Prerpints.org logo
Preprint
Article

Advantages of Ferroelectrics as a Component of Heterostructures for Electronic Purposes: A DFT Insight

Altmetrics

Downloads

95

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

20 September 2023

Posted:

21 September 2023

You are already at the latest version

Alerts
Abstract
The main advantage of using the ferroelectric material as a component of complex heterostructure is the ability to tune various properties of the whole system by means of external electric field. In particular, the electric field may change the polarization direction within the ferroelectric material and consequently affect the structural properties, which in turn affects the electronic and magnetic properties of the neighboring material. Besides, the ferroelectrics proceed the electrostriction phenomenon, which is promising to be used to affect the magnetic states of interface state in the heterostructure with a magnetic component. The interfacial phenomena are of a great interest since they provide an extended functionality useful for electronic devices of a new generation. Following an idea of utilizing a ferroelectric in heterostructures component in the present work we consider 2DEG, Rashba effect, the effect of magnetoelectric coupling and magnetostriction in order to emphasize the advantages of such heterostructures as components of devices. For this purpose model systems of LaMnO3/BaTiO3, La2CuO4/BaTiO3, Bi/BaTiO3 and Bi/PbTiO3, Fe/BaTiO3 heterostructures are investigated by density functional theory calculations.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

The presence of ferroelectric as a component of heterostructure gives us new outstanding functionality which can be used in possible electronic devices based on it. It is well established that the appearance of a two-dimensional gas (2DEG) or liquid is possible due to the presence of internal electrical polarization. That polarisation, for instance in LaAlO 3 /SrTiO 3 , arises due to the charge sequence in LaAlO 3 atomic layers. However, even without charged atomic layers 2DEG can occur thanks to the presence of spontaneous polarisation in the ferroelectric thin films [1,2,3,4,5,6]. That means that the electronic properties of the arising state can be tuned by an external field through changing the direction of the ferroelectric dipoles.
Another property which can be useful for electronic applications is magnetoelectric coupling. This property is associated with the possibility of controlling the ferromagnetic ordering at the interface due to interactions of spins through conduction electrons and with arising of multiferroic properties of the whole heterostructure. Multiferroic materials are compounds where at least two order parameters coexist in the same phase. One very important but the extremely rare group is ferroelectric ferromagnets, which have recently stimulated an increasing number of research activities for their scientific uniqueness and application in the novel multifunctional devices. Magnetoelectric materials are mainly interesting due to the possibility of controlling the magnetic properties by an external electric field [7,8,9,10,11]. Due to the extraordinary challenge of creating multiferroic compounds, it was essential to create superlattice multicomponent materials, which consists of a magnetic insulator in order to support spin-polarized 2DEG, and ferroelectric in order to manipulate the magnetic state using an electric field, i.e., to realize a converse magnetoelectric (ME) effect [12].
Besides, the presence of an electrostatic field in ferroelectrics due to spin-orbit (SO) coupling allows control of SO splitting by ferroelectric polarization, which is desirable property for spintronic applications. Natural materials demonstrating both gigantic and ideal states of Rashba are extremely rare [13,14], so computer simulations could help in this problem by investigating various combinations of materials.
The last effect also promising for electronic devices purposes is magnetostriction in combination with ferroelectricity. In particular, within the superlattice approach one can combine two materials with different features, when by changing the linear sizes of ferroelectric by applying an external electric field the lattice parameters of neighboring ferromagnet change as well leading to the change in magnetic moments. Such possibility promises to have a significant advantage in the development of new generation electronic devices. For instance, the magnetic tunnel junctions (MTJs) are of great interest to the experimental and theoretical community due to their applications in magnetic random-access memory (MRAM) devices. Besides, multiferroic materials are suitable for spin filter purposes [15,16]. Indeed, previous research demonstrated that the heterostructure based on iron and classical ferroelectric (Fe/BaTiO 3 ) can demonstrate an ideal crystallinity and heteroepitaxial growth [17]. Furthermore, what is more significant is that changing the polarization direction is able to affect the magnetization inside a ferromagnetic film [8]. The Fe/BaTiO 3 heterostructure was widely investigated previously being a simple example of a model system of ferromagnetic/ferroelectric combination [5,8,17,18,19,20,21,22].
Last 30 years a significant breakthrough in computational methods was achieved mainly thanks to the success of computer sciences. That made possible various calculations of electronic and magnetic properties of sufficiently big and complex systems. In particular, the most popular density functional theory was implemented in a wide range of codes. Indeed, the possibilities of that approaches based method are very extensive.
So, the present research is dedicated to the ab initio study within the DFT approach of heterostructures having a ferroelectric material as one of the components. The aim is to investigate the arising electronic and magnetic states and possibilities of controlling the interfacial properties (2DEG, Rashba effect, ME coupling, magnetostriction) via ferroelectric polarization reversal. For this purpose within the present research LaMnO 3 /BaTiO 3 , La 2 CuO 4 /BaTiO 3 , Bi/BaTiO 3 and Bi/PbTiO 3 , Fe/BaTiO 3 heterostructures were investigated in order to demonstrate the effect of polarization switching onto the electronic and magnetic state, as well as the Rashba effect.

2. Materials and Methods

In the present research structural, electronic and magnetic properties calculations were realized within the density functional theory [23]. Exchange and correlation effects were accounted using the generalized gradient approximation (GGA-PBE) [24]. The Kohn-Sham equations [25] were solved using projectively extended wave potentials and wave functions [26]. All calculations were carried out using the VASP-6.3 (Vienna Ab-initio Simulation Package) program [27] built into the MedeA computational software [28]. The cut-off of the plane wave was taken to be 400 eV, the convergence criterion for atomic relaxation was 0.02 eV/Å, and the convergence condition for self-consistent calculations was the invariance of the total energy of the system with an accuracy of 10 − 5 eV. The Brillouin zones were sampled using Monkhorst–Pack grids [29,30,31], including 7 × 7 × 1, 5×5×1 k-points depending on the particular heterostructure studied. The Gaussian smearing was 0.05 eV. A set of calculations was carried out with a simplified +U correction applied [32], which is used for a better description of the electronic properties of strongly correlated electrons: additional U value was applied to electrons of d and f orbitals in according to Ref. [33]. In particular, U = 4.4, 4, 4 eV for 3d orbitals of Ti, Cu and Mn and 8 ev for 4f orbitals of La, respectively, were applied.
The model of heterostructures was constructed in such a way that the BTO were served as an overlayer for LaMnO 3 /BaTiO 3 , La 2 CuO 4 /BaTiO 3 and LaMnO 4 /BaTiO 3 , the vacuum region was added in order to imitate the real heterostructures with both interface and surface. In the Bi/BaTiO 3 and Bi/PbTiO 3 heterostructures the results are presented for structures with no vacuum region as a comparison with previous research [34]. Lastly, the model of Fe/BaTiO 3 was as same as in Ref. [18] being a superlattice with no vacuum added also to focus on the interface and avoid surface impact.

3. Results

In this section the effect of the presence of ferroelectric material on the interfacial conducting state, onto the magnetic state, onto the size of Rashba-type splitting as well as the reverse magnetostriction and magnetoelectric coupling will be presented separately.

3.1. 2DEG

The area of perovskite based heterostructures was started by investigation of the appearing of a two-dimensional conducting state (2DEG) at the interface. The conductivity at the interface occurs due to either the polar nature of one of the components or due to the presence of defects [35]. Later, it has been shown that 2DEG can be created at the interface of non-polar oxides one of which is ferroelectric [1]. The main advantage of using ferroelectrics is a possibility to switch on and off the polarization and thus control the properties of the electron system. Moreover, ferroelectrics have a range of other outstanding properties which might expand the scope of applications in nanoscale electronic devices: there are spontaneous polarization switching, high dielectric permeability, dielectric nonlinearity, piezo- and pyro- activity, linear and quadratic electro-optical effects.
There are two systems studied in this frame within the present paper: heterostructure of antiferromagnet/ferroelectric, i.e., LaMnO 3 /BaTiO 3 (LMO/BTO), and ferroelectrics with high-temperature superconductor as La 2 CuO 4 /BaTiO 3 (LCO/BTO). Indeed, the creation of a 2DEG is possible when the electrostatic field along the slab is present in the system. That is possible whether due to the alternating charges in the atomic layers, or thanks to the ferroelectric polarization being directed normally to the interface plane.
In both studied systems bulk components are insulators: LMO is A-type antiferromagnetic, LCO is a ferromagnetic insulator, and BTO is an insulator as well [36,37].
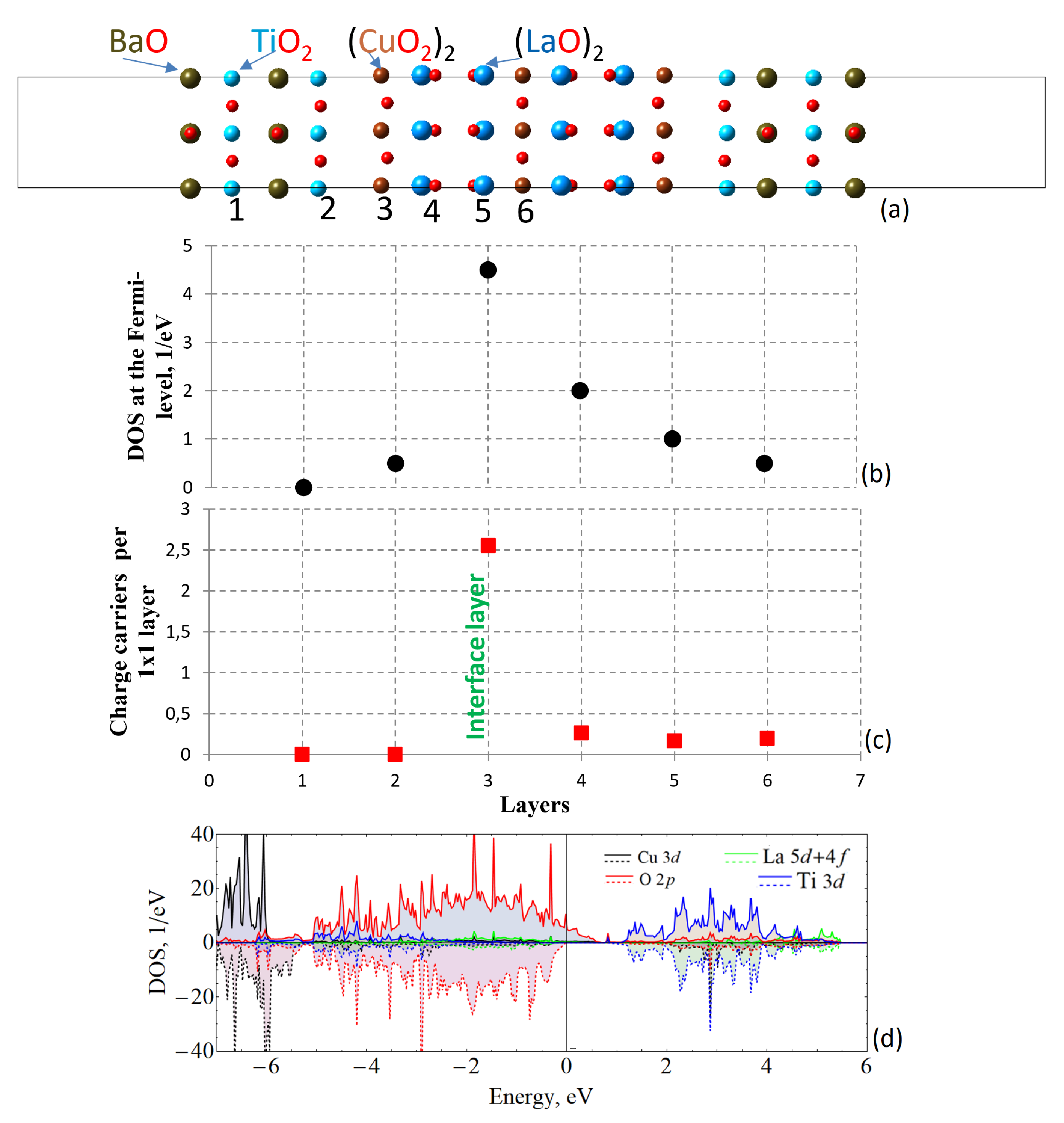
The unit cell for the LCO/BTO heterostructure is presented in Figure 1 (a) which consist of a middle slab of LCO as a substrate and BTO as an overlayer on both sides to make the cell symmetrical with respect to the central layer. It is seen from the density of states (DOS) in Figure 1 (d) that conduction state arises which is provided mostly by oxygen polarized electrons. These conducting electrons are located mostly within the interfacial CuO layer (Figure 1 (b-c)). In fact, the DOS at the Fermi level gradually increases from the surface of the ferroelectric towards the interfacial CuO layer and monotonously decreases towards the center of the LCO slab. The calculated number of charge carriers dependence is rather discrete, when carriers are present only within one atomic layer indicating the 2D conducting character.
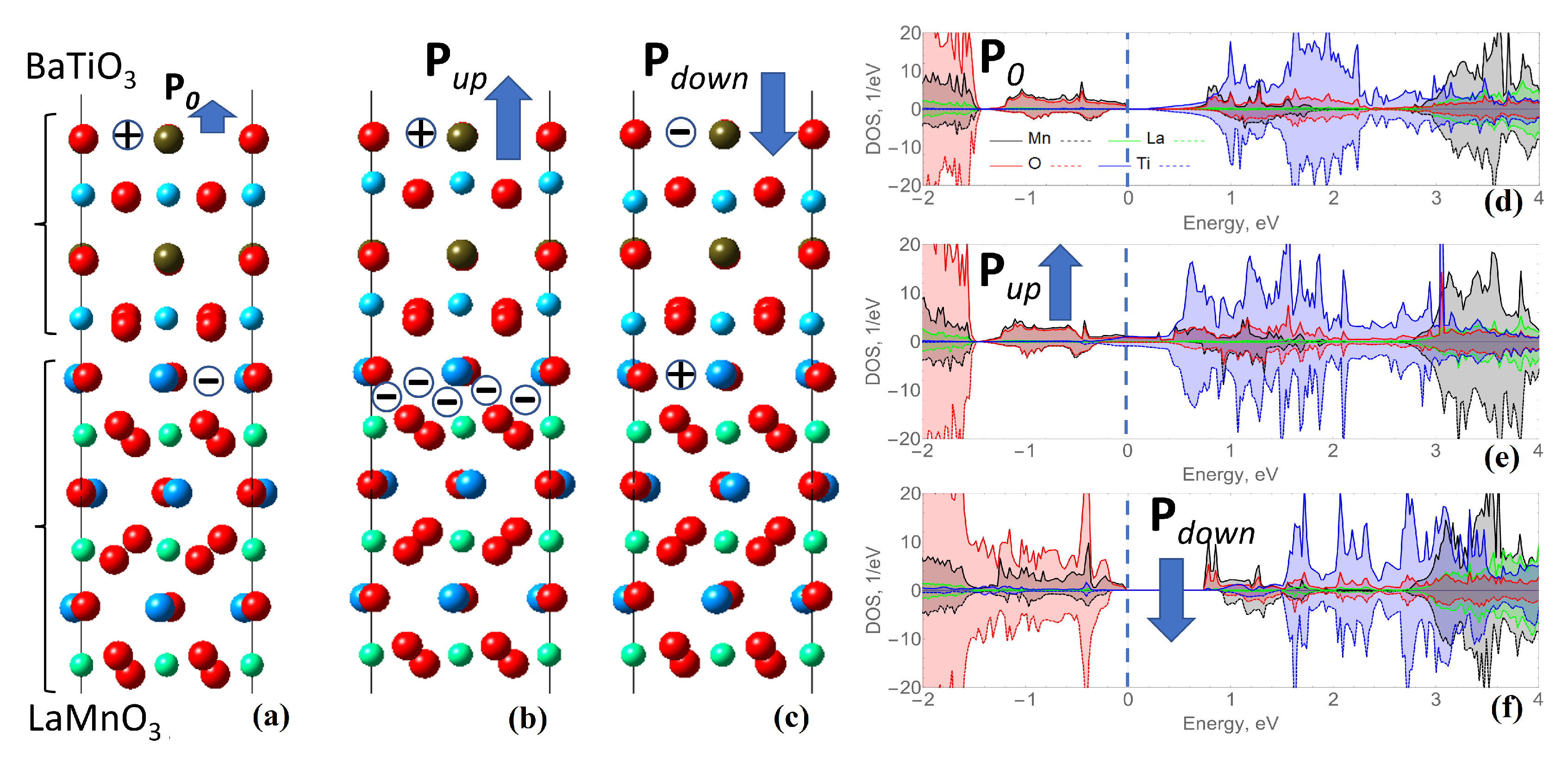
The other investigated heterostructure of LMO/BTO was constructed in the same way when the antiferromagnet LMO was surrounded by BTO overlayers on both sides as depicted in Figure 2 (a). The optimization of the cell led to the structural distortions associated with buckling within atomic layers. Most pronounced displacements were found close to the interface. These out-off plane shifts contribute to the potential build-up along the BTO overlayer giving rise to the internal field. However, the resulting electrostatic field is not sufficiently big to promote the significant electronic reconstruction and conductivity in the system as might be seen from Figure 2 (d) where the DOS at the Fermi-level is zero.
In the same way, increased polarization due to the artificial displacement of positive ions with respect to the negative oxygen ions immediately results in the increased charge carriers at the surface (holes) and interface (electrons) as depicted in Figure 2 (b). In terms of energy state the increased polarization shifts the Fermi-level up (Figure 2 d and e), so that Ti and Mn 3d states become closer to the Fermi-level. Contrary, the polarization towards the interface led to an opposite situation with holes located near the interface and electrons located near the surface as depicted in Figure 2 (c).
To sum up, the presence of an electrostatic field of ferroelectric material is favorable in the systems where 2DEG is a desirable property. There are at least two advantages of such component, specifically, the arising conducting phase might be switched by external field stimulus, secondly, the field within the ferroelectric material is an intrinsic feature and that means that the requirement of the ideal interface is not indispensable here and that makes the growth easier. Consequently, both features are privileges for electronic purposes.

3.2. Reverse Magnetoelectric (ME) Coupling

As was mentioned in the introduction section multiferroics are of a great scientific interest due to the range of their physical properties. Besides, this class of materials has a great potential for applications as switches, magnetic field sensors and memory devices [38]. However, pure multiferroics are rare and that is the reason for searching among the multicomponent superlattices mainly constructed from ferroelectrics and magnets.
In the previous section it was clearly demonstrated that the change in ferroelectric polarization direction switches the conductivity on and off. To test the possibilities, the distribution of magnetic moments within the antiferromagnetic slab of LMO was checked. It has to be noted that LMO is a pure antiferromagnet is a bulk, however in the slab geometry used in the present work due to the odd number of five MnO layers in the slab the order is ferromagnetic in total. That is different from the situation described, for instance, in Ref. [4] where an infinite cell without vacuum region was used for investigation. Within the model constructed in the present research the effect of changed polarization direction was also observed. As listed in Table 1 the initial optimized LMO/BTO heterostructure has an alternation of magnetic moments directed along and opposite to the z-axis. Such order is preserved for other considered cases. However, the magnitude changes. That change is insignificant, but the situation might change in the superlattice geometry what will be checked in further investigations.
To conclude, the ab initio observation of magnetic moments switching through the reverse magnetoelectric coupling requires an adjustment of geometry of the heterostructure. In particular, in the LMO/BTO structure considered here the change of polarization direction does not change the direction of magnetic moments of Mn ions, but changes the amplitude.

3.3. Rashba Effect

The Rashba effect constitutes the splitting of the electron conduction band along the spin due to the spin-orbit interaction. The effect is observed in structures where an effective electric field presents. These internal electric fields, due to the presence of spin-orbit interaction, lead to a splitting of the electronic states along the axis of the wave vectors. As a result, two dispersion surfaces are formed, which are connected at one Dirac point. A large and ideal Rashba-type splitting is desired for the application in spintronic devices. There are a few approaches that exist for enhancing the splitting. In particular, an introduction of heavy elements as a components of heterostructure may lead to an increase in the strength of spin-orbit (SO) coupling [39]. Another approach is to use polar semiconductors as a substrate for the heterostructure [40,41]. That allows to avoid the mixing of the Rashba states and the spin-degenerate substrate states, in order to create so-called ideal Rashba states. And the last most promising one is to use ferroelectric material in order to enhance the electric field across the heterostructure [42]. Besides, the use of ferroelectric would allow to tune the polarization, which in turn may lead to a change in the strength of SO coupling.
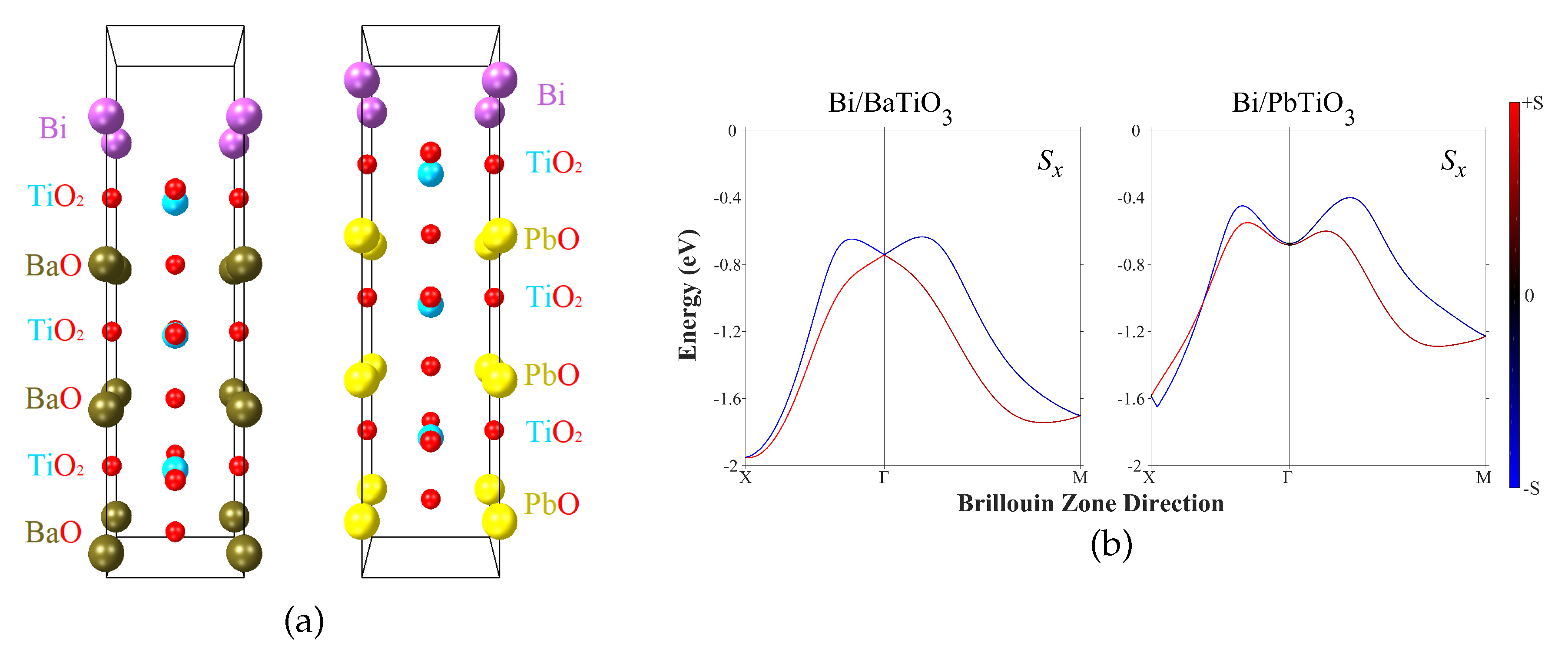
In the present research two heterostructures were considered BaTiO 3 /Bi and PbTiO 3 /Bi. Both consist of a ferroelectric substrate and heavy metal mono-layer. The BaTiO 3 /Bi heterostructure was investigated previously in Refs. [34,43]. Here we followed the heterostructure model proposed there but the vacuum region was not incorporated there. The structures of modeled BTO/Bi and PTO/Bi cells along with corresponding band structure are presented in Figure 3. The one band with splitting is presented there, which is the same for S x and S y components, whereas the out of plane component S z is negligibly small, so the spins are located and split within the interfacial plane. Two path directions in the Brillouin Zone were found X – G and G – M, where G is a gamma point.
Dispersions of surface states with characteristic features of Rashba-type splitting (shift of energy E R and Rashba wave vector k 0 ) were found for both BaTiO 3 /Bi and PbTiO 3 /Bi heterointerfaces. All data along with effective masses is collected in Table 2 along with ab initio data from [43].
All obtained results for Bi/BTO are in qualitative agreement with previously published data, the difference might be due to the computational parameters used. The replacement of BTO by PTO indeed increases the Rashba parameter by a factor of ≈1.7 which is a significant increase. Indeed, in PTO the ferroelectric polarization associated with displacements of positively charged Ti ions out of negatively charged oxygen planes is significantly higher. That can be seen from Figure 3. Thus the electrostatic field along the cell and perpendicular to the interface plane is higher, so that leads to a bigger splitting.
Further, the Bi mono-layer has been checked separately in order to ensure that the splitting occurs only when both spin-orbit coupling and field perpendicular to the interface plane coexist in the heterostructure. The Bi mono-layer with corresponding band structure is presented in Figure 4, where the splitting is present but not a Rashba-type.
Finally, we have checked the influence of applying a reverse field by shifting in the opposite direction with respect to the oxygen planes and freezing the atoms in the ferroelectric slab. That resulted in similar values as listed in Table 2. However, the increase of ferroelectric polarization might increase the splitting. That might be a subject of further investigations as well as the other combinations of heavy elements and other ferroelectrics.

3.4. Magnetostriction Effect

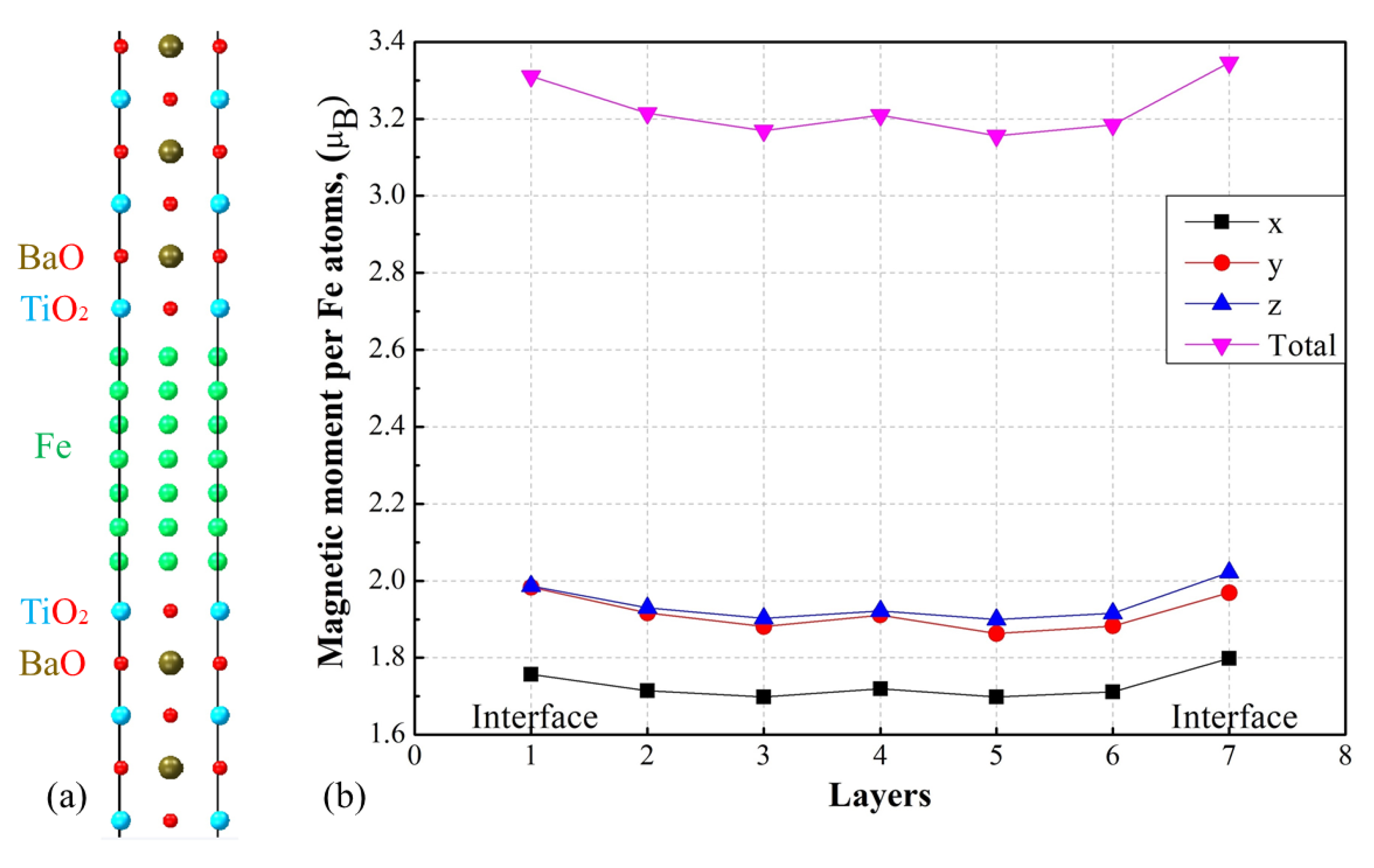
In order to study the effect of linear sizes compression of the ferroelectric onto the magnetic properties of the ferromagnet, the Fe/BaTiO 3 model system was chosen. The unit cell used in the calculations is depicted in Figure 5 (a), where BTO acts as a ferroelectric, and iron acts as a ferromagnetic overlayer. In this case the unit cell was constructed without vacuum region in order to exclude an impact of the surface and concentrate onto the ferroelectric slab properties. The system was constructed to be a total of 18 atomic layers in the periodic structure, 7 of which are layers of bcc iron. The initial value of the lattice parameter was equal to 4.05 Å, and the entire heterostructure was simultaneously compressed along the x axis by 0.2 Å and expanded along the y axis by the same value. After an optimization process taking into account spin-orbit interactions, the magnetic moments of the iron atoms in each layer of the ferromagnet were calculated, the data is presented in Figure 5 (b). Taking spin-orbit interactions into account during the calculation makes it possible to obtain magnetic moment values that have different directions, and not just the total value of magnetization of Fe layers.
The graph shows that all curves are symmetrical with respect to the middle of the layer and have the same character of a slight increase near the interfaces. Besides, there is a smooth decrease until the third layer, where a minimum is reached and a slight increase in the middle of the layer (number 4). The maximum value of the total magnetic moment was found to be ≈3.35 μ B , which is ≈0.6 μ B higher than the initial magnetic moment of iron (2.99 μ B ) calculated per Fe ion. The magnetic moments are predominantly directed along the y and y axes; their values do not differ much from each other and range from ≈1.86 μ B to ≈2.02 μ B . The magnitude of magnetization directed along the x axis is located in the region from ≈ 1.70 μ B to ≈ 1.80 μ B .
In the case of heterostructures without compression of the Fe/BTO heterostructure, the magnetic moments were directed along the z axis, the values along the x and y axes were negligibly small. The same result was obtained in our previous work, when the heterostructure was compressed isotropically along both the x and y axis by equal lengths [18]. Our results show that compression along only one axis and expansion along the other can affect the direction of magnetization along the xy plane so that the magnetic moment turns in the axis with expanded length. Further calculation are required in order to understand the conditions and the reason of the phenomenon.

4. Conclusions

In the paper we have demonstrated that the incorporation of ferroelectric as a component of heterostructure may enhance the desirable property of a heterostructure.
In the case of the creation of a interfacial conducting state the presence of a material with intrinsic ferroelectric polarization is favorable due to the opportunity to toggle the conductivity by means of external field. Using the example of two heterostructures, namely LaMnO 3 /BaTiO 3 and La 2 CuO 4 /BaTiO 3 we have seen that even without charged layers as in LaAlO 3 /SrTiO 3 , the 2DEG might arise within the interfacial layers. Furthermore, the other advantage concerns the growth conditions of the ferroelectric overlayer. Indeed, the alternation of charges in the LaAlO 3 /SrTiO 3 -type heterostructures and pure interface without defects are substantial conditions for a 2DEG. The field in ferroelectric arises anyway.
The second very important feature desirable for electronic applications, especially for memory devices, is reverse magnetoelectric coupling. The systems with the ability to change the magnetic ordering by means of electric stimulus are of particular interest due to higher energy-storage density. Within the present paper the effect of the ferroelectric polarisation onto the magnitude of magnetic moments in the LaMnO 3 /BaTiO 3 was observed.
The presence of ferroelectric material as a component of heterostructure with heavy metal as Bi may enhance the splitting thanks to the ferroelectric polarization. The external electric field may also increase the internal electrostatic field and slightly increase the splitting. The change of ferroelectric polarization direction does not change the Rashba parameter significantly.
Lastly, an impact of in-plane striction of ferroelectric BaTiO 3 onto the magnetic moments of ferromagnetic bcc iron was investigated. The striction in one direction (x-axis) and corresponding extension in the other direction (y-axis) results in the appearing of the component of magnetization vector in y and z direction with similar amplitude. Whereas in the fully optimized structure only the z-component is present.

Author Contributions

Conceptualization, I.P.; methodology, O.N. and D.T.; software, I.P.; validation, I.P., A.E. and O.N.; formal analysis, I.P.; investigation, I.P, A.E. and K.E.; resources, I.P.; data curation, R.M.; writing—original draft preparation, I.P.; writing—review and editing, O.N., D.T., R.M.; visualization, I.P.; supervision, V.K.; project administration, V.K.; funding acquisition, R.M. and V.K. All authors have read and agreed to the published version of the manuscript.

Funding

The work of I.P. and R.M. concerning LMO/BTO was funded by the Russian Scientific Foundation according to research project No. 21-12-00179. The part concerning the Magnetostriction effect was funded by the Russian Scientific Foundation according to research project No. 21-72-10178. The part of LCO/BTO was supported by the government assignment for FRC Kazan Scientific Center of RAS. V.K. acknowledges the financial support from the Slovenian Research Agency Program No. P1-0040.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

Computational resources were provided by the Laboratory for computer design of new materials and machine learning of Kazan Federal University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fredrickson, K.D.; Demkov, A.A. Switchable conductivity at the ferroelectric interface: nonpolar oxides. Phys. Rev. B 2015, 91, 115126. [Google Scholar] [CrossRef]
  2. Niranjan, M.K.; Wang, Y.; Jaswal, S.S.; Tsymbal, E.Y. Prediction of a switchable two-dimensional electron gas at ferroelectric oxide interfaces. Phys. Rev. Lett. 2009, 103, 016804. [Google Scholar] [CrossRef] [PubMed]
  3. Liu, X.; Tsymbal, E.Y.; Rabe, K.M. Polarization-controlled modulation doping of a ferroelectric from first principles. Phys. Rev. B 2018, 97, 094107. [Google Scholar] [CrossRef]
  4. Weng, Y.; Niu, W.; Huang, X.; An, M.; Dong, Sh. Ferroelectric control of a spin-polarized two-dimensional electron gas. Phys. Rev. B 2021, 103, 214101. [Google Scholar] [CrossRef]
  5. Cao, C.; Chen, S.; Deng, J.; Li, G.; Zhang, Q.; Gu, L.; Ying, T.P.; Guo, E.J.; Guo, J.G.; Chen, X. Two-Dimensional Electron Gas with High Mobility Forming at BaO/SrTiO3 Interface. Chinese Physics Letters 2022, 39, 047301. [Google Scholar] [CrossRef]
  6. Kabanov, V.V.; Piyanzina, I.I.; Lysogorskiy, Yu.V.; Tayurskii, D.A.; Mamin, R.F. Ab initio investigation of electronic and magnetic properties of antiferromagnetic/ferroelectric LaMnO3/BaTiO3 interface. Mater. Res. Express 2020, 7, 055020. [Google Scholar] [CrossRef]
  7. Niranjan, M.K.; Burton, J.D.; Velev, J.P.; Jaswal, S.S.; Tsymbal, E.Y. Magnetoelectric effect at the SrRuO3/BaTiO3 (001) interface: an ab initio study. Appl. Phys. Lett. 2009, 95, 052501. [Google Scholar] [CrossRef]
  8. Duan, C.G.; Jaswal, S.S.; Tsymbal, E.Y. Predicted magnetoelectric effect in Fe/BaTiO3 multilayers: ferroelectric control of magnetism. Appl. Phys. Lett. 2006, 97, 047201. [Google Scholar] [CrossRef]
  9. Niranjan, M.K.; Velev, J.P.; Duan, C.G.; Jaswal, S.S.; Tsymbal, E.Y. Magnetoelectric effect at the Fe3O4/BaTiO3 (001) interface: a first-principles study. Phys. Rev. B 2008, 78, 104405. [Google Scholar] [CrossRef]
  10. Demkov, A.A.; Niu, Q.; Li, Z.; Shi, J.; Wang, E. Magnetoelectric coupling and electric control of magnetization in ferromagnet/ferroelectric/normalmetal superlattices. Phys. Rev. B 2009, 80, 140415. [Google Scholar] [CrossRef]
  11. Baloni, M.; Sharma, R.Ch.; Singh, H.; Khan, B.; Singh, M.K.; Sati, P.Ch.; Thakur, V.N.; Kotnala, R.K.; Kumar, A. Energy storage and magnetoelectric coupling in neodymium (Nd) doped BiFeO3-PbTiO3 solid solution, Journal of Alloys and Compounds 2023, 946, 169333. [CrossRef]
  12. Piyanzina, I.I. , Mamin, R.F. Toward the ferroelectric field-effect transistor on BaTiO3/LaMnO3 heterostructure: DFT investigation. J. Mater. Sci. 2022, 57, 21620–21629. [Google Scholar] [CrossRef]
  13. Chen, M.; Liu, F. Prediction of giant and ideal Rashba-type splitting in ordered alloy monolayers grown on a polar surface. Natl. Sci. Rev. 2021, 8, nwaa241. [Google Scholar] [CrossRef]
  14. Bychkov, Yu.A.; Rashba, E.I. Properties of a 2D electron gas with lifted spectral degeneracy. Sov. Phys. - JETP Lett. 1984, 39, 78–81. [Google Scholar]
  15. Borek, S.; Braun, J.; Ebert, H.; Minár, J. Multiferroic heterostructures for spin filter applications: An ab initio study. Phys. Rev. B 2015, 92, 174408. [Google Scholar] [CrossRef]
  16. Fechner, M.; Maznichenko, I.V.; Ostanin, S.; Ernst, A.; Henk, J.; Bruno, P.; Mertig, I. Magnetic phase transition in two-phase multiferroics predicted from first principles. Phys. Rev. B 2008, 78, 212406. [Google Scholar] [CrossRef]
  17. Lu, N.; Zhang, P.; Zhang, Q.; Qiao, R.; He, Q.; Li, H.B.; Wang, Y.; Guo, J.; Zhang, D.; Duan, Z.; et al. Electric-field control of tri-state phase transformation with a selective dual-ion switch. Nature 2017, 546.7656, 124–128. [Google Scholar] [CrossRef]
  18. Piyanzina, I.; Evseev, K.; Kamashev, A.; Mamin, R. Ab Initio Characterization of Magnetoelectric Coupling in Fe/BaTiO3, Fe/SrTiO3, Co/BaTiO3 and Co/SrTiO3 Heterostructures. Magnetism 2023, 3, 215–225. [Google Scholar] [CrossRef]
  19. Leksin, P.V.; Garifyanov, N.N.; Garifullin, I.A.; Schumann, J.; Vinzelberg, H.; Kataev, V.; Klingeler, R.; Schmidt, O.G.; Buchner, B. Full spin switch effect for the superconducting current in a superconductor/ferromagnet thin film heterostructure. Appl. Phys. Lett. 2010, 97.10, 102505. [Google Scholar] [CrossRef]
  20. Zhao, Y.; Peng, R.; Guo, Y.; Liu, Z.; Dong, Y.; Zhao, S.; Li, Y.; Dong, G.; Hu, Y.; Zhang, J.; Peng, Y. Ultraflexible and malleable Fe/BaTiO3 multiferroic Heterostructures for functional devices. Adv. Funct. Mater. 2021, 31.16, 2009376. [Google Scholar] [CrossRef]
  21. Velev, J.P.; Duan, C.G.; Belashchenko, K.D.; Jaswal, S.S.; Tsymbal, E.Y. Effects of ferroelectricity and magnetism on electron and spin transport in Fe/BaTiO3/Fe multiferroic tunnel junctions. Journal of Applied Physics 2008, 103.7, 07A701. [Google Scholar] [CrossRef]
  22. Duan, C.G.; Sahoo, S.; Srinivas, P.; Jaswal, S.S.; Tsymbal, E.Y.; Binek, C. Ferroelectric control of magnetism in BaTiO3/Fe heterostructures via interface strain coupling. Phys. Rev. B 2007, 76.9, 092108. [Google Scholar] [CrossRef]
  23. Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci., 1996, 6.1, 15–50. [CrossRef]
  24. Perdew, J. P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett., 1996, 77.18, 3865. [CrossRef]
  25. Kohn, W.; Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev., 1965, 140.4A, A1133. [CrossRef]
  26. Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B, 1994, 50.24, 17953. [CrossRef]
  27. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B, 1996, 54.16, 11169. [CrossRef]
  28. MedeA version 3.7; MedeA is a registered trademark of Materials Design, Inc., San Diego, USA. Available online: https://www.materialsdesign.com/ (accessed on 20 september 2023).
  29. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev., 1976, 13, 125188. [Google Scholar] [CrossRef]
  30. Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev., 1994, 49.23, 16223. [CrossRef]
  31. Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev., 1989, 40.6, 3616. [CrossRef]
  32. Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B, 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
  33. Calderon, C.E.; Plata, J.J.; Toher, C.; Oses, C.; Levy, O.; Fornari, M.; Natan, A.; Mehl, M.J.; Hart, G.; Nardelli, M.B.; Curtarolo, S. The AFLOW standard for high-throughput materials science calculations. Comput. Mater. Sci., 2015, 108, 233–238. [Google Scholar] [CrossRef]
  34. Evseev, A.A.; Piyanzina, I.I.; Nedopekin, O.V.; Tayurskii, D.A. Ab initio investigation of Bi/BaTiO3 and Bi/PbTiO3 heterostructures for spintronic applications. Ferroelectrics, 2023, 605, 27–35. [Google Scholar] [CrossRef]
  35. Piyanzina, I.I.; Eyert, V.; Lysogorskiy, Yu.V.; Tayurskii, D.A.; Kopp, T. Oxygen vacancies and hydrogen doping in LaAlO3/SrTiO3 heterostructures: electronic properties and impact on surface and interface reconstruction. J. Phys. Condens. Matter., 2019, 31, 295601. [Google Scholar] [CrossRef]
  36. Piyanzina, I.I.; Mamin, R.F. Electronic and Magnetic Properties of the BaTiO3/LaMnO3 Interface: a DFT Study. J Supercond Nov Magn., 2022, 35, 2225–2229. [Google Scholar] [CrossRef]
  37. Kabanov, V. V,; Piyanzina, I. I.; ,Tayurskii, D.A.; Mamin, R.F. Towards high-temperature quasi-two-dimensional superconductivity. Phys. Rev. B, 2018, 98, 094522. [Google Scholar] [CrossRef]
  38. Ramesh, R.; Spaldin, N. Multiferroics: progress and prospects in thin films. Nature Mater, 2007 6, 21–29. [CrossRef]
  39. Ast, C.R.; Henk, J.; Ernst, A.; Moreschini, L.; Falub, C. M.; Pacilé, D.; Bruno, P.; Kern, K.; Grioni, M. Giant spin splitting through surface alloying. Phys. Rev. Lett., 2007, 98, 186807. [Google Scholar] [CrossRef]
  40. Singh, S.; Romero, A.H. Giant tunable Rashba spin splitting in a two-dimensional BiSb monolayer and in BiSb/AlN heterostructures. Phys.Rev. B, 2017, 95, 165444. [Google Scholar] [CrossRef]
  41. Eremeev, S.V.; Nechaev, I.A.; Koroteev, I.A.; Echenique, P. M.; Chulkov, E. V. Ideal two-dimensional electron system with a giant Rashba-type spin splitting in real materials:surfaces of bismuth tellurohalides. Phys. Rev. Lett., 2012, 108, 246802. [Google Scholar] [CrossRef] [PubMed]
  42. Lutz, P.; Figgemeier, T.; Abd El-Fattah, Z.M.; Bentmann, H.; Reinert, F. Large Spin Splitting and Interfacial States in a Bi/BaTiO3 Rashba Ferroelectric Heterostructure. Phys. Rev. Appl., 2017, 7, 044011. [Google Scholar] [CrossRef]
  43. Mirhosseini, H.; Maznichenko, I. V.; Abdelouahed, S.; Ostanin, S.; Ernst, A.; Mertig, I.; Henk, J. Toward a ferroelectric control of Rashba spin-orbit coupling: Bi on BaTiO3 (001) from first principles. Phys. Rev. B, 2010, 81, 073406. [Google Scholar] [CrossRef]
Preprints 85663 g001
Figure 1. (a) The unit cell of a La 2 CuO 4 /BaTiO 3 (LCO/BTO) heterostructure; (b) density of states (DOS) per atomic layers as denoted in (a); (c) charge carriers per 1×1 layer; (d) atom-resolved DOS.
Figure 1. (a) The unit cell of a La 2 CuO 4 /BaTiO 3 (LCO/BTO) heterostructure; (b) density of states (DOS) per atomic layers as denoted in (a); (c) charge carriers per 1×1 layer; (d) atom-resolved DOS.
Preprints 85663 g001
Preprints 85663 g002
Figure 2. Half unit cells of the LaMnO 3 /BaTiO 3 (LMO/BTO) heterostructure (a) fully optimized and with imposed polarization directed (b) towards the surface and (c) towards the interface (d-f) with corresponding atom-resolved density of states (DOS). P 0 denotes the initial polarization, P u p polarization directed toward the surface and P d o w n the interface, respectively. Plus and minus correspond to the character of positive and negative charges distribution.
Figure 2. Half unit cells of the LaMnO 3 /BaTiO 3 (LMO/BTO) heterostructure (a) fully optimized and with imposed polarization directed (b) towards the surface and (c) towards the interface (d-f) with corresponding atom-resolved density of states (DOS). P 0 denotes the initial polarization, P u p polarization directed toward the surface and P d o w n the interface, respectively. Plus and minus correspond to the character of positive and negative charges distribution.
Preprints 85663 g002
Preprints 85663 g003
Figure 3. (a) The unit cells and (b) corresponding band structures of investigated BTO/Bi and PTO/Bi heterointerfaces. Only S x component of splitted band is presented, whereas the S y component is the same, S z component is zero.
Figure 3. (a) The unit cells and (b) corresponding band structures of investigated BTO/Bi and PTO/Bi heterointerfaces. Only S x component of splitted band is presented, whereas the S y component is the same, S z component is zero.
Preprints 85663 g003
Preprints 85663 g004
Figure 4. The unit cells and corresponding band structure of a 2×2 Bi mono-layer with no Rashba-type splitting.
Figure 4. The unit cells and corresponding band structure of a 2×2 Bi mono-layer with no Rashba-type splitting.
Preprints 85663 g004
Preprints 85663 g005
Figure 5. (a) The unit cell of Fe/BaTiO 3 heterostucture used in calculations. (b) Corresponding magnetic moments distribution of Fe atoms calculated for each layer of Fe/BTO heterostructure within the applied in-plane striction along x-axis and extension along y-axis. Each curve corresponds to the resulted magnetisation magnitude for the x, y, z components of magnetization vector.
Figure 5. (a) The unit cell of Fe/BaTiO 3 heterostucture used in calculations. (b) Corresponding magnetic moments distribution of Fe atoms calculated for each layer of Fe/BTO heterostructure within the applied in-plane striction along x-axis and extension along y-axis. Each curve corresponds to the resulted magnetisation magnitude for the x, y, z components of magnetization vector.
Preprints 85663 g005
Table 1. Distribution of magnetic moments per Mn ions over atomic layers within the LaMnO 3 slab of LaMnO 3 /BaTiO 3 heterostructure.
Table 1. Distribution of magnetic moments per Mn ions over atomic layers within the LaMnO 3 slab of LaMnO 3 /BaTiO 3 heterostructure.
P 0 P d o w n P u p
Conductivity - - +
Interfacial layer -3.725 -4.165 -3.710
Second layer 3.670 3.635 3.705
Middle layer -4.170 -3.91 -3.710
Second layer 3.675 3.635 3.710
Interface layer -3.725 -4.165 -3.630
Table 2. Calculated Rashba splitting parameters: where E R and k 0 are the Rushba energy and momentum offset respectively, α R is a Rashba parameter, m * is an effective mass. The X – G and G – M denote the path in the Brillouin Zone. The results are shown for both fully optimized heterostructures of BaTiO 3 /Bi and PbTiO 3 /Bi with optimized polarization directed towards the interface.
Table 2. Calculated Rashba splitting parameters: where E R and k 0 are the Rushba energy and momentum offset respectively, α R is a Rashba parameter, m * is an effective mass. The X – G and G – M denote the path in the Brillouin Zone. The results are shown for both fully optimized heterostructures of BaTiO 3 /Bi and PbTiO 3 /Bi with optimized polarization directed towards the interface.
path X – G G – M
  E R , eV k 0 , Å − 1 α R , eVÅ m * , m e E R , eV k 0 , Å − 1 α R , eVÅ m * , m e
Bi/BTO 0.1 0.19 1.05 1.35 0.11 0.22 1.01 1.65
Bi/PTO 0.23 0.27 1.72 1.2 0.28 0.35 1.63 1.61
Bi/BTO [43] 0.16 0.22 1.45 1.14 0.18 0.25 1.42 1.36
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated