Preprint
Article
The Multivariate Regression Models Suggested as Tools for Categorizing Solitarious and Gregarious Groups of the Main Pest Locust, Schistocerca gregaria, Produce Reproducible Results
Altmetrics
Downloads
91
Views
52
Comments
0
This version is not peer-reviewed
Submitted:
20 September 2023
Posted:
21 September 2023
You are already at the latest version
Alerts
Abstract
Outbreaks of the desert locust Schistocerca gregaria affect some of the poorest parts of Africa, causing devastating catastrophes. Key to understanding and dealing with this problematic adaptation to environmental changes is comparing locusts that are gregarious (associated with outbreak states) and solitarious (associated with non-outbreak states) either in nature or after experimental treatments in laboratories. Categorising locusts and detecting changes in their phase status is key to such comparisons. Such comparisons are hitherto based on applying mathematical models that use behavioural parameters and that each laboratory has to build a new for each experiment. All such models used thus far for research on locusts are different from each other. That implies differences in the tools used for the different experiments and by the different laboratories and, thus, potential noise in the scientific results and interpretations too. Standardizing the way how we categorise locusts between laboratories and experiments is needed if we want to reduce noise and errors. It is even a must if we are to make the results and interpretations transferable and comparable between experiments and laboratories that work in such an important research area. Here, we use samples from independent S. gregaria population in order to further test the two models that were suggested earlier as standardizing tools for S. gregaria categorization. The outcomes of both models were largely replicated and reproducible. We report on how successful the two models were at categorizing solitarious, intermediate (transient) and gregarious nymph and adult samples. We highlight shortcomings and make more specific recommendations on the use of these models based on the differences they show as to their precision when categorizing the solitarious and gregarious S. gregaria nymph and adult samples.
Keywords:
Subject: Biology and Life Sciences - Insect Science
1. Introduction
Locust outbreaks recurrently devastate vast regions around the globe. Different species are responsible for such devastation, including Locusta migratoria (mainly in Asia)[1], Melanoplus sanguinipes (in North America)[2], Schistocerca piceifrons and Schistocerca cancellata (in South America)[3,4], Dociostaurus maroccanus (in Southern Europe)[5] and Chortoicetes terminifera (in Australia)[6], among other species. Schistocerca gregaria, the desert locust, is considered the most devastating pest locust due to its broad distribution range (from North-West Africa to India)[7,8] and to the damage it causes to regions that are already affected by extreme climate, poverty, war and corruption [9]. The especially stressing need to find ways to prevent, protect and help those poor areas against locust outbreaks makes S. gregaria a species of interest to science.
As other locust species, S. gregaria is usually found living in low population density conditions where individuals are at a state referred to as solitarious phase, at which locusts display sedentary behaviour, social avoidance and usually inconspicuous coloration. When climatic conditions change and become favourable, locusts experience an increase in their population size and a subsequent series of physiological (e.g.,[10,11,12,13]), behavioural (e.g.,[14,15,16,17]) and morphological changes (e.g., [18,19]). Their mobility increases and they start aggregating into massive swarms that eventually form locust outbreaks (a state associated with the gregarious phase). The differences between the two states (phases) of the locusts are adaptive responses to the change in the living environment that the locusts suffer. They co-occur in long-term solitarious and gregarious individuals. However, these differences are decoupled in short-term gregarious and solitarious locusts; meaning that solitarious locusts that have been just gregarized and gregarious locusts that are just solitarized will change behaviour and, later, color, but they won’t change morphometry if they don’t molt (e.g., [14,15,16,17,20]).
Molecular and genetics testing is becoming common strategy to all the fields of research that use S. gregaria (e.g., [21,22,23]), and we are entering into an era of functional testing in non-model species. Accordingly, research on S. gregaria is, as predicted in [24], increasingly shifting towards functional studies in quest of a better understanding and tackling of the locust plagues. Aware of all that, in 2017, we measured several morphological and behavioural traits (variables) from solitarious and gregarious S. gregaria locusts and we assessed the correlation between the changes in each of these variables and the locust phase. The variables that correlated the most with the locust phase were used for model building based on logistic regression formulae. The results of those formulae were transformed into probabilities of a locust being gregarious where Pgreg=0 was assigned to solitarious and Pgreg=1 was assigned to gregarious locusts.
After testing on additional solitarious, gregarious locusts, we suggested the use of two logistical regression models as standardized tools to detect changes in S. gregaria locust phase status or to distinguish between solitarious and gregarious S. gregaria samples [25].
One of the two models that we suggested in [25], the Sg_extended_corrected model, is based not only on behavioural variables but also included selected morphological variables that were proven to distinguish long-term solitarious S. grearia locusts from the gregarious locusts of the same species. The other model, the Sg_non-morphometric model was based only on selected behavioural variables. The first model was intended for experiments that compare different locust groups, log-term solitarious and long-term gregarious locust groups and groups of nymphs that have molted during the experiment (i.e., animals whose morphology is not the same between the two ends of the comparison), whereas the second model was intended for use on animals that do not change morphology between the two ends of the comparison (i.e., just solitarized and just gregarized locust groups that do not molt and change morphology during the experiment). A novelty that we introduced compared to the non-standardized ways how locusts were thus far categorized was that we normalized the movement-related variables, that are function of the animal’s body size, by the animal’s femur (see leg) size. The models were optimized and tested on different locust cages of different states (raised at different densities), sexes, developmental stages (adults and nymphs) and origin (populations). They were then tested on additional independent samples. They were reasonably able to distinguish solitarious from gregarious S. gregaria samples in all the different sets (in total we used 168 individuals from 12 sets of locusts). Nonetheless, the performance of the Sg_non-morphometry model was better than that of the Sg_extended_corrected model and this latter was useless for adult samples. We therefore wrote that “we suggest using the ‘Sg_extended_corrected’ model (that includes morphometric variables) for comparing different S. gregaria nymph samples. For testing adults or the same nymphs at different time points (if they do not molt), we suggest using the ‘Sg_non-morphometric’ model (that does not include morphometric variables).” [25].
In silico re-application of the models to our data successfully reproduced the model’s outcomes —at least “with two-digit accuracy or better” [26]. Still, interpretations in the same work [26] casted doubts on the standardization possibility and on how the models were built. Interpretations in that work led to predicting that the models “will not predict future observations as well as it appeared to predict on the present sample.” [26].
Since the prediction in [26] was based on theoretical analyses and interpretations and not on testing real locusts, here, we take advantage of the re-population and renewal of our laboratory locust colony —that was annihilated during the COVID-19 restriction period— in order to directly test and answer the question of whether the models would work in additional S. gregaria samples that are different from the ones tested in [25].
This report shows that, contrary to the prediction in [26], when used on additional, different, samples of actual solitarious and gregarious S. gregaria locusts, the models worked with similar relative performance and limitations as they did in [25]. We discuss on the reproducibility of the results and validity of the models and we refine our recommendation of using these models. We also signal the model’s advantages and limitations for time-saving and, more importantly, for standardizing the very important task of categorizing S. gregaria samples for the research on that locust’s phase change and population outbreaks.
2. Material and methods
We used S. gregaria of different phases (solitarious, transient and gregarious), stages (nymphs of different stages and adults), and sexes. The locusts were unrelated to the 12 sets of two origins that we used for the building and initial testing of the models in [25]. Even the personnel that reared the locusts and the one that measured the variables and video-recorded the locusts was different from the one that did that work in [25]. Furthermore, the personnel that applied the models using the gathered morphometric and behavioural data was unaware of (blind to) the locust raring condition and phase.
We raised the locusts at different densities as we describe in [25]. In brief, all the locusts shared some rearing conditions (31 degrees Celsius temperature, 14:10 light/dark period and the same food —cabbage and corn flakes), while they differed in other rearing conditions (the phase-related ones). The solitarious locusts were raised each in an individual small cage in complete visual, mechanical (contact) and chemical (olfactory) isolation from other locusts, in order to prevent them from turning gregarious. The gregarious locusts were raised in groups in large cages that allow mechanical, visual and olfactory contact between the locusts. The transient locusts were from a gregarious colony but they were reared for one generation at lower density. The videos were taken at mid-day and in the same room and 60 × 60 × 60 cm observation arena as described in [25]. The behavioural data were extracted from the videos using the R script that we provide in [25]. The morphometric data were measured for each individual after (not before) its video-recording —in order to avoid disturbing its behaviour. The probability of a locust being gregarious was separately calculated for each individual using the Sg_extanded_corrected and the Sg_non-morphometric models from [25]. The animals were tested only once —in order to avoid the effect of habituation. Animals that jumped strait to the arena’s walls were discarded, otherwise the data were considered no matter how the animal behaved. The personnel that applied the models was blind to the state of the locusts and no post-analysis filtering was applied to the data (i.e., data were considered even when they did not fit the individual locust’s phase status), in order to avoid subjective manipulation or bias of the results. Nymphs and adults were uncontrolled mixes of different sexes —since the models do not distinguish between sexes— and the nymphs were uncontrolled mixes of different stages —since the models do not distinguish between nymphal stages. First and second instar nymphs were not used in order to avoid possible effect of mechanical damage when handling them —they are too small and fragile for the handling required for the morphometrical measurements and behavioural observations needed for the present work.
In total we tested here 279 additional S. gregaria locusts grouped into 11 sets: two sets of solitarious nymphs of different sexes and stages, three sets of solitarious adults of both sexes, four sets of gregarious nymphs of different sexes and stages and two sets of gregarious adults of both sexes. In addition, we also tested two sets of gregarious locusts (adults and mixed stage nymphs of both sexes) that were transferred since eclosion to lower density cages —referred to as transient adults and transient nymphs.
All the variables and methods were as in [25]. As a reminder, the variables and formulae of both models are in Table 1 and, being the results of both models interpretable at the group/sample not the individual level, the models were assessed based on the mean values they assigned to each locust set (i.e., the means obtained for solitarious nymphs, transient nymphs, gregarious nymphs, solitarious adults, transient adults and gregarious adults).
In order to assess the differences between the locust samples used for this work, and before applying the models (see Table 1), the morphometric and behavioural variables that we extracted from the locust samples used in the present work were analyzed. For that we used the ANOVA design: variable ~ Phase + Age + Sex + Phase * Age; where phase had the levels gregarious, solitarious and transient; age had the levels adult and nymph; and sex had the levels female and male. The sex ratio of the samples was tested using Chi squared test, and Mann-Whitney test was used in Statistica 8.0 to compare the outcomes of each model between sample types. All other statistical analyses were performed using R project v4.1.2.
3. Results
The sets of locusts that we use here are significantly different from each other
Measurements of femur length, pronotum length, and head width showed statistically significant differences between phases (Figure 1A–C) and sexes (Figure 1G–I). Solitarious females showed higher values for femur and pronotum length, while gregarious females showed wider heads. Being all the mean values lower in nymphs, only femur length showed significant difference between the adults and nymphs of our sample (Figure 1D–F). The sex ratio of the sample was not biased towards any sex (χ2 2 = 2.847, P-value = 0.241).
None of the morphometric indices showed statistically significant differences between the current gregarious and solitarious samples (Figure 2A–C). Nevertheless, the pronotum to femur (P/F) and femur to head (F/H) indices showed differences between nymphs and adults. Both indices showed interactive effects of phase and age: solitarious nymphs showed higher values for these indices compared to gregarious nymphs, while adults showed no differences between phases but lower values compared to nymphs (P-value < 0.001 in both cases).
As expected, the behavioral variables (Figure 2D–L), elapsed time, distance, turn ratio and erratic movement, all positively related to hesitation and lethargy, showed statistically significant differences between phases, with higher values for solitarious locusts independently of their age. In addition, elapsed time and turn ratio showed differences between gregarious and transient individuals (P-values 0.036 and 0.009, respectively). Stops showed differences only for transient individuals, and a statistically significant interaction between age and phase was also seen for that variable (the stops): while solitarious nymphs took more time static compared to gregarious nymphs, this tendency was inverted in adults. The mean values of the analyzed variables per phase and age are in Supplementary Table S1.
We checked whether the statistical differences would change after normalization by femur length of six behavioral variables that are related to movement, and that could therefore be affected by locust size (i.e., elapsed time, total distance, average speed, average acceleration, C/T and erratic movement) (Figure 3A–F). Average speed and acceleration continued not showing statistical differences between gregarious and solitarious locusts; and elapsed time and erratic movement continued showing differences between such locusts. However, distance lost the significant differences between gregarious and solitarious locusts, while C/T —which is the last coordinate reached divided by the time spent to reach it— showed differences between the gregarious and the transient locusts.
The Sg_extended_corrected model is not accurate although it does distinguish between solitarious and gregarious nymphs
Application of the Sg_extended_corrected model to the data from nymphs allowed distinction between the solitarious and the gregarious S. gregaria nymphs. Accordingly, Figure 4A shows how solitarious nymphs had lower mean probability of being gregarious (Pgreg mean ± SE = 0.65 ± 0.09) than gregarious nymphs (Pgreg mean ± SE = 0.93 ± 0.03). Although the mean Pgreg value for solitarious was higher than 0.5, the difference between solitarious and gregarious Pgregs is statistically significant (Z-adjusted=4.330, p<0.0001). Indeed, the distribution of the Pgreg values was clearly different between the solitarious and gregarious nymphs, although it had a relatively broad range with some overlap observed (0.25 to 0.65 in solitarious nymphs, and 0.64 to 1.00 in gregarious nymphs). The standard deviations were clearly dependent on the sample sizes and, just as we found in [25], the model’s results are interpretable at the group and not the individual level (see Supplemental Tables S2 and S3 for details).
For transient nymphs, the Pgreg values were intermediate (0.71 ± 0.11) and the statistics suggest that those nymphs became not significantly different from the solitarious group (Z-adjusted=-1.097, p=0.273) and are no longer similar to the gregarious samples from where they came (Z-adjusted=2.670, p=0.008).
Taken all the three independent nymph groups together (i.e., when increasing the sample size), the model shows even clearer separation of the gregarious, transient and solitarious S. gregaria nymphs (Figure 4C).
Application of the Sg_extended_corrected model to adults gave mean Pgreg values of 0.92 ± 0.06 for solitarious adults and 0.95 ± 0.05 and 0.92 ± 0.03 for transient and gregarious adults, respectively. Thus, and just as it did in [25], it again reproducibly failed to assign acceptable differences in Pgreg values between solitarious and gregarious adult locusts —Z-adjusted=-0.271, p=0.787 for solitarious versus gregarious adults, Z-adjusted=-0.213, p=0.831 for solitarious versus transient adults, and Z-adjusted=-0.455, p=0.639 for gregarious versus transient adults (Figure 4B,D and Supplemental Tables S2 and S3).
Overall, and although the adult samples sizes were larger than the nymph ones, when applied to both stages at once, the model discriminates between phases (Z-adjusted=3.059, p=0.002) but, as seen before, there is a significant difference between developmental stages (Z-adjusted=2.378, P=0.017). Based on the distribution of the Pgreg, Figure 5 confirms how this model works for nymphs but not for adults.
The Sg_non-morphometric model does distinguish between solitarious and gregarious locusts
As in [25], here also, the Sg_non-morphometric model did distinguish well both between the solitarious and gregarious nymphs, with Pgreg mean ± SE values of 0.45 ± 0.09 and 0.83 ± 0.04, respectively (Z-adjusted=4.452, p<0.00001). It also distinguishes between the solitarious and gregarious adults, with Pgreg mean ± SE values of 0.29 ± 0.10 and 0.88 ± 0.03, respectively (Z-adjusted=6.825, p<0.000001 ) (Figure 6A,B). As in the previous model, transient locusts showed intermediate and gregarious Pgreg mean for nymphs (0.88 ± 0.08) and adults (1.00 ± 0.00), respectively. However, this model suggests that the transient nymphs and adults remained not statistically different from the gregarious group from which they came and did not become similar to solitarious locusts (Z-adjusted=-2.134, p=0.033, for solitarious versus transient nymphs, Z-adjusted=1.160, p=0.246, for gregarious versus transient nymphs, Z-adjusted=-4.829, p=0.000001, for solitarious versus transient adults, and Z-adjusted=-1.623, p=0.105 for gregarious versus transient adults).
The model therefore again distinguishes solitarious from gregarious locusts in both nymph and adult stages (Figure 6C,D and Supplemental Tables S2 and S3) and, just like when we used the Sg_extended_corrected model, the transient adults show high Pgreg in the Sg_non-morphometric model too.
Overall, the Sg_non-morphometric model differentiates between phases better than the Sg_extended_corrected (Z-adjusted=8.062, p<0,000001) while, contrary to this latter, it does not show any between-stage difference in performance (Z-adjusted=0.889, p=0.374). The distribution of Pgreg further supports the better outcome of the Sg_non-morphometric model both for nymphs and for adults (Figure 7).
4. Discussion
Locust outbreaks are a significant recurrent problem in several parts of the world, and outbreaks of the main pest locust, S. gregaria, are associated with the shift from the solitarious to the gregarious phase. The shift between phases occurs in response to changes in the environment (living conditions), and locusts of both phases show adaptations in form of notorious differences in almost every aspect of their biology (see references in the introduction section). In the absence of a clear qualitative or quantitative single morphological or behavioural marker that indicates the phase of a locust, some of the differences between solitarious and gregarious locusts could be combined so that we can infer the phase of the locusts or, at least, compare between locust groups or between different time points of the same locust group. This was thus far achieved using logistic regressions that combine different traits. The problem is that each single published work that differentiated between locust samples based on such method used a different combination of traits and a different logistic regression formula. That does not only imply spending time for building a new model for each experiment, it also means that the results might not be transferable or comparable between the different experiments and laboratories. Providing a time-saving tool is a good thing for science and standardizing methods is a must. That is why we aimed at providing an agnostic tool for time-saving and for standardizing the way solitarious and gregarious S. gregaria samples are categorized.
Our aim in this study is not to characterize the phenomenon of locust outbreaks per se (an issue already approached in several earlier works like [12,13,14,19,21,27,28,29,30,31,32,33,34,35,36,37] and that is still being analysed in even more works) but to test, experimental results in hand, whether the models in [25] are valid for categorising solitarious and gregarious S. gregaria samples as suggested in that work.
We thus will not discuss every single result in this work as, having successfully replicated our previous results, such discussion can be found in our earlier extensive work [25]. However, it is to highlight that here, as in [25], preliminary analyses on the selected traits of adult and nymph, males and females, and solitarious and gregarious S. gregaria showed expected size differences between males and females (with females generally larger) and between nymphs and adults (with adults generally larger). They also confirm that our solitarious and gregarious samples are indeed different (with both types of locust samples showing traits expected for their respective phase). They also reflect how no single morphological or behavioural trait is enough to distinguish between solitarious and gregarious S. gregaria groups.
The models that we test here introduce two novelties: normalization of the movement-related variables by the size of the locust and, in one model, including morphometric traits together with behavioural traits in the formula. Contrary to the false insinuations in [26], we do not suggest colorimetry for calculating Pgreg neither do we suggest our models for different species; we actually tested, proved and suggested the contrary. The models do not include colorimetry, and in [25] we textually state that the models are for S. gregaria, we test and prove that they are not applicable to another locust, Locusta migratoria, and, on purpose, we include Sg in the models names, logically in reference to S. gregaria not other species, and even the title of the work speaks about just one species “the main pest locust”.
Should we normalize by locust size?
This in principle should be as obvious as stating that dividing the distance travelled by the leg size of the traveller will allow more accurate comparison between the levels of activity of tall and short runners. Here, as in [25], we consider the fact that some movement (see behavioural) variables are function of, and could be affected by, the animal’s size. Such effect could distort the differences between solitarious and gregarious individuals. Here we corroborate that by showing how the variable distance (Figure 2E, Figure 3B), when not normalized by the animal’s size, shows a higher mean for solitarious locusts than for gregarious ones. Had we not normalized by femur length (a proxy of the animal’s size —as we explain in [25]), we would have had as a result and interpretation that the solitarious individuals have been walking more distance in the observation arena, so they were more active, than the gregarious individuals (which is contrary to what is proven and known about the differences between solitarious and gregarious S. gregaria). It is normalization that attenuates the effect of the larger body size on the distance travelled by the solitarious locusts. Movement-related variables are undoubtedly function of the leg size variable so, rather than introducing a leg size effect (often vaguely described as morphology in [26]), the normalization that we applied (a division), actually mathematically takes off (or at least attenuates) the leg-size effect from the movement-related variables (often vaguely described as behaviour in [26]) —introducing such effect would be mathematically true had we add or multiply by the leg size. Of course, we did not normalize any random behavioural variable (we normalized movement-related variables that we previously proved to be associated with S. gregaria phase) and we did not normalize by any random morphological variable, we used the femur size after explaining why it is the most suitable and valid proxy for leg and body size. Moreover, the model’s regression coefficients are calculated based on movement-related variables that were already femur-normalized (not on the non-normalized ones) —so the weight of each normalized variable (regression coefficient) is mathematically adequate to the values that that variable shows and to the association of such values with the locusts’ states.
Can morphometry and behaviour be in the same model?
S. gregaria’s phase change involves either morphological and behavioural or only behavioural changes and is a dynamic phenomenon, so that: (i) locusts can either remain at the same phase for a long time (see generations); they would have inherited that phase’s morphology and behaviour from previous generation(s), or they might have changed phase within their lifetime (so, contrary to their behaviour, their morphometry would not have changed). Worth mentioning here that the shift from solitarious to gregarious is more rapid than the shift from gregarious to solitarious. Furthermore, (ii) while adults change behaviour but maintain morphometry when they change phase within their adult lifetime (i.e., if they don’t inherit the phase from previous generation), nymphs change their morphology too if they molt after they change phase within their nymphal lifetime. There are therefore instances when the solitarious and gregarious S. gregaria locusts differ both in morphology and behaviour (i.e., long-term solitarious and gregarious locusts that inherited the phase or nymphs that molted after the phase change), and there are instances where the solitarious and gregarious locusts differ only in behaviour (i.e., the same locusts when they change phase within their lifetime and do not molt). In addition, (iii) there are morphology differences between developmental stages of the same sex and phase, (iv) there are morphology (including size) differences between males and females of the same phase and developmental stage, (v) there are size differences between individuals of the same sex, developmental stage and phase, and (vi) different locust samples normally have different sex proportions and (vii) are composed of individuals of different sizes, even when they are of the same developmental stage and phase. To all this one has to add the potential differences between populations and genetick backgrounds—we do not use the term strain as it is still for defining in locusts. Considering all these facts, different S. gregaria samples will therefore have morphological differences even when they are of the same phase, developmental stage and sex.
At the same time, if one is to use variables in order to differentiate between two states, then one has to select the variables that significantly differentiate those two states and use as many variables as possible in order to be as accurate as possible. Hence, it is expected that the most variables that are associated with the phase change one considers, the closer one is to reality and to correctly inferring the phase of a locust sample. Using morphological and behavioural variables for distinguishing locust samples that differ in morphology and behaviour should therefore be a plus.
As objection to introducing morphology, much was made of the potential situation of a locust that would be stimulated/induced into the gregarious phase and tested straightaway (non-long term gregarious); it was claimed that because such locust won’t change morphology, then using morphological variables in the model will be wrong. [26]. First, let us not forget that the models work at the group not individual level (since, when observed, some individuals may behave different to the expected given their phase). Now, such locusts do not change morphology and thus one should use the Sg_non-morphology model that we recommend for S. gregaria samples that do not change morphology. That the model’s regression coefficients are calculated based on movement-related variables that were already femur-normalized is not a problem since the weight of each normalized variable (regression coefficient) is mathematically adequate to the values that that variable shows and to the association of such values with the locusts’ states. Furthermore, and unless the animals remain unchanged —which would result in the model giving similar or same values for the before stimulation and after stimulation testings— locusts that were gregarized should change behaviour even when their morphology does not change. Thus, their movement-related variables will change. At the same time dividing the movement-related behavioural variables by the unchanged femur length of the same locusts (i.e., dividing by a constant) does not prevent detecting differences between states (movement-related behaviours) of the same locusts if they change behaviour (see phase); especially since the coefficients of the logistic regression are calculated on such normalized values. All that mathematically means that the model’s outcome will change for the same locusts after gregarizing or solitarizing them; and thus the model would detect that those locusts’ state has changed —it is expected that this detected difference will be less than the difference that we would detect if we apply a model that includes morphometrical variables to samples that changed morphometry too. The magnitudes of the differences detected will depend on the magnitude of the change of the variables of the model and, thus, on the magnitude of the change that the locusts would have experienced after being induced into a different phase.
Do the models do what we want them to do?
If they prove capable of categorising locust samples and detecting differences in their phase status, the models that we suggested in [25] should then allow standardizing tools for an essential aspect of many functional and comparative studies on S. gregaria locusts, i.e., to categorize solitarious and gregarious S. gregaria groups of adults and nymphs. Research on locust phase change is quite important and deserves standardized tools for one of its essential tasks. The tools that we suggested are just for classifying S. gregaria samples; they are not for inferring on the locust phase change phenomenon itself. However, the message in [26] is that standardization of such tools is not possible at all —which we think is just a subjectively arguable opinion that is based on unproven interpretations; such as the still to be defined locust strain concept and whether there are differences in the phase change phenomenon between such strains. Moreover, the same author, again based on theoretical evaluations (simulations) and personal views and interpretations on proven and unproven concepts, considered our models as flawed and not recommended and predicted that they won’t work in future samples as well as they did in the 2017 samples. The prediction literally was that the models “will not predict future observations as well as it appeared to predict on the present sample.” [26]. The models were criticised in a theoretical text that did not experimentally apply the models to real locusts to see whether they do what we say they do [26]. We thus think that rather than interpretatively arguing it is better to empirically test in a direct and objective way, and the new locusts that we have after renewing our locust colony (that was affected by the COVID-19 restrictions) provides a good material for that.
In fact, interpretation and indirect evaluations-based predictions themselves need testing. Direct testing of the models by applying them to real locust samples is quick (matter of hours), easy and feasible (in [25] we provide all the methods, formulae and even a script to facilitate that task). If the interpretations and consequent predictions in [26] were right, then directly testing the models by applying them to new well known S. gregaria samples should not allow correct categorization of those samples and, if the models correctly categorize the locusts samples, then we can safely state that, after being tested in [25] and replicated in [26], they are validated in the present work. In experimental sciences, experiments are more trustable than interpretations of concepts, these latter are what have to adapt to the empirical results not the other way around.
It is to highlight that the models were already successfully tested by us when we suggested them in [25]. It is also worth highlighting that the first data-based re-test of the models by others, although re-using our data, gave the same results as the ones that we had, and that the models were considered as “appeared” to work “well” in the 2017 samples [26].
Here we re-evaluate the models as if we were a different laboratory (what our criticiser should have done in the first place). So not only we use even more and different sets of real locusts —that are different from the ones that we used for building and the ones we used for testing the models in [25] — we also incorporate different researchers between whom communication of the results was reduced to the necessary minimum —in order to reduce or eliminate any potential subjective biasing of the results. Thus, here the models are tested in additional independent samples and the researchers who carried out the observations and data collection were different from the ones in [25]; while the researchers that applied the models were blind to the phase state of the analysed locusts.
In our original work [25] we wrote that “We suggest using the ‘Sg_extended_corrected’ model (that includes morphometric variables) for comparing different S. gregaria nymph samples. For testing adults or the same nymphs at different time points (if they do not molt), we suggest using the ‘Sg_non-morphometric’ model (that does not include morphometric variables).”. This was successfully replicated in the present work as: (i) the Sg_extended_corrected model only predicts phase for nymphs, and (ii) The Sg_non-morphometric model predicts the phase of both adults and nymphs.
Even the fact that we found in [25] that “The models that we provide here are useful for comparing different populations” because “the results are only applicable at the population (sample) level.” was replicated in the current work.
Furthermore, in [25] we wrote that “distinguishing between samples of intermediate densities falls beyond the models’ sensitivity”. Here we show that while both models show transient nymphs with intermediate Pgreg, transient adults appear more as gregarious and the statistical comparisons do not allow a clear interpretation of the change that these locusts experienced.
We therefore re-tested and corroborated again that the models built and initially tested in [25] can distinguish between solitarious and gregarious S. gregaria nymphs and adults. Although the models are useful for testing groups but not single individuals, we re-highlight —as we did in [25]— that experiments are done using samples (populations/groups) and not single individual locusts, and that individual locusts might behave in a way that is not the expected for their phase, due to uncontrolled or even stochastic reasons. Thus, we confirm that the models we suggest in [25] can be used for inferring the phase or for comparing samples/groups/populations of S. gregaria locusts (both different samples or the same sample between experimental times; e.g., when testing the effects of experimental manipulations such as the effect of drugs, gene silencing, etc. on the phase of S. gregaria). We thus reiterate that “The use of these models by multiple laboratories would standardize and homogenize methodologies to the benefit of reliable results and interpretations.”
Testing, replication and reproduction of the results are key to science, and science, is based on hypotheses-driven results that are prone to testing and rejection and that should stand valid as long as they are reproduced. The models we suggest for inferring the phase of S. gregaria —for the sake of standardizing methods between experiments and laboratories— were tested in two works, by different researchers and using a total of 447 locusts pertaining to 25 different sets of S. gregaria locusts of different origin, densities, developmental stages and sexes. The models consistently differentiated between solitarious and gregarious S. gregaria sets (see groups or populations) and they, thus, should do so whenever they are used —a fact that allows us to confidently re-suggest their use for the benefit of standardizing methodologies and saving time. We also highlight, as we did in [25], the better outcome of the Sg_non_morphometric model as compared to that of the Sg_extended_corrected model. All what we can add here is that both models work better in larger samples sizes (as shown by the results when we pool all the samples of the same phase together) and that, had we to chose, we would recommend the Sg_non_morphometric model more than the second.
That being said, the models, correct and capable of correctly categorizing solitarious and gregarious S. gregaria samples as thus far they proved to be, are not equally valid, they are not optimal, and are no doubt improvable. We would certainly applaud anyone who can rebuild and improve them using larger sample sizes. Being these models species-specific, we encourage colleagues working on other species to build and standardize tools for their work material.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
Author Contributions
Conceptualization, Mohammed Bakkali; Formal analysis, NOUREDDINE BAKKALI, Rubén Martín Blázquez, Abdelmounim Badih and Mohammed Bakkali; Investigation, Soumia Saadi; Writing – original draft, Mohammed Bakkali; Writing – review & editing, Soumia Saadi, NOUREDDINE BAKKALI, Rubén Martín Blázquez, Abdelmounim Badih and Mohammed Bakkali; Supervision, Mohammed Bakkali; Project administration, Mohammed Bakkali; Funding acquisition, Mohammed Bakkali.
Data Availability Statement
All data generated or analysed during this study are included in this published article and its supplementary information files.
Acknowledgments
M. Bakkali wants to thank the Agencia Estatal de Investigación, Ministerio de Ciencia e Innovación (Spain) for the grant Ref. PGC2018.097678.B.I00 that funded this work. M. Bakkali and S. Saadi want to thank the ERASMUS+ International Dimension Programme for the studentship at the University of Granada for the studentship to S. Saadi.
References
- P, U.B. , Grasshoppers and locusts.. Cambridge University Press Cambridge, UK., 1966.
- Dingle, H.; Mousseau, T.A.; Scott, S.M. Altitudinal variation in life cycle syndromes of California populations of the grasshopper, Melanoplus sanguinipes (F.). Oecologia 1990, 84, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Waloff, Z.; Green, S.M. Regularities in duration of regional desert locust plagues. Nature 1975, 256, 484–485. [Google Scholar] [CrossRef]
- A Poot-Pech, M.; Ruiz-Sánchez, E.; Ballina-Gómez, H.S.; Gamboa-Angulo, M.M.; Reyes-Ramírez, A. Olfactory Response and Host Plant Feeding of the Central American Locust Schistocerca piceifrons piceifrons Walker to Common Plants in a Gregarious Zone. Neotropical Èntomol. 2016, 45, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Latchininsky, A.V. , Moroccan locust dociostaurus maroccanus (thunberg, 1815): A faunistic rarity or an important economic pest? Journal of Insect Conservation 1998, 2, 167–178. [Google Scholar] [CrossRef]
- Key, K. , The regional and seasonal incidence of grasshopper plagues in australia. Bull. Coun. sci. industr. Res. Aust 1938, 87. [Google Scholar]
- Waloff, Z. , Upsurges and recessions of the desert locust plague; an historical survey. 1966.
- Pedgley, D. , Desert locust forecasting manual. Volumes i and ii. Centre for Overseas Pest Research.: 1981.
- Showler, A.T.; Lecoq, M. Incidence and Ramifications of Armed Conflict in Countries with Major Desert Locust Breeding Areas. Agronomy 2021, 11, 114. [Google Scholar] [CrossRef]
- Applebaum, S.W.; Heifetz, Y. Density-dependent physiological phase in insects. Annu. Rev. Èntomol. 1999, 44, 317–341. [Google Scholar] [CrossRef]
- Nishide, Y.; Tanaka, S. Yellowing, morphology and behaviour in sexually mature gynandromorphs of the desert locustSchistocerca gregaria. Physiol. Èntomol. 2012, 37, 379–383. [Google Scholar] [CrossRef]
- Stower, W.J.; Davies, D.E.; Jones, I.B. Morphometric Studies of the Desert Locust, Schistocerca gregaria (Forsk.). J. Anim. Ecol. 1960, 29, 309. [Google Scholar] [CrossRef]
- Symmons, P.M. A morphometric measure of phase in the desert locust, Schistocerca gregaria (Forsk.). Bull. Èntomol. Res. 1969, 58, 803–809. [Google Scholar] [CrossRef]
- Bouaïchi, A.; Roessingh, P.; Simpson, S.J. An analysis of the behavioural effects of crowding and re-isolation on solitary-reared adult desert locusts (Schistocerca gregaria) and their offspring. Physiol. Èntomol. 1995, 20, 199–208. [Google Scholar] [CrossRef]
- Bouaichi, A.; Simpson, S.J. Density-dependent accumulation of phase characteristics in a natural population of the desert locust Schistocerca gregaria. Physiol. Èntomol. 2003, 28, 25–31. [Google Scholar] [CrossRef]
- Simpson, S.J.; McCaffery, A.; HAeGELE, B.F. , A behavioural analysis of phase change in the desert locust. Biological Reviews 1999, 74, 461–480. [Google Scholar] [CrossRef]
- Tanaka, S.; Nishide, Y. Behavioral phase shift in nymphs of the desert locust, Schistocerca gregaria: Special attention to attraction/avoidance behaviors and the role of serotonin. J. Insect Physiol. 2013, 59, 101–112. [Google Scholar] [CrossRef] [PubMed]
- Gunn, D.; Hunter-Jones, P. , Laboratory experiments on phase differences in locusts. Anti-Locust Bull 1952, 12, 1–29. [Google Scholar]
- Stower, W. , The colour pattern of hoppers of the desert locust (schistocerca gregaria forskal). Anti-Locust Bull 1959, 75.
- Bouaïchi, A.; Simpson, S.J.; Roessingh, P. The influence of environmental microstructure on the behavioural phase state and distribution of the desert locust Schistocerca gregaria. Physiol. Èntomol. 1996, 21, 247–256. [Google Scholar] [CrossRef]
- Bakkali, M.; Martín-Blázquez, R. RNA-Seq reveals large quantitative differences between the transcriptomes of outbreak and non-outbreak locusts. Sci. Rep. 2018, 8, 9207. [Google Scholar] [CrossRef]
- Martín-Blázquez, R.; Chen, B.; Kang, L.; Bakkali, M. Evolution, expression and association of the chemosensory protein genes with the outbreak phase of the two main pest locusts. Sci. Rep. 2017, 7, 6653–6653. [Google Scholar] [CrossRef]
- Sugahara, R.; Saeki, S.; Jouraku, A.; Shiotsuki, T.; Tanaka, S. Knockdown of the corazonin gene reveals its critical role in the control of gregarious characteristics in the desert locust. J. Insect Physiol. 2015, 79, 80–87. [Google Scholar] [CrossRef]
- Bakkali, M. , A bird's-eye view on the modern genetics workflow and its potential applicability to the locust problem. C R Biol 2013, 336, 375–383. [Google Scholar] [CrossRef]
- Martín-Blázquez, R.; Bakkali, M. Standardization of multivariate regression models for estimation of the gregariousness level of the main pest locust. Èntomol. Exp. et Appl. 2017, 163, 9–25. [Google Scholar] [CrossRef]
- Ott, S.R. Regressions Fit for Purpose: Models of Locust Phase State Must Not Conflate Morphology With Behavior. Front. Behav. Neurosci. 2018, 12, 137. [Google Scholar] [CrossRef] [PubMed]
- Piou, C.; Zagaglia, G.; Medina, H.E.; Trumper, E.; Brizuela, X.R.; Maeno, K.O. Band movement and thermoregulation in Schistocerca cancellata. J. Insect Physiol. 2021, 136, 104328. [Google Scholar] [CrossRef] [PubMed]
- Hamouda, A.B.; Tanaka, S.; Hamouda, M.H.B.; Bouain, A. , Density-dependent phenotypic plasticity in body coloration and morphometry and its transgenerational changes in the migratory locust, locusta migratoria. Journal of Entomology and Nematology 2011, 3, 105–116. [Google Scholar]
- Chen, S.; Yang, P.; Jiang, F.; Wei, Y.; Ma, Z.; Kang, L. De Novo Analysis of Transcriptome Dynamics in the Migratory Locust during the Development of Phase Traits. PLOS ONE 2010, 5, e15633. [Google Scholar] [CrossRef]
- Chapuis, M.P.; Lecoq, M.; Michalakis, Y.; Loiseau, A.; Sword, G.A.; Piry, S.; Estoup, A. , Do outbreaks affect genetic population structure? A worldwide survey in locusta migratoria, a pest plagued by microsatellite null alleles. Molecular ecology 2008, 17, 3640–3653. [Google Scholar]
- Hägele, B.F.; Simpson, S.J. The influence of mechanical, visual and contact chemical stimulation on the behavioural phase state of solitarious desert locusts (Schistocerca gregaria). J. Insect Physiol. 2000, 46, 1295–1301. [Google Scholar] [CrossRef]
- Islam, M.S.; Roessingh, P.; Simpson, S.J.; McCaffery, A.R. Parental effects on the behaviour and colouration of nymphs of the desert locust Schistocerca gregaria. J. Insect Physiol. 1994, 40, 173–181. [Google Scholar] [CrossRef]
- Islam, M.S.; Roessingh, P.; Simpson, S.J.; Mccaffery, A.R. , Effects of population density experienced by parents during mating and oviposition on the phase of hatchling desert locusts, schistocerca gregaria. Proceedings of the Royal Society of London B: Biological Sciences 1994, 257, 93–98. [Google Scholar] [CrossRef]
- Roessingh, P.; Simpson, S.J.; James, S. , Analysis of phase-related changes in behaviour of desert locust nymphs. Proceedings of the Royal Society of London B: Biological Sciences 1993, 252, 43–49. [Google Scholar]
- Gillett, S.D. Social determinants of aggregation behaviour in adults of the desert locust. Anim. Behav. 1973, 21, 599–606. [Google Scholar] [CrossRef]
- Dingle, H.; Haskell, J.B. Phase Polymorphism in the Grasshopper Melanoplus differentialis. Science 1967, 155, 590–592. [Google Scholar] [CrossRef] [PubMed]
- Ellis, P.E. Changes in the social aggregation of locust hoppers with changes in rearing conditions. Anim. Behav. 1963, 11, 152–160. [Google Scholar] [CrossRef]
Figure 1.
Effect of the phase (solitarious versus gregarious), age (adult versus nymph) and sex on the morphometric traits used for building the models for inferring the phase of groups and populations of the desert locust Schistocerca gregaria. The X axix is the locust type (sex, age or phase) and the Y axis is the size of the trait in mm. The solitarious, transient and gregarious adult and nymph samples are different samples not the same sample in different states.
Figure 1.
Effect of the phase (solitarious versus gregarious), age (adult versus nymph) and sex on the morphometric traits used for building the models for inferring the phase of groups and populations of the desert locust Schistocerca gregaria. The X axix is the locust type (sex, age or phase) and the Y axis is the size of the trait in mm. The solitarious, transient and gregarious adult and nymph samples are different samples not the same sample in different states.
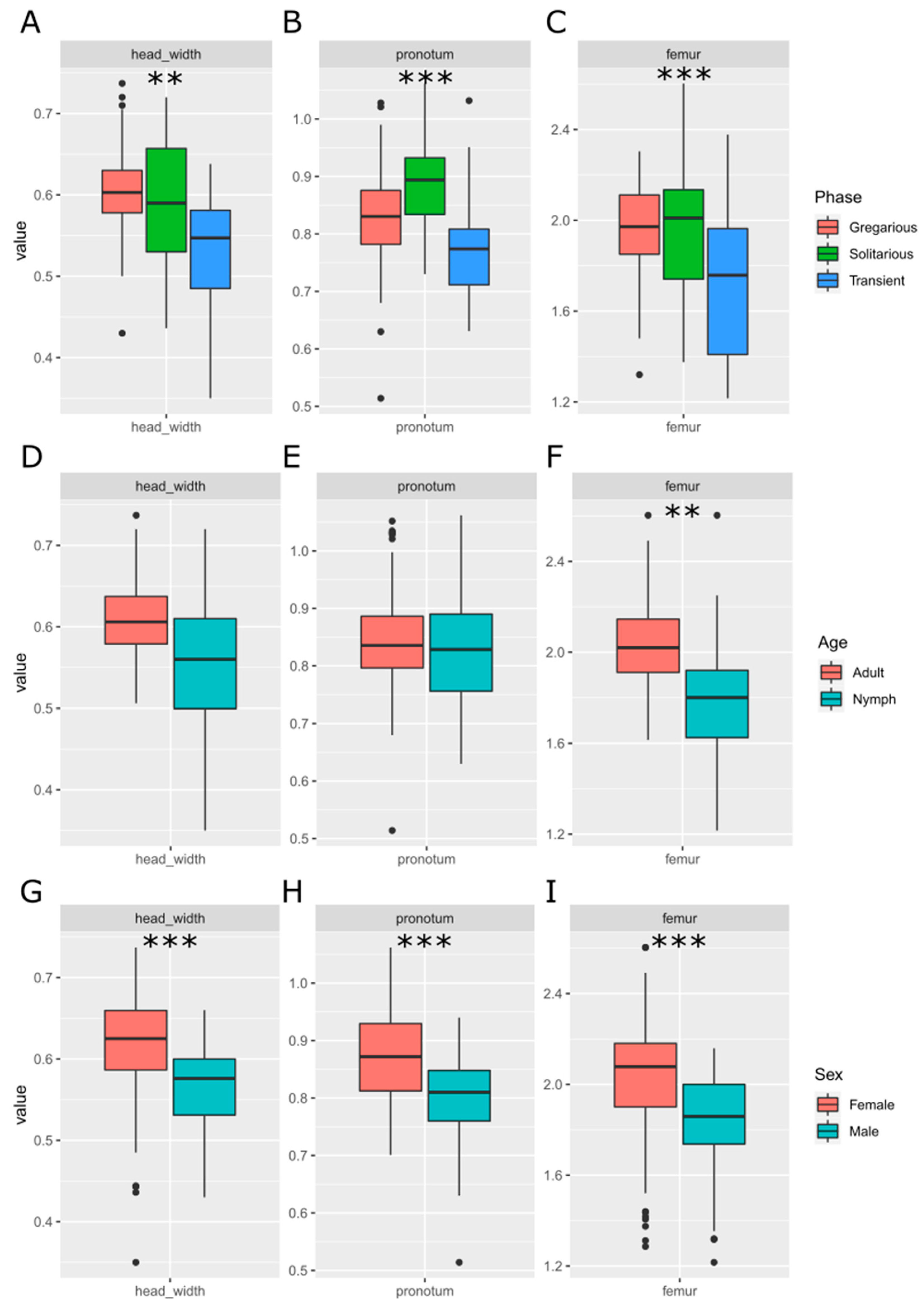
Figure 2.
Comparison of the morphometric and behavioural traits used for building the models between solitarious, transient and gregarious adults and nymphs of the desert locust Schistocerca gregaria used in this work. X axis are the samples (solitarious, transient or gregarious adults or nymphs) and the Y axis is the value of the trait analyzed. Abbreviations of the traits are as explained in Material and methods section.
Figure 2.
Comparison of the morphometric and behavioural traits used for building the models between solitarious, transient and gregarious adults and nymphs of the desert locust Schistocerca gregaria used in this work. X axis are the samples (solitarious, transient or gregarious adults or nymphs) and the Y axis is the value of the trait analyzed. Abbreviations of the traits are as explained in Material and methods section.
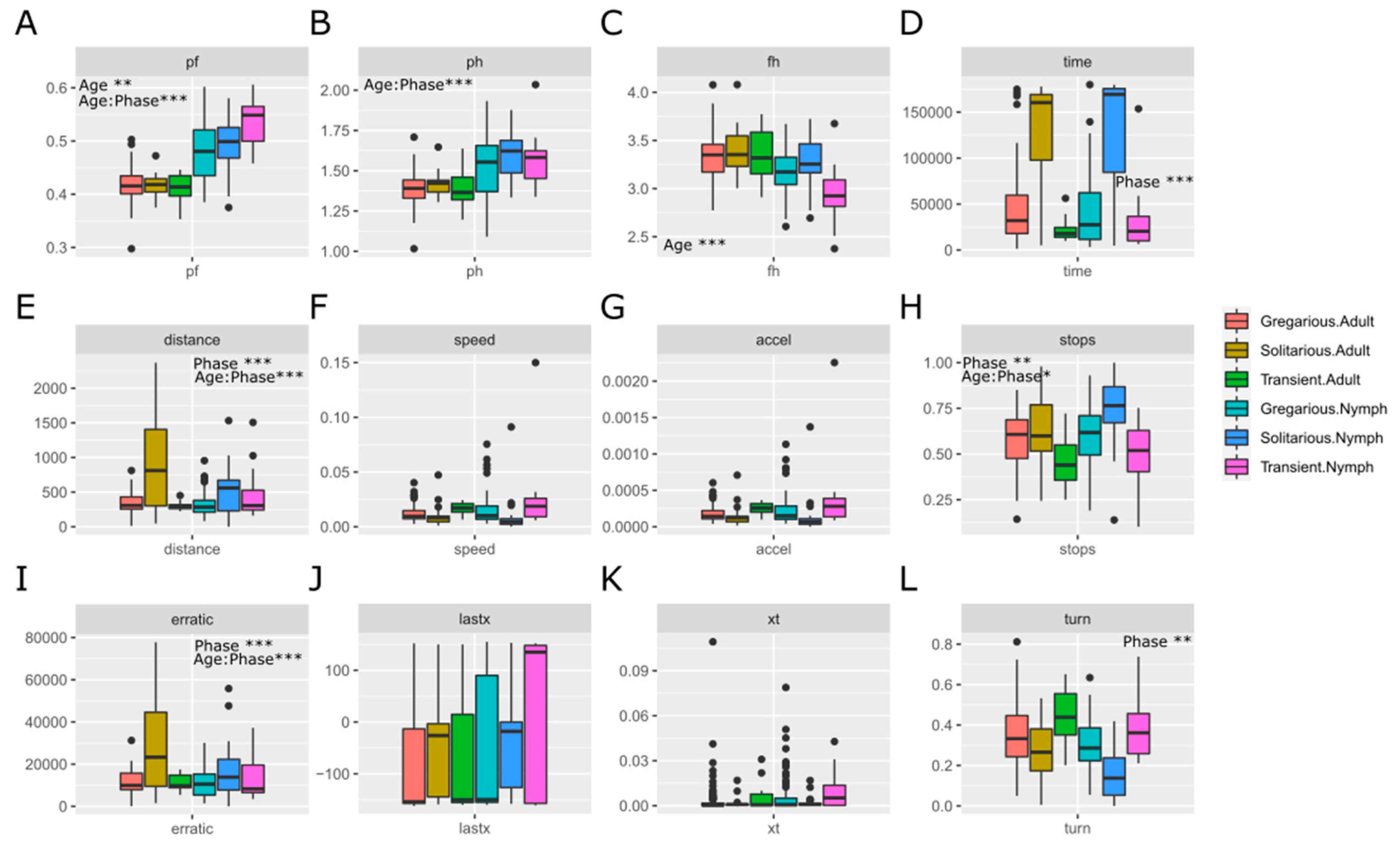
Figure 3.
Effect of the normalization of the movement-related behavioural traits used for building the models (abbreviation of the variables are as in Material and methods section) by the femur length (FemSt) of the solitarious, transient and gregarious adults and nymphs of the desert locust Schistocerca gregaria used in this work. Significant effects and interactions, as by ANOVA, are shown with asterisks in each corresponding graph.
Figure 3.
Effect of the normalization of the movement-related behavioural traits used for building the models (abbreviation of the variables are as in Material and methods section) by the femur length (FemSt) of the solitarious, transient and gregarious adults and nymphs of the desert locust Schistocerca gregaria used in this work. Significant effects and interactions, as by ANOVA, are shown with asterisks in each corresponding graph.
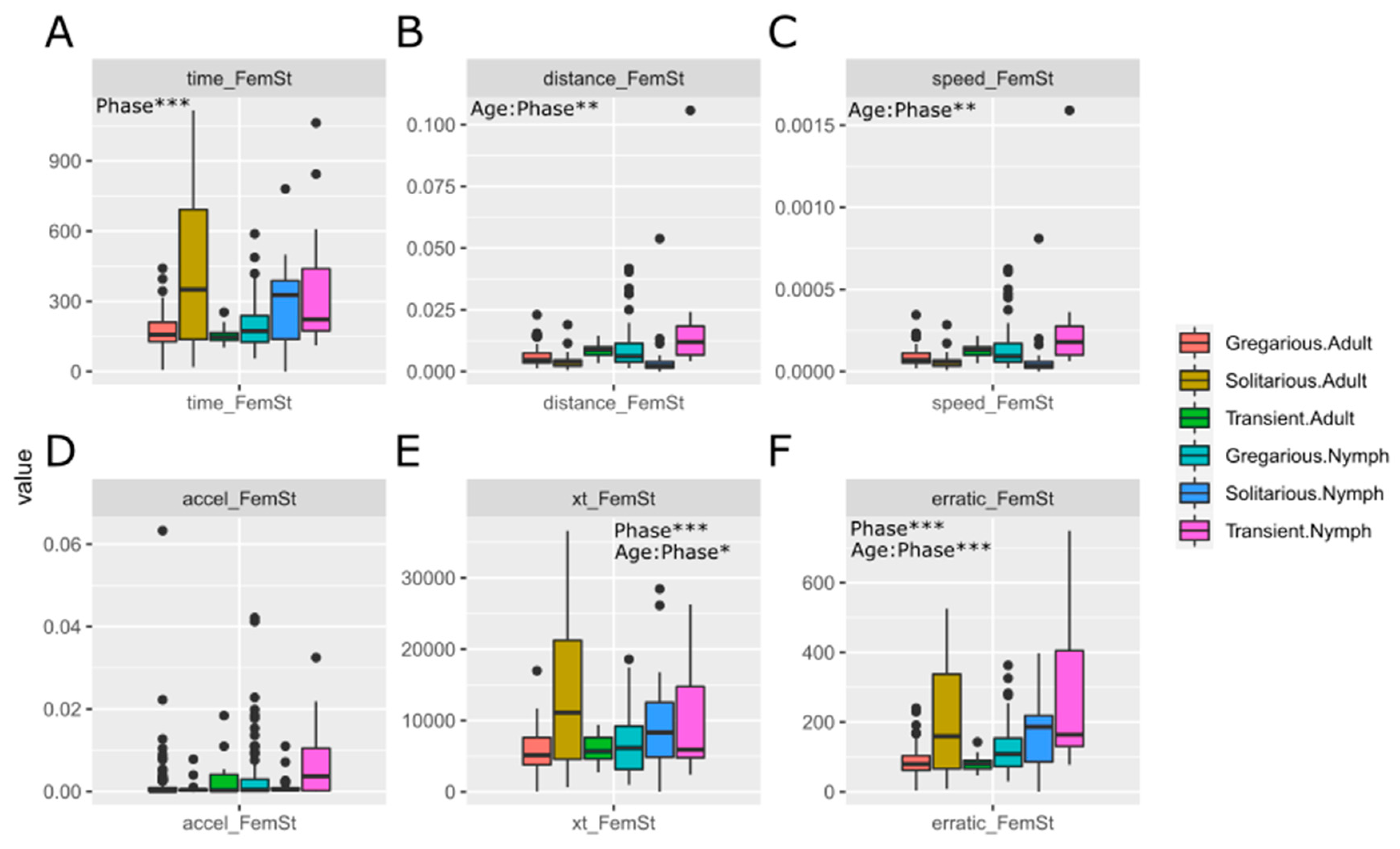
Figure 4.
Gregariousness probability (Pgreg), shown as percentage in the Y axis, as obtained after application of the Sg_extended_corrected model from [25] to the solitarious (green), transient (orange) and gregarious (red) nymphs (A and C) and adults (B and D) of the desert locust Schistocerca gregaria used in this work. GA: gregarious adults, GN: gregarious nymphs, SA: solitarious adults, SN: solitarious nymphs, TA: Transient adults, TN: transient nymphs.
Figure 4.
Gregariousness probability (Pgreg), shown as percentage in the Y axis, as obtained after application of the Sg_extended_corrected model from [25] to the solitarious (green), transient (orange) and gregarious (red) nymphs (A and C) and adults (B and D) of the desert locust Schistocerca gregaria used in this work. GA: gregarious adults, GN: gregarious nymphs, SA: solitarious adults, SN: solitarious nymphs, TA: Transient adults, TN: transient nymphs.
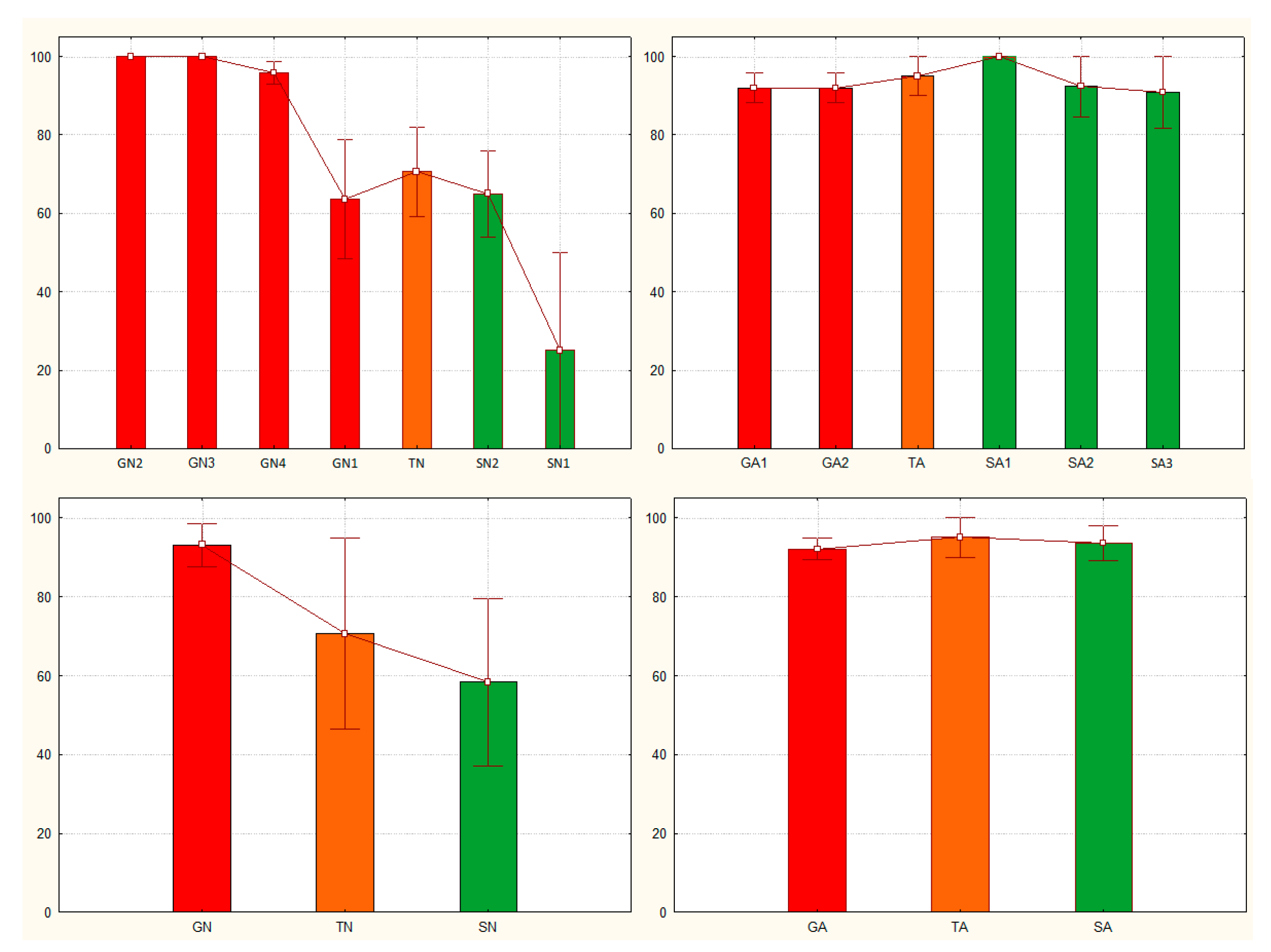
Figure 5.
Proportions of individuals that show 0 (green), between 0 and 1 (grey), and 1 (red) as gregariousness probability (Pgreg), shown as percentage in the Y axis, as obtained after application of the Sg_extended_corrected model from [25] to the solitarious nymphs (Sol_Nym) and adults (Sol_Ad), transient nymphs (Trans_Nym) and adults (Trans_Ad) and gregarious nymphs (Greg_Nym) and adults (Greg_Ad) of the desert locust Schistocerca gregaria used in this work. Sol_All, Trans_all and Greg_all are, respectively, the pooled solitarious, transient and gregarious adult and nymph samples.
Figure 5.
Proportions of individuals that show 0 (green), between 0 and 1 (grey), and 1 (red) as gregariousness probability (Pgreg), shown as percentage in the Y axis, as obtained after application of the Sg_extended_corrected model from [25] to the solitarious nymphs (Sol_Nym) and adults (Sol_Ad), transient nymphs (Trans_Nym) and adults (Trans_Ad) and gregarious nymphs (Greg_Nym) and adults (Greg_Ad) of the desert locust Schistocerca gregaria used in this work. Sol_All, Trans_all and Greg_all are, respectively, the pooled solitarious, transient and gregarious adult and nymph samples.
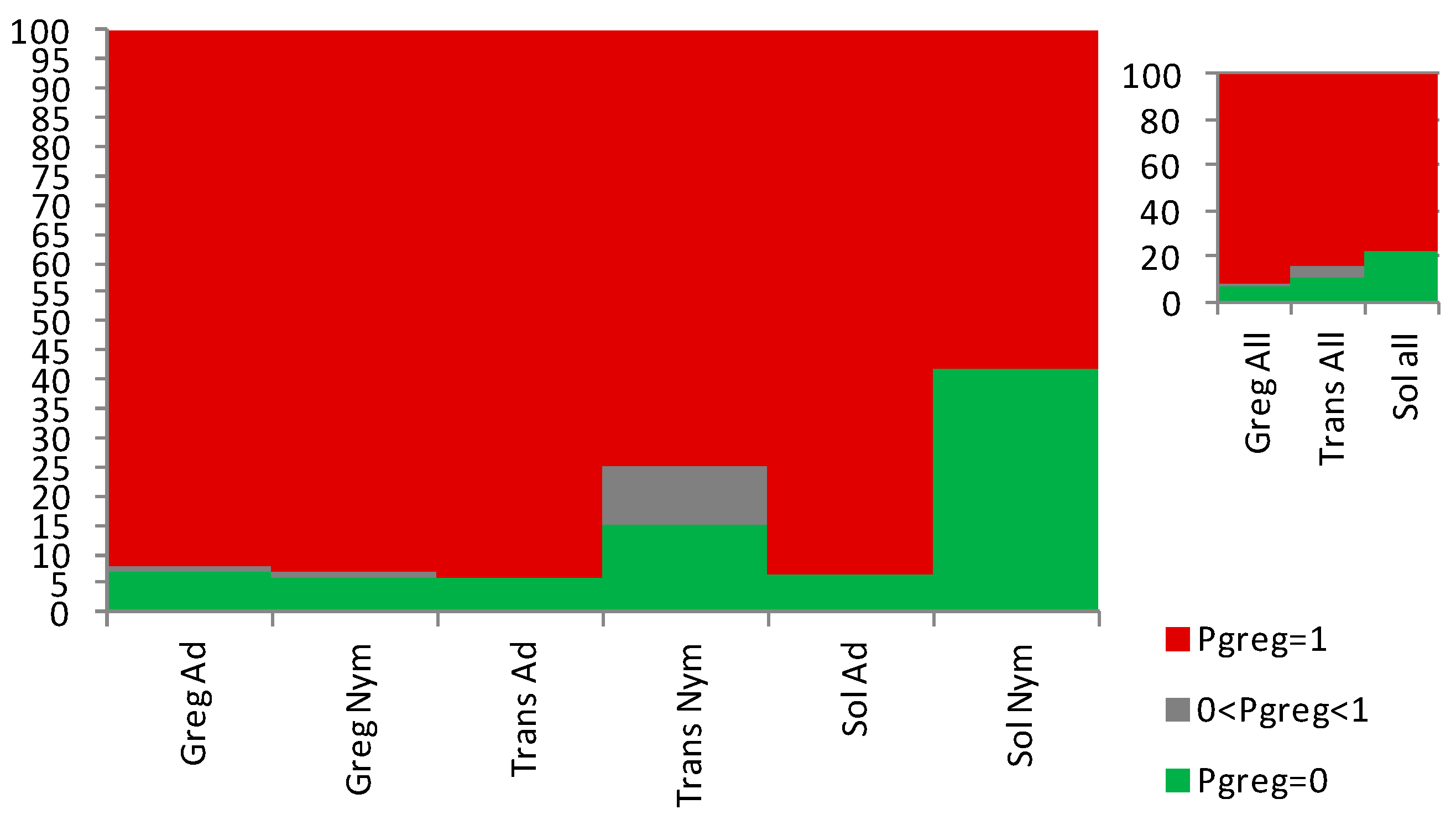
Figure 6.
Gregariousness probability (Pgreg), expressed as percentage in the Y axis, as obtained after application of the Sg_non-morphometric model from [25] to the solitarious (green), transient (orange) and gregarious (red) nymphs (A and C) and adults (B and D) of the desert locust Schistocerca gregaria uses in this work. GA: gregarious adults, GN: gregarious nymphs, SA: solitarious adults, SN: solitarious nymphs, TA: Transient adults, TN: transient nymphs.
Figure 6.
Gregariousness probability (Pgreg), expressed as percentage in the Y axis, as obtained after application of the Sg_non-morphometric model from [25] to the solitarious (green), transient (orange) and gregarious (red) nymphs (A and C) and adults (B and D) of the desert locust Schistocerca gregaria uses in this work. GA: gregarious adults, GN: gregarious nymphs, SA: solitarious adults, SN: solitarious nymphs, TA: Transient adults, TN: transient nymphs.
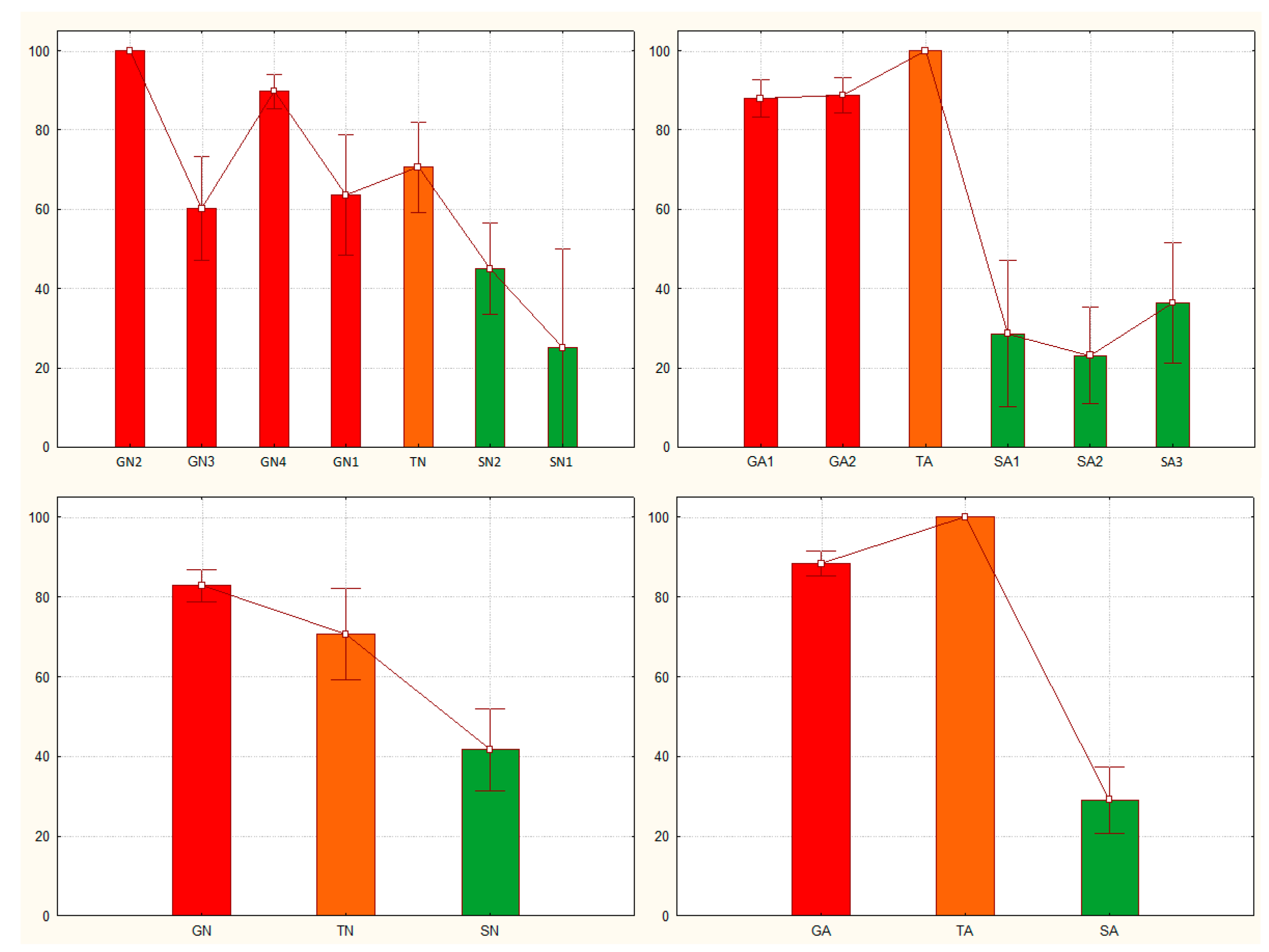
Figure 7.
Proportions of individuals that show 0 (green), between 0 and 1 (grey), and 1 (red) as gregariousness probability (Pgreg), shown as percentage in the Y axis, as obtained after application of the Sg_non-morphometric model from [25] to the solitarious nymphs (Sol_Nym) and adults (Sol_Ad), transient nymphs (Trans_Nym) and adults (Trans_Ad) and gregarious nymphs (Greg_Nym) and adults (Greg_Ad) of the desert locust Schistocerca gregaria used in this work. Sol_All, Trans_all and Greg_all are, respectively, the pooled solitarious, transient and gregarious adult and nymph samples.
Figure 7.
Proportions of individuals that show 0 (green), between 0 and 1 (grey), and 1 (red) as gregariousness probability (Pgreg), shown as percentage in the Y axis, as obtained after application of the Sg_non-morphometric model from [25] to the solitarious nymphs (Sol_Nym) and adults (Sol_Ad), transient nymphs (Trans_Nym) and adults (Trans_Ad) and gregarious nymphs (Greg_Nym) and adults (Greg_Ad) of the desert locust Schistocerca gregaria used in this work. Sol_All, Trans_all and Greg_all are, respectively, the pooled solitarious, transient and gregarious adult and nymph samples.
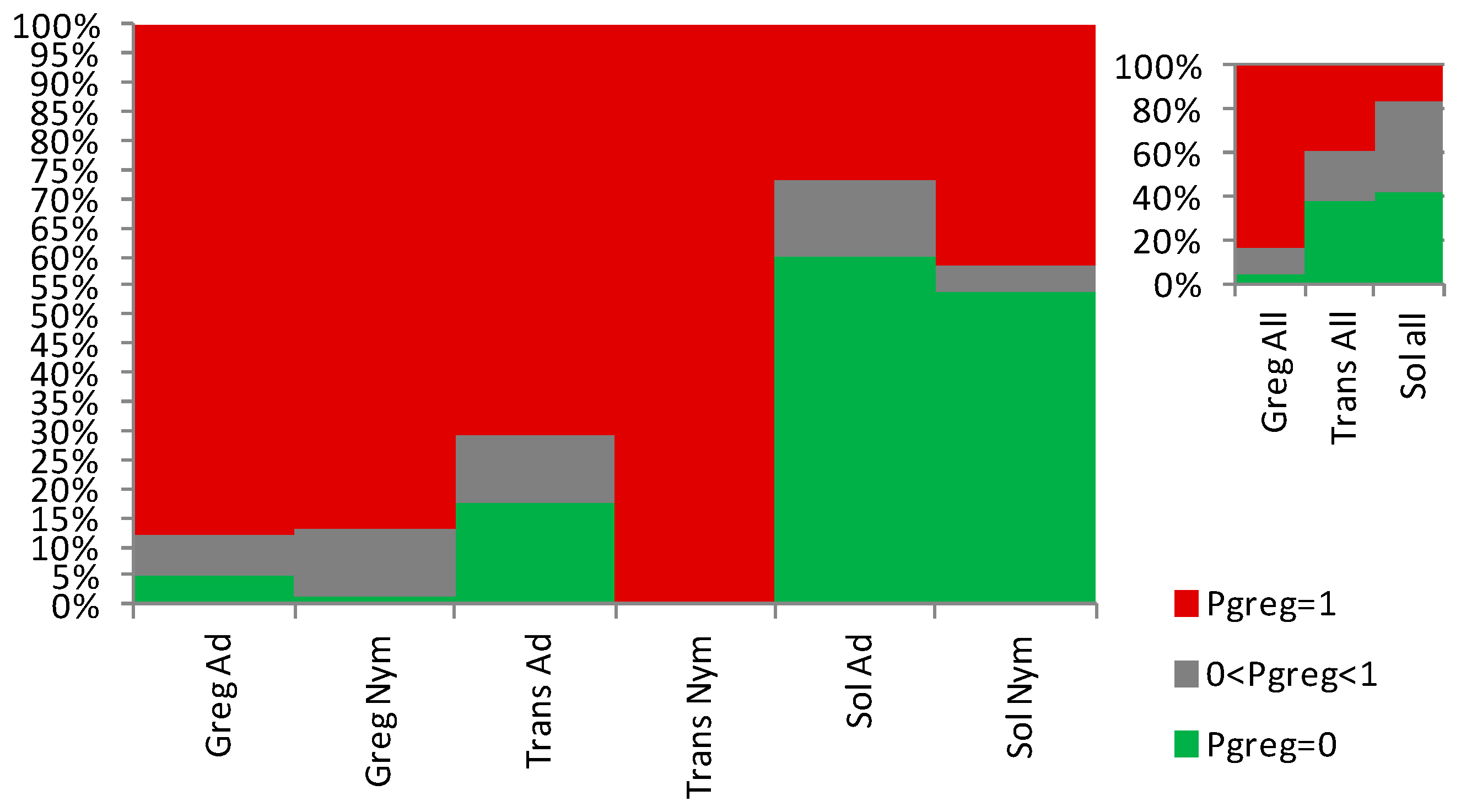
Table 1.
Variables, their coefficients (βvariable), Intercepts (β0) and correction factor (c) of the models for estimating Schistocerca gregaria’s probability of being gregarious. Each model’s equation being: η = intercept + (βP/F × P/F) + (βP/H × P/H) +…+ (βEM × EM). The probability of being gregarious is calculated as: Pgreg = eηc/(1 + eηc), where e is Euler’s number (2.718) and c is a correction factor. I= Sg_extended_corrected. II: Sg_non-morphometric.
Table 1.
Variables, their coefficients (βvariable), Intercepts (β0) and correction factor (c) of the models for estimating Schistocerca gregaria’s probability of being gregarious. Each model’s equation being: η = intercept + (βP/F × P/F) + (βP/H × P/H) +…+ (βEM × EM). The probability of being gregarious is calculated as: Pgreg = eηc/(1 + eηc), where e is Euler’s number (2.718) and c is a correction factor. I= Sg_extended_corrected. II: Sg_non-morphometric.
| Correction factor and variables of the model’s logistic regression formulae. | Constants and coefficients of the model: | ||
| I | II | ||
| C | 1/104 | 1 | |
| Intercept (β0) | −2.83 107 | 1.12 104 | |
| Pronotum-femur index | Pronotum-femur index (PF= pronotum dorsal length divided by hind femur length) | 5.11 107 | 0 |
| Pronotum-head index | Pronotum-head index (PH= pronotum dorsal length divided by head width) | −1.69 107 | 0 |
| Femur-head index | Femur-head index (FH= hind femur length divided by head width) | 9.39 106 | 0 |
| Choice | CH= a binary variable describing the side of the arena where the experimental animal was positioned at the end of the recording, with 0 being the blank side and 1 being the stimulus side | 1.03 106 | 8.45 103 |
| Elapsed time | ET= total time of the recording, maximum 3 minutes if the animal does not reaches one side of the observation arena earlier | −3.53 | 5.30 10−3 |
| Total distance | TD= total distance travelled by the experimental animal during the recording time | −6.68 102 | −21.3 |
| Average speed | AS= average of dividing the distance increments by the time increments at each time frame | 7.91 108 | −3.41 105 |
| Average acceleration | AA= average of dividing the speed increments by the time increments at each time frame | −2.53 105 | −1.47 104 |
| Last coordinate | LC= value of the observation arena’s X-axis coordinate where the animal was positioned at the end of the recording, ranging between 150 at the blank side and +150 at the stimulus side | −3.68 103 | −18.3 |
| Choice by time | CT or XT= last coordinate divided by the elapsed time | 1.90 107 | −6.46 104 |
| Stop ratio | SR= number of 67-ms time frames with no distance increment divided by the total number of time frames of the recording | −9.04 105 | −7.53 103 |
| Turn ratio | TR= number of time frames when the animal turned divided by total number of time frames of the recording. A deviation from the path is considered as turn if the angle increment between two consecutive time frames exceeds 9°, i.e., 5% of a full, 180° turn | −5.33 010 | 2.04 107 |
| Erratic movement | EM= the summed product of the turn angle and the distance per time frame | 29.1 | 0.435 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






