Prerpints.org logo
Preprint
Article

Finite Element Analysis (FEA) for Evaluation of Retention in a Conometric Connection for the Implant and Prosthesis.

Altmetrics

Downloads

111

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

20 September 2023

Posted:

21 September 2023

You are already at the latest version

Alerts
Abstract
Today, dental implantology is a reliable technique for the treatment of partial and total edentulism. The fixing of dentures on dental implants can be achieved by a number of different techniques. The choice of technique depends on the specific needs of the patient, the condition of the jawbone and the design of the prosthesis itself. Currently, the two most common types of prosthetic abutment connections are cemented or screwed connections, both of which have disadvantages and ad-vantages. The aim of this study is to analyze, with Finite Element Analysis (FEA), a new Cone Morse connection system between the prosthesis and implant. The connection retention has been analyzed by adopting three different approaches: analytical, in vitro and the FEA method. The systems formed by abutment, healing-cap, and crown with three different inclination conditions were modeled in 3D: 0°, 15° and 30°. With Ansys finite element software, the effect of tilt on system retention was studied. The FEA analysis showed comparable results with in vitro studies regarding the retention strength for an abutment-cap system with a taper of 4°, obtaining 66.6 N compared to 68 N calculated through an in vitro study. The inclination of the abutment affects the retention of the system because the hole made on the surface of the abutment, decreases the contact area between the components. The Cone Morse prosthesis implant connection system is the most stable and efficient system compared to the threaded or cemented system. Retention is influenced by factors such as abutment conicity, insertion strength and the contact surface be-tween components.
Keywords: 
Subject: Medicine and Pharmacology  -   Dentistry and Oral Surgery

1. Introduction

Implantology can be considered a safe method to solve problems of partial and total edentulism especially in patients with advanced age [1,2]. In modern implantology there are two diverse types of implant prosthesis support, which depend on the number and position of the implants. Treatment options include fixed or removable implant-prosthesis support. The removable prosthesis implant support consists of a prosthesis that is anchored to the implant with diverse ways of fixation: with screw or cemented. However, the two fixation systems have some disadvantages [3]. Although the use of cemented fixation seems ideal, the disadvantage lies in having to eliminate excess cement in the soft tissues around the implant structure. Some studies [4-9] have linked residual cement and the development of chronic peri-implant diseases, since residual cement could cause soft tissue inflammation and the relative resorption of the bone crest. Another problem is the removal of cement if the margins are located sub-gingivally. The greater the depth, the more difficult it is to detecting excess cement. In vitro studies have shown that it is possible to eliminate excess cement when the margin is positioned between 1.5 and 3mm apical at the soft tissue margin [10]. The screwed connection, on the other hand, involves greater complications, the inadequate preload of the screw, the misfit between the interface of the two components and the characteristics of the screw are considered to be the reasons that lead to the loosening of the screw or even fractures [11,12]. In a recent publication, Degidi et al. [13] proposed the use of the Morse cone connection between abutments and prostheses. This type of connection presents an interesting alternative thanks to its advantages compared to cemented or screwed connections. Since their introduction, their efficacy and benefits have been proved by many studies [14,15,16]. This type of connection consists in the coupling of two surfaces that have the same conicity: abutment (male) and cap (female) that are inserted compared to those without the use of screw or concrete (Figure 1).
When force is applied from the outside, retention occurs thanks to the friction that is formed between the two surfaces [17]. By analyzing the conometric connection system, the conformation of the abutment influences the retentive ability. It has been found that the greater the diameter at the base and the height, the greater the retentive ability from a study [18]. Applying a force from the outside in the direction coinciding with the axis of insertion of the cap, stress and deformation fields are generated that affect both the inside of the cap and the abutment. Such stress fields will remain even when the insertion force is removed. It is precisely these fields of stress and deformation that supply the retentive ability of the system. From studies conducted [19,20] it has been seen how the retentive force is inversely proportional to the taper angle of the cap, that is, the greater the angle and the lower the retentive force. Through a numerical-mathematical evaluation performed by Sinan Muftu et al. [19], the efficiency of the cone morse connection was evaluated given by the ratio insertion force and simplified extraction force in the following equation (1):
η = 2 cos ⁡ θ μ k μ k cos ⁡ θ − sin ⁡ θ
In order for the cap-to-abutment connection to be stable, efficiency η must be greater than 1, which means that the extraction force Fout is greater than the insertion force Fin and, therefore, there is no possibility of spontaneous loosening occurring. If we use the studies conducted by Sinan Muftu et al. [19] as a reference and consider equation (1), it is noted that efficiency is influenced by the taper angle and the coefficient of friction between the two surfaces. Therefore, an increase in the taper angle leads to a decrease in efficiency, in fact, the efficiency goes from about 1.6 with a taper angle of 2.5° to about 0.5 with a taper angle of 10° [20]. With regard to the coefficient of friction, on the other hand, the efficiency goes from 1.5 with a coefficient equal to 0.25 to about 1.8 with a coefficient equal to 0.85 [20]. From these first results, it is clear that to have suitable stability of the system it is necessary to have taper angles of less than 6° and a friction coefficient of about 0.3. With regards to the concept previously explained, retention is guaranteed by the presence of an adequate stress field in the absence of applied load. It should be noted that in order for the system to be efficient, the stresses caused by the insertion of the cap must not exceed the yield strength of the material [21]. A last aspect to consider concerns the insertion force which, due to the conical geometry of the system, generates contact pressures at the abutment cap interface of the resulting N according to equation 2 [19,20,21].
N = π E Δ z L c sin ⁡ 2 θ 6 b 2 2 3 b 2 2 − r a b 2 − L c sin ⁡ θ 3 r a b + L c sin ⁡ θ
Looking at the formula you can see how it is influenced by the taper angle θ and the length of the surfaces in contact L c . An increase of L c , leads to an increase in the retentive capacity of the system, in a linear manner for lengths between 1 mm and 5 mm [21]. From these first observations, we understand how the insertion force of the cap plays a fundamental role in defining the stability of the system, in the first place this force must be sufficient to firmly house the cap and, therefore, supply resistance to extraction forces. Secondly, it should avoid excessive plastic deformation of the cap and abutment due to interference. The analytical method to detect this force [21] has limitations because it is obtained according to severe restrictions as the cyclic loads of mounting and dismantling the cap leading to surface erosion phenomena, consequently decreasing the retention of the system [22], are not considered. In vitro studies have established that the connection has a retention that varies with the taper angle: 40.36 N for a taper angle of 6° and 235 N for an angle of 1° [23]. The aim of this study is to evaluate, through the finite element method (FEA), the force with which the cap must be inserted into a conometric connection of 4° and the effect that the inclination of the abutment (15°, 30°) has on the retention of the system and to compare the FEA results with the analytical ones presented by [19] and experimental [23] in order to assess which method is most suitable. The advantage of using the FEA method compared to other methods is that many factors that can influence system retention can be evaluated simultaneously in less time. Moreover, when comparing the vitro studies and the FEM method we can presume that the first is a destructive procedure as it foresees breaking the device to find the resistance limit, while the second has the advantage of being a non-destructive technique. The null hypothesis is to assume that the inclination of the abutment and the presence of the hole on the surface of the abutment (Figure 2) to insert the retention screw does not affect the performance of the system.

2. Materials and Methods

Three different systems, composed of the abutment and the cap of the AoN implant (AoN Implants, Grisignano di Zocco, Vicenza, Italy), were modeled using Autodesk Inventor 3D software, and afterwards, imported into ANSYS Workbench 2023. Figure 3 shows the abutment-cap and crown system in the 0° tilt configuration.
Figure 4 shows the 15° and 30° configurations of the cap-abutment system.
Finite element analysis was used to analyze the stress distribution on the abutment-cap system during cap insertion. The virtual models made with Autodesk Inventor have been converted to a .stp format, readable by the FEA analysis software Ansys Workbench (ANSYS Inc., Canonsburg, PA, USA). The implemented geometry did not consider the implant since the analysis of this study focuses on the cap-abutment connection zone. The FEA study involves performing the following steps:
  • Model creation: Start by creating a digital model of the structure or part to be analyzed. This model is divided into smaller parts called finite elements. Finite elements are simple geometric shapes such as triangles or quadrilaterals in 2D and tetrahedra or hexagons in 3D.
  • Definition of material properties: Each finite element has associated material properties, such as Young's modulus, Poisson's coefficient, strength, and other characteristics that depend on the material from which the part is made.
  • Application of loads: Loads are defined, such as forces, moments, pressures, constraints, and boundary conditions that simulate the real environment in which the structure runs.
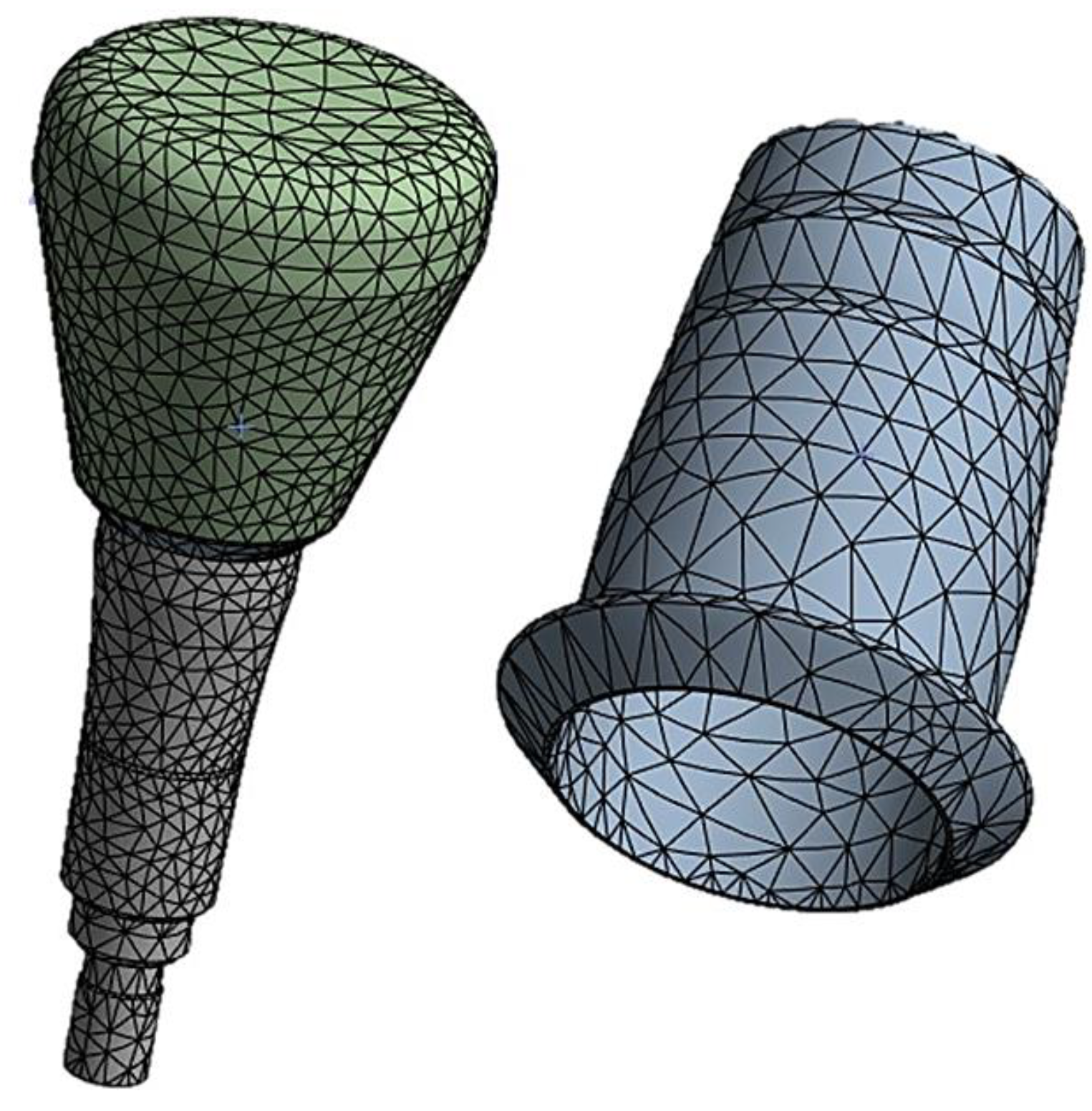
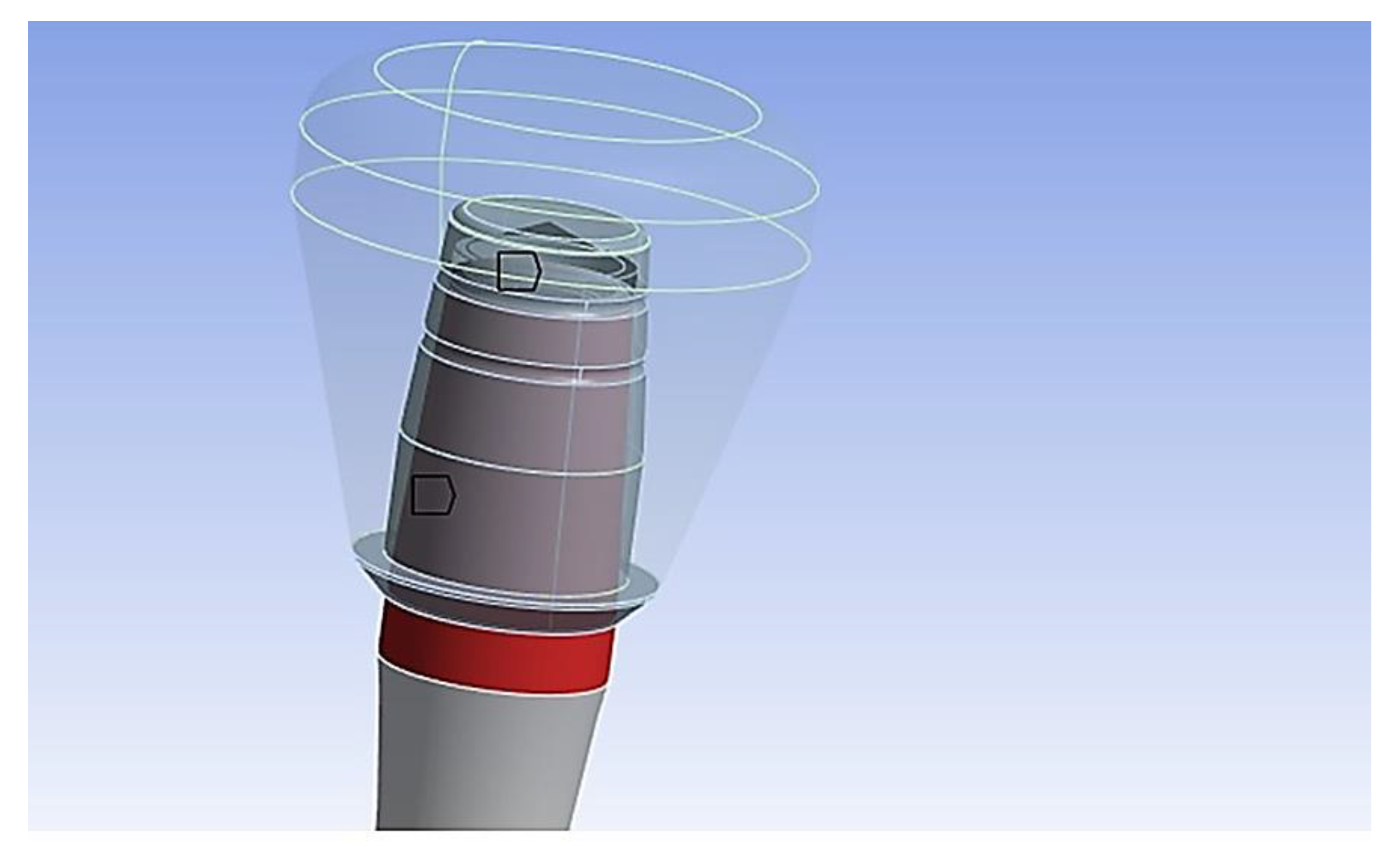
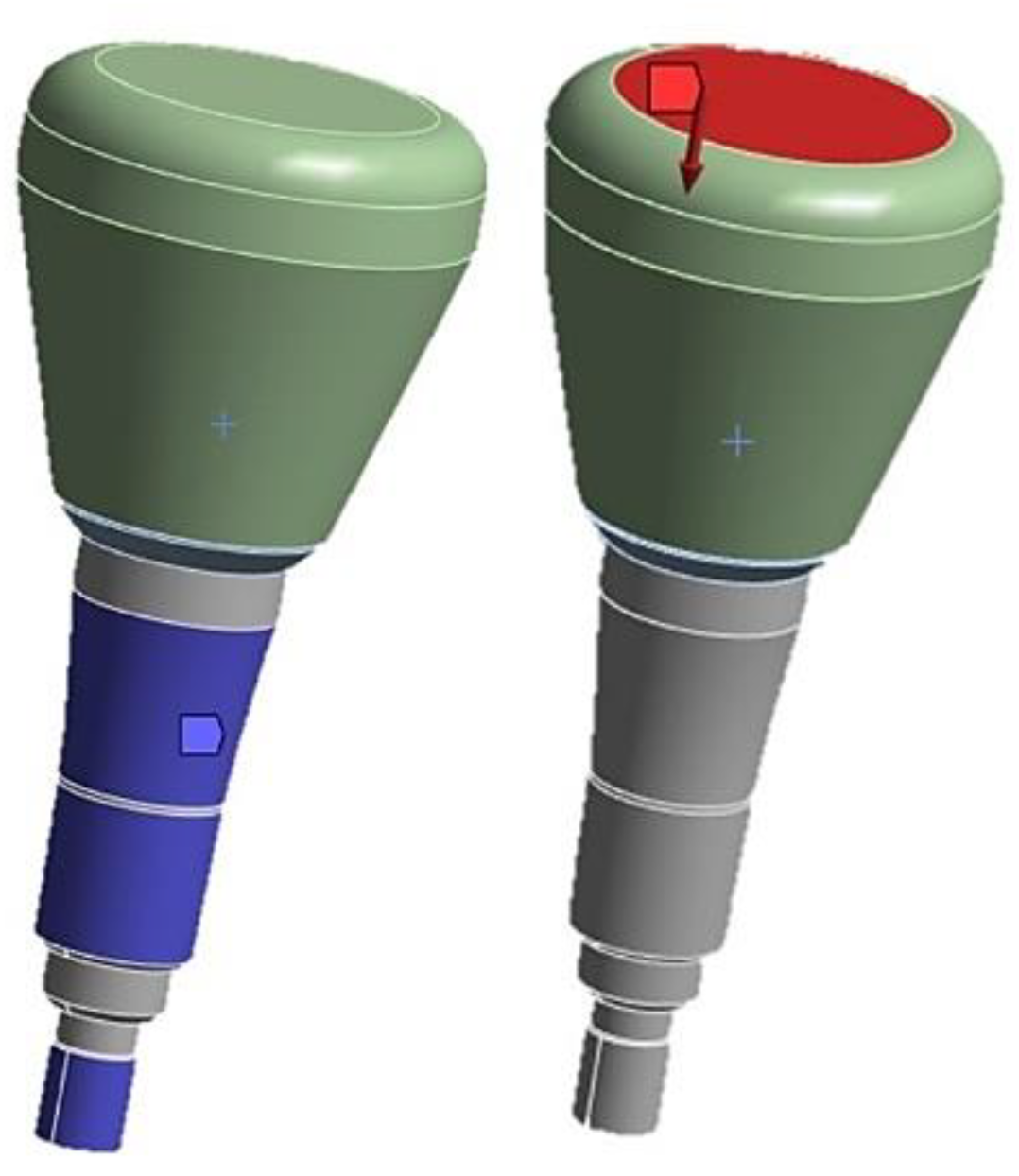
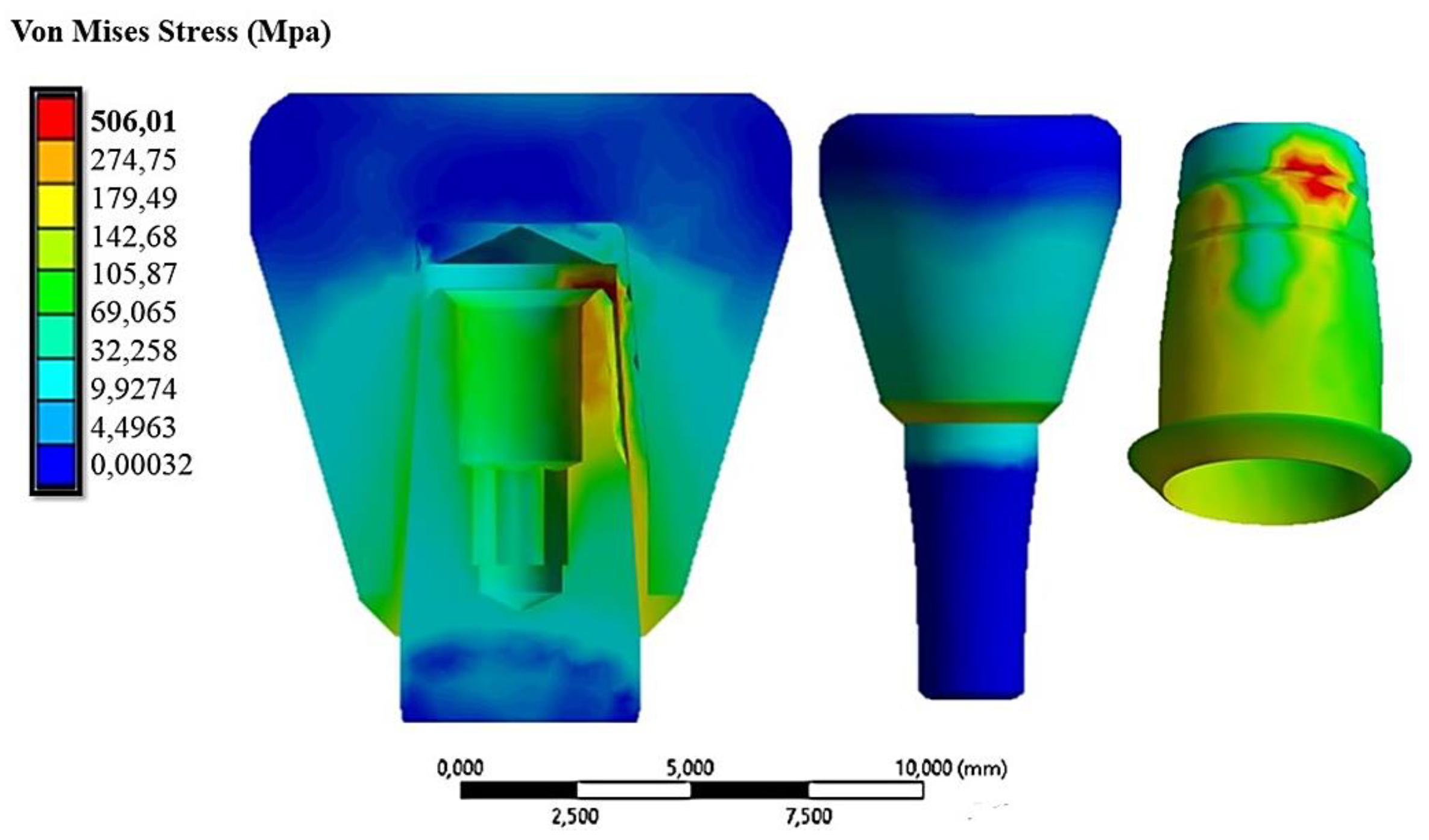
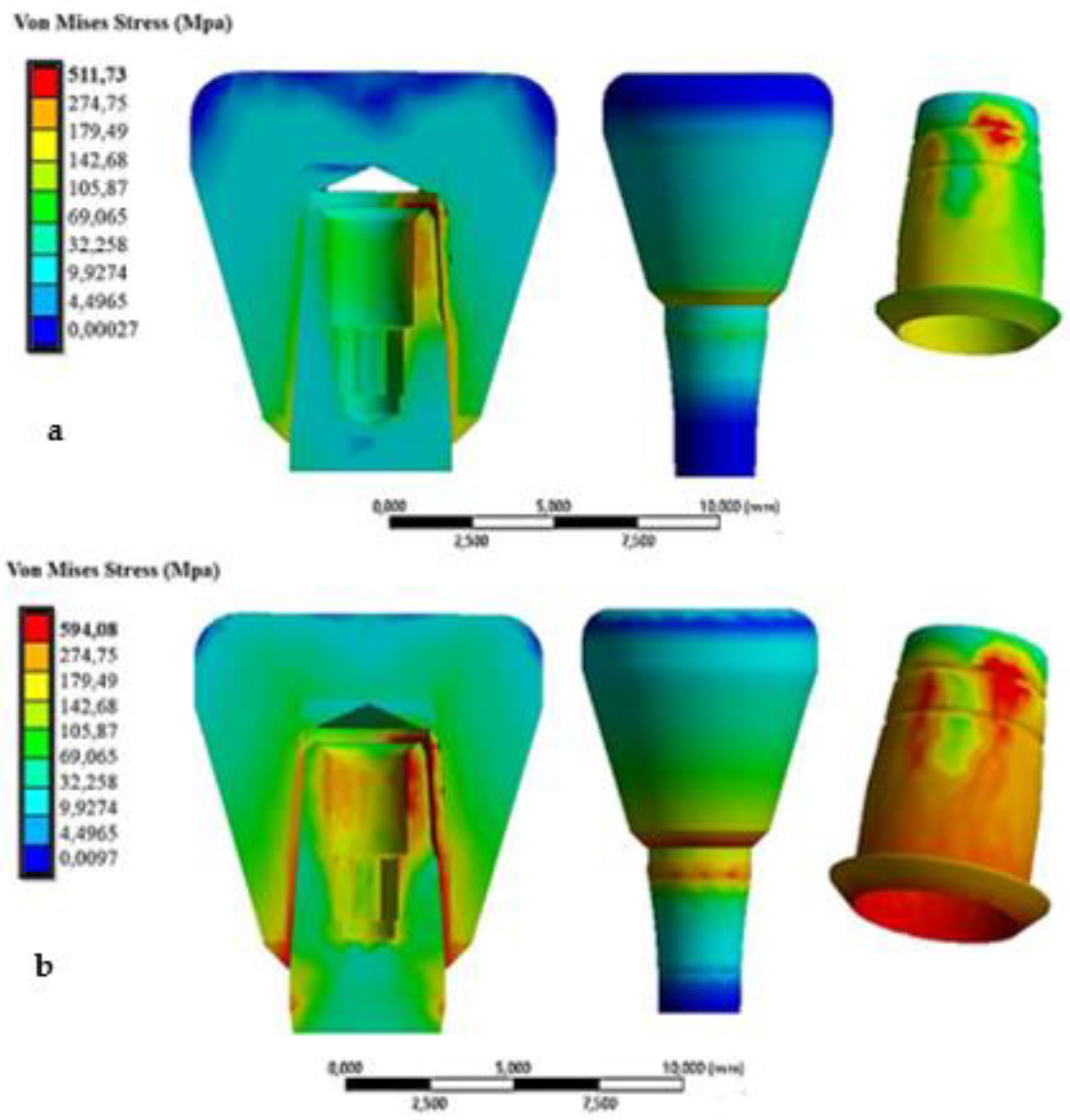
  • Discretization: The model is divided into finite elements and the nodes of these elements are assigned unknown variables being displacements, stresses, or other amounts of interest. Subsequently, the load/constraint conditions are assigned, and the results are analyzed. The cap-abutment model was discretized using Solid 187 4-knot tetrahedral elements using a 0.5 mm mesh [24]. At the abutment-cap contact, to better appreciate the stress distribution, the mesh was reduced to 0.3 mm (Figure 5).
After modeling the finite elements of the system, the properties of the materials used in this study were assigned. All materials have been considered homogeneous, linear, and isotropic, since the hypothesis in which the Von-Mises criterion used to analyze the results is based, assumes these considerations [25]. The properties of the materials are shown in Table 1 [26,27].
To analyze the cap-abutment system, the following contact modes between the two components were assigned (Figure 6).
Between the crown and the cap, on the other hand, a fixed type of contact was imposed without penetration. The contact analysis cap has been assigned the target element. "Target elements" (red) refer to finite elements in an FEA analysis that are considered particularly important or relevant to the analysis aim, while the "contact elements" model the contact surfaces between the parts (blue). The abutment was fully constrained, applying constraints on its side surface as shown in Figure 5. Whereas on the upper surface of the crown, a vertical load was applied along the direction of insertion of the cap with variable intensity between 10 N and 60 N. For this load it was considered to take as reference the hood insertion loads obtained from in vitro studies [29] (Figure 7).
For the analysis of the results, three methodologies were used in this study in order to decide which of the three supplies the reliable results. The first method used is an analytical method proposed by Muftu [19], with the aim of calculating the retention force of the cap knowing only the parameters related to the taper and the coefficient of friction. Using equation 1 the following data can be assumed: θ =4°, μ s =0,3= μ k . The efficiency of the system can be calculated as follows equation (3):
η = 2 cos ⁡ θ μ k μ k cos ⁡ θ − sin ⁡ θ = 1.52
The second method used is an experimental method proposed by Jose et al. [23] in which by using the graph obtained through in vitro tests, it is possible to calculate the retention of the system knowing only the conicity of the abutment (Figure 8).
The third method used is the FEA proposed in this study to compare results. In which from the application of the cap insertion load, we can evaluate both the Von-Mises Stress distribution and the axial displacements of the cap Δ z along the insertion direction. Using equation 4 the retention of the system can be calculated:
F r = π E Δ z L c sin ⁡ 2 θ 6 b 2 2 3 b 2 2 − r a b 2 − L c sin ⁡ θ 3 r a b + L c sin ⁡ θ
The data necessary for the calculation can be obtained thanks to the 3D model developed with inventor (AoN Implants, Grisignano di Zocco, Vicenza, Italy),   r a b =1,414 mm   b 2 =1,850 , L c =5mm, θ =4° μ s =0,3
After modeling with ANSYS software, the Von-Mises stress values were evaluated in the case of a non-angled and angled system of 15° and 30° respectively. Stress distributions are represented by color-coded maps, maximum stress in red and minimum stress in blue for qualitative analysis.

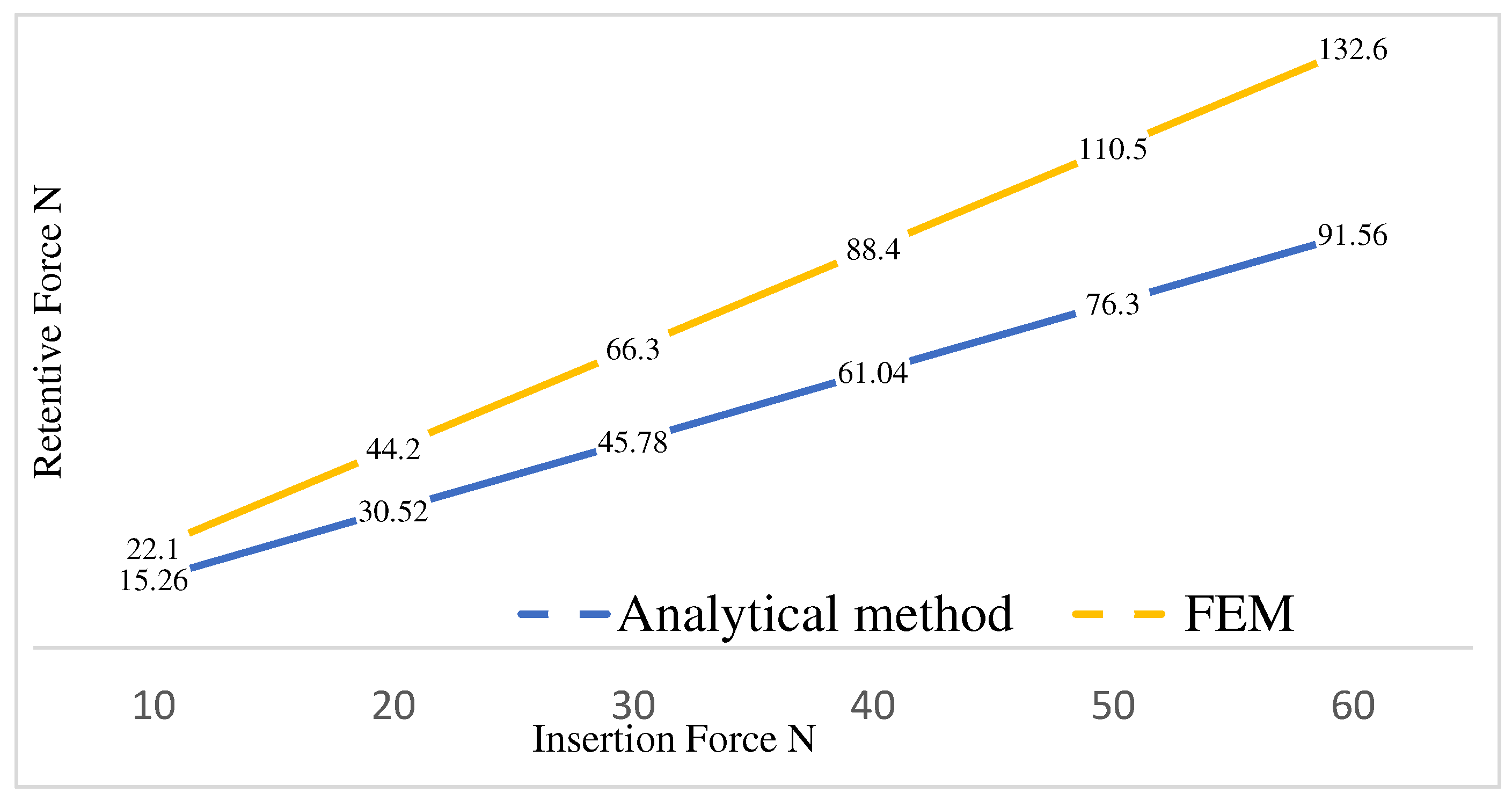
3. Results

Figure 9 shows the Von-Mises stress of the crown-cap abutment system for an insertion load of 10 N.
Von-Mises stress ranges between 0.0032 MPa and 506.01 Mpa. The maximum stress values are found on the cap because of its thinness and therefore stress is increased. The figure also shows how stress values are reached that vary between 35 MPa and 120 MPa in the area of contact with the cap on the crown made of zirconium. This stress field does not impair the mechanical behavior of the material since, as described in Table 1, the breakdown stress of Zirconia is approximately 551 MPa. In Figure 10, the displacement field compared to the cap is shown because the abutment has been fixed in all directions.
From Figure 8 we see how the cap has a field of displacements that varies along the axial direction. In fact, the maximum values are reached in the lower part of the same (red zone) where there are about 0.00273 mm of displacement. This value is also comparable with the FEA study conducted by Bressan et al [31]. Figure 9 demonstrates the stress distribution when the cap is inserted with a force of 30N and 60N.
Here, it is seen that as the coat insertion force increases, there is also an increase in the stresses on the system. In fact, it goes from about 511.73 MPa with an insertion of 30N to 594.08 MPa with an insertion of 60N. From this first analysis, it is clear that the most stressed part is the 594.08 MPa cap. This stress value, however, does not compromise the mechanical behavior of the hood since the resistance of the latter to yield strength is about 830 Mpa table 1. Also, from Figure 12 it is shown how on the abutment the stresses are higher in the case of an insertion with 60N of the cap. In fact, the circumferential stresses exerted by forcing increase the compressive stress on the outer surface of the abutment. Table 2 summarizes the results obtained (Von-Mises stress) and displacement along z of the hood for insertion loads varying between 10 N and 60 N.
Table 2 shows that as the insertion force increases, both an increase in the displacement of the cap and the Von Mises stress correspond. It can be said that there are no critical issues in the system as the yield strength of the 830 Mpa material for Titanium is never exceeded. Knowing both the insertion force and the vertical displacement of the cap, we can calculate the retention force for each load condition of the cap thanks to equation 2 and obtain the orange line in graphic 13.
Using the analytical method proposed by Muftu et al. [19] the blue line is obtained (Figure 13). It is seen that the analytical method, due to the multiple simplifications performed in the geometry, has lower values of removal force as a function of the insertion force. Observing the experimental method proposed by Jose L. et al. [23] for an insertion of the cap with a load of 30 N, it corresponds to a removal force of about 70 N (Figure 14).
From the three criteria presented, it is noted that the FEA finite element method has results closer to the values obtained experimentally through in vitro studies. In fact, for an insertion of the cap with 30 N using the FEA method there is about 66.3 N of retention force, using the analytical method there is 45.78 N, compared to the value of 68.8N obtained from in vitro studies. The time effect of tilt is studied using the same load data as above. Figure 15 shows the distribution of Von-Mises stress if the cap is inserted with a load of 10 N,30N and 60N in the 15° configuration.
From Figure 15, we can see how the 15° inclination of the abutment leads to an increase in stresses on the abutment and cap. In fact, considering the red areas, we notice that the maximum stress varies between 621.45 MPa with 10 N of insertion up to 645 Mpa with 60 N of insertion on the cap. In Figure 16 we can see that the Von Mises stress distribution is higher than in the case of 15°.
This is due to the fact that the inclination involves a decomposition of the forces also along the direction perpendicular to the axis of insertion of the cap. These tangential forces stress the abutment more, in fact in the configuration of 30 ° with a cap insertion force of 60 N stress values of about 756 Mpa are recorded on the abutment and on the lower part of the cap (figure 16 c). We can therefore say that the configuration of the abutment inclined at 30° registers higher stresses than the 15° and 0° configuration. By analyzing exclusively with the FEA method, we can calculate the retention of the system in the configurations of inclined abutments and compare it with the non-inclined configuration of the abutment (Figure 17).
From graph (Figure 17) shows how the retention at the same insertion force decreases with the inclination of the abutment. In fact, assuming that the cap is inserted with a force of 30 N, it is seen that in the case of no inclination, we have 66.3 N compared to 57.018 N for abutments inclined at 15 ° and 53.04 N for abutment inclined at 30 °. This phenomenon is because the hole for the insertion of the retention screw decreases the amount of surface that can be used for contact with the cap and therefore, there is a decrease in the retention ability of the system. Hence, it can be said that in order to have the same retention required by in vitro studies or about 70 N, it is necessary to increase the insertion force by about 10 N more than the non-inclined configuration where inclined abutments are concerned.

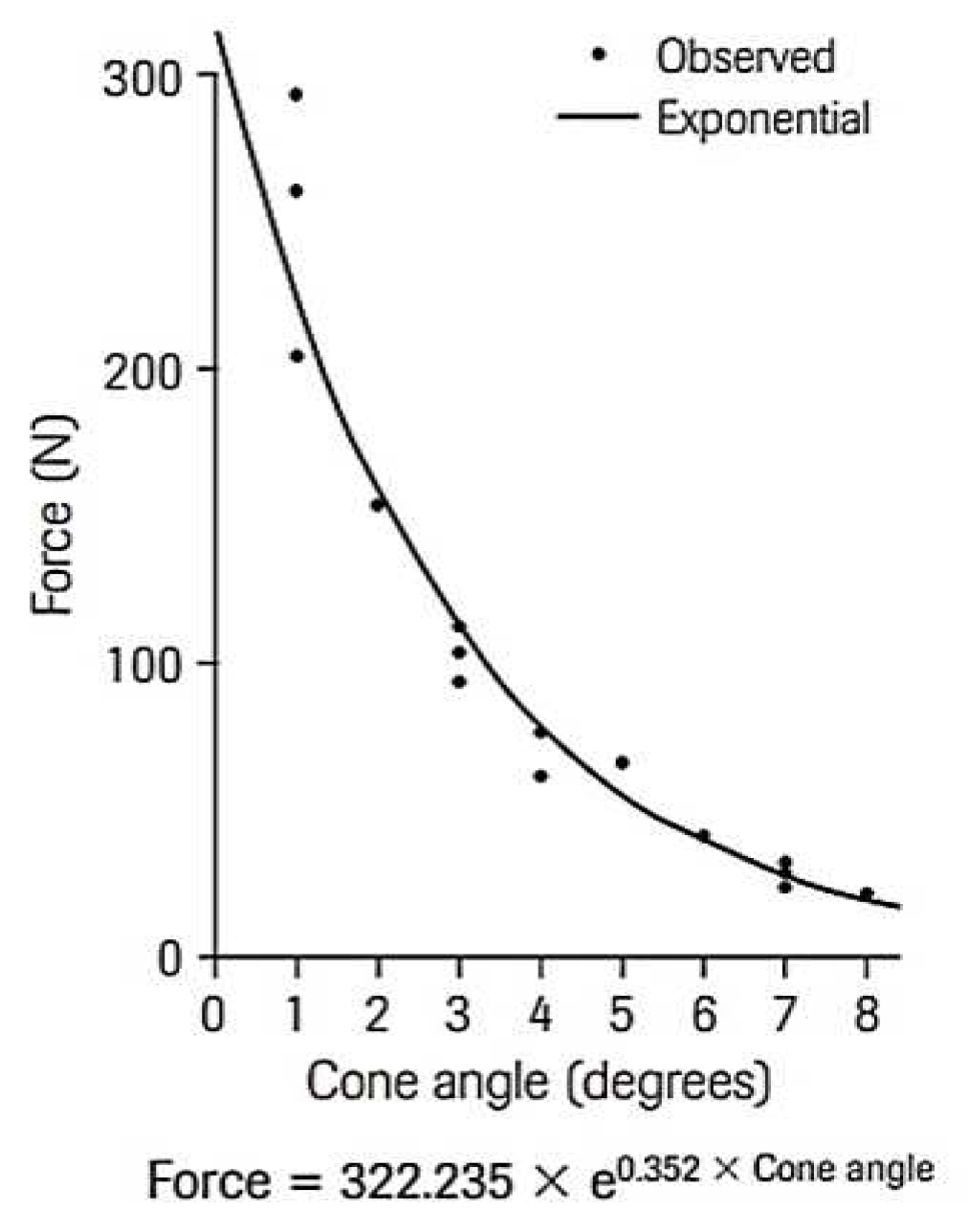
4. Discussion

The FEA method shown in this study has also been used in other works [32-35] to investigate the effect of the connection type on stress in the implant and surrounding bone. In particular, as has been seen by [29] the use of a screwed type of implant prosthesis retention system presented less stress than the conventional system with the use of cement. The explanation of this phenomenon is due to the fact that in the case of a screwed system, there are several separate components including: the implant, the abutment, the prosthetic screw, and the crown. The micro-gap does not guarantee a uniform stress distribution between the components and the implant. Therefore, it was concluded that in a cemented retention system, the stresses and deformations were higher. Also, photo-elastic studies [32,33] have shown this phenomenon and have found that the gap between the components of the implant can reduce or increase the stress that is transmitted to the bone due to micro-movements. Although the use of a retention system with screw can cause bone resorption due to the insufficiency of stress transmitted, in the case of a cemented connection, the stress generated by the masticatory load could discharge directly on the bone, rather than being dissipated between the prosthetic components. These factors can increase stress on the bone leading it to resorption. In fact, as was shown in a study [34] when the stress generated in the crestal area of the implant exceeds the elasticity of the bone, microfractures and resorption occur. Screwed prosthetics have the advantage of being removed without damaging the denture or implant with the only negative being the execution of the hole on the crown to insert the screw creates aesthetic problems and risks of fracture. Thanks to the conometric system, dental prostheses can reduce pressure on the surrounding gum tissue, helping to prevent long-term damage or irritation. In particular, SEM analyses analyzed the interface between cap and abutment, seeing that even after the application of the load, a relevant gap was not shown [35]. This leads to the following benefits, including a reduced risk of bacterial infiltration and more evenly transmitted stress. In the conometric connection, retention is given only by the frictional force that develops at the abutment-cap interface. The perfect fit between the two surfaces and the absence of marginal gap of the conometric connection is a fundamental requirement to avoid failures and bacterial infiltration [36,37]. In an attempt to further reduce inflammatory responses and maximize bone stability in the crestal area of the implant, many in vitro studies [38-40] have defined that in the conometric connection, the gap between abutment and cap (2.04-2.064 micron) was considered necessary to avoid bacterial infiltration phenomena. On the other hand, in the case of a cemented connection between abutment and cap, a gap of (145 microns) was seen [40]. Another problem is related to the removal of the prosthesis. Through a study by Degidi et al. [41] it was seen how prostheses that used a conometric retention system were easily removed. In fact, conometric prostheses are designed for easy removal and cleaning making the oral hygiene and prosthesis cleaning processes easier than those for cemented or adhesive dentures which had problems due to incomplete cement removal. The success rate of conometric prostheses is an important aspect of rehabilitation. Numerous studies [42-44] have described the follow-up period, noting a 97.77% success rate during a 2-year follow-up period. System retention understood as the ability of the prosthesis to remain stable and firmly in place inside the mouth during normal use is a key factor in long-term durability. As shown in the introductory part, the retention of the conometric connection depends on the first load with which the cap is inserted, the taper angle, the height, and the friction between the two surfaces [45,46]. Insufficient retention leads to loosening of the prosthesis with the related implant problems and bacterial infection. The influence of cap insertion-separation cycles on retention ability has been evaluated by many studies [47-49]. In particular, as shown in an in vitro study [50], retention decreases by about 40% from 5 cycles to 15 insertion-removal cycles. This phenomenon is due to the fact that with the increase in the number of cycles, the functional characteristics of the surfaces in contact vary. In addition, retention is reduced even if the plastic limit of the material is exceeded, as the state of residual stress due retention is no longer guaranteed. However, when similar materials are used, a cold fusion can develop between the abutment-cap contact surface, thus ensuring greater retention. Conversely, with a softer material than the abutment there is greater wear on the inner surface of the cap and therefore less retention [51]. In the oral environment, prostheses are subject to time-varying chewing forces, temperature variations and high humidity; all factors that worsen the condition of the cement causing loss of retention. In a study [52] the retention of a cemented and conometric system was measured, highlighting how the use of the conometric system led to an increase in retention as the phenomenon of cold welding between the two components occurred. While in the case of the cemented system there was a decrease in retention due to the loss of cement performance after 5 years. The evaluation of the retention of the cap-abutment connection has always been evaluated through in vitro studies. In particular, as shown by [53] the retention varies according to the conicity of the abutment in fact it goes from 40.46 N for 6 degrees of taper to 235 N for a taper of 1 degree. Bressan et al [54] also used the FEA method to analyze the retention of a morse cone connection by seeing that in the case of a gold cap there was in vitro a retention of 148.22 N compared to 150 N obtained by numerical analysis. However, there are no clear data in the literature on the minimum retention necessary for the crown and cap to remain in a stable position. During chewing, the depressive muscles apply displacement forces to the prosthesis. Therefore, the minimum retention force must be greater than the contraction force of these depressor muscles which turns out to be about 113 N [54,55]. Thanks to a numerical study [56] a mathematical model has been developed that allows, as a function of conicity, to qualitatively know the retention offered by the system. In particular, it can be seen that the retention increases exponentially decreasing the taper angle. The other method to evaluate system retention is through the use of numerical simulation, in particular FEA finite element analysis. This method now used in most engineering and medical applications allows to accurately simulate what happens from the point of view of mechanical behavior when the cap is inserted on the abutment. The process implemented in this study allowed to evaluate the retention of the system in the case of an abutment with a taper of 4° and define the necessary force with which the cap must be inserted to have sufficient retention. Thanks to the FEA analysis, it was also possible to evaluate the effect of the inclination of the abutment on retention. Therefore, the null hypothesis has not been confirmed because the inclined abutment supplies a hole for the insertion of the screw on the mating surface. This hole decreases the surface in contact with the cap thus obtaining a decrease in the retention ability of the connection. In addition, the retention also decreases with increasing angle of inclination of the abutment as the axial loads along the abutment are also broken down according to the components: mesial, distal, and buccal that vary with inclination. It is the non-axial components function as a lever on the cap decreasing the retention of the system.

5. Conclusion

Thanks to the finite element simulation performed in this study, it was possible to calculate the activation force of the cap to ensure the retention required by the in vitro studies, both in axial and inclined positioning of the abutment. Below are the main results obtained: There is a linear relationship between cap activation force and retentive force. The analytical method of Muftu et al. underestimates system retention. The FEA method shows comparable results with in vitro studies. For a connection with 4° conicity the retentive force obtained from in vitro studies is 68N. while with FEA analysis 66N. The force to activate the connection in the case of a 4° taper is about 30N. Values below 20N of activation force do not guarantee the required retention. The inclination of the abutment decreases the retention of the system. To overcome this phenomenon, it is necessary to increase the activation force by 10 N for abutments inclined between 15° and 30°. The state of stress acting on the system is greater in the case of inclined abutments. Despite the limitations with the FEA method, the results are consistent with in vitro studies. Further studies are needed to improve the model and also consider intraoral conditions and wear phenomena that can compromise the stability of the system.

Author Contributions

Conceptualization, B.T. and L.C.; methodology, M.C., T.R. and A.S.; software, M.C.; validation, B.T., A.P. and N.D.P.; formal analysis, M.C. and A.S.; investigation, M.C. and L.C.; resources, B.T.; data curation, N.D.P.; writing—original draft preparation, L.C., A.P., M.C. and B.T.; writing—review and editing, N.D.P. and T.R.; visualization, A.P.; supervision, B.T.; project administration, A.P. and B.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All experimental data to support the findings of this study are available contacting the corresponding author upon request.

Acknowledgments

The Authors gratefully thank AoN Implants Company, Grisignano di Zocco, Vicenza, Italy, for all the mathematical data on the implants.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Heydecke, G.; Thomason, J.M.; Awad, M.A.; et al. Do mandibular implant overdentures and conventional complete dentures meet the expectations of edentulous patients? Quintessence Int 2008, 39, 803–809. [Google Scholar]
  2. Musacchio, E.; Perissinotto, E.; Binotto, P.; et al. Tooth loss in the elderly and its association with nutritional status, socio-economic and lifestyle factors. Acta Odontol Scand 2007, 65, 78–86. [Google Scholar] [CrossRef]
  3. Michalakis, K.X.; Hirayama, H.; Garefis, P.D. Cement-Retained versus Screw-Retained Implant Restorations: A Critical Review.Int. J. Oral Maxillofac. Implants 2003, 18, 719–728. [Google Scholar]
  4. Wilson, T.G. Jr. The Positive Relationship Between Excess Cement and Peri-Implant Disease: A Prospective Clinical Endoscopic Study. J. Periodontol. 2009, 80, 1388–1392. [Google Scholar] [CrossRef]
  5. Salvi, G.E.; Cosgarea, R.; Sculean, A. Prevalence and Mechanisms of Peri-Implant Diseases. J. Dent. Res. 2017, 96, 31–37. [Google Scholar] [CrossRef]
  6. Bornstein, M.M.; Lussi, A.; Schmid, B.; Belser, U.C.; Buser, D. Early Loading of Nonsubmerged Titanium Implants with a Sandblasted and Acid-Etched (SLA) Surface: 3-Year Results of a Prospective Study in Partially Edentulous Patients. Int. J. Oral Maxillofac. Implants 2003, 18, 659–666. [Google Scholar] [PubMed]
  7. Abboud, M.; Koeck, B.; Stark, H.; Wahl, G.; Paillon, R. Immediate Loading of Single-Tooth Implants in the Posterior Region. Int. J. Oral Maxillofac. Implants 2005, 20, 61–68. [Google Scholar] [CrossRef]
  8. Tan, B.; Gillam, D.G.; Mordan, N.J.; Galgut, P.N. A Preliminary Investigation into the Ultrastructure of Dental Calculus and Associated Bacteria. J. Clin. Periodontol. 2004, 31, 364–369. [Google Scholar] [CrossRef] [PubMed]
  9. Schedle, A.; Franz, A.; Rausch-Fan, X.; Andreas, S.; Lucas, T.; Samorapoompichit, P.; Sperr, W.; Boltz-Nitulescu, G. Cytotoxic Effects of Dental Composites, Adhesive Substances, Compomers and Cements. Dent. Mater. 1998, 14, 429–440. [Google Scholar] [CrossRef]
  10. Agar, J.R.; Cameron, S.M.; Hughbanks, J.C.; Parker, M.H. Cement Removal from Restorations Luted to Titanium Abutments with Simulated Subgingival Margins. J. Prosthet. Dent. 1997, 78, 43–47. [Google Scholar] [CrossRef] [PubMed]
  11. Gehrke, P.; Hartjen, P.; Smeets, R.; Gosau, M.; Peters, U.; Beikler, T.; Fischer, C.; Stolzer, C.; Geis-Gerstorfer, J.; Weigl, P.; et al. Marginal Adaptation and Microbial Leakage at Conometric Prosthetic Connections for Implant-Supported Single Crowns: An In Vitro Investigation. Int. J. Mol. Sci. 2021, 22, 881. [Google Scholar] [CrossRef]
  12. Albrektsson, T.; Canullo, L.; Cochran, D.; De Bruyn, H. “Peri-Implantitis”: A Complication of a Foreign Body or a Man-Made “Disease”. Facts and Fiction. Clin. Implant Dent. Relat. Res. 2016, 18, 840–849. [Google Scholar] [CrossRef] [PubMed]
  13. Degidi, M.; Nardi, D.; Piattelli, A. One abutment at one time: non-removal of an immediate abutment and its effect on bone healing around subcrestal tapered implants. Clin Oral Implants Res. 2011, 22, 1303–7. [Google Scholar] [CrossRef] [PubMed]
  14. Waltenberger, L.; Wolfart, S. Safety Crown: a patient-centered, fully digital concept for immediate implant restoration following the one-abutment/one-time concept-a pilot case series of a new treatment concept. Int J Implant Dent. 2022, 8(1), 35. [Google Scholar] [CrossRef]
  15. Rathi, P.R.; Kolte, R.A.; Kolte, A.P. Comparative evaluation of peri-implant tissues in definitive and repeated abutment replacements: A randomized clinical trial. J Indian Soc Periodontol. 2022, 26, 44–50. [Google Scholar]
  16. Grandi, T.; Guazzi, P.; Samarani, R.; Garuti, G. Immediate positioning of definitive abutments versus repeated abutment replacements in immediately loaded implants: effects on bone healing at the 1-year follow-up of a multicentre randomised controlled trial. Eur J Oral Implantol. 2012, 5, 9–16. [Google Scholar] [PubMed]
  17. Albiero, A.M.; Benato, R.; Momic, S.; Degidi, M. Guided-Welded Approach Planning Using a Computer-Aided Designed Prosthetic Shell for Immediately Loaded Complete-Arch Rehabilitations Supported by Conometric Abutments. J. Prosthet. Dent. 2019, 122, 510–515. [Google Scholar] [CrossRef]
  18. Nardi, D.; Degidi, M.; Sighinolfi, G.; Tebbel, F.; Marchetti, C. Retention Strength of Conical Welding Caps for Fixed Implant Supported Prostheses. Int. J. Prosthodont. 2017, 30, 553–555. [Google Scholar] [CrossRef] [PubMed]
  19. Bozkaya, D.; Müftü, S. Efficiency considerations for the purely tapered interference fit (TIF) abutments used in dental implants. J Biomech Eng. 2004, 126, 393–401. [Google Scholar] [CrossRef]
  20. Prisco, R.; Troiano, G.; Laino, L.; Zhurakivska, K. Rotational tolerances of a titanium abutment in the as-received condition and after screw tightening in a conical implant connection. J Adv Prosthodont. 2021, 13, 343–350. [Google Scholar] [CrossRef]
  21. Aguirrebeitia, J.; Abasolo, M.; Müftü, S.; Vallejo, J. Influence of design and clinical factors on the removal force ratio in tapered implant-abutment interfaces. J Prosthet Dent. 2017, 117, 493–498. [Google Scholar] [CrossRef]
  22. Tuna, S.H.; Al-Chalabi, Z.S.; Kozak, E. Evaluation of the Effects of Repeated Insertion-Removal Cycles on the Retention of an Indexed Conometric Connection. Int J Oral Maxillofac Implants 2022, 37, 549–555. [Google Scholar] [CrossRef]
  23. Antonaya-Martin, J.; Del Rio-Highsmith, J.; Moreno-Hay, I.; Lillo-Rodríguez, J.; Gomez-Polo, M.; Celemin-Viñuela, A. CAD/CAM Conic Crowns for Predictable Retention in Implant-Supported Prostheses. Int. J. Prosthodont. 2016, 29, 230–232. [Google Scholar] [CrossRef] [PubMed]
  24. Brunski, J.B. In vivo bone response to biomechanical loading at the bone/dental-implant interface. Adv. Dent. Res. 1999, 13, 99–119. [Google Scholar] [CrossRef] [PubMed]
  25. Lanza, A.; Ruggiero, A.; Sbordone, L. Tribology and dentistry: a commentary. Lubricants 2019, 7, 52. [Google Scholar] [CrossRef]
  26. Di Pietro, N.; Ceddia, M.; Romasco, T.; De Bortoli Junior, N.; Mello, B.F.; Tumedei, M.; Specchiulli, A.; Piattelli, A.; Trentadue, B. Finite Element Analysis (FEA) of the Stress and Strain Distribution in Cone-Morse Implant–Abutment Connection Implants Placed Equicrestally and Subcrestally. Appl. Sci. 2023, 13, 8147. [Google Scholar] [CrossRef]
  27. Cipollina, A.; Ceddia, M.; Di Pietro, N.; Inchingolo, F.; Tumedei, M.; Romasco, T.; Piattelli, A.; Specchiulli, A.; Trentadue, B. Finite Element Analysis (FEA) of a Premaxillary Device: A New Type of Subperiosteal Implant to Treat Severe Atrophy of the Maxilla. Biomimetics 2023, 8, 336. [Google Scholar] [CrossRef]
  28. Lee, J.H.; Jang, H.Y.; Lee, S.Y. Finite Element Analysis of Dental Implants with Zirconia Crown Restorations: Conventional Cement-Retained vs. Cementless Screw-Retained. Materials (Basel) 2021, 14, 2666. [Google Scholar] [CrossRef]
  29. Kapos, T.; Evans, C. CAD/CAM technology for implant abutments, crowns, and superstructures. Int J Oral Maxillofac Implants 2014, 29, 117–36. [Google Scholar] [CrossRef]
  30. Mehl, C.; Harder, S.; Steiner, M.; Vollrath, O.; Kern, M. Influence of cement film thickness on the retention of implant-retained crowns. J Prosthodont. 2013, 22, 618–25. [Google Scholar] [CrossRef]
  31. Bressan, E.; Lops, D. Conometric Retention for Complete Fixed Prosthesis Supported by Four Implants: 2-Years Prospective Study. Clin. Oral Implants Res. 2014, 25, 546–552. [Google Scholar] [CrossRef]
  32. Mohanty, A.K.; Varghese, T.; Bhushan, P.; Mahapatro, R.K.; Kashi, A.B.; Kariyatty, P. Influence of Occlusal Stress on Implant Abutment Junction and Implant Bone Interface: A Finite Element Analysis Study. J Contemp Dent Pract. 2022, 23, 1190–1194. [Google Scholar] [PubMed]
  33. Ochiai, K.T.; Ozawa, S.; Caputo, A.A.; Nishimura, R.D. Photoelastic stress analysis of implant-tooth connected prostheses with segmented and nonsegmented abutments. J. Prosthet. Dent. 2003, 89, 495–502. [Google Scholar] [CrossRef] [PubMed]
  34. Aalaei, S.; Rajabi Naraki, Z.; Nematollahi, F.; Beyabanaki, E.; Shahrokhi Rad, A. Stress distribution pattern of screw-retained restorations with segmented vs. non-segmented abutments: A finite element analysis. J. Dent. Res. Dent. Clin. Dent. Prospect. 2017, 11, 149–155. [Google Scholar] [CrossRef]
  35. Sato, Y.; Shindoi, N.; Hosokawa, R.; Tsuga, K.; Akagawa, Y. A biomechanical effect of wide implant placement and offset placement of three implants in the posterior partially eden-tulous region. J. Oral Rehabil. 2000, 27, 15–21. [Google Scholar] [CrossRef] [PubMed]
  36. Gehrke, P.; Fischer, C.; Weinhold, O.; Dhom, G. Das konometrische Konzept für implantatgetragene Einzelkronen: die definitive Befestigung ohne Zement oder Schrauben. ZWR – Das Deutsche Zahnärzteblatt 2021, 130, 1–7. [Google Scholar] [CrossRef]
  37. Canullo, L.; Peñarrocha, M.; Monje, A.; Catena, A.; Wang, H.-L.; Peñarrocha, D. Association Between Clinical and Microbiologic Cluster Profiles and Peri-Implantitis. Int. J. Oral Maxillofac. Implants 2017, 32, 1054–1064. [Google Scholar] [CrossRef]
  38. Caricasulo, R.; Malchiodi, L.; Ghensi, P.; Fantozzi, G.; Cucchi, A. The Influence of Implant-Abutment Connection to Peri-Implant Bone Loss: A Systematic Review and Meta-Analysis. Clin. Implant Dent. Relat. Res. 2018, 20, 653–664. [Google Scholar] [CrossRef]
  39. Gehrke, P.; Burg, S.; Peters, U.; Beikler, T.; Fischer, C.; Rupp, F.; Schweizer, E.; Weigl, P.; Sader, R.; Smeets, R.; Schäfer, S. Bacterial translocation and microgap formation at a novel conical indexed implant abutment system for single crowns. Clin Oral Investig. 2022, 26, 1375–1389. [Google Scholar] [CrossRef]
  40. Gehrke, P.; Bleuel, K.; Fischer, C.; Sader, R. Influence of margin location and luting material on the amount of undetected cement excess on CAD/CAM implant abutments and cement-retained zirconia crowns: an in-vitro study. BMC Oral Health. 2019, 19, 111. [Google Scholar] [CrossRef]
  41. Degidi, M.; Nardi, D.; Sighinolfi, G.; Degidi, D. The conometric concept for the definitive rehabilitation of a single posterior implant by using a conical indexed abutment: A technique. J Prosthet Dent. 2020, 123, 576–579. [Google Scholar] [CrossRef]
  42. Degidi, M.; Nardi, D.; Piattelli, A. The Conometric Concept: Coupling Connection for Immediately Loaded Titanium-Reinforced Provisional Fixed Partial Dentures—A Case Series. Int. J. Periodontics Restor. Dent. 2016, 36, 347–354. [Google Scholar] [CrossRef] [PubMed]
  43. Degidi, M.; Nardi, D.; Sighinolfi, G.; Degidi, D.; Piattelli, A. The Conometric Concept: A two-year follow-up of fixed partial cerec restorations supported by cone-in-cone abutments. J. Prosthodont. 2019, 28, 780–787. [Google Scholar] [CrossRef]
  44. Lian, M.; Zhao, K.; Feng, Y.; Yao, Q. Prognosis of Combining Remaining Teeth and Implants in Double-Crown-Retained Removable Dental Prostheses: A Systematic Review and Meta-Analysis. Int J Oral Maxillofac Implants. 2018, 33, 281–297. [Google Scholar] [CrossRef] [PubMed]
  45. Stefano, M.D.; Ruggiero, A. Real contact area and friction: an overview of different approaches. Industrial Tribology, CRC Press, 2022, 1–23.
  46. Beuer, F.; Edelhoff, D.; Gernet, W.; Naumann, M. Parameters Affecting Retentive Force of Electroformed Double-Crown Systems. Clin. Oral Investig. 2010, 14, 129–135. [Google Scholar] [CrossRef] [PubMed]
  47. Zhang, R.-G.; Hannak,W. B.; Roggensack, M.; Freesmeyer,W.B. Retentive Characteristics of Ankylos SynCone Conical Crown System over Long-Term Use in Vitro. Eur. J. Prosthodont. Restor. Dent. 2008, 16, 61–66. [Google Scholar]
  48. Mangano, F.; Macchi, A.; Caprioglio, A.; Sammons, R.L.; Piattelli, A.; Mangano, C. Survival and complication rates of fixed restorations supported by locking-taper implants: a prospective study with 1 to 10 years of follow-up. J Prosthodont. 2014, 23, 434–44. [Google Scholar] [CrossRef]
  49. Tuna, S.H.; Al-Chalabi, Z.S.; Kozak, E. Evaluation of the Effects of Repeated Insertion-Removal Cycles on the Retention of an Indexed Conometric Connection. Int J Oral Maxillofac Implants 2022, 37, 549–555. [Google Scholar] [CrossRef]
  50. Kubo, K.; Koike, T.; Ueda, T.; Sakurai, K. Influence of the mechanical properties of resilient denture liners on the retention of overdenture attachments. J Prosthet Dent. 2018, 120, 431–438. [Google Scholar] [CrossRef]
  51. Türk, P.E.; Geckili, O.; Türk, Y.; Günay, V.; Bilgin, T. In vitro comparison of the retentive properties of ball and locator attachments for implant overdentures. Int J Oral Maxillofac Implants 2014, 29, 1106–13. [Google Scholar] [CrossRef]
  52. Al-Chalabi, Z.S.; Tuna, H.S. The effect of thermomechanical aging on the retention of a conometric system in a chewing simulator. J. Prosthodont. 2023, 1–8. [Google Scholar] [CrossRef] [PubMed]
  53. Ghodsi, S.; Zeighami, S.; Meisami, A.M. Comparing Retention and Internal Adaptation of Different Implant-Supported, Metal-Free Frameworks. Int J Prosthodont. 2018, 31, 475–477. [Google Scholar] [CrossRef]
  54. Bressan, E.; Lops, D. Conometric retention for complete fixed prosthesis supported by four implants: 2-years prospective study. Clinical oral implants research. 2013. [Google Scholar] [CrossRef] [PubMed]
  55. Schriwer, C.; Skjold, A.; Gjerdet, N.R.; Øilo, M. Monolithic Zirconia Dental Crowns. Internal Fit, Margin Quality, Fracture Mode and Load at Fracture. Dent. Mater. 2017, 33, 1012–1020. [Google Scholar] [CrossRef]
  56. Howes, D. Angled Implant Design to Accommodate Screw-retained Implant-supported Prostheses. Compend Contin Educ Dent. 2017, 38, 458–463. [Google Scholar] [PubMed]
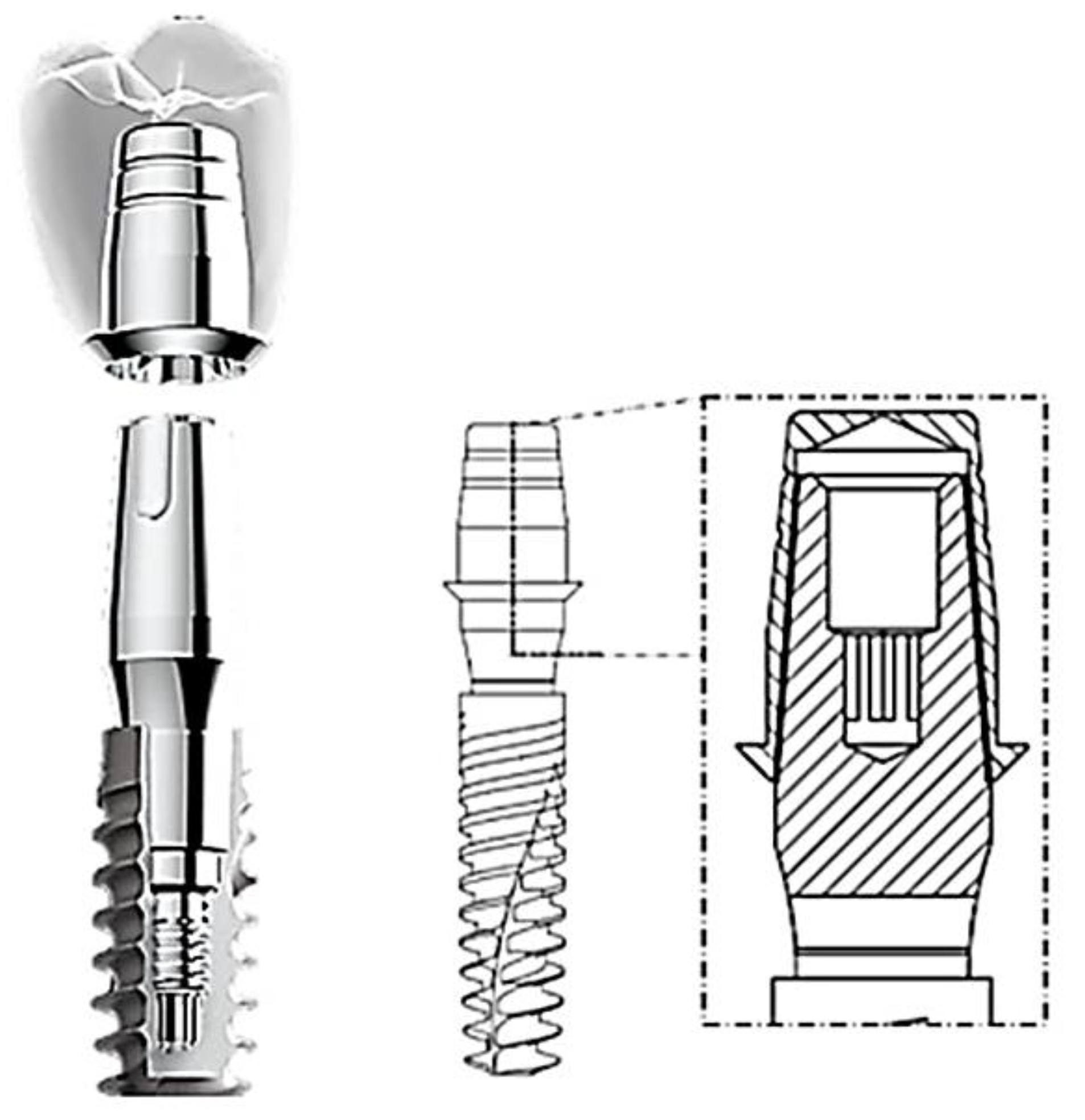
Preprints 85667 g001
Figure 1. Conometric connection between cap and abutment.
Figure 1. Conometric connection between cap and abutment.
Preprints 85667 g001
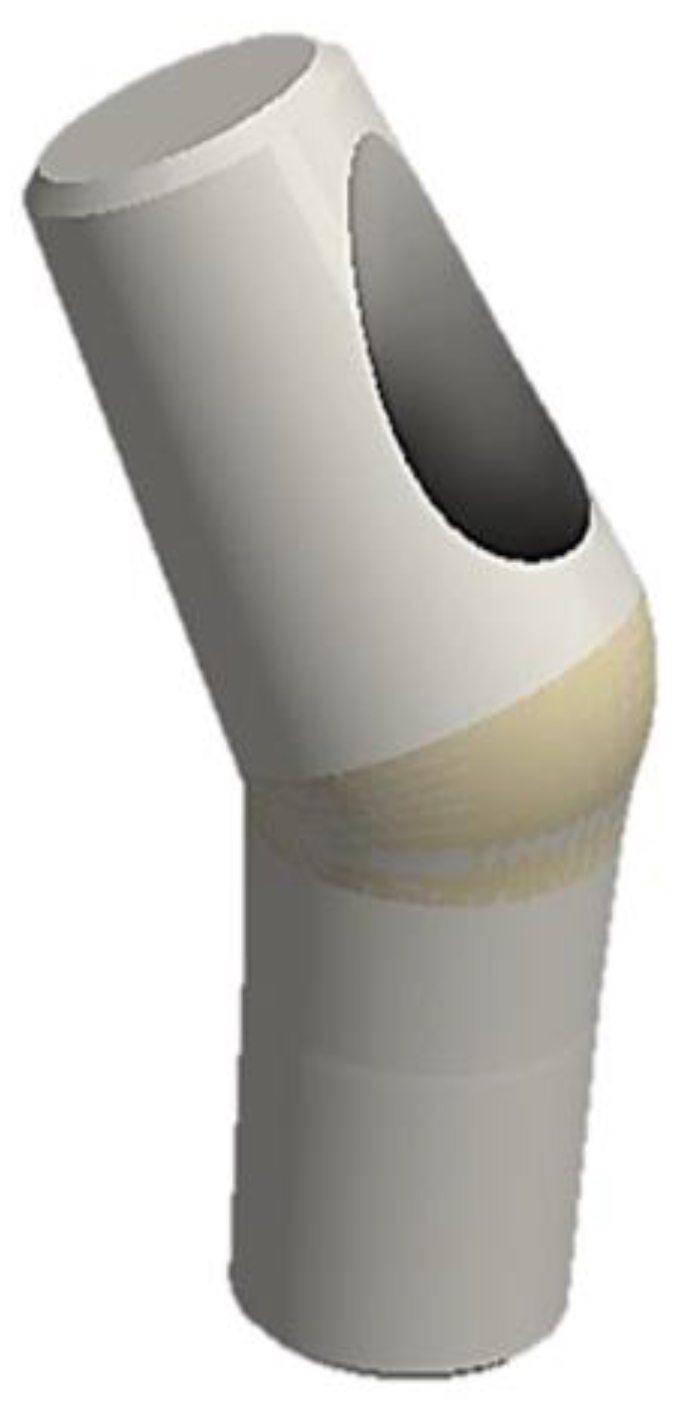
Preprints 85667 g002
Figure 2. Example of inclined stump with through hole for retention screw of the implant.
Figure 2. Example of inclined stump with through hole for retention screw of the implant.
Preprints 85667 g002
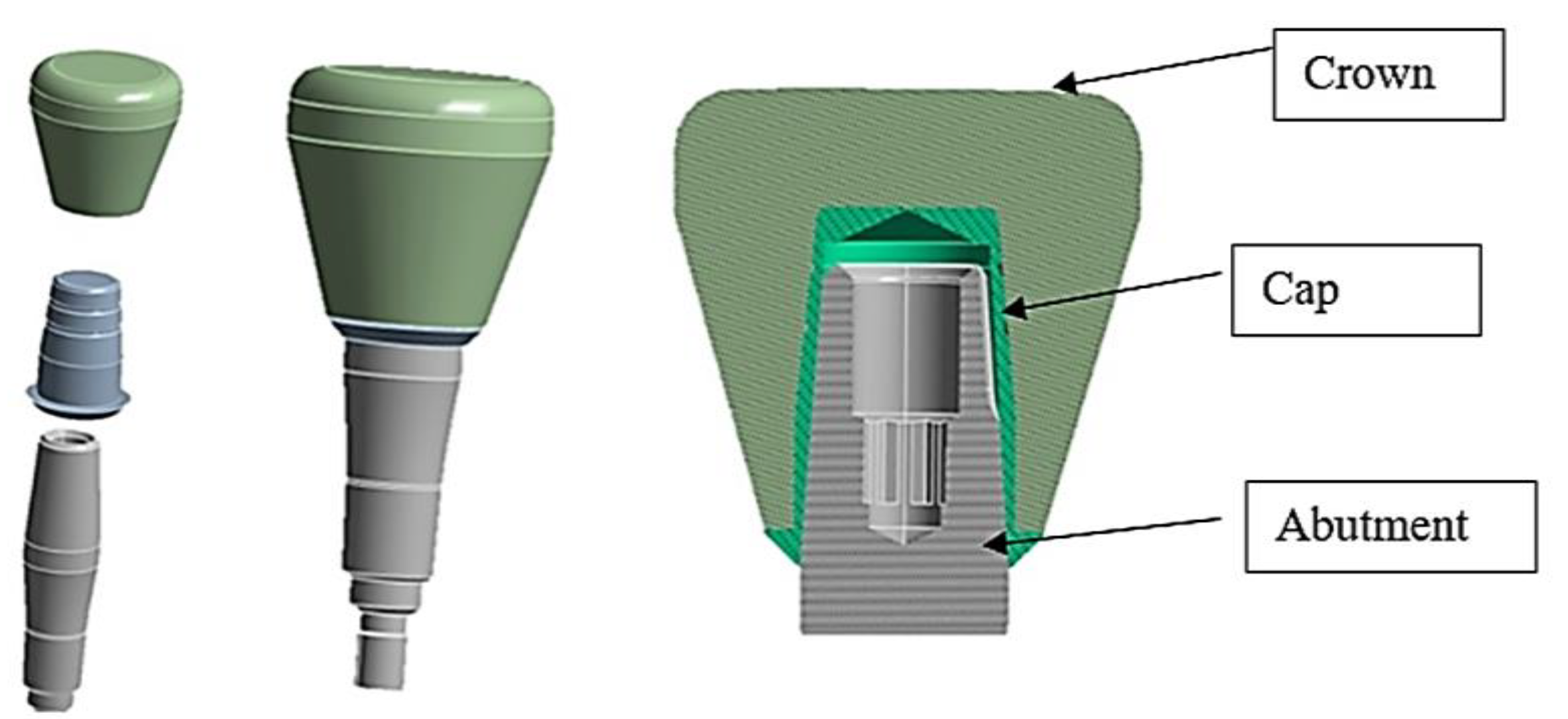
Preprints 85667 g003
Figure 3. 3D model of the crown, cap, and abutment system.
Figure 3. 3D model of the crown, cap, and abutment system.
Preprints 85667 g003
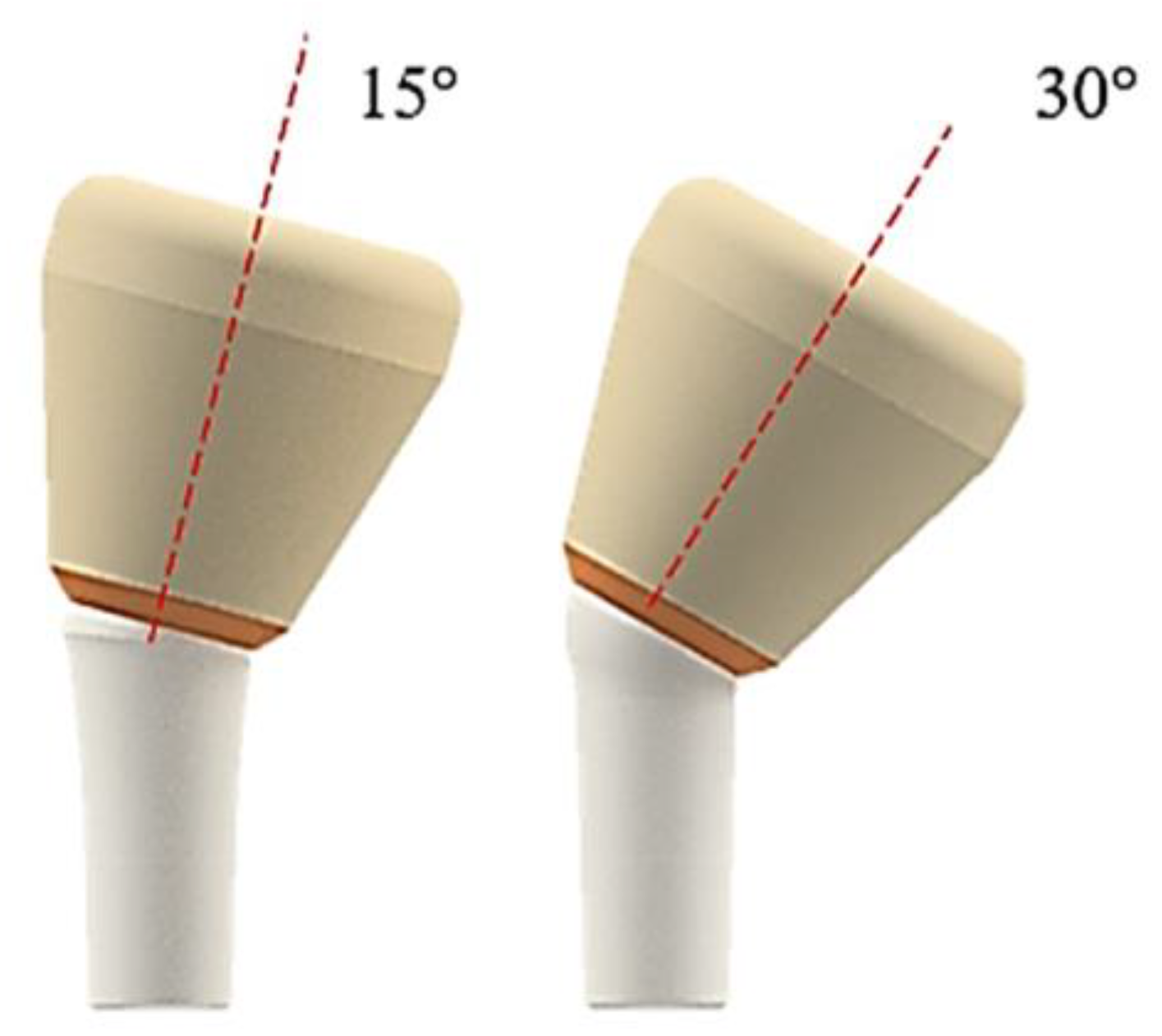
Preprints 85667 g004
Figure 4. 3D model of the crown system - cap and abutment inclined at 15° (on the left) and inclined at 30° (on the right).
Figure 4. 3D model of the crown system - cap and abutment inclined at 15° (on the left) and inclined at 30° (on the right).
Preprints 85667 g004
Preprints 85667 g005
Figure 5. Finite element model of the crown-cap-abutment system.
Figure 5. Finite element model of the crown-cap-abutment system.
Preprints 85667 g005
Preprints 85667 g006
Figure 6. Contact with friction (red) between cap and abutment The coefficient of friction used was 0.3 [28].
Figure 6. Contact with friction (red) between cap and abutment The coefficient of friction used was 0.3 [28].
Preprints 85667 g006
Preprints 85667 g007
Figure 7. On the left the constraint configuration, on the right the application of the load on the crown.
Figure 7. On the left the constraint configuration, on the right the application of the load on the crown.
Preprints 85667 g007
Preprints 85667 g008
Figure 8. Trend of the retention force of the cap-abutment system as a function of conicity [23].
Figure 8. Trend of the retention force of the cap-abutment system as a function of conicity [23].
Preprints 85667 g008
Preprints 85667 g009
Figure 9. Von Mises stress on the system for an insertion force of 10 N.
Figure 9. Von Mises stress on the system for an insertion force of 10 N.
Preprints 85667 g009
Preprints 85667 g010
Figure 10. Displacements along the cap-abutment system for an insertion force of 10 N.
Figure 10. Displacements along the cap-abutment system for an insertion force of 10 N.
Preprints 85667 g010
Preprints 85667 g011
Figure 12. Von-Mises stress distribution: (a) 30N; (b) 60 N (insertion force).
Figure 12. Von-Mises stress distribution: (a) 30N; (b) 60 N (insertion force).
Preprints 85667 g011
Preprints 85667 g012
Figure 13. Trend of the removal force as a function of the insertion force.
Figure 13. Trend of the removal force as a function of the insertion force.
Preprints 85667 g012
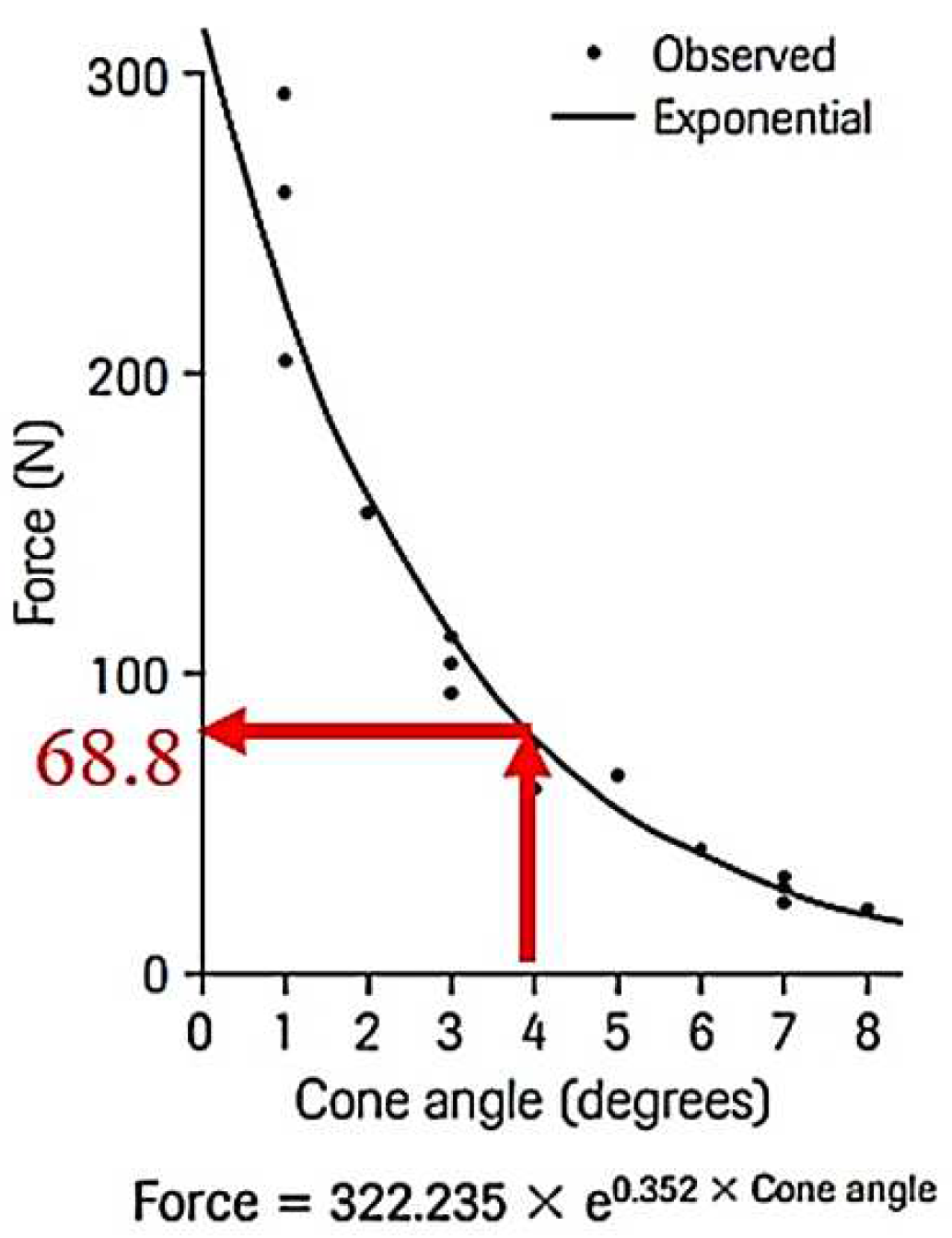
Preprints 85667 g013
Figure 14. Retention force as a function of the taper of the system for an insertion load of 30N [23].
Figure 14. Retention force as a function of the taper of the system for an insertion load of 30N [23].
Preprints 85667 g013
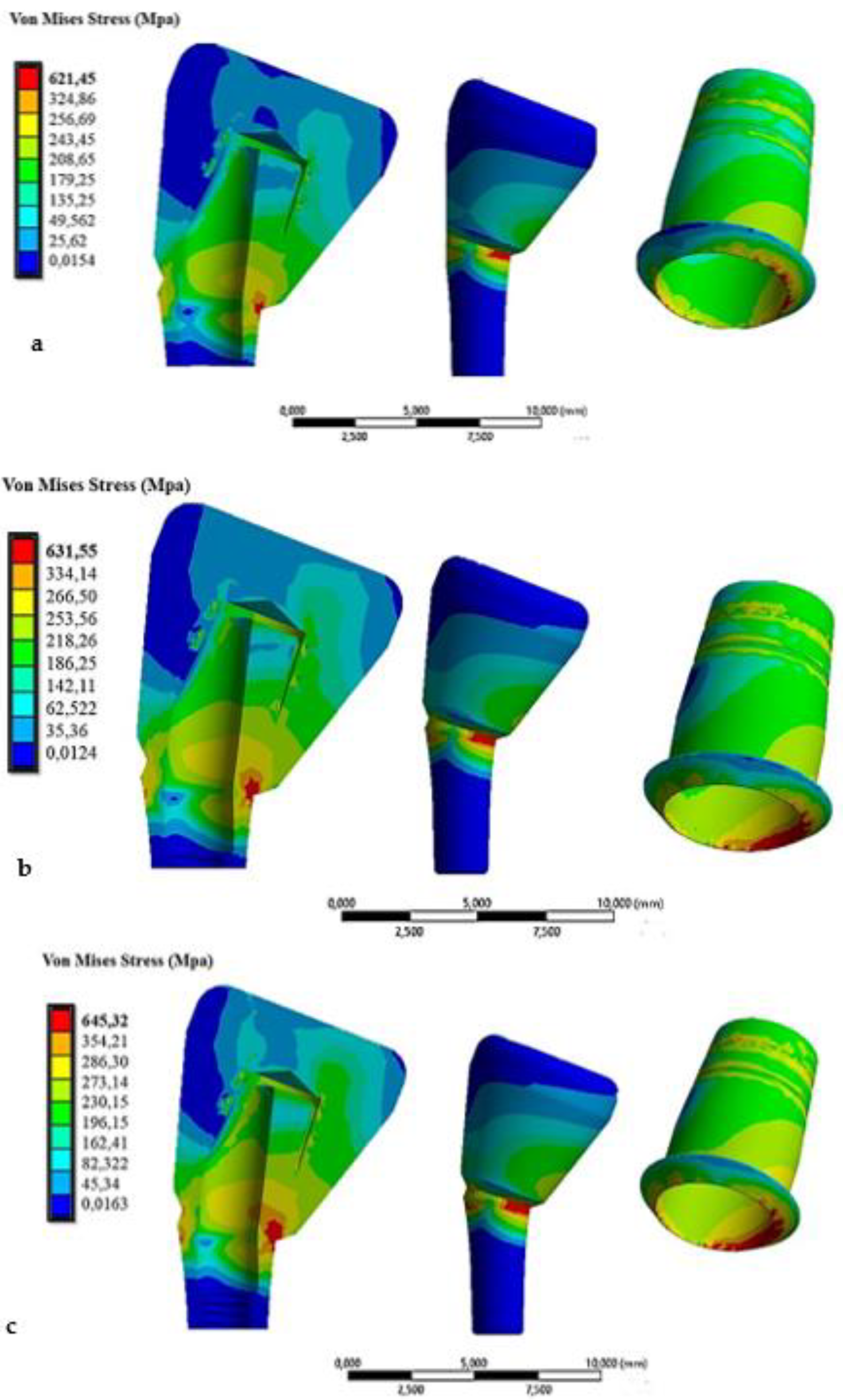
Preprints 85667 g014
Figure 15. Von-Mises stress distribution per abutment inclined at 15° (a) 10N, (b) 30 N, (c) 60N.
Figure 15. Von-Mises stress distribution per abutment inclined at 15° (a) 10N, (b) 30 N, (c) 60N.
Preprints 85667 g014
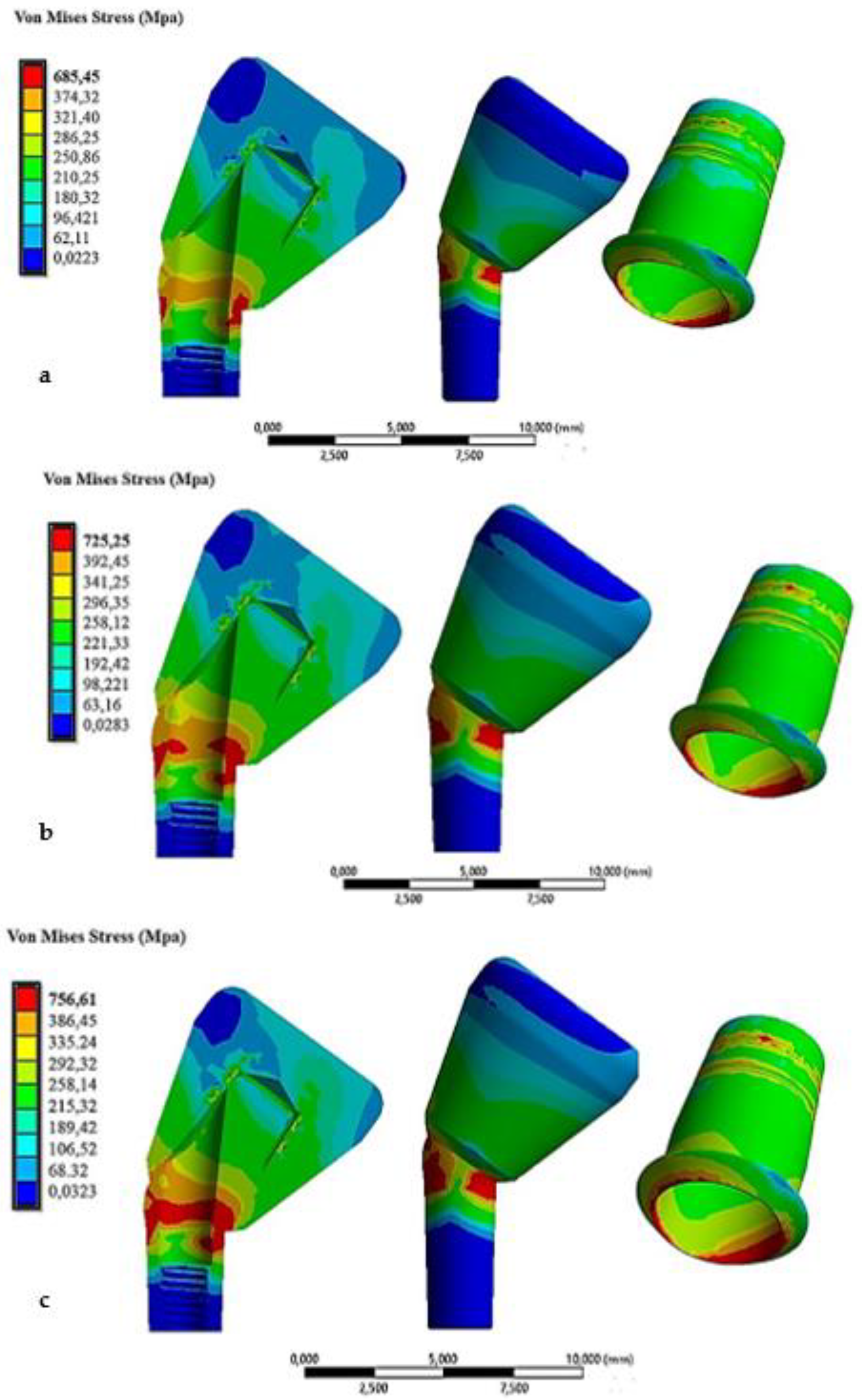
Preprints 85667 g015
Figure 16. Von-Mises stress distribution per abutment inclined at 30° (a) 10N, (b) 30 N, (c) 60N.
Figure 16. Von-Mises stress distribution per abutment inclined at 30° (a) 10N, (b) 30 N, (c) 60N.
Preprints 85667 g015
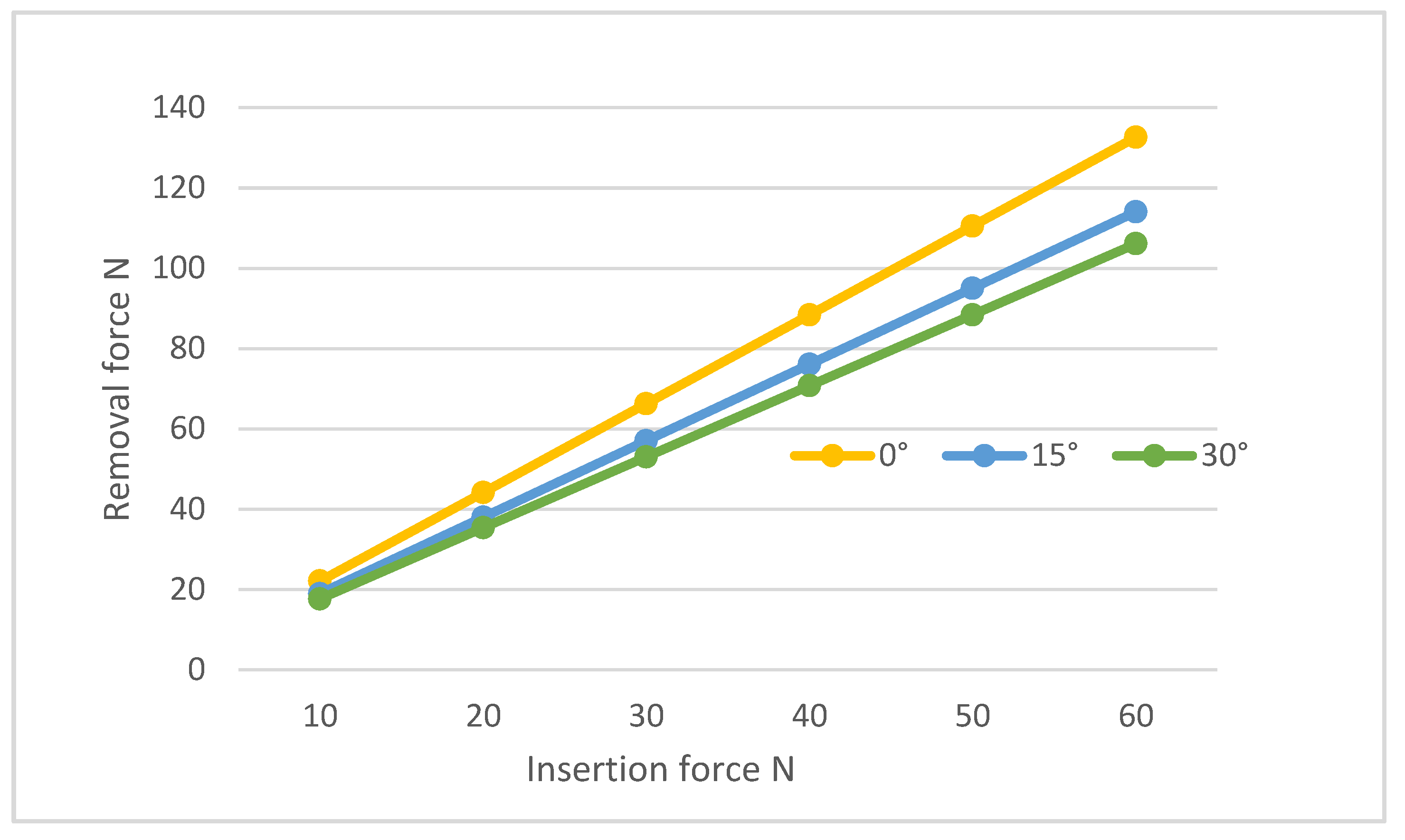
Preprints 85667 g016
Figure 17. Trend of the removal force as a function of the insertion force. For abutments inclined at 0°, 15° and 30°.
Figure 17. Trend of the removal force as a function of the insertion force. For abutments inclined at 0°, 15° and 30°.
Preprints 85667 g016
Table 1. Properties of materials used in the study.
Table 1. Properties of materials used in the study.
Young Modulus [GPa] Poisson Ratio Tensile Yield Strenght [MPa] Tensile Ultimate Strenght [MPa]
Titanium (Ti6Al4V) 110 0.3 830 900
Zirconia (Crown) 200 0.31 330 551
Table 2. Von-Mises stress and displacement along x of the cap for different insertion loads.
Table 2. Von-Mises stress and displacement along x of the cap for different insertion loads.
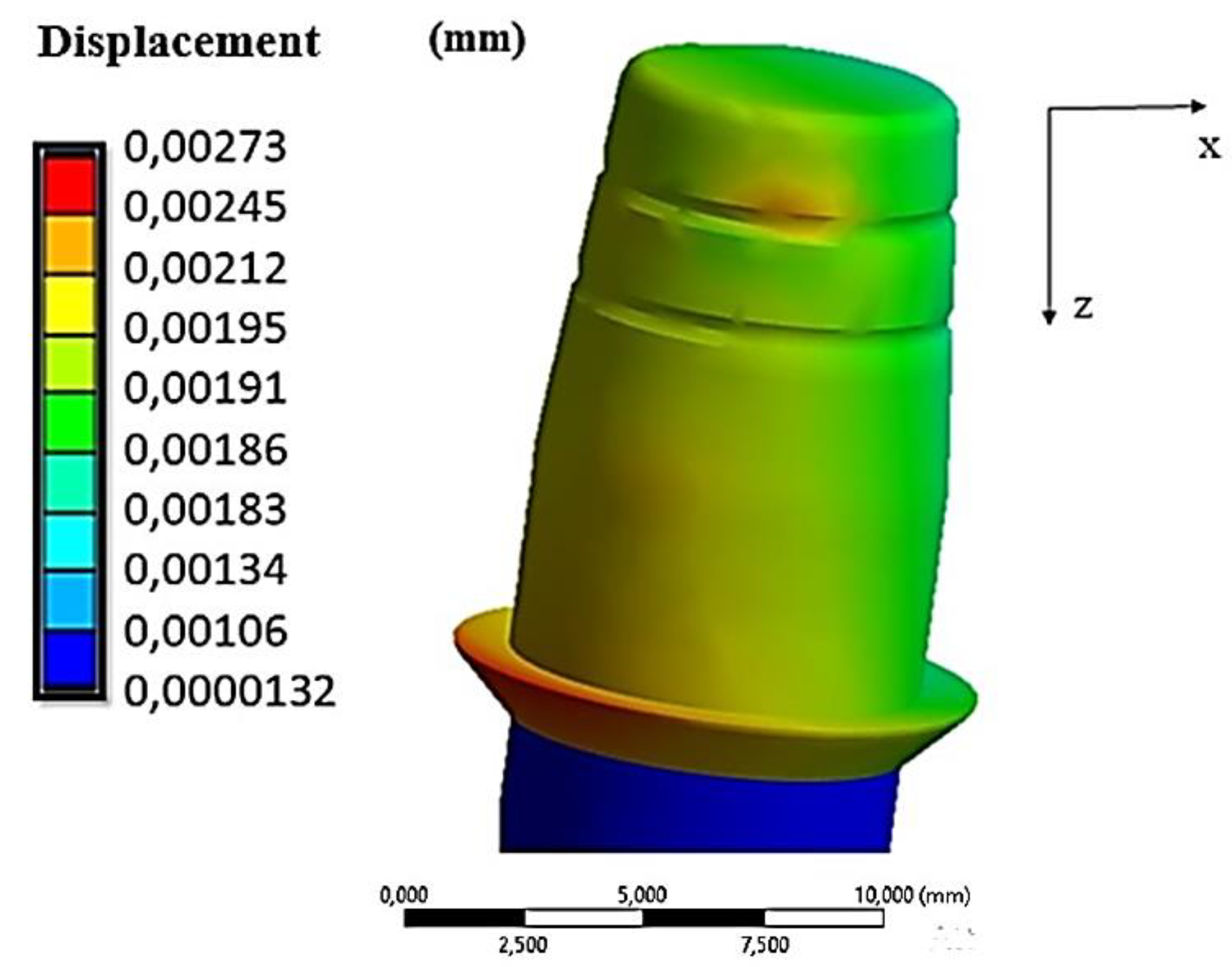
Insertion force N Displacement of coping (mm) Von Mises Stress MPa
10 0.00273 506.01
20 0.00546 508.52
30 0.00819 511.73
40 0.01092 530.56
50 0.013655 570.34
60 0.01638 594.08
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated