Preprint
Article
A Conversational Framework for Interstellar Discourse on Fundamental Physical Structures
Altmetrics
Downloads
102
Views
55
Comments
0
This version is not peer-reviewed
Submitted:
21 September 2023
Posted:
22 September 2023
You are already at the latest version
Alerts
Abstract
This paper considers the possibility that abstract thinking and advanced synthesis skills might be selection criteria for extraterrestrial civilizations to accept communication with mankind on Earth. For this purpose, a notation not relying upon the use of alphabet and numbers is proposed, in order to denote just some basic structures of current physical theories: vector fields, 1-form fields, and tensor fields of arbitrary order. An advanced civilization might appreciate the way here proposed to achieve a concise description of electromagnetism and general relativity, and hence it might accept the challenge of responding to our signals. The abstract symbols introduced in this paper to describe the basic structures of physical theories are encoded into black and white bitmap images that can be easily converted into short bit sequences and modulated on a carrier wave for radio transmission.
Keywords:
Subject: Physical Sciences - Space Science
1. Introduction
The modern theories of fundamental interactions have developed powerful tools for addressing some outstanding problems, i.e., what is the ultimate nature of gravity, and how to achieve unification of all fundamental interactions and guiding principles of physics. At a deeper level, however, yet another problem arises, i.e., how to develop a language which is universally understood by the scientific community. This is not a purely formal issue. For example, since the language of physics is mathematics, we might consider the question: if we use alphabets in order to express physical laws in mathematical form, what tells us that X is a vector field, rather than a topological space, or a point of a metric space, or a 1-form field? At present, several authors find a way out by using the so-called abstract indices, e.g., for vector fields, but this does not truly solve the problem, because it needs a second family of symbols taken from the alphabet, and on our planet no unique alphabet exists. Moreover, upstairs Latin indices are also used to denote families of 1-form fields, e.g., the tetrads , nor can we distinguish between a vector and a vector field unless we introduce for the former a letter to denote the point p at which the vector is considered. Hence one writes for the vector, and X for the vector field, which consists of a smooth (of class or less) assignment of as p is varying on the manifold of interest. Thus, unless we use twice the alphabet, no clear understanding of our notation is available, even though we refrain us completely from using coordinate descriptions.
At this stage, this seems to be just a well motivated but minor issue for modern science. However, if we consider the open problem of CETI, i.e., communication with extra-terrestrial intelligence, the associated perspective changes completely. So far, mankind has sent signals that contain a synthesis of our current understanding of biology, chemistry and physics. The lack of reply suggests considering, in our opinion, the following question: if an advanced extraterrestrial civilization receives sequences of signals from various parts of the Universe, but has no time to work hard on all of them, what features would convince them to select our own signals from the Earth? In our opinion, the more advanced they are, the more they would prefer to detect clear indication of original thinking in outlining the basic structures of the concepts we use, rather than the detailed operations that we perform upon them.
Our proposal is an abstract and simple notation, here called Physics Lingo, that serves as a bridge, connecting the abstract language of physics with the universal power of visual imagery. Rather than relying solely on traditional mathematical symbols and equations, Physics Lingo harnesses the expressive capacity of images by offering a unique perspective on transforming physical concept and theories into tangible visual representations. At the core of Physics Lingo lies the concept of encoding physics principles and theories, represented by abstract symbols, into digital bitmap images. Each bitmap image conveys specific meanings and forms the foundation for a visual language that can transcend linguistic barriers and communicate the richness of physics across the cosmos. The beauty of Physics Lingo lies not only in its ability to encode complex physics concepts, but also in its potential to serve as a means of extra-terrestrial interstellar communication. As we seek to establish contact with intelligent beings from distant star systems, the simplicity and universality of the bitmap images offer a promising platform for communication.
2. Physics Lingo: A Language for Cosmic Dialogue
The first non-trivial problem is: which branch of mathematics do we want to describe in the original synthesis of the structures and concepts that we use in our research and our teaching? As far as we can see, the basic geometric objects provide a good candidate in this respect. Our prescriptions are as follows.
- (i)
- Tangent vectors: rather than writing for the tangent vector at , which is an element of the tangent space , we write where the empty space within square brackets is a substitute for X, the dot downstairs is a substitute for the point p, and the arrow upstairs distinguishes a vector from its dual concept of 1-form or covector. We are therefore introducing a substitution map
- (ii)
- Vector fields: in this case, our substitution map acts according to
- (iii)
- 1-forms: we require thatwhere the arrow downstairs denotes the concept dual to the one in item (i).
- (iv)
- 1-form fields: we writewhere the dot has disappeared, as is the case in Equation (2), since we are dealing with a smooth assignment of 1-form as the point p is varying on the manifold M.
- (v)
- Tensor fields: a tensor field of type takes the formand, in particular, the Riemann curvature tensor, which is of type , can be denoted by
- (vi)
- The spacetime manifold , one of the great achievements of Einstein, can be expressed in the form
- (vii)
-
Vacuum Maxwell theory in curved spacetime can be described by the potential 1-form field A, its gauge curvature 2-form field , and the Hertz [1,2] 2-form P such thatThe simple but non-trivial tripletcan be represented in the formwhich, for the educated reader relevant for the CETI program, is enough for him/her to understand that this is a shorthand notation for the content of Equation (8).
- (viii)
- Tensor affinities are unfortunately denoted in the literature in the same way as tensor components, even though they do not transform in a homogeneous way under diffeomorphisms. Within our concise language, we propose instead to denote them in the formThe educated reader should understand that the resulting objects resemble tensor components, but do not transform tensorially under diffeomorphisms. Only arrows are appropriate for visual description of tensorial behaviour.
3. Some Peculiar Features of Interstellar Communication
When talking about interstellar communication, the general reader should bear in mind that, apart from the Pioneer plaques and Voyager records, every interstellar message has used microwave frequencies as the communication medium. Attention is restricted to a relatively narrow band, ranging from about 1 GHz to 10 GHz. This is said to be the microwave window, because it is one of the few regions of the electromagnetic spectrum that is unimpeded by Earth’s atmospheric gases [3]. The radio signals that we send have to travel through energy-absorbing clouds of interstellar dust and gas, hence they will be quite faint by the time they arrive at their destination. The probability that a message from Earth is detected is very low, because of the large number of possible frequencies to broadcast on. An alternative to microwave signals consists of optical communication based upon laser transmission, which however has a far higher energy requirement. Moreover, optical telescopes also require sophisticated equipment adaptations in order to make them capable of transmitting laser signals. Other important issues are the choice of wavelengths at which we should search for signals from extraterrestrial intelligence [4], and the estimate of mean number of radio signals crossing the Earth [5].
4. Encoding and Transmitting Physics Words
This section focuses on realizing digital signals that enable the receiver to build the simple images described by Equations (1)–(7) and (9). For this purpose, we leverage the bitmap representation, that has gained significant attention due to its simplicity and efficiency in data storage and transmission. Several studies focused on such a representation of digital images, by underlying its applicability to different fields (e.g., medicine [6], astronomy [7], document analysis [8]) and providing useful instruments to improve representation quality [9] or processing capabilities [10].
The bitmap representation of a black and white image subdivides the image in a fixed number of points (i.e., into a grid of small squares called pixels) and associates to each point or pixel a value that is either black or white. Each pixel is then assigned a binary value, where 1 represents black and 0 represents white. Figure 1 shows how the symbols reported in Equations (1)–(7) and (9) can be represented by grids that are 5 pixels wide and 8 pixels tall, so the bitmap representation for each symbol is a 8x5 grid. Then, the pixels stored in the bitmap grid can be converted into a sequence of bits, as depicted in Figure 1, by concatenating the bits of each row from the top to the bottom of the bitmap grid. Each bit in the sequence corresponds to a pixel in the image.
4.1. Signal Modulation
In order to transmit these data as a radio signal, the binary sequence needs to be modulated onto a carrier wave. Indeed, binary modulation enables the efficient transmission of digital information over long distances. The process begins with the binary signal (the sequence of 1s and 0s representing the digital information) that is modulated onto a radio wave carrier by using existing modulation schemes such as amplitude-shift keying (ASK), frequency-shift keying (FSK), or phase-shift keying (PSK). In ASK, the carrier’s amplitude is varied to represent the binary data, with one amplitude denoting a ’1’ and another amplitude representing a ’0’. FSK modulates the carrier’s frequency, assigning different frequencies to ’1’ and ’0’. PSK, on the other hand, alters the phase of the carrier wave to encode the binary signal. Through these modulation techniques, the binary signal is combined with the radio wave carrier, allowing it to propagate through the air.
For generating the signals corresponding to sequences of symbols such the ones reported in Equations (1)–(7) and (9), we concatenate in a single sequence the bit sequences corresponding to each symbol. Figure 2 summarizes in the last three images the bit encoding for the bitmap images in Equations (6), (7) and (9).
4.2. Generality of the Approach
The presented technique, which involves converting black and white images into a bitmap representation and then encoding them into bit sequences that are modulated onto a carrier wave, exhibits a remarkable generality in its applicability. In fact, it can be effectively employed for transmitting any black and white image, if the appropriate size of the grid is selected. By adjusting the grid size, the technique can accommodate images of different complexity by handling different levels of detail. As a final note, we want to stress that whatever message sent in the space and detected from anyone needs to be decoded for being interpreted and, thus, simpler the code used (as ours) higher the probability of having it decoded.
As an example, Figure 3 shows a portion of the limit set of a Fuchsian group [11], represented as bitmaps obtained by using grids of different size. As can be noticed, by lowering the grid dimension the quality of the image degrades but there is a saving in the total number of pixels and, thus, bits required to encode the original image. Indeed, by using a grid of size 730x380 pixels, the total number of bits needed to encode the image is 277400, while by using a grid of size 150x76 pixels the same image can be encoded by using 11400 bits only but obtaining a representation of worse quality.
5. Concluding Remarks
The topic of interstellar communications is still receiving a careful consideration in the modern literature, from different perspectives [12,13,14,15,16,17]. In particular, we agree with the author of Ref. [15] that other technological life exists; a relevant fraction of ETI wishes to explore the universe; travel velocities are sufficiently high to allow for probes that arrive at their destination intact, with a useful lifetime remaining; last, but not least, a relevant fraction of ETI appreciate data of some kind. Within this framework, our original contribution is, as far as we can see, twofold:
- (i)
- We have first proposed a concise notation for describing some basic geometric concepts used in modern physical theories [18].
- (ii)
- We have then shown in detail how to obtain bit encoding for the images in Equations (1)–(7) and (9), which might be exploited for interstellar communication, since the resulting synthesis skills might attract the attention of advanced civilizations which receive signals sent from the Earth. On reflection, even the skeptical reader might appreciate that the unification of space and time as depicted in the sixth image of Figure 3, the electromagnetic theory depicted in the seventh image therein, and the Riemann curvature represented in the eighth image, deserve careful consideration.
By working along similar lines, other original concise notations for scientific concepts might be hopefully developed, and a new longterm research program might be conceived. In particular, it might be challenging to perform a visualizable synthesis of mathematical and physical knowledge achieved so far, and to choose a suitable set of examples for interstellar quantum communications [17]. Although a more advanced civilization might have reached the stage where they depend substantially on artificial intelligence [12], we hope that the original synthesis initiated in this paper will enhance future efforts in achieving interstellar communication.
Author Contributions
G.E. was involved in the development of the abstract language to represent physical structures and theories; V.F. dealt with the digital representation of the abstract symbols of the language; G.E and V.F. wrote the paper.
Funding
This research received no external funding
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bouas, J. Hertz Potentials and Differential Geometry. PhD thesis, Texas A & M University, 2011.
- Cohen, J.M.; Kegeles, L.S. Electromagnetic fields in curved spaces: a constructive procedure. Phys. Rev. D 1974, 10, 1070–1084. [Google Scholar] [CrossRef]
- Oberhaus, D. Extraterrestrial Languages; The MIT Press, 2019.
- Townes, S. At what wavelengths should we search for signals from extraterrestrial intelligence? PNAS 1983, 80, 1147–1151. [Google Scholar] [CrossRef] [PubMed]
- Grimaldi, C.; Marcy, G.W. Bayesian approach to SETI. PNAS 2018, 115, E9755–E9764. [Google Scholar] [CrossRef] [PubMed]
- Deserno, T.M. Fundamentals of biomedical image processing. In Biomedical image processing; Springer, 2010; pp. 1–51.
- Dimov, D.; Dimov, A. Data driven approach to binarization of astronomical images. Proceedings of the 11th International Conference on Computer Systems and Technologies and Workshop for PhD Students in Computing on International Conference on Computer Systems and Technologies, 2010, pp. 478–484.
- Rivest-Hénault, D.; Farrahi Moghaddam, R.; Cheriet, M. A local linear level set method for the binarization of degraded historical document images. International Journal on Document Analysis and Recognition (IJDAR) 2012, 15, 101–124. [Google Scholar] [CrossRef]
- Sarkar, P.; Nagy, G.; Zhou, J.; Lopresti, D. Spatial sampling of printed patterns. IEEE Transactions on Pattern Analysis and Machine Intelligence 1998, 20, 344–351. [Google Scholar] [CrossRef]
- Guibas, L.J.; Stolfi, J. A Language for Bitmap Manipulation. ACM Trans. Graph. 1982, 1, 191–214. [Google Scholar] [CrossRef]
- Seade, J. Limit sets of discrete groups, School and Workshop, Geometry of discrete actions, ICTP, Trieste.
- Shostak, S. What ET will look like and why should we care. Acta Astron. 2010, 67, 1025–1029. [Google Scholar] [CrossRef]
- Shostak, S. Limits on interstellar images. Acta Astron. 2011, 68, 366–371. [Google Scholar] [CrossRef]
- Hippke, M. Interstellar communication. IX. Message decontamination is impossible. arXiv:1802.02180 [astro-ph.IM] 2018, arXiv:1802.02180 [astro-ph.IM] 2018. [Google Scholar]
- Hippke, M. Interstellar communication network. I. Overview and assumptions. Astron. J. 2020, 159, 85. [Google Scholar] [CrossRef]
- Berera, A. Quantum coherence to interstellar distances. Phys. Rev. D 2020, 102, 063005. [Google Scholar] [CrossRef]
- Hippke, M. Searching for interstellar quantum communications. Astron. J. 2021, 162, 1. [Google Scholar] [CrossRef]
- Esposito, G. Fondamenti di teoria classica dei campi; Amazon, 2023.
Figure 1.
Bitmap representation of the symbols in Equations (1)–(7) and (9) and bit sequence encoding for the symbol ’(’.
Figure 1.
Bitmap representation of the symbols in Equations (1)–(7) and (9) and bit sequence encoding for the symbol ’(’.
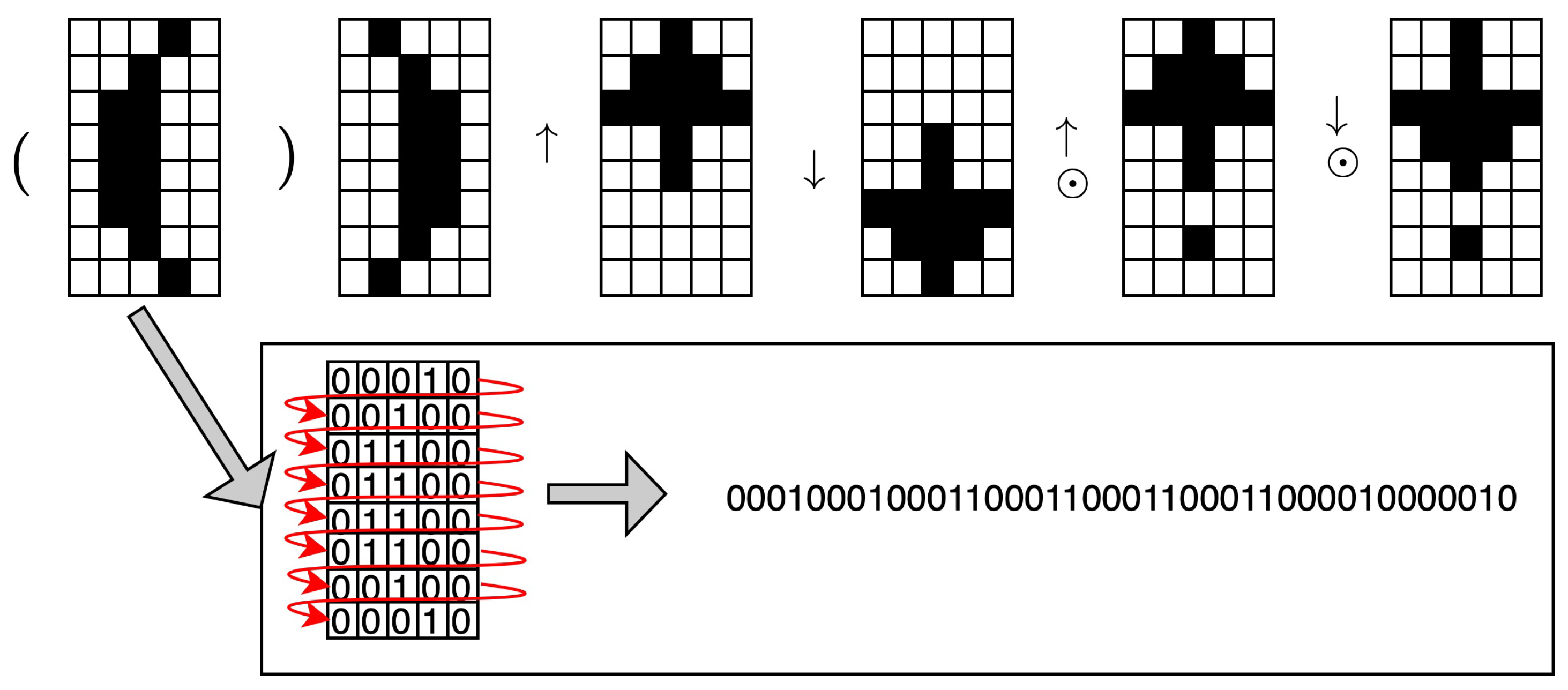
Figure 2.
Bit encoding for the images in Equations (6), (7) and (9). The first five images represent some basic geometric concepts, i.e. a vector, a vector field, a 1-form, a 1-form field, and a tensor field of type , respectively. The sixth image describes the spacetime manifold, while the seventh image is devoted to the electromagnetic theory of light, and the eighth image focuses on the Riemann curvature tensor.
Figure 2.
Bit encoding for the images in Equations (6), (7) and (9). The first five images represent some basic geometric concepts, i.e. a vector, a vector field, a 1-form, a 1-form field, and a tensor field of type , respectively. The sixth image describes the spacetime manifold, while the seventh image is devoted to the electromagnetic theory of light, and the eighth image focuses on the Riemann curvature tensor.
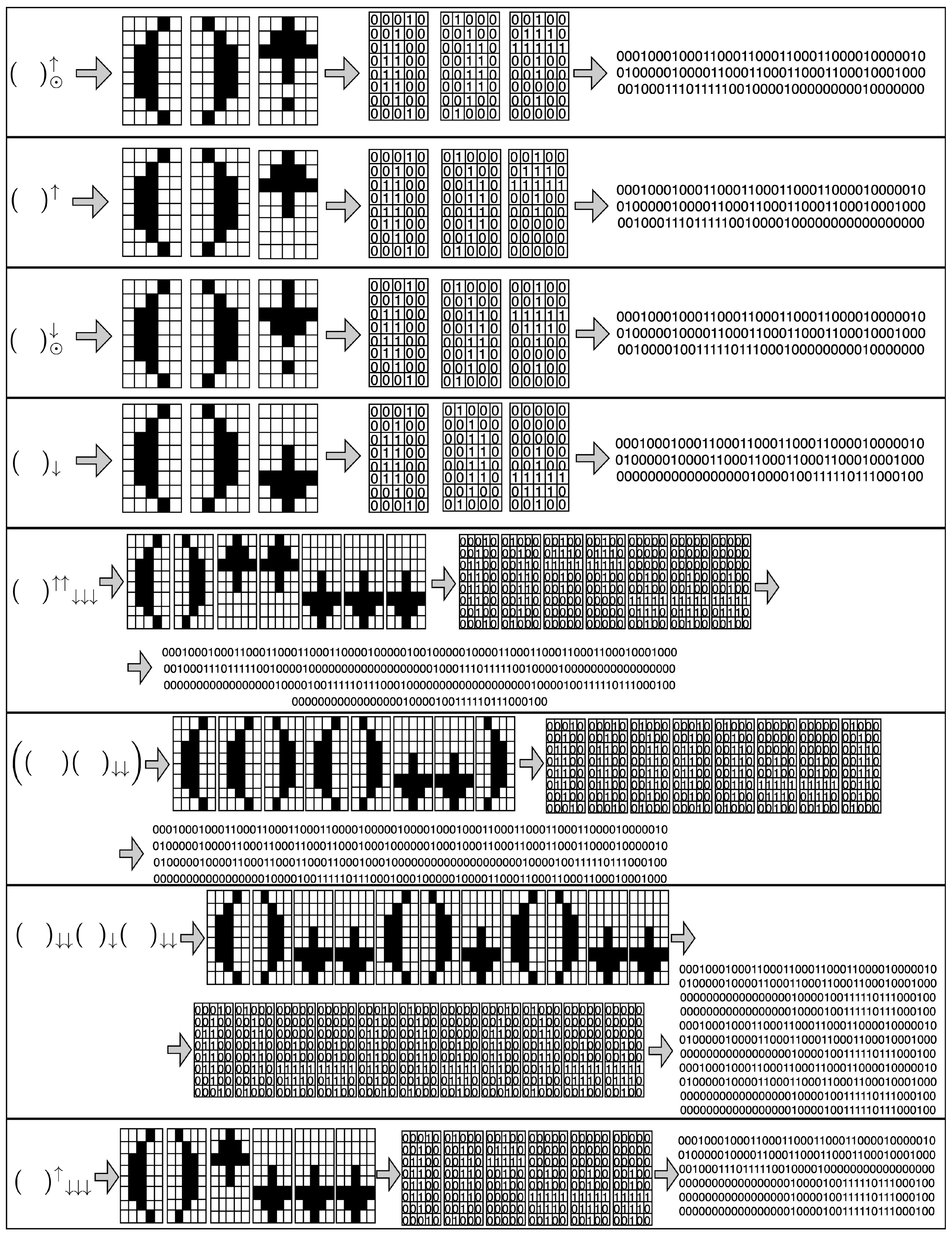
Figure 3.
Bitmap representation of a portion of the limit set of a Fuchsian group [11]
Figure 3.
Bitmap representation of a portion of the limit set of a Fuchsian group [11]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




