Prerpints.org logo
Preprint
Article

Graded Triply Periodic Minimal Surface Structures with Lightweight, High-Strength and Sound Absorption Produced by Laser Powder Bed Fusion

Altmetrics

Downloads

240

Views

88

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 September 2023

Posted:

25 September 2023

You are already at the latest version

Alerts
Abstract
In this research, a design method for the graded triply periodic minimal surface (TPMS) structures with lightweight, high-strength, and high sound absorption properties is proposed. The graded TPMS structures are controlled by linear, quadratic, and sine functions. Uniform TPMS and graded TPMS were manufactured by laser powder bed fusion (LPBF) with AlSi7Mg powder, and an acoustic impedance tube test, compression test, and digital image correlation (DIC) test were ap-plied to obtain the sound absorption and compression properties. The sound absorption coefficient of a uniform Gyroid increases as the number of layers and surface thickness increase, and it in-creases as element size decreases. The sound absorption peak shifts to low frequencies as the number of layers increases. The sound absorption property of Type-Ⅰ graded TPMS is superior to the Type-Ⅱ, and the G-LinearⅠ has the highest sound absorption properties among the three functions. It reveals that the graded TPMS has superior sound absorption performance at low and medium frequencies. The compression and DIC results of graded TPMS also show excellent mechanical properties and energy absorption characteristics.
Keywords: 
Subject: Physical Sciences  -   Acoustics

1. Introduction

The sound absorption materials with lightweight, high specific strength are popular research topics for their energy conservation and noise reduction [1]. However, many sound absorption materials currently have poor sound-absorbing effects at mid-to-low frequencies and low strength [2], and further improvements are needed to enhance the structure of the sound absorption materials. Porous structure material is generally used in sound absorption for its high porosity and permeability, and its surface contains numerous holes that match the wavelength of sound waves, particularly for sound absorption over wide frequency ranges [3]. The sound waves propagate inside the porous structures, and the acoustic energy is converted into heat energy due to the viscous losses. The porous structure also has high specific strength, high stiffness, and lightweight properties [4], and it is considered a potential material for aeronautics [5], aerospace [6], and building structures [7].
The common porous materials applied in sound absorption include foam structure [8], lattice structure [9], honeycomb structure [10], and triply periodic minimal surface (TPMS) [11]. Foam structures with low density and thermal conductivity, combined with their interesting mechanical properties, make them excellent thermal and sound insulators [12]. The TPMS structure is one potential sound absorption material because of its complex internal cavity structure. It can theoretically achieve a “cavity-like” effect on the back of the material and reflect the sound waves entering its interior. However, the TPMS structure is hard to be manufactured by traditional processing techniques due to its complex internal cavity structure. In recent years, with the rapid development of additive manufacturing technology that can prepare complex spatial structures, more possibilities have been provided for the design of new sound-absorbing material structures. Researchers prepared some porous structures using FDM additive manufacturing technology and conducted sound absorption tests, and they found that multilayered micro-channels with absorption averages up to 0.87 and noise reduction coefficient (NRC) up to 0.49 were produced [13]. The open-porous structures, including starlit, rhomboid, cartesian, and octagonal, were designed and manufactured by additive manufacturing technology with ABS material, and the results show that the starlit-shaped specimen has better sound absorption performance in comparison with the other structure types [14]. The different additive manufacturing technologies, including DLP, SLA, LCD, SLM, FDM, and FFF, were applied to manufacture the same porous structure, and it is demonstrated that the sound absorption measurements performed on samples with the same cellular design are very close, and additive manufacturing technologies are suitable for reproducing porous samples designed for sound absorption [15].
There is currently limited literature on the sound absorption performance of TPMS structures manufactured by additive manufacturing technology. Theoretically, the three TPMS structures, including F-RD, Gyroid, and Fischer Koch S, have multiple complete sound absorption bandgaps in the range of 200-2000 Hz [16]. The Gyroid structure has a 415 Hz wide bandgap structure near the center of 456 Hz, which provides a theoretical basis for the design of low-frequency sound absorption structures. Primitive, IWP, and Neovius surfaces were demonstrated that their sound absorption band gaps can be adjusted by topology optimization [17]. Based on stereolithography technology, the acoustic absorption properties of Diamond, Primitive and Gyroid have been researched [18], and the small unit cell or high volume fraction can enhance the effective frequency ranges. However, this experimental research on the sound absorption performance of TPMS structure shows that its low-frequency absorption performance is still poor, and that its absorption peak range is still in the range of 4000 Hz-6000 Hz. The sound absorption properties in mid-frequency and low-frequency of these homogenous TPMS mentioned above are not as ideal as the theoretical calculations. To further improve the low and medium frequency absorption performance and bandgap width of the TPMS structure, it is necessary to optimize the structural design to further enhance the sound absorption performance of TPMS.
Due to the gradient changes in its internal physical properties, the acoustic medium with gradient characteristics is receiving increasing attention from researchers[19]. To develop the acoustic absorber with high efficiency and thin thickness, four-layer gradient compressed porous metals were manufactured, and it was verified that the sound absorption coefficient reached 60.33% in 100-6000 Hz with 11 mm thickness [20]. A gradient structured fiber sponges with super elasticity and stretch-ability by combining humidity-assisted multistep electrospinning was demonstrated that the gradient change of porosity and pore diameter in the Z direction endowed the fibrous sponge material with high-efficiency absorption of broadband sound waves [21]. A gradient ceramsite structure with a high sound absorption coefficient was proposed [22], but the compressive and flexural strengths of gradient ceramsite structures is only greater than 3 MPa and 1 MPa, which is too low to be used for structural materials. It has been demonstrated that the improved sound absorption performance of the graded porous structure results from the decreased primary reflected energy associated with the increased absorbed energy [23].
Therefore, the gradient structure design can improve the sound absorption properties, but there are still important challenges in obtaining lightweight and high-strength sound-absorbing structures. There is a lack of research on the sound absorption of gradient TPMS. In this research, the influence of heights, surface thickness, and element size on the sound absorption property of TPMS was investigated, and the purpose was to obtain optimized structural design interval parameters. Based on this, the graded acoustic structures were designed by three graded functions, and the effects of the graded directions and functions on the sound absorption properties were analyzed to obtain the highly effective sound absorption material. Moreover, the mechanical properties of TPMS were obtained by compression tests and digital image correlation (DIC) tests to verify the efficient acoustic absorption materials with high strength and energy absorption.

2. Materials and Methods

2.1. Modelling of TPMS

2.1.1. Design of uniform TPMS

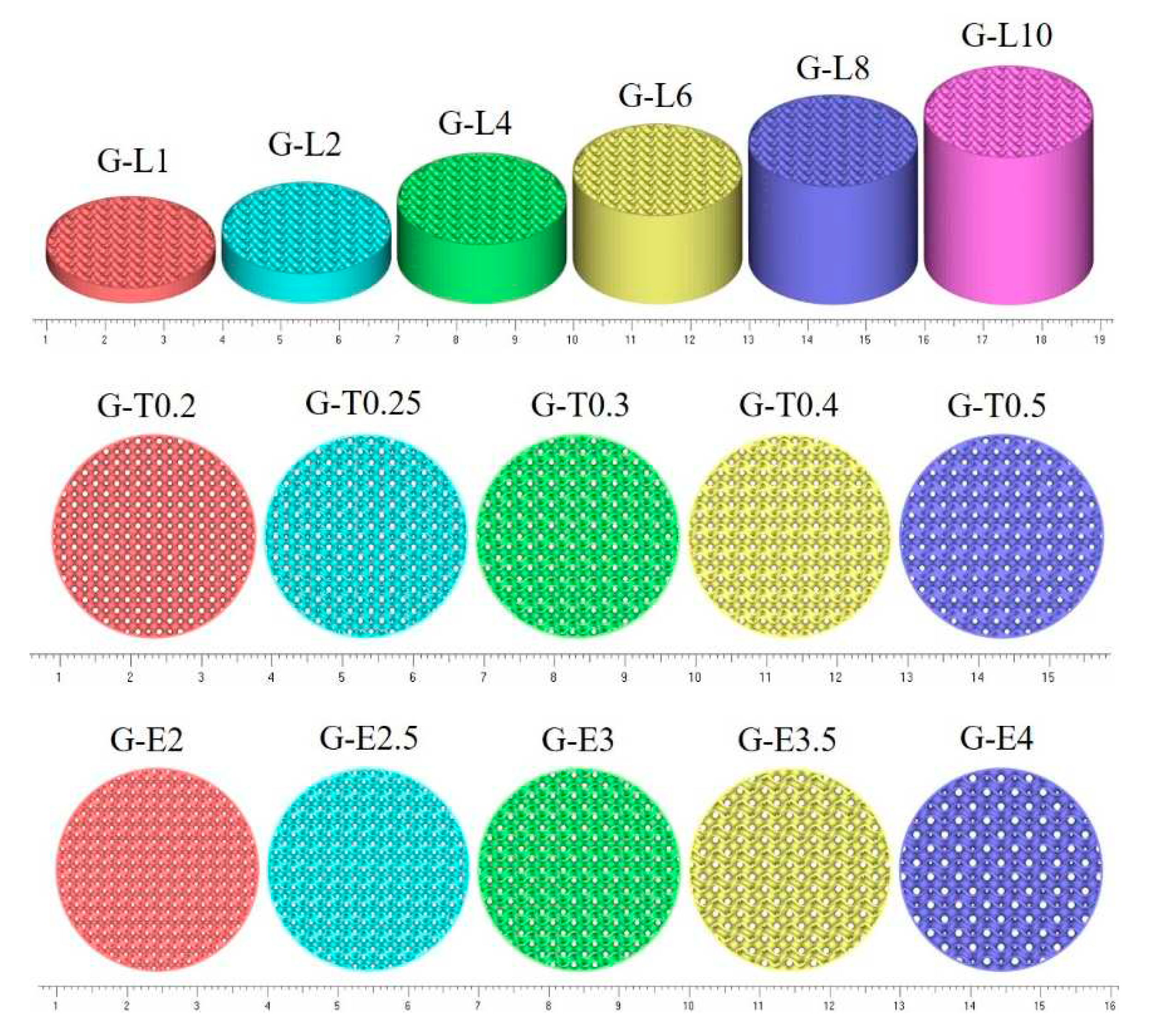
Gyroid surface structures were generated by MATLAB code with function (1). The element size of structure parameters was adjusted by parameter s in function (1), and the number of layers of Gyroid was adjusted by the calculation range (x, y, z) of function (1). After obtaining the surface structure of Gyroid, the solid structure was obtained by offset thickening of the surface in Materialise Magics software. The designed parameters of the Gyroid are listed in Table 1, and the models of uniform Gyroid structures are shown in Figure 1.
F g y r o i d = sin ⁡ 2 π x s × cos ⁡ 2 π y s + sin ⁡ 2 π y s × cos ⁡ 2 π z s + sin ⁡ 2 π z s × cos ⁡ 2 π x s  

2.1.2. Design of graded TPMS

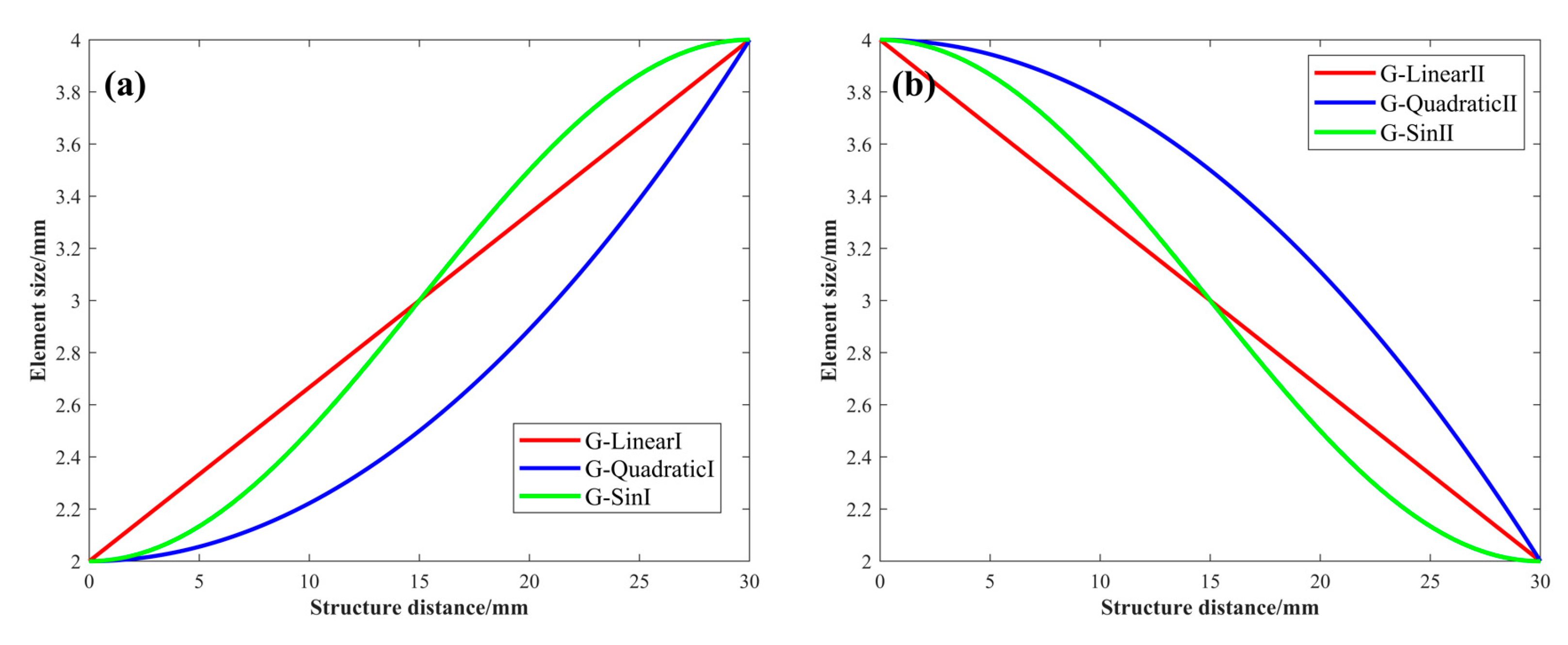
TPMS structures with graded element size can be obtained by the adjustment of parameter s in function (1), and the parameter s was set as a function related to the x coordinate, such as a linear function (2), a quadratic function (3), and a sin function (4). When z is 0, then s is equal to 2; when z is 30, then s is equal to 4. Therefore, the element size of the Gyroid was distributed from 2 mm to 4 mm along the z-axis with linear variation, quadratic variation, and sin variation, respectively. The functional relationship curves between element size and structural distance are shown in Figure 2, and the structural parameters of graded Gyroid structures are listed in Table 2.
s = 1 15 z + 2
s = 1 450 z 2 + 2
s = 3 + sin ⁡ ( π z 30 − π 2 )
Based on the graded function of element size, the graded Gyroid structures were designed and shown in Figure 3. The noise source was a power amplifier. Type-Ⅰ structure was defined when the noise waves flow from the end surface with small element size to the end surface with large element size, and Type-Ⅱ structure was defined when the noise waves flowed from the end surface with a large element size to the end surface with a small element size. It is worth noting that, when the thickness of the curved surface is the same, the smaller the unit size is, the lower the porosity is, and the higher the relative density is.

2.2. Additive manufacturing

The TPMS was produced by laser powder bed fusion (LPBF) equipment (Dimetal-280, produced by Laseradd Co., Ltd., Guangzhou, China), as shown in Figure 4, and the processing parameter for LPBF is shown in Table 3. The AlSi7Mg powder was supplied by Avimetal Powder Metallurgy Technology Co., Ltd., Beijing, China, and its particle size distribution is 15–53 μm (D10 = 22.56 μm, D50 = 38.37 μm, D90 = 60.90 μm). The chemical composition of AlSi7Mg powder is shown in Table 4. The contour scanning was applied in the manufacturing process, and spot compensation was set to 0.1mm.

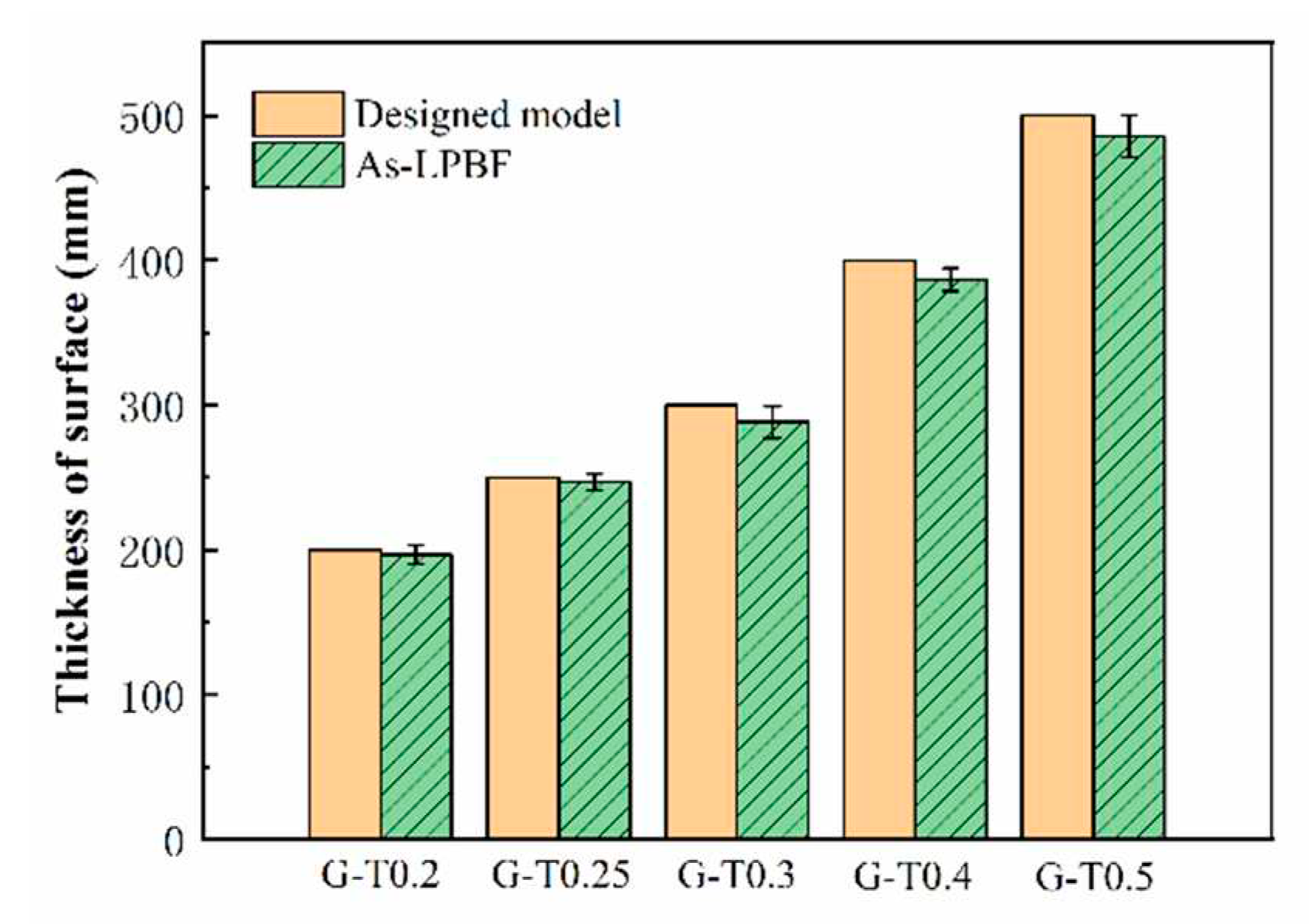
2.3. Dimensional accuracy measurement

The TPMS thickness was measured by a depth of field microscope (VHX-5000, KEYENCE Co., Shanghai, China), and each surface of the TPMS was measured five times.

2.4. Sound absorption coefficient test

Based on the method of the two-microphone transfer function and acoustic impedance tube, in accordance with the ASTM E1050-12 standard, the absorption coefficient of TPMS was measured by an impedance tube with a 29 mm diameter (SW4661, BSWA Technology Co. Ltd., China), as shown in Figure 5. TPMS structures were inserted into the impedance tube with the rigid backing. The measurement frequency is in the range of 500–6300 Hz. Two microphones were applied to collect the acoustic data, and the data was analyzed by VA-Lab software (BSWA Technology Co. Ltd., China).
The reflection coefficient R with rigid back was calculated by function (5).
R = H − e − j k s e j k s − H e j 2 k ( l + s )
H—the ratio of pressure between two microphones.
k—equal 2pf/c; wave number, m-1.
l—distance from the test sample to the centre of the nearest microphone, m.
s—centre-to-center spacing between microphones, m.
The normal incidence sound absorption coefficient α was calculated by function (6). Each structure has three test samples, and then the absorption coefficients of the three samples are averaged to obtain the absorption coefficient curve.
α = 1 − R 2
The 1/3 times frequency range includes 500 Hz, 630 Hz, 800 Hz, 1000 Hz, 1250 Hz, 1600 Hz, 2000 Hz, 2500 Hz, 3150 Hz, 4000 Hz, 5000 Hz, and 6300 Hz. The average absorption coefficient was calculated by function (7).
A α = ∑ α i 12
i: 500 Hz, 630 Hz, 800 Hz, 1000 Hz, 1250 Hz, 1600 Hz, 2000 Hz, 2500 Hz, 3150 Hz, 4000 Hz, 5000 Hz, and 6300 Hz.
The sound absorption properties of sound absorption materials are strongly influenced by the excitation frequency. Therefore, the first peak of sound absorption was analyzed, and the sound absorption coefficient α1 and frequency f1 at the first peak were obtained. The full width at half maximum (FWHM) of the first peak was calculated to evaluate the peak of sound absorption.

2.5. Mechanical and DIC test

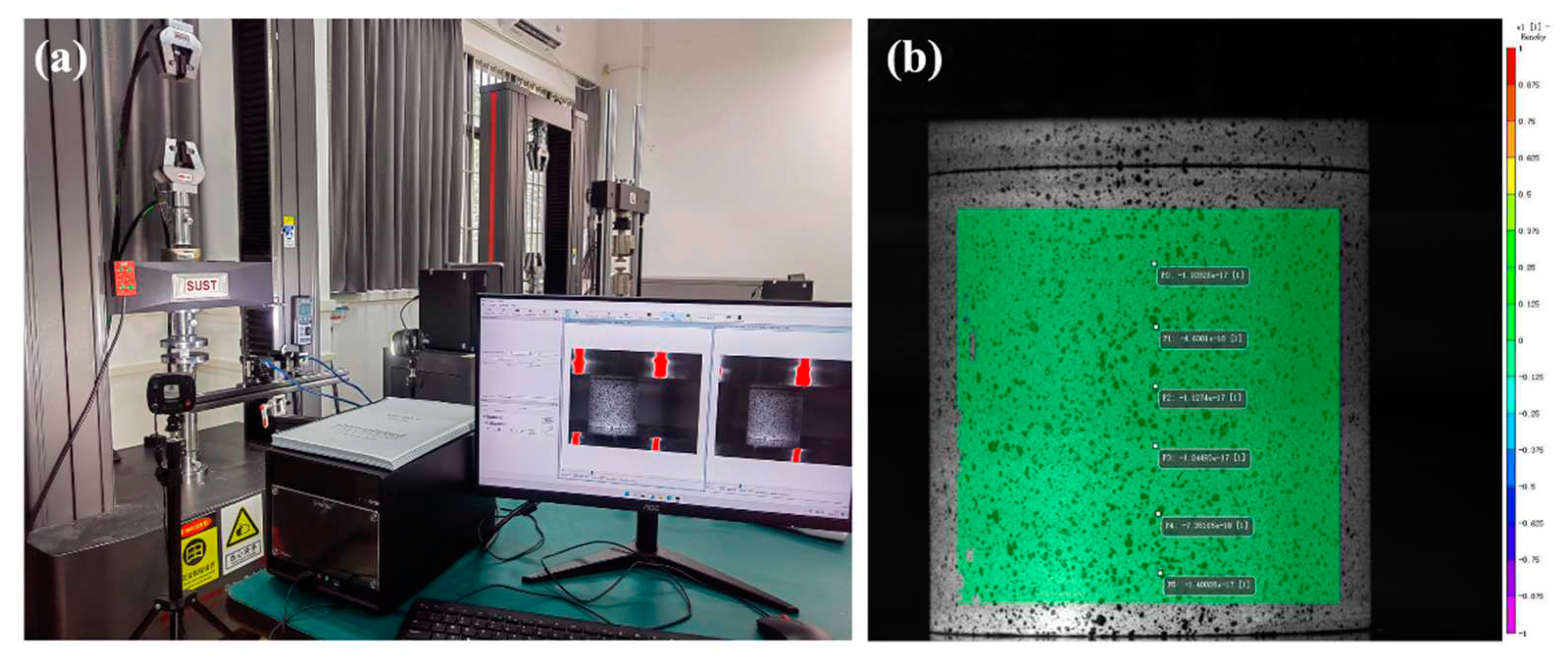
The compressive properties of TPMS were measured by a universal electronic testing machine (CMT5105-100kN, SUST Co., Ltd., China), and there are three duplicate samples. The displacement speed was set at 1 mm/min, and the data analysis reference standard ISO 13314:2011.
The compressive behavior of TPMS was detected by DIC equipment (VIC-3D, Correlated Solutions, Inc., U.S.A.), as shown in Figure 6a. Two cameras were used to capture images of the deformation of porous sound-absorbing structures. The pixel size of the CCD chip in the DIC camera is 3376*2704, and the displacement accuracy is 0.01 pixels. After the images were captured by two cameras, the region of interest (ROI) was set at the outline of the specimen. The relevant areas of the image through grayscale were located, and the surface displacement and strain distribution of the object were calculated. To compare the trend of strain changes at these six locations, six points were distributed in the middle of the specimen for the strain analysis, as shown in Figure 6b.

3. Results and discussion

3.1. Forming quality by LPBF

The uniform gyroid structures fabricated by LPBF are shown in Figure 7, and the dimensional accuracy measurement result is shown in Figure 8. It is noticed that the printing accuracy of the Gyroid is consistent with the designed model, and the size error is very small.

3.2. Sound absorption properties of uniform TPMS

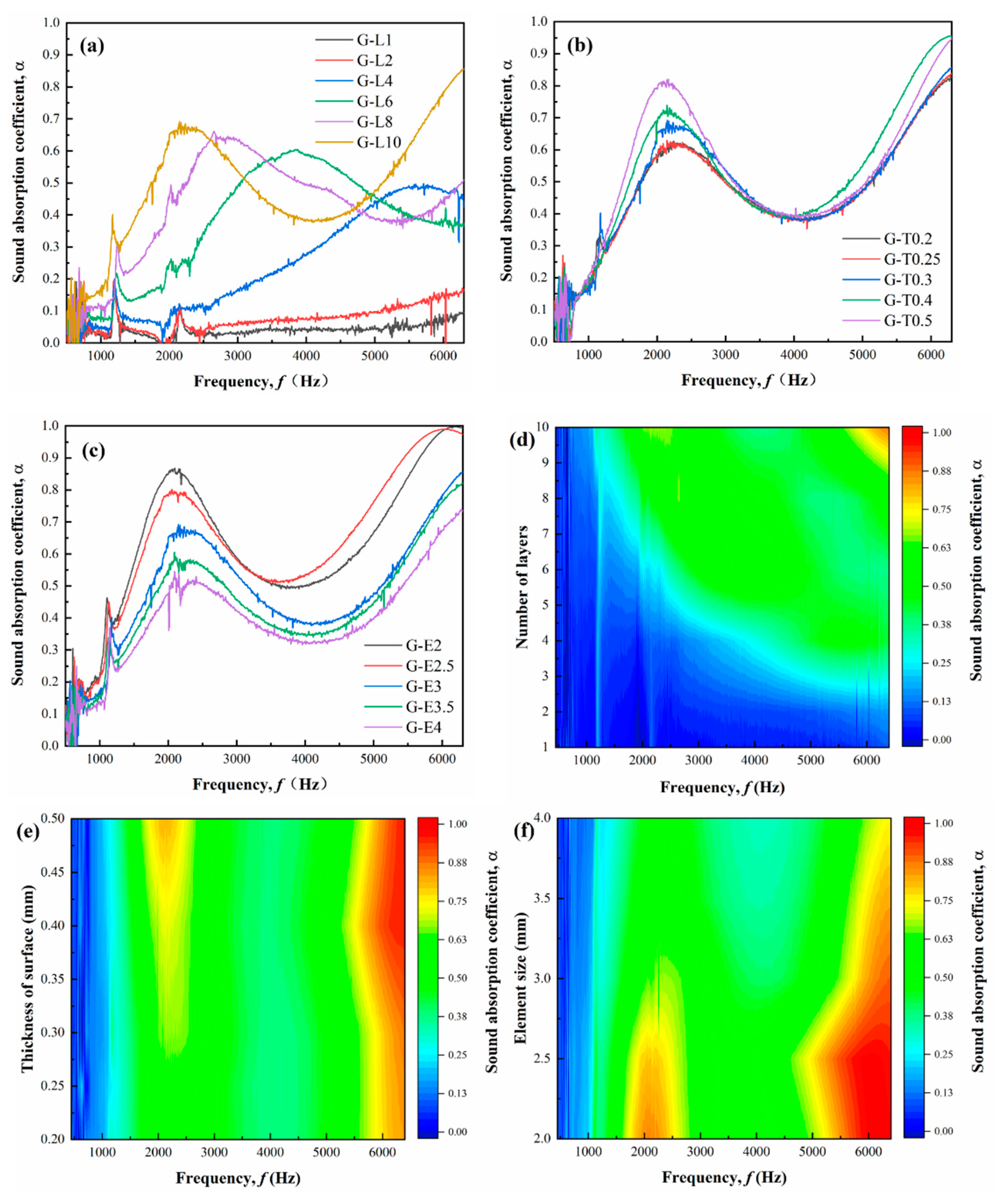
The influence of structural parameters of a uniform Gyroid on the sound absorption coefficient is presented in Figure 9, and the sound absorption properties are listed in Table 5. As shown in Figure 9a, the sound absorption coefficient increases slowly as the frequency increases when the number of layers is less than four. After the number of layers is equal to 4, the sound absorption curves have a peak at 5712 Hz. This frequency, corresponding to the sound absorption peak, shifts to low frequencies as the number of layers increases. This characteristic of moving toward low frequency as the height of the porous structure increases is also found in lattice structures [14]. When the frequency of the incident sound wave is close to the resonance frequency of the system, the air in the perforated plate hole will produce violent vibration friction, and the acoustic energy of the incident sound wave will be significantly attenuated, thus achieving the sound absorption effect. On the contrary, when the frequency of the incident sound wave is far away from the resonance frequency of the system, the sound absorption effect will be weakened. The resonance frequency shifts to 2234 Hz when the number of structural layers increases to ten. It means that increasing the number of layers of TPMS can increase its low-frequency sound absorption effect. However, the increasing number of layers will increase costs and structure thickness. The multi-peaks of sound absorption were observed in the Gyroid with 65% porosity manufactured by stereolithography [16], but the sound absorption peak is only 0.2864 at a frequency of 2264 Hz.
It is noticed that the FWHM of the first peak decreases as the number of layers increases, which means that the width of the first peak narrows. The average sound absorption coefficient increases with the number of layers increasing. The average sound absorption coefficient represents the average sound absorption capacity of the structure from 500 to 6300 Hz. The higher the average sound absorption coefficient, the better the broadband sound absorption effect of the structure. The sound absorption varies with the number of layers and frequency, as shown in Figure 9d, and the optimized design parameter region is located in the upper right corner of the contour.
The influence of the thickness of the surface on the sound absorption coefficient curves is shown in Figure 9b. The sound absorption coefficient at the first peak and flow resistance of the Gyorid increase as the thickness of Gyroid increases, but the frequency at the first peak changes slightly with the increase in thickness. It is demonstrated that the resonance frequency is independent of the thickness of the TPMS surface. The average sound absorption coefficient increases slowly as the thickness of the surface increases. The sound absorption contour with different thicknesses is shown in Figure 9e, and there are two high sound absorption coefficient regions. The first region is located near the frequency of 2000 Hz and has a thickness greater than 0.3 mm. The second region is located near the frequency of 6000 Hz.
The influence of element size on the sound absorption coefficient curves and the sound absorption contour is shown in Figure 9c and Figure 9f, respectively. When the size of the element is reduced from 4 mm to 2 mm, the α1 of the Gyroid increases by 58.97%, and α1 of G-E2 reaches 0.868, which means that the Gyroid with a small element size enhances sound absorption. The average sound absorption coefficient increases by 58.18% as the element size reduces from 4 mm to 2 mm. It is noticed that the flow resistance of G-E2 is 3917 Pa·s/m2, which is 3.6 times that of G-E4 with a 4 mm element size. The greater the flow resistance, the better the sound absorption performance [24]. Although the reduction of unit size can improve the sound absorption performance of the structure, when the element size is 2 mm, the porosity of the structure has decreased to 59.30%, and the weight of the structure has increased. Therefore, the element size can’t be designed too small. The change in sound absorption coefficient and weight should be considered comprehensively.

3.3. Sound absorption properties of graded TPMS

Based on the sound absorption results of uniform Gyroid, graded Gyroid structures were designed and manufactured. The influence of the graded porosity of Gyroid on the sound absorption coefficient is shown in Figure 10. According to the sound absorption coefficient curves, the sound absorption properties were calculated and listed in Table 6. The average sound absorption coefficient of G-QuadraticⅠ with a porosity of 66.84% is 6.75% higher than that of G-E2.5 with a porosity of 65.83%, and it is 27.33% higher than that of G-T0.4 with a porosity of 65.52%. It should be noted that the average sound absorption coefficient of G-QuadraticⅠ is the smallest among the three Type-Ⅰ gradient structures. Additionally, the first peak of sound absorption of all three Type-Ⅰ graded Gyroid structures is all greater than 0.9, which is higher than that of a uniform Gyroid. This result demonstrated that the graded porosity distribution can greatly improve the sound absorption performance of TPMS structures.
When the linear graded distribution is changed from type-Ⅱ to type-Ⅰ, the resonance frequency of the first peak shifts from 2772 Hz to 1534 Hz, and the sound absorption coefficient of the first peak also increases from 0.749 to 0.968. The average sound absorption coefficient of G-LinearⅠ is higher than that of G-LinearⅡ. The resonance frequency of the first peak of G-QuadraticⅠ and G-SinⅠ is 1680 Hz and 1528 Hz, respectively. The resonance frequency of the first peak of G-QuadraticⅡ and G-SinⅡ is 2610 Hz and 2834 Hz, respectively. It is indicated that no matter what type of function change is used, the resonance frequency of the type-Ⅰ structure moves to a lower frequency than that of the type-Ⅱ structure. The average sound absorption coefficient type-Ⅰ structure is higher than that of the type-Ⅱ structure, and the difference between these two types is the largest in the linear graded structure, reaching 33.22%. The flow resistance of G-LinearⅠ is 5082 Pa·s/m2, which is the highest among all TPMS models in this research. It is demonstrated that type-Ⅰ structure with a small element size on the side contacting the sound source has higher sound absorption properties. The type-Ⅱ structure with a large element size on the side contacting the sound source has lower sound absorption properties, and it can be inferred that the larger the size of the surface element, the larger the acoustic reflection surface area, the higher the reflection coefficient, and the lower the sound absorption coefficient. The average sound absorption coefficient of gradient foam metal is 0.6033 [20], which is only 4.83% higher than that of G-LinearⅠ, but there is no obvious resonance peak in the gradient foam metal.
It is noticed that the FWHM of type-Ⅰ is less than type-Ⅱ, and the FWHM of G-SinⅠ is the highest in all graded structures, but the first resonance frequency shifts 1306 Hz from the resonance frequency of G-SinⅡ to high frequency. Compared with GL-10, the FWHM of G-SinⅡ is 142.43% wider. This result illustrates that type-Ⅱ has a relatively wide high-frequency absorption performance. The general periodic structure will generate periodic scattering of sound waves, making it difficult to achieve sufficiently high broadband sound absorption. By designing impedance gradients, high surface porosity can reduce surface scattering at the interface, increase internal porosity, and improve the sound absorption effect.
The mechanism of sound absorption in graded TPMS is illustrated in Figure 10c. The sound wave enters the porous cavity from a small porous structure, and its element size increases from 2 mm to 4 mm. When the sound wave encounters the barrier and returns, the returned sound wave will be scattered many times because it will encounter the hole wall again, which is equivalent to the common sound resonator adding the cavity backing, resulting in the resonance frequency moving to the low frequency. This phenomenon is also observed in the microperforated panel (MPP), where the first peak frequency of the sound absorption coefficient moves to the low frequencies when the height of cavity 2 increases [25]. The large pores close to the sound source make acoustic waves easy to propagate into graded porous structures, and thus the materials have less reflection and more propagated acoustic energy [26]. However, the sound waves of Type-Ⅰ structures are more likely to scatter toward the entrance than those of Type-Ⅱ structures. Therefore, the sound absorption coefficient of Type-Ⅰ structure is higher than that of Type-Ⅱ structure. The superiority of sound absorption of graded porous structure was demonstrated in the two-dimensional continuously graded phononic crystal (CGPC) [27], and the graded structure enhanced acoustic scattering and lengthened the propagation path, subsequently dissipating energy.

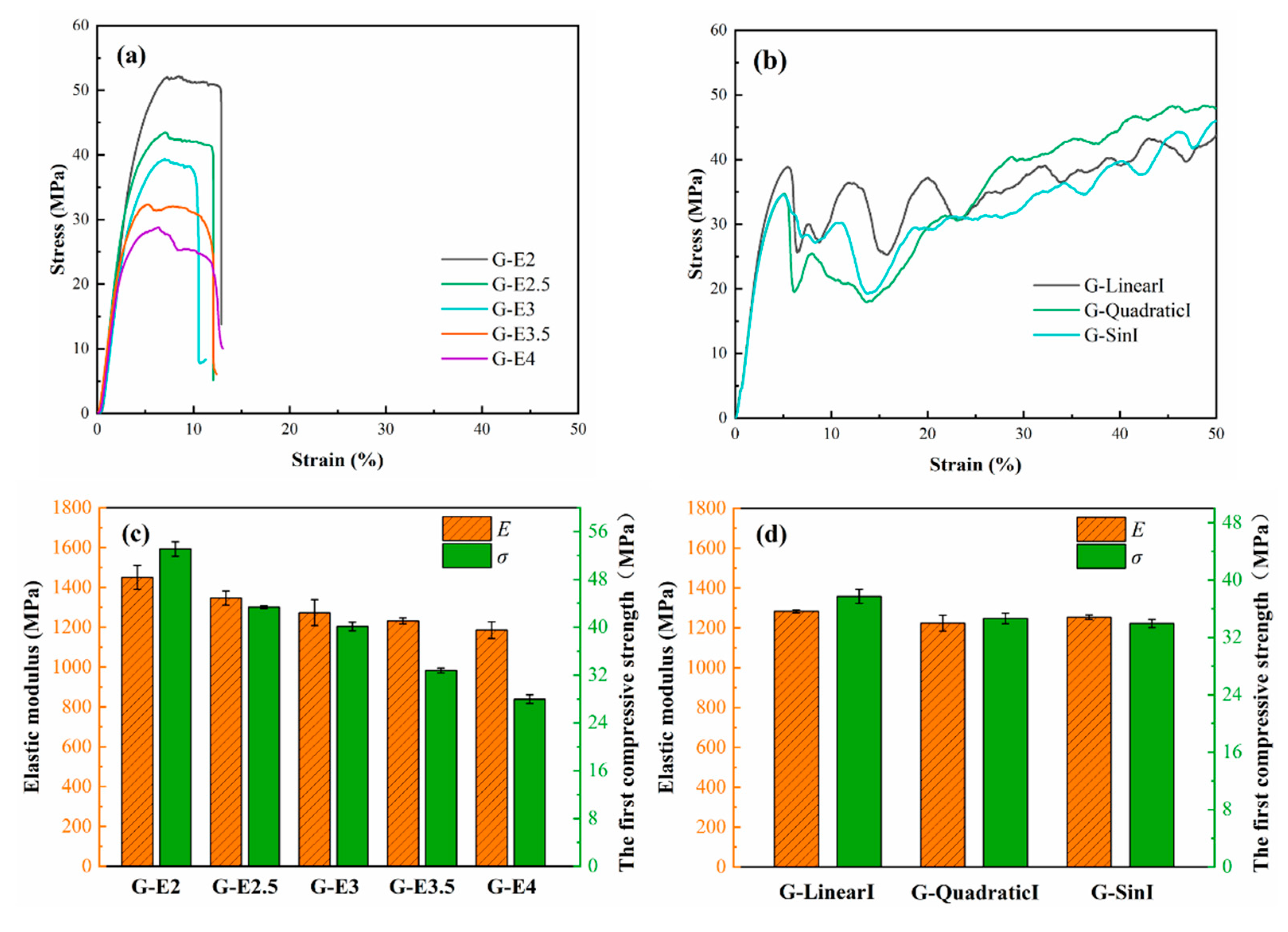
3.4. Mechanical properties of TPMS

The compression results of TPMS are shown in Figure 11. It shows that the uniform Gyroid all has a short yield plateau, and compressive failure strain is between 9.5% and 15%. The first compressive strength and elastic modulus of a uniform Gyroid decrease as the element size increases, as shown in Figure 11c. The compression curves of graded Gyroid structures all have a long yield plateau with over 50% strain, as shown in Figure 11b. There are multiple stress peaks in the yield plateau of graded Gyroid structures due to the fracture of aluminum alloy porous structures in a layer-by-layer way [28].
The elastic modulus of G-LinearⅠ, G-QuadraticⅠ, and G-SinⅠ is 1283.15 ± 8.51 MPa, 1223.62 ± 39.41 MPa, and 1253.77 ± 10.90 MPa, respectively. The difference in the elastic modulus of graded structures is not significant. Compared to uniform structures, the mechanical properties of graded structures have decreased slightly, but due to changes in the mechanical compression mode, their mechanical energy absorption performance has changed. The true first principal strain nephogram of uniform Gyroid and graded Gyroid structures is shown in Figure 12. The true first principal strain nephogram of G-LinearⅠ, G-QuadraticⅠ, and G-SinⅠ show a layer-wise failure pattern, and this phenomenon is also observed at G-FGS with graded structure shot by DIC [29]. This phenomenon is caused by the porosity-graded variation. The compressive strength of Gyroid with high porosity is weaker than that of Gyroid with low porosity, as illustrated in Figure 11c, and the part of the Gyroid with high porosity is prioritized when entering the yielding stage. Therefore, the graded TPMS shows a layer-wise failure pattern, which is common in graded porous structures [30] and graded material structures [31].
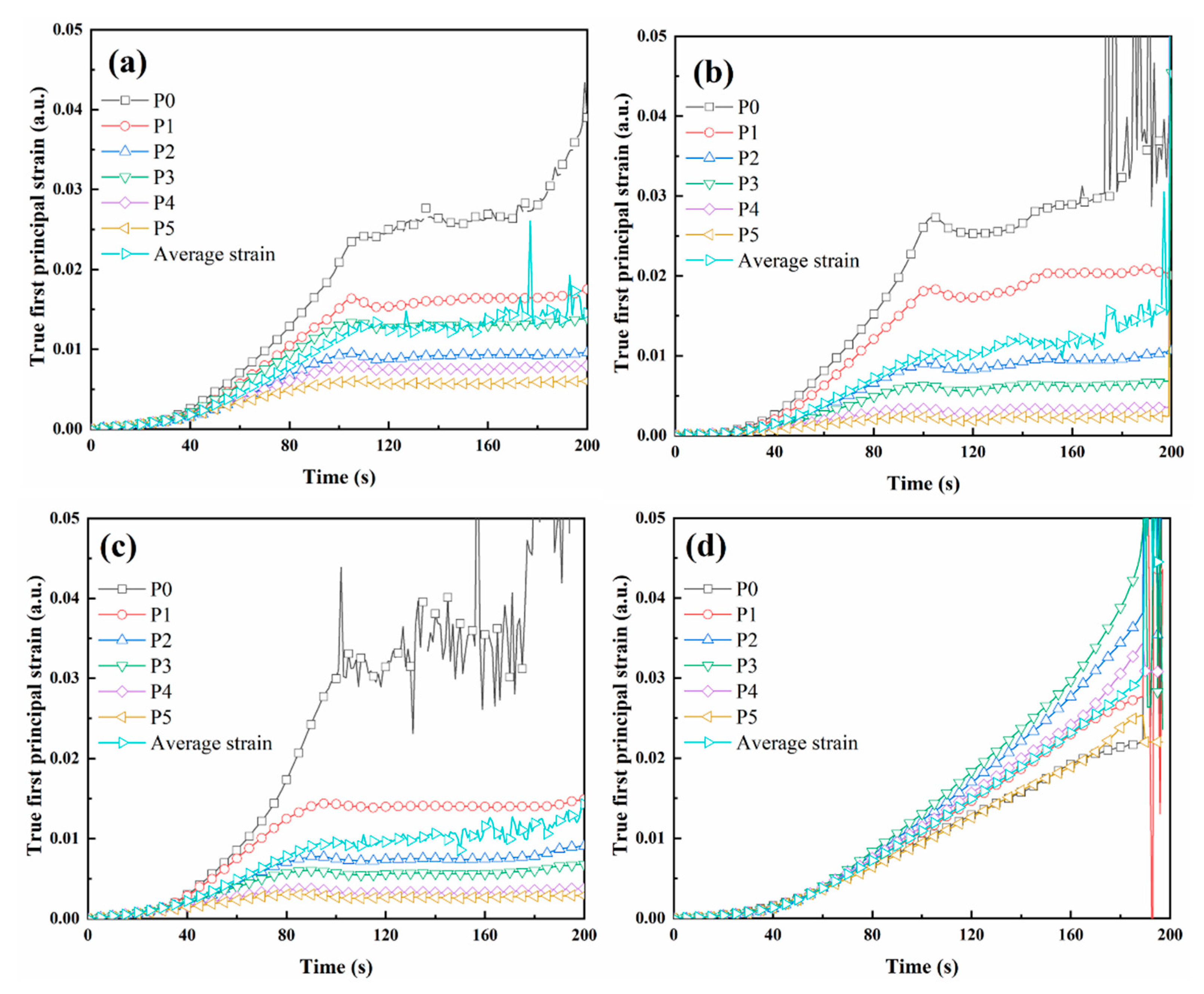
The strain-time curves of six points distributed at the surface of the graded Gyroid were analyzed by DIC, as shown in Figure 13a–c. The ranking of strain magnitude of G-LinearⅠ on the yield platform is P0 >P1 > P3 > P2 > P4 > P5. The ranking of strain magnitude of G-QuadraticⅠ on the yield platform is P0 > P1 > P2 > P3 >P4> P5. The ranking of strain magnitude of G-SinⅠ on the yield platform is P0 > P1 > P2 > P3 >P4> P5. This result shows that the strain decreases layer by layer from top to bottom. The influence of these three functions on the compressive strain of gradient structures lies in the varying magnitude of strain differences. The order of strain differences between P0 and P5 is G-SinⅠ > G-QuadraticⅠ > G-LinearⅠ. This result shows that the linear gradient of porosity has little effect on the structural strain difference, while the sinusoidal gradient has a greater impact on the strain difference.
The true first principal strain nephogram of uniform Gyroid and graded Gyroid structures is shown in Figure 12. The true first principal strain nephogram of G-LinearⅠ, G-QuadraticⅠ, and G-SinⅠ show a layer-wise failure pattern, and this phenomenon is also observed at G-FGS with graded structure shot by DIC [29]. This phenomenon is caused by the porosity-graded variation. The compressive strength of Gyroid with high porosity is weaker than that of Gyroid with low porosity, as illustrated in Figure 11c, and the part of the Gyroid with high porosity is prioritized when entering the yielding stage. Therefore, the graded TPMS shows a layer-wise failure pattern, which is common in graded porous structures [30] and graded material structures [31]. The strain-time curves of six points distributed at the surface of the graded Gyroid were analyzed by DIC, as shown in Figure 13a–c. The ranking of strain magnitude of G-LinearⅠ on the yield platform is P0 >P1 > P3 > P2 > P4 > P5. The ranking of strain magnitude of G-QuadraticⅠ on the yield platform is P0 > P1 > P2 > P3 >P4> P5. The ranking of strain magnitude of G-SinⅠ on the yield platform is P0 > P1 > P2 > P3 >P4> P5. This result shows that the strain decreases layer by layer from top to bottom. The influence of these three functions on the compressive strain of gradient structures lies in the varying magnitude of strain differences. The order of strain differences between P0 and P5 is G-SinⅠ > G-QuadraticⅠ > G-LinearⅠ. This result shows that the linear gradient of porosity has little effect on the structural strain difference, while the sinusoidal gradient has a greater impact on the strain difference.
The strain nephogram of G-E3 presents relatively uniform changes in the initial stage, and then high strain areas appear in the 45° direction and the middle. In the final stage, a 45° shearing band of G-E3 was observed at 180s. The 45° shearing band is commonly observed in the uniform porous structure[32,33]. The strain-time curves of six points distributed at the surface of the uniform Gyroid were analyzed by DIC, as shown in Figure 13d. The strains at these six points do not differ significantly during the initial stage of compression. When the true strain is greater than 0.01, the strain curves of the six points begin to separate significantly, and the difference gradually expands. The true strain growth rate is the fastest at points P2 and P3 in the middle region, while the true strain growth rate is the slowest at points P0 and P5. It indicates that the compression shear failure of uniform TPMS is due to greater strain near the diagonal structure part.
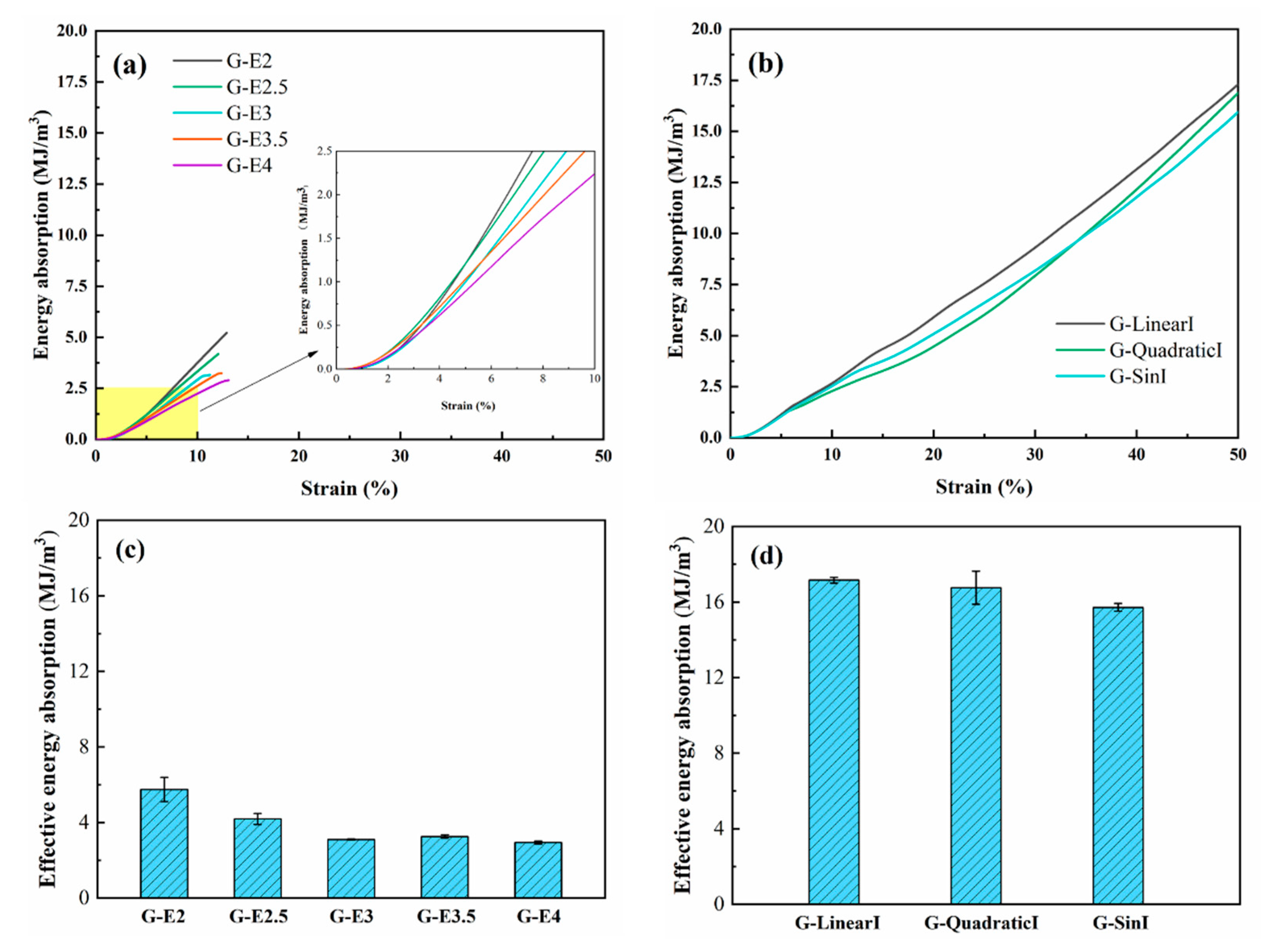
The energy absorption properties of TPMS are shown in Figure 14. The uniform Gyroid is all broken at strain values of 11%-13%, and then structures lose the ability. In terms of quasi-static energy absorption, uniform structures fail due to fractures caused by shear bands, as shown in Figure 12, resulting in lower energy absorption values. However, gradient structures compress layer by layer due to the high to low porosity of the structure, and each layer of the structure can play a buffering role in energy absorption. Therefore, the effective energy absorption strain values of graded Gyroid structures all exceed 50%, and the effective strain was set at 50% according to test standard ISO 13314:2011. The effective energy absorption of G-E2, G-E2.5, G-E3, G-E3.5, and G-E4 is 5.75 ± 0.64 MJ/m3, 4.19 ± 0.29 MJ/m3, 3.10 ± 0.04 MJ/m3, 3.26 ± 0.09 MJ/m3, and 2.94 ± 0.08 MJ/m3, respectively. It is demonstrated that the effective energy absorption increases with the increase in elemental size of the Gyroid. The effective energy absorption of G-Linear is 17.16 ± 0.15 MJ/m3, which is the highest among the three types of graded structures and is four times that of G-E2.5. It shows that the energy absorption properties of graded porous structures are superior to those of uniform porous structures, and this is also demonstrated in the rob-shaped gyroid structures [34].
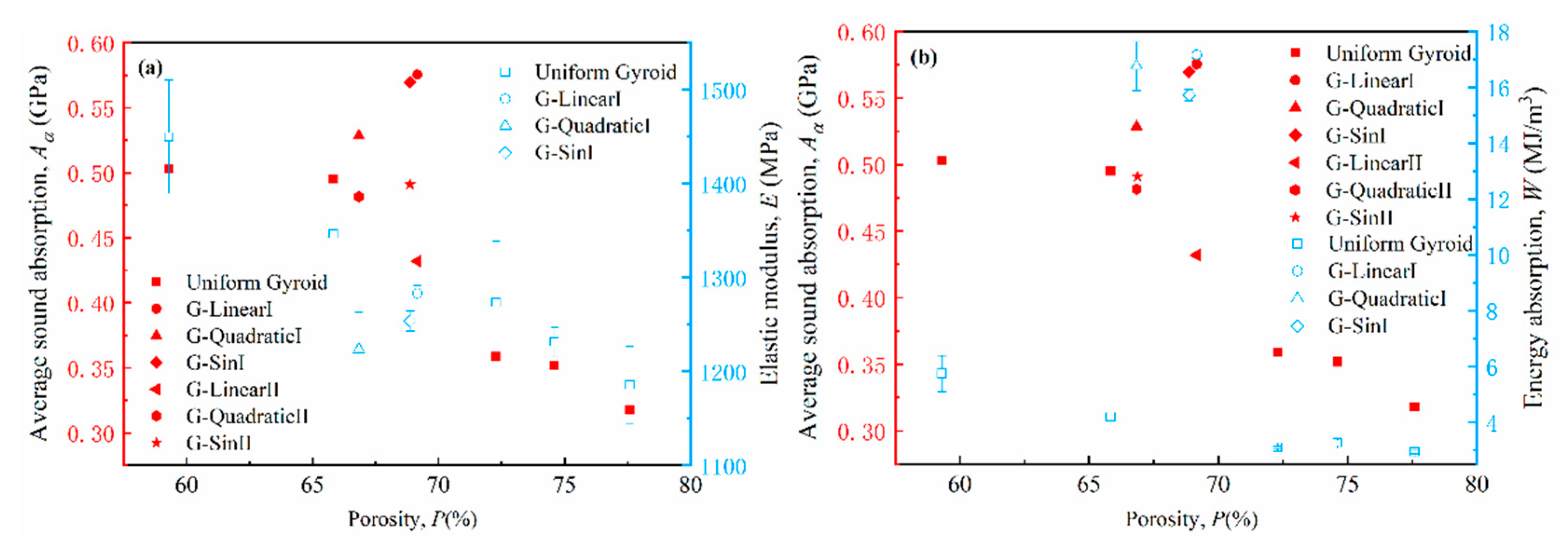
The sound absorption, elastic modulus and energy absorption performances of TPMS are shown in Figure 15. The average sound absorption and elastic modulus of uniform Gyroid is located at the diagonal position in the Figure 15a, and it is illustrated that the average sound absorption and elastic modulus decreases as the porosity increases. It is noticed that the sound absorption of G-SinⅠ and G-LinearⅠ are the highest among these structures, and their elastic modulus also is located at the diagonal position in the Figure 15a. The energy absorption of uniform Gyroid is located at the left lower corner of Figure 15b. The average sound absorption and energy absorption of G-SinⅠ and G-LinearⅠ are the highest and located at the middle upper position. It is proved that under the same weight, G-SinⅠ and G-LinearⅠ have better sound and energy absorption performance.

4. Conclusions

This study proposes a design method for the TPMS structure with lightweight, high-strength, and sound absorption. The sound absorption and compression properties of TPMS were investigated by acoustic impedance tube tests, compression tests, and DIC analysis, and the following conclusions were obtained:
(1) The frequency corresponding to the sound absorption peak shifts to low frequencies as the number of layers increases. The sound absorption coefficient of a uniform Gyroid increases as the number of layers increases, surface thickness increases, and element size decreases. Based on the contour of sound absorption, the optimized structural design interval parameters were obtained.
(2) The graded direction and function have an impact on the sound absorption property. Owing to the multiple scattering, the sound absorption property of Type-Ⅰ graded TPMS is superior to the Type-Ⅱ. It has been demonstrated that graded TPMS has good sound absorption performance at low frequencies. Comparing the three functions, G-LinearⅠ has the highest average sound absorption coefficient and the first sound absorption peaks, and it also has the lowest resonance frequency.
(3) The compressive yield plateau of uniform TPMS is short due to the 45° shearing band, and graded TPMS has a long yield plateau in a layer-wise failure pattern. The length of the yield plateau determines that the energy absorption value of graded TPMS is higher than that of uniform TPMS.

Author Contributions

Conceptualization, M.Z.; methodology, M.Z.; formal analysis, C.L., M.D.; investigation, M.Z., C.L.; data curation, M.Z., M.D., J.L.; writing—original draft preparation, M.Z.; writing—review and editing, C.L., M.D., Y.L., D.W.; visualization, C.L.; supervision, D.W.; project administration, M.Z.; funding acquisition, M.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Guangdong Basic and Applied Basic Research Foundation (No. 2023A1515012704, No.2021A1515110033), and Program for Scientific Research Start-up Funds of Guangdong Ocean University (No. 360302022201).

Data Availability Statement

Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rastegar, N.; Ershad-Langroudi, A.; Parsimehr, H.; Moradi, G. Sound-absorbing porous materials: a review on polyurethane-based foams. Iran. Polym. J. 2022, 31, 83–105. [Google Scholar] [CrossRef]
  2. Cao, L.; Fu, Q.; Si, Y.; Ding, B.; Yu, J. Porous materials for sound absorption. Composites Communications 2018, 10, 25–35. [Google Scholar] [CrossRef]
  3. Allard, J.; Atalla, N. Propagation of sound in porous media: modelling sound absorbing materials; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
  4. INVALID CITATION !!! [4, 5]).
  5. Palma, G.; Mao, H.; Burghignoli, L.; Göransson, P.; Iemma, U. Acoustic Metamaterials in Aeronautics. Appl. Sci. 2018, 8, 971. [Google Scholar] [CrossRef]
  6. Bheekhun, N.; Talib, A.R.A.; Hassan, M.R. Aerogels in Aerospace: An Overview. Advances in Materials Science and Engineering. 2013, 2013, 1–18. [Google Scholar] [CrossRef]
  7. Cobo, P.; Simón, F. Multiple-Layer Microperforated Panels as Sound Absorbers in Buildings: A Review. Buildings 2019, 9, 53. [Google Scholar] [CrossRef]
  8. Choe, H.; Sung, G.; Kim, J.H. Chemical treatment of wood fibers to enhance the sound absorption coefficient of flexible polyurethane composite foams. Compos. Sci. Technol. 2018, 156, 19–27. [Google Scholar] [CrossRef]
  9. Guo, J.; Xiao, Y.; Ren, H.; Chen, H.; Yu, D.; Wen, J. Broadband low-frequency sound insulation of double-panel metastructures with a perforated lattice truss-core sandwich plate. Mech. Syst. Signal Process. 2023, 200. [Google Scholar] [CrossRef]
  10. Xie, S.; Yang, S.; Yang, C.; Wang, D. Sound absorption performance of a filled honeycomb composite structure. Appl. Acoust. 2020, 162. [Google Scholar] [CrossRef]
  11. Xiang-Nan, K.; Bin, L.; Zhong-Hua, L.; Peng-Fei, Z.; Chao, S. Research on Sound Absorption Properties of Tri-Periodic Minimal Surface Sandwich Structure of Selective Laser Melting Titanium Alloy. Mater. Trans. 2023, 64, 861–868. [Google Scholar] [CrossRef]
  12. Gama, N.V.; Ferreira, A.; Barros-Timmons, A. Polyurethane Foams: Past, Present, and Future. Materials 2018, 11, 1841. [Google Scholar] [CrossRef]
  13. Johnston, W.; Sharma, B. Additive manufacturing of fibrous sound absorbers. Addit. Manuf. 2021, 41. [Google Scholar] [CrossRef]
  14. Monkova, K.; Vasina, M.; Monka, P.P.; Kozak, D.; Vanca, J. Effect of the Pore Shape and Size of 3D-Printed Open-Porous ABS Materials on Sound Absorption Performance. Materials 2020, 13, 4474. [Google Scholar] [CrossRef]
  15. Zieliński, T.G.; Opiela, K.C.; Pawłowski, P.; Dauchez, N.; Boutin, T.; Kennedy, J.; Trimble, D.; Rice, H.; Van Damme, B.; Hannema, G.; et al. Reproducibility of sound-absorbing periodic porous materials using additive manufacturing technologies: Round robin study. Addit. Manuf. 2020, 36. [Google Scholar] [CrossRef]
  16. Lu, J.Y.; AlZaabi, F.; Teneiji, M.A.; Lee, D.W. Acoustic band structures of Architectured Materials based on Triply Periodic Minimal Surfaces. In Proceedings of the 2021 Fifteenth International Congress on Artificial Materials for Novel Wave Phenomena (Metamaterials); 2021; pp. 1–3. [Google Scholar]
  17. Abueidda, D.W.; Jasiuk, I.; Sobh, N.A. Acoustic band gaps and elastic stiffness of PMMA cellular solids based on triply periodic minimal surfaces. Mater. Des. 2018, 145, 20–27. [Google Scholar] [CrossRef]
  18. Yang, W.; An, J.; Chua, C.K.; Zhou, K. Acoustic absorptions of multifunctional polymeric cellular structures based on triply periodic minimal surfaces fabricated by stereolithography. Virtual Phys. Prototyp. 2020, 15, 242–249. [Google Scholar] [CrossRef]
  19. Zhang, X.; Qu, Z.; Wang, H. Engineering Acoustic Metamaterials for Sound Absorption: From Uniform to Gradient Structures. iScience 2020, 23, 101110. [Google Scholar] [CrossRef]
  20. Yang, X.; Shen, X.; Bai, P.; He, X.; Zhang, X.; Li, Z.; Chen, L.; Yin, Q. Preparation and Characterization of Gradient Compressed Porous Metal for High-Efficiency and Thin-Thickness Acoustic Absorber. Materials 2019, 12, 1413. [Google Scholar] [CrossRef]
  21. Feng, Y.; Zong, D.; Hou, Y.; Yin, X.; Zhang, S.; Duan, L.; Si, Y.; Jia, Y.; Ding, B. Gradient structured micro/nanofibrous sponges with superior compressibility and stretchability for broadband sound absorption. J. Colloid Interface Sci. 2021, 593, 59–66. [Google Scholar] [CrossRef]
  22. Yang, K.; Long, G.; Tang, Z.; Pan, X.; Su, W.; Xie, Y. Mechanical and Acoustic Properties of Ceramsite Sound Absorbing Boards with Gradient Structure. Acoust. Aust. 2022, 50, 393–403. [Google Scholar] [CrossRef]
  23. Zhang, X.; Qu, Z.; Tian, D.; Fang, Y. Acoustic characteristics of continuously graded phononic crystals. Appl. Acoust. 2019, 151, 22–29. [Google Scholar] [CrossRef]
  24. Qunli, W. Empirical relations between acoustical properties and flow resistivity of porous plastic open-cell foam. Appl. Acoust. 1988, 25, 141–148. [Google Scholar] [CrossRef]
  25. Yan, S.; Wu, J.; Chen, J.; Mao, Q.; Zhang, X. Design of Honeycomb Microperforated Structure with Adjustable Sound Absorption Performance. Shock. Vib. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
  26. Zhang, X.H.; Qu, Z.G.; He, X.C.; Lu, D.L. Experimental study on the sound absorption characteristics of continuously graded phononic crystals. AIP Adv. 2016, 6, 105205. [Google Scholar] [CrossRef]
  27. Zhang, X.; Qu, Z.; Xu, Y. Enhanced sound absorption in two-dimensional continuously graded phononic crystals. Jpn. J. Appl. Phys. 2019, 58, 090904. [Google Scholar] [CrossRef]
  28. Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J.M. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef]
  29. Zhang, X.; Jiang, L.; Yan, X.; Wang, Z.; Li, X.; Fang, G. Revealing the apparent and local mechanical properties of heterogeneous lattice: a multi-scale study of functionally graded scaffold. Virtual Phys. Prototyp. 2022, 18. [Google Scholar] [CrossRef]
  30. Yang, L.; Mertens, R.; Ferrucci, M.; Yan, C.; Shi, Y.; Yang, S. Continuous graded Gyroid cellular structures fabricated by selective laser melting: Design, manufacturing and mechanical properties. Mater. Des. 2019, 162, 394–404. [Google Scholar] [CrossRef]
  31. Zhang, M.; Yang, Y.; Wang, D.; Song, C.; Chen, J. Microstructure and mechanical properties of CuSn/18Ni300 bimetallic porous structures manufactured by selective laser melting. Mater. Des. 2019, 165, 107583. [Google Scholar] [CrossRef]
  32. Liu, F.; Ran, Q.; Zhao, M.; Zhang, T.; Zhang, D.Z.; Su, Z. Additively Manufactured Continuous Cell-Size Gradient Porous Scaffolds: Pore Characteristics, Mechanical Properties and Biological Responses In Vitro. Materials 2020, 13, 2589. [Google Scholar] [CrossRef]
  33. Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
  34. Wang, Y.; Liu, F.; Zhang, X.; Zhang, K.; Wang, X.; Gan, D.; Yang, B. Cell-size graded sandwich enhances additive manufacturing fidelity and energy absorption. Int. J. Mech. Sci. 2021, 211, 106798. [Google Scholar] [CrossRef]
Preprints 85761 g001
Figure 1. Models of uniform Gyroid with different layers, surface thickness and element size.
Figure 1. Models of uniform Gyroid with different layers, surface thickness and element size.
Preprints 85761 g001
Preprints 85761 g002
Figure 2. The functional relationship curves between element size and structural distance.
Figure 2. The functional relationship curves between element size and structural distance.
Preprints 85761 g002
Preprints 85761 g003
Figure 3. Designed model of the graded Gyroid structures.
Figure 3. Designed model of the graded Gyroid structures.
Preprints 85761 g003
Preprints 85761 g004
Figure 4. Designed model of the graded Gyroid structures.
Figure 4. Designed model of the graded Gyroid structures.
Preprints 85761 g004
Preprints 85761 g005
Figure 5. Two-microphone impedance tube equipment.
Figure 5. Two-microphone impedance tube equipment.
Preprints 85761 g005
Preprints 85761 g006
Figure 6. DIC test: (a) DIC test equipment and (b) strain of six points were extracted by DIC.
Figure 6. DIC test: (a) DIC test equipment and (b) strain of six points were extracted by DIC.
Preprints 85761 g006
Preprints 85761 g007
Figure 7. Uniform Gyroid manufactured by LPBF.
Figure 7. Uniform Gyroid manufactured by LPBF.
Preprints 85761 g007
Preprints 85761 g008
Figure 8. Measurement of Gyroid with different thickness.
Figure 8. Measurement of Gyroid with different thickness.
Preprints 85761 g008
Preprints 85761 g009
Figure 9. Influence of structural parameters on the sound absorption curves of uniform Gyroid: (a) number of layers, (b) thickness of surface, and (c) element size. Influence of structure parameters on contour of sound absorption (d) number of layers, (e) thickness of surface, and (f) element size.
Figure 9. Influence of structural parameters on the sound absorption curves of uniform Gyroid: (a) number of layers, (b) thickness of surface, and (c) element size. Influence of structure parameters on contour of sound absorption (d) number of layers, (e) thickness of surface, and (f) element size.
Preprints 85761 g009
Preprints 85761 g010
Figure 10. Influence of the graded porosity of Gyroid on the (a) sound absorption coefficient, (b) average sound absorption coefficient, (c) mechanism of sound absorption of graded TPMS.
Figure 10. Influence of the graded porosity of Gyroid on the (a) sound absorption coefficient, (b) average sound absorption coefficient, (c) mechanism of sound absorption of graded TPMS.
Preprints 85761 g010
Preprints 85761 g011
Figure 11. Compression results of TPMS: (a) compressive stress-strain curves of uniform Gyroid, (b) compressive stress-strain curves of graded Gyroid, (c) compressive properties of uniform Gyroid, and (d) compressive properties of graded Gyroid.
Figure 11. Compression results of TPMS: (a) compressive stress-strain curves of uniform Gyroid, (b) compressive stress-strain curves of graded Gyroid, (c) compressive properties of uniform Gyroid, and (d) compressive properties of graded Gyroid.
Preprints 85761 g011
Preprints 85761 g012
Figure 12. The true first principal strain nephogram of TPMS analyzed by DIC.
Figure 12. The true first principal strain nephogram of TPMS analyzed by DIC.
Preprints 85761 g012
Preprints 85761 g013
Figure 13. The true first principal strain-time curves analyzed by DIC: (a) G-linear, (b) G-quadratic, (c) G-sin, and (d) G-E3.
Figure 13. The true first principal strain-time curves analyzed by DIC: (a) G-linear, (b) G-quadratic, (c) G-sin, and (d) G-E3.
Preprints 85761 g013
Preprints 85761 g014
Figure 14. Energy absorption of TPMS: (a) energy absorption curves of uniform Gyroid, (b) energy absorption curves of graded Gyroid, (c) effective energy absorption of uniform Gyroid, and (d) effective energy absorption of graded Gyroid.
Figure 14. Energy absorption of TPMS: (a) energy absorption curves of uniform Gyroid, (b) energy absorption curves of graded Gyroid, (c) effective energy absorption of uniform Gyroid, and (d) effective energy absorption of graded Gyroid.
Preprints 85761 g014
Preprints 85761 g015
Figure 15. (a) Sound absorption and elastic modulus performance of TPMS, (b) Sound absorption and energy absorption performance of TPMS.
Figure 15. (a) Sound absorption and elastic modulus performance of TPMS, (b) Sound absorption and energy absorption performance of TPMS.
Preprints 85761 g015
Table 1. Structural parameters of uniform Gyroid.
Table 1. Structural parameters of uniform Gyroid.
Specimens Number of layers h/mm Element size/mm Thickness/mm Porosity/%
G-L1 1 3 3 0.3 72.29
G-L2 2 6 3 0.3 72.29
G-L4 4 12 3 0.3 72.29
G-L6 6 18 3 0.3 72.29
G-L8 8 24 3 0.3 72.29
G-L10 10 30 3 0.3 72.29
G-T0.2 10 30 3 0.2 80.57
G-T0.25 10 30 3 0.25 75.21
G-T0.3 10 30 3 0.3 72.29
G-T0.4 10 30 3 0.4 65.52
G-T0.5 10 30 3 0.5 60.51
G-E2 15 30 2 0.3 59.30
G-E2.5 12 30 2.5 0.3 65.83
G-E3 10 30 3 0.3 72.29
G-E3.5 8.6 30 3.5 0.3 74.60
G-E4 7.5 30 4 0.3 77.59
Table 2. Structural parameters of graded Gyroid structures.
Table 2. Structural parameters of graded Gyroid structures.
Specimens Number of layers h/mm Element size/mm Thickness/mm Porosity/%
G-Linear I 10 30 2→4 0.3 69.16
G-Linear II 10 30 4→2 0.3 69.16
G-Quadratic I 10 30 2→4 0.3 66.84
G-Quadratic II 10 30 4→2 0.3 66.84
G-Sin I 10 30 2→4 0.3 68.87
G-Sin II 10 30 4→2 0.3 68.87
Table 3. The processing parameter for LPBF.
Table 3. The processing parameter for LPBF.
Laser Power
(W)		 Scanning Speed
(mm/s)		 Layer Thickness
(mm)		 Scanning Space
(mm)
150 1300 0.03 0.09
Table 4. Chemical composition of AlSi7Mg powder.
Table 4. Chemical composition of AlSi7Mg powder.
Element Al Si Mg Cu Fe Mn Ni O
Composition (wt. %) Bal. 6.730 0.678 0.045 0.281 0.198 0.012 0.070
Table 5. Sound absorption properties of uniform Gyroid.
Table 5. Sound absorption properties of uniform Gyroid.
Specimen Porosity (%) f1 (Hz) α1 FWHM (Hz) Aα Flow resistance (Pa·s/m2)
G-L1 72.29 - - - 0.038 4382
G-L2 72.29 - - - 0.055 2561
G-L4 72.29 5712 0.498 4379 0.152 3429
G-L6 72.29 3866 0.605 3938 0.253 2454
G-L8 72.29 2652 0.661 3929 0.313 1829
G-L10 72.29 2234 0.685 1624 0.359 1800
G-T0.2 80.57 2244 0.627 3224 0.374 1640
G-T0.25 75.21 2144 0.630 2866 0.375 1734
G-T0.3 72.29 2234 0.685 1624 0.359 1800
G-T0.4 65.52 2146 0.739 2656 0.415 2234
G-T0.5 60.51 2166 0.821 2323 0.430 2348
G-E2 59.30 2096 0.868 2747 0.503 3917
G-E2.5 65.83 2054 0.802 3081 0.495 3895
G-E3 72.29 2234 0.685 1624 0.359 1800
G-E3.5 74.60 2094 0.606 2890 0.352 1403
G-E4 77.59 2094 0.546 2991 0.318 1076
Table 6. Sound absorption properties of graded Gyroid.
Table 6. Sound absorption properties of graded Gyroid.
Specimen Porosity (%) f1 (Hz) α1 FWHM (Hz) Aα Flow resistance (Pa·s/m2)
G-Linear I 69.16 1534 0.968 2815 0.5755 5082
G-Linear II 69.16 2772 0.749 5436 0.4320 3032
G-Quadratic I 66.84 1680 0.936 2205 0.5284 3341
G-Quadratic II 66.84 2610 0.817 6009 0.4815 4026
G-Sin I 68.87 1528 0.964 3425 0.5697 4666
G-Sin II 68.87 2834 0.852 7411 0.4910 4545
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated