Preprint
Article
Relative Orderings of Modified Proportional Hazard Rates and Modified Proportional Reversed Hazard Rates Models
Altmetrics
Downloads
103
Views
13
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
21 September 2023
Posted:
22 September 2023
You are already at the latest version
Alerts
Abstract
In this paper, we identify several relative ordering properties of the modified proportional hazard rate and modified proportional reversed hazard rate models. For this purpose, we use two well-known relative orderings, namely the relative hazard rate ordering and the relative reversed hazard rate ordering. The investigation is to see how a relative ordering between two possible base distributions for the response distributions in these models is preserved when the parameters of the underlying models are changed. We will give some examples to illustrate the results and the conditions under which they are obtained.
Keywords:
Subject: Computer Science and Mathematics - Probability and Statistics
MSC: 62N05, 90B25, 62E10, 65C20
1. Introduction
The parameters of a distribution are typically considered to be real or perhaps vector values. In the literature, families of distributions are considered that are characterized by having a parameter that is itself a distribution function. These families are called semiparametric because they also contain a real parameter. Choosing the parameter that is first a distribution function is one possible way to use a semiparametric model. The underlying distribution is the formal name for this distribution function. In practice, the selection of an underlying distribution leads to the selection of a parametric model, but the selection is limited to families with the structure of the semiparametric model.
The underlying distribution F might already have one or more parameters, in which case a semiparametric family might provide a way to include a new parameter, extending the family from which F originates. One can imagine that the standard families of the Gamma and Weibull distributions are derived from the exponential distribution via semiparametric families that include a second parameter. The Weibull and Gamma families can both be found as special cases of a three-parameter family using the same technique. The study of semiparametric families is therefore advantageous for two reasons: it provides a new understanding of traditional distribution families, and it offers strategies for extending families to make data fitting more flexible (see, e.g., Marshall and Olkin [18]).
Stochastic orderings of random variables have long been a useful tool for making comparisons between probability distributions (see Müller and Stoyan [19], Shaked and Shanthikumar [23], Belzunce et al. [3], and Li and Li [16]). Some researchers used stochastic orders comparing distributions in terms of the magnitude of random variables to perform stochastic comparisons between semiparametric models, including those presented in equations (1), (5), and (9) in Section 2. To this end, we quantify the effect of varying the parameters of the model on the variation of the response variables and, furthermore, the effect of changing the underlying distribution on changing the distribution of the response variables using several known stochastic orders. For example, in the context of the proportional hazard rate (PHR) model for the case where is a random variable (frailty), Gupta and Kirmani [10] and subsequently Xu and Li [24] identified some stochastic ordering properties of the model. Considering the proportional reversed hazard rates (PRHR) model, Di Crescenzo [6] made some stochastic comparisons between two candidate distributions of the model that differ in their parameters. Kirmani and Gupta [13] derived some stochastic ordering results for the model proportional odds rates (POR) model.
Recently, however, many researchers have focused on stochastic orders that compare lifetime distributions according to aging behavior, namely the faster aging stochastic orders. One of the key ideas in reliability theory and survival analysis is stochastic aging. It broadly outlines the pattern of aging/degradation of a system over time. Three different notions of aging are presented in the literature: positive aging, negative aging, and no aging. Positive aging implies a stochastically decreasing remaining lifetime of the system, while negative aging implies just the opposite. The system does not mature with time if there is no aging. To study different characteristics of system aging, various aging classes (including increasing failure rate (IFR), decreasing failure rate (DFR), increasing failure rate on average (IFRA), decreasing failure rate on average (DFRA), increasing likelihood ratio (ILR), and decreasing likelihood ratio (DLR), to name a few) have been presented in the literature based on these three aging principles. The reader can consult Barlow and Proschan [2] and Lai and Xie [15] for further discussion on this topic. In addition to these ideas about aging, relative aging is a useful concept to use when studying system reliability. Relative aging is used to measure how a system changes over time relative to another system.
In real life, there are many situations where we deal with multiple systems of the same type (e.g., TVs from different manufacturers, CPUs from different brands, etc.). In these circumstances, we often encounter the following problem: how to determine whether one system is aging faster than others over time? The idea of relative aging provides a compelling answer to this problem. When dealing with the crossover hazards/medium remaining life phenomena, another component of relative aging proves helpful. Many real-life situations involve this type of circumstance. For example, when Pocock et al. [20] examined survival data on the effects of two different treatments on breast cancer patients and became aware of the phenomenon of crossover hazards. In addition, Champlin et al. [4] described several cases in which the superiority of one treatment over another lasted only for a short period of time. The above considerations suggest that increasing/decreasing hazard ratio models are a viable option in a variety of real-world scenarios. In fact, Kalashnikov and Rachev [12] have developed a concept of relative aging based on the monotonicity of the ratio of two hazard rate functions called relative hazard rate order. This concept is known as faster hazard rate aging. Sengupta and Deshpande [22] presented another idea in a similar way based on the monotonicity of the ratio of two cumulative hazard rate functions. Rezaei et al. [21] proposed a relative order based on the ratio of the reversed hazard rates of two random lifetimes and called it relative reversed hazard rate order.
The aim of this paper is to perform stochastic comparisons between two newly defined semiparametric models, the modified proportional hazard rate model and the modified proportional reversed hazard rate model, corresponding to the relative hazard rate and the relative reversed hazard rate order.
The rest of the paper is organized as follows. In Section 2 we give some advanced preliminary considerations and auxiliary results. In Section 3, we consider the modified proportional hazard rate model for comparison in terms of relative hazard rate order. In Section 4, we consider the modified proportional reversed hazard rate model to give some ordering properties according to the relative reversed hazard rate order. In Section 5, we conclude the paper with a more detailed summary and provide an outlook on possible future studies.
2. Preliminaries
In this section we give some mathematical definitions of the notions that will be utilized in this paper. In the literature, many semiparametric families of distributions have been introduced and studied. Among these models some of them find their applicability in the context of lifetime events. The Cox’s PHR model is of the important and frequently used such semiparametric family of distributions (see, Cox [5]). For a review on the PHR model we refer the reader to Kumar and Klefsjö [14]. Let us consider the parameter , called the frailty parameter, then the PHR model is defined as
where is the survival function (sf) of the response random variable and is the baseline sf. Let have an absolutely continuous distribution function (cdf) , with probability density function (pdf) Then, the hazard rate (hr) of , as important reliability quantity in survival analysis, measures the instantaneous risk for failure of a device with lifetime at a certain age (t, say). The hr of for all which fulfills is defined as follows:
It is well-known that h characterizes the underlying sf, , as follows:
Suppose that is the hr function associated with the sf (1), then, it is plainly seen that for every for which
In contrast to the PHR model, the PRHR model was introduced by Gupta et al. [9]. We refer the reader to Gupta and Gupta [11] for further descriptions of the PRHR model. In the PRHR model, a positive parameter, , called the resilience parameter, is considered. The PRHR model is then defined as
in which is the cdf of the response random variable and is the baseline cdf or the underlying distribution function in the model. The reversed hazard rate (rhr) of , as another reliability quantity, measures the risk for failure of a device (with original lifetime ) in the past at a certain time point t at which the device is found to be inactive. The rhr of for all which is derived via the following relation:
It has been verified that characterizes the underlying cdf, F, as below:
Let us now assume that is the rhr function of the distribution with the cdf (5). Then, it is readily realized for all for which that
Another reputable semiparametric family of distributions is the POR model (see, e.g., Marshall and Olkin [17]). This model is defined with cdf
In some situations the following model is alternatively utilized:
The odds rate function of , measures the relative odd of the event in terms of the event where t is some point of time. The odds rate function of for all which defined as follows:
We assume that is the odds rate function of the distribution with the cdf (9). Then, it is easily verified for all for which that
Balakrishnan et al. [1], utilized the PHR (resp. PRHR) model as baseline model in (9) (resp. (10)) to propose two new models, referred to as modified proportional hazard rates (MPHR) and modified proportional reversed hazard rates (MPRHR) models.
Suppose that is a baseline random variable with survival function . Let are independent and identically distributed (i.i.d.) lifetimes of n components of a system with a common distribution function . Then, are said to follow the MPHR model with tilt parameter , modified proportional hazard rate and baseline survival function (denoted as ) if, and only if,
For the case , (13) simply reduces to the PHR model. The MPHR model in (13) includes some well-known distributions such as extended exponential and extended Weibull distributions (Marshall and Olkin [18]), extended Pareto distribution (Ghitany [7]) and extended Lomax distribution (Ghitany et al. [8]).
On the other hand, suppose are i.i.d. lifetimes of n components of a system with a common distribution functions F. Then, are said to follow the MPRHR model with tilt parameter , modified proportional reversed hazard rate and baseline distribution function F (denoted as ) if and only if
Note that the PRHR model is a sub-model of (14) when .
We assume that the random variables X and Y have distribution functions F and G, survival functions and , density functions f and g, hazard rate functions and and reversed hazard rate functions and , respectively. To compare the magnitude of random variables some notions of stochastic orders are introduced below.
Definition 1.
Suppose that X and Y are two non-negative random variables which denote the lifetime of two systems. The random variable X is then said to be smaller than the random variable Y in the
- (i)
- usual stochastic order (denoted by ) if,
- (ii)
-
hazard rate order (denoted by ) if,or equivalently, if for all .
- (iii)
-
reversed hazard rate order (denoted by ) if,or equivalently, if for all .
- (iv)
- likelihood ratio order (denoted by ) if,
- (v)
- relative hazard rate order (denoted by ) if,.
- (vi)
- relative reversed hazard rate order (denoted by ) if,
Some stochastic orders in Definition 1 are connected to each other. In this regard, implies and also implies . Furthermore, gives and also yields For further relations and properties of the stochastic orders and we refer the reader to Shaked and Shanthikumar [23]. For more descriptions of the relative order we refer the reader to Kalashnikov and Rachev [12] and also Sengupta and Deshpande [22]. For further properties of the relative order the reader can see Rezaei et al. [21].
3. Results on relative orderings of MPHR distributions
In this section, we obtain a relative ordering property in the MPHR model according to the relative hazard rate order. We will consider the MPHR model in two settings where two sets of parameters and which are possibly different are assigned and also possibly different baseline sfs and are taken into account. Finding conditions on and and also conditions on and to establish the preservation of the relative hazard rate ordering property in the MPHR model is the main objective of this section.
Before stating next result we introduce some notation. Let and have pdfs f and g, and sfs and , respectively, and, further, and . Then, using (13), the sfs of and which are denoted by and , respectively, can be written as follows:
Now, let us denote by and the pdfs of and , which can be obtained by taking derivatives of cdfs in (15) as follows:
Appealing to (15) together with (16) the hazard rate function of and the hazard rate function of are acquired as:
where and are the hazard rate functions of and respectively, and the function is given by
We define here two measures of relative hazard rates of and with hazard rate functions and respectively. Let us denote two limiting points of hazard rates ratio as follows:
Theorem 1.
Let and have sfs and , respectively. Let and where and for every . Let be a function of , and , such that
If
then
Proof.
It suffices to prove that is non-increasing in . Since,
and, by assumption, is non-increasing in , thus it is sufficient to to show that is non-increasing in , which holds if, and only if,
Denote . We have:
where the last inequality follows from the fact that, for and ,
and that yields
as it implies that for all . The right hand side of inequality in (19) is negative, if and only if,
in which
The inequality in (20) is satisfied if
So, , for all which further implies that
□
In the following example, we show that the result of Theorem 1 is applicable.
Example 1.
Let us write when X follows Weibull distribution with shape parameter c and scale parameter d, with , having sf Suppose that and . Assume that and with and and, further, and We can observe that and have hrs and . Therefore,
Hence, We can observe that
and, on the other hand, we can see that
Thus, obviously, , and using Theorem 1 we conclude that . In Figure 1, the graph of is plotted to exhibit that it is non-increasing in
Remark 1.
In the context of Theorem 1, the obtained result is immediately followed when and . To prove this claim, note that if and , then, for all and for every , one has
Therefore, the parenthetical statement in right hand side of inequality given in (19) is non-positive. Thus, it is straightforward that if and and then . In this case the additional supremum condition in Theorem 1 could be omitted.
The following theorem states another setting for the parameters of two MPHR distributions so that the result of Theorem 1 is obtained under a different condition.
Theorem 2.
Let and have sfs and , respectively. Let and where and for every . Let be a function of , and also such that
If
then
Proof.
Similarly, as in the proof of Theorem 1, we need to demonstrate that is non-increasing in , which holds if, and only if,
Analogously as in the proof of Theorem 1, one has
in which the last inequality follows because, for and ,
and moreover that gives
which implies that for all . The right hand side of the inequality in (23) is negative, if and only if,
in which . The inequality in (24) stands valid if
Thus, , which in turn gives
□
The following example provides a situation where the result of Theorem 2 is applicable.
Example 2.
Suppose that follows gamma distribution with sf and has sf It is easily seen that the hrs of and are and , respectively. Therefore,
Now, since is non-increasing in t, thus We assume that and with and . It is observable that
and, in parallel, it is seen that
Therefore, clearly, , and thus an application of Theorem 2 concludes that . In Figure 2, the graph of is plotted to indicate that this ratio is non-increasing in
4. Results on relative orderings of MPRHR distributions
In this section, we investigate the relative reversed hazard rate ordering property in two MPRHR models with possibly different sets of parameters , where and , and also under possibly different baseline distributions F and G.
Figure 2.
Plot of the hazard rate ratio in Example 2 for and when
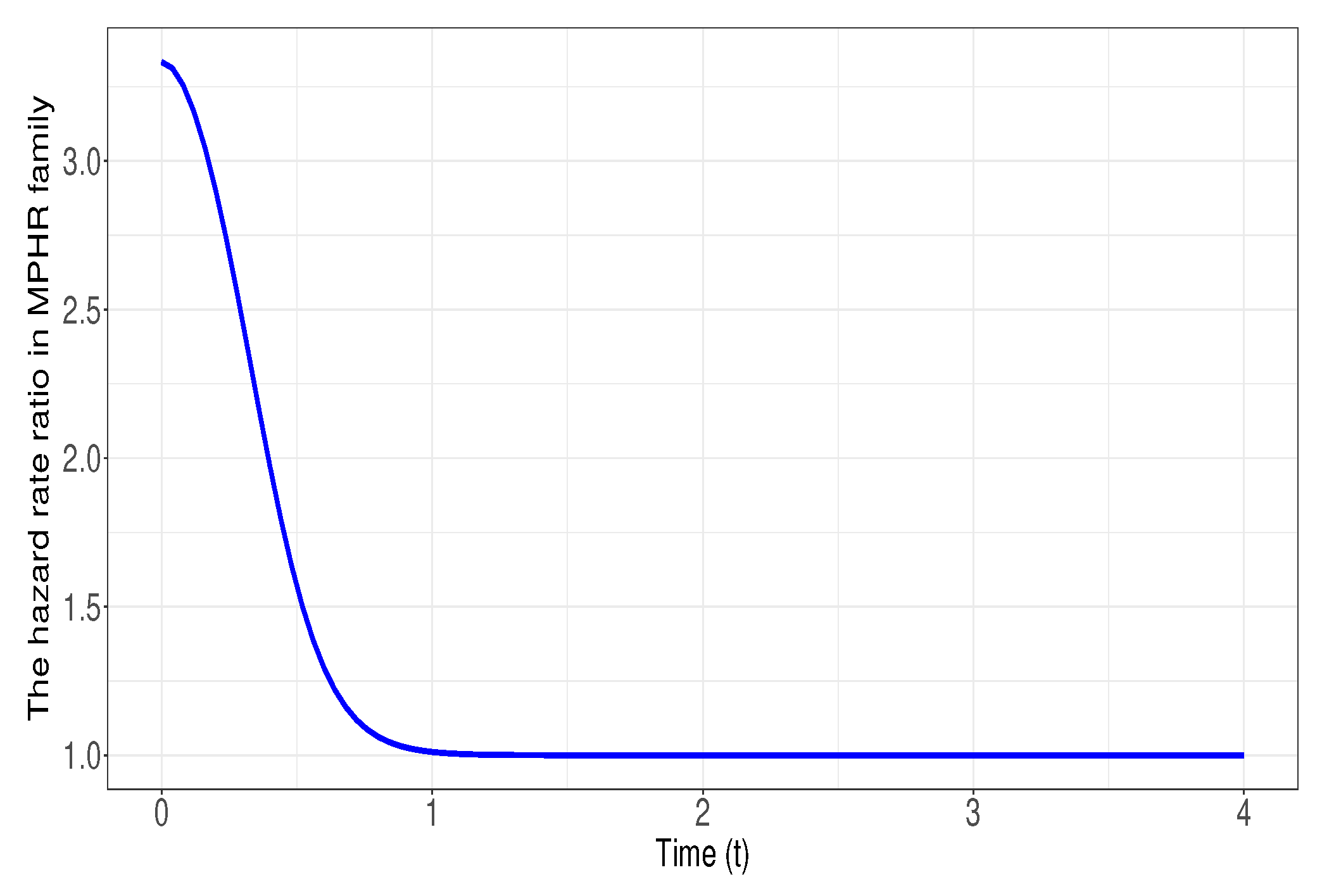
We start with introducing some notation. Let and have pdfs f and g, with underlying cdfs F and G, respectively. Let us assume that and and denote by and . Then, using (14), we have
Using (26), the pdfs of and (signified by and ) are acquired as below:
By dividing the pdfs in (27) into the cdfs given in (26), the reversed hazard rate function of and the reversed hazard rate function of are derived as follows:
where and are the reversed hazard rate functions of and respectively, and further the function is defined as
Now, let us define two measures of relative reversed hazard rates of and having reverenced hazard rate functions and respectively. The limiting points of reversed hazard rates ratio as follows:
Theorem 3.
Let and have cdfs F and G, respectively. Let and where and for every . Suppose that which is a non-negative function of is defined as
If
then
Proof.
To prove (29), it is sufficient to establish that is non-decreasing in . Following the equations (28), one has:
and, due to assumption, is non-decreasing in , thus it is enough to prove that is non-decreasing in . The latter statement is valid if, and only if,
We use the notation . We get
in which the last inequality is due to the fact that, for and whenever ,
and, further, that provides that
which further implies that for all . Note that the right hand side in (30) is non-negative, if and only if,
where the function is defined as below:
Now, it is sufficient to observe that the inequality in (31) is fulfilled if
Note that, since yields
hence, for all . Consequently, for all , using the characterization relation (7) one gets:
Thus, , for all which leads to
□
Example 3.
Let us assume whenever X has Inverse Weibull distribution with shape parameter c and scale parameter d, where and also . Then, X has cdf for We assume that and . Further, we suppose that and with and so that is the cdf of and It can be readily show that and have rhrs and , respectively. Thus,
Consequently, On can easily check that
and, simultaneously, one has
Therefore, one realizes that , and using Theorem 3 we deduce that . In Figure 3, the graph of is exhibited to indicate that it is non-decreasing in
Remark 2.
In the setting of Theorem 3, the derived result can be acquired when and . To verify this claim, one needs to observe that if and , then, for all and for , we have
Thus, the parenthetical statement in right hand side of inequality given in (30) is clearly non-negative. Hence, it is not hard to see that if and and then . In this setting the additional infimum condition in Theorem 3 can be removed.
In the next theorem, we obtain the result of Theorem 3 under different conditions.
Theorem 4.
Let and follow cdfs F and G, respectively. Suppose that and where and for every . Consider as a non-negative function of defined as
If
then
Proof.
In order to verify the implication in (33), as in the proof of Theorem 3, it suffices to show that
Analogously as in the proof of Theorem 3, we can get
where the last inequality is due to the fact that, for and for every ,
and moreover because , thus
from which one obtains for all . Now, one can see that the right hand side in (34) is non-negative, if and only if,
where the function is as defined in the proof on Theorem 3. It is now enough to see that the inequality in (35) is satisfied when
Now observe that gives
Therefore, for all . Hence, for all , by appealing to the relationship (7) we can write:
As a result, , for all providing that
□
Example 4.
Let have cdf and let have exponential distribution with cdf where is a common parameter in F and G. Note that for all where is the rhr of and is the rhr of , respectively. Hence, and also clearly, . Suppose that and such that and . In view of the notations and definitions in Theorem 4, we have
and on the other hand, one has
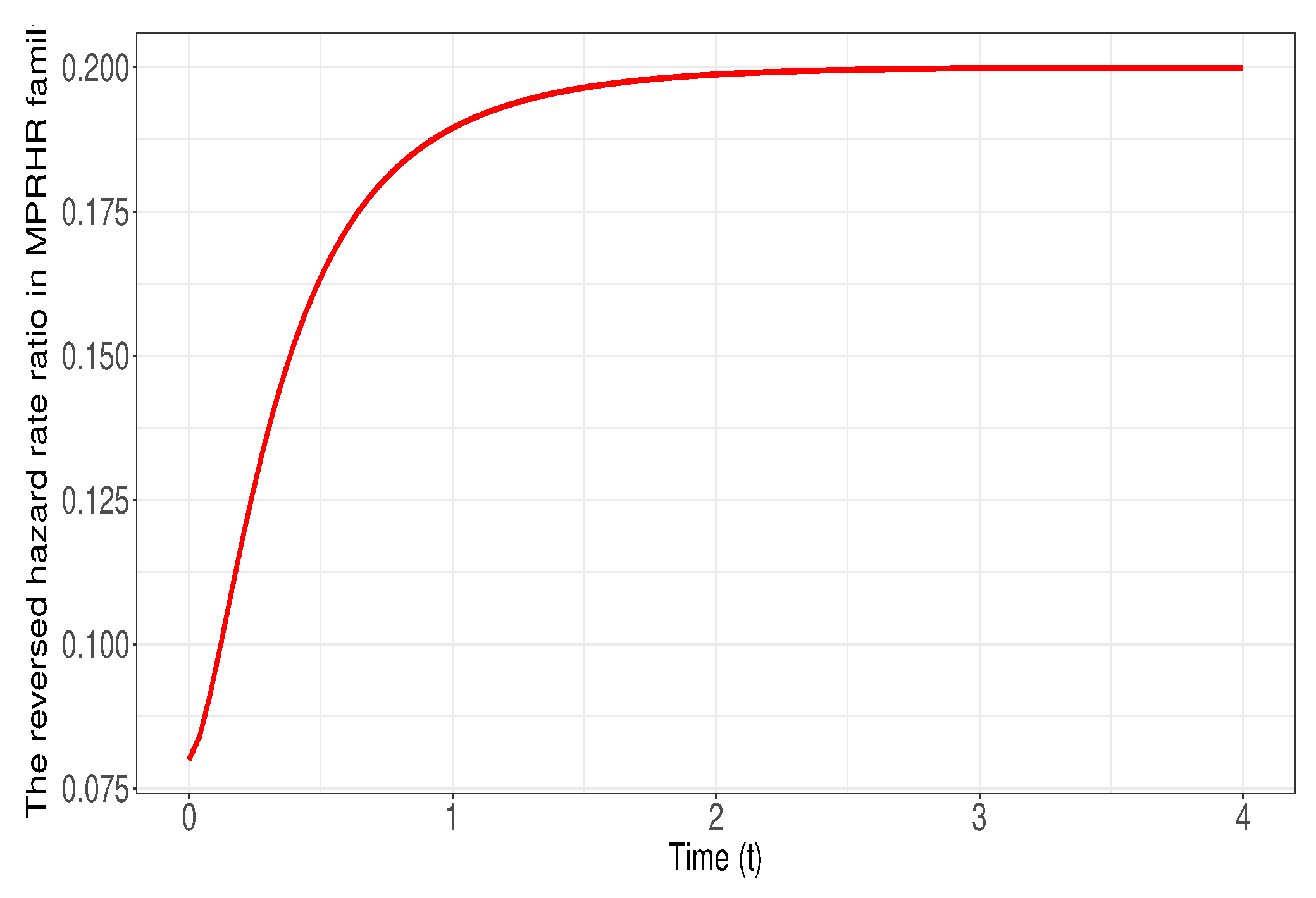
So, it is obvious that Therefore, Theorem 4 is applicable which provides that In Figure 4, the curve of , when is plotted to verify that it is non-decreasing in
5. Concluding Remarks
In this paper, we have examined two recently proposed semiparametric models, namely the MPHR model and the MPRHR model. As shown by Balakrishnan et al. [1], these models include as special cases three important models in the literature, namely the proportional hazard rate model, the proportional reversed hazard rate model, and the proportional odds ratio model. Because these three models have found many applications in the literature so far and because they are available to the two newly defined semiparametric models, it deserves an analytical study of the latter models because they cover and generalize the previous studies. The study of stochastic orderings for model comparisons has been done in the literature in various contexts, including reliability theory, survival analysis, actuarial analysis, risk theory, biostatistics, and many other areas. Stochastic orderings are very useful potential tools for model analysis. For example, stochastic orders are very useful for detecting underestimation and overestimation problems in models. Stochastic orderings are usually recognized as tools for making inferences about models without data. The ordering properties of probability distributions reveal other aspects of the distribution or a family of distributions that can be used for various purposes.
The study conducted in this paper addresses situations in which there is a relative ordering property between two candidates from the MPHR family and, moreover, two candidates from the MPRHR family of semiparametric distributions. In general, the base distributions were assumed to be unknown but to satisfy a relative ordering property according to either the relative hazard rate order () or the relative reverse hazard rate order (). It was assumed that the external parameters of the candidate models were generally different. Sufficient conditions were established for the conservation of the relative hazard rate order in the MPHR model and also for the conservation of the relative reverse hazard rate order in the MPRHR model. In the literature, for the preservation of the stochastic order in some scenarios, some stochastic orders are set as assumptions, which is a very strong condition. However, the conditions we found and presented in our work involve comparisons between two numbers, one of which is the supremum or infimum of a function and the other a function of the parameters of the models. With some examples we have shown that even very well known standard statistical distributions, such as Weibull, Gamma or reversed Weibull distributions, can be used as the basic distribution in the MPHR and MPRHR model.
In the future study we shall consider stochastic comparisons in the MPHR and the MPRHR models according to other stochastic orders such as likelihood ratio order (), hazard rate order (), reversed hazard rate order () and the usual stochastic order . In the context of MPHR model, in view of (16), when and follows pdfs and , respectively, then implies if
where . In addition, in the context of the MPHR model, when and follow sfs and , respectively, as given in (15), then implies if
where . In parallel, when the MPHR model is under consideration, as and have hrs and , respectively, as formulated in (17), then yields if
where is defined as before after (17). On the other hand, concerning the MPRHR model, by appealing to (27), and assumign that and have pdfs and , respectively, then implies if
where . Moreover, by considering the MPRHR model, as and follow cdfs and , respectively, as provided in (26), then implies if
where . Furthermore, when the MPRHR model is regarded, so that and have rhrs and , respectively, as written in (28), then yields if
in which is defined earlier after the equations (28). The analogous study can also be carried out in the context of other stochastic orders such as dispersive order, star order, and super-additive order.
Author Contributions
Methodology, MS; Software, MS; Validation, MM; Formal analysis, MS; Investigation, MK; Resources, MM; Writing – original draft, MS; Writing – review and editing, MK and MM; Visualization, MK and MM; Supervision, MM; Project administration, MS.
Acknowledgments
The authors acknowledge financial support from the Researchers Supporting Project number (RSP2023R464), King Saud University, Riyadh, Saudi Arabia.
References
- Balakrishnan, N. , Barmalzan, G. and Haidari, A. (2018). Modified proportional hazard rates and proportional reversed hazard rates models via Marshall-Olkin distribution and some stochastic comparisons. Journal of the Korean Statistical Society, 47, 127–138. [CrossRef]
- Barlow, R.E. and Proschan, F. (1975). Statistical theory of reliability and life testing: probability models (Vol. 1). New York: Holt, Rinehart and Winston.
- Belzunce, F. , Riquelme, C.M., Mulero, J. (2015). An introduction to stochastic orders. Academic Press.
- Champlin, R. , Mitsuyasu, R., Elashoff, R. and Gale, R.P. (1983). Recent advances in bone marrow transplantation. In R.P. Gale (ed.), UCLA symposia on molecular and cellular biology, vol. 7. New York, pp. 141–158.
- Cox, D.R. (1972). Regression models and life-tables. Journal of the Royal Statistical Society: Series B (Methodological), 34(2), 187–202. [CrossRef]
- Di Crescenzo, A. (2000). Some results on the proportional reversed hazards model. Statistics and Probability Letters, 50(4), 313–321. [CrossRef]
- Ghitany, M.E. (2005). Marshall-Olkin extended Pareto distribution and its application. International Journal of Applied Mathematics, 18(1), 17.
- Ghitany, M.E. , Al-Awadhi, F.A. and Alkhalfan, L. (2007). Marshall-Olkin extended Lomax distribution and its application to censored data. Communications in Statistics-Theory and Methods, 36(10), 1855–1866. [CrossRef]
- Gupta, R.C. , Gupta, P.L. and Gupta, R.D. (1998). Modeling failure time data by Lehman alternatives. Communications in Statistics-Theory and methods, 27(4), 887–904. [CrossRef]
- Gupta, R.C. and Kirmani, S.N.U.A. (2006). Stochastic comparisons in frailty models. Journal of Statistical Planning and Inference, 136(10), 3647–3658. [CrossRef]
- Gupta, R.C. and Gupta, R. (2007). Proportional reversed hazard rate model and its applications. Journal of statistical planning and inference, 137(11), 3525–3536. [CrossRef]
- Kalashnikov, V.V. and Rachev, S.T. (1986). Characterization of queueing models and their stability. In Yu.K. Prohorov et al. (eds.), Probability theory and mathematical statistics, vol. 2. Amsterdam: VNU Science Press, pp. 37-53.
- Kirmani, S.N.U.A. and Gupta, R.C. (2001). On the proportional odds model in survival analysis. Annals of the Institute of Statistical Mathematics, 53, 203–216. [CrossRef]
- Kumar, D. and Klefsjö, B. (1994). Proportional hazards model: a review. Reliability Engineering and System Safety, 44(2), 177–188. [CrossRef]
- Lai, C.D. and Xie, M. (2006). Stochastic ageing and dependence for reliability. Springer Science and Business Media.
- Li, H. and Li, X. (2013). Stochastic orders in reliability and risk. Honor of Professor Moshe Shaked. Springer, New York.
- Marshall, A.W. , Olkin, I. (1997). A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika, 84(3), 641–652.
- Marshall, A.W. and Olkin, I. (2007). Life distributions (Vol. 13). Springer, New York.
- Müller, A. and Stoyan, D. (2002). Comparison Methods for Stochastic Models and Risks. John Willey and Sons. Inc., New York.
- Pocock, S.J. , Gore, S.M. and Keer, G.R. (1982). Long-term survival analysis: The curability of breast cancer. Statistics in Medicine, 1, 93–104. [CrossRef]
- Rezaei, M. , Gholizadeh, B. and Izadkhah, S. (2015). On relative reversed hazard rate order. Communications in Statistics-Theory and Methods, 44(2), 300–308.
- Sengupta, D. and Deshpande, J.V. (1994). Some results on the relative ageing of two life distributions. Journal of Applied Probability, 31, 991–1003. [CrossRef]
- Shaked, M. and Shanthikumar, J.G. (Eds.). (2007). Stochastic orders. New York, NY: Springer New York.
- Xu, M. and Li, X. (2008). Negative dependence in frailty models. Journal of Statistical Planning and Inference, 138(5), 1433–1441. 5). [CrossRef]
Figure 1.
Plot of the hazard rate ratio in Example 1 for and when
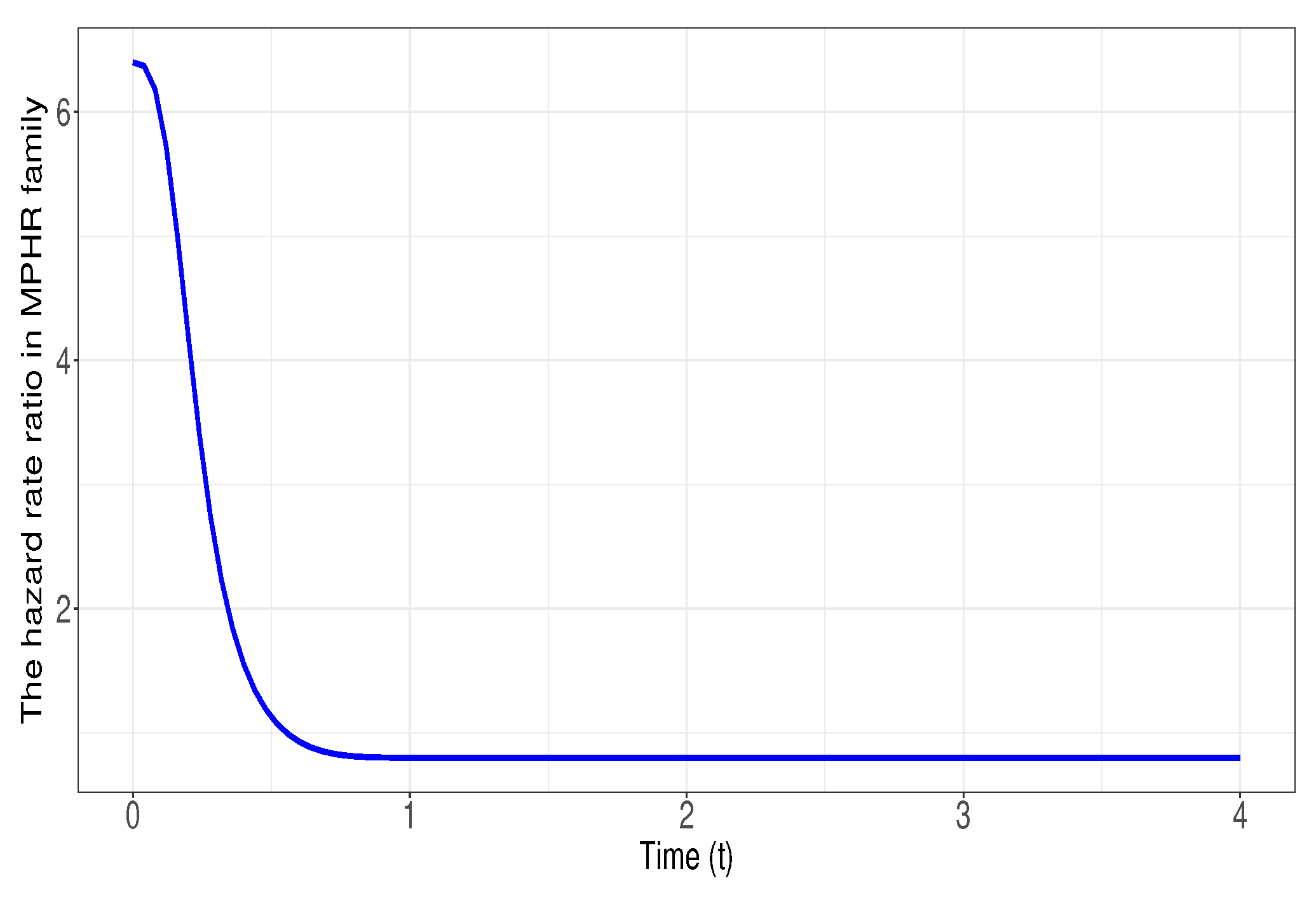
Figure 3.
Plot of the reversed hazard rate ratio in Example 3 for and when
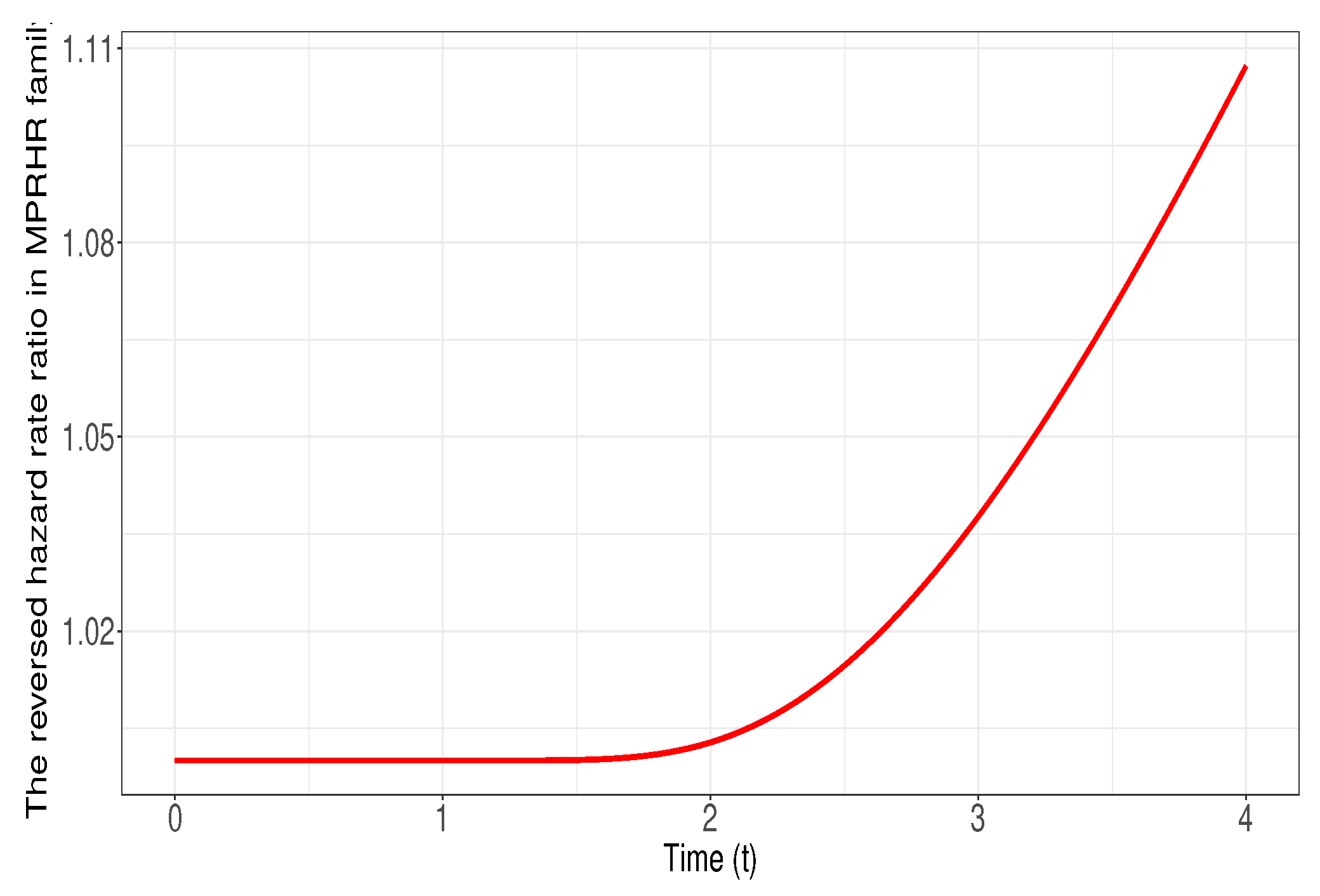
Figure 4.
Plot of the reversed hazard rate ratio in Example 4 for , and when
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






