Prerpints.org logo
Preprint
Article

Analysis of the Performance of a Hybrid Thermal Power Plant Using Anfis-Based Approaches

Altmetrics

Downloads

76

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 September 2023

Posted:

26 September 2023

You are already at the latest version

Alerts
Abstract
The hybridization of conventional thermal power plants by incorporation of renewable energy systems has witnessed widespread adoption in recent years. This trend aims not only to mitigate carbon emissions but also to enhance the overall efficiency and performance of these power generation facilities. However, calculating the performance of such intricate systems using fundamental thermodynamic equations proves to be both laborious and time-intensive. Nevertheless, possessing accurate and real-time insights into their performance is of utmost significance to ensure optimal plant operation, facilitate decision-making, and streamline power production planning. In this paper, we delve into the application of machine learning techniques, particularly hybrid methodologies, to predict the performance of power plants. Specifically, we employ three approaches: the Adaptive Neuro-Fuzzy Inference System (ANFIS), the ANFIS optimized via Particle Swarm Optimization (ANFIS-PSO), and the ANFIS optimized through Genetic Algorithm (ANFIS-GA). These techniques are alternatively applied to a complex hybrid thermal power plant, namely an Integrated Solar Combined Cycle Power Plant (ISCCPP). This ISCCPP comprises a steam turbine section, a gas turbine section, and a concentrated solar power system utilizing troughs as collectors. The energy transfer fluid, in conjunction with exhaust from the gas turbine section, heats water within a vessel or steam generator, producing steam to propel the steam turbine's rotor. Electricity generation is facilitated by both gas and steam turbines, which are coupled to a generator. The findings of this study underscore the accuracy and appropriateness of ANFIS-based models in evaluating and predicting the performance of intricate hybrid power plants. The ANFIS model exhibited an impressive overall coefficient of correlation of 0.9991. Notably, the integration of evolutionary algorithms (PSO and GA) into the ANFIS framework elevated model performance, yielding correlation coefficients of 0.9994 for ANFIS-PSO and 0.9997 for ANFIS-GA. It is noteworthy that ANFIS-GA demonstrated superior predictive capability. The modeling framework developed in this research offers valuable support to designers, energy managers, and decision-makers. It provides a robust and dependable tool to assess the performance of hybrid thermal power plants, which are poised for a global surge in numbers amid the ongoing energy transition.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

As part of a transition step to zero carbon emission, some classic thermal power plants have been hybridized with renewable energy, especially concentrated solar power system. On the other hand, hybridization of renewable energy is mainly driven by the challenge of the non-availability of renewable energy sources (sun, wind, geothermal, ocean, biomass, etc.) all the time throughout the year [1]. Not only does this affect the overall performance or efficiency of the system but reduces fossil fuel consumption and brings up the challenge of the computation of the said efficiency since the level of complexity of the system increases. Hybridizing thermal power plants is even the way for-ward if governments take energy transition and climate change seriously. Moreover, it can improve the overall efficiency of the power plant [2]. For the system studied in this research, the gas system and the solar system were interacting through the heating unit where low-grade energy in the exhaust gas from a gas turbine is used to produce steam by heating water in addition to solar heating through a heat transfer fluid which was flowing in a concentrated solar power system, parabolic troughs in this case. Engineers are very concerned and sensitive to the use of energy or the performance of systems or plants that they design or operate. With the increasing level of complexity of hybrid thermal power plants, it becomes much harder to assess or evaluate the performance of such systems from thermodynamics standpoint or governing equations [3]. Therefore, there is a need for alternative approaches such as those developed as part of machine learning.
Machine learning (ML) techniques have been adopted in recent years to model and analyze hybrid energy systems. ML models have been hybridized and refined with optimization strategies in a quest for better solutions. As a result, an outstanding rise in the accuracy, precision, robustness and generalization ability of the ML models in energy systems using hybrid models was noted. Hybridization of ML models was even reported to be effective in the advancement of prediction models [4,5], particularly for renewable energy systems. However, recent trends suggest that the research direction is moving toward customized ML models or models which are designed for a particular application. In other words, the highest degree of accuracy can be achieved through the development of a case-based ML model [6]. It was found that the enhancement of the predictability of renewable energy systems and demand enables the replacement of expensive standby power generation assets with advanced control and optimization systems [7]. In this study ANFIS, which is a combination of an Artificial Neural Network (ANN), and Fuzzy logic is used to evaluate the performance of an integrated solar combined cycle gas/steam power plant. Thereafter it was hybridized for the training phase, with evolutionary algorithms, namely Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) which are part of metaheuristic algorithms. Some studies have successfully applied ANFIS in the prediction of power generation in solar power plants, control and modelling of interconnected combined cycle gas turbine plants and diagnosis of these systems. However, until recently no work applying ANFIS model in the design or analysis of the efficiency or the performance of a combined cycle gas turbine was found in the literature [8]. To date this gap is further widened by the integration of renewable energy systems, namely solar systems in the conventional combined cycle gas turbines plants in an effort to reduce carbon footprint and increase the overall efficiency of the plants. Furthermore, there is a necessity to explore advanced optimization techniques to improve the prediction accuracy of the ANFIS model for these hybrid power systems. The present investigation is undertaken and motivated to fill this gap.
Some researchers have conducted related work, for example, Khosravi et al. [9] tried to determine the optimal design parameters of a solar-only power tower system using molten salt for storage. They used machine learning, specifically hybrid Adaptive neuro-fuzzy inference system with a combination of genetic algorithm and teaching-based optimization algorithm. They used four parameters as inputs, namely latitude, longitude, design point DNI (Direct Normal Irradiance) and SM (Solar Multiple) which is the ratio of the solar field size to the power block, all expressed as nominal thermal power. Three parameters (annual energy produced, levelized cost of energy and capacity factor) were used as output parameters in the analysis. An extremely high correlation coefficient close to 1 for the hybrid ANFIS-GATLBO was reported in this study.
Yaici and Entchev [10] investigated the suitability of Adaptive Neuro-Fuzzy Inference System (ANFIS) method for predicting the performance parameters of a solar thermal energy system (STES) used for household hot water and space heating applications. They found that the predicted values were in agreement with the experimental data with mean relative errors less than 1 %. The ANFIS results were compared to the ANN results, and it was found that the ANFIS approach performed slightly better than the ANNs one because of higher accuracy and reliability for the prediction of the performance of the energy system. However, the ANN model was more flexible in terms of implementation and reduced computation time.
Zaaoumi et al. [11] presented a comparison between ANN and ANFIS to predict the daily power output of a solar power plant in eastern Morocco. The plant itself is an integrated solar combined cycle (ISCC) which is made of a CSP plant and a natural gas-fired combined cycle (NGCC) power plant. The whole system has got two gas turbines fueled by natural gas, a steam turbine, two recovery boilers, a solar field (made of parabolic troughs) and a heat exchanger. The total installed capacity is 472 MW of which 20 MW is of solar source. For modelling purposes, six variables (daily direct normal irradiance, day of the month, mean wind speed, daily mean ambient temperature, relative humidity and previous daily electric production were used as inputs while the daily electricity generation of the plant was used as the output. They concluded that both ANN and ANFIS models had similar performance with regards to the prediction accuracy. The coefficient of correlation R2 was in the range of 0.94 for training and testing phases while the RMSE was in the range of 0.072 for training and 0.089 for testing.
In an effort to identify the operating variables that can improve the efficiency of a combined cycle gas turbine (CCGT), Rodriguez et al. [8] modelled the cycle using adaptive neuro-fuzzy inference system (ANFIS). Three input variables namely, the compression ratio in the gas cycle, the pressure of the bled steam for water heating and the heat lost to the steam turbine exhaust were considered. They found that the pressure ratio in the gas turbine had the most significant effect on the efficiency of the combined system. ANFIS results were compared to analytical results and found to be similar.
Azfal et al. [12] conducted a critical review of optimization techniques of thermal performance of solar energy devices using metaheuristic algorithms. Many power arrangements integrating solar PV, CSP (dish collectors, heliostats, parabolic troughs), geothermal well, etc. were covered. It was highlighted in this study that more research is needed in hybrid optimization strategies to solve complex obstacles and obtain high efficacy in solar energy systems. Evolutionary algorithms for multi-objective optimization of hybrid renewable energy systems were recommended for future research.
Reyes-Belmonte et al. [13] studied the optimization of an integrated solar combined cycle. The system was made of an open-air Brayton cycle which was thermodynamically connected to a base steam Rankine cycle and a CSP hybrid plant. The CSP plant was based on pressurized air-receiver technology assisted by a natural gas burner. For analysis, Thermoflex software tool was used. An exclusive contribution of thermal energy through the solar thermal receiver was first considered and then a mixed thermal contribution by solar energy and natural gas was examined. Scenarios of different configurations of the combined system were considered. It was found, among other things, that the overall system efficiency was far from modern conventional combined cycle systems whose conversion efficiencies are around 60 % because of pressure limitations for pressurized air-receivers.
An investigation of the performance of an integrated solar combined cycle (ISCC) plant situated in the tropical climate of southern Algeria was carried out by Achour et al. [14]. The plant was a combination of a parabolic trough solar field with a fossil fuel combined cycle which was made of two gas turbines and a steam turbine. The authors developed from first principles a model for each component of the plant and concluded that an overall thermal efficiency of about 60 % could be reached. It is worth noting that developing a thermodynamic model for such a complex system or plant is a very tedious process and some assumptions need to be properly made.
Temraz et al. [15] developed and validated a dynamic simulation model for an integrated solar combined cycle (ISCC) power plant in Karaymat in Egypt using APROS (Advanced PROcess Simulation), a design software. The power plant (135 MW total electrical power) consisted mainly of a parabolic trough collectors solar field, a gas turbine (70 MW), a steam turbine (65 MW) and a heat recovery steam generator (HRSG). The boiler was using hot water from the heat exchanger with the heat transfer fluid of the CSP field and also flue gas from the gas turbine. The model was initialized and turned using operational data measured from the plant. The authors concluded that the model represented reality with high accuracy and showed a good predictive capability. Once again it can be seen that the approach followed by the authors was tedious and did not make use of machine learning.
Benabdellah et al. [16] analyzed from thermodynamics point of view energy, exergy and economics of an integrated solar combined cycle (ISCC) power plant situated in Algeria. It was made of two gas turbines of 40 MW each, one steam turbine of 80 MW which was fed by two HRSG (Heat Recovery Steam Generator), one solar steam generator (SSG) and a solar field of a total area of 183.120 m2 and comprising 224 parabolic troughs collectors (PTC). The plant operates as ISCC-PTC during sunny times and as a conventional combined cycle plant in other times. Hence, the SSG works as a boiler in parallel to the HRSG to increase the steam quantity. They found that energy and exergy efficiencies were respectively 56.0 % and 53.29 %. The levelized cost of energy (LCOE) was promising but still higher than a simple combined cycle. The ISCC-PTC power plant allowed some saving in natural gas consumption and CO2 emission taxes. Many other researchers [17,18,19,20,21] have adopted similar thermodynamic analysis approaches to assess the performance of the integrated solar combined cycle power plant even in recent years.
From the existing literature and to our best knowledge it appears that some authors have tried to model the performance of hybrid thermal power plants by means of ANFIS but the hybridization of ANFIS with evolutionary algorithms (PSO and GA) has not been tried and investigated on hybrid (gas/steam/solar) systems yet.
The aim of this study is to investigate and demonstrate the capability of metaheuristic methods (PSO and GA) combined with ANFIS to accurately predict the performance of a hybrid solar/gas/steam power plant or an integrated solar combined cycle power plant. It promotes the hybridization of thermal power plant with renewable energy systems like solar systems where possible to mitigate the effects of climate change and shows that the challenge of prediction or real-time knowledge of the performance of such a complex plant for energy planning and sustainability can be overcome by making use of suitable machine learning approaches. Hence this paper contributes to the body of knowledge in the application of metaheuristic approaches in the modelling of hybrid thermal power plants.
The structure of this paper is as follows: Section 2 provides the methodology followed in this investigation for the implementation and deployment of ANFIS-based approaches, Section 3 shows and discusses results obtained and Section 4 is a summary of major findings of this research.

2. Materials and Methods

The methodology used in this work is shown in Figure 1. It takes into account data preparation, the procedure, modelling and results analysis.

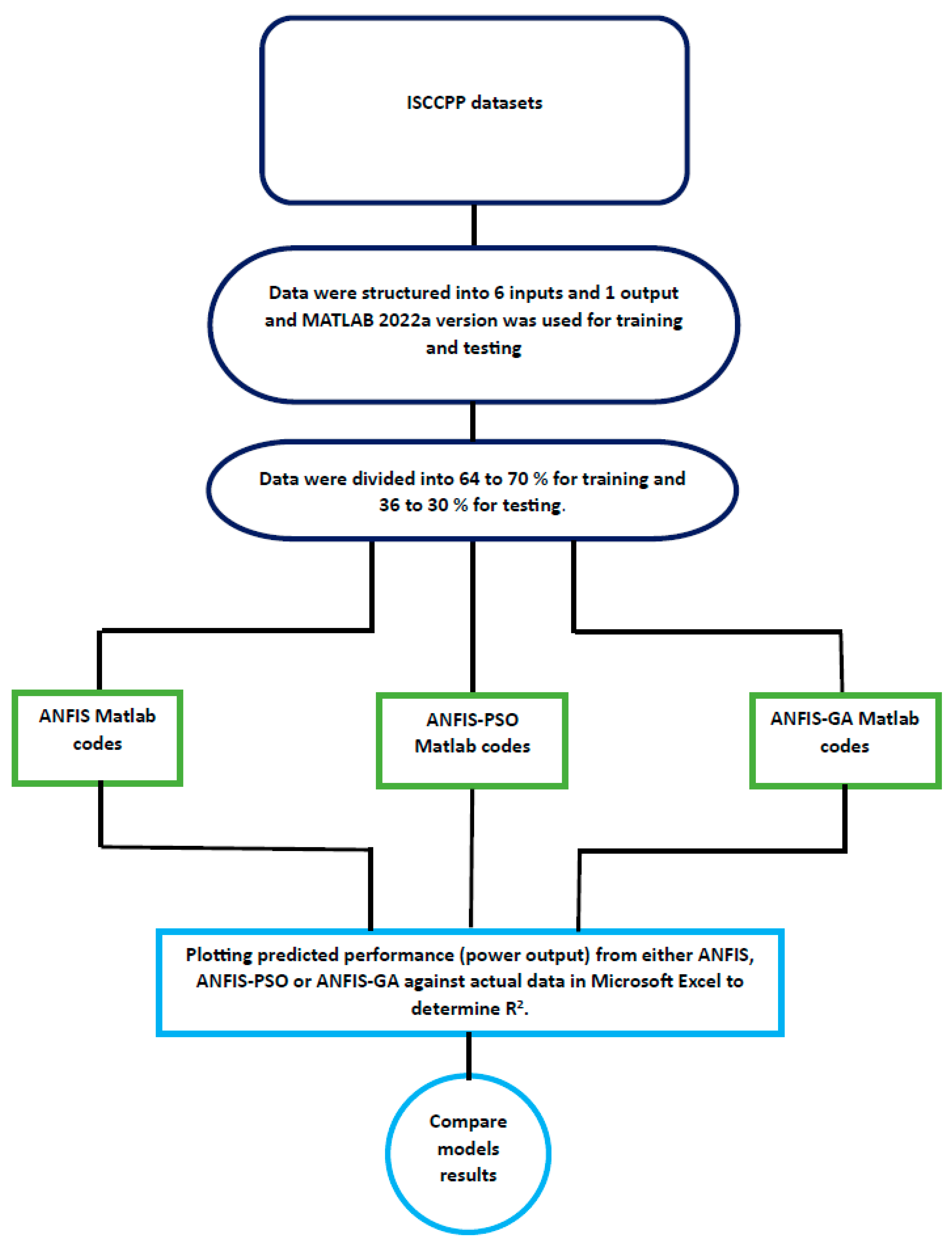
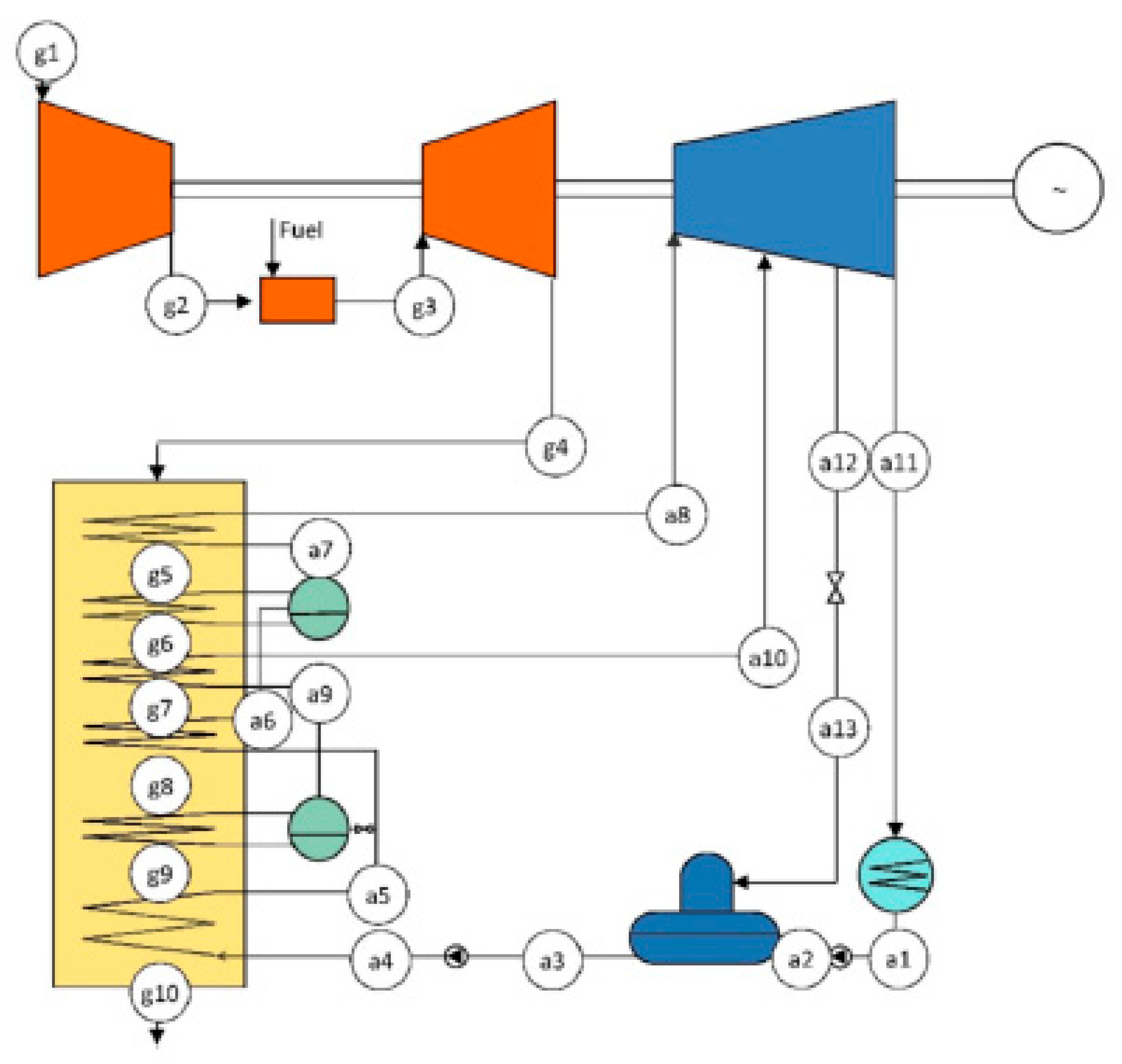
2.1. Data collection

The data used in this paper were obtained from Mendeley repository [22]. They were measured from an integrated solar combined cycle power plant comprising a gas turbine rated at 87.7 MW, a steam turbine rated at 37.1 to 42.4 MW and a concentrated solar power system in the form of parabolic troughs rated at 16 MW thermal. Steam was produced in the steam generator thanks to heat from the exhaust gas of the gas turbine and the heat transfer fluid from the CSP field as shown in Figure 2. The details of the hybrid power plant can be found in [23] and it is a good step towards carbon emission reduction or a transition from a fully fossil fuel-based energy generation to green or renewable energy.
Six parameters, namely ambient temperature (tamb), Direct Normal Irradiance (DNI), mass flow rate of air (ma), mass flow rate of gas or exhaust gas from the gas turbine (mg), mass flow rate of fuel or natural gas (mf) and mass flow rate of heat transfer fluid or thermal oil (mHTF) were used as input variables to the model while the power output of the plant was used the output parameter of the model. These input parameters were measured factors which influence the efficiency, or the power plant production from thermodynamic point of view. 108 data sets were used in this investigation and Table 1 shows a sample of it. For a full range of the data used in this study, tamb varied from -0.01 to 44 ⁰C, DNI from 0 to 909.669 W/m2, ma from 174.84 to 225.16 kg/s, mg from 178.72 to 230.5 kg/s, mf from 3.61 to 5.34 kg/s, mHTF from 85.33 to 85.34 kg/s and the power output of the plant (W_tot) from 93186.5 to 138940.8 kW.

2.2. Model development and implementation

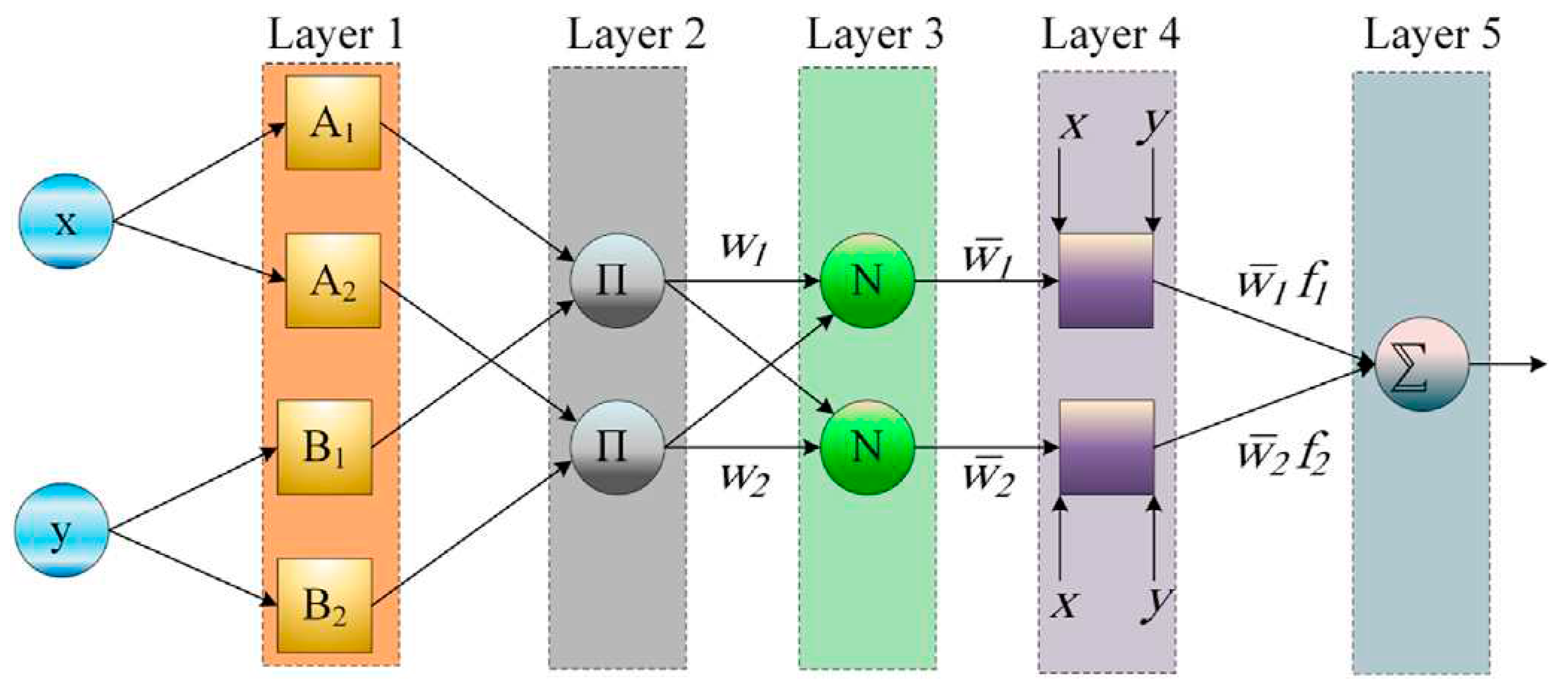
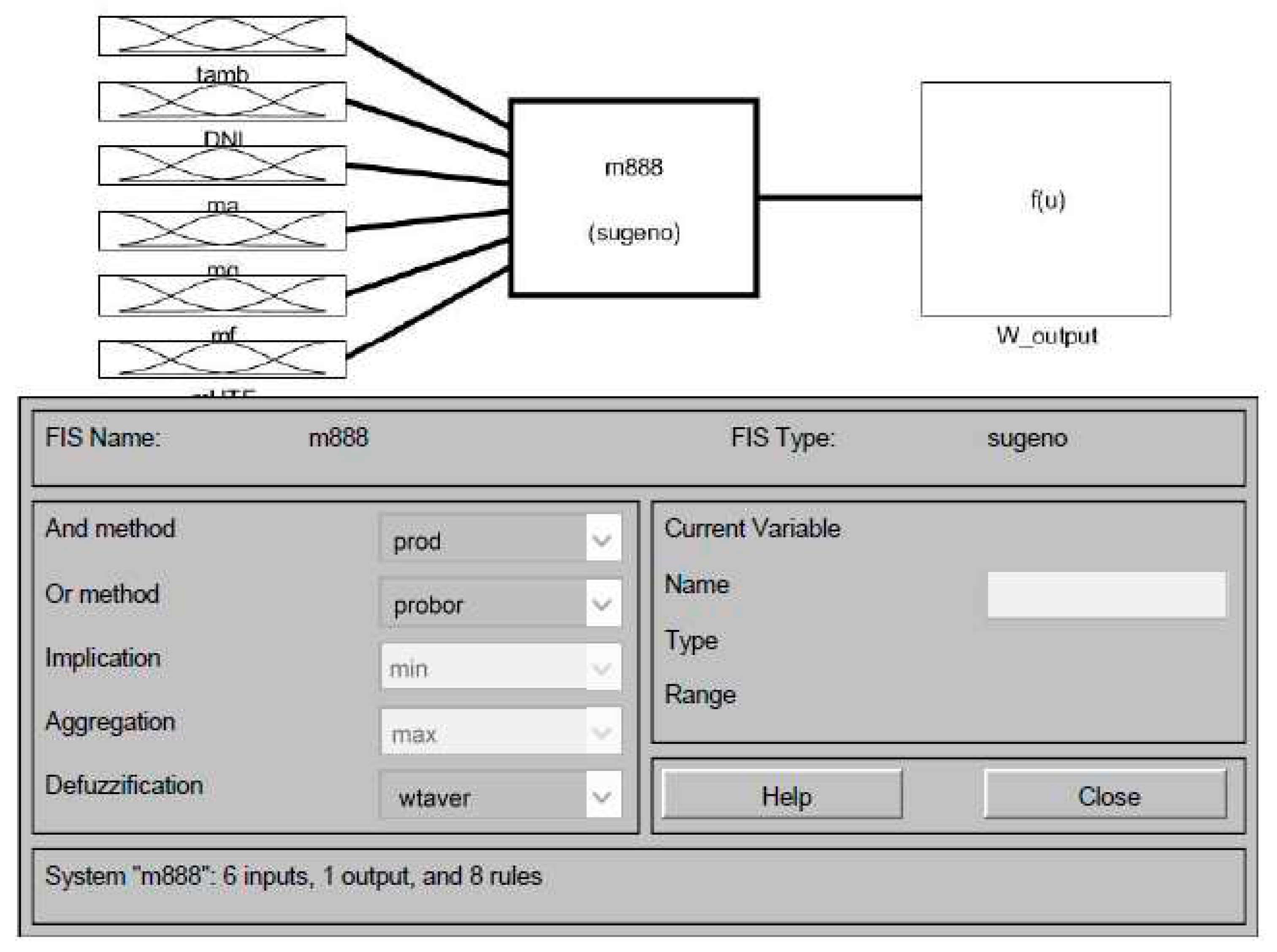
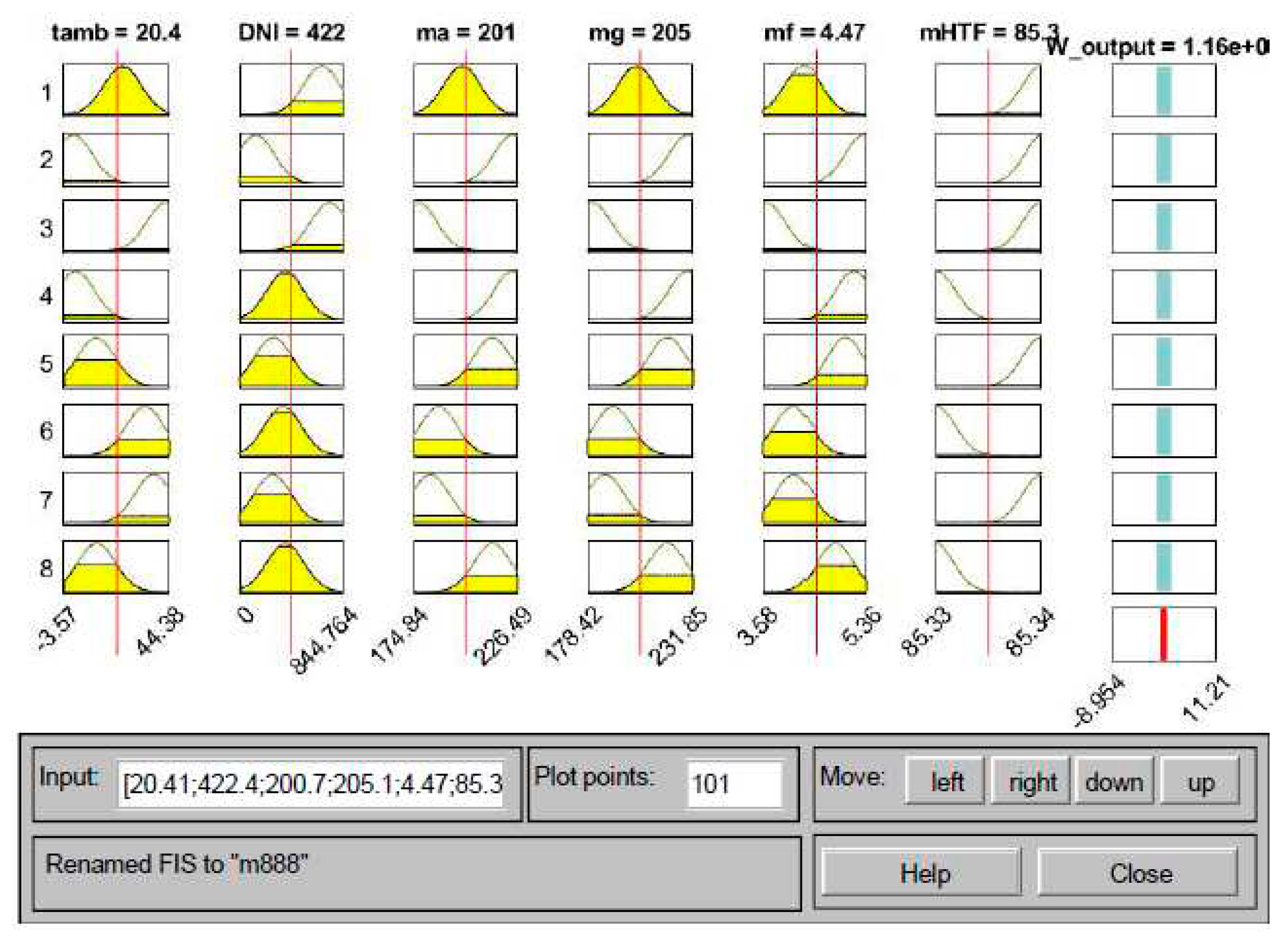
2.2.1. Adaptive Neuro-Fuzzy Inference System modelling

The analysis carried out in this paper uses Adaptive Neuro-Fuzzy System or ANFIS-based approaches to analyse the ISCCPP performance. Neuro-Fuzzy is actually a hybrid artificial intelligence technique that incorporates artificial neural networks and fuzzy logic. The development of this technique over the years has produced different types of fuzzy logic, namely the outstanding adaptive neuro-fuzzy inference system (ANFIS) which was discovered in 1993 by Jang. An ANFIS model borrows the structure and learning capability of the artificial neural network and the decision-making protocol of the fuzzy logic [24]. In other words, an ANFIS model is a hybrid method which combines the architecture of a fuzzy inference system with artificial neural network and provides the solution of a complex non-linear problem. The nodes in the feedforward network are flexible and change with specific parameters of the membership functions associated with fuzzy rules. Usually, an ANFIS model comprises 5 layers, namely fuzzy layer, product layer, normalized layer, de-fuzzy layer and the total output layer as shown in Figure 3. The de-fuzzy layer transforms a fuzzy set into a classical or crisp value. For training, the input and output data are obtained from parameters of the problem being analyzed and the ANFIS model presents a fuzzy inference system (FIS) for which parameters of the membership function are turned or refined by means of a classic optimization method or a metaheuristic optimization method. The optimization is done in the training step in order to minimize the error function or the difference between the targets or desired values and the output values [8]. A number of training algorithms have been presented in the literature, e.g.: back propagation as part of heuristic methods, evolutionary algorithms like Particle Swarm Optimization (PSO) and Genetic Algorithm (GA), etc. In the present study classic methods, PSO and GA were tried for training and compared for model performance analysis and assessment.
The first layer starts with the incoming signals or inputs x and y which are transferred to the neurons in Layer 2. The output can then be written using the membership function as:
O i 1 = μ A i x   o r   O i 1 = μ B i y ,   i = 1 ,   2
Where i is the node’s label and Ai or Bi is the linguistic label (small, very small, large, very large, etc) associated with the membership function. In other words, O i 1 is the membership function of Ai and Bi and it indicates the degree to which the given input x or y satisfies the quantifier Ai or Bi. There is a number of membership function types that can be used: trapezoidal, triangular, bell shaped, Gaussian, etc. It must be noted that Gaussian membership function is given by:
μ A i x = e x p − x − γ i α i 2
The same can be written for input y.
For bell shaped membership function,
μ A i x = 1 1 + x − γ i α i 2 β i
L a y e r   2 : O i 2 = ω i = μ A i x * μ B i y ,   i = 1 , 2 ,  
L a y e r   3 : O i 3 = ω ¯ i = ω i ∑ i = 1 2 ω i
L a y e r   4 : O i 4 = ω ¯ i f i = ω ¯ i p i x + q i y + r i
where p, q and r are coefficients of the ith neuron or node.
Layer 5: This is the last layer and has got an elementary neuron.
It computes the entire output as:
O i 5 = ∑ i ω ¯ i f i = ∑ i ω i f i ∑ i ω i

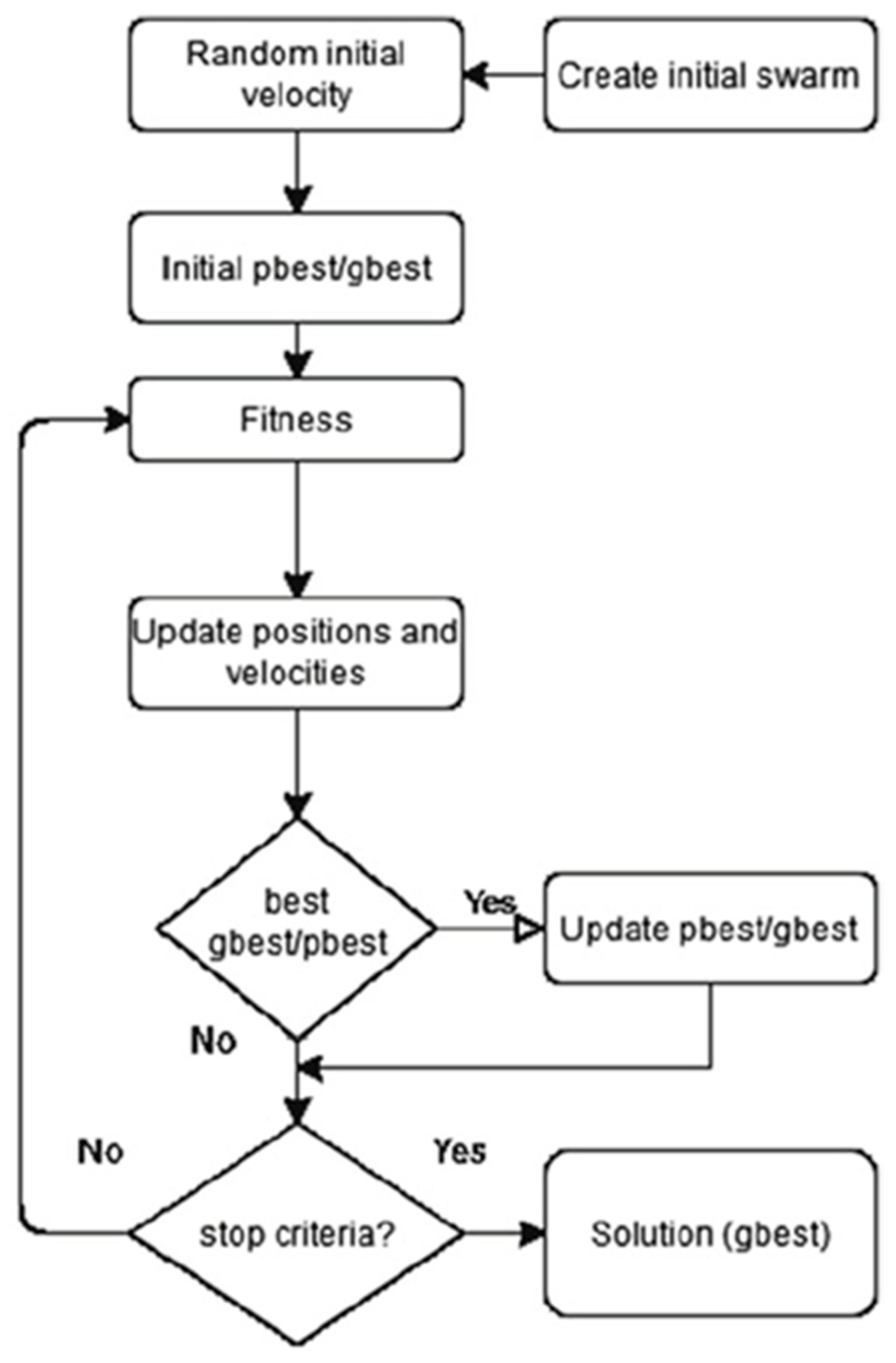
2.2.2. Particle Swarm Optimization

Particle Swarm Optimization (PSO) is a computational technique that optimizes a stochastic or non-linear problem by iteratively improving a candidate solution with regards to a defined fitness function. It was first presented by Kennedy and Eberhart in 1995 and simulates social behavior like the movement of organisms in a bird flock or fish school [26]. The approach helps solve a numerical problem by generating candidate solutions called particles and moving them around in the search space until the optimal solution is attained. The movement of each particle is guided by its knowledge of its personal best or local best position and the global best position of the swarm or population. In this way the swarm moves towards the best solution. The flowchart of the method is shown in Figure 4.
The velocity and the position of a particle are updated as follows [27]:
v i   t + 1 = v i t + C 1   r 1 t x P b e s t ,   i t − x i   t + C 2 r 2   ( t ) x G b e s t , i t − x i ( t )
x i t + 1 = x i t + v i ( t + 1 )
where x i t and x i t + 1 are particles’ positions in the search space at time step t and t+1. v i t and v i   t + 1 are the velocity vectors of particle i at time step t and t+1. x P b e s t ,   i t and x G b e s t , i t are the personal (local) and global best positions of particle i. C 1   and C 2 are the acceleration factors. r 1 t and r 2   ( t ) are random numbers between 0 and 1.

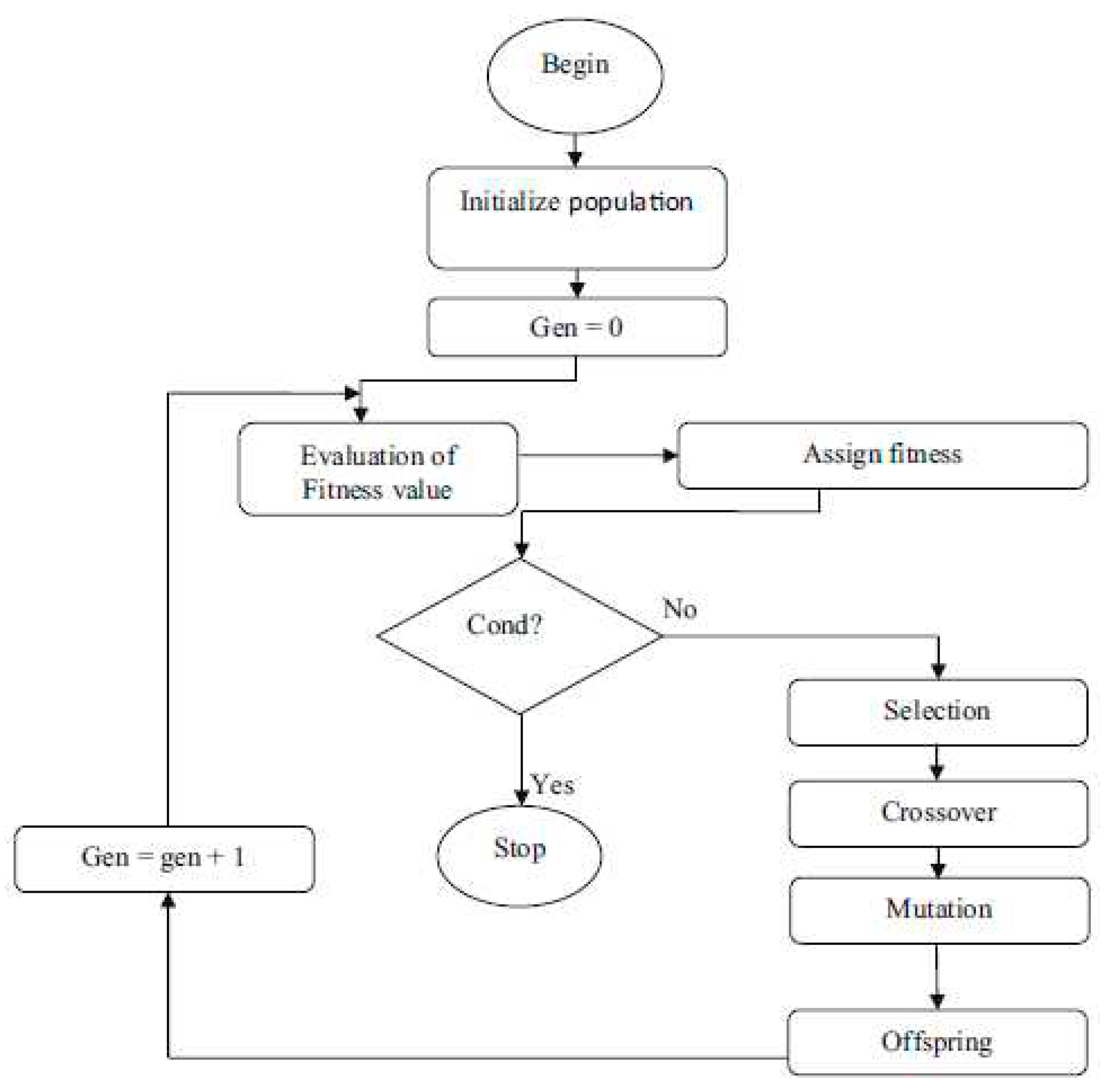
2.2.3. Genetic Algorithm

Genetic Algorithm (GA) is one of the algorithms which can explore a wide search space. The idea was introduced by John Holland in the 1960 s and 1970 s and was emulating natural biological genetics and evolution. An initial and unlimited population of solutions is randomly generated. Each solution is evaluated by calculating the values of the objective or fitness function. Solutions with fitter chromosomes stand a higher chance of being selected to participate in the next generation. Through this probabilistic approach, an intermediate population with a higher representation of the strong species is created. The intermediate population is allowed to undergo crossover through mutation and the next population is randomly generated. This process continues until the termination condition is satisfied [28]. In the genetic analogy which is a competition-based process, individuals or candidate solutions resemble chromosomes and the variables represent genes. Each solution is given an eligibility score that presents an individual’s “competition” abilities [29,30]. Figure 5 illustrates the flowchart of genetic algorithm.
Offspring population is created through the crossover operation which for example interchanges a subsequence of two of the selected chromosomes to generate two offsprings. It may be noted that GA makes use of a selection operator to implement the principle of natural selection or the survival of the fittest. Therefore, unlike the PSO where all the population members are kept in the process, not all the candidate solutions are kept as part of the population in genetic algorithm [31].

2.2.4. Hybrid ANFIS-PSO modelling

For the hybrid ANFIS-PSO model, data were divided into 69 data for training, 39 data for testing and they were loaded. A basic Fuzzy Inference System (FIS) was then generated. Its parameters were set and tuned in the training step by means of Particle Swarm Optimization (PSO). In the optimization phase the error function between the model outputs and the expected values is minimized until the required number of iterations (which was set at 1000) is reached. From this point results were plotted, testing phase could start, and its corresponding results were equally plotted. The main steps of the model are illustrated in the flowchart in Figure 5. Once training and testing plots were obtained, results data were exported to Microsoft Excel to generate regression plots and determine the coefficient of correlation R2.

2.2.5. Hybrid ANFIS-GA modelling

The approach followed for the hybrid ANFIS-GA model was similar to that of ANFIS-PSO until the setting of the FIS parameters. From this point an option could be chosen to conduct the training phase either by the Particle Swarm Optimization or by the Genetic Algorithm approach as depicted in Figure 6.

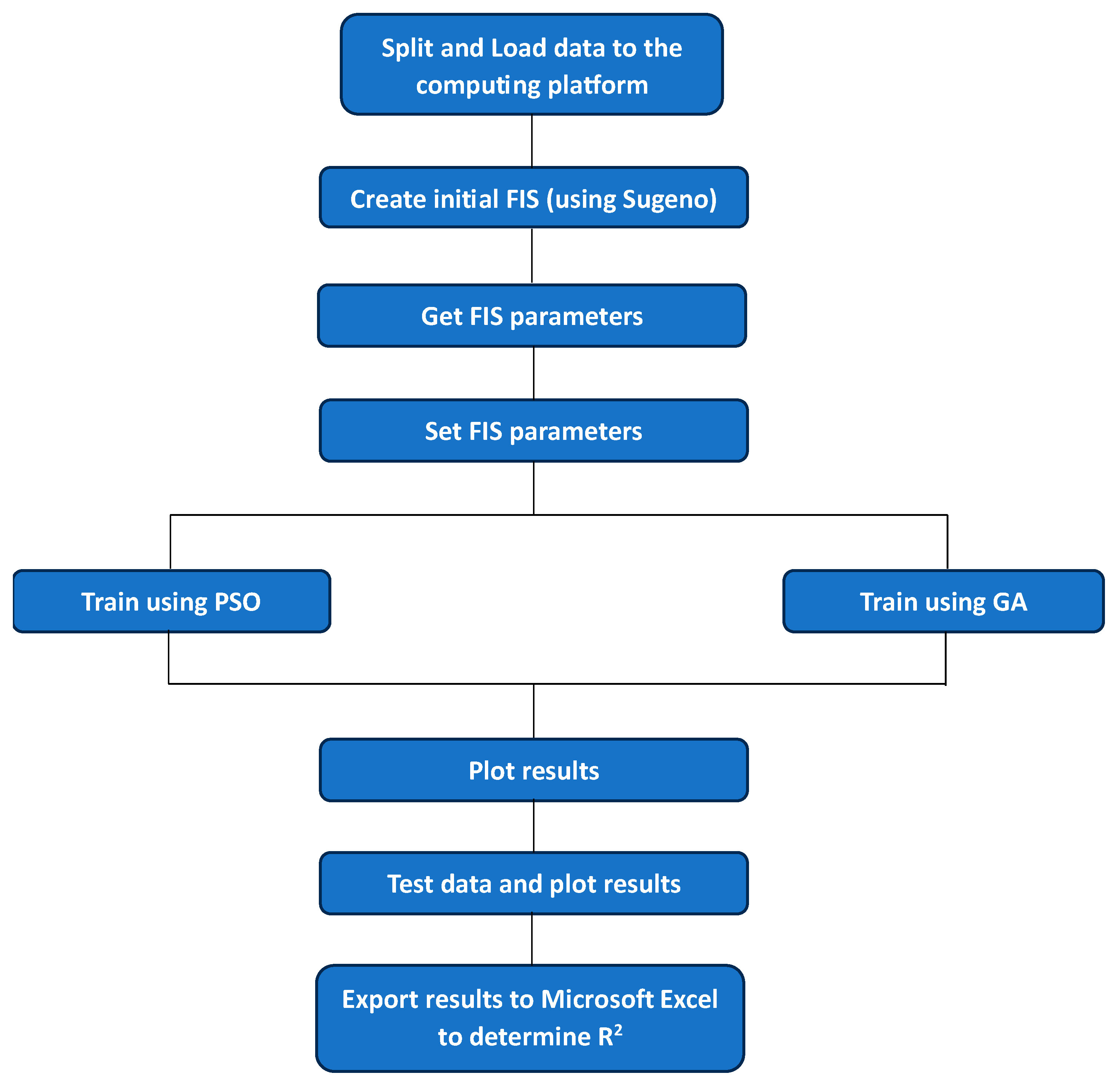
2.3. Procedure

The model was implemented in Matlab 2022a environment. The data were divided into 64 to 70 % datasets for training while the remaining 36 to 30 % were used for testing. The ANFIS model was firstly run with a classic training algorithm to get basic results. After importing data into the Neuro-Fuzzy Designer, a Fuzzy Inference System (FIS) was generated using Sugeno Fuzzy Inference System and subtractive clustering approach (with default parameters) was chosen as the number of input parameters was relatively high. The set FIS was trained using a hybrid learning strategy that combines gradient descent and linear and least squares methods. The maximum number of epochs was set to be 100 (refer to 3.1 for further details). After this stage the FIS was tested for generalization capability. Secondly the ANFIS model was optimized with Particle Swarm Optimization (refer to 3.2 for details) and finally with Genetic Algorithm (refer to 3.3 for details) for comparison purposes.

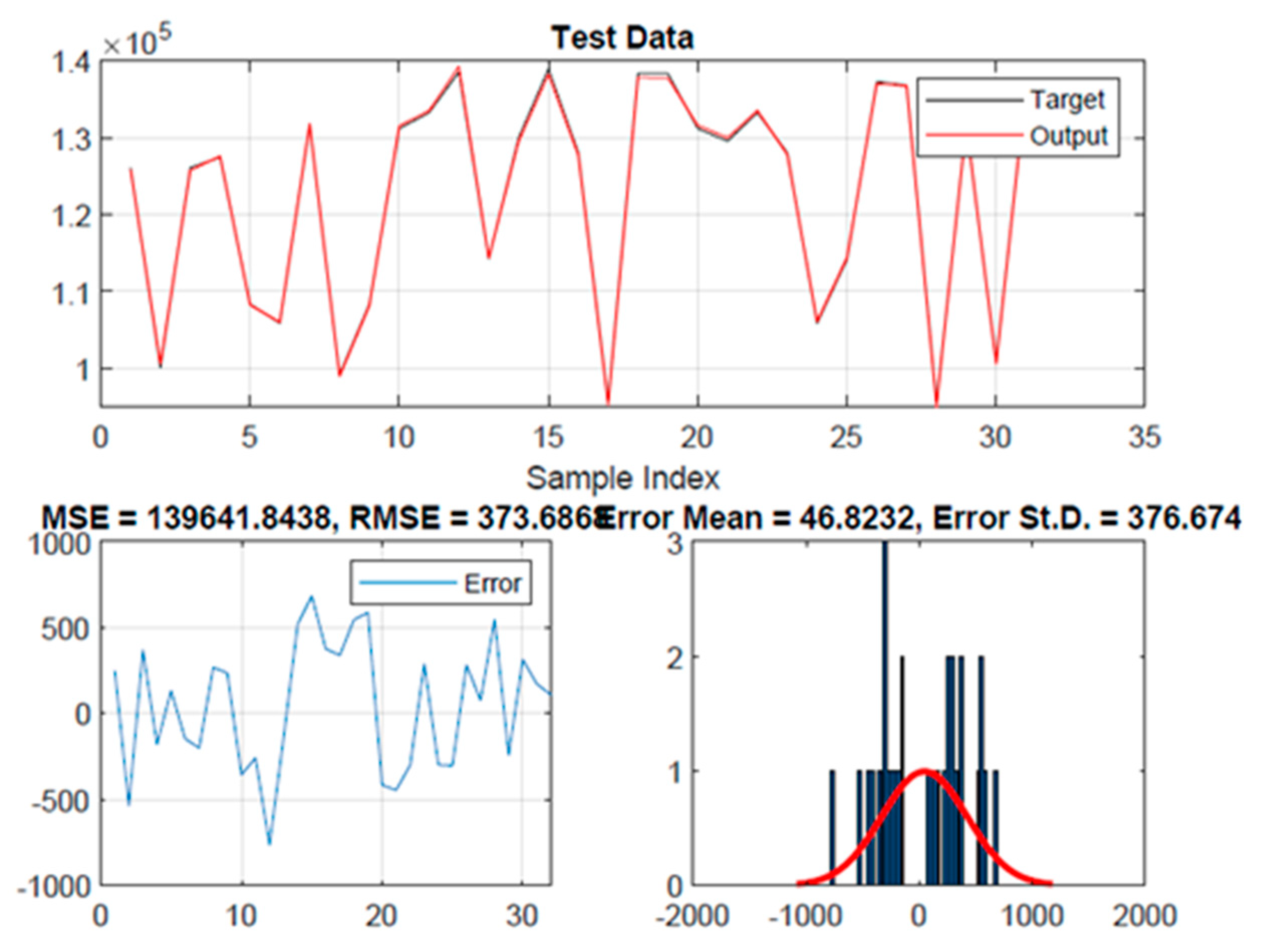
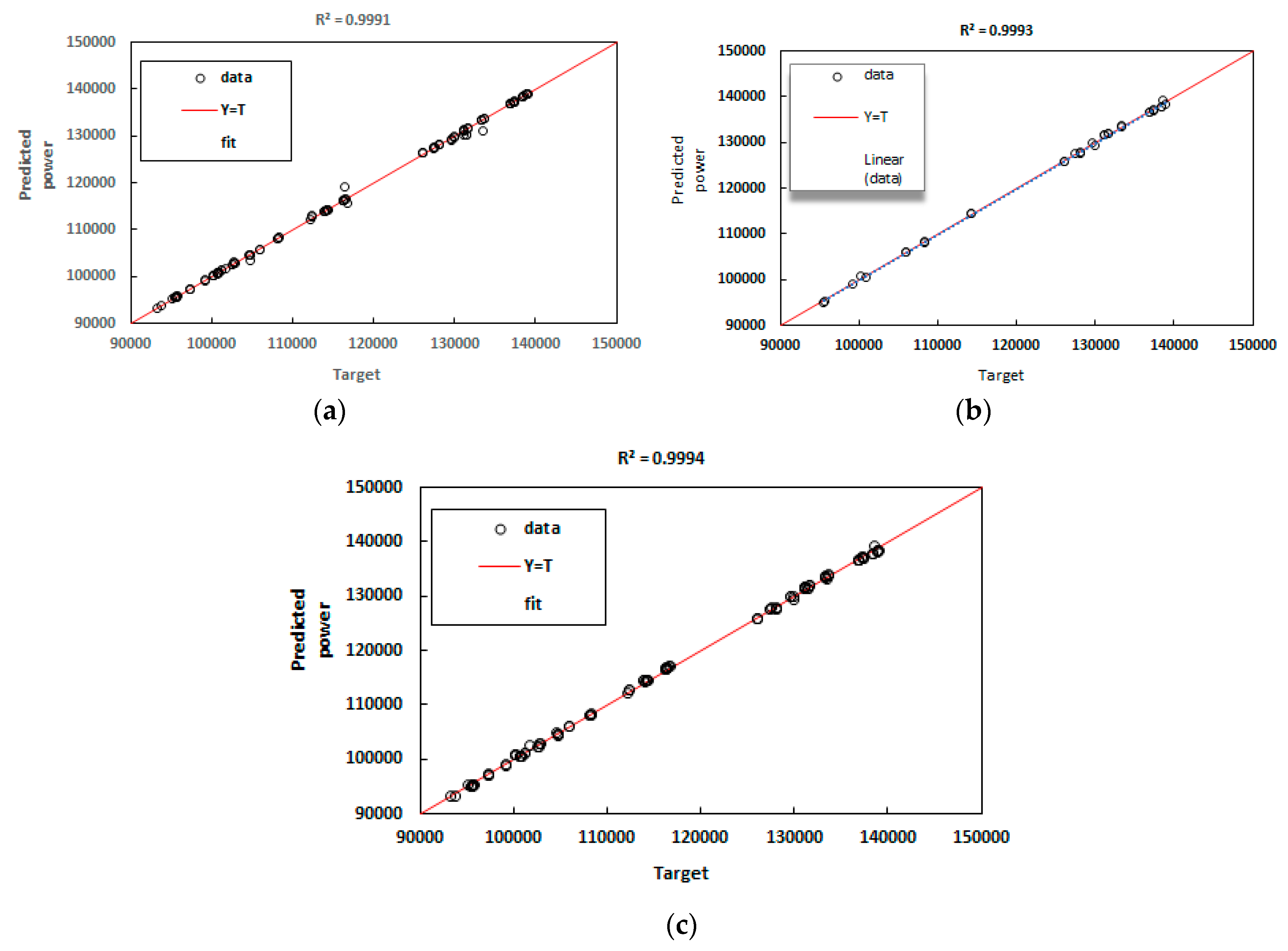
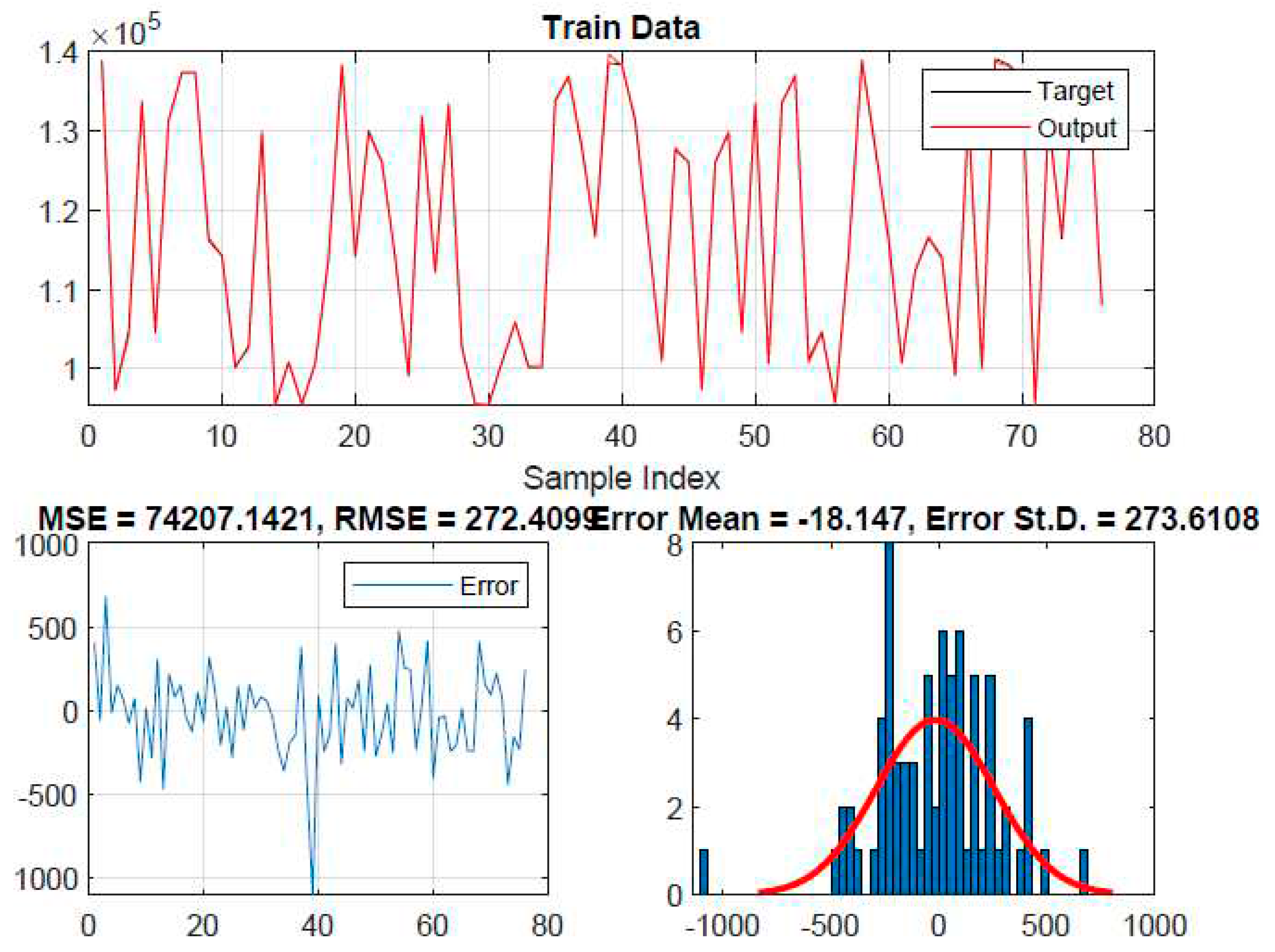
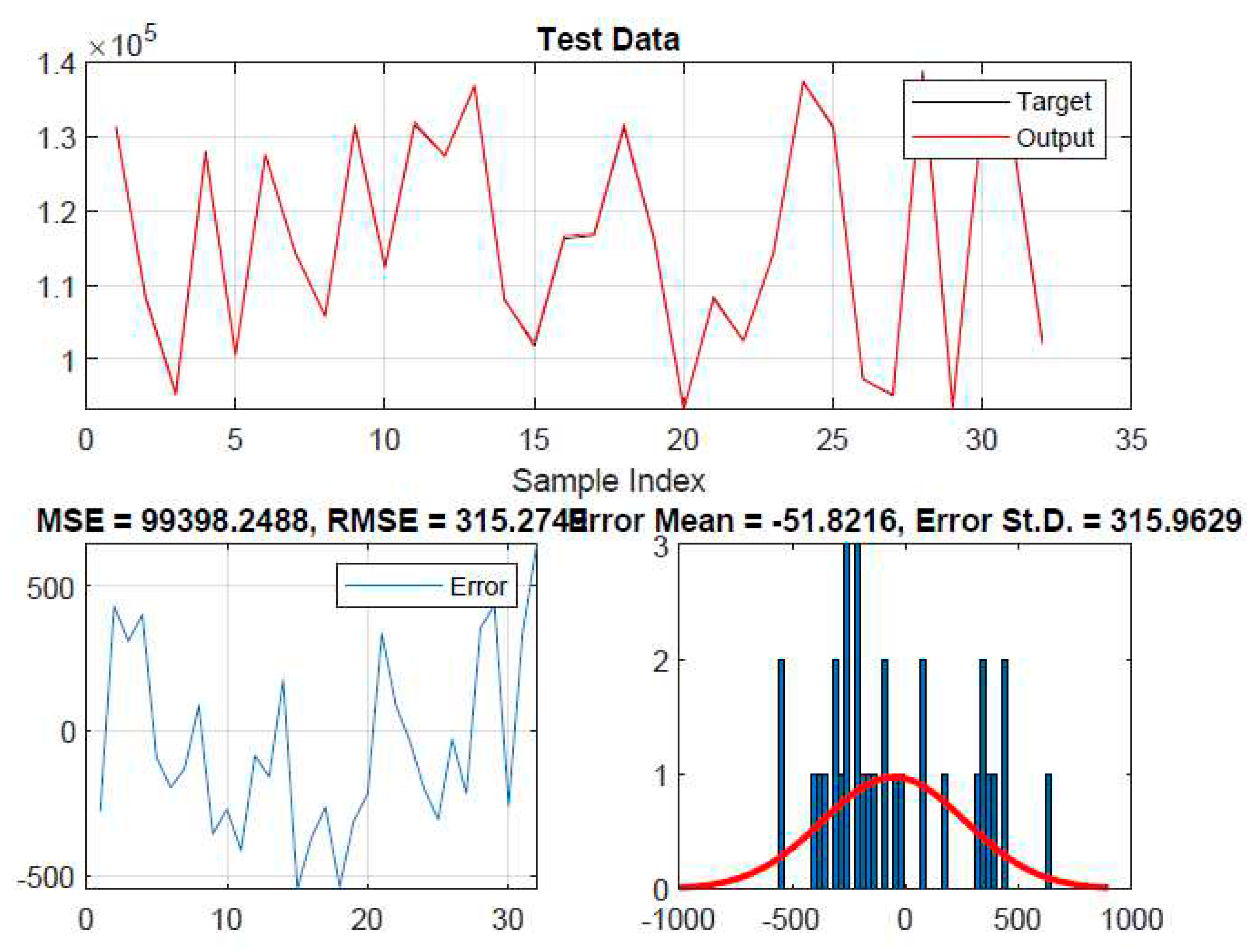
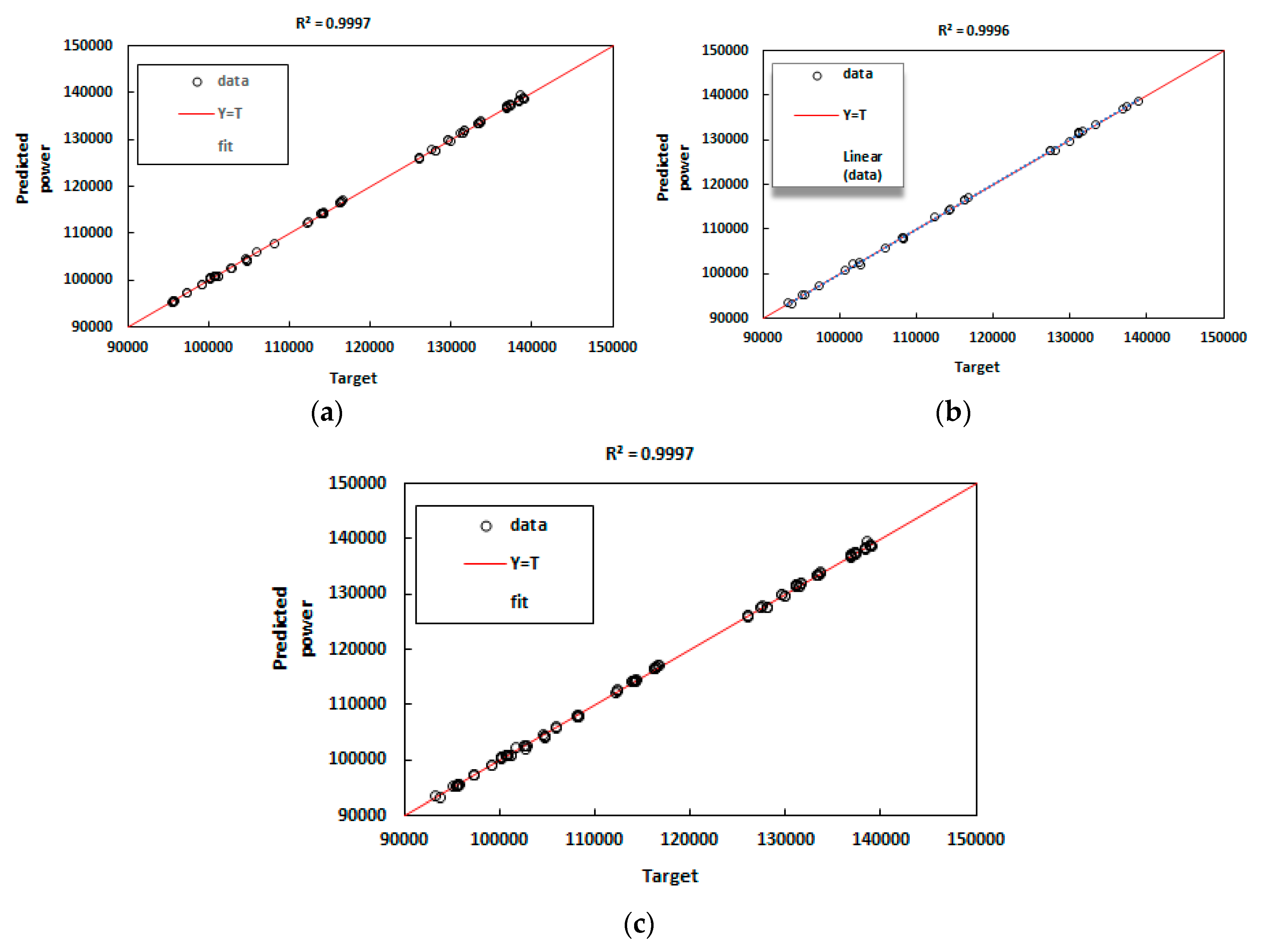
3. Results and discussion

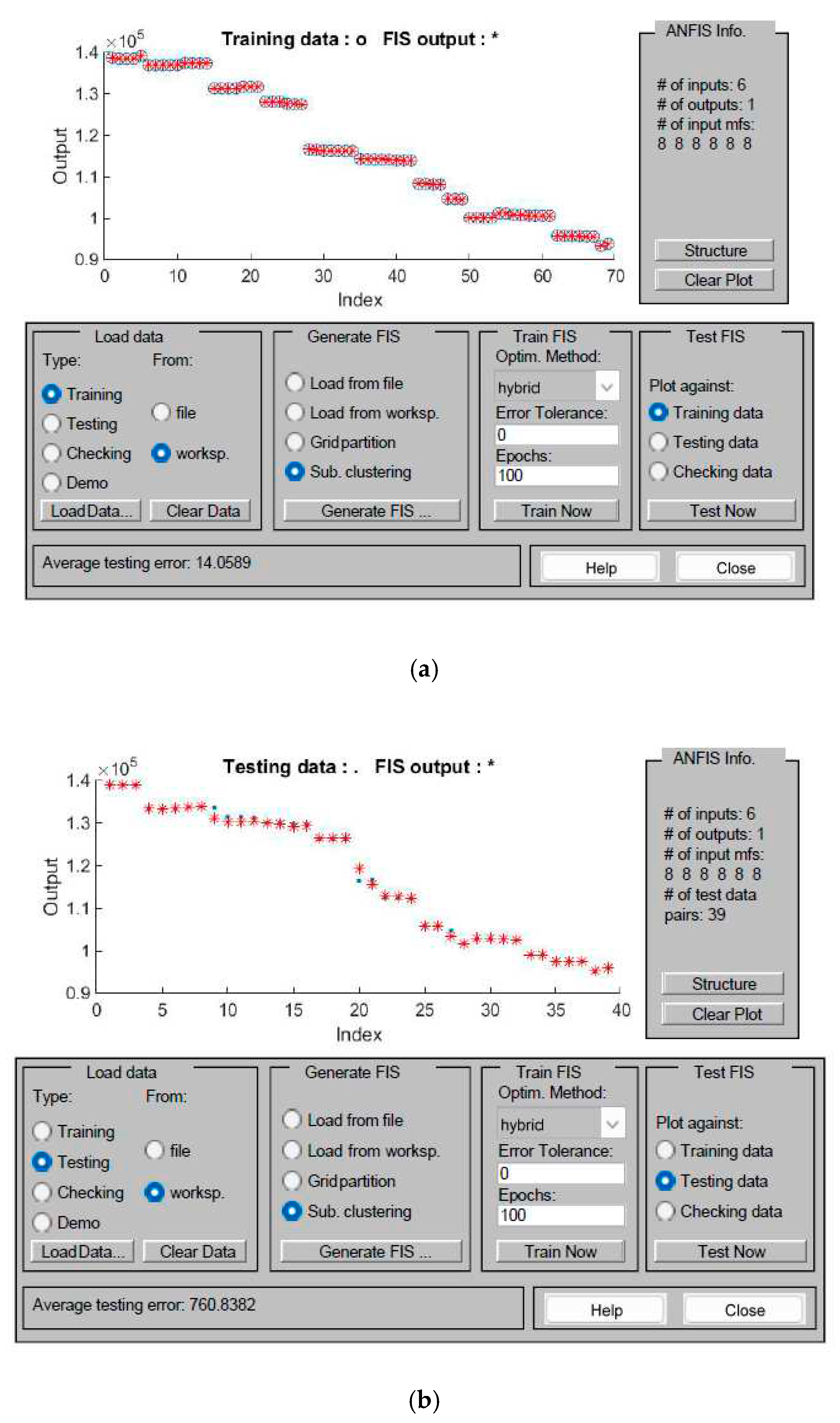
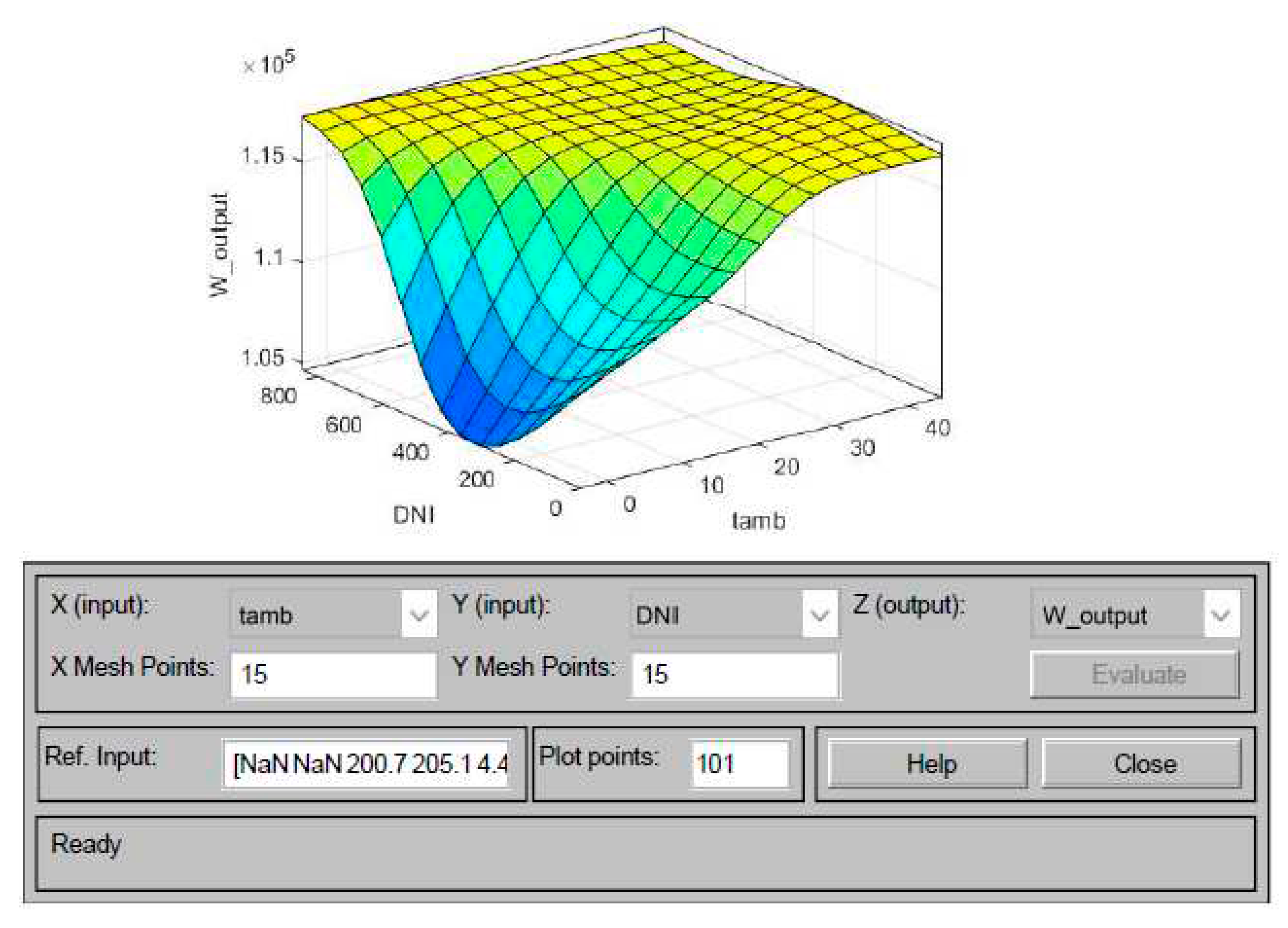
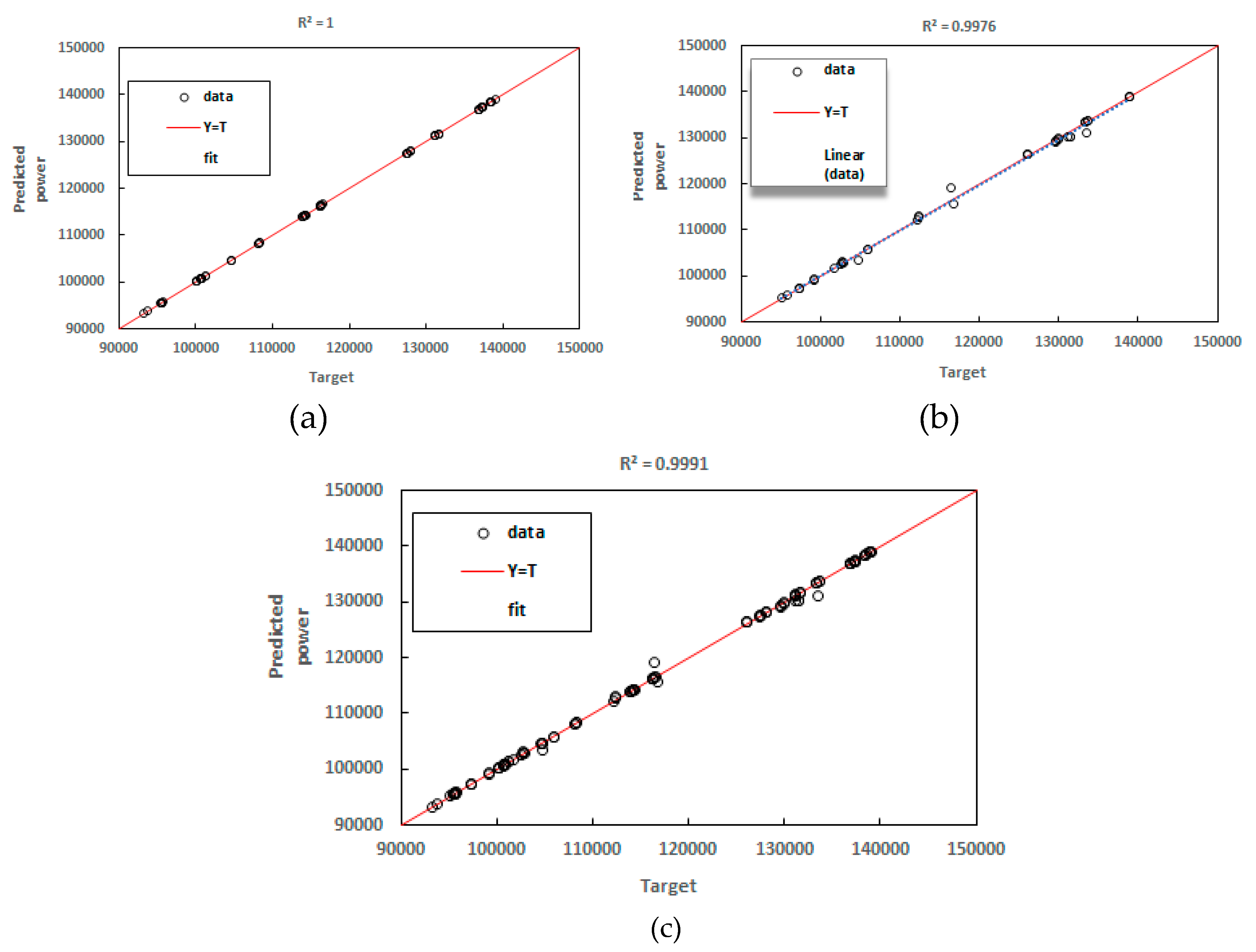
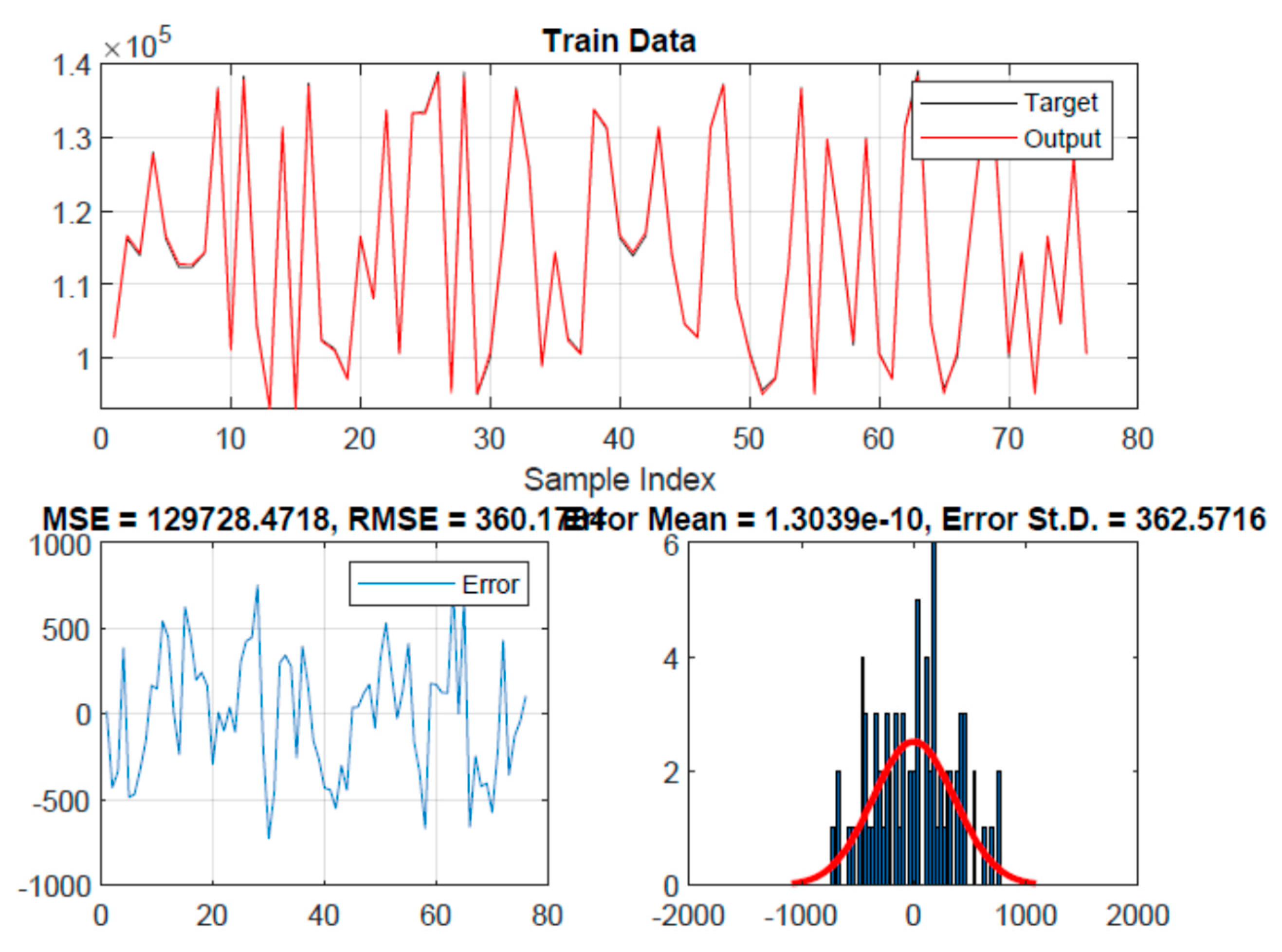
3.1. ANFIS

For the purpose of this investigation, data (training data and testing data) were loaded to the model, a FIS was generated and trained and then its reliability was tested with training data and with testing data as shown in Figure 7. The Takagi-Sugeno Fuzzy Inference System (FIS) was used and 8 gaussian membership functions were used for each input variable while a linear membership function was used for the output. A total of 8 rules were applied to define the FIS whose structure is shown in Figure 8.
It can be observed from Figure 7 that the set FIS is reliable for training and testing because errors are negligeable compared to the range of total power output.
Figure 9 displays a rule viewer of the model while Figure 10 shows the surface viewer for 2 input parameters, namely ambient temperature (tamb) and Direct Normal Irradiation (DNI). The output power (W_output) in Figure 9 is to be multiplied by 10^5. The rule viewer is equally showing reasonable results.
As expected, it can be observed from the surface viewer that the power output increases as the ambient temperature and the direct normal irradiation increase.
The ANFIS model appraisal was also conducted by means of the coefficient of correlation R2 obtained from the regression plots shown in Figure 11 for training, testing and overall results.
It emerges from Figure 11 that the ANFIS model performed well with an overall correlation coefficient of 0.9991.

3.2. ANFIS-PSO

The Matlab codes for running ANFIS-PSO were obtained from [24]. Particle Swarm Optimization is one of the widely known evolutionary algorithms or metaheuristic algorithms that are used to solve complex non-linear problems. It mimics the swarming behavior of creatures (insects, animals or birds). A swarm of particles is initially randomly generated. In the iterative search of the optimum solution each particle updates its position based on its prior experience and the experience of neighbors. The velocity with which the particle flies the search space is also consequently updated until the optimal or global best solution is found. The details of PSO can be found in [27,31]. For the purpose of this study, the following parameters were used: inertia weight w = 1, inertia weight damping ratio wdamp = 0.99, personal learning coefficient c1 = 1, global learning coefficient c2 = 2, number of rules = 10, maximum number of iterations = 1000 and the population size or swarm size nPop = 25. The corresponding ANFIS-PSO results are shown in Figure 12 and Figure 13.
It is clear from Figure 12 and Figure 13 that the ANFIS-PSO model outputs track very closely the expected or target data for training and for testing. For more insight, the regression plots are displayed in Figure 14.
It can be observed from Figure 14 that the ANFIS-PSO model performed well for training and for testing with an overall coefficient of correlation R2 = 0.9994. This performance metric is slightly higher than the one obtained with ANFIS model but the computation time was long.

3.3. ANFIS-GA

The genetic algorithm is one of the powerful optimization algorithms. It emulates the so-called biological evolution process in the nature or the natural selection of the fittest. The basic elements of a GA comprise: the fitness function, which is to get optimized, the population of chromosomes, the selection, by means of an operator, of chromosomes which will reproduce and the production through mutation, of the next generation in a random fashion. The crossover operation is employed to generate offsprings. It swaps a sequence or subsequence of the two selected chromosomes to create one or two offsprings depending on the strategy followed. The uniqueness of GA compared to PSO resides in the fact that unlike PSO, GA has got the selection operator for easy optimization and not all the individuals are retained as members of the population. This last factor somewhat reduces the computation time. The main steps in the deployment of a GA are initialization of the population, calculation of the fitness function, crossover, mutation, selection of survivor and finally terminate the process and keep the best if criteria is met. The details of GA can be found in [27].
In this investigation parameters of the ANFIS section were kept as in the case of PSO (number of rules = 10, nPop =25 and maximum iterations = 1000) and the following parameters were used for the GA: Crossover percentage pc = 0.4, number of offsprings nc = 2*round(pc*nPop) = 10, mutation percentage pm = 0.7, number of mutants nm = round(pm*nPop) = 18, gamma = 0.7, mutation rate mu = 0.15 and selection pressure beta = 8. The corresponding ANFIS-GA results are shown in Figure 15 and Figure 16.
It is obvious from Figure 15 and Figure 16 that as in the case of ANFIS-PSO, the ANFIS-GA model outputs track very closely the expected or target data for training and for testing. The corresponding regression plots are depicted in Figure 17.
It can be observed from Figure 17 that the ANFIS-GA model performed very well for training and for testing with an overall correlation coefficient R2 equal to 0.9997 which was slightly higher than the one obtained in the case of ANFIS-PSO and the corresponding MSE or RMSE was relatively lower than in the case of ANFIS-PSO. It was also noted that the computation time was relatively shorter than that required for ANFIS-PSO which may be attributed to the reduction of the population size due to the selection of the fittest.

4. Conclusion

In this investigation, the ANFIS model and the hybrid ANFIS model combined with evolutionary algorithms (PSO and GA) were alternatively employed to model and analyze the performance of a combined cycle gas turbine power plant integrated with a concentrated solar power system utilizing parabolic troughs. The results demonstrated remarkable accuracy and efficacy across all models, with coefficient of correlation (R²) values reaching an impressive 0.9991 for ANFIS, 0.9994 for ANFIS-PSO, and 0.9997 for ANFIS-GA. Additionally, the root mean square errors were consistently minimal, substantiating the precision of these ANFIS-based approaches. Notably, the accuracy exhibited an upward trajectory as the foundational ANFIS model was enriched through integration with metaheuristic optimization techniques. The application of evolutionary algorithms (PSO or GA) to hybridize ANFIS showcased its robustness and reliability in analyzing and predicting the integrated solar combined cycle power plant’s performance. However, it is essential to acknowledge that this hybridization, while enhancing accuracy, also led to an increase in computation time. Remarkably, among the ANFIS-based methodologies explored, the ANFIS-GA model emerged as a standout performer for the scenarios investigated in this study. The significance of this work is underscored by its revelation of the potential inherent in ANFIS-based methodologies for accurate performance prediction within hybrid thermal power plants. These methodologies present themselves as practical alternatives to more phenomenological approaches. As we look towards the future, several avenues for further exploration come to light:
  • Delve into the influence of clustering techniques, varying parameters, and the intrinsic model parameters on the ANFIS approach’s performance.
  • Thoroughly investigate the pivotal parameters of the hybrid ANFIS-PSO and ANFIS-GA models, discerning their impact on accurately forecasting the integrated solar combined cycle power plant’s performance.
In conclusion, this study illuminates the efficacy of ANFIS-based methodologies in precisely predicting hybrid thermal power plant performance. By leveraging the capabilities of evolutionary algorithms, these methodologies can serve as invaluable tools, offering a level of accuracy that is both robust and practical when compared to traditional phenomenological methodologies.

Author Contributions

Conceptualization, K.T.K. and….; methodology, K.T.K; software, K.T.K.; validation, K.T.K., I.O.O. and L.K.T.; formal analysis, K.T.K.; investigation, K.T.K; resources, L.K.T.; data curation, K.T.K.; writing—original draft preparation, K.T.K.; writing—review and editing, K.T.K and …..; visualization,…..; supervision, L.K.T; project administration, L.K.T.; funding acquisition, L.K.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data used in this study can be found at https://data.mendeley.com/datasets/crzxm8ggwn.

Acknowledgments

The authors thank the University of Johannesburg for financial support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Baypai, P.; Dash, V. Hybrid renewable energy systems for power generation in stand-alone applications: A Review. Renewable and sustainable Energy Reviews 2012, 16, 2926–2939. [Google Scholar]
  2. Ibrahim, T.K.; Mohammed, M.K.; Awad, O.I.; Rahman, M.; Najafi, G.; Basrawi, F.; Alla, A.N.A.; Mamat, R. The optimum performance of the combined cycle power plant: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 459–474. [Google Scholar] [CrossRef]
  3. Tüfekci, P. Prediction of full load electrical power output of a base load operated combined cycle power plant using machine learning methods. Int. J. Electr. Power Energy Syst. 2014, 60, 126–140. [Google Scholar] [CrossRef]
  4. Kumar, R.; Hynes, N.R.J. Prediction and optimisation of surface roughness in thermal drilling using integrated ANFIS and GA approach. Engineering science and Technology, an International Journal 2020, 23, 30–41. [Google Scholar] [CrossRef]
  5. Zahraee, S.M.; Assadi, M.K.; Saidur, R. Application of Artificial Intellingence Methods for hybrid Energy System optimisation. Renewable and Sustenable Energy Reviews 2016, 66, 617–630. [Google Scholar] [CrossRef]
  6. Mosavi, A.; Salimi, M.; Ardabili, S.F.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the Art of Machine Learning Models in Energy Systems, a Systematic Review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef]
  7. Sharifzadeh, M.; Sikinioti-Lock, A.; Shah, N. Machine-learning methods for integrated renewable power generation: A comparative study of artificial neural networks, support vector regression, and Gaussian Process Regression. Renew. Sustain. Energy Rev. 2019, 108, 513–538. [Google Scholar] [CrossRef]
  8. Rodríguez, M.B.R.; Rodríguez, J.L.M.; Fontes, C.d.H. Modeling of a Combined Cycle Gas Turbine (CCGT) Using an Adaptive Neuro-Fuzzy System. Therm. Eng. 2022, 69, 662–673. [Google Scholar] [CrossRef]
  9. Khosravi, A.; Malekan, M.; Pabon, J.J.G.; Zhao, X.; Assad, M.E.H. Design parameter modelling of solar power tower system using Adaptive neuro-fuzzy inference system optimized with a combination of genetic algorithm and teaching – based optimisation algorithm. Journal of cleaner Production 2020, 244, 118904. [Google Scholar] [CrossRef]
  10. Yaïci, W.; Entchev, E. Adaptive Neuro-Fuzzy Inference System modelling for performance prediction of solar thermal energy system. Renew. Energy 2016, 86, 302–315. [Google Scholar] [CrossRef]
  11. Zaaoumi, A.; Bah, A.; Alaoui, M.; Mechaqrane, A.; Berrehili, M. Application of artificial neural networks and adaptive neuro-fuzzy inference system to estimate the energy generation of a solar power plant in Ain Beni-Mathar (Morocco). Electronics, Computers and Artificial Intelligence (ECAI 2018) International conference. 28-30 June 2018, Iasi, Romania.
  12. Afzal, A.; Buradi, A.; Jilte, R.; Shaik, S.; Kaladgi, A.R.; Arıcı, M.; Lee, C.T.; Nižetić, S. Optimizing the thermal performance of solar energy devices using meta-heuristic algorithms: A critical review. Renew. Sustain. Energy Rev. 2023, 173, 112903. [Google Scholar] [CrossRef]
  13. Reyes-Belmonte, M.A.; Pino, F.J.; Romero, M.; Suarez, C.; Gongalez-Aguilar, J.; Guerro, J. Optimization of an Integrated solar combined cycle. AIP Conference Proceedings 2018, 2033, 210012. [Google Scholar]
  14. Achour, L.; Bouharkat, M.; Behar, O. Performance assessment of an integrated solar combined cycle in the southern of Algeria. Energy Rep. 2018, 4, 207–217. [Google Scholar] [CrossRef]
  15. Temraz, A.; Alobaid, F.; Link, J.; Elweteedy, A.; Epple, B. Development and validation of a Dynamic Simulation Model for an Integrated Solar Combined Cycle Power Plant. Energies 2021, 14, 3304. [Google Scholar] [CrossRef]
  16. Benabdellah, H.M.; Ghenaiet, A. Energy, exergy, and economic analysis of an integrated solar combined cycle power plant. Eng. Rep. 2021, 3, e12404. [Google Scholar] [CrossRef]
  17. Elmohlawy, A.E.; Ochkov, V.F.; Kazaudzhan, B.I. Evaluation of the performance and energy efficiency of integrated solar combined cycle power plant. Energy Sector Problems 2019, 21, 43–54. [Google Scholar] [CrossRef]
  18. Elmorsy, L.; Morosuk, T.; Tsatsaronis, G. Exergy-Based Analysis and Optimization of an Integrated Solar Combined-Cycle Power Plant. Entropy 2020, 22, 655. [Google Scholar] [CrossRef]
  19. Rashad, A.; Elweteedy, A.; Temraz, A.; Gomaa, A. Investigating an integrated solar combined cycle power plant. Global Journal of Engineering Sciences 2021, 1, 33552. [Google Scholar] [CrossRef]
  20. Dayem, A.A.; Metwally, M.N.; Alghamdi, A.; Marzouk, E. Numerical Simulation and Experimental Validation of Integrated Solar Combined Power Plant. Energy Procedia 2014, 50, 290–305. [Google Scholar] [CrossRef]
  21. Elmohlawy, A.E.; Ochkov, V.F.; Kazandzhan, B.I. Study and Prediction the Performance of an Integrated Solar Combined Cycle Power Plant. Energy Procedia 2019, 156, 72–78. [Google Scholar] [CrossRef]
  22. Available online: https://data.mendeley.com/datasets/crzxm8ggwn.
  23. Rovira, A.; Abbas, R.; Sánchez, C.; Muñoz, M. Proposal and analysis of an integrated solar combined cycle with partial recuperation. Energy 2020, 198, 117379. [Google Scholar] [CrossRef]
  24. Olayode, I.O.; Severino, A.; Tartibu, L.K.; Arena, F.; Cakici, Z. Performance Evaluation of a hybrid PSO Enhanced ANFIS Model in Prediction of Traffic Flow of Vehicles on Freeways: Traffic Data Evidence from South Africa. Infrastructures Infrastructures 2021, 7, 7010002. [Google Scholar] [CrossRef]
  25. Zayed, M.E.; Zhao, J.; Li, W.; Elsheikh, A.H.; Elaziz, M.A. A hybrid adaptive neuro-fuzzy inference system integrated with equilibrium optimizer algorithm for predicting the energetic performance of solar dish collector. Energy 2021, 235, 121289. [Google Scholar] [CrossRef]
  26. Kennedy, J.; Eberhart, R.C. Particle swarm optimisation. In the Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, Australia, 1942-1948. Piscataway, NJ: IEEE Service Center.
  27. Okwo, M. O.; Tartibu, L. K. Metaheuristic optimization: Nature-inspired algorithms swarm and computational intelligence, theory and applications. Springer Nature, 2020.
  28. Zolpakar, N.A.; Yasak, M.F.; Pathak, S. A review: use of evolutionary algorithm for optimisation of machining parameters. Int. J. Adv. Manuf. Technol. 2021, 115, 31–47. [Google Scholar] [CrossRef]
  29. Ceylan, Z.; Pekel, E.; Ceylan, S.; Bulkan, S. Biomass Higher Heating Value Prediction Analysis by ANFIS, PSO-ANFIS and GA-ANFIS. Global NEST Journal 2017, 20, 589–597. [Google Scholar]
  30. Rezakazemi, M.; Dashti, A.; Asghari, M.; Shiraziani, S. H2-Selective mixed matrix membranes modelling using ANFIS, PSO-ANFIS, GA-ANFIS. International Journal of Hydrogen Energy 2017, 42, 15211–15225. [Google Scholar] [CrossRef]
  31. Piotrowski, A. P.; Napiorkowski, J. J.; Piotrowska, A. E. Population size in particle swarm optimization. Swarm Evolutionary Computation 2020, 58, 100718. [Google Scholar] [CrossRef]
Preprints 85907 g001
Figure 1. Flowchart of the methodological approach.
Figure 1. Flowchart of the methodological approach.
Preprints 85907 g001
Preprints 85907 g002
Figure 2. Layout of the reference ISCCPP [23].
Figure 2. Layout of the reference ISCCPP [23].
Preprints 85907 g002
Preprints 85907 g003
Figure 3. Typical ANFIS model architecture [25].
Figure 3. Typical ANFIS model architecture [25].
Preprints 85907 g003
Preprints 85907 g004
Figure 4. Flow chart of PSO [27].
Figure 4. Flow chart of PSO [27].
Preprints 85907 g004
Preprints 85907 g005
Figure 5. Flow chart of Genetic Algorithm [28].
Figure 5. Flow chart of Genetic Algorithm [28].
Preprints 85907 g005
Preprints 85907 g006
Figure 6. Major steps of implementation of hybrid ANFIS-PSO and ANFIS-GA models.
Figure 6. Major steps of implementation of hybrid ANFIS-PSO and ANFIS-GA models.
Preprints 85907 g006
Preprints 85907 g007
Figure 7. Testing the FIS with: (a) training data and (b) Testing data.
Figure 7. Testing the FIS with: (a) training data and (b) Testing data.
Preprints 85907 g007
Preprints 85907 g008
Figure 8. Structure of the FIS used in this investigation.
Figure 8. Structure of the FIS used in this investigation.
Preprints 85907 g008
Preprints 85907 g009
Figure 9. Rule viewer for the trained ANFIS model.
Figure 9. Rule viewer for the trained ANFIS model.
Preprints 85907 g009
Preprints 85907 g010
Figure 10. Typical surface viewer of the trained ANFIS model.
Figure 10. Typical surface viewer of the trained ANFIS model.
Preprints 85907 g010
Preprints 85907 g011
Figure 11. ANFIS regression plots for: (a) training, (b) testing and (c) All data.
Figure 11. ANFIS regression plots for: (a) training, (b) testing and (c) All data.
Preprints 85907 g011
Preprints 85907 g012
Figure 12. ANFIS-PSO data plots for training.
Figure 12. ANFIS-PSO data plots for training.
Preprints 85907 g012
Preprints 85907 g013
Figure 13. ANFIS-PSO data plots for testing.
Figure 13. ANFIS-PSO data plots for testing.
Preprints 85907 g013
Preprints 85907 g014
Figure 14. ANFIS-PSO regression plots for: (a) training, (b) testing and (c) All data.
Figure 14. ANFIS-PSO regression plots for: (a) training, (b) testing and (c) All data.
Preprints 85907 g014
Preprints 85907 g015
Figure 15. ANFIS-GA data plots for training.
Figure 15. ANFIS-GA data plots for training.
Preprints 85907 g015
Preprints 85907 g016
Figure 16. ANFIS-GA data plots for testing.
Figure 16. ANFIS-GA data plots for testing.
Preprints 85907 g016
Preprints 85907 g017
Figure 17. ANFIS-GA regression plots for: (a) training, (b) testing and (c) All data.
Figure 17. ANFIS-GA regression plots for: (a) training, (b) testing and (c) All data.
Preprints 85907 g017
Table 1. A sample of dataset used in this investigation.
Table 1. A sample of dataset used in this investigation.
tamb (⁰C) DNI (w/m2) ma (kg/s) mg (kg/s) mf (kg/s) mHTF (kg/s) Power output (kW)
11.0767 162.547 214 219 5 85.34 128037.2
20.9667 749.527 201.47 205.76 4.3 85.34 116162.6
24.9233 447.82 196.51 200.81 4.3 85.33 112374.3
25.42 434.645 196.95 200.82 4.3 85.33 112389.7
22.9978 551.628 198.95 203.26 4.32 85.34 114308.4
0.61 88.15 223.85 229.14 5.29 85.34 136802.8
36.97 332.64 183.25 187.23 3.98 85.33 101213
-0.61 64.63 225.16 230.5 5.34 85.34 138351.3
33.025 137.475 187.24 191.48 4.24 85.34 104705.4
44 0 174.84 178.72 3.88 85.34 93186.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated