Refined Equivalent Modeling Method for Mixed Wind Farms Based on Small Sample Data

Preprint

Article

Refined Equivalent Modeling Method for Mixed Wind Farms Based on Small Sample Data

This version is not peer-reviewed.

Qianlong Zhu^*,1

,Wenjing Xiong,

Haijiao Wang,Xiaoqiang Jin

Qianlong Zhu^*,1

,Wenjing Xiong,

Haijiao Wang,Xiaoqiang Jin

¹ cite table in the main text

This version is not peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

21 September 2023

Posted:

25 September 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

For equivalent modeling of mixed wind farms (WFs), existing clustering indicators cannot consider the complex coupling characteristics between different types of wind turbines (WTs). This paper proposes a refined equivalent modeling method for mixed WFs based on artificial intelligence technology. Firstly, the electromechanical transient performance of mixed WFs is analyzed. The WT type, wind speed and direction, and voltage dip are considered the main factors affecting the external dynamic response of mixed WFs. Secondly, the equivalent node model is established, including the selection of independent and dependent variables. Then, the multiple artificial neural networks (ANNs) are trained one by one based on sample data, to explore the nonlinear relationship between the dependent variables and the independent variables. Finally, the electromechanical transient simulations of the power systems with a mixed WF is carried out by using the MATLAB platform. Simulation results show that the proposed model can reflect the external characteristics of the mixed WF in different wind scenarios and voltage dips.

Keywords:

Subject:

Engineering - Electrical and Electronic Engineering

1. Introduction

In recent years, large-scale wind farms (WFs) have become popular to reduce the consumption of fossil fuels in China [1,2]. The growing penetration of wind power brings deep changes in the dynamic performance of power systems, due to the low inertia and weak voltage support capability of wind power [3,4]. To ensure the safe and stable operation of the changing power systems, grid power operators must conduct extensive simulation analysis in advance. Large-scale WFs may consist of hundreds or even thousands of wind turbines (WTs), which could significantly enlarge the size of a model and then cause the “curse of dimensionality” [5]. Therefore, it is significant to develop the WF equivalent models for power system dynamic studies.

Currently, WTs are generally divided into 4 types, i.e., squirrel-cage induction generator (SCIG), wound rotor induction generator (WRIG), doubly-fed induction generator (DFIG), and permanent magnet synchronous generator (PMSG) [6,7]. In the early days, SCIG and WRIG were the mainstream WTs. Due to the lack of power converters, the rotor speeds of these WTs remain almost constant under different wind speeds. In addition, early SCIG- or WRIG-based WFs are not large. The differences in electrical distance and input wind speed between WTs are relatively small, leading to high behavioral correlations among WTs in large disturbance scenarios. Therefore, the single-machine equivalent modeling method, which aggregates the whole WF into one equivalent WT, is recommended for SCIG-based and WRIG-based WFs [8]. However, with the continuous expansion of the WF scale and the emergence of variable speed constant frequency WTs, it is difficult to reflect the external characteristics of WFs using the single-machine equivalent modeling method.

For DFIG- or PMSG- based WFs, there are differences in the operating characteristics of WTs within WFs, and the multi-machine equivalent modeling method, which clusters WTs into several groups and aggregates each group into one equivalent WT, generally reflects the dynamic characteristics of WFs better and has wider applications in practice [9]. During past few decades, to obtain a better performance on WT clustering, wind speed [10,11], rotor speed [12], the power characteristic curve [13,14], crowbar action [15,16], chopper action [17] and other quantities have been fully investigated to be selected as the clustering indicators. With these methods, the dynamic characteristics of DFIG- or PMSG- based WFs can be accurately represented.

The dynamic performance of DFIG and PMSG is better, but SCIG still exists in the power system because of its low maintenance, complication, and expenses [18,19]. From an economic perspective, WF operators will consider utilizing the complementarity between different types of WTs to build mixed WFs. At present, there is limited literature on equivalent modeling of mixed WFs. For a mixed WF composed of SCIG and DFIG, the WTs are firstly separated based on the WT type, and then a second clustering is performed based on wind speed [5]. In [20], the genetic algorithm is used to solve the equivalence problem of inconsistent parameters between WTs of the same type, but still used separate equivalence for SCIG and DFIG. For mixed WFs composed of SCIG and PMSG, references [21,22] also simply separate WTs based on type. It should be pointed out that within mixed WFs, there may be coupling characteristics between different types of WTs. Whether these coupling characteristics have an impact on the external characteristics of mixed WFs, whether the equivalent modeling method based on WT type differences can effectively reflect these coupling characteristics, and how to construct new clustering indicators if the existing ones cannot represent the coupling characteristics are the issues worth in-depth consideration and research. However, they are not mentioned in the aforementioned literature.

Accordingly, this paper proposes an innovative refined equivalent modeling method for mixed WFs. The main contributions are listed as follows:

(1): The method of using multiple artificial neural networks (ANNs) to identify the electromechanical transient power fluctuation curve of mixed WFs is introduced into the research on equivalent modeling. For small sample data scenarios, the established model has good performance.
(2): Meaningful insights into how to select the equivalent node model are provided. The WT type, wind speed and direction, and the fault voltage dip are select as the independent variables of the equivalent node model. The active power and reactive power at the point of connection (POC) are selected as the dependent variables.

The remainder of this paper is organized as follows. In Section 2, the ideas and methods based on artificial intelligence technology are introduced. The external characteristics of mixed WFs are discussed in detail in Section 3. In Section 4, the equivalent node modeling method for mixed WFs is established. The example analysis and conclusions are discussed in Section 5 and Section 6.

2. Ideas and Methods

Different from the coherence-based WF equivalent modeling method, we treat the whole WF as a black box and utilize artificial intelligence technology to explore the mapping relationship between inputs and outputs. The proposed modeling method has the following characteristics:

(1): It focuses on the input and output characteristics of WFs, without emphasizing the internal structure and operation principle. The WF structure modeling can be omitted.
(2): The ANN has a large number of connections, and the weights of the connection correspond to the model parameters. By adjusting these parameters, the ANN can approximate the outputs of nonlinear systems
(3): The time spending on modeling is only related to the ANN and its learning algorithm, and no longer depends on the type and number of WTs within one WF.

The difficulty of this equivalent modeling method lies in balancing the accuracy and generalization ability of the equivalent model, as well as obtaining data training sets. The wind speed and voltage dip are candidates for the inputs of the black-box model since they are crucial for the dynamic performance of WFs. In the electromechanical transient time scale, it is usually considered that the wind speed and direction remain constant, and the voltage dip during the fault period also remains unchanged. Considering that using a set of constants to explore the change rule of the whole dynamic curve of WFs may produce a large error, we adopt the way of training each time point separately, that is, using ANN each time only for the same time in different samples of the power data training. The proposed equivalent modeling method will establish several ANNs to fit the whole dynamic curve of WFs, but it is suitable for small sample data scenarios. The framework of this method is shown in Figure 1.

3. External Characteristics of Mixed WF

3.1. Composition of Mixed WF

Compared with WFs composed of same WTs, the concept of mixed WFs includes two meanings: one is the types of WTs in one WF are the same, but the parameters between the WTs are different. The other is that the types of WTs in one WF are different. The first one is relatively simple. The differences between the WTs are mainly reflected in the capacity, operation control mode, and control parameters. In this case, the external performance of the mixed WF will not deviate too much from the dynamic response of the WTs contained in it. Therefore, the equivalent WF model can still follow the single-machine model structure. For the second case, the differences between the WTs are directly reflected in the type of power generation technology and the topology. In this case, the mixed WF is the sum of the dynamic response of each type WTs, and its external characteristics may be different from the performance of any type of WTs. Therefore, the equivalent WF model can no longer simply follow the single-machine model structure.

Without loss of generality, we carry out an equivalent modeling study on mixed WFs for the second scenario, which integrates the simultaneous existence of three mainstream WTs, i.e., DFIG, PMSG, and SCIG. The parameters of the same type of WTs are identical. The topology of the mixed WF is shown in Figure 2. The model parameters are given in Table A1.

3.2. Influencing Factors of External Characteristics of Mixed WF

3.2.1. WT Type

As the core device in WFs, WTs play a decisive role in the external characteristics of WFs. In the electromechanical transient process, the dynamic response of the WT mainly depends on its operation control characteristics. Due to the differences in control topology and strategy, different types of WTs have their unique dynamic response, as shown in Figure 3.

The stator of DFIG is directly connected to the grid, and the rotor is connected to the grid through the power converter. The capacity of the power converter is generally 30 % of the capacity of DFIG. To protect the IGBT in the rotor-side converter from electrical and thermal overload, a crowbar circuit is usually added between the rotor and the converter. When the crowbar circuit is activated, the DFIG will lose its power regulation capability, resulting in the WT not only not providing reactive power support to the grid, but also needing to absorb part of the reactive power from the grid. After the crowbar circuit is out of service, the DFIG can restore the reactive power support to the grid.

PMSG is connected to the grid through a full-power converter. The increase in the capacity of the power converter makes the power regulation ability of the PMSG and the ability to withstand fault impacts significantly enhanced. Therefore, it is generally only necessary to install a chopper circuit at the DC bus of the power converter to protect the converter. Compared with DFIG, PMSG can continuously provide reactive power support to the grid during the fault period, and the output reactive power is higher than that of DFIG.

SCIG does not contain a power converter module, so its power regulation ability is relatively weak, resulting in relatively intense and lasting active power fluctuations in its dynamic response process. At the same time, it needs to absorb a large amount of reactive power from the grid.

3.2.2. Wind Speed and Direction

In practice, wind power operators will use the wind measurement device to record the wind condition information of WFs, mainly including wind speed and direction. The wind speed reflects the strength of the wind condition, and the wind direction determines the shielding relationship between the upstream and downstream WTs within the WF. Under the wake effect, wind speed and direction jointly determine the operating conditions of WTs and WFs. Moreover, the operating conditions of WTs and WFs before faults will affect their dynamic response.

It is worth noting that compared with WFs composed of same WTs, the external characteristics of mixed WFs are more obviously affected by wind conditions due to the difference in WT types. As shown in Figure 4, when the input wind speed is 16 m / s and the wind direction is 270 and 90 respectively, the distribution of wind resources in the wind field has an axisymmetric relationship. However, due to the influence of WT type differences, the external characteristics of the mixed WF show different fluctuation processes.

3.2.3. Fault Voltage Dip

As an important fault characteristic quantity, the voltage dip at the POC directly reflects the influence of the grid-side fault on the wind farm. We know that the voltage dip determines the speed change of the WT, the action of the protection circuit, and the amount of reactive power support provided to the grid, which in turn indirectly affects the external characteristics of the mixed WF, as shown in Figure 5.

3.3. External Characteristic Analysis

In power systems, the oscillation waveform in time domain simulation is generally in the form of variable period attenuation (divergence), and its characteristic parameters mainly include amplitude, attenuation coefficient, and oscillation period. The external characteristics of mixed WFs are the combination of the dynamic response process of multiple WTs under different types and different operating conditions. Although the oscillation waveforms between WTs are not the same, the power fluctuation after the convergence of multiple WTs should be smoother than that of a single one. Therefore, for an actual determined mixed WF, the fluctuation process of its external characteristics is generally rule-based. It increases the feasibility of treating the WF as a whole to identify its external characteristics.

4. Equivalent Node Modeling for Mixed Wind Farm

4.1. Equivalent Node Model

In the dynamic equivalent method of power systems, the equivalent model constructed by the coherent theory retains the model structure of the original power device. The advantage is that the existing structure can be directly used for analysis and calculation, but the detailed parameters of the system to be equivalent are needed in the modeling process. For the estimation equivalent modeling method, it directly treats the system as a black box, and the equivalent model is established based on the system identification theory by analyzing the dynamic process of the input and output variables of the system. The equivalent model established by this method is no longer limited to the original model structure of power devices. It provides theoretical support for the equivalent node model of mixed wind farms.

The nodes in power systems are described by a set of interrelated variables such as active power, reactive power, voltage amplitude, and phase angle. When the WF is connected to the grid, the change of voltage and frequency at the network node will directly affect the operation state of the WF, that is, the power output from the WF to the network node, which in turn affects the voltage and frequency of the power network. It can be seen that the equivalent node model of the WF should be used to characterize the external power characteristics of the WF. Therefore, the active power and reactive power at the POC are selected as the dependent variables of the equivalent node model. According to the analysis in Section 3.2, the external characteristics of mixed WFs are mainly affected by the WT type, the magnitude and direction of wind speed, and the fault voltage dip. Therefore, the above indicators are selected as the independent variables of the equivariant node model. Because the expression of WT type information needs a carrier, we take each WT as an input, and then distributes the wind speed and wind direction information of the WF to each WT according to the wake effect principle, and then uses the input wind speed of 21 WTs to replace the WT type and the wind speed and direction. Therefore, there are 22 input variables of the equivalent node model of the mixed WF, that is, the input wind speeds of 21 WTs and the voltage dip at the POC.

4.2. Experimental Design and Data Collection

The idea of the estimation equivalent modeling method is to extract the intrinsic law of the system by analyzing the sample data, so the selection of the sample must be representative, and also pay attention to the balance of the sample category. Based on the above principles, the wind direction is evenly divided into 16 azimuths according to the interval. The wind speed is divided into 21 wind speed segments according to the (1 m/s) step size between the wind turbine cut-in wind speed (3 m/s) and the cut-off wind speed (23 m/s). For the voltage dip, four cases of voltage drop to 0.2 pu, 0.4 pu, 0.6 pu, and 0.8 pu at the POC are considered, with a three-phase short-circuit occurring at the moment of 0.1 s, and is removed 150 ms later. Each combination of wind speed magnitude, wind direction, and voltage dip constitutes a set of input variables totaling 1344 sets.

According to the simulation waveform, during the fault period and the initial stage of fault removal, the fluctuation of the external characteristics of the WF is more severe, and then the fluctuation tends to be stable. Therefore, we adopt the variable step size sampling method, that is, in the 0 ~ 1 s and 1 ~ 3 s periods, the active power and reactive power of the WF are collected at intervals of 0.05 s and 0.5 s, respectively.

The sampled data have different physical meanings and different dimensions. To meet the requirements of ANN for training samples, it is necessary to scale the data, that is, the input and output data are limited to [0, 1] or [-1, 1] intervals [23]. In this paper, the linear scale transformation method is used, and the mathematical formula is as follows:

x^{'} = \frac{x - x_{\min}}{x_{\max} - x_{\min}}

(1)

Where

x

x_{\min}

x_{\max}

are the original value of the training sample, the minimum value, and the maximum value of the training sample, respectively.

4.3. ANN-Based Equivalent Modeling

ANN is widely used due to the ability to express the gradient method in a very indirect and explicit way, as well as with a distinct physical meaning. In this paper, the ANN is selected to construct the equivalent node model of mixed WFs, which mainly includes the following contents: the selection of input and output variables, the determination of the number of implied layers, the number of neurons, and the implementation of the learning algorithm. It can be seen from the previous analysis that the input variables are the input wind speeds of 21 WTs and the voltage dip at the POC. The output variables are the active power and reactive power of the mixed WF. It is worth noting that the accuracy of an ANN can be improved by increasing the number of neurons even if a network structure with a single hidden layer is used. Therefore, we set the number of hidden layers of the neural network to 1, and the number of neurons can be determined by the Kolmogorov theorem or the repeated test method. The learning algorithm adopts the error correction learning algorithm, and the modeling flow is shown in Figure 6.

5. Example Analysis

The proposed equivalent node modeling method for mixed WFs is implemented in the MATLAB platform, where the number of neurons in the hidden layer is

2 \times 22 + 1 = 45

, the learning efficiency is 0.05, and the additional momentum factor is 0.7.

An accurate assessment of the hybrid wind farm equivalent node model requires the construction of appropriate assessment metrics. Considering the numerical characteristics of active power and reactive power at the grid-connected point of wind farm, the average relative error index is used to evaluate the fitting accuracy of the equivalent node model to the active power, and the average absolute error index is used to evaluate the fitting accuracy of the equivalent node model to the reactive power. The formula is as follows:

E_{r} = \frac{1}{n} \sum_{i = 1}^{n} | \frac{Y_{f i} (k) - Y_{i} (k)}{Y_{i} (k)} |

(2)

δ = \max_{1 \leq i \leq n} | Y_{f i} (k) - Y_{i} (k) |

(3)

where

Y_{i} (k)

and

Y_{f i} (k)

are the electrical quantities of the detailed model and the equivalent model of the WF at the POC, respectively.

n

is the number of sampling points.

To verify the generalization ability of the resulting mixed WF equivalent node model, 20 groups of the WF are randomly generated with a combination of wind speed magnitude and direction as well as the voltage dip, and then the input wind speed of each unit is deduced based on the principle of the wake effect. According to equations (2) and (3), the error index of the equivalent node model of the WF under these 20 sets of test data conditions is shown in Table 1.

Table 1 shows that the power error metrics of the equivalent node model are relatively concentrated, which is mainly since the sample types were considered to be balanced in the experimental design session and the linear scale transformation was applied to the collected data. More importantly, we adopt a separate ANN training method for each sampling moment point, so that the error of the whole power curve is jointly determined by multiple ANNs, which in turn reduces the influence of the volatility of the output of a single ANN on the error index, and makes the established equivalent node model of hybrid wind farms have good stability. The performance of the equivalent node model at each time point under the No. 1 test data, which is the test group with the smallest error, is shown in Table 2.

Figure 7 shows the detailed model of the mixed WF and the power curve of the equivalent node model at the POC under the condition of No.20 test data. It can be seen that the error index of the equivalent node model is the largest under the condition of No.20 test data, but the dynamic response curve of the model can still characterize the fluctuation process of the detailed model of the WF in shape and trend. As an application of the estimation equivalence method for WFs, the equivalent node model of mixed WFs can reflect the external characteristics of mixed WFs, both in terms of the error index and the curve trend.

From Figure 7, it can be further seen that the equipotential node model fits the WF reactive power relatively better compared to the active power, which is mainly because the nonlinearity of the WF reactive power is weaker than that of the active power during the electromechanical transient process, and thus the ANN can converge to the globally optimal solution more easily.

6. Conclusions

In this paper, from the perspective of system identification modeling, an equivalent node model construction method for mixed WFs based on small sample data is proposed.

(1): During the electromechanical transient process, the external characteristics of the mixed WF are mainly affected by three factors: the WT type, the wind speed and direction, and the voltage dip at the POC. At the same time, the output active and reactive power will affect the frequency and voltage of the power systems. therefore, the input and output variables of the equivalent node model are determined.
(2): The ANN directly identifies the whole mixed WF as a black box, which avoids the selection and quantification of clustering indicators, as well as the equivalent parameters calculation of WTs, collection lines, grounding transformers, and control strategy.
(3): Based on the MATLAB platform, the establishment of the equivalent node model is realized, which makes the equivalent modeling of WFs no longer limited to the professional simulation platform, and it is also more convenient for the power dispatching department to use, enhancing the engineering practical value of the equivalent model.

Author Contributions

Conceptualization, Q. Z. and W. X.; methodology, Q. Z. and H. W.; software, X. J.; validation, Q. Z. and W. X.; formal analysis, Q. Z., W. X. and H. W.; investigation, Q. Z. and X. J.; resources, H. W.; data curation, W.X.; writing—original draft preparation, Q. Z.; writing—review and editing, Q. Z. and X.J.; visualization, H. W.; project administration, Q. Z. and W. X. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Open Fund of State Key Laboratory of Operation and Control of Renewable Energy & Storage Systems (China Electric Power Research Institute (No. NY80-22-002).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. Simulation parameters.

SCIG	Wind turbine
	Blade radius /m	48	Shaft system stiffness factor /(pu/rad)	1.11
	Inertia time constant /s	3.5	Rated wind speed /(m/s)	10
	Cut-in wind speed /(m/s)	3	Cut-out wind speed /(m/s)	23
	Squirrel-cage induction generator
	Rated power /MW	2	Rated frequency /Hz	50
	Rated voltage /kV	0.69	Stator impedance /pu	0.01+j0.1
	Rotor impedance /pu	0.01+j0.1	Stator and rotor mutual impedance /pu	J3
	Grounding transformer
	Rated capacity /MVA	5	Impedance /pu	3
	Rated Ratio /kV	25/0.575	Rated frequency /Hz	50
DFIG	Wind Turbine
	Blade radius /m	31	Shaft system stiffness factor /(pu/rad)	1.11
	Inertia time constant /s	4.32	Rated wind speed /(m/s)	12.5
	Cut-in wind speed /(m/s)	4.5	Cut-out wind speed /(m/s)	22
	Double-fed induction generators
	Rated power /MW	1.5	Rated frequency /Hz	50
	Rated voltage /kV	0.575	Stator impedance /pu	0.016+j0.16
	Rotor impedance /pu	0.023+j0.18	Stator and rotor mutual impedance /pu	j2.9
	Power converters
	Rated capacity of rotor-side converter /MVA	0.525	Rated capacity of grid-side converter /MVA	0.75
	DC Bus Rated Voltage /kV	1.15	DC side bus capacitance /F	0.01
	Crowbar circuit input threshold /pu	2	Crowbar circuit cut out threshold /pu	0.35
	Crowbar resistance /pu	0.1
	Grounding transformer
	Rated capacity /MVA	1.75	Rated frequency /Hz	50
	Rated Ratio /kV	25/0.575	Impedance /pu	0.06
PMSG	Wind turbine
	Blade radius /m	38	Shaft system stiffness factor /(pu/rad)	1.2
	Inertia time constant /s	4.6	Rated wind speed /(m/s)	12.5
	Cut-in wind speed /(m/s)	4.5	Cut-out wind speed /(m/s)	22
	Permanent magnet synchronous generator
	Rated power /MW	2	Rated frequency /Hz	50
	Rated voltage /kV	0.69	Rated DC bus voltage /kV	1.1
	Stator resistance /pu	0.0001	d-axis inductance of stator/ pu	1.5
	q-axis inductance of stator/ pu	1.5	DC bus capacitor/ F	0.01
	Grounding transformer
	Rated capacity /MVA	2.5	Rated frequency /Hz	50
	Rated Ratio /kV	25/0.69	Impedance /pu	0.06
Main Transformer	Rated capacity /MVA	150	Rated frequency /Hz	50
Main Transformer	Rated Ratio (kV)	220/25	Impedance /pu	0.135
Cable line	Unit resistance /(Ω/km)	0.1153	Unit inductance (/Ω/km)	j0.3297

References

Global Wind Energy Council. Global Wind Report 2021; Global Wind Energy Council: Brussels, Belgium, 2021; pp. 6–7. [Google Scholar]
Wu, J.; Xiao, J.; Hou, J.; Lyu, X. Development potential assessment for wind and photovoltaic power energy resources in the main desert–gobi–wilderness areas of China. Energies 2023, 16, 4559. [Google Scholar] [CrossRef]
Agarala, A.; Bhat, S.; Mitra, A.; Zycham, D.; Sowa, P. Transient stability analysis of a multi-machine power system integrated with renewables. Energies 2022, 15, 4824. [Google Scholar] [CrossRef]
Skibko, Z.; Hołdynski, G.; Borusiewicz, A. Impact of wind power plant operation on voltage quality parameters—example from Poland. Energies 2022, 15, 5573. [Google Scholar] [CrossRef]
Fernández, L. M.; García, C. A.; Saenz, J. R.; Jurado, F. Equivalent models of wind farms by using aggregated wind turbines and equivalent winds. Energy Convers. Manag. 2009, 50, 691–704. [Google Scholar] [CrossRef]
Wind Turbines—Part 27-1: Electrical simulation models—wind turbines, IEC 61400-27-1, Switzerland, 2015.
WECC Renewable Energy Modeling Task Force. WECC wind power plant dynamic modeling guidelines. USA: EPRI, 2014.
Trudnowski, D. J.; Gentile, A,; Khan, J. M.; Petritz, E. M. Fixed-speed wind-generator and wind-park modeling for transient stability studies. IEEE Trans. Power Syst. 2004, 19, 1911–1917. [CrossRef]
Chao, P.; Li, W.; Liang, X.; Xu, S.; Shuai, Y. An analytical two-machine equivalent method of DFIG-based wind power plants considering complete FRT processes. IEEE Trans. on Power Syst. 2021, 36, 3657–3667. [Google Scholar] [CrossRef]
Akhmotov, V.; Knudsen, H. An aggregate model of a grid-connected, large-scale, offshore wind farm for power stability investigations—importance of windmill mechanical system. International Journal of Electrical Power & Energy Systems 2002, 24, 709–717. [Google Scholar]
Brochu, J.; Larose, C.; Gagnon, R. Validation of single- and multiple-machine equivalents for modeling wind power plants[J]. IEEE Transactions on Energy Conversion 2011, 26, 532–541. [Google Scholar] [CrossRef]
Teng, W.; Wang, X.; Meng, Y.; Shi, W. Dynamic clustering equivalent model of wind turbines based on spanning tree. Journal of Renewable and Sustainable Energy 2015, 7, 1–15. [Google Scholar] [CrossRef]
Zhou, Y.; Zhao, L.; Matsuo, I. B. M.; Lee, W. J. A dynamic weighted aggregation equivalent modeling approach for the DFIG wind farm considering the Weibull distribution for fault analysis. IEEE Transactions on Industry Applications 2019, 55, 5514–5523. [Google Scholar] [CrossRef]
Jin, Y.; Wu, D.; Ju, P.; Rehtanz, C.; Wu, F.; Pan, X. Modeling of wind speeds inside a wind farm with application to wind farm aggregate modeling considering LVRT characteristic. IEEE Transactions on Energy Conversion 2020, 35, 508–519. [Google Scholar] [CrossRef]
Zhu, Q.; Ding, M.; Han, P. Equivalent modeling of DFIG-based wind power plant considering crowbar protection. Mathematical Problems in Engineering 2016, 2016, 1–16. [Google Scholar] [CrossRef]
Wu, Z.; Cao, M.; Li, Y. An equivalent modeling method of DFIG-based wind farm considering improved identification of Crowbar status. Proceedings of the CSEE 2022, 42, 603–614. [Google Scholar]
Zhu, Q.; Ding, M. Equivalent modeling of PMSG-based wind power plants considering LVRT capabilities: electromechanical transients in power systems. SpringerPlus 2016, 5, 2037. [Google Scholar]
Chandra, D. R.; Kumari, M. S.; Sydulu, M.; Grimaccia, F.; Mussetta, M.; Leva, S.; Duong, M. Q. Impact of SCIG, DFIG wind power plant on IEEE 14 bus system with small signal stability assessment. In Proceedings of the 2014 Eighteenth National Power Systems Conference, Guwahati, India, 18-20 December 2014. [Google Scholar]
Nafisa, M. T.; Jahan, E.; Mannan, M. A. Design and analysis of a grid-tied dual rotor PMSG and SCIG-based wind farms. In Proceedings of the 2021 IEEE 9th Region 10 Humanitarian Technology Conference, Bangalore, India, 30 September 2021 - 02 October 2021. [Google Scholar]
Li, H.; Yang, C.; Zhao, B.; Wang, H. S.; Chen, Z. Aggregated models and transient performances of a mixed wind farm with different wind turbine generator systems. Electr. Pow. Syst. Res. 2012, 1–10. [Google Scholar] [CrossRef]
Leon, A. E.; Mauricio, J. M.; Gomez-Exposito, A.; Solsona, J. A. An improved control strategy for hybrid wind farms. IEEE Trans. Sustain. Energ. 2010, 131–141. [Google Scholar] [CrossRef]
Teninge, A.; Roye, D.; Bacha, S.; Duval, J. Low voltage ride-through capabilities of wind plant combining different turbine technologies. Proceedings of 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 08-10 September 2009. [Google Scholar]
Zou, A,; Yang, C. ; Wang, Y. A new method for stability analysis of recurrent neural networks with interval time-varying delay. IEEE Trans. Neural Networ., 2010, 21, 339–344. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Framework of refined equivalent modeling method.

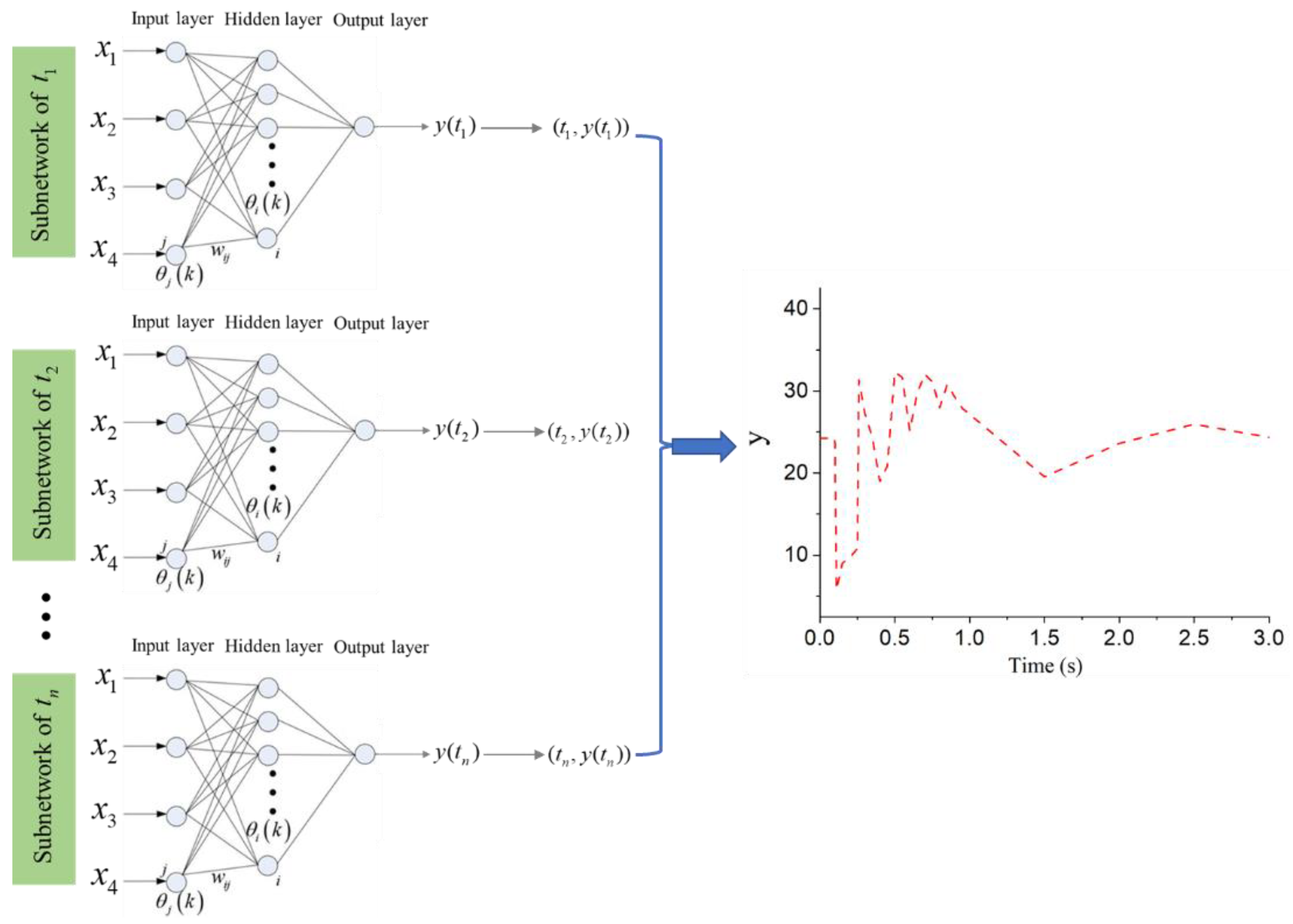
Figure 2. Mixed WF topology.

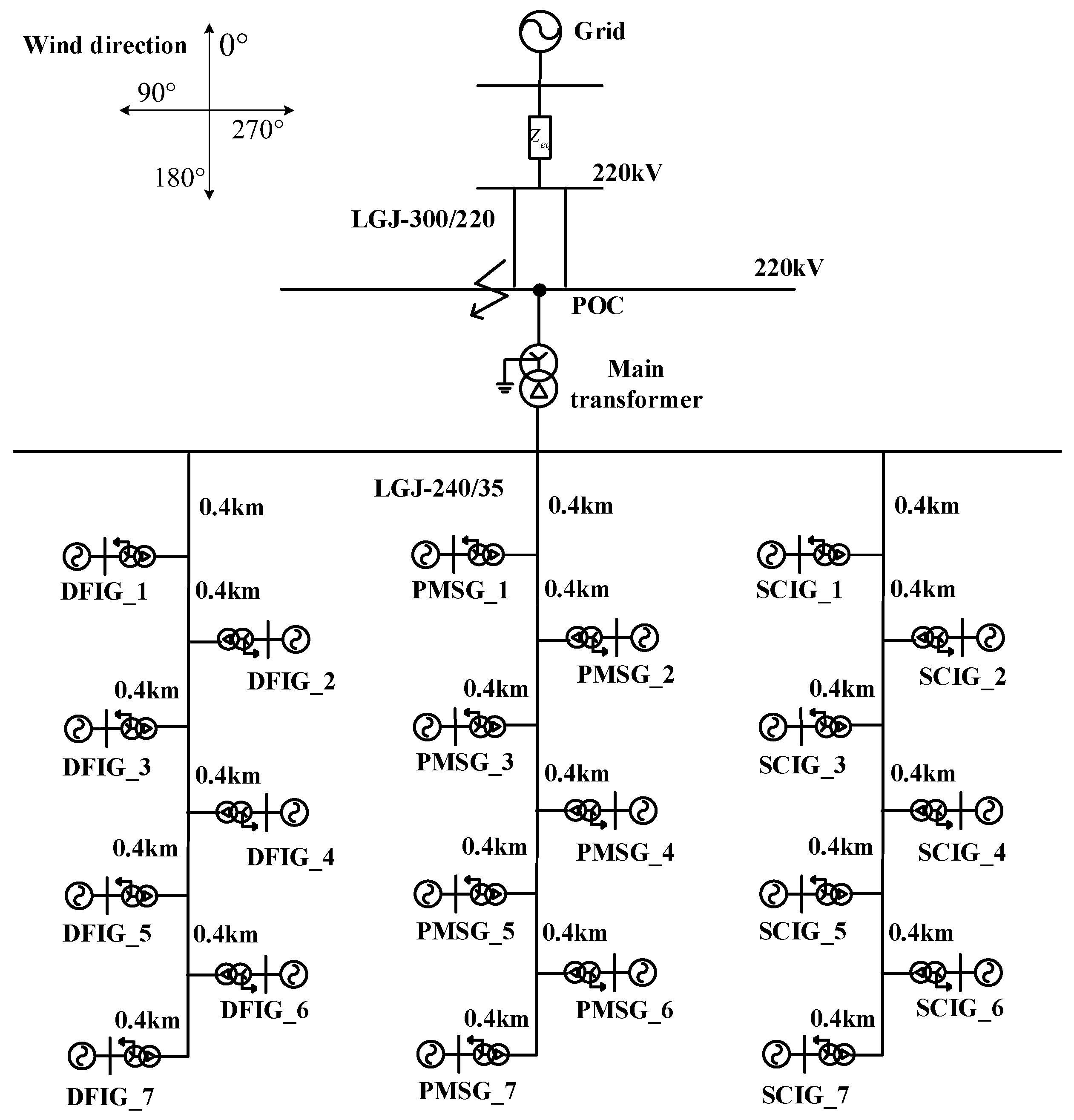
Figure 3. Dynamic response of different types of WTs.

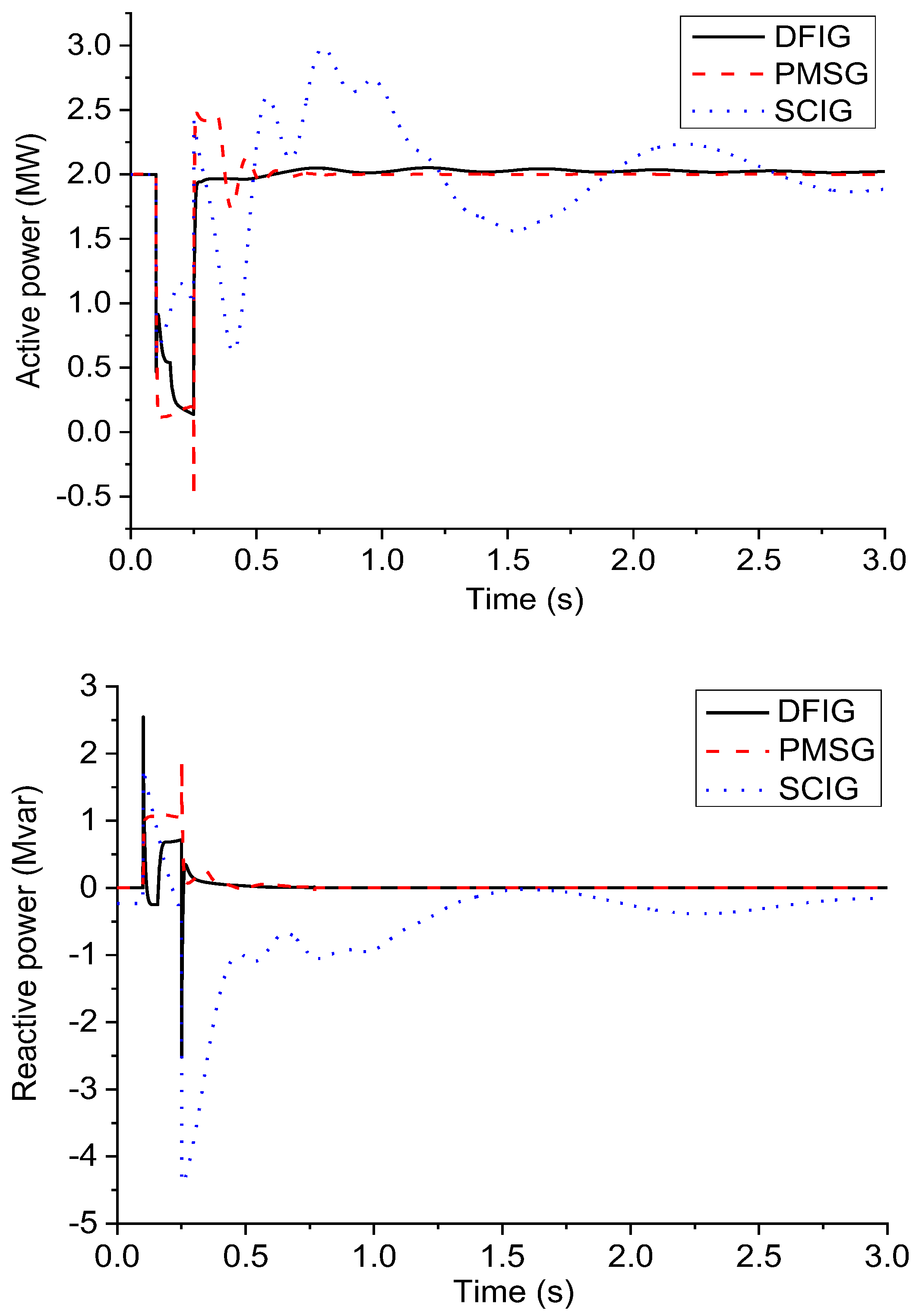
Figure 4. Characteristics of mixed WF under different wind conditions.

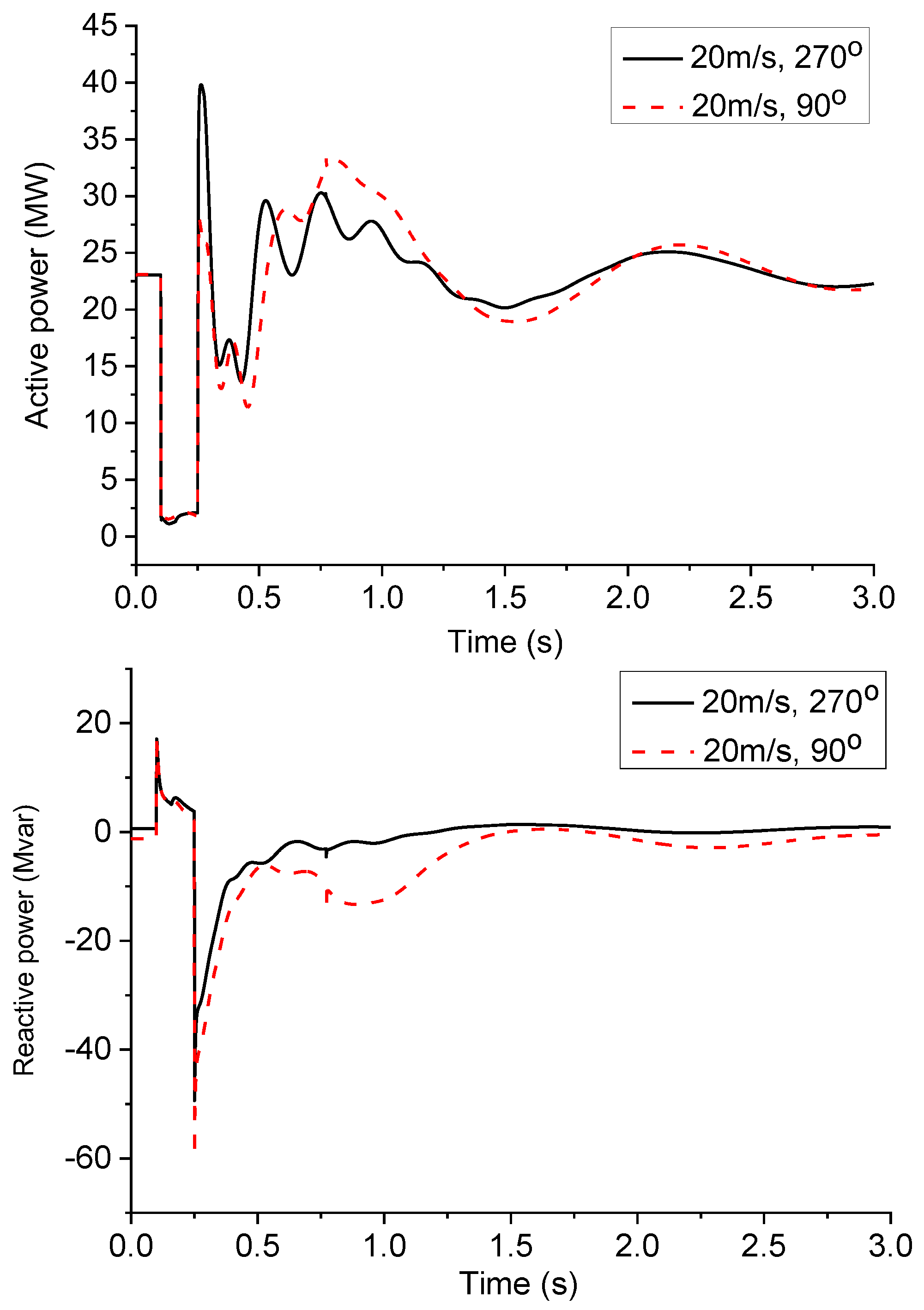
Figure 5. Characteristics of mixed WF under different voltage dips.

Figure 6. Flow chart of equivalent modeling for the mixed WF.

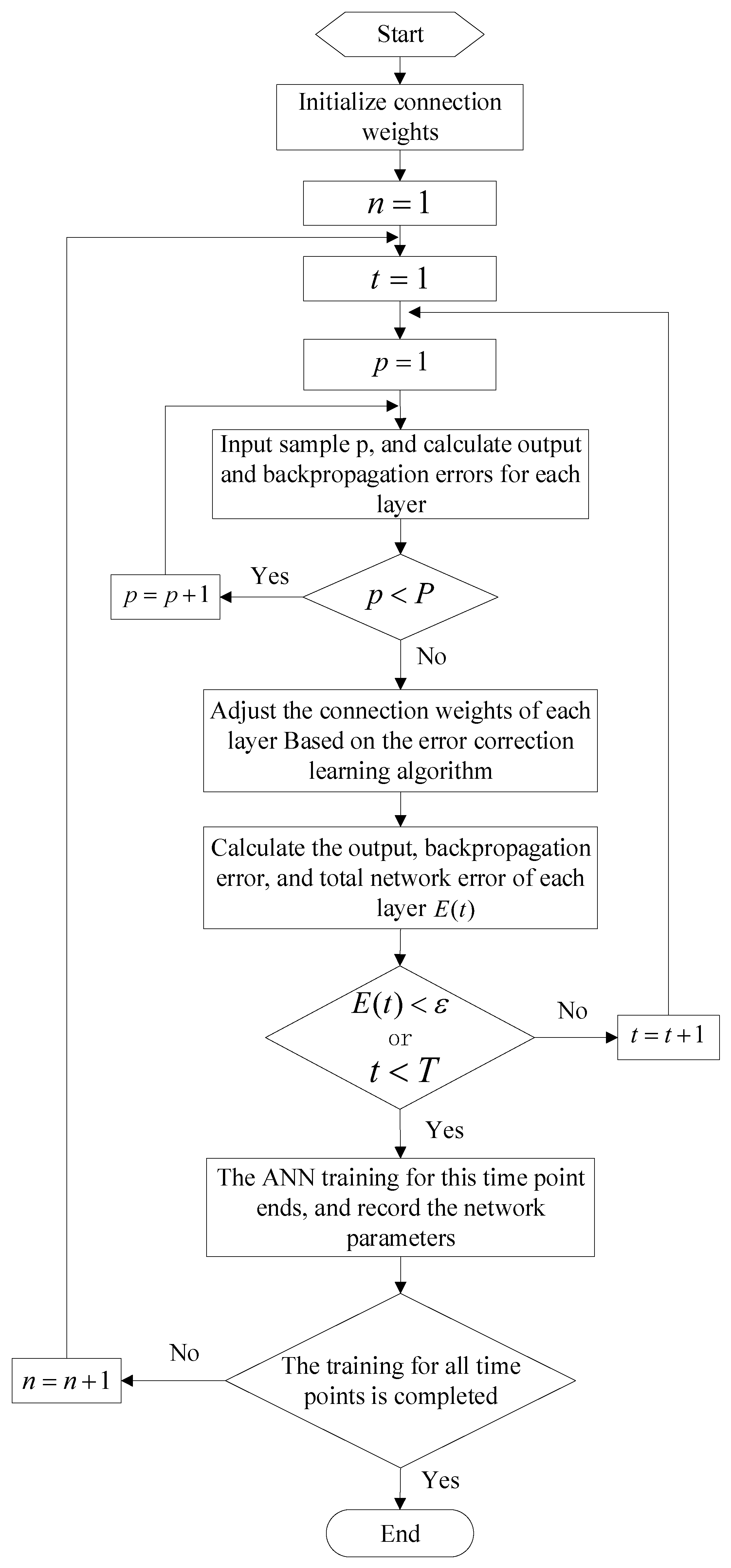
Figure 7. Dynamic power response of the mixed WF at POC.

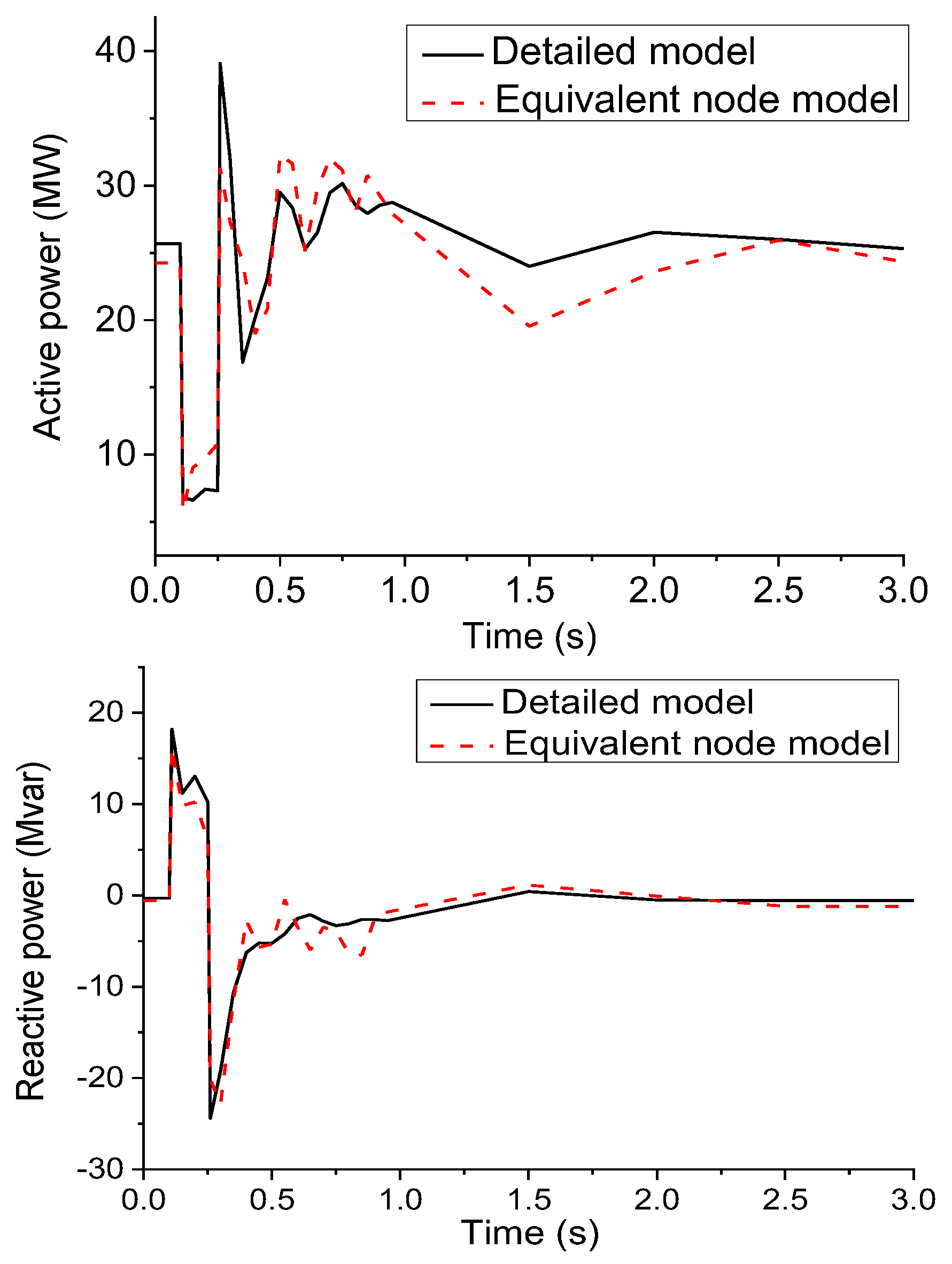
Table 1. Model error indices (sorted by active power error).

Serial Number	$Δ P$ (%)	$Δ Q$ (Mvar)	Serial Number	$Δ P$ (%)	$Δ Q$
1	5.78	0.267	11	9.89	0.676
2	6.31	0.383	12	10.05	0.872
3	7.11	0.465	13	10.23	0.765
4	7.50	0.496	14	10.45	0.696
5	7.68	0.561	15	10.86	0.723
6	8.43	0.605	16	11.32	0.705
7	8.60	0.622	17	11.57	0.912
8	9.12	0.593	18	11.68	0.725
9	9.26	0.536	19	12.22	1.160
10	9.53	0.623	20	13.18	1.362

Table 2. Output value of equivalent node model and actual value with the No. 1 test data.

Time	Active power			Reactive power
Time	Measured Value	Output value of equivalent node model	Mean relative error/%	Measured Value	Output value of equivalent node model	Mean relative error /Mvar
0.00	12.428	11.821	4.884	1.890	1.866	0.024
0.05	12.428	11.821	4.884	1.890	1.866	0.024
0.10	6.938	6.147	11.401	19.192	19.102	0.089
0.15	8.736	9.353	7.063	20.763	20.971	0.208
0.20	10.073	10.146	0.725	17.947	17.248	0.698
0.25	9.396	9.372	0.255	16.427	16.556	0.129
0.30	17.724	21.361	20.520	-9.978	-10.140	0.162
0.35	13.554	11.903	12.181	-6.177	-5.691	0.486
0.40	8.608	7.638	11.269	-2.853	-2.851	0.002
0.45	10.466	10.095	3.545	-1.594	-1.869	0.275
0.50	14.347	12.836	10.532	-1.269	-1.210	0.059
0.55	14.722	14.509	1.447	-0.415	-0.436	0.021
0.60	12.03	11.551	3.982	0.777	0.670	0.107
0.65	11.45	11.026	3.703	1.200	1.090	0.111
0.70	13.488	12.751	5.464	1.029	0.264	0.764
0.75	14.378	13.611	5.335	1.010	0.961	0.049
0.80	13.165	12.06	8.393	1.417	1.037	0.380
0.85	12.294	12.169	1.017	1.628	0.695	0.933
0.90	12.953	12.392	4.331	1.599	1.090	0.510
0.95	13.541	13.406	0.997	1.525	0.959	0.566
1.00	13.015	12.815	1.537	1.633	0.873	0.760
1.50	12.049	11.287	6.324	1.988	2.075	0.086
2.00	12.749	11.91	6.581	1.831	1.741	0.090
2.50	12.417	11.799	4.977	0.933	1.049	0.116
3.00	12.428	12.022	3.267	1.059	1.083	0.024

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Refined Equivalent Modeling Method for Mixed Wind Farms Based on Small Sample Data

Abstract

Keywords:

Subject:

1. Introduction

2. Ideas and Methods

3. External Characteristics of Mixed WF

3.1. Composition of Mixed WF

3.2. Influencing Factors of External Characteristics of Mixed WF

3.2.1. WT Type

3.2.2. Wind Speed and Direction

3.2.3. Fault Voltage Dip

3.3. External Characteristic Analysis

4. Equivalent Node Modeling for Mixed Wind Farm

4.1. Equivalent Node Model

4.2. Experimental Design and Data Collection

4.3. ANN-Based Equivalent Modeling

5. Example Analysis

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe