Prerpints.org logo
Preprint
Article

Nonlinear Finite Element Analysis and Fatigue Damage Assessment of Wind-Induced Vibration for the Tension Cable-Supported Power Transmission Structure

Altmetrics

Downloads

100

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 September 2023

Posted:

25 September 2023

You are already at the latest version

Alerts
Abstract
The tension cable-supported power transmission structure (TC-PTS) is a new type of power transmission structure suitable for mountainous terrain, which is sensitive to wind load. In this regard, a nonlinear finite element analysis model of wind-induced vibration is proposed for the TC-PTS, and the wind-induced vibration response of the structure is analyzed. Firstly, the tangent stiffness matrix of the three-dimensional truss element for the supporting suspension cable and transmission line, considering the geometric nonlinearity of structures, is derived through the relationship between the element elastic energy and its displacement. Subsequently, the element mass matrix and damping matrix of the supporting suspension cable and transmission line, as well as the element nodal load vector obtained from wind load equivalence are given. Then, based on the nonlinear finite element theory, the nonlinear dynamic equation of wind-induced vibration is established for the TC-PTS and solved by Newmark-β method combined with Newton-Raphson iterative method. Furthermore, the rain-flow counting method and Miner's linear fatigue cumulative damage theory were used for wind induced fatigue damage assessment. Finally, a two-span TC-PTS is selected as an example, and the wind-induced nonlinear vibration and fatigue damage assessment are analyzed through the proposed model. The results show that the proposed model has high computational accuracy and efficiency. With the increase of wind speed and wind direction angle, the maximum lateral displacement and tension of the supporting suspension cable and transmission line increase, and their degree of increase shows a nonlinear trend. In terms of the wind-induced fatigue analysis results of TC-PTS, the fatigue damage at the end of the supporting-conductor suspension cable is greater than the fatigue damage at its midpoint. Compared to the fatigue damage at the midpoint of the conductor, the fatigue damage at the end of the conductor is less affected by wind direction angle, and both are more significantly affected by the wind speed.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

As an electric energy infrastructure, a high-voltage transmission tower-line system is an important part of the transmission and distribution systems in the power grid [1]. With the boom in the development of power grid construction, the number of power transmission structures erected in mountainous terrains has been increasing [2]. However, the paths required for transmission line corridors in mountainous areas are becoming tighter, and the selection of tower locations is becoming increasingly difficult. For example, the transmission tower-line system in the Guangxi karst terrain, Xinjiang Danxia terrain, and other special complex mountainous terrain alignments and tower positions owing to terrain restrictions are often difficult to set up, resulting in a wide range of line rerouting.
Therefore, the electric power industry in recent years began to explore new power transmission structures suitable for mountainous areas, the tension cable-supported power transmission structure (TC-PTS) is one of the new overhead power transmission structure. The TC-PTS primarily consists of a conductor, ground wire, supporting-conductor suspension cable, supporting-ground wire suspension cable, tension-resistant insulator strings, and fixed brackets. The structural schematics are illustrated in Figure 1. Among them, the supporting suspension cable made of high-strength steel strands is the main load-bearing structure, which is usually fixed in mountain rock or rigid fixed brackets, the transmission line through the connection of fittings, and the supporting suspension cable to form a coupling system.
The supporting suspension cables and transmission lines in TC-PTS are large-span, highly flexible spatial suspension structures, which are typical wind-sensitive structures. In addition, the structure has mechanical characteristics such as large deformation and small strain, and the geometric nonlinear effect is significant. Compared with the transmission line and transmission tower-line systems, the transmission line of the TC-PTS forms a coupled system with supporting suspension cables, and its geometric nonlinear effect is more significant. Scholars have conducted a series of studies to address the wind-induced nonlinear vibration problem of transmission lines and transmission tower line systems. In early studies, transmission lines were usually considered as suspension structures; and their static and dynamic characteristics are analyzed [3,4,5]. With the development of the finite element method and large deformation theory, the wind-induced vibration analysis of transmission lines and tower-line systems is generally performed using a nonlinear finite element method. The mechanical model of the transmission line and tower-line system based on the truss element is convenient for performing various types of wind vibration and other static and dynamic analysis [6,7]. The mechanical model of the transmission line and tower-line system established by using a cable element and beam element can consider the torsional and bending capacity of the transmission line and then study complex wind vibration problems such as galloping [8,9,10,11]. Scholars have analyzed the dynamic models of transmission lines and tower-line systems and their wind-induced nonlinear vibration problems in detail through theoretical studies and numerical simulations, and have achieved significant research results. However, nonlinear dynamic modeling and wind-induced vibration analyses of TC-PTS have rarely been reported.
To this end, this study establishes a finite element model of TC-PTS based on 3D truss elements, then the nonlinear dynamic equations of the structure are formed, and the iterative solution process of the Newmark-β method combined with the Newton–Raphson method is provided. In addition, wind vibration fatigue assessment was performed by combining the rainfall counting method with the Miner linear fatigue cumulative damage theory. The remainder of this paper is organized as follows. Section 2 exhibits the simplified mechanical model of TC-PTS. The nonlinear finite element equation of wind-induced vibration and fatigue damage assessment method for TC-PTS are shown in Section 3. Subsequently, Section 4 provides an example and the corresponding discussion. Finally, some conclusions are summarized in Section 5.

2. Simplified mechanical model of TC-PTS

2.1. Structural parameters and boundary conditions

The simplified model and the structural parameters of the TC-PTS are shown in Figure 2. ls is the horizontal distance between the ends on both sides of the same suspension cable, lc is the horizontal distance between two adjacent spans of the suspension cable, hs is the height difference between the ends of both sides of the same suspension cable, hc is the height difference between the positions of the same span of the conductor or ground wire in the adjacent hanging points of the suspension cable, hwg is the height difference between the ends of the supporting-ground wire suspension cable and the corresponding ends of the supporting-conductor suspension cable.
The connections between the ends of the supporting suspension cables, fixed supports, and the connection between the transmission lines and corresponding suspension cables at the boundaries are hinged. Therefore, all the supports at the TC-PTS boundary can be considered as fixed hinged supports.

2.2. Initial shape of TC-PTS

To establish a finite element model of the TC-PTS that considers the geometric nonlinear effect, it is necessary to first obtain the initial shape and initial internal force under gravity loading. For the supporting suspension cables and transmission lines of the TC-PTS, its initial shape can be simplified as a parabolic model, and the functional expression required to establish this parabolic model is
y = 4 x f m ( 1 − x / l ) / l
where y is the vertical distance from the calculation point to the starting point, x is the horizontal distance from the calculation point to the starting point, l is the horizontal distance from the end point to the starting point, and fm is the spanning mid-arc droop calculated according to Eq. (2):
f m = q l 2 / ( 8 σ 0 cos β )
where q is the gravity load per element volume of the supporting suspension cable or transmission line, σ0 is the horizontal stress of the suspension cable, β is the angle of elevation difference, and tanβ = h/l , where h is hs or hc and l is the corresponding ls or lc.

2.3. The mechanical characteristics of TC-PTS

In TC-PTS, the supporting suspension cables and transmission lines are mainly subjected to tension, and to a lesser extent, they will also be subjected to bending and torsional moments. It is reasonable to neglect the bending and torsional capacities in wind vibration response analysis without considering torsion [12]. Therefore, in the TC-PTS wind vibration analysis, the supporting suspension cables and transmission lines were primarily considered for the axial tensile capacity.

3. Nonlinear finite element analytical model of wind-induced vibration and fatigue damage assessment for TC-PTS

3.1. Element stiffness matrix for supporting suspension cables and transmission lines

According to the mechanical characteristics of the TC-PTS, its supporting suspension and transmission line wind vibration are large deformation and small strain problems. Combined with the force characteristics of this power transmission structure, the finite element model shown in Figure 3 can be established using a 3D truss element by considering geometric nonlinear effects. Generally, the element stiffness matrix can be established using both the local and global coordinate systems. Compared with the stiffness matrix established in the local coordinate system [11,13,14], the element stiffness matrix in the global coordinate system [15,16,17] can be directly grouped into the system stiffness matrix. It can be directly grouped into a system stiffness matrix to effectively avoid the coordinate conversion process. For the three-dimensional truss element in the global coordinate system, the stiffness matrices are mostly derived using the principle of virtual work [15] and by deriving the truss ends [17]. However, the virtual work principle requires multiple integrals, and often results in implicit stiffness matrices that are difficult to apply directly, whereas the truss end strives for derivatives that require more complicated vector operations. Therefore, this study simplifies the operation through the relationship between the elastic energy of the 3D truss element and its deformation, and derives the explicit stiffness matrix of the 3D truss element under the global coordinate system.
In Figure 3, the physical quantities at the initial moment (C0 state) are known quantities, and the node vectors at both ends of the element in the global coordinate system are
{ a 0 i = { x i y i z i } T a 0 j = { x j y j z j } T
The principle of vector subtraction is then used to obtain the element vectors of the truss element in the global coordinate system.
a 0 e = a 0 j − a 0 i = { x j − x i y j − y i z j − z i } T
After time t, the truss element undergoes a displacement deformation movement to C1 state, and the displacement vector of the nodes at both ends of the element under the global coordinate system is
{ u i = { u i v i w i } T u j = { u j v j w j } T
From Eq. (3) and (5), the node vectors at both ends of the element in the global coordinate system are
{ a t i = a 0 i + u i a t j = a 0 j + u j
Therefore, the element vector of the truss element at time t is
a t e = a 0 e + u j − u i
According to the node displacement vector, the element displacement vector can be expressed as
u e = { u i v i w i u j v j w j } T
Eq. (7) can be further expressed as Eq. (8) as:
a t e = a 0 e + [ − I 3 × 3 I 3 × 3 ] u e
where I3×3 is the 3rd order element matrix.
At C0 state, the truss element in the state has no strain and its element length is
l 0 = | a 0 e | = a 0 e T a 0 e
At C1 state, the length of the truss element in the state is:
l t = | a t e | = a t e T a t e
At this point, the strain in the truss element is:
ε t = ( l t − l 0 ) / l 0
The truss element elastic energy tU at time t can be calculated using equation (13):
U t = ∫ V ∫ 0 ε t σ ( ε ) d ε d V
where: σ(ε) is the stress of the truss element, and the relationship between stress and strain in the linear elastic range is: σ(ε) = Eε , E is the Young’s modulus, V is the element volume, when the cross-section area of the truss element is a constant value of A, Eq. (13) can be further expressed as
U t = 1 2 E A l 0 ε t 2
The element tangent stiffness matrix at time t in the global coordinate system can be calculated using the Hessian matrix as follows:
K t e = ∂ 2 U t ∂ u t e ∂ u t e T
The final result of the element tangent stiffness matrix at time t is:
K t e = E A ε t l t [ I 3 × 3 − I 3 × 3 − I 3 × 3 I 3 × 3 ] + E A l t 3 [ a t e a t e T − a t e a t e T − a t e a t e T a t e a t e T ]
The element tangent stiffness matrix tKe shown in Eq. (16) is derived by introducing only the linear elasticity assumption and not the small deformation assumption, which is an exact tangent stiffness matrix at any displacement. Therefore, it is applicable to the case of arbitrarily large deformations and small strains.

3.2. Element mass matrix and damping matrix

The TC-PTS finite element model mass matrix is constructed using a consistent mass matrix with an element-consistent mass matrix as follows:
M e = l 0 ρ A 6 [ 2 I 3 × 3 I 3 × 3 I 3 × 3 2 I 3 × 3 ]
where 0l is the initial length of the element, ρ is the mass density of the element, respectively.
The element damping matrix is constructed using Rayleigh damping:
C t e = α v M e + β v K t e
where αv and βv are the Rayleigh damping constants calculated using Eq. (19) and Eq. (20):
α v = 2 ξ k 1 ω k 1 ω k 2 / ( ω k 1 + ω k 2 )
β v = 2 ( ξ k 2 ω k 2 − ξ k 1 ω k 1 ) / ( ω k 1 2 + ω k 2 2 )
where ωk1 and ωk2 are the intrinsic frequencies of the k1st and k2nd order modes, respectively; ξk1 and ξk2 is the damping ratio corresponding to the k1st and k2nd order modes, respectively. This can be considered as βv = 0 [18]. In which case, tCe is not affected by the change in structural displacement, namely, Ce.

3.3. Equivalent nodal load vector

The primary loads to which the TC-PTS was subjected were gravity and wind. The static and dynamic displacements of this power transmission structure are based on the gravity load equilibrium position. Therefore, when calculating the structural equivalent nodal load vector, the gravity load is equivalent to the internal nodal load vector at the reference position. For the truss elements of the TC-PTS finite element model, the wind load per unit length was calculated using equation (21):
F D = 1 2 ρ a i r V z 2 C D A m
where ρair is the air density, Vz is the wind speed, CD is the drag coefficient, Am is the windward projected area per unit length of the truss element, for supporting suspension cables: Am = dcosθ, for transmission lines: Am = dsinθ , d is the diameter of the truss element, and θ is the angle of the wind direction (shown in Figure 4).
Vz can be calculated using equation (22):
V z = V s ( z ) + V ( t )
where Vs(z) is the average wind speed, V(t) is the pulsating wind speed.
The pulsating wind speed V(t) is generated by the harmonic synthesis method [19]. The average wind speed Vs(z) can be calculated from the exponential law according to equation (23):
V s ( z ) = ( z / 10 ) α V 10
Where V10 is the reference average wind speed at the height of 10 m, z is the height, and α is the ground roughness coefficient. As TC-PTS is in the mountainous terrain, its ground roughness category can be considered as C. According to the “Code for Structural Loads of Buildings” [20], α is taken as 0.22.
The wind loads on the element are converted to element equivalent nodal loads, namely:
F t e = 1 2 l t [ F i x F i y F i z F j x F j y F j z ] T
where Fix is the equivalent nodal load of the wind load in the X-direction at node i, and the rest are similar.

3.4. Establishment of the nonlinear dynamic equation

The mass matrix, stiffness matrix, damping matrix, and equivalent nodal load vectors of each element of the TC-PTS were assembled respectively, and nonlinear dynamic equations of the structure were established at the reference position based on the updated Lagrange column equation:
M u ¨ t + Δ t + C u ˙ t + Δ t + Q t + Δ t − Q 0 = F t + Δ t
where u ¨ t + Δ t and u ˙ t + Δ t are the acceleration and velocity vectors of the structure at time t+Δt, M and C are the mass and damping matrix of the structure. Q t + Δ t and Q 0 are the internal load vectors, that is, the internal nodal load vectors at time t+Δt and the reference position, respectively. In addition, F t + Δ t is the equivalent nodal load vector of the structure at time t+Δt.
When Δt is sufficiently small, the displacement increment of the structure within a time step is small, and Q t + Δ t and tK can be approximated using the following linear relationship:
Q t + Δ t = Q t + K t u
where tQ is the internal nodal load vector at time t, tK is the stiffness matrix of the structure at time t, and u is the displacement increment within Δt, that is u = u t + Δ t − u t .
Combining Eq. (25) and Eq. (26), the nonlinear dynamic equations in the form of displacement increments are obtained.
M u ¨ t + Δ t + C u ˙ t + Δ t + K t u = F t + Δ t − [ Q t − Q 0 ]

3.5. Solution of the nonlinear dynamical equation

The Newmark-β method is used to solve the nonlinear finite element equations shown in Eq. (27). Because Eq. (26) is a linear approximation, the displacement increment of the solution produces a large error accumulation as the time step increases. Therefore, to improve the accuracy of the solution and avoid the accumulation of numerical instability within each time step, the Newton–Raphson iterative method was used in this study for balanced iterative calculation. The solution process is summarized as follows.
Step 1: Calculate the individual element characterization matrices K 0 e , M e , and C e based on the initial shape and strain of the element, and then assemble them to obtain the characterization matrices K 0 , M , and C f the structure.
Step 2: Apply the initial equivalent nodal load F 0 , and then calculate u ¨ 0 from the initial conditions u 0 and u ˙ 0 :
u ¨ 0 = M − 1 [ F 0 − C u ˙ 0 − K 0 u 0 ]
Step 3: Select the time step Δt and calculate the integration constant [21] using the known physical quantities at time t. The effective stiffness matrix was calculated before performing the iterations of K ^ t ( 0 ) :
K ^ t ( 0 ) = K t + c 0 M + c 1 C
Step 4: Perform Newton–Raphson iterations. Calculate the effective load vector F ^ t + Δ t at time t+Δt:
F ^ t + Δ t = F t + Δ t + M [ c 0 u t + c 2 u ˙ t + c 3 u ¨ t ] + C [ c 1 u t + c 4 u ˙ t + c 5 u ¨ t ]
From this, calculate the unbalanced force vector for the first iteration F ^ t + Δ t ( 0 ) :
F ^ t + Δ t ( 0 ) = F ^ t + Δ t − [ Q t ( 0 ) − Q 0 ] − [ c 0 M + c 1 C ] [ u t + Δ t ( 0 ) − u t ]
where Q t ( 0 ) is the internal nodal load vector before the first iteration, and u t + Δ t ( 0 ) is the displacement before the first iteration, namely, u t .
Solve for the displacement increment u ( 1 ) after the first iteration at time t+Δt:
u ( 1 ) = [ K ^ t ( 0 ) ] − 1 [ F ^ t + Δ t ( 0 ) ]
Step 5: Update K t ( 1 ) and Q t ( 1 ) and update the effective stiffness matrix K ^ t ( 1 ) and the displacement before iteration u t + Δ t ( 1 ) :
u t + Δ t ( 1 ) = u t + Δ t ( 0 ) + u ( 1 )
and the unbalanced force vector F ^ t + Δ t ( 1 ) :
F ^ t + Δ t ( 1 ) = F ^ t + Δ t − [ Q t ( 1 ) − Q 0 ] − [ c 0 M + c 1 C ] [ u t + Δ t ( 1 ) − u t ]
and calculate the displacement increment after the second iteration u ( 2 ) :
u ( 2 ) = [ K ^ t ( 1 ) ] − 1 [ F ^ t + Δ t ( 1 ) ]
Step 6: Determine whether the L2 norm of the unbalanced force vector F ^ t + Δ t ( 1 ) satisfies the convergence condition; if not, loop Step 5 until the convergence condition is satisfied; if so, end the Newton–Raphson iteration to obtain the final nonlinear displacement u t + Δ t at time t+Δt, and then obtain the velocity u ˙ t + Δ t and acceleration u ¨ t + Δ t at time t+Δt.

3.6. Wind-induced fatigue damage assessment of TC-PTS

Using the displacement time history and velocity time history obtained from the above TC-PTS wind vibration nonlinear finite element analysis model, the stress time history of each part of the TC-PTS can be derived. The rain-flow counting method was then used to process the stress time history and obtain the stress amplitude distribution statistically. Finally, the number of stress cycles in which fatigue damage occurs can be obtained using the S–N curve. The logarithmic form of the S–N curve is shown in Eq. (28):
lg N = C − m lg S
where N is the number of stress cycles in which fatigue damage occurs, C and m are the material fatigue parameters, and S is the stress amplitude.
The fatigue parameters for support suspension materials [22] were obtained from C = 13.84 and m = 3.5 . The fatigue parameters of the transmission line materials [23] are available for N ≤ 2 × 10 7 , C = 13.27 , and m = 5 , as well as for N > 2 × 10 7 , C = 14.40 , and m = 5.95 .
According to Miner’s linear fatigue cumulative damage criterion, the wind vibration fatigue damage of each part of the TC-PTS is as follows:
D = ∑ i = 1 k n i / N i
where D is the total fatigue damage value. When D = 1, fatigue damage occurs, k is the total number of stress amplitudes, n i is the number of times the ith stress amplitude occurs, and N i is the number of stress cycles corresponding to the ith stress amplitude where fatigue damage occurs.
In addition, wind vibration fatigue damage analysis of the supported suspension cables and transmission lines must consider the effect of the average stress. The Goodman model is often used to correct for the effect of the nonzero average stress Sm, namely:
S = S 0 ( 1 − S m / S t )
where S is the actual stress amplitude, S0 is the equivalent stress amplitude at zero average stress, Sm is the average stress, and St is the tensile strength of a material.

4. Example analysis

4.1. Example description

In this study, a two-span TC-PTS, as shown in Figure 5, was considered as the research object for wind vibration response analysis and fatigue damage assessment. In this study, the wind speed time duration was taken as 600 s, and the structural parameters of the two-span TC-PTS were ls = 1000 m, lc = 800 m, hwg = 20 m, hs = 0 m, and hc = 0 m, respectively, and the endpoints of the supporting-conductor suspension cables were considered to be fixed at a height of 300 m. All the calculations required for the analysis in this study were performed on a computer with an Intel i5-9400F CPU and 32 GB of RAM.
Using the proposed model, the first five orders of natural frequency and the first three orders of the vibration mode of this power transmission structure can be calculated, as shown in Table 1 and Figure 6, respectively. The results of the frequency analysis in Table 1 show that the first five orders of intrinsic frequencies of the supporting-conductor part are 77.89%, 78.65%, 78.28%, 78.30%, and 78.30% of the corresponding values of the supporting-ground wire part. The lower-order natural frequency of the supporting-conductor part was lower than that of the supporting-ground wire part. As shown in Figure 6, for the supporting-conductor part, the first-, second-, and third-order vibration modes were antisymmetric vertical bending, symmetric lateral bending, and antisymmetric lateral bending, respectively.
To verify the correctness and calculation accuracy of the proposed model, ANSYS was used to perform a modal analysis, and the results of the two calculations were compared. In the ANSYS model, the supporting suspension and transmission line were simulated using the Link180 element, and the structural parameters, boundary conditions, and other parameters were consistent with those of the model in this study. The ANSYS calculation results are also given in Table 1 and Figure 6, respectively, and it can be seen that the maximum absolute value of the relative error of the frequency results of the proposed model is 0.001%, which is a better accuracy, and vibration modes are also consistent.

4.2. Wind-induced vibration response of TC-PTS

4.2.1. Time history analysis of TC-PTS wind-induced vibration response

The time history analysis of wind-induced vibration response of TC-PTS was performed by considering the working conditions of the wind speed V 10 = 15 m / s and wind direction angle θ = 90 o . The mean square error (σ) of lateral displacement at each location along the conductor length is shown in Figure 7, and it can be seen that the mean square error of lateral displacement in the center of the conductor is the largest, which is 2.34 m, indicating that the location in the center of the conductor is more significantly affected by wind load, and the variance values of lateral displacement in the remaining locations are roughly symmetrical along the location in the center of the conductor. The lateral displacement time histories at the center of the conductor are shown in Figure 8, and the average and maximum values of the lateral displacement time histories in Figure 8 are listed in Table 2. The results in Table 2 and Figure 8 show that the average values of lateral displacement in the conductor under wind load in this condition is 23.33 m, and its maximum value is 29.70 m, the lateral displacement is distributed from the minimum value of 16 m to the maximum value of 29.70 m, with a large variation.
Similarly, the time history of the midpoint displacement of the conductor computed by ANSYS are plotted in Figure 8 and Table 2, whereas the computational efficiency of the proposed model is listed in Table 3. From Figure 8 and Table 2, it can be observed that the relative errors of the mean and maximum values of the lateral displacement time history obtained by the proposed model were 0.13% and 0.83%, respectively, and its accuracy was high. Simultaneously, the lateral displacement time history curves obtained by the proposed model have a consistent trend with the ANSYS results, which have a high degree of agreement. The results in Table 3 show that the computation time required by ANSYS to analyze the lateral displacement in the conductor was 35.88 min, whereas the computation time of the proposed model was 1.50 min, and its computational cost was only 4.19% of the former. Therefore, the proposed model can be applied to the wind-induced vibration nonlinear finite element analysis for TC-PTS more efficiently.

4.2.2. Effect of different wind direction angles on TC-PTS wind-induced vibration response

In this section, the influence of different wind direction angles (θ taken as 0°, 45°, 60°, and 90°) on the maximum lateral displacement of the transmission line and the maximum tension of the supporting suspension cables of TC-PTS at V 10 = 20 m / s are investigated. The variation in the maximum lateral displacement of the transmission line and the maximum tension of the supporting suspension cable with the wind direction angle θ is shown in Figure 9. In Figure 9a, it can be seen that the maximum lateral displacement of the transmission line increases with the increase in θ, and initially, it tends to be faster and slower subsequently. In Figure 9b, the maximum tension of the supporting suspension cable increases with the increase in θ. The change in the incremental magnitude of the maximum lateral displacement of the transmission line was also owing to the stress-stiffening effect of the structure. Considering the conductor as an example, the maximum lateral displacements of the conductor are 0.0071, 21.15, 28.12, and 32.96 m for wind direction angles of 0°, 45°, 60°, and 90°, respectively, and the most unfavorable wind direction angle for the maximum lateral displacement of the transmission line is 90°. The maximum tension of the supporting suspension cables increased with the wind direction angle because the downwind projected area of the transmission line was larger than that of the supporting suspension cables. As the wind direction angle increased, the global wind load on the structure increased. Therefore, the wind direction angle had a more significant effect on both the lateral displacement of the transmission line and the tension of the supporting suspension cables and the most unfavorable wind direction angle for the two-span TC-PTS was 90°.

4.2.3. Effect of different wind speeds on the wind-induced vibration response of TC-PTS

Based on the conclusions of the above analysis, this section examines the effect of the change of wind speed V10 on the maximum lateral displacement of the transmission line and the maximum tension of the supporting suspension cables under the most unfavorable wind direction angle of 90° working condition. The variation of the maximum lateral displacement of the transmission line and the maximum tension of the supporting suspension cable with the wind speed V10 at θ = 90 o is shown in Figure 10. In Figure 10a, it can be seen that the maximum lateral displacement of the transmission line increases with the increase of V10 , and the magnitude of the increase tends to be faster initially which becomes slow subsequently. This phenomenon is more obvious on the conductor. In Figure 10b, the maximum tension of the supporting suspension cables increases with the increase in V10 all the time. The change of the maximum lateral displacement increment of the transmission line is due to the stress stiffening effect of the structure, according to Eq. (16), the element tangent stiffness increases with the increase in displacement, and the lateral stiffness of the structure also increases gradually with the increase in displacement. When the lateral stiffness is larger, the increase in lateral displacement of the transmission line will slow down.
Maximum lateral displacement of transmission line considering the maximum lateral displacement of conductor as an example, the wind speed is 5, 10, 15, 20, 25, and 30 m/s, and the maximum lateral displacement of conductor is 2.83, 11.03, 22.48, 32.96, 40.16, and 44.78 m, respectively. The wind speed is from 5 m/s, and every increase of 5 m/s, the maximum lateral displacement of conductor increases by 8.20, 11.45, 10.48, 7.21, and 4.62 m, respectively. Therefore, in the case of smaller wind speed, the increase in wind speed will be higher. The maximum lateral displacement of the conductor increases by 8.20, 11.45, 10.48, 7.21, and 4.62 m. Therefore, the increase in wind speed increases the maximum lateral displacement of the transmission line more significantly when the wind speed is low, whereas the maximum lateral displacement of the transmission line is less affected by the wind speed when the wind speed is high. The change in the maximum tension of the supporting suspension cables is due to the fact that the suspension tension is required to balance the equivalent nodal loads, and the increase in wind speed increases the suspension tension all the time.
Maximum tension of supporting suspension cables taking the maximum tension of supporting-conductor suspension cable as an example, the wind speed starts from 5 m/s, and every increase of 5 m/s, the maximum tension of supporting-conductor suspension cable increases by 6.59, 11.05, 15.62, 20.38, and 25.47 kN, respectively, and the increment of the maximum tension is approximately linearly related to the wind speed, the maximum tension and the quadratic of the wind speed are approximately linearly correlated, at the wind speed is small, the maximum tension of the supporting suspension cable is less affected by wind speed, while in the wind speed is larger, the maximum tension of the supporting suspension cable is more significantly affected by wind speed.
Therefore, at lower wind speeds V10, the lateral displacement of the transmission line was more affected by the wind speed than the tension of the supporting suspension cable, and at higher wind speeds V10, the tension of the supporting suspension cable was more notably affected by wind speeds than the lateral displacement of the transmission line.

4.3. Wind-induced fatigue damage of TC-PTS

4.3.1. Wind-induced fatigue damage assessment of TC-PTS

To comprehensively analyze the wind vibration fatigue damage condition of the two-span TC-PTS, the ends and midpoint of the supporting-conductor suspension cable and conductor were selected as fatigue analysis parts. The ends and midpoint of the supporting-conductor suspension cable and conductor are points A, B, C, and D, respectively. The wind-induced fatigue damage of each fatigue analysis part of the two-span TC-PTS was calculated by considering the working conditions of wind speed V 10 = 15 m / s and wind direction angle θ = 90 o as examples. The stress time history of each fatigue analysis part is shown in Figure 11, and the corresponding mean stress, mean square deviation, and fatigue damage are listed in Table 4. It can be observed that, compared with point A, the stress mean value of point B is larger, but the mean square deviation is smaller, and its fatigue damage is smaller because the stress amplitude has a more significant effect on the fatigue damage value: the larger the mean square deviation, the more frequently the high stress amplitude occurs, and the more serious the corresponding fatigue damage. The mean stress value and mean square deviation of point C were greater than those of point D, and the fatigue damage value was also greater.

4.3.2. Effect of different wind direction angles on wind-induced fatigue damage of TC-PTS

At V 10 = 20 m / s , the influences of different wind direction angles θ on the fatigue damage of various parts of the TC-PTS are listed in Table 5. With a gradual increase in the wind direction angle, the wind load acting on the conductor is larger because of the coupling effect between the conductor and the supporting-conductor suspension cable, and the load borne by the supporting-conductor suspension cable also gradually increases. Therefore, the fatigue damage of each part increases, in the same working condition, the fatigue damage of the supporting-conductor suspension cable end (point A) is larger than that of the midpoint (point B), while the fatigue damage of the conductor end (point C) is smaller than that of the midpoint (point D). It is easy to see that among the wind direction angles, 90° wind direction angle has the most significant effect on the wind-induced fatigue damage of the TC-PTS.

4.3.3. Effect of different wind speeds on wind-induced fatigue damage of TC-PTS

Under the 90° wind direction angle condition, the effect of wind speed V10 change on the fatigue damage of each part of TC-PTS is shown in Table 6. As shown in the table, the wind-induced fatigue damage of each part increases with an increase in the wind speed V10 , and the fatigue damage at the end of the supporting-conductor suspension cable (point A) is larger than the fatigue damage of the midpoint (point B) under the same working conditions. With the gradual increase in wind speed V10, the fatigue damage of all parts of the supporting-conductor suspension cable and conductor showed a tendency to increase faster and then slower. The fatigue damage of all parts of the supporting-conductor suspension cable increased gradually from to 10-16 to 10-8, whereas the fatigue damage of all parts of the conductor increased gradually from to 10-25 to 10-7. When the wind direction angle was 90°, the wind load per unit length of the conductor was greater than that of the supporting-conductor suspension cable, and the fatigue damage of each part of the conductor increased more than that of the supporting-conductor suspension cable.

5. Conclusions

The TC-PTS is a new class of power transmission structures suitable for mountainous terrain. A nonlinear finite element model of the wind-induced vibration for the TC-PTS was established using the nonlinear finite element method. Wind-induced vibration response analysis and fatigue damage assessment were carried out for a two-span TC-PTS, and the effect of wind speeds and wind direction angles on wind-induced vibration response and fatigue damage of the TC-PTS were discussed. The main conclusions are as follows:
(1) The comparison results show that the natural frequency and displacement time history calculated by the proposed model are highly accurate and can accurately calculate the structural dynamic characteristics and dynamic response. The proposed model also has high computational efficiency, and the computational cost of obtaining the dynamic response is only 4.19% of that of ANSYS.
(2) The low-order natural frequency of the supporting-conductor part was lower than that of the supporting-ground wire part; however, both values were still of the same order of magnitude. The first three order vibration modes of the supporting-conductor part were antisymmetric vertical bending, symmetric side bending, and antisymmetric side bending.
(3) For the mean wind load, at smaller wind speeds, the lateral displacement of the transmission line is more affected by wind speeds than the tension of the supporting suspension cable, at larger wind speeds, the tension of the supporting suspension cable is more notably affected by wind speeds than the lateral displacement of the transmission line.
(4) The fatigue damage value at the end of the supporting-conductor suspension cable was larger than that at the midpoint; however, they were approximately of the same order of magnitude. For the conductor, under the wind direction angle condition, the midpoint fatigue damage value is greater than the end fatigue damage value, whereas under the wind speed condition, the end and midpoint fatigue damage values have no obvious comparison.
(5) The wind-induced vibration response and fatigue damage of TC-PTS were significantly affected by the wind direction angle, and the results of the arithmetic analysis showed that the most unfavorable wind direction angle for TC-PTS was 90°.

Author Contributions

Conceptualization, Z.L. and T.W.; methodology, T.W.; software, J.L. and B.W.; validation, Z.L., T.W. and J.L.; formal analysis, T.W.; investigation, T.W., B.W. and J.Y.; resources, Z.L.; data curation, B.W.; writing—original draft preparation, J.L.; writing—review and editing, J.L. and B.W.; visualization, B.W.; supervision, T.W.; project administration, T.W.; funding acquisition, T.W. All authors have read and agreed to the published version of the manuscript.

Funding

The research presented in this paper was conducted with the support of the Special Support of Chongqing Postdoctoral Research Project (Grant No. 2022CQBSHBT3009) and the Special Postdoctoral Support Project of Chongqing Research Institute of HIT (Grant No.KY506023002).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bai, H., Yi, T., Li, H., Ren, L. Multisensors on-site monitoring and characteristic analysis of UHV transmission tower. International Journal of Distributed Sensor Networks 2012, 8(11), 545148. [CrossRef]
  2. Lou, W., Wu, D., Liu, M., Zhang, L., Bian, R. Properties of mountainous terrain wind field and their influence on wind-induced swing of transmission lines. China Civil Engineering Journal 2018, 51(10), 46-55+77.
  3. Irvine, H. Cable structure; The MIT Press: New York, 1981. [Google Scholar]
  4. McClure, G., Lapointe, M. Modeling the structural dynamic response of overhead transmission lines. Computers and Structures 2003, 81(8/9/10/11), 825–834. [CrossRef]
  5. Kempner, L., Smith, S. Cross-rope transmission tower-line dynamic analysis. Journal of Structural Engineering ASCE 1984, 110(6), 1321–1335. [CrossRef]
  6. Tian, L, Pan, H., Ma, R., Dong, X. Seismic failure analysis and safety assessment of an extremely long-span transmission tower-line. Structural Engineering and Mechanics 2019, 71(3), 305–315.
  7. Fu, X., Li, H., Tian, L., Wang, J., Cheng, H. Fragility analysis of a transmission line subjected to wind loading. Journal of Performance of Constructed Facilities ASCE 2019, 33(4), 1–11.
  8. Yan, Z., Savory, E., Li, Z., Lin, W. Galloping of iced quad-conductors bundles based on curved beam theory. Journal of Sound and Vibration 2014, 33(6), 1657–1670.
  9. Yan, Z., Li, Z., Savory, E., Lin, W. Galloping of a single iced conductor based on curved-beam theory. Journal of wind engineering and industrial aerodynamics 2013, 123, 77–87. [CrossRef]
  10. Chunming, W., Bin, M., Tingting, S. Research on the wind-induced vibration coefficient of transmission tower-line system. Physics Procedia 2012, 24, 149–154. [CrossRef]
  11. Liu, X., Yan, B., Zhang, H., Zhou, S. Nonlinear numerical simulation method for galloping of iced conductor. Applied mathematics and mechanics 2009, 30(4), 489–501. [CrossRef]
  12. Yan, Z., Huang, J., Li, Z. Finite element model of bundle lines based on 6-dof node. Engineering Mechanics 2012, 29(8), 325–332.
  13. Zhu, Z., Meguid, S. Analysis of three-dimensional locking-free curved beam element. International Journal of Computational Engineering Science 2004, 5(03), 535–556.
  14. Zhu, Z., Meguid, S. Vibration analysis of a new curved beam element. Journal of Sound and Vibration 2008, 309(1-2), 86–95. [CrossRef]
  15. Chen, Z., Zeng, Q., Yan, Q. A UL formulation for internal force analysis of spatial frame structures with large displacement. China Civil Engineering Journal 1992, 25(5), 34–43.
  16. Shi, H., Salim, H. Geometric nonlinear static and dynamic analysis of guyed towers using fully nonlinear element formulations. Engineering Structures 2015, 99, 492–501. [CrossRef]
  17. Liu, S. Accurate analysis method on the tangential stiffness matrix of pinned straight rod element. Chinese Journal of Computational Mechanics 2014, 31(1), 48–53. [Google Scholar]
  18. Desai, Y., Yu, P., Popplewell, N., Shah, A. Finite element modelling of transmission line galloping. Computers & structures 1995, 57(3), 407–420.
  19. Jakob, M. Wind field simulation. Probabilistic Engineering Mechanics 1998, 13(4). [Google Scholar]
  20. Load code for the design of building structures. GB 50009-2012; China Architecture & Building Press: Beijing, China, 2012.
  21. Wang, X. Finite Element Method. Tsinghua University Press: Beijing, 2003. [Google Scholar]
  22. Yan, L., Li, J., He, X. Effect of central clamps on fatigue damage of suspenders of suspension bridge under joint action of fluctuating wind and vehicle loads. Journal of Central South University (Science and Technology) 1–14.
  23. Kong, D., Li, L., Long, X., Ye, Z. Parametric investigation on fatigue life of transmission line subjected to Aeolian vibration. Journal of Wuhan University of Technology 2010, 32(10), 53–57.
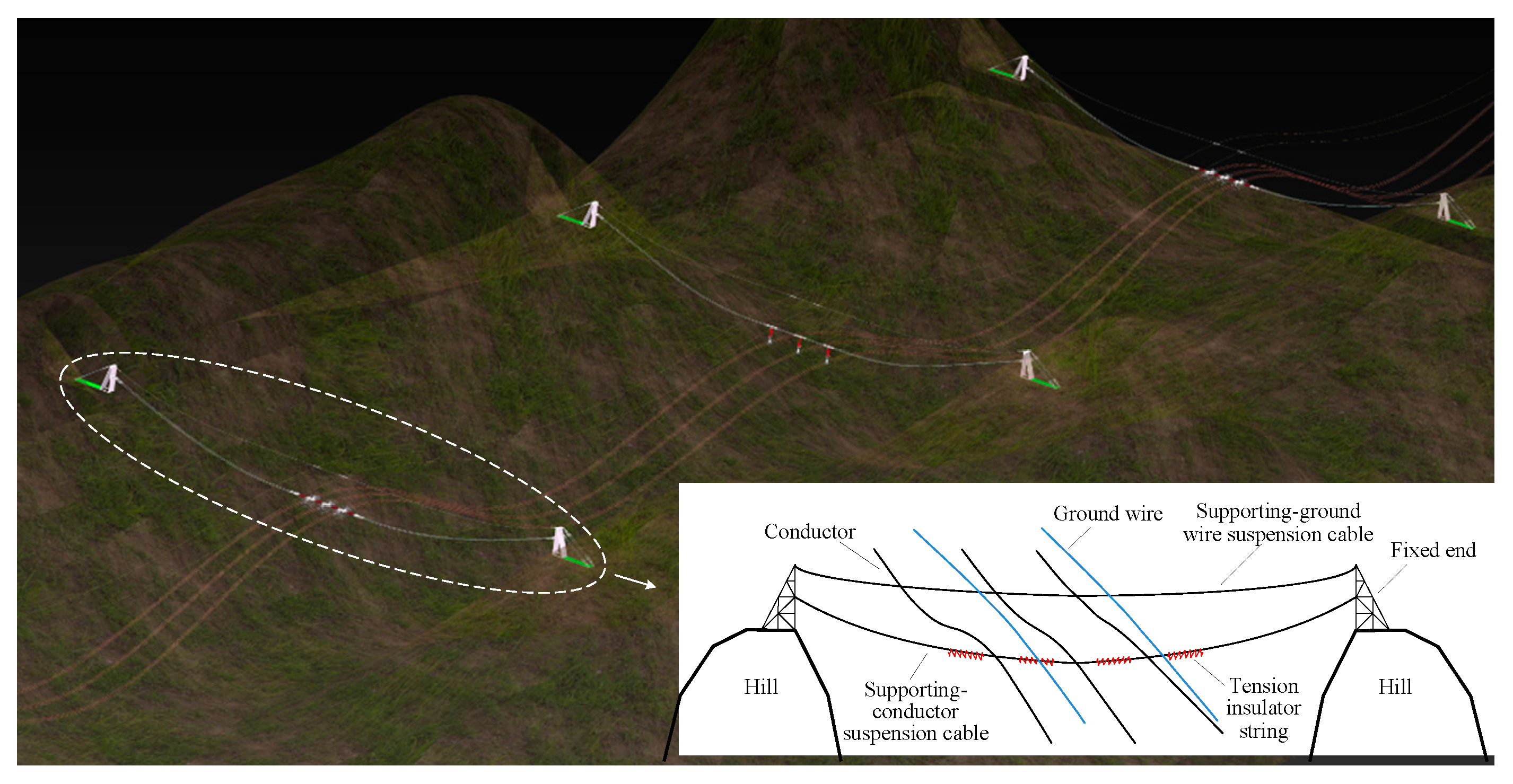
Preprints 86033 g001
Figure 1. Schematic diagram of the tension cable-supported power transmission structure.
Figure 1. Schematic diagram of the tension cable-supported power transmission structure.
Preprints 86033 g001
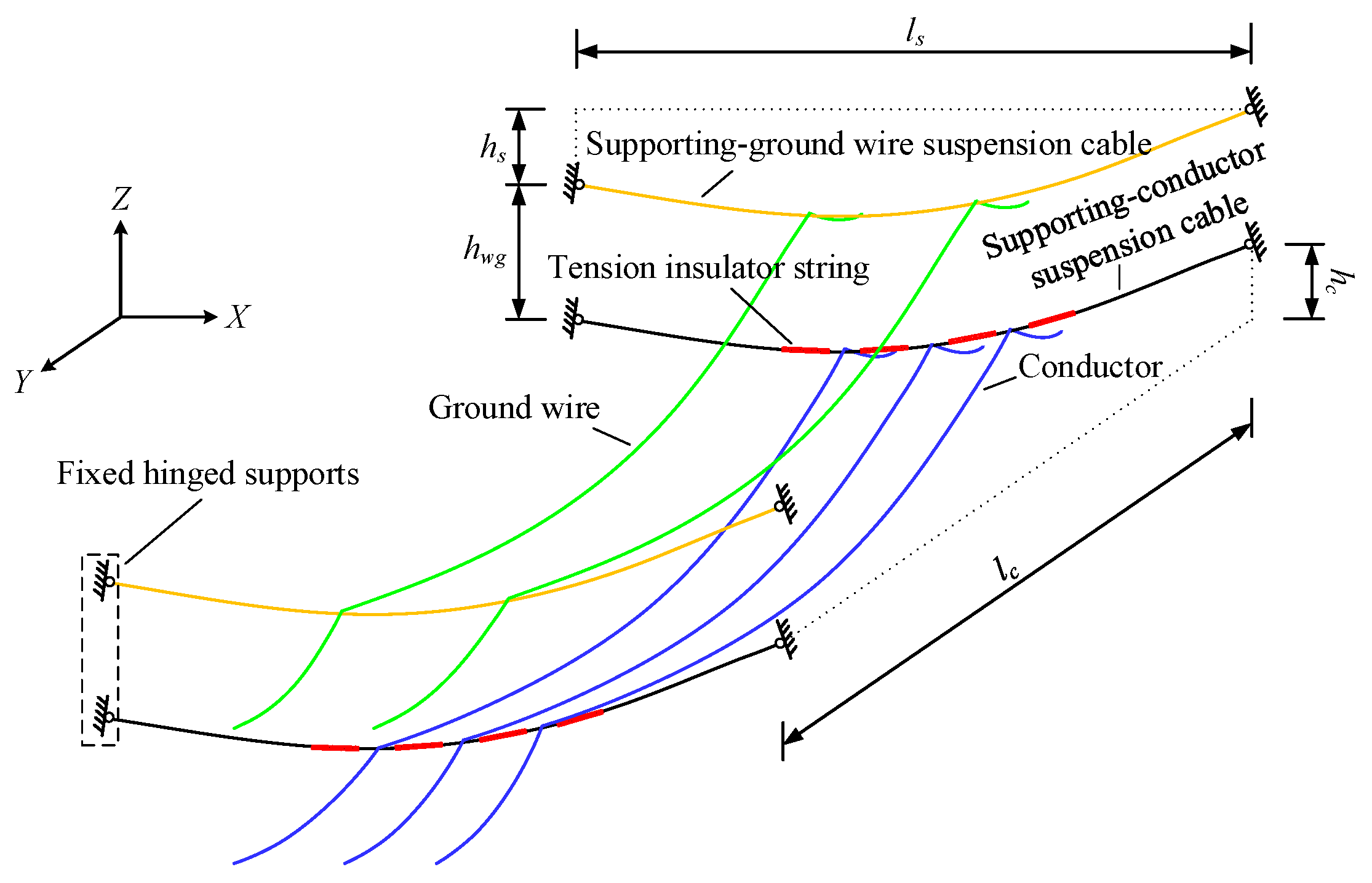
Preprints 86033 g002
Figure 2. Simplified model and structural parameters of the tension cable-supported power transmission structure.
Figure 2. Simplified model and structural parameters of the tension cable-supported power transmission structure.
Preprints 86033 g002
Preprints 86033 g003
Figure 3. Simplified finite element model and node displacements.
Figure 3. Simplified finite element model and node displacements.
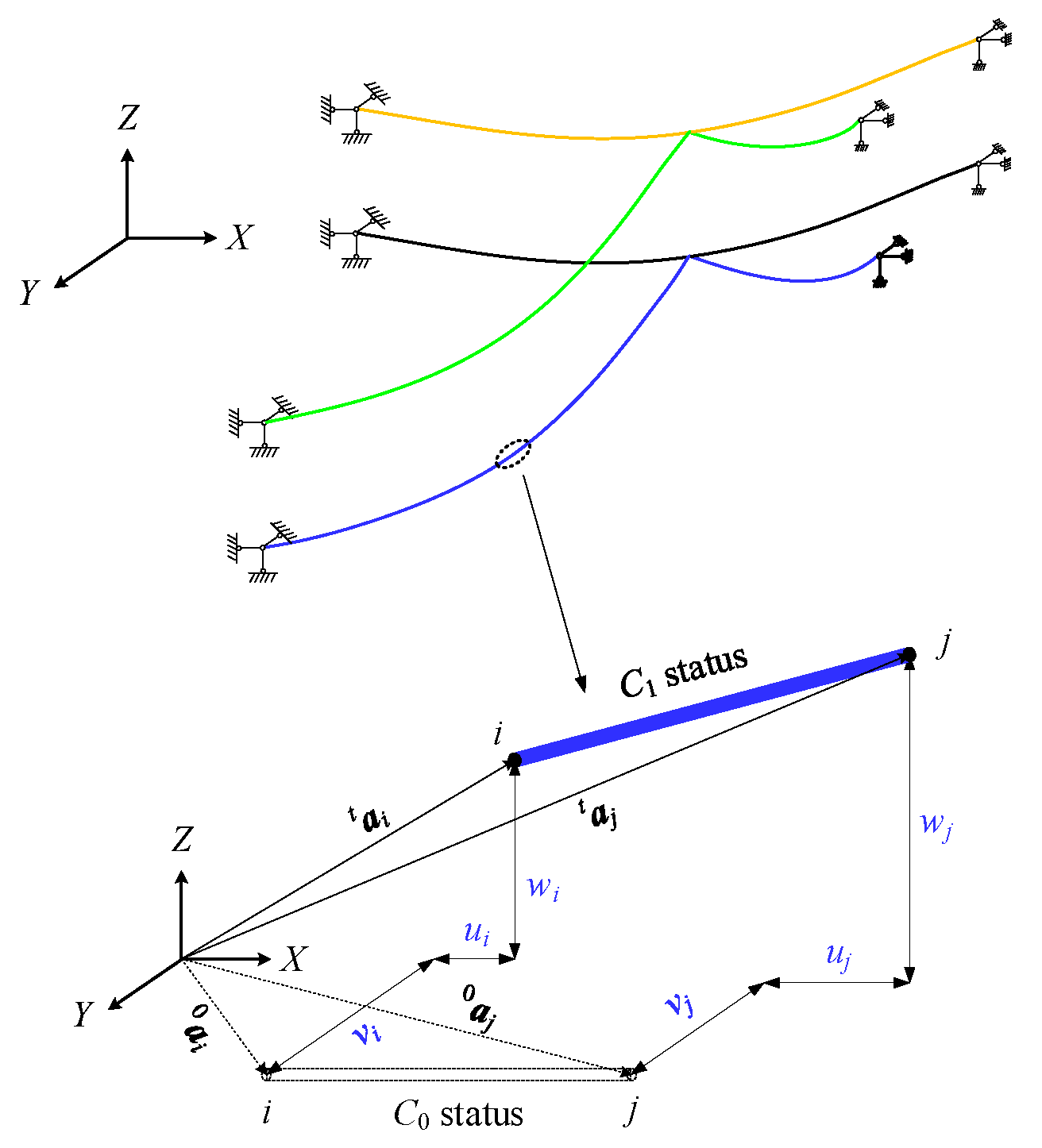
Preprints 86033 g003
Preprints 86033 g004
Figure 4. Schematic diagram of wind direction angle θ.
Figure 4. Schematic diagram of wind direction angle θ.
Preprints 86033 g004
Preprints 86033 g005
Figure 5. A two-span tension cable-supported power transmission structure.
Figure 5. A two-span tension cable-supported power transmission structure.
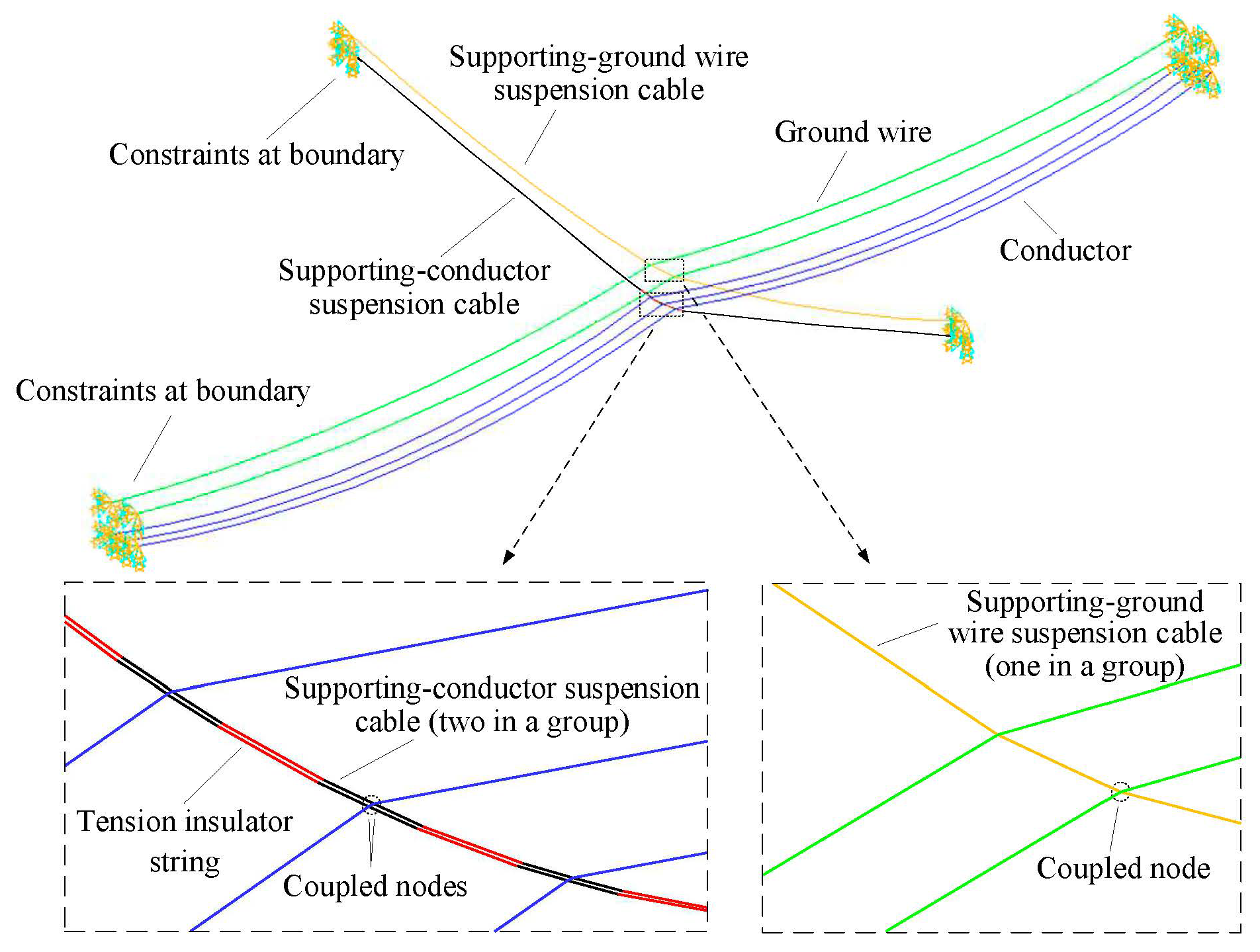
Preprints 86033 g005
Preprints 86033 g006
Figure 6. First three orders mode of vibration of the supporting-conductor part obtained by the proposed model (left) and ANSYS (right). (a) First order vibration mode; (b) Second order vibration mode; (c) Third order vibration mode.
Figure 6. First three orders mode of vibration of the supporting-conductor part obtained by the proposed model (left) and ANSYS (right). (a) First order vibration mode; (b) Second order vibration mode; (c) Third order vibration mode.
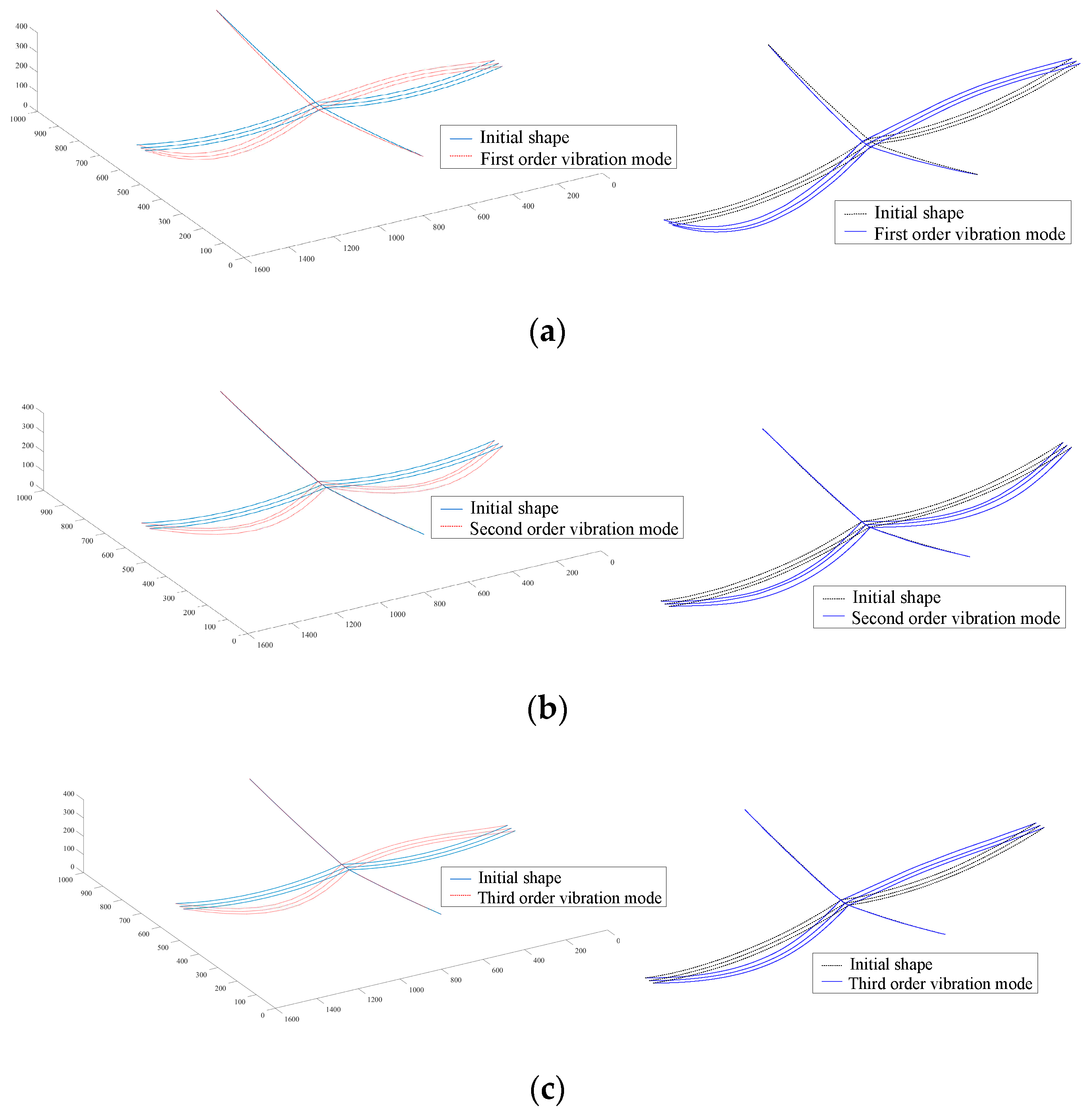
Preprints 86033 g006
Preprints 86033 g007
Figure 7. Mean square deviation of lateral displacement at each position of a single span conductor.
Figure 7. Mean square deviation of lateral displacement at each position of a single span conductor.
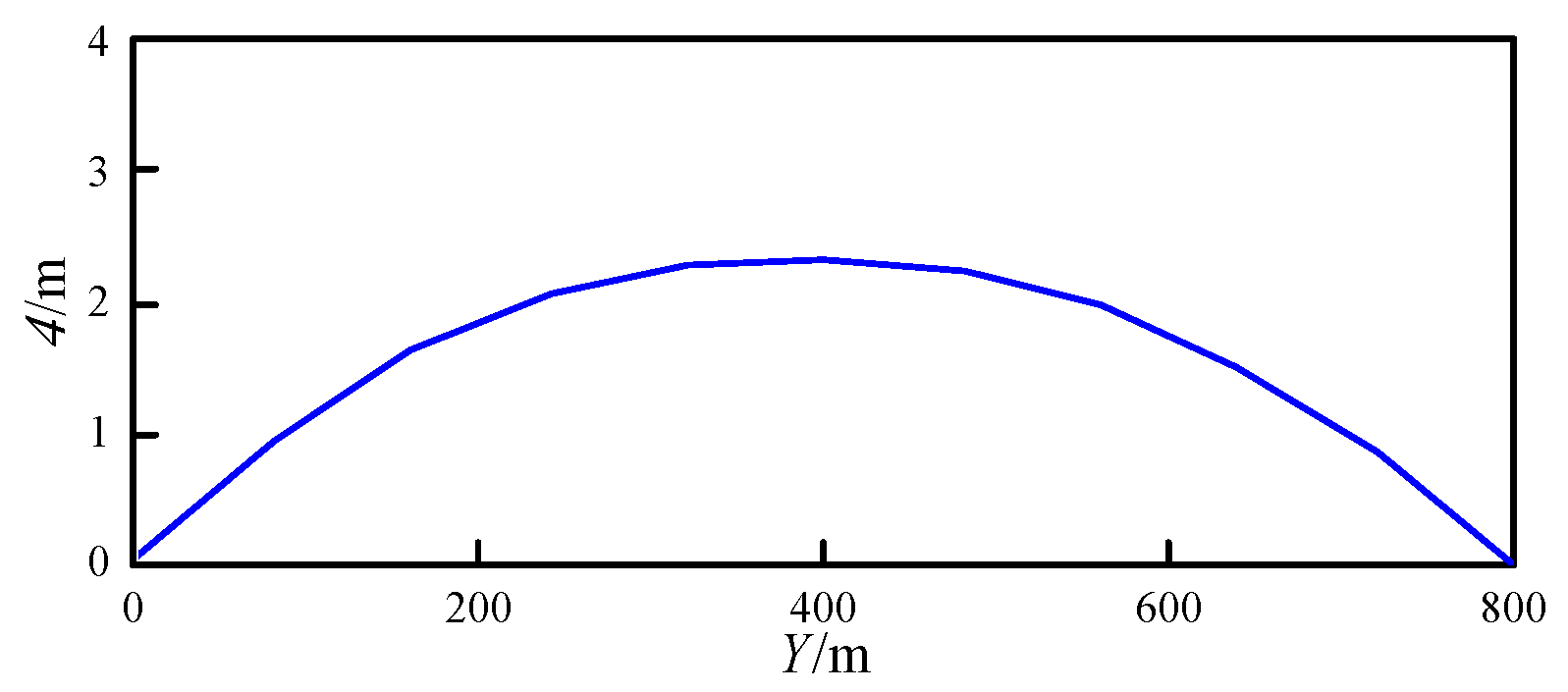
Preprints 86033 g007
Preprints 86033 g008
Figure 8. The lateral displacement time history of the conductor midpoint.
Figure 8. The lateral displacement time history of the conductor midpoint.
Preprints 86033 g008
Preprints 86033 g009
Figure 9. The influence of wind direction angle θ. (a) Maximum lateral displacement of the transmission line; (b) Maximum tension of the supporting suspension cable.
Figure 9. The influence of wind direction angle θ. (a) Maximum lateral displacement of the transmission line; (b) Maximum tension of the supporting suspension cable.
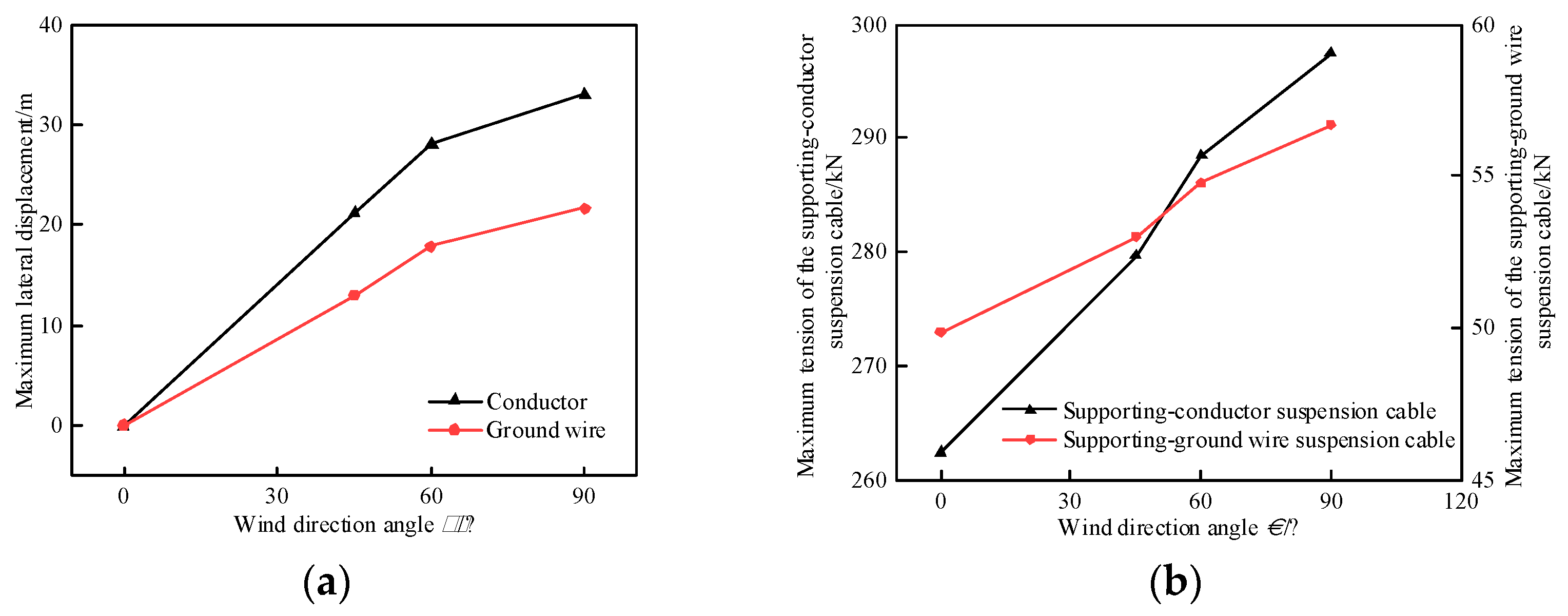
Preprints 86033 g009
Preprints 86033 g010
Figure 10. The influence of wind speed V10. (a) Maximum lateral displacement of the transmission line; (b) Maximum tension of the supporting suspension cable.
Figure 10. The influence of wind speed V10. (a) Maximum lateral displacement of the transmission line; (b) Maximum tension of the supporting suspension cable.
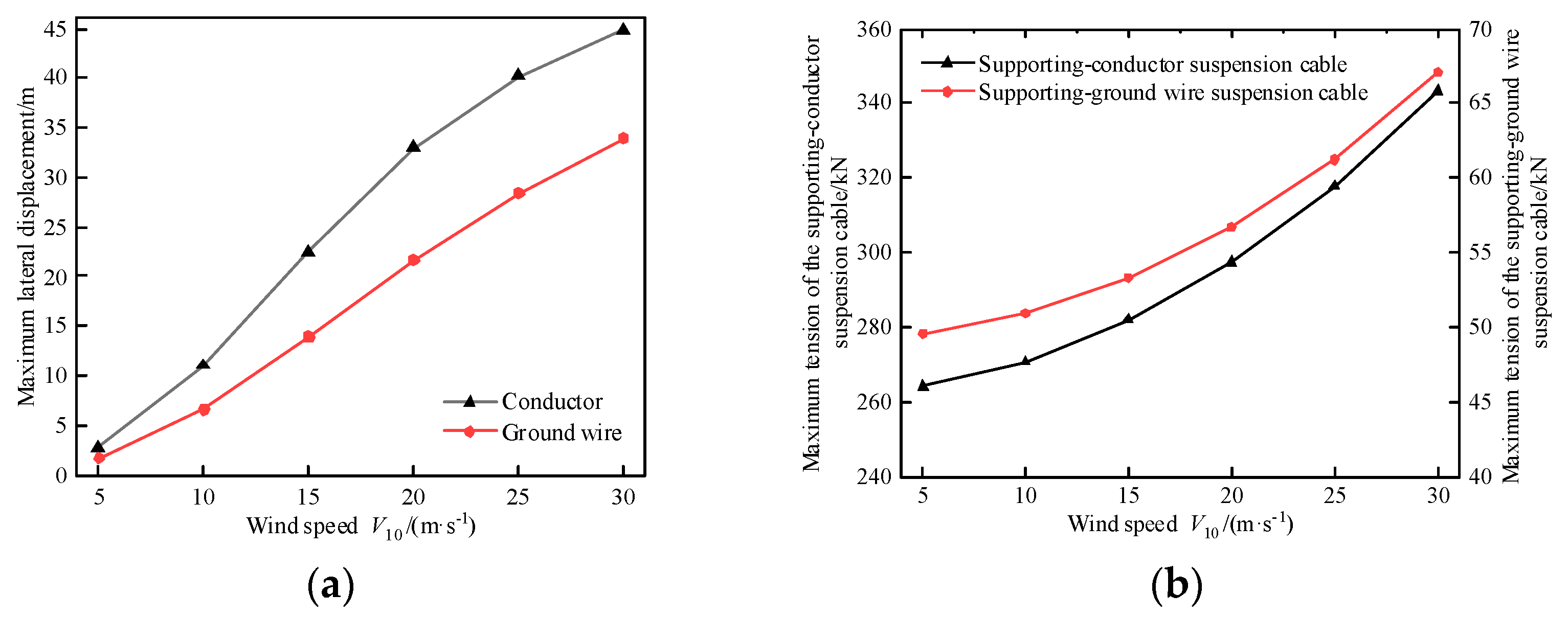
Preprints 86033 g010
Preprints 86033 g011
Figure 11. Stress time history of each part. (a) The supporting-conductor suspension cable; (b) The conductor.
Figure 11. Stress time history of each part. (a) The supporting-conductor suspension cable; (b) The conductor.
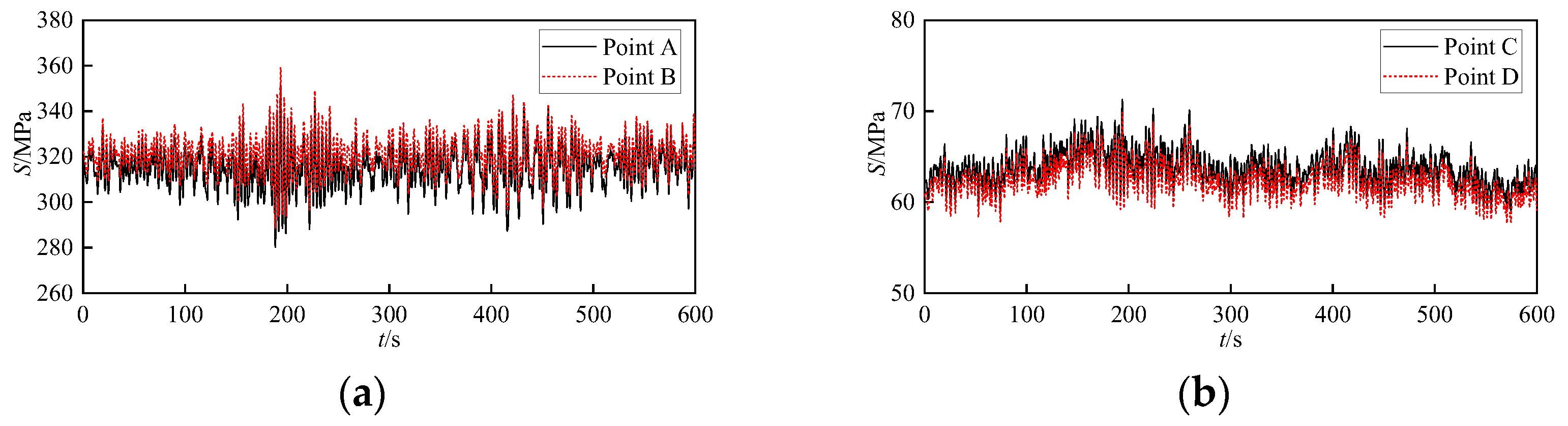
Preprints 86033 g011
Table 1. First five orders natural frequency of TC-PTS.
Table 1. First five orders natural frequency of TC-PTS.
Parts Frequency order Proposed model/(Hz) ANSYS/(Hz) Relative error/(%)
The supporting-conductor part first order 0.08063176 0.08063257 -0.001000
second order 0.08174143 0.08174136 0.000086
third order 0.08186433 0.08186437 -0.000053
fourth order 0.08188066 0.08188070 -0.000057
fifth order 0.08188298 0.08188303 -0.000058
The supporting-ground wire part first order 0.10351429 0.10351425 0.000046
second order 0.10393417 0.10393408 0.000087
third order 0.10457513 0.10457513 0.000000
fourth order 0.10457779 0.10457779 0.000000
fifth order 0.10457779 0.10457779 0.000000
Table 2. Average and maximum values obtained by the proposed model and ANSYS.
Table 2. Average and maximum values obtained by the proposed model and ANSYS.
Terms Average values Maximum values
Proposed model 23.33m 29.70m
ANSYS 23.36m 29.95m
Relative error/(%) 0.13 0.83
Table 3. Calculation efficiency obtained by the proposed model and ANSYS.
Table 3. Calculation efficiency obtained by the proposed model and ANSYS.
Terms Computing time/min Calculation efficiency/%
Proposed model 1.50 4.19
ANSYS 35.88 -
Table 4. Fatigue damage of each part.
Table 4. Fatigue damage of each part.
Part Mean value of stress/(MPa) Mean square deviation of stress/(MPa) Fatigue damage
Point A 315.04 9.12 9.70×10-11
Point B 320.96 8.37 7.79×10-11
Point C 63.70 1.87 1.41×10-12
Point D 62.36 1.83 4.96×10-13
Table 5. Fatigue damage of each part under different wind directions.
Table 5. Fatigue damage of each part under different wind directions.
Case Wind direction/(°)
0 45 60 90
Point A 2.91×10-12 4.43×10-11 2.72×10-10 1.80×10-9
Point B 3.30×10-12 1.29×10-11 1.43×10-10 8.87×10-10
Point C 2.01×10-14 1.17×10-13 1.33×10-12 6.13×10-11
Point D 1.50×10-14 5.25×10-13 9.28×10-12 4.11×10-10
Table 6. Fatigue damage of each part under different wind speeds.
Table 6. Fatigue damage of each part under different wind speeds.
Wind speed/( m·s-1) Point A Point B Point C Point D
5 1.40×10-15 1.31×10-16 1.14×10-24 2.64×10-25
10 2.87×10-12 1.59×10-13 5.13×10-18 1.47×10-16
15 9.70×10-11 7.79×10-11 1.41×10-12 4.96×10-13
20 1.80×10-9 8.87×10-10 6.13×10-11 4.11×10-10
25 7.72×10-9 3.84×10-9 1.59×10-8 8.39×10-8
30 5.81×10-8 1.70×10-8 8.03×10-7 3.32×10-7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated