Prerpints.org logo
Preprint
Article

TFR: Texture Defect Detection with Fourier Transform Using Normal Reconstructed Template of Simple Autoencoder

Altmetrics

Downloads

140

Views

33

Comments

0

This version is not peer-reviewed

Submitted:

23 September 2023

Posted:

25 September 2023

You are already at the latest version

Alerts
Abstract
Texture is essential information for image representation, capturing patterns, and structures. Consequently, texture plays a crucial role in the manufacturing industry and has been extensively studied in the fields of computer vision and pattern recognition. However, real-world textures are susceptible to defects, which can degrade the image quality and cause various issues. Therefore, there is a need for accurate and effective methods to detect texture defects. In this study, a simple autoencoder and Fourier transform were employed for texture defect detection. The proposed method combines Fourier transform analysis with the reconstructed template obtained from the simple autoencoder. Fourier transform is a powerful tool for analyzing the frequency domain of images and signals. Moreover, analyzing the frequency domain enables effective defect detection because texture defects often exhibit characteristic changes in specific frequency ranges. The proposed method demonstrates effectiveness and accuracy in detecting texture defects. Experimental results are presented to evaluate its performance and compare it with those of existing approaches.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

Defect detection can be classified into two types: texture defect detection and object defect detection. Both texture defect detection and object defect detection are visual inspection techniques used in manufacturing and production environments to identify product defects visually. However, each type focuses on detecting distinct types of defects and employs unique methods and objectives. Texture defect detection is primarily used to identify defects related to the texture of a product surface. It identifies irregularities in texture, color variations, pattern changes, and similar attributes on a product surface to detect defects. On the contrary, Object defect detection is utilized to detect flaws in components or parts within or outside the product. It identifies issues, such as flaws in the component shape, size, and composition, which could impact the functionality or safety of the product.
Texture defect detection is a crucial topic in image processing and computer vision because texture provides important information about patterns and structures in images. Texture defects are particularly significant in the manufacturing industry where they are essential for evaluating product quality and detecting defects in manufacturing processes.
In the manufacturing industry, it is crucial to ensure that products meet the required standards. Texture defects in products can significantly affect their quality. Texture defect detection allows for the identification and resolution of anomalies or irregularities in texture patterns or structures, enabling the evaluation of product quality. This study proposes a new approach that combines the Fourier transform and a convolutional autoencoder to effectively detect and address texture defects.
Texture defects can arise during the manufacturing process, and their detection is essential for maintaining product quality. By applying texture defect detection techniques, manufacturing companies can swiftly detect issues and take prompt action. Furthermore, texture defect detection offers advantages in terms of cost reduction. Companies can minimize the occurrence of defective products, reduce waste, and optimize production efficiency by implementing robust texture defect detection methods.
Manual inspection of texture defects is time-consuming and subjective. Automation of the texture defect detection process using computer vision technology enables faster and more objective evaluation. This study aims to contribute to the improvement of product quality, optimization of manufacturing processes, cost reduction, and automation by highlighting the importance of texture defect detection and proposing a novel approach that integrates the Fourier transform and a convolutional autoencoder.
Various techniques have been used for texture defect detection, including the combination of deep learning and image processing methods. In this study, the Fourier transform and a simple autoencoder were utilized for texture defect detection. Fourier transform is a useful tool for analyzing the frequency domain of images or signals, enabling the characterization of texture frequency properties. Because texture defects may exhibit characteristic changes in certain frequency ranges, analyzing the frequency domain using the Fourier transform allows for effective defect detection. Additionally, an autoencoder was employed to learn the normal characteristics of the textures and reconstruct them. An autoencoder is a model that encodes and reconstructs the input data into a latent space, thereby extracting features from the input data. In this study, an autoencoder was used to reconstruct the normal texture data and generate a template for normal reconstruction. This template is utilized for defect detection by analyzing the differences between the reconstructed texture and normal state. This study provides a detailed explanation of the reconstruction process of the autoencoder and a method for generating a normal reconstruction template for texture defect detection. The aim was to contribute a fresh perspective and advancements to the field of texture defect detection.
The contributions of this study are as follows:
  • Performance Improvement: The proposed simple autoencoder architecture achieved a high level of performance comparable to that of State-of-the-Art (SOTA) methods. Despite its simplicity, the autoencoder demonstrated effectiveness in texture defect detection, proving that efficient defect detection can be achieved without the need for complex deep learning models.
  • Integration of Techniques: This study employs a hybrid approach that combines deep learning and image processing methodologies to address texture defect detection. Specifically, deep learning was applied to achieve denoising and reconstruction tasks, whereas image processing methods were used to extract pertinent texture features and facilitate defect detection. This fusion of techniques yields notable benefits, including the elimination of the need for extensive data training. Consequently, this study proposes a streamlined and efficient methodology for texture defect detection achieved through the integration of deep learning and image processing techniques.
  • Experimentation and Analysis: Detailed experiments and analyses were conducted using the necessary parameters. Various parameters were adjusted and compared to optimize texture defect detection performance. This provides insights into the parameters that impact the performance most significantly and offers practical guidelines for real-world applications.
Through these contributions, this study demonstrates the potential for performance enhancement in texture defect detection and the benefits of combining deep learning and image processing techniques.

2. Related Work

2.1. Anomaly Detection with Reconstruction

In anomaly detection research, methods based on reconstruction have been widely studied. These methods typically involve training on normal data to generate reconstructed data and utilize the difference between the input anomalous data and the original image for detection. Models such as autoencoder and GAN are commonly employed for reconstruction and leveraging reconstruction errors for anomaly detection.
AnoGAN [1] proposes a basic approach to anomaly detection that combines unsupervised learning with a GAN. It learns the distribution of normal data by inputting only normal data and calculates anomaly scores to compare and detect anomalies. f-AnoGAN [2], an extension of AnoGAN [1], improves performance by introducing fast mapping techniques for new data and incorporating an Encoder into GAN for more refined reconstruction. The data generated by f-AnoGAN [2] exhibit high generation performance, and even experts find it difficult to distinguish them from real data. GANomaly [3] learns both generation and latent spaces using only normal data. Anomaly scores were computed based on the differences in latent vectors. Skip-GANomaly [4] extends GANomaly [3] with a U-Net-based network architecture and introduces adversarial training that includes a loss function for discriminator’s feature maps, leading to improved reconstruction performance. MemAE [5] overcomes the limitations of using an autoencoder for anomaly detection by incorporating a Memory Module, which makes reconstruction more challenging for abnormal samples. Although the autoencoder generalizes well, it can also reconstruct abnormal regions, which is a drawback. This study focuses on postprocessing methods to address this issue. OCGAN [6] is a model for one-class anomaly detection that learns latent representations of in-class examples and restricts the latent space to a given class. By utilizing a denoising autoencoder network and discriminator, it generates in-class samples and explores anomalies outside the class boundaries. This approach achieved high-performance results.
These studies [1,2,3,4,5,6] mainly focused on reconstruction-based methods for anomaly detection, in which training on normal data was used to assess and detect anomalies. Anomaly detection encompasses various subfields [7,8,9] that can be applied to real-life scenarios, including disease detection, accident detection, and fall detection.
Y. Zhao et al. [7] aimed to effectively detect plant diseases. However, the study mentions the issue of data imbalance between diseased and healthy samples and proposes a solution called DoublaGAN, which applies Super-Resolution to augment the diseased data. This research achieved the goal of detecting various plant diseases while enhancing the resolution by a factor of four and demonstrated high performance. J. Si et al. [8] introduced the structure of a Generative Adversarial Serial Autoencoder consisting of autoencoders connected in series. This study presents a method for detecting diseases in chili peppers using the GrabCut technique to segment pepper regions and apply a reconstruction process. It addresses the limitations of reconstruction and improves the performance by calculating all scores based on reconstruction. J. Si et al. [9] focused on detecting traffic accidents using black-box videos. The proposed method generates the next frame of the video using information from previous frames and compares it with the actual frame to detect accidents. However, this study mentioned the need to address the issue of background misclassification when dealing with moving videos.

2.2. Defect Detection

D. M. Tsai et al. [10] proposed the use of Fourier transform to detect defects in PCBs. This study demonstrated the ability to detect small irregular pattern defects by comparing the Fourier spectra of an image and a template, demonstrating the effectiveness of this method. While inspired by the idea of using templates, this approach differs from the proposed method in that it does not utilize Fourier spectrum comparison and incorporates the element of deep learning. J. Si et al. [11] serves as a preliminary study of the proposed method, introducing the ability to detect defects by applying the Fourier transform to the results of an autoencoder and removing specific components. Unlike [10], which used templates, this study demonstrates that improved performance can be achieved by focusing solely on component removal. Consequently, this study introduces additional methods and achieves performance enhancement for various textures.
DRAEM [12] presented a defect detection method based on reconstructing anomalous data, which deviates from the conventional approach of training on normal data for reconstruction. This method simultaneously learns two networks for reconstruction and discrimination to preserve and detect the defective regions. However, the goal of this study was to achieve performance improvement using a simple approach by training only on normal data without generating anomalous data. Thus, it may achieve a lower performance than the study mentioned. Y. Liang et al. [13] mentioned the limitations of the reconstruction capabilities of other methods and introduced a method for defect detection from a frequency perspective, which aligns with the viewpoint and approach of this study. Two novel methods, Frequency Decoupling, and Channel Selection, are proposed to reconstruct from various frequency perspectives and combine them for more accurate defect detection. N-Pad [14] introduced a defect detection method that uses the relative positional information of each pixel. Relative positional information is represented in eight directions. Using a loss function, this study demonstrates the utilization of this positional information. Anomaly Score was proposed using Mahalanobis and Euclidean distances, and various experiments on neighborhood sizes demonstrated the significance of the method.
J. Si et al. [15] focused on the application of reconstruction to the thermal images of solar panels for defect detection. As the distribution of thermal images is sensitive to color and lacks pronounced edge features, this study proposes a method that uses patches instead of reconstructing the entire image. The proposed method introduces a technique called “Difference Image Alignment Technique” by sorting pixel values, which enables easy detection of defects using only a few specific pixels. However, owing to the significant differences in the data characteristics between the focus of this study (manufacturing) and thermal images, the application may not be straightforward. C. C. Tsai et al. [16] introduces a defect detection method that considers the similarity between patches to extract representative and important information from images. By utilizing different-sized patches, the method performs representation learning based on different scales and applies K-means clustering and cosine similarity to improve defect detection. The advantages of randomly selecting multiple patches from an image and including local information through relative angles were demonstrated. However, while both the object and texture were detected in this study, it showed lower performance, specifically for texture detection, whereas this study focused solely on texture.
T. Liu et al. [17] proposes a method for enhancing the defect detection performance in grayscale images by applying post-processing techniques such as color space and image processing. The network was designed to reconstruct the original colors using grayscale images to avoid the incorrect classification of color information. This study showed an improved performance by incorporating various augmentation techniques and morphologies. Y. Shi et al. [18] is distinct from most other studies that have focused on image reconstruction. Instead, this study utilizes a pretrained model to extract feature maps from various layers, combine them, and perform reconstruction to better restore the features. By basing all content on diverse feature maps, the method can better preserve the defective regions in the results. H. Jinlei et al. [17], a divide-and-assemble approach was proposed to overcome the limitations of autoencoder models for unsupervised anomaly detection. By applying this approach, the reconstruction capability of the model was modulated. This study introduced a multi-scale blockwise memory module, adversarial learning, and meaningful latent representations to improve the performance of anomaly detection. The results demonstrate enhanced anomaly detection performance.

3. Texture Defect Detection

Noise is an inevitable factor that arises during image processing, and poses a significant challenge to image analysis and defect detection. Particularly, in defect detection, noise can complicate the accurate identification of areas where defects occur. This can result in elevated detection scores, potentially leading to false positives during defect detection.
In this study, we propose a defect detection method using deep learning networks and Fourier transformation. The proposed method involves the following steps:
Generation of Reconstructed Images through Denoising: Initially, a deep learning network was employed to perform the denoising process on the input images. This process generates reconstructed images from which fine details are removed. The network used in this step is a simple autoencoder with a straightforward structure trained only on normal images. The core objective is to generate images that closely resemble the input data, with a primary emphasis on noise removal.
Preservation Defect using Fourier Transform: Defect detection occurs during the inference phase. This process was used to create Normal Reconstructed Templates using a set of normal experimental data. The term ‘Normal Reconstructed Template’ refers to a collection of results generated by a model trained solely on normal videos. This approach utilizes the reconstruction mechanism of an autoencoder, acknowledging the limitations of precisely recreating the original imagery from normal videos. To overcome these limitations, the generated outcomes were treated as representative of the normal distribution. Consequently, by utilizing the Normal Reconstructed Template to construct differential images, it is possible to eliminate the normal distribution, highlighting only areas containing defects. One template was selected and the same Fourier transformation process was applied to it. Upon examining the Fourier spectrum, it is evident that a region affected by defects exhibits a dissimilarity compared to a normal region. Notably, the region afflicted with defects demonstrates a pronounced energy concentration, particularly within the high-frequency domain. To preserve the high-frequency components corresponding to the defective region exclusively, a high-pass filtering operation is executed. Subsequently, an inverse Fourier transform is applied to generate an image that corresponds specifically to the high-frequency component.
Generation of Difference Images and Binary-Level Thresholding: The difference images between each high-pass-filtered Normal Reconstructed Template and the input image were computed. In the difference image, pixels with nonzero values are regarded as potential defect regions, and higher values indicate a greater likelihood of defects. The difference image is converted into a binary image by applying a binary thresholding operation. This approach allows the creation of a defect score by representing items with a potential for defects as one and those with a lower likelihood as zero in a binary image. By generating a binary image, the defect score is formulated by counting the occurrences of the value one. A higher score implies a greater likelihood of the presence of defects. In binary images, pixels corresponding to defects possess values distinct from those of normal pixels. Through the binarization process, the defect regions can be effectively emphasized and represented.
The proposed method enables defect detection using the aforementioned steps. This allows for differentiation between normal and defective images, highlighting the regions where defects are present. The overall flow of the proposed method is shown in Figure 1.

3.1. Normal Texture Image Reconstruction

This model processes input images with a size of 256x256, which are composed of RGB color channels. Therefore, the input shape was (256, 256, 3) and consisted of 5 layers in depth. The proposed network is illustrated in Figure 2.
The autoencoder is composed of an encoder and a decoder. The input data were compressed into a low-dimensional latent vector through the encoder and then reconstructed back to the same size as the input image through the decoder.
The encoder part followed the structure of a Convolutional Neural Network (CNN). The first convolutional layer uses 64 filters, each applying a 3x3 kernel. It uses the ReLU activation function and applies ‘same’ padding to maintain the output size the same as the input. Subsequently, additional convolution layers were used to extract the spatial features of the image and gradually reduce its size. The output of the encoder was passed to the decoder for the restoration process. The decoder alternately used an up-sampling layer to match the size of each layer mentioned in the encoder. It also incorporates a skip-connection structure, in which the information from each layer of the encoder is brought and combined. Consequently, it generates high-quality output results of the same size as the input image.
This model combines basic L1 and L2 losses as its loss function. The L1 loss calculates the absolute error between the actual and predicted values, whereas the L2 loss calculates the squared error between them. By combining these two losses, the reconstruction loss (1) is computed and minimized during the model training process. This combined form of a simple loss function provides an approach for capturing various aspects of the errors in a balanced manner. By minimizing this combined loss, the model can effectively learn and optimize its parameters.
L r e c o n x , R x = λ L 1 L 1 x , R x + λ L 2 L 2 x , R x
In this study, this simple autoencoder structure was used for defect-detection tasks. The goal is to detect defects using this simple autoencoder structure. By effectively compressing and reconstructing the input data, autoencoders can detect and differentiate between normal and defective data.
Furthermore, this structure provides denoising effects. The encoder part extracts features from the input image and removes noise. This helps reduce noise in the input data. Noise refers to parts that can be misclassified as defects in the texture, such as patterns in the backgrounds of normal images. By removing the noise, the reconstructed image can be transformed into an image with a nearly uniform color that represents a normal distribution. This approach can help effectively distinguish defects or normal in the frequency band. With reduced noise, the input data represent clearer and more accurate frequency bands, making it easier to distinguish defect areas from the results of the Fourier transformation. Therefore, this simple autoencoder structure with denoising effects is highly suitable for Fourier transformation and can be effectively used for tasks such as defect detection and frequency-band division.

3.2. Application of Fourier Transform

The Fourier transform of a 2D image refers to the process of transforming an image from the spatial domain into the frequency domain, thereby allowing us to obtain information related to the frequency components of the image. The Fourier transform involves converting the original image into the frequency domain, performing the necessary operations, and restoring it back to the original domain through inverse transformation.
First, the given 2D square image (256, 256) is represented in the spatial domain using ( x ,   y ) coordinates. To perform the Fourier transform on this image, we use Equation (2): F ( u ,   v ) is a complex number representing the transformed result in the frequency domain and ( u ,   v ) represents the coordinates in the frequency domain. Equation (2) implies multiplying the complex exponential function in the frequency domain and the image value at each position in the spatial domain, and then summing them for all positions. This allowed us to obtain the frequency information of the image in the frequency domain.
F u , v = ∑ x = 0 N − 1 ∑ y = 0 N − 1 f x , y * e − j 2 π u x + v y N
The inverse Fourier transform is expressed in Equation (3). Importantly, the property of the Fourier transform is that when the original image is transformed and then inverse-transformed, it is restored to the original image. This represents the relationship between the Fourier transform and the inverse Fourier transform.
f x , y = 1 N 2 ∑ x = 0 N − 1 ∑ y = 0 N − 1 F u , v * e j 2 π u x + v y N
In this paper, multiple reconstructed results for a “Normal Reconstructed Template” representing normal data are defined as T ( x i ) . To determine the presence of defects, both the target image to be evaluated and the Normal Reconstructed Template are Fourier transformed to convert them into the frequency domain. In the frequency domain, the part with frequency 0 was placed at the center, and as the frequency increased, it shifted towards the edges of the frequency area through a shift process.
Next, a “Fourier Mask” is defined to remove the low-frequency components, as shown in Figure 3. For this purpose, an ideal mask with a radius of τ centered at the origin is created. This mask was used to perform pixel-wise operations on the Fourier-transformed result, effectively removing low-frequency components. This process retains only the high-frequency region where defects exist while eliminating the background and unwanted components. Finally, an inverse transformation was applied to convert the results from the frequency domain to the spatial domain. Consequently, only the defective regions of the texture image were preserved in the spatial domain.

3.3. Difference Images and Thresholding

Both F ( R x ) and F ( T x i ) generated through this process represent the results of removing the low-frequency range and preserving only the high-frequency range, respectively. Therefore, the Normal Reconstructed Template retains only fine high-frequency details while removing the rest. If we perform the same process using a normal image as the input, the difference from the Normal Reconstructed Template is very small. However, when an image with defects is used as the input, the defective parts are not completely eliminated through the process, and some noise from the background may remain. By subtracting the two generated images, the resulting difference image has nonzero values in the defective regions and values close to zero in the remaining areas. This difference image is then used to create the final map for defect detection. Finally, by applying a threshold value t h to the generated map, we can generate the final maps that allow us to determine the presence of defects. If the values exceeded the threshold, they were set to one. Otherwise, they are set to zero. This binary map indicates the presence of defects, where it is set to one, and absence, where it is set to zero. By calculating the total number of pixels in the generated map, we derived the scores for each image. Because the score range can vary significantly, we normalized the scores based on the scores of all the images and calculated an appropriate defect score. To fill the empty areas in the resulting image, a dilation operation was performed three times using a (5,5) kernel.
Therefore, the binary image obtained through this process has one in the locations of defects and zero in the unaffected areas. This enables defect detection, and by calculating the scores for the entire image and normalizing them, we determined the normalized defect score. Figure 4 shows the process of calculating the defect score.

4. Experimental Results

4.1. Datasets

In this study, we focus on texture defect detection using the MV-Tec AD [20]. This dataset consists of 5 textures and 10 objects, but we only evaluate the performance using 5 textures. However, available data are insufficient for both training and testing. Therefore, data augmentation was performed in this study. Table 1 lists the final composition of the dataset in terms of the number of samples in each texture category. Because we used only normal data for training, the majority of the data were used as training data. To balance the number of samples between the normal and defective data, augmentation techniques were applied to the normal data. This process increased the diversity of the training data and ensured an adequate number of defective samples, ultimately improving the performance of the model.

4.2. Training Details

For texture defect detection in this study, the following training approach was used. The pixel values of the input image data were normalized to fall within an interval of 0 to 1. Data augmentation was performed to generate diverse forms of training data. This augmentation procedure encompasses diverse techniques including shearing (20% magnitude), zooming (20% magnification), and both horizontal and vertical flipping. During the training process, the Adam optimizer was employed with an initial learning rate of 1e-4. Training was conducted for 500 epochs on the entire dataset, with a batch size of 16. In the loss function, the hyperparameter λ L 2 is set to 100 for L2 loss, and λ L 1 is set to 1 for L1 loss, resulting in a combination of simple loss functions.

4.3. Performance Evaluation and Ablation Study

The network proposed in this study was trained solely on normal data, which generated areas with distributions different from those of normal images when processing images containing defects. Figure 5 illustrates the images reconstructed from examples of defective data for each category. All the data in the figure contain defects, and the types of defects appear differently. The first row shows the original images with defects, whereas the second row shows the images reconstructed using the autoencoder. The original images exhibit patterns even in the background, indicating prominent features. However, the defective regions possess even more pronounced features. Therefore, by removing noise from the background, the defective regions can be highlighted more effectively. The overall reconstructed results appear blurred, with a significant reduction in background noise, except for the grid. Although the defective regions also become blurry, the removal of background patterns makes it easier to extract the defects. The grid exhibited a consistent pattern and closely resembled the original, except in areas with defects, where differences could be observed.
The reason for using Normal Reconstructed Templates is the limitations in the reconstruction performance of the network. Consequently, significant differences were observed when creating different images from the original images. In practice, even normal data cannot be perfectly reconstructed to match the original. Hence, this approach can help retain only the defect regions by maximizing the reconstructed outcomes for the original images. The Normal Reconstructed Template represents the restoration results of normal data and possesses various forms and patterns. These templates were used to generate difference images and were subsequently employed to detect the defective regions. Given that the network was trained exclusively on normal images, the processing of images containing defects led to reconstructed images that exhibited minor deviations in their distributions. Consequently, the adopted approach entails the computation of differences between the normal reconstructed templates and the regions within the images that manifest defects. This process facilitates the extraction of defects.
This approach allows the precise detection of defects by distinguishing between normal and defective regions. By removing non-defective areas through differences in the reconstructed images, the remaining areas were composed of defective regions, making the defects more distinct and enabling more accurate detection. Accordingly, this approach seeks to utilize the inherent constraints of the autoencoder’s reconstruction capabilities. It employs the Normal Reconstructed Template to improve defect detection performance. More accurate defect detection can be achieved by removing the normal areas and emphasizing the defective areas. The images reconstructed from normal data exhibit a variety of normal restoration templates. Therefore, selecting the most suitable template for each data category is crucial. Figure 6 presents the selection of appropriate templates for each category based on the experimental results. These templates can be utilized to generate difference images and consistently improve performance across all data. In addition, when generating difference images, the 10-pixel edge was excluded from the evaluation. This is because the edge exhibits a different distribution from the original owing to padding, which increases the likelihood of misclassification.
As mentioned in Section 3, we need to find the most suitable template by combining the Fourier mask, denoted as τ , and the binary-level thresholding represented by t h . To evaluate performance, we used the Area Under the Curve (AUC) as an evaluation metric. The AUC is a common metric used to assess the performance of classification models, ranging from 0 to 1, where a value closer to 1 indicates better performance. Because each category has different characteristics, they have different parameter values, and we explored various combinations of these parameters. Therefore, we used AUC to determine the optimal parameter combination for each category and selected the combination with the highest AUC value. Based on this, we inferred the AUC values for various parameter combinations. The results are presented in Table 2. The parameter combinations that showed the highest AUC for each category are as follows ( τ , t h ) : Carpet: (41, 11), Grid: (44, 20), Leather: (2, 6), Tile: (40, 2), Wood: (1, 11)
The overall average AUC was 93.1%. This indicates that our proposed simple method achieves a performance similar to that of the state-of-the-art approaches. These results demonstrate that the proposed method effectively detects defects despite its simplicity. However, the Carpet category had a relatively lower AUC than the other categories. This can be attributed to the relatively smaller difference between the defect regions and background in the Carpet category compared to the other categories. When the difference between the defect regions and the background is small, removing noise from the background may also result in the removal of defect regions, making accurate detection more challenging. Therefore, the Carpet category may require different parameter values and additional adjustments. We demonstrated that a simple method can achieve high performance. Additionally, because the optimal parameter combinations may vary for each category, it is important to adjust the parameter values accordingly. Thus, our method offers both flexibility and simplicity, making it applicable to various defect-detection problems.
Figure 7 shows a partial process of generating the final decision map for each category. The first column shows the reconstructed image. The second and third columns show the frequency-domain images of the input image and the normal reconstructed template, respectively. The fourth column illustrates the result of binary-level thresholding applied to the difference Fourier image. The white areas indicate defective regions, and it can be observed that the actual defective areas are well preserved.
Table 3 presents the results of evaluating various anomaly detection algorithms on different categories. The performance of each algorithm is measured by the Area Under the Curve (AUC) value, where a value of 1 indicates the presence of defects and 0 indicates their absence.
Analyzing the results for the Grid and Wood category, DAAD [19] shows high AUC values of 0.957 and 0.982, respectively, indicating its superior performance in anomaly detection. In the Leather category, the proposed method achieved the highest AUC value of 0.975. This suggests that the proposed method has a strong anomaly detection performance for Leather data. For the Tile category, the proposed method achieved the highest AUC value of 0.932. This indicates that the proposed method demonstrates excellent anomaly detection capability for Tile data. In the case of the carpet, although it exhibited a relatively low value of 0.874 compared with related studies, it demonstrated the highest value. This results in a 0.8% superior performance compared to DAAD [19].
Overall, AnoGAN [1] shows relatively lower performance across all categories, whereas GANomaly [3] and Skip-GANomaly [4] exhibit highly irregular results compared to the other categories. DAAD [19] demonstrated high performance for specific categories, but the proposed method showed excellent performance in all categories except Carpet. Notably, the proposed method stands out because it does not rely heavily on deep learning networks compared to previous studies, and it exhibits the smallest category-wise variation with the highest average AUC of 93.9%. The significant difference observed in the Leather category can be attributed to the simplicity of the background, which facilitates noise removal.
The method proposed in this study has two main aspects: using a simple autoencoder for a Normal Reconstructed Template and combining it with the Fourier transform to separate and remove defective features. Therefore, the performance was evaluated based on the usage of the Normal Reconstructed Template and Fourier transform. Without the Normal Reconstructed Template, performing only Fourier transform makes it extremely challenging to separate defective features in the frequency domain, resulting in a slightly higher AUC of 75.2% overall compared with the results. Especially in the “leather” category, it records a significantly low value of 0.344 when compared to other categories. This can be attributed to the characteristics of the data, as they possess an intensity that makes it difficult to detect defects using frequency bands, unlike other categories. When only the Normal Reconstructed Template was used along with the Fourier transform, it yielded a very low performance with an average AUC of 63.4% across all categories except for Leather. This indicates that using only the Normal Reconstructed Template to preserve defective regions is difficult for other categories, whereas the reconstructed results alone can preserve defective regions. In contrast, the proposed method, which combines both the Normal Reconstructed Template and Fourier transform, achieved the highest performance with an AUC of 93.9%. Therefore, the method proposed in this study demonstrates a higher performance compared to evaluating using the existing methods alone. In particular, although utilizing only the Fourier transform is a common approach when compared with this method, there was a performance improvement of 18.7%, achieving the highest performance across all categories.
The proposed approach uses a high-pass filter. In this study, a method based on an ideal filter is introduced. The ideal filter sets only the high-frequency region to one through the cutoff and the rest to zero. However, because of the tendency of filters to cause a ringing effect frequently, the Butterworth filter is preferred over the ideal filter. A significant point of comparison between the Butterworth and the ideal filter is the smoother transition of boundaries offered by the former. In this study, post-filtering, a binary image was generated through a post-processing step employing a threshold. The primary purpose is to retain only the defects. Consequently, both the ideal and Butterworth filters were resilient to the ringing effect. Table 5 presents the performance evaluation results corresponding to different filters. The preference for the ideal filter over the Butterworth filter, considering the generation of binary images, confirms its superior performance in terms of defect preservation.

5. Conclusions

This study proposes a method in the field of image analysis that combines a simple autoencoder and Fourier transform for texture defect detection. The experimental results showed that the proposed method achieved an overall high performance, although there were cases in which it did not show effectiveness for some data. Therefore, in future research, it will be necessary to enhance the performance of the proposed method by utilizing deep learning networks to improve noise removal. By developing and applying more sophisticated denoising techniques through deep learning networks, defect detection performance can be further improved. Additionally, future research directions include conducting comparative studies with other anomaly detection algorithms to validate the superiority of the proposed method and performing experiments on a wider range of datasets to evaluate its generalization performance.

Author Contributions

Conceptualization, J. Si and S. Kim; methodology, J. Si; software, J. Si; validation, J. Si; formal analysis, J. Si and S. Kim; investigation, J. Si; resources, S. Kim; data curation, J. Si; writing—original draft preparation, J. Si; writing—review and editing, S. Kim; visualization, J. Si; supervision, J. Si and S. Kim; project administration, S. Kim; funding acquisition, S. Kim. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Korea Institute for Advancement of Technology(KIAT) grant funded by the Korea Government(MOTIE) (P0024166 Development of RIC(Regional Innovation Cluster)).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Schlegl, T.; Seeböck, P.; Waldstein, S. M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In Proceedings of the International Conference on Information Processing in Medical Imaging, Boone. NC. USA, 25 June–30 June. 2017. 146-157. [Google Scholar]
  2. Schlegl, T.; Seeböck, P.; Waldstein, S. M.; Langs, G.; Schmidt-Erfurth, U. f-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks. Medical image analysis 2017, 54, 30–44. [Google Scholar] [CrossRef] [PubMed]
  3. Akçay, S.; Atapour-Abarghouei, A.; Breckon, T. P. GANomaly: Semi-supervised anomaly detection via adversarial training. In Proceedings of the Asian Conference on Computer Vision, Perth. Australia, 2 December–6 December 2018; pp. 622–637. [Google Scholar]
  4. Akçay, S.; Atapour-Abarghouei, A.; Breckon, T. P. Skip-GANomaly: Skip connected and adversarially trained encoder-decoder anomaly detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Budapest, Hungary, 14 July–19 July 2018; pp. 39–42. [Google Scholar]
  5. Gong, D.; Liu, L.; Le, V.; Saha, B.; Mansour, M. R.; Venkatesh, S.; Hengel, A. V. D. Memorizing normality to detect anomaly: Memory-augmented deep autoencoder for unsupervised anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1705–1714. [Google Scholar]
  6. Perera, P.; Nallapati, R.; Xiang, B. Ocgan: One-class novelty detection using gans with constrained latent representations. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Long Beach, CA, 16 June–20 June 2019; pp. 2898–2906. [Google Scholar]
  7. Zhao, Y.; Chen, Z.; Gao, X.; Song, W.; Xiong, Q.; Hu, J.; Zhang, Z. Plant disease detection using generated leaves based on DoubleGAN. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2021, 19, 1817–1826. [Google Scholar] [CrossRef]
  8. Si. J.; Kim. S. Chili Pepper Disease Diagnosis via Image Reconstruction Using GrabCut and Generative Adversarial Serial Autoencoder. arXiv. 2023, arXiv:2306.12057. [Google Scholar]
  9. Si. J.; Kim. S., Traffic Accident Detection in First-Person Videos Based on Depth and Background Motion Estimation. Journal of Korean Institute of Information Technology (JKIIT). 2021, 19, 25–34. [Google Scholar] [CrossRef]
  10. Tsai, D. M.; Huang, C. K. Defect detection in electronic surfaces using template-based Fourier image reconstruction. IEEE Transactions on Components, Packaging and Manufacturing Technology. 2018, 9, 163–172. [Google Scholar] [CrossRef]
  11. Si, J.; Kim., S. Surface Anomaly Detection of Wood Grain Image Using Fourier Transform : A Preliminary Study. Proceedings of Korean Institute of Information Technology Conference, Jeju, Korea, 1 December–3 December 2022; 2022; pp. 86–87. [Google Scholar]
  12. Zavrtanik, V.; Kristan, M.; Skočaj, D. Draem-a discriminatively trained reconstruction embedding for surface anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11 October–17 October 2021; pp. 8330–8339. [Google Scholar]
  13. Liang, Y.; Zhang, J.; Zhao, S.; Wu, R.; Liu, Y.; Pan, S. Omni-frequency channel-selection representations for unsupervised anomaly detection. arXiv. 2023, arXiv:2203.00259. [Google Scholar] [CrossRef] [PubMed]
  14. Jang, J.; Hwang, E.; Park, S. H. N-pad: Neighboring pixel-based industrial anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, 17 June–21 June 2023; pp. 4364–4373. [Google Scholar]
  15. Si, J.; Kim., S. Difference Image Alignment Technique of Reconstruction Method for Detecting Defects in Thermal Image of Solar Cells. Journal of Korean Institute of Information Technology (JKIIT). 2023, 21, 11–19. [Google Scholar]
  16. Tsai, C. C.; Wu, T. H.; Lai, S. H. Multi-scale patch-based representation learning for image anomaly detection and segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, Hawaii, 4 January–8 January 2022; pp. 3992–4000. [Google Scholar]
  17. Liu, T.; Li, B.; Zhao, Z.; Du, X.; Jiang, B.; Geng, L. Reconstruction from edge image combined with color and gradient difference for industrial surface anomaly detection. arXiv. 2022, arXiv:2210.14485. [Google Scholar]
  18. Shi, Y.; Yang, J.; Qi, Z. Unsupervised anomaly segmentation via deep feature reconstruction. Neurocomputing. 2021, 424, 9–22. [Google Scholar] [CrossRef]
  19. Jinlei, H.; Yingying, Z.; Qiaoyong, Z.; Di, X.; Shiliang, P.; Hong, Z. Divide-and-assemble: Learning block-wise memory for unsupervised anomaly detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Virtual, 11 October–17 October 2021; pp. 8791–8800. [Google Scholar]
  20. Bergmann, P.; Fauser, M.; Sattlegger, D.; Steger, C. MVTec AD--A comprehensive real-world dataset for unsupervised anomaly detection. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, Long Beach, CA, 16 June–20 June 2019; pp. 9592–9600. [Google Scholar]
Preprints 85964 g001
Figure 1. Overall architecture of the proposed method.
Figure 1. Overall architecture of the proposed method.
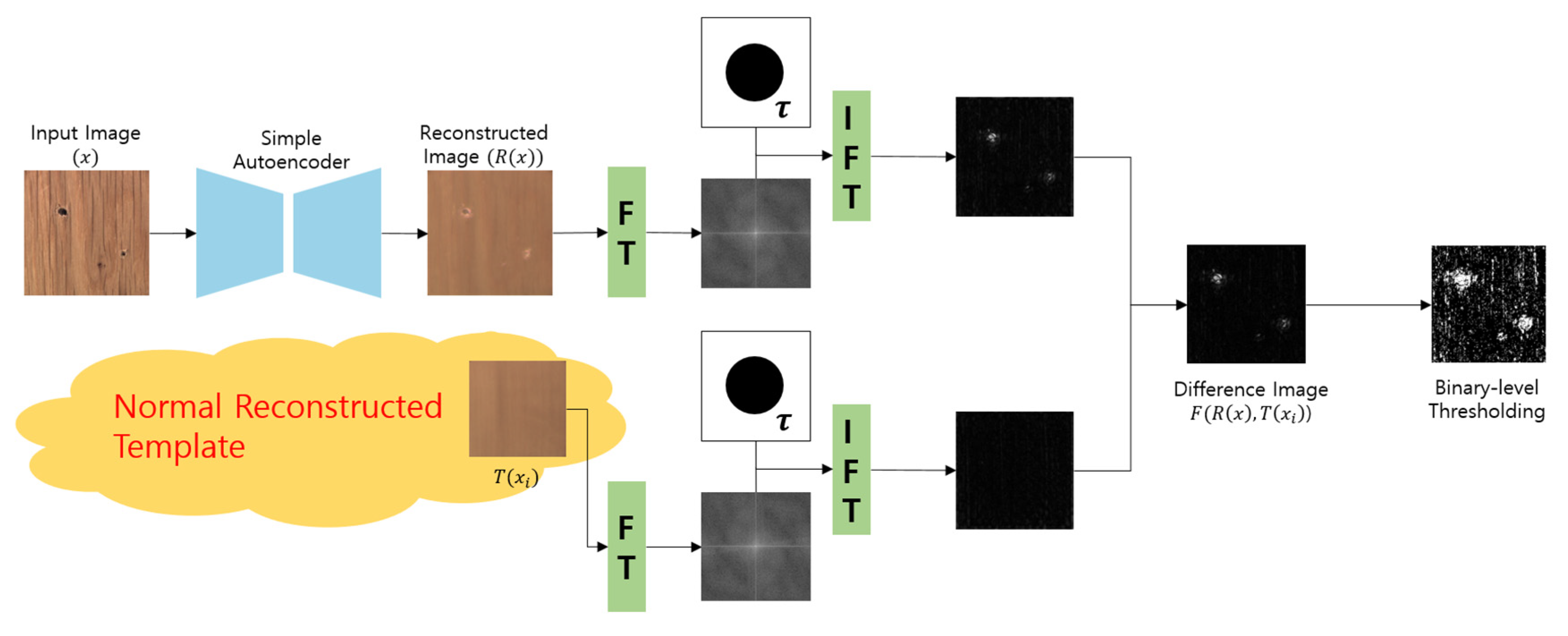
Preprints 85964 g001
Preprints 85964 g002
Figure 2. Model architecture for reconstruction.
Figure 2. Model architecture for reconstruction.
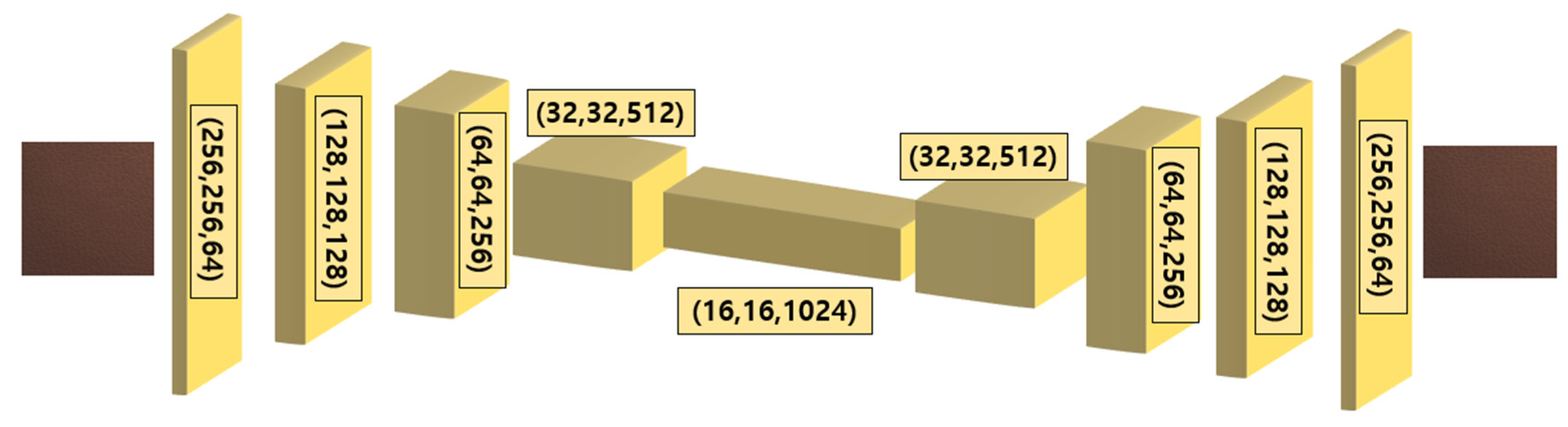
Preprints 85964 g002
Preprints 85964 g003
Figure 3. Fourier Mask and Pixel-wise.
Figure 3. Fourier Mask and Pixel-wise.
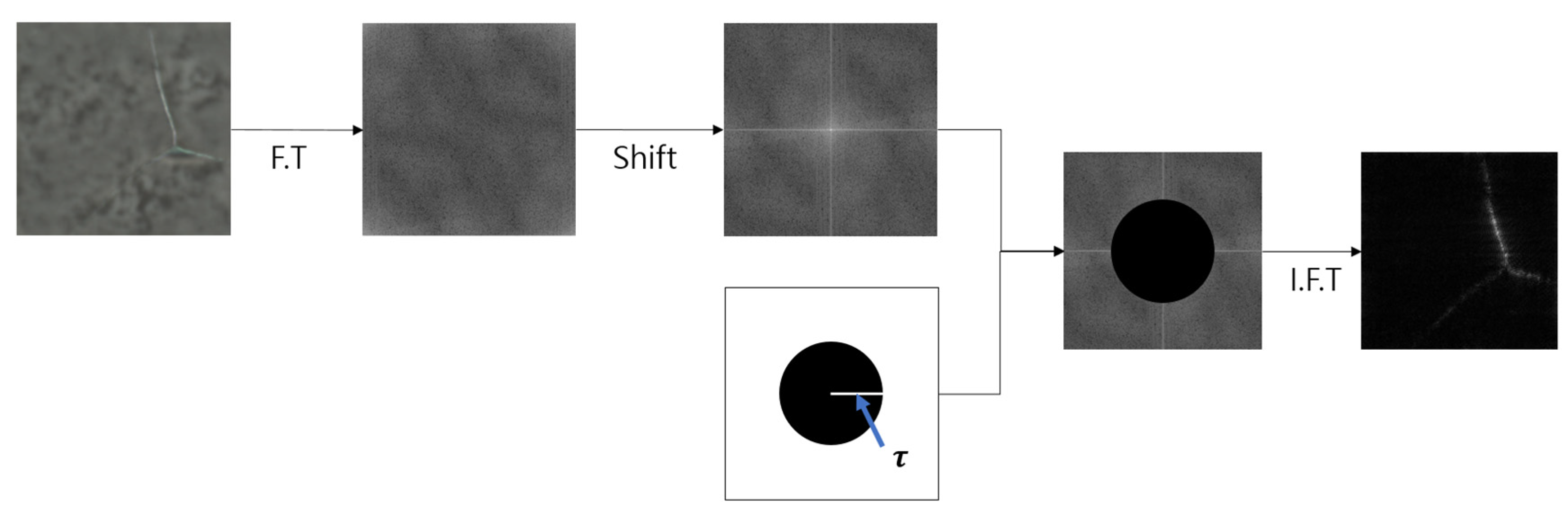
Preprints 85964 g003
Preprints 85964 g004
Figure 4. Process of calculating the defect score.
Figure 4. Process of calculating the defect score.
Preprints 85964 g004
Preprints 85964 g005
Figure 5. Some samples of reconstructed results for images with defects.
Figure 5. Some samples of reconstructed results for images with defects.
Preprints 85964 g005
Preprints 85964 g006
Figure 6. Normal Reconstructed Template.
Figure 6. Normal Reconstructed Template.
Preprints 85964 g006
Preprints 85964 g007
Figure 7. Process for locating defect detection (1st column: reconstruction, 2nd-3rd columns: Fourier transform results, 4th column: binary-level thresholding).
Figure 7. Process for locating defect detection (1st column: reconstruction, 2nd-3rd columns: Fourier transform results, 4th column: binary-level thresholding).
Preprints 85964 g007
Table 1. Detailed datasets with data augmentation.
Table 1. Detailed datasets with data augmentation.
Train (Normal) Test (Normal) Test (Defect)
Carpet 280 84 89
Grid 264 63 57
Leather 245 96 92
Tile 230 99 84
Wood 247 57 60
Table 2. Performance analysis (row: Fourier mask radius τ , column: threshold value t h ).
Table 2. Performance analysis (row: Fourier mask radius τ , column: threshold value t h ).
Carpet 7 8 9 10 11 12
37 0.736 0.727 0.720 0.715 0.712 0.713
38 0.732 0.731 0.730 0.726 0.725 0.731
39 0.763 0.758 0.758 0.762 0.766 0.771
40 0.815 0.820 0.822 0.821 0.825 0.822
41 0.869 0.871 0.874 0.864 0.845 0.836
42 0.845 0.827 0.812 0.783 0.759 0.743
Grid 18 19 20 21 22 23
42 0.907 0.815 0.920 0.931 0.925 0.913
43 0.918 0.918 0.921 0.919 0.915 0.902
44 0.919 0.934 0.939 0.933 0.922 0.903
45 0.928 0.934 0.937 0.929 0.919 0.889
46 0.923 0.931 0.929 0.929 0.915 0.890
47 0.931 0.924 0.926 0.921 0.906 0.867
Leather 4 5 6 7 8 9
1 0.910 0.932 0.924 0.901 0.892 0.871
2 0.955 0.964 0.975 0.900 0.824 0.788
3 0.968 0.951 0.888 0.847 0.825 0.793
4 0.953 0.914 0.887 0.845 0.785 0.760
5 0.946 0.909 0.859 0.800 0.752 0.722
6 0.948 0.890 0.846 0.787 0.745 0.716
Tile 1 2 3 4 5 6
37 0.685 0.898 0.818 0.766 0.696 0.643
38 0.695 0.915 0.820 0.748 0.685 0.637
39 0.727 0.896 0.786 0.743 0.685 0.631
40 0.736 0.932 0.786 0.741 0.679 0.625
41 0.735 0.914 0.794 0.735 0.667 0.625
42 0.733 0.923 0.791 0.723 0.655 0.625
Wood 7 8 9 10 11 12
1 0.875 0.897 0.929 0.953 0.976 0.962
2 0.886 0.910 0.939 0.932 0.938 0.935
3 0.914 0.918 0.944 0.940 0.939 0.946
4 0.906 0.930 0.917 0.918 0.918 0.917
5 0.901 0.925 0.911 0.904 0.912 0.910
6 0.900 0.911 0.898 0.906 0.915 0.912
Table 3. Performance analysis (row: Fourier mask radius τ , column: threshold value t h ).
Table 3. Performance analysis (row: Fourier mask radius τ , column: threshold value t h ).
AnoGAN [1] memAE
[5]		 OCGAN
[6]		 GANomaly [3] Skip-GANomaly [4] DAAD
[19]		 Ours
Carpet 0.337 0.386 0.348 0.699 0.795 0.866 0.874
Grid 0.871 0.805 0.855 0.708 0.657 0.957 0.939
Leather 0.451 0.423 0.624 0.842 0.908 0.862 0.975
Tile 0.401 0.718 0.806 0.794 0.850 0.882 0.932
Wood 0.567 0.954 0.959 0.834 0.919 0.982 0.976
Average 0.525 0.657 0.718 0.775 0.826 0.910 0.939
Table 4. Ablation Study.
Table 4. Ablation Study.
Normal Reconstructed Template X O O
Fourier Transform O X O
Carpet 0.791 0.659 0.874
Grid 0.885 0.508 0.939
Leather 0.344 0.634 0.975
Tile 0.819 0.505 0.932
Wood 0.923 0.867 0.976
Average 0.752 0.634 0.939
Table 5. Performance Comparison of Ideal Filter and Butterworth Filter.
Table 5. Performance Comparison of Ideal Filter and Butterworth Filter.
Filters Butterworth Ideal (ours)
Carpet 0.828 0.874
Grid 0.920 0.939
Leather 0.969 0.975
Tile 0.881 0.932
Wood 0.963 0.976
Average 0.912 0.939
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated