Prerpints.org logo
Preprint
Article

Study on the Rainwater Interception Process and Capacity of Urban Tree Organs in Shanghai

Altmetrics

Downloads

98

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 September 2023

Posted:

25 September 2023

You are already at the latest version

Alerts
Abstract
The process of rainfall interception by tree organs is crucial in mitigating the impact of intense rainfall on urban drainage systems, particularly in the context of climate change. this study selected ten commonly found tree species in Shanghai. Main parts of trees, including leaves, branches, and bark, were collected to analyze their ability to intercept rainwater. The optimized Artificial Rainfall Simulation System (ARSS) was applied to simulate the rainfall. The time-changing process of rainwater interception in three organs was measured during a 180-minute rainfall event which under four different rainfall intensities (4, 8, 12, and 16 mm/h, respectively). Process models of rainwater interception in different organs were fitted with adsorption kinetic equations. The rainwater interception process of tree organs complied with the quasi 2nd-order adsorption kinetic equation. The rainwater interception capacity of leaves, branches, and bark of ten urban tree species ranged from 0.05 to 0.34 mm, 0.13 to 0.24 mm, and 0.29 to 1.22 mm, respectively. The rainwater interception capacity of three organs significantly differs (p<0.05). It reveals that bark exhibits the highest rainwater interception ability. Coniferous tree species have a greater ability to intercept rainwater than broad-leaved tree species. There are also differences in the rainwater interception ability of trees in urban and natural areas.
Keywords: 
Subject: Environmental and Earth Sciences  -   Ecology

1. Introduction

The tree organs are the main components that intercept rainwater, and the accuracy of measuring their interception capacity affects the assessment of the canopy's overall interception capacity. The measurement of rainwater interception in plants is primarily conducted by manually wetting the surface of the organs using methods such as immersion [1,2,3] and artificial simulated rainfall [4,5,6].
The immersion method is currently the primary method used to measure the interception of rainwater by tree organs. This method involves immersing the tree organs in rainwater or distilled water that has been collected for a specific duration. Afterward, the organs are removed, and the difference between their fresh weight and wet weight is measured [1,2,7]. This measurement represents the amount of rainwater intercepted by the organs [8].
There are two main results of the research on organ rainwater interception using the immersion method. One reason is that the rainwater interception capacity of branches and trunks is significantly greater than that of leaves. Additionally, there are significant variations in the interception of rainwater by different types of vegetation [2,3]. The results showed that the rainwater interception capacity of Herwitz [9] on branches and trunks of tropical rainforest tree species ranged from 0.12 mm to 0.72 mm [9]. Leyton [10], Crockford [3], and others found that the rainwater interception capacity on branches and trunks of various Eucalyptus species ranged from 0.07-0.92 mm. The rainfall interception of broad-leaved trees, eucalyptus, and tropical rainforest trees [4,9] ranged from 0.07 mm to 0.11 mm. In the study of coniferous trees, the rainfall interception of branches of Picea koraiensis [11], Taxodium ascendens [2], slash pine [2], and Pinus densiflora [1] ranged from 0.13 mm to 1.26 mm. However, studies on coniferous tree species such as Pinus elliottii [2], Taxodium ascendens [2], Pinus sylvestris [1], Pinus radiata [12], Pinus pinaster [13], and Picea sitchensis [14] have shown that leaf rainfall interception ranges from 0.10 mm to 0.16 mm. The second reason is that there are significant differences in the rainwater interception capacity between shrub and tree leaves. The rainwater interception capacity of shrubs such as Caragana korshinskii, Hedysarum scoparium, and Artemisia ordosica, as studied by Wang [15] using the immersion method, ranges from 0.39 mm to 0.61 mm. This capacity is higher than that of tree leaves in previous studies. The measurement of rainfall interception by tree organs, particularly leaves, using the immersion method, is influenced by various factors, and its value varies significantly across different studies [3,4,16]. The factors that influence this fluctuation include the growth area of the tree, immersion time [1,2,3,7,9,17,18], whether the branch section is sealed, whether the blade is calculated on one side or both sides, and whether the air flow is taken into consideration. For the same species of Eucalyptus (Eucalyptus manniferu), Aston [4] measured 0.07 mm, while Crockford [3] measured 0.01-0.04 mm. For the leaf immersion time, Liu [2] argues that a shorter time aligns better with the actual rainfall interception function of leaves. Therefore, the recommended leaf immersion time is only 3 seconds. On the other hand, Llorens [1] believes that for maximum rainfall interception, the leaf needs to be fully soaked, requiring a longer immersion time of 60 minutes. Additionally, the immersion time for branches, and bark is even longer, ranging from 1 to 72 hours [2,3,9,17,18]. Under windy conditions, the rainwater interception capacity of the blade is significantly reduced. Herwitz [9] studied the rainwater interception capacity of leaves from various tropical rainforest trees, including Eucalyptus [4], as well as other broad-leaved trees. The study revealed that under windy conditions, the rainwater interception per unit area of leaves from broad-leaved trees would be reduced by 64-73%. In windy conditions, the reduction is 59-85%. The coniferous rainwater interception capacity of Pinus sylvestris was 0.10 mm and 0.04 mm under calm and windy conditions [1].
The immersion method is used to measure the water absorption capacity of an organ's surface under static conditions. In actual rainfall, organs are affected by factors such as rainfall intensity, rainfall duration, the dynamic impact of raindrops, and other variables. These factors can lead to dissimilation. Yu Kailiang [8,16,18,19,20] employed various techniques to assess the leaves of a single tree. Their findings revealed that the rainfall interception of the leaves, as measured by the artificial simulated rainfall method, was greater than that measured by the immersion method. It was speculated that the reason for this was that the continuous droplets formed on the surface of the leaves during the artificial simulated rainfall increased the interception of rainfall [21]. At present, the laboratory generally conducts artificial simulated rainfall moisture tests. In this method, the samples are placed under a simulated rainfall device, and the maximum rainwater interception capacity of trees is calculated by measuring the weight difference of the samples before and after rainfall [4,22]. The factors that affect the determination of rainfall interception include the intensity and duration of rainfall. The research object of rainfall interception using artificial simulation methods is typically the entire tree. Limited by the experimental conditions, the study primarily focuses on the seedling stage of the experimental object, making it challenging to determine the characteristics of larger tree species or mature trees. In Aston's study, eucalyptus seedlings [4,9] were selected, while in Li's study, seedlings at an early growth stage were chosen. For the determination of rainfall intensity, current research primarily focuses on the requirements for controlling soil and water loss in natural areas. The simulated rainfall intensity is usually more than 20 mm/h [4,19] for heavy rain and rainstorm intensity [4,5,9,15,18]. Only one rainfall intensity is set in many artificial simulated rainfall experiments, and only a few experiments have multiple rainfall intensities [19,23].
At present, related research mainly uses the methods of immersion and artificial rainfall to wet the surface of organs. The immersion method focuses on tree organs as the subject, but it does not consider the specific rainfall conditions. As a result, it cannot accurately determine the rainwater interception capacity of tree organs under varying rainfall intensities and durations. Artificial simulation rainfall methods can better simulate the natural wetting process [18,19] and are more widely used. However, current research primarily focuses on small trees or immature seedlings, making it challenging to determine the rainwater interception capacity of mature tree organs. Moreover, to quickly maximize the interception of rainfall by plants, the rainfall intensity is set to be more than 20 mm/h. This is significantly higher than the current natural rainfall conditions during rainstorms, which are typically greater than 16 mm/h [24,25]. This setting ignores the impact of different rainfall conditions, especially in urban areas where rainfall intensity is mostly moderate and light, on the capacity of tree organs to interception rainwater. Therefore, to accurately quantify the rainwater interception capacity of tree crowns under natural rainfall conditions, it is necessary to systematically establish rainfall intensity and duration conditions based on the characteristics of urban rainfall. This will allow for the implementation of artificial simulation experiments to study the wetting of organ surfaces. From a measurement perspective, the focus is primarily on natural areas, with only a few studies on urban trees that consider the entire tree as the subject. It is difficult to promote trees with different morphological characteristics and varying growth years. It is necessary to study the different components of urban trees, particularly their organs, in order to comprehensively assess the rainwater interception function of urban trees.

2. Materials and Methods

In this study, we measured rainwater interception by calculating the changes in organ weight before and after rainfall. The rainfall was simulated using an artificial rainfall simulation system (ARSS) for a duration of 180 minutes. The process of rainwater interception was modeled using an adsorption kinetic equation, which aims to calculate the rainwater interception capacity (rainwater interception capacity) of tree organs.

2.1. Research sample

The tree organ sampling points were in the Minhang Campus of Shanghai Jiao Tong University (31°01'12'' N, 121°25'33” E). The campus is in the southwest of Shanghai Minhang District (Figure 1), covering an area of 309.25 hectares. It has a rich variety of plant species, with 314 species belonging to 74 families and 188 genera. This includes the major tree species that are commonly found in gardens and green spaces in Shanghai. The trees were planted more than 20 years ago, with good environmental conditions, standard management, and vigorous growth. The simulated rainfall experiments were conducted in the controlled greenhouse of the School of Agriculture and Biology, Shanghai Jiao Tong University (Figure 1). The controlled greenhouse can prevent the influence of ambient air flow, temperature, and wind speed changes on the measurement of rainwater interception capacity.

2.2. Selection method of urban tree species

According to the results of the study on the characteristics of urban vegetation types in Shanghai City [26,27,28], the green plant communities in the central urban area of Shanghai are mainly consist of deciduous broad-leaved forests and evergreen broad-leaved forests. The second most common vegetation types are evergreen deciduous broad-leaved mixed forests and evergreen coniferous forests. In this study, five species of evergreen broad-leaved trees, three species of deciduous broad-leaved, as well as two species of coniferous trees in Shanghai were selected (Table 1), including Golden Rain Tree (Koelreuteria paniculata, KOP), London Planetree (Platanus × acerifolia, PCA), Japanese zelkova (Zelkova serrata, ZES), Camphor Tree (Cinnamomum camphora, CIC), Japanese blueberry tree (Elaeocarpus decipiens, ELD), Glossy privet (Ligustrum lucidum, LIL), Southern magnolia (Magnolia Grandiflora, MAG), Fragrant tea olive (Osmanthus fragrans, OSF), Deodar cedar (Cedrus deodara, CED), Dawn redwood (Metasequoia glyptostroboides, MEG), 20 sample trees were selected for each species from the Minhang campus of Shanghai Jiao Tong University (Figure 1).
According to the research results of Diameter at Breast Height (DBH) of urban trees by Wang [29] and Shi [30], the age distribution curve of DBH for trees mainly exhibits an inverted "J" shape in natural areas and an "L" shape in urban areas. According to the research results of DBH distribution range of urban trees in China, the DBH of common trees in urban built-up areas of Shanghai mainly distributes in 10-35 cm [29]. The trees in urban green space are mainly young and middle-aged forests with low maturity and small DBH in the whole growth process of trees. Therefore, mature trees from middle-aged forests were selected as the sample trees for this study to best represent the overall characteristics of common trees in the city. The selection of sample trees requires good growth vigor and normal crown type.

2.3. Sample collection of urban tree organs

During the investigation, samples were collected from the leaves, branches, and bark of trees. There should be no natural rainfall for at least 8 days before collecting the leaves, branches, and bark [31], to ensure that there is no residual water on the sample surface from the last rainfall. After the sample collection, put it into the incubator and take it back to the laboratory for testing.

2.3.1. Leaf collection method

Before conducting the rainwater interception measurement experiment, 100 leaves with healthy growth and no signs of dryness, disease, or insect pests were randomly selected from five different positions on each broad-leaved tree species (see Figure 2). For each coniferous tree species, 100 leaves were randomly selected from eleven positions on sample trees that exhibited good growth and showed no signs of dryness, disease, or insect pests.

2.3.2. Branch collection and sample preparation

The diameter of branches will significantly affect the rainwater interception capacity [24]. Therefore, based on the growth patterns of branches, the branches can be classified into large, medium, and small branches. The branches with growing leaves can be classified as third-class branches, the branches growing on the trunk can be classified as first-class branches, and the branches between the first-class and third-class branches can be classified as second-class branches. Before each simulated rainfall experiment, branches from sample trees to be tested were collected. After removing the leaves, the branches without leaves were sorted and cut based on their grades. Then, each grade of branches was standardized to a length of 10 cm (Figure 3), with 30 branches per grade, resulting in a total of 90 branches for each rainfall experiment, and 3600 branches were sampled for standardization for 40 rainfall events in this study. The cross sections of branch samples were sealed with impermeable silica gel to prevent water from entering the xylem during the rainfall test.

2.3.3. Bark collection and sample preparation

Three pieces of phloem were collected from the trunk of a sample tree to create a square bark sample. The side length of each piece was between 3 and 5 cm (Figure 3). a total of 1200 bark samples were collected for 40 rainfall events in this study. Except for the outer surface of the bark samples, the other five surfaces are sealed with impermeable silicone to prevent water from entering the xylem during the rainfall test.

2.4. Trial production method of artificial rainfall simulation system

To accurately quantify the rainwater interception capacity of tree organs in the context of Shanghai's rainfall characteristics, we designed and constructed an artificial simulation rainfall system (ARSS, Figure 4). This device has the capability to simulate four distinct levels of rainfall intensity: 4mm/h, 8mm/h, 12mm/h, and 16mm/h. The related patent has been authorized by the China National Intellectual Property Administration. The design of ARSS considers the specific meteorological classification standards for 1-hour rainfall intensity, which include light rain (< 2.5 mm/h), moderate rain (2.5-8.0 mm/h), heavy rain (8.1-16.0 mm/h), and rainstorm (> 16.0 mm/h) [24,25]. Based on an analysis of 30 years of rainfall data in Shanghai, it was observed that approximately 90% of rainfall events had an intensity of less than 4 mm per hour [32,33]. To accurately represent the maximum rainfall intensity, we have set the rainfall intensity levels at 16 mm/h, 12 mm/h, 8 mm/h, and 4 mm/h. This approach not only aligns with meteorological standards but also reflects the specific rainfall characteristics observed in Shanghai. Additionally, in order to maximize rainwater interception by tree organs, we set the rainfall duration to 180 minutes, which is consistent with previous research [5,34,35].
Previous studies that have utilized artificial rainfall simulations have primarily concentrated on examining the dynamics of soil erosion and water runoff during high-intensity rainfall events [4,36,37,38,39]. Furthermore, research on rainwater interception in natural forest canopies has primarily focused on heavy rainfall intensities, typically ranging from 10 to 150 mm/h [5,22,34,40,41]. However, there is a noticeable gap in the availability of artificial rainfall simulation devices capable of accurately replicating the specific rainfall patterns characteristic of urban areas. We used two primary methods for improvement. Firstly, we utilized a frequency conversion water pump to regulate water pressure and outlet flow. Secondly, we implemented a new design for the outlet nozzle (see Figure 4, nozzle sketch). Unlike the conventional nozzle design that directs water vertically downward, limiting the coverage area and resulting in intense rainfall, our new nozzle design modifies the spray direction to increase the coverage area while maintaining consistent water pressure and yield conditions. This adjustment effectively reduced the intensity of rainfall, aligning it with the desired specifications. To simulate light rain intensity (4mm/h) more accurately, we adjusted the nozzle's spray direction to a 45° angle upwards along the horizontal direction, causing the water to fall in a parabolic trajectory (see Figure 4, spray angle diagram), meeting the requirements of the simulated rainfall test [42].

2.5. Artificial simulated rainfall simulation test

Rainfall and its uniformity were measured using a rainfall gauge (Davis 7825, USA). The actual evenness of the 40 rainfall events ranged from 90.4% to 94.4%. The average actual rainfall intensities of 4 mm/h, 8 mm/h, 12 mm/h, and 16 mm/h were 4.23 ± 0.32 mm, 8.26 ± 0.17 mm, 12.09 ± 0.59 mm, and 16.25 ± 0.46 mm, respectively (Table 2). The results showed that the distribution of rainfall was uniform and met the test requirements.

2.6. Calculation method for rainwater interception process and capacity of tree organs

We conducted 40 simulated rainfall events using ARSS. Each time, we measured the rainwater interception process and capacity of three organs of a specific tree species. Each tree species experienced four simulated rainfall events of varying intensities. To minimize wilting and sunburn of tree organs during in vitro sampling, the sampling and experiments were conducted in late summer and early autumn, when deciduous tree species were not undergoing the process of shedding their leaves. The specific time was from September to November in 2018 and 2019.
For each rainfall experiment, we prepared a sample-package which conclude 100 leaf samples, 90 branch samples, and 30 bark samples from a certain tree species. The sample-package was evenly divided into 10 groups (group1 to group10), with each group containing 10 leaf samples, 9 branch samples, and 3 bark samples.
The rainwater interception process and capacity test experimental procedure involve a series of steps. First, the fresh weight (FW, g) and area(A) of the samples were measured. Secondly, a predetermined rainfall intensity was established, and a sample-package which conclude 10 groups of organ samples was placed in ARSS. Thirdly, the ARSS was activated and remained in operating mode. We extracted one group sample at each rainfall time interval of 5, 10, 20, 30, 50, 70, 90, 120, 150, and 180 minutes, respectively. Then, the weight of organ samples with rainwater (RW, g) was measured as soon as the samples were extracted.
The rainwater interception capacity will increase with the duration of rainfall, however, it's not clear the max capacity of rainfall interception because the value still raises when the experiment ended [3,4,9]. This study introduced an adsorption kinetic equation to address this question. The equation fits the rainwater interception at different rainfall time.
The organ rainwater interception at rainfall time t (It, mm) was calculated as follows:
I t = 10 R W t − F W / A
Where：
It, the rainwater interception of organ at time t (mm), RWt, the organ weight with rainwater at time t (g), FW, the flesh weight of organ sample (g), A, the area of organ surface, t represents the rainfall time (min).
The specific analysis methods are as follows: using Origin 2018 software, the pseudo 1st-order adsorption kinetic equation and the pseudo 2nd-order adsorption kinetic equation are applied to analyze the results of the organ rainwater interception test. The pseudo 1st-order kinetic model assumes that rainwater interception is controlled by diffusion steps, while the pseudo 2nd-order kinetic model assumes that rainwater interception is controlled by a chemical adsorption mechanism. According to the correlation coefficient, the most suitable fitting equation was selected, and the initial rainwater interception rate and maximum rainwater interception of organs were calculated.
The pseudo 1st-order adsorption kinetic equation is as follows:
l n I e − I t = ln ⁡ I e − k 1 t
The pseudo 2nd-order adsorption kinetic equation is as follows：
t I t = 1 k 2 I e 2 + t I e      
Where:
Ie represents the rainfall interception at equilibrium (mm), It represents the rainfall interception at time t (mm), K1 represents the rate constant of the pseudo 1st-order kinetic equation, K2 represents the rate constant of the pseudo 2nd-order kinetic equation, t represents the rainfall time (min).

3. Results

3.1. Dynamic analysis of rainwater interception process of tree organs

The fitting lines of the pseudo 1st-order adsorption kinetic equation and the pseudo 2nd-order adsorption kinetic equation for organ rainwater interception are shown in Figure 5, Figure 6 and Figure 7. The fitting lines of the pseudo 2nd-order adsorption kinetic equation are more consistent with the process of rainwater interception. In the first 50 minutes, the interception of rainwater increased rapidly, after that, the rate of increase gradually slowed down and eventually reached a state of equilibrium.

3.2. Analysis of dynamic parameters of rainwater interception by tree organs.

To analyze the variation in rainwater interception among different types of leaves over time, we calculated the average values for four simulated rainfall events based on 10-time intervals. Each average value was based on 40 leaves, 36 branches, and 12 bark samples. The curve fitting of rainwater interception and time of leaves was carried out using pseudo 1st-order and pseudo 2nd-order dynamic equations. The results are shown in Table 3, Table 4 and Table 5.
The fitting results indicate that the pseudo 2nd-order kinetic model has a higher correlation coefficient (R2) compared to the pseudo 1st-order kinetic model when fitting the process of organ rainwater interception. This suggests that the process of organ rainwater interception and adsorption aligns better with the pseudo 2nd-order kinetic equation, indicating that the adsorption process is similar to chemical adsorption [43].

3.3. Rainwater interception in different tree organs

In this section, we analyzed the differences in average organ rainwater interception values among ten trees that were tested. The aim was to characterize the variations in rainwater interception capacity among different organs of common trees in urban areas, as well as to compare and analyze the differences in rainwater interception among the ten tree species.
According to the calculation results of the pseudo 2nd-order adsorption kinetic equation (Table 3, Table 4 and Table 5), the rainwater interception capacity of leaves from ten urban trees ranged from 0.05 mm to 0.34 mm. The Deodar cedar leaves exhibited the highest rainwater interception capacity, whereas the London planetree leaves showed the lowest capacity. The rainwater interception capacity of two coniferous trees was greater than that of broad-leaved trees. The rainwater interception capacity of 10 urban tree branches ranged from 0.13 mm to 0.24 mm. The branches of the Deodar cedar had the highest rainwater interception capacity, while the branches of the Japanese blueberry tree had the lowest rainwater interception capacity. The rainwater interception capacity of two coniferous tree branches was higher than that of broad-leaved tree branches. The rainwater interception capacity of ten urban tree barks ranges from 0.29 mm to 1.22 mm. The Camphor tree bark exhibits the highest rainwater interception capacity, whereas the Glossy privet bark has the lowest capacity.
The mean rainwater interception values in different organs of the ten tested trees were significantly different (P < 0.01). Additionally, there were significant differences between the bark and leaf, as well as between the bark and branch (P < 0.05). The rainwater interception in bark was significantly greater than that in leaf and branch, but there was no significant difference between leaf and branch. Specific to each tree species, the results of variance analysis of rainwater interception in different organs (Figure 8) showed that for Deodar cedar, the order of rainwater interception in organs was bark > leaf > branch. For the other nine tree species, the rule of rainwater interception was bark > branch > leaf. Duncan's multiple comparison results showed that there were two types of differences in rainwater interception among the ten tree organs. One finding was that there was no significant difference in rainwater interception between leaves and branches, but there were significant differences between them and bark (P < 0.05). This was observed in various tree species, including Golden rain Tree, Japanese blueberry tree, and Deodar cedar. The other reason was that there were significant differences in rainwater interception among leaves, branches, and bark (P < 0.05), including London planetree, Japanese zelkova, Camphor tree, Glossy privet, Fragrant tea olive, and Dawn redwood.
The results of the variance analysis (Figure 8) showed that the order of leaf rainwater interception capacity was coniferous > evergreen broad-leaved > deciduous broad-leaved. The rainwater interception capacity of coniferous trees was significantly higher than that of deciduous broad-leaved and evergreen broad-leaved trees (P < 0.05). However, there was no significant difference between deciduous broad-leaved and evergreen broad-leaved trees (P > 0.05). The order of rainwater interception capacity was coniferous > deciduous broad-leaved > evergreen broad-leaved. The rainwater interception capacity of coniferous trees was significantly higher than that of deciduous broad-leaved and evergreen broad-leaved trees (P < 0.05). However, there was no significant difference between the rainwater interception capacity of deciduous broad-leaved and evergreen broad-leaved trees (P > 0.05). The order of bark rainwater interception capacity was coniferous > deciduous broad-leaved > evergreen broad-leaved. The rainwater interception capacity of coniferous branches was significantly higher than that of deciduous broad-leaved and evergreen broad-leaved trees (P < 0.05). There was no significant difference in bark rainwater interception capacity among the three life forms.

4. Discussion

The capacity of tree organs to intercept rainwater is a result of the long-term evolutionary process, which is influenced by rainfall characteristics and the tree's living environment. This capacity reflects how effectively tree organs utilize rainwater and emphasizes the role of trees in the water cycle.

4.1. Differences in rainwater interception capacity among tree species' organs

In this study, significant variations were observed in the rainwater interception capacity of organs among the different tree species that were tested. The rainwater interception capacity of leaves from 10 tree species ranged from 0.05 mm (London planetree) to 0.34 mm (Deodar cedar). The rainwater interception of branches ranged from 0.13 mm (Japanese blueberry tree) to 0.24 mm (Deodar cedar). The rainwater interception capacity of bark ranged from 0.29 mm (Glossy privet) to 1.22 mm (Camphor tree). This is similar to the findings of previous studies on the rainwater interception capacity of leaves and branches in different tree species, such as slash pine (Taxodium ascendens), blue fruit tree [2], Pinus densiflora [1], and Eucalyptus [4,9]. There are three reasons for the variation in rainwater interception capacity among different trees. Firstly, the surface characteristics of organs in different tree species can cause differences in rainwater interception capacity [2,5,15]. Secondly, the use of different measurement methods can also lead to discrepancies. Some studies have shown that the amount of rainwater interception capacity, as measured by artificial simulated rainfall, is higher than that measured by the immersion method [8,16,18,19,20]. Additionally, different intensities of artificially simulated rainfall can also yield varying measurement results [24,44,45].

4.2. Differences in rainwater interception capacity among different tree organs

In this study, the results of rainwater interception of different organs of 10 trees were as follows: the average rainwater interception of leaves was 0.12mm (± 0.08), the average rainwater interception of branches was 0.18 mm (± 0.05), and the average rainwater interception of bark was 0.64 mm (± 0.33). The rainwater interception ability of leaves, branches and bark was as follows: bark > branches > leaves. There was no significant difference in rainwater interception between leaves and branches. However, there were significant differences between bark and leaves (P < 0.05), as well as between bark and branches (P < 0.05). Additionally, the rainwater interception of bark was significantly greater than that of leaves and branches, which is consistent with previous research findings. In the studies of Liu [2], Herwitz [9], Aston [4], Llorens [1], the rainwater interception of leaves ranged from 0.01 mm to 0.10 mm and in the studies of Liu [2], Llorens [1], the rainwater interception of branches and bark ranged from 0.48 mm to 1.26 mm. These results showed that the rainwater interception of rainwater in branches and bark was higher than that in leaves [46,47], because the rainwater interception of rainwater in branches and bark was higher than that in leaves [1,2] in unit area and in crown surface area [9]. In this study, there are two rules of rainwater interception of different organs of specific tree species: one is that there is no significant difference in rainwater interception between leaves and branches, and there are significant differences between leaves and bark, and between branches and bark (P < 0.05), and the rainwater interception of bark is significantly greater than that of leaves and branches, including Golden rain tree, Japanese blueberry tree, Southern magnolia, Deodar cedar; the other is rainwater interception The order of rainwater interception was bark > Branch > leaf, including Platanus acerifolia, Zelkova, Deodar cedar, Glossy privet, Fragrant tea olive and Dawn redwood. The latter law is similar to the existing research. Herwitz [9] conducted research on mature Eucalyptus in similar areas. The results showed that the rainwater interception capacity of branches was significantly greater than that of leaves. The research on coniferous trees also showed that the rainwater interception capacity of branches and bark was significantly greater than that of leaves [1,2].

4.3. Difference of rainwater interception capacity of different life form tree species

Among the ten tree species tested in this study, the order of rainwater interception by leaves, branches, and bark was coniferous trees > broad-leaved trees. There was a significant difference in the rainwater interception of leaves among tree species of different life forms [1,2,12,13,14]. This finding is consistent with previous studies, which showed that coniferous tree species have a higher ability to intercept rainwater compared to broad-leaved tree species. However, there was no significant difference in rainwater interception between broad-leaved forests and coniferous forests [1,2,3,9,10,11]. The reasons why coniferous leaves have a stronger rainwater interception ability compared to broad-leaved trees are as follows: Firstly, coniferous leaves have been found to have a stronger rainwater interception ability [3,4,16]. Secondly, the growth structure of coniferous leaves is mostly clustered, which leads to raindrops being trapped between two or more coniferous needles [1], thereby increasing their rainwater interception capacity.

4.4. Differences in rainwater interception capacity of tree organs between urban and natural areas

In this study, the interception of rainwater by the leaves of broad-leaved trees ranged from 0.05 mm to 0.12 mm, which is consistent with the findings of Aston [4] and Herwitz [9] who studied the rainwater interception of tropical broad-leaved trees (0.01 mm - 0.18 mm). In this study, the leaf rainwater interception of coniferous tree species ranged from 0.15 mm to 0.36 mm. The results of previous studies on leaf rainwater interception of various coniferous tree species, including Pinus elliottii [2], Taxodium ascendens [2], Pinus densiflora [1], Pinus armandii [12], Pinus coastal [13], and Picea rigida [14], showed that the range of leaf rainwater interception was from 0.10 mm to 0.16 mm.
According to the research findings on selected tree species, urban common coniferous trees have a higher rainwater interception capacity compared to natural coniferous trees. This finding aligns with previous research that shows urban tree species have a higher overall rainwater interception rate compared to natural areas [48,49,50]. According to the results of this experiment and existing research, we can explain the differences in rainwater interception capacity and natural area of urban tree organs in this study from two aspects. One aspect is the difference in morphological structure of tree organs. In response to changes in urban air quality and rainfall patterns, as well as the impact of artificial pruning, urban trees undergo various changes in plant physiology, morphological structure, and even surface structure of their organs. These changes result in alterations in their capacity to intercept rainwater. Another factor is the variability in rainfall conditions, which varies across different studies. In this study, the rainfall intensity is simulated to mimic urban rainfall characteristics. However, in studies on rainwater interception by trees in natural environments, due to experimental limitations and varying objectives, most studies use a higher rainfall intensity. Nonetheless, there are only slight differences in the results. The findings indicate that increasing or decreasing rainfall intensity to a certain extent can affect the rainwater interception by trees. This is one of the reasons why the rainwater interception in this experiment differs from that in natural areas.

5. Conclusions

This study demonstrates significant variations in the rainwater interception capabilities among different tree species. It reveals that bark exhibits the highest rainwater interception ability, while there is no significant difference in rainwater interception ability between branches and leaves. Coniferous tree species have a greater ability to intercept rainwater than broad-leaved tree species. There are also differences in the rainwater interception ability of trees in urban and natural areas, which may be attributed to variations in the physiological and morphological characteristics of trees.
To gain a deeper understanding of the mechanisms and functions of tree rainwater interception, future research should focus on the rainwater interception strategies employed by various tree species in different habitats. Additionally, it is important to examine the internal and external factors that influence rainwater interception.

Author Contributions

Conceptualization, B. W., and J. G.; methodology, J. G.; validation, Y. Z.; formal analysis, Y. Z..; investigation, J. G.; data curation, J. G.; writing—original draft preparation, B. W. and J. G.; writing—review and editing, J. G.; visualization, Y. Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Shanghai Engineering Research Center of Urban Trees Ecological Application, grant number 17DZ2252000; 2023 Shanghai Botanical Garden Youth Project, grant number ZWQ202304.

Data Availability Statement

Data available on request from the authors.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Llorens, P.; Gallart, F. A simplified method for forest water storage capacity measurement. J Hydrol 2000, 240, 131–144. [Google Scholar] [CrossRef]
  2. Liu, S. Estimation of rainfall storage capacity in the canopies of cypress wetlands and slash pine uplands in North-Central Florida. J Hydrol 1998, 207, 32–41. [Google Scholar] [CrossRef]
  3. Crockford, R.; Richardson, D. Partitioning of rainfall in a Eucalypt forest and Pine plantation in southeastern Australia: III Determination of the canopy storage capacity of a dry sclerophyll Eucalypt forest. Hydrol. Processes 1990, 4, 157–167. [Google Scholar] [CrossRef]
  4. Aston, A. Rainfall interception by eight small trees. J Hydrol 1979, 42, 383–396. [Google Scholar] [CrossRef]
  5. Li, X.; Xiao, Q.; Niu, J.; Dymond, S.; van Doorn, N.S.; Yu, X.; Xie, B.; Lv, X.; Zhang, K.; Li, J. Process-based rainfall interception by small trees in Northern China: the effect of rainfall traits and crown structure characteristics. Agric For Meteorol 2016, 218, 65–73. [Google Scholar] [CrossRef]
  6. Calder, I.R. Rainfall interception and drop size-development and calibration of the two-layer stochastic interception model. Tree Physiol 1996, 16, 727–732. [Google Scholar] [CrossRef]
  7. Wang, J. Redistribution of rainfall and chemical characteristics of rainfall components in evergreen broad-leaved forest in Tiantong. Doctoral thesis, East China Normal University, Shanghai, 2008. [CrossRef]
  8. Yu, K.; Chen, N.; Yu, S.; Wang, G. Effects of species composition on rainfall interception capacity of alpine meadow vegetation. Acta Ecol. Sin. 2011, 31, 5771–5779. [Google Scholar]
  9. Herwitz, S.R. Interception storage capacities of tropical rainforest canopy trees. J Hydrol 1985, 77, 237–252. [Google Scholar] [CrossRef]
  10. Leyton, L.; Reynolds, E. R. C; Thompson, F. B. Rainfall interception in forest and moorland. In Proceedings of the International Symposium on Forest Hydrology, New York, 1967, 163-178.
  11. Hutchings, N.J.; Milne, R.; Crowther, J.M. Canopy storage capacity and its vertical distribution in a Sitka spruce canopy. J Hydrol 1988, 104, 161–171. [Google Scholar] [CrossRef]
  12. Kelliher, F.M.; Whitehead, D.; Pollock, D.S. Rainfall interception by trees and slash in a young Pinus radiata D. Don stand. J Hydrol 1992, 131, 187–204. [Google Scholar] [CrossRef]
  13. Lankreijer, H.; Hendriks, M.; Klaassen, W. A comparison of models simulating rainfall interception of forests. Agric For Meteorol 1993, 64, 187–199. [Google Scholar] [CrossRef]
  14. Teklehaimanot, Z.; Jarvis, P.; Ledger, D. Rainfall interception and boundary layer conductance in relation to tree spacing. J Hydrol 1991, 123, 261–278. [Google Scholar] [CrossRef]
  15. Wang, X.P.; Zhang, Y.F.; Hu, R.; Pan, Y.X.; Berndtsson, R. Canopy storage capacity of xerophytic shrubs in Northwestern China. J Hydrol 2012, 454, 152–159. [Google Scholar] [CrossRef]
  16. Monson, R.K.; Grant, M.C.; Jaeger, C.H.; Schoettle, A.W. Morphological causes for the retention of precipitation in the crowns of alpine plants. Environ Exp Bot. 1992, 32, 319–327. [Google Scholar] [CrossRef]
  17. Ilek, A.; Kucza, J.; Morkisz, K. Hydrological properties of bark of selected forest tree species. Part 2: Interspecific variability of bark water storage capacity Folia For. Pol., Ser. A 2017, 59, 110–122. [Google Scholar] [CrossRef]
  18. Garcia-Estringana, P.; Alonso-Blázquez, N.; Alegre, J. Water storage capacity, stemflow and water funneling in Mediterranean shrubs. J Hydrol 2010, 389, 363–372. [Google Scholar] [CrossRef]
  19. Keim, R.F.; Skaugset, A.E.; Weiler, M. Storage of water on vegetation under simulated rainfall of varying intensity. Adv Water Resour 2006, 29, 974–986. [Google Scholar] [CrossRef]
  20. Wohlfahrt, G.; Bianchi, K.; Cernusca, A. Leaf and stem maximum water storage capacity of herbaceous plants in a mountain meadow. J Hydrol 2006, 319, 383–390. [Google Scholar] [CrossRef]
  21. Beysens, D.; Steyer, A.; Guenoun, P.; Fritter, D.; Knobler, C. How does dew form? Phase Transit. 1991, 31, 219–246. [Google Scholar] [CrossRef]
  22. Dunkerley, D.L.; Booth, T.L. Plant canopy interception of rainfall and its significance in a banded landscape, arid western New South Wales, Australia. Water Resour Res. 1999, 35, 1581–1586. [Google Scholar] [CrossRef]
  23. Li, X.; Niu, J.; Zhang, L.; Xiao, Q.; McPherson, G.E.; Van Doorn, N.; Yu, X.; Xie, B.; Dymond, S.; Li, J. A study on crown interception with four dominant tree species: a direct measurement. Hydrol. Res. 2015, 47, 857–868. [Google Scholar] [CrossRef]
  24. Peng, H.; Zhao, C.; Feng, Z.; Xu, Z.; Wang, C.; Zhao, Y. Canopy interception by a spruce forest in the upper reach of Heihe River basin. Northwestern China. Hydro. Processes 2014, 28, 1734–1741. [Google Scholar] [CrossRef]
  25. Koch, K.; Bhushan, B.; Barthlott, W. Multifunctional surface structures of plants: an inspiration for biomimetics. Prog. Mater. Sci. 2009, 54, 137–178. [Google Scholar] [CrossRef]
  26. Fogg, G. Adhesion of water to the external surfaces of leaves. Discuss Faraday Soc. 1948, 3, 162–166. [Google Scholar] [CrossRef]
  27. Challen, S. The retention of aqueous suspensions on leaf surfaces. J Pharm Pharmacol. 1962, 14, 707–714. [Google Scholar] [CrossRef] [PubMed]
  28. Fang, H. Status and comprehensive evaluation of urban green space plant communities in Shanghai. Master's thesis, East China Normal University, Shanghai, 2006.
  29. Wang, B. Urban vegetation and urban vegetation. Acta Sci. Nat. Univ. Sunyatseni 1998, 4, 9–12. [Google Scholar]
  30. Shi Y.; Jin H.; Bao Z.; Ge Y. Tree structure characteristics of urban built-up area of China. Chin. Lands. Archit. 2016, 32:77-82.
  31. Liu, S. A new model for the prediction of rainfall interception in forest canopies. Ecol. Modell. 1997, 99, 151–159. [Google Scholar] [CrossRef]
  32. Ning J.; Li T. Statistics of rainfall characteristics and calculation of rainwater storage tank volume in Shanghai. China Water Wastewater 2006, 22:48-51. [CrossRef]
  33. Gao, J.; Qi, L. Characteristics and influence of short duration heavy rainfall in Shanghai. Meteorol. Environ. Res. 2015, 28, 52–60. [Google Scholar] [CrossRef]
  34. Huo, Y.; Bi, H.; Zhu, Y.; Xu, H.; Wang, X.; Chang Y., F. Experiment on rainfall characteristics of QYJY-503C artificial rainfall simulator [J]. Bull. Soil Water Conserv. 2015, 13, 31–36. [Google Scholar] [CrossRef]
  35. Xiao, Q.; McPherson, E.G. Surface water storage capacity of twenty tree species in Davis, California. J. Environ. Qual. 2016, 45, 188–198. [Google Scholar] [CrossRef]
  36. Li, J.; Tang, Y.; Li, B. The influence of indoor simulated rainfall intensity on the stability of gravel soil slope. Gansu Water Res. Hydropower Technol 2013, 49, 21–23. [Google Scholar]
  37. Xia, D.; Zhang, X.; Fang, Y.; Jia, S. Rainfall intensity ratio control based on rainfall spray control system. Lab Res. Explor 2010, 29, 4–7. [Google Scholar] [CrossRef]
  38. Geng X.; Zheng F.; Liu L. Effect of rainfall intensity and slope gradient on soil erosion process on purple soil hill slopes. J. Sediment Res. 2010, 6:48-53.
  39. Meyer, L.D.; Harmon, W.C. Multiple-Intensity Rainfall Simulator for Erosion Research on Row Sideslopes. Trans Asae 1979, 22, 0100–0103. [Google Scholar] [CrossRef]
  40. Pei, T.; Zheng, Y.; Simulation and model of canopy rainfall distribution process I. models of throughfall, trunk runoff and Canopy Interception under constant rainfall intensity. For. Sci. (Beijing, China) 1996, 32, 1–10. [Google Scholar]
  41. Liu Y.; Peng H.; Meng W.; Bie Q.; Wang Y. Zhao C. Artificial rainfall interception characteristics in alpine meadows under different grazing scenarios in the upper reach of Heihe River. J. Lanzhou Univ., Nat. Sci. 2013:10-12.
  42. Müller, C.; Riederer, M. Plant surface properties in chemical ecology. J Chem Ecol. 2005, 31, 2621–2651. [Google Scholar] [CrossRef]
  43. Wan, D.; Liu, H.; Zhao, X.; Qu, J.; Xiao, S.; Hou, Y. Role of the Mg/Al atomic ratio in hydrotalcite-supported Pd/Sn catalysts for nitrate adsorption and hydrogenation reduction. J Colloid Interface Sci. 2009, 332, 151–157. [Google Scholar] [CrossRef]
  44. Klaassen, W.; Bosveld, F.; De Water, E. Water storage and evaporation as constituents of rainfall interception. J Hydrol 1998, 212-213, 36-50. [CrossRef]
  45. Bassette, C.; Bussiere, F. Partitioning of splash and storage during raindrop impacts on banana leaves. Agric For Meteorol. 2008, 148, 991–1004. [Google Scholar] [CrossRef]
  46. Hancock, N.H.; Crowther, J.M. A technique for the direct measurement of water storage on a forest canopy. J Hydrol 1979, 41, 105–122. [Google Scholar] [CrossRef]
  47. Wang Zhijie. Studies on the Rainfall Features inside the Coastal Protection Forest of Casuarina equisetifolia. Fujian For Sci Technol 2000, 4, 10–13. [Google Scholar] [CrossRef]
  48. Livesley, S.J.; Baudinette, B.; Glover, D. Rainfall interception and stem flow by eucalypt street trees – The impacts of canopy density and bark type. Urban For Urban Green 2014, 13, 192–197. [Google Scholar] [CrossRef]
  49. Crockford, R.; Richardson, D. Partitioning of rainfall in a eucalypt forest and pine plantation in southeastern Australia: IV The relationship of interception and canopy storage capacity, the interception of these forests, and the effect on interception of thinning the pine plantation. Hydrol. Processes 1990, 4, 169–188. [Google Scholar] [CrossRef]
Preprints 86044 g001
Figure 1. The location of study area. SJTU, Shanghai Jiao Tong University.
Figure 1. The location of study area. SJTU, Shanghai Jiao Tong University.
Preprints 86044 g001
Preprints 86044 g002
Figure 2. Collection position of leaves.
Figure 2. Collection position of leaves.
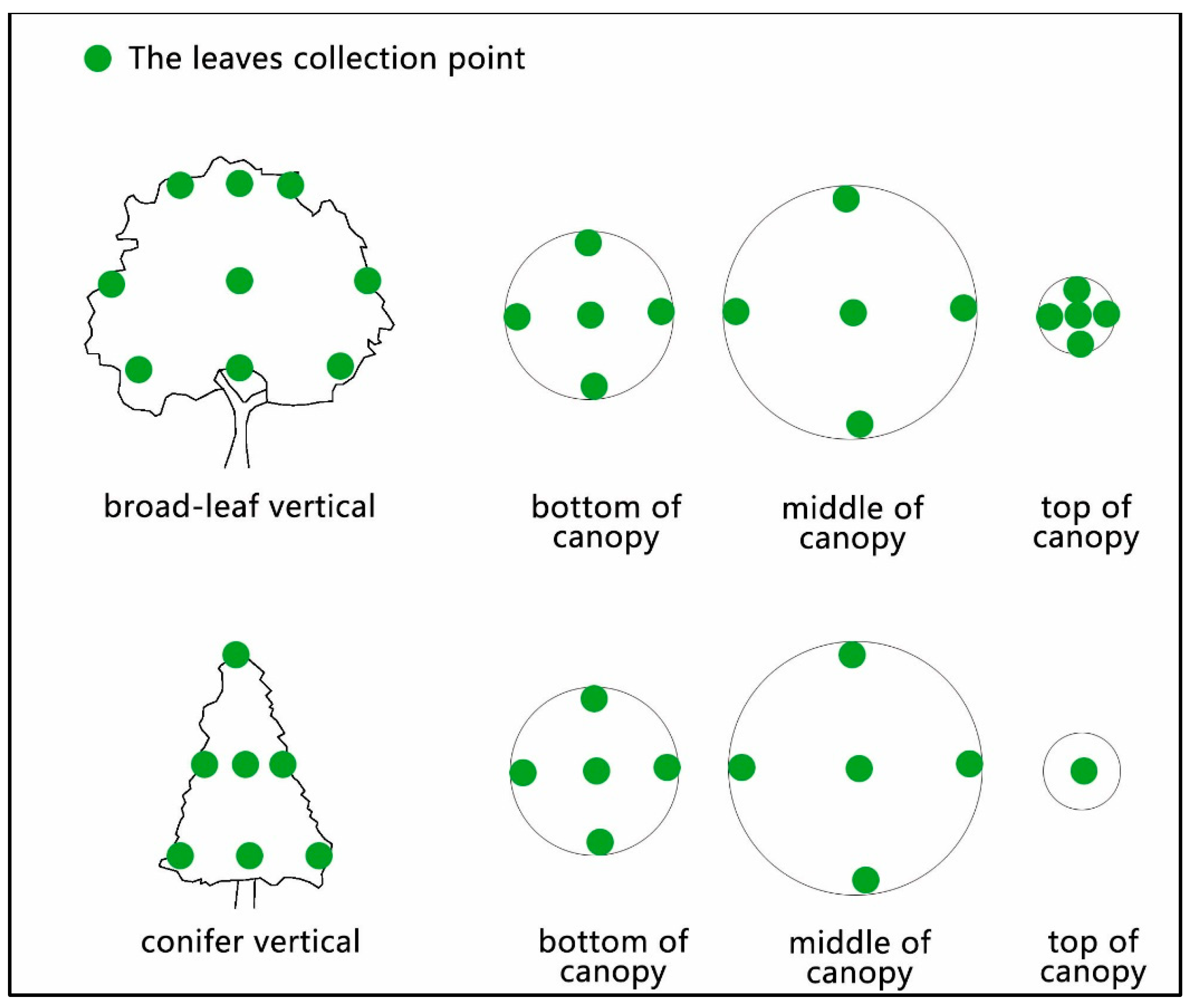
Preprints 86044 g002
Preprints 86044 g003
Figure 3. Organ samples.
Figure 3. Organ samples.
Preprints 86044 g003
Preprints 86044 g004
Figure 4. Artificial rainfall simulation system (ARSS). Note: 1. Water pipe, φ = 15mm; 2. Variable frequency water pump, power 900W; 3. Suction pipe, φ = 25mm; 4. Water tank, volume = 500L; 5. Outlet nozzle; 6. Outer frame of simulated rainfall, 6m * 4m * 10m.
Figure 4. Artificial rainfall simulation system (ARSS). Note: 1. Water pipe, φ = 15mm; 2. Variable frequency water pump, power 900W; 3. Suction pipe, φ = 25mm; 4. Water tank, volume = 500L; 5. Outlet nozzle; 6. Outer frame of simulated rainfall, 6m * 4m * 10m.
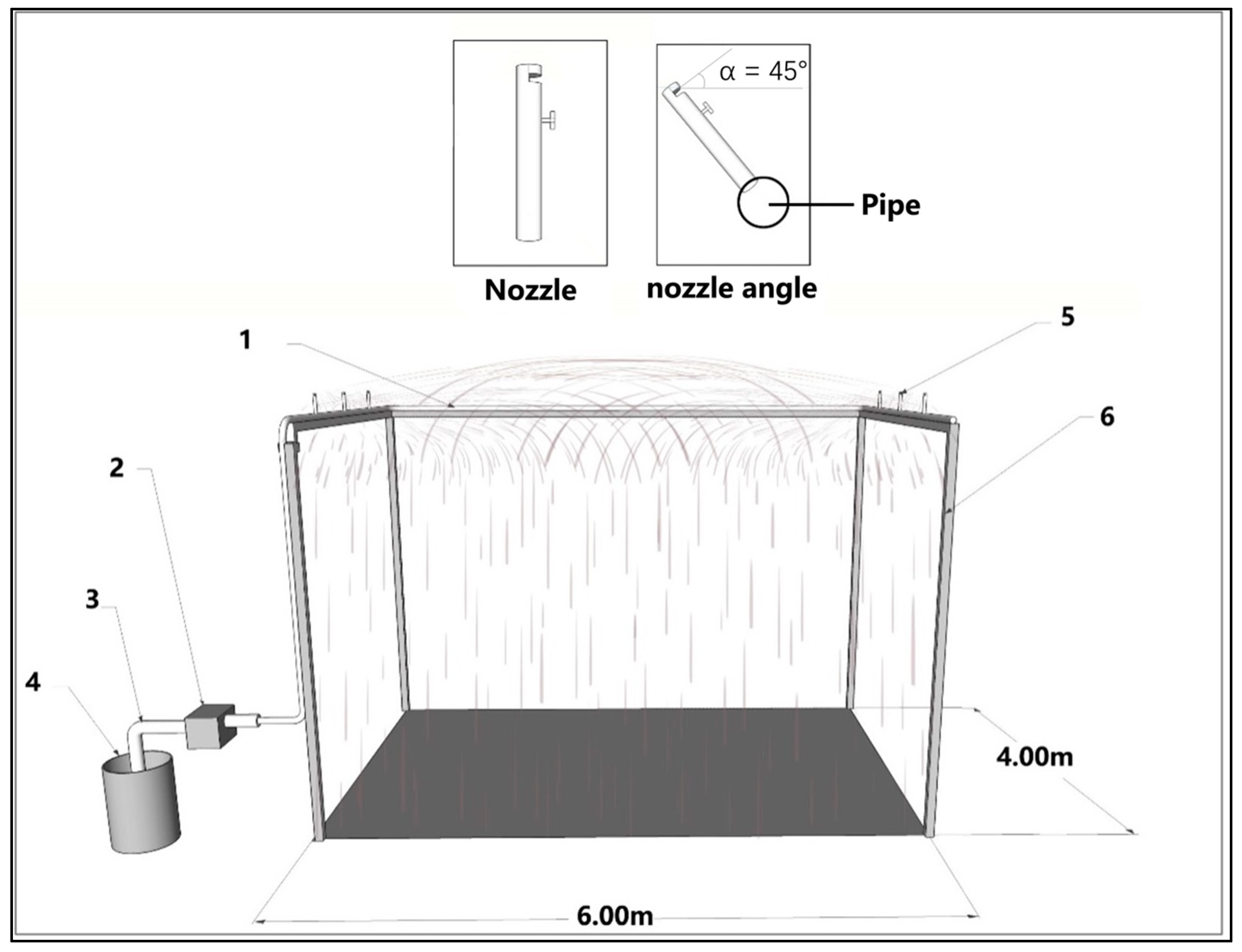
Preprints 86044 g004
Preprints 86044 g005
Figure 5. Leaf rainwater interception process fitting. Note: I, Rainwater interception (mm); 1st-order, The pseudo 1st-order adsorption kinetic equation; 2nd-order, The pseudo 2nd-order adsorption kinetic equation; KOP, Golden Rain Tree; PCA, London Planetree; ZES, Japanese zelkova; CIC, Camphor Tree; ELD, Japanese blueberry tree; MAG, Southern magnolia; OSF, Fragrant tea olive; CED, Deodar cedar; MEG, Dawn redwood.
Figure 5. Leaf rainwater interception process fitting. Note: I, Rainwater interception (mm); 1st-order, The pseudo 1st-order adsorption kinetic equation; 2nd-order, The pseudo 2nd-order adsorption kinetic equation; KOP, Golden Rain Tree; PCA, London Planetree; ZES, Japanese zelkova; CIC, Camphor Tree; ELD, Japanese blueberry tree; MAG, Southern magnolia; OSF, Fragrant tea olive; CED, Deodar cedar; MEG, Dawn redwood.
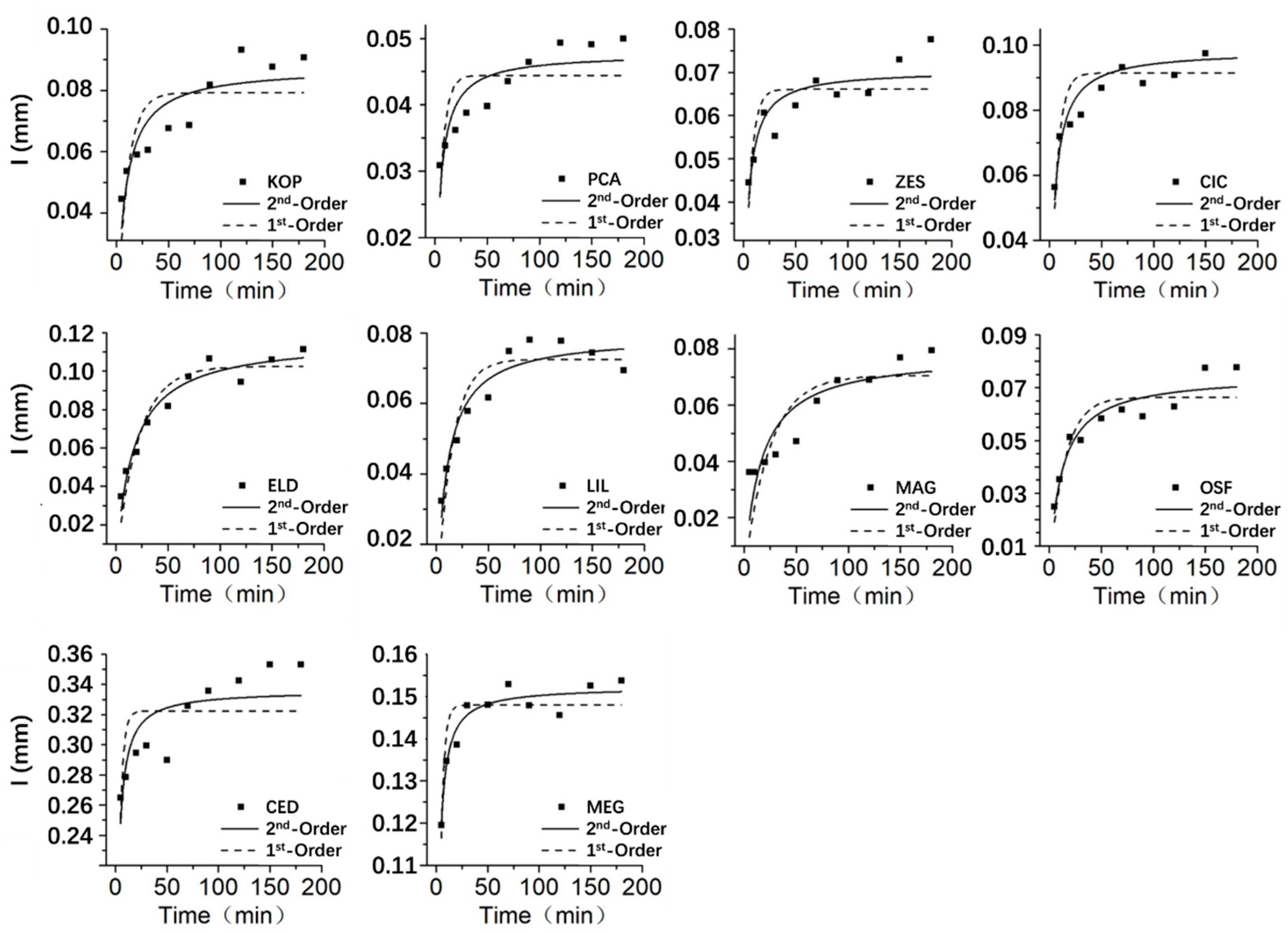
Preprints 86044 g005
Preprints 86044 g006
Figure 6. Branch rainwater interception process fitting.
Figure 6. Branch rainwater interception process fitting.
Preprints 86044 g006
Preprints 86044 g007
Figure 7. Bark rainwater interception process fitting.
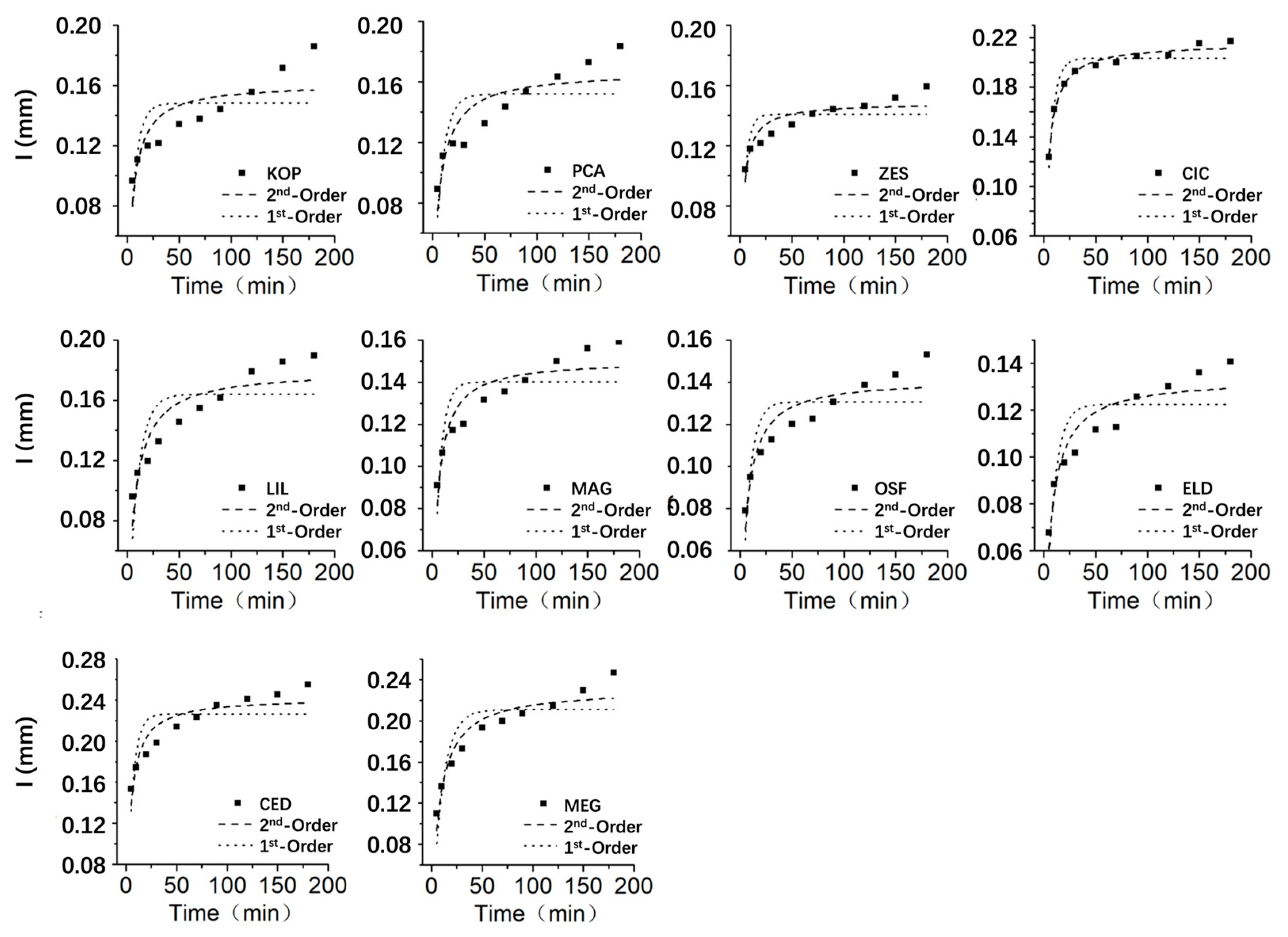
Figure 7. Bark rainwater interception process fitting.
Preprints 86044 g007
Table 1. Species selected.
Table 1. Species selected.
Common name Scientific name Life form Species code
Golden Rain Tree Koelreuteria paniculata Deciduous broad KOP
London Planetree Platanus × acerifolia Deciduous broad PCA
Japanese zelkova Zelkova serrata Deciduous broad ZES
Camphor Tree Cinnamomum camphora Evergreen broad CIC
Japanese blueberry tree Elaeocarpus decipiens Evergreen broad ELD
Glossy privet Ligustrum lucidum Evergreen broad LIL
Southern magnolia Magnolia Grandiflora Evergreen broad MAG
Fragrant tea olive Osmanthus fragrans Evergreen broad OSF
Deodar cedar Cedrus deodara Coniferous CED
Dawn redwood Metasequoia glyptostroboides Coniferous MEG
Table 2. Simulate rainfall information.
Table 2. Simulate rainfall information.
No. Tree Set rainfall
Intensity
(mm/h)		 Average actual
rainfall Intensity
(mm/h)		 Rainfall uniformity
(%)		 Rainfall
Time
(min)
1 Golden Rain Tree 4 4.32 90.4 180
2 8 8.13 91.2 180
3 12 11.68 92.1 180
4 16 16.53 91.7 180
5 London Planetree 4 4.42 90.4 180
6 8 8.31 91.2 180
7 12 11.18 92.1 180
8 16 15.79 91.5 180
9 Japanese zelkova 4 3.48 90.2 180
10 8 8.51 91.2 180
11 12 12.38 92.1 180
12 16 16.57 91.9 180
13 Camphor Tree 4 4.51 90.4 180
14 8 8.23 91.2 180
15 12 11.68 92.1 180
16 16 15.33 91.1 180
17 Japanese blueberry tree 4 4.46 90.4 180
18 8 8.04 91.2 180
19 12 11.81 92.1 180
20 16 15.73 91.4 180
21 Glossy privet 4 4.25 90.4 180
22 8 8.48 91.2 180
23 12 11.82 92.1 180
24 16 16.44 91.6 180
25 Southern magnolia 4 4.28 90.4 180
26 8 8.17 91.2 180
27 12 12.82 92.1 180
28 16 16.71 94.4 180
29 Fragrant tea olive 4 4.24 91.2 180
30 8 8.48 92.1 180
31 12 11.67 90.4 180
32 16 16.48 91.2 180
33 Deodar cedar 4 3.79 91.2 180
34 8 8.11 92.1 180
35 12 13.01 90.4 180
36 16 16.17 91.2 180
37 Dawn redwood 4 4.52 92.1 180
38 8 8.14 90.4 180
39 12 12.84 91.2 180
40 16 16.79 92.3 180
Table 3. Leaf rainwater interception adsorption kinetic fitting parameters of different tree species.
Table 3. Leaf rainwater interception adsorption kinetic fitting parameters of different tree species.
Tree Pseudo 1s-order Pseudo 2nd-order
Ie (mm) k1 R2 Ie (mm) k2 R2
Golden Rain Tree 0.08 0.10 0.50 0.09 0.015 0.74
London Planetree 0.04 0.18 0.44 0.05 0.053 0.76
Japanese zelkova 0.07 0.18 0.53 0.07 0.038 0.76
Camphor Tree 0.09 0.16 0.56 0.10 0.023 0.77
Japanese blueberry tree 0.10 0.05 0.89 0.12 0.005 0.95
Glossy privet 0.07 0.07 0.83 0.08 0.013 0.91
Southern magnolia 0.07 0.04 0.54 0.08 0.008 0.71
Fragrant tea olive 0.07 0.07 0.79 0.07 0.011 0.89
Deodar cedar 0.32 0.30 0.30 0.34 0.017 0.74
Dawn redwood 0.15 0.31 0.75 0.15 0.048 0.92
Table 4. Branch rainwater interception adsorption kinetic fitting parameters of different tree species.
Table 4. Branch rainwater interception adsorption kinetic fitting parameters of different tree species.
Tree Pseudo 1st-order Pseudo 2nd-order
Ie (mm) k1 R2 Ie (mm) k2 R2
Golden Rain Tree 0.15 0.15 0.38 0.16 0.012 0.66
London Planetree 0.15 0.13 0.49 0.17 0.010 0.75
Japanese zelkova 0.14 0.23 0.49 0.15 0.025 0.80
Camphor Tree 0.20 0.17 0.89 0.22 0.013 0.98
Japanese blueberry tree 0.12 0.12 0.66 0.13 0.012 0.87
Glossy privet 0.16 0.11 0.54 0.18 0.008 0.80
Southern magnolia 0.14 0.16 0.57 0.15 0.016 0.84
Fragrant tea olive 0.13 0.14 0.61 0.14 0.014 0.84
Deodar cedar 0.23 0.17 0.55 0.24 0.011 0.84
Dawn redwood 0.21 0.10 0.72 0.23 0.006 0.90
Table 5. Bark rainwater interception adsorption kinetic fitting parameters of different tree species.
Table 5. Bark rainwater interception adsorption kinetic fitting parameters of different tree species.
Tree Pseudo 1st-order Pseudo 2nd-order
Ie (mm) k1 R2 Ie (mm) k2 R2
Golden Rain Tree 0.36 0.08 0.69 0.34 0.003 0.89
London Planetree 0.42 0.06 0.71 0.47 0.002 0.86
Japanese zelkova 1.05 0.10 0.66 1.16 0.001 0.87
Camphor Tree 1.13 0.12 0.88 1.22 0.001 0.94
Japanese blueberry tree 0.41 0.10 0.53 0.45 0.003 0.77
Glossy privet 0.25 0.07 0.77 0.29 0.003 0.89
Southern magnolia 0.35 0.08 0.67 0.44 0.002 0.90
Fragrant tea olive 0.34 0.11 0.64 0.37 0.004 0.86
Deodar cedar 0.82 0.15 0.64 0.88 0.002 0.87
Dawn redwood 0.53 0.17 0.63 0.54 0.004 0.88
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated