Prerpints.org logo
Preprint
Article

Adaptive Learning in Agent-Based Models: An Approach for Analyzing Human Behavior in Pandemic Crowding

Altmetrics

Downloads

162

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Preprints on COVID-19 and SARS-CoV-2

Submitted:

20 September 2023

Posted:

25 September 2023

You are already at the latest version

Alerts
Abstract
This study assesses the impact of incorporating an adaptive learning mechanism into an agent-based model (ABMS) simulating behavior on a university campus during the course of a pandemic outbreak, with a particular case on the COVID-19 pandemic. The aim is to reduce overcrowding and infections on campus through the use of Reinforcement Learning (RL). Our findings indicate that RL is a viable approach for effectively representing agents’ behavior within this context. The results reveal specific temporal patterns of overcrowding violations. While our study successfully mitigated campus crowding, it had limited influence on altering the course of the epidemic. This highlights the necessity for comprehensive epidemic control strategies that consider the role of individual decision-making influenced by adaptive learning, along with the implementation of targeted interventions. This research significantly contributes to our understanding of adaptive learning within complex systems and offers valuable insights for shaping future public health policies in similar community settings. Future research directions encompass exploring various parameter settings and updating representations of the disease’s natural history.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

In healthcare modeling, especially in the context of a pandemic, it has become increasingly evident that understanding how human behavior influences disease transmission is important. Over a span of just a few years, the COVID-19 Pandemic sent the world into an unprecedented health crisis, requiring extensive global efforts to combat its effects. During this period, governments and agencies were compelled to rapidly develop and adapt public health policies to address the challenges posed by the pandemic [1]. The COVID-19 pandemic underscored the importance of modeling and simulating complex systems, particularly those related to human behavior and public health responses.
Traditional modeling methods often encounter challenges in accurately representing how people respond to crises of such magnitude. Recent research has suggested that how people act in social situations plays an important role in how a pandemic develops [2]. For this reason, strengthening physical distancing measures within micro-communities could positively affect epidemic outcomes [3,4]. Therefore, it is critical to identify aspects of social conduct that could significantly influence clustering patterns in crowded places. In addition, social behavior has been successfully reproduced in a simulated environment through adaptive-learning methodologies [5,6,7,8,9].
Agent-based Modeling and Simulation (ABMS) is a powerful tool to study epidemics and other complex systems [10]. Namely, this technique has received considerable attention in the field of social simulation due to its capacity to represent intricate social behavior and even human emotions [6,11]. An agent-based model is essentially a computer program that simulates an artificial world of interacting multi-faceted agents [12].
Reinforcement Learning (RL) offers a good opportunity for this research as it enables agents in the agent-based model to exhibit adaptive behavior in response to evolving conditions during a COVID-19 outbreak within a university campus. This adaptability enhances the realism of the simulation, reflecting the intricacies of human decision-making during a health crisis. RL is an artificial intelligence paradigm comprising mathematical methods to model goal-oriented learning and decision-making [13]. Certainly, RL is different from other schemes as it focuses on agent-based learning, meaning that an idealized agent interacts with its environment and learns from those experiences to achieve a predefined goal.
A central subject in Reinforcement Learning is the exploration-exploitation dilemma [14]. Actually, the RL scheme works as a trial-and-error feedback process, where an action in the current state leads to a new state and reveals a reward, whose value is used to refine future decisions. In that sense, in each step, the agent must decide whether to explore different actions that might provide a good reward or use (exploit) a previous action that resulted in good rewards. This means, the agent is not taught what actions to take; instead, it should be able to determine, by itself, what action derives satisfactory results under a particular circumstance.
Most problems in RL can be mathematically idealized according to the Markov Decision Processes(MDP) framework [15]. Markov Decision Processes (MDP) are a classical formalization of sequential decision-making, where the problem is framed as an extended Markov Chain [16]. The steps involved in a typical RL method framed as an MDP generally include a sequence of discrete time steps. First, the agent performs an action A t derived from the current state S t and reward R t . Then, a scalar reward R t + 1 is received, and the agent moves to state S t + 1 . Based on the last reward, the agent will determine if the previous action A t was good or bad.
Q-learning is a derived Temporal Difference (TD) algorithm that is able to find an optimal policy for a learning problem framed as an MDP [13]. The optimality condition is assured if infinite exploration time and a partially random initial policy are given. Q-learning can estimate each state’s values without demanding a model of the environment. Hence making it especially useful for agent-based models where the emergent patterns command system behavior. Oppositely to TD, Q-learning estimates the state-action values Q ( S t , A t ) , which represent how good is to perform action A t in the state S t . Particularly, these approximations are meant to converge to q * ( S t , A t ) .
Algorithm 1: Q-learning for estimating an optimal policy π * [13]
Preprints 85705 i001
Equation 1 describes Q-learning’s update rule. Algorithm 1 describes the solution of the Q-learning scheme. All state-action value pairs are initialized with a random value in a range matching the reward signal. Then, the learning procedure is divided into episodes, which are sub-sequences of agent-environment interactions. In this paper, an episode will be conceived as a simulation run. Next, an initial state S and action A are selected for each episode by using an action selection method like ϵ -greedy. An ϵ -greedy selection chooses the best action 1 − ϵ percent of the time and a random one otherwise. Having taken action A, a reward R and new state S ′ are observed. Subsequently, the state-action value Q ( S , A ) is updated with Equation 1 and S is replaced with S ′ . If S is a terminal state, then the episode ends, and a new one is built.
Q S t , A t ← Q S t , A t + α R t + 1 + γ max a Q S t + 1 , a − Q S t , A t
The potential of combining Reinforcement Learning with Agent-Based Modeling and Simulation for modeling human behavior during pandemics, specifically focusing on COVID-19, is evident. Consequently, it is essential to gain insights into the dynamics of COVID-19 and its interplay with individual behavior within semi-enclosed communities like university campuses.

1.1. Natural history of Covid-19

The natural history of a disease is the course an illness takes in an individual from its medical onset until its inevitable conclusion into full recovery or death. It is generally understood as a detailed description of a disease’s development without treatment. Outstandingly, this paper focuses on simulating how a COVID-19 outbreak progresses inside a semi-enclosed community. Notwithstanding, by the time this study was conducted, no official comprehensive natural history had been published detailing each process’s mathematical ingredients. By that means, several epidemiological publications were surveyed on the topic to develop a basic scheme.
Several authors have pointed out that the compartmental SEIR scheme furnishes a satisfactory structure for modeling the disease under study [17,18,19]. Evidence reveals that COVID-19 involves an exposure stage where the individual holds the virus but cannot transmit it to others [20]. Consequently, the examined sickness is abstracted as an infectious disease that can be explained through five independent compartments. In particular, individuals are classified as either Susceptible (S), Exposed (E), Infected (I), Recovered (R), or Dead (D).
Every agent holds an internal mechanism that controls its disease’s stage. At the start of the simulation, most individuals are susceptible, meaning they are vulnerable to COVID-19. Either they have not been exposed to the virus so far or have such a low viral load that is unrepresentative of its condition. Suppose a susceptible subject meets an infected community member within a small radius. In that case, the former is more likely to be exposed. In essence, exposed individuals are agents that contracted the disease but are currently incapable of disseminating it. However, newly exposed individuals will become infectious in a matter of days, according to the distribution of the latency period. Certainly, infected people can either die or survive, as it greatly depends on the patient’s condition. Discernibly, this epidemic system and related agent interactions are assumed to be governed by random processes that can be fitted to probabilistic distributions. The selected COVID-19 natural history is based on the first strain of the SARS-CoV-2 virus presented in Figure 1.
An essential aspect of COVID-19’s natural history is the probability of exposure due to close contact with an infected individual. Remarkably, He et al. [21] suggest that this component may well be modeled as the likelihood of a G a m m a distribution with parameters α , β , and λ described in Equation 2. The proposed approach designates that the exposure progression rate g ( t ) is a function of the time the infected subject has been able to spread the virus. The recommended distribution uses a shift parameter λ because evidence shows that virus carriers can spread the virus up to 2.4 days before symptoms’ onset [21].
g ( t ) ∼ G a m m a ( α = 2.11 , β = 1.3 , λ = − 2.4 )
f ( t ) ∼ L o g n o r m a l ( μ = 1.621 , σ = 0.418 )
Another critical feature in the representation of the epidemic process is the latency period. The latency period is defined as the time interval between an individual getting exposed and later being capable of spreading the virus to others [22]. He et al. [21] indicate that spreadability is proportional to the appearance of the first symptoms. Accordingly, this period can be specified in terms of the incubation period (time between the exposition and symptoms’ onset) by shifting it 2.4 days to the past. In addition, Lauer et al. [23] estimate the distribution of the incubation period as a L o g n o r m a l distribution with parameters μ and σ as depicted in Equation 3.
As previously mentioned, at the time of this study, it was assumed that an infected individual would either die or make a full recovery, with the latter resulting in complete immunity. Additionally, when an agent becomes infected, a random process is employed to classify the agent into a specific patient type. This classification plays a crucial role in determining future outcomes, considering the well-established fact that COVID-19 affects individuals differently. For instance, Ferguson et al. [24] propose a patient classification based on the severity of its symptoms. Following the cited grading, infected agents are categorized according to empirical probability P ( t y p e ) , as shown in Equation 4.
P ( t y p e ) = 0.30 , t y p e = No symptoms 0.55 , t y p e = Moderate symptoms 0.10 , t y p e = Severe symptoms 0.05 , t y p e = Critical symptoms
Once a patient type is assigned, the simulation must determine whether the agent will survive or not and schedule the corresponding event. In fact, Liu et al. [25] state that the severity of symptoms influences mortality. Having that in mind, the authors suggest that death rates are about 15% for patients with severe symptoms and 50% for critical subjects, as shown in Equation 5.
P ( d y i n g | t y p e ) = 0.15 , t y p e = Severe symptoms 0.50 , t y p e = Critical symptoms 0 otherwise
It is assumed that neither death nor recovery follows a constant time duration after infection. Instead, the time until discharge is considered a random variable with positive values. To address this, we conducted a goodness-of-fit test using the Kolmogorov–Smirnov test based on patient records from Xu et al. [26]. The resulting distribution is presented in Equation 6.
d ( t ) ∼ G a m m a ( α = 1.99 , β = 7.77 )
Certainly, understanding the disease dynamics of Covid-19 highlights ABMS potential for modeling disease transmission. ABMS ability to represent social interactions, individual decision-making, and system-level behaviors makes it an excellent tool in epidemic modeling.

1.2. ABMS in epidemic modeling

Mathematical modeling is a fundamental tool for analyzing strategies to control the effects of an epidemic outbreak [27,28,29,30,31]. It offers a formal structure that allows modelers to develop practical solutions to real-world problems. Numerous authors have successfully applied these methods to model outbreaks since the 16th century [32,33,34,35]. The integration of a modeling-based approach for epidemic management has improved general well-being conditions and assisted government agencies in developing effective public health policies [35,36].
Research on epidemiology models has focused on the development of compartment-based models [32,35]. In essence, a compartmental model divides the population into subgroups by fitting the disease to a natural history structure and estimating related parameters from available data [32,37]. Most of these compartment-based models can be solved and analyzed using simple differential equation techniques, and, as a consequence, these have proven to be very useful in real epidemic scenarios [32,38,39,40].
However, these approaches are generally very rough simplifications of an epidemic event with strong assumptions on the internal processes and homogeneous mixing of people. Besides, these studies have commonly ignored individual heterogeneity and multifaceted interactions between individuals. They commonly assume that contacts are static and interactions are not necessarily spatially related. Moreover, there is evidence of a consensus among agent-based modelers about traditional modeling methods lacking the necessary tools to understand such complex systems thoroughly [27,41,42].
Another approach for epidemics modeling focuses on the use of Agent-based modeling and simulation. Many researchers have worked with agent-based models to explain the emergent epidemic behavior of simple interactions within a community [33,43,44,45,46,47,48]. According to Miksch et al. [33], a significant benefit of agent-based epidemic modeling is that it allows exceptional flexibility to design very elaborate epidemic processes. For instance, Perez and Dragicevic [42] implemented a GIS-enabled ABMS to simulate a generic city-wide epidemic incorporating attributes like gender, age, ethnicity, and many others to determine the susceptibility of different community groups. As noted by the authors, traveling individuals are more likely to get exposed, and as a consequence, the infection tends to concentrate in places like schools and universities. Later, Crooks and Hailegiorgis [44] applied ABMS to explore the dynamics of cholera transmission in a refugee camp in Kenya. They modeled factors in family and friendship relationships and goal-oriented agent behavior for determining where to move.
Additionally, Crooks and Hailegiorgis [44] performed a set of experiments to determine the effects of geographical interactions and concluded that geospatial setups truly determine the outcomes of an epidemic. Another example is Weligampola et al.[48], where the authors introduce the Pandemic Disease Simulation (PDSIM) framework, an innovative agent-based model that addresses the impact of the COVID-19 pandemic on diverse communities. PDSIM incorporates attributes like gender, age, ethnicity, and other individual characteristics to assess the susceptibility of different community groups to the COVID-19 pandemic. The framework allows the simulation of disease propagation, the identification of vulnerable groups, and the assessment of containment measures’ effectiveness, offering valuable insights for informed decision-making and the development of resilient and sustainable societies. All these studies support the notion that individual attributes and interactions admittedly affect the course of an epidemic.
A substantial number of studies have applied ABMS to reproduce compartmental-like behavior using the SEIR scheme. The SEIR scheme is an equation-based model that divides the population into susceptibles, exposed, infected, and recovered to model how an infectious disease spreads in a closed community. The interest in modeling diseases with varying viral loads (like Dengue, Zika, and COVID-19) has increased over the last 20 years [31,42,43,44]. Most of these SEIR-based models hold a standard list of personal attributes such as age, gender, health status, and homeplace. Equally important, some of these studies incorporate common patterns such as close-proximity infections [42], fitting probability distributions to several stages of the transmission process [49], individual daily routines such as working and resting [44], transportation networks [50], and geospatial demography [51].
Several recent agent-based studies have specifically focused on modeling the dynamics of the COVID-19 pandemic and assessing control measures. For instance, Al-Shaery et al. [52] developed an agent-based model to investigate the effectiveness of measures like buffers, face masks, and capacity limitations in controlling COVID-19 spread during mass-gathering events. Similarly, Asgary et al. [53] developed an agent-based simulation tool to analyze the spread of COVID-19 in long-term care facilities. The tool uses a contact matrix based on previous research in these facilities and accurately predicts resident deaths within a minimal variation of 0.1. Another example is Dong et al. [54], which introduces an agent-based model designed to address the ongoing COVID-19 pandemic, particularly focusing on Shanghai’s Huangpu District. The model incorporates real-world geographic and population data, along with details of COVID-19 transmission and WHO data. It aims to simulate the virus’s spread and account for factors like population movement, detection, and treatment, as well as the impact of other similar diseases on testing resources. Through validation against official COVID-19 data, the model serves as an epidemiological risk assessment system tailored to China’s COVID-19 characteristics. It offers insights into adjusting intervention strategies and individual health behaviors, ultimately aiding in informed decision-making for effective pandemic prevention and control in China. Additionally, Jahn et al. [55] developed a dynamic agent-based population model to compare different vaccination strategies. They found that to minimize COVID-19-related hospitalizations and deaths, elderly and vulnerable persons should be prioritized for vaccination until further vaccines are available. Sun et al. [56] introduced an agent-based model together with a particle filter approach as a method for studying the evolution of COVID-19. With this model, they introduced a novel method for evaluating the effective reproduction number.
Given the framework of disease spread within university settings, Alvarez Castro and Ford [57] focused on students in Newcastle University accommodation using a geospatial agent-based simulation to demonstrate how measures like face masks, early lockdowns, and self-isolation can significantly reduce infections among students. Both their research and ours use ABMS to investigate the dynamics of COVID-19 transmission within a university campus. Nevertheless, there are differences in their research focuses and principal findings. Their study primarily assesses diverse control measures within the student community at Newcastle University accommodations. Their ABMS approach effectively utilizes spatial data and mathematical epidemiological modeling to replicate disease spread, yielding consistent results with prior studies. Their research highlights the adaptability of their ABMS for regions with accessible geospatial data, offering valuable insights into high-risk locations for effective strategies. In contrast, our research emphasizes integrating adaptive learning, specifically Reinforcement Learning, to model and influence agents’ behavior during a pandemic, focusing on university campuses. While our study successfully reduces campus crowding, it emphasizes the need for comprehensive epidemic control strategies considering individual decision-making influenced by adaptive learning and targeted interventions.

1.3. Adaptive learning in ABMS

There is a growing body of literature on adaptive learning in agent-based models that holds that habits and past experiences heavily influence people’s social behavior [6,8,9]. Recent developments in agent-based modeling have demonstrated the potential of adaptive learning mechanisms, such as Reinforcement Learning, to significantly enhance the modeling and simulation of epidemic scenarios [8].
For example, Popescu et al. [58] developed a psychology-based framework to model human emotions during disaster evacuation. Their study provides new insights into mapping emotions to membership functions so that agents take actions according to a probabilistic algorithm that combines personal and emotional data. In another study, Abdolmaleki et al. [6] integrated Reinforcement Learning methods with a multi-agent system designed to simulate city fires. This research sought to create an adaptive mechanism that allows a single firefighter to learn strategies to keep people safe. Precisely, their study employed various well-known RL algorithms, including Temporal Difference, SARSA, and Q-learning.
In the context of epidemic modeling, Guo et al. [59] developed a framework called Pandemic Control decision-making via large-scale ABMS and deep Reinforcement learning (PaCAR). It utilizes large-scale agent-based simulation and reinforcement learning to find optimal control policies that minimize infection spread and government restrictions simultaneously. It includes a realistic simulator for cities or states with vaccine settings and a reinforcement learning architecture with a reward system based on economic benefit. This framework outperforms existing methods and is adaptable to different pandemic variants like Alpha and Delta in COVID-19.
Similarly, Zong and Luo [60] presented a reinforcement learning framework for COVID-19 resource allocation. The approach involves creating an agent-based epidemic environment to simulate transmission dynamics across multiple states. A multi-agent reinforcement learning algorithm is then developed, taking into account the time-varying characteristics of the environment. The study applies this framework to determine optimal lockdown resource allocation strategies considering factors such as population age distribution and economic conditions. Results demonstrated that this approach enables more flexible resource allocation strategies, aiding decision-makers in optimizing the deployment of limited resources for infection prevention during the COVID-19 pandemic. Kompella et al. [61] proposed a novel agent-based pandemic simulator that, unlike traditional models, is able to model fine-grained interactions among people at specific locations in a community. Unlike traditional models, they utilized an RL-based methodology for optimizing fine-grained mitigation policies within this simulator.
Furthermore, Kadinski et al. [62] employed machine learning inside of an agent-based model to propose a response and recovery approach for contamination events in water distribution systems. Kadinski and Ostfeld [63] also proposed an agent-based model coupled to a hydraulic simulation where the decision-making of the individual agents is based on a fuzzy logic system reacting to a contamination event in a water network.
In a different context, Harati et al. [64] used a conceptual Agent-Based Model to simulate interactions between a group of agents and a governing agent. They included six Temporal Difference Reinforcement Learning algorithms used by the governing agent to influence the group of agents to perform an action that benefits the governing agent. Their research investigates the emergence of new social norms within an agent framework, using recognition and good reputation as incentives for agent cooperation, even without penalties. They employ agent-based simulations to explore norm development. This demonstrates the benefits of using incentives for agent behavior and integrating adaptive learning techniques into agent-based models.
Likewise, Augustijn et al. [65] explored the impact of disease transmission and governmental interventions on COVID-19. Their work offers a fresh perspective in the realm of ABMS models by departing from traditional rule-based government agents and adopting Machine Learning (ML) algorithms for decision-making. In their study, governments engage in collaborative, data-driven decision processes, sharing experiences to combat disease spread. They evaluated several ML algorithms, with c4.5 and Random Forest proving effective in enhancing government risk perception. Their research underscores the potential of ML-guided government decision-making to optimize disease control efforts, complementing our exploration of adaptive learning techniques in ABMS for epidemic modeling.
In summary, the literature reviewed shed light on the evolving landscape of agent-based modeling, particularly in its capacity to comprehend and influence agent behavior within complex systems, such as disease diffusion and government interventions. The integration of Reinforcement Learning into Agent-Based Models represents a notable advancement, enabling the modeling of dynamic human behavior during epidemics. This adaptation allows agents to flexibly adjust their strategies in response to changing conditions and personal experiences. This innovation not only aligns with the broader application of artificial intelligence but also opens up promising avenues for more precise and responsive epidemic modeling, thus contributing to the enhancement of public health strategies. Little has been found about combining agent-based models and adaptive learning techniques to model epidemic scenarios. For all practical purposes, there is evidence that much of the available literature pays particular attention to disaster-recovery scenarios and has utilized artificial intelligence methods.
Existing research highlights the importance of adopting specific social rules based on agent-based learning for modeling long-term effects. While these studies provide valuable insights into social learning as a product of individual decision-making, certain aspects remain relatively unexplored. For instance, many studies lack detailed explanations of their proposed ABMS, making them more persuasive if accompanied by formal experimental designs featuring confidence intervals and statistical significance tests. Consequently, this study tackles these modeling gaps by employing a comprehensive experimental design that includes ANOVA tables and confidence interval analyses.
The remainder of the paper is organized as follows. First, it presents the materials and methods, beginning with a thorough model description that outlines the core aspects of our research approach. Following that, we delve into the input analysis, providing insights into how we prepared and handled the data for our study. Then, we provide details on the model implementation, explaining the technical aspects of how our agent-based model and adaptive learning techniques were integrated. Followed by the results section, where we first delve into the details of the adaptive learning integration with ABMS, ending with the experimentation, where we explain the specific experiments conducted and the outcomes of these simulations. Finally, the paper concludes with a discussion where we assess the significance of our findings in the context of the broader field of adaptive learning within agent-based modeling.

2. Materials and Methods

This research involves the integration of adaptive learning mechanisms into an ABMS model that simulates crowding patterns within a university campus during a COVID-19 outbreak. Specifically, the research utilizes techniques for crowding reduction based on Reinforcement Learning to enhance the outcomes of epidemic simulations within this micro-community setting. The proposed model aims to describe the effects of blending adaptive learning techniques in an agent-based model that simulates crowding patterns in a university during a COVID-19 outbreak. Indeed, the primary objective is to test whether RL-based crowding-reduction techniques can improve an epidemic’s outcome within a micro-community. Accordingly, the model should reproduce compartment-based epidemic curves to allow assessing the impact of applying adaptive learning to the forenamed curves.
The ABMS model considers the daily routines of students and university staff as they move between various campus facilities, interacting and potentially contributing to the emergence of a COVID-19 epidemic. In this model, adaptive learning refers to agents’ ability to adjust their behavior based on data gathered from their actions in the simulated environment. Essentially, each community member selects their next destination by weighing the perceived risk associated with available facilities, which relates to crowd size. This programming encourages individuals to avoid large gatherings, and as a result, each agent learns to choose routes through facilities that minimize campus congestion.
The evaluation of the model focuses on its capacity to reproduce important patterns. It aims to simulate a simplified version of the progression of COVID-19, resembling the SEIRD (susceptible, exposed, infected, recovered, discharged)-based epidemic behavior observed in conventional models [66]. While exact precision is not required, achieving a reasonable degree of similarity is essential to evaluate how external factors influence the course of the epidemic. Furthermore, the model should illustrate that densely populated areas result in more infections, acknowledging spatial factors such as crowding that play a role in COVID-19 transmission. Lastly, the model should exemplify how adaptive features effectively alleviate congestion on the campus, aligning with our objective to comprehend how social learning influences the outcomes of outbreaks.

2.1. Model description

The model description in this study was designed using the ODD (Overview, Design Concepts, and Details) protocol for describing agent-based models [67]. The overview component of our model defines its purpose, entities, state variables, and process overview. This model aims to simulate the daily dynamics of a micro-community during a COVID-19 outbreak. As a result, the agent-based model considers three core processes: daily campus routine, transmission, and learning. Firstly, the daily campus routine describes how agents move around campus following their schedule. Secondly, the transmission process explains how the disease spreads through close contact with infected individuals. Lastly, the learning process describes how people learn to avoid crowds by trial and error.
Additionally, the model has four types of entities: students, campus staffers, places, and the environment. Students and campus staff are referred to as agents. They represent real-life community members, so they emulate the epidemic interactions between individuals on campus. Each agent has a predetermined weekly routine. A routine is a set of scheduled activities an agent performs in several places. During the initialization process, each agent is assigned a plan according to its type. For instance, students follow an academic program comprised of classes, laboratories, lectures, and other educational activities, while staffers follow a traditional office calendar. Following a plan means going to a facility, staying there for a predetermined amount of time, and leaving for the next activity once the current event ends.
A place is a location on campus where agents perform their activities or transit to other spots. A site is considered an entity as it behaves as a distinct unit with an internal state. There are 87 places on campus of different types, such as teaching facilities, eating places, common areas, parking lots, transit areas, entrances, and exits. These are required to estimate the population density at each simulation step. Also, agents walk through or stay at these places, depending on their routine. Finally, the environment is a single entity that keeps track of the simulation and controls when the outbreak starts. Explicitly, this entity manages global behavior and, therefore, is critical to perform the experiments. Table 1, Table 2, and Table 3 describe the state variables of the agents, places, and environment respectively.
The proposed model utilizes two-dimensional GIS polygons to represent the spatial layout. Consequently, agents interact within an environment resembling the reference campus’s scale. This results in spatial dimensions having a nearly 1:1 relationship with real-life proportions. The simulated university encompasses an area of approximately 130,000 square meters, chosen to mirror the actual campus dimensions in Medellín, Colombia. In contrast, each time step corresponds to one hour, and the simulations run for a duration of 150 days. This temporal extent was chosen to provide ample time for simulating an epidemic that could potentially affect the entire campus population.
A student day schedule can be described as follows: The Students arrive at a campus entrance, update their current location, and then proceed to their next academic activity by taking the fastest route available. During this time, students inform each visited place to update the population density and count of people present. While participating in an event, students remain in the facility, and upon its conclusion, they decide on their next course of action. This involves either relaxing in a common area or proceeding to their next activity. The decision to have lunch on campus is predetermined during initialization, so if a student chooses to dine on campus, they select an eating location, have their meal, and depart upon completion of the meal. After completing all daily activities, students head to a random exit for their journey home.
The schedule for the staff is similar to that of students. On weekdays, staff members arrive at a campus entrance, update their current location, proceed to their workplace, work until noon, and then have lunch. Subsequently, they return to their office and continue working until the end of their shift. At the end of the workday, staff members head to a random exit to make their way home.
The transmission process describes how COVID-19 spreads throughout the campus. At the beginning of the simulation, the environment entity schedules the occurrence of the first active case. In this scenario, a randomly selected individual is marked as infected, and their compartmental state is updated accordingly. Infected individuals follow their usual routines, with the distinction that they can potentially expose nearby susceptible individuals to the disease. When an infected agent comes into close proximity with a susceptible community member, a random process determines whether the contact results in infection. If successful, the exposed individual is categorized as exposed. Subsequently, another random process establishes the current stage’s duration and schedules the infected state’s assignment. Additionally, the agent notifies its current location to update the infection count. Eventually, the agent becomes infected and can potentially transmit the virus to others. Furthermore, a stochastic mechanism determines whether the agent succumbs to the infection or becomes immune, scheduling the corresponding state update.

2.2. Input Analysis

In this section, some components related to input parameters and data sources used in our ABMS model will be presented. The parameters of the ABMS are listed in Table 4, with each parameter being accompanied by a brief description, measurement unit, and default value.
In addition to the input parameters, several data files from external sources are also required to run the model. For instance, shapefiles (.shp extension) are needed to build the campus geography inside the GIS projection. Specifically, these files contain a geometrical representation of each one of the facilities in the simulation. Moreover, additional CSV files are expected that characterize each of the available amenities’ attributes. In particular, each place holds an id, an area in square meters, a state that determines if the site is currently active or not, and a link to another location in case it is required. Furthermore, another file is needed to select the areas that correspond to workplaces, as each staffer will be assigned to one of those.
Moreover, a supplementary routes file is mandatory as it defines how facilities are connected to each other in a network structure. As previously mentioned, agents walk around campus to their selected next location, meaning they must pass by different places to reach their final destination. That is why, to simplify the traversal process, a graph-based structure was designated. The regarded graph is built by taking the facilities as nodes and the distance between them as arcs. On top of that, Dijkstra’s algorithm is used to find the shortest route between an origin and a destination.
Similarly, a group’s file is also compulsory. This file contains the academic schedule to use as a reference for the student’s routine. Particularly, the program comprises subject groups, each featuring a subject id, a day of the week, a start time, an end time, a student capacity, and a facility. The idea is that a student enrolls in several groups, determining what he or she must do during the week.
It is important to note that not all agent behaviors in our model rely on data; some involve estimating important parameters based on expert insights and available information about the variables. For instance, certain processes lacked specific data, such as the duration of lunch breaks in the cafeterias and the timing of the lunch period. We gathered estimated values through stakeholder consultations and interviews with logistics personnel in these cases. Stakeholders reported an estimated mean duration of 45 minutes for lunch breaks, ranging from 15 to 75 minutes. Logistics personnel interviews indicated a typical midday meal time frame from 11:30 am to 2:00 pm. A similar approach was applied to model several other secondary processes, utilizing input from Universidad EAFIT’s staff. However, when data was available, we conducted fitting procedures using Goodness-of-Fit tests.
Table 5 summarizes the main stochastic elements in the model. It is important to consider that We use a Bernoulli distribution with an unknown parameter p to determine whether a community member arrives on campus in a vehicle; this is relevant as car entrances differ from pedestrian ones. Parameter p is set as a model input parameter because different car-based restriction scenarios will be evaluated in future works. In addition, a uniform walking speed in meters per minute is defined in the 70 to 100 limit as it renders a lower and upper bound of reported velocities for different age ranges [68].

2.3. Model implementation

Our ABMS model was implemented in the Repast Simphony platform, an open-source framework for simulating agent-based systems. Repast Simphony is based on object-oriented programming principles and provides a broad toolkit for effectively modeling and analyzing dynamic systems. Its open-source nature allows collaboration with other modelers, and compatibility across different operating systems is ensured by its Java-based design. Moreover, organized and modular model development is facilitated by Repast Simphony, which is deemed essential for complex simulations. The platform’s scalability accommodates simulations on various scales. For a broader overview, Figure 2 presents the components of our model, and Figure 3 exhibits a rough blueprint of the syndicated classes and their interactions.
The agent-based model is divided into seven modules, each one of them responsible for a specific task. The central module, simulation, is in charge of orchestrating the model’s execution. Plainly, the aforementioned building block interacts with other peer constituents to set up the model and manage scheduled events. On the other hand, one of the initial configuration tasks is loading all the necessary data, which is, by the way, the data loader module’s job. Pointedly, the former module is in command of accessing external data sources and transforming them into POJOs (Plain old Java objects). Once the bootstrapping ends, the simulation instantiates all the agents, in this case, all students, staffers, and locations.
The agent behavior unit operates how agents interact with each other and with the environment. In detail, the antecedent module is responsible for enforcing each community member’s daily routine. On the side, the natural history artifact guides disease dynamics. As mentioned before, one of its primary inputs is the patient type, an internal attribute every individual holds, as infected subjects are classified in accordance with the severity of their symptoms.
Moreover, all those previously discussed agent interactions, behaviors, and internal mechanisms are present in a simulated geospatial environment. As previously stated, facilities are materialized into polygons. The GIS-enabled environment supports the integration of a weighted-graph-based structure that emulates on-campus routes. All the earlier features are supported by the geography management module. Last but not least, the learning and output management modules are self-explanatory under precedent descriptions. Conversely, seamless orchestration is the key to success. Each module might work independently from others, but its dependencies allow for contract-based synergies that enable strait-laced modularization and low coupling.
Initialization refers to the process that sets up to model before its actual simulation. In this case, this agent-based model requires several initial steps before it is ready to emulate the campus dynamics. At initialization, the different types of agents are created according to the parameters described in Table 4. First, the program reads all shapefiles and extracts the corresponding GIS polygons to build the facility agents. Each place entity is generated by reading both its associated shape and attributes file. Once all sites are instantiated, the simulation builder reads the workplace file to keep references to the office locations for later usage.
After forging all site agents, the routes file is read into a weighted graph structure. Recall that the nodes represent locations on campus, and edges refer to distances between those places. Now, suppose that the routing algorithm is embedded into the agents, meaning that each time a student wants to go to a specific location, it is responsible for calculating the fastest route to its destination. In reality, the foregoing approach is impractical, as it is very likely that lots of agents will need to calculate the same paths repeatedly. That is why an initial procedure is implemented to calculate the shortest route between all possible localities. Found courses are stored in a hashed map with unique keys that designate the origin and destination pair. The proposed method is sketched in Algorithm 2.
Algorithm 2: Calculation of shortest paths between localities
Preprints 85705 i002
Following route building, the program loads the groups’ file into a collection of objects. Later, student agents are produced according to the simulation parameters. Remember that two sets of students are created: the initial susceptible and those that will get infected once the outbreak is activated. The specifics of the student initialization will be discussed in a bit. In the meantime, as soon as the application holds a list of students, it continues by assigning them a schedule according to the previously read academic plan. The foretold assignment was designed to be straightforward, with no intricate heuristics to balance the student population, as it was deemed unnecessary. Precisely, schedules are allotted randomly. Outright, a random number of groups to enroll n is generated for each agent according to the Binomial distribution in Table 5. Then, the algorithm shuffles the groups’ list and selects n arbitrary groups with at least one available spot if that is possible. If the affirmative case, the student is enrolled in the mentioned course. Otherwise, if no single group is attached, the agent is removed from the simulation. The suggested randomized procedure is outlined in Algorithm 3.
Algorithm 3: Student’s schedule assignment
Preprints 85705 i003
The staffer agents are immediately materialized and added to the simulation context. At this point, all agents have been embodied. Though, a few inner details were left undisclosed. For instance, how the internal features of each agent type are initialized. To all intents and purposes, all community members are made ready as follows. First, the vehicle usage attribute is fixed according to the Bernoulli distribution in Table 5. Next, if the individual was marked for spontaneous infection, the corresponding transition is programmed to comply with the outbreak tick parameter in Table 4. Later, the learning mechanism is turned on, and the state-value pairs are set to their initial values. Afterward, the agent is sent home to an undetermined location outside the campus. Finally, all weekly recurring events are timetabled in line with the agent’s type.
Weekly recurring events are a core component in the model under examination. The prior is true because the ABMS was coded in an event-based fashion, where agent interactions are orchestrated through a prearranged set of repeating events. As a rule, the following four types of activities are anticipated: academic or work-related ones, the arrivals to campus, the departures to home, and having lunch. These are implemented separately for the students and staffers as they hold dissimilar routines. Namely, students arrive on campus according to their assigned schedule, showing up a few minutes before their first academic activity. Albeit, staffers arrive close to 7:00 a.m. at the start of the working shift. Similarly, students return home after their last activity, whilst staffers have a pre-established exit hour.
During the model’s development, a visual aid was implemented for illustration and shallow validation purposes in the form of a 2D geo-map. Figure 4 presents the forenamed graphical representation of the model’s workings. Respectively, the mentioned depiction is remarkably appropriate for observing global behavior such as crowding and outbreak progression. To be specific, blue dots symbolize susceptible individuals. Colors change as the disease proceeds to orange for exposed, red for infected, green for recovered, and black for dead.

3. Results

In this section, we present the outcomes of our research, investigating how reinforcement learning impacts social distancing on a simulated campus and, by extension, its influence on the spread of COVID-19. Our main objective was to determine if RL-driven adjustments in behavior could effectively reduce crowding on campus and potentially mitigate the virus’s transmission. Having discussed the theoretical foundations and detailed our experimental setup in previous sections, the focus is now on integrating RL-based adaptive learning into the ABMS model. Additionally, we evaluate the influence of this adaptive learning on campus density and the evolution of the COVID-19 outbreak within our simulation scenarios. We analyze the effects of different RL parameters, such as learning rate ( α ), exploration probability ( ϵ ), and discount factor ( γ ), on key metrics like campus density and epidemic dynamics. Through rigorous statistical analysis, we assess the practical implications of these findings, shedding light on the potential of RL-based strategies to reshape social behavior during a pandemic.

3.1. Adaptive learning integration with ABMS

In this subsection, we go into the specifics of the adaptive mechanism we have employed. It is important to recall that our aim with this mechanism is to facilitate agents in learning social distancing behaviors while preserving the normalcy of campus life. We operate under the assumption that individuals within the community are rational and prioritize avoiding infection. This inherent drive motivates them to adapt their behaviors to minimize exposure to potential risks willingly. It is important to note that in our scenario, agents act solely based on their personal experiences and not due to external influences.
Our chosen learning approach is grounded in a Q-learning scheme with ϵ -greedy action selection. We opted for this strategy due to its adaptability, versatility, and ease of implementation. Among the various tabular methods we explored, Q-learning offers a straightforward method for estimating state-action values and is well-suited for navigating a dynamic environment comprising thousands of knowledgeable agents vying for limited resources. Each agent operates independently, mirroring the concurrent adaptation of a small-sized community within the simulation.
There are four fundamental components in our proposed design. Firstly, we have the representation, which defines what states, actions and values signify. Secondly, initialization outlines how the scenarios are set up initially. Thirdly, action selection elucidates the process of choosing the next action in the current state. Lastly, value update elucidates how estimations are revised based on the reward signal. Regarding representation, states correspond to specific locations on campus, with each state representing a distinct available location to visit. Actions, on the other hand, symbolize the act of moving from one location to another. The value associated with a state-action pair indicates the desirability of selecting a particular destination while currently situated in another place. Consequently, the value function is modeled as a lookup table comprising Q ( s , a ) entries, where ’s’ represents the state and ’a’ denotes an available action.
Only the following amenities are considered in the learning process: teaching facilities, common areas, and eating places. It is evident that there is a vast amount of Q values as locations are taken in pairs. On the subject of initialization, preliminary experiments suggested the best setup was leaving all initial figures at zero, thus implying that all places have the same attractiveness factor in the first iteration. The referred situation does not match the classical scheme that recommends a random initialization procedure.
An ϵ -greedy strategy was implemented in the matter of action selection. The idea behind this procedure is that actions should be picked considering the exploration-exploitation dilemma. To be exact, the best available action, referring to the one with the highest Q figure, is selected with probability 1 − ϵ , while a random one is chosen in the opposite case. By way of explanation, the examined method is sketched in Algorithm 4.
Regarding the Q values’ update, a reward signal was picked to outcome positive figures for safe places and negative amounts for sites that exceed the ideal social distancing measure (as described in Table 4). The proposed payment for landing in a certain location is described by Equation 7, where the social distancing is measured in meters, and the current density of the place is estimated as the number of people in that location over its superficial area in square meters. As an illustration, if the social distancing policy is set to 2 meters, then densities over the 0.5 p e o p l e m 2 mark will be considered threatening.
R = 1 social distancing measure − current density of the location
Algorithm 4: ϵ -greedy action selection
Preprints 85705 i004
Considering the four preceding ingredients, the learning scheme can be summarized in Algorithm 5. Essentially, adaptation only happens when the agent faces site selection circumstances. It is crucial to clarify that the convergence of the algorithm greatly depends on the parameter configuration, as careful attention is required to balance the exploration-exploitation dilemma [13]. For that purpose, a three-factor factorial design of experiments is applied to analyze each parameter’s effects. Despite everything, results are expected to show different outcomes, good or bad, under each scenario. Anyhow, the intention was not to reveal pleasing results in all examined situations; instead, the idea is to identify the key differences under various settings.
Algorithm 5: Q-learning scheme for crowding reduction
Preprints 85705 i005
In order to assess the influence of the implemented RL-based adaptive features, a base scenario is defined. The selected reference settings render a population of 10,000 students and 200 staffers and fix both the infectious radius and social distancing measure to 2 meters. Besides, we use a uniform random procedure to select facilities (similar to an ϵ = 1 setup). Therefore, the picked parameter values are the same as those reported in the default value column in Table 4. However, bear in mind that learning parameters α , γ , and ϵ have no effect at all in the course of the earlier described scenario. For descriptive purposes, mean on-campus densities for ten repetitions are shown in Figure 5.
Figure 5 reveals recurrent patterns of density peaks over the 0.5 p e o p l e m 2 threshold, which indicates that the current crowding dynamics do not comply with recommended social practices. However, a more in-depth analysis is required to identify the temporal fragment that poses the greatest threat to the community. Next, some descriptive statistics for the density output are reported in Table 6.
Table 6 shows that the mean density on campus is around 0.10 people per square meter, meaning that agents are 10 meters apart on average. Still, the median value is utterly different from the aforesaid measure, suggesting the presence of outliers. Yet, anomaly detection techniques are not applicable here as the outliers are of special interest in the analysis. Having said that, the recorded high skewness value exhibits a significant positive asymmetry. Simultaneously, the kurtosis figure displays a slight tendency of greater deviations to the mean that conforms with previous findings. In summary, computed metrics agree that density values are not homogeneous and that outliers’ demeanor is meaningful. Along with it, a histogram of densities is plotted in Figure 6 according to Sturge’s criteria.
As expected, the histogram in Figure 6 provides further details on the distribution of the density figures. For instance, around 60% of the measurements are lower than the 0.1 people per square meter mark, while only 0.9 percent of the values are actually larger than the social distancing measure. In simpler terms, results show that potentially dangerous situations happen less than 1% of the time.
For good measure, Figure 6 could raise some doubts about the densities’ distribution since the graphic may lead to thinking that these could be drawn from a mixing of two random variables. One way of making sure that results are legit is by means of an analysis of independence. By this study’s standards, the densities should follow some foreseeable structure, given that gatherings are based upon the academic schedule. Due to this, an overlapped scatter plot should evince non-random patterns, and an autocorrelation plot is likely to exhibit substantial correlations for some lag values. Figure 7 conveys the previously mentioned diagrams.
Unsurprisingly, Figure 7 illustrates that densities are not random at all. For all intents and purposes, density values follow a temporal arrangement that bears a linear association with the three preceding data points. To continue with the analysis, two box-plots are brought into the examination to browse how densities behave in various temporal groupings. Figure 8 presents the above-stated charts.
A closer inspection of Figure 8 shows noticeable differences between the examined temporal partitions. For instance, it is apparent from the figure on the left that weekends’ densities are almost negligible. Besides, Friday’s quantities do not exceed the 0.35 bar, implying that unfavorable gatherings are not likely to occur from Friday to Sunday. At the same time, Monday to Thursday’s maximum measurements are close to the 0.5 benchmark, with the highest values being recorded on Tuesdays. Setting aside, the figure on the right shows that bigger congregations happen close to lunchtime, where most agents look for a place to eat in one of the few available. Other distinctive top figures are seen near common arrival and departure times, suggesting that agents crowd in places near the entrances and exits at these time frames. Altogether, evidence suggests that Tuesdays close to lunchtime deliver the utmost risk of clustering. For a proper validation of the last statement, Table 7 presents the mean confidence intervals for the densities each day and in the whole week.
Evidence in Table 7 supports that Tuesdays hold noticeably larger gatherings than any other day of the week. Now, in relation to the comparison with the implemented learning method, a reference densities curve should be selected. In this case, the maximum weekly density time series is picked, the reason being that it suppresses the effect of the weekend figures and allows for a smoother comparison with experimental results. Figure 9 displays the aforementioned data points on the right.
What is interesting about the data in Figure 9 is that maximum densities seem to shift randomly near the 0.55 yardstick up to the 80th day. Then, the specified figures go down a little bit and converge near 0.53. Noticeably, the above behavior matches the scheduled outbreak progression since it starts at day 60 and should begin reporting dead cases in the following 15 to 20 days. The differences suggest that the epidemic itself reduces the maximum crowding values by 0.02, which is not meaningful at all.
Base epidemic outcomes are showcased in Figure 10. It is apparent from the graphic that a broad compartmental dynamics holds on the grounds that the manifested behavior resembles a classical SEIRD scheme. Despite that, notable differences are revealed since irregularities are detected in the susceptible and exposed curves. The results are quite revealing in several ways. First, a peak of 9424 infected subjects on day 16 conveys that COVID-19 progresses astonishingly fast in a semi-enclosed community where no action is taken, recording a 0.92 prevalence rate in a couple of weeks from the initial case. Second, a 3.9% mortality rate is registered, comparable to recently reported fatalities ratios [69]. Finally, a rather odd phenomenon is observed in the exposed curve, as the data does not follow a bell-shaped form; more precisely, exposed cases break in the middle and go up a few days later. The last proceeding could be explained due to the latency term being around 2.4 days shorter than the incubation period and no new infections appearing on weekends.
Robinson [70] states that multiple replications are required to obtain a good enough estimate of a model’s mean performance. Unequivocally, a central question is: How many simulation runs need to be performed? A rule of thumb hints that at least five repetitions should be carried out. Howbeit, a precise derivation is preferred instead. For instance, a statistically reliable method involves rearranging the confidence interval formula, as shown in Equation 8. Where X is the variable of interest, X ¯ is its expected value, σ ^ is its estimated standard deviation, α is the selected significance level, and d is the percentage deviation of the confidence interval about the mean. Now, taking the maximum weekly density as the variable under study, a significance level of five percent ( α = 0.05 ) and a deviation of ten percent ( d = 0.10 ), n = 5.39 minimum replications are obtained. Therefore, at least six simulation runs are recommended per experiment. Indeed, that means that the initial ten runs are sufficient.
n = σ ^ · t n − 1 , α / 2 d X ¯ 2

3.2. Experimentation

Preceding results show that the learning-lacking scenario does not comply with the social distancing policy. Thus, a design of experiments is aimed to determine the effect of RL-based social distancing with different sets of parameters. Truly, it would be ideal to examine a vast array of parameter settings. Still, extensive simulation times constrain the number of trials to perform in a reasonable time and with limited computing resources. Consequently, a 2 k factorial design is chosen, where k is the number of factors to analyze. Specifically, k = 3 factors are considered according to parameters α , γ , and ϵ . Table 8 presents the figures selected as the low and high levels for each experimental factor.
Factor’s levels were selected intuitively following their effects. Namely, α was assigned a 0.1 low level as smaller values will likely lead to imperceptible corrections and a 0.25 high level as larger figures could potentially head to oscillatory behavior. Similar arguments were examined while choosing the bounds of the remaining parameters. Table 9 describes the proposed 2 3 factorial design.
The experiments were repeated six times, as previously stated, to capture the variability of the model’s outcomes up to a 10% confidence interval deviation from the mean. Remarkably, results show that agents are absolutely capable of learning to avoid crowds on campus. Thus validating the hypothesis that the suggested RL-based approach is suitable for implementing the adaptive learning mechanism. As expected, maximum weekly densities reduce progressively while agents accumulate experiences in their daily activities. Figure 11 exhibits the mentioned behavior.
Figure 11 contrasts the base scenario with the eight experiments. What is striking about the outcomes is that all parameter settings significantly reduce maximum weekly densities with respect to the base case. Notwithstanding, some scenarios provide better results than others. For example, Experiment 2 affords the greatest decline in supreme densities and ends up in a situation where on-campus gatherings are, on average, below the 0.40 mark (10 points below the recommended social distancing policy). Extraordinarily, all experiments render a behavioral shift that positions the community in a sweet spot regarding compliance with the minimum physical distancing measures. Table 10 displays some relevant density figures for each one of the scenarios.
What stands out in Table 10 is that the experiments with the highest relative reduction in the maximum weekly densities (Experiments 2 and 6) share the same parameter values for ϵ and γ . All in all, evidence suggests that the second setup is a local optimum with respect to the chosen experimental space. Nevertheless, the aforementioned settings are not guaranteed to be a globally optimal selection of learning parameters. Undoubtedly, a more in-depth optimization procedure is required to establish the Pareto set of learning factors to procure the maximum decline in density figures. Having said that, the obtained density reductions represent ideal learning configurations, meaning that these figures do not necessarily reflect actual human behavior. In contrast, those values portray fanciful conditions that could lead to the lowest attainable crowding level on campus.
Results show that a significant drop in density values is plausible through a well-calibrated learning mechanism. However, an essential question is: Do these improvements have a meaningful impact on the epidemic? The answer is not straightforward. We will start the analysis by visually inspecting the outcomes. Figure 12 contrasts the experiments’ active cases curves against the reference scenario. In fact, both graphics show that Experiment 1 seems to drive a massive decrease in the number of infections, leading to a bit more than 1800 people not being exposed at all. One could argue that the first scenario has a positive effect on the outbreak. But are these results statistically significant?
Table 11 presents two other relevant figures to grasp how different the base scenario and the experiments are. The relative mean cumulative difference measures how large is the average distance between the base scenario’s accumulated active cases curve and the same one for a certain experiment with respect to the population size (N). If the precedent is positive, one could allege that the base scenario produces a relatively higher number of infections on average than the experiment under consideration. Equation 9 presents the formulation of the earlier mentioned metric.
c d ¯ % = 1 N 1 k ∑ i = 1 k A R i − A E i
Where, k is the number of hours the epidemic lasts, A R i is the accumulated active cases at hour i in the reference scenario, and A E i is the same as the last one for the experiment under study. Also, the spline difference measurement estimates the area between the two previously mentioned curves. If the area is greater than zero, then the base case furnishes a larger number of contagions than its counterpart in at least one timeframe.
Results in Table 11 are inconsistent with the preceding findings. Unmistakably, both figures should have the same sign if one time series dominates the other one. Nonetheless, signs do not always match, suggesting that the base curve does not entirely surpass the opposite. It is apparent from the data that absolute relative mean differences, excluding Experiment 1, are lower than 2.5%, bespeaking that infections in the base and test scenarios are not strongly dissimilar. Unusually, Experiment 1’s metrics diverge significantly from the remainder, which should not be the case as Experiments 1 and 2 only differ in 0.15 in the discount factor, hence implying the presence of outliers. So far, there is no concrete evidence yielding that adaptive learning has a substantial impact on the outbreak at all. But are Experiment 1’s results legit? Figure 13 deep dives in this issue.
As predicted, Experiment 1’s results are not reliable. The computed confidence intervals are so broad that they reveal an immense variability in the outputs. Closer inspection unveiled that one of the simulation runs did not lead to a massive outbreak as patient zero recovered very quickly. Thus, the outcomes of Experiment 1 should be ignored in the analysis. As yet, the employed analysis techniques have fallen short. So, non-parametric procedures are put in the mix. Table 12 displays the p-values of three non-parametric tests to examine if the base scenario and the experiments have sufficient differences to classify them as belonging to separate sets of samples.
Friedman’s test is an ideal statistic to estimate if a particular factor influences the outputs of a process that is measured several times. In particular, its null hypothesis states that the medians of the examined groups of samples are all the same. On the other hand, Wilcoxon’s and Kruskal-Wallis’s tests employ the mean for the comparison. As Table 12 shows, most experiments reject Friedman’s H 0 , alluding to the median cumulative cases are distinct. Notwithstanding, the remaining tests are never rejected, denoting that no solid evidence confirms the experiments and the reference scenario are statistically different on average. Thereupon, formal methods have proven that although RL-based learning has a meaningful impact on campus densities, nothing suggests the same happens with the epidemic. In addition, the ANOVA procedure in Table 13 confirms the verdict.
In synch with earlier resolutions, Table 13 unfolds that no factor or combination of factors is significant in the epidemic outcomes, the reason being that all the p-values are higher than the 0.05 significance level. Consequently, all evidence points in the same direction. As an illustration, Figure 14 displays the estimated effect of each parameter. Unsurprisingly, these effects are quite similar to each other as the ANOVA technique is unable to determine each factor’s influence and, therefore, distributes the impact across the parameters space.
Overall, these results indicate that RL-based learning successfully reduces crowds on campus to the point that the social distancing policy is obeyed on average. However, no statistically significant proof was found of the effect of adaptive learning regarding the epidemic results. The current hypothesis on that matter is that COVID-19 is so contagious that physical distancing in a small semi-enclosed community helps but is not enough to render a substantial decline in the number of infected subjects.

4. Discussion and Conclusions

This study explored the impact of introducing an adaptive learning system into an agent-based model simulating a university campus during an epidemic. Our primary aim was to assess whether this mechanism could effectively reduce gatherings and stationary infections on campus. Our findings demonstrate that implementing an adaptive learning mechanism, mainly through Reinforcement Learning, is feasible. Our results align with previous research that has successfully applied adaptive learning techniques to optimize control policies during epidemics. This highlights the adaptability and effectiveness of Reinforcement Learning in representing how people make goal-oriented decisions in complex, semi-enclosed environments, such as a university campus during an epidemic.
However, the results also provide insights into the subtle aspects of the impact of adaptive learning. While the adaptive learning mechanism led to meaningful reductions in campus crowding, the extent of this effect varied across scenarios. In some cases, agents maintained a considerable distance from one another, significantly exceeding the recommended physical distancing policy. However, in other instances, this effect was less pronounced. These variations emphasize the intricacies of human behavior and the challenges of precisely predicting outcomes within semi-enclosed communities like campuses. Moreover, our study revealed a temporal aspect of crowding violations. We observed that these violations predominantly occurred on Tuesdays during lunch hours. This temporal pattern underscores the necessity for targeted interventions on specific days and times to ensure adherence to social distancing measures.
It is important to note that while our study successfully reduced campus crowding, it did not substantially alter the epidemic’s course. This highlights the importance of comprehensive epidemic control strategies that consider individual decision-making influenced by adaptive learning. Moreover, focusing only on social distancing may not include all important aspects of disease control, and our study’s limited timeframe may have hindered the detection of significant impacts from this specific measure. This emphasizes the need to thoroughly evaluate various control measures to comprehend their combined influence on epidemic dynamics.
In summary, this study’s main objective was to assess the effects of integrating adaptive learning into an agent-based model within a university campus epidemic scenario. While adaptive learning can effectively reduce campus crowding, its impact on the epidemic is limited. This emphasizes the importance of multifaceted epidemic control strategies considering individual behavior influenced by adaptive learning.
Future research may include exploring diverse parameter settings to optimize campus density reduction while maintaining realistic social behaviors. Updating the model’s natural history representation based on the latest COVID-19 research is essential. Additionally, comparing our agent-based model with compartmental models, particularly considering geospatial interactions, could provide valuable insights. Computing meaningful epidemic figures and validating the model with accurate data at an appropriate aggregation level will further contribute to understanding adaptive learning in epidemic control within semi-enclosed communities like university campuses.

Author Contributions

Following the criteria for authorship and contribution, the roles of the authors are specified as follows. Paula Escudero served as the primary advisor for David Romero’s research work, providing substantial guidance throughout the conception, design, and execution of the study. Paula Escudero was crucial in directing the research efforts, offering critical insights into various aspects of the project, and supervising the overall research process. Paula Escudero was actively involved in drafting and revising several sections of the manuscript, contributing significantly to its intellectual content. David Romero, on the other hand, was primarily responsible for the modeling and implementation aspects of the research. He mainly focused on exploring the integration of Reinforcement Learning (RL) into Agent-Based Modeling and Simulation (ABMS). His contributions included extensive study and experimentation on using RL within the ABMS framework. Both authors, Paula Escudero, and David Romero, approved the final submitted version of the manuscript and jointly ensured the accuracy and integrity of the work.

Funding

This research received no external funding

Informed Consent Statement

Not applicable

Acknowledgments

We want to express our sincere appreciation to the Universidad EAFIT, specifically Juan David Jurado Tapias, Gloria Stella Sepulveda Cossio, Jhon Alexanders Miranda Echeverri, Nicolás Rengifo Campo, Mariana Gómez Piedrahita, and Francisco Iván Zuluaga Díaz for all their valuable insights and support to this research.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ABMS Agent-based Modelling and Simulation
RL Reinforcement Learning
MDPI Multidisciplinary Digital Publishing Institute
DOAJ Directory of open access journals
TLA Three letter acronym
LD Linear dichroism

References

  1. UN Economic Commission for Latin America and the Caribbean. Latin America and the Caribbean and the COVID-19 pandemic: Economic and social effects, 2020.
  2. Van Bavel, J.J.; Baicker, K.; Boggio, P.S.; Capraro, V.; Cichocka, A.; Cikara, M.; Crockett, M.J.; Crum, A.J.; Douglas, K.M.; Druckman, J.N.; et al. Using social and behavioural science to support COVID-19 pandemic response. Nature Human Behaviour 2020, pp. 1–12.
  3. Talic, S.; Shah, S.; Wild, H.; Gasevic, D.; Maharaj, A.; Ademi, Z.; Li, X.; Xu, W.; Mesa-Eguiagaray, I.; Rostron, J.; et al. Effectiveness of public health measures in reducing the incidence of covid-19, SARS-CoV-2 transmission, and covid-19 mortality: systematic review and meta-analysis. bmj 2021, 375. [Google Scholar] [CrossRef] [PubMed]
  4. Glass, R.J.; Glass, L.M.; Beyeler, W.E.; Min, H.J. Targeted social distancing designs for pandemic influenza. Emerging infectious diseases 2006, 12, 1671. [Google Scholar] [CrossRef] [PubMed]
  5. Ferreira, E.; Lefèvre, F. Social signal and user adaptation in reinforcement learning-based dialogue management. In Proceedings of the Proceedings of the 2nd Workshop on Machine Learning for Interactive Systems: Bridging the Gap Between Perception, Action and Communication, 2013; pp. 61–69.
  6. Abdolmaleki, A.; Movahedi, M.; Salehi, S.; Lau, N.; Reis, L.P. A Reinforcement Learning Based Method for Optimizing the Process of Decision Making in Fire Brigade Agents. In Proceedings of the Progress in Artificial Intelligence; Antunes, L.; Pinto, H.S., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2011; pp. 340–351. [Google Scholar]
  7. Izquierdo, S.S.; Izquierdo, L.R.; Gotts, N.M. Reinforcement learning dynamics in social dilemmas. Journal of Artificial Societies and Social Simulation 2008, 11, 1. [Google Scholar]
  8. Steinbacher, M.; Raddant, M.; Karimi, F.; Camacho Cuena, E.; Alfarano, S.; Iori, G.; Lux, T. Advances in the agent-based modeling of economic and social behavior. SN Business & Economics 2021, 1, 99. [Google Scholar]
  9. Cases, B.; Rebollo, I.; Graña, M. A hybrid spatial—social—logical model explaining human behaviour in emergency situations. Logic Journal of the IGPL 2011, 20, 625–633. [Google Scholar] [CrossRef]
  10. Epstein, J.M. Modelling to contain pandemics. Nature 2009, 460, 687–687. [Google Scholar] [CrossRef]
  11. Tomas, S. Design of agent-based models: developing computer simulations for a better understanding of social processes; Tomas Bruckner, 2011.
  12. Hamill, L.; Gilbert, G.N. Agent-based modelling in economics; Wiley Online Library, 2016.
  13. Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction; MIT press, 2018.
  14. Hofmann, K.; Whiteson, S.; De Rijke, M. Balancing exploration and exploitation in learning to rank online. In Proceedings of the European Conference on Information Retrieval. Springer; 2011; pp. 251–263. [Google Scholar]
  15. Ratitch, B.; Precup, D. Using MDP characteristics to guide exploration in reinforcement learning. In Proceedings of the European Conference on Machine Learning. Springer; 2003; pp. 313–324. [Google Scholar]
  16. White, C.C. A survey of solution techniques for the partially observed Markov decision process. Annals of Operations Research 1991, 32, 215–230. [Google Scholar] [CrossRef]
  17. He, S.; Peng, Y.; Sun, K. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dynamics 2020, pp. 1–14.
  18. Hou, C.; Chen, J.; Zhou, Y.; Hua, L.; Yuan, J.; He, S.; Guo, Y.; Zhang, S.; Jia, Q.; Zhao, C.; et al. The effectiveness of quarantine of Wuhan city against the Corona Virus Disease 2019 (COVID-19): A well-mixed SEIR model analysis. Journal of medical virology 2020. [Google Scholar] [CrossRef]
  19. Fan, R.G.; Wang, Y.B.; Luo, M.; Zhang, Y.Q.; Zhu, C.P. SEIR-Based COVID-19 Transmission Model and Inflection Point Prediction Analysis. Dianzi Keji Daxue Xuebao/Journal of the University of Electronic Science and Technology of China 2020, 49. [Google Scholar]
  20. Novel, C.P.E.R.E.; et al. The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19) in China. Zhonghua liu xing bing xue za zhi= Zhonghua liuxingbingxue zazhi 2020, 41, 145. [Google Scholar]
  21. He, X.; Lau, E.H.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nature medicine 2020, 26, 672–675. [Google Scholar] [CrossRef] [PubMed]
  22. Liu, Z.; Magal, P.; Seydi, O.; Webb, G. A COVID-19 epidemic model with latency period. Infectious Disease Modelling 2020, 5, 323–337. [Google Scholar] [CrossRef] [PubMed]
  23. Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Annals of internal medicine 2020, 172, 577–582. [Google Scholar] [CrossRef] [PubMed]
  24. Ferguson, N.; Laydon, D.; Nedjati Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba Perez, Z.; Cuomo-Dannenburg, G.; et al. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand. Imperial College London 2020. [Google Scholar]
  25. Liu, Y.; Yan, L.M.; Wan, L.; Xiang, T.X.; Le, A.; Liu, J.M.; Peiris, M.; Poon, L.L.; Zhang, W. Viral dynamics in mild and severe cases of COVID-19. The Lancet Infectious Diseases 2020. [Google Scholar] [CrossRef] [PubMed]
  26. Xu, B.; Gutierrez, B.; Mekaru, S.; Sewalk, K.; Goodwin, L.; Loskill, A.; Cohn, E.L.; Hswen, Y.; Hill, S.C.; Cobo, M.M.; et al. Epidemiological data from the COVID-19 outbreak, real-time case information. Scientific data 2020, 7, 1–6. [Google Scholar] [CrossRef]
  27. Willem, L. Agent-based models for infectious disease transmission: exploration, estimation & computational efficiency. PhD thesis, Universiteit Antwerpen, 2015.
  28. Farkas, J.Z.; Gourley, S.A.; Liu, R.; Yakubu, A.A. Modelling Wolbachia infection in a sex-structured mosquito population carrying West Nile virus. Journal of mathematical biology 2017, 75, 621–647. [Google Scholar] [CrossRef]
  29. Guo, P.; Liu, T.; Zhang, Q.; Wang, L.; Xiao, J.; Zhang, Q.; Luo, G.; Li, Z.; He, J.; Zhang, Y.; et al. Developing a dengue forecast model using machine learning: A case study in China. PLoS neglected tropical diseases 2017, 11, e0005973. [Google Scholar] [CrossRef]
  30. Morrison, T.E. Reemergence of chikungunya virus. Journal of virology 2014, 88, 11644–11647. [Google Scholar] [CrossRef]
  31. Okabe, Y.; Shudo, A. A mathematical model of epidemics—a tutorial for students. Mathematics 2020, 8, 1174. [Google Scholar] [CrossRef]
  32. Brauer, F.; Castillo-Chavez, C.; Feng, Z.; Brauer, F.; Castillo-Chavez, C.; Feng, Z. Introduction: A Prelude to Mathematical Epidemiology. Mathematical Models in Epidemiology 2019, pp. 3–19.
  33. Miksch, F.; Urach, C.; Einzinger, P.; Zauner, G. A Flexible Agent-Based Framework for Infectious Disease Modeling. Information and Communication Technology Lecture Notes in Computer Science 2014, p. 36–45. [CrossRef]
  34. Allen, L.J. A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis. Infectious Disease Modelling 2017, 2, 128–142. [Google Scholar] [CrossRef] [PubMed]
  35. Afzal, A.; Saleel, C.A.; Bhattacharyya, S.; Satish, N.; Samuel, O.D.; Badruddin, I.A. Merits and limitations of mathematical modeling and computational simulations in mitigation of COVID-19 pandemic: A comprehensive review. Archives of Computational Methods in Engineering 2022, 29, 1311–1337. [Google Scholar] [CrossRef] [PubMed]
  36. Chubb, M.C.; Jacobsen, K.H. Mathematical modeling and the epidemiological research process. European journal of epidemiology 2010, 25, 13–19. [Google Scholar] [CrossRef] [PubMed]
  37. Brauer, F.; Driessche, P.V.d.; Wu, J.; Allen, L.J.S. Mathematical epidemiology; Springer, 2008.
  38. Whang, S.; Choi, S.; Jung, E. A dynamic model for tuberculosis transmission and optimal treatment strategies in South Korea. Journal of Theoretical Biology 2011, 279, 120–131. [Google Scholar] [CrossRef] [PubMed]
  39. Syafruddin, S.; Noorani, M. SEIR model for transmission of dengue fever in Selangor Malaysia. IJMPS 2012, 9, 380–389. [Google Scholar]
  40. Mettle, F.O.; Osei Affi, P.; Twumasi, C. Modelling the Transmission Dynamics of Tuberculosis in the Ashanti Region of Ghana. Interdisciplinary Perspectives on Infectious Diseases 2020, 2020. [Google Scholar] [CrossRef]
  41. Hunter, E.; Mac Namee, B.; Kelleher, J.D. A taxonomy for agent-based models in human infectious disease epidemiology. Journal of Artificial Societies and Social Simulation 2017, 20. [Google Scholar] [CrossRef]
  42. Perez, L.; Dragicevic, S. An agent-based approach for modeling dynamics of contagious disease spread. International Journal of Health Geographics 2009, 8, 50. [Google Scholar] [CrossRef]
  43. Sanchez, P.J.; Sanchez, S.M. A scalable discrete event stochastic agent-based model of infectious disease propagation. 2015 Winter Simulation Conference (WSC) 2015. [Google Scholar] [CrossRef]
  44. Crooks, A.T.; Hailegiorgis, A.B. An agent-based modeling approach applied to the spread of cholera. Environmental Modelling & Software 2014, 62, 164–177. [Google Scholar] [CrossRef]
  45. Miksch, F.; Pichler, P.; Espinosa, K.J.P.; Casera, K.S.T.; Navarro, A.N.; Bicher, M. An agent-based epidemic model for dengue simulation in the Philippines. 2015 Winter Simulation Conference (WSC) 2015. [Google Scholar] [CrossRef]
  46. Kuhlman, C.J.; Ren, Y.; Lewis, B.; Schlitt, J. Hybrid Agent-based modeling of Zika in the united states. 2017 Winter Simulation Conference (WSC) 2017. [Google Scholar] [CrossRef]
  47. Palomo-Briones, G.A.; Siller, M.; Grignard, A. An agent-based model of the dual causality between individual and collective behaviors in an epidemic. Computers in biology and medicine 2022, 141, 104995. [Google Scholar] [CrossRef]
  48. Weligampola, H.; Ramanayake, L.; Ranasinghe, Y.; Ilangarathna, G.; Senarath, N.; Samarakoon, B.; Godaliyadda, R.; Herath, V.; Ekanayake, P.; Ekanayake, J.; et al. Pandemic Simulator: An Agent-Based Framework with Human Behavior Modeling for Pandemic-Impact Assessment to Build Sustainable Communities. Sustainability 2023, 15. [Google Scholar] [CrossRef]
  49. Tuite, A.; Gallant, V.; Randell, E.; Bourgeois, A.C.; Greer, A. Stochastic agent-based modeling of tuberculosis in Canadian Indigenous communities. BMC Public Health 2017, 17. [Google Scholar] [CrossRef] [PubMed]
  50. Jung, H.J.; Jung, G.S.; Kim, Y.; Khan, N.T.; Kim, Y.H.; Kim, Y.B.; Park, J.S. Development and appplication of agent-based disease spread simulation model : The case of Suwon, Korea. 2017 Winter Simulation Conference (WSC) 2017. [Google Scholar] [CrossRef]
  51. Using data-driven agent-based models for forecasting emerging infectious diseases. Epidemics 2018, 22, 43–49. [CrossRef]
  52. Al-Shaery, A.M.; Hejase, B.; Tridane, A.; Farooqi, N.S.; Jassmi, H.A. Agent-based modeling of the Hajj Rituals with the possible spread of COVID-19. Sustainability 2021, 13, 6923. [Google Scholar] [CrossRef]
  53. Asgary, A.; Blue, H.; Solis, A.O.; McCarthy, Z.; Najafabadi, M.; Tofighi, M.A.; Wu, J. Modeling COVID-19 Outbreaks in Long-Term Care Facilities Using an Agent-Based Modeling and Simulation Approach. International Journal of Environmental Research and Public Health 2022, 19, 2635. [Google Scholar] [CrossRef]
  54. Dong, T.; Dong, W.; Xu, Q. Agent Simulation Model of COVID-19 Epidemic Agent-Based on GIS: A Case Study of Huangpu District, Shanghai. International Journal of Environmental Research and Public Health 2022, 19, 10242. [Google Scholar] [CrossRef]
  55. Jahn, B.; Sroczynski, G.; Bicher, M.; Rippinger, C.; Mühlberger, N.; Santamaria, J.; Urach, C.; Schomaker, M.; Stojkov, I.; Schmid, D.; et al. Targeted covid-19 vaccination (tav-covid) considering limited vaccination capacities—an agent-based modeling evaluation. Vaccines 2021, 9, 434. [Google Scholar] [CrossRef]
  56. Sun, C.; Richard, S.; Miyoshi, T.; Tsuzu, N. Analysis of COVID-19 spread in Tokyo through an agent-based model with data assimilation. Journal of Clinical Medicine 2022, 11, 2401. [Google Scholar] [CrossRef] [PubMed]
  57. Alvarez Castro, D.; Ford, A. 3D agent-based model of pedestrian movements for simulating COVID-19 transmission in university students. ISPRS International Journal of Geo-Information 2021, 10, 509. [Google Scholar] [CrossRef]
  58. Popescu, M.; Keller, J.M.; Zare, A. A framework for computing crowd emotions using agent based modeling. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence for Creativity and Affective Computing (CICAC); 2013; pp. 25–31. [Google Scholar]
  59. Guo, X.; Chen, P.; Liang, S.; Jiao, Z.; Li, L.; Yan, J.; Huang, Y.; Liu, Y.; Fan, W. PaCAR: COVID-19 pandemic control decision making via large-scale agent-based modeling and deep reinforcement learning. Medical Decision Making 2022, 42, 1064–1077. [Google Scholar] [CrossRef] [PubMed]
  60. Zong, K.; Luo, C. Reinforcement learning based framework for COVID-19 resource allocation. Computers & Industrial Engineering 2022, 167, 107960. [Google Scholar]
  61. Kompella, V.; Capobianco, R.; Jong, S.; Browne, J.; Fox, S.; Meyers, L.; Wurman, P.; Stone, P. Reinforcement learning for optimization of COVID-19 mitigation policies. arXiv preprint arXiv:2010.10560 2020. arXiv:2010.10560 2020.
  62. Kadinski, L.; Salcedo, C.; Boccelli, D.L.; Berglund, E.; Ostfeld, A. A hybrid data-driven-agent-based modelling framework for water distribution systems contamination response during COVID-19. Water 2022, 14, 1088. [Google Scholar] [CrossRef]
  63. Kadinski, L.; Ostfeld, A. Incorporation of COVID-19-inspired behaviour into agent-based modelling for water distribution systems’ contamination responses. Water 2021, 13, 2863. [Google Scholar] [CrossRef]
  64. Harati, S.; Perez, L.; Molowny-Horas, R. Promoting the emergence of behavior norms in a principal–agent problem—An agent-based modeling approach using reinforcement learning. Applied Sciences 2021, 11, 8368. [Google Scholar] [CrossRef]
  65. Augustijn, E.W.; Aguilar Bolivar, R.; Abdulkareem, S. Using Machine Learning to drive social learning in a Covid-19 Agent-Based Model. AGILE: GIScience Series 2023, 4, 19. [Google Scholar] [CrossRef]
  66. Fonseca i Casas, P.; Garcia i Carrasco, V.; Garcia i Subirana, J. SEIRD COVID-19 formal characterization and model comparison validation. Applied Sciences 2020, 10, 5162. [Google Scholar] [CrossRef]
  67. Grimm, V.; Berger, U.; DeAngelis, D.L.; Polhill, J.G.; Giske, J.; Railsback, S.F. The ODD protocol: a review and first update. Ecological modelling 2010, 221, 2760–2768. [Google Scholar] [CrossRef]
  68. Knoblauch, R.L.; Pietrucha, M.T.; Nitzburg, M. Field studies of pedestrian walking speed and start-up time. Transportation research record 1996, 1538, 27–38. [Google Scholar] [CrossRef]
  69. Rajgor, D.D.; Lee, M.H.; Archuleta, S.; Bagdasarian, N.; Quek, S.C. The many estimates of the COVID-19 case fatality rate. The Lancet Infectious Diseases 2020, 20, 776–777. [Google Scholar] [CrossRef] [PubMed]
  70. Robinson, S. Simulation: The Practice of Model Development and Use, 2nd edition; 2014.
Preprints 85705 g001
Figure 1. Selected natural history for COVID-19 transmission
Figure 1. Selected natural history for COVID-19 transmission
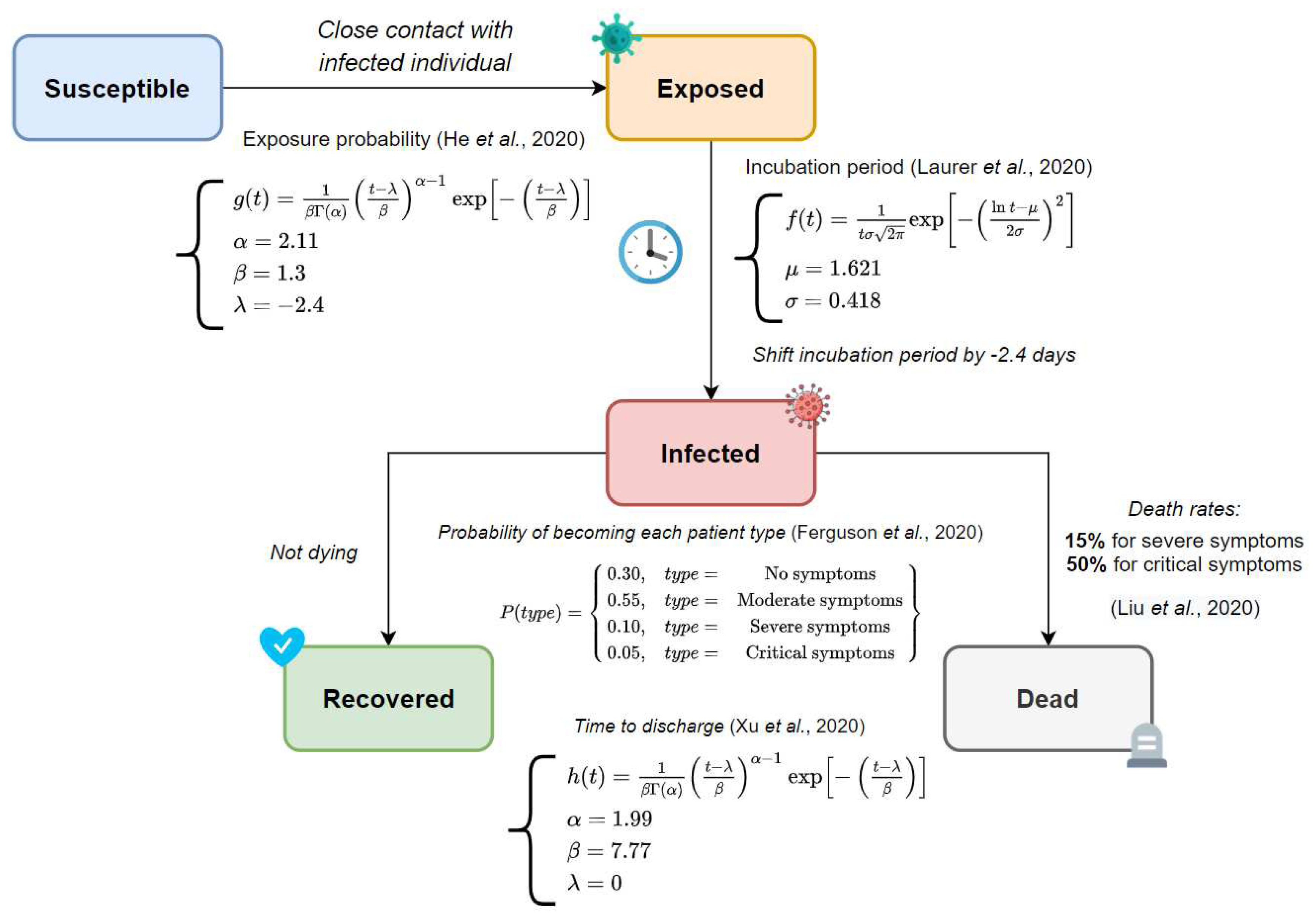
Preprints 85705 g001
Preprints 85705 g002
Figure 2. Component model
Figure 2. Component model
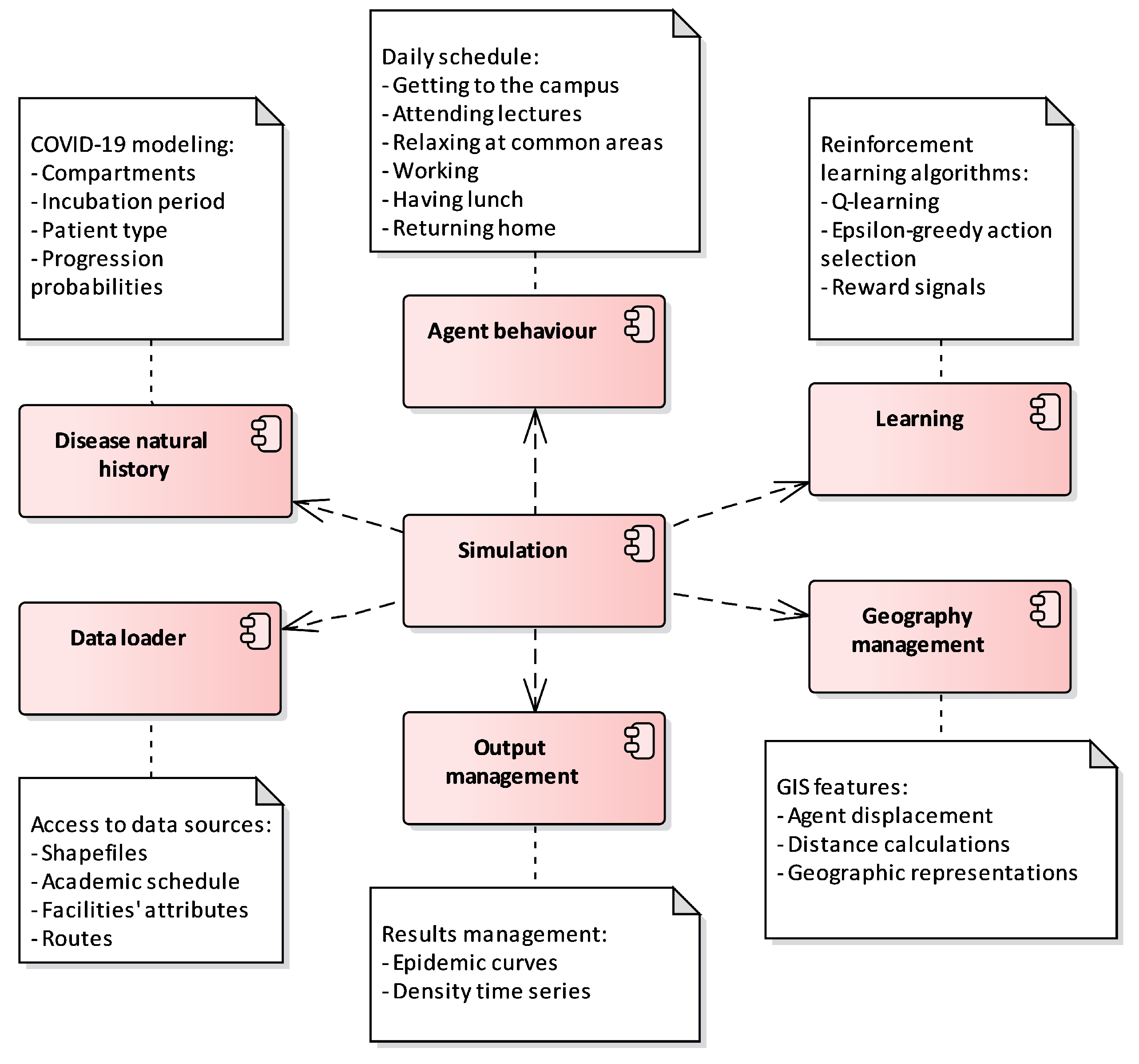
Preprints 85705 g002
Preprints 85705 g003
Figure 3. Blueprint of the class diagram
Figure 3. Blueprint of the class diagram
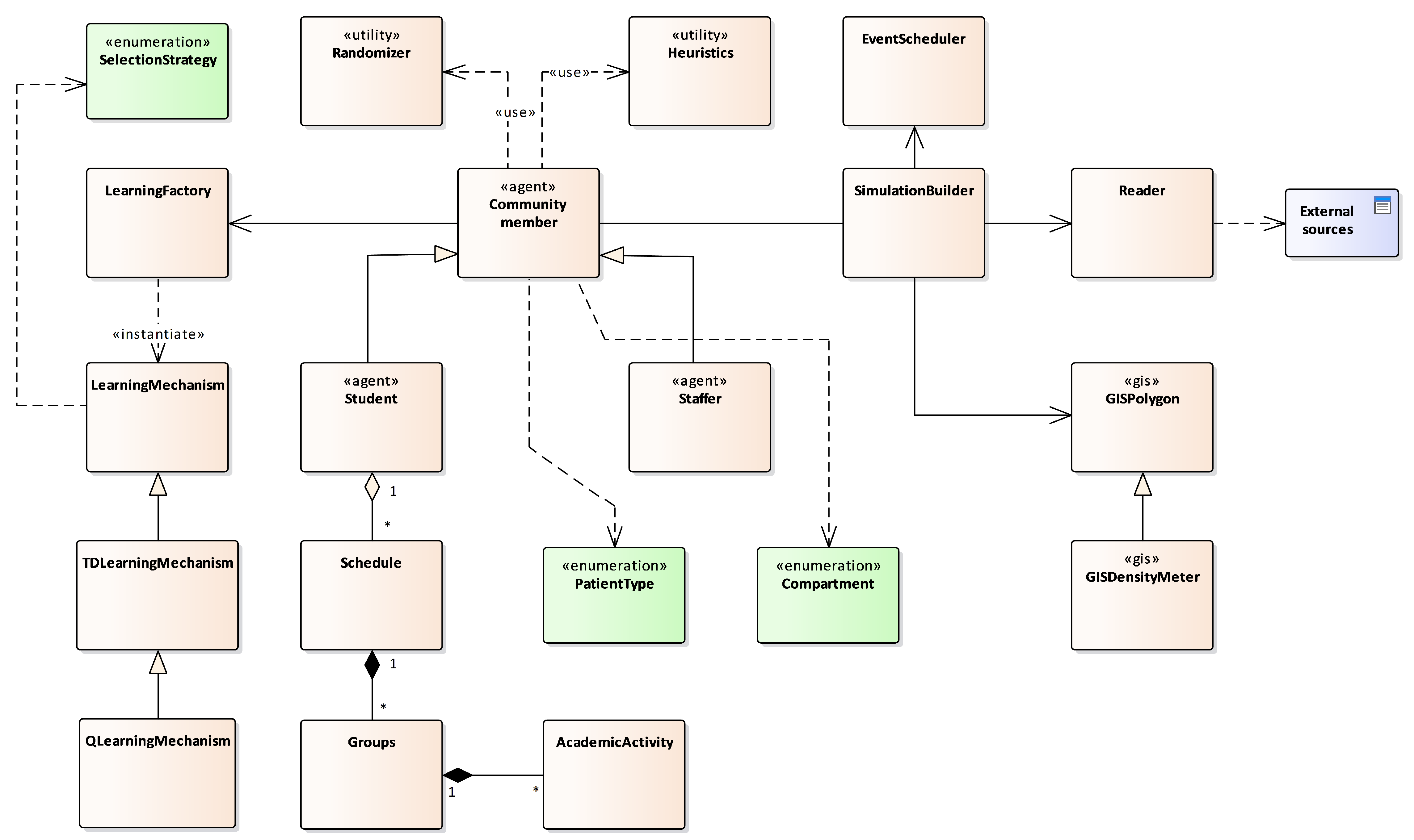
Preprints 85705 g003
Preprints 85705 g004
Figure 4. Model’s visualization
Figure 4. Model’s visualization
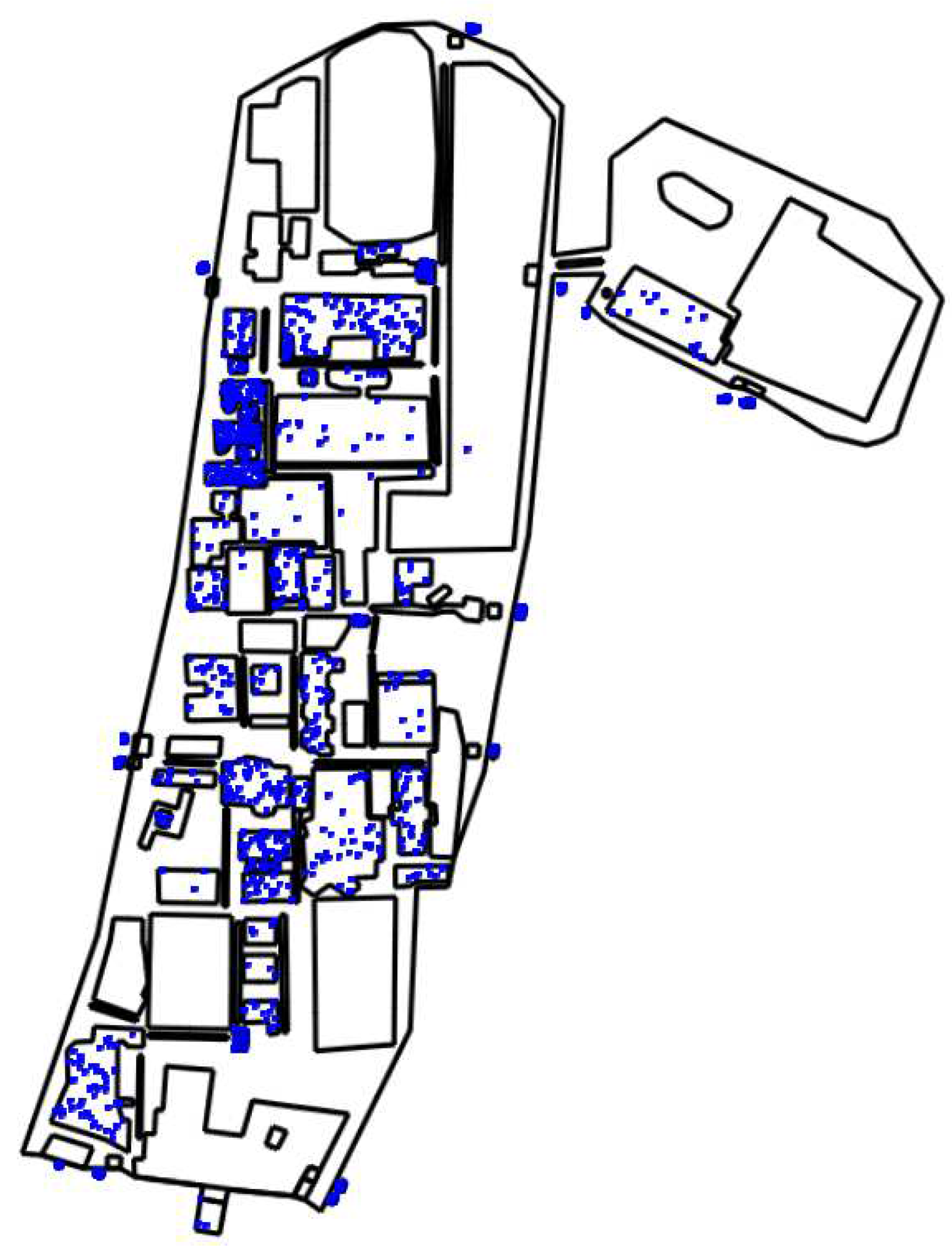
Preprints 85705 g004
Preprints 85705 g005
Figure 5. Base mean densities on campus
Figure 5. Base mean densities on campus
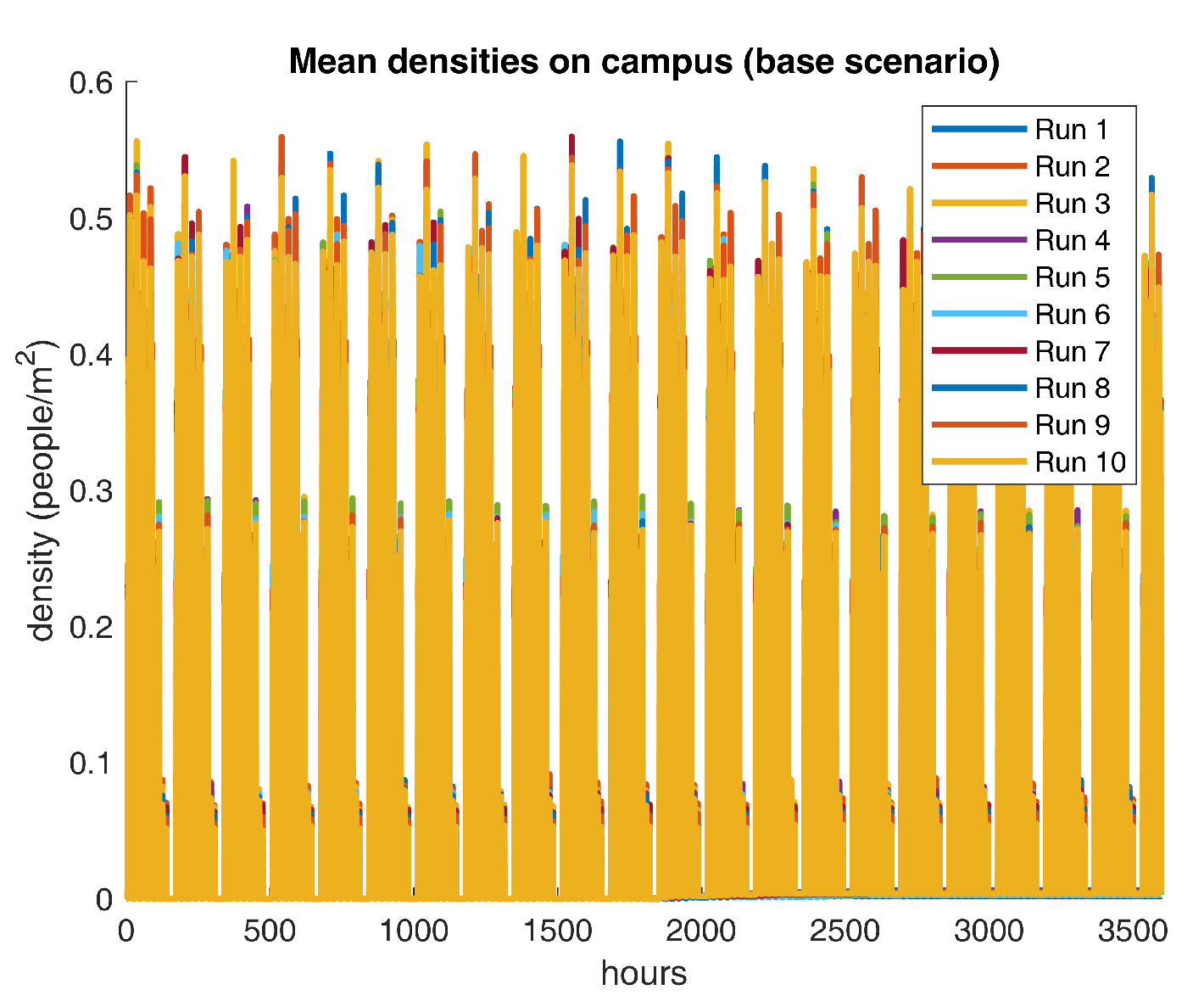
Preprints 85705 g005
Preprints 85705 g006
Figure 6. Histogram of base densities
Figure 6. Histogram of base densities
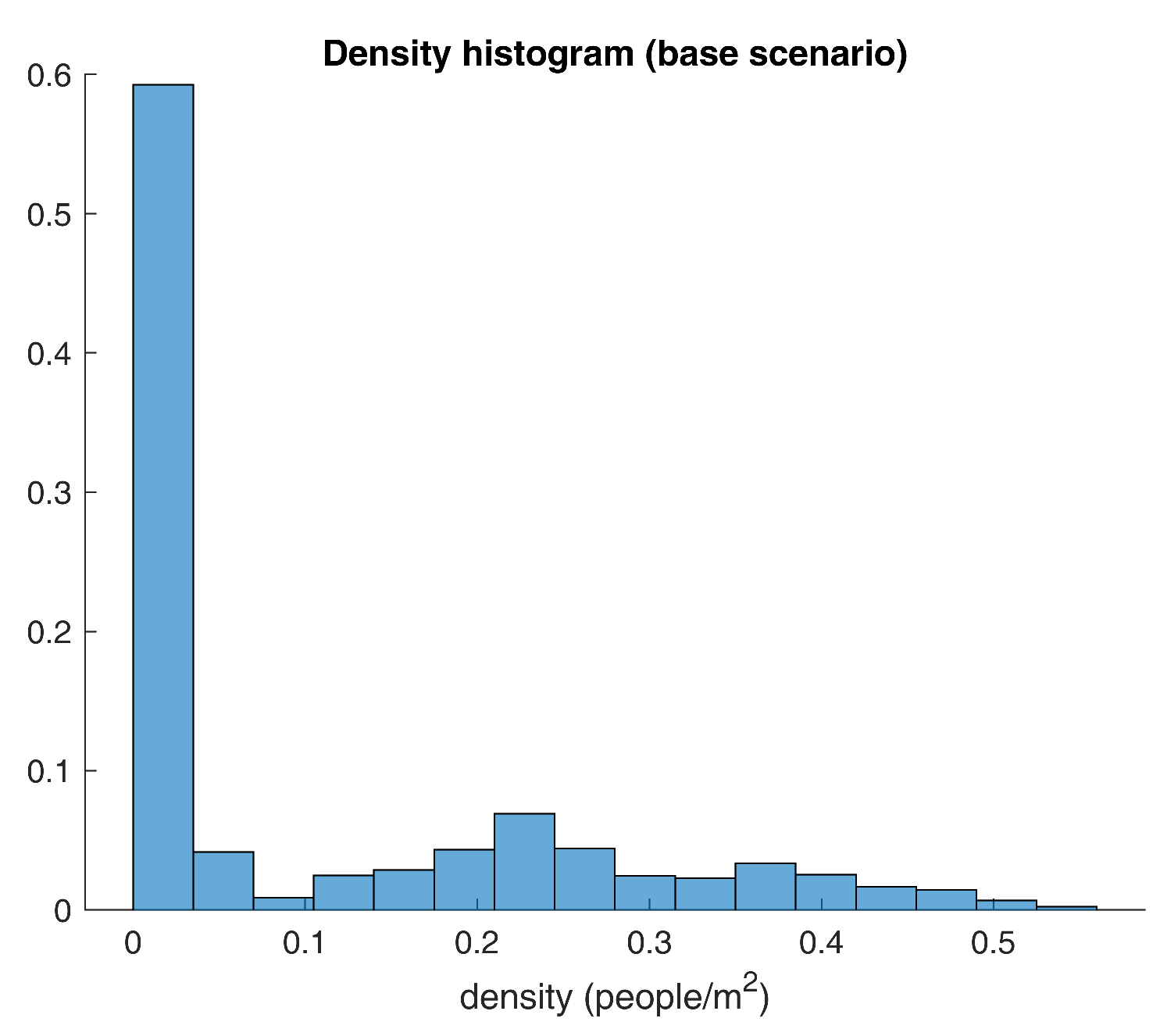
Preprints 85705 g006
Preprints 85705 g007
Figure 7. Base densities’ independence analysis
Figure 7. Base densities’ independence analysis
Preprints 85705 g007
Preprints 85705 g008
Figure 8. Base densities’ boxplots
Figure 8. Base densities’ boxplots
Preprints 85705 g008
Preprints 85705 g009
Figure 9. Densities’ boxplots
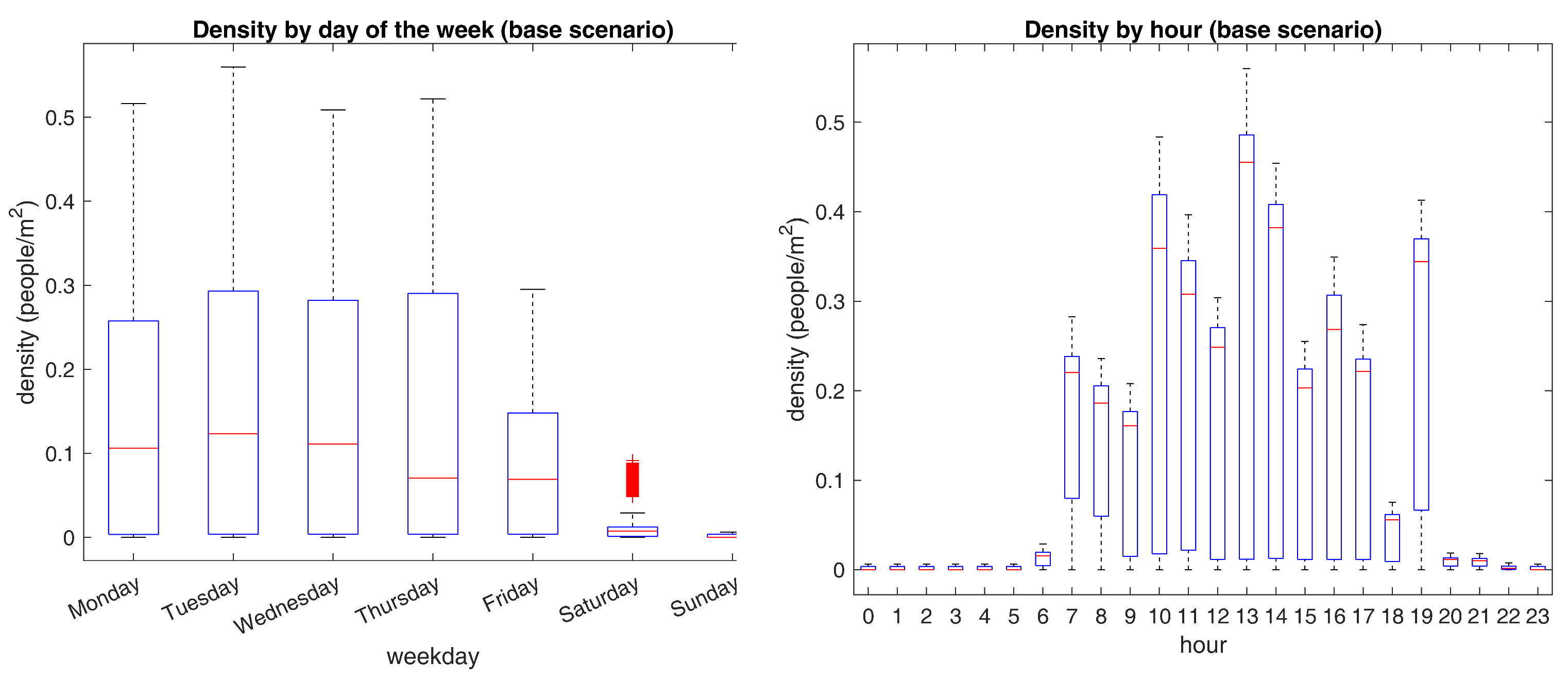
Figure 9. Densities’ boxplots
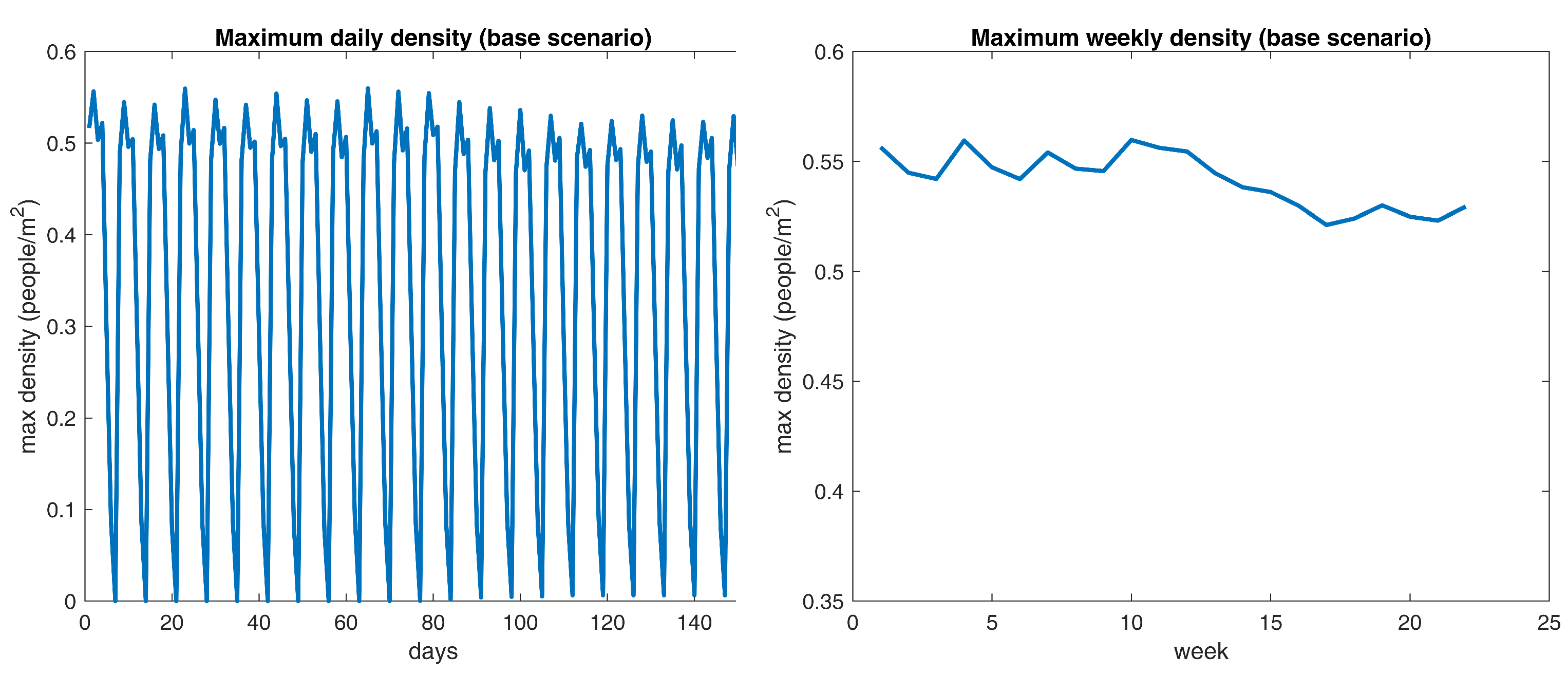
Preprints 85705 g009
Preprints 85705 g010
Figure 10. Base epidemic curves
Figure 10. Base epidemic curves
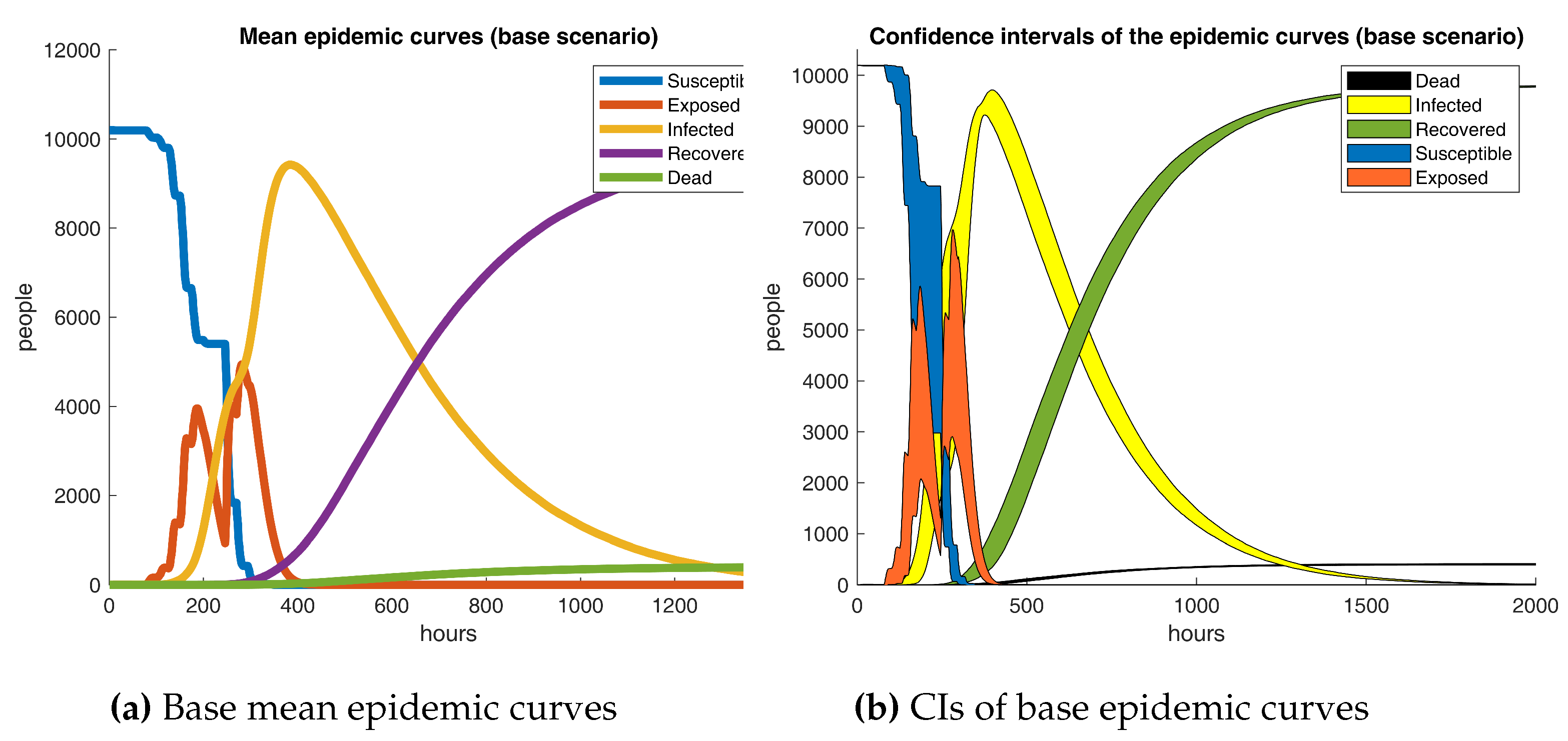
Preprints 85705 g010
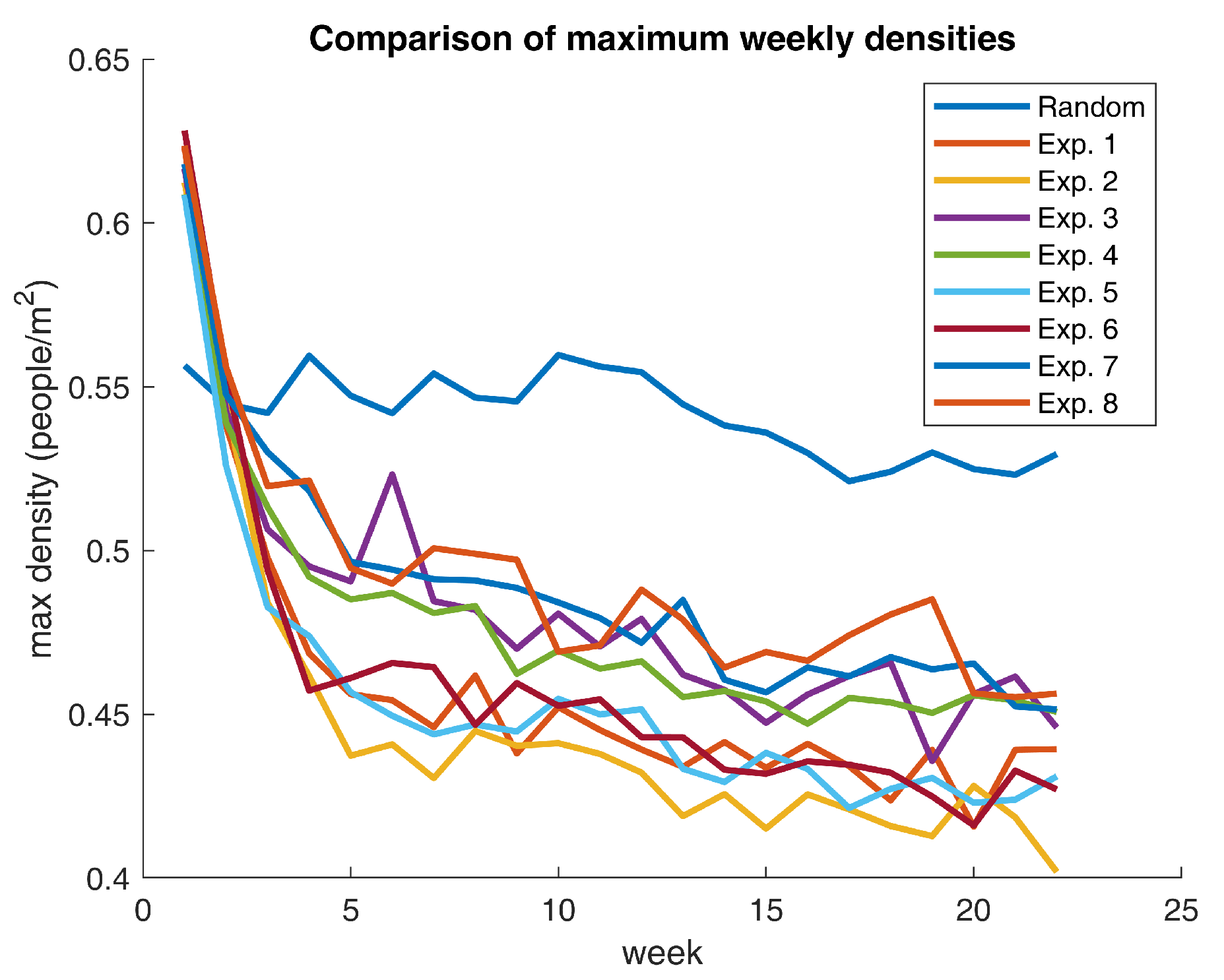
Preprints 85705 g011
Figure 11. Comparison of maximum weekly densities
Figure 11. Comparison of maximum weekly densities
Preprints 85705 g011
Preprints 85705 g012
Figure 12. Comparison of active cases
Figure 12. Comparison of active cases
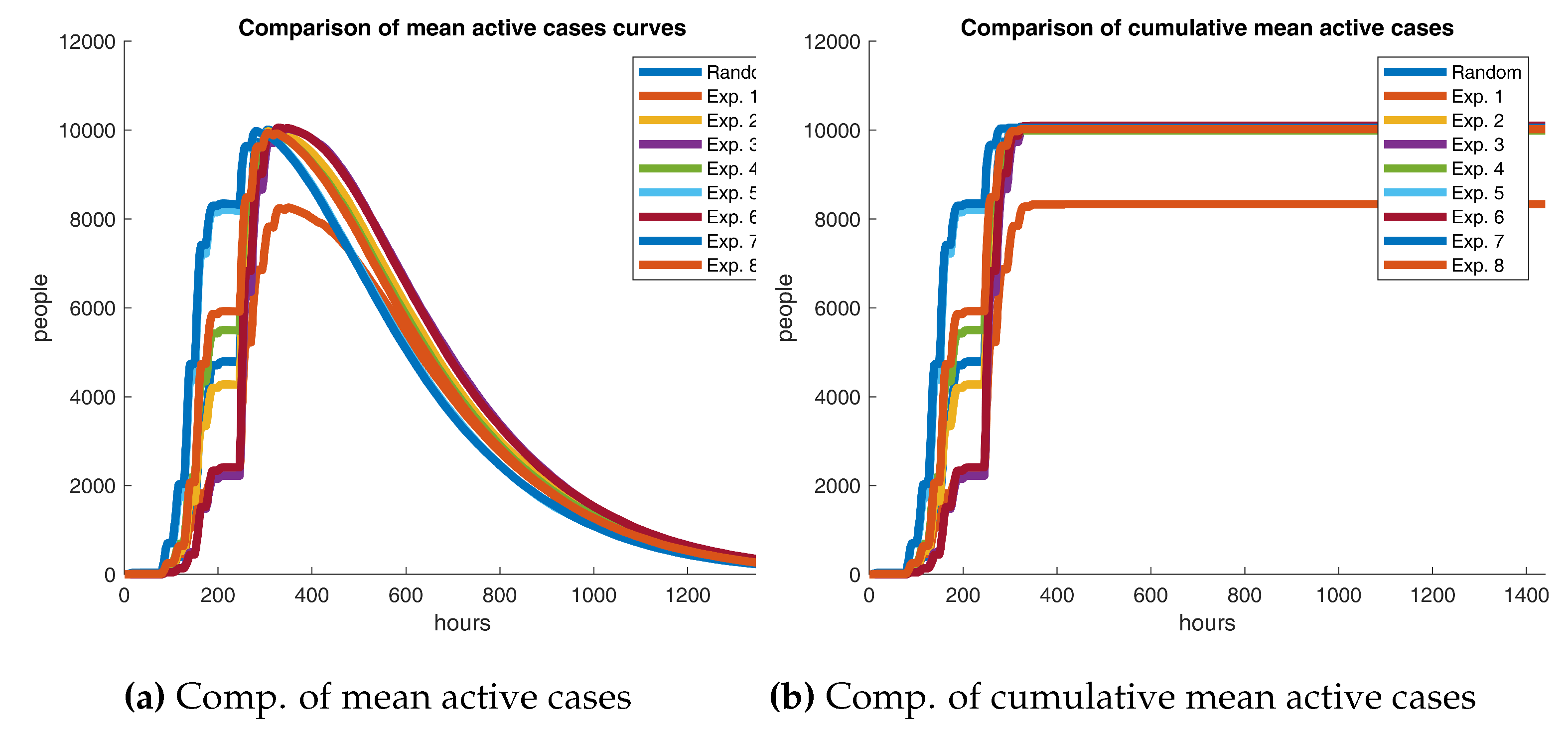
Preprints 85705 g012
Preprints 85705 g013
Figure 13. Confidence intervals in Experiments 1 and 2
Figure 13. Confidence intervals in Experiments 1 and 2
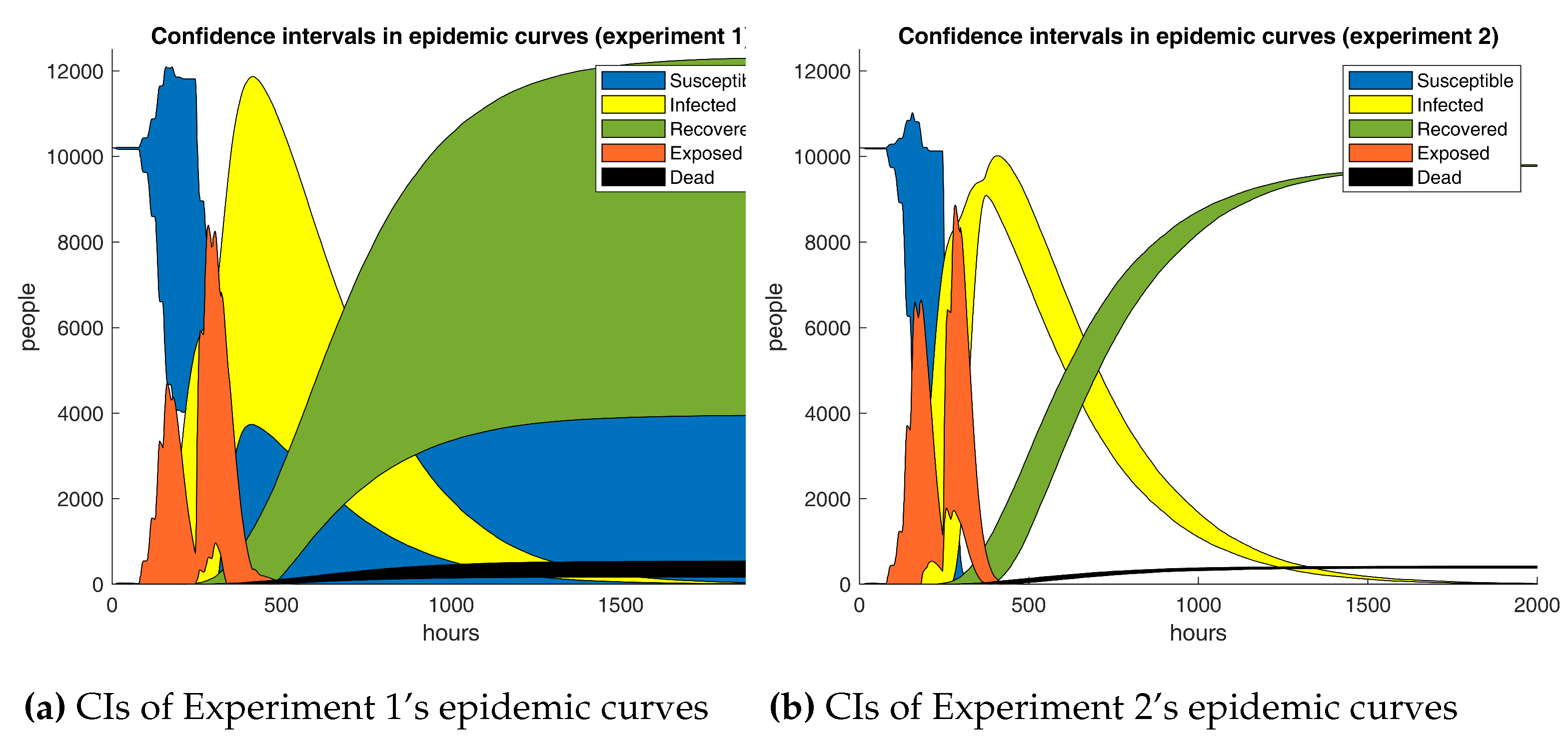
Preprints 85705 g013
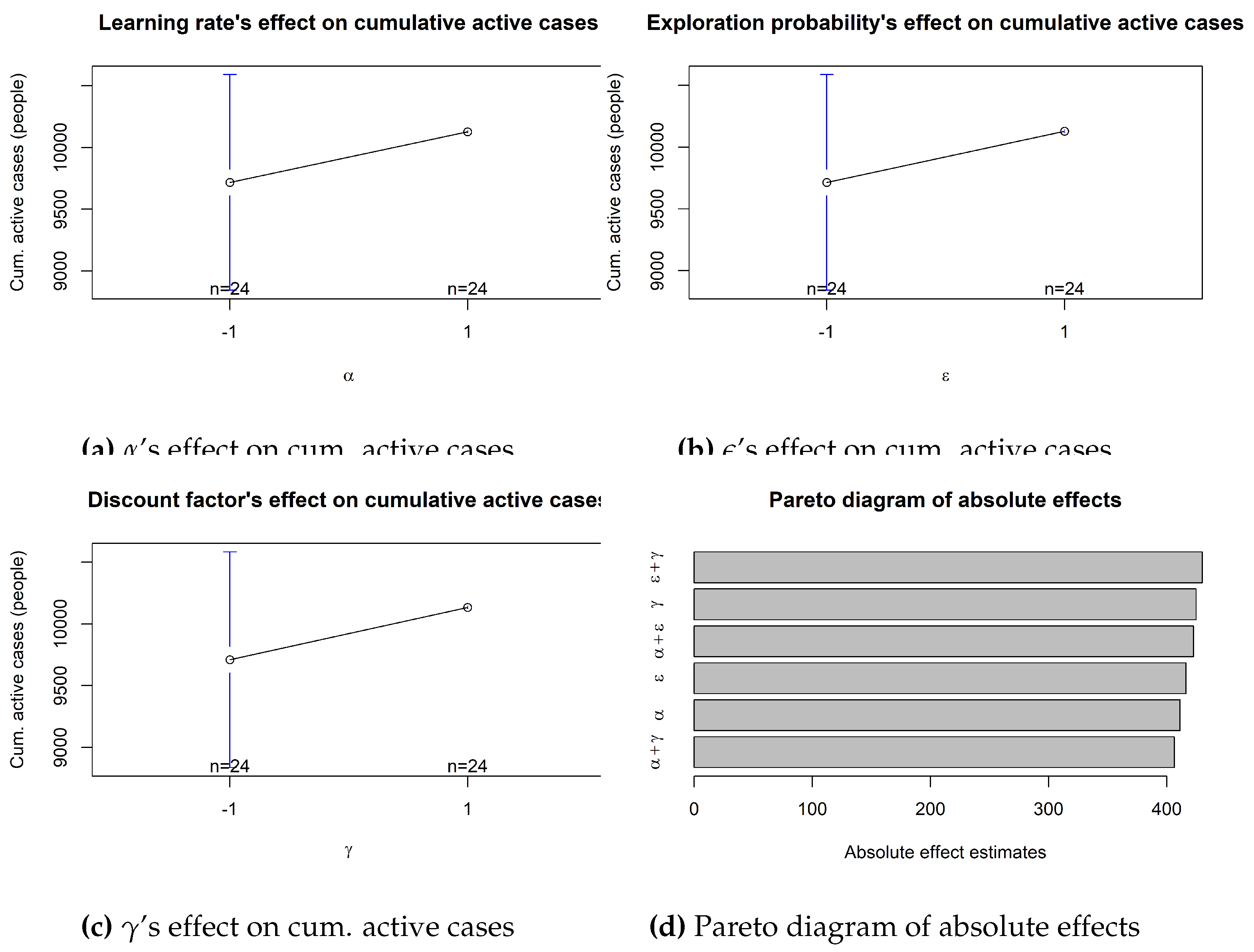
Preprints 85705 g014
Figure 14. Estimation of factor effects
Figure 14. Estimation of factor effects
Preprints 85705 g014
Table 1. Agent entities’ state variables
Table 1. Agent entities’ state variables
Variable name Brief description
Current location This variable represents the place the agent is currently located in. It is a reference to a place instance. Furthermore, this reference changes over time as the agent moves around campus.
Current compartment This variable represents the current epidemic state of the agent. An agent can be in only one of the following states: susceptible (S), exposed (E), infected (I), immune (R), or dead (D). Besides, the current compartment is dynamic as the disease progresses according to estimated random processes.
Routine This variable is a list of scheduled activities the agent has to perform every single week. Indeed, both students and staffers have a different list of events. For example, both agent types lunch at noon, but students attend classes and staffers work. Specifically, weekly routines are assumed unchanged during the simulation.
Learning state-value pairs This variable is a list of state-value pairs that represent the learning mechanism of each agent. This list holds a numeric representation (in the − 1 , 0.5 range) for each facility’s perceived danger. In addition, this list changes as the agent visits new places and updates its perceptions.
Table 2. Places’ state variables
Table 2. Places’ state variables
Variable name Brief description
Current population This variable measures the total population count inside the place. As a consequence, this counter is dynamic as people follow their routines. Naturally, this variable is an integer in the range 0 , N , where N is the total population in the simulation.
Area This variable holds the area of the place. As a result, it is a constant assigned during the initialization phase. The area of a site is a real number in the range 0 , A , where A is a finite real number.
Population density This variable measures the population density inside the place. Because of this, it is dynamic as people walk around the campus. Also, the density is a real number in the range 0 , D , where D is a finite real number.
Infections count This variable measures the number of infections that happened inside the place. As a result, it is dynamic as people interact with each other, and the virus spreads on campus. Clearly, this counter is an integer in the 0 , N , where N is the total population in the simulation.
Table 3. Environment’s state variables
Table 3. Environment’s state variables
Variable name Brief description
Clock This variable holds the current simulation time. For this reason, this it is measured in ticks.
Time to the first COVID-19 case This variable holds a time reference for the appearance of the first COVID-19 case on campus. As a consequence, it is defined as the number of ticks to the aforementioned event.
Table 4. Input parameters
Table 4. Input parameters
Parameter Brief description Unit Default value
Susceptible students This count is the initial number of susceptible students in the simulation. people 10.000
Susceptible staffers This count is the initial number of susceptible staffers in the simulation. people 200
Outbreak tick This input is the number to ticks to activate the outbreak scenario. hours 1440
Infected students This count is the number of students to spontaneously infect once the scheduled outbreak tick is reached. people 1
Infected staffers This count is the number of staffers to spontaneously infect once the scheduled outbreak tick is reached. people 0
Infection radius This radius is the maximum distance in which an effective contact is possible. meters 2
Social distancing This input measures the ideal minimum social distance between two agents. meters 2
Selection strategy This input determines whether a random or learning-based action selection is applied when facing a facility choice situation. - random
Learning rate This input is the α parameter in Equation 1. - 0.1
Discount factor This input is the γ parameter in Equation 1. - 0.8
Epsilon This input is the ϵ parameter used in the ϵ -greedy action selection. - 0.1
Vehicle usage ratio This input is the p parameter for the vehicle usage’s Bernoulli distribution. probability 0.3
Table 5. Summary of main stochastic elements of the model
Table 5. Summary of main stochastic elements of the model
Element Brief description Distribution
Lunchtime This random variable describes the moment an agent haves lunch on a particular day. Uniform ( 11.5 , 14 )
Lunch duration This random variable describes the duration in hours of an agent’s lunch. Normal ( μ = 0.66 , σ = 0.16 )
Arrival shift to an academic activity This random variable describes the number of minutes the student arrives before a given activity. Normal ( μ = 0.16 , σ = 0.08 )
Vehicle usage This random variable describes the probability of an agent having a vehicle. Bernoulli ( p )
Walking speed This random variable describes an agent’s walking speed (meters per minute). Uniform ( 70 , 100 )
Groups to enroll This random variable describes the number of groups an agent enrolls in. Binomial ( n = 7 , p = 0.71 )
Exposure probability This random variable describes the probability a susceptible individual getting exposed to the virus. Equation 2
Incubation period This random variable describes the length of the incubation period in days. Equation 3
Patient type This random variable describes the probability of an agent becoming each patient type. Equation 4
Death decision This random variable describes the probability of an agent dying from COVID-19. Equation 5
Time to discharge This random variable describes the number of days for an agent to recover or die from the disease. Equation 6
Table 6. Base densities’ basic statistics
Table 6. Base densities’ basic statistics
Statistic Value
Mean 0.1053
Median 0.0112
Std. dev. 0.1436
Minimum 0
Maximum 0.5597
Skewness 1.1383
Kurtosis 3.0050
Table 7. Mean confidence intervals for the base densities in a week
Table 7. Mean confidence intervals for the base densities in a week
Day Lower bound Upper bound
Monday 0.1413 0.1494
Tuesday 0.1616 0.1708
Wednesday 0.1528 0.1616
Thursday 0.1532 0.1621
Friday 0.0854 0.0904
Saturday 0.0130 0.0141
Sunday 0.0016 0.0017
Week 0.1038 0.1067
Table 8. Experimental factor levels
Table 8. Experimental factor levels
Factor Low level (-) High level (+)
Learning rate ( α ) 0.1 0.25
Exploration probability ( ϵ ) 0.1 0.25
Discount factor ( γ ) 0.8 0.95
Table 9. 2 3 factorial design of experiments
Table 9. 2 3 factorial design of experiments
Experiment Learning rate ( α ) Exploration probability ( ϵ ) Discount factor ( γ )
1 - - -
2 - - +
3 - + -
4 - + +
5 + - -
6 + - +
7 + + -
8 + + +
Table 10. Experiments’ key density figures
Table 10. Experiments’ key density figures
Experiment Mean Std. dev. Relative reduction (%)
1 0.0936 0.1266 17.01
2 0.0941 0.1269 24.09
3 0.0965 0.1311 15.77
4 0.0961 0.1306 14.87
5 0.0954 0.1297 18.58
6 0.0958 0.1292 19.33
7 0.0981 0.1328 14.72
8 0.0982 0.1329 13.83
Table 11. Experiments’ key epidemic figures
Table 11. Experiments’ key epidemic figures
Experiment Rel. mean cumulative difference ( c d ¯ % ) Spline difference
1 16.49 835190
2 0.30 -19820
3 1.49 -12080
4 0.35 -25393
5 -2.04 -13349
6 1.19 -30501
7 -2.16 -21410
8 0.16 -4282
Table 12. Experimental non-parametric tests
Table 12. Experimental non-parametric tests
Experiment Friedman’s p-value Wilcoxon’s p-value Kruskal-Wallis’ p-value
1 0 0.0619 0.0619
2 0 0.7289 0.7289
3 0 0.9182 0.9182
4 0.3294 0.5986 0.5986
5 0 0.6627 0.6627
6 0 0.3914 0.3914
7 0 0.4356 0.4356
8 0 0.9106 0.9106
Table 13. Analysis of variance of factor’s effects
Table 13. Analysis of variance of factor’s effects
Factor DF Sum Sq. Mean Sq. F stat. p-value
α 1 2029108 2029108 0.946 0.337
ϵ 1 2078753 2078753 0.969 0.331
γ 1 2165376 2165376 1.01 0.321
α + ϵ 1 2143343 2143343 1 0.323
α + γ 1 1981688 1981688 0.924 0.342
ϵ + γ 1 2219230 2219230 1.035 0.315
α + ϵ + γ 1 2153498 2153498 1.004 0.322
Residuals 40 85767210 2144180
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated