Preprint
Article
Deep Supervised Hashing by Fusing Multiscale Deep Features
Altmetrics
Downloads
122
Views
109
Comments
0
This version is not peer-reviewed
Submitted:
22 September 2023
Posted:
26 September 2023
You are already at the latest version
Alerts
Abstract
Deep networks-based hashing has gained significant popularity in recent years, particularly in the field of image retrieval. However, most existing methods only focus on extracting semantic information from the final layer, disregarding valuable structural information that contains important semantic details crucial for effective hash learning. To address this limitation and improve image retrieval accuracy, we propose a novel deep hashing method called Deep Supervised Hashing by Fusing Multiscale Deep Features (DSHFMDF). Our approach involves extracting multiscale features from multiple convolutional layers and fusing them to generate more robust representations for efficient image retrieval. Experimental results on CIFAR10 and NUS-WIDE datasets demonstrate that our method surpasses the performance of state-of-the-art hashing techniques.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
The internet and communication advancements have led to an overwhelming influx of images on the web [1,2,3], creating a challenge for accurate and efficient large-scale data retrieval. To address this, hash-based image retrieval techniques [4] have gained attention due to their ability to generate compact binary codes, offering computational efficiency and storage advantages.
These techniques can be classified as data-independent and data-dependent approaches. Data-independent methods, such as locality-sensitive hashing (LSH) [5], use random projections as hash functions but suffer from limitations. They do not utilize auxiliary information, leading to poor retrieval accuracy, and require longer codes, consuming more storage [5,6,7]. In contrast, data-dependent methods leverage training information to learn hashing functions, resulting in shorter codes with improved performance. They can be further categorized as unsupervised [8,9,10,11] or supervised hashing methods [12,13,14,15,16,17,18].
Deep hashing techniques [19,20,21,22] have arisen as a result of the achievements made by deep neural networks in computer vision tasks. These methods, as opposed to traditional hashing methods, possess the ability to effectively extract high-level semantic features and facilitate end-to-end frameworks for generating binary codes. Nevertheless, a drawback of numerous existing deep hashing techniques [23,24,25] is their reliance on features from the penultimate layer in fully connected networks, which serve as global image descriptors but fail to capture local characteristics.
To overcome these challenges, this paper proposes a novel deep hashing method, called Deep Supervised Hashing by Fusing Multi-scale Deep Features (DSHFMDF), which effectively captures multi-scale object information. Specifically, it extracts features from different network stages, fuses them at the fusion layer, and encodes them into robust hash codes. The network used various hashing results based on different scale features, enhancing retrieval recall without sacrificing precision. The key contributions of this paper are as follows:
- DSHFMDF employs multiple feature scales to learn binary codes, which are then fused together to enhance retrieval performance.
- The research paper presents a novel deep hashing method that integrates the learning of feature representations and binary codes within a unified framework.
- Through experimental assessments conducted on two extensive datasets, DSHFMDF demonstrates superior performance compared to existing methods in real-world applications.
2. Related Works
In recent years, hashing methods have gained significant attention in the field of image retrieval due to their ability to efficiently store large amounts of data and process it quickly [6,26]. The fundamental objective of hashing is to transform input data with high-dimensional, such as images, into hash codes with low-dimensional. By doing so, hashing methods aim to reduce the Hamming distance between similar image pairs while maximizing it for dissimilar pairs, enabling efficient and accurate image retrieval.
The existing literature on hashing methods can be broadly categorized into two types: supervised and unsupervised approaches. Supervised hashing methods utilize labeled data, whereas unsupervised methods operate without the use of any supervision. Unsupervised hashing methods, such as Locality Sensitive Hashing (LSH) [27], Spectral Hashing (SH) [28], and Iterative Quantization (ITQ) [8] is a technique that seeks to learn hash functions through unlabeled training samples. These approaches convert input images into binary codes, enabling efficient storage and retrieval. While LSH has been one of the most widely used unsupervised hashing approaches, other methods like SH and ITQ have also been successfully employed in subsequent studies.
Supervised hashing techniques, on the other hand, leverage the availability of labeled data to improve the accuracy of the generated hash codes. These methods outperform unsupervised approaches in terms of retrieval performance. Some notable supervised hashing methods include Supervised Hashing with Kernels (KSH) [29], Minimal Loss Hashing (MLH) [30], and Supervised Discrete Hashing (SDH) [31]. KSH introduces a nonlinear hash function in kernel space to capture complex relationships between image features and their corresponding labels. Instead of directly optimizing hash functions, MLH employs structured Support Vector Machines (SVM) to create an objective function for learning hash functions. In contrast, SDH prioritizes the generation of top-notch hash codes without any relaxation by redefining the optimization objective.
Due to the swift progress in deep neural networks, deep hashing methods have emerged as a powerful approach in image retrieval. These methods leverage the extensive feature representations provided by deep neural networks to achieve superior performance compared to traditional hand-crafted feature-based approaches. Various deep hashing algorithms have been proposed, including CNNH [32], Deep Pairwise- supervised Hashing (DPSH) [32], HashGAN [33], Zhuang et al. [34], Deep Triplet Quantization (DTQ) [35], Supervised Learning of Semantics-Preserving Hash (SSDH) [36], Wang et al. [37], and Similarity-Adaptive Deep Hashing (SADH) [38].
CNNH is an algorithm that focuses on learning hash codes by utilizing features extracted from Convolutional Neural Networks (CNNs). It follows a two-step process where the hash function learning and feature representation learning are performed independently. By leveraging the rich and high-level representations captured by CNNs, CNNH aims to generate effective hash codes for image retrieval tasks. In contrast, DPSH takes a Bayesian approach to establish a relationship between hash codes and pairwise labels. It optimizes this relationship to learn hash functions that can effectively preserve the pairwise similarities among the data samples. By considering the pairwise label information, DPSH aims to learn more discriminative hash codes that can improve the retrieval performance. HashGAN, on the other hand, introduces the use of Wasserstein Generative Adversarial Networks (GANs) to enhance the training process. It exploits pairwise similarity or dissimilarity information to generate hash codes within a Bayesian framework. By leveraging the power of GANs, HashGAN can effectively increase the amount of training data and generate high-quality hash codes. In the study by Zhuang et al., they propose a binary CNN classifier that incorporates a triplet-based loss. This loss function is designed to learn both semantic links and hashing functions simultaneously. By considering triplets of samples with their corresponding similarities or dissimilarities, the binary CNN classifier aims to learn hash codes that not only preserve the semantic relationships among data samples but also enhance the retrieval accuracy. DTQ takes a different approach by combining a triplet quantization strategy within a supervised deep learning framework. It jointly optimizes the quantization and feature learning processes to generate discriminative hash codes. By considering the relationships among triplets of samples, DTQ aims to learn hash codes that can preserve the relative distances between data samples and improve retrieval performance. SSDH introduces a novel approach where hash functions are built as new fully connected layers (FC Layers). The learning of hash codes is achieved by minimizing the specified classification error. By incorporating the hash functions as additional layers within the network architecture, SSDH aims to learn compact and discriminative hash codes that can effectively preserve the semantic information of the data. Wang et al. provide a general framework for distance-preserving linear hashing that incorporates deep hashing approaches. This framework aims to learn hash functions that can preserve the pairwise distances between data samples, enabling efficient similarity search. By integrating deep hashing algorithms into the framework, Wang et al. propose an effective way to learn discriminative hash codes for image retrieval tasks. SADH is a two-step hashing algorithm that leverages the output representations from the fully connected layers (FC Layers) to update the similarity graph matrix. By utilizing the FC Layer outputs, SADH aims to improve the optimization process of hash codes. This approach focuses on capturing the intrinsic structure of the data and refining the hash codes accordingly, leading to enhanced retrieval performance. Overall, these approaches showcase various strategies to leverage deep learning techniques for the task of image hashing. They aim to learn effective hash codes by exploiting the power of deep neural networks, considering pairwise relationships, incorporating Bayesian frameworks, and optimizing the hash functions based on different objectives and constraints.
While many hashing methods focus on using features from the last fully connected layer (FC), it has been recognized that extracting different types of features can lead to a more comprehensive image description and enhance retrieval performance. Several approaches have been suggested for multiple-levels image retrieval. For instance, Lin et al. propose DDH [39], which combines end-to-end learning, divide-and-encode, and hash code learning into a unified framework. DDH employs a stack of convolutional pooling (conv-pool) layers to obtain multi-scale features by combining the outputs of the third pooling layer and the fourth convolutional layer. In their work, Yang et al. present Feature Pyramid Hashing (FPH) [40], a novel architecture for image hashing that incorporates two pyramids, namely vertical and horizontal pyramids. FPH is designed to effectively capture intricate visual details and semantic information, thereby enabling the retrieval of fine-grained images. Ng et al. introduce a ground-breaking method called multi-level supervised hashing (MLSH) [41] for image retrieval. MLSH focuses on constructing and training distinct hash tables that utilize various levels of features, such as semantic and structural information. By incorporating multiple levels of information, MLSH aims to enhance the accuracy of image retrieval.
In summary, hashing methods in image retrieval have witnessed significant advancements in recent years. From unsupervised approaches to supervised and deep hashing techniques, researchers have explored various methods to learn effective hash functions and generate compact hash codes for efficient image retrieval. Furthermore, the incorporation of multi-level features has shown promise in improving retrieval performance by capturing both fine-grained details and high-level semantics.
3. Proposed method
In this section, we provide a comprehensive explanation of our proposed approach, Deep Supervised Hashing by Fusing Multiscale Deep Features (DSHFMDF). We start by defining the problem of learning hash codes and subsequently introduce the architecture of our model. Finally, we describe the objective function of our proposed DSHFMDF method.
3.1. Problem definition
Let represent training dataset consisting of N image. Here, denotes the ground truth labels for the samples, where K represents the number of classes. The pairwise label matrix indicates the semantic similarity between training image samples, with . If , it signifies that samples and are semantically similar, whereas indicates that they are not. The objective of deep hashing methods, is to learn a deep hash function that encodes each input into . Here, L represents the length of the binary codes.
3.2. Model architecture
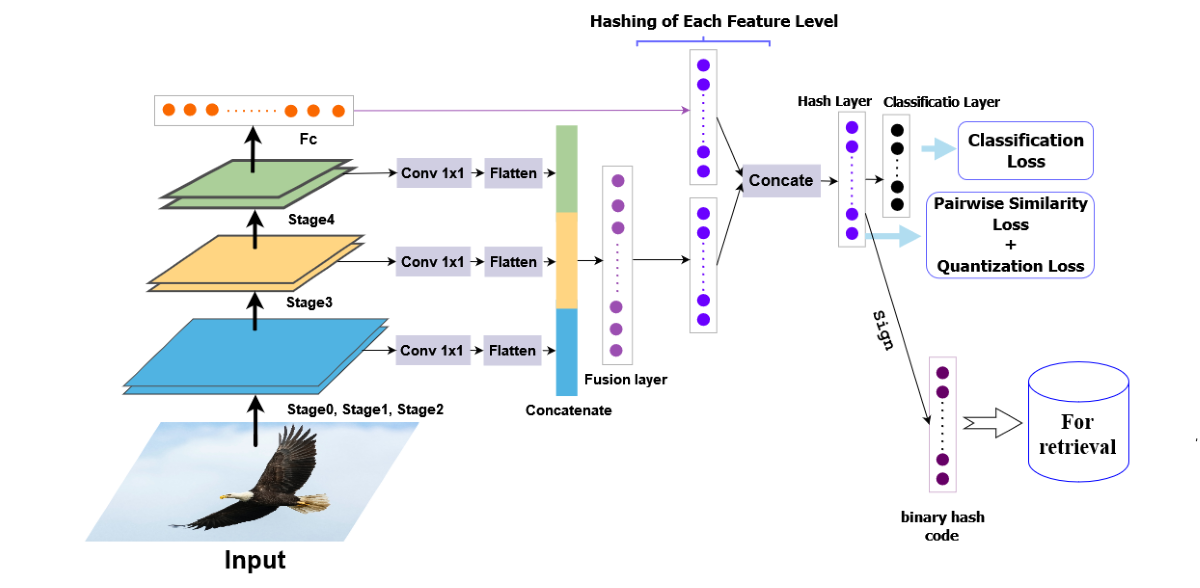
Our proposed approach for the model architecture is designed to be comprehensive and effective, consisting of five main components: (1) feature extraction; (2) feature reduction; (3) feature fusion; (4) hash coding; (5) and classification. By providing a more detailed and bulky description, we can better understand the intricacies of each component and how they contribute to the overall functionality of the model.
To begin with, the feature extraction stage plays a crucial role in capturing relevant information from the input image. In our approach, we leverage the VGG-19 network as the backbone, which is a deep convolutional neural network known for its ability to extract rich and discriminative features. The VGG-19 architecture is comprised of several layers, each responsible for extracting features at different levels of abstraction.
During the feature extraction process, we extract features from multiple levels of the VGG-19 network. This includes extracting low-level features that capture structural information at a local level, such as edges and corners, as well as high-level features that capture more abstract and semantic information about the image. By considering features from multiple levels, we aim to capture both fine-grained details and high-level semantic concepts in the image representation.
After feature extraction, we move on to the feature reduction stage, where we aim to reduce the dimensionality of the extracted features while preserving their discriminative power. To achieve this, we employ a 1×1 convolutional kernel, which acts as a linear combination of the features from different levels. This process helps enhance the depth and robustness of the extracted features while reducing redundancy.
Next, we proceed to the feature fusion layer, which consists of 1024 nodes. At this layer, we connect and combine the different feature levels, allowing for the integration of both low-level and high-level information. This fusion of features from multiple levels helps capture a comprehensive representation of the image, combining both local structural details and global semantic information.
In order to approximate hash codes, we perform a non-linear mapping of the features from the fusion layer and the fully connected layer (FC). This mapping is accomplished using hash layers, which consist of L nodes representing the desired length of the hash codes. The non-linear mapping ensures that the generated hash codes capture the essential characteristics of the image representation in a compact and efficient manner.
Moving forward, we concatenate the two hashing layers, resulting in a consolidated representation of the hash codes. This concatenated layer is then connected to the final hashing layer, which further refines the representation and prepares it for classification. By arranging the architecture in this manner, we aim to enhance the preservation of semantic information in the generated hash codes, ensuring that they possess meaningful and discriminative properties.
The classification layer is the last component of our model architecture. It contains neurons equal to the number of classes in the dataset, allowing the network to classify the images based on the learned representations. The classification layer takes advantage of the discriminative power of the hash codes to accurately assign images to their respective classes.
Through the comprehensive approach outlined above, our model utilizes different hashing outcomes based on the various feature levels. This leads to improved image retrieval performance, as the hash codes capture both local and global information. Furthermore, the learning process of the hash codes ensures the preservation of pairwise similarity and the maintenance of semantic information. This results in more meaningful and effective image retrieval based on the learned representations.
Table 1.
Specifics of the feature extraction network are as follows. It is important to note that we utilize the features from layers marked with ’ # ’. For the sake of simplicity, we have omitted the ReLU and Batch Normalization layers.
Table 1.
Specifics of the feature extraction network are as follows. It is important to note that we utilize the features from layers marked with ’ # ’. For the sake of simplicity, we have omitted the ReLU and Batch Normalization layers.
| Conv Block | Layers | Kernel Size | Feature Size |
|---|---|---|---|
| 1 | Conv2D | ||
| Conv2D# | |||
| MaxPooling | |||
| 2 | Conv2D | ||
| Conv2D# | |||
| MaxPooling | |||
| Conv2D | |||
| 3 | Conv2D | ||
| Conv2D | |||
| Conv2D# | |||
| MaxPooling | |||
| Conv2D | |||
| 4 | Conv2D | ||
| Conv2D | |||
| Conv2D# | |||
| MaxPooling | |||
| Conv2D | |||
| 5 | Conv2D | ||
| Conv2D | |||
| Conv2D# | |||
| MaxPooling |
Figure 1.
Deep Supervised Hashing by Fusing Multiscale Deep Features(DSHFMDF).
3.3. Objective function
To ensure the learning of similarity-preserving hash codes, our DSHFMDF approach employs three loss functions: pairwise similarity loss, quantization loss, and classification loss. These losses are combined to train our model effectively.
3.3.1. Pairwise Similarity Loss:
Our DSHFMDF strives to maintain the resemblances between pairs of input data in a Hamming space. We evaluate pairwise similarity by utilizing the inner product. In particular, the inner product between hash codes, and , is precisely defined as .
Given the binary codes and the pairwise labels , The formulation of the likelihood of pairwise labels’ is expressed in the following manner:
where , and .
This formulation implies that a larger inner product corresponds to a smaller and a higher value of . Thus, when , the binary codes and are considered similar.
Upon calculating the negative log-likelihood of labels on S, we encounter the subsequent optimization problem:
The optimization problem described above seeks to minimize Hamming distance inter similar samples while maximizing the distance between dissimilar points. This objective is in line with the goals of pairwise similarity-based hashing techniques.
3.3.2. Quantization Loss:
In practical applications, binary hash codes are commonly used to measure similarity. However, optimizing discrete hash codes within a CNN presents challenges. To overcome this, we propose a continuous form of hash coding. The output of the hash layer is defined as and set .
To minimize the discrepancy inter continuous and discrete hash codes, we introduce the quantization loss as the second objective:
Here, Q represents the mini-batch size.
3.3.3. Classification Loss:
To ensure the robust learning
of multi-scale features throughout the deep network, we employ cross-entropy loss (classification loss) to classify the classes. The formulation of the classification loss is given by:
In this context, denotes the true label, and represents the softmax output of the i-th training sample belonging to the k-th class.
To summarize, the overall loss function is obtained by combining the losses from pairwise similarity, pairwise quantization, and classification.
4. Experiments
We validate effectiveness of our approach using two publicly available datasets: NUS-WIDE and CIFAR-10. Firstly, we provide a concise overview of these datasets, followed by an exploration of our experimental configurations. Section 4.3 presents the evaluation metrics and baseline methods. Finally, in the concluding section, we present the results of our method, including validations and comparisons with several state-of-the-art hashing techniques.
Table 2.
The Mean Average Precision (MAP) scores for Hamming ranking on CIFAR-10 and NUS-WIDE datasets with different numbers of bits. The MAP values are computed based on the top 5,000 retrieved images for the NUS-WIDE dataset.
Table 2.
The Mean Average Precision (MAP) scores for Hamming ranking on CIFAR-10 and NUS-WIDE datasets with different numbers of bits. The MAP values are computed based on the top 5,000 retrieved images for the NUS-WIDE dataset.
| CIFAR-10 (MAP) | NUS-WIDE (MAP) | |||||||
|---|---|---|---|---|---|---|---|---|
| Method | 12 bits | 24 bits | 32 bits | 48 bits | 12 bits | 24 bits | 32 bits | 48 bits |
| SH [28] | 0.127 | 0.128 | 0.126 | 0.129 | 0.454 | 0.406 | 0.405 | 0.400 |
| ITQ [8] | 0.162 | 0.169 | 0.172 | 0.175 | 0.452 | 0.468 | 0.472 | 0.477 |
| KSH [29] | 0.303 | 0.337 | 0.346 | 0.356 | 0.556 | 0.572 | 0.581 | 0.588 |
| SDH [31] | 0.285 | 0.329 | 0.341 | 0.356 | 0.568 | 0.600 | 0.608 | 0.637 |
| CNNH [42] | 0.439 | 0.511 | 0.509 | 0.522 | 0.611 | 0.618 | 0.625 | 0.608 |
| DNNH [21] | 0.552 | 0.566 | 0.558 | 0.581 | 0.674 | 0.697 | 0.713 | 0.715 |
| DHN [20] | 0.555 | 0.594 | 0.603 | 0.621 | 0.708 | 0.735 | 0.748 | 0.758 |
| HashNet [43] | 0.609 | 0.644 | 0.632 | 0.646 | 0.643 | 0.694 | 0.737 | 0.750 |
| DPH [44] | 0.698 | 0.729 | 0.749 | 0.755 | 0.770 | 0.784 | 0.790 | 0.786 |
| LRH [45] | 0.684 | 0.700 | 0.727 | 0.730 | 0.726 | 0.775 | 0.774 | 0.780 |
| Ours | 0.779 | 0.827 | 0.835 | 0.845 | 0.823 | 0.851 | 0.851 | 0.863 |
4.1. Datasets
CIFAR-10 [46] database, as described in the work by Krizhevsky et al. (2009), comprises a collection of 60,000 images categorized into 10 classes. Each image has a dimension of 32×32 pixels. Following the approach outlined in [45]), we randomly choose 100 images per class to serve as queries, resulting in a total of 1,000 test instances. The remaining images form the database set. Additionally, we randomly select 500 images per category (totaling 5,000) from the database to create the training set.
NUS-WIDE [47] database, introduced by Chua et al. (2009), is a comprehensive collection of approximately 270,000 images sourced from Flickr. It consists of 81 different labels or concepts. For our experiment, we randomly choose 2,100 images from 21 class to form the query database set, while the remaining images serve as the database. Furthermore, we randomly select 10,000 images from the database set to construct the training dataset.
4.2. Experimental settings
To implement DSHFMDF, we utilize PyTorch as our framework. As a base network, we employ a VGG-19 convolutional network that has been pre-trained on the ImageNet dataset [48]. Throughout our experiments, we train our network using the Adam algorithm [49] with a learning rate of . As for the hyperparameters of the cost function, we assign a value of 0.01 to alpha and 0.1 to beta.
4.3. Evaluation metrics
In order to assess the performance of various approaches, we employ four evaluation metrics: (MAP) Mean Average Precision , (PR) Precision-Recall curves , Precision curve within Hamming radius 2, and Precision curves with top N returned results (P@N).
We conduct a comparison between our proposed DSHFMDF method and several classical or state-of-the-art methods, which encompass five unsupervised shallow methods, and two traditional supervised hashing techniques, and 8 deep supervised hashing technique. In the case of the multi-label CIFAR-10 and NUS-WIDE datasets, samples are considered similar if they share the same semantic labels. Conversely, if the samples have different semantic labels, they are considered dissimilar.
4.4. Results Discussion
The results obtained from our experiments on the CIFAR-10 and NUS-WIDE datasets, evaluating the performance of various hash code lengths, are presented in Table 2. The table clearly shows that our proposed DSHFMDF (Deep Supervised Hashing by Fusing Multiscale Deep Feature) method outperforms all the compared methods by a significant margin. Specifically, when compared to SDH (Supervised Discrete Hashing), which is considered one of the top shallow hashing methods, DSHFMDF demonstrates substantial improvements with absolute increases of 49.4% and 24% in average Mean Average Precision (MAP) on the CIFAR-10 and NUS-WIDE datasets, respectively. This highlights the effectiveness of our approach in generating high-quality hash codes for image retrieval tasks.
Furthermore, our results indicate that deep hashing methods, including DSHFMDF, outperform traditional hashing techniques. This can be attributed to the ability of deep hashing methods to generate more robust feature representations, leveraging the power of deep neural networks. Among the deep hashing techniques, DSHFMDF surpasses the second-best method, LRH (Learning to Hash with Rank Supervision), achieving an average MAP increase of 11.1% and 8.3% on the CIFAR-10 and NUS-WIDE datasets, respectively. These findings highlight the superiority of DSHFMDF in capturing and preserving semantic information in the hash codes, leading to improved retrieval performance.
In order to provide a more detailed analysis of our results, we present precision curves (P@H = 2) in Figure 2a and Figure 3a, which illustrate the retrieval performance of different methods. Notably, the precision curves clearly demonstrate that our proposed DSHFMDF model consistently outperforms the other methods as the code length increases. This indicates that our method maintains the highest precision rate even when longer hash codes are used, showcasing its effectiveness in producing accurate and reliable retrieval results.
To further evaluate the performance of DSHFMDF, we analyze its Precision-Recall (PR) performance and Precision at N (P@N) measures compared to other approaches. Figure 2b, Figure 3b, Figure 2c, and Figure 3c present the PR performance and P@N results for the CIFAR-10 and NUS-WIDE datasets, respectively. In Figure 2c and Figure 3c, it is evident that the proposed DSHFMDF method achieves the highest precision when using 48-bit hash codes. This demonstrates its effectiveness in generating precise retrieval results. Additionally, Figure 2b and Figure 3b show consistently high precision levels at low recall, which is of great importance in precision oriented retrieval tasks and finds practical application in various systems.
In conclusion, our DSHFMDF method surpasses the compared methods across multiple evaluation aspects, highlighting its superiority in image retrieval tasks. To provide visual evidence of its effectiveness in removing irrelevant images, we present Figure 4, which showcases the retrieval accuracy of various image categories in the CIFAR-10 dataset using DSHFMDF with 48-bit binary codes. The figure includes the query images in the first column, while the subsequent columns display the retrieved images using DSHFMDF. This example further emphasizes the ability of our approach to accurately retrieve relevant images and demonstrates its practical utility.
Overall, our extensive experiments and detailed analysis validate the superiority of the proposed DSHFMDF method in generating high-quality hash codes, improving retrieval performance, and achieving accurate and precise image retrieval results.
5. Conclusion
This paper presents an end-to-end approach called Deep Supervised Hashing by Fusing Multiscale Deep Features (DSHFMDF) for image retrieval. Our proposed method focuses on generating robust binary codes by optimizing the similarity loss, quantization loss, and semantic loss. Moreover, the network leverages various hashing results based on multiscale features, thereby enhancing retrieval recall while preserving precision. Through extensive experiments on two image retrieval datasets, we demonstrate the superiority of our method over other state-of-the-art hashing techniques. Furthermore, the scalability of our model enables its application in various computer vision tasks, offering robust representative features.
Author Contributions
Conceptualization, A.R. and K.B.; methodology, K.B.; software, A.R.; validation, K.B. and A.R.; formal analysis, A.R., A. B. and K.B.; investigation, K.B. and A. B.; writing–original draft preparation, A.R. and K.B.; writing–review and editing, K.B. and A.R.; visualization, A.R. and A. B.; supervision, K.B. and A.B.; project administration, K.B.; funding acquisition, K.B. All authors have read and agreed to the published version of the manuscript.”
Funding
`This research received no external funding”.
Data Availability Statement
Publicly available datasets were analyzed in this study. These data can be found here: http://www.cs.toronto.edu/~kriz/cifar.html , https://paperswithcode.com/datasets (all accessed on 20 July 2023).
Conflicts of Interest
“The authors declare no conflict of interest.”.
Abbreviations
The following abbreviations are used in this manuscript:
| DSHFMDF | Deep Supervised Hashing by Fusing Multiscale Deep Features |
| CBIR | Content-Based Image Retrieval |
| FPN | Feature Pyramid Network |
| CNN | Convolutional Neural Network |
| DCNN | Deep Convolutional Neural Network |
References
- Yan, C.; Shao, B.; Zhao, H.; Ning, R.; Zhang, Y.; Xu, F. 3D room layout estimation from a single RGB image. IEEE Transactions on Multimedia 2020, 22, 3014–3024. [Google Scholar] [CrossRef]
- Yan, C.; Li, Z.; Zhang, Y.; Liu, Y.; Ji, X.; Zhang, Y. Depth image denoising using nuclear norm and learning graph model. ACM Transactions on Multimedia Computing, Communications, and Applications (TOMM) 2020, 16, 1–17. [Google Scholar] [CrossRef]
- Li, S.; Chen, Z.; Li, X.; Lu, J.; Zhou, J. Unsupervised variational video hashing with 1d-cnn-lstm networks. IEEE Transactions on Multimedia 2019, 22, 1542–1554. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Sebe, N.; Shen, H.T.; et al. A survey on learning to hash. IEEE transactions on pattern analysis and machine intelligence 2017, 40, 769–790. [Google Scholar] [CrossRef]
- Gionis, A.; Indyk, P.; Motwani, R.; et al. Similarity search in high dimensions via hashing. In Proceedings of the Vldb, 1999, Vol. 99, pp. 518–529.
- Andoni, A.; Indyk, P. Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. Communications of the ACM 2008, 51, 117–122. [Google Scholar] [CrossRef]
- Indyk, P.; Motwani, R. Approximate nearest neighbors: towards removing the curse of dimensionality. In Proceedings of the Proceedings of the thirtieth annual ACM symposium on Theory of computing, 1998, pp. 604–613.
- Gong, Y.; Lazebnik, S.; Gordo, A.; Perronnin, F. Iterative quantization: A procrustean approach to learning binary codes for large-scale image retrieval. IEEE transactions on pattern analysis and machine intelligence 2012, 35, 2916–2929. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, J.; Mu, Y.; Kumar, S.; Chang, S.F. Compact hyperplane hashing with bilinear functions. arXiv 2012, arXiv:1206.4618 2012. [Google Scholar]
- Gong, Y.; Kumar, S.; Rowley, H.A.; Lazebnik, S. Learning binary codes for high-dimensional data using bilinear projections. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2013, pp. 484–491.
- Lin, G.; Shen, C.; Wu, J. Optimizing ranking measures for compact binary code learning. In Proceedings of the European Conference on Computer Vision. Springer, 2014, pp. 613–627.
- Kulis, B.; Darrell, T. Learning to hash with binary reconstructive embeddings. Advances in neural information processing systems 2009, 22. [Google Scholar]
- Strecha, C.; Bronstein, A.; Bronstein, M.; Fua, P. LDAHash: Improved matching with smaller descriptors. IEEE transactions on pattern analysis and machine intelligence 2011, 34, 66–78. [Google Scholar] [CrossRef]
- Lin, G.; Shen, C.; Suter, D.; Van Den Hengel, A. A general two-step approach to learning-based hashing. In Proceedings of the Proceedings of the IEEE international conference on computer vision, 2013, pp. 2552–2559.
- Lin, G.; Shen, C.; Shi, Q.; Van den Hengel, A.; Suter, D. Fast supervised hashing with decision trees for high-dimensional data. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2014, pp. 1963–1970.
- Chen, Z.; Zhou, J. Collaborative multiview hashing. Pattern Recognition 2018, 75, 149–160. [Google Scholar] [CrossRef]
- Cui, Y.; Jiang, J.; Lai, Z.; Hu, Z.; Wong, W. Supervised discrete discriminant hashing for image retrieval. Pattern Recognition 2018, 78, 79–90. [Google Scholar] [CrossRef]
- Song, J.; Gao, L.; Liu, L.; Zhu, X.; Sebe, N. Quantization-based hashing: a general framework for scalable image and video retrieval. Pattern Recognition 2018, 75, 175–187. [Google Scholar] [CrossRef]
- Erin Liong, V.; Lu, J.; Wang, G.; Moulin, P.; Zhou, J. Deep hashing for compact binary codes learning. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 2475–2483.
- Zhu, H.; Long, M.; Wang, J.; Cao, Y. Deep hashing network for efficient similarity retrieval. In Proceedings of the Proceedings of the AAAI conference on Artificial Intelligence, 2016, Vol. 30.
- Lai, H.; Pan, Y.; Liu, Y.; Yan, S. Simultaneous feature learning and hash coding with deep neural networks. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 3270–3278.
- Cakir, F.; He, K.; Bargal, S.A.; Sclaroff, S. Hashing with mutual information. IEEE transactions on pattern analysis and machine intelligence 2019, 41, 2424–2437. [Google Scholar] [CrossRef] [PubMed]
- Gordo, A.; Almazán, J.; Revaud, J.; Larlus, D. Deep image retrieval: Learning global representations for image search. In Proceedings of the European conference on computer vision. Springer, 2016, pp. 241–257.
- Jiang, Q.Y.; Li, W.J. Asymmetric deep supervised hashing. In Proceedings of the Proceedings of the AAAI conference on artificial intelligence, 2018, Vol. 32.
- Shen, F.; Gao, X.; Liu, L.; Yang, Y.; Shen, H.T. Deep asymmetric pairwise hashing. In Proceedings of the Proceedings of the 25th ACM international conference on Multimedia, 2017, pp. 1522–1530.
- Jin, Z.; Li, C.; Lin, Y.; Cai, D. Density sensitive hashing. IEEE transactions on cybernetics 2013, 44, 1362–1371. [Google Scholar] [CrossRef]
- Datar, M.; Immorlica, N.; Indyk, P.; Mirrokni, V.S. Locality-sensitive hashing scheme based on p-stable distributions. In Proceedings of the Proceedings of the twentieth annual symposium on Computational geometry, 2004, pp. 253–262.
- Weiss, Y.; Torralba, A.; Fergus, R. Spectral hashing. Advances in neural information processing systems 2008, 21. [Google Scholar]
- Liu, W.; Wang, J.; Ji, R.; Jiang, Y.G.; Chang, S.F. Supervised hashing with kernels. In Proceedings of the 2012 IEEE conference on computer vision and pattern recognition. IEEE, 2012, pp. 2074–2081.
- Norouzi, M.; Fleet, D.J. Minimal loss hashing for compact binary codes. In Proceedings of the ICML; 2011. [Google Scholar]
- Shen, F.; Shen, C.; Liu, W.; Tao Shen, H. Supervised discrete hashing. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 37–45.
- Li, W.J.; Wang, S.; Kang, W.C. Feature learning based deep supervised hashing with pairwise labels. arXiv 2015, arXiv:1511.03855 2015. [Google Scholar]
- Cao, Y.; Liu, B.; Long, M.; Wang, J. Hashgan: Deep learning to hash with pair conditional wasserstein gan. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 1287–1296.
- Zhuang, B.; Lin, G.; Shen, C.; Reid, I. Fast training of triplet-based deep binary embedding networks. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 5955–5964.
- Liu, B.; Cao, Y.; Long, M.; Wang, J.; Wang, J. Deep triplet quantization. In Proceedings of the Proceedings of the 26th ACM international conference on Multimedia, 2018, pp. 755–763.
- Yang, H.F.; Lin, K.; Chen, C.S. Supervised learning of semantics-preserving hash via deep convolutional neural networks. IEEE transactions on pattern analysis and machine intelligence 2017, 40, 437–451. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhou, W.; Tian, Q.; Li, H. A general framework for linear distance preserving hashing. IEEE Transactions on Image Processing 2017, 27, 907–922. [Google Scholar] [CrossRef]
- Shen, F.; Xu, Y.; Liu, L.; Yang, Y.; Huang, Z.; Shen, H.T. Unsupervised deep hashing with similarity-adaptive and discrete optimization. IEEE transactions on pattern analysis and machine intelligence 2018, 40, 3034–3044. [Google Scholar] [CrossRef]
- Lin, J.; Li, Z.; Tang, J. Discriminative Deep Hashing for Scalable Face Image Retrieval. In Proceedings of the IJCAI; 2017; pp. 2266–2272. [Google Scholar]
- Yang, Y.; Geng, L.; Lai, H.; Pan, Y.; Yin, J. Feature pyramid hashing. In Proceedings of the Proceedings of the 2019 on International Conference on Multimedia Retrieval, 2019, pp. 114–122.
- Ng, W.W.; Li, J.; Tian, X.; Wang, H.; Kwong, S.; Wallace, J. Multi-level supervised hashing with deep features for efficient image retrieval. Neurocomputing 2020, 399, 171–182. [Google Scholar] [CrossRef]
- Xia, R.; Pan, Y.; Lai, H.; Liu, C.; Yan, S. Supervised hashing for image retrieval via image representation learning. In Proceedings of the Twenty-eighth AAAI conference on artificial intelligence, 2014.
- Cao, Z.; Long, M.; Wang, J.; Yu, P.S. Hashnet: Deep learning to hash by continuation. In Proceedings of the Proceedings of the IEEE international conference on computer vision, 2017, pp. 5608–5617.
- Bai, J.; Ni, B.; Wang, M.; Li, Z.; Cheng, S.; Yang, X.; Hu, C.; Gao, W. Deep progressive hashing for image retrieval. IEEE Transactions on Multimedia 2019, 21, 3178–3193. [Google Scholar] [CrossRef]
- Bai, J.; Li, Z.; Ni, B.; Wang, M.; Yang, X.; Hu, C.; Gao, W. Loopy residual hashing: Filling the quantization gap for image retrieval. IEEE Transactions on Multimedia 2019, 22, 215–228. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G.; et al. Learning multiple layers of features from tiny images 2009.
- Chua, T.S.; Tang, J.; Hong, R.; Li, H.; Luo, Z.; Zheng, Y. Nus-wide: a real-world web image database from national university of singapore. In Proceedings of the Proceedings of the ACM international conference on image and video retrieval, 2009, pp. 1–9.
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. Imagenet large scale visual recognition challenge. International journal of computer vision 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980 2014. [Google Scholar]
Figure 2.
The results obtained by comparing various methods on the CIFAR-10 dataset using three evaluation metrics.
Figure 2.
The results obtained by comparing various methods on the CIFAR-10 dataset using three evaluation metrics.
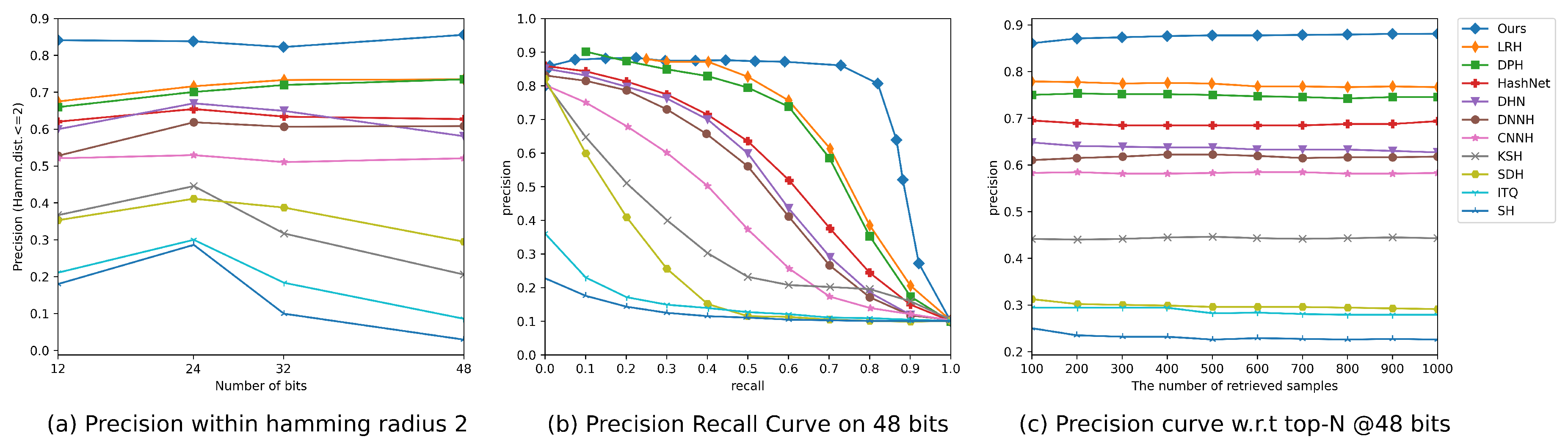
Figure 3.
The results of comparing different approaches on the NUS-WIDE dataset using three evaluation metrics.
Figure 3.
The results of comparing different approaches on the NUS-WIDE dataset using three evaluation metrics.
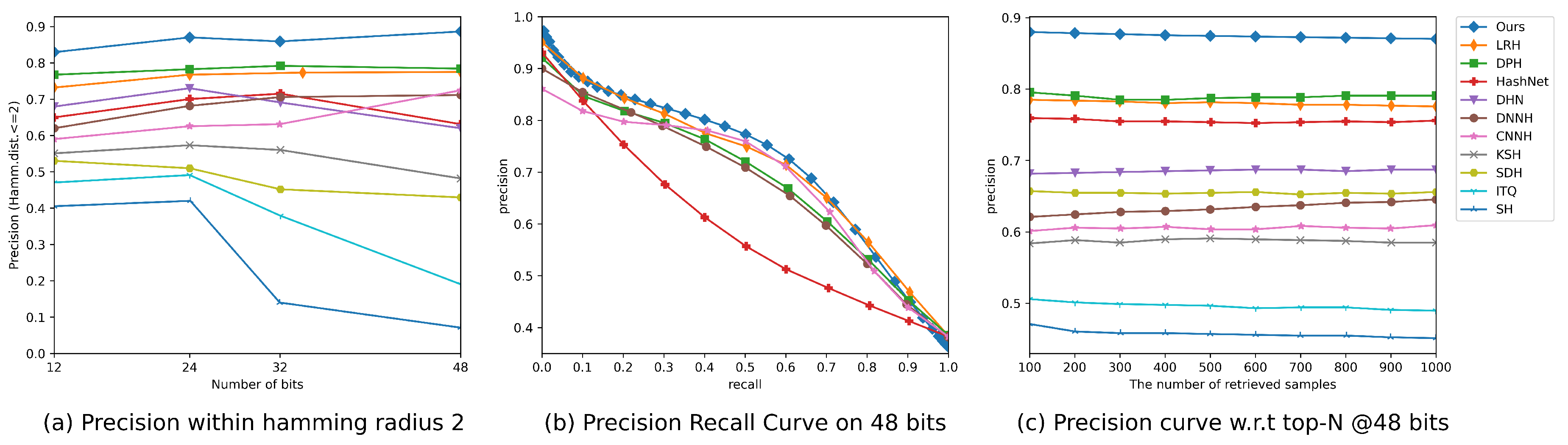
Figure 4.
The top 20 retrieved results from the CIFAR-10 dataset using DSHFMDF with 48-bit hash codes are presented. The query images are displayed in the first column, while the subsequent columns showcase the retrieval results obtained by DSHFMDF.
Figure 4.
The top 20 retrieved results from the CIFAR-10 dataset using DSHFMDF with 48-bit hash codes are presented. The query images are displayed in the first column, while the subsequent columns showcase the retrieval results obtained by DSHFMDF.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






