Prerpints.org logo
Preprint
Article

Neuro Fuzzy GreyWolf Optimisation Method for Diagnosing the Liver Disorders

Altmetrics

Downloads

159

Views

73

Comments

0

This version is not peer-reviewed

Artificial Intelligence and Fuzzy Systems

Submitted:

25 September 2023

Posted:

26 September 2023

You are already at the latest version

Alerts
Abstract
The hybrid method proposed in the study, ANFIS-GWO, combines the Adaptive Neuro-Fuzzy Inference System (ANFIS) with Grey Wolf Optimization (GWO) for the diagnosis of liver disorders. ANFIS is a powerful tool that combines the advantages of neural networks and fuzzy logic to create a hybrid model capable of handling complex and uncertain data. GWO is a metaheuristic optimization algorithm inspired by the social behaviour of grey wolves. In the ANFIS-GWO method, the hyperparameters of ANFIS are optimized using GWO. This optimization process aims to fine-tune the ANFIS model based on the available dataset, which consists of 7 characteristic attributes and 354 samples related to liver diseases. By adopting the hyper-parameters, the ANFIS-GWO method enhances the overall performance and accuracy of the diagnostic system. To evaluate the effectiveness of the ANFIS-GWO intelligent medical system, the study employs classification accuracy, sensitivity, and specificity analysis. Classification accuracy measures the overall correctness of the system in predicting liver disease cases. Sensitivity refers to the system’s ability to correctly identify individuals with liver disorders, while specificity measures its ability to correctly identify those without liver disorders. Experimental results demonstrate that the performance of the ANFIS-GWO method surpasses that of traditional Fuzzy Inference Systems (FIS) and ANFIS models that do not undergo an optimization phase. This suggests that the integration of GWO optimization significantly improves the diagnostic accuracy of the ANFIS model for liver disease diagnosis.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Expert systems are indeed a branch of Artificial Intelligence (AI) that leverages human expertise to solve complex or ill-structured problems where a specific algorithmic solution may not be readily available. These systems are designed to mimic the decision-making capabilities of human experts in a specific domain. They utilize knowledge and inference techniques to address challenging problems that typically require significant human expertise for their resolutions. [1]. Expert systems [2] are built upon a knowledge base, which contains a collection of domain-specific information and rules. This knowledge base is created by capturing the expertise of human specialists in the form of if-then rules or logical statements. The inference engine, a key component of expert systems, applies these rules to the available data or user input to make informed decisions or provide recommendations.
The aim of expert systems is to emulate the problem-solving and decision-making abilities of human experts [3]. They can handle complex situations, analyze data, and provide explanations and justifications for their conclusions. Expert systems are particularly useful in domains where expert knowledge is scarce, expensive, or time-consuming to obtain.
By utilizing expert systems, organizations can leverage the expertise of specialists even in the absence of direct human involvement [4]. These systems have found applications in various fields, such as medicine, finance, engineering, and troubleshooting complex technical issues. They have proven effective in assisting professionals, enhancing decision-making processes, and providing valuable insights and guidance in complex problem domains.
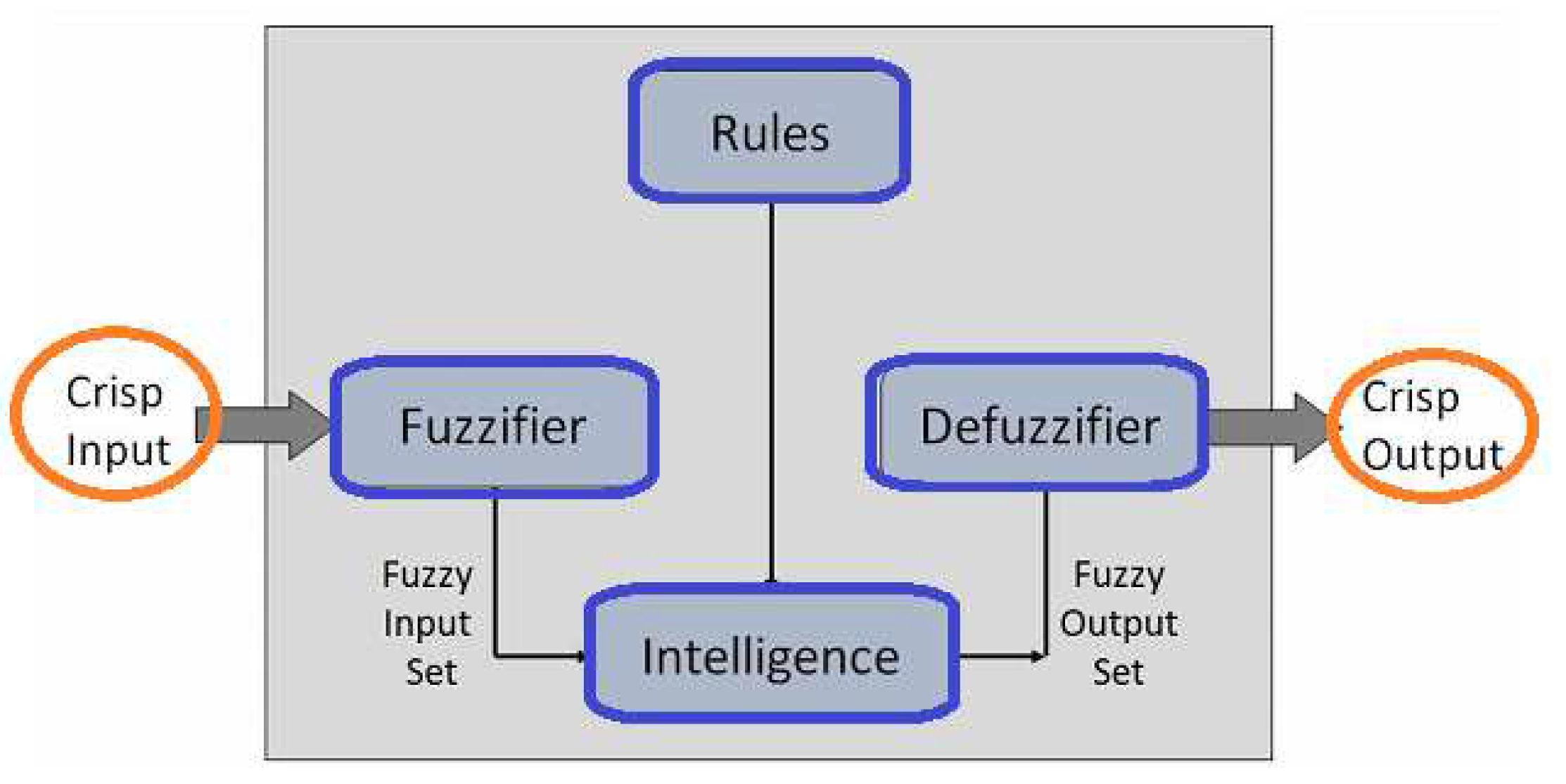
A fuzzy expert system can be a specific knowledge-based system, which is formed of fuzzification, knowledge database, inference rules, and defuzzification parts and applies fuzzy logic instead of Boolean logic to consider data in the deduction mechanism. This system is adopted to describe decision-making problems where there is no scientific algorithm exists, although alternatively, the problem solution can be considered heuristically, which is based on specialists in the form of If-Then rules. A fuzzy expert system can be sufficiently supplied to the problem, which gives uncertainty emitting from fuzziness, ambiguity or subjectivity. In the 21st century, the applications of fuzzy expert systems have been tremendously expanding throughout scientific research topics such as diagnosing and predicting the various risks of diseases [5,6,7], civil engineering applications, evaluating the educational service qualities and for modelling different aspect of indeterministic business situations.
Preprints 86026 g001
Figure 1. The scheme of a fuzzy expert system
Figure 1. The scheme of a fuzzy expert system
Preprints 86026 g001
The liver plays a vital role in detoxifying medications and removing waste products generated from the breakdown and formation of red blood cells. It also produces bile, blood clotting factors, and stores glycogen, while regulating sugar and fat metabolism. Additionally, it aids in fat digestion and defends against microbes and toxins present in food [8]. The prevalence of liver disorders and associated mortality has significantly increased in recent years. Timely detection of these disorders can effectively mitigate their impact and enable better control and treatment. Diagnosis of diseases is a complex task influenced by human error, highlighting the importance of expert systems. These systems utilize artificial intelligence (AI) techniques, such as machine learning, fine-tuning [9], neural networks, Deep learning [10], ensemble models [11], transfer learning [12] and so on, to assist medical professionals in diagnosing diseases based on symptom analysis and laboratory tests [13]. By leveraging expert systems, we can reduce costs, save time, and improve diagnostic accuracy. In our research, we focus on diagnosing liver disorders using a hybrid adaptive neuro-fuzzy inference technique. Our approach involves selecting the adaptive neuro-fuzzy inference system (ANFIS) due to its advantages, such as simplicity, flexibility, robustness to erroneous data, ability to model complex non-linear functions, reliance on expert knowledge, and compatibility with conventional control systems. We also apply Grey Wolf swarm optimization (GWO), a popular swarm intelligence technique, to optimize the hyper-parameters of ANFIS. These hyper-parameters include the number and type of fuzzy membership functions and the enhancement of fuzzy rules. The utilization of GWO significantly impacts diagnostic performance, improving the accuracy of liver disorder diagnosis.
The primary objective of this article is to examine and compare the advantages and limitations of existing approaches and theories in enhancing and modelling fuzzy expert systems using optimization algorithms. The focus is on evaluating the performance of the proposed hybrid adaptive neural fuzzy inference system for diagnosing liver disorders utilizing the Bupa dataset. To achieve this goal, a thorough investigation of the relevant fuzzy inference system technique is conducted. The intention is to provide a comprehensive study that explores the potential benefits and drawbacks associated with various approaches and theories in the context of improving and modelling fuzzy expert systems for liver disorder diagnosis.
The remaining sections of this article are organized as follows. Section 2 provides an overview of the dataset used in the study, presenting its details. In Section 3, a comprehensive explanation of fuzzy expert systems is provided, highlighting their intricacies. Section 4 focuses on reviewing the structure of adaptive neural fuzzy inference systems. Additionally, Section 5 delves into the technical specifications of the particle swarm optimization method and explores its diverse applications. The experimental results and implications are presented in Section 6. Finally, Section 7 presents the concluding remarks summarizing the findings and contributions of the study.

2. Bupa Liver Disorders Data-Set

The dataset utilized in this research paper aims to enhance the investigation of liver disorders based on their characteristics. The dataset was collected by Richard S. Forsyth [14] and was introduced to the UCI (University of California, Irvine) in 1995 [1].
It contains a total of 345 samples, with each sample consisting of 7 attributes. The first five attributes in the dataset are associated with various variable substances obtained from a male blood test. The sixth attribute represents the quantity of alcohol consumption, while the seventh attribute is used to classify individuals as either healthy or ill. Detailed information about the attributes can be found in Table 1.
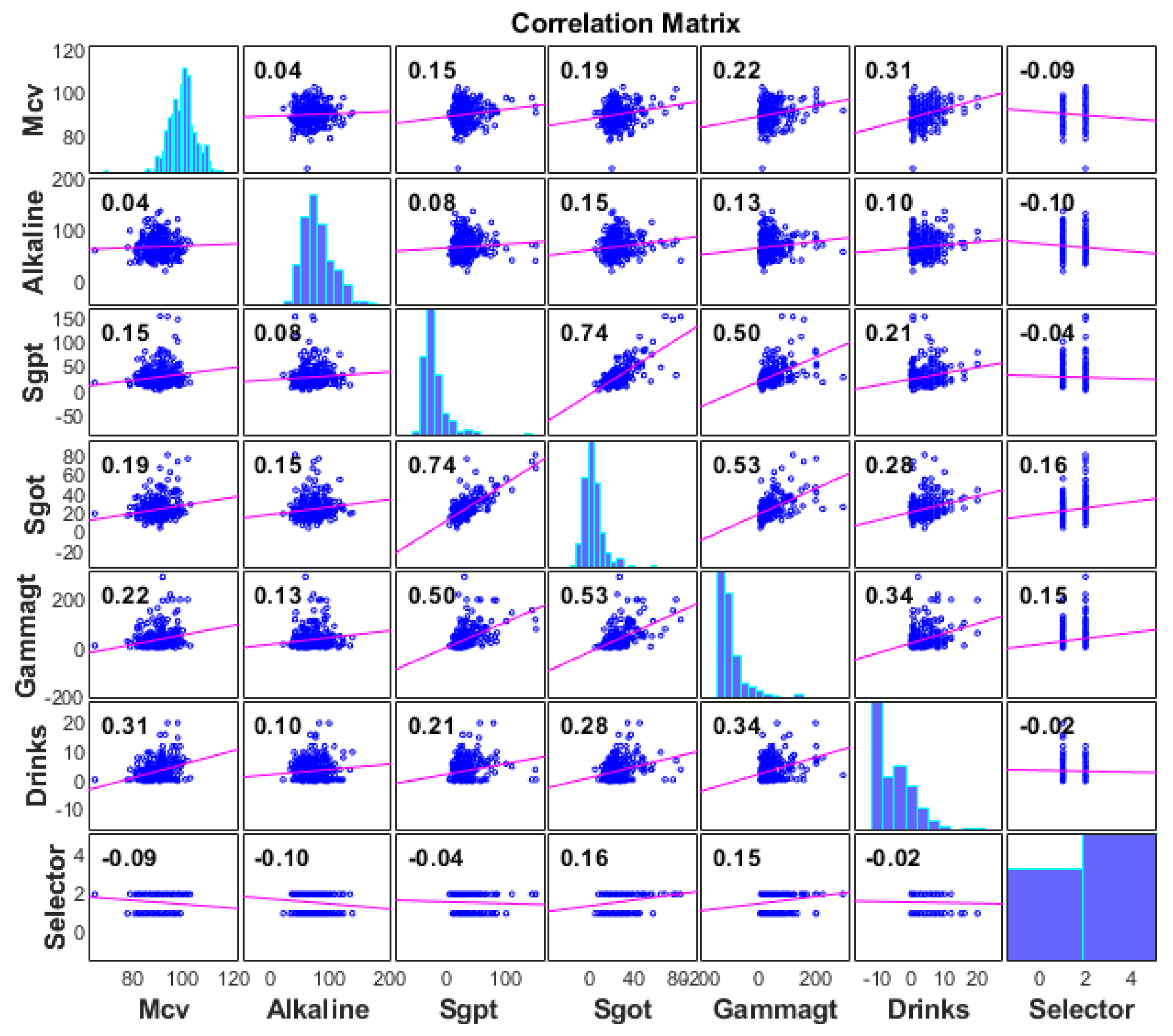
Figure 2 represents the correlation coefficients between the features and liver disorder. As can be seen, the highest correlation is 0.16 between the SGOT and disorder; however, other features have a low and negative correlation. In total, the highest meaningful correlations are between Drinking alcohol and MCV at 0.31. Furthermore, the correlation between SGPT and SGOT is considerable. The dataset is continuous, and there is no missing or destroyed data.

3. Fuzzy Expert Systems (FES)

The original formulation of fuzzy logic theory was introduced by Zadeh [15] as a means of handling imprecise and well-defined human knowledge. Figure 3 illustrates the basic structure of a fuzzy logic system. The process of fuzzification involves converting crisp input information into fuzzy linguistic values using various membership functions. In a fuzzy expert system, fuzzification is often necessary as the input values from sensors or detectors are typically deterministic numerical values. The inference engine takes fuzzy inputs and rules, generating fuzzy productions as a result. It is important to represent the fuzzy rule base in the form of "IF-THEN" rules that incorporate linguistic variables. The final component of a fuzzy expert system is defuzzification, which is responsible for converting fuzzy outputs into crisp values. Figure 1 provides a visual representation of the structure of a fuzzy expert system.
Over the past 30 years, fuzzy rule-based systems have played a significant role in artificial intelligence, specifically in the interpretation of complex medical data. These systems have demonstrated the ability to uncover meaningful relationships within datasets, which has been applied in various clinical scenarios for diagnosis, treatment, and outcome prediction. This section presents a survey of different artificial intelligence techniques and highlights their critical clinical applications in expert systems. Artificial neural networks and knowledge-based systems have been the most commonly utilized analytical tools in medical research. Additionally, other artificial intelligence systems, including evolutionary algorithms, swarm intelligence, and hybrid systems, have been employed in diverse clinical settings. The potential of artificial intelligence and expert systems extends to almost every field of medicine. To provide a comprehensive overview, Table 2 showcases the practical application of various AI techniques such as fuzzy sets, neural networks, evolutionary algorithms, and swarm intelligence in diagnosing a wide range of diseases. Moreover, Table 2 offers a brief review of different methods specifically focused on analyzing liver disorders in the past two decades.
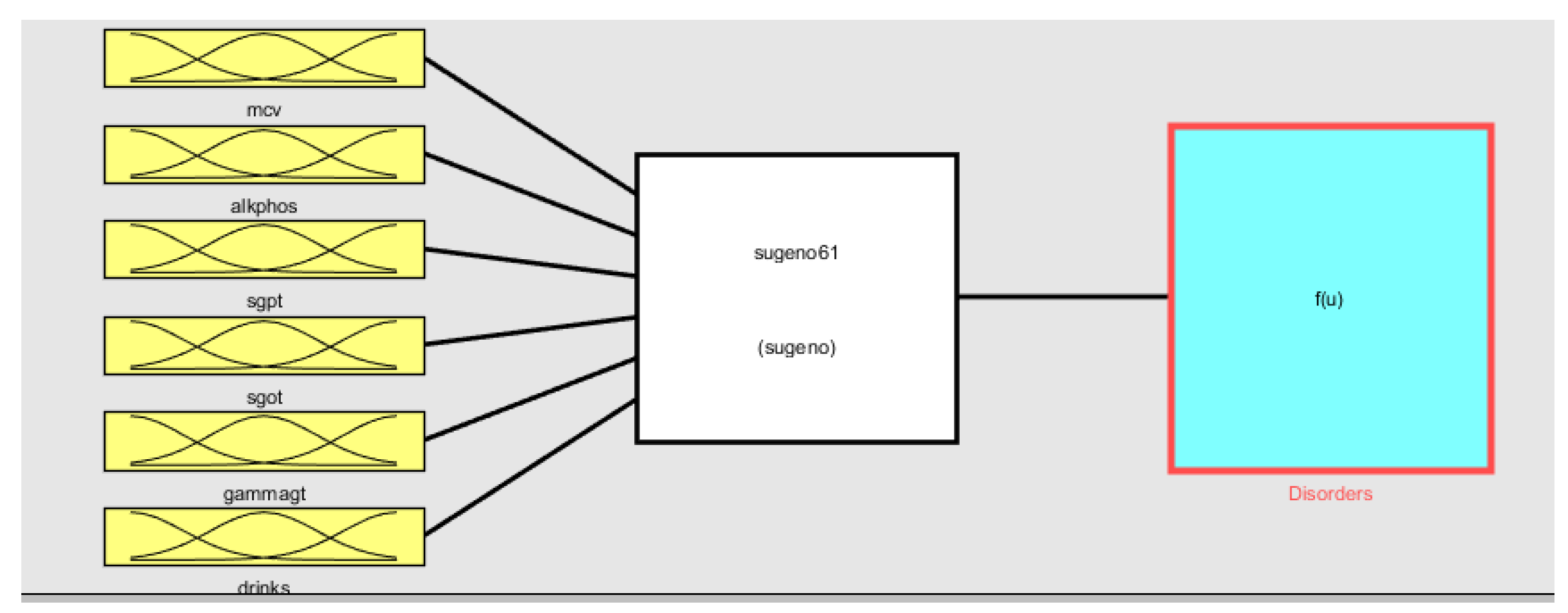
Preprints 86026 g003
Figure 3. The scheme of the Liver Disorders Diagnostic Fuzzy Inference System
Figure 3. The scheme of the Liver Disorders Diagnostic Fuzzy Inference System
Preprints 86026 g003

4. Adaptive Neural Fuzzy Inference System (ANFIS)

ANFIS, short for Adaptive Neuro-Fuzzy Inference System, is a type of artificial neural network (ANN) that operates based on the principles of the Takagi-Sugeno fuzzy inference system. It was initially developed in the early 1990s [43]. By combining both ANN and fuzzy logic principles, ANFIS offers a unique framework that capitalizes on the advantages of both approaches. The fuzzy inference system (FIS) within ANFIS consists of a collection of fuzzy rules (IF-THEN) that can learn to approximate nonlinear functions. As a result, ANFIS is considered a versatile estimator. To improve the efficiency and optimization of ANFIS, one can utilize genetic algorithms to handle the relevant parameters [44]. ANFIS (Adaptive Neuro-Fuzzy Inference System) [45] is based on the concept of utilizing fuzzy logic principles to construct a fuzzy inference system (FIS) comprising a set of fuzzy rules. These rules are structured as "IF-THEN" statements and aim to approximate intricate nonlinear functions. 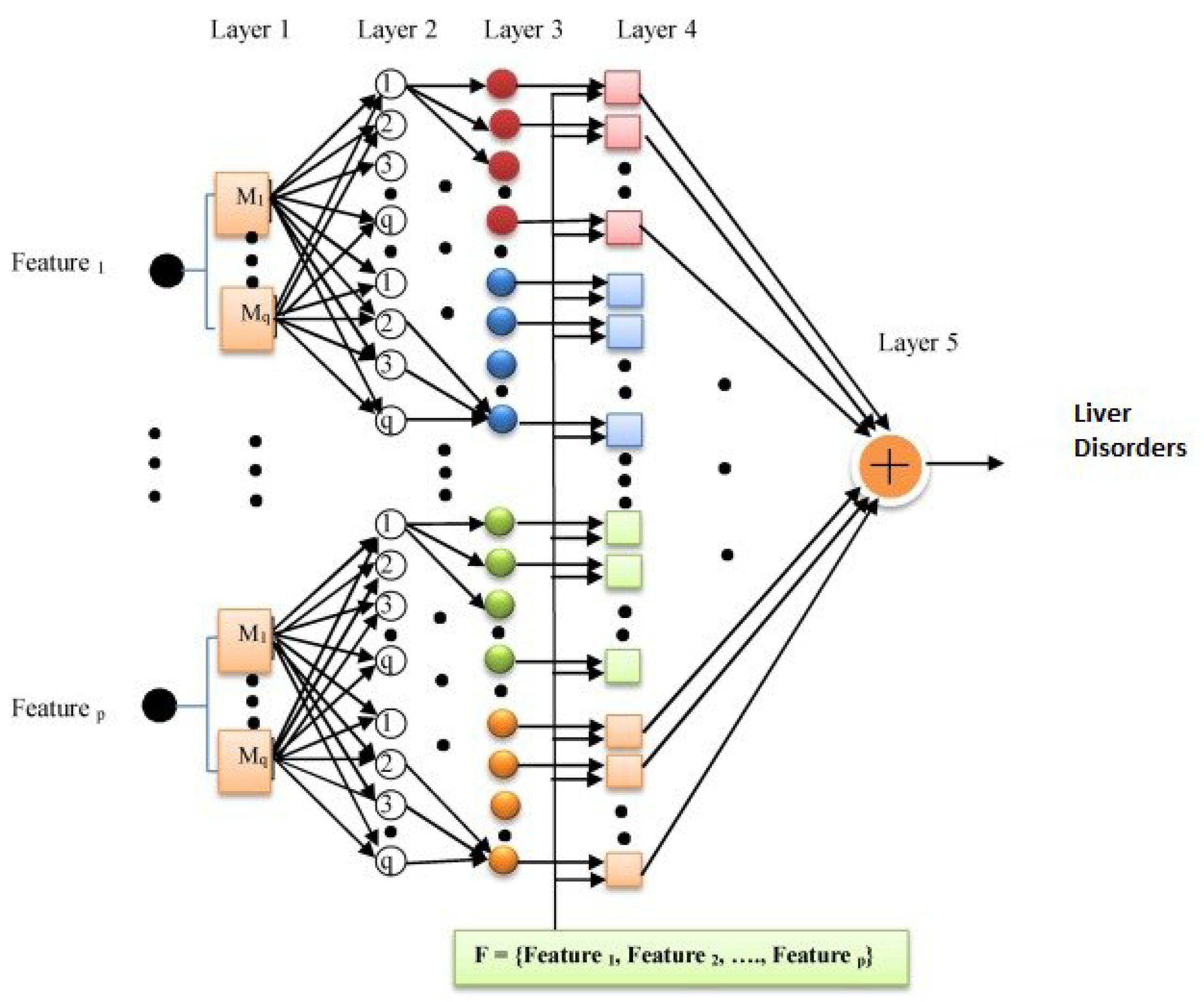The learning process in ANFIS involves fine-tuning the parameters of the fuzzy rules to enhance the model’s accuracy [46]. The ANFIS architecture (See Figure 4) comprises five layers. The initial layer called the fuzzification layer, receives input values and assigns membership degrees using predefined membership functions. These functions determine the extent to which the input values belong to specific fuzzy sets [47]. The second layer, referred to as the rule layer, calculates the firing strengths for each fuzzy rule by combining the membership degrees of the input variables. Each rule is associated with parameters that govern its firing strength. The third layer normalizes the firing strengths by dividing each value by the sum of all firing strengths. This normalization process ensures that the contribution of each rule is appropriately scaled. The fourth layer, known as the defuzzification layer, combines the normalized firing strengths with the consequent parameters of the fuzzy rules. It computes the weighted average of the consequent parameters based on the normalized firing strengths, generating defuzzified values as outputs. The final layer represents the overall output of the ANFIS model. It receives the defuzzified values from the preceding layer and produces the final output based on the specific task or problem under consideration.
ANFIS models can be trained using various learning algorithms, such as gradient descent or hybrid approaches that combine gradient-based and least-squares techniques. Genetic algorithms can also be employed to optimize the model’s parameters and enhance its performance. In summary, ANFIS offers a flexible and adaptive framework for modelling complex systems by integrating the interpretability of fuzzy logic with the learning capabilities of neural networks. It has been successfully utilized across various domains, including forecasting, classification, control systems, and decision-making tasks.
ANFIS (Adaptive Neuro-Fuzzy Inference System) provides several technical advantages in modelling and problem-solving, as follows.
  • ANFIS excels at approximating complex nonlinear functions by employing fuzzy rules [49]. It can effectively capture intricate relationships between input and output variables, surpassing traditional mathematical models.
  • The interpretability and linguistic representation of fuzzy logic with the powerful learning capabilities [50] and pattern recognition of neural networks is another benefit of ANFIS. This fusion enables comprehensive comprehension of the modelled system.
  • Adaptability and learning capabilities [51] can be found by ANFIS. Through parameter adjustments in fuzzy rules during training, ANFIS continually enhances accuracy and performance. This adaptability is particularly valuable in dynamic systems subject to changes.
  • ANFIS yields interpretable models due to the linguistic representation of fuzzy rules [52]. The "IF-THEN" structure facilitates easy understanding and analysis by domain experts, which is crucial for domains emphasizing explainability and transparency.
  • Supporting various learning algorithms, including gradient descent, hybrid techniques, and genetic algorithms [53], can be considered by ANFIS. This versatility allows practitioners to choose optimal learning approaches, improving training efficiency and model performance.

5. Grey Wolf Swarm Optimization

The Grey Wolf Optimizer [54] (GWO) is a swarm intelligent optimization algorithm proposed by Seyedali Mirjalili and others in 2014. It draws inspiration from the hierarchical leadership structure and hunting behaviour of wolves in nature. Research conducted by Seyedali Mirjalili and colleagues has demonstrated that the standard GWO algorithm outperforms other optimization algorithms such as PSO, GSA, DE, and FEP. The GWO algorithm offers several advantages, including its simplicity, fast convergence speed [55], high precision in searching for optimal solutions, and ease of implementation. These characteristics make it well-suited for practical engineering problems and hold significant theoretical research value. Although GWO is a relatively new algorithm in the field of biological intelligence, research on it is still in its early stages. The theory and development of the algorithm are not yet perfect. To fully harness the superior performance of GWO, further exploration and research are required.
To replicate the internal leadership structure of wolves, the GWO algorithm categorizes wolves into four distinct types: alpha, beta, delta, and omega. Among these, the alpha, beta, and delta wolves represent the best, second-best, and third-best individuals, respectively, while the remaining wolves are classified as omega. Within the GWO algorithm, the hunting or optimization process is guided by the alpha, beta, and delta wolves. They lead other wolves (W) towards the most promising areas in the search space. During the iterative search process, the potential position of the prey (optimal solution) is evaluated by the alpha, beta, and delta wolves. The locations of the wolves are then updated in the optimization process using Equations (1) and (2).
D → = C → · X P → ( t ) − X → ( t ) X → ( t + 1 ) = X P → ( t ) − A → · D →
Where t represents the t t h iteration, A and C are coefficient vectors, ( X P ) is the position vector of prey, and X represents the wolf position. The vectors A and C can be expressed by:
A → = 2 a · r 1 → − a → C → = 2 · r 2 →
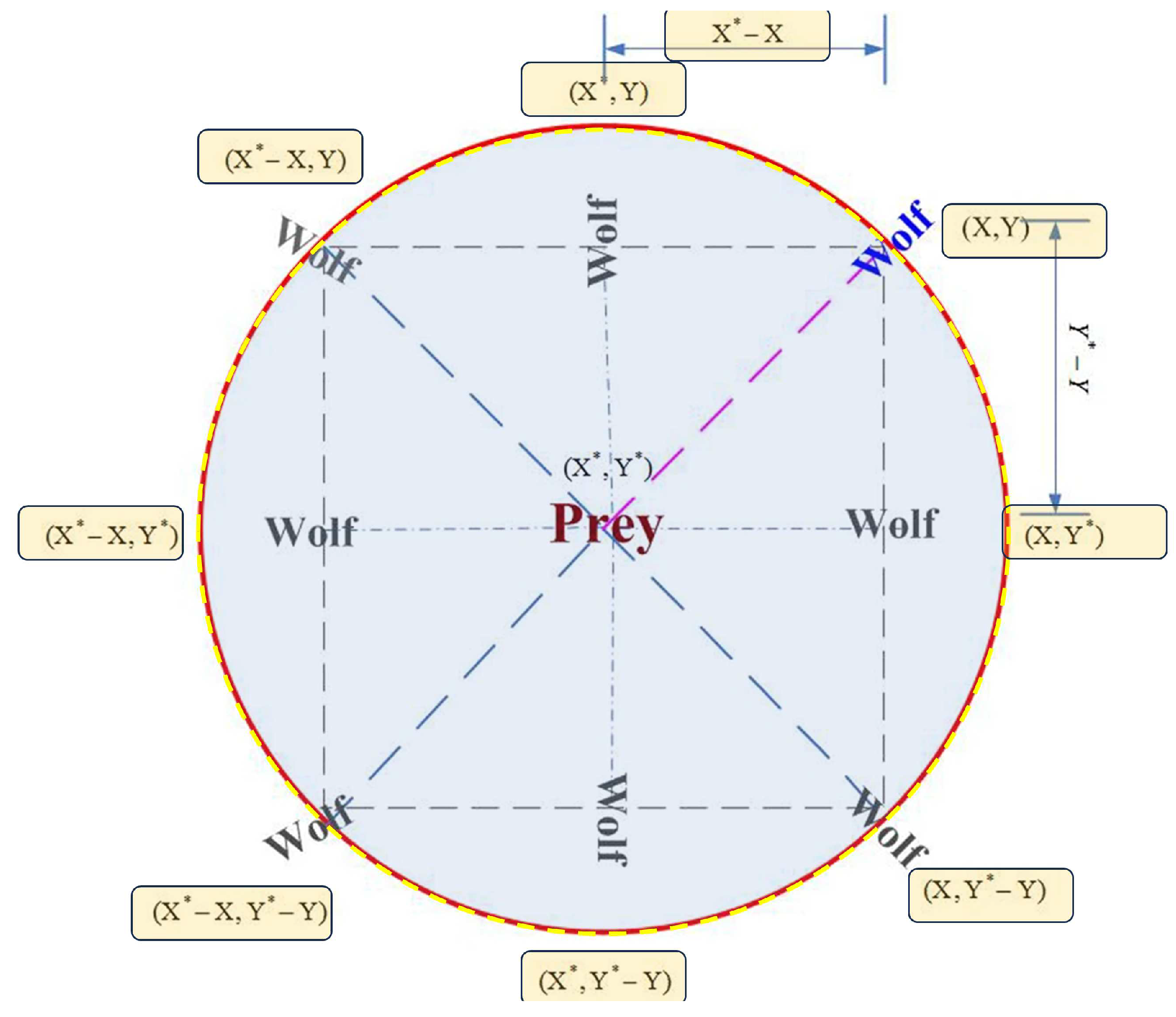
Where the coefficient linearly decreases from 2 to 0 with the increasing iteration number, (r1 ) and (r2 ) are random vectors located in the scope [0,1]. The principles underlying the position updating rules described in Equations (1) is visually represented in Figure 1. The figure illustrates how a wolf positioned at coordinates (X, Y) can adjust its position around the prey based on the aforementioned updating formulas. Although Figure 1 only displays seven possible positions for the wolf to move to, by adjusting the random parameters C and A, it becomes possible for the wolf to relocate itself to any position within the continuous space near the prey.
In the GWO algorithm, it is always assumed that the positions of the alpha, beta, and delta wolves are likely to correspond to the position of the prey, which represents the optimal solution. Throughout the iterative search process, the alpha, beta, and delta wolves represent the best, second-best, and third-best individuals obtained thus far, respectively. On the other hand, the remaining wolves, referred to as omega, adjust their locations based on the positions of the alpha, beta, and delta wolves. Mathematical formulas are employed to re-adjust the positions of the omega wolves. The conceptual model depicting the process of a wolf updating its position is presented in Figure 2.
D → α = C 1 → · X α → − X → D → β = C 2 → · X β → − X → D → δ = C 3 → · X δ → − X →
In the equations mentioned, X α , X β , and X δ represent the position vectors of the alpha, beta, and delta individuals, respectively. C1, C2, and C3 denote randomly generated vectors, and X represents the position vector of the current individual. Equations (3) calculate the distances between the position of the current individual and the positions of the alpha, beta, and delta individuals, respectively. The final position vectors of the current individual are then determined by the following calculations:
X 1 → = X α → − A 1 → · D α → → X 2 → = X β → − A 2 → · D β → X 3 → = X δ → − A 3 → · D δ → → X → ( t + 1 ) = X 1 → + X 2 → + X 3 → 3
Where A1, A2, and A3 are randomly generated vectors, and t represents the number of iterations.
Preprints 86026 g005
Figure 5. The coordination vectors of the particles in GWO and possible next locations.
Figure 5. The coordination vectors of the particles in GWO and possible next locations.
Preprints 86026 g005
The ability to explore and exploit plays a crucial role in determining the search performance of an algorithm. In the context of GWO, exploration refers to a wolf deviating from its original search path to a certain extent and venturing into new directions. This reflects the wolf’s capability to explore unknown regions and discover potentially promising solutions. Exploitation, on the other hand, involves a wolf continuing its search more meticulously along its original trajectory, ensuring a thorough examination of the regions that have already been explored.
Finding the right balance between exploration and exploitation is a significant research question in optimizing the GWO algorithm. It involves determining how to enable the algorithm to strike a suitable compromise between exploring new areas and exploiting the knowledge gained from previously explored regions. By achieving this balance, the algorithm can effectively search the solution space and improve its overall performance.

6. Neural Fuzzy Grey wolf Optimization Inference System (ANFIS-GWO)

Developing an accurate fuzzy rule base is a critical aspect of building a fuzzy system. Typically, domain specialists are responsible for creating these rules and defining the membership functions, as their expertise directly influences the meaning and effectiveness of the system. While acquiring fuzzy rules can be relatively straightforward, obtaining appropriate membership functions can be challenging and time-consuming. The membership functions play a significant role in characterizing the fuzzy system and determining its performance through its type and parameters. Unfortunately, there are no established techniques available for managing them. Fuzzy systems can be viewed as search spaces, where each point in the space represents a rule set and membership functions. Evolutionary algorithms such as Genetic Algorithms (GAs), particle swarm optimization (PSO), and other similar approaches are well-suited for exploring these spaces [56].
Combining an Adaptive Neuro-Fuzzy Inference System (ANFIS) with the Grey Wolf Optimization (GWO) method involves integrating the optimization capabilities of GWO into the learning process of ANFIS. Here is a general approach to combining ANFIS with GWO:
  • Initialize the GWO population: Generate an initial population of grey wolves with random positions.
  • Evaluate the fitness: Evaluate the fitness of each grey wolf in the population by using ANFIS to measure the performance of the fuzzy inference system.
  • Update the alpha, beta, delta, and omega positions: Identify the alpha (best), beta, delta, and omega positions based on the fitness evaluations.
  • Update the position of each grey wolf: Update the position of each grey wolf using the GWO equations, which involve leveraging the alpha, beta, delta, and omega positions to simulate the movement and search behaviour of the grey wolves.
  • Design an initial FIS, which serves as the starting point for optimization.
  • Fine-tune the parameters of the FIS using GWO. This process involves precise adjustments to align the model’s error function with the desired performance.
  • Identify the best FIS solution based on the minimum Root Mean Square Error (RMSE), indicating the optimal balance between accuracy and error.
  • Perform ANFIS training: Use the updated positions of the grey wolves to adjust the parameters of the fuzzy rules in ANFIS. This involves updating membership functions, rule weights, and other parameters through the learning process.
  • Repeat steps 6-8: Iterate through steps 6 to 8 until a termination criterion is met, such as reaching a maximum number of iterations or achieving a desired level of performance.
By combining ANFIS with GWO, several benefits can be obtained. Frist, GWO improves the optimization process of ANFIS by exploring the search space more effectively. The optimization capabilities of GWO help ANFIS find better parameter values, leading to improved accuracy and performance. Secondly, GWO’s ability to guide the search process can accelerate the convergence of ANFIS. This can result in a reduced number of training iterations needed to achieve the desired performance. Furthermore, The combined approach of ANFIS with GWO can help improve the generalization ability of the model. GWO helps avoid overfitting by effectively exploring the solution space and finding a good balance between underfitting and overfitting. Meanwhile, GWO assists in automatically tuning the parameters of ANFIS, reducing the need for manual parameter tuning. This can save time and effort in model development. Last but not least, the combination of ANFIS and GWO can enhance the robustness of the model by providing a more reliable and accurate representation of the underlying data patterns. Overall, combining ANFIS with GWO allows for improved optimization, faster convergence, enhanced generalization, automatic parameter tuning, and increased robustness, making it a powerful approach for solving complex problems.

7. Experimental outcomes

In this section, we established a structured framework for systematically evaluating the efficacy of three methods, ANFIS, FIS, and ANFIS-GWO, for the diagnosis of liver disorders. Subsequently, we conducted an analysis to assess the performance of GWO control parameters, aiming to demonstrate the sensitivity of GWO in relation to optimal parameter selection.

7.1. GWO’s control parameters tuning

Achieving an appropriate equilibrium between exploration and exploitation processes is crucial in swarm intelligence methods [57], and it heavily relies on the accurate initialization of control parameters. Control parameters, including population size, crossover probability rate, mutation size, and alpha value, exert a significant impact on the behaviour of the swarm throughout the optimization process [58]. The population size determines the number of individuals in the swarm, directly influencing both diversity and exploration capabilities. The crossover probability rate determines the likelihood of genetic material exchange among individuals, facilitating the exploitation of advantageous solutions. The mutation size governs the magnitude of random perturbations applied to individuals, promoting exploration within the search space [59]. Meanwhile, the alpha value regulates the influence of the global best position on individual movement, ensuring a delicate balance between exploration and exploitation. By meticulously initializing and fine-tuning these control parameters, swarm intelligence methods can effectively navigate the search landscape, facilitating the discovery of optimal solutions while maintaining a harmonious interplay between exploration and exploitation.
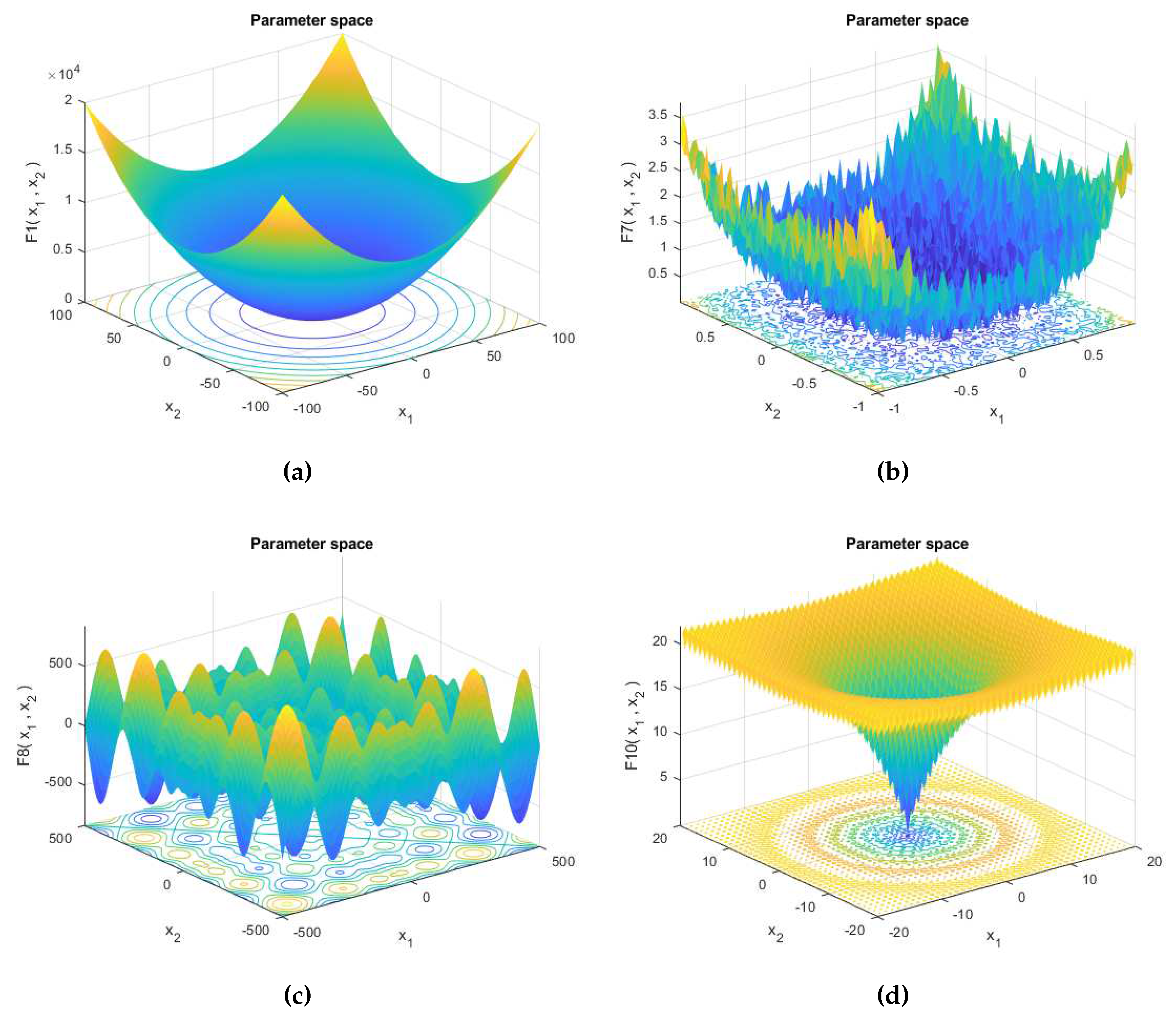
In this investigation, we conducted performance testing of the Grey Wolf Optimizer (GWO) using four well-known optimization benchmarks sourced from the CEC2005 package [60]. Various population sizes were employed in the testing process. The two dimensions of the optimization benchmark are depicted in Figure 6 . F1 represents an unimodal benchmark characterized by a single global optimum. On the other hand, F7 and F8 are multi-modal benchmarks that pose a significant challenge for most optimization methods in finding the global optimum. Lastly, F10 presents an intriguing optimization benchmark featuring one global optimum and numerous local optima. Addressing the issue of stagnation becomes particularly challenging when dealing with problems that exhibit multiple local optima.
In Figure 7(a), we can see the convergence speed of GWO with various population sizes, 5, 10, 25, 50 and 100 solutions for F1. As F1 is an unimodal function, increasing the population size leads to reducing the convergence rate; thus smaller population size can perform better. This is because a smaller population size reduces the likelihood of premature convergence to local optima. By having fewer individuals, the exploration of the search space becomes less dense, allowing the algorithm to focus on refining and converging towards the global optimum more efficiently [61]. In unimodal benchmarks, where the objective function exhibits a single peak, a larger population size can lead to increased competition among individuals, resulting in more exploration across different regions of the search space. This extensive exploration may slow down the convergence process towards the global optimum [62]. Conversely, a smaller population size tends to accelerate convergence by reducing exploration, enabling individuals to converge more rapidly towards the global optimum.
On the other hand, it can be seen in Figure 7(c) a large population sizes can perform better than small sizes in multimodal benchmarks. This is due to the capability of larger populations to engage in more extensive exploration of the search space, thereby increasing the likelihood of discovering and converging towards multiple optima. In multi-modal benchmarks, characterized by having multiple peaks in the objective function, a larger population size facilitates a more comprehensive exploration of diverse regions within the search space [63]. With a greater number of individuals, the algorithm can simultaneously search for and converge towards multiple optima. This heightened exploration capacity helps prevent premature convergence to suboptimal solutions and enhances the probability of identifying global optima or multiple global optima.
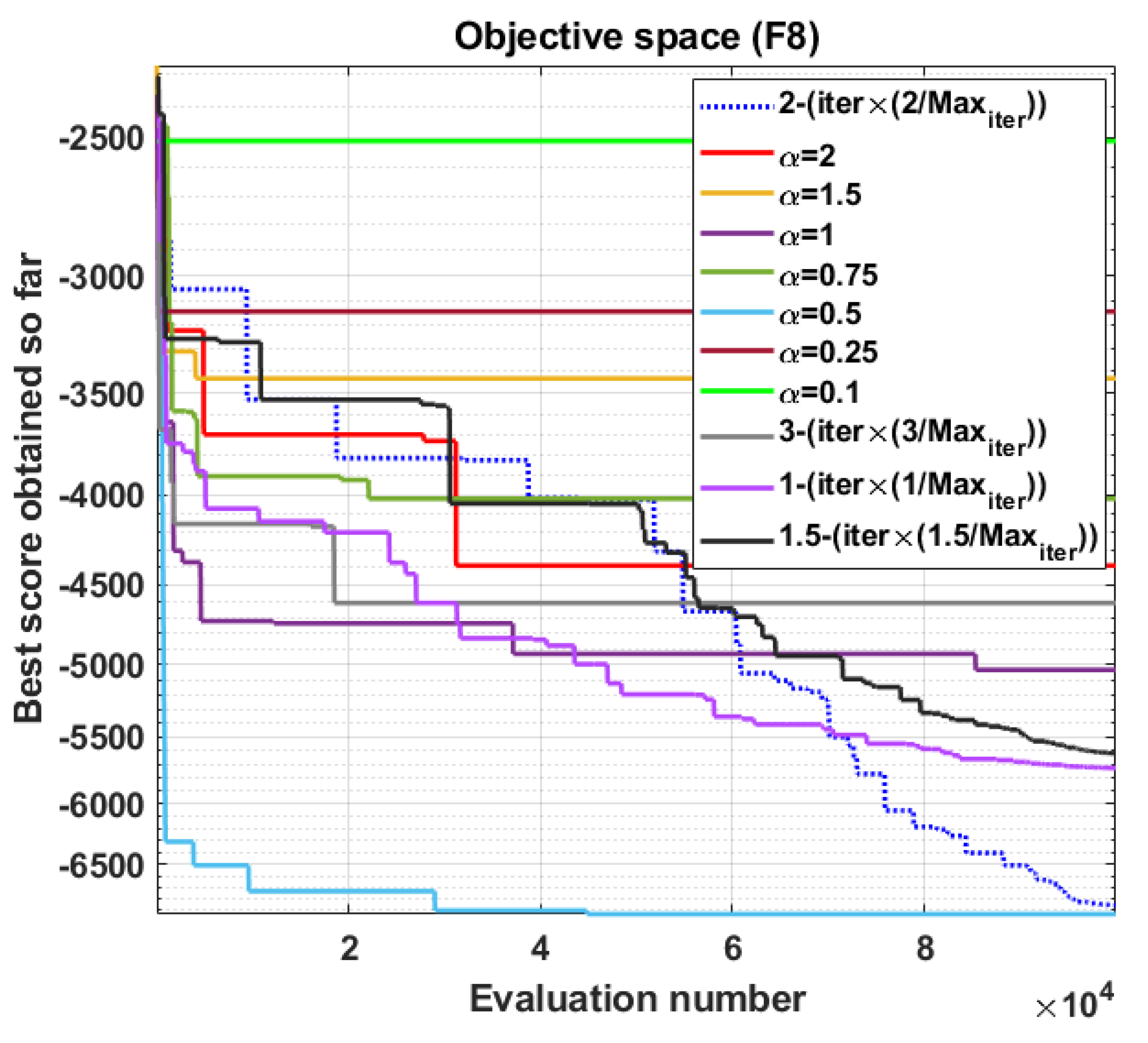
The alpha parameter in GWO is the second most significant parameter, as it plays a crucial role in balancing exploration and exploitation. Figure 8 illustrates the impact of different alpha values on the performance of GWO. Interestingly, when alpha had a fixed value of 0.5, it exhibited a notable convergence rate compared to the standard linear decrease from 2 to zero. However, other alpha values did not yield satisfactory results. Additionally, we tested other constant values, such as 1, 1.5, and 3, in the dynamic formula for alpha, but none of them outperformed the value of 2. Overall, these findings highlight the significance of selecting an appropriate alpha value to achieve optimal performance in GWO, with a fixed value of 0.5 demonstrating promising results compared to the conventional linear decrease from 2 to zero.

7.2. Diagnosis liver disorders results

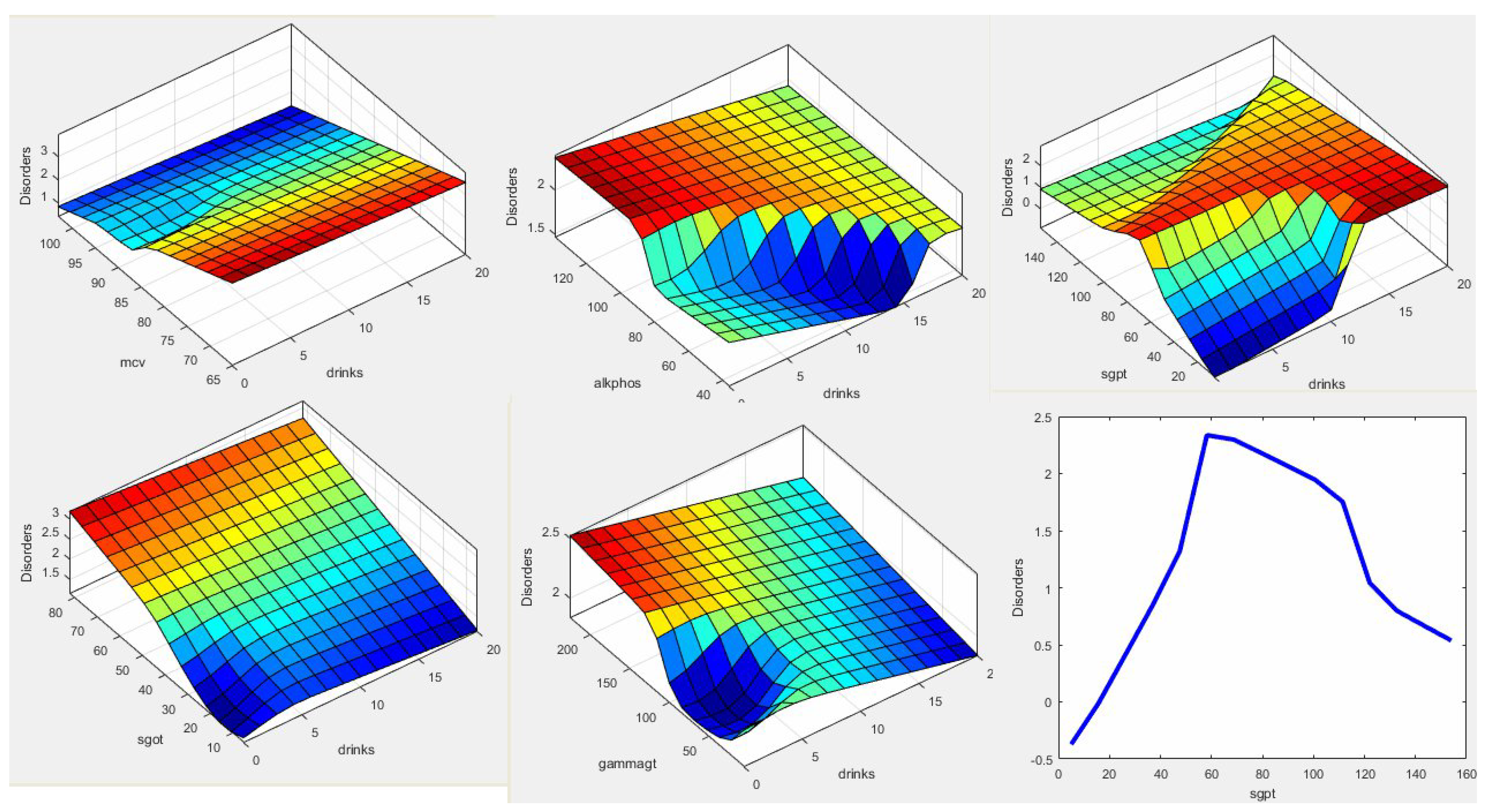
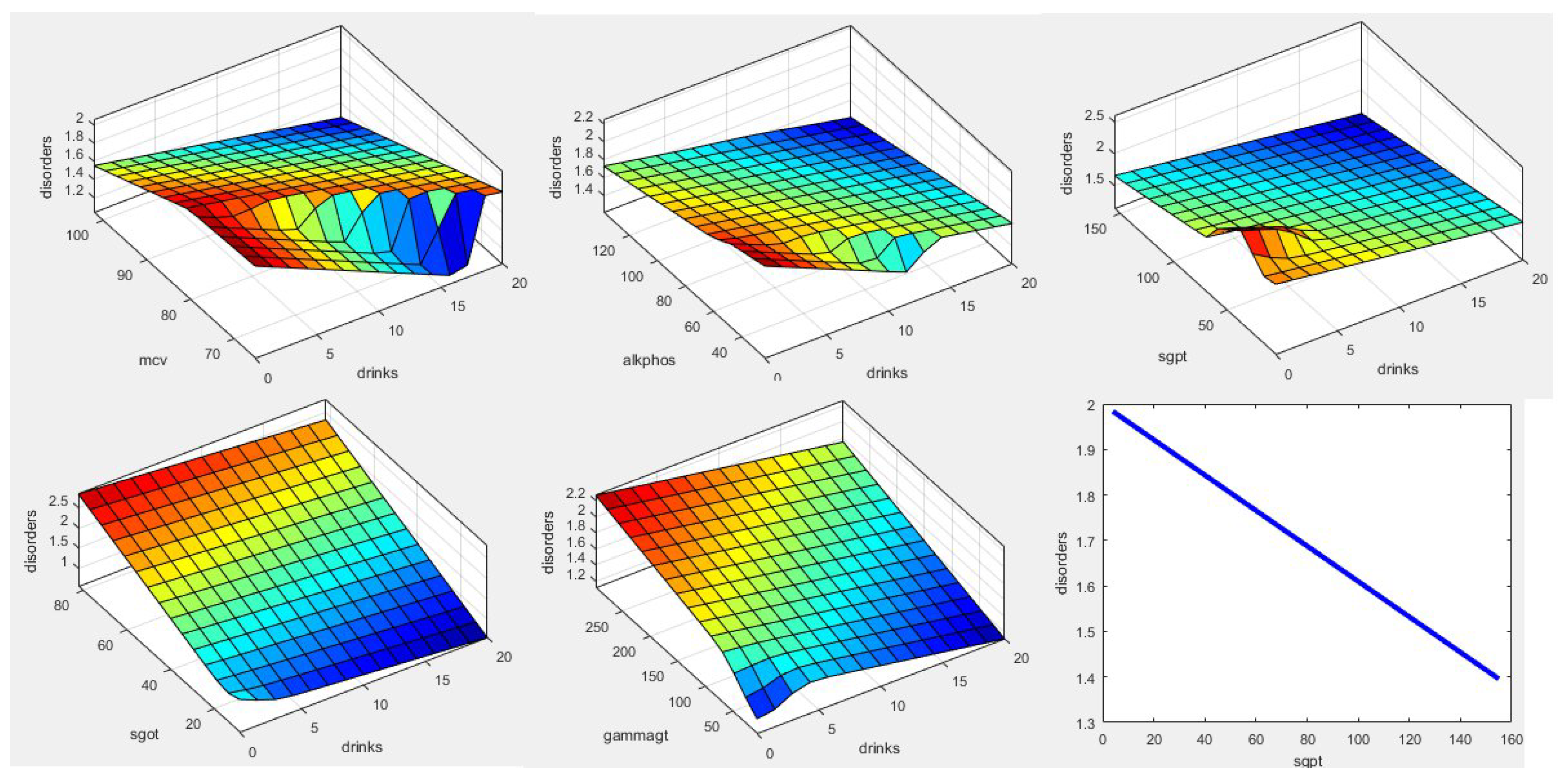
The proposed ANFIS and ANFIS-GWO performances are evaluated by the dataset of Liver disorders (Bupa). Both Figure 9 and Figure 10 present the fuzzy relationships among the five features with drinks level in ANFIS and ANFIS-GWO. It can be seen that the used ANFIS-GWO is able to enhance the achieved model.
Based on the information provided, Table 3 presents the statistical analysis results of various models for classifying liver disorders. The models evaluated in terms of classification accuracy are as follows:
ANFIS-GWO: A hybrid model combining Adaptive Neuro-Fuzzy Inference System (ANFIS) with Grey Wolf Optimization (GWO). ANFIS: The standard ANFIS model. SVM: Support Vector Machine. SGD: Stochastic Gradient Descent. MLP: Multilayer Perceptron. KNN: K-Nearest Neighbors. Decision Tree: A decision tree-based model. XGBoost: A gradient boosting-based model.
According to the results presented in Table 3, the best-performing models in terms of classification accuracy are ANFIS-GWO with an accuracy of 51%, followed by ANFIS with 44%, and SVM with 42%. It is also mentioned that this arrangement holds true for the average validation error as well.

8. Conclusions

This study introduced a hybrid adaptive neural fuzzy expert system that utilizes Grey Wolf Swarm Optimization (GWO) in Matlab’s Simulink for distinguishing between liver disease and healthy conditions. By employing this recommended approach, the classification accuracy can be improved by 7% compared to the ANFIS system based on the dataset. Statistical analysis was employed to develop meaningful attributes and fuzzy rules. The significance of identifying significant and relevant fuzzy rules without relying on specialists highlights the potential for knowledge discovery. The key advantages of using the fuzzy inference system (FIS) as a knowledge acquisition mechanism include the adaptability to handle varying numbers of rules and the ability to efficiently explain the acquired rules. These findings suggest promising research avenues for utilizing GWO and fuzzy expert systems in various classification problems. Based on the results, the proposed hybrid system outperforms previously studied approaches in terms of accuracy and reliability.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

References

  1. Feigenbaum, E.A. Expert systems in the 1980s. State of the art report on machine intelligence. Maidenhead: Pergamon-Infotech 1981.
  2. Saibene, A.; Assale, M.; Giltri, M. Expert systems: Definitions, advantages and issues in medical field applications. Expert Systems with Applications 2021, 177, 114900. [Google Scholar] [CrossRef]
  3. Rodger, J.A. An expert system gap analysis and empirical triangulation of individual differences, interventions, and information technology applications in alertness of railroad workers. Expert Systems with Applications 2020, 144, 113081. [Google Scholar] [CrossRef]
  4. Mazhar, T.; Nasir, Q.; Haq, I.; Kamal, M.M.; Ullah, I.; Kim, T.; Mohamed, H.G.; Alwadai, N. A Novel Expert System for the Diagnosis and Treatment of Heart Disease. Electronics 2022, 11, 3989. [Google Scholar] [CrossRef]
  5. Adeli, A.; Neshat, M. A fuzzy expert system for heart disease diagnosis. Proceedings of International Multi Conference of Engineers and Computer Scientists, Hong Kong, 2010, Vol. 1, pp. 28–30.
  6. Neshat, M.; Sepidname, G.; Eizi, A.; Amani, A. A new skin color detection approach based on fuzzy expert system. Indian Journal of Science and Technology 2015, 8, 1–11. [Google Scholar] [CrossRef]
  7. Moya, A.; Navarro, E.; Jaén, J.; González, P. Fuzzy-description logic for supporting the rehabilitation of the elderly. Expert Systems 2019, p. e12464. 1246. [Google Scholar]
  8. Farokhzad, M.R.; Ebrahimi, L. A novel adaptive neuro fuzzy inference system for the diagnosis of liver disease. International Journal of Academic Research in Computer Engineering 2016, 1, 61–66. [Google Scholar]
  9. Neshat, M.; Momin, M.M.; Truong, B.; van der Werf, J.; Lee, S.; Lee, S. Finetuning hyper-parameters increases the prediction accuracy in single-step genetic evaluation. Proceedings of 12th World Congress on Genetics Applied to Livestock Production (WCGALP) Technical and species orientated innovations in animal breeding, and contribution of genetics to solving societal challenges. Wageningen Academic Publishers, 2022, pp. 1352–1355.
  10. Dehkordi, A.A.; Hashemi, M.; Neshat, M.; Mirjalili, S.; Sadiq, A.S. Brain Tumor Detection and Classification Using a New Evolutionary Convolutional Neural Network. arXiv 2022, arXiv:arXiv:2204.12297. [Google Scholar] [CrossRef]
  11. Hajam, M.A.; Arif, T.; Khanday, A.M.U.D.; Neshat, M. An Effective Ensemble Convolutional Learning Model with Fine-tuning for Medicinal Plant Leaf Identification 2023.
  12. Dadgar, S.; Neshat, M. Comparative Hybrid Deep Convolutional Learning Framework with Transfer Learning for Diagnosis of Lung Cancer. International Conference on Soft Computing and Pattern Recognition. Springer, 2022, pp. 296–305.
  13. Rajabi, M.; Hossani, S.; Dehghani, F. A literature review on current approaches and applications of fuzzy expert systems. arXiv arXiv:arXiv:1909.08794.
  14. Liver Disorders. UCI Machine Learning Repository, 1990. [CrossRef]
  15. Zadeh, L.A. Soft computing and fuzzy logic. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi a Zadeh; World Scientific, 1996; pp. 796–804.
  16. Neshat, M.; Yaghobi, M.; Naghibi, M. Designing an expert system of liver disorders by using neural network and comparing it with parametric and nonparametric system. 2008 5th International Multi-Conference on Systems, Signals and Devices. IEEE, 2008, pp. 1–6.
  17. Neshat, M.; Yaghobi, M.; Naghibi, M.; Esmaelzadeh, A. Fuzzy expert system design for diagnosis of liver disorders. 2008 International Symposium on Knowledge Acquisition and Modeling. IEEE, 2008, pp. 252–256.
  18. Neshat, M.; Zadeh, A.E. Hopfield neural network and fuzzy Hopfield neural network for diagnosis of liver disorders. 2010 5th IEEE International Conference Intelligent Systems. IEEE, 2010, pp. 162–167.
  19. Neshat, M.; Masoumi, A.; Rajabi, M.; Jafari, H. Diagnosing hepatitis disease by using fuzzy hopfield neural network. Annual Research & Review in Biology 2014, pp. 2709–2721. 2709. [Google Scholar]
  20. Neshat, M.; Adeli, A.; Masoumi, A. A Survey on Artificial Intelligence and Expert System for Liver Disorders. ARPN Journal of Systems and Software 2013, 3. [Google Scholar]
  21. Selvaraj, G.; Janakiraman, S. Improved feature selection based on particle swarm optimization for liver disease diagnosis. International Conference on Swarm, Evolutionary, and Memetic Computing. Springer, 2013, pp. 214–225.
  22. Satarkar, S.; Ali, M. Fuzzy expert system for the diagnosis of common liver disease. International Engineering Journal For Research & Development 2015, 1, 2–7. [Google Scholar]
  23. Hashmi, A.; Khan, M.S. Diagnosis blood test for liver disease using fuzzy logic. International Journal of Sciences: Basic and Applied Research (IJSBAR) 2015, 20, 151–183. [Google Scholar]
  24. Singh, A.; Pandey, B. An Efficient Diagnosis System for Detection of Liver Disease Using a Novel Integrated Method Based on Principal Component Analysis and K-Nearest Neighbor (PCA-KNN). In Intelligent Systems: Concepts, Methodologies, Tools, and Applications; IGI Global, 2018; pp. 1015–1030.
  25. Mirmozaffari, M. Developing an expert system for diagnosing liver diseases. European Journal of Engineering Research and Science 2019, 4, 1–5. [Google Scholar] [CrossRef]
  26. Kim, S.; Jung, S.; Park, Y.; Lee, J.; Park, J. Effective liver cancer diagnosis method based on machine learning algorithm. 2014 7th International Conference on Biomedical Engineering and Informatics. IEEE, 2014, pp. 714–718.
  27. Das, A.; Das, P.; Panda, S.S.; Sabut, S. Adaptive fuzzy clustering-based texture analysis for classifying liver cancer in abdominal CT images. International Journal of Computational Biology and Drug Design 2018, 11, 192–208. [Google Scholar] [CrossRef]
  28. Xian, G.m. An identification method of malignant and benign liver tumors from ultrasonography based on GLCM texture features and fuzzy SVM. Expert Systems with Applications 2010, 37, 6737–6741. [Google Scholar] [CrossRef]
  29. Polat, K.; Güneş, S. An expert system approach based on principal component analysis and adaptive neuro-fuzzy inference system to diagnosis of diabetes disease. Digital Signal Processing 2007, 17, 702–710. [Google Scholar] [CrossRef]
  30. Polat, K.; Güneş, S. Hepatitis disease diagnosis using a new hybrid system based on feature selection (FS) and artificial immune recognition system with fuzzy resource allocation. Digital Signal Processing 2006, 16, 889–901. [Google Scholar] [CrossRef]
  31. Chen, H.L.; Liu, D.Y.; Yang, B.; Liu, J.; Wang, G. A new hybrid method based on local fisher discriminant analysis and support vector machines for hepatitis disease diagnosis. Expert Systems with Applications 2011, 38, 11796–11803. [Google Scholar] [CrossRef]
  32. Neshat, M.; Yaghobi, M. Designing a fuzzy expert system of diagnosing the hepatitis B intensity rate and comparing it with adaptive neural network fuzzy system. Proceedings of the World Congress on Engineering and Computer Science, 2009, Vol. 2, pp. 797–802.
  33. Neshat, M.; Sargolzaei, M.; Nadjaran Toosi, A.; Masoumi, A. Hepatitis disease diagnosis using hybrid case based reasoning and particle swarm optimization. ISRN Artificial Intelligence 2012, 2012. [Google Scholar] [CrossRef]
  34. Neshat, M.; Yaghobi, M. FESHDD: fuzzy expert system for hepatitis B diseases diagnosis. 2009 Fifth International Conference on Soft Computing, Computing with Words and Perceptions in System Analysis, Decision and Control, 2009.
  35. Adeli, M.; Bigdeli, N.; Afshar, K. New hybrid hepatitis diagnosis system based on Genetic algorithm and adaptive network fuzzy inference system. 2013 21st Iranian conference on electrical engineering (ICEE). IEEE, 2013, pp. 1–6.
  36. Ahmad, W.; Ahmad, A.; Iqbal, A.; Hamayun, M.; Hussain, A.; Rehman, G.; Khan, S.; Khan, U.U.; Khan, D.; Huang, L. Intelligent hepatitis diagnosis using adaptive neuro-fuzzy inference system and information gain method. Soft Computing 2018, pp. 1–8.
  37. Ahmad, G.; Khan, M.A.; Abbas, S.; Athar, A.; Khan, B.S.; Aslam, M.S. Automated Diagnosis of Hepatitis B Using Multilayer Mamdani Fuzzy Inference System. Journal of healthcare engineering 2019, 2019. [Google Scholar] [CrossRef]
  38. Affane, A.; Lebre, M.A.; Mittal, U.; Vacavant, A. Literature review of deep learning models for liver vessels reconstruction. 2020 Tenth International Conference on Image Processing Theory, Tools and Applications (IPTA). IEEE, 2020, pp. 1–6.
  39. Rabbi, M.F.; Hasan, S.M.; Champa, A.I.; AsifZaman, M.; Hasan, M.K. Prediction of liver disorders using machine learning algorithms: a comparative study. 2020 2nd International Conference on Advanced Information and Communication Technology (ICAICT). IEEE, 2020, pp. 111–116.
  40. Balasubramanian, K.; Ananthamoorthy, N. Improved adaptive neuro-fuzzy inference system based on modified glowworm swarm and differential evolution optimization algorithm for medical diagnosis. Neural Computing and Applications 2021, 33, 7649–7660. [Google Scholar] [CrossRef]
  41. Napte, K.; Mahajan, A. Deep Learning based Liver Segmentation: A Review. Revue d’Intelligence Artificielle 2022, 36, 979. [Google Scholar] [CrossRef]
  42. Huang, L.; Sun, H.; Sun, L.; Shi, K.; Chen, Y.; Ren, X.; Ge, Y.; Jiang, D.; Liu, X.; Knoll, W.; others. Rapid, label-free histopathological diagnosis of liver cancer based on Raman spectroscopy and deep learning. Nature Communications 2023, 14, 48. [Google Scholar] [CrossRef] [PubMed]
  43. Jang, J.S.R.; others. Fuzzy modeling using generalized neural networks and kalman filter algorithm. AAAI, 1991, Vol. 91, pp. 762–767.
  44. Tahmasebi, P.; Hezarkhani, A. A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation. Computers & geosciences 2012, 42, 18–27. [Google Scholar]
  45. Walia, N.; Singh, H.; Sharma, A. ANFIS: Adaptive neuro-fuzzy inference system-a survey. International Journal of Computer Applications 2015, 123. [Google Scholar] [CrossRef]
  46. Wang, J.S.; Lee, C.G. Self-adaptive neuro-fuzzy inference systems for classification applications. IEEE Transactions on Fuzzy systems 2002, 10, 790–802. [Google Scholar] [CrossRef]
  47. Chopra, S.; Dhiman, G.; Sharma, A.; Shabaz, M.; Shukla, P.; Arora, M. Taxonomy of adaptive neuro-fuzzy inference system in modern engineering sciences. Computational Intelligence and Neuroscience 2021, 2021. [Google Scholar] [CrossRef] [PubMed]
  48. Nilashi, M.; Ahmadi, H.; Shahmoradi, L.; Ibrahim, O.; Akbari, E. A predictive method for hepatitis disease diagnosis using ensembles of neuro-fuzzy technique. Journal of infection and public health 2019, 12, 13–20. [Google Scholar] [CrossRef]
  49. Iwendi, C.; Mahboob, K.; Khalid, Z.; Javed, A.R.; Rizwan, M.; Ghosh, U. Classification of COVID-19 individuals using adaptive neuro-fuzzy inference system. Multimedia Systems 2021, pp. 1–15.
  50. Mohiyuddin, A.; Javed, A.R.; Chakraborty, C.; Rizwan, M.; Shabbir, M.; Nebhen, J. Secure cloud storage for medical IoT data using adaptive neuro-fuzzy inference system. International Journal of Fuzzy Systems 2022, 24, 1203–1215. [Google Scholar] [CrossRef]
  51. Zeinalnezhad, M.; Chofreh, A.G.; Goni, F.A.; Klemeš, J.J. Air pollution prediction using semi-experimental regression model and Adaptive Neuro-Fuzzy Inference System. Journal of Cleaner Production 2020, 261, 121218. [Google Scholar] [CrossRef]
  52. Wu, J.; Hu, R.; Li, M.; Liu, S.; Zhang, X.; He, J.; Chen, J.; Li, X. Diagnosis of sleep disorders in traditional Chinese medicine based on adaptive neuro-fuzzy inference system. Biomedical Signal Processing and Control 2021, 70, 102942. [Google Scholar] [CrossRef]
  53. Farhadi, S.; Salehi, M.; Moieni, A.; Safaie, N.; Sabet, M.S. Modeling of paclitaxel biosynthesis elicitation in Corylus avellana cell culture using adaptive neuro-fuzzy inference system-genetic algorithm (ANFIS-GA) and multiple regression methods. PloS one 2020, 15, e0237478. [Google Scholar] [CrossRef]
  54. Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Advances in engineering software 2014, 69, 46–61. [Google Scholar] [CrossRef]
  55. Wang, J.S.; Li, S.X. An improved grey wolf optimizer based on differential evolution and elimination mechanism. Scientific reports 2019, 9, 7181. [Google Scholar] [CrossRef] [PubMed]
  56. Muthukaruppan, S.; Er, M.J. A hybrid particle swarm optimization based fuzzy expert system for the diagnosis of coronary artery disease. Expert Systems with Applications 2012, 39, 11657–11665. [Google Scholar] [CrossRef]
  57. Hatta, N.; Zain, A.M.; Sallehuddin, R.; Shayfull, Z.; Yusoff, Y. Recent studies on optimisation method of Grey Wolf Optimiser (GWO): a review (2014–2017). Artificial intelligence review 2019, 52, 2651–2683. [Google Scholar] [CrossRef]
  58. Slowik, A.; Kwasnicka, H. Evolutionary algorithms and their applications to engineering problems. Neural Computing and Applications 2020, 32, 12363–12379. [Google Scholar] [CrossRef]
  59. Meng, Z.; Pan, J.S.; Tseng, K.K. PaDE: An enhanced Differential Evolution algorithm with novel control parameter adaptation schemes for numerical optimization. Knowledge-Based Systems 2019, 168, 80–99. [Google Scholar] [CrossRef]
  60. Mohammed, H.M.; Umar, S.U.; Rashid, T.A.; others. A systematic and meta-analysis survey of whale optimization algorithm. Computational intelligence and neuroscience 2019, 2019. [Google Scholar] [CrossRef]
  61. Zhou, S.; Xing, L.; Zheng, X.; Du, N.; Wang, L.; Zhang, Q. A self-adaptive differential evolution algorithm for scheduling a single batch-processing machine with arbitrary job sizes and release times. IEEE transactions on cybernetics 2019, 51, 1430–1442. [Google Scholar] [CrossRef]
  62. Mohamed, A.W.; Suganthan, P.N. Real-parameter unconstrained optimization based on enhanced fitness-adaptive differential evolution algorithm with novel mutation. Soft Computing 2018, 22, 3215–3235. [Google Scholar] [CrossRef]
  63. Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. Population size in particle swarm optimization. Swarm and Evolutionary Computation 2020, 58, 100718. [Google Scholar] [CrossRef]
Preprints 86026 g002
Figure 2. Correlation matrix plot: visualizing the relationships among variables and target"
Figure 2. Correlation matrix plot: visualizing the relationships among variables and target"
Preprints 86026 g002
Preprints 86026 g004
Figure 4. The five layers architecture of an Adaptive Neuro-Fuzzy Inference System from [48]
Figure 4. The five layers architecture of an Adaptive Neuro-Fuzzy Inference System from [48]
Preprints 86026 g004
Preprints 86026 g006
Figure 6. Optimisation benchmark functions, a) F1, b) F7, c) F8, and d)F10
Figure 6. Optimisation benchmark functions, a) F1, b) F7, c) F8, and d)F10
Preprints 86026 g006
Preprints 86026 g007
Figure 7. A performance comparison of GWO with various population sizes Optimisation benchmark functions, a) F1, b) F2, c) F3, and d) F7
Figure 7. A performance comparison of GWO with various population sizes Optimisation benchmark functions, a) F1, b) F2, c) F3, and d) F7
Preprints 86026 g007
Preprints 86026 g008
Figure 8. Hyper-parameter analysis of GWO for the control parameter α with seven fixed values and four linearly decreased strategies.
Figure 8. Hyper-parameter analysis of GWO for the control parameter α with seven fixed values and four linearly decreased strategies.
Preprints 86026 g008
Preprints 86026 g009
Figure 9. The fuzzy relationship among the effective variables of Liver disorders with different levels of drink values BY ANFIS
Figure 9. The fuzzy relationship among the effective variables of Liver disorders with different levels of drink values BY ANFIS
Preprints 86026 g009
Preprints 86026 g010
Figure 10. The fuzzy relationship among the effective variables of Liver disorders with different levels of drink values BY ANFIS-GWO.
Figure 10. The fuzzy relationship among the effective variables of Liver disorders with different levels of drink values BY ANFIS-GWO.
Preprints 86026 g010
Table 1. Bupa Liver Disorders Dataset
Table 1. Bupa Liver Disorders Dataset
# Feild Description
1 MCV means corpuscular volume Alkphos
2 ALP Alkaline phosphates
3 Sgpt alanine aminotransferase
4 Sgot aspartate aminotransferase
5 Gammagt gamma-glut amyl Tranpeptidase
6 Drinks number of half-pint equivalents of alcoholic beverages Drunk per day
7 Selector field used to split data into two sets.
Table 2. A brief survey of the AI method applications for diagnosing Liver disorders.
Table 2. A brief survey of the AI method applications for diagnosing Liver disorders.
Authors Methods Disease Year
Neshat et al. [16,17,18,19,20] Bayesian parametric method and Parzen window non parametric method, Fuzzy Expert System, Hopfield Neural Network and Fuzzy Hopfield Neural Network Liver Disease 2008, 2009, 2010, 2013, 2014
Selvaraj et al.[21] particle swarm optimization Liver Disease 2013
Satarkar et al.[22] Fuzzy expert system Liver Disease 2015
Hashemi et al. [23] fuzzy logic Liver Disease 2015
Singh et al.[24] Principal Component Analysis and K-Nearest Neighbor (PCA-KNN) Liver Disease 2018
Mirmozaffari et al. [25] expert system Liver Disease 2019
Kim et al. [26] neural network and fuzzy neural network Liver Cancer 2014
Das et al. [27] Adaptive fuzzy clustering-based texture analysis Liver Cancer 2018
Xian et al. [28] GLCM texture features and fuzzy SVM Liver Tumors 2010
Polat et al. [29] adaptive neuro-fuzzy inference system Diabetes Disease 2007
Polat et al. [30] artificial immune recognition system with fuzzy resource allocation Hepatitis Disease 2006
Chen et al.[31] local fisher discriminant analysis and support vector machines Hepatitis Disease 2011
Neshat et al. [32,33,34] Adaptive Neural Network Fuzzy System, Hybrid Case Based Reasoning and PSO, Fuzzy expert system Hepatitis B 2009, 2012
Adeli et al. [35] Genetic algorithm and adaptive network fuzzy inference system Hepatitis 2013
Ahmad et al. [36,37] adaptive neuro-fuzzy inference system, Multilayer Mamdani Fuzzy Inference System Hepatitis Disease 2018, 2019
Affane et al. [38] Deep learning models liver vessels reconstruction 2020
Rabbi et al. [39] Machine learning models Liver disorders 2020
Balasubram et al. [40] Improved ANFIS + Glow Worm Swarm +DE Liver Cancer 2021
Napte et al. [41] Deep learning models Liver Segmentation 2022
Huang et al. [42] Raman spectroscopy and deep learning liver cancer 2023
Table 3. Statistical analysis of the proposed model (ANFIS-GWO) compared with seven models for diagnosing Liver disorders.
Table 3. Statistical analysis of the proposed model (ANFIS-GWO) compared with seven models for diagnosing Liver disorders.
SVM SGD
MSE RMSE MAE R-value R2 MSE RMSE MAE R-value R2
Min 0.203 0.450 0.203 0.263 0.069 Min 0.246 0.496 0.246 0.136 0.018
Max 0.348 0.590 0.348 0.574 0.329 Max 0.435 0.659 0.435 0.498 0.248
Mean 0.280 0.527 0.280 0.422 0.190 Mean 0.339 0.580 0.339 0.318 0.123
Median 0.283 0.532 0.283 0.415 0.172 Median 0.355 0.596 0.355 0.305 0.099
STD 0.056 0.053 0.056 0.103 0.088 STD 0.064 0.056 0.064 0.149 0.096
MLP KNN
MSE RMSE MAE R-value R2 MSE RMSE MAE R-value R2
Min 0.246 0.496 0.246 0.248 0.062 Min 0.275 0.525 0.275 0.131 0.017
Max 0.362 0.602 0.362 0.550 0.302 Max 0.406 0.637 0.406 0.362 0.131
Mean 0.295 0.541 0.295 0.394 0.167 Mean 0.349 0.590 0.349 0.262 0.076
Median 0.283 0.532 0.283 0.410 0.168 Median 0.355 0.596 0.355 0.262 0.069
STD 0.041 0.038 0.041 0.103 0.080 STD 0.040 0.034 0.040 0.082 0.043
Decision Tree XGBoost
MSE RMSE MAE R-value R2 MSE RMSE MAE R-value R2
Min 0.275 0.525 0.275 0.026 0.001 Min 0.246 0.496 0.246 0.149 0.022
Max 0.464 0.681 0.464 0.445 0.198 Max 0.406 0.637 0.406 0.496 0.246
Mean 0.367 0.603 0.367 0.259 0.093 Mean 0.325 0.567 0.325 0.328 0.124
Median 0.355 0.596 0.355 0.300 0.091 Median 0.319 0.565 0.319 0.357 0.127
STD 0.070 0.058 0.070 0.157 0.073 STD 0.062 0.054 0.062 0.120 0.080
ANFIS ANFIS-GWO
MSE RMSE MAE R-value R2 MSE RMSE MAE R-value R2
Min 0.203 0.450 0.203 0.367 0.134 Min 0.188 0.434 0.188 0.426 0.181
Max 0.319 0.565 0.319 0.562 0.316 Max 0.275 0.525 0.275 0.606 0.368
Mean 0.273 0.521 0.273 0.441 0.202 Mean 0.234 0.482 0.234 0.514 0.271
Median 0.304 0.552 0.304 0.386 0.149 Median 0.246 0.496 0.246 0.472 0.222
STD 0.047 0.047 0.047 0.084 0.078 STD 0.038 0.039 0.038 0.085 0.090
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated