Prerpints.org logo
Preprint
Review

Measurements and Evaluations of the Atmospheric Transparency at Short Millimeter Wavelengths at the Candidate Sites for Millimeter and Submillimeter Wave Telescopes

Altmetrics

Downloads

123

Views

57

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 September 2023

Posted:

26 September 2023

You are already at the latest version

Alerts
Abstract
Radio astronomical observations at millimeter and submillimeter wavelengths are a very important tool of astrophysical research. However, there is a huge area in the northern Eurasia, including the whole Russian territory, which lacks sufficiently large radio telescopes effectively operating at these wavelengths. In this review we describe our long-term efforts to find suitable sites for such radio telescopes in this area, that is, sites with good atmospheric transparency at millimeter and submillimeter waves. We describe methods and instruments used for measurements and evaluations of the atmospheric opacity. They include special radiometric systems, which are used for estimations of the atmospheric opacity from the sky brightness measurements. Evaluation of the precipitable water vapor from such measurements by the artificial neural network is discussed. Alternative approaches use global atmospheric models and signals of the Global Navigation Satellite Systems. To date, a long-term radiometric monitoring has been performed at several candidate sites and atmospheric conditions for many sites have been evaluated using global atmospheric models. Several sites with the best atmospheric transparency at millimeter and submillimeter wavelengths have been selected. They can be effectively used for astronomical observations at least in the major atmospheric transparency windows at 1.3 mm and 0.85 mm. These results can be also used for space communications and radar systems.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

Radio astronomical observations at millimeter and submillimeter wavelengths are a very important tool of astrophysical research (e.g., [1]). They provide a unique opportunity for detailed investigations of the interiors of the cold dense interstellar clouds of gas and dust which represent cradles of new stars. The emission peak of these clouds lies in this band. Millimeter and submillimeter waves are very rich in the spectral lines of various molecules, atoms and ions, which can serve as diagnostic tools of physical conditions and chemical content. At these wavelengths the highest angular resolution can be achieved which is very important for studies of compact objects, in particular active galactic nuclei. These studies are facilitated by a lower interstellar scattering in comparison with longer radio wavelengths. Bright examples of such a study are recent images of the “shadows” of supermassive black holes in the centers of M87 and our Milky Way galaxies [2,3]. These results have been obtained with the Event Horizon Telescope (EHT), which is a global VLBI network of sufficiently large millimeter-wave observatories operating at the 1.3 mm wavelength. Nowadays there are about 10 such observatories in the world. The success of the EHT stimulates the project of its extension, known as the next-generation EHT (ngEHT) [4]. Many locations in the world are considered as candidate sites for new EHT telescopes (e.g., [5]). There is a huge area in the northern Eurasia, including the whole Russian territory, which lacks such facilities although many years ago a construction of the 70-m radio telescope intended for operation at short millimeter wavelengths started on the Suffa plateau in Uzbekistan[6] (it was frozen after the USSR collapse) and there are relevant new projects and proposals [7,8,9,10].
The main obstacle to ground-based radio astronomy observations at short millimeter and submillimeter wavelengths, in addition to the technical challenges, is the atmospheric opacity, caused primarily by water and molecular oxygen. The observations are possible only in the so-called “atmospheric transparency windows” – the bands of relatively high transparency between the strong spectral lines of these molecules. The main windows discussed here are those centered at ∼90 GHz, ∼140 GHz, ∼225 GHz and ∼350 GHz. They are usually referred to as the 3 mm, 2 mm, 1.3 mm and 0.8 mm windows, respectively. However, even in these windows the opacity can be quite high. Radio astronomical observations at the sea level are possible only in the 3 mm and 2 mm windows. At higher frequencies high-altitude locations should be used.
While the oxygen absorption is stable and can be rather easily evaluated, the water content is highly variable. Water in the atmosphere is present in two forms – water vapor and liquid water (the latter one mainly in clouds). The amount of water vapor is usually characterized by the PWV (Precipitable Water Vapor) parameter, which is the vertically integrated amount of water vapor in the atmosphere. It is usually measured in millimeters. The amount of liquid water is parameterized by Liquid Water Path (LWP) measured in g m − 2 or in μ m (e.g. [5]). The zenith opacity (optical depth) of the atmosphere in dependence on frequency ( ν ) is related to these parameters by the following expression:
τ ( ν ) = τ O 2 ( ν ) + β ( ν ) P W V + γ ( ν ) L W P ,
where τ O 2 ( ν ) is the molecular oxygen contribution to this opacity, β ( ν ) is the specific absorption coefficient per PWV unit and γ ( ν ) is the specific absorption coefficient per LWP unit. The suitability of a site for radio astronomy observations is primarily characterized by the opacity statistics in atmospheric windows or by the PWV statistics, which are related to each other under clear sky conditions, although the LWP statistics is also important.
Both τ O 2 ( ν ) and β ( ν ) are determined by the vertical distributions of the atmosphere physical parameters (pressure and temperature), molecular oxygen and water vapor. They can be derived empirically for a certain site or calculated using the existing models of the atmosphere in conjunction with spectroscopic databases (e.g., [11,12]). Then, nowadays global dynamic models of the atmosphere with a high spatial and temporal resolution are available (see below). The dependencies of the microwave absorption by molecular oxygen and water vapor on physical parameters and altitude in the atmosphere were analyzed many years ago [13]. In paper [14] the dependencies of τ O 2 ( ν ) and β ( ν ) on altitude for the 1.3 mm window were calculated. The dependence of the molecular oxygen optical depth on altitude (h) is well described by the exponential function:
τ O 2 ( ν ) = α ( ν ) e − h h 0 ,
where α ( ν ) is the O 2 optical depth at the sea level and h 0 is the characteristic height usually adopted to be 5.3 km [15], although it can be somewhat different in different seasons [13].
Atmospheric transparency research is important not only for radio astronomy but also for telecommunications and radars. Millimeter-wave communication channels can provide the highest throughput (e.g., [16,17,18,19,20,21,22]) but are strongly affected by the atmosphere. Millimeter-wave radars are promising facilities for monitoring space debris and dangerous asteroids (e.g., [23,24,25,26]).
There are several ways to measure the atmospheric opacity and PVW, which are described in Section 2. In Section 3 we present some results of such investigations. They are discussed in Section 4.

2. Instruments and Methods

2.1. Methods for measuring atmospheric opacity

The optical depth of the atmosphere in zenith can be measured by several methods. Direct measurements of the opacity in a flat layered atmosphere are based on the Bouguer’s law:
I ( ν ) = I 0 ( ν ) e − τ ( ν ) cos θ ,
where I 0 ( ν ) is the intensity of cosmic source emission within the antenna beam, as it would be measured without atmosphere, I ( ν ) is the measured intensity of this emission and θ is the zenith angle. By measurements of I ( ν ) at different zenith angles, the optical depth in zenith τ ( ν ) can be retrieved. This method requires a long time for a substantial change of the zenith angle, stable atmospheric conditions during this time and negligible or well known dependence of the antenna response on the zenith angle. The flat layered model is valid at θ ≲ 85 ∘ (e.g. [15]).
In practice the value of the zenith opacity (optical depth) at millimeter wavelengths is usually derived from measurements of the atmosphere emission [15]. The sky brightness temperature in a flat layered atmosphere, neglecting the cosmic microwave background, equals to
T s ( θ , ν ) = T a ( ν ) 1 − e − τ ( ν ) cos θ ,
where T a is the mean temperature of the atmosphere:
T a ( ν ) = ∫ 0 ∞ κ ( ν , l ) T ( l ) exp [ − ∫ 0 l κ ( ν , l ′ ) d l ′ ] d l ∫ 0 ∞ κ ( ν , l ) exp [ − ∫ 0 l κ ( ν , l ′ ) d l ′ ] d l ,
where T ( l ) is the air temperature along the line of sight and κ ( ν , l ) is the total air absorption coefficient, d l = d h / cos θ and h is the height. The value of the mean temperature of the atmosphere is discussed in [27]. At a relatively low opacity T a ∼ ( 0.90 ⋯ 0.95 ) T 0 , where T 0 is the ambient temperature. At a higher opacity the mean temperature increases, as expected, to ∼ T 0 . Therefore, T a depends on the zenith angle.
In principle the zenith optical depth can be derived using Eq. (4) from the absolute measurements of the sky brightness temperature. However this method requires a precise absolute calibration of the brightness measurements, which can be challenging. A typical widely used approach, known as a “sky dip” (described below), is based on relative measurements of the sky brightness at several (minimum two) zenith angles.

2.2. Measurements of the atmosphere optical depth by the “sky dip” method

2.2.1. Basics of the “sky dip” method

From the measurements at two zenith angles ( θ 1 and θ 2 ) the optical depth of the atmosphere in zenith in the first approximation can be obtained as [15]
τ = 1 sec θ 2 − sec θ 1 ln u 0 − u 1 u 0 − u 2 .
Here u 1 and u 2 are the receiver responses at the zenith angles θ 1 and θ 2 , respectively, while u 0 is the response for the input emission with the brightness temperature T 0 . Most frequently a reference angle near the horizon, where the optical depth should be high, is used for this purpose. Some variants of this method, which use measurements at 3 zenith angles and a reference area near the horizon, are considered in [28]. From measurements of the sky brightness in a range of zenith angles the optical depth can be derived by fitting the measurement results with a function corresponding to Eq. (4) (which can be also expressed in the logarithmic form) assuming a constant mean atmosphere temperature. In this case a reference signal is needed anyway. Some examples of such devices are the 225 GHz tipping radiometers at the site of the 30-m IRAM radio telescope (D.L. John, private communication) and at the Large Millimeter Telescope (LMT) site [29].

2.2.2. A dual-band radiometer for measuring the atmospheric opacity developed at the Institute of Applied Physics RAS

About 10 years ago a dual-band radiometer MIAP-2 for measuring the atmospheric opacity was developed and manufactured at the Institute of Applied Physics of the Russian Academy of Sciences and GYCOM company [30]. The radiometer operates in the 3 mm and 2 mm atmospheric windows.
At the front-end of the 3 mm channel a broad-band millimeter wave amplifier is used with the specified frequency range 84–99 GHz. In fact, it has no rejection of lower frequencies, which leads to contamination of the measurements by the strong contribution of the molecular oxygen absorption band near 60 GHz. The problem was partly fixed by installation of a waveguide filter with the cross-section of 1 × 2 mm 2 , which has the cutoff frequency of ∼75 GHz [31]. Nevertheless, the contribution of the low frequencies remains significant and its consequences are discussed below.
The front-end of the 2 mm channel includes the local oscillator on a Gunn diode with a built-in frequency doubler, a balanced mixer on Schottky-barrier diodes (SBDs), an intermediate-frequency amplifier (IFA), and a detector for a range of 4–8 GHz. The local oscillator frequency is 140 GHz. The channel detects the emission in both lower and upper sidebands, which are 132–136 GHz and 144–148 GHz, respectively.
At the front-ends of both channels the modulator-calibrators are used. This device is described in detail in [32]. It is based on chains of series–parallel connected SBDs, placed into the standard cross-section waveguide. It can serve as a modulator of the input signal or as a source of a calibration signal. Depending on the current, it can be in 3 states: (1) open (transmitting the input signal with low losses), (2) locked with the equivalent brightness temperature of 155–180 K (“cold” calibration level) and (3) locked with the equivalent brightness temperature of ∼300 K (“warm” calibration level). These features enable both sky-dip measurements and absolute measurements of the sky brightness temperature.
Both channels are equipped with the lens antennas, which are misphased conically-shaped feed horns with a bent fracture and lenses. The half-power beam width of the antennas (with lenses) in both bands is about 2.5 ∘ . The elevation scan is provided by the rotating common mirror in front of both horns, oriented at the angle of 45 ∘ , and a mirror drive system, which is based on a stepper motor. The zenith angle range is from 0 ∘ to 90 ∘ , and the step is 0.7 ∘ .
Three measurement modes are possible. In the first one the measurements are performed at two zenith angles and at the angle near the horizon as a reference (see Section sec:basics). In the second mode the data at 5 zenith angles are acquired. The angle near the horizon is not mandatory. At last, the absolute measurements of the sky brightness are possible.
As mentioned above, the frequency responses of the channels, especially in the 3 mm band, are not well defined. This can create problems with the interpretation of the measurement results. In [33] an attempt is done to determine the effective frequencies of the channels by comparison of the experimental values of the coefficients in Eq. (1) with the values obtained from the model calculations for a range of frequencies. The experimental values were obtained using independent measurements of the PWV amount. As a result, it was found that the effective frequencies of the 3 mm and 2 mm channels are 79.7 and 134 GHz, respectively. The effective frequency of the 3 mm channel is lower than the specified frequency range of the 3 mm amplifier. It shows that the contribution of the molecular oxygen absorption band near 60 GHz is significant in this channel and should be taken into account.
Two pieces of such a radiometer have been manufactured, however the second one lacks the 2 mm channel. At the same time it has a better constrained frequency response of the 3 mm channel.

2.3. Measurements of the precipitable water vapor (PWV) by water vapor radiometers

In some cases the information on the PVW value and its fast variations is of primary interest. They lead to phase shifts and fluctuations, which should be taken into account in radio interferometry. Although such information can be retrieved from the measurements of the opacity in the atmospheric windows described above, a more effective approach is to perform such measurements at frequencies near the H 2 O transitions. Usually for this purpose the transitions at ∼22 GHz and ∼183 GHz are used. For example, all 12-m ALMA antennas are equipped with the 183 GHz water vapor radiometers [34]. At the Institute of Applied Astronomy of the Russian Academy of Sciences a dual-band water vapor radiometer operating at ∼21 GHz and ∼31 GHz was developed [35]. It is actively used for atmospheric measurements (e.g., [36,37]).

2.4. Evaluation of the atmospheric opacity from global atmospheric models

Atmospheric transparency can be estimated on the basis of the approach used for modeling path delay in the neutral atmosphere [38]. The publicly available data provided by the NASA Global Modeling and Assimilation Office model GEOS-FPIT1 are used [8]. They evaluate atmosphere parameters (in particular, air temperature, total atmospheric pressure, and partial pressure of water vapor) using various ground, air-born, and space-born measurements that are assimilated into a dynamic model. Current models have 72 levels in altitude, 0 . 25 ∘ × 0 . 31 ∘ spatial grid and 3 hours resolution in time. Atmospheric absorption at any frequency can be calculated for any selected location by using standard spectroscopic parameters as described in [8]. The values of the zenith opacity obtained in this way are in good agreement with the results of sky-dip measurements at the LMT and other sites, including measurements with the MIAP-2 radiometer at 2 mm on Suffa plateau [39].
Similar data are provided by the Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2) [40,41] and the European Center for Medium-Range Weather Forecast ReAnalysis (ERA5) [42].

2.5. Evaluation of the precipitable water vapor (PWV) from the Global Navigation Satellite System (GNSS) data

The development of the Global Navigation Satellite Systems (GNSS) provides an opportunity for estimations of PWV from measurements of delays of the navigation signals [43,44,45]. Taking into account the surface temperature and pressure, the PWV values can be estimated from these delays with a low uncertainty. Nowadays this method is widely used for this purpose, including evaluation of results obtained from the global atmospheric models mentioned above (e.g., [46,47,48,49,50,51,52,53,54,55,56,57]).

2.6. Evaluation of the precipitable water vapor (PWV) from the sky-dip data by the artificial neural network

The direct comparison of the results obtained by the different methods may be problematic. The low PWV values in dry atmosphere are barely detectable by humidity sensors in aerosonde. Wet conditions and high opacity lead to small variations in brightness temperature on different angles, leading to higher errors in τ and PVW estimations. The spatial-temporal resolution of the dynamic atmospheric models is limited, it is lower than typical sizes of the topographic features such as mountains and typical times of the variations of the PWV values. Since that, different methods should be cross-validated and extrapolated to the same scale.
Recently we proposed the statistical approach for the determination of the PWV values based on machine learning algorithms and MIAP-2 data [58]. The idea was to use non-linear regression to calculate PWV values from the MIAP data using the receiver responses on different angles in the 2 mm and 3 mm bands as the input data, without addressing to the physical model. The training set is based on the one year monitoring session near the Badary observatory (2016–2017). The observatory was equipped with the water vapor radiometer (WVR) and GNSS receivers capable for tropospheric delay estimations. We found that the GNSS and WVR data are consistent. We use the GNSS data as the target values for the statistical model fitting and the k Nearest Neighbors (kNN) [59] and artificial neural network (ANN) as the regression models. We utilize the individual component analysis to speed up the learning process. As a result, the regression model encapsulates the instrumental transfer function and the PWV fraction in the microwave absorption (Eq. eq:tau). The bias introduced by the flat layered atmospheric model was also excluded. The coefficient of determination R 2 on the validation part of the dataset was 0.8 for kNN and 0.86 for ANN with symmetrical deviations from the trend line [58]. The result of this findings was that the PWV may be consistently determinated from the sky dip data using the statistical approach.
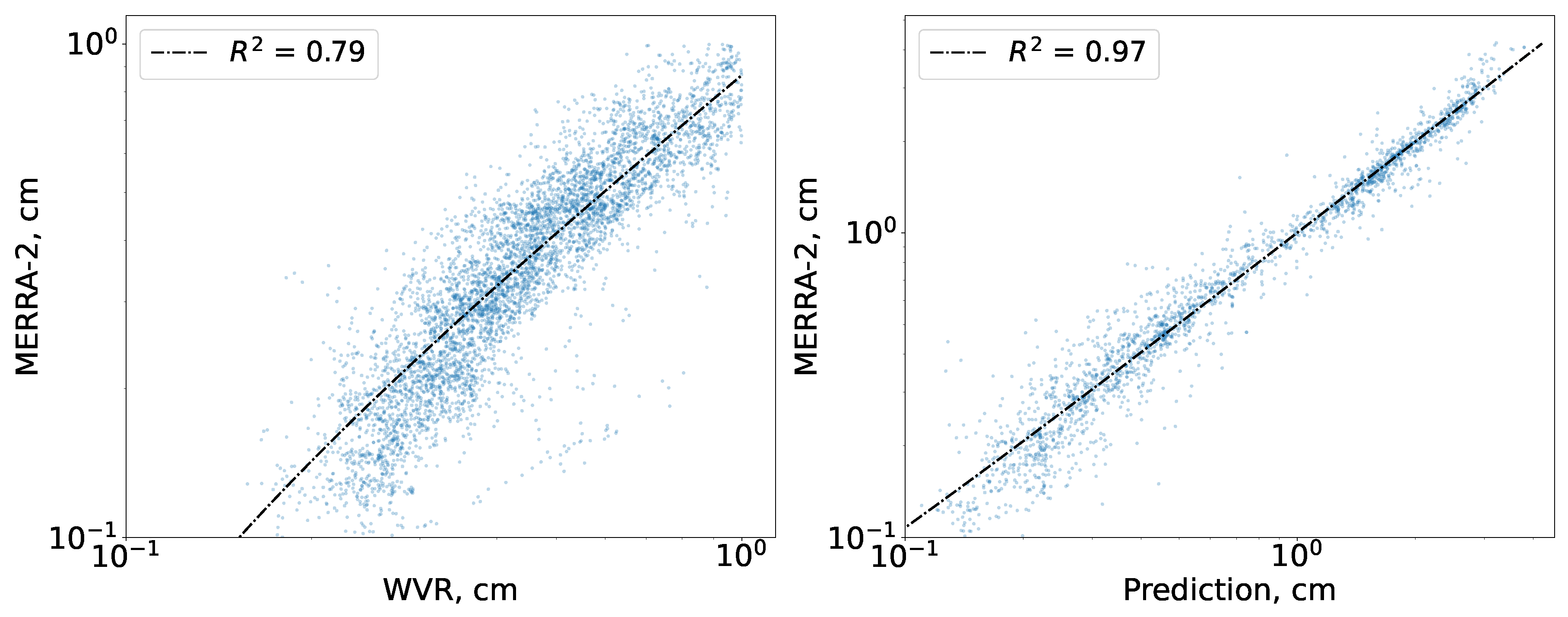
We use similar approach to construct statistical model based on the two sessions obtained in Svalbard (2018-2019) and Badary (2016-2017). The target values are based on publicly available MERRA-2 model’s PWV data and ANN regressor. The input data was the MIAP-2 measurements 2×6×3 vector (bands, angles, n m = t MERRA / t MIAP , number of MIAP measurements per MERRA-2 timestamp). We found that PWV estimations based on WVR data are biased from MERRA-2 data in dry conditions (Figure 1). The resulting R 2 was 0.98 on validation dataset trained on Badary data only and 0.96 for Svalbard and Badary combined dataset. The time-series and scatter plot are presented in Figures 1 and 2. The results show a good agreement between the predicted and the PWV MERRA-2-based and GNSS-based values. The lower R 2 value is probably caused by the different impact of the absorption in O 2 and LWP in different sites that cannot be represented by the single regression model. Still, the predictive ability of the model is very high at the full variety of the atmospheric conditions during the sessions.
Preprints 86045 g001
Figure 1. Left panel: the scatter diagram between the WVR and MERRA-2. Right panel: correlation between the target PWV values (MERRA-2) and the predicted values on the validation dataset.
Figure 1. Left panel: the scatter diagram between the WVR and MERRA-2. Right panel: correlation between the target PWV values (MERRA-2) and the predicted values on the validation dataset.
Preprints 86045 g001
Preprints 86045 g002
Figure 2. Time-series plot of the PWV in MERRA-2 data (target values), GNSS-based data and predicted by ANN from Badary session, one month partial selection.
Figure 2. Time-series plot of the PWV in MERRA-2 data (target values), GNSS-based data and predicted by ANN from Badary session, one month partial selection.
Preprints 86045 g002
This approach can be applied to different types of the data acquiring methods and should produce the statistically coherent results. The R 2 traces the predictive ability of the statistical model and can test the validity of the different non-direct methods testing astroclimatic measurements or atmospheric model predictions in specific places. We assume the MERRA-2 model as the reference, but it can also be tested by different direct PWV drone-based measurements or aerosonde that is too rare to serve as training set.

3. Results

3.1. Monitoring of the millimeter-wave atmospheric opacity at selected sites

To date, atmospheric absorption studies with the MIAP-2 radiometers have been carried out at several sites in Russia and Uzbekistan [31,60,61,62,63,64,65]. However, a long-term monitoring covering all seasons is limited to the RT-70 radio telescope construction site on the Suffa plateau in Uzbekistan (altitude 2400 m), site of the BTA telescope of the Special Astrophysical Observatory (SAO) in the North Caucasus (altitude 2040 m) and the Badary observatory in the Baikal region (altitude 813 m). Among these sites, the best atmospheric transparency has been observed on the Suffa plateau. From these measurements the PWV values were derived, which are in good agreement with the satellite and aerosonde data [31]. Then, expected optical depth in other atmospheric transparency windows was evaluated. The monthly averaged values of the optical depth in zenith at 1.3 mm are ∼0.3 in winter and ∼0.8 in summer. The corresponding monthly averaged PVW values are ∼4 mm in winter and ∼14 mm in summer.
In addition to long-term monitoring, short-term measurements of atmospheric absorption have been carried out in several locations: the Muus-Khaya peak in Yakutia (altitude 1950 m), the Terskol peak in Caucasus (altitude 3150 m), Svalbard (altitude 36 m), Caucasian Mointain Observatory (altitude 2112 m), Mondy, Sayans in Buryatia (altitude 2006 m), Karadag in Crimea (altitude 105 m). Measurements have recently begun in the eastern Caucasus [65]: in Dagestan (Mount Mayak, 2700 m and Mount Shalbuzdag 4142 m) and in North Ossetia (Stolovaya Mountain, ∼3000 m).
The Muus-Khaya peak is located in the region of the “Pole of Cold”. The measurements were done in July and gave quite good results for this season: PVW∼5 mm [60], which is significantly better than at the RT-70 site on the Suffa plateau in summer. The expected PWV value in winter is 1–2 mm, which makes this peak a promising site for millimeter and submillimeter astronomy. The short measurement on the Terskol peak did not show good results. The one day measurements on Elbrus in August 2021 gave rather high opacity, too. Promising preliminary data were obtained for the eastern Caucasus. In May 2023, a long (over half a year) expedition ended in the vicinity of Kurapdag (Chirag village), which basically confirmed the previously formulated hypothesis about the lower humidity of the eastern Caucasus compared to the western one. An interesting feature was observed on Karadag. The millimeter-wave absorption there strongly depends on the wind direction and can drop to quite low values when dry air enters from the steppe Crimea [28].
All the data collected during numerous expeditions, including the semi-annual expedition to Dagestan that ended in May 2023, where the results have not yet been processed or published, are posted in the open access archive [66].

3.2. Some results of the opacity evaluations from the NASA data

Evaluations of the atmospheric opacity from the NASA data as described in Section sec:nasamethod have been performed for more than 40 sites around the globe [8]. They include analysis of the seasonal variations of the opacity. The main conclusion of this research is that the best place for submillimeter astronomy in the Eastern hemisphere is the high-altitude (4300–4500 m) plateau in Eastern Pamirs. The atmospheric transparency at this site is comparable to that in the Atacama desert in Chile and is much better than on the Suffa plateau in Uzbekistan, where the 70-m radio telescope is constructed. Typical PWV values in winter are as low as 0.8–0.9 mm. The extent of the plateau is rather large, baselines up to ∼130 km are possible. Similar conditions exist in Tibet.

4. Discussion

4.1. Degradation of the telescope sensitivity due to atmospheric opacity

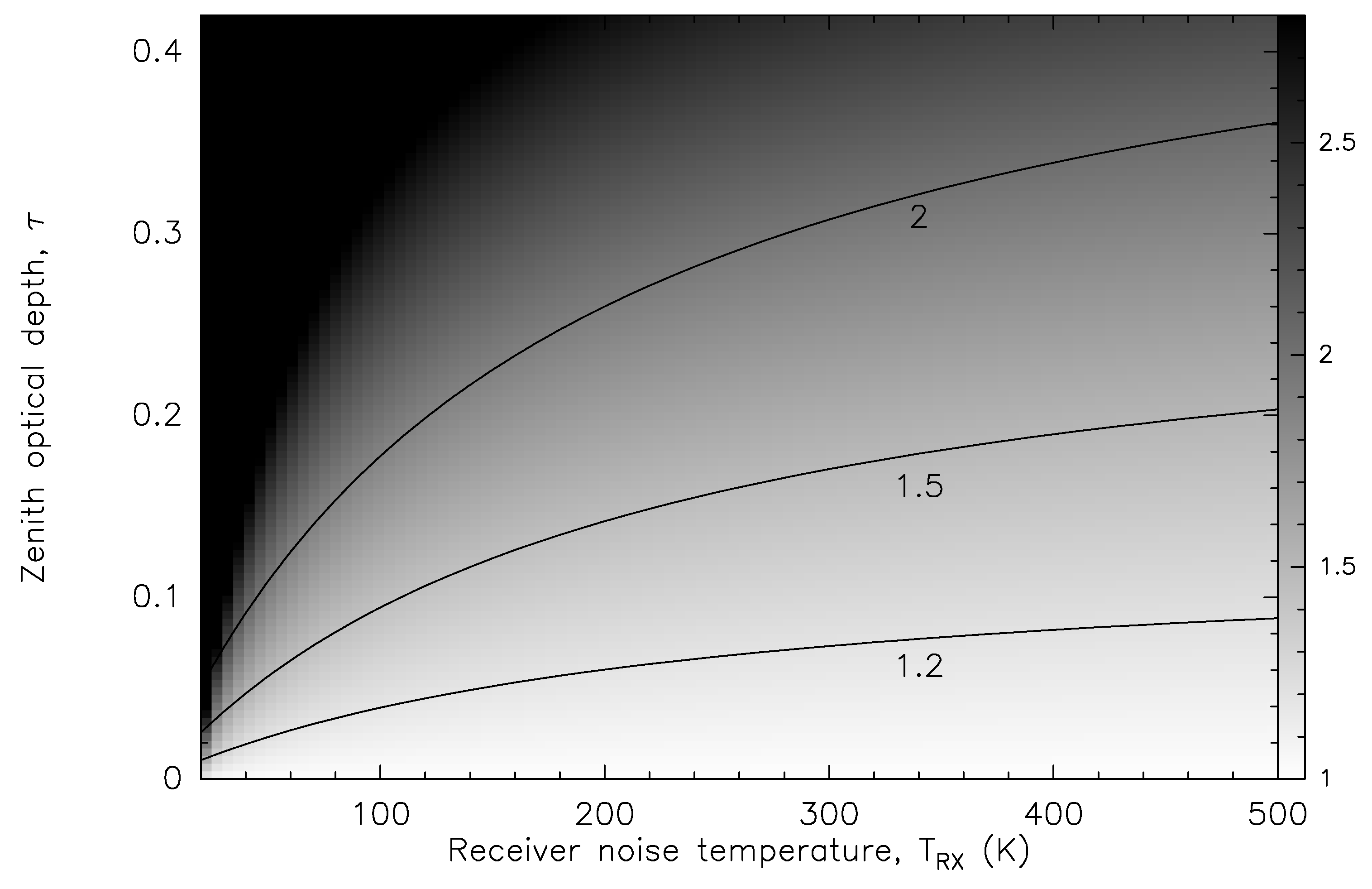
Atmospheric opacity leads to deterioration of the telescope sensitivity in any case. However, it is worth obtaining numerical estimates of this deterioration. In particular it can help to understand better an acceptable value of the opacity in various conditions. For this purpose we will estimate the quantity, which can be called a “degradation factor”:
R D = T SYS * T RX ,
where T RX is the receiver noise temperature and T SYS * is the system temperature “above the atmosphere”, i.e. calculated from the system temperature at the receiver front-end taking into account the attenuation in the atmosphere. Neglecting antenna losses and background emission
T SYS * = T RX e τ cos θ + T a e τ cos θ − 1 .
In case of no opacity R D = 1 . The plot of the degradation factor R D in dependence on the receiver noise temperature T RX and zenith opacity τ for the zenith angle θ = 45 ∘ , assuming T a = 250 K, is presented in Figure 3. For example, if the degradation factor of 1.5 is considered to be acceptable and the receiver noise temperature is T RX ∼ 100 K, then the required zenith opacity is τ ≲ 0.1 . It is worth noting that the integration time required to achieve the same sensitivity, varies as R D 2 . In case of T RX ≫ T a , which happens at very high frequencies, the degradation factor approaches e τ / cos θ . Then, R D = 1.5 implies τ ≈ 0.29 at θ = 45 ∘ .
Preprints 86045 g003
Figure 3. The degradation factor R D (gray scale) in dependence on the receiver noise temperature T RX and zenith opacity τ for the zenith angle θ = 45 ∘ , assuming T a = 250 K. The curves correspond to R D = 1.2 , 1.5 and 2 (from bottom to top).
Figure 3. The degradation factor R D (gray scale) in dependence on the receiver noise temperature T RX and zenith opacity τ for the zenith angle θ = 45 ∘ , assuming T a = 250 K. The curves correspond to R D = 1.2 , 1.5 and 2 (from bottom to top).
Preprints 86045 g003

4.2. The effect of cloudiness

The coefficient γ in Eq. (1) is approximately 2.5 × 10 − 3 and 3.5 × 10 − 3 μ m − 1 at 230 and 345 GHz, respectively, with weak temperature dependence [67]. It means that LWP of 100 μ m (which is equivalent to 100 g m − 2 ) contributes about 0.25 to the opacity at 230 GHz. The median values of LWP for different cloud classes are from ∼10 to ∼40 g m − 2 [68,69]. In [5] the LWP statistics is presented for the existing and candidate EHT sites. The median values are well below 100 μ m for most sites. Therefore, in most cases the opacity in clouds at 1.3 mm is ≲0.1 and cannot fully prevent the radio astronomical observations.
However the problem is that clouds are usually very inhomogeneous, which leads to spatial and temporal fluctuations of the opacity and of the sky brightness. Their influence can hardly be sufficiently suppressed even by the usual beam switching technique. As a result, these fluctuations make practically impossible observations of weak sources, especially in continuum. Spectral line observations are less affected because the fluctuations are synchronous in all channels and can be subtracted at the data reduction. However, a more frequent calibration is needed.

4.3. Comparison of the candidate sites for millimeter-wave telescopes in Eurasia

A long-term monitoring of atmospheric opacity with the MIAP-2 radiometers has been performed at several sites in Russia and Uzbekistan, as described in Section sec:monitor (the RT-70 radio telescope construction site on the Suffa plateau, site of the BTA telescope in Caucasus and the Badary observatory). Among these sites, the best conditions for millimeter-wave astronomy have been observed on the Suffa plateau. However, these conditions are far from being excellent and hardly allow for regular observations at wavelengths λ ≲ 2 mm. At 1.3 mm only episodic observations can be possible in winter, when the monthly averaged value of zenith opacity at this wavelength drops to ∼0.3 (somewhat lower estimates of the opacity for this site are obtained in [5]).
Promising results have been obtained in the short summer measurements on the Muus-Khaya peak in Yakutia (Section sec:monitor). However, a long-term monitoring at this site is needed. Short measurements on the Terskol peak are not conclusive.
Investigations with various methods (e.g., [8,39,65,70,71,72,73,74]) reveal other promising sites in Eurasia with better conditions in comparison with the Suffa plateau. In paper [8] based on the NASA GEOS-FPIT model, the Eastern Pamirs and Tibet are shown to be the best places. According to [71] based on the ERA5 re-analysis, very good conditions exist at the Ali 1 site in Tibet (PWV ∼0.4 mm in winter) and at Muztag-Ata in the Chinese Pamirs (PWV ∼0.7 mm in winter). Comparable conditions exist in the Sayan Mountains. The Khulugaisha peak, in terms of its characteristics, is close to the sites of Tibet and Pamirs (PWV ∼0.6 mm in winter). There are promising sites in Altai and Dagestan, in particular the Khorai and Kurapdag mountains [71]. The Terskol peak is also rather good in terms of PWV [39,75] but not so good concerning cloudiness. The Aktashtau peak in Uzbekistan (3383 m) located near the RT-70 construction site, has PWV statistics similar to Terskol [71]. With PWV ≲ 2 mm, astronomical observations at least in the 1.3 mm and 0.85 mm atmospheric windows can be quite efficient. Even lower PWV values, ∼0.5 mm, make possible observations in the higher frequency windows.
It is worth noting that in rugged terrains the spatial resolution of the global models can be insufficient to characterize atmospheric conditions on certain sites (e.g. on local peaks). This emphasizes the importance of local measurements with radiometric systems or GNSS devices. So far, our measurements have been performed at 3 and 2 mm. Measurements in the 1.3 mm window would be very important.
In this consideration of the candidate sites for new millimeter and submillimeter wave telescopes we have taken into account only the atmospheric opacity. However, there are other criteria which should be also considered. One of them is stability of the atmosphere [76,77]. Enhanced instability can lead to strong phase fluctuations [78] and anomalous refraction (e.g., [79]). This factor is still poorly investigated.
A new large millimeter wave telescope should be an efficient part of the global VLBI network (EHT). The estimates show that from this point of view the Caucasus region is the most effective with the existing EHT configuration (Andrey Lobanov, private communication). However, the situation will change if a large millimeter wave telescope is built in eastern Asia. In this case, places like the Pamirs and Tibet will have an advantage.

5. Conclusions

Our studies of the atmospheric transparency at the candidate sites for millimeter and submillimeter telescopes continue for about 10 years already by various methods. The considered sites are located in Russia and in the nearby surroundings (in particular, in Uzbekistan). The atmospheric optical depth has been measured with the dual-band tipping radiometer and evaluated from the global atmospheric models. Several sites have been selected, which can be effectively used for astronomical observations at least in the major atmospheric transparency windows at 1.3 mm and 0.85 mm. The investigations continue. More detailed studies of several recently suggested sites are planned as well as an extension of the measurements to the 1.3 mm atmospheric window.

Author Contributions

Conceptualization, I.Z.; methodology, I.Z., A.L., V.V. and P.M.; formal analysis, I.Z. A.L., V.V., P.M. and T.K.; writing—original draft preparation, I.Z.; writing—review and editing, I.Z., A.L., V.V. and P.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the IAP RAS state program FFUF-2021-0005.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Acknowledgments

We are grateful to everyone who supported these works and took part in the measurements and estimates of atmospheric opacity considered here, as well as in discussions of the results obtained.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study.

Abbreviations

MDPI Multidisciplinary Digital Publishing Institute
GNSS Global Navigation Satellite Systems
NASA National Aeronautics and Space Administration
VLBI Very Long Baseline Interferometry
EHT Event Horizon Telescope
LWP Liquid Water Path
PWV Precipitable Water Vapor
WVR Water Vapor Radiometer

References

  1. Wilson, T.L.; Guilloteau, S. Millimeter Astronomy; 2018. [CrossRef]
  2. Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; et al.; Event Horizon Telescope Collaboration First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophysical Journal Letters 2019, arXiv:astro-ph.GA/1906.11238875, L1. [Google Scholar] [CrossRef]
  3. Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; et al.; Event Horizon Telescope Collaboration First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophysical Journal Letters 2022, 930, L12. [Google Scholar] [CrossRef]
  4. Doeleman, S.S.; Barrett, J.; Blackburn, L.; Bouman, K.; Broderick, A.E.; Chaves, R.; Fish, V.L.; Fitzpatrick, G.; Fuentes, A.; Freeman, M.; et al. Reference Array and Design Consideration for the next-generation Event Horizon Telescope. arXiv e-prints 2023, p. arXiv:2306.08787. arXiv:2306.08787. [CrossRef]
  5. Raymond, A.W.; Palumbo, D.; Paine, S.N.; Blackburn, L.; Córdova Rosado, R.; Doeleman, S.S.; Farah, J.R.; Johnson, M.D.; Roelofs, F.; Tilanus, R.P.J.; Weintroub, J. Evaluation of New Submillimeter VLBI Sites for the Event Horizon Telescope. Astrophysical Journal Supplement 2021, arXiv:astro-ph.IM/2102.05482253, 5. [Google Scholar] [CrossRef]
  6. Artemenko, Y.N.; Balega, Y.Y.; Baryshev, A.M.; Bubnov, G.M.; Etnaer, A.; Kardashev, N.S.; Gimmelman, V.G.; de Graauw, T.M.; Gunbina, A.; Eghamberdiev, S.A.; Kogan, B.L.; Kolachevsky, N.N.; Koshelets, V.P.; Lagerweij, G.; Lesnov, I.V.; Likhacheva, L.N.; Likhachev, S.F.; Mansfeld, M.; Marchiori, G.; Rampini, F.; Shanin, G.I.; Schekinov, Y.A.; Zinchenko, I.I.; Vdovin, V.F. New stage of the Suffa Submm Observatory in Uzbekistan Project. ISSTT 2019 – 30th International Symposium on Space Terahertz Technology, Proceedings Book, 2019, pp. 196–201.
  7. Wang, N. Xinjiang Qitai 110 m radio telescope. Scientia Sinica Physica, Mechanica & Astronomica 2014, 44, 783–794. [Google Scholar]
  8. Lapinov, A.V.; Lapinova, S.A.; Petrov, L.Y.; Ferrusca, D. On the benefits of the Eastern Pamirs for sub-mm astronomy. Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy X; Zmuidzinas, J.; Gao, J.R., Eds., 2020, Vol. 11453, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, p. 114532O. arXiv:astro-ph.IM/2012.04647. [CrossRef]
  9. Khaikin, V.; Lebedev, M.; Shmagin, V.; Zinchenko, I.; Vdovin, V.; Bubnov, G.; Edelman, V.; Yakopov, G.; Shikhovtsev, A.; Marchiori, G.; Tordi, M.; Duan, R.; Li, D. On the Eurasian SubMillimeter Telescopes Project (ESMT). 2020 7th All-Russian Microwave Conference (RMC), 2020, pp. 47–51. [CrossRef]
  10. Marchiori, G.; Rampini, F.; Tordi, M.; Spinola, M.; Bressan, R. Towards the Eurasian Submillimeter Telescope (ESMT): Telescope concept outline and first results. Ground-Based Astronomy in Russia. 21st Century, 2020, pp. 378–383.
  11. Liebe, H.J. MPM—An atmospheric millimeter-wave propagation model. International Journal of Infrared and Millimeter Waves 1989, 10, 631–650. [Google Scholar] [CrossRef]
  12. Urban, J. Moliere (v5): a versatile forward- and inversion model for the millimeter and sub-millimeter wavelength range. Journal of Quantitative Spectroscopy and Radiative Transfer, 2004, 83, 529–554. [Google Scholar] [CrossRef]
  13. Zhevakin, S.A.; Naumov, A.P. The propagation of centimeter, millimeter, and submillimeter radio waves in the earth’s atmosphere. Radiophysics and Quantum Electronics 1967, 10, 678–694. [Google Scholar] [CrossRef]
  14. Bubnov, G.; Vdovin, V.; Khaikin, V.; Tremblin, P.; Baron, P. Analysis of variations in factors of specific absorption of sub-terahertz waves in the earth’s atmosphere. 2020 7th All-Russian Microwave Conference (RMC), 2020, pp. 229–232. [CrossRef]
  15. Kislyakov, A.G.; Stankevich, K.S. Investigation of the absorption of radio waves in the troposphere using radioastronomical methods. Radiophysics and Quantum Electronics 1967, 10, 695–708. [Google Scholar] [CrossRef]
  16. Kallfass, I.; Antes, J.; Schneider, T.; Kurz, F.; Lopez-Diaz, D.; Diebold, S.; Massler, H.; Leuther, A.; Tessmann, A. All Active MMIC-Based Wireless Communication at 220 GHz. IEEE Transactions on Terahertz Science and Technology 2011, 1, 477–487. [Google Scholar] [CrossRef]
  17. Hirata, A.; Kosugi, T.; Takahashi, H.; Takeuchi, J.; Togo, H.; Yaita, M.; Kukutsu, N.; Aihara, K.; Murata, K.; Sato, Y.; Nagatsuma, T.; Kado, Y. 120-GHz-Band Wireless Link Technologies for Outdoor 10-Gbit/s Data Transmission. IEEE Transactions on Microwave Theory Techniques 2012, 60, 881–895. [Google Scholar] [CrossRef]
  18. Wang, C.; Lin, C.; Chen, Q.; Lu, B.; Deng, X.; Zhang, J. A 10-Gbit/s Wireless Communication Link Using 16-QAM Modulation in 140-GHz Band. IEEE Transactions on Microwave Theory Techniques 2013, 61, 2737–2746. [Google Scholar] [CrossRef]
  19. Tsvetkov, A.I.; Fokin, A.P.; Sedov, A.S. First Experiments on Data Transmission Using a Sub-THz Gyrotron. Journal of Infrared, Millimeter, and Terahertz Waves 2019, 40, 696–702. [Google Scholar] [CrossRef]
  20. O’Hara, J.F.; Ekin, S.; Choi, W.; Song, I. A Perspective on Terahertz Next-Generation Wireless Communications. Technologies 2019, 7. [Google Scholar] [CrossRef]
  21. Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless Communications and Applications Above 100 GHz: Opportunities and Challenges for 6G and Beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
  22. Jiang, W.; Zhang, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Renzo, M.D.; Schotten, H.D.; LUO, F.L.; El-Bawab, T.S.; Juntti, M.; Debbah, M.; Leung, V.C.M. Terahertz Communications and Sensing for 6G and Beyond: A Comprehensive View 2023. [CrossRef]
  23. Tolkachev, A.; Yegorov, E.; Shishlov, A. Radar and communication systems: Some trends of development. Quasi-Optical Control of Intense Microwave Transmission. Springer, 2005, pp. 353–370.
  24. Kempkes, M.A.; Hawkey, T.J.; Gaudreau, M.P.; Phillips, R.A. W-band transmitter upgrade for the haystack ultrawideband satellite imaging radar (HUSIR). 2006 IEEE International Vacuum Electronics Conference held Jointly with 2006 IEEE International Vacuum Electron Sources. IEEE, 2006, pp. 551–552.
  25. Linde, G.J.; Ngo, M.T.; Danly, B.G.; Cheung, W.J.; Gregers-Hansen, V. WARLOC: A high-power coherent 94 GHz radar. IEEE Transactions on Aerospace and Electronic Systems 2008, 44, 1102–1117. [Google Scholar] [CrossRef]
  26. Balega, Y.; Bubnov, G.; Glyavin, M.; Gunbina, A.; Danilevsky, D.; Denisov, G.; Khudchenko, A.; Lesnov, I.; Marukhno, A.; Mineev, K.; Samsonov, S.; Shanin, G.; Vdovin, V. Atmospheric Propagation Studies and Development of New Instrumentation for Astronomy, Radar, and Telecommunication Applications in the Subterahertz Frequency Range. Applied Sciences 2022, 12, 5670. [Google Scholar] [CrossRef]
  27. Kislyakov, A.G. Effective path length and mean temperature of the atmosphere. Radiophysics and Quantum Electronics 1966, 9, 282–287. [Google Scholar] [CrossRef]
  28. Bubukin, I.T.; Rakut’, I.V.; Agafonov, M.I.; Pankratov, A.L.; Troitskii, A.V.; Lapchenko, V.A.; Gorbunov, R.V.; Zinchenko, I.I.; Nosov, V.I.; Vdovin, V.F. Analysis of the Results of Astroclimate Research at the Kara-Dag Radioastronomical Station in Crimea and the Possibilities for Reducing the Influence of the Atmosphere on Millimeter-Band Radioastronomical Observations. Soviet Journal of Experimental and Theoretical Physics 2019, 129, 35–45. [Google Scholar] [CrossRef]
  29. Ferrusca, D.; Contreras R., J. Weather monitor station and 225 GHz radiometer system installed at Sierra Negra: the Large Millimeter Telescope site. Ground-based and Airborne Instrumentation for Astronomy V; Ramsay, S.K.; McLean, I.S.; Takami, H., Eds., 2014, Vol. 9147, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, p. 914730. [CrossRef]
  30. Nosov, V.I.; Bolshakov, O.S.; Bubnov, G.M.; Vdovin, V.F.; Zinchenko, I.I.; Marukhno, A.S.; Nikiforov, P.L.; Fedoseev, L.I.; Shvetsov, A.A. A dual-wave atmosphere transparency radiometer of the millimeter wave range. Instruments and Experimental Techniques 2016, 59, 374–380. [Google Scholar] [CrossRef]
  31. Bubnov, G.M.; Artemenko, Y.N.; Vdovin, V.F.; Danilevsky, D.B.; Zinchenko, I.I.; Nosov, V.I.; Nikiforov, P.L.; Shanin, G.I.; Raupov, D.A. The Results of Astroclimate Observations in the Short-Wave Length Interval of the Millimeter-Wave Range on the Suffa Plateau. Radiophysics and Quantum Electronics 2017, 59, 763–771. [Google Scholar] [CrossRef]
  32. Fedoseev, L.I.; Bozhkov, V.G.; Genneberg, V.A.; Petrov, I.V.; Shkaev, A.P. Radiometer of the 3-mm wave range with a modulator-calibrator. Radiophysics and Quantum Electronics 2007, 50, 858–863. [Google Scholar] [CrossRef]
  33. Bubnov, G.M.; Grigor’ev, V.F.; Zinchenko, I.I.; Zemlyanukha, P.M.; Il’in, G.N.; Kabanov, D.M.; Nosov, V.I.; Vdovin, V.F. Consistent Determination of the Integral Humidity and Effective Optical Depth of the Atmosphere in the Millimeter Wavelength Range Using Wideband Radiometers. Radiophysics and Quantum Electronics 2020, 62, 820–829. [Google Scholar] [CrossRef]
  34. Nikolic, B.; Bolton, R.C.; Graves, S.F.; Hills, R.E.; Richer, J.S. Phase correction for ALMA with 183 GHz water vapour radiometers. Astronomy & Astrophysics 2013, arXiv:astro-ph.IM/1302.6056]552, A104. [Google Scholar] [CrossRef]
  35. Arsaev, I.E.; Bykov, V.Y.; Il’in, G.N.; Yurchuk, E.F. Water Vapor Radiometer: Measuring Instrument of Atmospheric Brightness Temperature. Measurement Techniques 2017, 60, 497–504. [Google Scholar] [CrossRef]
  36. Dembelov, M.G.; Bashkuev, Y.B. Estimation of the Tropospheric Moisture Content Derived from GPS Observations, Radio Sounding Data, and Measurements with a Water Vapor Radiometer. Atmospheric and Oceanic Optics 2022, 35, 359–365. [Google Scholar] [CrossRef]
  37. Dembelov, M.G.; Bashkuev, Y.B. Moisture content of the troposphere from GPS observations and water vapor radiometer measurements. 28th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics; Matvienko, G.G.; Romanovskii, O.A., Eds., 2022, Vol. 12341, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, p. 123415M. [CrossRef]
  38. Petrov, L. Modeling of path delay in the neutral atmosphere: a paradigm shift. arXiv e-prints 2015. arXiv:1502.06678. [CrossRef]
  39. Bubukin, I.T.; Rakut, I.V.; Agafonov, M.I.; Pankratov, A.L.; Lapinov, A.V.; Petrov, L.Y. On Atmospheric Absorption Values at Millimeter Waves on the Suffa Plateau and Karadag Landfill. Radiophysics and Quantum Electronics 2023, 65, 719–727. [Google Scholar] [CrossRef]
  40. Global Modeling And Assimilation Office.; Pawson, S. MERRA-2 inst1 2d int Nx: 2d, 1-Hourly, Instantaneous, Single-Level, Assimilation, Vertically Integrated Diagnostics V5.12.4, 2015. [CrossRef]
  41. Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; Wargan, K.; Coy, L.; Cullather, R.; Draper, C.; Akella, S.; Buchard, V.; Conaty, A.; da Silva, A.M.; Gu, W.; Kim, G.K.; Koster, R.; Lucchesi, R.; Merkova, D.; Nielsen, J.E.; Partyka, G.; Pawson, S.; Putman, W.; Rienecker, M.; Schubert, S.D.; Sienkiewicz, M.; Zhao, B. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). Journal of Climate 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
  42. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; Simmons, A.; Soci, C.; Abdalla, S.; Abellan, X.; Balsamo, G.; Bechtold, P.; Biavati, G.; Bidlot, J.; Bonavita, M.; De Chiara, G.; Dahlgren, P.; Dee, D.; Diamantakis, M.; Dragani, R.; Flemming, J.; Forbes, R.; Fuentes, M.; Geer, A.; Haimberger, L.; Healy, S.; Hogan, R.J.; Hólm, E.; Janisková, M.; Keeley, S.; Laloyaux, P.; Lopez, P.; Lupu, C.; Radnoti, G.; de Rosnay, P.; Rozum, I.; Vamborg, F.; Villaume, S.; Thépaut, J.N. The ERA5 global reanalysis. Quarterly Journal of the Royal Meteorological Society 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
  43. Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. Journal of Geophysical Research 1992, 97, 15–787. [Google Scholar] [CrossRef]
  44. Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. Journal of Applied Meteorology 1994, 33, 379–386. [Google Scholar] [CrossRef]
  45. Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Rocken, C.; Solheim, F.; van Hove, T.; Ware, R.; McClusky, S.; Herring, T.A.; King, R.W. GPS Meteorology: Direct Estimation of the Absolute Value of Precipitable Water. Journal of Applied Meteorology 1996, 35, 830–838. [Google Scholar] [CrossRef]
  46. Wang, J.; Zhang, L.; Dai, A.; van Hove, T.; van Baelen, J. A near-global, 2-hourly data set of atmospheric precipitable water from ground-based GPS measurements. Journal of Geophysical Research (Atmospheres) 2007, 112, D11107. [Google Scholar] [CrossRef]
  47. Manandhar, S.; Lee, Y.H.; Meng, Y.S.; Yuan, F.; Ong, J.T. GPS-Derived PWV for Rainfall Nowcasting in Tropical Region. IEEE Transactions on Geoscience and Remote Sensing 2018, 56, 4835–4844. [Google Scholar] [CrossRef]
  48. Zhang, W.; Zhang, H.; Liang, H.; Lou, Y.; Cai, Y.; Cao, Y.; Zhou, Y.; Liu, W. On the suitability of ERA5 in hourly GPS precipitable water vapor retrieval over China. Journal of Geodesy 2019, 93, 1897–1909. [Google Scholar] [CrossRef]
  49. Jiang, J.; Zhou, T.; Zhang, W. Evaluation of Satellite and Reanalysis Precipitable Water Vapor Data Sets Against Radiosonde Observations in Central Asia. Earth and Space Science 2019, 6, 1129–1148. [Google Scholar] [CrossRef]
  50. Zhao, Q.; Yao, Y.; Yao, W.; Zhang, S. GNSS-derived PWV and comparison with radiosonde and ECMWF ERA-Interim data over mainland China. Journal of Atmospheric and Solar-Terrestrial Physics 2019, 182, 85–92. [Google Scholar] [CrossRef]
  51. Zhu, D.; Zhang, K.; Yang, L.; Wu, S.; Li, L. Evaluation and Calibration of MODIS Near-Infrared Precipitable Water Vapor over China Using GNSS Observations and ERA-5 Reanalysis Dataset. Remote Sensing 2021, 13. [Google Scholar] [CrossRef]
  52. Wang, S.; Xu, T.; Nie, W.; Jiang, C.; Yang, Y.; Fang, Z.; Li, M.; Zhang, Z. Evaluation of Precipitable Water Vapor from Five Reanalysis Products with Ground-Based GNSS Observations. Remote Sensing 2020, 12. [Google Scholar] [CrossRef]
  53. Ziskin Ziv, S.; Yair, Y.; Alpert, P.; Uzan, L.; Reuveni, Y. The diurnal variability of precipitable water vapor derived from GPS tropospheric path delays over the Eastern Mediterranean. Atmospheric Research 2021, 249, 105307. [Google Scholar] [CrossRef]
  54. Huang, L.; Mo, Z.; Liu, L.; Zeng, Z.; Chen, J.; Xiong, S.; He, H. Evaluation of hourly PWV products derived from ERA5 and MERRA-2 over the Tibetan Plateau using ground-based GNSS observations by two enhanced models. Earth and Space Science 2021, 8, e2020EA001516. [Google Scholar] [CrossRef]
  55. Rosell, P.A.; Mackern Oberti, M.V.; Rivera, J.A.; Euillades, P.A. 10-Year assessment of GNSS integrated water vapour in the SIRGAS network. Journal of South American Earth Sciences 2023, 130, 104539. [Google Scholar] [CrossRef]
  56. Wu, J.; Su, M.; Shen, X.; Qiao, L.; Zheng, J. Assessment of the performance of GPS-PWV and rainfall event prediction by using precise products from different analysis centers. Earth Science Informatics 2023, 16, 2199–2210. [Google Scholar] [CrossRef]
  57. Sarkar, S.; Kuttippurath, J.; Patel, V. Long-term changes in precipitable water vapour over India derived from satellite and reanalysis data for the past four decades (1980–2020). Environmental Science: Atmospheres 2023, 3, 749–759. [Google Scholar] [CrossRef]
  58. Bubnov, G.; Zemlyanukha, P.; Dombek, E.; Vdovin, V. Machine learning methods for Precipitable Water Vapor estimation by radiometric data in millimetre wavelength. Journal of Physics Conference Series, 2021, Vol. 2015, Journal of Physics Conference Series, p. 012024. [CrossRef]
  59. Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Transactions on Information Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
  60. Bubnov, G.M.; Abashin, E.B.; Balega, Y.Y.; Bolshakov, O.S.; Dryagin, S.Y.; Dubrovich, V.K.; Marukhno, A.S.; Nosov, V.I.; Vdovin, V.F.; Zinchenko, I.I. Searching for New Sites for THz Observations in Eurasia. IEEE Transactions on Terahertz Science and Technology 2015, 5, 64–72. [Google Scholar] [CrossRef]
  61. Bubnov, G.M.; Vdovin, V.F.; Bukov, V.Y.; Makarov, T.A.; Il’in, G.N.; Zinchenko, I.I. Millimeter-wave astroclimate investigations on Badary observatory near Baikal lake. 2017 XXXIInd General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS). IEEE, 2017, pp. 1–4.
  62. Bubnov, G.; Vdovin, V.F.; Zemlyanukha, P.M.; Okunev, V.S.; Grigor’yev, V.F. Svalbard astroclimate research: expedition and first results. European Physical Journal Web of Conferences, 2018, Vol. 195, European Physical Journal Web of Conferences, p. 09002. [CrossRef]
  63. Agafonov, M.I.; Bubnov, G.M.; Bubukin, I.T.; Vdovin, V.F.; Gorbunov, R.V.; Zinchenko, I.I.; Lapchenko, V.A.; Nosov, V.I.; Pankratov, A.L.; Rakut, I.V. The Results of Observing the Astroclimate on the Crimean Peninsula in the Shortwave Part of the Millimeter Wavelength Range. Astrophysical Bulletin 2018, 73, 387–392. [Google Scholar] [CrossRef]
  64. Marukhno, A.S.; Bubnov, G.M.; Vdovin, V.F.; Voziakova, O.V.; Zemlyanukha, P.M.; Zinchenko, I.I.; Mingaliev, M.G.; Shatsky, N.I. Analysis of the Millimeter-Band Astroclimate at the Caucasus Mountain Observatory. Ground-Based Astronomy in Russia. 21st Century; Romanyuk, I.I.; Yakunin, I.A.; Valeev, A.F.; Kudryavtsev, D.O., Eds., 2020, pp. 184–188. [CrossRef]
  65. Balega, Y.Y.; Bataev, D.K.S.; Bubnov, G.M.; Vdovin, V.F.; Zemlyanukha, P.M.; Lolaev, A.B.; Lesnov, I.V.; Marukhno, A.S.; Marukhno, N.A.; Murtazaev, A.K.; Khaykin, V.S.; Khudchenko, A.V. Direct Measurements of Atmospheric Absorption of Subterahertz Waves in the Northern Caucasus. Physics - Doklady 2022, 67, 1–4. [Google Scholar] [CrossRef]
  66. Bubnov, G. Astroclimate measurements on several points over Eastern hemisphere in 2-mm and 3-millimeter atmospheric transparency windows using tipping radiometer. Zenodo, 202. [CrossRef]
  67. Paine, S. The am atmospheric model. Zenodo, 2019. [CrossRef]
  68. Rogers, R.R.; Yau, M.K. A Short Course in Cloud Physics; Elsevier, 1989.
  69. Unglaub, C.; Block, K.; Mülmenstädt, J.; Sourdeval, O.; Quaas, J. A new classification of satellite-derived liquid water cloud regimes at cloud scale. Atmospheric Chemistry & Physics 2020, 20, 2407–2418. [Google Scholar] [CrossRef]
  70. Panchuk, V.E.; Afanas’ev, V.L. Astroclimate of Northern Caucasus - Myths and reality. Astrophysical Bulletin 2011, 66, 233–254. [Google Scholar] [CrossRef]
  71. Khaikin, V.B.; Shikhovtsev, A.Y.; Mironov, A.P.; Qian, X. A study of the astroclimate in the Dagestan mountains Agul region and at the Ali Observatory in Tibet as possible locations for the Eurasian SubMM Telescopes (ESMT). The Multifaceted Universe: Theory and Observations - 2022, 2022, p 72. [Google Scholar] [CrossRef]
  72. Shikhovtsev, A.Y.; Khaikin, V.B.; Mironov, A.P.; Kovadlo, P.G. Statistical Analysis of the Water Vapor Content in North Caucasus and Crimea. Atmospheric and Oceanic Optics 2022, 35, 168–175. [Google Scholar] [CrossRef]
  73. Shikhovtsev, A.Y.; Kovadlo, P.G.; Khaikin, V.B.; Kiselev, A.V. Precipitable Water Vapor and Fractional Clear Sky Statistics within the Big Telescope Alt-Azimuthal Region. Remote Sensing 2022, 14, 6221. [Google Scholar] [CrossRef]
  74. Bolbasova, L.A.; Shikhovtsev, A.Y.; Ermakov, S.A. Statistics of precipitable water vapour above the sites of the 6-m Big Telescope Alt-azimuthal and new 3-m Large Solar Telescope using ERA5 data. MNRAS 2023, 520, 4336–4344. [Google Scholar] [CrossRef]
  75. Shikhovtsev, A.Y.; Khaikin, V.B.; Kovadlo, P.G.; Baron, P. Optical Thickness of the Atmosphere above the Terskol Peak. Atmospheric and Oceanic Optics 2023, 36, 78–85. [Google Scholar] [CrossRef]
  76. Abahamid, A.; Vernin, J.; Benkhaldoun, Z.; Jabiri, A.; Azouit, M.; Agabi, A. Seeing, outer scale of optical turbulence, and coherence outer scale at different astronomical sites using instruments on meteorological balloons. Astronomy & Astrophysics 2004, 422, 1123–1127. [Google Scholar]
  77. Shikhovtsev, A.Y.; Kovadlo, P.G.; Kopylov, E.A.; Ibrahimov, M.A.; Ehgamberdiev, S.A.; Tillayev, Y.A. Energy spectra of atmospheric turbulence for calculating C n 2 parameter. I. Maidanak and Suffa observatories in Uzbekistan. Atmosphere 2021, 12, 1614. [Google Scholar] [CrossRef]
  78. Thompson, A.R.; Moran, J.M.; Swenson, George W., J. Interferometry and Synthesis in Radio Astronomy, 3rd Edition; 2017. [CrossRef]
  79. Altenhoff, W.J.; Baars, J.W.M.; Wink, J.E.; Downes, D. Observations of anomalous refraction at radio wavelengths. A&A 1987, 184, 381–385. [Google Scholar]
1
http://gmao.gsfc.nasa.gov
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated