Prerpints.org logo
Preprint
Article

Magnetic Whispering-Gallery Super-resonance Spoiling in a Drude-Kerr Optical Cavity

Altmetrics

Downloads

131

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 September 2023

Posted:

26 September 2023

You are already at the latest version

Alerts
Abstract
High-quality optical Fano resonances, which exist in a spherical dielectric microparticle in the spatial configurations of the "whispering-gallery modes" (WGMs) and recently are referred to as the “super-resonances”, possess extremal sensitivity not only to the micro-cavity size and shape but also to the optical properties of the particulate material. The increase in the power of light radiation coupling into a super-resonance can lead to the manifestation of strong optical nonlinearity of the resonator material due to the cubic nonlinearity (optical Kerr effect) and generation of free electron plasma in certain regions of the spherical microcavity. In fact, an optically linear medium of the resonance cavity transforms into a Drude-Kerr-type medium with a strong dependence on input laser intensity. With the help of the finite-elements numerical simulations, we theoretically analyze the transformations of the resonant contour for a number of high-quality WGMs excited in a lanthanum-glass microsphere exposed to an optical radiation of different intensity. We show that in a certain input intensity range, the competition of Kerr and plasma optical nonlinearities can stop and even reverse the Stokes shift of the super-resonance observed in a pure Kerr medium. Additionally, optical ionization and plasma generation within the mode volume significantly reduce the strength of the magnetic super-resonance and lead to its spoiling and frequency splitting.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

I. Introduction

Recently, much research attention has been paid to the study of resonant optical effects in dielectric photonics structures, in particular, microspheres, due to the wide range of extraordinary optical effects exhibited under resonance conditions. This is due to both fundamental interest and numerous potential applications of such resonators. Dielectric wavelength scaled (mesoscale) particles with Mie size parameter xa = 2πR/λ of the order of a few tens (where R is particle radius, λ is the optical radiation wavelength) occupy a less-explored niche between subwavelength nanoparticles (xa < 1) and particles which obey the geometrical optics laws (xa > 100) [1].
Effective control of optical radiation implies the possibility of manipulating the electric and especially the magnetic components simultaneously. However, in the optical range due to the lowering contribution of electron spin states the magnetic response of dielectric materials found in nature is extremely weak. At the same time, the dielectric particles with a small size parameter and high refractive index can possess a non-zero induced magnetic moment [2]. Studies in the field of high-quality spherical dielectric resonators have shown that different regimes of light-matter interactions can be significantly enhanced when the WGMs are resonantly excited in the cavity [3]. Recently, it has been shown that in the so-called super-resonance regime [4,5], weakly scattering mesoscale dielectric spheres can support Fano resonances of the internal magnetic and electric fields with very high-quality factor (Q) values.
One of the specific feature of the spatial distribution of resonant optical field in an open spherical cavity is the location of the so-called "hot spots" [6] at the sphere poles due to the specific behavior of the internal Mie modes with a huge amplification of the intensities of the electric and magnetic components [4,5]. The latter is associated with the formation of regions in which the local wave vectors can exceed the wave vector of the incident radiation by orders of magnitude [7] due to the presence of optical nanovortices, analogous to the generation of strong magnetic fields in microcoils [8]. Significantly, the presence of nanovortices is not related to the features of the incident optical beam, but is due solely to the scattering of a plane linearly polarized wave, which does not have any intrinsic phase or amplitude singularities. Obviously, at such extremely large fields inside a dielectric microresonator its material can exhibit noticeable optical nonlinearity, in particular due to the optical Kerr effect, thermo-optic effect, radiation pressure, etc. [9,10].
The studies on the nonlinear optics in mesoscale dielectric microspheres have a long history and are presented in many publications, e.g., Refs. [11,12,13,14,15,16,17]. A review of recent advances in the field of nonlinear optics in glass microspheres is presented, e.g., in [10,11,12,13,14,15,16,17,18]. In particular, it was reported that the presence of giant internal field in the hot spots of a dielectric sphere at WGM resonance can lead to a noticeable lowering of the energy threshold for light-induced ionization of the particulate material [19,20], which can stimulate the optical breakdown (OB) and effective generation of a supercontinuum [21,22]. Meanwhile, the free-electron plasma localized inside the spherical particle in the shadow pole is characterized by the pronounced dynamics and may exhibit a complex spatial shape [23]. One can also expect that the field enhancement due to high-order Fano resonance [4] in the above conditions will lead to a reduced ionization threshold similar to that of monomer ionization by high-power femtosecond pulses [24].
Worthwhile noting, in the most of published works on the impact of the Kerr-type optical nonlinearity on the resonance conditions of high-Q eigenmodes in dielectric spherical particles are studied either the frequency shift of the resonance peak or nonlinear mode splitting, while the overall deformation and possible spoiling of the resonant contour as a whole is not considered. Also, we are not aware of any published works which report the joint action of the Kerr-type nonlinearity and the electron plasma emerged in a dielectric mesoscale sphere on the properties of high-order WGM resonances. The majority of studies known to the authors refer to the electric field resonances, while the magnetic field in a WGM resonance was specially considered only in linear scattering regime for liquid mesoscale particles (water droplets with the size parameter xa ~ 70) [4]. The present work is aimed to fill this gap and presents the analysis of the above-mentioned problems.

II. Problem Formulation for a “Resonator-In-Capillary” Model

In the following, the excitation and detection of WGMs in a dielectric microsphere is analyzed according to the popular optical scheme with an evanescent electromagnetic field using a capillary coupled into the WGM resonator (WGMR) [25]. To this end, we consider the following problem formulation (see, Figure 1a). A dielectric sphere of radius R having a high refractive index (RI) and extremely small intrinsic absorption is placed inside a glass capillary in such a way that the sphere touches the capillary walls. For simplicity, the particle is illuminated by a laser radiation propagating inside the walls of the capillary without accounting for light reflection from its outlets. Lanthanum doped optical glass (OHARA S-LAM7) having a complex refractive index m2 = 1.75 - i⋅10- [8] at the wavelength λ = 550 nm [26] is chosen as the WGMR material. The glass capillary is a hollow annular core fiber (HACF) with a real refractive index n1 = 1.5 [27]. In practice, to direct optical radiation mainly into the capillary walls one of its ends is tapered by fusing to a cone and docked to a standard single-mode fiber [28].
As a result of diffraction coupling of the optical field which leaks out of the capillary walls with the WGMR, inside its volume the optical eigenmodes are excited in the spatial form of an annular field region confined close to the sphere surface (Figure 1b). The eigenmodes contain the regions with extremely high field intensity ("hot spots"), where favorable conditions are realized for the manifestation of the optical nonlinearity of the particle substance. In turn, this changes the phase-matching conditions of the optical field in resonance and affects the WGM parameters (quality factor, resonance frequency). Obviously, in contrast to the linear case, the WGM properties should depend on the intensity of the excitation field in the capillary.
During the simulations, the spectral range of the input optical radiation was specially chosen to include several neighboring resonances in spherical WGMR with different Q-factors and linewidths.
Thus, in the case under study two resonances are selected: (a) the super-resonance TE95,1 with high quality factor Q = 1.6⋅105 excited at the wavelength λ = 519.585 nm, and (b) the resonant WGM TE90,2 with multiple lower Q- factor, Q = 4⋅104 , at the wavelength λ = 517.13 nm. The spectral positions of the selected resonances are shown in Figure 1c as a function of the dimensionless Mie parameter Mie xa. Practically, the excitation of a WGM resonance is usually detected by the transmission minimum, T = Iout/Iin, of the waveguide coupled to the resonator, as presented in Figure 1d. Here, Iin and Iout are the optical intensities (more exactly, the powers) at the input and output ports of the WGMR, respectively, while on the x-axis in this graph the relative detuning from the resonance frequency ω0 is plotted: δ = ω − ω 0 / Γ , where Γ = ω0/Q denotes the resonance halfwidth.
The optical field coupled with the eigenmode of a spherical particle illuminated through its rim is considered within the stationary problem formulation by the numerical solution of the homogeneous wave equation accounting for resonator medium optical nonlinearity:
∇ × ∇ × E r − k 0 2 ε ′ E 2 E r = 0
where k0 = 2π/λ is the wave number in free space, and ε′[E2] = ε + Δε is the nonlinear dielectric permittivity of medium depending on the optical field intensity E2. The character of the functional dependence ε[E2] is determined by specific nonlinear processes occurring in the WGMR material in a strong optical field. In transparent dielectrics, such physical processes are primarily cubic optical nonlinearity, manifested as the optical Kerr effect, and photoionization of the medium with the generation of underdense free-electron plasma. Both of these physical mechanisms tend to deform the electronic shells of the atoms, thus changing the polarizability of the medium which is expressed in the appearance of a nonlinear additive Δm to the linear refractive index m:
Δ m = Δ n − i κ N L = γ I + n p l − i α p l / 2 k 0 n
Here, γ is the parameter of cubic (Kerr) nonlinearity, I = c n E 2 / 8 π stays for the optical intensity, c is speed of light, while n = Re m denotes the real part of the complex refractive index. The contribution of plasma nonlinearity to RI additive Δm can be decomposed into real npl and imaginary αpl parts, the latter being the sum of optical losses for molecule photoionization κi and intrinsic plasma absorption κpl: α p l = 2 k 0 n κ i + κ p l . Clearly, the plasma RI additive is proportional to the spatial distribution of free electron concentration ρe formed as a result of medium photoionization in WGM field.
In turn, the density ρe of free-electrons is governed by the kinetic equation accounting for direct multiphoton (MPI) and impact molecule ionization, as well as for the electron number decay due to the recombination with neutrals and ions. In the single ionization approximation, the equation for ρe dynamics in an equilibrium plasma has the following form: [29]
∂ ρ e ∂ t = ν m p i ( I ) ρ n t − ρ e + ν i I − ν r ρ e ,
where νmpi is the MPI rate, ρ n t is the density of the neutral molecules (atoms), νi is the impact ionization rate, and ν r is the free-electron recombination rate which usually is considered as a constant. Equation (3) does not take into account the diffusion of free electrons from the plasma region because the characteristic time of ambipolar diffusion of electrons generated mainly in the “hot spot” area is estimated to be tens of picoseconds, which is an order of magnitude longer than the characteristic time of radiative recombination of plasma free charges, τr = 1/νr ~ 1 ps.
The photoionization rate νmpi of molecules is calculated via the p-photon absorption process which is characterized by the rate coefficient ν I ( p ) and determined by the Keldysh ionization model: [30] ν m p i I = ν I ( p ) I p / E i ρ n t , where Ei is the energy bandgap of dielectric. The optical response of plasma is modelled by the Drude model [31], which neglects the real energy distribution of free electrons and considers some average electron with a constant mean transit time τ c between collisions. In this case, the frequency of ionization of an atom by electron impact ν i depends linearly on the product of optical wave intensity I and the avalanche ionization cross section of the atom σc(λ): ν i = I σ c / E i . Then, within the Drude medium model the addition to the refractive index due to the plasma nonlinearity is expressed as: n p l = − ρ e / 2 ρ c n , while the nonlinear absorption due to MPI and plasma "heating" reads as: α p l = 1 / 2 ρ e σ c + ν I ( p ) I p − 1 ρ n t − ρ e / ρ n t . Here, the parameter ρ c = σ c λ τ c c − 1 is introduced, which defines the critical plasma electron density, above which the plasma becomes completely opaque to optical radiation with the wavelength λ. The main parameters of the numerical model presented above for fused silica in the visible spectral region [29], [32] are summarized in Table 1.
The solution to Eq. (3) in the approximation of a step-wise optical pulse of the duration tp has the following form:
ρ e ( t p ) = ν m p i η 1 − exp − η t p ,
Here, the parameter η = ν m p i + ν r − ν i combines the rates of free electron sources and sink and actually determines the threshold intensity for optical breakdown of medium Ibd providing ρ e → ∞ at t → ∞ .
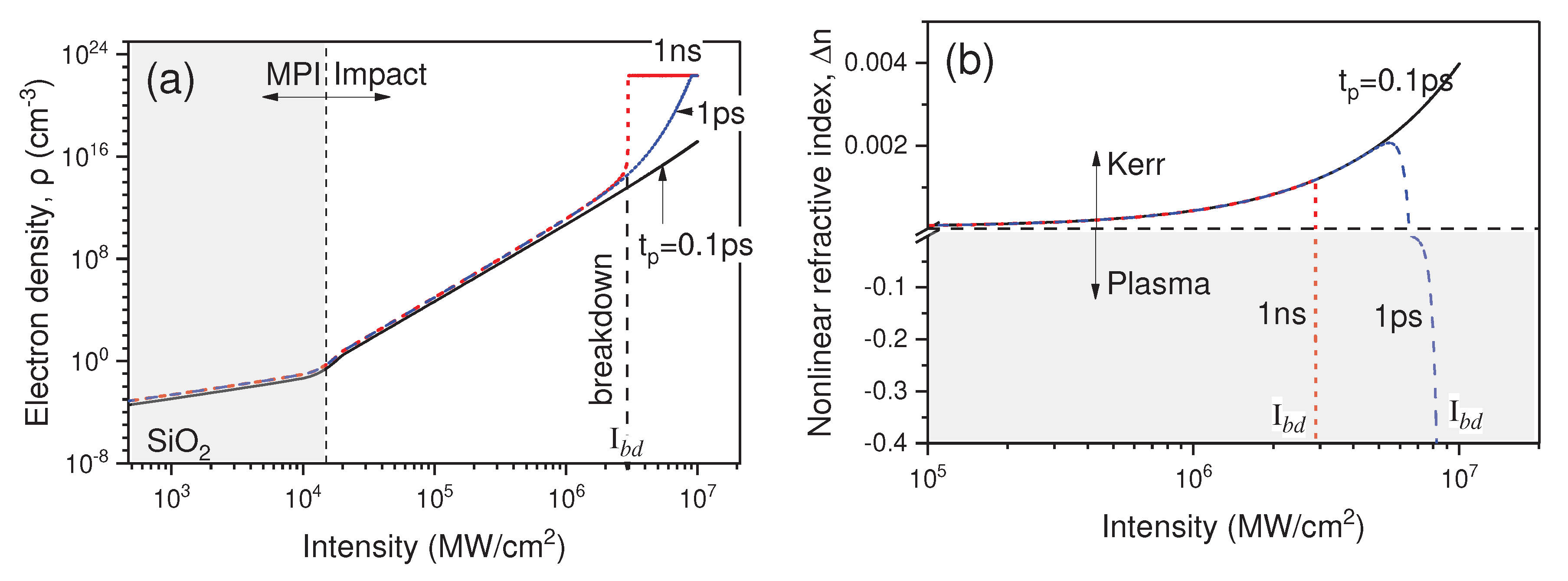
Indeed, noting that in a dense dielectric at moderate optical intensities the condition νmpi << νi is usually fulfilled, then from the condition η = 0 one immediately obtains the expression for OB threshold as: Ibd = νrEi/ σc , which according to the Table 1 gives the value Ibd ≈ 2 TW/cm2 in silica. Worth noting that this value determines the lowest OB threshold in a glass microparticle illuminated by a continuous wave (CW) optical radiation (tp→∞). For pulsed radiation, the threshold intensity Ibd increases with laser pulse shortening. For example, for tp = 1 ns, the calculation of the electron concentration dynamics gives Ibd ≈ 2.9 TW/cm2 (Figure 2a), while for much shorted pulse, tp = 0.1 ps, the optical breakdown is not realized up to the intensity Ibd ≈ 100 TW/cm2. Summarizing, when the intensity of the optical wave in any point of the medium exceeds the specific threshold value, I > Ibd (tp), an avalanche-like growth of free-electron concentration is developed and the appearance of regions with quasi-metal optical properties, i.e., extremely high optical absorption and reflectivity should be expected.
In accordance with the dynamics of optical intensity and plasma electron concentration in the “hot spots” area, the nonlinear additive Δn to the refractive index of medium also changes, as shown in Figure 2b. According to Eq. (2), at small values of optical intensity I, the cubic (Kerr) nonlinearity dominates giving a positive increase of the refractive index Δn ~ I. With the intensity increasing up to the sub-breakdown values, I ~ Ibd, the free-electron density also increases which leads first to compensation of the Kerr additive and then to an avalanche-like fall of Δn in the negative value region.
In our simulation, the computer package COMSOL Multiphysics is used, which performs the numerical solution of the wave equation to obtain the optical fields in a spherical resonator-capillary structure by the finite elements method (FEM). Without limiting the generality of the considered problem, we use an axisymmetric 2D-problem formulation which allows us to model a realistic 3D-problem by calculating the fields in only one half-plane in cylindrical coordinates, r , z , φ = 0 , π / 2 . In this case, the entire photonic structure is surrounded by a rectangular region of perfectly absorbing layers (PML) to prevent wave reflection from the outer boundaries of the simulation domain. Input and output of optical radiation are performed through COMSOL coaxial ports by specifying the HE11 fiber mode with circular polarization. For the discretization of all computational domains a triangular mesh is used with the boundary element edges less than λ/20. For the numerical solution of the system of coupled equations (1)-(2), a standard nonlinear solver is chosen based on the Newton's iterative method with damping. The linear step of this solver is carried out using the parallelized method for large sparse systems of algebraic equations (MUMPS). Typically, the reliable convergence of the numerical problem solved is achieved at the number of iterations of about 30 with the optimal parameters of the nonlinear solver.

III. Results and Discussion

Before addressing the results of the numerical simulations on WGM resonances excitation in a cavity with Drude-Kerr-type medium, it is instructive to demonstrate the effect of optical nonlinearity using simple analytical analysis. For simplicity, we consider only the cubic addition to the refractive index of the resonator material as a nonlinear mechanism: Δn(I) = γI.
It is worth noting that the appearance of nonlinear RI additive Δn changes the resonance conditions for the eigenmodes and shifts the resonant wavelengths to the Stokes region. Qualitatively, this result can be explained by considering the expression for the resonance size parameter xa which is inversely proportional to the refractive index of the particle: [33] x a ≈ l 2 − 1 / n e f f , where neff = n + Δn, and l is the mode azimuthal number (e.g., l = 95 for TE95,1 mode). As seen, an increase in the effective refractive index of spherical particle due to the emergence of regions with Kerr nonlinearity (Δn << n) leads to a proportional redshift of the resonance: Δω/ω0 ≈ -Δn/n.
In turn, approximating the spectral shape I(ω) of the resonant contour by a Lorentzian function:
I ω = Γ 2 2 π I a ω − ω 0 2 + Γ / 2 2 ∝ I a 4 δ 2 + 1 = I a L δ
and setting the nonlinear change of the parameter δ as, δ → δ(1 + f(Δn)), one obtains a deformed resonance line in a Kerr-type medium:
I * δ ∝ I a 4 δ + C / 4 δ 2 + 1 2 + 1 = I a L δ + C L δ
Here, L δ = 1 / 4 δ 2 + 1 is reduced Lorentzian profile, and C = ξ ω 0 γ I a / Γ n = ξ Q γ I a / n is the parameter depending on the resonance quality factor Q, resonance intensity Ia, reduced mode volume ξ, and Kerr nonlinearity coefficient γ. Note that the volume ξ occupied by a high-Q WGM usually does not exceed a few percent of the total volume of a spherical resonator.
Figure 3(a) illustrates the deformation of the resonant contour of an eigenmode when increasing the optical nonlinearity of the intracavity medium according to Eq. (6), while Figure 3(b) depicts the results of the numerical solution of Eqs. (1)-(2) in the same intensity range. As seen, the analytical evaluations and exact numerical calculations are in good qualitative agreement. With the increasing of parameter C, an increasingly pronounced deformation of the resonance spectral contour is observed caused by the peak shifting to the Stokes frequency band with simultaneous broadening of the resonance line, Γ →ΓC.
Now consider the results of the numerical simulations of WGM spectral contour transformation excited in a spherical resonator in the conditions of optical nonlinearity manifestation of the plasmonic and Kerr types. The capillary wall transmittance T, magnetic field intensity H2 (normalized to the initial value), and peak value of nonlinear refractive index Δnpeak of the resonator material are shown in Figure 4(a-f) in the dependence on the frequency detuning δ for two eigenmodes of the resonant glass sphere. The optical intensity I0 of the wave propagating inside the capillary walls and coupling to a WGM is chosen as the dependent parameter.
It follows from the analysis of these figures that at relatively low input radiation intensities, the red shift of the centers and asymmetry of the spectral contours of both WGM resonances are realized, which is in good agreement with the analytical estimates for a purely Kerr medium presented above in Figure 3(a). This indicates that in this intensity range the Kerr addition to the refractive index of the sphere is dominant (Figure 4c and f).
However, starting from the values I0 = 25 MW/cm2 and 150 MW/cm2 for TE95,1 and TE90,2 eigenmodes, respectively, the spectral contour of WGM acquires significant deformations due to plasma formation in the “hot spot” regions. The emerging electron plasma tends to lower the effective refractive index of the medium and simultaneously causes energy losses of the eigenmode. As a result, intensity dips appear in the Stokes wing of the spectral contour and the magnitude of the magnetic field in resonance decreases (Figure 4b and e).
At even higher input intensities inside the capillary, I0 = 100 MW/cm2 and 300 MW/cm2 for TE95,1 and TE90,2, the optical breakdown of the medium is realized at the “hot spots”. In this case, as can be seen in Figure 4, in a certain frequency range shown in the figures by shaded rectangles the nonlinear RI additive Δn becomes negative, the optical absorption increases sharply (not shown), and the eigenresonance either practically disappears (Figure 4a and b) or splits into several weaker sub-resonances (Figure 4d and e).
Two key parameters of a resonant contour in a nonlinear medium, the frequency shift Δδ from the unperturbed value and magnetic field intensity in resonance H max 2 , are shown in Figure 5(a) and (b) as the functions of input intensity of the excitation optical field. As seen, as the parameter I0 increases, for both resonance modes there is a tendency for peak intensity decrease and frequency redshift. Obviously, the higher-Q mode, TE95,1, is characterized by a larger-scale change in the parameters Δδ and H max 2 . Here, the competition between Kerr and plasmonic nonlinearities manifests itself in a nonmonotonic Δδ dependence on the input intensity. Indeed, up to a certain I0 value, I0 ≈ 50 MW/cm2, a monotonic shift of the resonant contour to the Stokes band is caused due to the Kerr effect, and above this I0 value, the parameter Δδ starts to decrease again (in modulus) that indicates the increasing impact of the plasma nonlinearity which imposes the Drude-type polarizability to the resonator medium.
of resonances for (a) TE95,1 and (b) TE90,2 WGMs of a sphere as a function of the input optical intensity.
Our estimates show that under the considered conditions by taking into account nonlinear plasma formation in the “hot spots”, the magnetic flux intensity B = μ0H (μ0 is vacuum permeability) for TE95,1 super-resonance can reach about 10 Tesla, while for TE90,2 mode this value is a bit lower, B ≈ 4 Tesla. Note, that a similar level of magnetic flux strength of about 8 Tesla was reported in [34] for atomic hydrogen under two-color with 50-fs structured laser pulse excitation at considerably higher laser intensity - 1015 W/cm2.

IV. Conclusion

The presence of resonances of the internal optical field in a spherical dielectric particle strictly follows from the Lorenz-Mie theory. Following this theory, high-quality high-order optical Fano resonances (the mode number is several tens) excited in a spherical non-dissipative dielectric mesoscale particle are characterized by high sensitivity to changes in the size and optical properties of the particle material. At sufficiently high intensity of the optical pulse incident onto a dielectric resonator, the strong optical nonlinearity of the resonator material is manifested mainly in the poles of the spherical resonator corresponding to the position of the “hot spots” due to the optical Kerr effect, light-induced ionization and the generation of free-electron plasma.
By means of numerical simulations, we theoretically demonstrate the effect of the resonant contour transformation of high-Q WGMs in a mesoscale glass sphere placed in a capillary depending on the intensity of pulsed optical radiation illuminating the particle. We show that in a certain intensity range, the Stokes shift of the WGM resonance due to the Kerr effect can be stopped and even reversed due to the competition of plasmonic and Kerr optical nonlinearities. Additionally, the optical ionization and plasma formation in the eigenmode volume significantly decrease both the intensity of the magnetic super-resonance in the pole region of the sphere and lead to its spoiling (becomes non-Lorentzian or non-Fano).
Our findings pav the way for an all-optical approach for the obtaining the strong magnetic fields of the order of tens Tesla at relatively moderate laser intensities. The considered effects of strong magnetic field generation in a wavelength-scale dielectric particle can be of interest both for fundamental physics of magnetic field in laboratory conditions [35] and for studying the interaction of optical radiation with matter in the problems of nonlinear magneto-optics [36].

Data availability

Data underlying the results presented in this paper may be obtained from the authors upon reasonable request.

Author Contributions

I.M. and O.M. author proposed the original idea, edit a paper. Y.G. wrote a draft, edit a paper and made simulations.

Acknowledgments

Y.G. thanks the Ministry of Science and Higher Education of Russia (IAO SB RAS) for funding for this work. I.M. and O.M. thank Tomsk Polytechnic University Development Program for supporting this work.

Conflict of Interest

The authors have no conflicts to disclose.

References

  1. Luk’yanchuk, A. Bekirov, Z. Wan, I. V. Minin, O. V. Minin, A. Fedyanin, “Optical phenomena in dielectric spheres with the size of several light wavelength (Review),”. Physics of Wave Phenomena 2022, 30, 283.
  2. Kuznetsov, A. Miroshnichenko, Y. H. Fu, Z. JingBo, B. Luk’yanchuk, “Magnetic light,”. Sci Rep 2012, 2, 492. [Google Scholar]
  3. Kozyreff, G.; Dominguez-Juarez, J.; Martorell, J. Nonlinear optics in spheres: from second harmonic scattering to quasi-phase matched generation in whispering gallery modes. Laser Photon- Rev. 2011, 5, 737–749. [Google Scholar] [CrossRef]
  4. Minin, I.V.; Minin, O.V.; Zhou, S. High-Order Fano Resonance in a Mesoscale Dielectric Sphere with a Low Refractive Index. JETP Lett. 2022, 116, 144–148. [Google Scholar] [CrossRef]
  5. Minin, O.V.; Zhou, S.; Minin, I.V. Generation of Giant Magnetic Fields in a Hollow Mesoscale Sphere. JETP Lett. 2023, 118, 201–207. [Google Scholar] [CrossRef]
  6. Calandrini, E.; Cerea, A.; De Angelis, F.; Zaccaria, R.P.; Toma, A. Magnetic hot-spot generation at optical frequencies: from plasmonic metamolecules to all-dielectric nanoclusters. Nanophotonics 2018, 8, 45–62. [Google Scholar] [CrossRef]
  7. Minin, I.V.; Minin, O.V. Mesotronics: Some New, Unusual Optical Effects. Photonics 2022, 9, 762. [Google Scholar] [CrossRef]
  8. Morita, H.; Fujioka, S. Generation, measurement, and modeling of strong magnetic fields generated by laser-driven micro coils. Rev. Mod. Plasma Phys. 2023, 7, 1–45. [Google Scholar] [CrossRef]
  9. Zhang, P.; Jung, S.; Lee, A.; Xu, Y. Radiation-pressure-induced nonlinearity in microdroplets. Phys. Rev. E 2015, 92, 063033–063033. [Google Scholar] [CrossRef]
  10. Frigenti, G.; Farnesi, D.; Conti, G.N.; Soria, S. Nonlinear Optics in Microspherical Resonators. Micromachines 2020, 11, 303. [Google Scholar] [CrossRef]
  11. Braunstein, D.; Khazanov, A.M.; Koganov, G.A.; Shuker, R. Lowering of threshold conditions for nonlinear effects in a microsphere. Phys. Rev. A 1996, 53, 3565–3572. [Google Scholar] [CrossRef]
  12. Zemlyanov, Yu. Geints, “Resonance excitation of light field in weakly absorbing spherical particles by a femtosecond laser pulse. 2001; 14. [Google Scholar]
  13. Pavlyukh, Y.; Hübner, W. Nonlinear Mie scattering from spherical particles. Phys. Rev. B 2004, 70, 245434. [Google Scholar] [CrossRef]
  14. Biswas, S.K.; Kumar, S. Impact of Kerr nonlinearity on the whispering gallery modes of a microsphere. Opt. Express 2015, 23, 26738–26753. [Google Scholar] [CrossRef]
  15. Kumar, S.; Biswas, S.K. Impact of Kerr nonlinearity and stimulated Raman scattering on the whispering gallery modes of an optical microsphere. J. Opt. Soc. Am. B 2016, 33, 1677–1687. [Google Scholar] [CrossRef]
  16. Devi, A.; De, A.K. Theoretical investigation on optical Kerr effect in femtosecond laser trapping of dielectric microspheres. J. Opt. 2017, 19, 065504. [Google Scholar] [CrossRef]
  17. Ghalanos, G.; Silver, J.M.; Del Bino, L.; Moroney, N.; Zhang, S.; Woodley, M.T.M.; Svela, A. ; Del'Haye, P. Kerr-Nonlinearity-Induced Mode-Splitting in Optical Microresonators. 2020, 124, 223901. [CrossRef]
  18. Strekalov, D.V.; Marquardt, C.; Matsko, A.B.; Schwefel, H.G.L.; Leuchs, G. Nonlinear and quantum optics with whispering gallery resonators. J. Opt. 2016, 18, 123002. [Google Scholar] [CrossRef]
  19. Zemlyanov, A.A.; Geints, Y. \. Intensity of optical field inside a weakly absorbing spherical particle irradiated by a femtosecond laser pulse. Opt. Spectrosc. 2004, 96, 298–304. [Google Scholar] [CrossRef]
  20. Efimenko, E.S.; Malkov, Y.A.; Murzanev, A.A.; Stepanov, A.N. Femtosecond laser pulse-induced breakdown of a single water microdroplet. J. Opt. Soc. Am. B 2014, 31, 534–541. [Google Scholar] [CrossRef]
  21. Favre, C.; Boutou, V.; Hill, S.C.; Zimmer, W.; Krenz, M.; Lambrecht, H.; Yu, J.; Chang, R.K.; Woeste, L.; Wolf, J.-P. White-Light Nanosource with Directional Emission. Phys. Rev. Lett. 2002, 89, 035002. [Google Scholar] [CrossRef]
  22. Geints, Y.E.; Kabanov, A.M.; Matvienko, G.G.; Oshlakov, V.K.; Zemlyanov, A.A.; Golik, S.S.; Bukin, O.A. Broadband emission spectrum dynamics of large water droplets exposed to intense ultrashort laser radiation. Opt. Lett. 2010, 35, 2717–2719. [Google Scholar] [CrossRef]
  23. Yang, Z.; Zhang, C.; Zhang, H.; Lu, J. The propagation loss of ultrashort laser pulses in water clouds. Plasma Phys. Control. Fusion 2023, 65, 085015. [Google Scholar] [CrossRef]
  24. Gao, X.; Arefiev, A.V.; Korzekwa, R.C.; Wang, X.; Shim, B.; Downer, M.C. Spatio-temporal profiling of cluster mass fraction in a pulsed supersonic gas jet by frequency-domain holography. J. Appl. Phys. 2013, 114, 034903. [Google Scholar] [CrossRef]
  25. Wang, J.; Zhang, X.; Yan, M.; Yang, L.; Hou, F.; Sun, W.; Zhang, X.; Yuan, L.; Xiao, H.; Wang, T. Embedded whispering-gallery mode microsphere resonator in a tapered hollow annular core fiber. Photon- Res. 2018, 6, 1124–1129. [Google Scholar] [CrossRef]
  26. M. N. Polyanskiy, "Refractive index database," https://refractiveindex.info. Accessed on 2023-09-05: https://refractiveindex.info/?
  27. Yang, Y.; Wang, Z.; Zhang, X.; Zhang, Q.; Wang, T. Recent progress of in-fiber WGM microsphere resonator. Front. Optoelectron. 2023, 16, 1–38. [Google Scholar] [CrossRef]
  28. Yang, Y.; Zhang, X.; Liu, X.; Wang, Z.; Yu, Y.; Wang, J.; Wang, T. In-fiber zigzag excitation for whispering-gallery modes via evanescent wave and free space coupling. Opt. Express 2020, 28, 31386–31396. [Google Scholar] [CrossRef]
  29. E Geints, Y.; A Zemlyanov, A. Numerical simulations of ultrashort laser pulse multifilamentation in fused silica: plasma channels statistics. J. Opt. 2015, 18, 015501. [Google Scholar] [CrossRef]
  30. L. V. Keldysh, “Ionization in the Field of a Strong Electromagnetic Wave,” Sov. Phys. 1307; 20.
  31. Self-focusing: Past and Present, Shen Y.R., Boyd R.W., and Lukishova S.G., еds. Springer, 2009.
  32. Couairon, A.; Sudrie, L.; Franco, M.; Prade, B.; Mysyrowicz, A. Filamentation and damage in fused silica induced by tightly focused femtosecond laser pulses. Phys. Rev. B 2005, 71, 125435. [Google Scholar] [CrossRef]
  33. Schiller, S. Asymptotic expansion of morphological resonance frequencies in Mie scattering. Appl. Opt. 1993, 32, 2181–2185. [Google Scholar] [CrossRef]
  34. Sederberg, S.; Kong, F.; Corkum, P.B. Tesla-Scale Terahertz Magnetic Impulses. Phys. Rev. X 2020, 10, 011063. [Google Scholar] [CrossRef]
  35. Battesti, R.; Beard, J.; Böser, S.; Bruyant, N.; Budker, D.; Crooker, S.A.; Daw, E.J.; Flambaum, V.V.; Inada, T.; Irastorza, I.G.; et al. High magnetic fields for fundamental physics. Phys. Rep. 2018, 765-766, 1–39. [Google Scholar] [CrossRef]
  36. Kimel, A.; Zvezdin, A.; Sharma, S.; Shallcross, S.; de Sousa, N.; García-Martín, A.; Salvan, G.; Hamrle, J.; Stejskal, O.; McCord, J.; et al. The 2022 magneto-optics roadmap. J. Phys. D: Appl. Phys. 2022, 55, 463003. [Google Scholar] [CrossRef]
Preprints 86072 g001
Figure 1. Computational model of a "resonator-in-capillary". (a) 3D perspective view, and (b) cross-sectional view of a spherical microparticle with the radius R and refractive index m2 placed inside a capillary with core diameter D and RI of walls n1. (c, d) Resonance contours and spatial profiles of TE95,1 and TE90,2 eigenmodes of the spherical resonator plotted for (c) normalized square of magnetic field amplitude H2 (“magnetic intensity”) and (d) optical transmission T of the capillary walls.
Figure 1. Computational model of a "resonator-in-capillary". (a) 3D perspective view, and (b) cross-sectional view of a spherical microparticle with the radius R and refractive index m2 placed inside a capillary with core diameter D and RI of walls n1. (c, d) Resonance contours and spatial profiles of TE95,1 and TE90,2 eigenmodes of the spherical resonator plotted for (c) normalized square of magnetic field amplitude H2 (“magnetic intensity”) and (d) optical transmission T of the capillary walls.
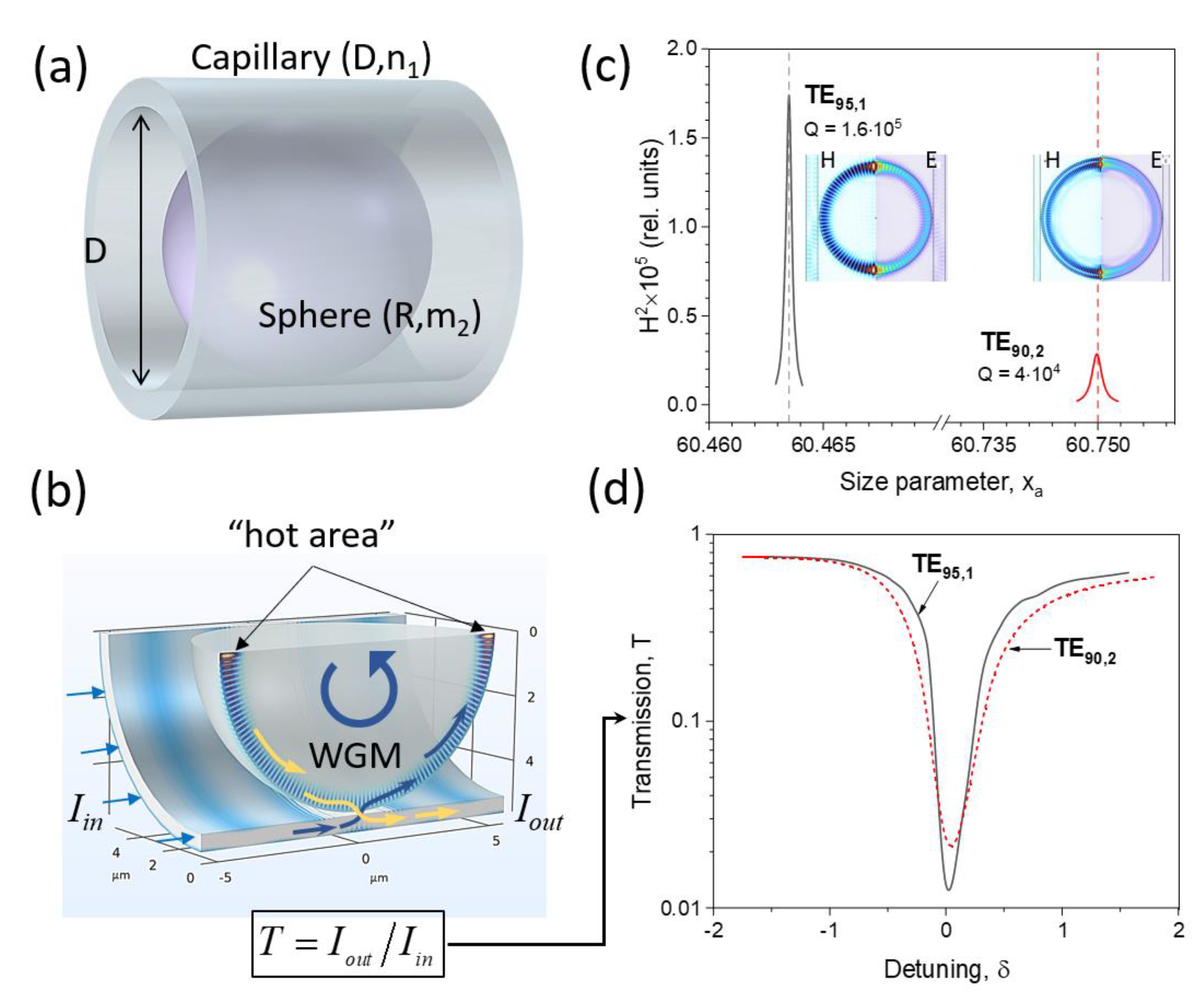
Preprints 86072 g001
Preprints 86072 g002
Figure 2. (a) Free-electron density ρe calculated by Eq. (5) and (b) nonlinear RI additive Δn calculated by Eq. (2) for silica glass at different input optical intensity and laser pulse duration tp.
Figure 2. (a) Free-electron density ρe calculated by Eq. (5) and (b) nonlinear RI additive Δn calculated by Eq. (2) for silica glass at different input optical intensity and laser pulse duration tp.
Preprints 86072 g002

Name Symbol Value
Kerr nonlinearity (cm2/W) γ 3.5·10-16
Energy bandgap (eV) E i 9.0
Electron mean transport time between collisions (fs) τ c 1.7
MPI order p 4
MPI rate (W(1-p)·cm(2p-3)) ν I ( p ) 1.21·10-49
Avalanche cross section (cm2) σ c 4.7·10-18
Electron recombination rate (fs-1) ν r 6.7·10-3
Neutrals density (cm-3) ρ n t 2.1·1022
Preprints 86072 g003
Figure 3. Deformation of the resonance spectral contour in a Kerr medium, (a) according to the analytical estimates Eq. (7) and (b) according to numerical calculations at different intensities I0 of incident optical radiation.
Figure 3. Deformation of the resonance spectral contour in a Kerr medium, (a) according to the analytical estimates Eq. (7) and (b) according to numerical calculations at different intensities I0 of incident optical radiation.
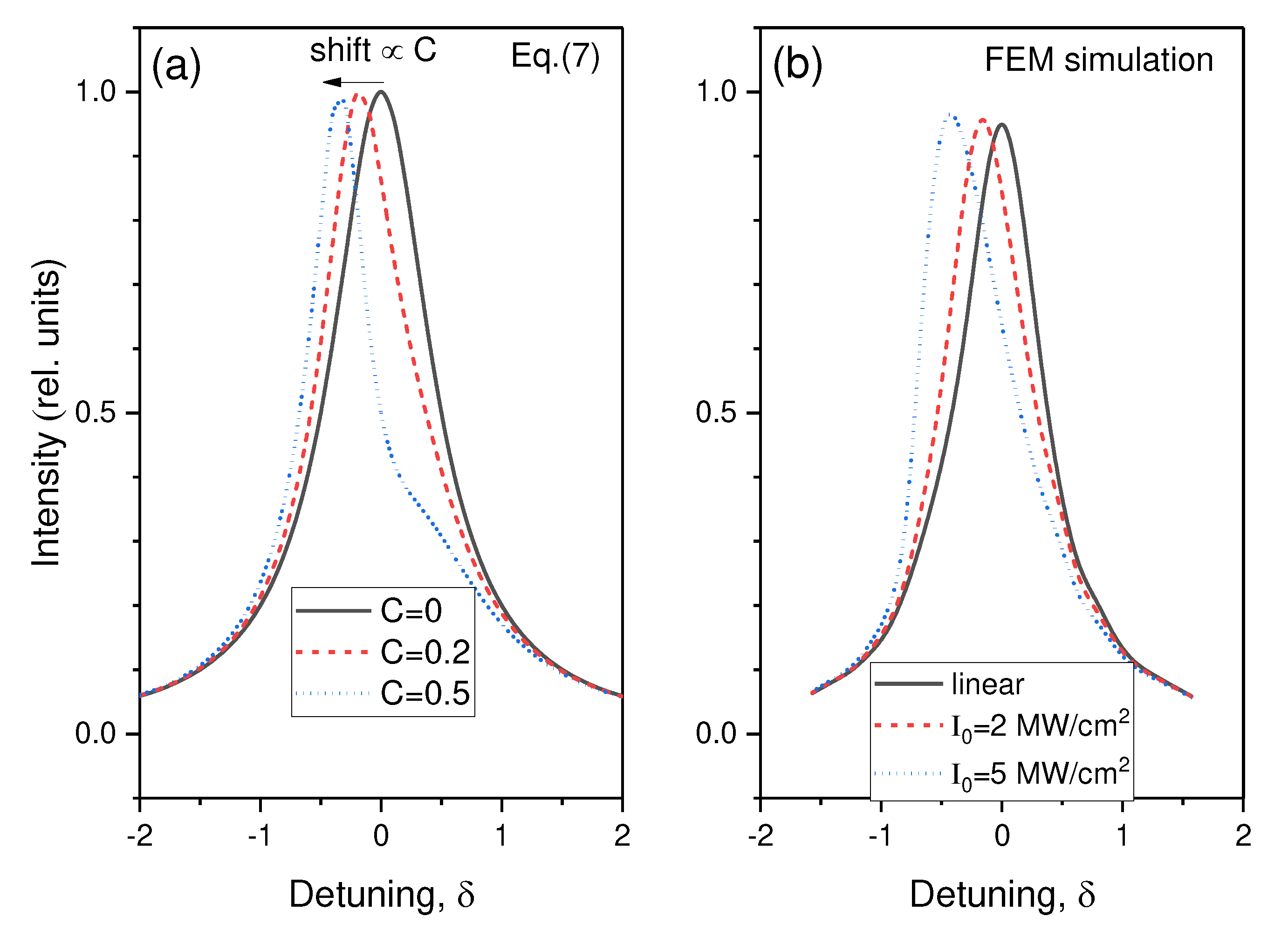
Preprints 86072 g003
Preprints 86072 g004
Figure 4. Parameters of the WGM resonances for (a-c) TE95,1 and (d-f) TE90,2 in a cavity with a Drude-Kerr optical nonlinearity for different incident optical wave intensity I0. (a, d) Transmittance T of the capillary walls, (b, e) square of the normalized magnetic field amplitude H2, (c, f) peak change of the nonlinear refractive index Δnpeak. The shaded regions depict the optical breakdown (OB) regions in the resonator material.
Figure 4. Parameters of the WGM resonances for (a-c) TE95,1 and (d-f) TE90,2 in a cavity with a Drude-Kerr optical nonlinearity for different incident optical wave intensity I0. (a, d) Transmittance T of the capillary walls, (b, e) square of the normalized magnetic field amplitude H2, (c, f) peak change of the nonlinear refractive index Δnpeak. The shaded regions depict the optical breakdown (OB) regions in the resonator material.
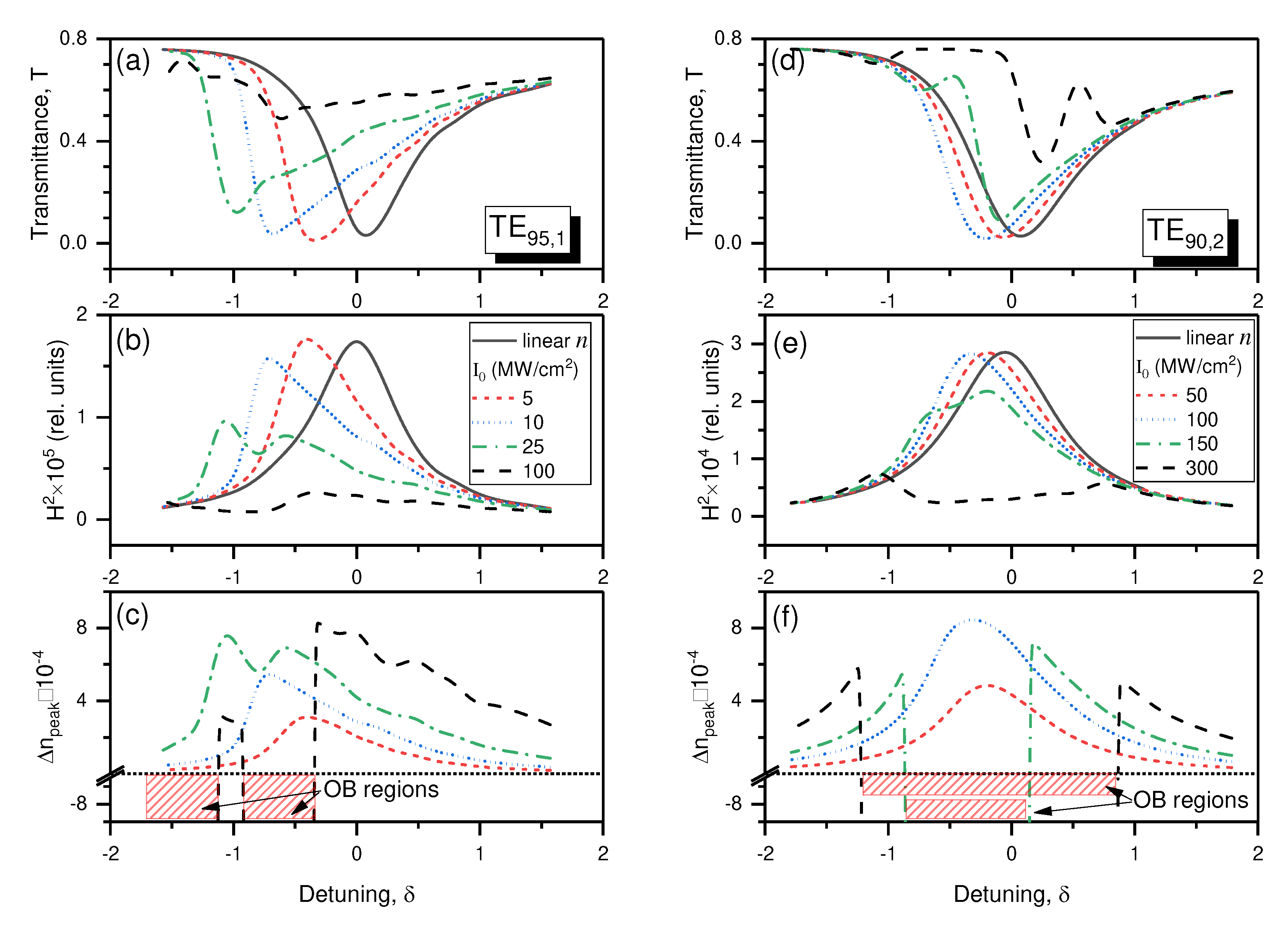
Preprints 86072 g004
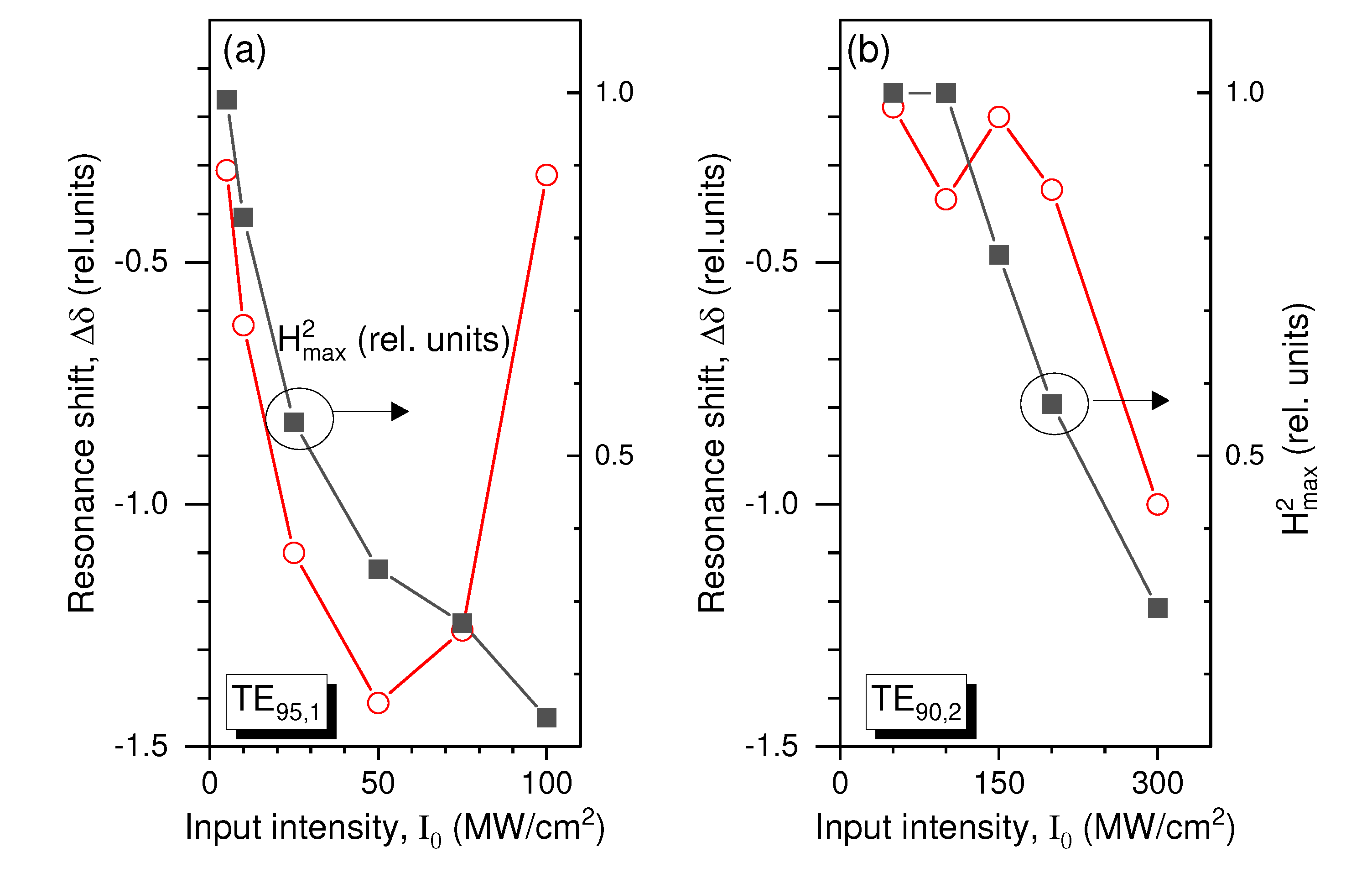
Preprints 86072 g005
Figure 5. Frequency shift Δδ and magnetic intensity H max 2
Figure 5. Frequency shift Δδ and magnetic intensity H max 2
Preprints 86072 g005
Table 1. Nonlinear optical parameters for fused silica (λ = 532 nm).
Table 1. Nonlinear optical parameters for fused silica (λ = 532 nm).
Name Symbol Value
Kerr nonlinearity (cm2/W) γ 3.5·10-16
Energy bandgap (eV) E i 9.0
Electron mean transport time between collisions (fs) τ c 1.7
MPI order p 4
MPI rate (W(1-p)·cm(2p-3)) ν I ( p ) 1.21·10-49
Avalanche cross section (cm2) σ c 4.7·10-18
Electron recombination rate (fs-1) ν r 6.7·10-3
Neutrals density (cm-3) ρ n t 2.1·1022
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated