Aggravation of Health Problems Subsequent to COVID-19 Lockdown

Covid-19 pandemic has greatly affected the whole world since the beginning and it continues to affect it. The main aim of this study is to show how Covid-19 affect other mortal diseases; cancer, heart diseases, and diabetes in near future. With this purpose two mathematical models are proposed via Ordinary Differential Equations (ODEs); one for the relationship between Covid-19 and cancer and one for the relationship between Covid-19, diabetes and heart diseases. Afterwards, stability analyses of these models are demonstrated. In order to see the effect of parameters on the disease compartments, sensitivity analysis is applied. Results of sensitivity analysis revealed that huge percentage of people are still scared of visiting doctors and this may lead a massive increase in the diagnosis of other diseases for upcoming years. Moreover, figures displayed that there exists a relationship between diabetes and heart diseases. Especially, diabetes patients should be careful about their health situations and take care of their heart. In order to provide these, awareness of people should be developed.

Keywords:

Subject: Computer Science and Mathematics - Mathematical and Computational Biology

1. Introduction

Epidemiology is the field of study that analyzes the ways among illness and health by addressing the facts of population [1]. Studies in this area are mostly interested in infectious diseases till the twentieth century. Recently, other than transmitted diseases by infection, diseases like cardiac heart diseases, diabetes and stroke that can induce the deaths worldwide have become a significant concern of health sciences [1].

New field is derived from the interaction among epidemiology and genetics in many years that lead to result a new discipline named genetic epidemiology. This new area concentrates on genetic parameters’ connection with environmental parameters during the presence of the disease in human population. Genetic epidemiology provides benefits to comprehend the interaction between genetic roots and the major chronic disorders like coronary heart diseases, cancer and diabetes [2].

Cardiovascular disorders (CVDs) belong to the category of disorders among blood veins and the heart. There is a variety of cardiovascular disorders (CVDs) including coronary heart, cerebrovascular peripheral arterial, rheumatic heart, congenital heart, pulmonary embolism and deep vein thrombosis [3].

Coronary heart disease (CHD) is a disorder of the blood veins providing the heart muscle [4]. One of the major chronic diseases is CHD worldwide and there are risk factors that increased CHD dramatically such as tobacco use, high cholesterol, unhealthy diet, alcohol use, and physical inactivity. Additionally, one significant risk of CHD is to have family history, especially having a family member which is a man under age 55 or a woman under age 65 with CHD. Approximately 17,9 million people passed away due to CVDs in 2019. CVD is a leading cause of deaths globally with 32%. Also, stroke and heart attacks are death causes with 85% [5].

Cancer is another disorder that includes a wide group of diseases. It is descriptive of unpreventable abnormal cells or damaged cells growth through almost anywhere in human parts or organs. Cancer doesn’t differentiate between age, gender, family background and other categories. However, statistics of cancer let us recognize the similarities and differences between categories identified with sex, age, ethnic groups, etc. The mathematical model proposed in [6] provides a picture of cancer rates in time by collecting information statistically. Cancer is classified by founding in a first place of a human body like lung cancer, colon cancer, skin cancer, breast cancer, and prostate cancer. It can also be classified by cells types like soft tissues ones such as muscle, nerves, blood vessels or deep skin [7,8].

According to the basic cancer facts, there are plenty of factors to raise the risk of having cancer. High tobacco use, high alcohol use, and being overweight are some of these factors. They can be called alterable within the realm of possibility. On the other hand, there are other risks factors that cannot be modifiable like inherited genetic mutation [8]. Globally, due to cancer, roughly 10 million people passed away in 2020 [9]. In other words, one in six deaths is because of a cancer in 2020. The most common cancers are breast cancer with 2.26 million cases, lung cancer with 2.21 million cases and colon and rectum cancer with 1.93 million cases. Prostate cancer and skin (non-melanoma) cancer are next in the line [10]. In 2022, the estimation of new cases and deaths is 1.9 million and 609.360, respectively only in the US. Moreover, cancer is the second major death cause in the US [11].

Diabetes mellitus, called simply diabetes, is a disease caused by insufficient insulin production by the pancreas. It leads uncontrolled amount of glucose or sugar in the human body [12]. The most well-known categories are type-1 diabetes (5%), and type-2 diabetes (95%) in obesity community. There are other categories of diabetes like Diabetes LADA, Diabetes MODY and gestational diabetes which are rare and occur in the mutation of single gene [13]. Statistically, around 442 million people have diabetes worldwide while 1.5 million people deaths are ground on diabetes every year [14].

Mathematical models allow us to foresee the future outcomes of an epidemic or health issues. Beside this, they might be used as interpretive tools for the clarification of basic principles of transmission or extension [15,16]. Kermack and McKendrick increased the level of mathematical epidemiology by proposing a new model depends upon the spread of contagious diseases in 1927 [1]. The first mathematical modelling of contagious diseases was structured by Daniel Bernoulli to determine the impact of smallpox inoculation in the population. Due to the description of complicated mutual interaction among human (or animal) hosts’ environment and biology, modern contagious disease epidemiology depends mostly on mathematical models [17].

Recently, the most well-known contagious disease is Coronavirus disease (COVID-19) caused by SARS-CoV-2 virus. COVID-19 is transmitted by liquid particles from the mouth or nose of an infected person. It is categorized as a pandemic disease since it affected many countries within international boundaries [18,19]. At the beginning, there was a big concern about the contagiousness and fatality since the structure of the disease were unknown. However, with the vaccination and some restrictions, the fatality of the disease is taken under control. Hence, almost every restriction is started to be lifted.

In the last years, many articles are published in the field of mathematical modelling that analyses Covid-19. The article [20] is about Covid 19’s epidemic development by using a mathematical model in China. It proposes an SEIR (a varied Susceptible, Exposed, Infectious, Recovered) model [21]. [22,23] studied the effect of vaccination on Covid-19 while [24] focuses on both vaccination and mobility. [25] discussed the change in health behavior during the Covid-19 lockdown in United Kingdom by applying descriptive statistics. Methods of another field, machine learning, are applied in the paper [26] with the purpose of examining transfusion of best convalescent plasma for the critical Covid-19 patients. The paper [27] deliberated over the artificial intelligence techniques about the detection and classification of medical images of Covid-19.

Mathematical modelling has a remarkable role not only in infectious(epidemic/pandemic) diseases but also in chronic diseases as well. In health sciences, mathematical models can be applied in order to identify dynamics and aspects of diseases like cancer, coronary heart disease (CHD) and diabetes. In [28], proposed mathematical models provide approaches for a better understanding of the parameters of chronic disorders.

In this paper, the main aim is to present the effect of Covid-19 on other significant diseases; cancer, heard diseases and diabetes. This study is constructed to warn people and increase their awareness so that the necessity of doctor and hospital visits for the upcoming years can be reduced. On that note, two mathematical models are proposed; one for the relationship between cancer and Covid-19, and one for the relationship between heart diseases, diabetes and Covid-19. It is aimed to indicate how doctor controls are important for the future of human beings and how Covid-19 will affect these doctor visits in a bad way. In section 2 and section 3, models are given with necessary existence theorems and proofs. Section 4 includes the sensitivity analysis results as a numerical simulation. The results are explained in Section 5 and conclusions are given in the last part.

2. Materials and Methods

In this study, compartmental mathematical models are constructed. For the analysis of models, invariance, basic reproduction number and equilibrium points properties are obtained and proved. Furthermore, for the effectiveness of parameters, sensitivity analysis is applied. All data used in this paper are gathered from the references [29,30,31,32,33].

3. Construction and Analysis of the First Model

In this section, the first model of the paper is proposed and the entity of the solution is demonstrated. The model is constructed with the help of Ordinary Differential Equations (ODEs) with the aim of obtaining the change in compartments at time

t

. Then, analysis of the model is given.

3.1. Mathematical Model Formulation

The whole population,

N

, is divided into 2 compartments. That is,

N (t) = S (t) + C (t)

, at time

t

. Model is constructed as follows:

\frac{d S}{d t} = π - f_{1} C S - (o + b) S - μ S + γ C + c C,

(1)

\frac{d C}{d t} = f_{1} C S + (o + b) S - μ C - η C - γ C - c C .

In Table 1 and Table 2, descriptions of variables and parameters are explained, respectively. In the study, parameter

c

(the negative effect of Covid-19), defines the rate of cancer individuals who waves doctor checks aside because of lockdowns or Covid-19 scares. As a result, individuals cannot be diagnosed earlier with cancer.

Theorem 1.

Let

(S, C)

be the solution of the constructed system with the initial conditions

S \geq 0

and

C \geq 0

. Then, the following set

Λ = \{(S, C) \in R_{+}^{2} : S + C \leq π\}

is invariant and positive. Moreover, all of the solutions in

R_{+}^{2}

stay in

Λ

with respect to the constructed system.

Proof of Theorem 1.

By adding all of the terms that are on the right side of the proposed system,

\frac{d N}{d t} = π - μ (S + C) - η C

is obtained. From the equality, it can be seen that

\frac{d N}{d t} \leq π

always holds. Applying integration with respect to

t

to the both sides yields

N (t) e^{t} \leq π e^{t} + k,

for some arbitrary constant

k

. Applying Rota and Birkhoff to the above differential inequality, it is obtained that as

t

tends to infinity,

\infty

0 \leq N \leq π

holds. As a result, the solutions of the system enter the region

Λ .

Hence, the model is feasible in terms of biology which is enough to consider the dynamics on the model in

Λ

. □

3.2. Equilibrium Points

For the constructed model, two equilibrium points, disease-free and endemic equilibrium point, are evaluated. At the disease-free equilibrium point, denoted by

E_{0,1}

, the disease is expected to die out. In other words, for the presented model,

E_{0,1}

is the point where cancer disease does not exist in the population. The endemic equilibrium point,

E_{*, 1}

, is defined as the point where the disease is maintained with no need of external inputs [34].

E_{0, 1}

of this model is unique and it obtained as

E_{0, 1} = (S_{0, 1}, C_{0, 1}) = (\frac{π}{o + b + μ}, 0) .

It is obvious that

E_{0, 1}

attracts the region so that

E_{0, 1} = \{(S_{0, 1}, C_{0, 1}) \in R_{2}^{+} : C = 0\} .

Endemic equilibrium point, denoted by

E_{*, 1}

, consists of

S_{*, 1}

and

C_{*, 1}

. That is,

E_{*, 1} = (S_{*, 1}, C_{*, 1}),

where

S_{1}

is the solution of

A {(S_{*, 1})}^{2} + B S_{*, 1} + F = 0,

for

A = f_{1} [(o + b) (1 + γ + c) - k], B = (μ + η + γ + c) [(o + b) (1 - γ - c) + μ] - f_{1} π, F = - (μ + η + γ + c) π,

and

C_{*, 1} = \frac{(o + b) S_{*, 1}}{μ + η + γ + c - f_{1} S_{*, 1}} .

On the other hand, the quadratic equation that depends on

S_{*, 1}

exists only if

\frac{μ}{o + b} < γ + c

holds.

Theorem 2.

Disease Free Equilibrium,

E_{0, 1}

, is globally asymptotically stable whenever

γ + c > f_{1}

Proof of Theorem 2.

Consider the Lyapunov function

V (S, C) = S - S_{0, 1} - S_{0, 1} \ln (\frac{S}{S_{0, 1}}) + C .

The above function is always positive and at the point

E_{0, 1}

, it is equal to

0

. So, for the stability, it is enough to show that

\dot{V}

is negative definite.

\dot{V} = \dot{S} - S_{0, 1} \dot{\frac{S}{S}} + \dot{C} = π - (f_{1} C + o + b + μ) S + (γ + c) C - \frac{S_{0, 1}}{S} [π - (f_{1} C + o + b + μ) S + (γ + c) C] + (f_{1} C + o + b) S - (μ + η + γ + c) C .

Since

π = S_{0, 1} (o + b + μ)

π - (f_{1} C + o + b + μ) S + (γ + c) C - \frac{S_{0, 1}}{S} [π - (f_{1} C + o + b + μ) S + (γ + c) C] + (f_{1} C + o + b) S - (μ + η + γ + c) C = π (2 - \frac{S_{0, 1}}{S}) + (f_{1} - γ - c) \frac{C}{S} S_{0, 1} .

It is clear that

2 - \frac{S_{0, 1}}{S} < 0

. Hence, for the condition

\dot{V} < 0

f_{1} - γ - c < 0

should hold. Therefore,

E_{0, 1}

is globally asymptotically stable if

γ + c > f_{1}

. □

Theorem 3.

Endemic Equilibrium,

E_{*, 1}

, is globally asymptotically stable.

Proof of Theorem 3.

For the proof of above theorem, the following Lyapunov function is constructed.

W (S, C) = S_{*, 1} g (\frac{S}{S_{*, 1}}) + C_{*, 1} g (\frac{C}{C_{*, 1}}),

where

g (x) = x - 1 - \ln x

. The function

W

is positive and

W (S_{*, 1}, C_{*, 1}) = 0

. So, it is enough to show that

\dot{W} < 0

\dot{W} = \dot{S} - S_{*, 1} \dot{\frac{S}{S}} + \dot{C} - C_{*, 1} \dot{\frac{C}{C}} = π - f_{1} C S - (o + b) S - μ S + γ C + c C - \frac{S_{*, 1}}{S} [π - f_{1} C S - (o + b) S - μ S + γ C + c C] + f_{1} C S + (o + b) S - (μ + η + γ + c) C - \frac{C_{*, 1}}{C} [f_{1} C S + (o + b) S - (μ + η + γ + c) C] = π (2 - \frac{S_{*, 1}}{S}) - μ S - (μ + η) C < 0,

since

2 - \frac{S_{*, 1}}{S} < 0

. Thus,

E_{*, 1}

is globally asymptotically stable. □

4. Construction and Analysis of the Second Model

In this section, the model is proposed with the proof of existence of the solution. Afterwards, analyses of equilibrium points are given.

4.1. Mathematical Model Formulation

The population which is stated by

N

, is separated into 3 compartments

N (t) = S (t) + H (t) + D (t)

, at time

t

. Model is built as follows:

\frac{d S}{d t} = Λ - (b + o) S - (f_{1} H - f_{2} D) S + (c_{1} + γ_{1}) H + (c_{2} + γ_{2}) D - μ S, \frac{d H}{d t} = (b + k_{1} o) S + f_{1} H S - (c_{1} + γ_{1} + μ + η_{1} + a) H + e D, \frac{d D}{d t} = (1 - k_{1}) o S + f_{2} D S - (c_{2} + γ_{2} + μ + η_{2} + e) D + a H .

(2)

The explanation of variables and parameters are given in Table 3 and Table 4. In the study, parameters

c_{1}

and

c_{2}

(negative effect of Covid-19), defines the rate of heart and diabetes patients, respectively, who waves doctor visits aside because of lockdowns or Covid-19 scary. As a result, individuals cannot be diagnosed earlier with the diseases.

Theorem 4.

Assume that

(S, H, D)

is the solution of the constructed system above with the initial conditions

S \geq 0, H \geq 0,

and

D \geq 0

. Then, the following set

π = \{(S, H, D) \in R_{+}^{3} : S + H + D \leq Λ\}

is positive, invariant, and the solutions in

R_{+}^{3}

stay in

π

with respect to the constructed system.

Proof of Theorem 4.

Addition of all of the terms that are on the right side of the system gives

\frac{d N}{d t} = Λ - μ (S + H + D) - η_{1} H - η_{2} D .

From the above equality, it is obvious that

\frac{d N}{d t} \leq Λ

. Integrating both sides with respect to

t

yields

N (t) e^{t} \leq Λ e^{t} + m,

for some constant

m

. Applying Rota and Birkhoff to the above differential inequality, it is obtained that as

t

tends to infinity,

0 \leq N \leq Λ

holds. As a result, the solutions of the system enter the region

π .

Therefore, it is certain that the model is feasible by means of biology and it is enough to consider the dynamics on the model in

π

. □

4.2. Equilibrium Points

In the proposed model, there are two equilibrium points; disease-free equilibrium point, denoted by

(E_{0, 2})

, and endemic equilibrium point, denoted by

(E_{*, 2})

E_{0, 2}

of this model is obtained as

E_{0, 2} = (S_{0, 2}, H_{0, 2}, D_{0, 2}) = (\frac{Λ}{o + b + μ}, 0, 0) .

Here

E_{0, 2}

attracts the region so that

E_{0, 2} = \{(S_{0, 2}, H_{0, 2}, D_{0, 2}) \in R_{3}^{+} : H = D = 0\} .

Endemic equilibrium point, denoted by

E_{*, 2}

, consists of

S_{*, 2}

and

C_{*, 2}

. That is,

E_{*, 2} = (S_{*, 2}, C_{*, 2}, D_{*, 2}),

where

S_{*, 2}

is the solution of

A {(S_{*, 2})}^{4} + B {(S_{*, 2})}^{3} + E {(S_{*, 2})}^{2} + F S_{*, 2} + G = 0,

for

A = (b + k_{1} o) f_{2}^{2} + f_{1} f_{2}^{2} (1 - k_{1} o - b + o + μ),

G = - Λ (c_{2} + γ_{2} + μ + η_{2} + e) [(c_{1} + γ_{1} + μ + η_{1} + a) (c_{2} + γ_{2} + μ + η_{2} + e) - e a]

and so

Theorem 5.

Disease Free Equilibrium,

E_{0,2}

, is globally asymptotically stable whenever

f_{1} < c_{1} + γ_{1}

and

f_{2} < c_{2} + γ_{2}

Proof of Theorem 5.

Consider the Lyapunov function

T (S, H, D) = S (\frac{S}{S_{0,2}} - 1 - \ln (\frac{S}{S_{0, 2}})) + H + D .

Here, the constructed function

T

is always positive and equals to zero at

E_{0,2}

. So, it will be enough to show that

\dot{T} < 0

holds.

since

Λ = S_{0} (o + b + μ)

. It is obvious that

2 - \frac{S_{0}}{S} < 0

. Hence,

E_{0,2}

is globally asymptotically stable if

f_{1} < c_{1} + γ_{1}

and

f_{2} < c_{2} + γ_{2}

. □

Theorem 6.

Endemic Equilibrium Point,

E_{*, 2}

, is globally asymptotically stable if

\frac{D_{*, 2}}{D} - \frac{H_{*, 2}}{H} < 0

Proof of Theorem 6.

Consider the Lyapunov function

X (S, H, D) = S_{*, 2} (\frac{S}{S_{*, 2}} - 1 - \ln (\frac{S}{S_{*, 2}})) + H_{*, 2} (\frac{H}{H_{*, 2}} - 1 - \ln (\frac{H}{H_{*, 2}})) + D_{*, 2} (\frac{D}{D_{*, 2}} - 1 - \ln (\frac{D}{D_{*, 2}})) .

The constructed function

X

is positive for each value and equals to

0

E_{*, 2}

. It is enough to show that

\dot{X} < 0

is true.

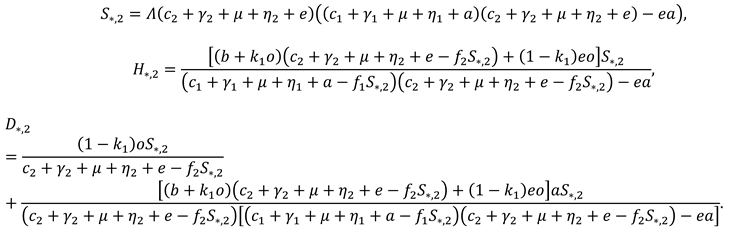
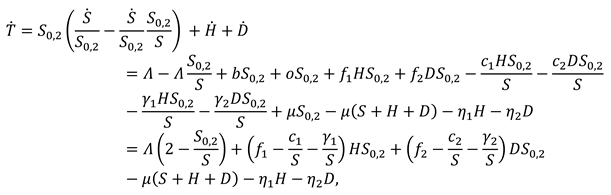
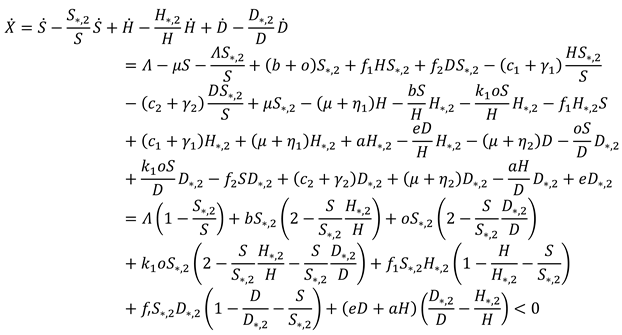
5. Sensitivity Analysis and Numerical Simulations

Sensitivity analysis is a method that can be applied to the parameters of any mathematical model with the purpose of identifying the effect of parameters on compartments. The main idea of this analysis is to show how a small change in parameters can affect the disease to exist or die out [29]. In this section, sensitivity analysis of the parameters is given for both models, separately. Data for the parameters are taken from the references [30,31,32,33,34].

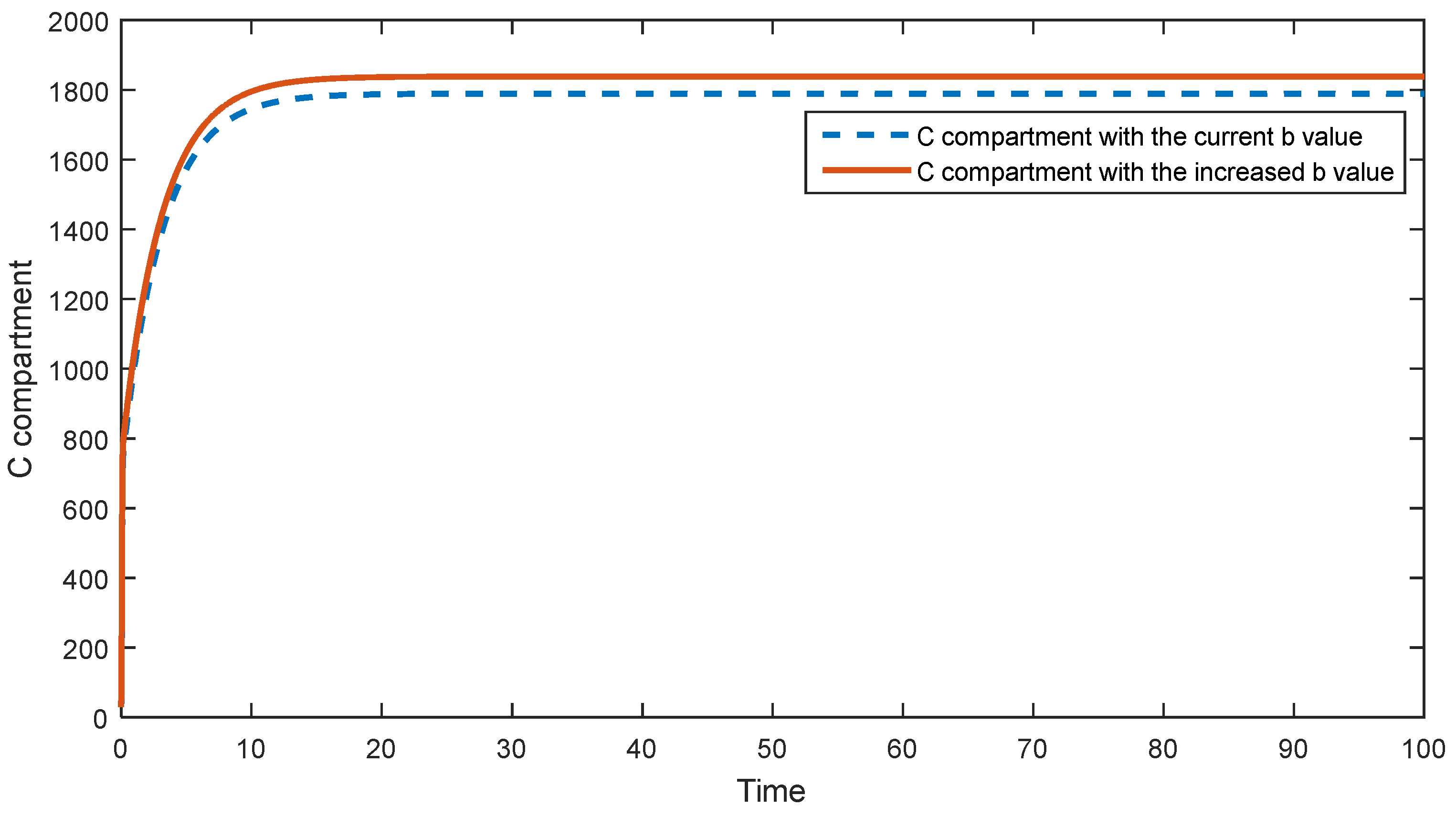
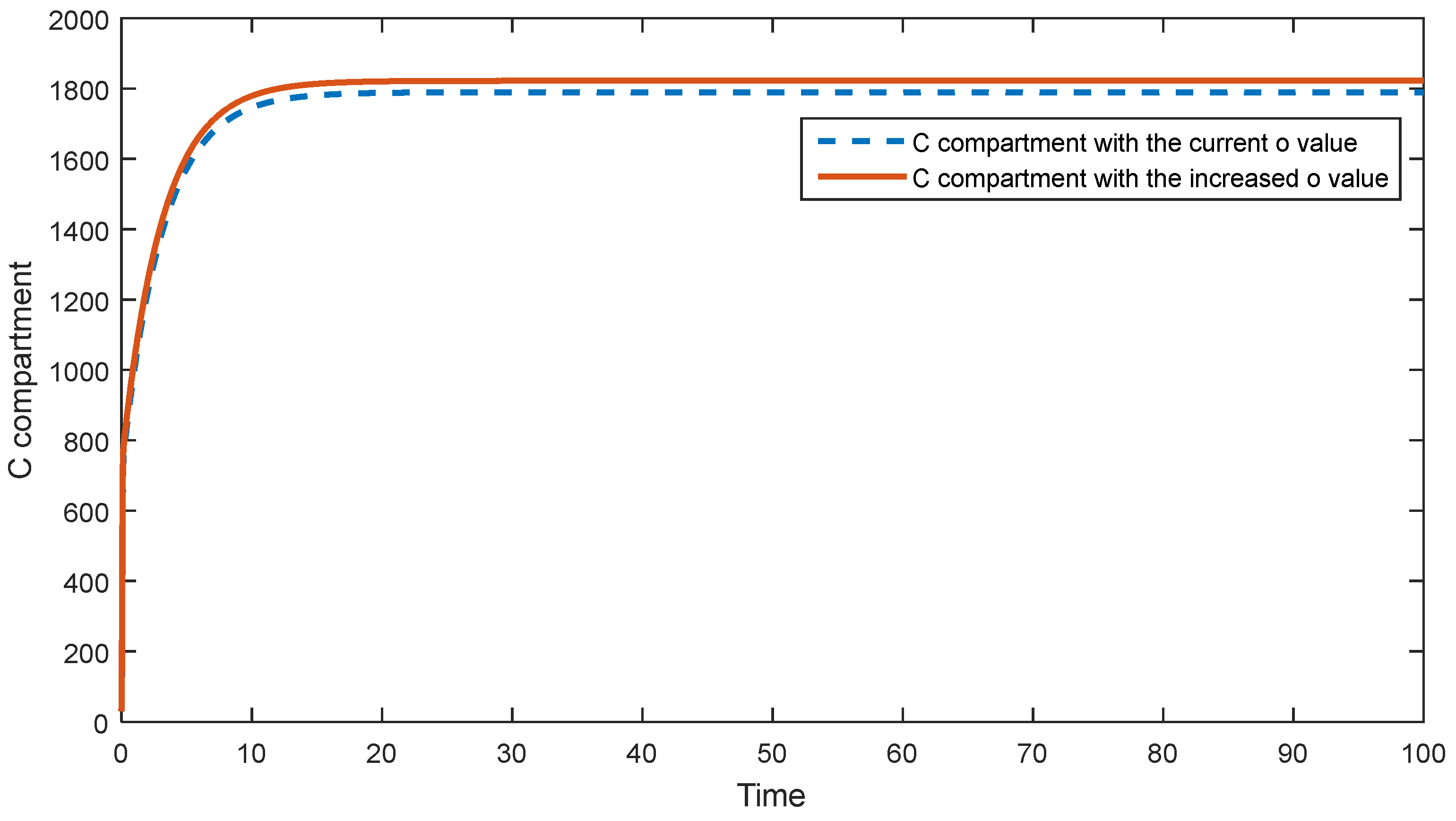
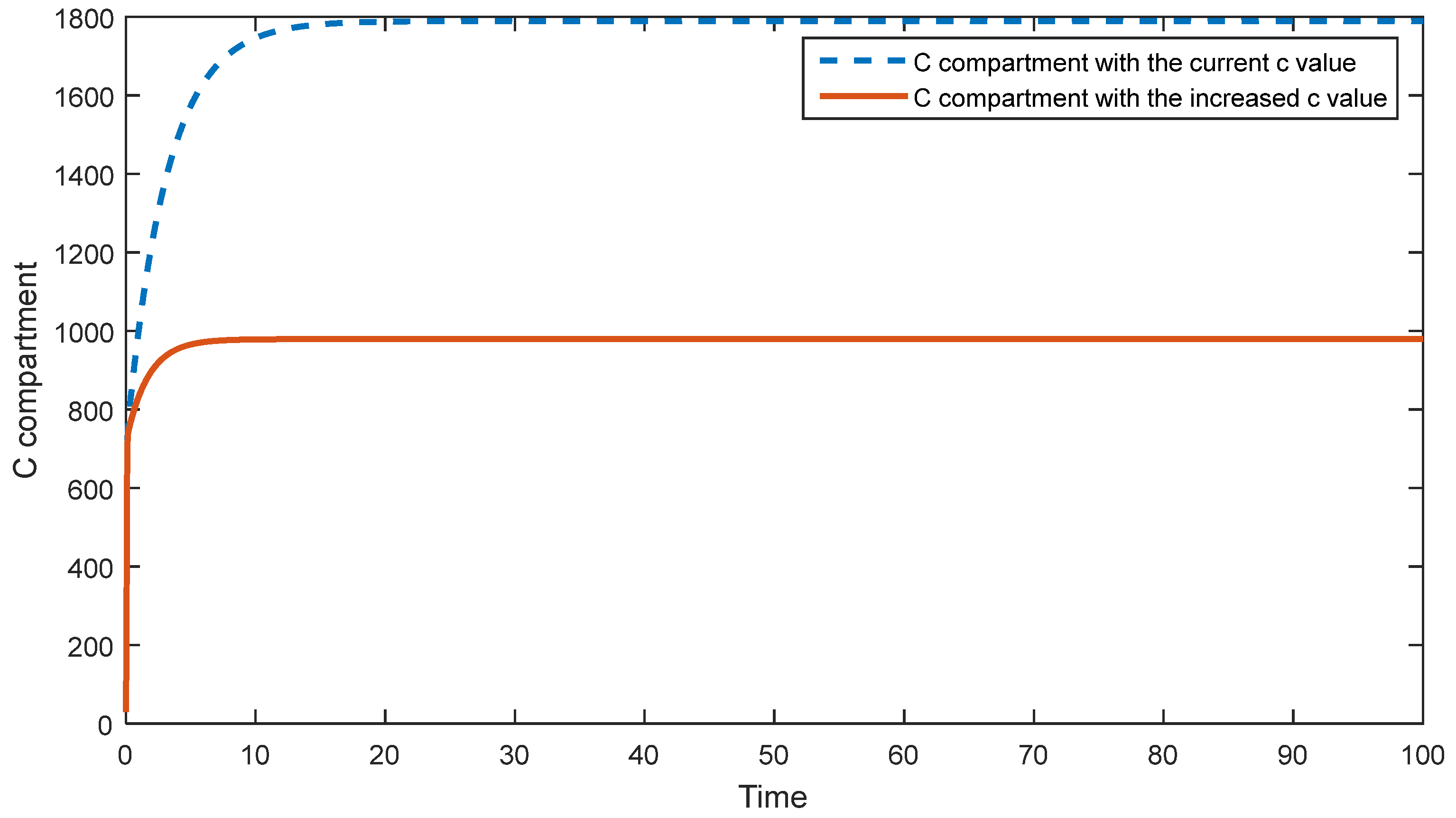
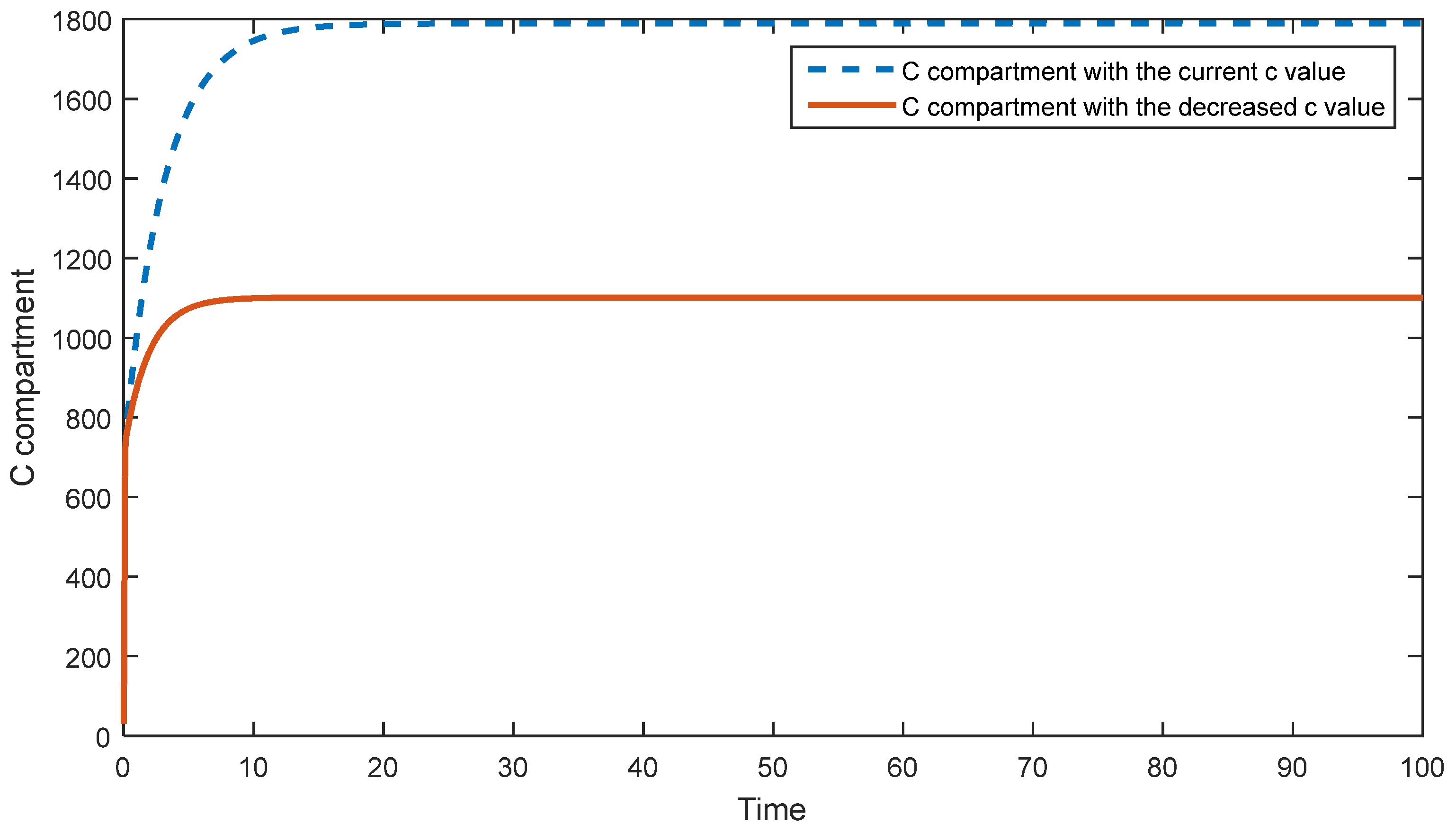
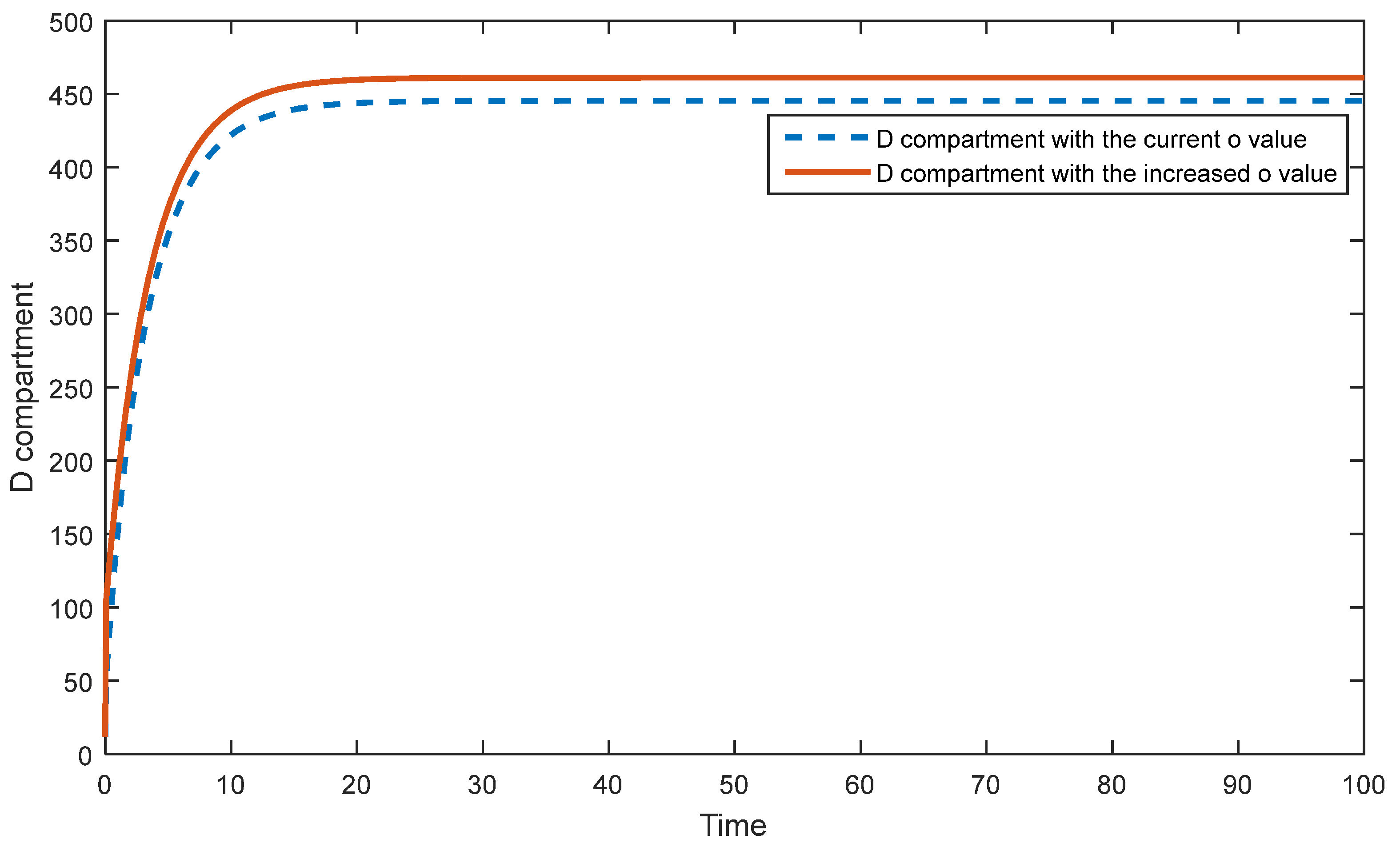
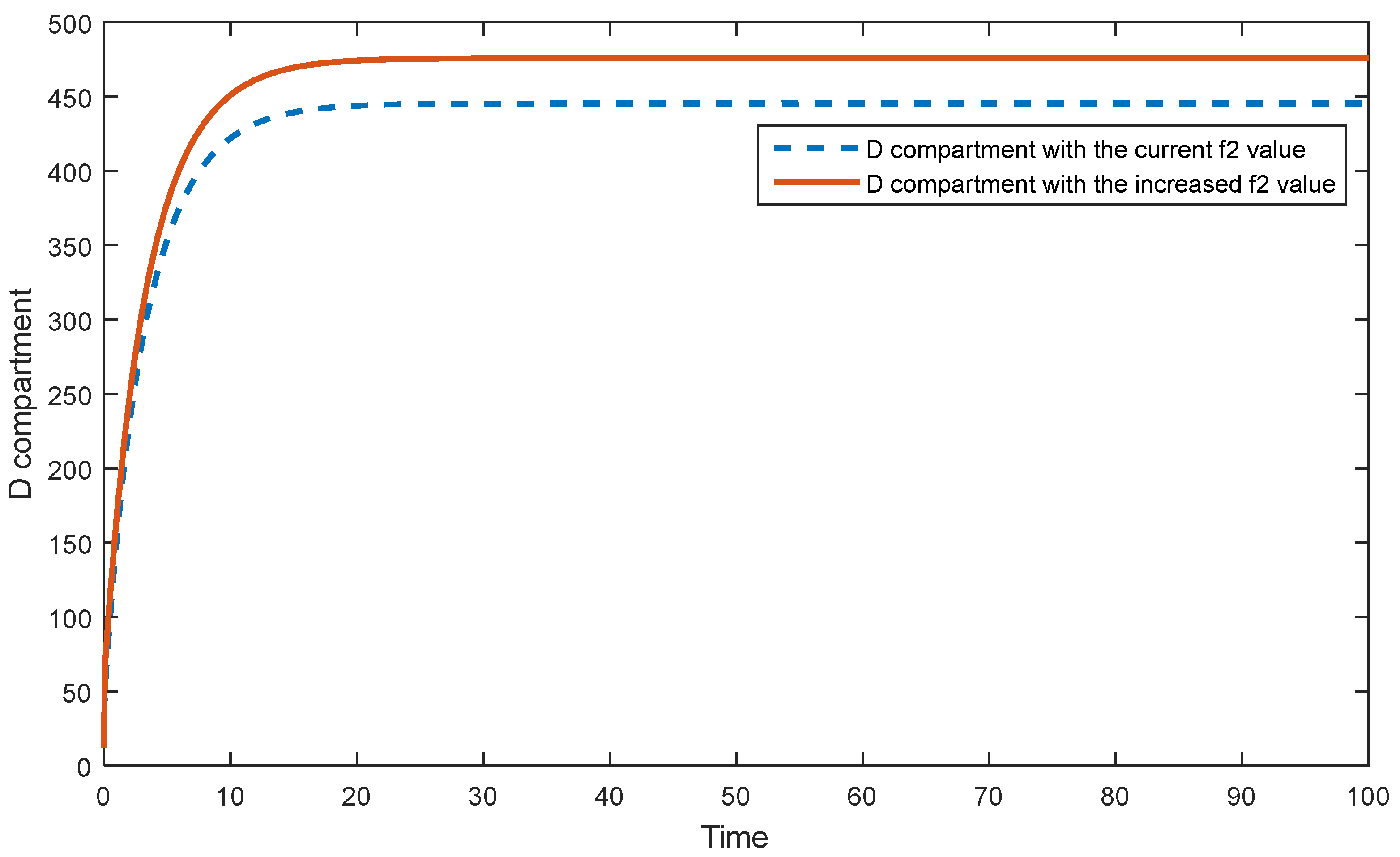
5.1. Sensitivity Analysis of the First Model

In this part, sensitivity analysis is implemented to the parameters of the first model.

Figure 1 and Figure 2 shows the expected pattern of Cancer Patients when the values of

b

and

c

are increased, respectively. In both cases, increase in the parameters will cause an increase in the

C

compartment.

Figure 3 and Figure 4 presents the effect of the parameter

c

when it is increased and decreased, respectively.

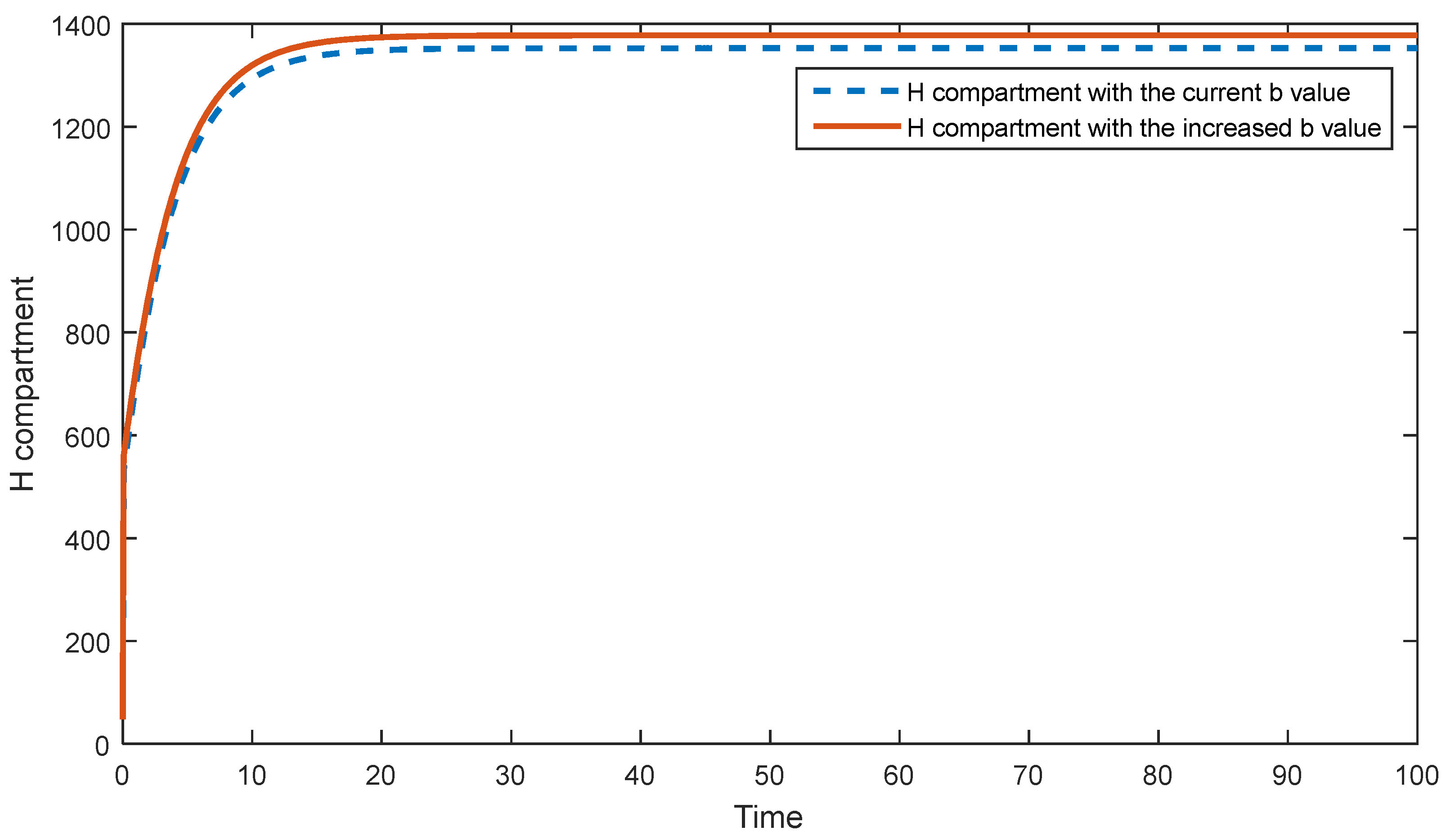
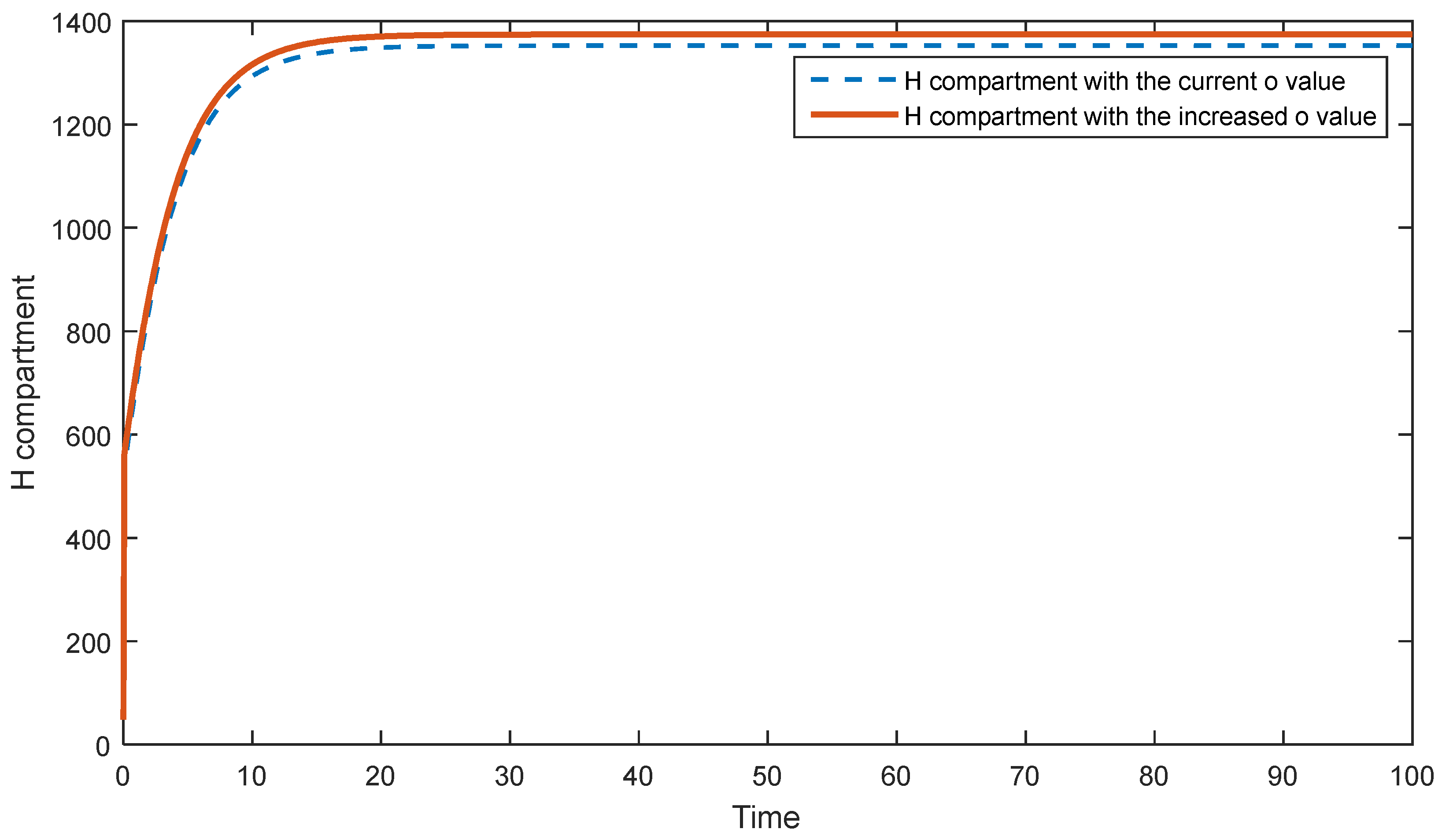
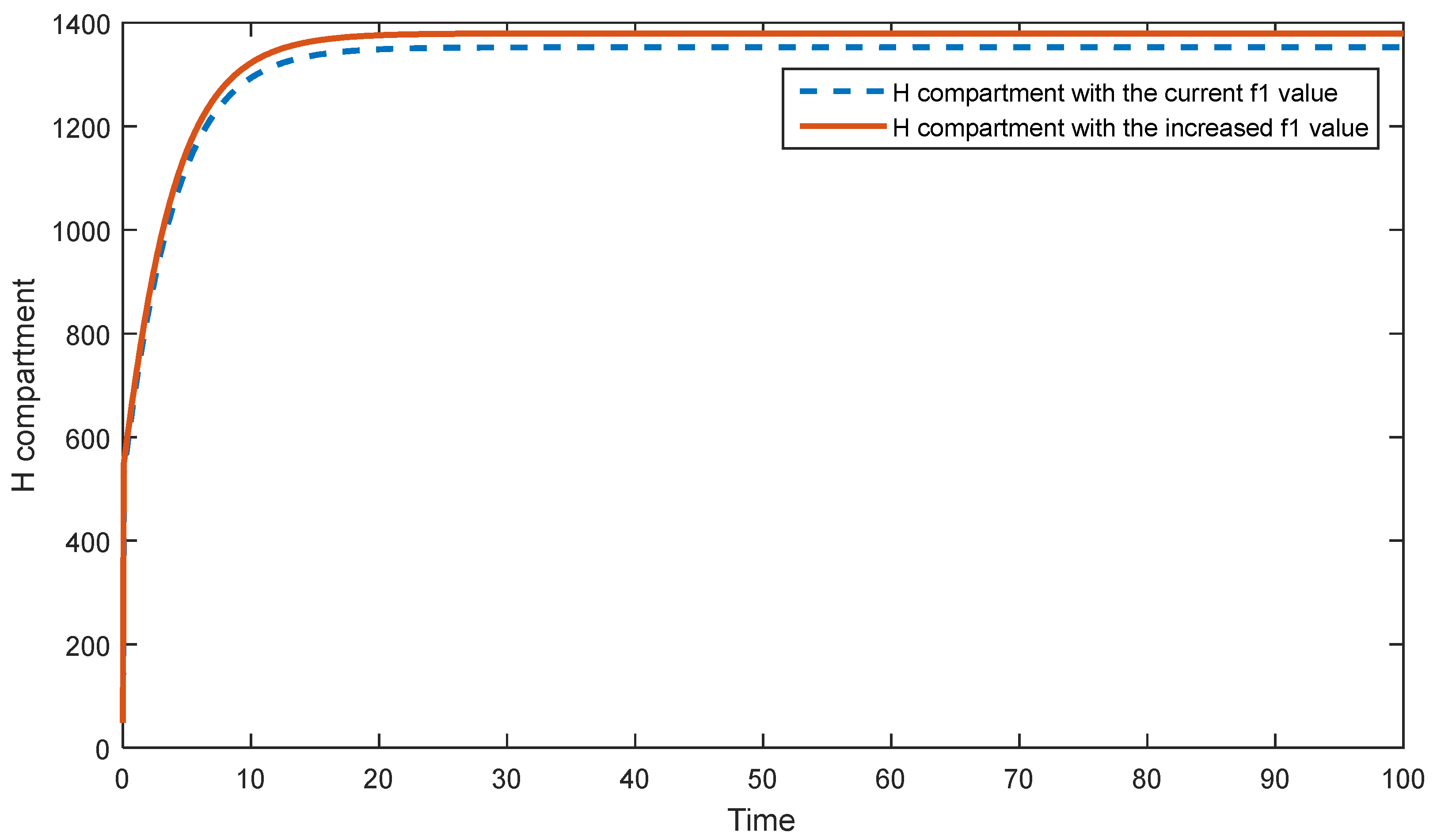
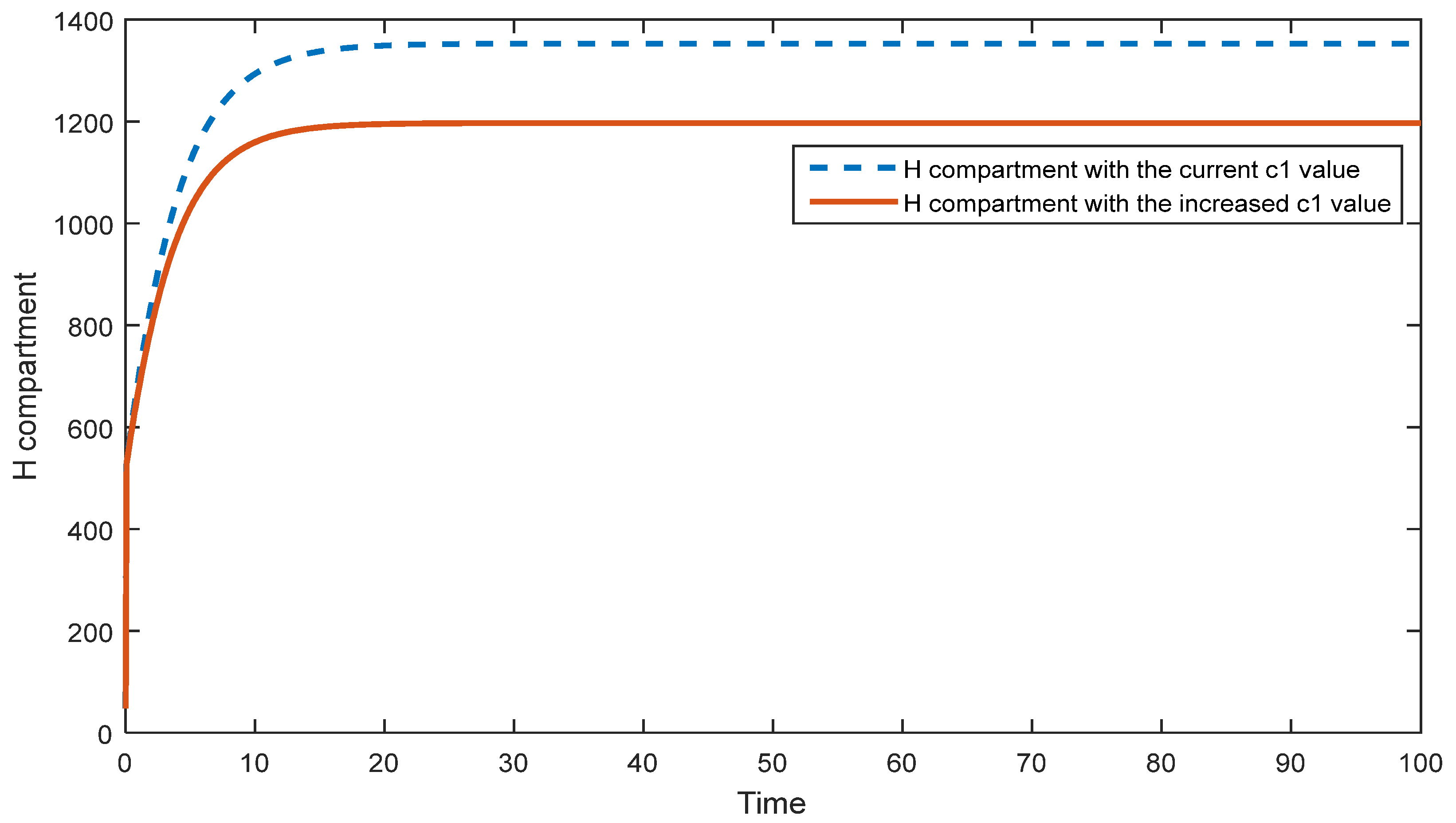
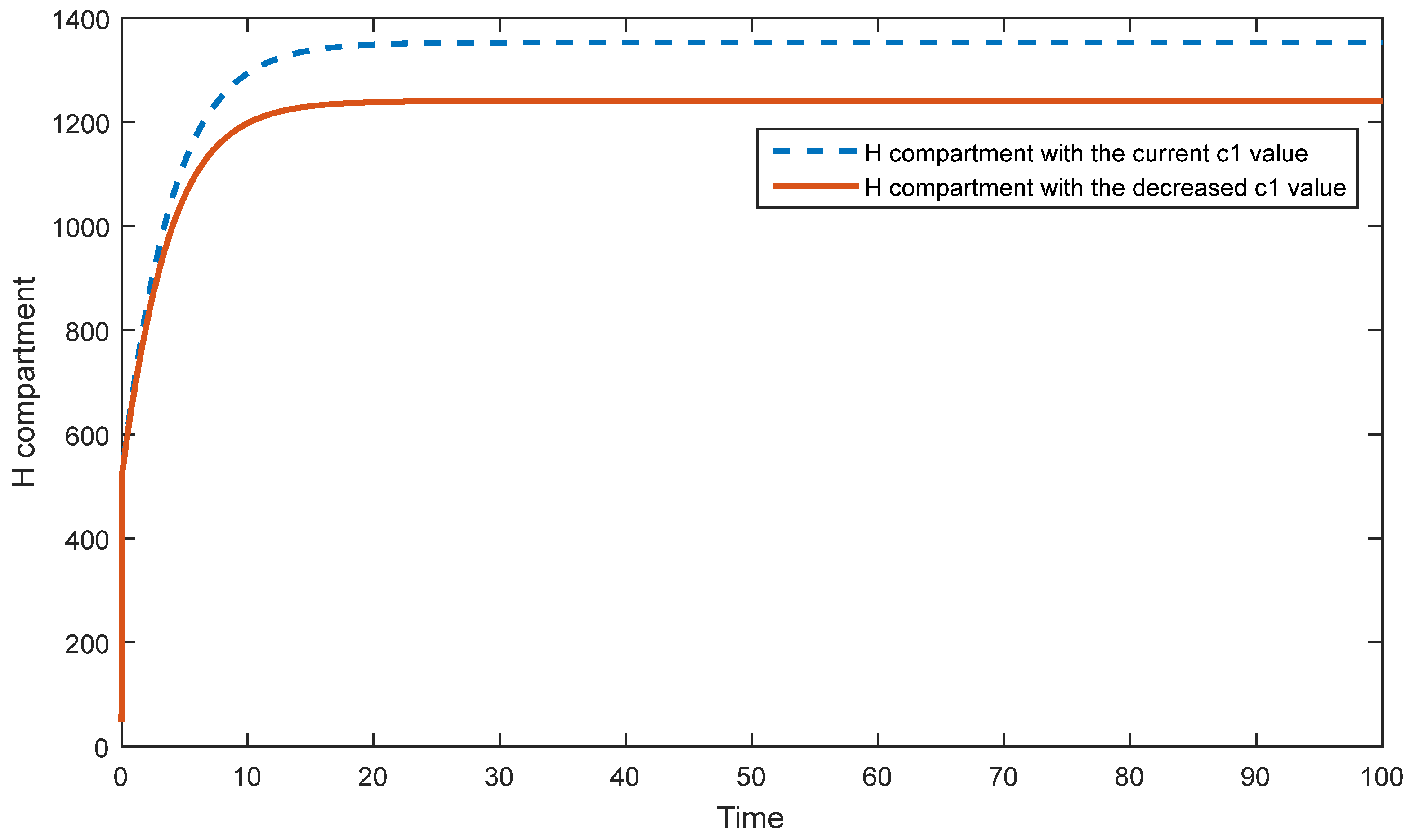
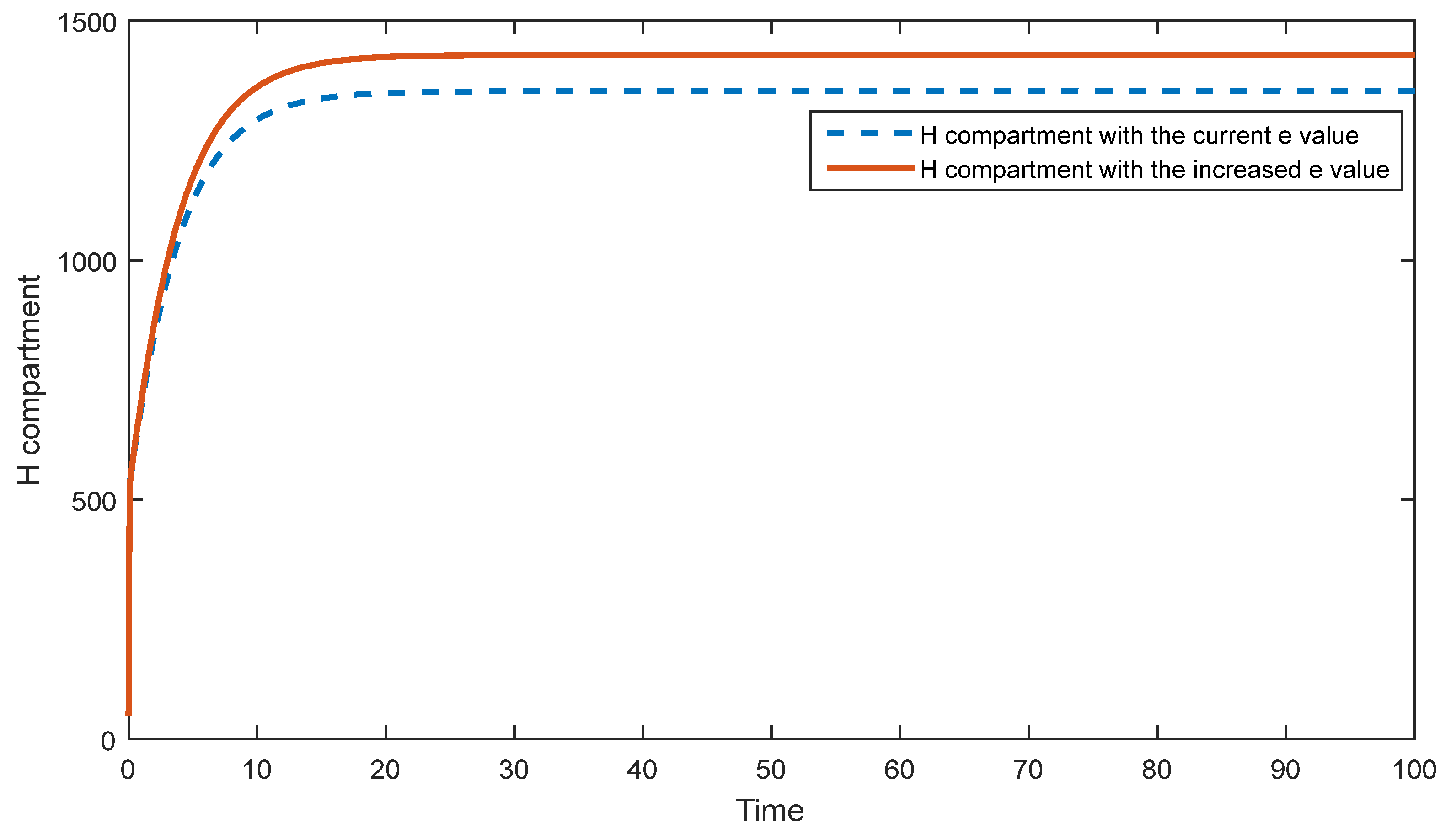
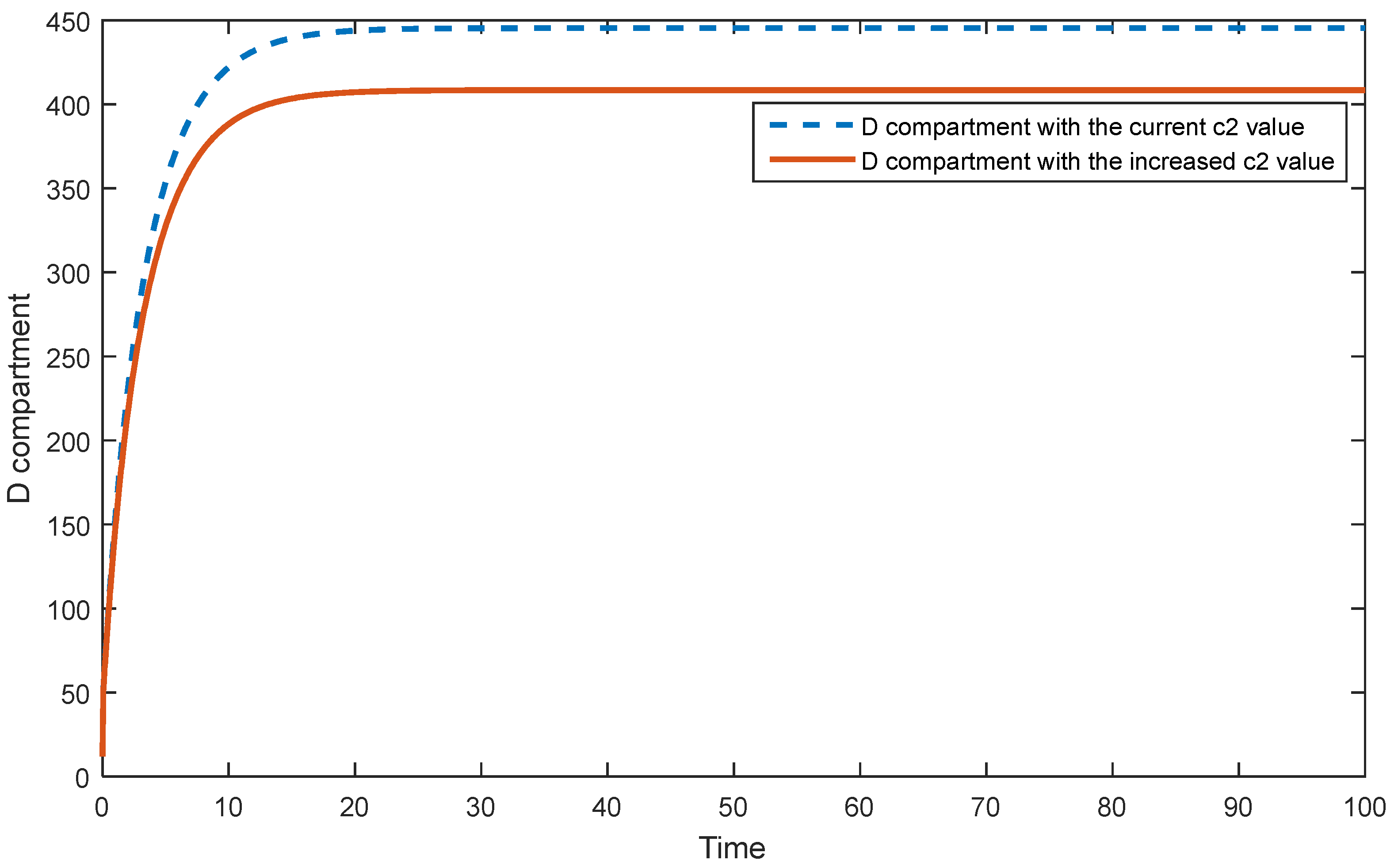
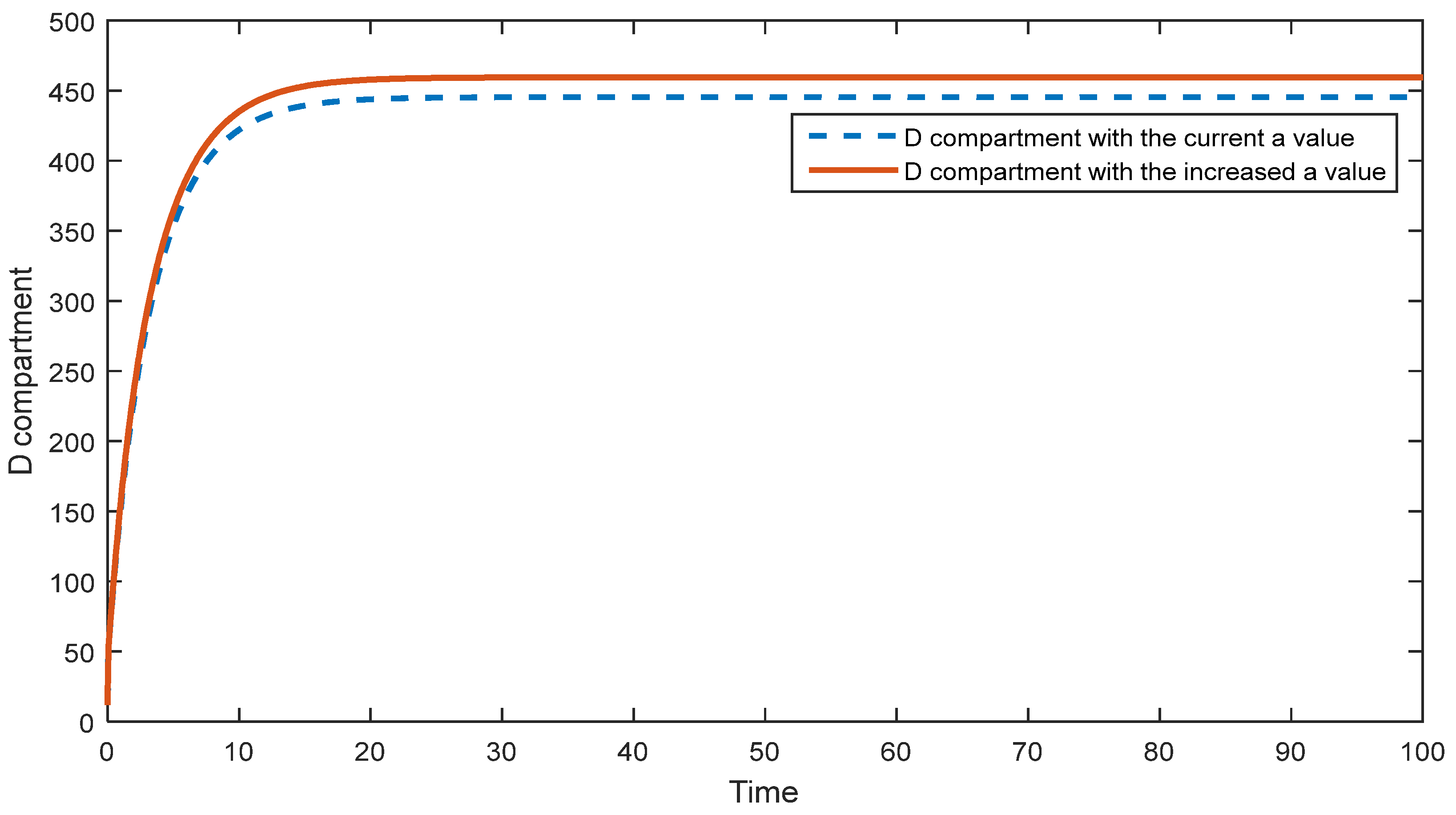
5.2. Sensitivity Analysis of the Second Model

In this part, sensitivity analysis is implemented to the parameters of the second model.

In Figure 5 and Figure 6, effects of the parameters

b

and

o

on the compartment

H

is given, respectively. Increase in both parameters will lead an increase in the compartment

H

as can be seen from the figures.

Figure 7 represents what is expected to happen in the compartment

H

when the percentage of hereditary,

f_{1}

, increases. Figure 8 and Figure 9 shows the compartment capacity in the case of increase or decrease of the parameter

c_{1} .

Figure 10 demonstrates the pattern of heart-diseased individuals in the case of increase in diabetes.

The effect of obesity parameter,

o

, on the compartment

D

is presented in Figure 11 while Figure 12 shows the effect of hereditary parameter,

f_{2}

, on the same compartment.

Figure 13 and Figure 14 are revealed in order to show the significance of Covid-19 parameter,

c_{2}

, on the compartment

D

6. Results and Discussion

The main purpose of this study is to show how Covid-19 will affect the future of the chronic diseases, cancer, heart diseases and diabetes. In this regard, two mathematical models are proposed and proved with required theorems. The first model consists of cancer-diagnosed and susceptible individuals while in the second model heart disease patients, diabetic patients and susceptible individuals are included. The reason of two separate models is the unrelated connection of cancer with heart diseases and diabetes.

In the analysis of the first model, disease-free equilibrium,

E_{0,1}

, and endemic equilibrium,

E_{*, 1}

, points are found with their existence proofs. Moreover, globally asymptotically stability property of both points is proved under some conditions. This results in a comment that there can be a population without cancer disease at the point

E_{0,1}

and endemic situation at the point

E_{*, 1}

In the same manner, analysis of the second model showed that there exist two equilibrium points for this model; disease-free equilibrium point,

E_{0,2}

and endemic equilibrium,

E_{*, 2}

, point. Both points are globally asymptotically stable with necessary conditions which means that both environment is possible for the diseases.

In Section 5, sensitivity analysis is applied to the parameters of both models. This analysis aims to specify the effects of parameters on the compartments C, H and D. Figure 1 and Figure 2 is the result of increase in smoking and obesity, respectively. Increase in both parameters will lead an increase in the cancer compartment. However, even with a slight difference, the effect of smoking is bigger than the effect of obesity in the compartment C. In this model the figure that shows the effect of hereditary transmission,

f_{1}

, is not given since the model didn’t give a meaningful result in this case. The reason of this situation may be arisen from the population studied in this paper. Since the compartment C includes all cancer patients (not a specific cancer type), the effect couldn’t be seen.

Figure 3 is drawn to show the expectation when the effect of the parameter c is increased. As expected, the more people being scared of seeing doctors will lead a huge decrease in the diagnosis of cancer. Figure 4 presents the situation of cancer compartment with decreased c value. In this case, an increase is assumed again. However, this increase is much smaller than the increase in Figure 3. Both of the Figure 3 and Figure 4 is a warning for the world about the Covid-19 pandemic. This problem can be solved by increasing the awareness of people and encouraging them for not postponing their doctor visits.

Figure 5 and Figure 6 displays the effect of smoking and obesity on heart disease patients. According to the figures, increase in both parameters will make a rise in the

H

compartment. Hereditary plays an important role in heart diseases which is proposed in Figure 7. Nevertheless, the most significant parameter for heart diseases is Covid-19,

c_{1}

. It is obvious that

c_{1}

is a very efficient parameter for the future patterns of heart diseases. Both increase and decrease in this parameter make a fall in the compartment

H

, which emphasizes the importance of awareness about doctor visits and Covid-19.

Figure 11 and Figure 12 demonstrates the pattern of diabetes patients when obesity and hereditary are increased, respectively. Although the increase in the parameters causes a rise in the pattern of

D

compartment, the effect of hereditary,

f_{2}

, is more. The effect of Covid-19 is meaningful in

D

compartment as well. In Figure 13, increase in parameter

c_{2}

causes a fall in the compartment

D

because of undiagnosed patients. However, for the compartment

D

, even with a slight fall in the parameter

c_{2}

, diagnosis with diabetes will be more (Figure 14). Figure 10 and Figure 15 are a warning that accentuates the relationship between diabetes and heart diseases.

Figure 14. Sensitivity analysis of the parameter

c_{2}

in the compartment

D

, when it is decreased.

Figure 14. Sensitivity analysis of the parameter

c_{2}

in the compartment

D

, when it is decreased.

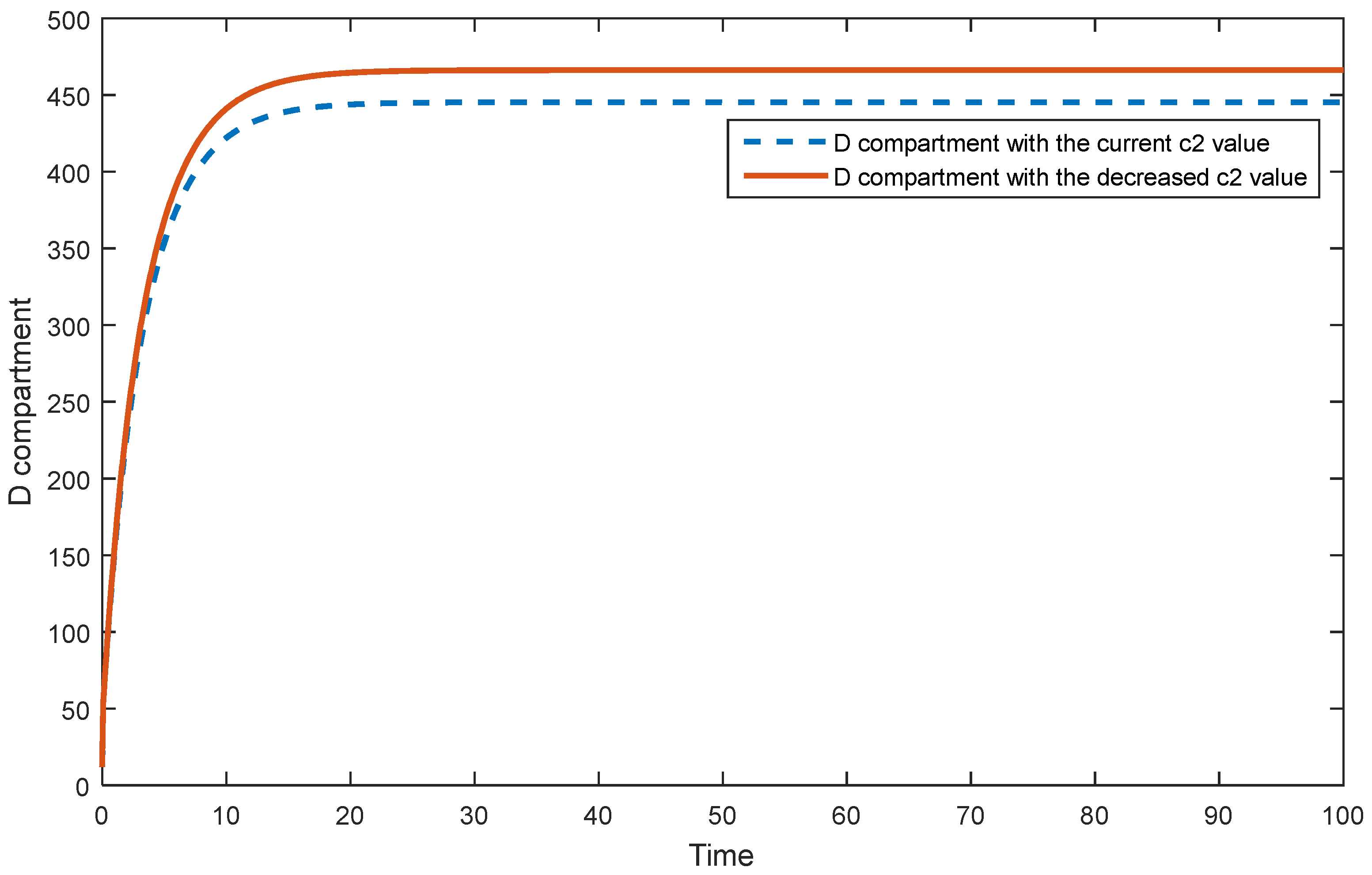
7. Conclusions

As a result of figures of models, it is concluded that obesity is an effective parameter for the studied diseases so that increase in any of them will affect the patients negatively. Smoking affects cancer and heart disease patients badly in the case of utilization. Hereditary is a significant parameter for the patients of diabetes and heart diseases. Hence, people with family history of these diseases should make their doctor visits properly. Besides, there is a relationship that cannot be ignored between diabetes and heart disease patients. As maintained in Figure 10 and Figure 15, people being diagnosed with diabetes should be more careful and conscious about heart diseases.

On the other hand, both of the models indicated that the most dangerous parameter for the diseases is

c

, which is the result of Covid-19 pandemic. In conclusion, the results showed that being aware of Covid-19 and its results may lead a decrease in deaths due to cancer, heart diseases and diabetes. In that way and with the doctor visits, people can enable be diagnosed earlier and get treatment.

Author Contributions

Conceptualization, F.N.E., N.G. and E.H.; methodology, F.N.E., S.Q. and N.G.; software, N.G. and A.S.; validation, F.N.E., E.H. and S.Q.; formal analysis, N.G.; investigation, E.H.; resources, F.N.E. and N.G.; data curation, E.H.; writing—original draft preparation, F.N.E., S.Q. and N.G.; writing—review and editing, F.N.E., N.G. and E.H..; visualization, S.Q. and A.S.; supervision, E.H.; project administration, E.H.; funding acquisition, none. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All data generated or analyzed during this study are included in this article.

Acknowledgments

As authors, we would like to thank the members of Mathematics Research Center of Near East University.

Conflicts of Interest

The authors declare no conflict of interest.

References

Martcheva, M. Introduction. In An Introduction to Mathematical Epidemiology, 1st ed.; Springer: New York, 2015; pp. 1–8. [Google Scholar]
Khoury, M.J.; Beaty, T.H.; Cohen, B.H. Scope and strategies of genetic epidemiology. In Fundamentals of Genetic Epidemiology, 1st ed.; Oxford University Press: New York, 1993; Volume 19. [Google Scholar]
Gan, W.Q.; Buxton, J.A.; Scheuermeyer, F.X.; Palis, H.; Zhao, B.; Desai, R.; Janjua, N.Z.; Slaunwhite, A.K. Risk of cardiovascular diseases in relation to substance use disorders. Drug Alcohol Depend. 2021, 229, 109132. [Google Scholar] [CrossRef] [PubMed]
World Health Organization. Cardiovascular diseases (CVDs). Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 29 August 2023).
United Kingdom National Health Service. Cardiovascular disease. Available online: https://www.nhs.uk/conditions/cardiovascular-disease/ (accessed on 29 August 2023).
National Cancer Institute. Cancer Statistics. Available online: https://www.cancer.gov/about-cancer/understanding/statistics (accessed on 29 August 2023).
Imran Khan Cancer Appeal. What is Cancer? Available online: https://www.ikca.org.uk/cancer-information/what-is-cancer/ (accessed on 29 August 2023).
American Cancer Society. Soft Tissue Sarcoma. Available online: https://www.cancer.org/cancer/types/soft-tissue-sarcoma.html (accessed on 29 August 2023).
WHO, International Agency for Research on Cancer. Cancer Today. Available online: https://gco.iarc.fr/today/home (accessed on 29 August 2023).
World Health Organization. Cancer. Available online: https://www.who.int/news-room/fact-sheets/detail/cancer (accessed on 29 August 2023).
American Cancer Society. Available online: https://www.cancer.org/content/dam/cancer-org/research/cancer-facts-and-statistics/annual-cancer-facts-and-figures/2022/2022-cancer-facts-and-figures.pdf (accessed on 29 August 2023).
Kalra, S.; Zargar, A.H.; Jain, S.M.; Sethi, B.; Chowdhury, S.; Singh, A. K.; Thomas, N.; Unnikrishnan, A.G.; Thakkar, P.B.; Malve, H. Diabetes insipidus: The other diabetes. Indian J. Endocrinol. Metab. 2016, 20, 9–21. [Google Scholar] [PubMed]
Chaudhary, N.; Tyagi, N. Diabetes mellitus: An Overview. Int. J. Res. Dev. Pharm. Life Sci. 2018, 7, 3030–3033. [Google Scholar] [CrossRef]
World Health Organization. Diabetes. Available online: https://www.who.int/news-room/fact-sheets/detail/diabetes (accessed on 29 August 2023).
Keeling, M.J.; Danon, L. Mathematical modelling of infectious diseases. Br. Med. Bull. 2009, 92, 33–42. [Google Scholar] [CrossRef] [PubMed]
Alridha, A.H.; Al-Jilawi, A.S.; Alsharify, F.H.S. Review of Mathematical Modelling Techniques with Applications in Biosciences. IJCSM 2022, 3, 135–144. [Google Scholar] [CrossRef]
White, P.J.; Enright, M.C. Mathematical models in infectious disease epidemiology. Infectious Diseases 2010, 70–75. [Google Scholar] [CrossRef]
Columbia University Irving Medical Center. Responding to the COVID-19 Pandemic. Available online: https://www.publichealth.columbia.edu/news/responding-covid-19-pandemic (accessed on 29 August 2023).
Our World in Data. Available online: https://ourworldindata.org/coronavirus (accessed on 29 August 2023).
Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; Liang, J.; Liu, X.; Li, S.; Li, Y.; Ye, F.; Guan, W.; Yang, Y.; Li, F.; Luo, S.; Xie, Y.; Liu, B.; Wang, Z.; Zhang, S.; Wang, Y.; Zhong, N.; He, J. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef] [PubMed]
Mwalili, S.; Kimathi, M.; Ojiambo, V.; Gathungu, D.; Mbogo, R. SEIR model for COVID-19 dynamics incorporating the environment and social distancing. BMC Res. Notes 2020, 13, 352. [Google Scholar] [CrossRef] [PubMed]
Jentsch, P.C.; Anand, M.; Bauch, C.T. Prioritising COVID-19 vaccination in changing social and epidemiological landscapes: a mathematical modelling study. Lancet Infect. Dis. 2021, 21, 1097–1106. [Google Scholar] [CrossRef] [PubMed]
Matrajt, L.; Eaton, J.; Leung, T.; Brown, E.R. Vaccine optimization for COVID-19: who to vaccinate first? Sci. Adv. 2021, 7, eabf1374. [Google Scholar] [CrossRef] [PubMed]
Kaymakamzade, B.; Hincal, E.; Gokbulut, N.; Sanlidag, T. Analyzing the Relationship Between Covid-19 and Proportions of Vaccine & Mobility. In Decision Analysis Applied to the Field of Environmental Health. Professional Practice in Earth Sciences; Uzun Ozsahin, D., Uzun, B., Sanlidag, T., LaMoreaux, J., Eds.; Springer: Cham, 2022; pp. 65–76. [Google Scholar]
Naughton, F.; Ward, E.; Khondoker, M.; Belderson, P.; Minihane, A.M.; Dainty, J.; Hanson, S.; Holland, R.; Brown, T.; Notley, C. Health behaviour change during the UK COVID-19 lockdown: Findings from the first wave of the C-19 health behaviour and well-being daily tracker study. Br. J. Health Psychol. 2021, 26, 624–643. [Google Scholar] [CrossRef] [PubMed]
Albahri, O.S.; Al-Obaidi, J.R.; Zaidan, A.A.; Albahri, A.S.; Zaidan, B.B.; Salih, M.M.; Qays, A.; Dawood, K.A.; Mohammed, R.T.; Abdulkareem, K.H.; Aleesa, A.M.; Alamoodi, A.H.; Chyad, M.A.; Zulkifli, C.Z. Helping doctors hasten COVID-19 treatment: Towards a rescue framework for the transfusion of best convalescent plasma to the most critical patients based on biological requirements via ml and novel MCDM methods. Comput. Methods Programs Biomed. 2020, 196, 105617. [Google Scholar] [CrossRef] [PubMed]
Albahri, O.S; Zaidan, A.A.; Albahri, A.S.; Zaidan, B.B.; Abdulkareem, K.H.; Al-qaysi, Z.T.; Alamoodi, A.H.; Aleesa, A.M.; Chyad, M.A.; Alesa, R.M.; Kem, L.C.; Lakulu, M.M.; Ibrahim, A.B.; Rashid, N.A. Systematic review of artificial intelligence techniques in the detection and classification of COVID-19 medical images in terms of evaluation and benchmarking: Taxonomy analysis, challenges, future solutions and methodological aspects. J. Infect. Public Health 2020, 13, 1381–1396. [Google Scholar] [CrossRef] [PubMed]
Panetta, J.C.; Chaplain, M.A.J.; Adam, J.A. The mathematical modelling of cancer: a review: Mathematical models in medical and health science. In Mathematical models in medical and health science; Webb, G.F. (eds); Vanderbilt University Press, 1998; pp. 281–309. [Google Scholar]
World Health Organization. Cardiovascular diseases (CVDs). Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 29 August 2023).
Cancer Research, UK. Worldwide cancer statistics. Available online: https://www.cancerresearchuk.org/health-professional/cancer-statistics/worldwide-cancer#heading-Zero (accessed on 29 August 2023).
Taylor, C.J.; Ordonez-Mena, J.M.; Roalfe, A.K.; Lay-Flurrie, S.; Jones, N.R.; Marshall, T.; Hobbs, F.D.R. Trends in survival after a diagnosis of heart failure in the United Kingdom 2000-2017: population based cohort study. BMJ 2019, 364, l223. [Google Scholar] [CrossRef] [PubMed]
Cardiovascular disease. Available online: https://fingertips.phe.org.uk/profile-group/cardiovascular-disease-diabetes-kidney-disease/profile/cardiovascular/data#page/4/gid/1938133107/pat/159/par/K02000001/ati/15/are/E92000001/iid/241/age/187/sex/4/cat/-1/ctp/-1/yrr/1/cid/4/tbm/1 (accessed on 29 August 2023).
Salehidoost, R.; Mansouri, A.; Amini, M.; Yamini, S.A.; Aminorroaya,A. Diabetes and all-cause mortality, a 18-year follow-up study. Sci. Rep. 2020, 10, 3183. [Google Scholar] [CrossRef] [PubMed]
Endemic (epidemiology). Available online: https://www.wikidoc.org/index.php/Endemic_(epidemiology) (accessed on 29 August 2023).

Figure 1. Sensitivity analysis of the parameter

b

in the compartment

C

Figure 1. Sensitivity analysis of the parameter

b

in the compartment

C

Figure 2. Sensitivity analysis of the parameter

o

in the compartment

C

Figure 2. Sensitivity analysis of the parameter

o

in the compartment

C

Figure 3. Sensitivity analysis of the parameter

c

in the compartment

C

, when it is increased.

Figure 3. Sensitivity analysis of the parameter

c

in the compartment

C

, when it is increased.

Figure 4. Sensitivity analysis of the parameter

c

in the compartment

C

, when it is decreased.

Figure 4. Sensitivity analysis of the parameter

c

in the compartment

C

, when it is decreased.

Figure 5. Sensitivity analysis of the parameter

b

in the compartment

H

Figure 5. Sensitivity analysis of the parameter

b

in the compartment

H

Figure 6. Sensitivity analysis of the parameter

o

in the compartment

H

Figure 6. Sensitivity analysis of the parameter

o

in the compartment

H

Figure 7. Sensitivity analysis of the parameter

f_{1}

in the compartment

H

Figure 7. Sensitivity analysis of the parameter

f_{1}

in the compartment

H

Figure 8. Sensitivity analysis of the parameter

c_{1}

in the compartment

H

, when it is increased.

Figure 8. Sensitivity analysis of the parameter

c_{1}

in the compartment

H

, when it is increased.

Figure 9. Sensitivity analysis of the parameter

c_{1}

in the compartment

H

, when it is decreased.

Figure 9. Sensitivity analysis of the parameter

c_{1}

in the compartment

H

, when it is decreased.

Figure 10. Sensitivity analysis of the parameter

e

in the compartment

H

Figure 10. Sensitivity analysis of the parameter

e

in the compartment

H

Figure 11. Sensitivity analysis of the parameter

o

in the compartment

D

Figure 11. Sensitivity analysis of the parameter

o

in the compartment

D

Figure 12. Sensitivity analysis of the parameter

f_{2}

in the compartment

D

Figure 12. Sensitivity analysis of the parameter

f_{2}

in the compartment

D

Figure 13. Sensitivity analysis of the parameter

c_{2}

in the compartment

D

, when it is increased.

Figure 13. Sensitivity analysis of the parameter

c_{2}

in the compartment

D

, when it is increased.

Figure 15. Sensitivity analysis of the parameter

a

in the compartment

D

, when it is decreased.

Figure 15. Sensitivity analysis of the parameter

a

in the compartment

D

, when it is decreased.

Table 1. Descriptions of Variables.

Variables	Descriptions
$S$	Susceptible Individuals
$C$	Cancer Patients

Table 2. Descriptions of Parameters.

Parameters	Descriptions
$π$	Recruitment rate
$f_{1}$	Transmission rate of hereditary
$o$	Rate of obese individuals being cancer
$b$	Rate of smokers being cancer
$γ$	Recovery rate
$c$	Negative effect of Covid-19
$η$	Disease-caused death rate
$μ$	Natural death rate

Table 3. Descriptions of Variables.

Variables	Descriptions
$S$	Susceptible Individuals
$H$	Heart disease patients
$D$	Diabetes patients

Table 4. Descriptions of Parameters.

Parameters	Descriptions
$Λ$	Recruitment rate
$b$	Rate of smokers being a heart patient
$k_{1} o$	Rate of obese individuals being a heart patient
$(1 - k_{1}) o$	Rate of obese individuals being diabetes
$f_{i}, i = 1, 2$	Transmission rate of hereditary
$c_{i}, i = 1, 2$	Negative effect of Covid-19
$γ_{i}, i = 1, 2$	Survival rate of diseases
$μ$	Natural death rate
$η_{1}$	Heart-disease caused death rates
$η_{2}$	Diabetes caused death rates
$a$	Transmission rate from $H$ to $D$
$e$	Transmission rate from $D$ to $H$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Aggravation of Health Problems Subsequent to COVID-19 Lockdown

Abstract

1. Introduction

2. Materials and Methods

3. Construction and Analysis of the First Model

3.1. Mathematical Model Formulation

3.2. Equilibrium Points

4. Construction and Analysis of the Second Model

4.1. Mathematical Model Formulation

4.2. Equilibrium Points

5. Sensitivity Analysis and Numerical Simulations

5.1. Sensitivity Analysis of the First Model

5.2. Sensitivity Analysis of the Second Model

6. Results and Discussion

7. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe