Preprint
Review
Irreversible Thermodynamics of Seawater Evaporation
Altmetrics
Downloads
112
Views
107
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.pdf (254.93KB )
This version is not peer-reviewed
Submitted:
25 September 2023
Posted:
26 September 2023
You are already at the latest version
Alerts
Abstract
Under typical marine conditions of about 80 % relative humidity, evaporation of water from the ocean is an irreversible process accompanied by entropy production. In this article, equations are derived for the latent heat of irreversible evaporation and the related non-equilibrium entropy balance at the sea surface. To achieve this, linear irreversible thermodynamics is considered in a conceptual ocean evaporation model. The equilibrium thermodynamic standard TEOS-10, the International Thermodynamic Equation of Seawater – 2010, is applied to irreversible evaporation under the assumption of local thermodynamic equilibrium. The relevance of local-equilibrium conditions for irreversible thermodynamics is briefly explained. New equations are derived for the mass flux of evaporation and for the associated non-equilibrium enthalpies and entropies. The estimated entropy production rate of ocean evaporation amounts to 0.004 W m^(-2) K^(-1) as compared to the average terrestrial global entropy production of about 1 W m^(-2) K^(-1).
Keywords:
Subject: Physical Sciences - Thermodynamics
1. Introduction
The marine troposphere acts as a giant natural desalination plant. The evaporation of water from aqueous solutions is a fundamental process relevant to various disciplines such as meteorology, hydrology, climatology, physiology or technology. However, its theoretical description, observation, measurement and numerical modelling are still only insufficiently well understood and advanced. Edmond Halley (1687) was the first who estimated oceanic evaporation rates, finding that “the whole Mediterranean must lose in Vapour, in a Summers-day, at least 5280 Millions of Tons.”1 John Dalton (1798) concluded from his experiments that the evaporation flux is driven by the liquid’s vapour pressure, by saying that “the quantity of any liquid evaporated in the open air is directly as the force of steam from such liquid”2.
Globally, the dominating energy source for the dynamics and the warming of the atmosphere is not the terrestrial thermal radiation trapped by greenhouse gases, rather, it is the latent heat of water vapour evaporated from the oceans (Feistel and Hellmuth 2021).“The by far largest part of heat conveyed to the air is in the form of latent heat during subsequent condensation along with cloud formation. … The heat budget over the sea is mainly controlled by the latent heat released to the air”3. „For the atmosphere, the globally averaged net radiative cooling approximately balances the globally averaged latent-heat release. The latent heat is supplied by the evaporation of water from the surface”4. “This way, the heat released to the air in latent form is larger by a multiple than the [sensible] heat transferred immediately to the air”5. The devastating power of evaporation from the exceptionally warm Mediterranean has recently become evident again by an unprecedented flooding of Slovenia and atypical gale-force winds in summer over the Baltic Sea, caused by the cyclone Petar (German name: Zacharias) in August 2023, and also mid September by torrential rain poured over Greece and Libya by “Daniel”, the deadliest Mediterranean tropical-like cyclone in recorded history.
Climate models estimate the ocean-atmosphere heat flux to within a relatively poor uncertainty of at least (Josey et al. 2013; Cronin et al. 2019), a range being 1000 times as large as the mean atmospheric warming rate of just (Feistel 2015; Gorfer 2022; von Schuckmann et al. 2023). This reason suggests a conclusion that, strictly speaking, current climate models are unable to estimate with requisite significance the rate of global warming of the troposphere. Within the given uncertainty of the model prediction, the atmosphere may either warm up much faster than observed, or may even cool down. Moreover, although “the climate of the Earth is ultimately determined by the temperatures of the oceans”6, “most CMIP6 [Coupled Model Intercomparison Project Phase 6] models fail to provide as much heat into the ocean as observed”7. Among other reasons, to this mismatch a biased parameterisation of evaporation fluxes may also contribute (Feistel and Hellmuth 2023). The observationally and theoretically complex and challenging process of oceanic evaporation warrants enhanced efforts for improving its physical description.
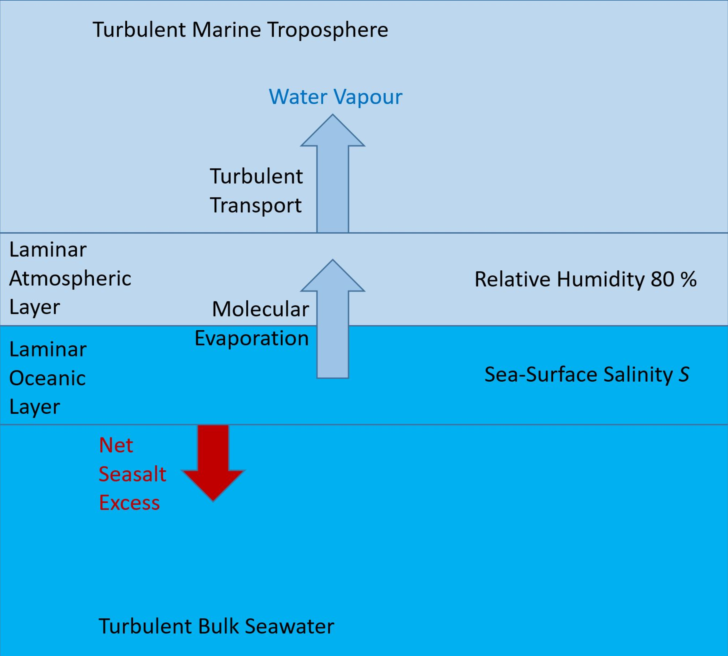
In Figure 1, a typical measured microstructure of a temperature profile immediately above the sea surface is shown. A laminar layer in the submillimetre range is distinguished by its vertical gradient while the air column above appears as isothermal with turbulent fluctuations. The thickness of the laminar layer is decreasing with the wind speed (Hupfer et al. 1975). Near-surface humidity profiles are described by Avery (1972).
In this paper, the irreversible thermodynamics of seawater evaporation is described theoretically in a simplified conceptual model as depicted in Figure 2. Similar models had already been employed previously by Wüst (1920), Sverdrup (1936), Montgomery (1940) or Albrecht (1940). For the evaporation mass flux across the laminar layer, Sverdrup (1936: eq. 10 therein) used the equation
Here, is an empirical coefficient expressing the characteristic diffusion time, is the layer thickness, is the saturation vapour pressure of water/seawater and is the partial pressure of water vapour of humid air above the sea surface. Montgomery (1940: eq. 24 therein) considered specific humidity q in place of vapour pressure e in eq. (1), an approximation still being used by various modern climate models (Gill, 1982; Stewart 2008; Rapp 2014). Both forms are known as Dalton equation today.
Evaporation occurs successively in two distinct physical steps. First, thermally fast water molecules escape from the condensed phase (water, seawater, ice, moist soil), and second, they are carried away in the gas phase by molecular or turbulent diffusion. The transfer of water across the phase boundary is driven by the difference between the chemical potentials of water in the two phases. The systematic loss of the fastest molecules of the condensed phase is lowering the skin temperature (Zülicke and Hagen 1998; Zülicke 2005) and the implied loss of heat (i.e., enthalpy) takes the form of latent heat added to the humid air.
Chemical potentials were introduced by J. Willard Gibbs (1878) as chemical equilibrium conditions of composite systems. They cannot be measured directly, and for seawater and humid air they have become available numerically for the first time by TEOS-10, the Thermodynamic Equation of Seawater 2010 (IOC et al. 2010; Feistel et al. 2010, 2016; Feistel 2012, 2018). In irreversible thermodynamics (Glansdorff and Prigogine 1971), the driving force for a mass flux is the gradient of the chemical potential divided by the temperature. This applies to seawater evaporation as well (Kraus and Businger 1994). If the evaporation flux is rigorously expressed this way, the Dalton equation (1) can be derived as a certain approximation thereof (Feistel and Hellmuth 2023).
TEOS-10 had been recommended as an international standard by IOC-UNESCO in 2010 at Paris and by IUGG in 2011 at Melbourne. It is defined and explained in the TEOS-10 Manual (IOC et al. 2010), which, together with several background papers, is freely available from the internet at http://www.TEOS-10.org. Empirical equations with their numerical coefficients are defined in a series of IAPWS documents (IAPWS AN6-19 2016). Functions for numerous thermodynamic properties are implemented as open source code in the SIA (“Sea-Ice-Air”) and the GSW (“Gibbs Seawater”) libraries (Wright et al. 2010), also available from the TEOS-10 web page. In an appendix of Feistel et al. (2022), additional explicit TEOS-10 code is provided for the calculation of relative fugacity, a real-gas alternative to conventional relative humidity, as defined mathematically by Feistel and Lovell-Smith (2017). Simplified TEOS-10 equations for application at the sea surface are reported in an appendix of Feistel and Hellmuth (2023).
This paper is structured as follows. Section 2 provides a short introduction to non-equilibrium thermodynamics and the role which local equilibrium plays in it. Section 3 derives the thermodynamic equation for the evaporation flux, expressed in terms of relative fugacity of water vapour in humid air, showing that its empirical rate constant deviates systematically from Dalton equations used in numerical climate models. Section 4 proves that the formula for the latent heat of reversible evaporation remains valid also for the irreversible non-equilibrium situation observed naturally at the oceans. By contrast, the entropy of irreversible evaporation, Section 5, includes an additional entropy production term proportional to the distance from equilibrium of the ocean-atmosphere interface which may as well be expressed in terms of the relative fugacity. A Summary concludes this paper, and Appendix A provides a list of formula symbols used.
In a steady-state regime, the water vapour entering by evaporation the laminar layer, see Figure 2, is conveyed away at the same rate in the layers above (Sverdrup 1936). While this paper is focussed on the immediate air-sea interface, a wealth of related literature is available regarding the parameterisation of the turbulent vertical water-vapour flux in the near-surface layer of the troposphere in terms of wind speed and water surface roughness. A brief introduction and review, in particular concerning the Monin Obukhov Similarity Theory (MOST) and a compilation of vapor-pressure and specific-humidity based Dalton coefficients from the literature, is separately added to this paper in a supplement.
2. Irreversible Thermodynamics and Local Equilibrium
Numerous textbooks on irreversible thermodynamics are available (Landau and Lifschitz 1966a; Glansdorff and Prigogine 1971; Falkenhagen et al. 1971; De Groot and Mazur 1984; Feistel and Ebeling 2011), however, most of those do not cover irreversible processes in multiphase composite systems or at phase boundaries, such as required for clouds or for the ocean-atmosphere interface. Here is a brief introduction.
The heat content of a given sample with a temperature T is described thermodynamically by two different quantities, entropy N and enthalpy H. Note that here N is used for entropy rather than S to avoid confusion with traditional ocean salinity variable. The relations of N and H to heat are evident from their relations to the isobaric heat capacity, , either by
or by
both being defined at constant pressure, . The difference between the two measures of heat is the Gibbs energy (also known as free enthalpy or Gibbs free energy)
These extensive quantities may vary over time t due to internal processes (subscript i) or exchange across the boundary (subscript e):
According to the 2nd Law of Thermodynamics, reversible processes are defined by zero entropy production, , and, by contrast, irreversible processes by , while processes with are physically impossible. After an irreversible change, the system may never return to its former state without exchange with its surrounding because the entropy once produced cannot be destroyed again but may only be exported to the outside world. Note that entropy production does not necessarily imply a warming but may as well be associated with structural relaxation (Kirkaldy 1965; Feistel 2019), such as weathering or mixing.
Entropy production can always be expressed as a bilinear sum
Here, are the Onsager forces describing the deviation from equilibrium, such as temperature or concentration gradients. are the associated fluxes driven by those forces. At equilibrium, both and vanish. Reversible processes may occur at but . As long as the forces are sufficiently weak, fluxes may be represented as linear functions of the forces,
expressing the rationale of linear irreversible thermodynamics. If the Onsager coefficients do not depend on the forces, the Prigogine theorem holds, saying that steady states establish minimum entropy production (Prigogine and Wiaume 1946). This theorem quantifies the principle of Le Chatelier and Braun that fluxes always tend to reduce the forces. Under these conditions, instabilities, spontaneous self-organisation or chaos are excluded.
Expressing the 1st Law of Thermodynamics, reversible as well as irreversible processes at constant T and p, such as evaporation or condensation, are characterised by conservation of enthalpy, . Under these conditions, the 2nd Law implies for reversible and for irreversible processes. According to Gibbs (1878), may be expressed as the sum
of the mass-specific chemical potentials and the masses of the sample’s constituents. For a pure substance, its chemical potential equals its specific Gibbs energy, .
In meteorology and oceanography, additional practical measures of the heat content are potential temperature and conservative temperature , as defined, respectively, in terms of entropy, , and enthalpy, . Potential temperature of a parcel with in-situ temperature T at pressure p is implicitly given by the actual temperature of that parcel after lifting or lowering it isentropically in the gravity field to the surface pressure :
This definition works for atmosphere and ocean as well. This way, is some equivalent measure of entropy, mainly designed for reversible excursion processes. Equilibrium entropy may be determined experimentally up to an arbitrary constant which may only be concluded from statistical models (Planck 1906; Feistel and Wagner 2005, 2006; Feistel 2019) or by formal specification of an arbitrary reference state (Feistel et al. 2008). While the definition (11) is independent of the choice of this arbitrary constant, other common definitions are ambiguous in this respect, such as that of Gill (1982: eq. 3.7.7). Potential temperature is less suited as a conservative tracer if the parcel undergoes irreversible internal mixing by which additional entropy is produced. In such a case the potential temperature is formally rising even though no extra heat has entered the parcel. To reduce this effect, potential enthalpy H* has been defined (McDougall 2003; IOC et al. 2010; McDougall et al. 2023) by
Conservative temperature is specific potential enthalpy conveniently scaled to a temperature unit, . In oceanography, this conversion constant is specified as the isobaric heat capacity of seawater at the ocean standard state. Being defined so far for oceanography only, the use of this measure in the atmosphere would be straightforward.
Geophysical fluids such as troposphere or ocean are typically in non-equilibrium states but may successfully be described thermodynamically under the assumption of local equilibrium. This means that sufficiently small volumes (termed “cells” here) exist in which the particle velocities obey a statistical Maxwell distribution so that a local temperature may reasonably be assigned to such a cell. A well-defined temperature is an indispensable precondition for proper definitions of entropy, Gibbs energy, and chemical potentials. As a consequence of local equilibrium, entropy production does not occur within a cell but only due to fluxes between adjacent cells whose spatial property differences then constitute the Onsager forces. Usual equilibrium thermodynamics applies to local-equilibrium cells, described by their specific entropy, , specific enthalpy, , specific volume, , mass fractions, , and specific internal energy, .
In statistical equilibrium thermodynamics, the so-called micro-canonical ensemble provides a fundamental thermodynamic potential in the form entropy, , as a function of internal energy, U, volume, V, and the masses of chemical species, m, see eq. (19) below. All arguments of this potential are extensive quantities subject to conservation laws. Specific entropy expressed as a function of specific energy, u, specific volume, v. and the mass fractions of the constituents,, ,
obeys Gibbs’ fundamental equilibrium relation in the form (Fofonoff 1962; Glansdorff and Prigogine 1971: eq. 2.15 therein)
Here, because of the local equilibrium, the cell’s entropy change is caused exclusively by exchange processes through the cell’s border, , and does not include any internal entropy production contributions, . Hence, the sign of the derivative in eq. (14) is not restricted in any way by the 2nd Law.
If, for example, two cells of the same mass, each at local equilibrium but away from mutual equilibrium, are included in an isolated parcel (without any exchange with its surrounding), , see Figure 3, the change of its total entropy is confined to the entropy production rate inside the parcel, . Adding up the entropies, eq. (14), of the two cells, while accounting for the conservation laws of energy, , of volume, , and of matter of each constituent, , the parcel’s total entropy will increase at the rate
Here, differences of intensive quantities between adjacent cells are the thermodynamic forces, , and , respectively, which drive, in direction to relaxation to mutual equilibrium, the particular exchange fluxes of extensive quantities per unit mass, internal energy, , occupied volume, and matter, , across the boundary separating the cells. Similarly, in the general case of an inhomogeneous non-equilibrium parcel, corresponding spatial gradients between its neighbouring cells with respect to the related partial differentials of entropy (14) constitute the appropriate three-dimensional Onsager-force vectors (Glansdorff and Prigogine 1971),
Fluxes driven by these forces give rise to irreversible entropy production among the spatial arrangement of cells. Note that because of the identity , one of eqs. (18) is not independent of the remaining ones and may be omitted.
At this point, for clarity and honesty, it may be important to mention that for the description of entropy production in terms of irreversible forces and fluxes, the existence of local equilibria and their temperatures, as argued above, is sufficient but not necessary. The fundamental statistical definition of entropy,
had first been proposed by Max Planck (1906) as a mathematical tool supporting his discovery of energy quanta of thermal radiation. Here, W is the number of microstates which are consistent with the given macroscopic boundary conditions. At that time, Planck attributed the origin of this formula to Boltzmann (1877, 1896), so that (2.17) became generally known as the “Boltzmann entropy” with the “Boltzmann constant” , which has recently become the key to the current SI definition of the kelvin (BIMP 2019). The famous entropy formula is engraved at Boltzmann’s monument in Vienna, Figure 4.
However, the work of Boltzmann (1877, 1896) does not include eq. (19) in an explicit form. In a text written in 1945 that appeared only shortly after his death, Planck (1948) revealed his own authorship. “Als Resultat … stellte sich heraus, … daß dabei k die sog. absolute Gaskonstante vorstellt … Sie wird öfters verständlicherweise als die Boltzmannsche Konstante bezeichnet. Dazu ist allerdings zu bemerken, daß Boltzmann diese Konstante weder jemals eingeführt noch meines Wissens überhaupt daran gedacht hat, nach ihrem numerischen Wert zu fragen. … Was nun die Größe W anbetrifft, so erwies es sich, um diese Größe als Wahrscheinlichkeit deuten zu können, als notwendig, eine neue universelle Konstante einzuführen, die ich mit h bezeichnete und … das elementare Wirkungsquantum nannte. Damit war also das Wesen der Entropie im Sinne Boltzmanns auch in der Strahlung festgestellt.”8
Let the state of an arbitrary physical object, which consists of many elements, may sufficiently well be characterised by some set of macroscopic properties. If a number of different, random microstates of the elements exists to each particular macrostate of the object, then an entropy value may be associated with that macrostate according to Planck’s entropy formula (19). This entropy is statistically well-defined regardless of the existence of local equilibria or temperatures. Note, however, that by a formal temperature can be assigned to such an object or its parts as far as the object’s energy is a well-defined physical quantity (Planck 1906, Landau and Lifschitz 1966b: §9).
If the object is isolated from its environment, the latter cannot affect its entropy, . If the object’s state is changing anyway, this change is subject to the 2nd Law in the form of the bilinear sum,
where the flux vector is and the conjugate forces are (Landau and Lifschitz 1966a; Feistel and Ebeling 2011). So far, to the authors’ knowledge, no system could be demonstrated to violate the inequality (20). Equations (15)-(18) represent just a special case of this fundamental concept, as applied here to oceanic evaporation. The statistical entropy (19) is relevant as residual Pauling entropy at the zero point, such as of ice Ih, and for other frozen structures such as information carriers (Feistel 2019).
Returning to geophysics, in the gravity field, fluids become vertically stratified. At equilibrium, the fluid has constant vertical profiles of the temperature and of each chemical potential while entropy and concentrations possess individual vertical gradients (Guggenheim 1949; Landau and Lifschitz 1966b). At a perfectly (turbulently) mixing state, by contrast, entropy and concentrations have vertically constant profiles while temperature has an adiabatic gradient (McDougall and Feistel 2003; Feistel and Ebeling 2011) together with the chemical potentials (Feistel and Hagen 1994; Feistel and Feistel 2006). The uniform chemical compositions observed of environmental dry air and sea salt do in fact result from that mixing. The mixing state is a non-equilibrium state which permanently produces entropy (Feistel 2011a; Feistel and Ebeling 2011) because of non-vanishing fluxes (16) - (18) between fluid cells in close contact after those had arrived adiabatically from different pressure levels, and due to hydrodynamic viscous friction.
3. Onsager Force and Flux of Evaporation
Previously, oceanographers such as Wüst (1920), Sverdrup (1936) and Albrecht (1940) used the “vapour-pressure jump” at the sea surface as the driving force for evaporation, in agreement with Dalton (1798). In modern irreversible thermodynamics, this jump is more correctly expressed by the difference between the chemical potentials of water in seawater and in humid air (Kraus and Businger 1994), such as by the Onsager force (18) across the phase boundary (Doney 1994).
Having been unavailable numerically in a sufficiently consistent way before 2010, more recently those chemical potentials may be derived from the Gibbs potential of seawater, the specific Gibbs energy , and from that of humid air, , provided by TEOS-10, the Thermodynamic Equation of Seawater – 2010 (IOC et al. 2010; Feistel 2018; Feistel and Hellmuth 2023), the current international geophysical standard for thermodynamic properties of seawater, ice and humid air. The Gibbs potentials do not depend on the respective sample masses, m. Their composition variables are absolute salinity, S, the mass fraction of dissolved salt in seawater, and the mass fraction A of dry air in humid air. The chemical potential of water in seawater with a solute mass and the water mass is calculated from
and the chemical potential of water vapour in humid air with a dry-air mass and the water-vapour mass from
The chemical potential of water in seawater may formally be expressed by the fugacity, , in the form (Guggenheim 1949; Prausnitz et al. 1999)
Here, the ideal-gas chemical potential is defined asymptotically by the low-pressure limit of , using an arbitrary auxiliary reference pressure ,
The specific gas constant, , is the molar gas constant, , divided by the molar mass of water, . Denoting by the molar mass of sea salt (Millero et al. 2008), the mole fraction of water in seawater is,
Similar to eq. (23), the chemical potential of water vapour in humid air is
with the mole fraction ,
of water vapour. The molar mass of dry air is denoted by . The fugacity of water vapour in humid air is (Feistel et al. 2015).
By its definition (26), the fugacity of an ideal gas equals its partial pressure, . The ideal-gas chemical potentials of water vapour in humid air and of liquid water in seawater are identical functions describing the water substance, so that their difference is, according to eq. (24),
The resulting difference
is regarded as the affinity of vapourisation (Kraus and Businger 1994: p. 42).
Assuming the same temperature on both sides of the air-sea interface with a thickness , the evaporation force (18) follows from (29) to be
For mole fractions close to unity, , the Lewis fugacity rule (Prausnitz et al. 1999: Section 5.1 therein) holds that
Here, the fugacity of water vapour in saturated humid air, , equals that of pure liquid water, . The resulting equation for the evaporation mass flux from the sea surface with salinity is
The relative fugacity, , of water vapour in humid air is defined by (Feistel and Lovell-Smith 2017)
The Onsager coefficient of evaporation is and the fugacity-based empirical mass transfer coefficient is .
In ideal-gas approximation of the fugacities,, that is,
the evaporation flux (32) is driven by the ratio of vapour pressures or of specific humidities, , in contrast to their difference,
in the Dalton equation of the form of eq. (1) or (35) typically used in numerical climate models (Stewart 2008).
Note that for ocean salinities (Wüst 1920). Approximating , comparison with (32) shows that
Accordingly, along with global warming the evaporation rates (35) of climate models increase exponentially in comparison to (32), as follows from the Clausius-Clapeyron formula for the saturated vapour pressure. This bias may contribute to the fact that latest climate models systematically underestimate the warming of the oceans (Weller et al. 2022), perhaps by accelerating the hydrological cycle, even though observation suggests and most models assume that relative humidity at the sea surface is largely unaffected by global warming (Rapp 2014; Feistel and Hellmuth 2021, 2023).
4. Evaporation Enthalpy
Along with the mass flux of water evaporating from the oceans at a rate of about 1000 mm per year, the heat of solar irradiation is transferred as latent heat to the troposphere. The thermodynamic equation for the latent heat, , of reversible evaporation of seawater into humid air was derived to read (Feistel et al. 2010; Feistel and Hellmuth 2023)
Let , respectively, be the partial masses of liquid water, dissolved sea salt, water vapour and dry air involved in the evaporation process. In Equation (37), is the specific enthalpy of humid air as a function of the mass fraction of dry air, temperature and pressure . The specific (or absolute) humidity is . Similarly, is the specific enthalpy of seawater as a function of the mass fraction of salt dissolved, also known as absolute (or specific) salinity of IAPSO Standard Seawater with Reference Composition (Millero et al. 2008). Evaporation is reversible (without production of entropy) if the chemical potentials of water in seawater, eq. (21), and of water vapour in humid air, eq. (22), take equal values, so that the phase equilibrium condition has the form
The specific entropies are related to the Gibbs energies and the enthalpies by (Feistel et al. 2010)
and
so that the entropy of reversible evaporation is
However, the typical sea-surface relative humidity is about 80 %rh (Rapp 2014; Feistel and Hellmuth 2021), and the related evaporation is an irreversible process accompanied by entropy production (Feistel and Ebeling 2011; Feistel 2019: Appendix C). The question arises of how large the related errors are if the reversible eqs. (37), (41) are applied to irreversible evaporation, i.e., if eq. (38) is violated.
At constant T and p, the total enthalpy of a two-box system consisting of one sample with seawater and one with humid air, such as displayed in Figure 2, is
If a mass portion of water, , is transferred from the seawater box to the air box, the latent heat of isobaric-isothermal evaporation is given by the implied change of total enthalpy
that is,
or, rearranged,
This formula is independent of any interaction between the two boxes as well as of the kind of water transfer mechanism involved. It is concluded that the agreement of eq. (45) with eq. (37) shows that the formula (37) for the reversible evaporation enthalpy as considered by Feistel and Hellmuth (2023) is valid also for irreversible evaporation at mutually independent values of the four given variables .
5. Evaporation Entropy
At constant T and p, the total entropy of a two-box system consisting of a sample with seawater and one with humid air, is
If a mass of water evaporates, the entropy increases at a rate of
which, similar to eq. (45), leads to
Making use of eqs. (39), (40), this formula results in
Here, the quantity
is the difference between the chemical potential of water in seawater and that of water in humid air, that is, their distance from mutual chemical equilibrium. This distance can be expressed in terms of the relative fugacity, , of humid air, eqs. (29), (32),
Here, the relative fugacity of humid air is (Feistel et al. 2015; Feistel and Lovell-Smith 2017),
where is the water-vapour mole fraction of saturated humid air. For ideal gases, the relative fugacity equals the conventional relative humidity (Lovell-Smith et al. 2016), .
According to eq. (49), the entropy of irreversible evaporation is, in contrast to eq. (41),
Note that the additional irreversible contribution has a negative sign if the air above the sea surface (with ) is almost or fully saturated,
This means that in such a case the mass flux is directed from the atmosphere to the ocean, that is, evaporation is replaced then by condensation of water vapour.
The sea-air entropy flux can be split into a reversible part, , and the remaining irreversible part, ,
Irreversible evaporation means that along with the mass flux density of water, the ocean exports entropy at the rate while the atmosphere imports entropy at the larger rate . This is reversed during irreversible condensation, when the ocean receives more entropy than the atmosphere is losing by this process.
Note that in the literature, the specific latent heat of vaporisation is sometimes given by the difference of the specific entropies and , respectively, of pure liquid water and water vapour, such as (Gill 1982: eq. 3.4.1 therein; Quasem et al. 2023: eqs. 6.1 and 6.5 therein),
This expression neglects the molecular interaction between water and either sea salt or dry air, and it applies only to saturated vapour which is formed reversibly, without producing additional entropy as it typically occurs at the ocean surface where the relative humidity deviated from its equilibrium value.
For an assessment of the relevance of the irreversible contribution to Eq. (53), the ocean-atmosphere entropy flux density of evaporation may be considered in comparison to the mean global entropy export of about from the top of the atmosphere (Ebeling and Feistel 1982), which corresponds to an atmospheric cooling rate of about 2 K day ̶ 1 (Feistel and Ebeling 2011: Section 3.4). Assuming an oceanic evaporation mass flux of eq. (32) with a Dalton constant of (Feistel and Hellmuth 2023: eqs. 22, 24 therein), a temperature of , a relative humidity of and a salinity of , the related fluxes are estimated to be approximately , and (Feistel and Ebeling 2011: Eq. 3.98 therein). Thus, in this rule-of-thumb estimate the entropy produced by irreversible evaporation contributes only about 0.4 % to the global entropy export of the Earth while the reversible flux amounts to about one third. This reversible flux originates mainly from the entropy production occurring during the absorption of high-temperature solar irradiation by the comparatively cold terrestrial ocean (Feistel and Ebeling 2011; Feistel 2011a,b). An alternative, more careful estimate of the oceanic entropy flux by Yan et al. (2004) amounts to almost .
6. Summary
Owing to the difference of chemical potentials of water between seawater and humid air, evaporation of water from the ocean surface is an irreversible process. Regardless of that, in the literature the latent heat of vaporisation is mostly derived from equilibrium thermodynamics. In this paper, the formalism of linear irreversible thermodynamics is applied to a conceptual evaporation model. Assuming local equilibrium conditions in the ocean and in the troposphere, thermodynamic equations provided by the geophysical standard TEOS-10 may be exploited, in particular by using mutually consistent equations for enthalpy, entropy and chemical potentials of seawater and humid air without ideal-gas approximations being required. The resulting form of the Dalton equation (32) for the evaporation mass flux,
is expressed in terms of relative fugacity of humid air, , which is a real-gas-corrected version of conventional definitions of relative humidity. The new Dalton equation predicts constant evaporation rates at constant sea-surface relative humidity, in contrast to Dalton equations implemented in most climate models which suggest an accelerated hydrological cycle under those conditions, implying numerical ocean cooling.
From the entropy balance at the air-sea interface, the equation for the latent heat of evaporation, eq. (45),
is demonstrated to be equally valid for reversible as well as irreversible evaporation. By contrast, the evaporation entropy, eq. (53),
includes an additional irreversible term proportional to the evaporation rate that vanishes at equilibrium. This new non-equilibrium term is missing in previous incomplete textbook definitions such as eq. (56),
for the latent heat of vaporisation in terms of entropies of water and vapour.
Acknowledgement:
The authors are grateful to Thomas Foken for providing the data shown in Figure 1 and various references. This article contributes to the tasks of the IAPSO/SCOR/IAPWS Joint Committee on the Properties of Seawater (JCS). The contribution of O. Hellmuth was provided within the framework of the research theme 2 “Aerosols and clouds, long-term processes and trends” of Leibniz Institute for Tropospheric Research (TROPOS), Leipzig and is part of the TROPOS activities within the framework of the EU project “Aerosol, Clouds and Trace gases Research InfraStructure” (ACTRIS).
Nomenclature
| Symbol | Quantity | Basic SI Unit |
| A | Mass fraction of dry air in humid air, | |
| Unit conversion constant | ||
| Isobaric heat capacity | ||
| Fugacity-based Dalton coefficient | ||
| Humidity-based Dalton coefficient | ||
| Partial pressure of water vapour of humid air | ||
| Saturation vapour pressure of water | ||
| Fugacity of water vapour in humid air | ||
| Ideal-gas fugacity of water vapour | ||
| Fugacity of water in seawater | ||
| Gibbs energy (or free enthalpy), | ||
| Specific Gibbs energy, Gibbs function | ||
| Gibbs energy of humid air | ||
| Specific Gibbs energy of humid air | ||
| Gibbs energy of seawater | ||
| Specific Gibbs energy of seawater | ||
| Enthalpy, | ||
| Specific enthalpy, | ||
| Specific enthalpy of humid air | ||
| Specific enthalpy of seawater | ||
| Potential enthalpy | ||
| Any Onsager flux | ||
| Entropy flux | ||
| Irreversible entropy flux | ||
| Reversible entropy flux | ||
| Evaporation mass flux of water | ||
| Specific entropy of evaporation | ||
| specific latent heat of vaporisation | ||
| Specific latent heat of evaporation | ||
| Vector of masses | ||
| Mass | ||
| Molar mass of dry air, | ||
| Mass of dry air in humid air | ||
| Mass of substance k | ||
| Molar mass of sea salt, | ||
| Mass of dissolved sea salt | ||
| Mass of water vapour | ||
| Molar mass of water, | ||
| Mass of water solvent | ||
| Entropy | ||
| Entropy production | ||
| Pressure | ||
| Reference pressure, surface pressure | ||
| Specific humidity, | ||
| Saturation specific humidity | ||
| Molar gas constant, | ||
| Specific gas constant of water, | ||
| Absolute salinity, | ||
| ITS-90 temperature | ||
| Time | ||
| Internal energy | ||
| Specific internal energy, | ||
| Volume | ||
| Specific volume | ||
| Vector of mass fractions | ||
| Mass fraction of substance k, | ||
| Mass-flux driving force | ||
| Any Onsager force | ||
| Onsager force vector of mass | ||
| Onsager force vector of internal energy | ||
| Onsager force vector of volume | ||
| Mole fraction of water vapour in humid air | ||
| Saturation mole fraction of water vapour in humid air | ||
| Onsager force of water evaporation | ||
| Mole fraction of liquid water in seawater | ||
| Laminar layer thickness | ||
| Conservative temperature | ||
| Potential temperature | ||
| Sverdrup’s diffusion coefficient (characteristic time) | ||
| Specific entropy, | ||
| Specific entropy of humid air | ||
| Specific entropy of seawater | ||
| Specific entropy of water vapour | ||
| Specific entropy of liquid water | ||
| Chemical potential | ||
| Vector of chemical potentials | ||
| Ideal-gas chemical potential of water vapour | ||
| Ideal-gas chemical potential of liquid water | ||
| Chemical potential of substance k | ||
| Chemical potential of water vapour in humid air | ||
| Chemical potential of water in seawater | ||
| Chemical potential difference of water | ||
| Relative fugacity | 1 | |
| Onsager coefficient | ||
| Onsager coefficient of water evaporation |
References
- Albrecht, F. (1940): Untersuchungen über den Wärmehaushalt der Erdoberfläche in verschiedenen Klimagebieten. Reichsamt für Wetterdienst, Wissenschaftliche Abhandlungen Bd. VIII, Nr. 2, Springer, Berlin, Heidelberg, https://www.springer.com/de/book/9783662425305.
- Avery, K.R. (1972): Literature Search for Atmospheric Humidity Profile Models From the Sea Surface to 1000 Meters. NOAA Technical Memorandum EDS NODC-1, Silver Spring, MD.
- BIPM (2019): The International System of Units (SI). 9th edition of the SI Brochure, available from the BIPM. https://www.bipm.org/en/publications/si-brochure.
- Boltzmann, L. (1877): On the Relationship between the Second Main Theorem of Mechanical Heat Theory and the Probability Calculation with Respect to the Results about the Heat Equilibrium. Sitzb. d. Kaiserlichen Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Klasse, Wien, Austria, LXXVI, Abt II, pp. 373–435.
- Boltzmann, L. (1896): Vorlesung über Gastheorie, Band 1. Wiener Sitzungsberichte, Johann Ambrosius Barth, Leipzig.
- Cronin, M.F., Gentemann, C.L., Edson, J., Ueki, I., Bourassa, M., Brown, S., Clayson, C.A., Fairall, C.W., Farrar, J.T., Gille, S.T. et al. (2019): Air-sea fluxes with a focus on heat and momentum. Front. Mar. Sci. 6, 430. [CrossRef]
- Dalton, J. (1798): Experimental Essays, on the Constitution of mixed GASES; on the Force of STEAM or VAPOUR from Water and other Liquids in different temperatures, both in a Torricellian Vacuum and in Air; on EVAPORATION; and on the Expansion of GASES by Heat. Mem. Lit. Philos. Soc. Manch. 1798, 5, 535–602. Available online: https://www.biodiversitylibrary.org/part/308525 (accessed 14 March 2023).
- de Groot, S.R.; Mazur, P. (1984): Non-Equilibrium Thermodynamics; Dover Publications: New York, NY, USA.
- Doney, S.C. (1994): Irreversible Thermodynamic Coupling between Heat and Matter Fluxes across a Gas/Liquid Interface. J. Chem. Soc. Faraday Trans. 90, 1865-1874. [CrossRef]
- Ebeling, W., Feistel, R. (1982): Physik der Selbstorganisation und Evolution. Akademie-Verlag, Berlin.
- Falkenhagen, H., Ebeling, W., Hertz, G. (1971): Theorie der Elektrolyte. S. Hirzel Verlag, Leipzig.
- Feistel, R. (2011a): Radiative entropy balance and vertical stability of a gray atmosphere. Eur. Phys. J. B 82, 197–206. [CrossRef]
- Feistel, R. (2011b): Entropy Flux and Entropy Production of Stationary Black-Body Radiation. J. Non-Equilib. Thermodyn. 36, 131–139. [CrossRef]
- Feistel, R. (2012): TEOS-10: A New International Oceanographic Standard for Seawater, Ice, Fluid Water, and Humid Air. Int. J. Thermophys. 33, 1335–1351. https://doi.org/10.1007/s10765-010-0901-y.
- Feistel, R. (2015): Salinity and relative humidity: climatological relevance and metrological needs. Acta Imeko 4, 57-61, http://dx.doi.org/10.21014/acta_imeko.v4i4.216.
- Feistel, R. (2018): Thermodynamic properties of seawater, ice and humid air: TEOS-10, before and beyond. Ocean Sci. 14, 471–502. https://doi.org/10.5194/os-14-471-2018.
- Feistel, R. (2019): Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-Equilibrium States. Entropy 21, 799. [CrossRef]
- Feistel, R., Ebeling, W. (2011): Physics of Self-Organization and Evolution. Wiley-VCH, Weinheim.
- Feistel, R., Feistel, S. (2006): Die Ostsee als thermodynamisches System. In: Schimansky-Geier, L., Malchow, H., Pöschel, T. (eds): Irreversible Prozesse und Selbstorganisation. Logos-Verlag, Berlin, p. 81-98. [CrossRef]
- Feistel, R., Hagen, E. (1994): Thermodynamic Quantities in Oceanography. In: Majumdar et al. (eds): The Oceans: Physical-Chemical dynamics and Human Impact. The Pennsylvania Academy of Science, p.1-13.
- Feistel, R., Hellmuth, O. (2021): Relative Humidity: A Control Valve of the Steam Engine Climate. J. Hum. Earth Future 2, 140–182. [CrossRef]
- Feistel, R., Hellmuth, O. (2023): Thermodynamics of Evaporation from the Ocean Surface. Atmosphere 14, 560. [CrossRef]
- Feistel, R., Hellmuth, O., Lovell-Smith, J. (2022): Defining relative humidity in terms of water activity: III. Relations to dew-point and frost-point temperatures. Metrologia 59, 045013. [CrossRef]
- Feistel, R., Lovell-Smith, J.W. (2017): Defining relative humidity in terms of water activity. Part 1: Definition. Metrologia 54, 566–576. [CrossRef]
- Feistel, R., Lovell-Smith, J., Hellmuth, O. (2015): Virial Approximation of the TEOS-10 Equation for the Fugacity of Water in Humid Air. Int. J. Thermophys. 36, 44–68. [CrossRef]
- Feistel, R., Wagner, W. (2005): High-pressure thermodynamic Gibbs functions of ice and sea ice. J. Mar. Res. 63, 95–139.
- Feistel, R., Wagner, W. (2006): A new equation of state for H2O ice Ih. J. Phys. Chem. Ref. Data 35, 1021–1047. [CrossRef]
- Feistel, R.; Wielgosz, R.; Bell, S.A.; Camões, M.F.; Cooper, J.R.; Dexter, P.; Dickson, A.G.; Fisicaro, P.; Harvey, A.H.; Heinonen, M.; et al. (2016): Metrological challenges for measurements of key climatological observables: Oceanic salinity and pH, and atmospheric humidity. Part 1 - Overview. Metrologia 53, R1–R11. https://doi.org/10.1088/0026-1394/53/1/R1.
- Feistel, R., Wright, D.G., Kretzschmar, H.-J., Hagen, E., Herrmann, S., Span, R. (2010): Thermodynamic properties of sea air. Ocean Science 6, 91–141. [CrossRef]
- Feistel, R., Wright, D.G., Miyagawa, K., Harvey, A.H., Hruby, J., Jackett, D.R., McDougall, T.J., Wagner, W. (2008): Mutually consistent thermodynamic potentials for fluid water, ice and seawater: A new standard for oceanography. Ocean Sci. 4, 275–291. [CrossRef]
- Fofonoff, N.P. (1962): Physical properties of sea water. In: Hill, M.N. (ed): The Sea, vol. 1, pp. 3–28, Wiley-Interscience, New York.
- Foken, Th., Kitajgorodskij, S.A., Kuznecov, O.A. (1978): On the Dynamics of the Molecular Boundary Layer Above the Sea. Boundary-Layer Meteorology 15, 289-300. [CrossRef]
- Gibbs, J.W. (1878): On the Equilibrium of Heterogeneous Substances. Transactions of the Connecticut Academy of Arts and Sciences III, 108-520.
- Glansdorff, P., Prigogine, I. (1971): Thermodynamic Theory of Structure, Stability and Fluctuations; Wiley-Interscience: London, UK; New York, NY, USA; Sydney, Australia; Toronto, ON, Canada.
- Gorfer, M. (2022): Monitoring of climate change and variability in atmospheric heat content based on climate records and reanalyses. Wegener Center Scientific Report 94-2022, Wegener Center Verlag, University of Graz, Austria. https://unipub.uni-graz.at/obvugrhs/content/titleinfo/6751357.
- Guggenheim, E.A. (1949): Thermodynamics. North-Holland, Amsterdam.
- Halley, E. (1687): An estimate of the quantity of vapour raised out of the sea by the warmth of the sun; derived from an experiment shown before the Royal Society at one of their late meetings. Philos. Trans. 16, 366–370. [CrossRef]
- Hupfer, P., Foken, Th., Panin, G. (1975): Existence and Structure of the Laminar Boundary Layer of the Atmosphere in the Near-Shore Zone of the Sea. Zeitschrift für Meteorologie 25, 94-102.
- IAPWS AN6-16 (2016): Advisory Note No. 6: Relationship between Various IAPWS Documents and the International Thermodynamic Equation of Seawater - 2010 (TEOS-10). http://www.iapws.org.
- IOC, SCOR, IAPSO (2010): The International Thermodynamic Equation of Seawater—2010: Calculation and Use of Thermodynamic Properties. Intergovernmental Oceanographic Commission, Manuals and Guides No. 56, UNESCO (English), p. 196, Paris. Available online: http://www.TEOS-10.org (accessed on 26 November 2022).
- Josey, S.A., Gulev, S., Yu, L. (2013): Exchanges through the ocean surface. In: Siedler, G., Griffies, S.M., Gould, J., Church, J.A. (eds): Ocean Circulation and Climate. A 21st Century Perspective. Elsevier, Amsterdam, S. 115–140. [CrossRef]
- Kirkaldy, J.S. (1965): Thermodynamics of Terrestrial Evolution. Biophysical Journal 5, 965-979. [CrossRef]
- Kraus, E.B., Businger, J.A. (1994): Atmosphere-Ocean Interaction. Oxford University Press, New York, Clarendon Press, Oxford.
- Landau, L.D., Lifschitz, E.M. (1966a): Hydrodynamik. Akademie-Verlag, Berlin, Germany.
- Landau, L.D., Lifschitz, E.M. (1966b): Statistische Physik. Akademie-Verlag, Berlin, Germany.
- Lovell-Smith, J.W., Feistel, R., Harvey, A.H., Hellmuth, O., Bell, S.A., Heinonen, M., Cooper, J.R. (2016): Metrological challenges for measurements of key climatological observables. Part 4: Atmospheric relative humidity. Metrologia 53, R39–R59. [CrossRef]
- McDougall, T. J. (2003): Potential enthalpy: A conservative oceanic variable for evaluating heat content and heat fluxes. Journal of Physical Oceanography, 33, 945-963. [CrossRef]
- McDougall, T.J., Barker, P.M., Feistel, R., Roquet, F. (2023): A Thermodynamic Potential of Seawater in terms of Conservative Temperature. Submitted to Ocean Science. Preprint egusphere-2023-1568. [CrossRef]
- McDougall, T.J., Feistel, R. (2003): What causes the adiabatic lapse rate? Deep-Sea Research I 50, 1523–1535. [CrossRef]
- Millero, F.J., Feistel, R., Wright, D.G., McDougall, T.J. (2008): The Composition of Standard Seawater and the Definition of the Reference-Composition Salinity Scale. Deep-Sea Res. Part I, 55, 50–72. [CrossRef]
- Montgomery, R.B. (1940): Observations of Vertical Humidity Distribution Above the Ocean Surface and Their Relation to Evaporation. Papers in Physical Oceanography and Meteorology 7, 2-30. [CrossRef]
- Planck, M. (1906): Vorlesungen über die Theorie der Wärmestrahlung. Johann Ambrosius Barth, Leipzig.
- Planck, M. (1948): Wissenschaftliche Selbstbiographie. Johann Ambrosius Barth, Leipzig.
- Prausnitz, J.M., Lichtenthaler, R.N., Gomes de Azevedo, E. (1999): Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd edn. Prentice Hall, Englewood Cliffs, NJ.
- Prigogine, I., Wiaume, J.M. (1946): Biologie et thermodynamique des phénomènes irréversibles. Experientia 2, 451-453. [CrossRef]
- Quasem, N.A.A., Generous, M.M., Qureshi, B.A., Zubair, S.M. (2023): Thermodynamic and Thermophysical Properties of Saline Water; Models, Correlations and Data for Desalination and Relevant Applications. Springer, Cham, Switzerland.
- Randall, D.A. (2012): Atmosphere, Clouds, and Climate. Princeton University Press, Princeton.
- Rapp, D. (2014): Assessing Climate Change - Temperatures, Solar Radiation, and Heat Balance. Springer, Cham, Switzerland.
- Stewart, R.H. (2008): Introduction to Physical Oceanography; Texas A & M University: College Station, TX, USA. [CrossRef]
- Sverdrup, H.U. (1936): Das maritime Verdunstungsproblem. Annalen der Hydrographie und maritimen Meteorologie 54, 41-47.
- Von Schuckmann, K. et al. (2023): Heat stored in the Earth system 1960–2020: where does the energy go? Earth Syst. Sci. Data 15, 1675–1709. [CrossRef]
- Weller, R.A., Lukas, R., Potemra, J., Plueddemann, A.J., Fairall, C., Bigorre, S. (2022): Ocean Reference Stations: Long-Term, Open-Ocean Observations of Surface Meteorology and Air–Sea Fluxes Are Essential Benchmarks. Cover. Bull. Am. Meteorol. Soc. 103, E1968–E1990. [CrossRef]
- Wright, D.G., Feistel, R., Reissmann, J.H., Miyagawa, K., Jackett, D.R.,Wagner, W., Overhoff, U., Guder, C., Feistel, A., Marion, G.M. (2010): Numerical implementation and oceanographic application of the thermodynamic potentials of liquid water, water vapour, ice, seawater and humid air – Part 2: The library routines. Ocean Sci. 6, 695–718. [CrossRef]
- Wüst, G. (1920): Die Verdunstung auf dem Meere. Veröffentlichungen des Instituts für Meereskunde an der Universität Berlin, Geographisch-naturwissenschaftliche Reihe 54, 1-95.
- Yan, Y., Gan, Z., Qi, Y. (2004): Entropy budget of the ocean system. Geophysical Research Letters 31, (L14311), 1-4. [CrossRef]
- Zülicke, Ch. (2005): Air–sea fluxes including the effect of the molecular skin layer. Deep-Sea Research II 52, 1220–1245. [CrossRef]
- Zülicke, Ch., Hagen, E. (1998): Impact of the Skin Effect on the Near-Surface Temperature Profile. Physics and Chemistry of the Earth 23, 531-535. [CrossRef]
| 1 | Halley (1687): p. 368 |
| 2 | Dalton (1789): p. 537 |
| 3 | Albrecht (1940): p. 36,77 |
| 4 | Randall (2012): p. 176 |
| 5 | Albrecht (1940): p. 77 |
| 6 | Rapp (2014): p. 420 |
| 7 | Weller et al. (2022): p. E1968 |
| 8 | Planck (1948): p. 28, 29 |
Figure 1.
Microstructure of temperature in the atmospheric layer immediately above the sea surface, measured on 15 April 1975 at the Caspian Sea (Foken et al. 1978). Data courtesy Thomas Foken, priv. comm.
Figure 1.
Microstructure of temperature in the atmospheric layer immediately above the sea surface, measured on 15 April 1975 at the Caspian Sea (Foken et al. 1978). Data courtesy Thomas Foken, priv. comm.
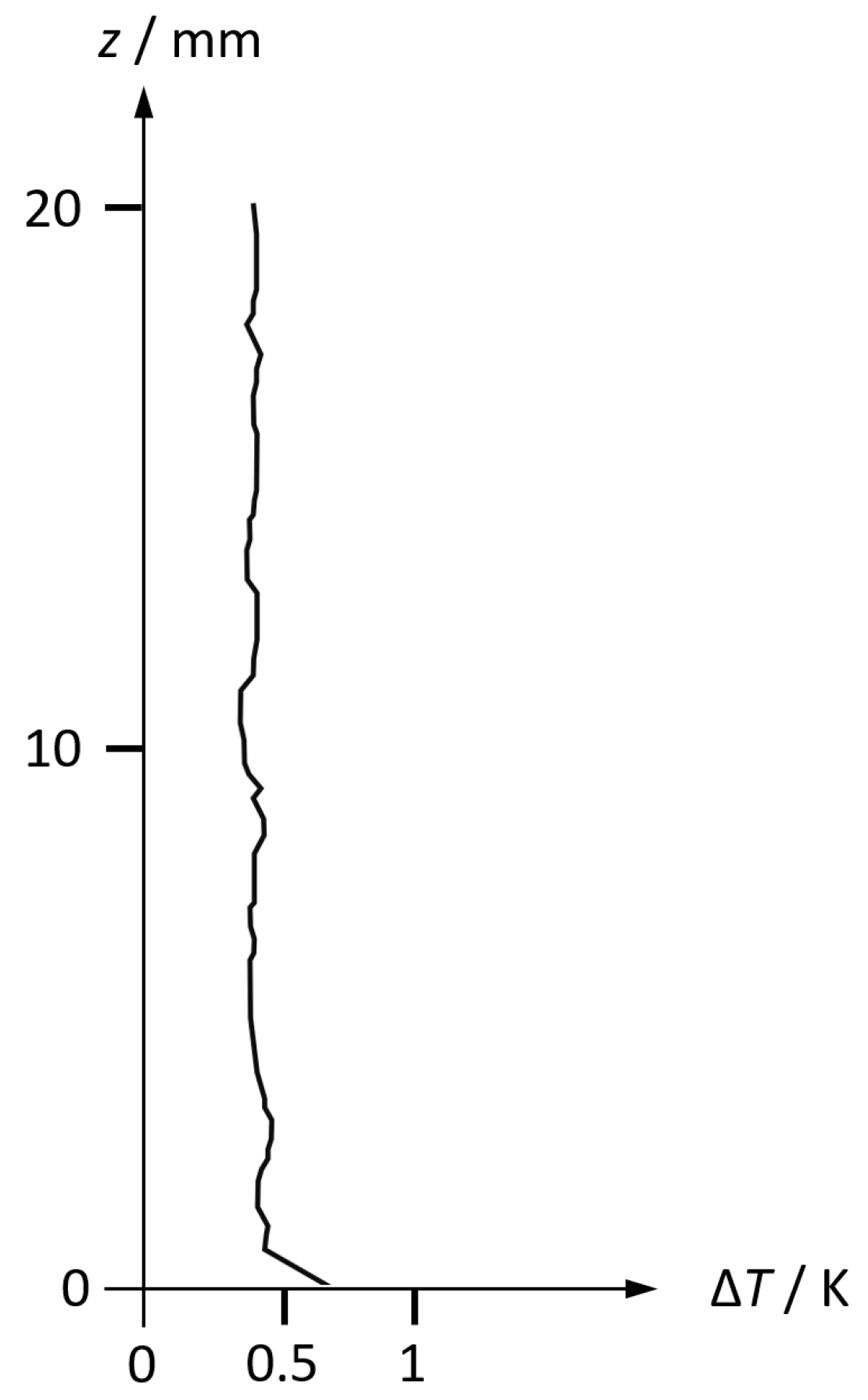
Figure 2.
Schematic of a conceptual model of seawater evaporation. The ocean-atmosphere interface is embedded in laminar layers on both the liquid and the gas sides. These layers are assumed to be sufficiently thin so that molecular transport may establish homogeneous distributions of specific humidity, salinity and temperature. Outside those layers, humid air and seawater may be turbulently mixed.
Figure 2.
Schematic of a conceptual model of seawater evaporation. The ocean-atmosphere interface is embedded in laminar layers on both the liquid and the gas sides. These layers are assumed to be sufficiently thin so that molecular transport may establish homogeneous distributions of specific humidity, salinity and temperature. Outside those layers, humid air and seawater may be turbulently mixed.
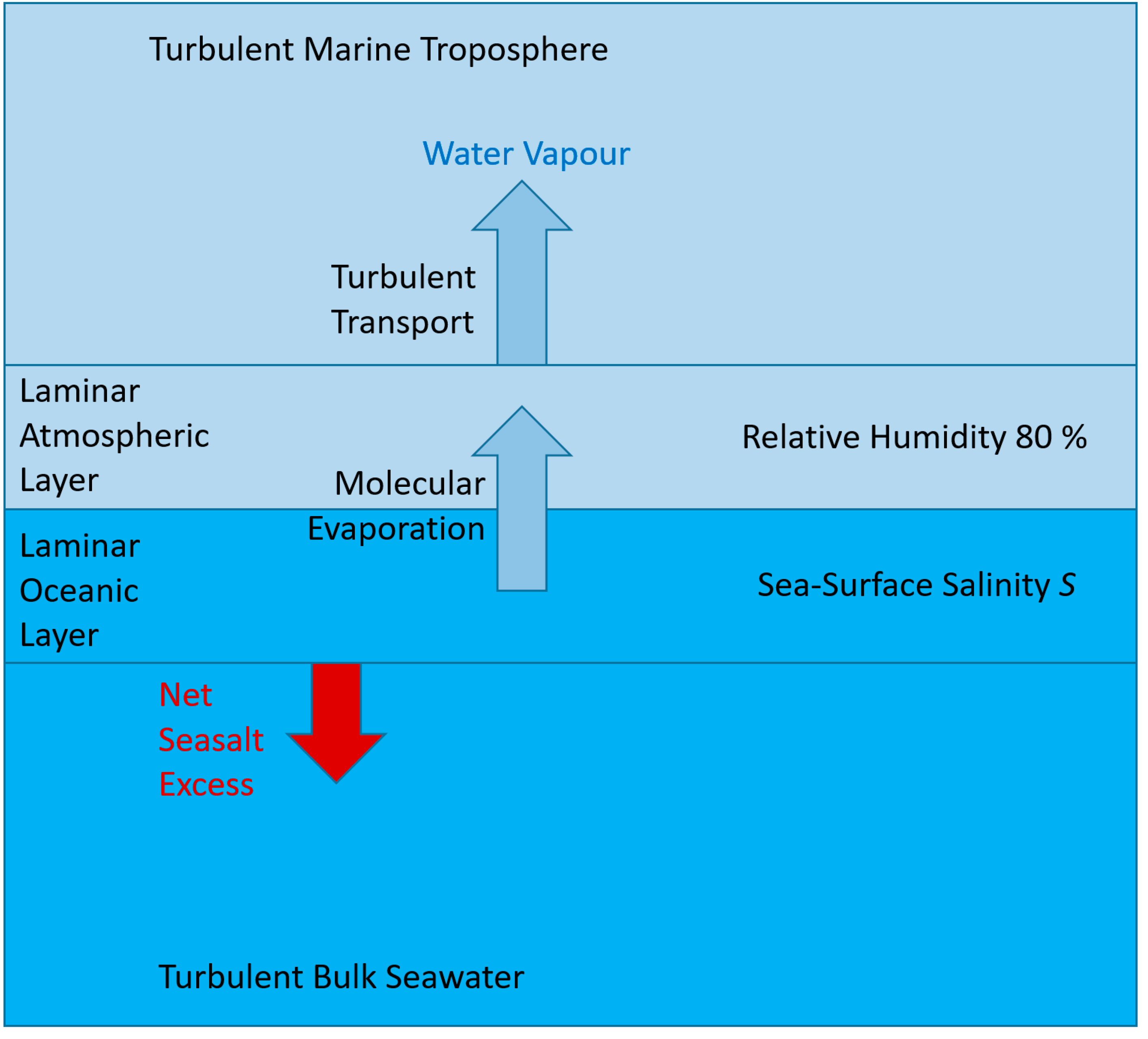
Figure 3.
Schematic of an isolated non-equilibrium parcel consisting of two different, local-equilibrium cells with equal masses, subject to mutual exchange. Accordingly, for the entire parcel the 2nd Law takes the form, , and the 1st Law is .
Figure 3.
Schematic of an isolated non-equilibrium parcel consisting of two different, local-equilibrium cells with equal masses, subject to mutual exchange. Accordingly, for the entire parcel the 2nd Law takes the form, , and the 1st Law is .
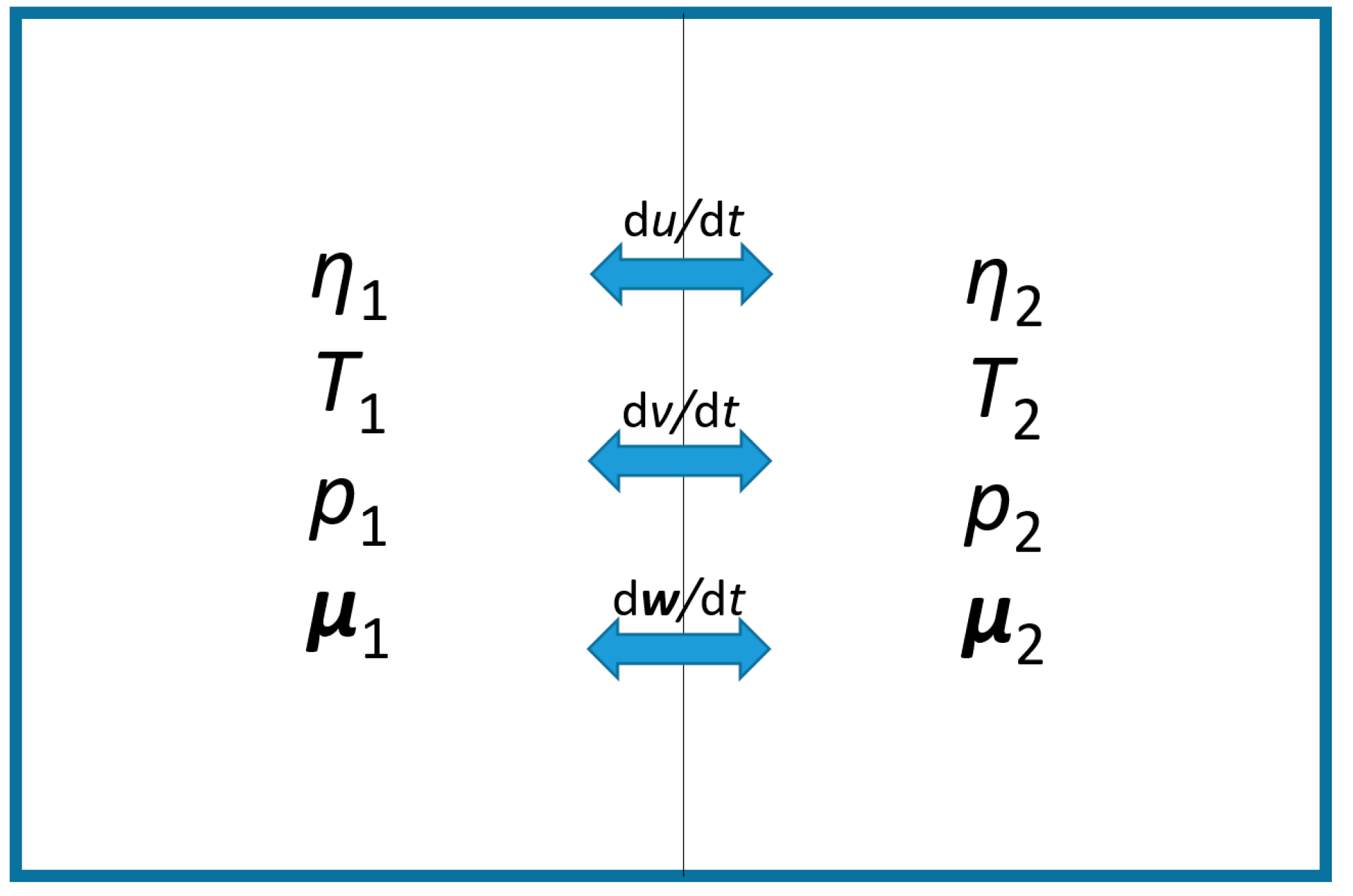
Figure 4.
Equation of statistical entropy, ascribed to Ludwig Boltzmann, as engraved at the Vienna Central Cemetery. This fundamental entropy definition does not presuppose the existence local equilibria or temperatures. Photo taken in October 2010.
Figure 4.
Equation of statistical entropy, ascribed to Ludwig Boltzmann, as engraved at the Vienna Central Cemetery. This fundamental entropy definition does not presuppose the existence local equilibria or temperatures. Photo taken in October 2010.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






