Preprint
Article
Membrane Potential: The Ignored Shape
Altmetrics
Downloads
118
Views
45
Comments
0
This version is not peer-reviewed
Submitted:
25 September 2023
Posted:
26 September 2023
You are already at the latest version
Alerts
Abstract
Membrane potential generation and maintenance are fundamental parts of membrane theory. However, since its inception, theories and assumptions have remained simple, whereas the amount of knowledge available has only grown. Unfortunately, this simplification and reductionism lead to its loss of validity on both microscopic and macroscopic scales. This article shows that assumptions made outside the context of factual reality lead to contradictions that cannot be compared with science. Membrane theory must be thoroughly revised, taking into account all forgotten and unanswered assumptions and questions to conform to facts and science to maintain credibility.
Keywords:
Subject: Biology and Life Sciences - Life Sciences
1. Introduction
This article is the fourth in a series of articles on membrane theory and its contradictions.
- Any diffusion? [1]
- The enigma of ion pumps [2]
- The Tamagawa experiment [3]
- The ignored shape
- The mathematical problem
In the first article in this series, we showed that simple diffusion or facilitated diffusion cannot be one of the sources of membrane potential (MP). The principles adopted and acknowledged in chemistry and physics are not considered or adopted in biology and biophysics. It was about fundamental theory and basic assumptions. Without these, all the mechanisms induced by the theory become invalid.
The second showed that diffusion at the microscopic level also becomes hampered or impossible. Indeed, if we accept the presence of ion channels in the membrane, we must accept working conditions that match the underlying theoretical conditions. This is not the case; some important questions remain unanswered and the absence of those answers invalidates the accepted hypothesis.
The Tamagawa experiment, the third in the series, showed that potentials can exist in an electrolyte solution in the absence of diffusion. The adsorption principle is perfectly accepted in chemistry and resolves many of the contradictions that membrane theory tries to avoid.
This fourth and penultimate section deals with the intermediate level: the cellular level and the level directly above; tissue. The cell, by its shape, offers intrinsic properties that can already modify or influence the behavior of the whole system and make it deviate from the extrapolations that were expected. We will find three major discrepancies that call into question the validity of the model.
2. Material and Discussion
2.1. Diffusion discrepancies
We previously found that diffusion was largely compromised both from a theoretical point of view [1] and microscopic topology [2] as a motor for the generation of membrane potential.
Although the model was studied as a single entity, there are many single-celled beings living in the same environment, and many multicelled beings, as well as many creatures. This implies that our basic model must be fully functional in the presence of other cells. The properties described in the basic model must stand the test of numbers and must not be altered or impeded in any way by the presence of other cells.
One of the first features of the cell model is independence; a unicellular being can live autonomously in its environment without the help of any other cell.
The cell model studied in isolation in an environment allows us to simplify our thinking and gives us some visibility on the interactions that may occur with the said environment but not with other organisms that may have been present.
This independence is taken to the extreme in membrane theory because each ion present in the electrolytes would be independent of the others by the mere presence of the water molecules surrounding them [4]. Obviously, this independence disappears when it comes to acting at a distance on the other side of a cell membrane. The actions of an ion whose effective distance exceeds the distance of the nearest ion would be stronger than those performed by the latter. The theory contains contradictions that are weakly or not logically argued. The authors tuned the action and electrostatic force of the ions according to their theories. The rigor is lacking because it has been built up by a historical empirical pile-up that is not questioned. However, it is now more questioned whether, on the scale of ions and molecules, the chemical and electrostatic forces are predominant [5].
Most cell envelopes are ovoid, cylindrical, or even spherical. Therefore, the convexity is almost constant towards the outside of the cell. Figure 1 highlights the first problem that has never been raised in our thinking about transmembrane exchange.
It is perfectly clear that diffusion can only take place asymmetrically. There is a convergence when the gradient is from the outside to the inside and a clear divergence when the gradient is from the inside to the outside. This can also be expressed as follows: The concentration should naturally increase when the diffusion is directed toward the cell, and, in contrast, the concentration should decrease when the diffusion is directed toward the outside.
It can also be said that the same concentration gives different effects depending on the direction of application. Membrane theory ignores this asymmetry from the beginning by simplifying and limiting the problem of diffusion to a single plane, whereas the phenomenon is always exercised in a volume that always has a shape. By definition, there is a bottleneck for material entering the cell and it appears that it is easier to get material out of the cell.
This can also be summarized as follows. Ions should flow out more easily than they flow in. This could be perfectly suitable for potassium outflow, but we have already made a major contradiction with respect to this leakage [1].
2.2. Vectors have a single direction
The role of potassium in the cell remains a kind of mystery. Current theory limits it to maintaining a concentration gradient between the external and internal environments. This gradient is thought to be electrogenic and therefore a major component of the membrane potential.
This would make it a major osmolyte. We usually present the membrane as flat because it allows us to highlight the different sequences and processes that can occur there. This electrogenic hypothesis would validate electrodiffusion as the source of the ionic movement carried out by the pumps. However, one of the conditions imposed by electrodiffusion is the direction of ion flow. This direction is necessarily linked to the electric field generated by the potential difference between the inside and outside of the cell, which are considered to be the electrodes of the membrane capacitance. If we accept this view of the model, when we know that the membrane is not homogeneous in its physical composition [6], then we have to admit that the electric field is linked to its composition and is also not constant and nonuniform. Understanding the phenomenon of membrane potential and action potential therefore merits a finer-grained approach that eliminates all integration steps.
Figure 2 shows the problem raised by reductionism and simplification of the model. The model imposes a flow that is perpendicular to the membrane surface, and this flow by definition has a direction that can be symbolized by a vector (a red arrow on the diagram). It is also theorized that diffusion occurs perpendicular to the membrane surface. This simple statement should be a warning, as the shape of most cells is not flat. Point X is the origin of this flow for two cells that are close together. We are already obliged to accept one piece of evidence: The direction of the vector is not identical even in the event of a flow of the same value. This perfectly contradicts the conditions of application of our theory. It is not possible for point X to generate two flows of the same amplitude but in opposite directions. What works on a microscopic scale is no longer validated on a larger scale.
2.3. Electric field
We also accept the principle that there is an electric field across the membrane. We would like it to be just as constant to validate our hypothesis. It would be just as nice if this electric field were also perfectly uniform, so as not to disturb the elegance and, above all, the simplicity of the theory [7,8].
Unfortunately, we have learned and found that the membrane is not as smooth and homogeneous as desired and that the distribution of ions on its surface depends on its composition and protein inclusions. Figure 3 shows a very small area where only a few ion channels have been randomly distributed. These channels are supposed to operate with cations for some and anions for others. If this theory is correct, then we must admit that they all contain ions aligned in a single file.
Our hypothesis assumes the presence of significant positive or negative charges, since they are close to each other but arranged vertically, as ion channel theory would have it, but quite far apart [9]. It is also clear that it is not the membrane itself, with its insulating properties, that could retain the said ions. The simulation shows some electric field lines that run from the ion channels. The diameter of these lines depends on the field amplitude. Obviously, with only eight ion channels and a few field lines, the diagram is already a mess. Reality is more complex on a larger scale.
In addition, the theory explains the forces at work in the thickness of the membrane but does not provide information about the effect of the electric field inside or outside the cell. What is the effect of the electric field on the ions at these points? Simple analysis shows that the passage of ions through the channels would be strongly impeded. I would go so far as to assert, without any real dispute, that movement is not or is no longer possible.
In addition, the presence of these localized and opposing charges creates rather random field lines that dictate the movement of ions as they approach the surface. The passage of ions through the ion channels thus becomes purely hypothetical but unlikely.
2.4. curvature
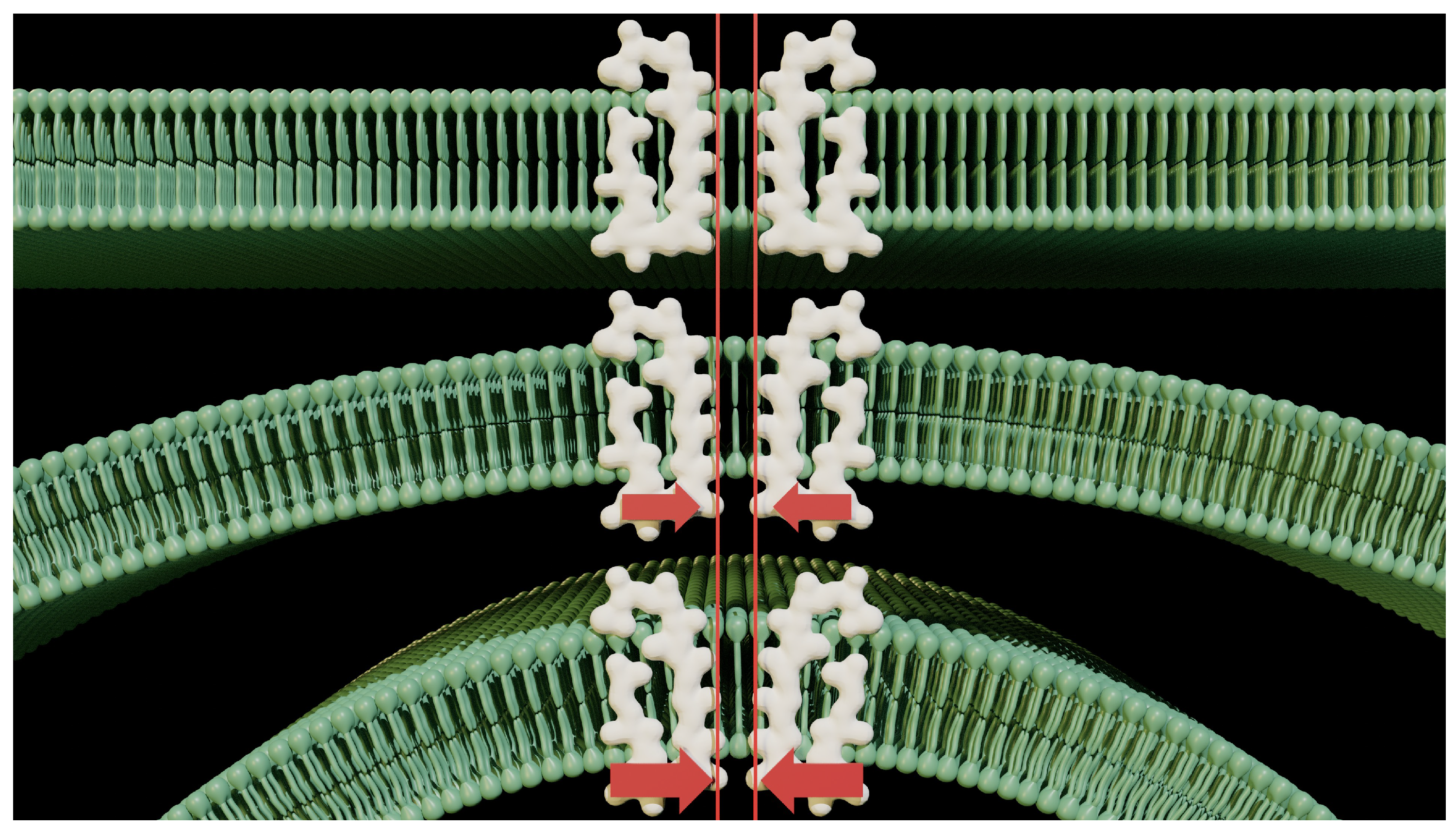
We also usually present only a part of the membrane for our explanations. This habit is also complemented by the flatness of the membrane. It is practical, and it is true that at this level of scale we can make this kind of approximation. Figure 4 shows three pieces of membrane with different and increasing curvatures.
The curvature of the membrane applies pressure to the lower edge of the pore of the ion channel, opening the outer mouth. This brings out a force that is neglected in normal ion channel operation. This force is in addition to the electrostatic interactions that take place inside the pores [2]. Electrostatic forces always predominate over diffusion at the molecular level. In fact, their magnitudes are much greater than those of the random motion that drives diffusion. The latter is also questionable, as it has not been verified in the case of ions with similar mobility, and there is no experimental evidence to validate it.
Even Nernst, in his famous experiment [10], was obliged to insert a luxury of precautions that we cannot encounter in the cell. This obvious and indisputable fact makes it even more difficult, if not impossible, for membrane theory to function as defined. It is, in fact, a sequence of operations or events that cannot take place because they depend on each other.
3. Conclusions
Examination of all the steps required for membrane theory to function correctly reveals major contradictions and a scientific basis that is not always perfect or credible. Based on the shape of the cell, and trying to apply the model to a more real or multi-cellular environment, it becomes clear that it does not work. Membrane theory needs to be totally reconsidered if it is to be a credible pillar of biology, even if some of its assumptions and foundations have to be modified.
Author Contributions
Conceptualization, B.D. and H.T. and V.M.; investigation, B.D.; writing—original draft preparation, B.D. and H.T. and V.M; writing—review and editing, B.D. and H.T. and V.M; visualization, B.D.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was not subsidized.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Delalande, B.; Tamagawa, H.; Matveev, V. Membrane Potential: Any Diffusion? [CrossRef]
- Delalande, B.; Tamagawa, H.; Matveev, V. Membrane Potential: The Enigma of Ion Pumps. [CrossRef]
- Delalande, B.; Tamagawa, H.; Matveev, V. Membrane Potential: The Tamagawa Experiment. [CrossRef]
- Hille, B. Ion channels of excitable membranes, 3rd ed ed.; Sinauer: Sunderland, Mass, 2001. [Google Scholar]
- Galassi, V.V.; Wilke, N. On the Coupling between Mechanical Properties and Electrostatics in Biological Membranes. Membranes 2021, 11, 478. [Google Scholar] [CrossRef] [PubMed]
- Funk, R.H.; Scholkmann, F. The significance of bioelectricity on all levels of organization of an organism. Part 1: From the subcellular level to cells. Progress in Biophysics and Molecular Biology 2023, 177, 185–201. [Google Scholar] [CrossRef] [PubMed]
- Goldman, D.E. POTENTIAL, IMPEDANCE, AND RECTIFICATION IN MEMBRANES. The Journal of General Physiology 1943, 27, 37–60. [Google Scholar] [CrossRef] [PubMed]
- A. L. Hodgkin, P. Howrowicz. The influence of potassium and chloride ions on the membrane potential of single muscle fibers. J. Physiol. 1959, 148, 127–160. [Google Scholar] [CrossRef]
- Gouaux, E.; MacKinnon, R. Principles of Selective Ion Transport in Channels and Pumps. Science 2005, 310, 1461–1465. [Google Scholar] [CrossRef] [PubMed]
- Maex, R. On the Nernst–Planck equation. Journal of Integrative Neuroscience 2017, 16, 73–91. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Diffusion asymmetry. Two axon fractions are shown at a distance. The shape of the cell is often convex to the outside environment. This leads to a divergence of functioning from possible diffusion. There is an asymmetry that is due to diffusion theory, but it is not contained in the assumptions of membrane theory.
Figure 1.
Diffusion asymmetry. Two axon fractions are shown at a distance. The shape of the cell is often convex to the outside environment. This leads to a divergence of functioning from possible diffusion. There is an asymmetry that is due to diffusion theory, but it is not contained in the assumptions of membrane theory.
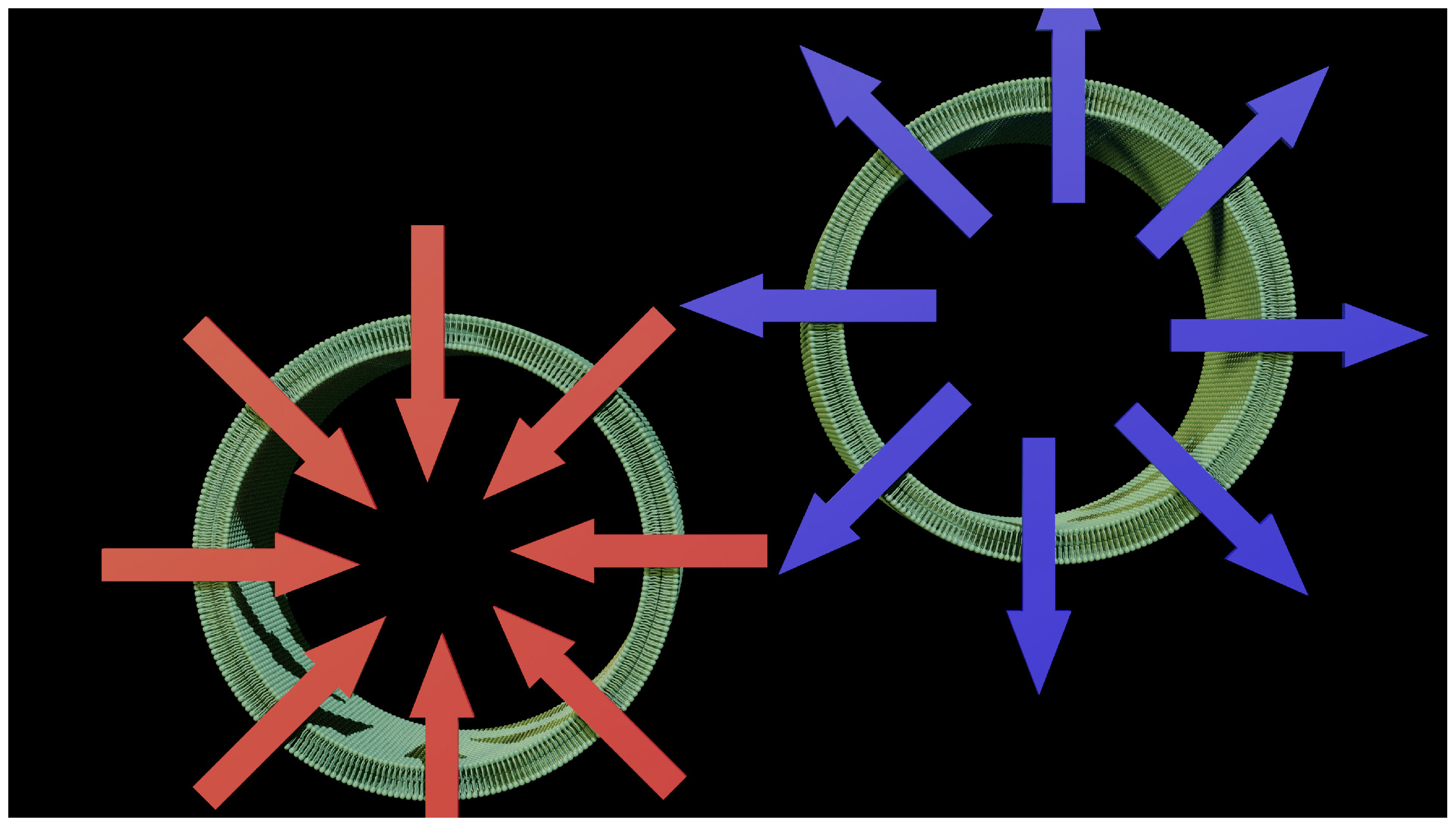
Figure 2.
Diffusion discrepancies. Two axon fractions are shown at a distance. Point X should be at the origin of two diffusion flows that are almost in opposite directions. That is impossible, or you would have to modify the theory to change the forces involved. This no longer works with diffusion.
Figure 2.
Diffusion discrepancies. Two axon fractions are shown at a distance. Point X should be at the origin of two diffusion flows that are almost in opposite directions. That is impossible, or you would have to modify the theory to change the forces involved. This no longer works with diffusion.

Figure 3.
Simulation of charges inside some ion channels and the electric field lines they impose. The resulting field may appear constant at a certain distance by mathematical integration, but it is, in fact, extremely complex. The field lines impose the movement and direction of the ions approaching the surface.
Figure 3.
Simulation of charges inside some ion channels and the electric field lines they impose. The resulting field may appear constant at a certain distance by mathematical integration, but it is, in fact, extremely complex. The field lines impose the movement and direction of the ions approaching the surface.
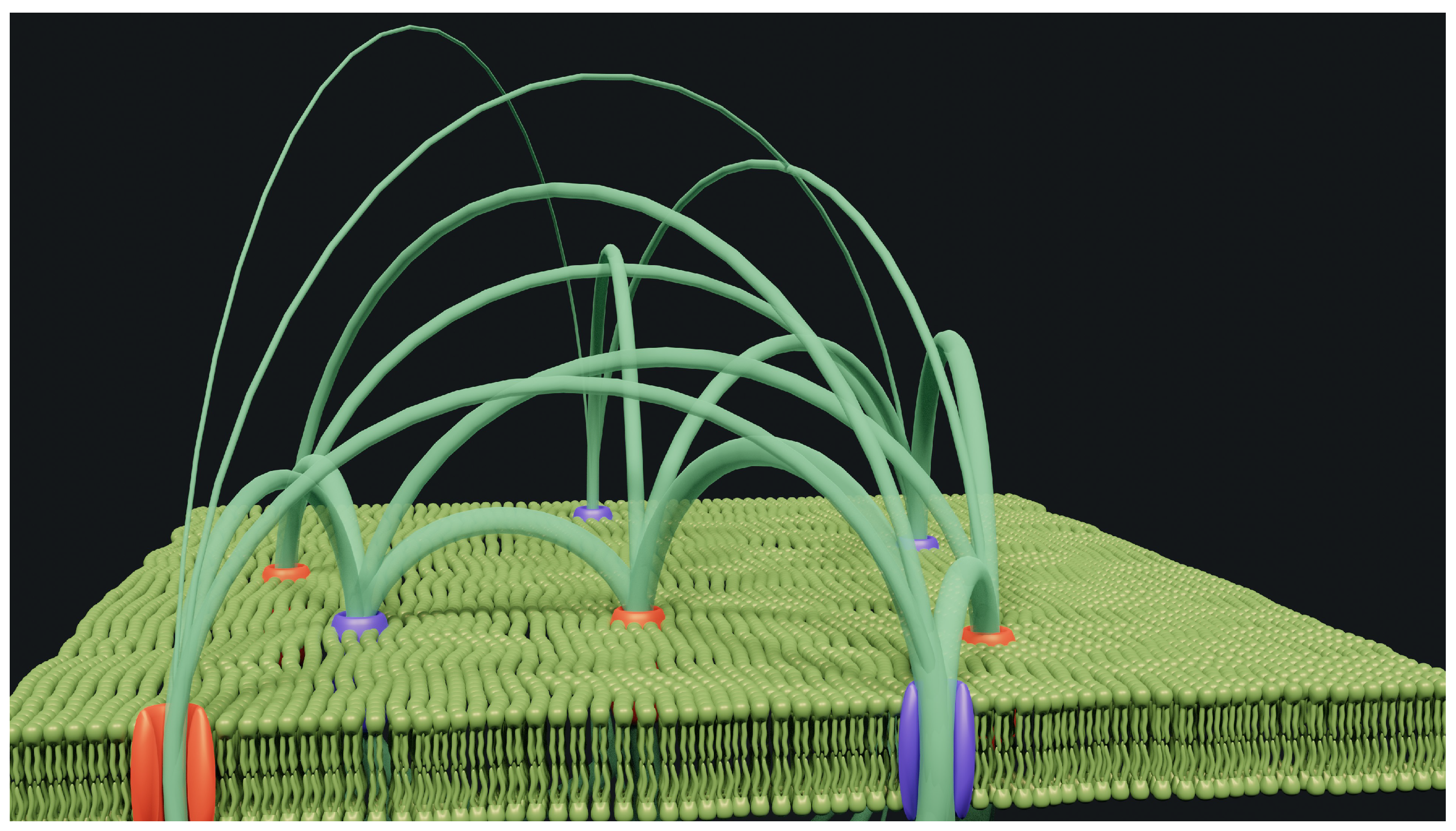
Figure 4.
The curvature of the membrane imposes an asymmetrical force on the lipid components. While it’s customary to show a horizontal section of membrane to demonstrate our hypotheses, we lose sight of the reality of the local situation. It is possible to understand that the function of ion channels is disrupted by membrane curvature. It’s also possible to question the forces that then close the channels, preventing any exchange.
Figure 4.
The curvature of the membrane imposes an asymmetrical force on the lipid components. While it’s customary to show a horizontal section of membrane to demonstrate our hypotheses, we lose sight of the reality of the local situation. It is possible to understand that the function of ion channels is disrupted by membrane curvature. It’s also possible to question the forces that then close the channels, preventing any exchange.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






