An Adaptive Mixup Hard Negative Sampling for Zero-Shot Entity Linking

Recently, the focus of entity linking research has centered on the zero-shot scenario, where the entity mention to be labeled at the time of testing was never observed during the training phase or may belong to a different domain than the source domain. Current studies have used BERT as the base encoder as it effectively establishes distributional links between source and target domains. The currently available negative sampling methods all use an extractive approach, which makes it difficult for the models to learn diverse and more challenging negative samples. To address this problem, we propose a generative negative sampling method, Adaptive_mixup_hard, which generates more difficult negative entities by fusing the features of both positive and negative samples on top of hard negative sampling and introduces a transformable adaptive parameter W to increase the diversity of negative samples. Next, we fuse our method with the Biencoder architecture and evaluate its performance under three different score functions. Ultimately, experimental results on the standard benchmark dataset Zeshel demonstrate the effectiveness of our method.

Keywords:

Subject:

Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Entity Linking(EL) is a critical task in the field of Natural Language Processing (NLP), whose core goal is to associate entity mentions appearing in a document (e.g., names of people, places, organizations, etc.) with their referent entity in a knowledge base (e.g., Wikipedia, Freebase, etc.). The EL task generally consists of the following main steps: entity detection, candidate entity generation, and candidate entity ranking. It should be noted that the specific steps and methods of EL tasks may vary in different application scenarios and tasks. In some tasks, entity detection may not be necessary because the entities in the text are already explicitly labeled. However, in an end-to-end EL task[1,2], it is usually necessary to include all these steps to complete the entity linking process. EL has received much attention due to its wide range of applications in various tasks, including information retrieval[3], content analysis[4], etc. However, significant progress has been made in building EL systems, and most of the existing research works[5,6] are based on the assumption that entity sets are shared between the train and test sets. However, in practice, textual data may come from different domains, topics, and sources, thus presenting diversity and heterogeneity in the data distribution. It also means that the train and test sets may come from different domain distributions, ultimately leading to disjoint entity sets in different domains. This situation highlights the need and importance of zero-shot entity linking[7,8].

The main goal of zero-shot EL is to address two aspects of the problem. Firstly, it aims to deal with unknown entities, having the ability to successfully link entities that have never been seen in the training data to the correct entities in the knowledge graph or entity repository. Secondly, it aims to build EL models that are more general so that they can be adapted to the challenges of different domains, topics, and data distributions, thus increasing the generality and robustness of the models to satisfy the information needs of multiple domains. However, labeled data is often costly to produce or difficult to access in certain specialist areas (e.g., legal). To delve deeper into this problem, [8] constructed the Zeshel dataset, containing 16 specialized domains, divided into 8 domains for training and 4 domains each for validation and testing, which covers rich textual content for mentions and entities. Without adopting resources (e.g., structured knowledge base) or assumptions (e.g., labeled mentions, a shared entity set), they expand the scope of zero-shot EL to promote the generalizability of the EL system on unseen domains.

To date, a body of work[9,10,11,12,13] has emerged on zero-shot EL, most of which uses BERT[14] as the base encoder. These research efforts have mainly focused on the candidate generation phase, which has a crucial impact on the candidate ranking in EL systems. [11] was based on encoding mentions and entities using a Biencoder[9] architecture, followed by a Sum-Of-Max(SOM) score function to compute the similarity between them and training the model using either hard negative sampling or mixed-p negative sampling. [13] proposed a Transformational Biencoder, which introduced a transformation into the Biencoder to encode mentions and entities and adopted an In-Domain negative sampling strategy, which they sorted all entities in the golden entity domain over a training period to take the top-k entities as hard negatives.

Concerning current negative sampling methods in the field of zero-shot EL, we note that they generally employ an extractive strategy, resulting in a lack of diversity in the selected negative samples, thus limiting the ability of the model to acquire richer knowledge. Furthermore, hard negative sampling aims to select more challenging negative samples to expose the model to more challenging tasks. However, the negative samples selected by the current hard negative sampling strategy are not yet challenging enough. Another problem is that the current zero-shot EL task is usually divided into two phases: candidate entity generation and ranking. These two phases of the task usually take a significant amount of time. Therefore, in the candidate entity generation phase, we believe that not only do we need to improve the recall of candidate entities to provide a richer pool of candidates for the candidate entity ranking phase, but we also need to improve the accuracy so that the model can match the ultimately correct entities in the candidate entity generation phase. These improvements will help to increase the performance and efficiency of the zero-shot EL system.

In this paper, we propose an Adaptive_mixup_hard generative negative sampling method based on the hard negative sampling method. The main innovation of the method is to generate more difficult negative samples by fusing the positive sample features of the current mention with negative sample features. In the generation process, a transformable adaptivity parameter W is introduced, which enables the model to generate rich and diverse negative samples during the training process to compensate for the shortcomings of the existing extractive negative sampling methods. In addition, this method inherits the feature that the negative entities selected by hard negative sampling are semantically different from the golden entities but closer in the embedding space, which helps to improve the differentiation between the golden entity and the negative entities. Therefore, we combine this negative sampling method with the Biencoder architecture to form a new model Biencoder_AMH. In the model, we adopt three different score functions (DUAL, Pooling Mean, and SOM) for similarity calculation. Through the validation of a large number of experiments, our model achieves a certain amount of improvement in the top-64 recalls and accuracy compared to previous work, which makes an essential contribution to the research of matching to the final correct entity in the candidate entity generation stage. Notably, our model achieves different degrees of improvement in each of the r@k(k=4, 8, 16, 32, 64) metrics, which indicates that our approach not only improves the performance but also provides a strong support for the research in the candidate entity ranking stage. More importantly, we show results at a finer granularity, demonstrating that the improvement in model performance is not limited to a single domain in the test set but grows on multiple domains, which is more in line with the context and goal of zero-shot entity linking.

Our contributions can be summarized as follows:

We propose an Adaptive_mixup_hard negative sampling, a method variant on hard negative sampling that enables the model to cope with more demanding challenges. Subsequently, we merge this method with the Biencoder[9] architecture to construct a new model Biencoder_AMH.
Our negative sampling method is a generative approach that generates a diversity of negative samples, which helps the model learn the data distribution more comprehensively and reduces the potential risk of overfitting, improving the model’s generalization performance.
After extensive experimental validation, our method achieves not only a significant improvement in top-64 recalls but also a certain degree of improvement in accuracy when compared with other negative sampling strategies (Random, Hard, Mixed-p) under three different score functions (DUAL, Pooling Mean, SOM).

2. Related Works

We discuss related work to better contextualize our contributions. The entity linking task can be divided into candidate generation and ranking. Previous work has used frequency information, alias tables, and TF-IDF-based methods to generate candidates. For candidate ranking, [5,15,16,17], and [18] have established state-of-the-art(SOTA) results using neural networks to model context word, span and entity. It has also been shown that fine-grained entity type information helps to link[19,20,21].

In the EL domain, negative sampling strategies aim to efficiently select negative samples to optimize the performance of EL tasks. [8] proposed the zero-shot entity linking task. Recently, the strategy of negative sampling has been widely used in the candidate generation phase in the domain of zero-shot entity linking. [9] followed [22] by using hard negatives in training. They obtained hard negatives by finding the top 10 predicted entities for each training example and added these extra hard negatives to the random in-batch negatives. [11] demonstrated the results obtained with different negative sampling strategies(Random, Hard, and Mixed-p) on different architectures and showed theoretically and empirically that hard negative mining always improves performance for all architectures. [13] thought that negatives that are lexically similar, semantically different, and close to the golden entity representation are more difficult. As a result, they considered the domain of the golden entity. They sorted all entities in the golden entity domain over a training period to take the top-k entities as hard negatives. However, the negatives generated by the above methods are not difficult enough. Therefore, we generate more difficult negatives based on hard negative sampling by incorporating the features of the golden entity, allowing the model to face more difficult challenges.

In the candidate generation, [8] used BM25, a variant of TF-IDF, to measure the similarity between mentions with their contexts and candidate entities with their descriptions. Numerous applications to the Zeshel dataset have sprung up following this work. Among them, BERT[14] is found to be a highly regarded encoder. [9] proposed a Biencoder architecture in which textual descriptions of mentions and entities are encoded using two independent BERT encoders. Then, the dot product is used as a scorer and is referred to by [11] as DUAL. Due to BERT, the Biencoder provides a robust baseline for the task. In the study by [10], they used repeated location embedding based on the BERT architecture to address the problem of remote modeling in entity text description. [11] used the Biencoder framework. However, they used the more expressive SOM[23] score function to measure the correlation between mentions and entities and, as a result, achieved better results on the task. [13] proposed a Transformational Biencoder, which introduced a transformation into the Biencoder[9] to improve the generalization performance of zero-shot EL over unknown domains. Accordingly, we also combined our negative sampling approach with the Biencoder architecture and notably achieved some improvements on three different score functions(DUAL, Pooling Mean, and SOM).

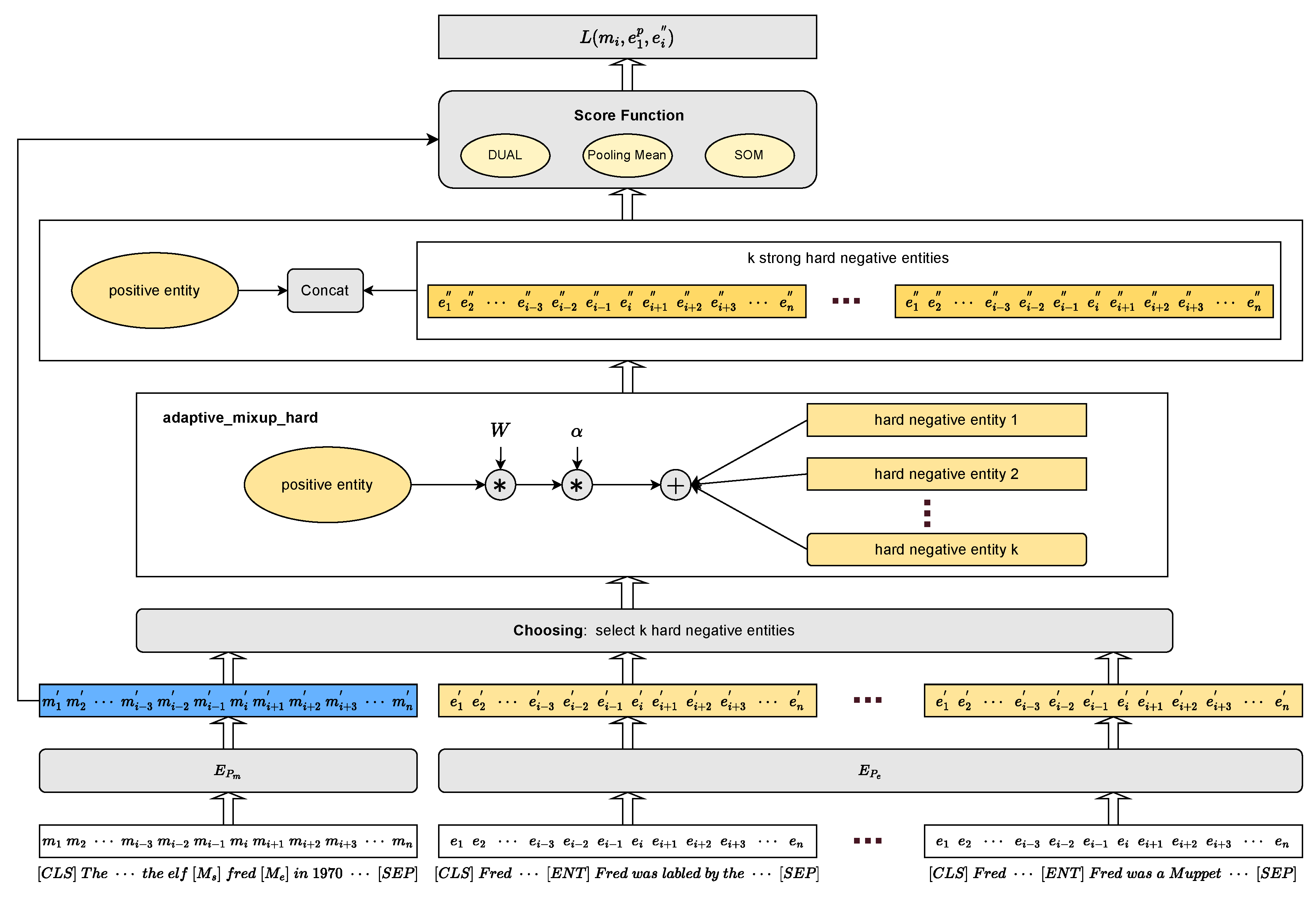
Figure 1. Biencoder_AMH consists of three main parts: Biencoder, Adaptive_mixup_hard and Score Function.

3. Methodology

In this section, we describe our adaptive_mixup_hard negative sampling strategy, a method variant on hard negative sampling, inspired via [24]. We then combine our negative sampling approach with the Biencoder[9] and multiple similarity calculations(DUAL, Pooling Mean, and SOM) to propose our model Biencoder_AMH. First, we formally present the task definition in Section 3.1. Next, in Section 3.2 we introduce the Biencoder. Then, we describe our adaptive_mixup_hard negative sampling strategy in Section 3.3. Finally, we present our model Biencoder_AMH in Section 3.4.

3.1. Task Definition

The entity linking task is expressed as follows. Given a mention m in a document and a set of entities

Ψ = {\{e_{i}\}}_{i = 1, . . ., n}

, EL aims to identify the referring entity

e \in Ψ

that corresponds to the mention m. The goal is to obtain an EL model on the train set of mention-entity pairs

D^{T r a i n} = {\{(m_{i}, e_{i}) | e_{i} \in Ψ\}}_{i \in [1, n]}

, that correctly labels mentions in the test set

D^{T e s t}

D^{T r a i n}

and

D^{T e s t}

are usually assumed to be from the same domain. We assume that the title and description of the entities are available, which is a common setting in entity linking[5,8].

In this paper, we focus on the study of the zero-shot EL[8], where both

D^{T r a i n} = {\{D_{s r c}^{i}\}}_{i = 1, . . ., n_{s r c}}

and

D^{T e s t} = {\{D_{t g t}^{i}\}}_{i = 1, . . ., n_{t g t}}

are found to contain multiple sub-datasets from different domains. At the same time, the knowledge base is separated into training and test time. Formally, denote

κ_{t r a i n}

and

κ_{t e s t}

to be the knowledge base in training and test, we require

κ_{t r a i n} \cap κ_{t e s t} = ϕ

. The collection of text documents, mentions, and entity dictionaries are separated for training and testing, so linked entities are not visible during the test.

Below, we will describe the three negative sampling methods that are already available.

Random: The negatives are sampled uniformly at random from all entities of a batch in training data. It can help the model deal with unknown entities in various situations but may lead to a training process that lacks guidance for specific textual contexts.
Hard: It is a more challenging strategy that tries to select semantically similar negatives to positive examples. In this way, the model will face more incredible difficulty in learning and will need a better understanding of the meaning of the entity in different contexts. It aims to help models capture semantic information better, but it can also lead to a more strenuous training process.
Mixed-p: p percent of the negatives are hard, the rest are random. It maintains a degree of diversity in the training process while introducing a degree of challenge. Previous works have shown that such a combination of random and hard negatives can be effective. [11] finds the performance is not sensitive to the value of p, In this paper, We choose a p-value of 50%.

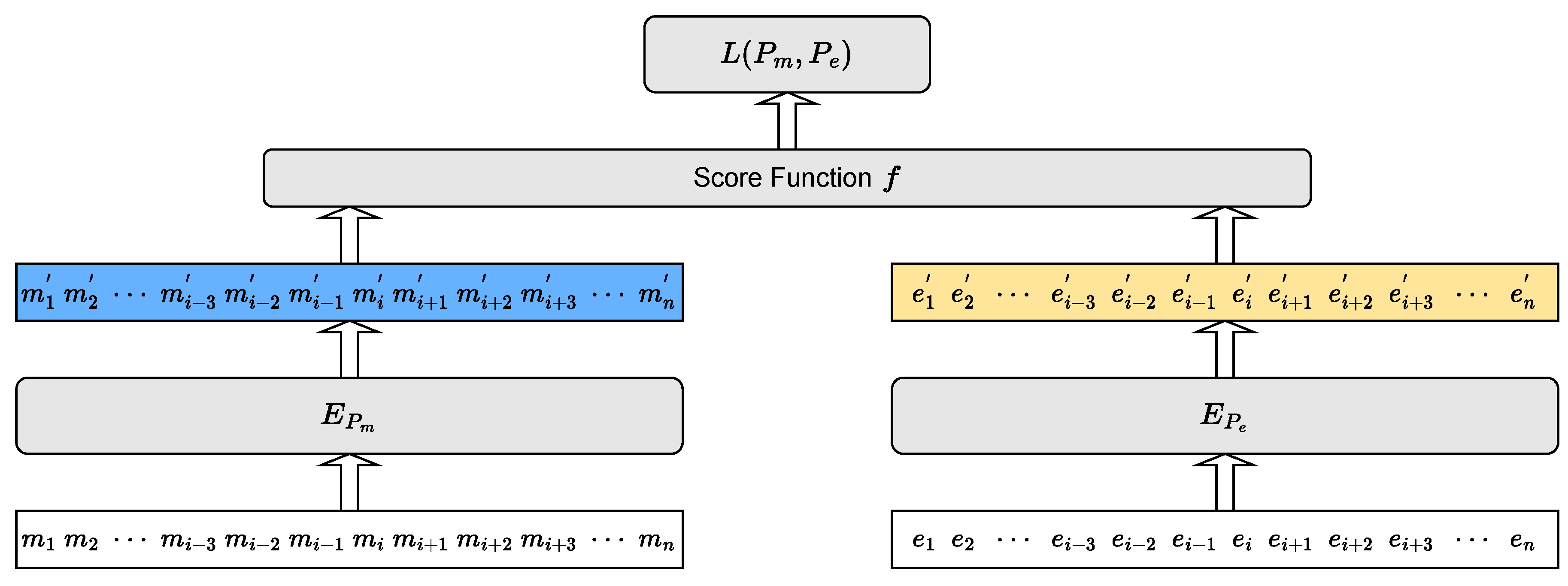
3.2. Biencoder

Our model is based on the Biencoder[9], which independently embeds mentions and corresponding entities into the same representation space. As shown in Figure 2, the Biencoder comprises a text encoder

E_{P_{m}}

for encoding mentions, a text encoder

E_{P_{e}}

for encoding entities, and a score function f for calculating the relevant scores for mention-entity pairs.

E_{P_{m}}

and

E_{P_{e}}

share the same architecture but have independent parameters,

P_{m}

and

P_{e}

and BERT[14] is employed to model

E_{P_{m}}

and

E_{P_{e}}

. This approach allows for real-time reasoning because candidate representations can be cached.

Given a pair of the mention-entity

(m, e)

, the representation of mention m is composed of the left context

(c t x t_{l})

and right context

(c t x t_{r})

of the mention, as well as the mention itself. Specifically, we construct the input for each mention m as:

m = [C L S] c t x t_{l} [M s] m e n t i o n [M e] c t c t_{r} [S E P]

(1)

Likewise, the entity representation e is also composed of word pieces of the entity title and description. Therefore, the input to our entity e is:

e = [C L S] t i t l e [E N T] d e s c r i p t i o n [S E P]

(2)

Where [CLS], [Ms], [Me], [ENT], and [SEP] are special tokens to mark the boundaries of the different pieces of information. For instance, [ENT] is a special token to separate entity title and description representation. More specifically, the input of mention m is represented after tokenization as

T_{m} = {\{m_{t}\}}_{t = 1, . . ., n_{m}}

and the entity e is denoted as

T_{e} = {\{e_{t}\}}_{t = 1, . . ., n_{e}}

. Then, both input context

T_{m}

and candidate entity

T_{e}

are encoded into vectors

V_{m} \in R^{n_{m} \times d}

and

V_{e} \in R^{n_{e} \times d}

\begin{matrix} V_{m} & = E_{P_{m}} (T_{m}) \\ V_{e} & = E_{P_{e}} (T_{e}) \end{matrix}

(3)

where d denotes the dimension of representations.

The problem of the entity linking is then reduced to using a score function f, i.e.,

f (V_{m}, V_{e})

to quantify the similarity between

V_{m}

and

V_{e}

. In the current mention-entity pair

(m, e)

, if the entity e is the golden entity, the score

f (V_{m}, V_{e})

should be high, or low if otherwise.

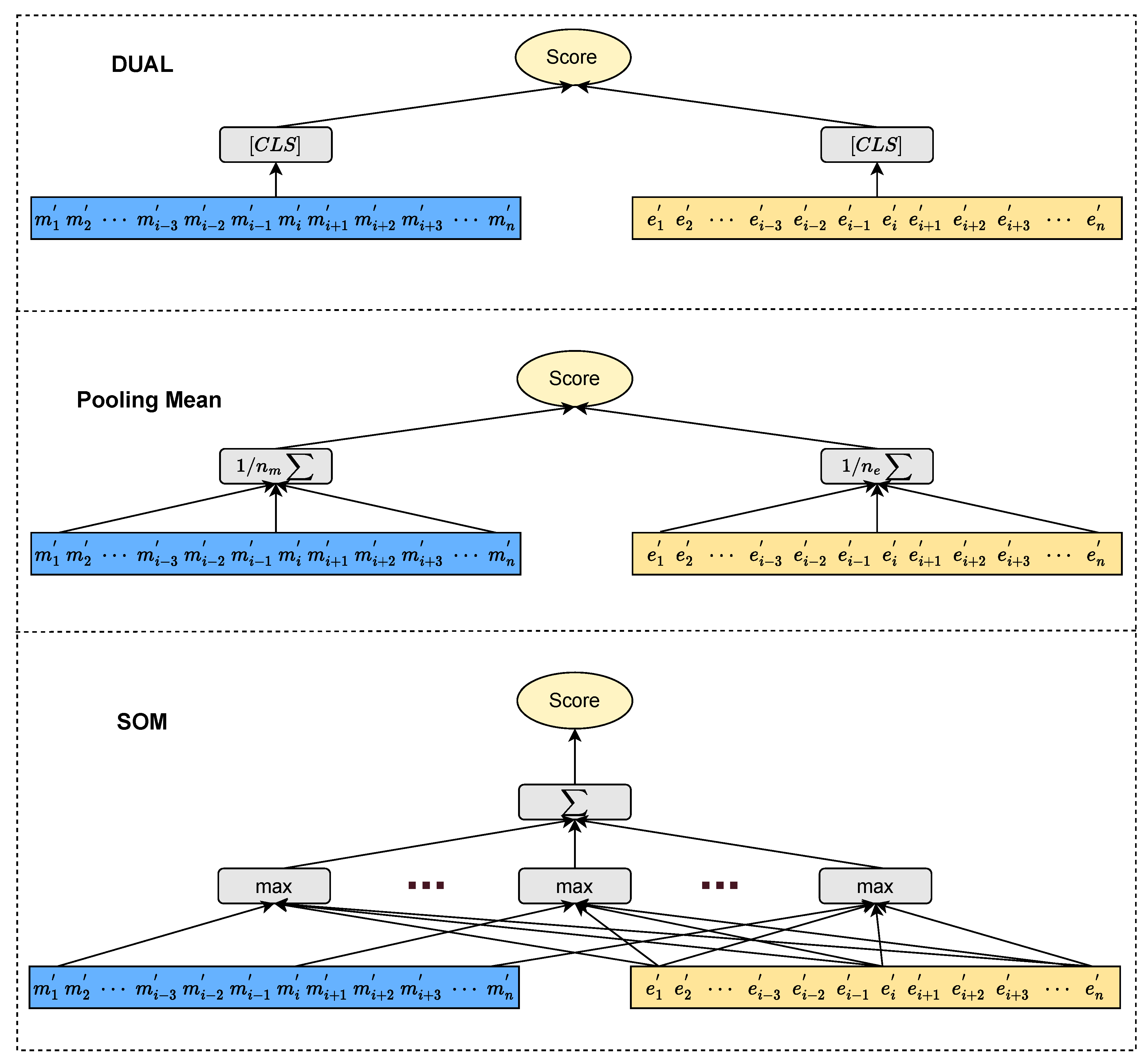
As shown in Figure 3, we will introduce the three existing score functions. [9] defines a DUAL score function that chooses the

[C L S]

representations

v_{[C L S]}^{m} \in R^{1 \times d}

and

v_{[C L S]}^{e} \in R^{1 \times d}

of the respective representations

V_{m}

and

V_{e}

to compute the score

f (V_{m}, V_{e})

DULA:

f (V_{m}, V_{e}) = v_{[C L S]}^{m} {(v_{[C L S]}^{e})}^{T}

(4)

Pooling Mean can be used to average pool the embeddings in a text fragment of the mention and entity to obtain an overall representation of the text fragment. Doing so allows the text snippet to be represented as a vector, reflecting the average features. Pooling Mean computes

f (V_{m}, V_{e})

as follows.

Pooling Mean:

f (V_{m}, V_{e}) = \frac{1}{n_{m}} \sum_{t = 1}^{n_{m}} v_{t}^{m} {(\frac{1}{n_{e}} \sum_{t = 1}^{n_{e}} v_{t}^{e})}^{T}

(5)

In addition, [11] followed the architecture of [9] and presented that the SOM scorer[23] produces better results than DUAL. However, it is worth noting that the SOM scorer comes at the cost of increased computational cost due to considering all hidden states of

V_{m}

and

V_{e}

in the scorer. It means SOM takes more time than DUAL and Pooling Mean in the training and prediction phases. SOM computes

f (V_{m}, V_{e})

as follows.

SOM:

f (V_{m}, V_{e}) = \sum_{t = 1}^{n_{m}} \underset{t^{^{'}} = 1}{\overset{n_{e}}{m a x}} v_{t}^{m} {(v_{t^{^{'}}}^{e})}^{T}

(6)

Eventually, train the network to maximize the score of the correct entity relative to the (randomly sampled) entities of the same batch([25,26]). Concretely, the total loss

L

is computed as:

\begin{matrix} L (P_{m}, P_{e}) = \frac{1}{B} \sum_{i = 1}^{B} (- f (E_{P_{m}} (T_{m_{i}}), E_{P_{e}} (T_{e_{i, 1}})) + \\ \frac{1}{B} \sum_{i = 1}^{B} ({log}_{} \sum_{j = 1}^{B} exp (f (E_{P_{m}} (T_{m_{i}}), E_{P_{e}} (T_{e_{i, j}})))) \end{matrix}

(7)

Where

{\{(m_{i}, e_{i, 1})\}}_{i = 1, . . ., B}

are golden mention-entity pairs in the training set, and

\{e_{i, 2}, . . ., e_{i, B}\}

are

B - 1

negative entities for the i-th mention in a batch.

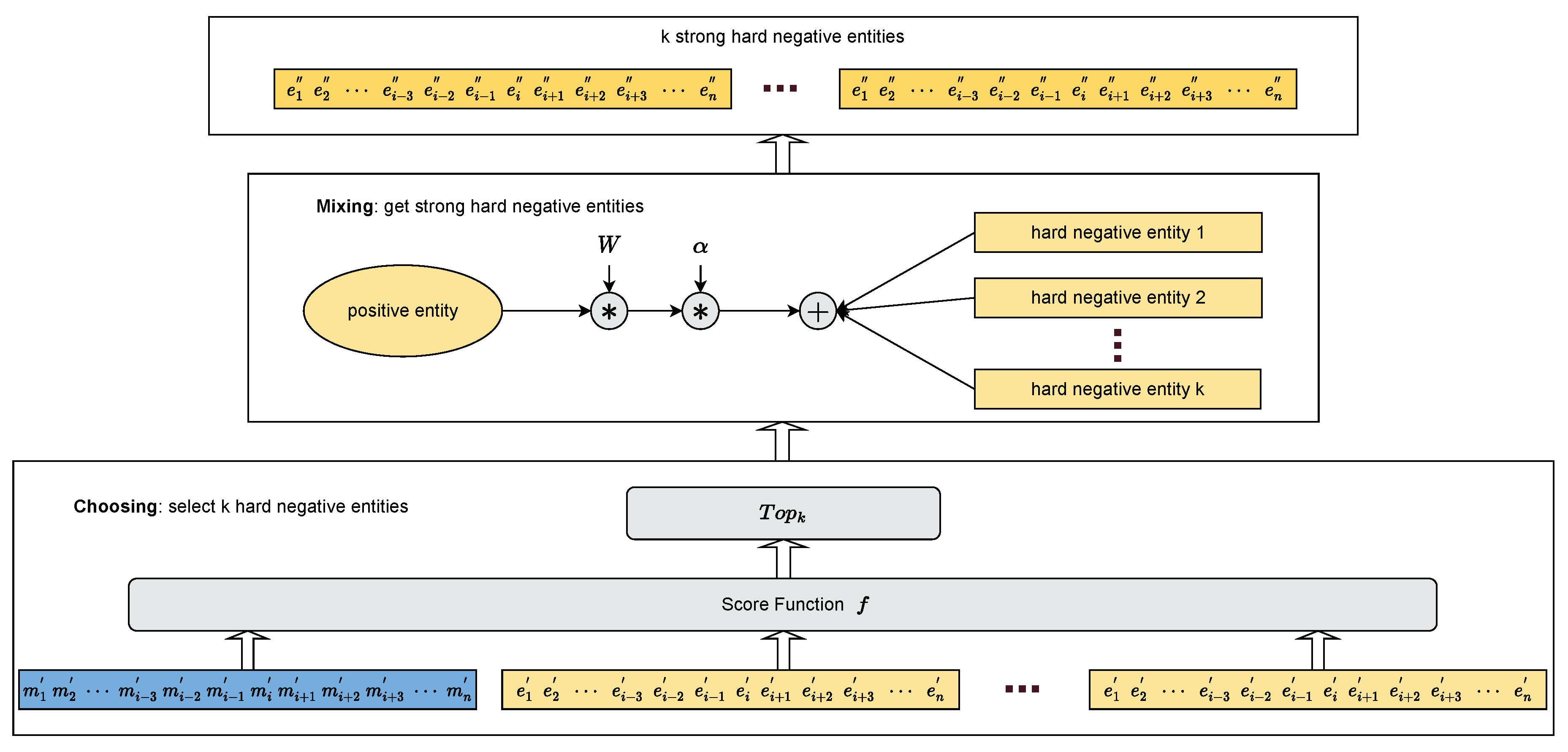
3.3. Adaptive_mixup_hard

It is known that hard negative sampling makes it more difficult for the model to learn, allowing it better to understand the meaning of entities in different contexts. However, the negative samples obtained under this sampling are still not challenging enough for zero-shot entity linking. Therefore, as shown in Figure 4, we propose the adaptive_mixup_hard(AMH) negative sampling, a method variant on hard negative sampling following a two-stage pipeline: choosing and mixing. This method improves the robustness of the model by fusing the features of positive entity

V_{e}^{p}

and negative entities

V_{e}^{n}

to obtain more difficult negative samples(strong hard negatives), enabling the model to face more complicated tasks.

Below, we will describe the two-stage process of the AMH negative sampling.

Choosing: For the mention-entity pairs

{(m_{i}, e_{i})}_{i = 1, . . ., B}

in a batch, they are encoded into vectors

{(V_{m_{i}}, V_{e_{i}})}_{i = 1, . . ., B}

. Then, for each mention m in a batch, there is one positive entity

V_{e, 1}^{p}

and the rest are its corresponding negative entities

{(V_{e, i}^{n})}_{i = 2, . . ., B}

. Next, we use the scoring function f to compute the scores of the mentions with their corresponding negative entities. According to hard negative sampling, we select the top k highest scores among the negative entities as the hard negative entities

{(V_{e, i}^{n})}_{i = 1, . . ., K}

. The hard negative entities are computed as:

{(V_{e, i}^{n})}_{i = 1, . . ., K} = T o p_{k} \{f (V_{m}, V_{e, 2}^{n}), . . ., f (V_{m}, V_{e, B}^{n})\}

(8)

Mixing: This process is crucial to our approach and aims to synthesize strong, hard negative entities to improve the robustness of the model. Considering that it may be counterproductive to train the model if it is too difficult to fuse the negative entities of the positive entity features at the beginning, we introduce an adaptive parameter

W \in [0, 1]

. Its calculation is as follows:

W = \frac{exp (f (V_{m}, V_{e, 1}^{p}))}{exp (f (V_{m}, V_{e, 1}^{p})) + \sum_{i = 1}^{K} exp (f (V_{m}, V_{e, i}^{n}))}

(9)

During the training process, W will increase to progressively increase the difficulty of negative entities, which allows the model to learn more diverse representations. It is worth noting that W will eventually increase to 1. Therefore, we also introduce an additional hyper-parameter

α \in (0, 1]

to control the difficulty of synthesizing new negative entities. The strong hard negative entity

V_{e, i}^{s t r o n g} \in R^{n_{e} \times d}

is computed as:

V_{e, i}^{s t r o n g} = α \cdot W \cdot V_{e, 1}^{p} + V_{e, i}^{n}

(10)

It is worth noting that for different score functions, different

α

values cause the model to perform differently and that there is a critical value at which the model performs best. We will describe this in more detail in Section 4.5.

Figure 4. Architecture of adaptive_mixup_hard

3.4. Biencoder_AMH

Eventually, we combine Biencoder, Adaptive_mixup_hard, and Score Function to form our new model Biencoder_AMH. More specifically, we form the new model Biencoder_AMH_DUAL using DUAL as the score function. Similarly, depending on the different score functions Pooling Mean and SOM, we will also form Biencoder_AMH_Pooling_Mean and Biencoder_AMH_SOM, respectively. Because, depending on the scoring function f, our negative sampling strategy AMH has different rules for the first stage of choosing.

As shown in Figure 1, first, we follow the Biencoder architecture and use BERT[14] to encode mentions with their contexts and entities with their descriptive information to obtain their encoded representations

V_{m}

and

V_{e}

, respectively. Then according to our method AMH, we first filter a batch to get K hard negative entities

{(V_{e, i}^{n})}_{i = 1, . . ., K}

and one positive entity

V_{e, 1}^{p}

corresponding to the current mention m, and finally fuse the features of each negative entity with those of the positive entity to get K strong hard negative entities

{(V_{e, i}^{s t r o n g})}_{i = 1, . . ., K}

. Finally, we input

V_{m}

V_{e, 1}^{p}

and

{(V_{e, i}^{s t r o n g})}_{i = 1, . . ., K}

into the scoring function f and use BCEWithLogitsLoss to calculate the loss

L

. Concretely, for each training pair

(m_{i}, e_{i})

in a batch of B pairs, the loss is computed as:

\begin{matrix} L (m_{i}, e_{i}) = - {log}_{} (s i g m o i d (f (V_{m_{i}}, V_{e_{i, 1}}^{p}))) - \\ \sum_{j = 1}^{K} {log}_{} (1 - s i g m o i d (f (V_{m_{i}}, V_{e_{i, j}}^{s t r o n g}))) \end{matrix}

(11)

where

V_{m_{i}}

indicates the code corresponding to the current mention m.

V_{e_{i, 1}}^{p}

and

V_{e_{i, j}}^{s t r o n g}

denote the coding of the positive entity and strong hard negative entity corresponding to m respectively.

s i g m o i d (\cdot)

is a function that maps the model’s output to the probability space, facilitating probability estimation and the computation of cross-entropy loss.

4. Experiments

In this section, we only empirically investigate our model on the Zeshel[8], a challenging dataset for zero-shot entity linking. We have conducted in-depth research and experiments on all three similarity calculations(DUAL, Pooling Mean, and SOM)[23].

4.1. Dataset

Zeshel is a prevailing benchmark dataset for zero-shot entity linking and contains 16 specialized domains from Wikia, divided into 8 domains for training and 4 domains each for validation and testing. The train, validation, and test sets have 49K, 10K, and 10K examples, respectively. Table 1 shows the details of this dataset, including the number of entities and mentions.

4.2. Evaluation Protocol

EL systems typically follow a two-stage pipeline: (1) a candidate generation stage, training an entity retriever to select the top-k candidate entities for each mention; (2) a candidate ranking stage, training a ranker to identify the golden entity among selected candidate entities. Candidate generation is critical to the performance of candidate ranking because if no golden entity is retrieved in the top-k candidates, the model can never recover the golden entity during the candidate ranking process. So, we follow the evaluation protocol of the previous work[8,9,11] and evaluate at the candidate generation stage. We report accuracy and top-64 recall for models on the validation and testing sets.

4.3. Implementation Details

We experiment with BERT-base[14] for our models. We directly use the preprocessed dataset provided by [9]. We tune the models over {5, 10, 15, 30} epochs using a batch size of 64 for mention-entity pairs. We only consider the learning rate as 2e-5. We perform a grid search to select the best set of hyper-parameters:

α

in [0.1, 0.2, 0.3,...,1] for DUAL and Pooling Mean and K in [1, 2, 4, 6, 8, 10, 12, 14, 16, 18] for SOM. Our models are implemented in PyTorch and optimizied with Adam[27]. All models are trained on one NVIDIA 3090 24GB, and the results are the average over 3 runs using different random seeds.

4.4. Performance Comparison

In this section, we compare our model against recent work[8,9] and different negative sampling methods for candidate generation. In addition, we consider the comparison of accuracy rates. These works use the Biencoder and generate negative entities for optimization. DUAL, Pooling Mean, and SOM scorers are employed in this work.

4.4.1. Main Results

The model comparison results are shown in Table 2. Hard and mixed negative examples for all architectures always yield considerable improvements over random negative examples. It is worth noting that for top-64 recalls, our negative sampling strategy performs better than these three negative sampling strategies. More specifically, regarding the DUAL scorer on the test, We find that our negative sampling strategy improves over random negative sampling by 3.65%, over hard negative sampling by 1.31%, and over mixed negative sampling by 1.36%. Concerning the Pooling Mean scorer on the test, We observe that our method improves over random negative sampling by 3.69%, over hard negative sampling by 1.81%, and over mixed negative sampling by 2.76%. The final average improvement in SOM scorer on the test is particularly significant, being 2.04% over random negative sampling, 1.28% over hard negative sampling, and 2.21% over mixed negative sampling, respectively. These results indicate the effectiveness of our sampling strategy. We also find that SOM yields better results over DUAL and Pooling Mean, while hard sampling leads to better optimization. However, SOM is more expensive and time-consuming to compute.

Interestingly, We also take accuracy into account. We observe that our method achieves better performance compared to other negative sampling strategies concerning DUAL and Pooling Mean. However, to the SOM, hard negative sampling performs better. In addition, in terms of accuracy, DUAL and Pooling Mean yield better results over SOM, and Pooling Mean is slightly better on the test.

4.4.2. Domain Zero-Shot Performance

Our main results show that we achieved the best performance on both validation and testing sets with respect to the top-64 recalls. To show that this improvement is actual for all test domains and not a result of a specific test domain, we show more fine-grained results. Specifically, we report the domain zero-shot performance on the testing sets over different choices of architecture and negative examples. Table 3 shows the results for the different testing domains.

Obviously, the results on the test domains "Forgotten Realms" and "Lego" are better than the other two domains. For the DUAL, our method exhibits the best performance in all domains. However, our method is 0.67% lower than hard negative sampling for Pooling Mean on the domain "Lego" and 0.08% lower than random negative sampling for SOM on the domain "Forgotten Realms". Overall, our method has shown better results on the different ways of calculating similarity, and the results on domains "Star Trek" and "YuGiOh" gain a significant boost, 85.07% and 78.25%, respectively.

4.5. Impact of $α$

In this section, we investigate the sensitivity of DUAL and Pooling Mean in terms of the hyper-parameter

α

. Recall

α

indicates the corresponding restriction after a strong hard negative sample is produced by fusing the current negative sample with the positive sample, where the range of

α

is set between 0 and 1. A smaller

α

means this strong hard negative sample is slightly weaker and vice versa. However, this does not mean that the stronger this strong negative sample is, the better, and at the same time, it is not the weaker, the better, but rather, for different similarity calculation structures, there exists an intermediate value in the range of settings that makes the current performance optimal. Table 4 and Table 5 contend to show the results obtained under different

α

for DUAL and Pooling Mean, which will be analyzed in the following.

In Table 4, we find that DUAL achieves the best performance for top-64 recalls with

α

of 0.3 and for accuracy with

α

of 0.7 on the test. Meanwhile, with increasing

α

, the performance of top-64 recalls decreases. In Table 5, we observe that Pooling Mean achieves the best performance for top-64 recalls with

α

of 0.3 and for accuracy with

α

of 0.8 on the test. By adjusting the

α

, we still find that Pooling Mean performs better than DUAL in terms of accuracy, being 0.29% higher, while for top-64 recalls, DUAL is better by 0.08%. At the same time, at some value of

α

, the

α

will show a difference of about 1% compared to the

α

in the case that shows the best performance, indicating the importance of controlling

α

. Considering the time and computational cost, we do not analyze the results presented by SOM under different

α

4.6. Impact of K

In this section, we investigate the sensitivity of SOM in terms of the hyper-parameters K. K in our method denotes the number of negative samples formed after fusion with positive sample features. We have selected only some of the K to compare the results of the test. Table 6 illustrates the specific results. As with the hyper-parameter

α

introduced in the previous section, there also exists an intermediate value for the number of strongly negative samples K after fusing the positive sample features, allowing the current model to exhibit optimal performance to the SOM. It is also predicted that this should be true for the other two similarity computation structures(DUAL and Pooling Mean).

In Table 6, we find that SOM achieves the best performance for top-64 recalls with K of 10 and for accuracy with K of 16 on the test. In addition, comparing with Table 2 for the highest accuracy of 32.74% on the test demonstrated for SOM in hard negative sampling, the model achieves a result of 34.15% at a K of 16, a 1.41% improvement. Thus, by adjusting the value of K on the SOM, our method will also show better performance in terms of accuracy than other negative sampling strategies. It follows that controlling the value of K is also particularly important for our approach.

4.7. Analyzing the number of candidates

In a two-stage entity linking system, the choice of the number of candidates retrieved influences the overall model performance. Previous work has typically used a fixed number of k candidates where k ranges from 5 to 100(for instance, [17] and [5] choose k = 30, [8] choose k = 64). According to [9] and Table 7, When k is larger, the recall accuracy increases; however, the ranking stage accuracy will likely decrease. Further, increasing k would often increase the run-time on the ranking stage.

In the following, we will analyze the importance of the number of candidate entities k in three aspects.

(i): Accuracy: A smaller number of candidate entities improves the accuracy of the system in selecting the correct entity. If there are too many candidate entities, the system may experience difficulties because there may be many similar entities, making it difficult for the model to make the correct selection.
(ii): Coverage: An increase in the number of candidate entities can increase the coverage of the system. In zero-shot entity linking, certain entities may not be covered in the candidate entity set, which can result in those entities not being linked correctly. A more comprehensive candidate entity set can improve the chances of successful linking, especially for rare or nonexistent entities in the training data.
(iii): Efficiency: The number of candidate entities is also related to the efficiency of the linking process. Fewer candidate entities mean the system needs less time and computational resources for entity linking.

However, increasing the number of candidate entities may also lead to problems such as increased noise and interference and reduced entity linking accuracy. Therefore, a balance needs to be found between the number of candidate entities and the accuracy of entity linking. As shown in Table 7, our method shows better performance for r@k(k=4, 8, 16, 32, 64) compared to other negative sampling strategies to the SOM, which lays a solid foundation for future research on the number of candidate entities k in the entity ranking stage.

5. Conclusion

We introduce the adaptive_mixup_hard(AMH) negative sampling, a method variant on hard negative sampling to obtain more difficult negative samples to improve the robustness and performance of the model on the task of zero-shot entity linking. Furthermore, we also combine our negative sampling method with the Biencoder architecture to form our new model Biencoder_AMH and test its performance on three different score functions(DULA, Pooling Mean, and SOM). Our work shows the performance of our method compared to other negative sampling methods(Random, Hard, and Mixed-p) under the same score function. Our experimental analysis demonstrates that our approach generally performs better on both validation and testing sets. More importantly, this improvement is genuine for essentially all test domains and not as a result of a specific test domain. In addition, we conduct extensive experiments to optimize the hyper-parameters

α

and K in our method and demonstrate that our method provides a solid foundation for the subsequent entity ranking stage. However, in the fusion of features of positive and negative samples, we currently only consider the control of the weights of features of positive samples, so we are thinking about whether we need to control the weights of negative samples simultaneously. We leave this thought for future work.

Author Contributions

Conceptualization, S.C. and X.W.; methodology, S.C.; software, S.C.; validation, S.C., X.W., Y.C. and Z.W.; formal analysis, S.C.; investigation, X.W.; resources, S.C.; data curation, Y.C. and Z.W.; writing—original draft preparation, S.C.; writing—review and editing, S.C.; visualization, X.W., Y.C. and Z.W.; supervision, M.M. and J.Z.; project administration, M.M; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Natural Science Foundation of Xinjiang Uyghur Autonomous Region under Grant No.2021D01C079.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/lajanugen/zeshel

Acknowledgments

The authors would like to thank the anonymous reviewers for their contribution to this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

Li, B.Z.; Min, S.; Iyer, S.; Mehdad, Y.; tau Yih, W. Efficient One-Pass End-to-End Entity Linking for Questions. arXiv 2020, arXiv:cs.CL/2010.02413]. [Google Scholar]
Ayoola, T.; Tyagi, S.; Fisher, J.; Christodoulopoulos, C.; Pierleoni, A. ReFinED: An Efficient Zero-shot-capable Approach to End-to-End Entity Linking. In Proceedings of the Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies: Industry Track; Association for Computational Linguistics: Hybrid: Seattle, Washington + Online, 2022; pp. 209–220. [Google Scholar] [CrossRef]
Lin, T.; Etzioni, O.; et al. Entity linking at web scale. In Proceedings of the Proceedings of the joint workshop on automatic knowledge base construction and web-scale knowledge extraction (AKBC-WEKEX), 2012, pp.; pp. 84–88.
Weng, J.; Lim, E.P.; Jiang, J.; He, Q. TwitterRank: Finding Topic-Sensitive Influential Twitterers. In Proceedings of the Proceedings of the Third ACM International Conference on Web Search and Data Mining; WSDM ’10; Association for Computing Machinery: New York, NY, USA, 2010; pp. 261–270. [Google Scholar] [CrossRef]
Ganea, O.E.; Hofmann, T. Deep Joint Entity Disambiguation with Local Neural Attention. arXiv 2017, arXiv:cs.CL/1704.04920]. [Google Scholar]
Cao, Y.; Hou, L.; Li, J.; Liu, Z. Neural collective entity linking. arXiv 2018, arXiv:1811.08603 2018. [Google Scholar]
Sil, A.; Cronin, E.; Nie, P.; Yang, Y.; Popescu, A.M.; Yates, A. Linking Named Entities to Any Database. In Proceedings of the Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning; Association for Computational Linguistics: Jeju Island, Korea, 2012; pp. 116–127. [Google Scholar]
Logeswaran, L.; Chang, M.W.; Lee, K.; Toutanova, K.; Devlin, J.; Lee, H. Zero-shot entity linking by reading entity descriptions. arXiv 2019, arXiv:1906.07348 2019. [Google Scholar]
Wu, L.; Petroni, F.; Josifoski, M.; Riedel, S.; Zettlemoyer, L. Scalable Zero-shot Entity Linking with Dense Entity Retrieval. 2020, arXiv:cs.CL/1911.03814]. [Google Scholar]
Yao, Z.; Cao, L.; Pan, H. Zero-shot Entity Linking with Efficient Long Range Sequence Modeling. In Proceedings of the Findings of the Association for Computational Linguistics: EMNLP 2020. Association for Computational Linguistics; 2020. [Google Scholar] [CrossRef]
Zhang, W.; Stratos, K. Understanding hard negatives in noise contrastive estimation. arXiv 2021, arXiv:2104.06245 2021. [Google Scholar]
Tang, H.; Sun, X.; Jin, B.; Zhang, F. A bidirectional multi-paragraph reading model for zero-shot entity linking. In Proceedings of the Proceedings of the AAAI conference on artificial intelligence, 2021, Vol.; pp. 3513889–13897.
Sun, K.; Zhang, R.; Mensah, S.; Mao, Y.; Liu, X. A Transformational Biencoder with In-Domain Negative Sampling for Zero-Shot Entity Linking. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2022; Association for Computational Linguistics: Dublin, Ireland, 2022; pp. 1449–1458. [Google Scholar] [CrossRef]
Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805 2018. [Google Scholar]
He, Z.; Liu, S.; Li, M.; Zhou, M.; Zhang, L.; Wang, H. Learning Entity Representation for Entity Disambiguation. In Proceedings of the Proceedings of the 51st Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers); Association for Computational Linguistics: Sofia, Bulgaria, 2013; pp. 30–34. [Google Scholar]
Sun, Y.; Lin, L.; Tang, D.; Yang, N.; Ji, Z.; Wang, X. Modeling mention, context and entity with neural networks for entity disambiguation. In Proceedings of the Twenty-fourth international joint conference on artificial intelligence; 2015. [Google Scholar]
Yamada, I.; Shindo, H.; Takeda, H.; Takefuji, Y. Joint Learning of the Embedding of Words and Entities for Named Entity Disambiguation. In Proceedings of the Proceedings of the 20th SIGNLL Conference on Computational Natural Language Learning; Association for Computational Linguistics: Berlin, Germany, 2016; pp. 250–259. [Google Scholar] [CrossRef]
Kolitsas, N.; Ganea, O.E.; Hofmann, T. End-to-end neural entity linking. arXiv 2018, arXiv:1808.07699 2018. [Google Scholar]
Raiman, J.; Raiman, O. Deeptype: multilingual entity linking by neural type system evolution. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence, 2018, Vol.; p. 32.
Onoe, Y.; Durrett, G. Fine-grained entity typing for domain independent entity linking. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence, 2020, Vol.; pp. 348576–8583.
Khalife, S.; Vazirgiannis, M. Scalable graph-based individual named entity identification. arXiv 2018, arXiv:1811.10547 2018. [Google Scholar]
Gillick, D.; Kulkarni, S.; Lansing, L.; Presta, A.; Baldridge, J.; Ie, E.; Garcia-Olano, D. Learning Dense Representations for Entity Retrieval 2019, arXiv:cs.CL/1909.10506].
Khattab, O.; Zaharia, M. Colbert: Efficient and effective passage search via contextualized late interaction over bert. In Proceedings of the Proceedings of the 43rd International ACM SIGIR conference on research and development in Information Retrieval, 2020, pp.; pp. 39–48.
Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond empirical risk minimization. arXiv 2017, arXiv:1710.09412 2017. [Google Scholar]
Lerer, A.; Wu, L.; Shen, J.; Lacroix, T.; Wehrstedt, L.; Bose, A.; Peysakhovich, A. PyTorch-BigGraph: A Large-scale Graph Embedding System. arXiv 2019, arXiv:cs.LG/1903.12287]. [Google Scholar]
Humeau, S.; Shuster, K.; Lachaux, M.A.; Weston, J. Poly-encoders: Transformer Architectures and Pre-training Strategies for Fast and Accurate Multi-sentence Scoring. arXiv 2020. [Google Scholar]
Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. Computer Science 2014. [Google Scholar]

Figure 2. Architecture of Biencoder

Figure 3. Architecture of Score Function

Table 1. Statistic of the Zeshel dataset.

Domains	Entities	Mentions
		Train	Evaluation
Training
American Football	31929	3898	743
Doctor Who	40281	8334	1521
Fallout	16992	3286	593
Final Fantasy	14044	6041	1156
Military	104520	13063	2764
Pro Wrestling	10133	1392	262
Star Wars	87056	11824	2706
World of Warcraft	27677	1437	255
Validation
Coronation Street	17809	0	1464
Muppets	21344	0	2028
Ice Hockey	28684	0	2233
Elder Scrolls	21712	0	4275
Testing
Forgotten Realms	15603	0	1200
Lego	10076	0	1199
Star Trek	34430	0	4227
YuGiOh	10031	0	3374

Table 2. Accuracy and top-64 recalls over different choices of architecture and negative examples

Model	Negatives	Val		Test
		r@1	r@64	r@1	r@64
BM25	-	-	76.22	-	69.13
Wu et al. (2020)	-	42.79	89.36	40.82	79.13
DUAL	Random	40.47	87.73	38.20	77.82
	Hard	42.94	89.48	40.45	80.16
	Mixed-50	43.10	89.29	40.75	80.11
	ours	45.30	90.01	42.90	81.47
Pooling Mean	Random	36.22	86.04	35.71	77.70
	Hard	40.19	88.14	39.09	79.58
	Mixed-50	40.42	88.25	38.65	78.63
	ours	43.93	89.36	43.10	81.39
SOM	Random	23.19	90.10	19.45	83.01
	Hard	30.55	91.14	32.74	83.77
	Mixed-50	15.91	91.34	24.84	82.84
	ours	25.56	91.83	31.19	85.05

Table 3. Top-64 recalls on Different Domains over different choices of architecture and negative examples

Model	Negatives	Domains
		Forgotten Realms	Lego	Star Trek	YuGiOh
DUAL	Random	89.42	88.82	80.32	66.66
	Hard	91.25	89.24	83.06	69.35
	Mixed-50	91.08	88.99	83.04	69.38
	ours	91.83	89.49	85.05	70.45
Pooling Mean	Random	89.50	88.24	79.87	67.04
	Hard	91.33	89.66	82.11	68.64
	Mixed-50	91.00	88.49	81.90	66.63
	ours	92.00	88.99	84.36	71.19
SOM	Random	94.33	92.99	82.49	76.08
	Hard	94.25	92.91	83.84	76.70
	Mixed-50	93.67	92.58	82.38	76.11
	ours	94.25	93.08	85.07	78.25

Table 4. Accuracy and top-64 recalls for different

α

under adaptive_mixup_hard for DUAL

Table 4. Accuracy and top-64 recalls for different

α

under adaptive_mixup_hard for DUAL

		$α$ =0.1	$α$ =0.2	$α$ =0.3	$α$ =0.4	$α$ =0.5	$α$ =0.6	$α$ =0.7	$α$ =0.8	$α$ =0.9	$α$ =1
Val	r@1	44.37	43.96	45.30	45.33	45.70	45.19	46.57	45.37	46.59	44.68
	r@64	90.18	89.68	90.01	89.75	89.76	89.71	89.61	89.47	89.90	89.22
Test	r@1	42.46	42.56	42.90	42.60	43.38	43.24	43.80	42.76	43.69	42.43
	r@64	80.94	81.06	81.47	80.95	81.46	81.13	80.98	80.55	80.73	80.57

Table 5. Accuracy and top-64 recalls for different

α

under adaptive_mixup_hard for Pooling Mean

Table 5. Accuracy and top-64 recalls for different

α

under adaptive_mixup_hard for Pooling Mean

		$α$ =0.1	$α$ =0.2	$α$ =0.3	$α$ =0.4	$α$ =0.5	$α$ =0.6	$α$ =0.7	$α$ =0.8	$α$ =0.9	$α$ =1
Val	r@1	43.28	44.74	43.93	43.67	43.28	42.82	44.80	45.79	45.35	44.16
	r@64	89.43	89.40	89.36	89.30	89.02	88.92	89.12	89.28	89.57	89.00
Test	r@1	41.41	42.36	43.10	42.69	42.23	42.05	43.02	44.09	43.47	42.31
	r@64	80.70	80.88	81.39	80.91	80.75	80.17	80.19	80.65	80.37	80.20

Table 6. Accuracy and top-64 recalls for different K under adaptive_mixup_hard for SOM

		K=1	K=2	K=4	K=6	K=8	K=10	K=12	K=14	K=16	K=18
Test	r@1	29.98	28.89	31.70	32.47	31.00	31.19	32.90	31.36	34.15	31.81
Test	r@64	82.65	83.39	84.11	84.70	83.91	85.05	83.83	83.28	84.83	83.59

Table 7. Top-k recalls over different choices of negative examples for SOM

Model	Negatives	r@k
		r@4	r@8	r@16	r@32	r@64
SOM	Random	50.92	62.28	71.41	77.69	83.01
	Hard	62.61	70.30	76.18	80.02	83.77
	Mixed-50	54.22	65.03	72.97	78.38	82.84
	ours	62.94	71.08	76.76	80.81	84.83

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Adaptive Mixup Hard Negative Sampling for Zero-Shot Entity Linking

Abstract

Keywords:

Subject:

1. Introduction

2. Related Works

3. Methodology

3.1. Task Definition

3.2. Biencoder

3.3. Adaptive_mixup_hard

3.4. Biencoder_AMH

4. Experiments

4.1. Dataset

4.2. Evaluation Protocol

4.3. Implementation Details

4.4. Performance Comparison

4.4.1. Main Results

4.4.2. Domain Zero-Shot Performance

4.5. Impact of α

4.6. Impact of K

4.7. Analyzing the number of candidates

5. Conclusion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.5. Impact of $α$