Prerpints.org logo
Preprint
Review

Heuristics and Rescheduling in Prioritised Multi-Robot Path Planning: A Literature Review

Altmetrics

Downloads

139

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 September 2023

Posted:

27 September 2023

You are already at the latest version

Alerts
Abstract
The benefits of multi-robot systems are substantial, bringing gains in efficiency, quality, and cost, and are useful in a wide range of environments from warehouse automation, to agriculture, and even extend in part to entertainment. In multi-robot system research, the main focus is on ensuring efficient coordination in the operation of the robots, both in task allocation and navigation. However, much of this research seldom strays from theoretical bounds; there are many reasons for this, with the most prominent and impactful being resource limitations. This is especially true for research in areas such as multi-robot path planning (MRPP) and navigation coordination. This is a large issue in practice as many approaches are not designed with meaningful real-world implications in mind and are not scalable to large multi-robot systems. This survey aims to look into the coordination and path-planning issues and challenges faced when working with multi-robot systems, especially those using a prioritised planning approach and identify key areas which are not well-explored and the scope of applying existing MRPP approaches to real-world settings.
Keywords: 
Subject: Computer Science and Mathematics  -   Robotics

1. Introduction

Robotics, Automation and Artificial Intelligence (AI) have a great influence on many domains which were traditionally relied on the human workforce. By replacing human-based roles, with robotics, AI-based tools designed solely for the task, able to work with less error and fatigue, and with enhanced communication speed and cooperation, the throughput of businesses can be increased along with the quality of the goods produced. With higher-quality automation and decreasing costs for robots, the potential for autonomous systems has soared. As these trends continue, more systems will see much more mass automation [1]. With these developments and the need to address wider spatial contexts, multi-robot systems (MRS) have seen a significant increase in their use over the last decade. An example of the benefits of MRS is shown in [2], where strawberry harvesting logistics were improved by 20-30% with the use of autonomous robots to deliver fruit from pickers to storage. MRS has already seen promising development in fully autonomous coordination such as in warehouses [3], agriculture [4], search and rescue [5], and drone shows [6].
A large factor impacting the effective deployment of MRS is Multi-Robot Path Planning (MRPP), that being, the ability to define paths each robot should take through the environment from its location to its respective goal, which both minimises the total distance each robot is taking through the network and more importantly avoids all potential collisions with other robots.
The computational complexity of considering continuous space for MRPP is prohibitively high for large environments, even for a small MRS. To enable efficient planning in large environments, MRPP algorithms may utilise a discrete topological perspective of the environment. In this topological perspective, the environment is modelled as a graph or network with nodes identifying key points, and edges describing how these points connect to one another, this utility effectively describes the navigable connections between spaces in which the robot can use. With the utilisation of these representations, the complexity of the space is minimised to only the aspects of key importance and allows MRPP algorithms to work more efficiently such as in [7], though the planning can be done without such a map, instead opting for the use or metric representations such as in [8] despite a trade-off in scalability.
Even with the topological representation of the environment, MRPP has been proven to be NP-Hard [9], wherein the joint state space grows exponentially as the complexity increases. With the complexity increasing alongside either the total number of robots or the size of the map. This means that finding optimal routes through a topology requires more processing resources or time, as there are more options and possibilities which must be explored. This restricts the scalability and thus deployment of large MRS in potentially congested spaces or domains.
The purpose and contributions of this survey are focused on three aims. Firstly, and primarily, to consolidate the variety of prioritised multi-robot path planning approaches, and the rationale behind them to form a single, referable source from which researchers can begin their study in this area. Secondly, to identify areas within the space of prioritised planning which warrant further exploration. Many approaches use simulations for their development, thus there is potential for further development when considered in practice on physical robots. Thirdly, to identify and provide solutions for common weaknesses in evaluation methodologies, which otherwise limit the transferability of efficacy into actual deployments.
There has been extensive research on multi-robot systems and the efficient coordination among robots within a system, with some overlap in the focus areas of research between multi-robot systems and multi-agent systems. Where multi-agent systems can consider agents as physical (such as robots or humans), software (as in simulated or projected robots), or general constructs (of mobile or stationary entities), they may not contain any robots at all, multi-robot systems exclusively consider robots as the agents. In the context of this survey, consider the terms robot and agent to be synonymous. Similarly, as many of the MRPP approaches discussed in this survey rely on explicit communications between the robots, multi-robot networks and networks are used synonymously to MRS.
Similarly, domains which have vastly different contexts share the same or similar research challenges, and the algorithms developed for a specific context in one domain may also be applicable in another domain. For instance, agricultural transportation logistics [7], and pipe routing [10] are both capable of utilising versions of prioritised planning implementations to optimise path assignments to individual robots. Thus this survey will be useful for research in domains where prioritised planning has a role to play.
The remaining paper is broken into four sections, beginning with Section 2 in which we detail the common challenges to MRPP, looking in depth into the specifics of why the four main issues of completeness, deadlocks, scalability, and communication are challenging, along with what can be done to help manage them. Section 3 contains the categorical breakdown of MRPP approaches, including a brief description of how each category fits within the two classifications groups of Inter-Agent Communication and Decision-Making Topology. A detailed analysis of prioritised planning approaches follows in Section 4, where the two fundamental components of prioritised planning, Heuristics and Rescheduling, are detailed alongside a breakdown of motion planning algorithms, which are the cornerstones of routing. In Section 5, we discuss our findings in commonly identified limitations with research across the literature, namely, the ideas of static scoring of edges, batch assignment of tasks, a drive for context generality, a lack of Heuristic-focused works, and lack of supporting topology manipulation. We then summarise these findings in the conclusion in Section 6.

2. Core Challenges in MRPP Algorithms

While developing an MRPP algorithm, many design challenges need to be addressed. Often these challenges are mutually exclusive, with one or more other constraints failing when the MRPP algorithm is designed to conform to one constraint. A short description of the five main challenges to MRPP is given below in this section.

2.1. Completeness

In MRPP solutions, the main aim is to find a set of routes which robots within an MRS may use to reach their respective targets, subject to some constraints. Whilst it is often a guarantee that such a set of assignments may exist, it is not always possible to find it [9]. Completeness, the most important challenge faced with MRPP approaches, is used to define whether an approach can guarantee that if a solution exists which allows all agents to reach their targets, it will be identified.

2.2. Optimality

For any collection of robots, their start locations and targets, there is always an optimal collective route, that is the collection of routes which each robot can take in order to minimise a collective objective measured by a metric such as the total distance travelled by all robots through the network [8]. The metric chosen is most commonly either, make-span (time the last robot arrives) or flow-time (sum of all route lengths). The key idea is that there is some optimal assignment of routes which can be matched but cannot be beaten.
Optimality refers to the ability of the MRPP algorithm to guarantee the identification of an optimal solution given enough computing time, i.e. the ability to find the optimal route from start to target given such a route exists. This is an issue on which much of the research into MRPP is focused, as the computational complexity of finding the optimal route is much higher.

2.3. Deadlocks

Deadlock situations are a significant concern for MRPP solutions and deployments. Deadlocks refer to a situation in which a robot is unable to find a route through the environment because it is trapped by another robot. Often, this is caused by planning inefficiencies such as incorrect assessment of priorities, or sub-optimal waiting points. In [11], the authors designed an abstract concept detailing the causes of deadlocks which they used to evaluate the efficacy of a range of prioritised planning approaches. While their aim was to detail specifically prioritised planning issues, the theory can be extended beyond. They summarised the causes of deadlocks into two key situations. In the first, the cause of the deadlock is the result of a high-priority lying in the path required by a low-priority robot, and in the second situation, the cause is a high-priority robot following behind a low-priority robot.
Papers such as [12], have attempted to resolve these common types of deadlocked situations using methods which discourage navigation around the initial movement areas of other agents. These methods, while simple, are effective in managing many causes of deadlocks.
While not as prevalent of an issue, approaches must also ensure they do not fall into the risks of Livelock (i.e. robots circle around one another unable to move forward) and Starvation (where resources, such as nodes of special interest, are locked up under different processes) as these can also be critical problems to a deployed system.

2.4. Scalability

The largest challenge to the successful deployment of MRS is its scalability, where the performance is not degraded with an increase in the size of the MRS or the working environment. The grand aim of MRS is to have many robots coordinating and working fully autonomously for long periods of time. There are three primary components which impact the scalability; the size of the map, the number/length of tasks, and the quantity of robots. As these grow, the complexity of the joint state space increases with them at an exponential rate due to more data requiring processing and more situations which need evaluation. This type of growth leads to a slower processing system overall [9].
Effective approaches to combat this are the utilisation of distributed and decentralised deployments. These can help unburden a centralised coordination system which would otherwise be handling all the processing by itself [13]. This, however, comes with other scalability problems such as communication or synchronisation overheads.
Decentralisation is effective at spreading the workload; however, it is not enough alone, the processing requirement is only divided by the total number of decentralised processors. So if the number of robots exceeds the capacity for a decentralised unit, the coordination must be decentralised further so that the number of robots per processor is stable.
Distributed processing is used widely with autonomous robots, where even if the primary coordination system is centralised, elements of the motion planning can be run locally for each agent. For instance, an agent can be given a simple goal or path from the coordination system allowing it to compute its own motion trajectories. This type of offloading allows for scalability issues to be lessened as a minimal amount of information needs to be computed centrally. With full utilisation of distributed coordination, robots can make all decisions themselves utilising technologies such as swarm behaviour, or potential fields [14].

2.5. Communication

Communication is another challenge within MRS which must be overcome. In any MRPP approach, there must be a method for robots to share information, either via a wireless data connection or via physical observations of their environment. Without such channels, agents in centralised or decentralised systems are unable to plan/share their routes, and agents in distributed systems are unable to share their intentions on their movements.
This challenge can have critical impacts on not just the efficiency of a system, but also on safety. If communications slow down too much and processing takes too long, hazards can appear and become critical before the coordinator has time to react and recalculate routes. This is especially troublesome in MRS involving both robots and humans sharing the same workspace. Where even though local navigation, can work to avoid direct collisions, robots suddenly moving in unexpected manners can cause accidents indirectly.
When utilising wireless data communication, which is the most common approach, it is important to understand the coupling between the robots and the environment. Many aspects of the environment can impact the reliability of such a system. Many materials can have significant impacts on the quality of wireless signals, stone walls of caving/mining robots, or metal infrastructure in warehouses/factories can significantly impact the reliability of wireless technologies, and the radiation in nuclear decommissioning can prevent any signals from passing through. In outdoor environments such as agricultural robots, the reliability of 4G is not always guaranteed, and even in a well-suited environment such as an office or school, issues such as blackouts and bandwidth limitations can also occur [15]. In real-world settings, there are many elements which can cause communication issues and are easily overlooked when solely working in simulation.
Communication overhead scales linearly with the number of agents in a system where the agents are only required to communicate with the coordinator, however when robots are all communicating their locations in a distributed manner without the use of a central coordinator, this can result in a lot of communication processing for each robot and each coordinator, and if they must process a lot of information with each communication there is also potential for error accumulation [14]. Many coordination issues can arise if a piece of information, such as a robot’s location, is sent but gets delayed, corrupted or inaccurate, even if it does eventually get received.

3. General Classifications of MRPP Algorithms

There are two classification systems of which all MRPP approaches can be described, Inter-Agent Communication (IAT) and Decision-Making Topology (DMT). IAC describes how much communication occurs between robots during routing, while DMT describes the number of processing units active throughout the planning and control.

3.1. Inter-Agent Communication

Within the path planning in an MRPP implementation, agents can present different levels of consideration to other agents in their proximity, this is shown through their communication with one another. The complexity of their interactions can be described on a scale, where on one end is a coupled approach where all agents are considered together, and the other is a decoupled approach where agents do not use this communication directly, between which is a combination where communication is rarely used.

3.1.1. Coupled

In a coupled approach, the routes of all agents are planned together within the same configuration space. Due to the interdependence with the configuration space, coupled approaches are at risk of scalability issues. As described above, the time it takes to find an optimal collision-free trajectory is dependent on the amount of complexity within the planning space. Where the search space increases exponentially with the number of agents, this can lead to large MRPP situations, struggling to find an optimal route.
While coupled approaches can take longer to process, the results are often much better than decoupled approaches as searching the entire joint state space can lead to identifying more complex and optimal solutions which may not be so easily discoverable using decoupled methods as described in Section 3.1.2.

3.1.2. Decoupled

Decoupled approaches work by ignoring the links and connections between agents, instead making use of conflict resolution. This often works with agents each initially planning their routes independently either online (computed by the robots) such as in [8] or offline (computed by an external machine) such as in [7], with these routes then being passed through some comprehensive conflict resolution phase.
Due to the limited exploration of the state space, and no consideration of other agents within the route generation stage, decoupled approaches are not always able to guarantee the optimal set of trajectories for each agent, however, they are able to guarantee a reasonable set of trajectories where possible, within a polynomial time. As this type of approach is quicker to find a valid route, it is better suited for scenarios with more robots, and for use in human-robot shared spaces. In these scenarios, swiftly calculating new routes to avoid collisions in a dynamic environment is key to ensuring both safety and efficiency. As much of the processing for decoupled MRPP algorithms is not reliant on a joint state space, these approaches are also much more effective than coupled approaches when the domain makes use of a distributed or decentralised topology.

3.1.3. Dynamic Coupling

While most approaches are either coupled or decoupled, there exist some methods which utilise both. In these approaches, agents may perform their own decoupled planning and re-couple the fleet to resolve issues. Alternatively, they may perform re-coupling to some agents in their proximity and decoupling to the rest of the agents in the system. There are many approaches which utilise this dynamic coupling behaviour but the general principle is that the state of coupling is not explicitly fixed.
Depending on the scope of the re-coupling, there are two broad sets in which re-coupling approaches may fall, Total Re-Coupling (TRC) requires all agents in the system to reconnect for conflict resolution, and Partial Re-Coupling (PRC) only requires agents which are in the local proximity to the conflict to join in with resolution.

Total Re-Coupling (TRC):

These types of approaches are commonplace in distributed decision-making topologies (see Sec.3.2.3) where algorithms are designed so each robot can limit communication with the fleet without adverse effects [16].

Partial Re-Coupling (PRC):

Algorithms like the ones produced by [17] and [18], take advantage of PRC to identify the optimal route for all agents in a distributed topology. In their approaches, when agents are within a local distance from one another, they plan in a joint state space, however, once apart, they make use of a decoupled approach. This style of approach is useful for environments with limited network coverage.

3.2. Decision Making Topology

The Decision Making Topology (DMT) defines the structure of the decision-making systems, that is the number of Processing Units (PU) responsible for generating the trajectories of the robots and performing the conflict resolution. There are many types of decision-making topologies that can be broadly categorised based on their level of decentralisation. A fully centralised (centralised) topology has a single processing unit for many robots, and a fully decentralised system (distributed) deploys each robot with its own processing unit. Between these are what can be referred to as decentralised approaches, where there are many processing units, but less than one per robot [19]. Centralised, decentralised and distributed DMT are shown in Figure 1.a-c. These categories can be broken down further based on the coupling which happens between agents.
Inherently, these structures can be considered synonymous with network communication topology, especially for the centralised and some types of decentralised topologies. However, it is important to note the distinction between network communication topology and decision-making topology. A DMT is focused on how the agents and servers implement control over one another. e.g., In Figure 1.d, while it is say possible for Agent 1 to communicate to Agent 3 via Agent 2, the limits of coordination for Agent 1, would be only with Agent 2. Overall, the DMT defines the limits in how agents make decisions together, rather than the availability of communication.

3.2.1. Centralised

The centralised topology consists of a communication network of a star, where a Single Processing Unit (SPU) functions as the central coordinator. This SPU handles all decision-making processes related to task assignment, route planning, and conflict resolution.
Compared with decentralised and distributed topologies, centralised topologies, have a significant reduction in communication overhead. Each agent communicates only with the SPU, meaning the amount of open connections is limited to the number of agents in the system. This allows for simple and straightforward approaches to be developed such as the prioritised planning method developed by [20].
The biggest risk of making use of a centralised approach is scalability. As the number of robots increases, having only one processing unit can lead to an overburdened system which is slow to generate even the simplest of results. This can be especially risky when the SPU is responsible for many other critical functionalities such as navigation safety analysis.

3.2.2. Decentralised

Decentralised decision-making topologies are characterised by their use of multiple coordinators each of which is responsible for a subset of the overall system. Two approaches which emphasise their unique benefits clearly are sub-fleet control and sub-region control.
In the sub-fleet control, coordinators assume responsibility for a subset of robots. The coordinator in each group is responsible for calculating routes, and then communicating these with either a central coordinator or the network of other decentralised coordinators. Approaches such as platooning or virtual structures, come under this definition. In Leader-Follower Platooning, a single leader takes the lead and agents entering their vicinity relinquish their own control to follow the leader [14]; in virtual structures, agents will become a part of a temporary collective to maintain a geometric shape [14].
In the sub-region control, the distribution of the coordinators is environment or topology-based. In this structure, the coordinators take responsibility for managing defined regions within the network. This method can be seen in [21], where the decentralised coordinators each manage a defined junction, taking control of autonomous vehicles which approach it and coordinating their movement through the junction. Decentralised approaches help manage the computational load away from a central coordinator, but may still struggle to keep up with demand as the number of agents distributed in the system increases.

3.2.3. Distributed

Distributed decision-making topologies, like decentralised methods, make use of a collection of processing units. However, unlike decentralised methods, distributed methods of MRPP do not risk scalability issues, whereas each robot works as its own processing unit, the number of processing units scales proportionally with the number of robots.
In distributed topologies, algorithms are designed so that each robot is able to perform its own planning and organise its conflict resolution locally. Distributed approaches are often also decoupled approaches however this is not always the case, a coupled approach may make use of a distributed decision-making topology to offset elements of its processing which work independently. These types of distributed approaches can be grouped based on how much re-coupling occurs in the conflict resolution (see Sec.3.1.3).
These types of topologies are distinct in their architecture from centralised and decentralised methods due to the absence of independent cloud-based/edge-server coordinators. However, not all distributed topologies are identical in structure. Depending on the application, environment, and robots; the topology may be either fully or partially connected. In a fully-connected distribution, every robot will be in communication with every other robot, allowing for all robots to coordinate as a collective [22], when conflict resolution is conducted for an individual robot, every agent is capable of contributing.
This is in contrast to a partially-connected distribution, in which robots might only be allowed to connect to the resolution if they have a necessity to do so such as if they are in proximity to the agent needing replanning. In practice, these types of connected distributions are necessary due to communication constraints, where agents are unable to maintain a consistent or reliable connection to a single server, and must instead act as relays for information [16,23].

4. Prioritised Multi-Robot Path Planning

Prioritised planning, developed by [20], is a commonly used decoupled approach to MRPP. It is a combination of two components, a prioritisation schema, and a motion planning system.
In traditional prioritised planning, each agent is assigned a priority then their routes are planned in the priority order, with each subsequent agent planning around those with a priority higher than itself. These priorities are defined by a priority schema, which orders the agents based on some predefined metrics such as the distance to their respective targets (see Sec.4.1). The routes themselves are calculated by the motion planning system (see Sec.4.2), which makes use of a planning algorithm such as A*.
As the agents defined with the higher priorities plan first, they will often be planning on an empty map, i.e., so long as a valid route is possible, these higher-priority agents are guaranteed to reach their goal. In contrast, agents defined with a lower priority plan their routes in a more restricted space navigating around the other robots which are treated as dynamic objects. Due to the limitation on navigable routes, a route is not always guaranteed for the lower-priority robots. The complexity of the MRPP is thus reduced with prioritised planning with the decoupled and prioritised approach and can be used in large MRS deployments. However, it may also result in an incomplete MRPP in some conditions as discussed above, and would require dynamically adjusting the underlying prioritisation schema or the motion planning system to get a complete solution.
More details on the prioritisation schema and the planning algorithms are discussed in the following subsections.

4.1. Prioritisation Schema

Prioritisation schema defines the approach to prioritise the agents, which is then used for ordering the agents in the decoupled path planning phase.

4.1.1. Heuristics

The approach used to set the priority order of the robots is referred to as the Heuristic. This subsection aims to highlight a broad range of heuristics found in the literature on prioritised planning. While some heuristics may work well generally, tailoring the chosen heuristic to the complexity and arrangement of the environment may lead to better results. These heuristics are summarised in Table 1 with brief descriptions and corresponding key publications.

Static Ordering

The initial ordering for the priority schema developed for use by [20], made use of the order the agents were added to the network as their heuristic. A similar heuristic was also used in [25], in which the agents were assigned static scores based on their identity, and always gave way to agents which had a higher priority. By itself, this ordering is not able to combat issues prevalent with larger and more complex scenarios.

Road-map Distance

In [27], the author made use of a heuristic which defined the ordering of agents based on their travel distance through a road-map to their respective targets, with the furthest from their target having the highest priority. Conceptually, this was the first well-known use of knowledge-based heuristics in prioritised planning with a coupling to the environment (see Figure 2).
A similar approach is utilised in [28], where the authors simultaneously perform task assignment and path planning. This results in the prioritisation schema being closely coupled to the resulting make-span, and being more accurate to the reality of the routing than either Euclidean distance or road-map distance.

Planning Time

Another approach which relied on network knowledge was designed by [30], in which agents were assigned a priority based on how long it took them to find a route. In this, the intent was that agents which took a long time to find a route would benefit more from planning in an emptier map, and should thus get a higher priority. Just as with using Road-map distance, this worked well to support the prioritised planning and return priorities quickly which is key for a scalable centralised approach. However due to varying hardware on different robots in a distributed decision-making topology making use of heterogeneous robots, this can prove to be unreliable with the current implementation. An alternative implementation could instead prioritise based on the total FLOPS during planning which would be more consistent across evaluations of distributed processing where each agent utilises unique hardware and sub-processes.

Naive & Coupled Surroundings

In [26], the author developed a heuristic making use of knowledge about the local environment. Later titled Naive Surroundings by [8], this heuristic scored agents based on how many other agents were in their local vicinity. The intent behind this approach is that agents which have a more cluttered workspace would struggle more to find a route out of the workspace and may become trapped by other agents moving through it with higher priorities.
It is termed naive as it does not consider the effect of the agent on these objects. This is in contrast to the Coupled Surroundings heuristic developed by [8] which instead counts the number of obstacles, where an obstacle can be defined as a collection of objects which the robot cannot move between. So not being able to move between two objects classifies them as a single obstacle, thus coupling the robot to its environment.

Path Prospects

The author of [8] worked to develop their own knowledge-based heuristic titled Path Prospects, in this, the agents are scored based on the number of surrounding paths which are available to them, calculated by counting the number of obstacles and the number of effective obstacles between them and their target by analysing the homology classes of trajectories (the number of distinct routes which can be created to join two points). Obstacles are regarded as any obstruction, while Effective Obstacles are regarded as regions the robot is unable to navigate through due to the constraints of its footprint on the environment (See Figure 3). The researchers also evaluated the effectiveness of constraining the search algorithm to areas with more promising minimal route options (Forwards Looking).
They evaluated a total of seven heuristics, comparing the two variants of path prospects (one which dealt with tie-breaks using random assignment, and one which used optimal route length), naive and coupled surroundings [26], optimal route length adapted from [24], random assignment and forwards looking. Their results showed for simulations comparing theirs to the benchmarks set out, they were able to achieve a higher optimality with respect to completeness, which offered a good balance between make-span and flow time.

4.1.2. Rescheduling

As discussed earlier, the original prioritised planning as defined by [20] is incomplete; i.e., the prioritisation of the robots can result in a situation where the robots with lower priority do not have a route to be found, and thus failing the overall planning. Rescheduling is a modification to the priority schema which exists to prevent such planning failures. However, it can also be extended to optimise the assignments to improve the ordering of agents. Inherently, decoupled approaches are not optimal as planning for each robot is done independently. However, some of the rescheduling approaches are able to guarantee a high percentage of optimality, while many others are unable to give a theoretical guarantee of optimality in polynomial time. Some of the commonly used rescheduling approaches are discussed below and summarised in Table 2.

Full Search

One of the first approaches to tackle optimality was completed by [31], where the author implemented a full state space search by calculating routes with all combinations of priorities. The result itself is able to guarantee optimality, however not in a reasonable amount of time. As described by [31] at the time, the only way to guarantee optimality is to perform a complete search through every combination of priority orderings. However, as some approaches below show, a reasonably high percentage of optimality can be reached while leaving some search spaces unexplored, [24,35].

Random Rescheduling

The search for scalable optimality with the use of rescheduling first began in 2001 when [32] employed an approach making use of Random Rescheduling (RR). In this, whenever a deadlock occurred, the priority scheme was randomised, and the plan was recomputed. Whilst simple, this was developed before the development of knowledge-based heuristics. This design was successful at avoiding many deadlocks, however, due to the random nature of the approach, it was not guaranteed to do so quickly.

Hill-Climbing Search

RR was later improved on by [24] with the use of a Hill-Climbing Search. In this, initial priorities are randomly allocated and the set of routes calculated, then random pairs of agents are selected and their priorities swapped. This repeats iteratively until a more optimal set of routes is found, restarting from scratch occasionally to prevent being stuck in a local minima. This approach had a much more reasonable search space to explore than [31], and was still scalable, however took time to recompute routes each time an amendment was made.

Continuous Enhancement

In [29], the author proposed a more complex solution to rescheduling called Continuous Enhancement (CE). In this approach, all robots start with a very low priority value, and rescheduling will be triggered when a robot cannot find a route after updating the priority by two possible static values (a conservative value or a large value). While still quite simple, this was proven to work in many situations, and as the author describes, "the algorithm is very robust against dynamic changes and erroneous robot behaviour".
CE was later improved by [33], where maximum priorities were assigned when an agent failed to find any route. This approach, named Deterministic Rescheduling is much simpler then its predecessor, decreasing the total number of plans in attempting to find a route. This approach uses the intuition that if the routing fails, this is due to the complexity of the local environment, and this may not be resolved by moving it up one or two places. This follows the same concept as the Naive Surroundings by [24].

Local Priority Adjustment

In the approach by [34], Local Priority Adjustment (LPA) was used. When a deadlock occurred, all agents with routes crossing within a certain radius of the deadlock were identified. Recomputing routes with all possible partial configurations of their priorities. This method, while seemingly intensive, was able to perform similarly to alternatives, being effective at improving the quality of priority assignments.

Priority Tuning

A similar approach to LPA was taken in 2019 where [35] made use of a method called Priority Tuning. In this approach, regardless of whether a deadlock occurred, once planning is completed, the agents with the least optimal routes would have their scores swapped with agents with slightly better scores, then the agents would all replan their routes with the new orderings. This would continue until there was no considerable change in the results. This approach showed a gradual improvement in scores as more time was offered to the algorithm, before converging on a likely optimal assignment meaning it can also be classified as an Anytime Algorithm once all deadlocks have been eliminated. The authors also with this paper included an asynchronous approach to prioritised planning, which was employed to accelerate the tuning process. Their results show the asynchronous prioritised planning method was able to achieve higher convergence scores in a reasonable time.

4.2. Motion Planning Algorithms

Motion Planning Algorithms describe the process in which a route through a map from a start to a goal is calculated. They are the fundamental part of route planning which nearly all MRPP implementations build upon. In [36], the authors put together an assessment of the practical benefits and drawbacks of utilising various approaches of motion planning algorithms, assessing both their real-world applicability and contexts in which they surpass one another.

4.2.1. Static Algorithms

Static algorithms are the most fundamental component of motion planning. They are named as such because once the optimal route is identified, any changes to the environment (e.g. a previously traversable area becomes untraversable due to the presence of another agent) mean the search must be restarted from the beginning.
A well-known and widely-used basis for many static algorithms is Dijkstra [37], which identifies the shortest path to visit by iterating through edges connected from the start node, and at each node computing the distance from the start. This approach spreads out in all directions until the target node is reached, and the path is determined by stepping backwards from the target.
An improvement to this was developed named A* [38], in which an additional computation was included where a heuristic estimation of distance (usually the Euclidean distance) to the target was added to the distance from the start node. This addition allowed the algorithm to prioritise searching in the direction of the target node, leading to a more narrowed search space.
These approaches can both be implemented as a forward or backward approach, by swapping the target and start nodes.

4.2.2. Replanning Algorithms

Replanning algorithms are designed to manage and modify identified routes, to ensure they remain optimal as the environment around the agent changes. Unlike static algorithms, these work without the need to restart the search. The algorithms Dynamic A* (D*) [39] and D* Lite [40] are the most well-known replanning algorithms.
D* Lite is a modified version of a backwards A* approach. It works by performing replanning on small portions of the network when changes are identified, before propagating forwards towards the agent. It is designed to improve efficiency by limiting the impact on states not affected by the changes in the topology and restricting attention to states which are important for repairing the current solution, essentially it only repairs parts which have become invalid.

4.2.3. Anytime Algorithms

Anytime approaches aim to identify a valid solution first, then perform continuous improvement to attain a better optimality. The Anytime Repairing A* (ARA*) [41] is an effective anytime algorithm which identifies a sub-optimal route quickly using a loose bound defined based on the search time, then repeating elements of the search, tightening the bound and optimising the route.
ARA* is designed to reuse sections of the results of its previous searches to decrease the computational requirement of the algorithm. Despite having a fast optimal route generation, implementations such as ARA* cannot respond to dynamic environments. Even if an optimal route has been found, if the topology of the environment is updated the algorithm must start from scratch.
Anytime approaches work well for single robot path planning, when there is no coupling, however, for conditions where many robots are restricted and have to plan around one another this type of algorithm does not work well.

4.2.4. Replanning Anytime Algorithms

The replanning algorithm Anytime Dynamic A* (AD*) [42], was developed to use the section reuse component within ARA* and the invalidated section repairing component within D* Lite. The fusing of these components enables the algorithm to boast a strong efficiency in planning around dynamic obstacles while avoiding them.

5. Discussion

In the literature analysed, there were a few key areas which affect the efficiency of the MRPP algorithms, and need to be addressed. While the research as a whole is quite broad, in scope and evaluation, most work makes two key assumptions which define their algorithmic approach. The first assumption (which we have named as Batch Assignment) is that the planning is carried out in batches. At the point of planning, every agent is considered to be idle, and this could lead to unnecessary delays or route replanning for agents which are still in motion. The second assumption (which we have named Static Scoring) is that the priority for each point along a reserved route is homogeneous, meaning a priority defined at the start of the route determines every point along it.
These assumptions have led to much of the existing research lacking accurate transferability when taken out of a single route planning instance, and into practice in a physical deployment. Additionally, we have identified a broader weakness in heuristic research as a whole (which we have named Context Generality), in which the published works rarely tie the developed heuristics into the contextual domain directly. We have also identified a shortcoming in the area of heuristic research, where only a fraction of papers actually had the developed heuristic as the focus of the paper.
Finally, we have found a shortcoming in the exploration of cross-approach optimisations, where there has been little exploration in evaluating the utility of combining other approaches from the areas of topological manipulation, which should have a clear improvement on scalability for larger environments (due to the discretisation of the environment) and work well alongside Prioritised Planning.

Batch Assignment 

The key concept here is that route planning is done in batches. In a classical Prioritised MRPP scenario, a system will start with all robots idle. Each robot will be assigned a priority and they will plan their motion accordingly. Each robot would execute its navigation route by navigating to the goal. There are four different scenarios depending on how many goals are assigned to each robot, and how the routes are planned for each goal.
  • Scenario 1: All robots have only one target so will stop at g o a l 1 , as in [8,20,24,27,29,30].
  • Scenario 2: Robots wait at g o a l n till all other robots have completed g o a l n before planning routes and start moving to g o a l n + 1 .
  • Scenario 3: Each robot completes its g o a l n , and receives a new smaller priority, so as not to disrupt existing routes when moving to g o a l n + 1 .
  • Scenario 4: All robots which complete g o a l n receives g o a l n + 1 . All robots delete existing routes, and planning restarts with one robot planning to its g o a l n + 1 and others still replanning to their g o a l n .
Due to the efficacy in evaluating the quality of single-instance plans, Scenario 1 is used often. However, this has led to approaches, not fully exploring the viability for practical deployments. As discussed in [28], minimising the flow time can be thought of as trying to get agents to an idle state as quickly as possible so that they can take on new tasks, however, this does not fully resolve the underlying issues.
Scenario 2 is an extrapolation of how subsequent uses of Scenario 1 would result. It does not fully utilise the available resources but does remove the likelihood of live-locks in the rescheduling phase.
For Scenario 3, the only way to guarantee a non-disruptive route is to utilise a priority value below the robots which already have routes, for any knowledge-based heuristics, this weakens their intended meaning.
Scenario 4, is a disruptive form of Scenario 2, where all resources are used, but with significantly increased processing due to unnecessary replanning. Routes being blocked can result in live-locked agents.

Static Scoring 

Another issue identified here with the heuristics occurs when planning or replanning is carried out only for some robots while others are in motion (similar to Scenario 3 in Batch Processing). Once planning is completed for a robot, using a knowledge-based heuristic for the planning schema, every edge in the route can be thought of as being reserved with the score given by this heuristic. Although a robot moves through its reserved route, the score which had been calculated to reserve the edges in the route remains the same as when the routing began. This leads to inconsistencies with the results of replanning where the robots which replanned their routes may have new scores computed, but these new accurate scores are being compared against historical existing scores to decide the winner to reserve the routes. As the purpose of knowledge-based heuristics is to bring relevant knowledge of the system into the planning schema, this is only partially achieved when the information being applied is historical and inaccurate to the new state of the robot.
It is only when priorities are integrated into live motion planning such as in [25,26,30], utilise reassignment as in [28,29], or apply to individual edges as in [7], does the scoring become reliable at all instances. For most approaches, however, this is not the case.

Context Generality 

Prioritisation schema heuristics can be categorised into four levels based on their relation to context dependence and use. Abstract heuristics take no information from the state of the system, relying only on meta information such as what would be found in a configuration file. System-based heuristics can be categorised as taking general information from the system, applicable in nearly any context. Context-based heuristics can be described as taking information directly relevant to the deployed domain. Combined heuristics are simply the combination of multiple independent heuristics to improve assignments.
Due to the wide applicability of System-Based heuristics, most research neglects potentially useful context information in favour of more widely applicable approaches. It is understandable that applications using these types of prioritisation schema are less likely to garner wider attention due to their limited use cases. However, it is still worth noting their absence and potential. For example, in a warehouse environment, the payload weight/size could be a contributing factor to a viable heuristic due to the instability of the load if encountering lots of starts and stops during transit; in a horticultural fruit logistics setting the time since the harvest could be a deciding factor as the shelf life of the fruit will be reduced if left in the heat after harvested from the plant; or in the domain of autonomous vehicles, an increase in the number of pedestrians in an area near school zones may work as a good prioritisation consideration. Table 3 shows how some of the heuristics discussed in Section 4.1.1 may be categorised based on the descriptions above.

Heuristic Focus 

Throughout this review, it has become evident that there is relatively little active research in prioritised MRPP focusing on improving the heuristics. The majority of the MRS research focused on optimising rescheduling for distributed fleet management. Of the heuristics discussed within this survey alone, only around half of the novel heuristics were developed as the sole focus of the paper.

Topology Manipulation 

In order to reduce the MRPP problem’s complexity, topology manipulation works by modifying the structure of the environment considered for planning. This can be done in one of two ways.
Topology Generation (generating internal structures within the topology) has been used in approaches like Probabilistic Roadmaps [43], Rapidly Expanding Random Trees [44], and Sub-Dimensional Expansion [17] to great effect, but have not been explored alongside prioritised planning.
Topology Decomposition (decreasing the state space by combining components together) has been used in approaches such as Road-Map Decomposition [45], Component-Based Map Decomposition [46], and Junction-Based Map Decomposition [21] to improve on scalability, with [46] being one of very few works to utilise prioritised planning alongside topology manipulation to great effect.

6. Conclusion

As evidenced through this literature review, despite its general applicability and rapid conflict-resolution speed, prioritised MRPP is not under much active research. However, as shown in [7] and here, there is still potential for improving the generalised efficiency of prioritised MRPP approaches by focused research on heuristic developments and rescheduling approaches, and framework developments to improve generalised efficiency.
Prioritised planning has been well-explored on the surface in both the topological domain, in the form of online and offline path planning, and in the continuous domain, in the form of online motion planning. Due to the simple frameworks supporting heuristics and rescheduling, these are able to be applied quite broadly across many domains, which has undoubtedly helped in facilitating their interoperability. While they have been well explored over varying decision-making topologies, systems utilising dynamic-coupling inter-agent communication have not received the same attention.
There is also a lot of potential for developments in finding optimality in heterogeneous systems and new domains with combined heuristic research. Given the relatively small selection of available heuristics, the exploration of context-based heuristics may spark more creative solutions to system-based heuristics so the usefulness of context-based heuristics must not be understated. Further, rescheduling approaches have been generally limited to works utilising coupled and dynamic coupling inter-agent communications, however have not widely considered the impacts on communication challenges in this process, despite being a critical restriction on their utility.
Approaches have shown a lot of potential when utilised alongside other innovations in the problem specifications such as the topological representations. However, further innovations such as topology manipulations are under-explored, although their combined utility seems to be an area for scalability optimisation.
Prioritised planning is a powerful architecture, with concepts applicable in both online and offline planning, and able to be utilised in both the topological and continuous domains. Yet, despite its conceptual simplicity, its potential is under-explored in a number of directions.

Author Contributions

Conceptualization, J.R.H. and G.P.D.; validation, J.R.H.; investigation, J.R.H. and G.P.D.; writing—original draft preparation, J.R.H.; writing—review and editing, J.R.H. and G.P.D.; visualization, J.R.H. and G.P.D.; supervision, G.P.D.; project administration, G.P.D.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Institutional Review Board Statement

Not applicable

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rizk, Y.; Awad, M.; Tunstel, E.W. Cooperative Heterogeneous Multi-Robot Systems: A Survey. ACM Comput. Surv. 2019, 52. [Google Scholar] [CrossRef]
  2. Das, G.P.; Cielniak, G.; From, J.; Hanheide, M. Discrete Event Simulations for Scalability Analysis of Robotic In-Field Logistics in Agriculture – A Case Study. In Proceedings of the ICRA 2018 Workshop on Robotic Vision and Action in Agriculture; 2018. [Google Scholar]
  3. Fernandez Carmona, M.; Parekh, T.; Hanheide, M. Making the Case for Human-Aware Navigation in Warehouses. In Proceedings of the Towards Autonomous Robotic Systems; Althoefer, K.; Konstantinova, J.; Zhang, K., Eds.; Springer International Publishing: Cham, 2019; pp. 449–453. [Google Scholar]
  4. Bechar, A.; Vigneault, C. Agricultural robots for field operations: Concepts and components. Biosystems Engineering 2016, 149, 94–111. [Google Scholar] [CrossRef]
  5. Drew, D.S. Multi-agent systems for search and rescue applications. Current Robotics Reports 2021, 2, 189–200. [Google Scholar] [CrossRef]
  6. O’Malley, J. There’s no business like drone business [drone light shows]. Engineering & Technology 2021, 16, 72–79. [Google Scholar]
  7. Heselden, J.R.; Das, G.P. CRH*: A Deadlock Free Framework for Scalable Prioritised Path Planning in Multi-robot Systems. In Proceedings of the Annual Conference Towards Autonomous Robotic Systems. Springer; 2021; pp. 66–75. [Google Scholar]
  8. Wu, W.; Bhattacharya, S.; Prorok, A. Multi-Robot Path Deconfliction through Prioritization by Path Prospects. arXiv preprint arXiv:1908.02361, 2019. [Google Scholar]
  9. Yu, J.; LaValle, S. Structure and intractability of optimal multi-robot path planning on graphs. Proceedings of the AAAI Conference on Artificial Intelligence 2013, 27. [Google Scholar] [CrossRef]
  10. Belov, G.; Du, W.; De La Banda, M.G.; Harabor, D.; Koenig, S.; Wei, X. From multi-agent pathfinding to 3D pipe routing. In Proceedings of the Thirteenth Annual Symposium on Combinatorial Search; 2020. [Google Scholar]
  11. Dewangan, R.K.; Shukla, A.; Godfrey, W.W. Survey on prioritized multi robot path planning. In Proceedings of the 2017 IEEE international conference on smart technologies and management for computing, communication, controls, energy and materials (ICSTM). IEEE, 2017; pp. 423–428. [Google Scholar]
  12. Cap, M.; Novak, P.; Kleiner, A.; Selecky, M. Prioritized Planning Algorithms for Trajectory Coordination of Multiple Mobile Robots. IEEE Trans. Autom. Sci. Eng. 2015, 12, 835–849. [Google Scholar] [CrossRef]
  13. Mao, W.; Liu, Z.; Liu, H.; Yang, F.; Wang, M. Research progress on synergistic technologies of agricultural multi-robots. Applied Sciences 2021, 11, 1448. [Google Scholar] [CrossRef]
  14. Soni, A.; Hu, H. Formation control for a fleet of autonomous ground vehicles: A survey. Robotics 2018, 7, 67. [Google Scholar] [CrossRef]
  15. Prorok, A.; Malencia, M.; Carlone, L.; Sukhatme, G.S.; Sadler, B.M.; Kumar, V. Beyond robustness: A taxonomy of approaches towards resilient multi-robot systems. arXiv preprint arXiv:2109.12343, 2021. [Google Scholar]
  16. De Hoog, J.; Jimenez-Gonzalez, A.; Cameron, S.; de Dios, J.R.M.; Ollero, A. Using mobile relays in multi-robot exploration. In Proceedings of the Proceedings of the Australasian Conference on Robotics and Automation (ACRA’11), Melbourne, Australia, 2011, pp.; pp. 7–9.
  17. Wagner, G.; Choset, H. M*: A complete multirobot path planning algorithm with performance bounds. 2011 IEEE/RSJ Int. Conf. Intell. Robot. Syst. 2011, 3260–3267. [Google Scholar]
  18. Wagner, G.; Kang, M.; Choset, H. Probabilistic path planning for multiple robots with subdimensional expansion. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation. IEEE; 2012; pp. 2886–2892. [Google Scholar]
  19. Blumenkamp, J.; Morad, S.; Gielis, J.; Li, Q.; Prorok, A. A framework for real-world multi-robot systems running decentralized GNN-based policies. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA). IEEE; 2022; pp. 8772–8778. [Google Scholar]
  20. Erdmann, M.; Lozano-Pérez, T. On multiple moving objects. Algorithmica 1987, 2, 477–521. [Google Scholar] [CrossRef]
  21. Zhao, W.; Liu, R.; Ngoduy, D. A bilevel programming model for autonomous intersection control and trajectory planning. Transp. A Transp. Sci. 2019, 1–25. [Google Scholar] [CrossRef]
  22. Patwardhan, A.; Murai, R.; Davison, A.J. Distributing collaborative multi-robot planning with gaussian belief propagation. IEEE Robotics and Automation Letters 2022, 8, 552–559. [Google Scholar] [CrossRef]
  23. Bayer, J.; Faigl, J. Decentralized topological mapping for multi-robot autonomous exploration under low-bandwidth communication. In Proceedings of the 2021 European Conference on Mobile Robots (ECMR). IEEE; 2021; pp. 1–7. [Google Scholar]
  24. Bennewitz, M.; Burgard, W.; Thrun, S. Finding and optimizing solvable priority schemes for decoupled path planning techniques for teams of mobile robots. Rob. Auton. Syst. 2002, 41, 89–99. [Google Scholar] [CrossRef]
  25. Clark, C.M.; et al. Randomized motion planning for groups of nonholonomic robots. In Proceedings of the Proceedings of the 6th International Symposium on Artificial Intelligence, 2001., Robotics and Automation in Space: i-SAIRAS.
  26. Clark, C.M.; Bretl, T.; Rock, S. Applying kinodynamic randomized motion planning with a dynamic priority system to multi-robot space systems. In Proceedings of the Proceedings, IEEE Aerospace Conference. IEEE. 2002, Vol. 7, pp. 7–7.
  27. Van Den Berg, J.P.; Overmars, M.H. Prioritized motion planning for multiple robots. 2005 IEEE/RSJ Int. Conf. Intell. Robot. Syst. IROS 2005, 2217–2222. [Google Scholar]
  28. Chen, Z.; Alonso-Mora, J.; Bai, X.; Harabor, D.D.; Stuckey, P.J. Integrated task assignment and path planning for capacitated multi-agent pickup and delivery. IEEE Robotics and Automation Letters 2021, 6, 5816–5823. [Google Scholar] [CrossRef]
  29. Regele, R.; Levi, P. Cooperative multi-robot path planning by heuristic priority adjustment. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE; 2006; pp. 5954–5959. [Google Scholar]
  30. Velagapudi, P.; Sycara, K.; Scerri, P. Decentralized prioritized planning in large multirobot teams. In Proceedings of the IEEE/RSJ 2010 Int. Conf. Intell. Robot. Syst. 2010; pp. 4603–4609. [Google Scholar]
  31. Azarm, K.; Schmidt, G. Conflict-free motion of multiple mobile robots based on decentralized motion planning and negotiation. Proc. - IEEE Int. Conf. Robot. Autom. 1997, 4, 3526–3533. [Google Scholar] [CrossRef]
  32. Bennewitz, M.; Burgard, W.; Thrun, S. Optimizing Schedules for Prioritized Path Planning of Multi-Robot Systems. In Proceedings of the IEEE Int. Conf. Robot. Autom., 2001, Vol. 1, pp. 271–276.
  33. Andreychuk, A.; Yakovlev, K. Two techniques that enhance the performance of multi-robot prioritized path planning. Proc. Int. Jt. Conf. Auton. Agents Multiagent Syst. AAMAS 2018, 3, 2177–2179. [Google Scholar]
  34. Ma, H.; Harabor, D.; Stuckey, P.J.; Li, J.; Koenig, S. Searching with Consistent Prioritization for Multi-Agent Path Finding. Proc. AAAI Conf. Artif. Intell. 2019, 33, 7643–7650. [Google Scholar] [CrossRef]
  35. Hu, B.; Cao, Z. Minimizing task completion time of prioritized motion planning in multi-robot systems. In Proceedings of the IEEE Int. Conf. Syst. Man Cybern. IEEE, 2019, Vol. 2019-Octob, pp. 1018–1023.
  36. Ferguson, D.; Likhachev, M.; Stentz, A. A guide to heuristic-based path planning. In Proceedings of the Proc. Int. Work. Plan. under Uncertain. Auton. Syst. Int. Conf. Autom. Plan. Sched. 2005; pp. 1–10. [Google Scholar]
  37. Dijkstra, E.W.; et al. A note on two problems in connexion with graphs. Numerische mathematik 1959, 1, 269–271. [Google Scholar] [CrossRef]
  38. Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE transactions on Systems Science and Cybernetics 1968, 4, 100–107. [Google Scholar] [CrossRef]
  39. Stentz, A. The Focussed D* Algorithm for Real-Time Replanning. In Proceedings of the Int. Jt. Conf. Artif. Intell., number August. 1995. [Google Scholar]
  40. Koenig, S.; Likhachev, M. Improved Fast Replanning for Navigation in Unknown Terrain. IEEE Trans. Robot. 2002, 21, 354–363. [Google Scholar] [CrossRef]
  41. Likhachev, M.; Gordon, G.; Thrun, S. ARA *: Anytime A * with Provable Bounds on Sub-Optimality. Adv. Neural Inf. Process. Syst. 2004, 767–774. [Google Scholar]
  42. Likhachev, M.; Ferguson, D.; Gordon, G.; Stentz, A.; Thrun, S. Anytime dynamic a*: An anytime, replanning algorithm. In Proceedings of the ICAPS 2005 - Proc. 15th Int. Conf. Autom. Plan. Sched. 2005; pp. 262–271. [Google Scholar]
  43. Kavraki, L.E.; Svestka, P.; Latombe, J.C.; Overmars, M.H. Probabilistic Roadmaps for Path Planning in High-Dimensional Configuration Spaces. In Proceedings of the IEEE Trans. Robot. Autom. 1996. [Google Scholar]
  44. LaValle, S.M.; Kuffner, J.J. Randomized kinodynamic planning. Int. J. Rob. Res. 1999, 20, 378–400. [Google Scholar] [CrossRef]
  45. Ryan, M. Multi-robot path-planning with subgraphs. In Proceedings of the Proc. 2006 Australas. Conf. Robot. Autom. ACRA 2006, 2006. [Google Scholar]
  46. Ryan, M.R. Exploiting subgraph structure in multi-robot path planning. J. Artif. Intell. Res. 2008, 31, 497–542. [Google Scholar] [CrossRef]
Preprints 86264 g001
Figure 1. Communication Structures: (a) Centralised: single central server; (b) Decentralised: localised servers communicating information; (c) Fully-Distributed: no servers, agents broadcast all information directly; (d) Uneven-Distributed: Agents only communicate required information with a subset of agents.
Figure 1. Communication Structures: (a) Centralised: single central server; (b) Decentralised: localised servers communicating information; (c) Fully-Distributed: no servers, agents broadcast all information directly; (d) Uneven-Distributed: Agents only communicate required information with a subset of agents.
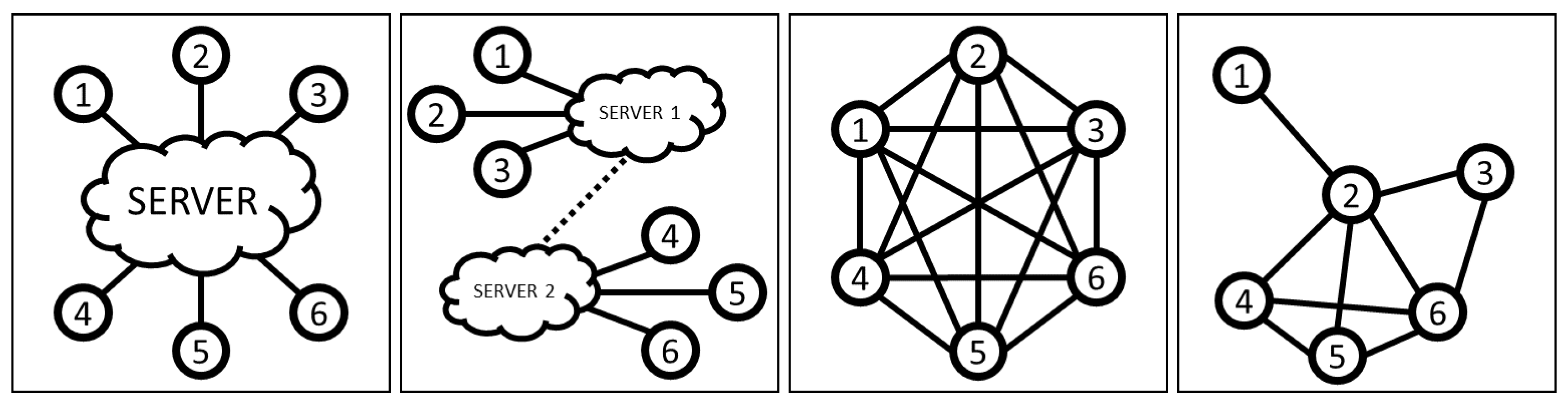
Preprints 86264 g001
Preprints 86264 g002
Figure 2. Impact of environmental constraints on optimal assignments; Robot 1 has a small Euclidean distance to the Goal, but would take a longer route along a road map than Robot 2.
Figure 2. Impact of environmental constraints on optimal assignments; Robot 1 has a small Euclidean distance to the Goal, but would take a longer route along a road map than Robot 2.
Preprints 86264 g002
Preprints 86264 g003
Figure 3. Generated Homology Class of Trajectories [8]: (a) Generation ignoring coupling of a robot on the environment (Obstacles); (b) Generation considering environmental constraints of robot footprint (Effective Obstacles).
Figure 3. Generated Homology Class of Trajectories [8]: (a) Generation ignoring coupling of a robot on the environment (Obstacles); (b) Generation considering environmental constraints of robot footprint (Effective Obstacles).
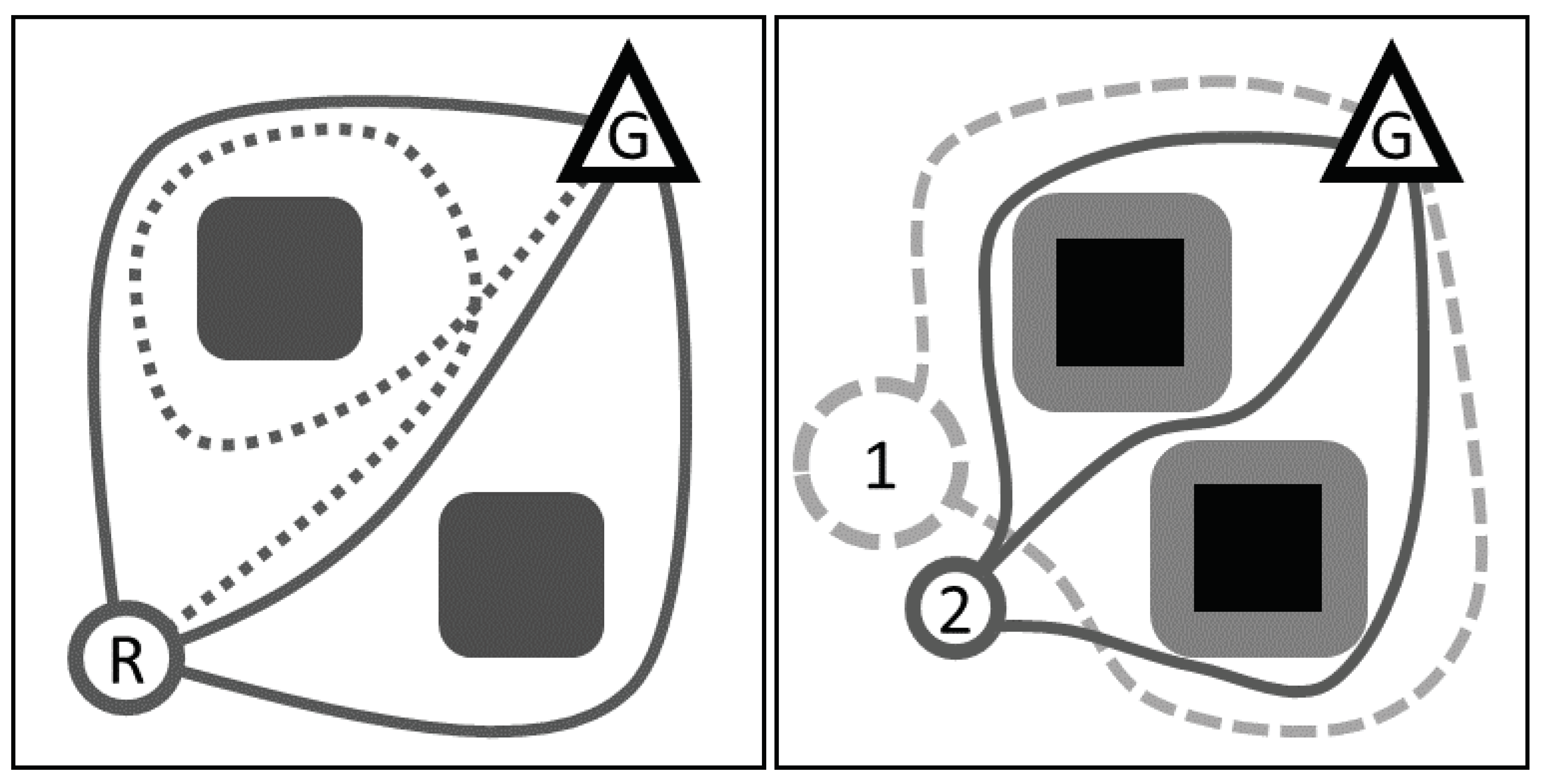
Preprints 86264 g003
Table 1. Overview of heuristics used in prioritised MRPP
Table 1. Overview of heuristics used in prioritised MRPP
  Identifier Description
[20] Static Ordering 1 Prioritised based on order added to network
[24] Hill-climbing Search Randomly swap priorities to search for better routes
  Random Ordering Prioritised Randomly
[25] Static Ordering 2 Agents given priorities based on their ID
[26] Naive Surroundings Counts number of other agents in local workspace
[27] Road-map Distance Furthest robot gets priority
[28] Coupled Ordering Schema coupled with effective routing lengths
[29] Continuous Enhancement Blocked robots have scores increased
[30] Planning Time Total time to identify route in empty workspace
[8] Path Prospects-R Total number of distinct routes (with random tie-break)
  Path Prospects-LF Total number of distinct routes (with Euclidean tie-break)
  Coupled Surroundings Counts the number of objects in the local workspace which obstruct robot
  Forwards Looking Naive Surroundings with restricted-search to low-route regions
Table 2. Summary of priority modification heuristics used in rescheduling.
Table 2. Summary of priority modification heuristics used in rescheduling.
  Identifier Description
[20] Prioritised Planning Core algorithm
[31] Full Search Considers all possible configurations
[32] Random Rescheduling Random switching of priorities
[24] Hill-climbing Search Randomly swap priorities to search for better routes
[33] Deterministic Rescheduling when an agent fails, it gets max score
[34] Local Priority Adjustment Only conflict onlookers are required to replan
[35] PriorityTuning Robots with least optimal routes, have priorities increased and replan till convergence
Table 3. Examples and concepts of heuristics based on Context Generality
Table 3. Examples and concepts of heuristics based on Context Generality
Generality Name / Description  
Abstract Random Ordering [24]
  Static Ordering [20]
Road-map Distance [27]
System-Dependent Planning Time [30]
  Path Prospects [8]
Combined Task-Priority Grading + Navigation Distance [7]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated