Test of Volatile Behaviors with the Asymmetric Stochastic Volatility Model: an Implementation on nasdaq-100

Preprint

Article

Test of Volatile Behaviors with the Asymmetric Stochastic Volatility Model: an Implementation on nasdaq-100

Altmetrics

Downloads

111

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

26 September 2023

Posted:

28 September 2023

You are already at the latest version

Alerts

Abstract

ABSTRACT The present study aimed to investigate the presence of asymmetric stochastic volatility and leverage effects within the Nasdaq-100 index. This index is widely regarded as an important indicator for investors. We focused on the nine leading stocks within the index, which are highly popular and hold significant weight in the investment world. These stocks are Netflix, PayPal, Google, Intel, Microsoft, Amazon, Tesla, Apple, and Meta. The study covered the period between 03/01/2017 and 30/01/2023, and we employed the Eviews and WinBUGS applications to conduct the analysis. We began by calculating the logarithmic difference to obtain the return series. We then performed a sample test with 100,000 iterations, excluding the first 10,000 samples to eliminate the initial bias of the coefficients. This left us with 90,000 samples for analysis. Using the results of the asymmetric stochastic volatility model, we evaluated both the Nasdaq-100 index as a whole and the volatility persistence, predictability, and correlation levels of individual stocks. This allowed us to evaluate the ability of individual stocks to represent the characteristics of the Nasdaq-100 index. Our findings revealed a dense clustering of volatility, both for the Nasdaq-100 index and the nine individual stocks. We observed that this volatility is continuous but has a predictable impact on variability. Moreover, with the exception of Intel, all the stocks in the model exhibited both leverage effects and the presence of asymmetric relationships, as did the Nasdaq-100 index as a whole. Overall, our results show that the characteristics of stocks in the model are similar to the volatility characteristic of the Nasdaq-100 index and have the ability to represent it.

Keywords:

Subject: Business, Economics and Management - Economics

Introduction

The integration of markets with each other, while offering positive opportunities for financial depth, has also brought about adverse fluctuations. Indeed, crises that may occur in another country, financial turmoil, or other news affecting markets have disrupted the macroeconomic balances of other countries as a result of this integration, leading to more complex economies in those countries (Beine, at.all 2010). Asymmetric volatility, also known as volatility asymmetry, refers to the situation in which new information leads to different levels of price changes. In other words, the presence of asymmetric effects implies that positive and negative shocks do not have an equal impact on the volatility of the return series. (Cappiello, at all. 2006). Although asymmetric effects and leverage effects are sometimes used interchangeably, they actually carry distinct meanings. The leverage effect is an indicator that reflects the varying impact of different shocks on the stock market. According to the leverage effect, a decrease (increase) in asset prices increases (decreases) the leverage levels of companies and consequently amplifies (diminishes) the risk borne by equity shareholders, leading to an increase (decrease) in the stock’s volatility.

Integration of markets with each other, although it provides positive opportunities for financial depth, has also brought along negative fluctuations. Indeed, crises that may occur in another country, financial disturbances, or other news affecting markets have disrupted the macroeconomic balances of other countries as a result of this integration, thus leading to more complex economies for countries. It is at this point that these factors have begun to be taken into account in the formulation of countries’ macroeconomic policies, and the need to mitigate negative effects and maximize positive returns for market participants has increased. With this momentum, especially since the global liberalization process after the 1980s, the importance of the concept of volatility has increased both in theory and practice.

Although the concept of volatility is perceived at an equivalent level to risk in terms of meaning, it should not actually be considered within the same framework as risk. This is because the concept of risk presents undesirable, negative outcomes, whereas the concept of volatility provides us with the volatility (fluctuation) of an asset in a positive or negative direction from a financial perspective. The concept of volatility is particularly an indicator aimed at measuring the width of deviation from the average value of a specific series in financial literature.

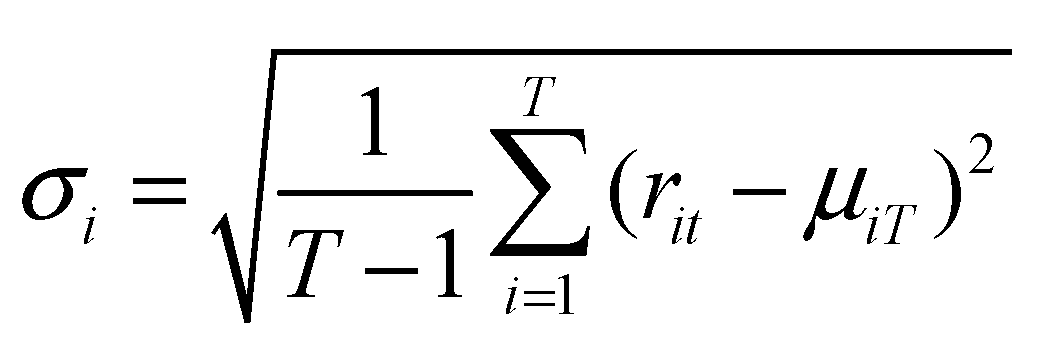
When different countries engage in mutual competition in certain products, a crisis in one country can deeply affect the macroeconomic structure of another. The contagion effect can manifest itself, for example, when a devaluation in one country makes the products produced by rival countries relatively expensive in terms of trade, thereby triggering a crisis in those countries. The 1998 Russian crisis can be cited as an example of this situation.

Especially in recent times, there has been an increasing research trend aimed at examining the interaction of volatility between countries and markets. This trend has provided financial market participants with the opportunity to diversify their portfolios more effectively. Volatility interaction in financial markets is crucial for asset pricing, exchange rates, trade strategies, risk hedging, and the development of effective regulatory strategies. Asymmetric volatility, also known as volatility asymmetry, refers to a situation where new information leads to different levels of price changes. In other words, the presence of asymmetric effects indicates that positive and negative shocks do not have an equal impact on the volatility of returns in series.

The leverage effect is an indicator that shows the different levels of impact of these different shocks on the stock market. According to the leverage effect, a decrease (increase) in asset prices increases (decreases) the leverage level of companies and therefore increases (decreases) the risk borne by shareholders. As a result, the volatility of the stock increases (decreases).

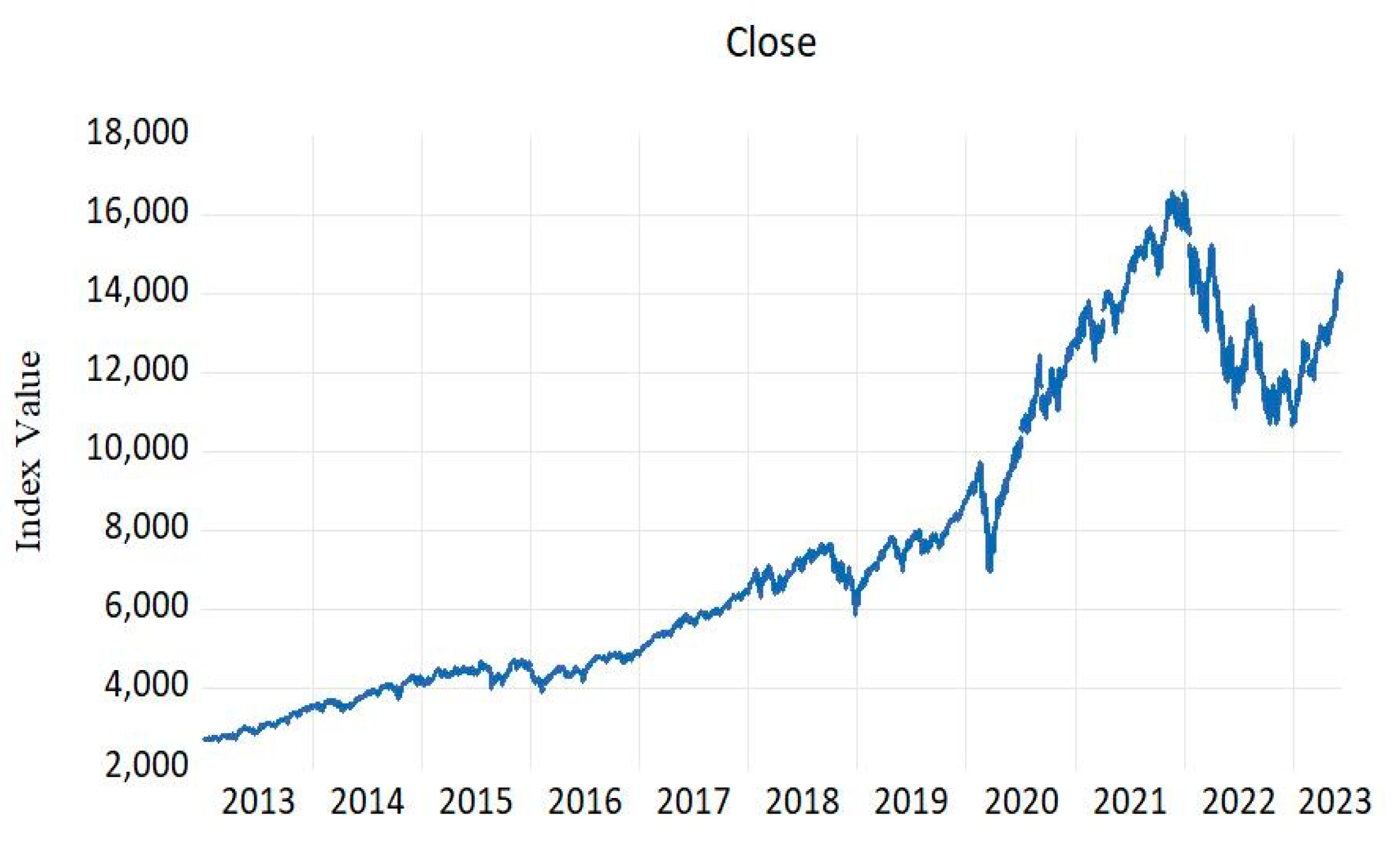
Figure 1. Index Value of Nasdaq (2013-2023). Source. https://www.nasdaq.com/market-activity/index/comp/historical.

Literature Review

Stock market volatility is a key area of interest in financial research due to its influence on pricing, risk management, and investment decisions. In the past decade, significant attention has been given to exploring asymmetric stochastic volatility and the leverage effect in stock returns. These phenomena provide valuable insights into the dynamics and risk characteristics of stock markets. This comprehensive literature review aims to consolidate the current state of knowledge by examining articles published in the last 10 years.

Numerous studies have investigated asymmetric stochastic volatility using advanced econometric techniques. For instance, Johnson et al. (2012) examined the presence of asymmetric volatility in the US stock market and found strong evidence supporting its existence. They employed a GARCH (Generalized Autoregressive Conditional Heteroskedasticity) framework and demonstrated that negative shocks have a more significant impact on volatility than positive shocks. Similarly, Li and Li (2016) explored the Chinese stock market and identified significant asymmetric volatility, indicating that negative shocks lead to larger and more persistent volatility responses compared to positive shocks.

Furthermore, recent research by Engle et al. (2017) focused on investigating asymmetric volatility in international stock markets. They employed a regime switching GARCH model and found evidence of asymmetric volatility across different countries and regions. Their results indicated that negative shocks have a more pronounced impact on volatility, suggesting the presence of asymmetry in stock market dynamics.

The leverage effect, which explores the relationship between stock returns and subsequent volatility, has also been extensively studied in the past decade. Researchers have focused on understanding the asymmetric impact of positive and negative returns on future volatility. For instance, Bollerslev et al. (2013) investigated the leverage effect in the European stock markets and found that negative stock returns are associated with higher subsequent volatility, while positive returns are linked to lower subsequent volatility. They employed a GARCH framework and provided robust empirical evidence of the leverage effect.

Similarly, Liu et al. (2015) examined the leverage effect in the context of emerging markets. They employed a multivariate GARCH model and confirmed a negative relationship between stock returns and future volatility, indicating the presence of the leverage effect. Their findings suggested that downside risk plays a more significant role in shaping stock market dynamics than upside risk.

Researchers have utilized various econometric methodologies to analyze asymmetric stochastic volatility and the leverage effect in stock returns. Advanced models such as GARCH, EGARCH (Exponential GARCH), and stochastic volatility models have been widely employed.

For instance, Ding et al. (2014) applied a threshold GARCH model to investigate asymmetric volatility in the Chinese stock market. They found strong evidence of asymmetry during different market regimes, suggesting that stock returns have different effects on volatility depending on the market conditions. The threshold GARCH model allowed for a more accurate representation of the nonlinear relationship between returns and volatility.

In another study, Chen, and Gao (2019) employed a Markov-switching asymmetric power GARCH approach to explore asymmetric volatility in Chinese stock markets. Their findings supported the presence of significant asymmetry in different market conditions. The Markov-switching approach captured the regime-switching dynamics of volatility, allowing for a more comprehensive analysis of asymmetric volatility.

The empirical evidence from the past 10 years consistently supports the presence of asymmetric stochastic volatility and the leverage effect in stock returns. For instance, studies by Lu and Lai (2012), Guo et al. (2016), and Wu et al. (2018) provide further confirmation of these phenomena across different stock markets and asset classes.

Understanding the presence of asymmetric stochastic volatility and the leverage effect has profound implications for investors, policymakers, and researchers. These phenomena can significantly impact risk management strategies, option pricing, and portfolio allocation decisions. By incorporating these effects into financial models and risk management practices, investors can make more informed decisions and effectively manage their portfolios.

Future research directions may involve exploring the impact of asymmetric volatility on derivative pricing, investigating the role of market sentiment in shaping asymmetry and examining the cross-country variations in the leverage effect. Additionally, the development of more advanced econometric models that can capture the complexities of asymmetric volatility and the leverage effect would contribute to a deeper understanding of these phenomena.

In conclusion, this comprehensive literature review provides an in-depth understanding of the presence of asymmetric stochastic volatility and the leverage effect in stock returns. The synthesis of articles published in the past 10 years demonstrates robust empirical evidence supporting the existence of these phenomena. By incorporating these effects into financial models and risk management practices, investors and policymakers can make more informed decisions. Future research endeavors should continue to explore and refine our understanding of these phenomena, contributing to the advancement of financial econometrics and investment strategies.

Econometric Method

The development of integration among financial markets has made the volatility structure of assets increasingly important, alongside the optimization of returns. Engle’s (1982) study first introduced the modeling of volatility, marking a fundamental starting point for volatility modeling. Before this study, modeling of the mean of financial asset returns was performed, but with Engle’s work, the variance modeling was also included. Engle’s study noted that the variance changes over time and that the constancy of variance is not always valid due to unexpected shocks. This study became popularly known as Autoregressive Conditional Heteroscedasticity (ARCH) in the literature (Engle, 1982).

Subsequently, (Bollerslev 1986) proposed the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model by extending the ARCH model, thus contributing to deterministic volatility models. In the following years, studies were conducted to investigate the impact of positive and negative news on volatility, which led to the inclusion of symmetric and asymmetric deterministic models in the literature, depending on whether the effects of positive and negative news on volatility are the same or different (Hentschel, 1995).

With Taylor’s (1986) study, Stochastic Volatility (SV) models have introduced a different perspective on the volatility structure of assets as an alternative approach to deterministic models in modeling volatility. The main characteristic of stochastic volatility models is that volatility is included as an unobservable, i.e., latent, variable in the analyses. While the volatility structure can be modeled deterministically as an observable variable in ARCH-type models, it is treated as an unobservable variable in alternative stochastic volatility models (Broto & Ruiz, 2004). Another advantage of stochastic volatility models, compared to GARCH models, is that they provide more effective parametric results, particularly in one-period-ahead forecasts (Das & Ghanem, 2009).

The presence of asymmetric relationships was first addressed in the literature by (Harvey and Shephard 1996). In this study, they related the sign of the volatility obtained using the Kalman filter to the return series. Similarity functions in this study were calculated using the Quasi-Maximum Likelihood (QML) method.

According to Harvey and Shephard’s model:

y_{t} = σ ε_{t} e^{h_{t} / 2} t = 1, ...., T,

(1)

h_{t + 1} = ϕ h_{t} + η_{t} η_{t} \sim N (0. σ_{η}^{2})

In equation (1), the parameter σ represents the scaling factor and includes a constant term effect on ht. ε_t represents a zero-mean random variable. Furthermore, when the absolute value of ϕ is less than 1, h_t and therefore y_t are stationary. According to Harvey and Shephard, there is a correlation relationship between the error terms of the mean and volatility models that exhibits simultaneous movement, represented as corr(ε_t,η_t) = ρ.

After Harvey and Shephard’s (1996) research, Jacquier et al. (2004) contributed by developing an asymmetric stochastic volatility model for discrete time, and modeled their work in a structure that takes the MCMC method in this study.

\begin{array}{l} y_{t} = \sqrt{h_{t}} ε_{t} \\ \log h_{t} = α + δ \log h_{t - 1} + η_{t} \end{array}

(2)

According to this model, the covariance matrix rt ≡(ε_t,η_t)ꞌ ∑*. Accordingly, ∑*:

It is expressed as

\sum_{}^{*} = (\begin{matrix} 1 \\ ρ σ_{η} \end{matrix} \begin{matrix} ρ σ_{η} \\ σ_{η}^{2} \end{matrix})

(3)

If the coefficient ρ is negative, ε_t changes will be higher and will occur simultaneously. On the other hand, a positive development is associated with a decrease in ε_t volatility. Even for intermediate correlation values, an asymmetric leverage effect can be exhibited. This situation shows that in the Jacquier et al. (2004) study, the expected value of E[h_t] will be 60% higher for negative shocks than for positive shocks when the correlation coefficient is -0.6 and ε_t value is 1.5. (Jacquier et al., 2004).

The contributions to the asymmetric stochastic volatility model continued with the study by (Yu 2005). In this study, Yu criticized the work of (Jacquier et al. 2004) and proposed the following model for asymmetric stochastic volatility:

\begin{array}{l} y_{t} = σ_{t} ε_{t} \\ \ln σ_{t + 1}^{2} = α + ϕ \ln σ_{t}^{2} + ρ σ_{η} σ_{t + 1}^{- 1} y_{t + 1} + σ_{η} \sqrt{1 - ρ^{2}} w_{t + 1} \end{array}

(4)

According to Equation (4), Yu (2005) proposed a representation of the model that incorporates intertemporal correlation instead of contemporaneous correlation, i.e., corr(ε_t, η_t+1) = ρ. In addition, it was observed that the MCMC method provided more reliable results compared to the QML method by comparing them. Yu also combined Harvey and Shephard’s (1996) model with Jacquier et al.’s (2004) model to create the following model:

\begin{array}{l} y_{t} = σ_{t} ε_{t} \\ \ln σ_{t + 1}^{2} = α + ϕ \ln σ_{t}^{2} + σ_{η} (ρ_{1} ε_{t} + ρ_{2} ε_{t + 1} + \sqrt{1 - ρ_{1}^{2} - ρ_{2}^{2}} w_{t + 1} \end{array}

(5)

In this model, correlations are allowed at both time delays, but with varying degrees of correlation.

Another contribution to asymmetric SV models was made by (Asai and McAleer 2005). They proposed a model that explains asymmetric relationships based on the direct negative correlation between changes in volatility and returns, which they referred to as a dynamic asymmetric volatility model. The model is expressed as follows:

\begin{array}{l} h_{t + 1} = μ + ϕ h_{t} + η_{t} η_{t} \sim N (0, σ η^{2}) \end{array}

(6)

E (ε_{t} η_{t}) = ρ σ_{η}

(7)

μ

: The constant term of the volatility model

ϕ

: Volatility persistence (continuity)

ε_{t}

: Error term of the mean model

η_{t}

: Error term of the volatility model

ρ

ε_{t}

and

η_{t}

represents the correlation coefficient between them.

In display (7), when the significance of the coefficient r is considered, an asymmetric relationship can be observed, and when the r coefficient is less than 0, dynamic leverage effects on volatility can be observed. Stochastic volatility models work with Bayesian techniques and methods such as Effective Importance Sampling (EIS) and Monte Carlo Markov Chain (MCMC) are quite popular. In this study, the MCMC method is used to calculate the dynamic leverage effect on volatility. The main purpose of MCMC methods is to produce variables by repeatedly sampling a Markov chain. (Kim et al., 1998). The main idea underlying the method is to calculate the joint posterior distribution function of the parameters to be estimated by multiplying the prior distribution function and the likelihood function of the data set. The prior density function is expressed in equation (8):

ρ (γ, ϕ, σ η, h 0, ...., h n) = ρ (γ, ϕ, σ η) ρ (h 0 | γ, σ η) \prod_{t = 1}^{n} ρ (h t | h t - 1, γ, ϕ, σ η)

(8)

The posterior distribution function is shown by equation (9):

p (γ, ϕ, σ η, h 0, ...., h n | y 1 ... yn) \propto p (γ) p (ϕ) p (σ η) p (h 0 | γ, σ η) \prod_{t = 1}^{n} p (h t | ht - 1, γ, ϕ, σ η) \prod_{t = 1}^{n} (y t | h t)

(9)

Data Set and Empirical Findings

In our study, we focused on the companies that form the foundation of the Nasdaq-100 index and constitute a significant part of the market value, namely Netflix (NFLX), Paypal (PYPL), Google (GOOGL), Intel (INTC), Microsoft (MSFT), Amazon (AMZN), Tesla (TSLA), and Apple (AAPL). For each of these stocks, we applied the ASV model using 1529 observations for the period between 03.01.2017 and 31.01.2023. According to this:

The above table shows the market value and weight of each stock in the index. It is observed that the 9 major stock units have approximately 45% value weight in the Nasdaq-100 market value. In the selection of stocks for the study, not only market value was taken into consideration, but also the popularity of the constituents among investors in the Nasdaq-100 was considered and used in the modeling. Accordingly, stocks such as Microsoft, Apple, Amazon, and Google are at the top of the ranking in terms of market capitalization and weight, while other stocks with low market capitalization and weight were included in the study due to their popularity among market participants. It can be argued that all of the stocks we have selected are suitable for testing the Nasdaq-100 characteristic in terms of both market value and popularity. The descriptive statistics of the return series and their corresponding graphs are presented in Table 2 and Figure 2, respectively:

When examining the values of descriptive statistics in Table 2, particularly the skewness referred to as the third moment and kurtosis known as the fourth moment, it is demonstrated that financial asset returns possess a leptokurtic characteristic that does not support the assumption of normal distribution. This information is further supported by the Jarque-Bera statistics. Additionally, the statistical significance of the probability values indicates the reliability of the values presented in Table 2. Figure 2 confirms that the differenced return series exhibit a stationary process over time, validating its suitability for our analysis.

In this study, a model was constructed using return series, where the return series were obtained using the ln(P_t/P_t-1)x100 equation, and model predictions were made using the WinBugs 1.4 program. In this context, 100,000 iterations were sampled, and the first 10,000 samples were excluded to remove the initial bias of the coefficients, and the remaining 90,000 samples were used for analysis. Therefore, the high number of samples is expected to produce more accurate parametric results, and the exclusion of the first 10% is intended to remove dependence on the initial values (prior distributions). Distribution assumptions for the study were made using the values in Yasuhiro Omori’s (2012) study through MCMC estimation. Accordingly, the reference values of μ ~Inverse-Normal(-10,1), ρ~Inverse-Uniform(-1,1), ϕ~Inverse-Beta(20,1.5),

σ_{η}^{2}

~Inverse-Gamma(2.5,0.025) were used as prior distributions. The initial values used for the ASV model parameters were μ = -9,

σ_{η}^{2}

=100, ρ=-4, ϕ=0.95. The ASV model parameter results for the selected stocks are presented in detail in Table 3 :

According to the results obtained from the model for Netflix, all five parameters were statistically significant at the 5% level of significance. One of these parameters

ϕ_{N F L X}

represents the persistence of volatility (volatility clustering) and provides a result close to 1 with a value of 0.89, indicating a high level of volatility clustering and the persistence of volatility continuity. Another important parameter for measuring volatility, the coefficient

σ_{η N F L X}

, expresses the standard deviation of the error term of the volatility model for Netflix. This parameter is used to calculate the variance of the error term of the volatility model and to represent the variability of volatility as variance. Consequently, it takes a value such as (

σ_{η N F L X}^{2}

= 0.197) which indicates that the variability of Netflix stock volatility is close to zero. The parameter

ϕ

being close to 1 and the parameter

σ_{η}^{2}

being close to 0 indicate that the structure of Netflix stock volatility is not highly floating. The coefficient

ρ_{N F L X}

which is another important parameter, expresses the direct relationship between changes in volatility and returns for Netflix. According to the model results, this parameter has a coefficient of -0.26 at the 5% level of statistical significance, indicating that there is an asymmetric relationship between changes in volatility and returns, and the negative value of the parameter coefficient indicates the presence of a weak leverage effect. Additionally, the low Monte Carlo error values from the model results prove that the model’s error margin is also very low.

The next section of the table presents the statistical significance of all parameter values based on the model results obtained for the PayPal stock. The persistence parameter of potential volatility clustering

ϕ_{P Y P L}

is statistically significant at the 5% level and close to 1 with a value of 0.95, indicating the presence of intense volatility clustering and thus, the continuity of volatility. Another parameter for measuring volatility, the coefficient

σ_{η P Y P L}

obtains an approximate value of 0.29, representing the variability of volatility as variance, with a result of approximately (

σ_{η P Y P L}^{2}

=0.088). This indicates that the variability of PayPal stock volatility is low. These results demonstrate the predictability of PayPal volatility. Another important parameter, the coefficient

ρ_{P Y P L}

expresses the direct correlation between changes in volatility and returns for PayPal. The model results indicate that this parameter is statistically significant for PayPal, indicating the presence of an asymmetric effect between changes in volatility and returns. Furthermore, the negative sign of this parameter signifies the existence of a leverage effect between shock effects on PayPal returns and volatility, with a significant but weak level of -0.33.

According to the model results obtained for Google stock, all stochastic model parameters are statistically significant. The parameter for volatility persistence

ϕ_{G O O G L}

is statistically significant and, due to its value of 0.92, it indicates a high level of clustering of volatility, suggesting the presence of volatility persistence. The parameter

σ_{η G O O G L}

has a coefficient value of 0.37, and the resulting variance of this value is approximately (

σ_{η G O O G L}^{2}

= 0.138), indicating a low level of volatility variability in the market for Google. These parameter values suggest that the predictability of Google stock volatility can be estimated. Another parameter, the coefficient

ρ_{G O O G L}

, represents the direct relationship between changes in Google stock volatility and Google returns. The model results for Google indicate that this parameter is statistically significant at a 5% level of significance, indicating the presence of both asymmetric effects and leverage effects between changes in volatility and returns.

According to the results of the model obtained for Intel stock, except for the

ρ_{I N T C}

parameter, all others are statistically significant. The

ϕ_{X L M}

parameter, with a value close to 0.90 and near 1, indicates that the stock has a high degree of volatility clustering. The

σ_{η I N T C}

coefficient in the model for Intel also obtains a value of approximately 0.47, and as a result of the variance, this indicator takes a value of approximately (

σ_{η I N T C}^{2}

=0.22). The fact that the value of 0.22 is relatively far from zero suggests that the volatility of Intel is high, and that the predictability of the stock’s volatility is somewhat lower than that of other stocks examined in the study. The

ρ_{I N T C}

parameter, which helps us to express the direct correlation relationship between changes in volatility and returns, although supporting an asymmetric relationship and leverage effect as a coefficient, is statistically insignificant at the 5% significance level in the model result. This indicates that there is no asymmetric relationship and leverage effect between changes in volatility and returns. Therefore, one of the findings for the Intel stock is that changes in volatility exhibit symmetric behavior.

According to the model results for Microsoft, all parameters are statistically significant.

ϕ X M S F T

indicates a high level of volatility persistence with an approximate value of 0.95. The

σ η M S F T

parameter obtains a value of approximately 0.31, and as a result of the variance, this indicator yields a value of approximately (

σ_{η M S F T}^{2}

= 0.096). Accordingly, the volatility variability for Microsoft stock is at a low level. The

ρ_{M S F T}

parameter demonstrates a statistically significant and strong correlation at a 5% significance level, with a coefficient of -0.48, indicating the presence of both asymmetric and leverage effects between shocks experienced by Microsoft returns and shocks experienced by Microsoft volatility.

According to the model results for Amazon, all parameters demonstrate statistical significance.

ϕ_{A M Z N}

indicates a dense volatility clustering with an approximate value of 0.95. The

σ_{η A M Z N}

parameter obtains a value of approximately 0.307, and as a result of the variance, this indicator yields a value of approximately (

σ_{η A M Z N}^{2}

= 0.094). Therefore, the volatility variability for Amazon stock is at a low level. The proximity of the

ϕ

parameter to 1 and the

σ_{η}^{2}

parameter to 0 indicates that the volatility of Amazon stock is predictable. The

ρ_{A M Z N}

parameter demonstrates a statistically significant correlation at a 5% significance level, with a coefficient of -0.31, indicating the presence of both an asymmetric relationship and leverage effect between shocks experienced by Amazon returns and shocks experienced by Amazon volatility.

According to the model results for Tesla, all parameters exhibit statistical significance.

ϕ_{T S L A}

indicates a high level of volatility persistence with an approximate value of 0.91. The

σ_{η T S L A}

parameter obtains a value of approximately 0.38, and as a result of the variance, this value yields an approximate result of (

σ_{η T S L A}^{2}

= 0.15). Therefore, the volatility variability for Tesla stock is at a low level. The trade-off relationship between the

ϕ

and

σ_{η}^{2}

parameters support the predictability of volatility for Tesla. The

ρ_{T S L A}

parameter demonstrates a statistically significant and weak correlation at a 5% significance level, with a coefficient of -0.171, indicating the presence of both asymmetric effects and leverage effects between shocks experienced by Tesla returns and shocks experienced by Tesla volatility.

According to the model results for Apple, all parameters are statistically significant.

ϕ_{A A P L}

indicates a dense volatility clustering with an approximate value of 0.94. The

σ_{η A A P L}

parameter obtains a value of approximately 0.30, and as a result of the variance, this indicator yields an approximate result of (

σ_{η A A P L}^{2}

= 0.09). Therefore, the volatility variability for Apple stock is at a low level. When examining the relationship between

ϕ

and

σ_{η}^{2}

, it supports the predictability of Apple stock volatility. The

ρ_{A A P L}

parameter demonstrates a statistically significant correlation at a 5% significance level, with a coefficient of -0.4572, indicating the presence of both asymmetric relationship and leverage effect between shocks experienced by Apple returns and shocks experienced by Apple volatility.

According to the model results for Meta, all parameters exhibit statistical significance.

ϕ M E T A

indicates a high level of volatility persistence with an approximate value of 0.92. The

σ_{η M E T A}

parameter obtains a value of approximately 0.42, and as a result of the variance, this indicator yields an approximate value of (

σ_{η M E T A}^{2}

= 0.18). Therefore, the volatility variability for Meta stock is at a low level. The

ρ M E T A

parameter demonstrates a statistically significant correlation, with a coefficient of -0.27, between shocks experienced by Meta returns and shocks experienced by Meta volatility. This indicates the presence of both leverage effect and asymmetric relationship.

According to the model results for the Nasdaq-100 index, all parameters are statistically significant.

ϕ_{N D X}

indicates a highly dense volatility clustering with an approximate value of 0.96, signifying persistence in volatility. The

σ_{η N D X}

parameter obtains a value of approximately 0.28, and as a result of the variance, this indicator yields an approximate value of (

σ_{η N D X}^{2}

= 0.08). Therefore, the volatility variability for the Nasdaq index is at a low level. When examining the relationship between

ϕ

and

σ_{η}^{2}

, it supports the predictability of the index’s volatility. The

ρ_{N D X}

parameter demonstrates a statistically significant and strong correlation at a 5% significance level, with a coefficient of approximately -0.64, indicating the presence of both leverage effect and asymmetric relationship between shocks experienced by Nasdaq returns and shocks experienced by Nasdaq volatility. The model results also suggest that other stocks included in the Nasdaq index exhibit high volatility clustering and display similar characteristics in terms of asymmetric structure and the presence of leverage effects, except for Intel stock. These findings highlight the common features and fluctuations in the Nasdaq-100 index based on positive and negative shocks in the market.

Conclusion

There has recently been a growing tendency among financial market participants to examine the volatility interaction among markets, enabling them to diversify their portfolios more effectively and allocate their investments with greater efficiency. The interaction of volatility in financial markets is crucial for asset pricing, currency and trading strategies, hedging, and effective regulatory strategies. Numerous studies in the literature have measured the spread of volatility on various indices of different countries, considering their relationships with other financial asset types and indices. However, studies that utilize ASV models for the Nasdaq-100 index and its major stocks are limited. Therefore, this study used dynamic leverage-effective stochastic volatility models to make predictions for major stocks within the Nasdaq-100. Subsequently, an ASV model was estimated for the Nasdaq-100 index itself, and the results were compared with those obtained from individual stock predictions.

The correlation relationship between the volatility continuity of stocks, the predictability of volatility, and the impact of shocks on the volatility of currencies in response to shocks that occur in their own returns were evaluated based on the results obtained from the dynamic leverage-effective SV model predictions. Based on these results, the presence of volatility density was determined for all stocks included in the analysis. In general, when considering stocks as a whole, it was empirically proven that there is a high volatility clustering for all stocks, and that this volatility is continuous and predictable. Another limitation of our study is to determine the presence of asymmetric relations/leverage effects for these stocks. Our findings have shown that there is no asymmetric relationship between changes in volatility and returns for the Intel financial asset and no leverage effect for this stock. In this context, an asymmetric relationship and leverage effect were found in all eight of the other stocks.

According to the results of the ASV model that fully encompasses the Nasdaq-100 index, there is a high volatility clustering and low volatility variability, thereby proving that volatility is predictable. Additionally, the strong correlation between the shocks experienced by Nasdaq returns and the shocks experienced by its volatility indicates the presence of both leverage effect and asymmetric relationship.

When compared to other literature studies, the results obtained for the stocks and indexes in our study closely match those of other studies. Specifically, similar findings were obtained in terms of their volatile structures. This can be attributed to the fact that, generally speaking, the volatile process of financial markets is more visible in terms of variable variance compared to other tools, and price forecasting predictions can show unusual trends. The empirical results obtained in our study are particularly important for the selection of indexes/stocks to be added to the portfolio, portfolio management, determination of risk level, and risk hedging. Similarly, the measurement of volatility level is an important indicator for providing investment strategies.

With the increasing number of studies focusing on examining volatility structures, our research provides valuable information on the careful selection of investment opportunities for various indices and other financial assets with high volatility structures. In this sense, our study is one of the ways to investigate the mentioned volatility structures, and it is believed to shed light on the complex volatility structure by helping researchers with various empirical research techniques in this area. The research can be extended by including other popular tools to better understand the volatility dynamics in financial markets and can offer more comprehensive insights for investors to embrace the nature of financial markets.

Conflicts of Interest

Research and publication ethics were complied with in the study.There is no conflict of interest between the authors of the study that could affect the results.

References

Asai, M.; McAleer, M. Dynamic asymmetric leverage in stochastic volatility models. Econometric Reviews, 2005, 24, 317–332. [Google Scholar] [CrossRef]
Beine, M.; Cosma, A.; Vermeulen, R. The dark side of global integration: Increasing tail dependence. Journal of Banking & Finance 2010, 34, 184–192. [Google Scholar]
Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. Journal of econometrics 1986, 31, 307–327. [Google Scholar] [CrossRef]
Bollerslev, T.; Osterrieder, D.; Sizova, N.; Tauchen, G. Risk and return: Long-run relations, fractional cointegration, and return predictability. Journal of Financial Economics 1986, 108, 409–424. [Google Scholar] [CrossRef]
Broto, C.; Ruiz, E. Estimation methods for stochastic volatility models: a survey. Journal of Economic surveys 2004, 18, 613–649. [Google Scholar] [CrossRef]
Brownlees, C.; Engle, R.F. SRISK: A conditional capital shortfall measure of systemic risk. The Review of Financial Studies 2017, 30, 48–79. [Google Scholar] [CrossRef]
Cappiello, L.; Engle, R.F.; Sheppard, K. Asymmetric dynamics in the correlations of global equity and bond returns. Journal of Financial econometrics 2006, 4, 537–572. [Google Scholar] [CrossRef]
Chen, H.; Li, Y.; Liu, Y. Dual capabilities and organizational learning in new product market performance. Industrial Marketing Management 2015, 46, 204–213. [Google Scholar] [CrossRef]
Chen, T.; Gao, Z.; He, J.; Jiang, W.; Xiong, W. Daily price limits and destructive market behavior. Journal of econometrics 2019, 208, 249–264. [Google Scholar] [CrossRef]
Das, S.; Ghanem, R. A bounded random matrix approach for stochastic upscaling. Multiscale Modeling & Simulation 2009, 8, 296–325. [Google Scholar]
Ding, H.; Chong, T.T.L.; Park, S.Y. Nonlinear dependence between stock and real estate markets in China. Economics Letters 2009, 124, 526–529. [Google Scholar] [CrossRef]
Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica: Journal of the econometric society 1982, 987–1007. [Google Scholar] [CrossRef]
Harvey, A.C.; Shephard, N. Estimation of an asymmetric stochastic volatility model for asset returns. Journal of Business & Economic Statistics 1996, 14, 429–434. [Google Scholar]
Hentschel, L. All in the family nesting symmetric and asymmetric garch models. Journal of financial economics 1995, 39, 71–104. [Google Scholar] [CrossRef]
Jacquier, E.; Polson, N.G.; Rossi, P.E. Bayesian analysis of stochastic volatility models with fat-tails and correlated errors. Journal of Econometrics 2004, 122, 185–212. [Google Scholar] [CrossRef]
Li, Q.; Chen, Y.; Jiang, L.L.; Li, P.; Chen, H. A tensor-based information framework for predicting the stock market. ACM Transactions on Information Systems (TOIS) 2016, 34, 1–30. [Google Scholar] [CrossRef]
Lu, X.F.; Lai, K.K. Relationship between stock indices and investors’ sentiment index in Chinese financial market. Xitong Gongcheng Lilun Yu Shijian/System Engineering Theory and Practice 2012, 32, 621–629. [Google Scholar]
Taylor, S.J. Modelling financial time series. world scientific. 2008.
Wang, Y.; Pan, Z.; Wu, C. Volatility spillover from the US to international stock markets: A heterogeneous volatility spillover GARCH model. Journal of forecasting 2018, 37, 385–400. [Google Scholar] [CrossRef]
Wildeman, C.; Wakefield, S.; Turney, K. Misidentifying the effects of parental incarceration? A comment on Johnson and Easterling (2012). Journal of Marriage and Family 2013, 75, 252–258. [Google Scholar] [CrossRef]
Yu, J. On leverage in a stochastic volatility model. Journal of Econometrics 2005, 127, 165–178. [Google Scholar] [CrossRef]
Zhu, H.; Guo, Y.; You, W.; Xu, Y. The heterogeneity dependence between crude oil price changes and industry stock market returns in China: Evidence from a quantile regression approach. Energy Economics 2016, 55, 30–41. [Google Scholar] [CrossRef]
Beine M, Antonio C, Robert, V. The dark side of global integration: Increasing tail dependence. Journal of Banking & Finance 2010, 34, 186.
Poon, Ser-Huang. A practical guide to forecasting financial market volatility. John Wiley & Sons, 2005. p.1.
Knight, John, L. ; Stephen, E.S.; Jun, Y. Theory & methods: Estimation of the stochastic volatility model by the empirical characteristic function method. Australian & New Zealand Journal of Statistics 2002, 44, 320. [Google Scholar]
Hepsağ, A.; Burcay, Y.A. Analysis of Volatility Spillovers Between the Bank Stocks Traded In Istanbul Stock Exchange and New York Stock Exchange. Eurasian Econometrics, Statistics & Emprical Economics Journal 2016, 1, 54–72. [Google Scholar]

Figure 2. Graphs of the return series for units used in the study. Source : Prepared by the authors with Eviews model output.

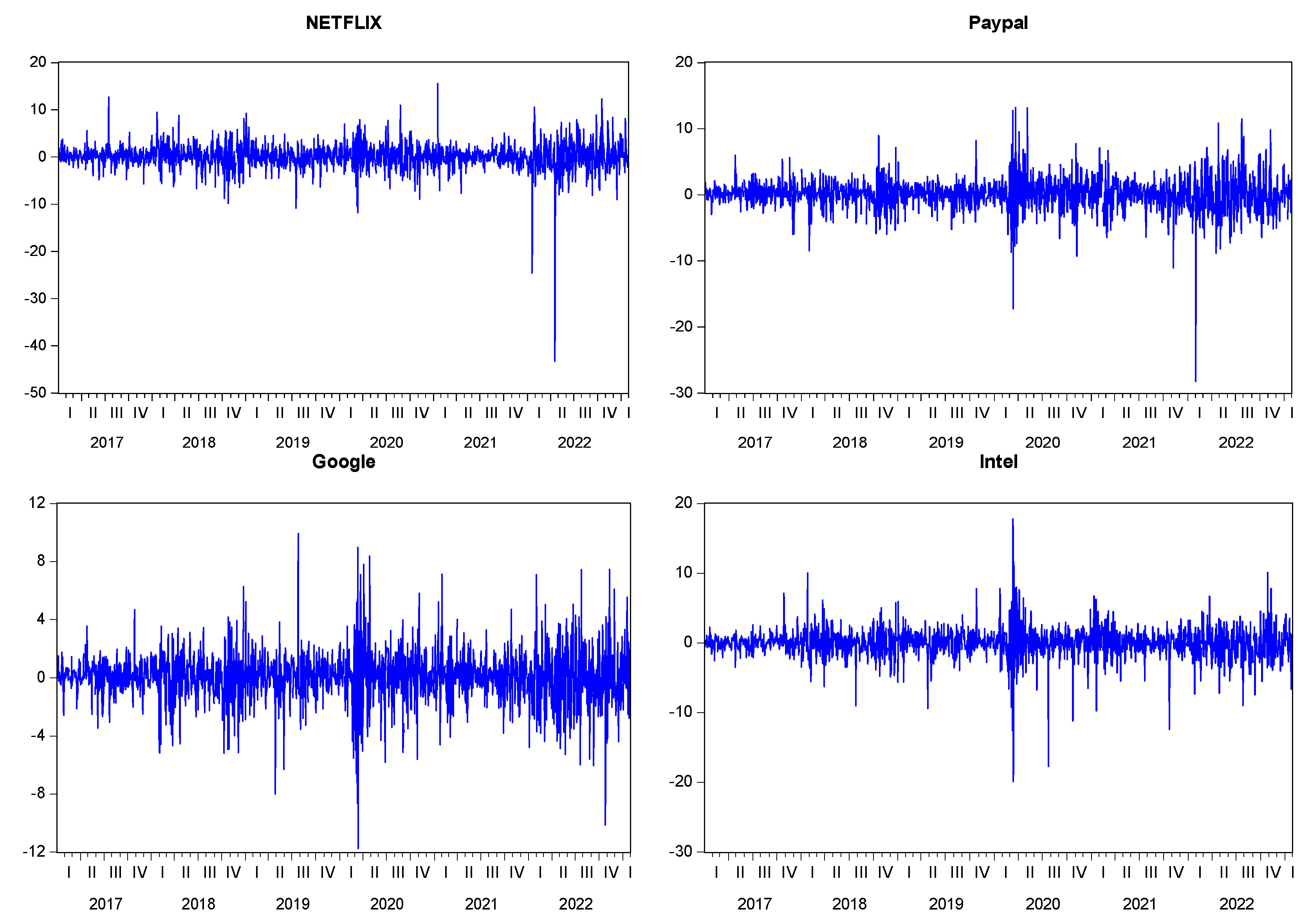
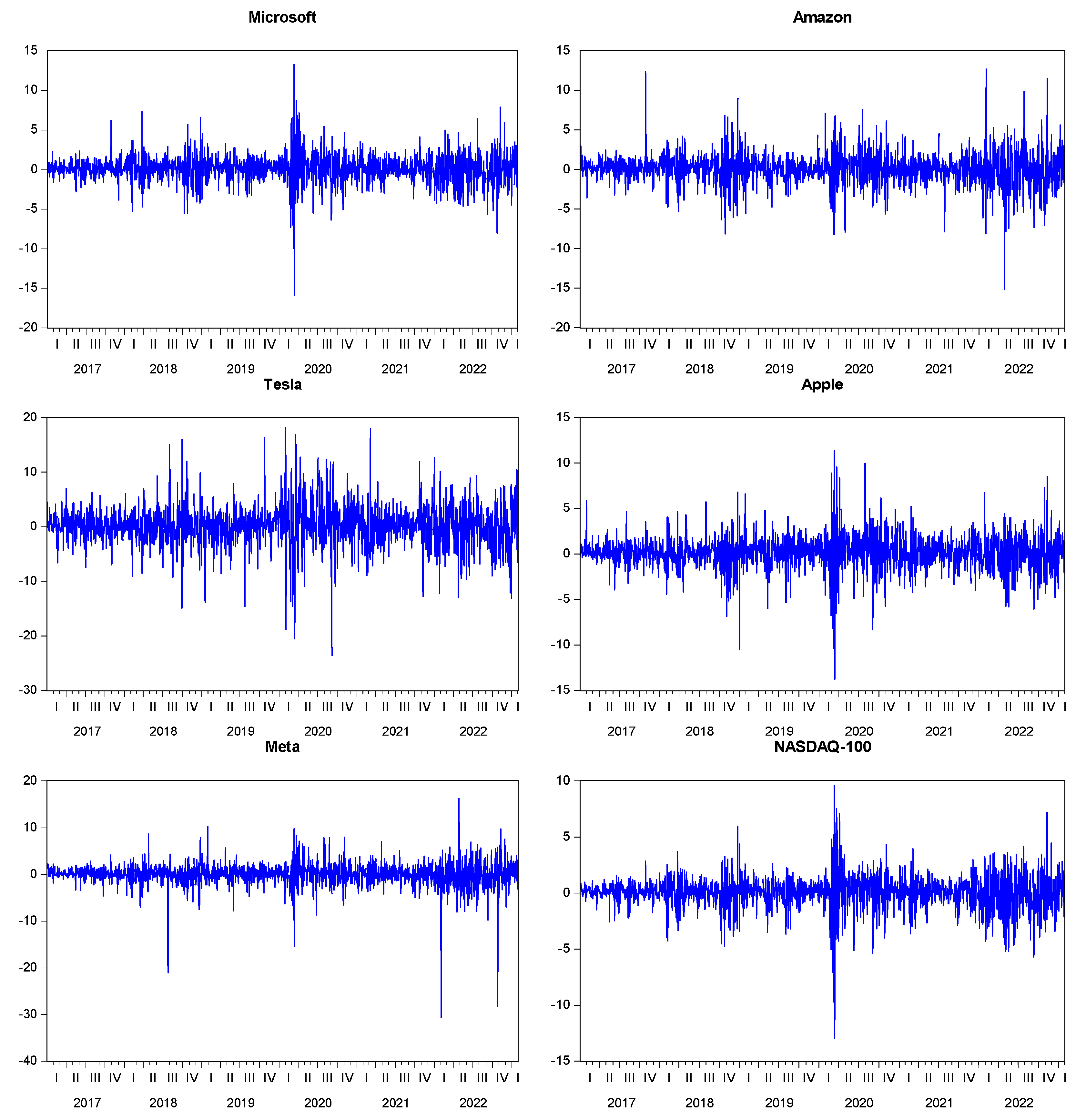
Table 1. Stock Unit and Total Market Values.

Stock Units	Weight	Market Cap
Netflix (NFLX)	1.183	152.15B
Paypal (PYPL)	0.655	85.02B
Google (GOOGL)	3.856	1346.38B
Intel (INTC)	1.02	133.10B
Microsoft (MSFT)	12.704	2076.94B
Amazon (AMZN)	6.205	1040.57B
Tesla (TSLA)	3.478	586.81B
Apple (AAPL)	12.458	2599.66B
Meta (META)	3.762	561.97B
Share of weight of selected stock units in Nasdaq-100	45.3%

Source : https://www.investing.com (Access Date : 14.04.2023).* The data in the table represent the values dated 14.04.2023.

Table 2. Descriptive statistics for selected stocks and Nasdaq-100.

	Mean	Median	Max	Min	Std.Dev.	Skewness	Kurtosis	Jaque-Bera	Observ.
Netflix	0.066767	0.060609	15.57580	-43.25785	2.91336	-2.352770	39.37181	85690.94	1529
Paypal	0.046133	0.141896	13.19908	-28.22361	2.56625	-0.828519	16.11873	11139.20	1529
Google	0.060985	0.117574	9.937953	-11.76673	1.85228	-0.213550	7.485203	1293.245	1529
Intel	-0.006024	0.027141	17.83241	-19.89573	2.24193	-0.688648	15.56109	10172.82	1529
Microsoft	0.095379	0.114790	13.29290	-15.94535	1.82829	-0.281769	11.07498	4174.352	1529
Amazon	0.065845	0.134587	12.69489	-15.13979	2.13178	-0.066113	8.217492	1735.396	1529
Tesla	0.162378	0.153386	18.14450	-23.65179	3.90274	-0.160801	7.111724	1083.660	1529
Apple	0.109191	0.100778	11.31576	-13.77082	1.97528	-0.239893	8.314467	1814.016	1529
Meta	0.015878	0.095097	16.20644	-30.63906	2.58517	-2.278320	30.02081	47837.76	1529
Nasdaq-100	0.058981	0.142970	9.596641	-13.00315	1.55111	-0.563345	10.12499	3315.057	1529

Source: Prepared by the authors with Eviews model output.

Table 3. ASV model results for selected stocks.

		Average	Std. Deviation	MC Error	Confidence interval (%95)
Netflix	$μ N F L X$	-7.66*	0.1139	0.001695	[-7.883	-7.434]
	$ϕ N F L X$	0.8924*	0.02707	0.001188	[0.8309	0.938]
	$ρ N F L X$	-0.2646*	0.06833	0.002161	[-0.3937	-0.128]
	$σ ε N F L X$	0.02175*	0.001241	1.86E-05	[0.01942	0.02431]
	$σ η N F L X$	0.4439*	0.05926	0.002913	[0.3404	0.5704]

Paypal	$μ P Y P L$	-7.831*	0.1543	0.002254	[-8.139	-7.53]
	$ϕ P Y P L$	0.9491*	0.01248	4.94E-04	[0.9226	0.9714]
	$ρ P Y P L$	-0.3322*	0.08333	0.003402	[-0.4987	-0.1655]
	$σ ε P Y P L$	0.01999*	0.001541	2.25E-05	[0.01709	0.02317]
	$σ η P Y P L$	0.2972*	0.03858	0.001937	[0.2214	0.3733]

Google	$μ G O O G L$	-8.383*	0.1268	0.002224	[-8.63	-8.129]
	$ϕ G O O G L$	0.9215*	0.01969	8.55E-04	[0.8771	0.9535]
	$ρ G O O G L$	-0.3583*	0.07304	0.002555	[-0.496	-0.2094]
	$σ ε G O O G L$	0.01515*	9.64E-04	1.70E-05	[0.01337	0.01717]
	$σ η G O O G L$	0.3712*	0.05256	0.002648	[0.2823	0.4878]

Intel	$μ I N T C$	-8.282*	0.1318	0.001662	[-8.545	-8.025]
	$ϕ I N T C$	0.8998*	0.02401	9.59E-04	[0.8461	0.9403]
	$ρ I N T C$	-0.03947	0.07039	0.002135	[-0.1751	0.1032]
	$σ ε I N T C$	0.01594*	0.00105	1.33E-05	[0.01395	0.01809]
	$σ η I N T C$	0.4699*	0.05503	0.002553	[0.3705	0.5871]

Microsoft	$μ M S F T$	-8.378*	0.1474	0.002543	[-8.661	-8.082]
	$ϕ M S F T$	0.9473*	0.01169	4.51E-04	[0.9218	0.9676]
	$ρ M S F T$	-0.4777*	0.07406	0.003024	[-0.6154	-0.3219]
	$σ ε M S F T$	0.0152*	0.001127	1.94E-05	[0.01316	0.01758]
	$σ η M S F T$	0.3097*	0.03565	0.001757	[0.2458	0.3869]

Amazon	$μ A M Z N$	-8.145*	0.1559	0.001881	[-8.453	-7.835]
	$ϕ A M Z N$	0.9486*	0.01267	4.95E-04	[0.9212	0.971]
	$ρ A M Z N$	-0.311*	0.07536	0.002833	[-0.453	-0.1597]
	$σ ε A M Z N$	0.01709*	0.001335	1.61E-05	[0.0146	0.01989]
	$σ η A M Z N$	0.3069*	0.03812	0.00188	[0.2327	0.3848]

	$μ T S L A$	-6.912*	0.117	0.001967	[-7.141	-6.68]
Tesla	$ϕ T S L A$	0.9054*	0.02913	0.00138	[0.8389	0.9507]
	$ρ T S L A$	-0.171*	0.06829	0.00199	[-0.302	-0.03438]
	$σ ε T S L A$	0.0316*	0.001853	3.13E-05	[0.02814	0.03544]
	$σ η T S L A$	0.3834*	0.06485	0.003367	[0.2778	0.525]

Apple	$μ A A P L$	-8.152*	0.1297	0.002441	[-8.402	-7.891]
	$ϕ A A P L$	0.9399*	0.01398	5.85E-04	[0.91	0.9647]
	$ρ A A P L$	-0.4572*	0.06836	0.002619	[-0.5849	-0.3176]
	$σ ε A A P L$	0.01701*	0.001108	2.09E-05	[0.01498	0.01934]
	$σ η A A P L$	0.3033*	0.03991	0.002017	[0.2274	0.3831]

Meta	$μ M E T A$	-7.993*	0.1438	0.001843	[-8.275	-7.71]
	$ϕ M E T A$	0.9226*	0.01698	6.44E-04	[0.8868	0.9529]
	$ρ M E T A$	-0.2733*	0.07024	0.002171	[-0.4083	-0.1338]
	$σ ε M E T A$	0.01842*	0.001327	1.71E-05	[0.01596	0.02117]
	$σ η M E T A$	0.4193*	0.04682	0.002173	[0.3292	0.5127]

Source: Prepared by the authors with WinBUGS 14 model output. *Table values represent statistical significance at the 5% level.

Table 4. ASV model results for the Nasdaq-100 index.

	Average	Std. Deviation	MC Error	Confidence interval (%95)
$μ N D X$	-8.663*	0.146	0.002249	[-8.943	-8.366]
$ϕ N D X$	0.9583*	0.007543	2.79E-04	[0.9419	0.9716]
$ρ N D X$	-0.6386*	0.0574	0.002418	[-0.7446	-0.5156]
$σ ε N D X$	0.01318*	9.69E-04	1.48E-05	[0.01143	0.01526]
$σ η N D X$	0.281*	0.02688	0.001313	[0.2338	0.3367]

Source: Prepared by the authors with WinBUGS 14 model output. * Table values express statistical significance at the 5% significance level.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Test of Volatile Behaviors with the Asymmetric Stochastic Volatility Model: an Implementation on nasdaq-100

Abstract

Introduction

Literature Review

Econometric Method

Data Set and Empirical Findings

Conclusion

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe