1. Introduction
Entry into the abdomen is a critical step in abdominal laparoscopic procedures. Although routinely performed in operating theatres across the world, entry into the abdomen is not without risk. (i.e. injury to aorta, inferior vena cava, iliac vessels and hollow and solid viscera) is a significant complication, and is associated with a high mortality rate [
1]. Potential contributing factors to large vessel or bowel injury include inexperience/unskilled surgeons, inappropriate insertion of the device used to enter the abdomen, and forceful thrust of the entry device into the abdomen [
1].
Implementation of procedural skills trainers (referred to as
trainers) during surgical training has been proposed to improve safety during laparoscopic abdominal entry[
2]. The introduction of trainers may create more skilled surgeons and mitigate the need for procedural practice on patients during early phases of skill acquisition. Development of such a trainer (i.e., for entry into the abdomen during laparoscopic surgery) requires replication of the haptic fidelity of a patient.
Before designing a trainer, it is imperative to understand how injury can occur during entry into the abdomen. Appreciation of 1) the entry procedure, and 2) the anatomy of the abdominal wall is required to develop an effective trainer.
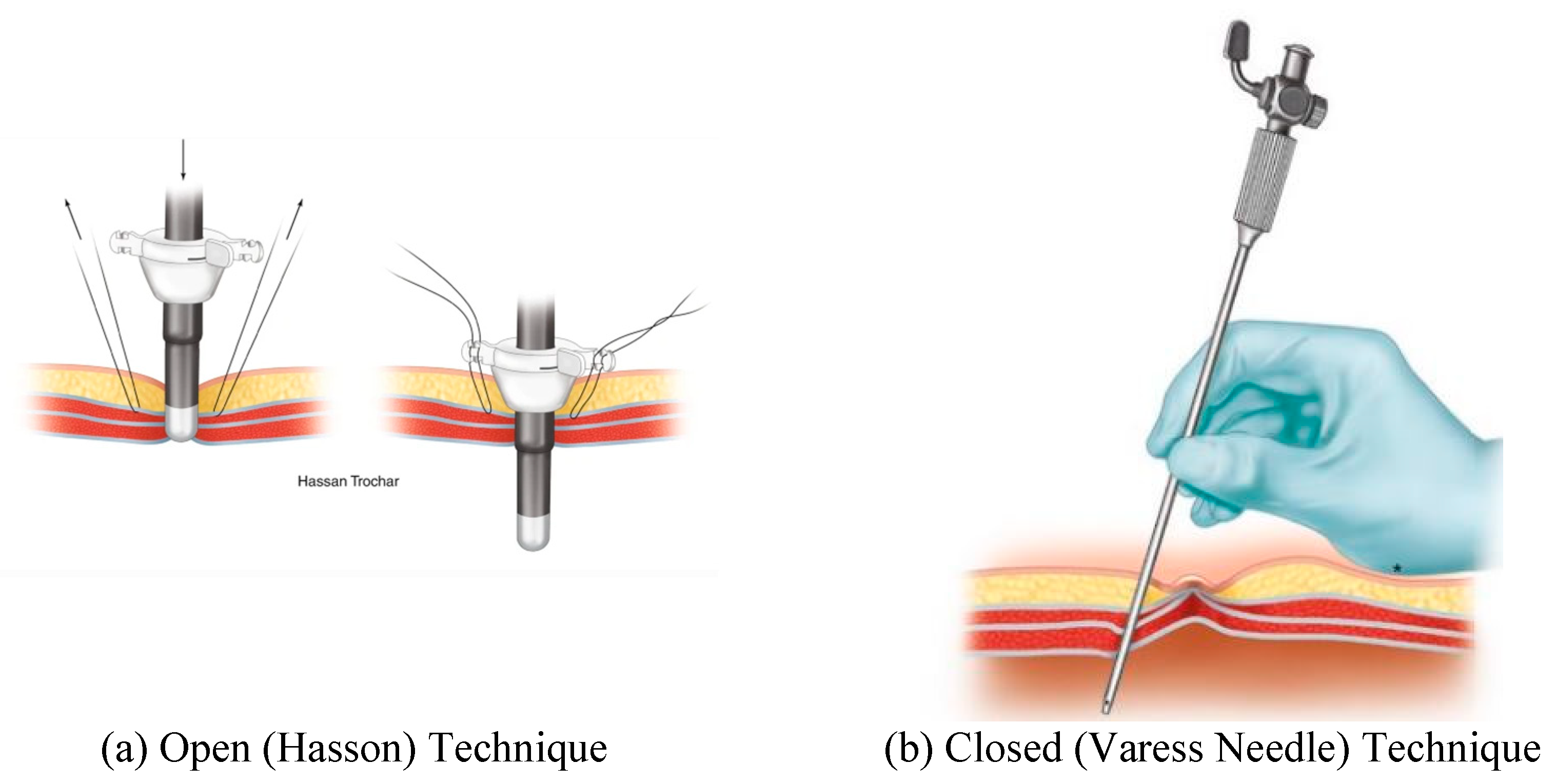
During laparoscopic entry into the abdomen, insufflation through a primary port is undertaken to separate the viscera from ventral abdominal wall. This primary port is often placed at the umbilicus using an open or closed technique.
The open (Hasson) technique involves an incision in the umbilicus and dissection of the subcutaneous tissue and fasciae under direct visualization. Stay sutures are placed in the fascial layers for subsequent use in stabilizing the port. The peritoneum is opened (bluntly or by sharp dissection) and a cannula is advanced into the abdomen for insufflation.
The closed technique involves the use of a Veress needle. The linea alba is commonly used for closed entry as it is the only significant structure between the superficial tissues and parietal peritoneum. The skin and subcutaneous tissue is dissected, and then the skin and fascia are elevated. The Veress needle is passed through the incision to enter the peritoneum with an angled approach. There is tactile feedback as the needle traverses the linea alba, then peritoneum. After insufflation the Veress needle is removed, and the primary trocar is placed in the same tract.
Figure 1.
Open and closed port entry are shown in this figure. Panel (a) displays an example of Hasson port entry. Image from
Figure 1.3, Ref. [
3]. Panel (b) demonstrates entry using the closer (Veress needle) technique and image from
Figure 1.4, Ref. [
3].
Figure 1.
Open and closed port entry are shown in this figure. Panel (a) displays an example of Hasson port entry. Image from
Figure 1.3, Ref. [
3]. Panel (b) demonstrates entry using the closer (Veress needle) technique and image from
Figure 1.4, Ref. [
3].
Knowledge of the anatomical arrangement of abdominal wall structures and tissue planes is critical for safe entry into the abdomen. A brief description of the relevant clinical anatomy (adapted from Last’s Anatomy (9
th Edition)) [
4] is provided here however the reader is directed to specialist texts for further detail.
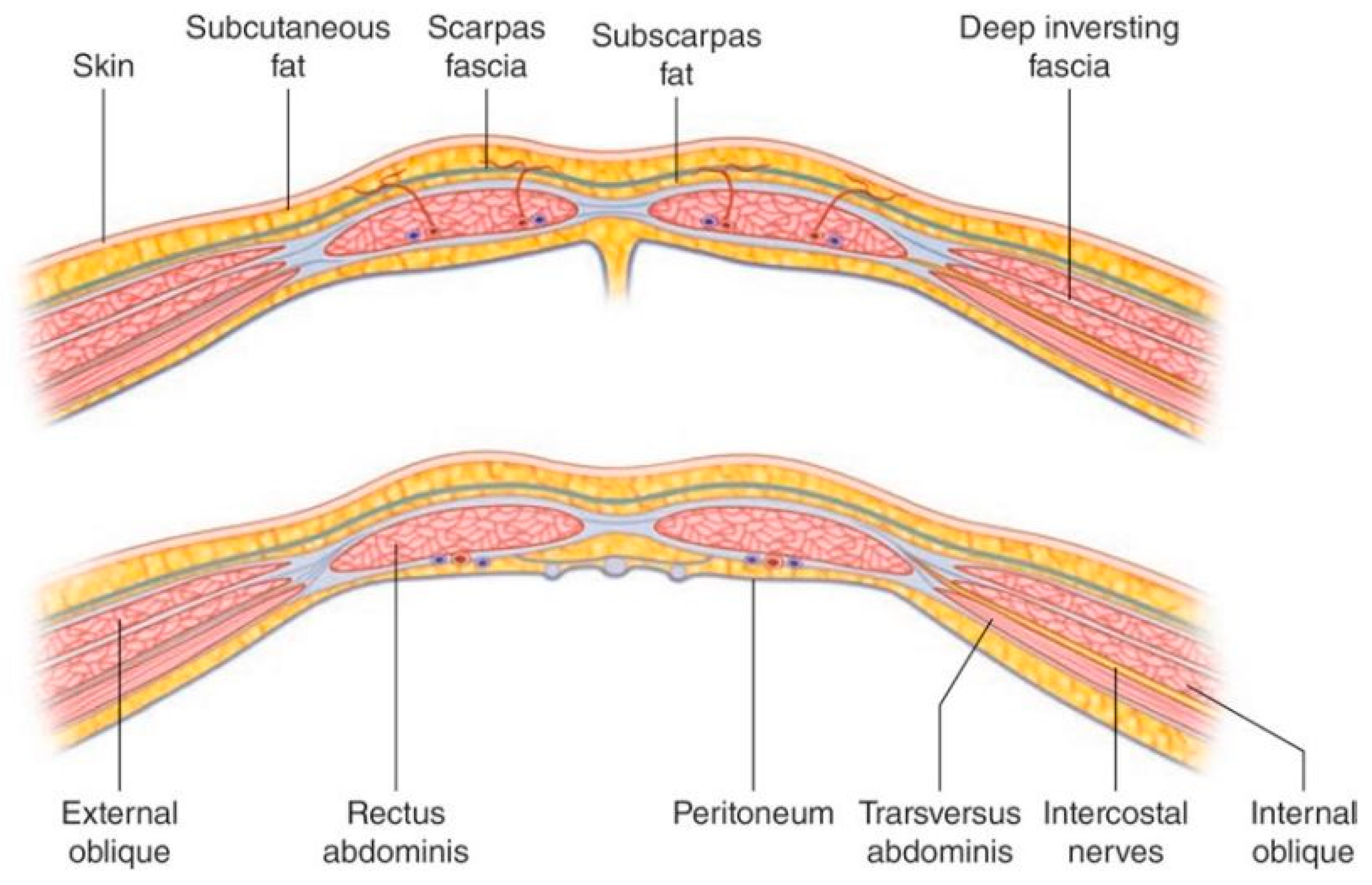
The anterior abdominal wall is comprised of skin, superficial fascia (subcutaneous fat), muscle and fascial layers and peritoneum. The tissue comprising the wall and the number of layers changes depending on location within the abdominal wall. Deep to the skin, the superficial fascia is dual layer comprised of Camper’s fascia (superficial layer of superficial fascia) and Scarpa’s fascia (membranous layer of superficial fascia). These layers of superficial fascia extend beyond the abdomen to the thorax and pelvis.
There are three muscular layers of the abdominal wall which remain separate laterally and fuse in the midline as the rectus abdominus. The external oblique muscle is the most superficial of the lateral muscles. The muscle arises from the lower eight ribs and becomes aponeurotic by its broad insertion from the iliac crest and anterior superior iliac spine to the pubic tubercle. Aponeurotic fibers with a free upper border running horizontally from the fifth rib to xiphisternum, run anterior to the rectus abdominus muscle and attach to other aponeurotic layers to form the linea alba. This aponeurosis therefore contributes to the anterior rectus sheath (described below). The muscle fibers of the external oblique run obliquely caudomedially.
The next muscular layer, deep to the external oblique muscle is the internal oblique. It originates from the lumbar fascia, iliac crest and lateral two thirds of the inguinal ligament. Muscle fibers run towards the costal margin to which they attach. The muscle gives way to aponeurotic fibers at the tip of the ninth costal cartilage, and the aponeurosis contributes to the rectus sheath and fuses with other aponeuroses to form the linea alba.
The transversus abdominus is the deepest of the three lateral muscles. It has a broad origin from the costal margin, lumbar fascia, iliac crest, and inguinal ligament. The muscle fibers become aponeurotic and also contribute to the rectus sheath.
The rectus abdominus is a paired muscle running from the pubic symphysis and pubic crest to the fifth to seventh costal cartilages. The two muscles are separated by linea alba. The rectus abdominus is divided into smaller bellies by tendinous intersections (usually three) that penetrate the superficial layer of the muscle. It is encased by the rectus sheath (
Figure 2) which is formed by the aponeuroses of the lateral abdominal wall muscles. The anterior rectus sheath is structured differently about a point 2.5 cm below the umbilicus (the arcuate line). Above the arcuate line, the anterior rectus sheath is formed by the fusion of the aponeurosis of the external oblique and the superficial layer of the split aponeurosis of the internal oblique. The posterior layer of the rectus sheath above the arcuate line is formed by the posterior layer of the aponeurosis of the internal oblique and that of the transversus abdominus.
The splitting of the internal oblique aponeurosis forms the semilunar line which runs from the pubic tubercle to the ninth costal cartilage. In the region superior to the costal margin, the anterior rectus sheath is comprised only of the aponeurosis of the external oblique. Below the arcuate line all three aponeuroses pass anterior to the rectus muscle; the posterior rectus sheath is absent. The arcuate line is formed by the transition from the internal oblique aponeurosis laminating to encase the rectus abdominus superiorly to passing with the aponeurosis of the transversus abdominus anteriorly to the rectus muscle. The aponeurotic fibers interdigitate in the midline to form the linea alba. Deep to the rectus abdominus and transversus abdominis is the transversalis fascia, extraperitoneal fat and the parietal peritoneum.
Designing a trainer with high haptic fidelity likely requires a selection of synthetic materials that closely replicate the mechanical properties of the tissues (i.e., the anterior abdominal wall) being modelled [
6,
7]. Specifically, mechanical properties to be considered are Shore hardness and tensile properties [
8]. Few studies, however, report on the mechanical properties of the layers of the abdomen or the abdomen as a composite, specifically in the context of laparoscopic trocar placement.
In this work, we characterize the tensile properties of a partial composite and the tissues that comprise the human abdominal wall. This work presents the tensile properties of the anterior abdominal wall, specifically, the elastic modulus, ultimate tensile strength, and strain at failure. This work contributes to our broad research goal of using human data to inform the design of a surgical skill trainer focusing on entry into the abdomen during laparoscopic procedures.
2. Materials and Methods
The human tissues collected were anterior rectus sheath, posterior rectus sheath, linea alba, rectus abdominis muscle, external oblique muscle, internal oblique muscle, transversus abdominis muscle, and parietal peritoneum. These tissues were extracted from a total of 15 cadavers. Five of the cadavers were fresh-never-frozen (FNF) and tissue had been harvested within 72-96 hours post-mortem. The ten frozen (FF) cadavers had undergone at least 1 freeze-thaw cycle prior to tissue dissection and extraction. The mean age of donors was 81 and 82 years for FF and FNF specimens, respectively. The mean number of days from death to dissection of FNF donors was 4.25, while the mean number of days between removal from freezing was 45.3 days after an average of 2.2 freeze-thaw cycles for FF specimens. The available donor characteristics are reported in
Table 1.
The tissues from FNF cadavers were collected upon arrival at the Gross Anatomy Facility (GAF) at the University of Queensland (UQ), which was typically between 24–96 hours postmortem. Tissues from FF cadavers were collected after the specimens thawed at room temperature for approximately 24–48 hours. Ethical approval was obtained from the University of Queensland (2021/HE002373) and performed in accordance with the following legislation: Transplantation and Anatomy, 1979 (Qld) [
9], Transplantation and Anatomy Regulations, 2017 (Qld) [
10], Criminal Code, 1899 (Qld) [
11], and Work Health and Safety, 2011 (Qld) [
12].
2.1. Extraction of Abdominal Wall Tissues
Approaches for tissue dissection were developed with reference to Grant’s Dissector [
13] and Gray’s Anatomy [
14]. Tissues were extracted unilaterally from a site devoid of previous surgery. A skin incision was made along the midclavicular line extending from the inferior costal margin to approximately 10 cm inferior to the umbilicus. Camper’s and Scarpa’s fasciae were identified and divided sharply to expose the superficial surface of external oblique muscle. The plane superficial to the external oblique was entered bluntly and extended medially to the semilunar line, and laterally to raise a 10 cm flap of skin and subcutaneous fascia. The external oblique was divided sharply 1 cm lateral to the semilunar line and separated from the underlying internal oblique by blunt dissection. Blunt dissection was continued laterally to isolate approximately 10 cm of the external oblique muscle. The external oblique was divided superiorly and inferiorly such that it could be reflected laterally to allow access to the internal oblique. The above dissections were repeated for the internal oblique and transversus abdominus muscles. Following isolation of the anterolateral muscles, a 5x5 cm tissue sample was extracted from each. Finally, a 5x5 cm section of peritoneum (with transversalis fascia) was extracted from the lateral abdominal wall deep to transversus abdominus. In vivo orientation muscle samples were labeled and prepared for subsequent analysis.
Next, the anterior rectus sheath was divided medial to the semilunar line and above the umbilicus. Fibrous attachments to the tendinous intersections were divided sharply, and the anterior rectus sheath was reflected medially towards the linear alba. A section of rectus abdominus (between tendinous intersections) was lifted off the posterior rectus sheath. The anterior rectus sheath, rectus abdominus, posterior rectus sheath, musculofascial composites and linear alba were sampled.
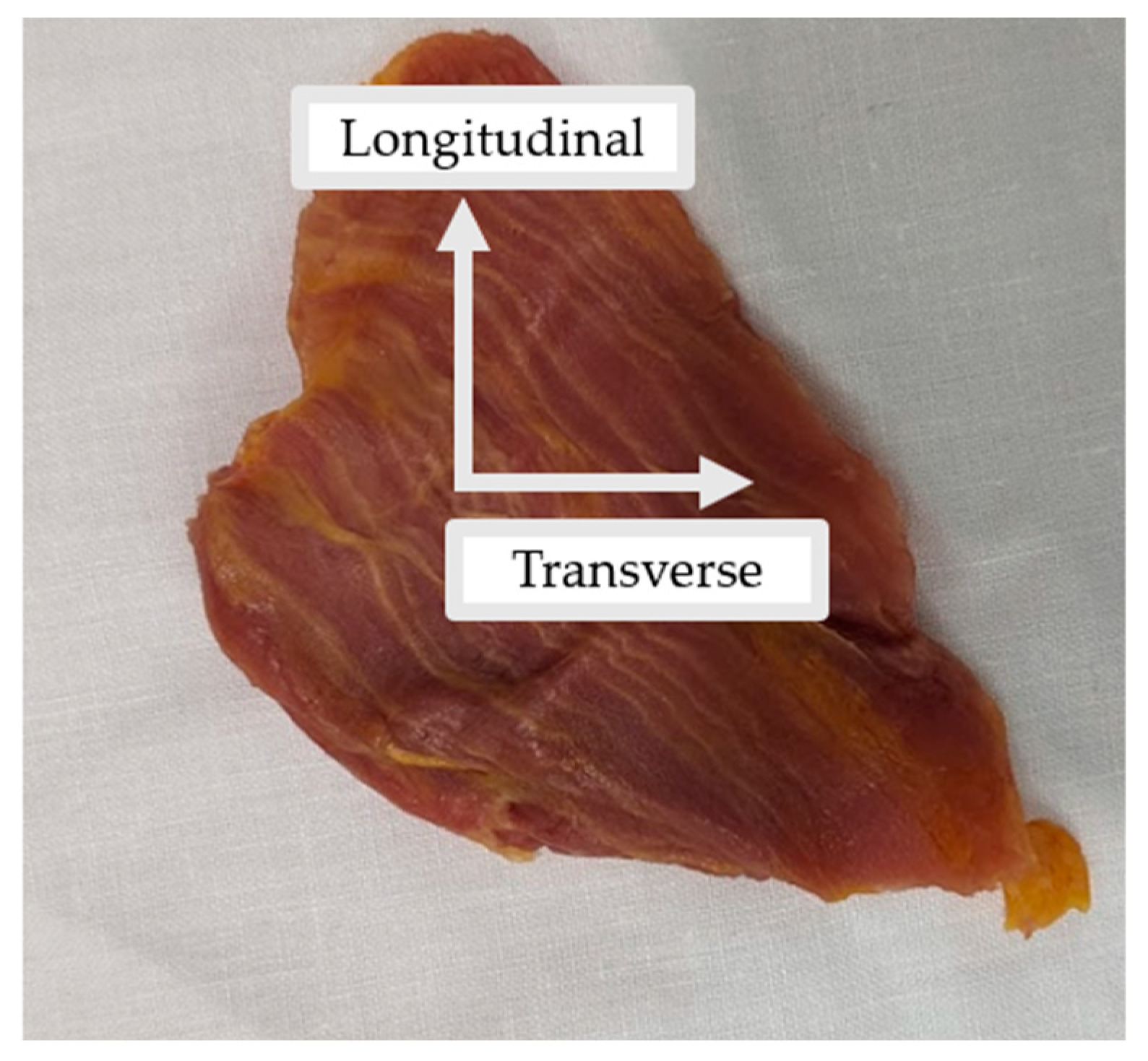
All tissues were kept in their in vivo orientation and cut into rectangular samples in the transverse and longitudinal directions (
Figure 3). Where possible, multiple samples of the same tissues were collected. In some instances (e.g., peritoneum or posterior rectus sheath), there were adhesions, which made it difficult to extract individual tissue layers.
Table 2 summarizes the total number of samples taken from each tissue type.
Figure 1.
Example of the external oblique muscle extracted in its in vivo orientation. The longitudinal and transverse axes demonstrate the orientation in which samples were cut for mechanical testing.
Figure 1.
Example of the external oblique muscle extracted in its in vivo orientation. The longitudinal and transverse axes demonstrate the orientation in which samples were cut for mechanical testing.
Table 1.
Summary of the tissues collected from each specimen (1-15). The samples highlighted in blue indicate FNF specimens.
Table 1.
Summary of the tissues collected from each specimen (1-15). The samples highlighted in blue indicate FNF specimens.
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
TOTAL |
| Anterior Rectus Sheath |
2 |
2 |
2 |
2 |
2 |
2 |
4 |
2 |
4 |
2 |
2 |
4 |
4 |
4 |
4 |
42 |
| Posterior Rectus Sheath |
— |
2 |
— |
— |
2 |
2 |
— |
— |
1 |
2 |
2 |
3 |
2 |
2 |
2 |
20 |
| Linea Alba |
— |
2 |
2 |
2 |
— |
2 |
2 |
2 |
2 |
2 |
2 |
— |
— |
— |
4 |
22 |
| Peritoneum |
— |
2 |
2 |
2 |
2 |
1 |
3 |
2 |
1 |
2 |
1 |
1 |
3 |
— |
4 |
26 |
| Rectus Abdominis |
4 |
2 |
2 |
2 |
2 |
2 |
2 |
— |
2 |
1 |
1 |
1 |
4 |
3 |
4 |
32 |
| External Oblique |
3 |
2 |
2 |
2 |
2 |
2 |
— |
2 |
4 |
2 |
2 |
3 |
4 |
— |
4 |
34 |
| Internal Oblique |
— |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
— |
4 |
— |
4 |
28 |
| Transversus Abdominis |
— |
2 |
1 |
— |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
3 |
4 |
— |
4 |
28 |
| Composite |
— |
2 |
— |
— |
2 |
— |
— |
— |
— |
— |
— |
— |
3 |
— |
— |
7 |
| TOTAL |
9 |
18 |
13 |
12 |
16 |
15 |
15 |
12 |
18 |
15 |
14 |
15 |
28 |
9 |
30 |
239 |
Tissue samples were adhered to the smooth side of 320 Grit Paper (3M, Maplewood, Minnesota, USA) using cyanoacrylate (Loctite ®, Henkel, Düsseldorf, Germany) to prevent slippage within the grips of the testing machine (
Figure 4).
After samples were adhered to Grit Paper, a vernier calipers was used to measure sample gauge length, width, and thickness (± 0.02 mm). Tissue measurements are summarized in
Table 3. All mechanical tests were performed at room temperature (18–21 °C) in the GAF, and tissues were kept hydrated with a specimen wetting solution prepared by the UQ GAF staff.
Table 2.
Median (interquartile range [IQR]) of length, width, and thickness are summarized in the table below.
Table 2.
Median (interquartile range [IQR]) of length, width, and thickness are summarized in the table below.
| Tissue |
Sample Size |
Length
(mm) |
Width
(mm) |
Thickness
(mm) |
| Anterior Rectus Sheath |
42 |
14.25 (12.43) |
7.22 (3.73) |
0.59 (0.38) |
| Posterior Rectus Sheath |
20 |
12.17 (7.98) |
5.95 (2.38) |
0.32 (0.39) |
| Linea Alba |
22 |
7.87 (4.57) |
5.90 (2.52) |
0.88 (0.76) |
| Peritoneum |
26 |
12.29 (7.31) |
5.82 (2.35) |
0.39 (0.29) |
| Rectus Abdominis |
25 |
13.14 (4.66) |
6.66 (2.48) |
1.82 (0.74) |
| External Oblique |
33 |
14.02 (7.31) |
7.78 (3.96) |
2.26 (1.28) |
| Internal Oblique |
28 |
12.78 (6.74) |
6.64 (2.22) |
2.07 (0.92) |
| Transversus Abdominis |
26 |
12.47 (6.57) |
6.52 (3.47) |
0.93 (0.53) |
| Composite |
7 |
8.90 (2.50) |
7.36 (1.36) |
2.40 (0.48) |
2.2. Tensile Testing
Tensile testing was conducted using a ST-1001 Universal Testing Machine (Salt, Incheon, Republic of Korea). The Universal Testing Machine (UTM) has a maximum load cell capacity of 5 kilonewtons (kN) (± 0.0333 newton [N] resolution), and data were recorded with a sample rate of 194 Hz. Samples were positioned in screw grips (Side-Action Grips 5kN, Salt Incheon, Republic of Korea) and tightened to “finger-tightness.”
Since the goal of this research is to select synthetic materials that match tissue properties, tissues were not pre-conditioned [
8]. Strain rate was selected based on similar work [
15], and was conducted at a quasi-static strain rate of 5 mm/min. Data collection began once tissues were pre-stressed to 0.2 N and were tested to failure. The point of failure was visually inspected and noted as being either upper third, middle third, bottom third, or within the grips (
Figure 5). Tissue failure was defined as not occurring in the grips and as either of the following conditions: 1) a 90% drop in the applied load or 2) when the applied load fell to zero.
Figure 2.
Example of muscle tissue failure within the UTM. The figure also shows the visual approximations of tissue failure. In
Figure 5, the sample was noted to have failed in the middle third of the sample.
Figure 2.
Example of muscle tissue failure within the UTM. The figure also shows the visual approximations of tissue failure. In
Figure 5, the sample was noted to have failed in the middle third of the sample.
After testing was completed, load (N) and displacement (mm) outputs from the Light-Salt testing software (Salt, Incheon, Republic of Korea) were collected to generate stress-strain curves.
2.3. Tensile Data from Stress-Strain Curves
Using load and displacement outputs from the Light-Salt testing software, stress and strain were calculated. An assumption of incompressibility was made, meaning that the materials were not considered to be porous, and volume was conserved [
16]. Therefore, engineering stress (
σ) was calculated by dividing force (
F) over the original cross-sectional area (
A0) (Equation 1).
The original cross-sectional area (
A0) was assumed to be rectangular and calculated by multiplying sample width (
w) by thickness (
t) (Equation 2).
Engineering strain (
ε) was calculated by dividing the change in specimen length (
Δl) by the gauge length (
l0) (Equation 3).
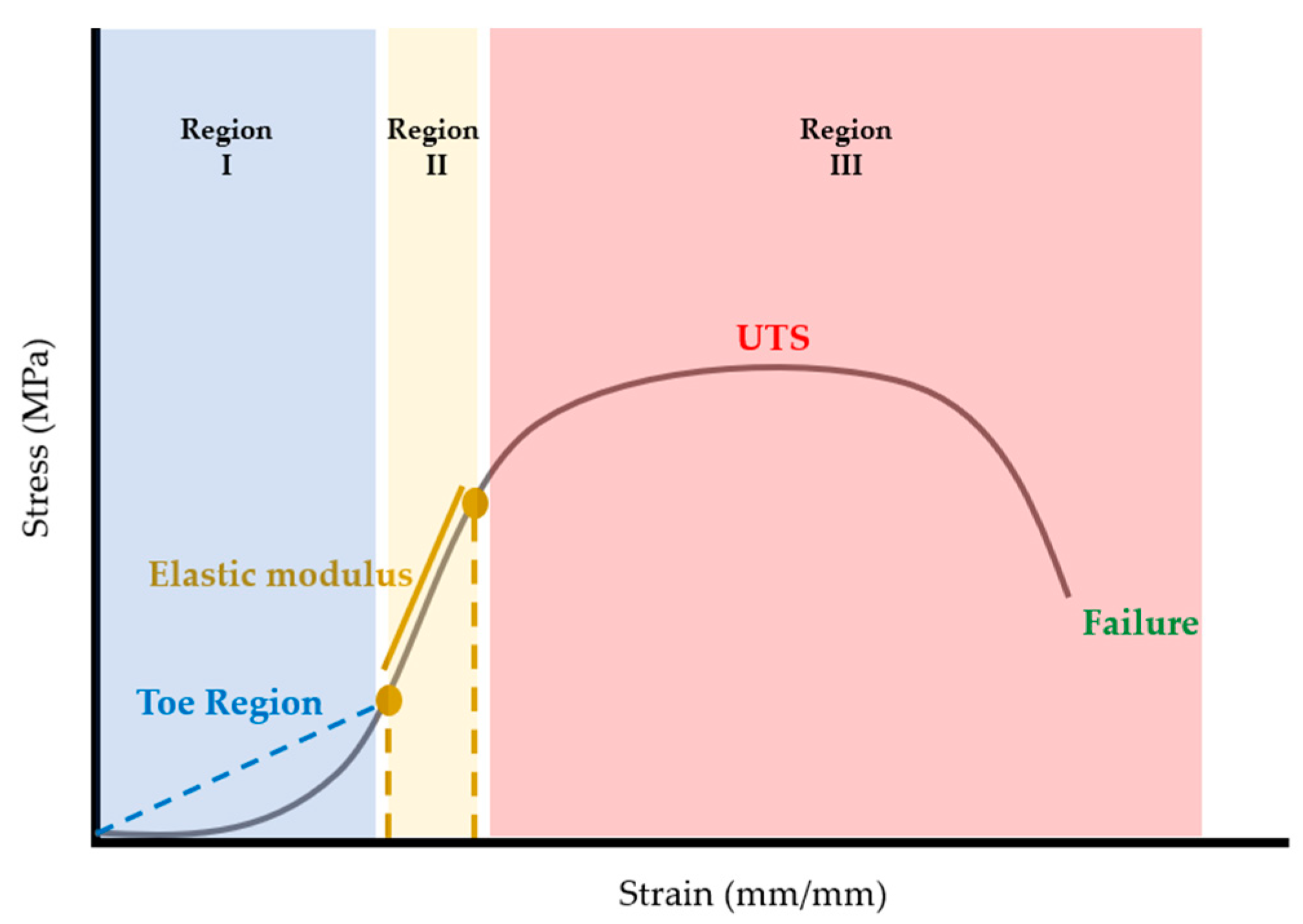
Once calculated, stress-strain curves for each sample were plotted using MATLAB (R2022b, The Mathworks, Natick Massachusetts, USA). Once plotted, elastic modulus, ultimate tensile strength (UTS), and strain at failure were extracted from the stress-strain curves. Considering that stress-strain curves of biological tissues exhibit nonlinear or hyperelastic curves [
16], the elastic modulus was calculated as the first linear portion of the stress-strain curve (
Figure 6). In biological materials, the toe region (Region I) is the initial, nonlinear portion of the stress-strain curve where there is a small amount of stiffness due to crimped collagen fibers [
17]. Following the toe region, is the linear region (Region II) of the curve [
16]. In this study, the elastic modulus was calculated from Region II by selecting two points and calculating the slope between the two points (
Figure 6). The ultimate tensile strength (UTS) was calculated as the maximum stress in the portion of the curve in Region III (
Figure 6). Strain at failure was selected from the strain value at failure of the material (
Figure 6).
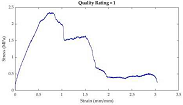
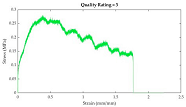
After plotting stress-strain curves, graphical quality of the curves was assessed. The rating system (developed by the authors) is described in
Table 4. Curves that were too noisy (rating of 4) could not reliably provide tensile properties and were excluded from the dataset. A total of 10 stress-strain curves were excluded because of this. All excluded data were muscle samples: rectus abdominis (7), external oblique (2), and transversus abdominis (1).
Table 3.
Stress-Strain curve rating system, descriptions, and curve examples.
As mentioned in
Section 2.3, location of failure was noted for tissue specimens. The elastic modulus for specimens that failed in the grips was calculated. However, because the specimens did not meet failure criteria, UTS and strain at failure could not be calculated.
2.4. Data Analysis
Tensile properties from stress-strain curves were collated within a master spreadsheet using Excel® (Version 2210, Microsoft ®, Redmond, Washington, USA). Shapiro-Wilk tests for normality were conducted, and Mann-Whitney U tests were used to compare FF and FNF tensile properties for each tissue type. Statistical testing was performed in SPSS® (29.0.0.0, IBM®, Armonk, New York, USA). Scatter and bar charts were created in MATLAB (R2022b, The Mathworks, Natick Massachusetts, USA).
3. Results
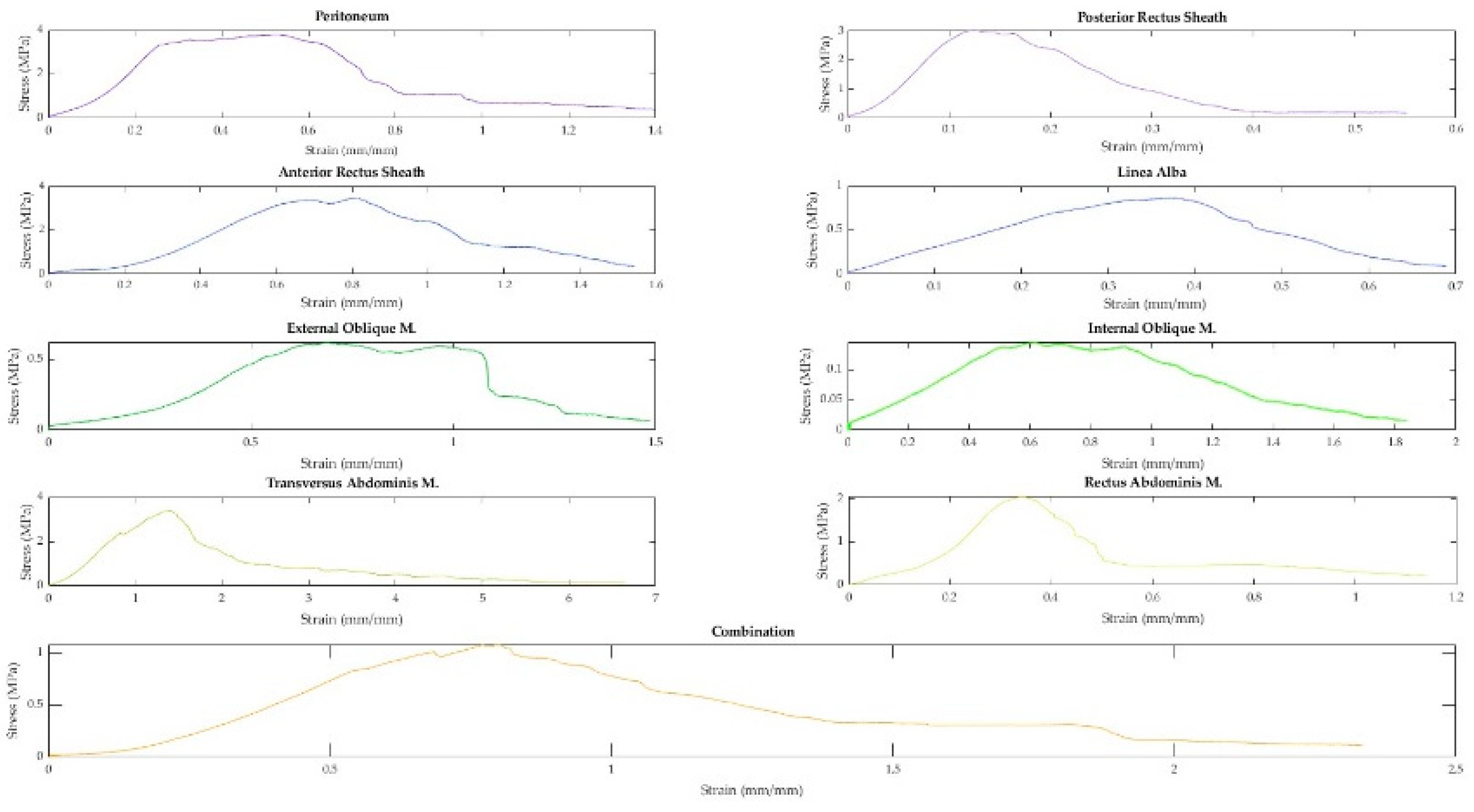
A total of 91 fresh-never-frozen (FNF) and 138 fresh-frozen (FF) tissues were extracted from the abdominal walls of 15 different cadavers. Representative curves from each tissue type and a combination sample are displayed in Figure 7. As demonstrated in Figure 7, when tested in uniaxial tension, the tissues of the abdominal wall exhibit nonlinear elastic stress-strain curves. Toe regions were observed in 158 samples. The median strain value where the toe region ends was 14.05%. The median strain for the end of the elastic region was 37.52%.
Figure 3.
Representative stress-strain curves of abdominal wall tissues.
Figure 3.
Representative stress-strain curves of abdominal wall tissues.
3.1. Inter- and Intra-Cadaveric Differences in Tensile Properties
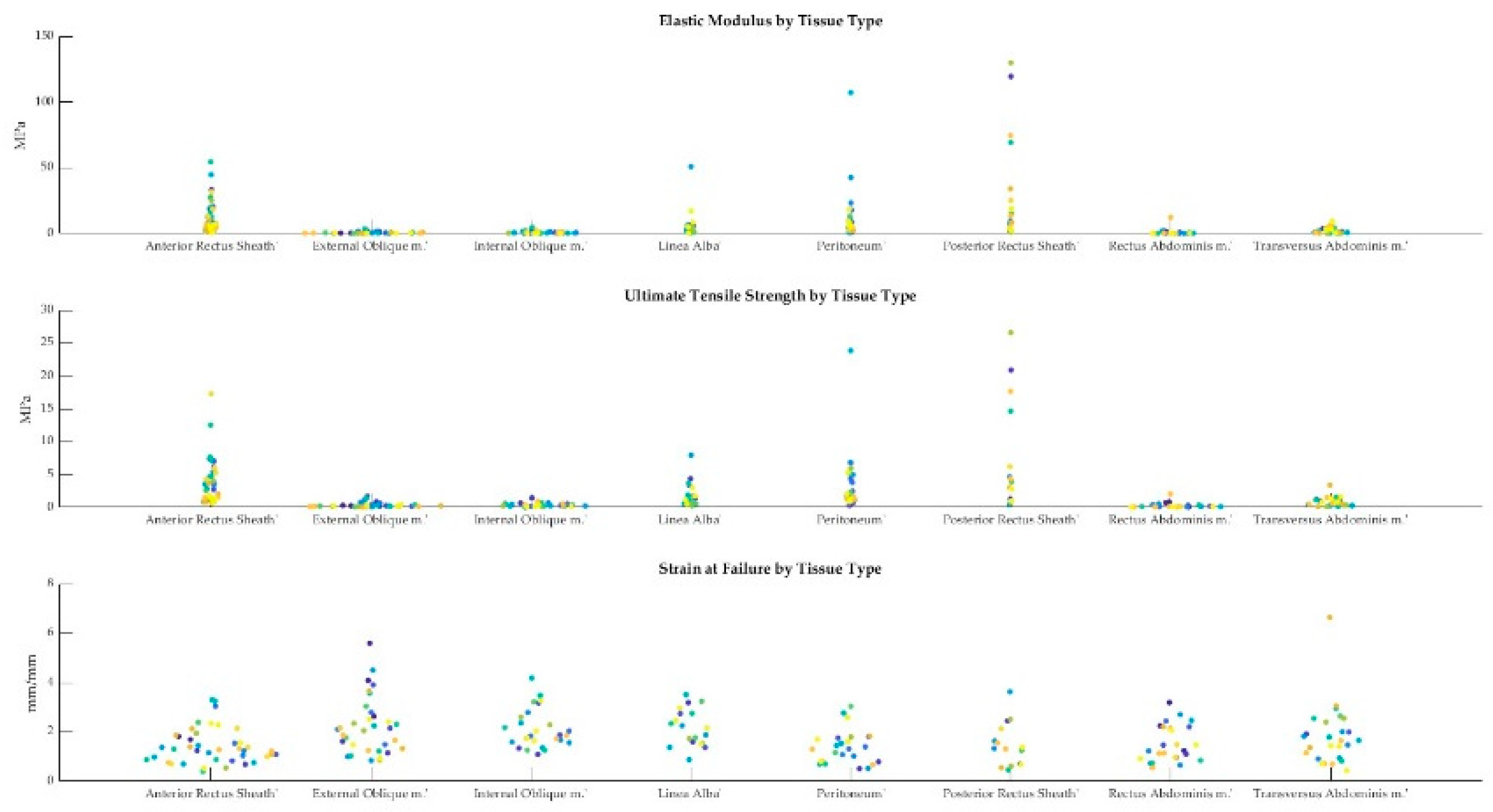
As described in section 2.3, the elastic modulus, ultimate tensile strength, and strain at failure were obtained from the stress-strain curves for each sample. A swarmchart (Figure 8) shows the spread of the mechanical properties between and among cadavers.
Figure 4.
Swarmcharts for tensile properties (elastic modulus, ultimate tensile strength, and strain at failure) are shown for the various tissue types of the anterolateral abdominal wall. Each cadaveric specimen is represented by the same color. Points of the same color indicate multiple tissue samples from the same cadaver. The points of the swarmchart are jittered on the x-axis for ease of visualization [
19].
Figure 4.
Swarmcharts for tensile properties (elastic modulus, ultimate tensile strength, and strain at failure) are shown for the various tissue types of the anterolateral abdominal wall. Each cadaveric specimen is represented by the same color. Points of the same color indicate multiple tissue samples from the same cadaver. The points of the swarmchart are jittered on the x-axis for ease of visualization [
19].
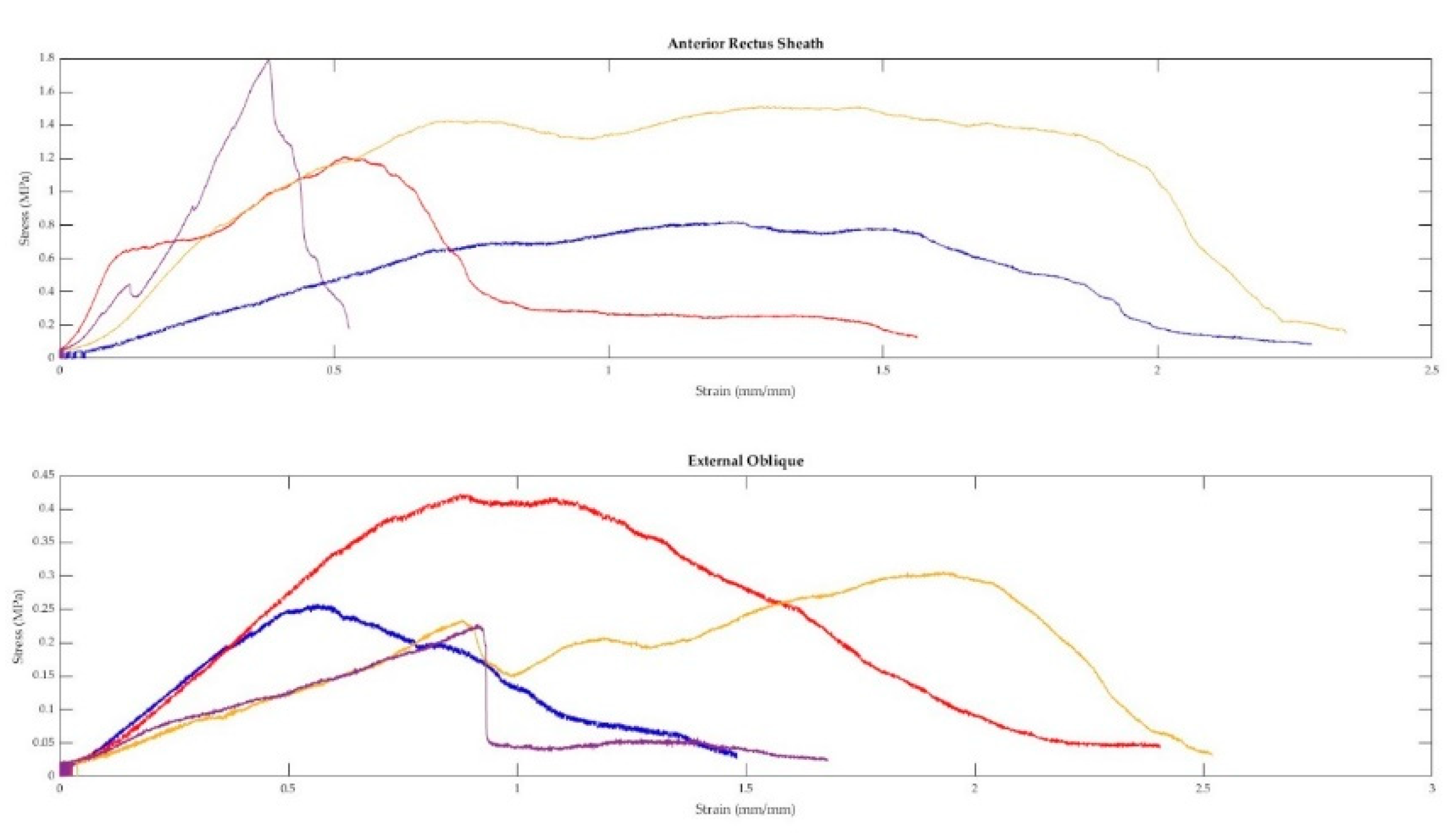
As seen in Figure 8, there is a larger spread of elastic moduli and ultimate tensile strength values for the fascia (anterior/ posterior rectus sheaths and linea alba) and peritoneum, whereas the tensile properties of the various muscles seem to be less variable. The intra-cadaveric tissue variability of fascia (anterior rectus sheath) versus muscle (external oblique) is again illustrated in Figure 9. Figure 9 demonstrates the broader range of values for tensile properties from anterior rectus sheath samples (Elastic modulus: 0.95–6.88 Megapascals [MPa]; UTS: 0.82–1.79 MPa; Strain at Failure: 52.79%–234.45%) compared to samples from the external oblique muscle (Elastic modulus: 0.21–0.59 MPa; UTS: 0.23–0.42 MPa; Strain at Failure: 93.28%–251.95%).
Figure 5.
Four anterior rectus sheath and four external oblique muscle samples were taken from the same cadaver and tested in tension. The above figure displays the stress-strain curves from each sample.
Figure 5.
Four anterior rectus sheath and four external oblique muscle samples were taken from the same cadaver and tested in tension. The above figure displays the stress-strain curves from each sample.
3.2. Fresh-Never-Frozen (FNF) and Fresh-Frozen (FF) Tensile Properties
Tensile property data from different cadaveric preservations (i.e., FNF and FF) were collated by tissue type (Table 5). As seen in Table 5, the median values for the elastic moduli of fresh frozen tissues were generally stiffer than those of FNF cadavers. The three exceptions were posterior rectus sheath, peritoneum, and transversus muscle. The UTS was generally higher for FF tissue except for the posterior rectus sheath and transversus muscle. Values for strain at failure were higher in FNF cadavers for five of the tissue types (anterior rectus sheath, posterior rectus sheath, peritoneum, internal oblique muscle, and composite).
Tissue tensile properties by cadaveric preparation were Mann-Whitney U test. The median elastic modulus was significantly higher in the external oblique of FF (0.57 vs. 0.24 MPa, p = 0.009), and the median ultimate tensile strength was significantly higher in the external oblique of FF (0.28 vs. 0.16 MPa, p = 0.015). A significant difference in medians was also detected for UTS of the rectus abdominis (FF significantly greater than FNF [0.14 vs. 0.06 MPa, p = 0.014]). However, it should be noted that in the case of the rectus abdominis comparisons, there was a small sample size for FNF tissues.
Table 4.
Median (Interquartile range [IQR]) are displayed below for separate tissues and as a composite. Values are given for fresh-never-frozen (FNF) and fresh-frozen (FF) cadavers. Outputs from the Mann-Whitney U test are included in the footer of this table.
Table 4.
Median (Interquartile range [IQR]) are displayed below for separate tissues and as a composite. Values are given for fresh-never-frozen (FNF) and fresh-frozen (FF) cadavers. Outputs from the Mann-Whitney U test are included in the footer of this table.
| Cadaveric Preparation |
Tissue |
Elastic Modulus
(MPa) |
Ultimate Tensile Strength
(MPa) |
Strain at Failure (%) |
| FNF |
Anterior Rectus Sheath |
6.02 (10.14) |
1.54 (3.02) |
132.92 (139.00) |
| Posterior Rectus Sheath |
14.32 (57.62) |
4.14 (13.34) |
134.92 (116.00) |
| Linea Alba |
2.67 (6.87) |
0.87 (1.28) |
195.96 (126.00) |
| Peritoneum |
6.79 (6.09) |
1.80 (3.99) |
145.54 (118.00) |
| Rectus Abdominis |
0.19* |
0.06*§
|
92.21* |
| External Oblique |
0.24 (0.37) †
|
0.16 (0.16) ‡
|
196.07 (86.00) |
| Internal Oblique |
0.42 (0.68) |
0.20 (0.22) |
185.67 (87.00) |
| Transversus Abdominis |
2.75 (5.24) |
0.79 (0.99) |
141.61 (169.00) |
| Composite |
1.64* |
0.89* |
233.43* |
| FF |
Anterior Rectus Sheath |
8.29 (15.76) |
3.45 (4.51) |
124.54 (84.00) |
| Posterior Rectus Sheath |
7.31 (67.69) |
3.02 (14.04) |
133.33 (190.00) |
| Linea Alba |
3.92 (3.80) |
1.40 (2.88) |
225.44 (138.00) |
| Peritoneum |
4.42 (14.15) |
2.24 (3.66) |
135.71 (108.00) |
| Rectus Abdominis |
0.30 (0.88) |
0.14 (0.32) |
135.60 (152.00) |
| External Oblique |
0.57 (1.27) |
0.28 (0.48) |
215.06 (243.00) |
| Internal Oblique |
0.58 (1.11) |
0.40 (0.41) |
185.46 (127.00) |
| Transversus Abdominis |
0.81 (2.44) |
0.49 (0.94) |
182.43 (118.00) |
| Composite |
1.12 (2.79) |
0.53 (1.22) |
195.55 (68.00) |
3.3. Composite Tissue vs. Separated Tissues
The composite contained the tissue layers in the following order: anterior rectus sheath, rectus abdominis muscle, posterior rectus sheath, parietal peritoneum. As previously detailed in
Table 2 (
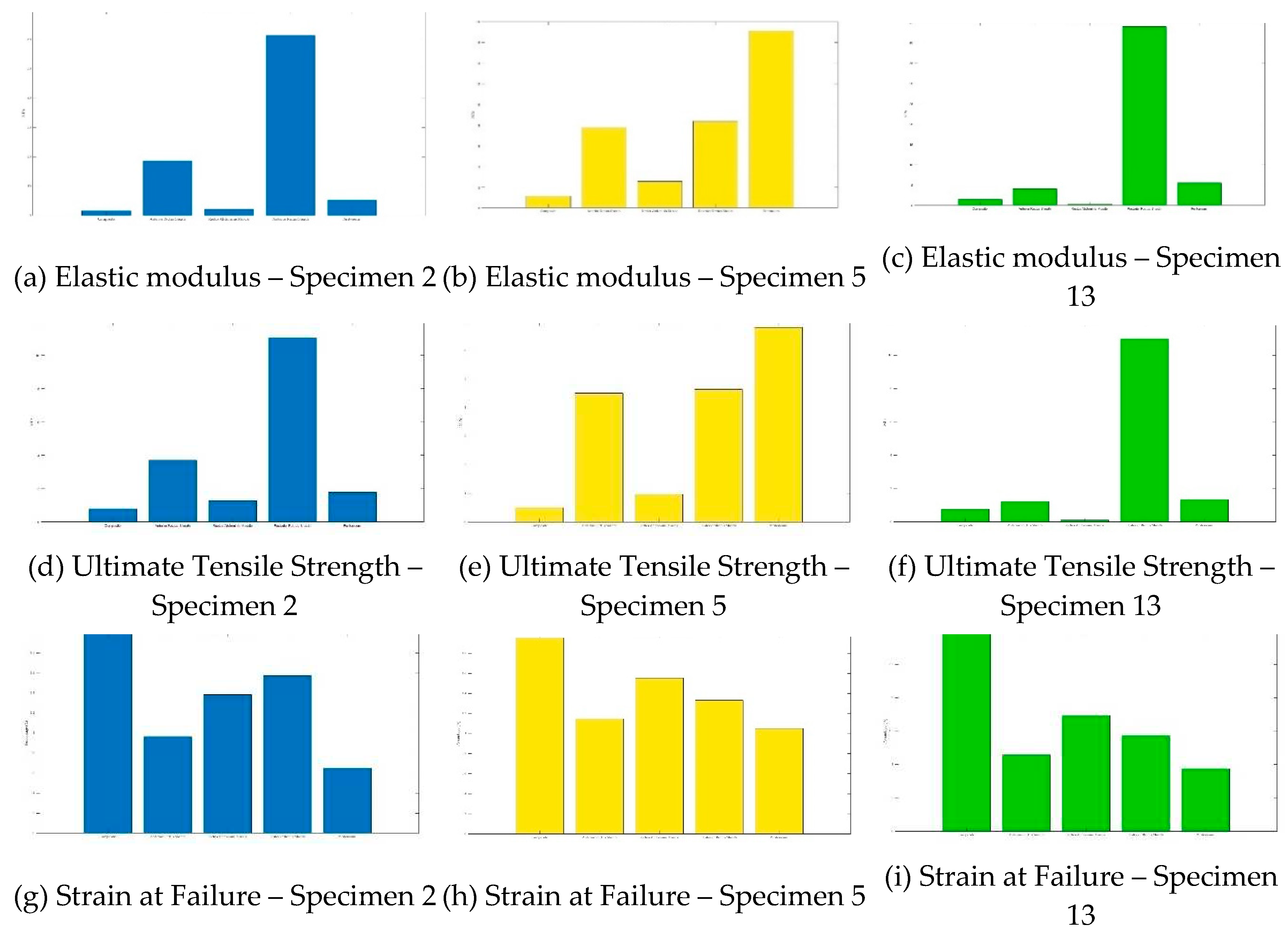
Section 2.1), a total of 7 composite samples were extracted from 3 different cadavers. The tensile properties of the composites of each cadaver were compared to the tensile properties of the tissues that comprise the composite (Figure 10). Interestingingly, when comparing the composite tissue to that of its individual parts, the tensile properties do not seem to have an easily discernable pattern.
Figure 6.
The bar graphs show comparisons of composite samples and their individual tissues (anterior rectus sheath, rectus abdominis, posterior recuts sheath, parietal peritoneum) for elastic modulus (a–c), ultimate tensile strength (UTS) (d–f), and strain at failure (g–i). Samples were taken from three different cadavers: Specimen 2 (blue), Specimen 5 (green), and Specimen 13 (yellow). The x-axes for all bar charts are in the following order: composite, anterior rectus sheath, rectus abdominis muscle, posterior rectus sheath, and peritoneum.
Figure 6.
The bar graphs show comparisons of composite samples and their individual tissues (anterior rectus sheath, rectus abdominis, posterior recuts sheath, parietal peritoneum) for elastic modulus (a–c), ultimate tensile strength (UTS) (d–f), and strain at failure (g–i). Samples were taken from three different cadavers: Specimen 2 (blue), Specimen 5 (green), and Specimen 13 (yellow). The x-axes for all bar charts are in the following order: composite, anterior rectus sheath, rectus abdominis muscle, posterior rectus sheath, and peritoneum.
4. Discussion
In this study, the mechanical characteristics of anterior abdominal wall tissues were investigated. Uniaxial tensile tests were conducted for eight different tissue types and a partial composite, and tensile properties were extracted from the plotted stress-strain curves. While there was variability in the shapes of the stress-strain curves, generalizations can be made. All of the curves could be classified as nonlinear elastic or hyperelastic. Most curves had an initial toe region, in which the tissue sample could withstand an appreciable amount of strain without a large change in stress. Following the toe region, a linear region was observed. Generally, this region was found within a strain range of 14%–42%. The toe and elastic region findings are consistent with what has been reported in the literature for similar tissues [
20].
Following the linear region, two generalizations about the stress-strain curves in the failure region could be made: 1) the linear region led to a singular peak in the curve, or 2) the linear region led to a series of peaks (usually two) with the second peak being higher. Similar findings have also been reported in the literature [
21]. After the maximum stress (UTS) in the stress-strain curves, the curves generally had a dramatic drop in stress followed by a gradually decreasing slope until the definition of failure was met. As previously reported in similar tissues, throughout the curve, there are multi-picks, which are likely due to strips of tissue rupturing until the specimen meets the definition of failure [
20,
21].
Like the stress-strain curves, variability of the mechanical properties of human tissues has been reported within and between cadaveric donor specimens [
20,
21]. The variability is likely due to several factors such as the non-homogenous microstructure of tissues, tissue hydration, and donor-specific factors (e.g., age, pathology, sex, etc.) [
18,
21,
22,
23,
24] Unfortunately, we cannot explore the specific contributions of the aforementioned factors without corresponding video analysis from the mechanical testing, chemical analysis, and/or histological testing.
4.1. Mechanical Properties of the Anterior Abdominal Wall
To the authors’ knowledge, this is the first article that reports on the mechanical characteristics of different tissue types and composites from cadaveric abdominal walls, utilizing uniaxial tensile testing. In this study, a total of 229 abdominal wall tissue samples from 15 different cadavers were tested in uniaxial tension at a quasi-static rate until failure. When assessing our data, there is a mixed agreement between our values and values from the literature.
In this study, we assessed the mechanical properties of the four anterior abdominal muscles: external oblique, internal oblique, transversus abdominus, and rectus abdominus. Th median elastic moduli of the individual muscles closely align with values published by Cardoso [
15] (values given as our median vs. mean from Cardosa): rectus abdominis (0.26 MPa vs. 0.52 MPa), external oblique (0.41 MPa vs. 1.00 MPa), internal oblique (0.53 MPa vs. 0.65 MPa), and transversus abdominis (0.95 MPa vs. 1.03 MPa). The UTS values for the individual muscles were also comparable to work done by Cardosa [
15] (values give as our median vs. mean from Cardosa): rectus abdominis (0.13 MPa vs. 0.23 MPa), external oblique (0.25 MPa vs. 0.57 MPa), internal oblique (0.32 MPa vs. 0.39 MPa), transversus abdominis (0.73 MPa vs. 0.73 MPa). Data for strain at failure was not available in the literature, however, we can ascertain that this study would have likely had similar results to Cardosa [
15] had they been reported. This is made on the assumption that our values of stretch at UTS were similar to those reported by Cardosa [
15] (our mean stretch vs. Cardosa’s mean stretch): Rectus abdominis (1.52 vs 1.60), external oblique (1.89 vs. 1.98), internal oblique (1.87 vs. 1.94), transversus abdominis (1.79 vs. 2.19).
The tensile properties for the anterior rectus sheath from this study were also similar to the available literature values for elastic modulus and UTS. The elastic modulus from this study (6.98 MPa) fell between the range in the literature: (5.6 MPa [
20]–9.06 MPa [
15]), as did our UTS value (2.70 MPa) vs. (2.2 MPa [
20]–2.86 MPa [
15]. However, our strain at failure (128%) was dissimilar to the available literature values (26.09%–6.62%) [
25]. It is unclear if this is due to a definition in failure or differences in methodology, as neither are well defined in the study from which the comparable data was extracted [
25].
The elastic modulus of the linea alba from this study (3.92 MPa) fell within the literature values, however this was noted to be a wide range (8 MPa–72 MPa [
26]). The wide range in values from the literature is a result of the directionality (i.e., anisotropy) of testing (longitudinal vs. transverse). When the data from this study filtered to match the testing properties of the comparable study [
26] (i.e., data from fresh-frozen cadavers and moduli from transverse and longitudinal directions instead of collated), our average elastic modulus values followed a similar pattern of a larger elastic modulus in the transverse direction (9.54 MPa) compared to the longitudinal direction (3.79 MPa). However, the values from this study were still lower than those reported in the literature [
26]. Values for UTS and strain at failure were not available in the literature.
Previous work on the posterior rectus sheath and peritoneum is limited. One study [
21] reported a range for the UTS of the transversalis fascia, which contributes to the posterior rectus sheath. The transversalis fascia obtained in this study was obtained from below the arcuate line and in the inguinal canal [
21]. In contrast, this study obtained posterior rectus sheath from above the arcuate line from behind the rectus abdominis muscle. The posterior rectus sheath obtained in this study would have been comprised of fibers from the aponeuroses of the external and internal oblique muscles. Despite the slight differences in composition and location, the UTS range from the literature (0.63 MPa–1.99 MPa [
21]) was similar to the value of the posterior rectus sheath UTS from this study (3.92 MPa).
Ranges for strain at failure are reported for the posterior rectus sheath in two studies. One from the same study reporting UTS (i.e., transversalis fascia) [
21] and the second from a study that had reported values for strain at failure of the anterior rectus sheath [
25]. The reported values are 71–104% and 30.77%–35.04%, respectively [
21,
25]. The literature ranges are lower than the value from this study (133%), however, this is likely due to both differences in definition and methodology.
While there are no available values for elastic modulus of the posterior rectus sheath, we can conclude that the values from this study would be similar to those obtained by Kirilova et al [
21] based upon similarities in the toe region modulus. Kirilova et al calculated a secant modulus in the toe region (strain of 5–10%) and found the toe modulus to be approximately 2.82 MPa–8.42 MPa [
21]. Utilizing the same methodology, the toe modulus from this study was found to be approximately 13.37 MPa.
In this study the composite studied was comprised of anterior rectus sheath, rectus abdominis muscle, posterior rectus sheath, and peritoneum, and it was difficult to readily identify a pattern in the mechanical properties of the composite vs. the individual tissues comprising the composite. Although human studies of composites were not identified, two animal studies assessing bilayer abdominal wall tissue mechanics were found [
27,
28]. In general, the literature findings were similar to ours: 1) separated layers had different mechanical properties to the composite, 2) large strains were observed, and 3) the composite was less compliant than its corresponding muscle layer. These findings are likely due to the difference in the arrangement of the extracellular connective tissue matrix and muscles, therefore, composites are likely to behave in an intermediate way than their separated tissues [
28]. The phenomenon of composites having intermediate properties was described as “myofascial force transmission” [
28] and is something to be considered in the future testing of composites.
4.2. Study Strengths and Limitations
This study presents novel findings, specifically, tissue stress-strain curves, mechanical properties for abdominal wall tissues, and mechanical testing of a partial abdominal wall composite. In this study, we aim for repeatability by presenting a thorough description of our methods. The current testing conditions were adapted from those previously published [
15] and generated comparable results; suggesting these protocols can be replicated.
This study also reports mechanical values for fresh-never-frozen (FNF), and fresh-frozen (FF) cadavers. Comparison of FNF and FF cadavers (especially soft tissues) remains to be investigated, however, it is generally assumed that the mechanical properties are similar. This work provides preliminary evidence of slight differences in tensile properties, however further analysis is required. Future analyses studying the effects of cadaveric preservation on soft tissue tensile properties are planned.
Some weaknesses of this study include cadaver characteristics, general methodology, and absent reporting on anisotropy. The use of cadavers to study human tissues is essential for destructive mechanical testing such as tensile testing. However, as is the case in this study, doners are generally of advanced age. The effects of aging and pathology on human tissues are likely to be greater and skew the data towards increased stiffness. Additionally, mechanical properties may differ between in vivo tissues and those tested ex vivo. Resultant discrepancy between tested properties, and those of in vivo tissue may impact the design of trainers and should be considered in future studies.
In this study, the methodology has been reported in detail, but some adjustments will be applied in future work. We did not take tissue measurements after pre-stressing the tissues. Tissue is known to be pre-stressed, and future protocols will consider a similar method used by Hernandez et al to account for initial strains [
27]. Furthermore, values for pre-stress can be extracted from studies using MRI data to calculate physiological stresses [
29]. Additional changes to the tensile testing protocol include the use of high-speed cameras for recording slippage at the grips and an extensometer for changes in tissue measurements. The inclusion of both will improve the repeatability of our experiments and reliability of our data. Despite the methodological limitations, the similarity in tensile property values to those in the literature is encouraging.
Finally, we did not characterize the anisotropy of the tissues of the abdominal wall. Human tissues are known to be anisotropic. However, it should be noted that this data has been collected, and analyses are planned. Anisotropy was out of the scope of our initial characterizations of the tissues of the abdominal wall.
5. Conclusions
This study presents initial characterizations of tissues from the anterior abdominal wall from 15 different fresh-never-frozen and fresh-frozen cadavers. In this work, representative stress-strain curves and tensile properties for eight different tissues and a partial composite are presented. Most of the work presented here is novel, however, in the few instances where similar values are presented in the literature, we demonstrate that the tensile properties of human tissues are reproducible. Future work will include analyses on the preservation effects of cadavers and anisotropy of the tissues of the anterior abdominal wall.
Regarding our overall goal of designing trainers with high-haptic fidelity, this study presents initial mechanical values that can be used to select synthetic materials. As observed, human data has a range of values for mechanical properties, therefore, our future studies will focus on the sensitivity of physicians to this range of data. Future studies will also try to assess whether tensile properties contribute to the haptics physicians feel during procedures. Although there is much work to be done in this field of research, the findings from this study reveal exciting opportunities to revolutionize how we approach tactile feedback in the design of procedural training devices.
Author Contributions
Conceptualization, K.K. and M.M..; methodology, K.K.; software, K.K.; validation, K.K.; formal analysis, K.K, H.F., K.S., M.W..; investigation, K.K., R.L., R.H., H.F., K.S., M.W. ; resources, K.K., M.M.; data curation, K.K., R.L., R.H., H.F., K.S., M.W..; writing—original draft preparation, K.K., R.L., R.H., H.F., K.S., M.W.; writing—review and editing, K.K., R.L., R.H., H.F., K.S., M.W, M.M.; visualization, K.K.; supervision, K.K., M.M..; project administration, K.K. and M.M..; funding acquisition, K.K. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Australian Research Training Program and the Wellcome Leap SAVE program.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of The University of Queensland (protocol code 2021/HE002373 and date of approval: 24-January-2022) for studies involving humans.
Informed Consent Statement
Informed consent was obtained from all donors as part of the Body Donor Program at the University of Queensland.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to acknowledge the staff at the University of Queensland’s Gross Anatomy Facility.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krishnakumar:, S.; Tambe, P. Entry complications in laparoscopic surgery. Journal of Gynecological Endoscopy and Surgery 2009, 1, 4–11. [Google Scholar] [CrossRef] [PubMed]
- Kostis, S.; Chung, K.C. Application of the "see one, do one, teach one" concept in surgical trianing. Plastic Reconstructive Surgery 2013, 131, 1194–11201. [Google Scholar]
- Davis, K.G.; Coviello, L. Tools. In Laparoscopic colectomy: A Step-by-Step Guide; Stein, L.R., Ed.; Springer Nature: Switzerland, AG, 2020; pp. 1–14. [Google Scholar]
- Last, R.J. Last’s anatomy: regional and applied; Ninth, ed, McMinn, R., Eds.; Elsevier Australia: Chatswood, New South Wales, AU, 2020; pp. 375–404. [Google Scholar]
- Goldberg, I.; Docimo, S. Normal radiographic anatomy of anterior abdominal 2all. In Fundamentals of Hernia Radiology; Docimo, S., Blatnik, J.A., Pauli, E.M., Eds.; Springer Nature: Switzerland AG.
- Coles, T.R.; Meglan, D.; John, N.W. The role of haptics in medical training simulators: A survey of the state of the art. IEEE Trans Haptics 2011, 4, 51–66. [Google Scholar] [CrossRef] [PubMed]
- Favier, V.; Subsol, G.; Duraes, M.; Captier, G.; Gallet, P. Haptic fidelity: The game changer in surgical simulators for the next decade? Frontiers in Oncology 2021. [Google Scholar] [CrossRef] [PubMed]
- Preis, A.; riedle, H.; Benke, E.; Franke, J. Matching of mechanical properties of biological tissues and technical materials for the fabrication of anatomical models by material jetting. In Proceedings of the 14th Joint Conference on biomedical engineering systems and technologies (SCITEPRESS - Science and Technology Publications 2021); p.p. 189-94.
- Transplantation and Anatomy Act 1979. Queensland Health. Available online: https://www.legislation.qld.gov.au/view/html/inforce/current/act-1979-074 (accessed on 12 September 2023).
- Transplantation and Anatomy Regulation 2017. Queensland Health. Available online: https://www.legislation.qld.gov.au/view/html/inforce/current/sl-2017-0148 (accessed on 12 September 2023).
- Criminal Code Act 1899. Queenlsand Government. Available online: https://www.legislation.qld.gov.au/view/html/inforce/current/act-1899-009 (accessed on 12 September 2023).
- Work Health and Safety Act 2011. Queensland Government. Available online: https://www.legislation.qld.gov.au/view/html/inforce/current/act-2011-018 (accessed on 12 September 2023).
- Tank, P.W. The Abdomen. In Grant’s Dissector; Lippincott Williams & Wilkins: Philadelphia, PA US; pp. 89–100.
- Gray, H. Muscles and fasciae of the abdomen. In Gray’s Anatomy; Barnes & Noble, Inc.: New York, NY, US, 2010; pp. 329–341. [Google Scholar]
- Cardoso, M.H.S. Experimental study of the human anterolateral abdominal 2all: Biomechanical Properties of Fascia and Muscles. Master’s Thesis, Faculty of Biomedical Engineering, University of Porto, Porto, Portugal, 2011. [Google Scholar]
- Roeder, R.K. Mechanical characterization of biomaterials. In Characterization of biomaterials; Bandyopadhyay, A., Bose, S., Eds.; Elsevier Inc.: Waltham, Massachussetts, US, 2011; pp. 49–104. [Google Scholar]
- Galbusera, F.; Innocent, B. Ligament and Tendon Biomechanics. In Human orthopedic biomechanics: fundamentals, devices, and applications; Academic Press: London, UK, 2022; pp. 137–149. [Google Scholar]
- Fung, Y. Chapter 7: Bioviscoelastic solids. In Biomechanics: Mechanical properties of living tissues; Springer: New York, New York, US, 1993; pp. 242–320. [Google Scholar]
- Swarmchart. The MathWorks, Inc.: Natick, MA US. Available online: https://au.mathworks.com/help/matlab/ref/swarmchart.html (accessed on 12 September 2023).
- Ben Abdelounis, H; Nicolle, S.; Ottenio, M.; Beillas, P.; Mitton, D. Effect of two loading rates on the elasticity of the human anteiror rectus sheath. Journal of the Mechanical Behavior of Biomedical Materials 2013, 20, 1–5. [Google Scholar] [CrossRef]
- Kirilova, M.; Stoytchev, S.; Pashkouleva, D.; Kavardzhikov, V. Experimental study of the mechanical properties of human abdominal fascia. Medical Engineering and Physics 2011, 33, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Horwood, A.; Chockalingam, N. Principles of tissue stress. In Clinical biomechanics in human locomotion: origins and principles; Elsevier: London, England, UK, 2023. [Google Scholar]
- Hollinsky, C.; Sandber, S. Measurement of the tensile strength of the ventral abdominal wall in comparison with scar tissue. Clinical Biomechanics 2007, 22, 88–92. [Google Scholar] [CrossRef] [PubMed]
- Sherman, V.R.; Yang, W.; Meyers, M.A. The materials science of collagen. Journal of the Mechanical Behavior of Biomedical Materials 2015, 52, 22–50. [Google Scholar] [CrossRef] [PubMed]
- Rath, A.M.; Zhang, J.; Chevrel, J.P. The sheath of the rectus abdominis muscle: an anatomical and biomechanical study. Hernia 1997, 1, 139–142. [Google Scholar] [CrossRef]
- Cooney, G.M.; Iake, S.P.; Thompson, D.M.; Castile, R.M.; Winter, D.C.; Simms, C.K. Uniaxial and biaxial tensile stress-stretch response of human linea alba. Journal of the Mechanical Behavior of Biomedical Materials 2016, 63, 134–140. [Google Scholar] [CrossRef] [PubMed]
- Hernandez, B.; Pena, E.; Pascual, G.; Rodriguez, M.; Calvo, B.; Doblare, M.; Bellon, J.M. Mechanical and histological characterization of the abdominal muscle. A previous step to modelling hernia surgery. Journal of the Mechanical Behavior of Biomedical Materials 2011, 4, 392–404. [Google Scholar] [CrossRef] [PubMed]
- Hwang, W.; Carvalho, J.C.; Tarlovsky, I.; Boriek, A.M. Passive mechanics of canine internal abdominal muscles. Journal of Applied Physiology 2005, 98, 1829–1835. [Google Scholar] [CrossRef] [PubMed]
- Forstemann, T.; Trzewik, J.; Holste, J.; Batke, B.; Konerding, M.A.; Wolloscheck, T.; Hartung, C. Forces and deformations of the abdominal wall - a mechanical and geometrical approach to the linea alba. Journal of Biomechanics 2011, 44, 600–606. [Google Scholar] [CrossRef] [PubMed]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).