Balanced Definition of Thresholds for Mode-Tracking in a Long-Term Seismic Monitoring System

In recent years, the use of long-term seismic monitoring systems for the protection of structures is becoming increasingly widespread. This is because more and more awareness is gradually developing regarding the importance of keeping structures under observation so as to prevent any damage scenarios. Within the field of Structural Health Monitoring, data driven techniques allow to process and analyze data collected on site. This paper presents a Mode Tracking procedure to obtain the time-histories of the natural frequencies of a monumental structure. The procedure is applied on the Sanctuary of Vicoforte, an important monumental structure site in Piedmont known for its imposing oval dome and characterized by a permanent structural monitoring system. Through the procedure presented in the paper it has been possible to obtain and observe the time series of the first natural frequencies of the structure considering various aspects, including the temperature variation.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Structural Health Monitoring (SHM) of civil structures has spread over last decades and nowadays it is the area that study and analyses the structural health state and its monitoring ^[1]. In this context, SHM techniques play an important role in making our structures safe. When studying the health state of structures, a key concept is represented by the state of damage. The structure is defined as "damaged" when it no longer performs in its ideal condition but can still work satisfactorily and safely, it could be defined as a non-optimal situation [2]. This definition implies that the analysis of the damage state of a structure is based on the comparison between two different states of the system, one of which represent the initial state and a second state in which the potential onset of damage is studied. The study of damage identification in structural and mechanical systems focuses precisely on this problem [3]. In order to be able to study the different states of the structure and therefore a possible evolution of damage, it has to define the characteristics of the structure that allow to understand what state it is in, such, for example, the natural frequencies and modes of the system. Data-driven approaches in SHM are usually used in the case of data coming from permanent or long-term monitoring systems installed on buildings since a lot of samples are available, [4]. These kinds of data can be influenced by variations caused by changes in the external environment or by noise, which must be isolated and removed in order to be able to study the actual health state without external effects. In addition, processing errors can lead to a misinterpretation of the path of natural frequencies when monitored over time. For example, for each new identification task it is necessary to attribute each identified mode to a previously identified time series, which then distinguishes a specific mode of vibration over time (mode-tracking problem). If the automatic process with which new frequency values are attributed to the historical series of a specific mode fails, the error made could be interpreted by the damage detection or identification algorithms as the onset of anomaly. It is therefore essential to study this problem carefully when installing permanent monitoring, particularly when the installed system is sparse (few sensors) as the mode coupling errors rise drastically due to the drastic loss of robustness of the parameter used to correlate the different modes of vibration (e.g., Modal Assurance Criterion, MAC).

For this reason, in this paper, a procedure to obtain tracking of natural frequencies of structures is presented. The data used come from the seismic permanent monitoring system installed on the Sanctuary of Vicoforte. The paper is divided as follows: in Section 2 the long-term dynamic monitoring systems are shown and a focus is made on the case study of the Sanctuary of Vicoforte; then in Section 3 the Mode tracking procedure has been explain in general terms, while in Section 4 the procedure applied in this specific case is presented together with the results. Finally, in Section 5 the conclusions are illustrated together with the problems encountered in the applied procedure and future developments.

2. Long-term seismic monitoring program

Since damage identification is determined by changes in the dynamic response of systems [3], a meaningful step of SHM process is the extraction of dynamic features of the structures, i.e., natural frequencies and modal shapes. Natural frequencies are obtained from the signals recorded by in situ sensors (e.g., accelerometers) of dynamic monitoring systems through system identification tasks [5]. In general, when dealing with structural monitoring, to get a comprehensive view of the health state of the structure, it is useful to combine static structural systems with dynamic ones. This is because dynamic monitoring aims to provide a dynamic or seismic response of the structure that characterizes the structure from a global point of view. There are different types of dynamic monitoring systems: one-time monitoring, periodic monitoring and continuous or permanent monitoring. In the first two cases, the instruments are used to perform dynamic tests by measuring characteristic vibrations of the structure induced by external forcing or natural phenomena. In the case of permanent monitoring, the structures are equipped with sensor systems capable of recording the vibrations of the structure whenever a microquake occurs or a significant source of vibration exceeds a certain threshold (trigger-based monitoring). They are also capable of continuously recording the vibration of the structure under ambient conditions. In this case it is referred to as Vibration Based SHM (VB-SHM) [5]. Continuous dynamic monitoring, through the remote and instantaneous reading of signals, such as displacements, velocities, and accelerations, can enable real-time or near real-time knowledge of useful information about the overall health state of the structure and the onset or development of serious damage states. Therefore, once the signals have been recorded, stored, and pre-processed, the modal parameters identification, both in operating conditions and in extreme conditions, is of fundamental interest [6]. The importance of operational modal analysis arises from the dependence of the dynamic behavior of the structure on its intrinsic characteristics, such as mass, stiffness, damping, etc., therefore, if no changes occur within the building (such as structural damage), the dynamic behavior of the structure remains constant (unless the presence of operational and environmental changes); on the contrary, in the presence of damage phenomena, changes occur in the dynamic parameters of the structure [6]. These data coming from permanent monitoring system are applied in data driven approaches for VB-SHM and then statistical models of the system can be defined, and noise levels and environmental variations are established naturally [4],[7]. Then, system identification aims to extract information regarding the behavior of the structure when responding to a dynamic load [5].

2.1. The case of the Sanctuary of Vicoforte

The Sanctuary of Vicoforte (CN) is one of the main monumental structures of the Baroque, whose importance is also due to its imposing dome. With a major axis of 37.23 m and a minor axis of 24.89 m, it is the largest oval masonry dome in the world [8]. More information about the Sanctuary of Vicoforte can be found in [6,8,9,10,11].

Figure 1. The Sanctuary of Vicoforte: (a) Front external view; (b) Top external view.

Over the years, the Sanctuary of Vicoforte has been interested by various type of investigation [8],[12,13,14]. Moreover, the evolution of the damage in the Sanctuary has been monitored since 1985 when the first strengthening system was installed [8]. A static sensor system was placed in 2004 and has been refurbished within the last year. Finally, since 2015 the Sanctuary has been equipped with a permanent dynamic system that allows to monitor the health state of the structure in almost real time. In this paper, the focus is only on the permanent dynamic system because the data used for the analyses in this study were derived from it.

The permanent monitoring of the lantern-dome-drum system of the Sanctuary of Vicoforte consists of 12 accelerometers. Their positions are shown in Figure 2: three orthogonal accelerometers are installed at the base of the crypt in order to record the ground accelerations; nine accelerometers are located at differents height on the lantern-dome-drum system along both longitudinal, transversal and vertical directions. The acquisition system is designed as a master/slave scheme to limit the distortion due to cable length that becomes significant over 50 m length [5]. Once the signals of acceleration are acquired by the accelerometers, they are then used to estimate in an automatic way the natural frequencies and mode shapes of the Sanctuary [6]. The dynamic system data are available from 2016 to present with some interruptions due to various causes such as bad weather or modifications and maintenance performed to the system. Figure 3 shows the days when acceleration data are available.

3. Mode tracking

Once the dynamic parameters of the structure are estimated through automated Operational Modal Analysis (OMA) techniques, an important and challenging step consists of progressively assign the identified modal properties of different identification tasks performed over time, to a particular vibration mode. This process is known as Mode (or Modal) Tracking (MT) and is commonly achieved by comparing estimated natural frequencies and their associated mode shapes with the modal properties of a set of reference modes [15]. The reference modes are obtained from an identification task in which most of the structure modes are identified or can be derived from one-time monitoring and in situ tests [16]. There are several examples where effective modal tracking procedures are shown and experimentally validated [15],[17],[18]. However, the MT procedure may vary from structure to structure especially in the case of monumental ones, and the result may also be affected by external factors such as environmental conditions that can cause changes in the dynamic response of the structure. In the present application a set of reference modes is compared with each identification task result. The comparison is performed in terms of Modal Assurance Criterion (MAC). The MAC between each reference mode and each mode identified in several tasks is calculated. Within the comparison of a single identification task result, the mode with maximum MAC with a specific reference mode is attributed to the time-history of that reference mode. However, the identification tasks can fail to identify all the reference modes, or the correlation (maximum MAC value) may be too low to consider a new identified mode associated to a previous reference time-history. For this reason, a threshold on the minimum value of acceptable maximum MAC is imposed, under which the mode remain unclassified, and the time history is filled-up with no number, i.e., Not a Number (NaN) value.

4. Application: definition of thresholds for mode tracking

In the case of the Sanctuary of Vicoforte, the modal parameters of the structure are estimated through an automatic modal identification procedure fully described in [5],[6]. Once this procedure was applied for the entire acquisition period (Figure 3), it has been possible to obtain the time series of the natural frequencies and their mode shapes through the MT procedure. In this study, to evaluate the coupling between the reference modes and the remaining vibration modes obtained from the identification process, MAC was used [19]. In particular, the analysis was performed in terms of MAC threshold values, which allowed the tracking of the natural frequencies. The threshold on the error in mode correlation,

e_{t h r}

, was evaluated with Eq. (1).

e_{t h r} = 1 - {M A C}_{t h r}

(1)

A MAC threshold equal to 0.95 was considered as starting point, because this value was used in the stabilization process [6]. Then this value has been changed, taking into account the following aspects:

Outlier analysis.
Total number of missing values, i.e. Not a Number.
Problem of classification, this means that there are many trends at different frequencies rather than just one that oscillates within small ranges.

Thus, the choice of the threshold value took into account the reduction in the number of outliers, also considering the Standard Deviation (StD),

σ

, of the time series obtained, as reported in Eq. (2).

σ = \sqrt{\frac{1}{N - 1} \sum_{i = 1}^{N} {| x_{i} - μ |}^{2}}

(2)

N is the number of samples, x is the observation and

μ

is the mean of

x_{i}

, see Eq. (3)

μ = \frac{1}{N} \sum_{i = 1}^{N} x_{i}

(3)

At the same time, as the outliers decreased, the increase in missing values, m_v, was taken into account so as not to lose any useful information (Eq. (4)).

N_{N a N} = \sum_{i = 1}^{N} m_{v}

(4)

where

N_{N a N}

is the total number of missing values. In addition, the results of the latter may depend on several factors such as the number of data available from the identification process or the reference mode chosen. Regarding the latter, it can be characterized by different frequency values and mode shapes, which are influenced by environmental factors such as temperature [4],[20]. For this reason, in the present study, it has been decided to take as reference three different moments referring to different periods of the year corresponding to different seasons: the first reference set of modes in February (low temperature, Section 4.1), the second in May (mild temperature, Section 4.2) and finally the third in August (high temperature, Section 4.3). In all cases, the first seven frequencies have been analyzed as they can be considered the most stable, in fact they are characterized by higher identification percentages. Therefore, the following modes have been evaluated: the first and second transversal (f₁ and f₆), the first and second longitudinal (f₂ and f₇), the first torsional (f₃) and the first and second local modes of the dome (i.e., ovalization) (f₄ and f₅).

4.1. Low temperature case

The low temperature analysis takes the identification of February 5, 2018, as the reference set of modes. Since the analysis involves the first seven frequencies, it has been appropriate to choose this one as a reference set because there are twelve modes in it.

The first step of the analysis was the choice of the threshold MAC according to a trial-and-error procedure that took into account the aspects listed above. Therefore, the threshold value has been calibrated from the starting point of 0.95 and increased (Figure 4). The analysis was first improved on f₁, f₂ and f₃ and then extended to f₄, f₅, f₆ and f₇. By increasing the value from 0.9500 to 0.9899, it is possible to observe a reduction of outliers and Standard Deviation; however, from a certain point onwards there could be also a loss of meaningful information since the number of NaN values in the natural frequencies increases. Figure 5 shows the trend of Standard Deviation and missing value as MAC thresholds change. In all three cases (f₁, f₂ and f₃), StD decreases while N_nan increases. Based on this and referring to the third frequency, a MAC_thr = 0.9750 was chosen as the optimal value.

The second step consists in obtaining the tracking of the remaining frequencies using MAC threshold; however, by carrying out an analysis taking into account all seven frequencies with a threshold of 0.9750, new outliers are introduced with values very far from the mean value. These results are shown in Figure 6 and Figure 7. Since this procedure causes a large variation in the time series of the first three frequencies, it has been decided to proceed by analyzing the frequencies in blocks, i.e., f₁-f₃, f₄-f₅, f_6-f₇, and find a different threshold for each of these blocks. Once the same procedure of f₁-f₃ block has been adopted, an optimal value of MAC_thr=0.9890 has been found in the case of f₄-f₅ because by increasing the value the frequency tracking does not vary considerably, i.e., neither Standard Deviation nor number of missing value change. By further increasing this value and reaching up to approximately 0.9930 the outliers decrease markedly, however together with them a lot of data is lost and consequently it is necessary to carefully evaluate whether the reduction of the Standard Deviation is more convenient than a significant loss of data. Finally, in the case of f₆-f₇ has been chosen a MAC_thr = 0.9892. The results are shown in Figure 8, while the tables show the different value of MAC threshold considered in both case of f₄-f₅ and f₆-f₇ and the relative number of missing value and Standard Deviation (Table 1 and Table 2); the highlighted values are those chosen.

Figure 5. Number of missing value (NaN) and Standard deviation for different MAC thresholds (normalized values) (a) f₁, (b) f₂ and (c) f_3.

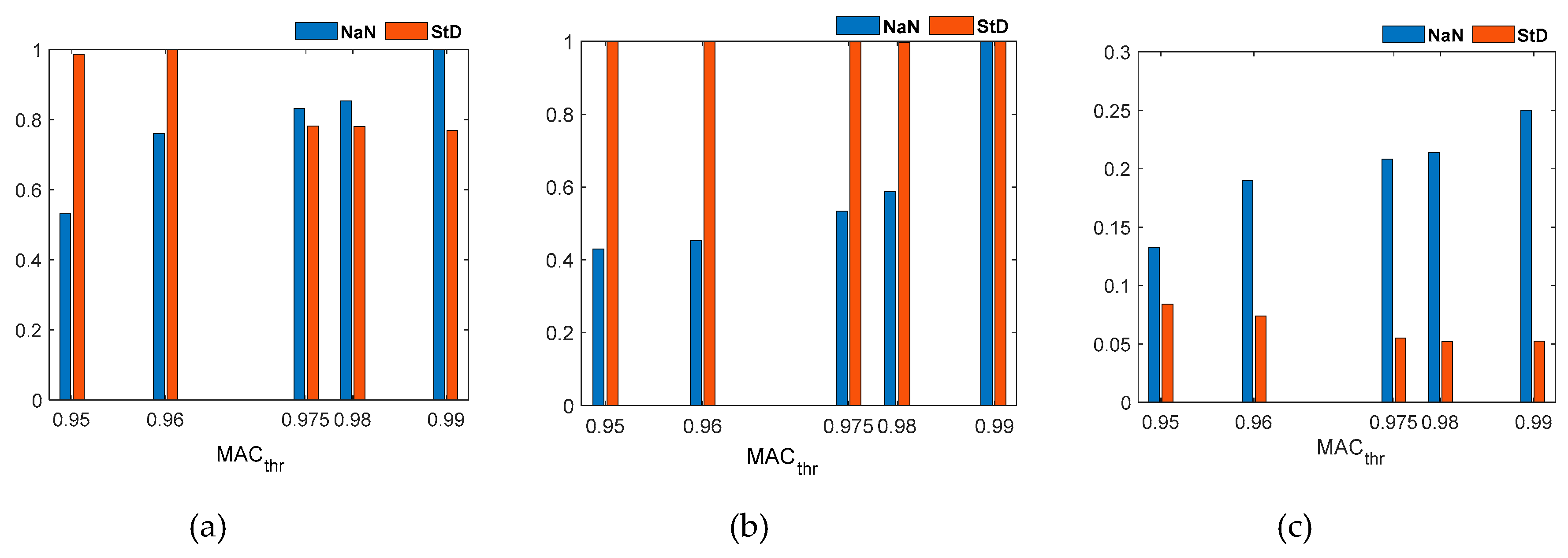
Figure 5. Comparison between different MT approaches: f₁, f₂ and f₃ time series considering only the first three frequencies with a MAC threshold of 0.9750 (left) and f₁, f₂ and f₃ time series considering seven frequencies (f₁-f₇) with a MAC threshold of 0.9750 (right).

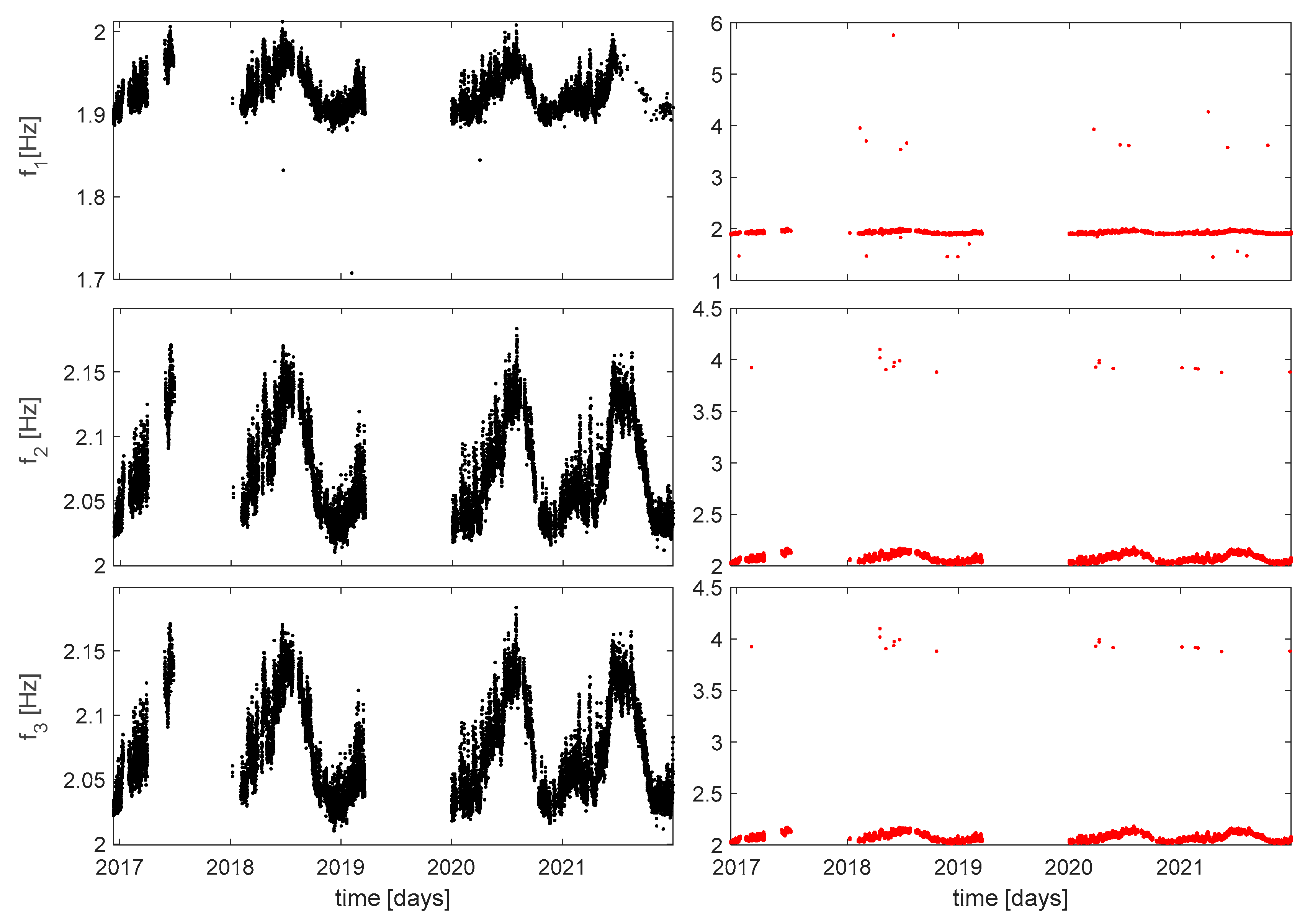
Figure 6. Number of missing value (NaN) and Standard Deviation (StD) comparison considering only the first three frequencies with a MAC threshold of 0.9750 and considering seven frequencies (f₁-f₇) with a MAC threshold of 0.9750: (a) f₁, (b) f₂ and (c) f_3.

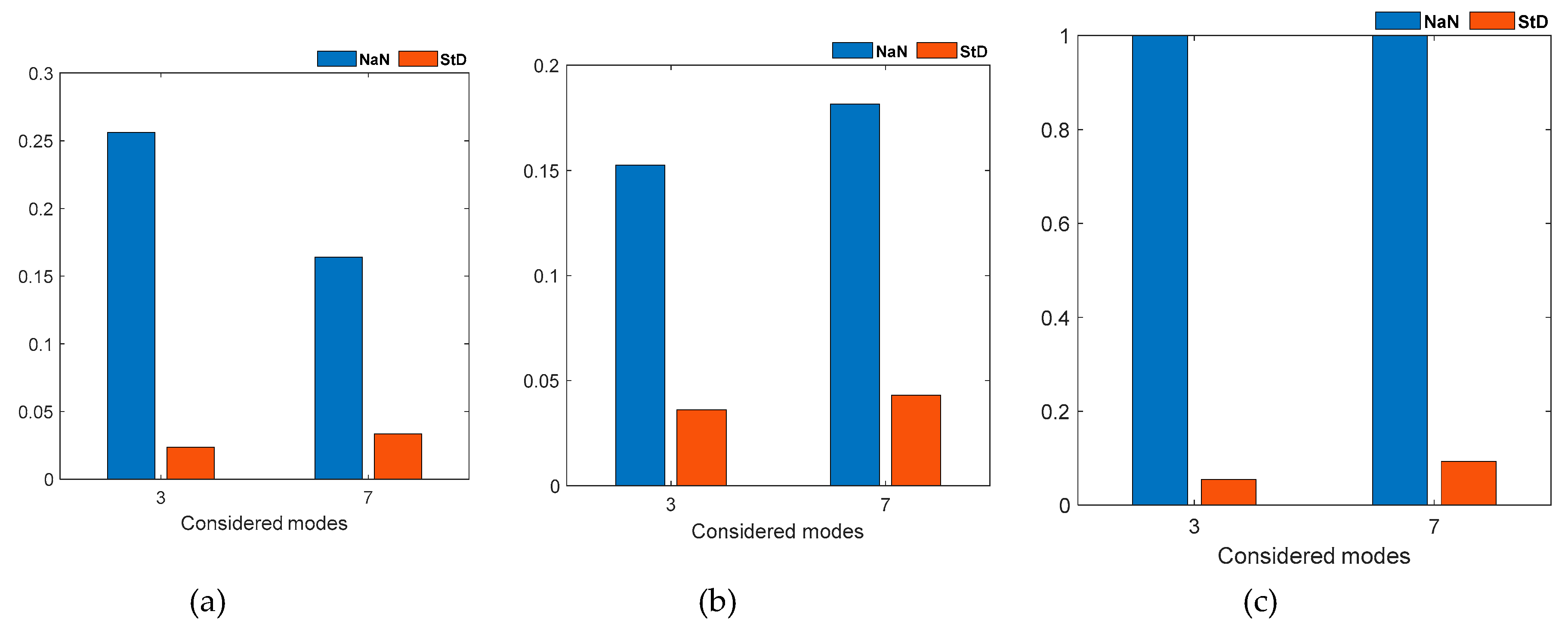
Figure 7. (a) Time series of f₄ and f₅ with a MAC threshold of 0.9890 and (b) time series of f₆ and f₇ with a MAC threshold of 0.9892.

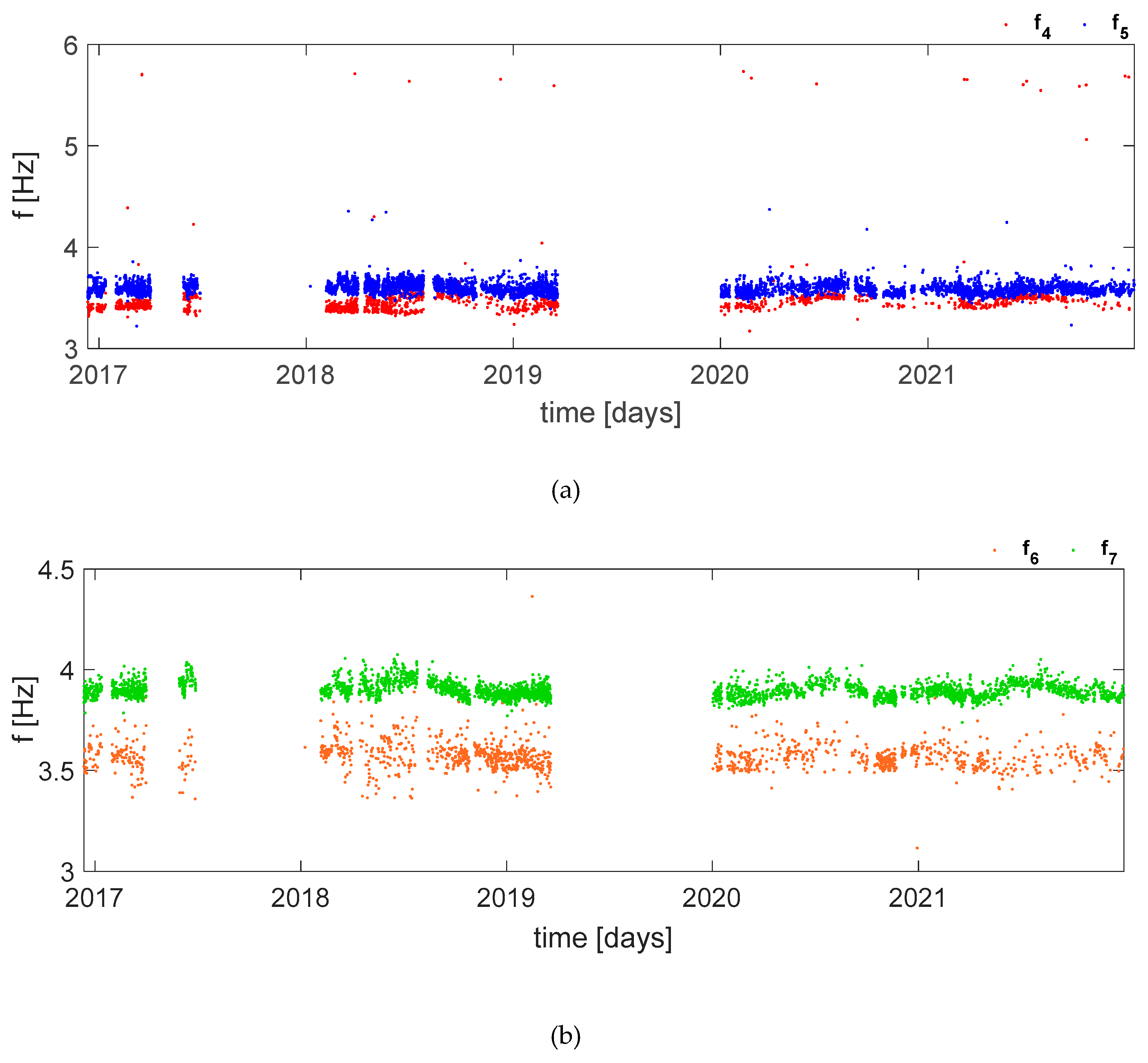
Table 1. Summary table with the MAC threshold values for f₄ and f₅ in the case of low temperature.

	MAC _thr	NaN	StD
f₄	0.9750	7569	0.2789
	0.9850	11275	0.2401
	0.9877	12370	0.2531
	0.9890	12856	0.2458
	0.9930	13919	0.1178
f₅	0.9750	8539	0.0890
	0.9850	8718	0.0639
	0.9877	8829	0.0594
	0.9890	8895	0.0587
	0.9930	9364	0.0546

Table 2. Summary table with the MAC threshold values for f₆ and f₇ in the case of low temperature.

	MAC _thr	NaN	StD
f₆	0.9750	3484	0.0908
	0.9850	9495	0.0985
	0.9877	11989	0.0924
	0.9892	13059	0.0697
	0.9940	14387	0.1246
f₇	0.9750	8229	0.0405
	0.9850	9862	0.0384
	0.9877	10612	0.0379
	0.9892	11159	0.0379
	0.9940	13260	0.0360

4.2. Mild temperature case

In the second case, the results of the identification of May 15, 2018 are considered as reference mode. Also in this case, a threshold of 0.95 has been always taken as the starting value. For the first three frequencies it has been possible to consider the same value used in the previous case (Section 4.1), i.e. 0.9750, as this result has been considered acceptable (Figure 9a). To obtain the trend of f₄ and f₅ it has been started from the value of MAC_thr = 0.989 used in the case of low temperature. In this case, however, this value is not adequate as both frequencies are characterized by many outliers which do not allow for a well-defined trend. As a subsequent step, a lower value of 0.9777 was considered and a worsening was found, as in the case of f₅ the outliers increased while for f₄ there was a classification problem that generates multiple behaviors within the same frequency. For this reason it was decided to test a value higher than 0.989 and therefore a MAC threshold equal to 0.9920 was considered and the tracking improves as the trend of both frequencies begins to be cleaner, however various outliers are present. Further increasing and testing different values, the best result is given by 0.9955 as many outliers are eliminated and there is not much data loss (Figure 9b). In the case of f₆ and f₇, even in this case it has been used the starting value of low temperature, i.e. 0.9892, some difficulties were encountered in finding a single value that would make tracking acceptable in the case of both frequencies. For this reason, it has been decided to analyze the two frequencies independently; but even in this case satisfactory results were not achieved, consequently the first type of results were maintained with a MAC_thr = 0.9800 (Figure 9c). Table 3 shows the different value of MAC threshold considered in the case of f₄-f₇ and the relative number of missing value and Standard Deviation.

4.3. High temperature case

The high temperature analysis takes the identification of August 14, 2018 as the reference mode. Also in this case the MAC threshold value used for low and mild temperatures works well for the first three frequencies; therefore in the case of f₁-f₃ the value 0.9750 was used. However, for all the other frequencies considered, the analysis in this case is more difficult because they are more characterized by classification errors, consequently it is really challeging to be able to isolate a defined behavior that represents the actual tracking of the frequency studied. In this case, given the large presence of outliers, instead of starting from the value of 0.95, it was decided to start from the maximum value of 0.99 and then decrease to observe the progressive restocking of the time series. Furthermore, MT was performed independently for f₄ to f₇. For f₄ a value of 0.9930 was chosen and an acceptable trend was obtained; even in the case of f₆ it was possible to define a MAC threshold value which allowed to trace the time series and this is equal to 0.9701. While, for f₅ and f₇ it was not possible to find a value of MAC threshold because in first case a lot of data is lost, so it is not possible to have a defined trend since it seems to be different behaviors at different frequencies; in the second case, the main problem is due to the presence of two different trend around 3 and 4.5 Hz that make the tracking result unacceptable. For these last reason, for high temperature only the times series of f₁-f₄ and f₆ are shown (Figure 10).

Figure 9. (a) Time series of f₁,f₂ and f₃ with a MAC threshold of 0.9750 , (b) time series of f₄ with a MAC threshold of 0.9930 and (c) time series of f₆ with a MAC threshold of 0.9701.

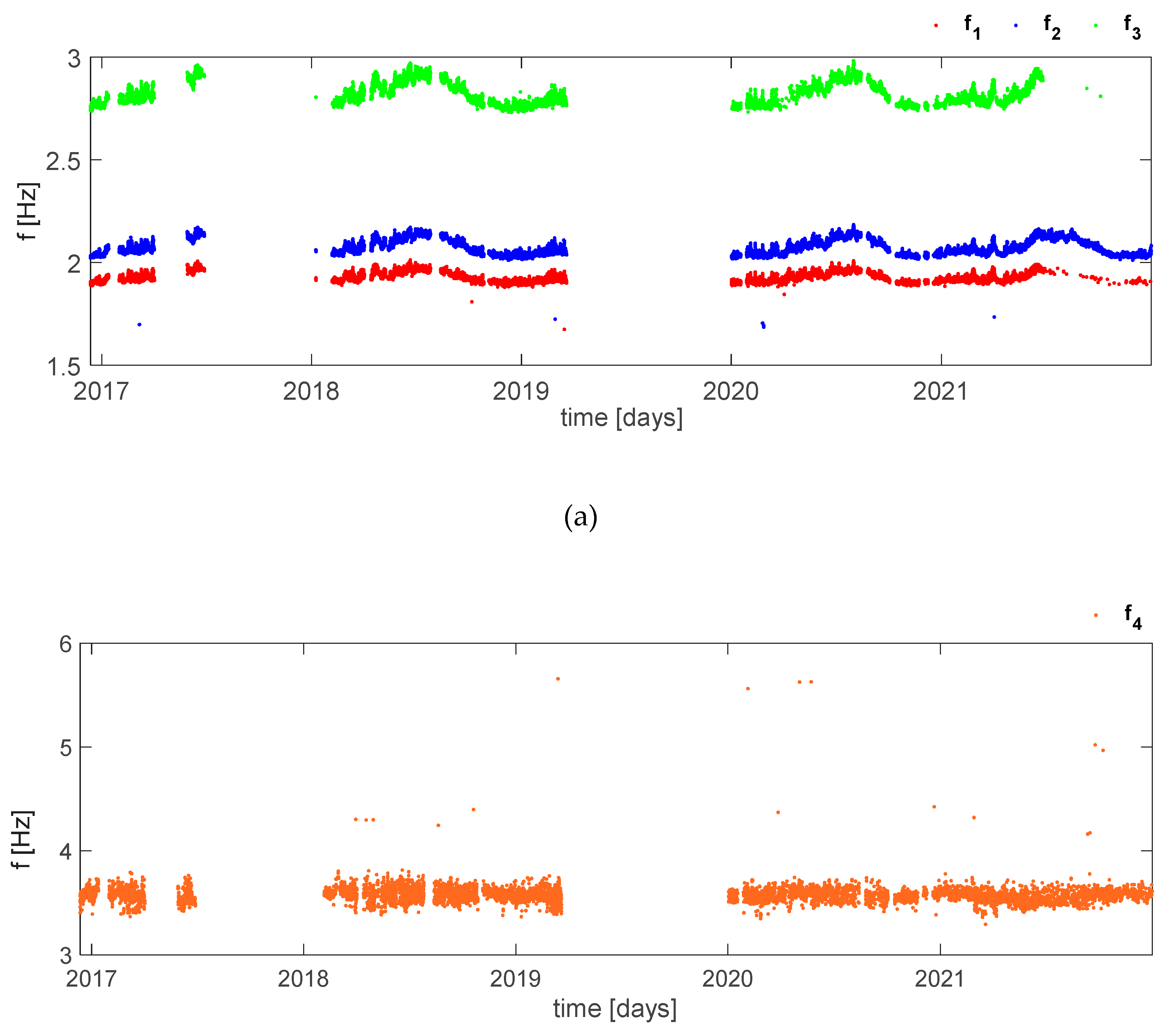
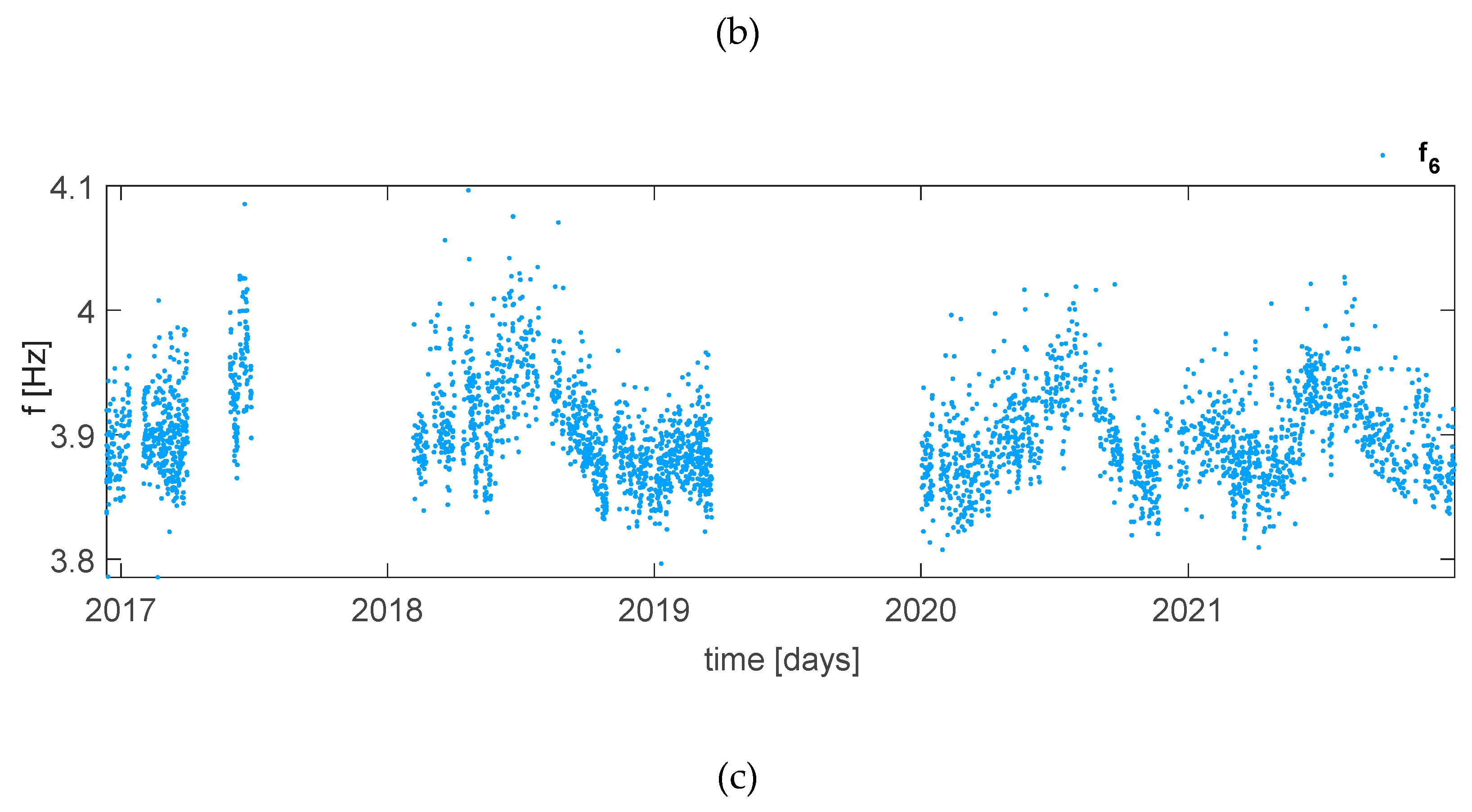
Table 4. Summary table with the MAC threshold values for f₄ and f₆ in the case of high temperature.

	MAC _thr	NaN	StD
f₄	0.9650	2137	0.1097
	0.9700	3116	0.0951
	0.9930	11372	0.0658
	0.9950	12724	0.0498
	0.9988	14387	0.0450
f₆	0.9700	11132	0.0418
	0.9701	11149	0.0383
	0.9705	11222	0.0382
	0.9740	11755	0.0377
	0.9750	11897	0.0376

4.4. Comparison of results

In the case of low temperature (Section 4.1), it has been possible to extract the tracking of frequencies for all considered modes, i.e., from f₁ to f_7. From the results obtained, it can be seen that tracking is more satisfactory in the case of lower and more stable frequencies in fact there is a lower number of NaN and less oscillation around the mean value. Secondly, for mild temperature (Section 4.2), even if it is possible to track all seven first frequencies, in the case of the higher modes the results obtained cannot be defined satisfactory as in the case of low reference temperatures since it is not possible to define a rather "clean" trend. Finally, in the last case (Section 4.3) with the exception of the first easily obtainable frequencies, in the rest of the cases it is very hard to define the trend, for this reason only some of the time series have been reported. For the first three frequencies, it could be said that they are less sensitive to the choice of the reference mode; in fact, from Figure 4, Figure 9a and Figure 10a and the below (Table 5), it can be seen that the mean and Standard Deviation are almost unchanged, the only variation occurs in the number of missing value.

5. Conclusions

A procedure of Mode Tracking is presented in order to obtain the time series of frequencies identified from the data collected by the seismic long-term monitoring system installed on the Sanctuary of Vicoforte. To achieve the aim of the study, it was decided to use the MAC threshold as a parameter for frequencies tracking. Furthermore, given the influence that environmental factors such as temperature can have on frequencies, cases at different temperatures were analyzed by choosing three different reference identifications corresponding to three different periods of the year as reference modes. In this way it was possible to analyze the trend at low, mild, and high temperatures. From the analysis performed in this study, it is possible to state that the mode tracking procedure cannot be defined univocally for all structures. In the case of the first three frequencies, which can be defined as the most stable, the procedure remained unchanged and in fact it has been possible to use the same MAC threshold value for the three reference periods. For these frequencies, the trends obtained are almost similar as demonstrated by the mean, Standard Deviation and missing values which are almost constant. On the contrary, in the case of the higher and less stable modes, it was necessary not only to vary the threshold MAC value but it was also necessary to change and adapt the procedure used based on the single case; despite this, in the case of mild temperature, the times series of higher modes are characterized by a significant number of missing value, while for high temperature, it was not possible to obtain the time series for the fifth and seventh frequencies.

From this application it appeared that the choice of parameter to obtain mode tracking, in this case the MAC threshold, should be calibrated case-by-case, both based on the different systems analyzed but also based on the mode analyzed within it. In fact, this procedure could be clearer and more immediate for simple concrete structures such as concrete arches, while in the case of monumental masonry buildings some more difficulties could arise. Another factor that could make the procedure more difficult could be the overlap of frequency ranges between the different modes, which would complicate obtaining correct tracking. In addition, there are cases where operational and environmental variations strongly influence the modal properties of the structure, so it should be necessary to take into account the variability due to these external conditions to obtain a correct estimate of the modal parameters. For these reasons, automating the calibration of the MAC threshold parameter could be very challenging. In fact, even if it was developed an algorithm that takes into account the aspects listed in Section 4, it would not be easy to define exact criteria for which the right threshold value could be obtained. A final check by an expert would always be necessary.

Finally, from the analyzes obtained in this study, the results of the low temperature case have been considered, i.e., those considered most reliable, to carry out simulations capable of providing more information on the relationship between the environmental temperature and the mechanical properties of the system; this topic will be the subject of future studies.

Author Contributions

Conceptualization, S.C., G.M., C.G., R.E., R.C; methodology, S.C. and G.M..; software, S.C. and G.M.; validation, S.C. and G.M.; formal analysis, S.C. and G.M.; investigation, S.C. and G.M.; resources, S.C. and G.M.; data curation, S.C., G.M., G.C and R.E.; writing—original draft preparation, S.C.; writing—review and editing, S.C., G.M., R.C., G.C. and R.E. visualization, S.C.,G.M. and R.C.; supervision, R.C.; project administration, R.C.; funding acquisition, R.C. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This research was partially supported by the Amministrazione del Santuario di Vicoforte and the Fondazione Cassa di Risparmio di Cuneo (CRC).

Conflicts of Interest

The authors declare no conflict of interest.

References

Staszewski, W. J.; Robertson, A. N. Time-Frequency and Time-Scale Analyses for Structural Health Monitoring. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2007, 365, 449–477. [Google Scholar] [CrossRef] [PubMed]
Worden, K.; Dulieu-Barton, J. M. An Overview of Intelligent Fault Detection in Systems and Structures. Struct Health Monit 2004, 3, 85–98. [Google Scholar] [CrossRef]
Farrar, C. R.; Worden, K. An Introduction to Structural Health Monitoring. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
Ceravolo, R.; Coletta, G.; Miraglia, G.; Palma, F. Statistical Correlation between Environmental Time Series and Data from Long-Term Monitoring of Buildings. Mech Syst Signal Process 2021, 152. [Google Scholar] [CrossRef]
Pecorelli, M. L.; Ceravolo, R.; Epicoco, R. An Automatic Modal Identification Procedure for the Permanent Dynamic Monitoring of the Sanctuary of Vicoforte. International Journal of Architectural Heritage 2020, 14, 630–644. [Google Scholar] [CrossRef]
Rodolfo, E. Identificazione Modale Automatica Di Tipo Stochastic Subspace per Il Monitoraggio Di Grandi Edifici Monumentali. MsC Thesis, Politecnico di Torino, Torino.
Ceravolo, R.; Pistone, G.; Fragonara, L. Z.; Massetto, S.; Abbiati, G. Vibration-Based Monitoring and Diagnosis of Cultural Heritage: A Methodological Discussion in Three Examples. International Journal of Architectural Heritage 2016, 10, 375–395. [Google Scholar] [CrossRef]
Ceravolo, R.; De Marinis, A.; Pecorelli, M.; Zanotti Fragonara, L. Monitoring of Masonry Historical Constructions: 10 Years of Static Monitoring of the World’s Largest Oval Dome. Struct Control Health Monit 2016, 24. [Google Scholar] [CrossRef]
Chiorino, M. A.; Spadafora, A.; Calderini, C.; Lagomarsino, S. Modeling Strategies for the World’s Largest Elliptical Dome at Vicoforte. International Journal of Architectural Heritage 2008, 2, 274–303. [Google Scholar] [CrossRef]
Casalegno, C.; Ceravolo, R.; Chiorino, M. A.; Pecorelli, M.; Zanotti Fragonara, L. Soil-Structure Modeling and Updating of the “Regina Montis Regalis” Basilica at Vicoforte, Italy. In 9th International Conference on Structural Analysis of Historical Constructions; Mexico City, Mexico, 2014.
Coletta, G. Monitoring of Architectural Heritage with Machine Learning Methods. PhD Thesis, Politecnico di Torino, Torino, 2022. [Google Scholar]
Aoki, T.; Tanigawa, Y.; Hatanaka, S.; Yuasa, N.; Hamasaki, H.; Chiorino, M. A.; Roccati, R. Nondestructive Testing of the Sanctuary of Vicoforte. In 13th Int. Brick and Block Masonry Conference; 2004; pp 1109–1118.
Scandella, L.; Lai, C. G.; Spallarossa, M.; Corigliano, M. Ground Shaking Scenarios at the Town of Vicoforte, Italy. Soil Dynamics and Earthquake Engineering 2011, 31. [Google Scholar] [CrossRef]
Chiorino, M. A.; Ceravolo, R.; Spadafora, A.; Zanotti Fragonara, L.; Abbiati, G. Dynamic Characterization of Complex Masonry Structures: The Sanctuary of Vicoforte. International Journal of Architectural Heritage 2011, 296–314. [Google Scholar] [CrossRef]
Pereira, S.; Magalhães, F.; Gomes, J. P.; Cunha, Á. Modal Tracking under Large Environmental Influence. J Civ Struct Health Monit 2022, 12, 179–190. [Google Scholar] [CrossRef]
Miraglia, G.; Cavanni, V.; Crocetti, A.; Len-Ticchia, E.; Ceravolo, R. Digital Twinning for the Prognosis of Spatial Architectures: Morandi’s Underground Pavilion in Turin.
Cabboi, A.; Magalhães, F.; Gentile, C.; Cunha, Á. Automated Modal Identification and Tracking: Application to an Iron Arch Bridge. Struct Control Health Monit 2016, 24. [Google Scholar] [CrossRef]
Desforges, M. J.; Cooper, J. E.; Wright, J. R. Mode Tracking during Flutter Testing Using the Modal Assurance Criterion.
Randall J. Allemang. The Modal Assurance Criterion – Twenty Years of Use and Abuse. In Sound & vibration, 37; 2003; pp 14–23.
Coletta, G.; Miraglia, G.; Gardner, P.; Ceravolo, R.; Surace, C.; Worden, K. A Transfer Learning Application to FEM and Monitoring Data for Supporting the Classification of Structural Condition States. In European Workshop on Structural Health Monitoring. EWSHM 2020. Lecture Notes in Civil Engineering; 2020. [CrossRef]

Figure 2. Permanent dynamic monitoring system: (a) Plan, (b) longitudinal section and (c) cross section.

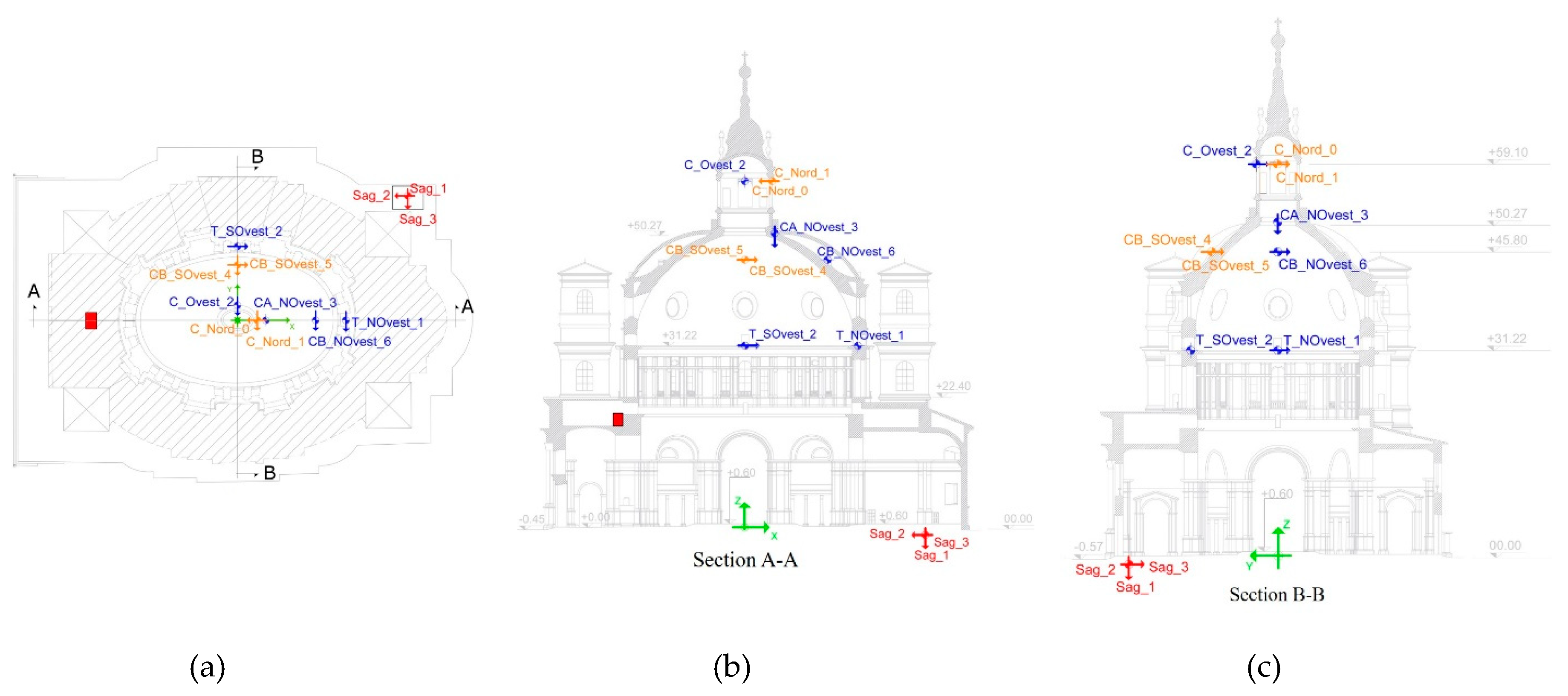
Figure 3. Days with available recordings from the permanent systems of the Sanctuary of Vicoforte.

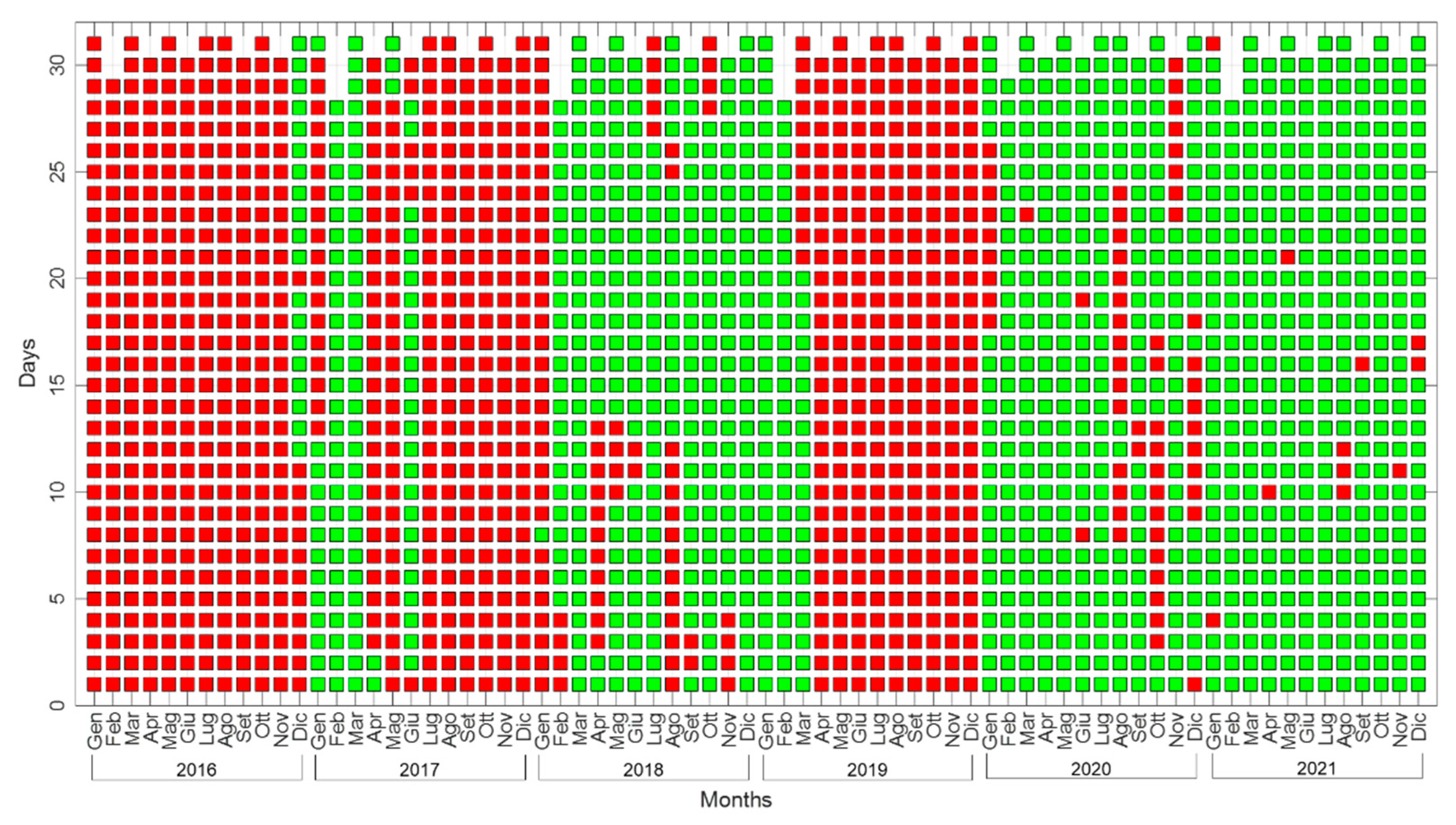
Figure 4. f₁, f₂ and f₃ comparison based on different values of MAC threshold.

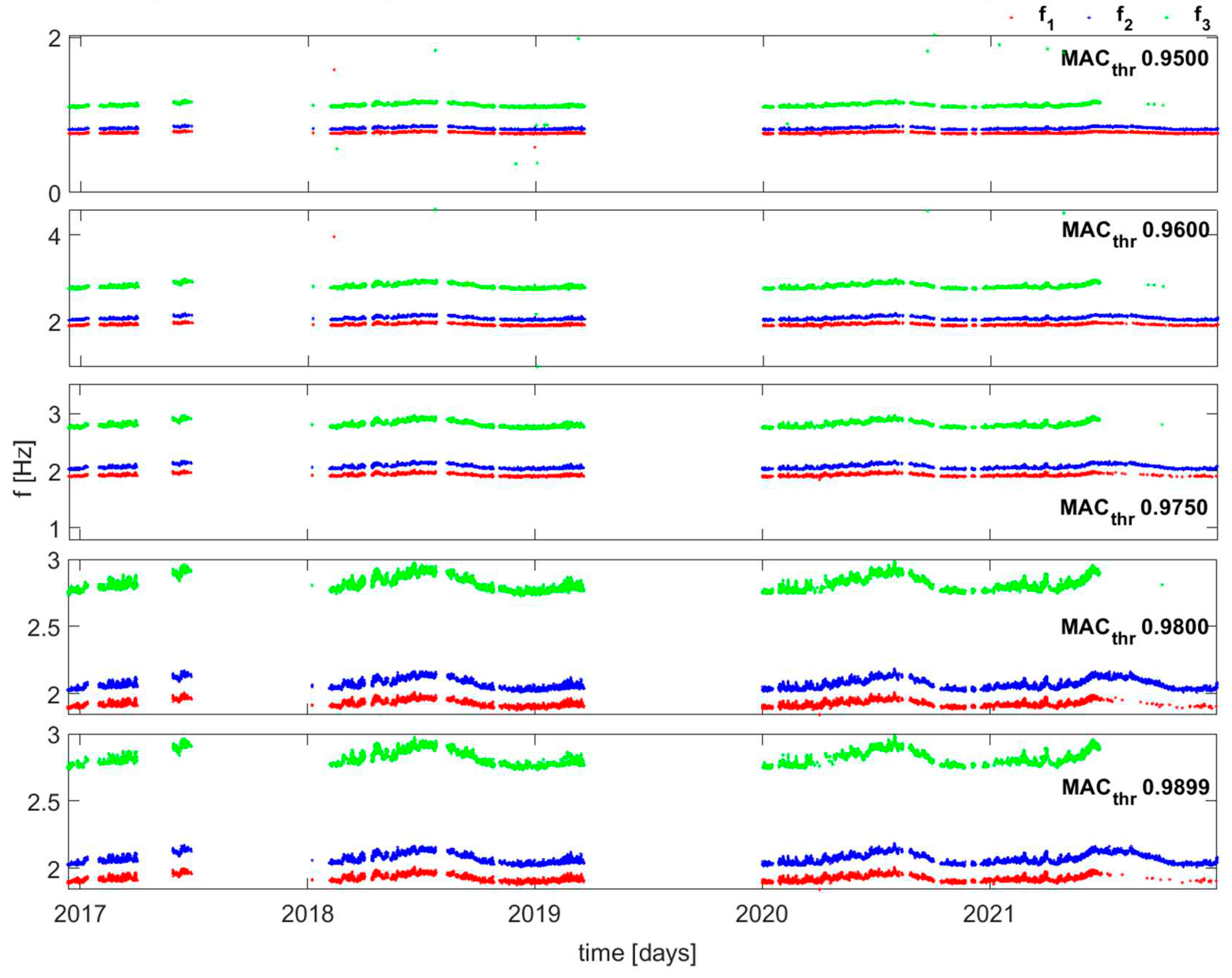
Figure 8. (a) Time series of f₁,f₂ and f₃ with a MAC threshold of 0.9750 (b) Time series of f₄ and f₅ with a MAC threshold of 0.9955, (c) time series of f₆ and f₇ with a MAC threshold of 0.9800.

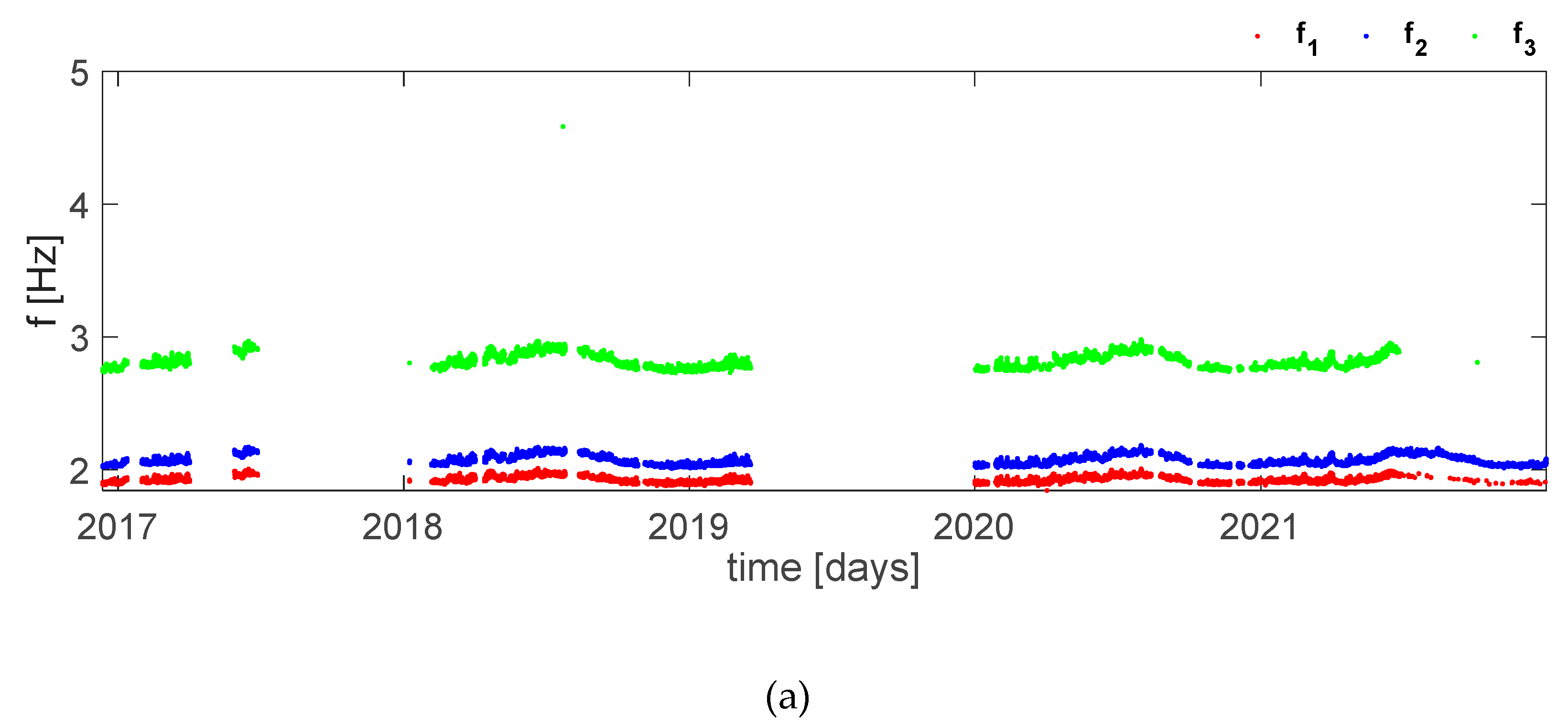
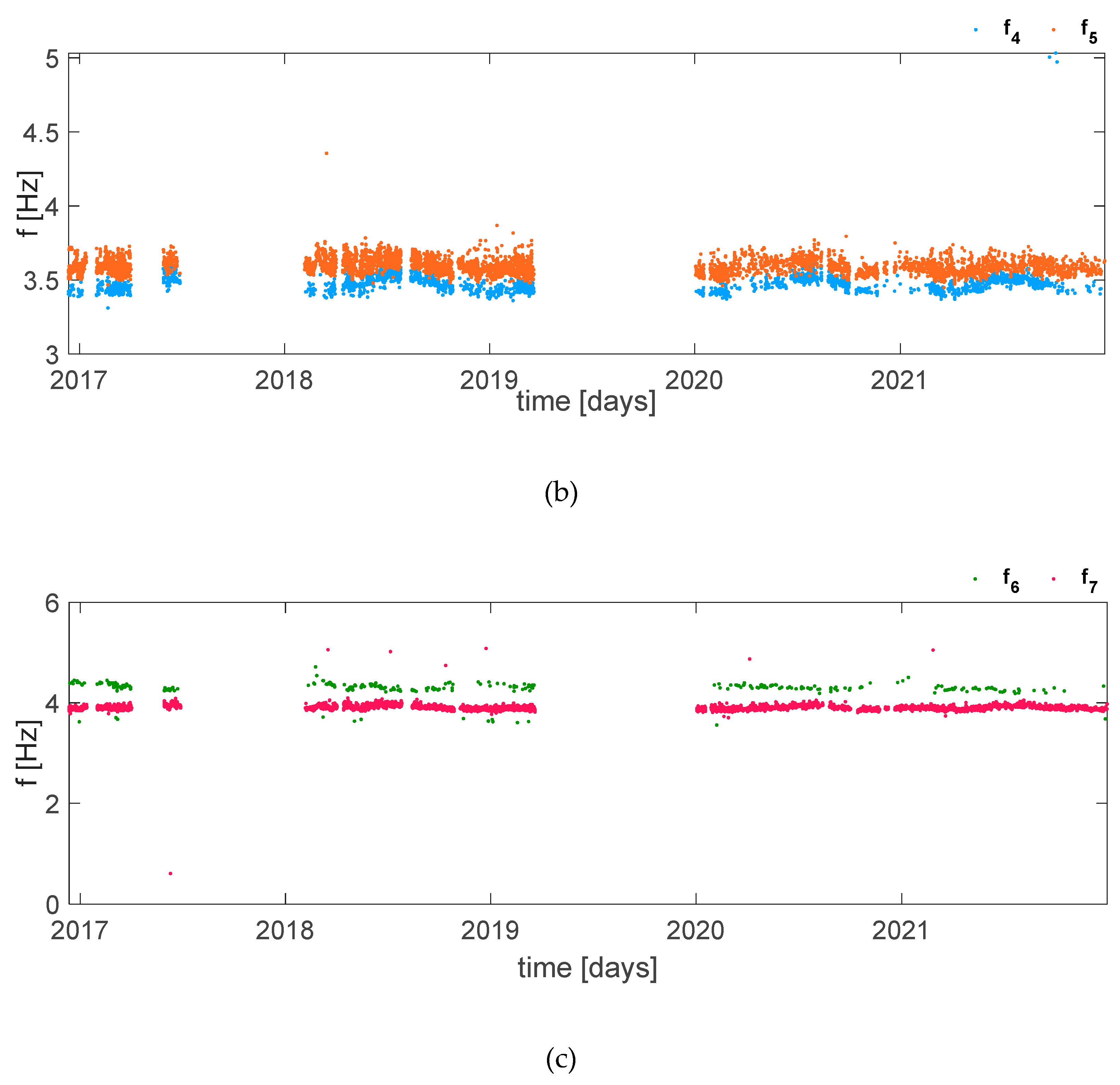
Table 3. Summary table with the MAC threshold values for f₄-f₇ in the case of mild temperature.

	MAC _thr	NaN	StD
f₄	0.9777	5862	0.2177
	0.9890	9496	0.1247
	0.9920	10558	0.1006
	0.9955	12363	0.0723
	0.996	12683	0.0667
f₅	0.9777	8356	0.0807
	0.9890	8668	0.0568
	0.9920	8968	0.0544
	0.9955	10040	0.0515
	0.9960	10341	0.0495
f₆	0.9700	13704	0.2252
	0.9750	13935	0.1674
	0.9780	14068	0.1618
	0.9800	14149	0.1497
	0.9892	14440	0.2269
f₇	0.9700	8167	0.1274
	0.9750	8825	0.0915
	0.9780	9329	0.0746
	0.9800	9732	0.0729
	0.9892	12283	0.0378

Table 5. Mean value, Standard Deviation (StD) and missing value (NaN) for different temperatures for the first three frequencies.

		Low T	Mild T	High T
f₁	μ	1.926	1.926	1.926
	StD	0.0235	0.0234	0.0236
	N_nan	3006	2958	2949
f₂	μ	2.072	2.072	2.073
	StD	0.0362	0.0362	0.0376
	N_nan	1791	1773	3108
f₃	μ	2.826	2.824	2.823
	StD	0.0551	0.0592	0.0544
	N_nan	11734	8268	8353

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer