Prerpints.org logo
Preprint
Article

Exploring the Femtosecond Filamentation Threshold in Liquid Media Using a Mach-Zehnder Interferometer

Altmetrics

Downloads

113

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 September 2023

Posted:

28 September 2023

You are already at the latest version

Alerts
Abstract
We experimentally study the supercontinuum (SC) induced by femtosecond filament in different liquid media, and determine the relative measurement value of filamentation threshold Pth for these media by using a Mach-Zehnder interferometer (MZI). It is found that the value of Pth is higher than the critical power for self-focusing Pcr, which can be attributed to the strong dispersion effect. Changing the focal length of the focusing lens affect the measured results of the filamentation threshold: In the case of shorter focal length, linear focusing (i.e., geometrical focusing) regime dominates, and the measured values of Pth for different media are almost the same; as the focal length becomes larger, self-focusing starts to play a role, making the values of Pth for different media different from each other. This work provides an effective approach to study the femtosecond filamentation process in liquid media, and helpful to further understand the physical process of supercontinuum induced by femtosecond filament in liquid media.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Since Braun et al. first discovered the phenomenon of laser filamentation in the air [1], there have been numerous theoretical and experimental studies on laser filamentation in the transparent media [2,3,4,5]. It is well known that the nonlinear filamentation phenomenon is attributed to the dynamic balance between the Kerr self-focusing and plasma defocusing effects [2]. When the femtosecond laser pulse transmits through a transparent medium, self-focusing effect will occur if its peak power exceeds the critical power for self-focusing Pcr.
When the pulse intensity exceeds the ionization threshold of the medium, it is high enough to ionize molecules producing numerous plasmas. Then the defocusing effect of the plasmas balances the self-focusing effect, thus limiting the peak intensity of the femtosecond laser pulse. The long and bright plasma channel formed at this time is called "filament". When the peak power of femtosecond laser pulse is higher than the filamentation threshold Pth, filamentation occurs. Since SC is a typical nonlinear phenomenon that occurs during femtosecond filamentation, in experiments, once the SC can be detected, the femtosecond filament has been formed.
In general, dispersion, self-phase modulation (SPM), self-steepening, intensity clamping and other nonlinear processes play a key role in determining the spectral range of SC [6,7,8,9,10]. SC can be generated by femtosecond filament in various transparent nonlinear media [11], and the spectral shape is similar, indicating that the generation of SC is a common feature of laser-matter interaction. Since the entire spectral range of SC maintains the polarization characteristics and spatiotemporal coherence of the original laser pulse, it is widely used as a broadband light source in time-resolved spectrum [12,13], optical communication [14], remote sensing [15,16], biomedical imaging [17] and few-cycle femtosecond pulses generation [18], etc.
Compared with gaseous media, liquid media has a higher nonlinear refractivity, which makes it easier to generate filaments and generate ultrabroad band continuum with relatively high intensity. While for solid media, they may cause optical damage under the action of intense laser pulses. Liquid media can easily change the thickness of the media, making it attractive for many experiments in nonlinear optics. There have been numerous reports on SC generation in liquid media [19,20,21]. For example, Wittmann et al. [22] studied the spectral superbroadening of femtosecond pulses in water, heavy water, ethanol, and fused silica under strong focusing conditions. In addition, studies have been conducted to control SC in transparent liquid media, such as doping a small amount of protein in water to inhibit SC broadening [23,24] or doping metal nanoparticles to enhance SC broadening [25].
The critical power for self-focusing Pcr and filamentation threshold Pth of femtosecond laser in different media have been studied extensively. Usually for longer pulse (e.g., picosecond pulses) and lower dispersion medium (e.g., air), Pth is identical to Pcr. However, for higher dispersion medium or ultrashort pulse, Pth is higher than Pcr. As for the measurement of Pth and Pcr, quite a few methods have been developed. For example, by using the moving focus method, the value of Pcr in air [26], helium [27] and flame [28] has been measured. Liang et al. [29] experimentally determine the value of Pcr for femtosecond vortex beams in air by measuring fluorescence using a photomultiplier tube. Akturk et al. [30] proposed a P-scan method to successfully distinguish linear, moving focus, filamentation, and multi-filamentation regimes in gases, and obtained the critical power of femtosecond Gaussian beam.
Since direct observation of femtosecond filaments in liquid media is not very convenient, it is often necessary to use other methods to diagnose filaments in experiments. In our previous work, by utilizing the interference of the SC induced by femtosecond filament, the actual value of filamentation threshold is determined by the Mach-Zehnder interferometer [31]. The SC generated by femtosecond filament in the transparent medium can be used as a coherent light source, after the spectral signal passes through the MZI, the interference patterns can be formed. For this reason, it is reasonable to judge the formation of filaments by the appearance of interference patterns in the field of view.
In this paper, the SC spectra induced by femtosecond filament in different liquid media are measured. We aim at measuring the relative measurement value of filamentation threshold Pth for higher dispersion media by using the MZI, and discussing the discrepancy between Pth and Pcr. In addition, the influence of the focal length of the focusing lens on the relative measurement value of filamentation threshold is also discussed.

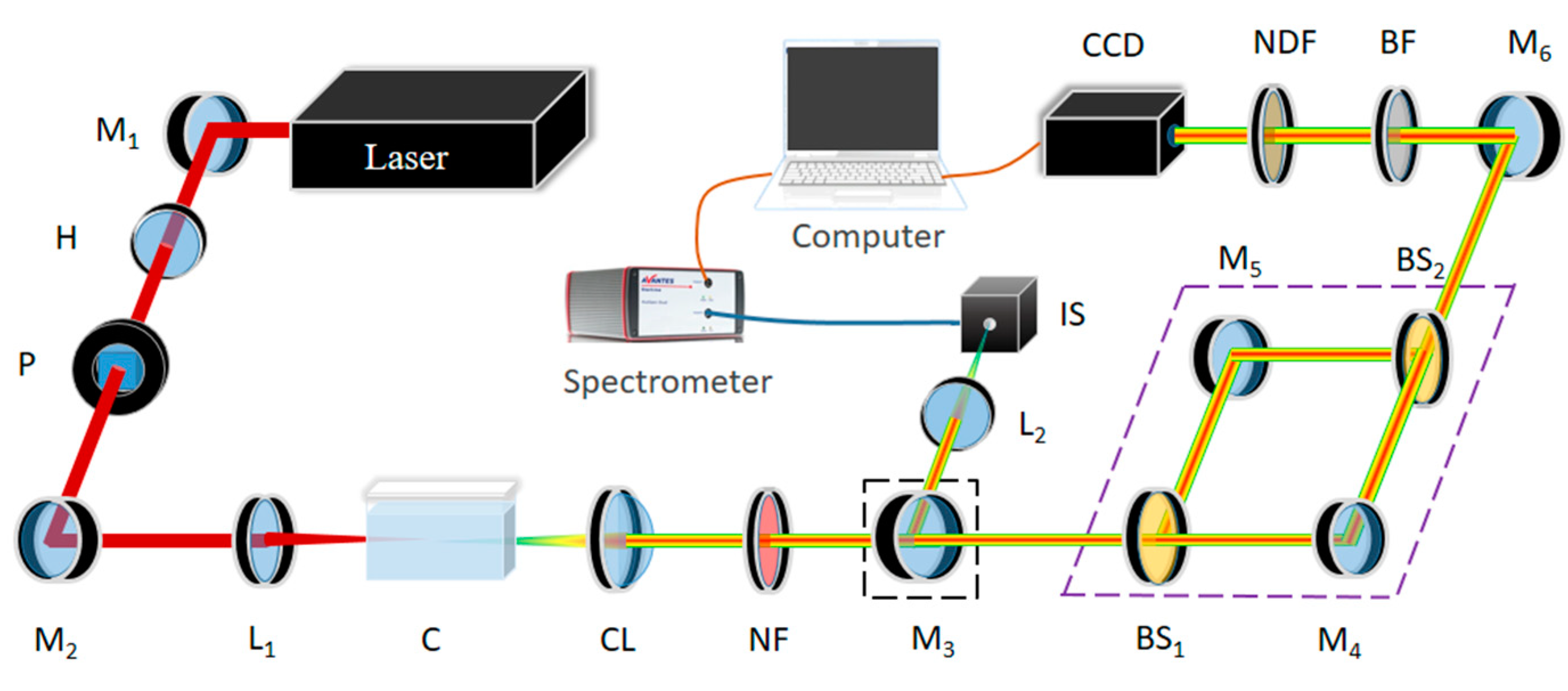
2. Experiment setup

The experiment is conducted by using an amplified Ti: sapphire laser system. The central wavelength, duration and repetition rate of the emitted pulses are 800 nm, 35 fs and 1 kHz, respectively. Figure 1 shows the schematic diagram of the experimental setup. The energy attenuator consists of a half-wave plate H and a polarizing beam-splitter P, which can adjust the pulse energy to the desired value. After passing through the focusing lens L1 (f = 400 mm), the incident laser beam is focused on the quartz cuvette (50 mm×10 mm×40 mm) filled with liquid samples, forming filaments. To avoid the generation of SC by femtosecond filamentation on the walls of the cuvette, the laser beam is focused close to the center of the cuvette, and then the position of the cuvette is fixed. The generated SC is collimated by the collimating lens CL (f = 75 mm), and then enters the notch filter NF which blocks the spectral components around 800 nm. The collimated SC is collected by the integrating sphere IS after being focused by the focusing lens L2 (f = 100 mm) and guided to the spectrometer (Avantes, AvaSpec Fast 1650F-USB2) through an optical fiber. After the spectra are measured, M3 is removed and the collimated SC enters into the MZI (marked by the dashed purple frame). After the SC passes through a band-pass filter BF and a neutral density filter NDF, the interference patterns of spectral signal are recorded by a CCD. In our experiment, five different liquid sample are selected: water, anhydrous ethanol, 95% ethanol, NaCl solution and glucose solution. The concentration of NaCl and glucose solutions are 25 mg/mL, 50 mg/mL and 100 mg/mL, respectively.

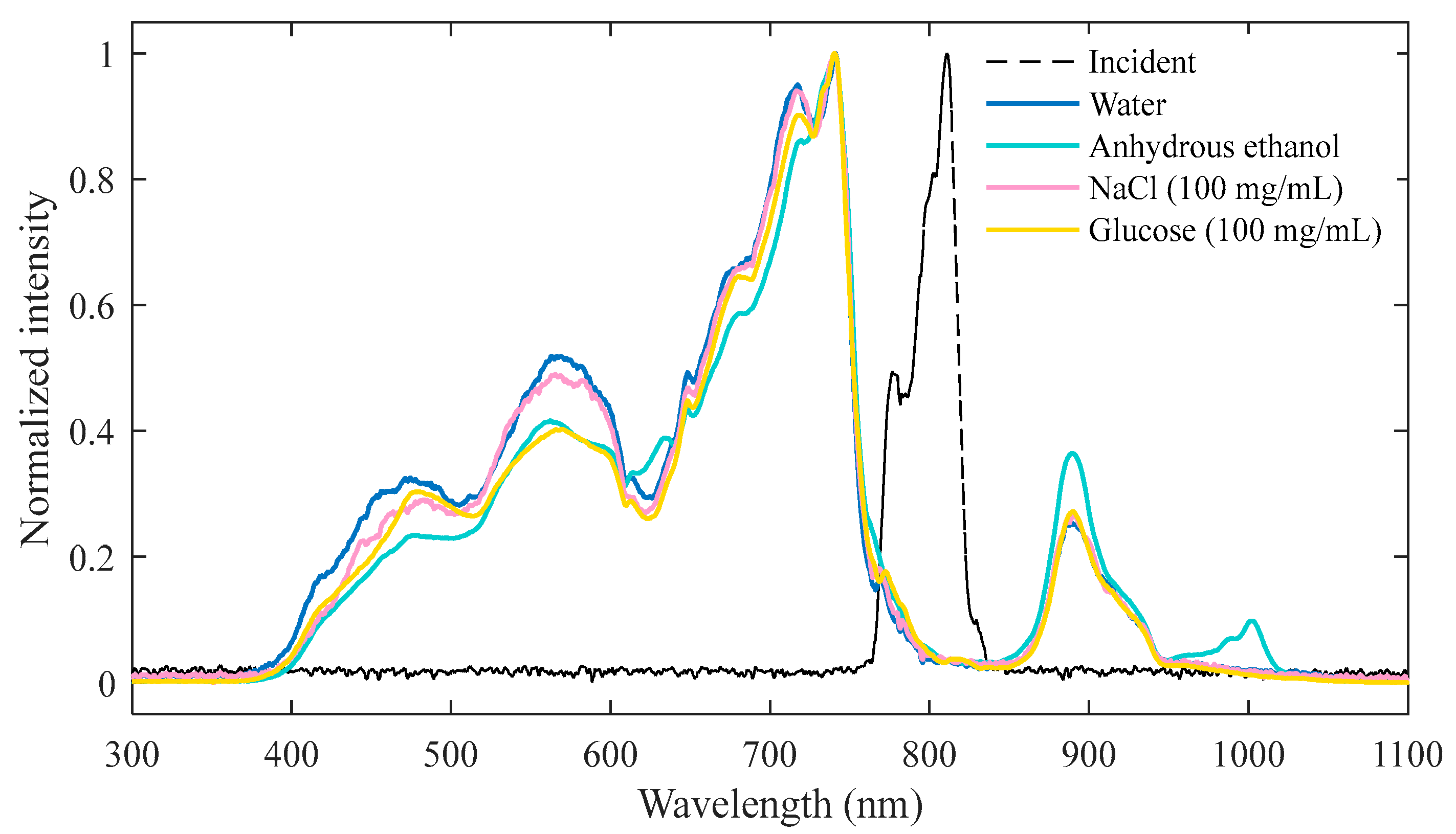
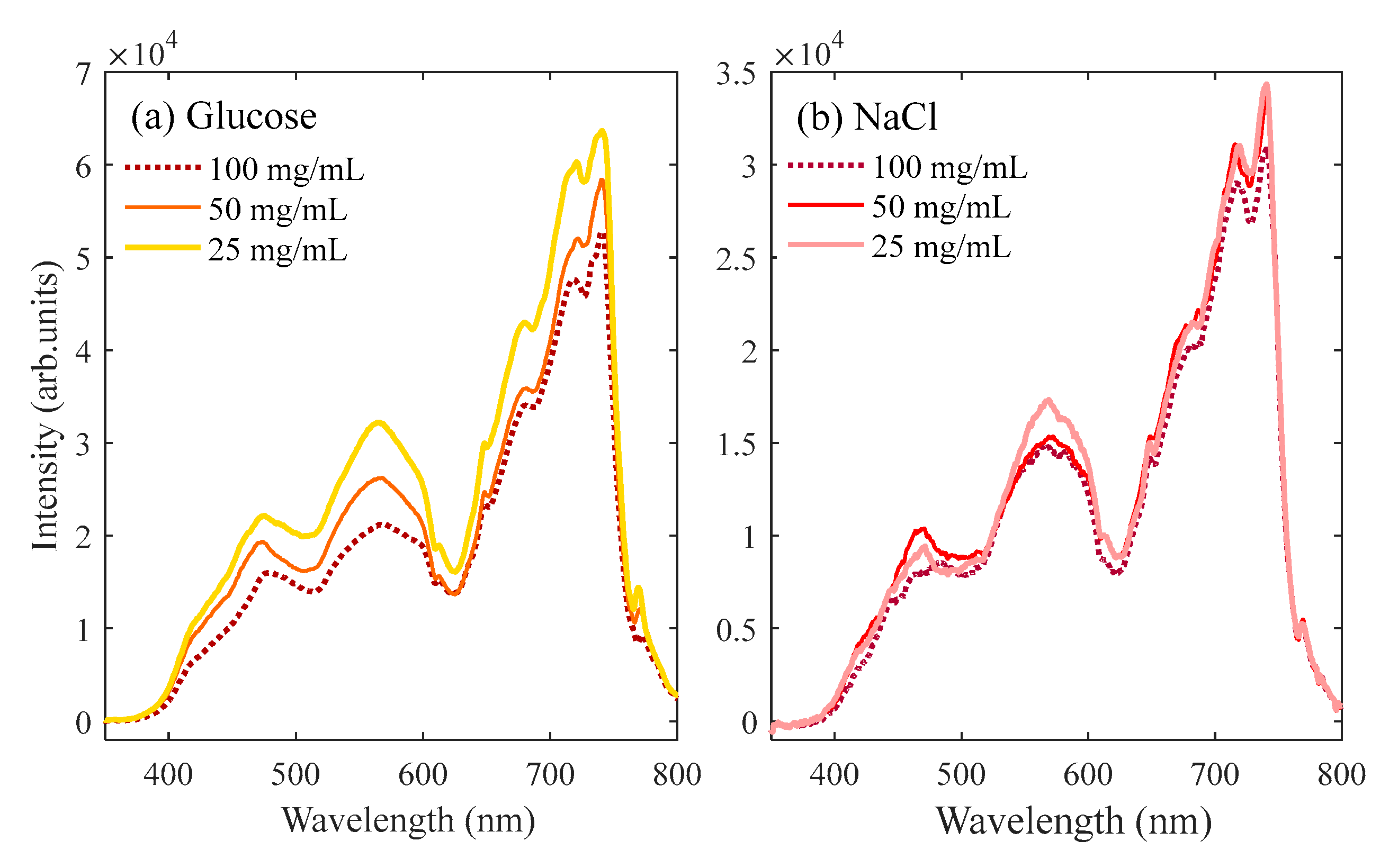
3. Results and discussion

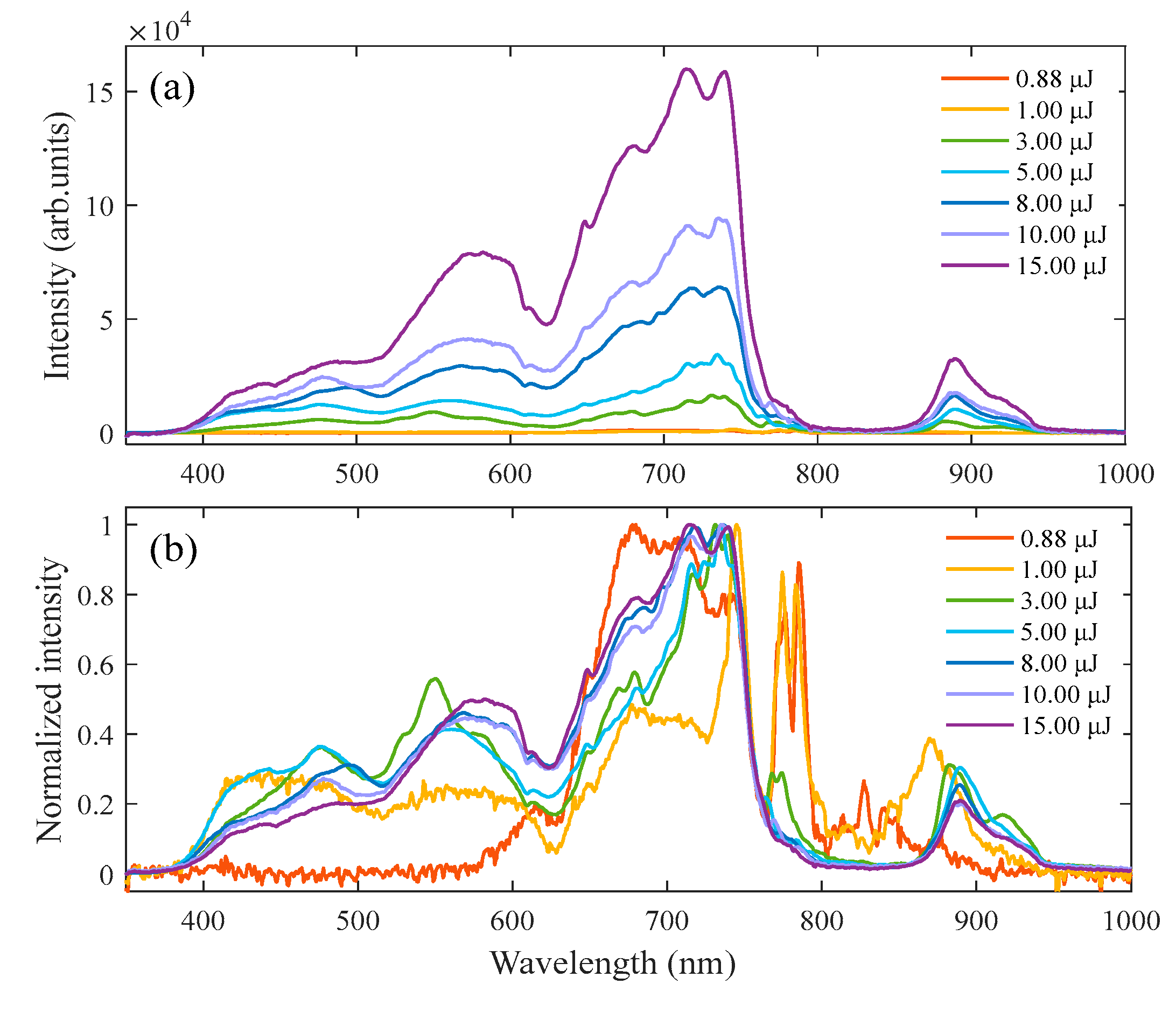
3.1. Supercontinuum

As femtosecond laser pulses form filaments in transparent media, nonlinear effects such as the SPM and self-steepening cause the spectral broadening, which covers the entire visible light band and is also known as supercontinuum /white light [32,33]. The spectral broadening induced by SPM can be described by following equation [2]:
Δ ω = - ∂ Δ φ ∂ t = ω 0 z c ( - n 2 ∂ I ( r , t ) ∂ t + 1 2 n 0 ρ c ∂ ρ e ( r , t ) ∂ t ) ,
where Δ φ is variation of the phase of the laser pulse, ω 0 is the central wavelength of the laser pulse, z is the propagation distance of the laser pulse in the medium, n 2 is the second-order nonlinear refractive index of the medium, ρ e ( r , t ) is the plasma density and ρ c = ε 0 m e ω 0 2 / e 2 is the plasma critical density( ε 0 , e and m e are the permittivity of vacuum, electron charge and electron mass respectively). Figure 2 shows the SC induced by femtosecond filament in water at different incident pulse energies. In liquid media, it is difficult to observe the femtosecond filament directly. The generation of the SC can usually be regarded as the sign of filament formation [2,34].
As can be seen from Figure 2(a), the SC is generated when the pulse energy reaches around 0.88 μJ, and the spectral range of the SC covers the entire visible wavelength band. In addition, the spectral intensity of the SC increases with the increase of pulse energy. From Figure 2(b), it is obvious that the normalized spectra undergo the asymmetric broadening, and there is a stronger shift towards the blue side of the spectrum than towards the red one. This asymmetric broadening is caused by the processes such as space-time focusing, self-steepening and plasma formation that arises from free electrons generated by multiphoton ionization (MPI) [23,35]. The free electrons generated by MPI give rise to a plasma that induces a spectral shift. As the incident pulse energy increases, the intensity of the SC increases and the ratio of the signal intensity of the blue part of the spectrum to the signal intensity of the center wavelength increases rapidly. The second term on the right-hand side of equation (1), the spectral broadening is proportional to the variation rate of plasma density with time. The variation of plasma density with time can be described as following equation [36,37]:
∂ ρ e ∂ t = W ( I ) ( ρ a t - ρ e ) + υ i ρ e + a ρ e 2
The first term at the right-hand side of this equation describes MPI in the filamentation dynamics, the second term is the contribution of the cascade ionization, and the third term describes the radiative electron recombination. We mainly consider the first term because for shorter laser pulses, MPI becomes the dominant process [38] and the latter two terms have relatively small effects. It can be seen from the equation (2) that the variation rate of plasma density with time is related to the pulse intensity in the filament which is clamped to a certain value, that is, the clamped intensity [39]. Therefore, the spectral range of the SC is independent of incident pulse energy and related to the clamped intensity. It is also observed that the spectrum extends to around 380 nm, and this value remains almost constant even when the incident pulse energy changes. In other words, spectrum broadening is not closely related to pulse energy/power, and intensity clamping is an important factor limiting the SC. Furthermore, linear chromatic dispersion [40], multi-photon absorption and plasma defocusing play important roles in the SC suppression [9]. It is necessary to consider the differences between the SC generated in different liquid media. The SC induced by femtosecond filament in different liquid media are shown in Figure 3.
Figure 3 shows that there is a marked dip near 620 nm in the SC, which is caused by the inverse Raman effect of water molecules [24,41]. The same dip in SC generated in anhydrous ethanol is due to the ionization of anhydrous ethanol to produce water molecules. Therefore, the position of the dip is irrespective of conditions like levels of additives introduced into the water, or variations in laser intensity and focusing conditions that have been represented in Ref. 24. It can be seen from Figure 3 that compared with pure water, the addition of additives suppresses the blue side of the white light spectrum. At the same pulse energy, the intensity of SC signals produced in different media is different, but the spectral shape and spectral broadening range remain almost consistent. In addition, we explore the SC generated in glucose and NaCl solutions with different concentrations. Figure 4 shows the SC induced by femtosecond filament in the glucose and NaCl solutions with different concentrations.
Figure 4(a) shows the SC generated in glucose solutions with different concentrations when the incident pulse energy is 10 μJ. It is evident that the blue-side components of the white light spectra are suppressed with the increase of glucose concentration. The degree of suppression is mainly related to concentrations of the glucose solution: the higher the concentrations of the solution, the more the SC is suppressed. Figure 4(b) shows the SC generated in NaCl solutions with different concentrations, and the results are similar to those in glucose solutions. As the concentration of NaCl solution increases, the short-wavelength spectrum of the SC is suppressed. The suppression occurs mainly on the blue side of the spectra, indicating that the addition of additives can affect the process of MPI free electrons generation. NaCl completely dissociates into sodium ions and chloride ions in water, increasing the concentration of the solution can increase the ion concentration in the solution. This leads to stronger interactions between water molecules and ions. Similarly, increasing the concentration of a glucose solution enhances the interactions between glucose molecules, reducing the possibility of ionization and thus affecting the electron yield. The difference in electron density will inevitably affect the self-phase modulation and affect the generation of white light. The electron density decreases with the increase of additives in water, thus the plasma effect is weakened, resulting in the suppression of the spectrum in the short-wavelength direction. In other words, the additives act as an electron capture in water. For the electron scavenging mechanism, it mainly includes the following two processes: one is the simple electron attachment, generating anion formation; the other one is the dissociative attachment process, where a low energy electron is temporarily attached to the additives via resonance, and the generated temporary negative ion rapidly dissociates into fragments, one of which is an anion [24]. The additive may participate in one or both processes, resulting in supercontinuum spectral compression in the short wavelength direction. Moreover, the absorption and scattering of light by additives in water may also contribute to the suppression of SC [42].

3.2. Self-focusing critical power and filamentation threshold

Femtosecond filamentation is usually accompanied by the generation of SC, which can be detected to determine the formation of the femtosecond filament. However, due to some spectral components being undetectable in cases of low pulse energy, the actual value of the filamentation threshold Pth is difficult to determine by the spectroscopic technology. Considering this problem, we use the SC induced by femtosecond filament in different liquid media as a coherent light source, which is introduced into MZI. Interference patterns can be generated and the pulse power at which the interference pattern emerges can be defined as the actual value of Pth. Figure 5 shows the interference patterns of 600 nm spectral signal in pure water and anhydrous ethanol, which are recorded by a CCD, when the focal length of the focusing lens is 400 mm.
When the pulse energy is lower, no interference pattern can be observed, indicating that no filament is formed in the water. As the pulse energy increases to a certain value (e.g., 0.88 μJ), as shown in Figure 5(a), interference patterns begin to flicker in view field, indicating that filamentation occurs. In the case of anhydrous ethanol, a filament also appears when the incident pulse energy is around 0.88 μJ, as shown in Figure 5(a'). This pulse power can be defined as the filamentation threshold Pth, which is also used as the criterion to determine the femtosecond filamentation threshold in the previous work [19]. Using the MZI, the actual filamentation threshold at low pulse energy can be accurately determined by interferometry. As the pulse energy increases to 1.0 μJ, we observe a stable fringe pattern. Further increasing the pulse energy forms multiple filaments, giving rise to a more complex interference pattern, until at higher power levels the fringe pattern becomes smeared.
If the input pulse is temporally Gaussian type, the critical power for self-focusing can be calculated by the following equation:
P c r = 3.77 λ 0 2 / 8 π n 0 n 2 ,
where λ 0 is the central wavelength of femtosecond laser pulse, n 0 and n 2 are the linear and nonlinear refractive indices of the medium [43,44]. The pulse energy can be measured by the pulse energy meter when the interference pattern appears (i.e., when the filament appears). The power (femtosecond filamentation threshold Pth) at this time can be calculated by the following equation:
P = E i n / （ π / 2 τ p ） ,
where τ p is the pulse duration. In the experiment, the initial pulse duration is approximately 50 fs, measured by an autocorrelator meter placed in front of the focusing lens L1. The filament is formed in different solutions (water, anhydrous ethanol, 95% ethanol, NaCl (100 mg/mL) and glucose (100 mg/mL) solutions) when the femtosecond laser pulse focused through focusing lenses with focal lengths of 1000 mm, 750 mm, 400 mm and 250 mm, respectively. Figure 6 shows the variations of the Pth with the focal length of the focusing lens in different liquid media. Table 1 provides the detailed values of Pth and Pcr of different media when using focusing lenses with different focal lengths. The n 0 and n 2 of water and anhydrous ethanol are reported from previous studies [45]. Based on their values, the n 0 and n 2 of 95% ethanol can be estimated. The formula to calculate the refractive index of a mixture is called the "Lorentz-Lorenz equation." It is given by [46]:
n a b = ϕ a n a + ϕ b n b ,
n a b , n a and n b are the refractive indices of solution, solvent, and solute, respectively, ϕ a and ϕ b are the volume fractions of the respective components in the solution. Taking linear refractive index n 0 as an example, the n 0 of water ( n a =1.33) and anhydrous ethanol ( n b =1.36), and the respective volume fraction of the mixture ( ϕ a =0.05, ϕ b =0.95). Substituting these values into the equation (5), the n 0 of 95% ethanol ( n a b ) is 1.3585. Similarly, it can be concluded that the n 2 of 95% ethanol is 7.52×10-16 cm2/W. The n 0 of the glucose and NaCl solutions in the Table 1 refer to data from Tan et al. [47]. The missing boxes in the Table 1 are caused by the lack of literature on the nonlinear refractive index values of glucose and NaCl solutions.
It can be clearly seen from Figure 6 that when using a focusing lens with a longer focal length (f = 1000 mm), there is a significant difference in Pth in the five kinds of media. As the focal length decreases, Pth gradually tends to converge to constant values, and they seem to be close when f = 250 mm. In the case of water, the critical power for self-focusing Pcr is 1.76 MW. When f = 250 mm, the value of Pth is 12.45 MW, and when f = 1000 mm, the value of Pth is 22.02 MW. As the focal length increases, the value of Pth gradually increases, and always remains higher than Pcr. The difference between Pth and Pcr can be attributed to the strong dispersion effect. It should be noted that dispersion plays a key role in the filamentation for ultrashort femtosecond laser pulse in water. Group velocity dispersion in transparent media increases the pulse duration and thus the peak power decreases during propagation. Therefore, we use the initial pulse duration to calculate Pth, which is much higher than the Pcr [48]. In addition, the dispersion of the lens itself has some effects. When using the same focusing lens, the effect of the dispersion caused by the lens on the measured value of Pth is consistent and can be ignored.
During the femtosecond filamentation, the core of the filament is fed by the surrounding energy reservoir, which can contain as much as 90% of the total pulse energy [49,50,51]. When an external focusing lens is used, the energy reservoir surrounding the filament core is confined to a smaller volume, resulting in a higher intensity at the self-focus when the laser pulse self-focuses [52]. The filament is formed through the balance among geometrical focusing, Kerr self-focusing, and defocusing by plasma and diffraction. The effective peak plasma density in the plasma column is highly dependent on the focal length [52]. When f = 250 mm, the measured values of Pth for different media are almost the same, which is 12.40±0.30 MW. This is because when the focal length of the focusing lens is small, far less than the self-focusing length of the beam, the beam focusing is mainly affected by the lens, that is, linear focusing is dominant in the filamentation region. Intensity clamping and thus electron density clamping do not occur in the linear focusing regime, the peak electron density and plasma channel diameter increase with energy [53]. In tight focusing geometry, the competition between plasma defocusing and self-focusing no longer play a significant role in intensity clamping [54]. It is well known that different liquid media have different refractive index and dispersion characteristics, which play a certain role in linear focusing. However, the measured values of Pth for different liquids are almost consistent when f = 250 mm, indicating that in the case of tight focusing, the effect of the medium itself on linear focusing is not significant. We use these liquid samples with similar linear refractive indices, so the influence on the geometrical focusing of the beam is relatively small after passing through the liquid samples. Therefore, in the case of shorter focal length (f = 250 mm), the measured values of Pth are less affected by the type and concentration of media.
However, when the focal length of the focusing lens increases, it can be observed that the measured values of Pth increase, and Pth for different media vary from each other. This is because the longer the focal length, the weaker the converging ability of the focusing lens, thus more energy is required to reach the filamentation threshold. As the focal length increases, self-focusing phenomenon gradually appears and takes effect. The linear and nonlinear refractive indices of liquid media play a greater role in the nonlinear focusing of the light beam, which can lead to varying degrees of ionization. Nonlinear focusing is more susceptible to the medium, so that the measured values of Pth for different media are quite different. The time dispersion caused by a long focal length lens is so small that we can ignore its effect on the threshold measurement. Therefore, it is speculated that in the case of longer focal length, self-focusing is dominant, and the type and concentration of media have a drastic impact on the measured values of Pth.

4. Conclusions

In our work, the SC generated by femtosecond filament in different liquid media is studied experimentally. It is found that, at the same pulse energy, the intensity of SC signals produced in different media is different, while the spectral shape and spectral broadening range remain almost consistent. The relative measurement value of filamentation threshold Pth in liquid media is measured using a Mach-Zehnder interferometer. It is found that, due to the influence of dispersion effect, the value of Pth is much higher than the critical power for self-focusing Pcr. In addition, changing the focal length of the focusing lens can affect the measured value of the Pth. Under the condition of shorter focal length, linear focusing plays a major role, and the measured values of Pth for different media are almost the same, since in the case of tight focusing, the effect of the medium itself on linear focusing is not significant. However, with the increase of focal length, the value of Pth increases gradually, and the difference between the values of Pth for different media is more obvious. This is because self-focusing phenomenon takes effect, nonlinear focusing is more susceptible to the influence of media. This work provides an effective approach for investigating the femtosecond filamentation process in liquid media. However, the method also has limitations, such as the determination of interference patterns depends on the detection efficiency of CCD. Nevertheless, the relative measurement of Pth in liquid media provided by this method can still serve as a reference.

Author Contributions

Conceptualization, Y.Z. and S.L.; methodology, Y.Z. and S.L.; software, Y.Z.; validation, Y.Z. and C.L.; formal analysis, Y.Z. and C.L.; investigation, Y.Z. and Y.X.; resources, S.L. and M.J.; data curation, Y.Z. and Y.X.; writing—original draft preparation, Y.Z.; writing—review and editing, Y.Z. and S.L.; visualization, Y.Z. and S.L.; supervision, A.C., S.L. and M.J.; project administration, A.C., S.L. and M.J.; funding acquisition, A.C., S.L. and M.J. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China (Grant No. 2019YFA0307701); National Natural Science Foundation of China (Grant Nos. 11704145 and 11974138); and the Education Department of Jilin Province (Grant No. JJKH20200937KJ).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on reasonable request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Braun, A.; Korn, G.; Liu, X.; Du, D.; Squier, J.; Mourou, G. Self-channeling of high-peak-power femtosecond laser pulses in air. Opt. Lett. 1995, 20, 73–75. [Google Scholar] [CrossRef] [PubMed]
  2. Couairon, A.; Mysyrowicz, A. Femtosecond filamentation in transparent media. Phys. Rep. 2007, 441, 47–189. [Google Scholar] [CrossRef]
  3. Papazoglou, D.G.; Tzortzakis, S. In-line holography for the characterization of ultrafast laser filamentation in transparent media. Appl. Phys. Lett. 2008, 93, 041120. [Google Scholar] [CrossRef]
  4. Dharmadhikari, A.K.; Alti, K.; Dharmadhikari, J.A.; Mathur, D. Control of the onset of filamentation in condensed media. Phys. Rev. A. 2007, 76, 033811. [Google Scholar] [CrossRef]
  5. Couairon, A.; Bergé, L. Modeling the filamentation of ultra-short pulses in ionizing media. Phys. Plasmas 1999, 7, 193–209. [Google Scholar] [CrossRef]
  6. Kolesik, M.; Wright, E.M.; Moloney, J.V. Dynamic nonlinear X-waves for femtosecond pulse propagation in water. Phys. Rev. Lett. 2004, 92, 253901. [Google Scholar] [CrossRef]
  7. Faccio, D.; Averchi, A.; Lotti, A.; Kolesik, M.; Moloney, J.V.; Couairon, A.; Di Trapani, P. Generation and control of extreme blueshifted continuum peaks in optical Kerr media. Phys. Rev. A. 2008, 78, 033825. [Google Scholar] [CrossRef]
  8. Porras, M.A.; Dubietis, A.; Kučinskas, E.; Bragheri, F.; Degiorgio, V.; Couairon, A.; Faccio, D.; Di Trapani, P. From X- to O-shaped spatiotemporal spectra of light filaments in water. Opt. Lett. 2005, 30, 3398–3400. [Google Scholar] [CrossRef]
  9. Kolesik, M.; Katona, G.; Moloney, J.V.; Wright, E.M. Physical factors limiting the spectral extent and band gap dependence of supercontinuum generation. Phys. Rev. Lett. 2003, 91, 043905. [Google Scholar] [CrossRef]
  10. Faccio, D.; Averchi, A.; Couairon, A.; Dubietis, A.; Piskarskas, R.; Matijosius, A.; Bragheri, F.; Porras, M.A.; Piskarskas, A.; Di Trapani, P. Competition between phase-matching and stationarity in Kerr-driven optical pulse filamentation. Phys. Rev. E. 2006, 74, 047603. [Google Scholar] [CrossRef]
  11. Gaeta, A.L. Catastrophic collapse of ultrashort pulses. Phys. Rev. Lett. 2000, 84, 3582–3585. [Google Scholar] [CrossRef] [PubMed]
  12. Kovalenko, S.A.; Schanz, R.; Hennig, H.; Ernsting, N.P. Cooling dynamics of an optically excited molecular probe in solution from femtosecond broadband transient absorption spectroscopy. J. Chem. Phys. 2001, 115, 3256–3273. [Google Scholar] [CrossRef]
  13. Harilal, S.S.; Kautz, E.J.; Phillips, M.C. Time-resolved absorption spectroscopic characterization of ultrafast laser-produced plasmas under varying background pressures. Phys. Rev. E. 2021, 103, 013213. [Google Scholar] [CrossRef] [PubMed]
  14. Smirnov, S.V.; Ania-Castanon, J.D.; Ellingham, T.J.; Kobtsev, S.M.; Kukarin, S.; Turitsyn, S.K. Optical spectral broadening and supercontinuum generation in telecom applications. Opt. Fiber Technol. 2006, 12, 122–147. [Google Scholar] [CrossRef]
  15. Rairoux, P.; Schillinger, H.; Niedermeier, S.; Rodriguez, M.; Ronneberger, F.; Sauerbrey, R.; Stein, B.; Waite, D.; Wedekind, C.; Wille, H.; Wöste, L.; Ziener, C. Remote sensing of the atmosphere using ultrashort laser pulses. Appl. Phys. B. 2000, 71, 573–580. [Google Scholar] [CrossRef]
  16. Brown, D.M.; Shi, K.; Liu, Z.; Philbrick, C.R. Long-path supercontinuum absorption spectroscopy for measurement of atmospheric constituents. Opt. Express 2008, 16, 8457–8471. [Google Scholar] [CrossRef]
  17. Tu, H.; Boppart, S.A. Coherent fiber supercontinuum for biophotonics. Laser Photon. Rev. 2013, 7, 628–645. [Google Scholar] [CrossRef]
  18. Bergé, L.; Rolle, J.; Köhler, C. Enhanced self-compression of mid-infrared laser filaments in argon. Phys. Rev. A. 2013, 88, 023816. [Google Scholar] [CrossRef]
  19. Zhang, H.; Zhang, Y.; Lin, S.; Chang, M.; Yu, M.; Wang, Y.; Chen, A.; Jiang, Y.; Li, S.; Jin, M. Testing the coherence of supercontinuum generated by optical vortex beam in water. J. Phys. B: At. Mol. Opt. Phys. 2021, 54, 165401. [Google Scholar] [CrossRef]
  20. Brodeur, A.; Ilkov, F.A.; Chin, S.L. Beam filamentation and the white light continuum divergence. Opt. Commun. 1996, 129, 193–198. [Google Scholar] [CrossRef]
  21. Golub, I. Optical characteristics of supercontinuum generation. Opt. Lett. 1990, 15, 305–307. [Google Scholar] [CrossRef] [PubMed]
  22. Wittmann, M.; Penzkofer, A. Spectral superbroadening of femtosecond laser pulses. Opt. Commun. 1996, 126, 308–317. [Google Scholar] [CrossRef]
  23. Santhosh, C.; Dharmadhikari, A.K.; Alti, K.; Dharmadhikari, J.A.; Deepak, M. Suppression of ultrafast supercontinuum generation in a salivary protein. J. Biomed. Opt. 2007, 12, 020510. [Google Scholar] [CrossRef] [PubMed]
  24. Santhosh, C.; Dharmadhikari, A.K.; Dharmadhikari, J.A.; Alti, K.; Mathur, D. Supercontinuum generation in macromolecular media. Appl. Phys. B. 2010, 99, 427–432. [Google Scholar] [CrossRef]
  25. Vasa, P.; Singh, M.; Bernard, R.; Dharmadhikari, A.K.; Dharmadhikari, J.A.; Mathur, D. Supercontinuum generation in water doped with gold nanoparticles. Appl. Phys. Lett. 2013, 103, 111109. [Google Scholar] [CrossRef]
  26. Liu, W.; Chin, S.L. Direct measurement of the critical power of femtosecond Ti: sapphire laser pulse in air. Opt. Express 2005, 13, 5750–5755. [Google Scholar] [CrossRef]
  27. Bernhardt, J.; Simard, P.T.; Liu, W.; Xu, H.L.; Théberge, F.; Azarm, A.; Daigle, J.F.; Chin, S.L. Critical power for self-focussing of a femtosecond laser pulse in helium. Opt. Commun. 2008, 281, 2248–2251. [Google Scholar] [CrossRef]
  28. Li, H.; Chu, W.; Zang, H.; Xu, H.; Cheng, Y.; Chin, S.L. Critical power and clamping intensity inside a filament in a flame. Opt. Express 2016, 24, 3424–3431. [Google Scholar] [CrossRef]
  29. Liang, W.; Li, D.; Chang, J.; Xi, T.; Ji, L.; Li, D.; Zhang, L.; Hao, Z. Experimentally determined critical power for self-focusing of femtosecond vortex beams in air by a fluorescence measurement. Opt. Express 2023, 31, 1557–1566. [Google Scholar] [CrossRef]
  30. Akturk, S.; D’Amico, C.; Franco, M.; Couairon, A.; Mysyrowicz, A. A simple method for determination of nonlinear propagation regimes in gases. Opt. Express 2007, 15, 15260–15267. [Google Scholar] [CrossRef]
  31. Li, S.; Wang, X.; Zhang, Y.; Yu, M.; Wang, Y.; Liu, F.; Jin, M. Femtosecond filamentation in water studied by the interference of supercontinuum. Phys. Scr. 2023, 98, 015501. [Google Scholar] [CrossRef]
  32. Kasparian, J.; Sauerbrey, R.; Mondelain, D.; Niedermeier, S.; Yu, J.; Wolf, J.P.; André, Y.B.; Franco, M.; Prade, B.; Tzortzakis, S.; Mysyrowicz, A.; Rodriguez, M.; Wille, H.; Wöste, L. Infrared extension of the supercontinuum generated by femtosecond terawatt laser pulses propagating in the atmosphere. Opt. Lett. 2000, 25, 1397–1399. [Google Scholar] [CrossRef] [PubMed]
  33. Théberge, F.; Châteauneuf, M.; Ross, V.; Mathieu, P.; Dubois, J. Ultrabroadband conical emission generated from the ultraviolet up to the far-infrared during the optical filamentation in air. Opt. Lett. 2008, 33, 2515–2517. [Google Scholar] [CrossRef] [PubMed]
  34. Chin, S.L. Femtosecond laser filamentation, New York: Springer, 2010; pp. 13.
  35. Bergé, L.; Skupin, S.; Nuter, R.; Kasparian, J.; Wolf, J.P. Ultrashort filaments of light in weakly ionized, optically transparent media. Rep. Prog. Phys. 2007, 70, 1633. [Google Scholar] [CrossRef]
  36. Yablonovitch, E.; Bloembergen, N. Avalanche ionization and the limiting diameter of filaments induced by light pulses in transparent media. Phys. Rev. Lett. 1972, 29, 907–910. [Google Scholar] [CrossRef]
  37. Feng, Q.; Moloney, J.V.; Newell, A.C.; Wright, E.M.; Cook, K.; Kennedy, P.K.; Hammer, D.X.; Rockwell, B.A.; Thompson, C.R. Theory and simulation on the threshold of water breakdown induced by focused ultrashort laser pulses. IEEE J. Quantum Electron. 1997, 33, 127–137. [Google Scholar] [CrossRef]
  38. Noack, J.; Vogel, A. Laser-induced plasma formation in water at nanosecond to femtosecond time scales: calculation of thresholds, absorption coefficients, and energy density. IEEE J. Quantum Electron. 1999, 35, 1156–1167. [Google Scholar] [CrossRef]
  39. Liu, W.; Petit, S.; Becker, A.; Aközbek, N.; Bowden, C.M.; Chin, S.L. Intensity clamping of a femtosecond laser pulse in condensed matter. Opt. Commun. 2002, 202, 189–197. [Google Scholar] [CrossRef]
  40. Kolesik, M.; Katona, G.; Moloney, J.V.; Wright, E.M. Theory and simulation of supercontinuum generation in transparent bulk media. Appl. Phys. B. 2003, 77, 185–195. [Google Scholar] [CrossRef]
  41. Jones, W.J.; Stoicheff, B.P. Inverse Raman spectra: induced absorption at optical frequencies. Phys. Rev. Lett. 1964, 13, 657–659. [Google Scholar] [CrossRef]
  42. Li, H.; Shi, Z.; Wang, X.; Sui, L.; Li, S.; Jin, M. Influence of dopants on supercontinuum generation during the femtosecond laser filamentation in water. Chem. Phys. Lett. 2017, 681, 86–89. [Google Scholar] [CrossRef]
  43. Wilkes, Z.W.; Varma, S.; Chen, Y.H.; Milchberg, H.M.; Jones, T.G.; Ting, A. Direct measurements of the nonlinear index of refraction of water at 815 and 407 nm using single-shot supercontinuum spectral interferometry. Appl. Phys. Lett. 2009, 94, 211102. [Google Scholar] [CrossRef]
  44. Dubietis, A.; Gaižauskas, E.; Tamošauskas, G.; Di Trapani, P. Light filaments without self-channeling. Phys. Rev. Lett. 2004, 92, 253903. [Google Scholar] [CrossRef] [PubMed]
  45. Boyd, R.W. Nonlinear optics, 3rd ed.; Academic press, 2008; pp. 212.
  46. Heller, W. Remarks on refractive index mixture rules. J. Phys. Chem. 1965, 69, 1123–1129. [Google Scholar] [CrossRef]
  47. Tan, C.Y.; Huang, Y.X. Dependence of refractive index on concentration and temperature in electrolyte solution, polar solution, nonpolar solution, and protein solution. J. Chem. Eng. Data 2015, 60, 2827–2833. [Google Scholar] [CrossRef]
  48. Luther, G.G.; Moloney, J.V.; Newell, A.C.; Wright, E.M. Self-focusing threshold in normally dispersive media. Opt. Lett. 1994, 19, 862–864. [Google Scholar] [CrossRef]
  49. Kandidov, V.P.; Kosareva, O.G.; Golubtsov, I.S.; Liu, W.; Becker, A.; Akozbek, N.; Bowden, C.M.; Chin, S.L. Self-transformation of a powerful femtosecond laser pulse into a white-light laser pulse in bulk optical media (or supercontinuum generation). Appl. Phys. B. 2003, 77, 149–165. [Google Scholar] [CrossRef]
  50. Liu, W.; Gravel, J.F.; Théberge, F.; Becker, A.; Chin, S.L. Background reservoir: its crucial role for long-distance propagation of femtosecond laser pulses in air. Appl. Phys. B. 2005, 80, 857–860. [Google Scholar] [CrossRef]
  51. Liu, W.; Théberge, F.; Arévalo, E.; Gravel, J.F.; Becker, A.; Chin, S.L. "Experiment and simulations on the energy reservoir effect in femtosecond light filaments. Opt. Lett. 2005, 30, 2602–2604. [Google Scholar] [CrossRef]
  52. Théberge, F.; Liu, W.; Simard, P.T.; Becker, A.; Chin, S.L. Plasma density inside a femtosecond laser filament in air: Strong dependence on external focusing. Phys. Rev. E 2006, 74, 036406. [Google Scholar] [CrossRef]
  53. Reyes, D.; Baudelet, M.; Richardson, M.; Fairchild, S.R. Transition from linear-to nonlinear-focusing regime of laser filament plasma dynamics. J. Appl. Phys. 2018, 124, 053103. [Google Scholar] [CrossRef]
  54. Kiran, P.P.; Bagchi, S.; Arnold, C.L.; Krishnan, S.R.; Kumar, G.R.; Couairon, A. Filamentation without intensity clamping. Opt. Express 2010, 18, 21504–21510. [Google Scholar] [CrossRef] [PubMed]
Preprints 86337 g001
Figure 1. Schematic diagram of the experimental setup. M1-M6: plane mirror; H: half-wave plate; P: polarizing beam-splitter; L1 and L2: focusing lens; Cuvette: cuvette filled with liquid samples; CL: collimating lens; NF: notch filter; BS1 and BS2: beam splitter; IS: integrating sphere; BF: band-pass filter; NDF: neutral density filter.
Figure 1. Schematic diagram of the experimental setup. M1-M6: plane mirror; H: half-wave plate; P: polarizing beam-splitter; L1 and L2: focusing lens; Cuvette: cuvette filled with liquid samples; CL: collimating lens; NF: notch filter; BS1 and BS2: beam splitter; IS: integrating sphere; BF: band-pass filter; NDF: neutral density filter.
Preprints 86337 g001
Preprints 86337 g002
Figure 2. (a) SC induced by femtosecond filament in water at different incident pulse energies, and (b) the normalized spectra of (a). The focal length of focusing lens adopted is 400 mm.
Figure 2. (a) SC induced by femtosecond filament in water at different incident pulse energies, and (b) the normalized spectra of (a). The focal length of focusing lens adopted is 400 mm.
Preprints 86337 g002
Preprints 86337 g003
Figure 3. SC generated in different liquid media using a focusing lens with a focal length of 400 mm when the incident pulse energy is 10 μJ.
Figure 3. SC generated in different liquid media using a focusing lens with a focal length of 400 mm when the incident pulse energy is 10 μJ.
Preprints 86337 g003
Preprints 86337 g004
Figure 4. SC generated in (a) glucose and (b) NaCl solutions with different concentrations using a 400 mm focusing lens. The pulse energy is 10 μJ.
Figure 4. SC generated in (a) glucose and (b) NaCl solutions with different concentrations using a 400 mm focusing lens. The pulse energy is 10 μJ.
Preprints 86337 g004
Preprints 86337 g005
Figure 5. (a)-(d) Interference patterns of 600 nm spectral signals in water recorded by a CCD with pulse energies of 0.88 μJ, 1.0 μJ, 2.0 μJ, and 4.0 μJ, respectively. (a')-(d') Interference patterns of 600 nm spectral signals in anhydrous ethanol at the corresponding pulse energy. The focal length of the focusing lens is 400 mm.
Figure 5. (a)-(d) Interference patterns of 600 nm spectral signals in water recorded by a CCD with pulse energies of 0.88 μJ, 1.0 μJ, 2.0 μJ, and 4.0 μJ, respectively. (a')-(d') Interference patterns of 600 nm spectral signals in anhydrous ethanol at the corresponding pulse energy. The focal length of the focusing lens is 400 mm.
Preprints 86337 g005
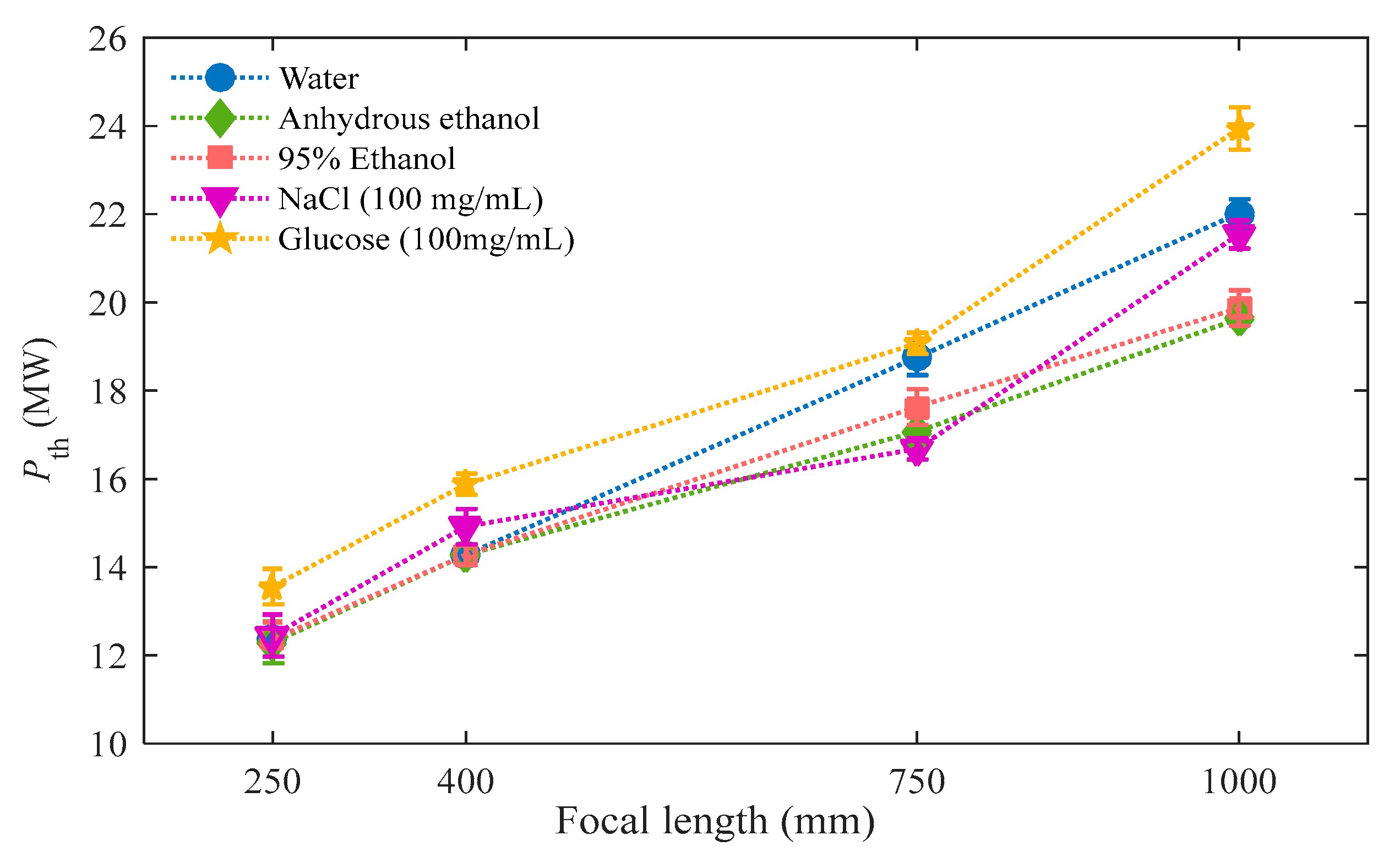
Preprints 86337 g006
Figure 6. Variations of the filamentation threshold Pth in different liquid media with the focal length of the focusing lens.
Figure 6. Variations of the filamentation threshold Pth in different liquid media with the focal length of the focusing lens.
Preprints 86337 g006
Table 1. Filamentation threshold Pth and critical power for self-focusing Pcr of different media when using focusing lenses with different focal lengths.
Table 1. Filamentation threshold Pth and critical power for self-focusing Pcr of different media when using focusing lenses with different focal lengths.
Material n 0 n 2 Pcr(MW) Pth(MW)
f = 1000 mm f = 750
mm		 f = 400
mm		 f = 250
mm
Water 1.33 4.1×10-16 1.76 22.02 18.67 14.20 12.45
Anhydrous ethanol 1.36 7.7×10-16 0.92 19.63 17.07 14.36 12.29
95% Ethanol 1.3585 7.52×10-16 0.94 19.79 17.55 14.20 12.29
NaCl
(100 mg/mL)		 1.3521 21.54 16.76 14.84 12.45
Glucose
(100 mg/mL)		 1.3481 23.94 19.15 15.79 13.56
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated