Reinforcement Learning and Stochastic Optimization with Deep Learning based Forecasting on Power Grid Scheduling

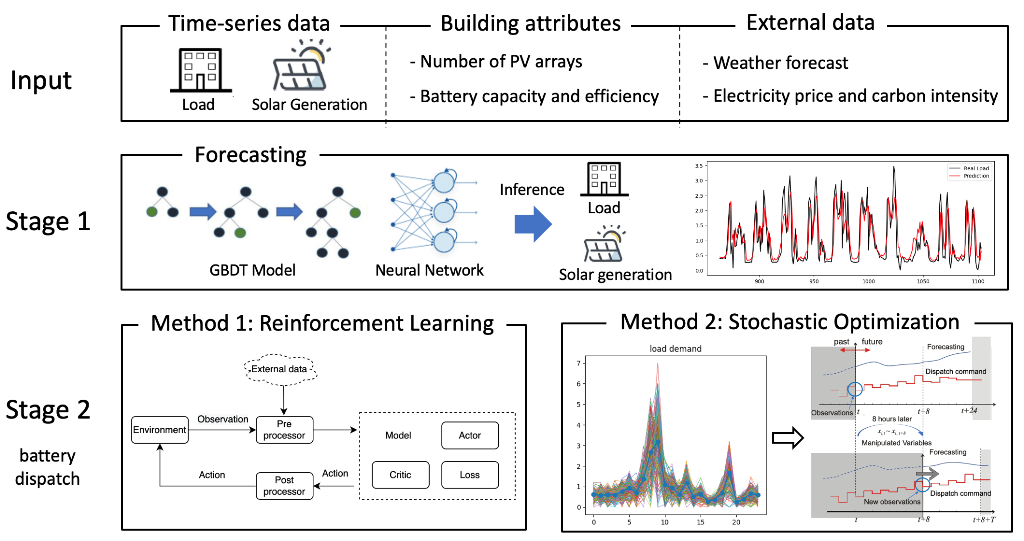
1. Introduction

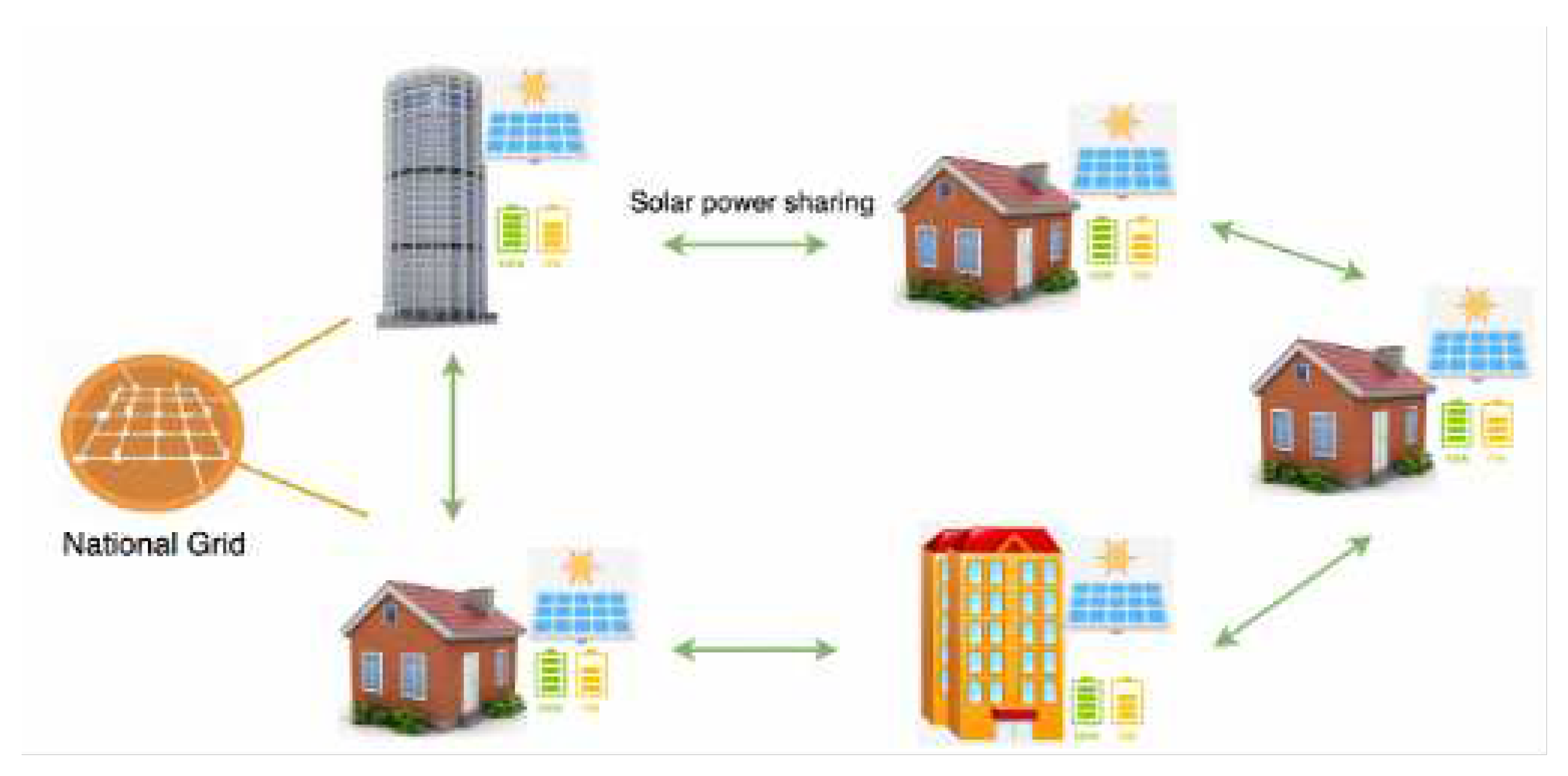
Nowadays, with the rapid development of artificial intelligence (AI), household appliances and equipment intelligence are gradually popularized. More and more families are installing home solar power generation equipment and small-scale energy storage equipment, not only to meet their own electricity needs but also to sell excess power through the sharing network. If we can make home electricity use more efficient, then the community power grid will be more economical and low-carbon. Furthermore, the efficient and stable of community power gird can provide a guarantee for the stability of the national power grid.

Electricity research generally includes Large-scale Transmission Grids (short for LTG) and Small-scale Micro-Grids (short for SMG). LTG focuses on high-voltage and long-distance power transmission, while SMG focuses on electricity consumption in small areas such as schools, factories, or residential areas. We focus on smart scheduling techniques in SMG. For example, Figure 1 shows a case of SMG. Households can generate electricity from solar energy, store the excess power and share with neighbors on the grid network (green arrows). When neither self-generated power nor shared network can provide enough electricity, power is supplied by the national grid (orange lines). The national grid generates electricity through wind power, hydroelectric and thermal. The cost of electricity and carbon emissions vary over time. In this paper, we use an AI-based approach to enable efficient scheduling of household storages. The AI-based scheduling method leads to economical and decarbonized electricity use.

In the power generation process, increasing the proportion of new energy sources is one of the important methods to reduce carbon emissions. The use of new energy sources, such as wind power and solar power, reduces carbon emissions for the grid network, but adds more uncertainty to the entire power network. For example, solar power generation is affected by the weather, and if future weather changes cannot be accurately predicted, then this will affect the scheduling program of other power generation methods in the power network. Uncertainty in new energy generation poses a great challenge to traditional dispatch systems /citecamacho2013model,olivares2014trends. We categorize the uncertainty as Data drift: the relation between input data and the target variables changes over time [1]. For example, the sequential transition in time-series of renewable energy generation can be fluctuated (e.g., wind power and solar power).

For the problem of uncertainty, classical methods, such as model predictive control (MPC), use rolling control to correct the parameters by realizing the feedback of rolling [2,3]. However, the effect is not up to expectation in practical applications. Taking industrial application as an example, the sequential MPC framework can usually be decomposed into point prediction of target variables (e.g., solar power generation), followed by deterministic optimization, which is unable to capture the uncertainty of probabilistic data distribution [4,5]. To solve the above problems, stochastic-based methods have been proposed, and they are able to eliminate the effects caused by some uncertainties.

Taking into account the uncertainty in forecasting, it is possible to improve energy efficiency by 13% to 30% [6,7]. Stochastic-based methods mainly include two types, one that requires prior knowledge of system uncertainty [8,9], and another that is based on scenarios, generating values for multiple random variables [10,11]. Additionally, adaptive methods are also applied in the presence of uncertainty [12,13,14]. In this paper, better generalization capability is achieved by combining stochastic optimization with online adaptive rolling updates.

Despite some recent progress, it is difficult for the existing system to meet the demand of real-time scheduling due to the huge number of SMGs and high model complexity. Under the requirement of real-time scheduling, the attempt of reinforcement learning in power grids is gradually emphasized.

Reinforcement learning has been proven to give real-time decisions in several domains and has the potential to be effectively applied in the power grid scenarios. In Large-scale Transmission Grids (LTG), reinforcement learning has not yet been successfully applied due to security concerns. In Small-scale Micro-Grids (SMG), where economy is more important (security can be guaranteed by the up-level grid network), reinforcement learning is gradually starting to be tried. In reinforcement learning, the model learns by trial and error through constant interaction with the environment [15], and ultimately obtains the best cumulative reward. Training for reinforcement learning usually relies on a simulation environment, which is assumed to be provided in this paper. Unlike the existing single agent approach, in this paper, we propose a multi-agent reinforcement learning method to adapt grid scheduling task. The main contributions in this paper are:

• To adapt to uncertainty, we propose two modules to achieve robust scheduling. One module combines deep learning-based prediction techniques with stochastic optimization methods, while the other module is an online data augmentation strategy, including stages of model pretraining and finetuning.
• In order to realize sharing rewards among buildings, we propose to use multi-agent PPO to simulate each building. Addition, We provide the ensemble method between reinforcement learning and optimization methods.
• The proposed method won the 1st place of the NeurIPS Challenge Competition. We conduct extensive experiments on real-world scenario and the results demonstrate the effectiveness of our proposed framework.

2. Problem Statement

Generally, SMG contains various type of equipments, including solar generation meachines (denoted as $\mathcal{G}$), storage devices (denoted as $\mathcal{S}$), other user devices (denoted as $\mathcal{U}$). $\mathcal{M}$ denotes the matkets, such as carbon and electricity. The total decision steps is set to T. We define the load demand of user as: $L_{u,t}$, where step $t\in \mathcal{T}=\{1,\dots ,T\}$ and $u\in \mathcal{U}$. $p_t$ is the market price as time t per unit or the average price among $\mathcal{M}$.

The variables in SMG include electricity need from national gird (denoted as $P_{\mathrm{grid},t}$), the power generation of device $g\in \mathcal{G}$ (denoted as $P_{g,t}$), the charging or discharging of storage(denoted as $P_{s,t}^{+}$ or $P_{s,t}^{-}$) and the state of charge of device $s\in \mathcal{S}$ (denoted as $E_{s,t}$). We define the decision variables as: $X=\{P_{\mathrm{grid},t},P_{g,t},P_{s,t}^{+},P_{s,t}^{-},E_{s,t}\}$, where $t\in \mathcal{T}$, $s\in \mathcal{S}$, $g\in \mathcal{G}$, then the objective is to minimize the total cost of all markets, which defined as:

$$\underset{X}{\mathrm{minimize}}\sum _{t=1}^T{p}_t·P_{\mathrm{grid},t}$$

(1)

s.t.:

$$\begin{array}{ccc}\hfill & P_{\mathrm{grid},t}\ge 0\hfill & \hfill t\in \mathcal{T}\end{array}$$

(1a)

$$\begin{array}{ccc}\hfill & P_{g,t}^{\min }\le P_{g,t}\le P_{g,t}^{\max }\hfill & \hfill g\in \mathcal{G},t\in \mathcal{T}\end{array}$$

(1b)

$$\left.\begin{array}{cc}\hfill & 0\le P_{s,t}^{+}\le {P_{s,t}^{+}}^{\max }\hfill \\ \hfill & 0\le P_{s,t}^{-}\le {P_{s,t}^{-}}^{\max }\hfill \\ \hfill & P_{s,t}^{+}·P_{s,t}^{-}=0\hfill \end{array}\right\}s\in \mathcal{S},t\in \mathcal{T}$$

(1c)

$$\begin{array}{ccc}\hfill & E_{s,t}^{\min }\le E_{s,t}\le E_{s,t}^{\max }\hfill & \hfill s\in \mathcal{S},t\in \mathcal{T}\\ \hfill & E_{s,t}=E_{s,t-1}+P_{s,t}^{+}-P_{s,t}^{-}\hfill & \hfill s\in \mathcal{S},t\in \mathcal{T}\setminus \left\{1\right\}\end{array}$$

(1d)

$$P_{\mathrm{grid},t}+\sum _{g\in \mathcal{G}}{P}_{g,t}+\sum _{s\in \mathcal{S}}{P}_{s,t}^{-}=\sum _{s\in \mathcal{S}}{P}_{s,t}^{+}+\sum _{u\in \mathcal{U}}{L}_{u,t}t\in \mathcal{T}$$

(1e)

To facilitate the understanding of the above constraints, we explain each formula with details:

(1a)

Electricity need bounds from national grid: larger than zero and without upper bounds;

(1b)

($P_{g,t}^{\min }$) denotes the lower bound of electricity generation device, such as solar generation, while the ($P_{g,t}^{\max }$) denotes the upper one.

(1c)

(${P_{s,t}^{+}}^{\max }$) represents the upper limit for battery/storage charging at timestamp t, while (${P_{s,t}^{-}}^{\max }$) represents the upper limit for discharging.

(1d)

$E_{s,t}^{\min }$ represents the lower value of soc (state of charge), while $E_{s,t}^{\max }$ denotes the upper one; And the seconde equation denotes the updating of the soc;

(1e)

This equation makes sure the power grid is stale (the sum of power generation is equal to the sum of power consumption).

In practical application scenarios, it is not possible to obtain exact data on market prices, new energy generation and user loads in advance when conducting power scheduling. Therefore, it is necessary to predict these values before making decisions. In the following, we will provide a detailed introduction to our solution.

3. Framework

3.1. Feature Engineering

Feature engineering provides input for the subsequent modules, including the forecasting module, reinforcement learning module, and optimization method module. We extract features for each building (the detailed building information will be introduced in the subsequent dataset section). Due to the different scales of features, we normalize all features X as follows:

$$x^{new}=\frac{x^{old}}{max\left(X\right)-min\left(X\right)+ϵ}$$

(2)

where $x^{new}$ is the normalized output, $max\left(X\right)$ denotes the max value of each domain, while $min\left(X\right)$ represents the minimum, and $ϵ$ is a value that prevents the denominator from being zero.

Moreover, to eliminate the influence of some outliers, we also performed data denoising processes as:

$$x^{new}=\left\{\begin{array}{cc}(1+\alpha )\ast avg\left(X\right),\hfill & \mathrm{if}{x}^{old}\ge (1+\alpha )\ast avg\left(X\right)\hfill \\ (1-\alpha )\ast avg\left(X\right),\hfill & \mathrm{if}{x}^{old}\le (1-\alpha )\ast avg\left(X\right)\hfill \\ x^{old},\hfill & \mathrm{else}\hfill \end{array}\right.$$

(3)

where $\alpha$ is a pre-set adjustable parameter, $avg\left(X\right)$ represents the average value of the feature. We truncate the outliers that exceed a certain percentage of the average value.

We show the key feature components of continuous modules. For forecasting module:

• The user loads of past months;
• The electricyty generation of past months;
• The radiance of solar direct or diffuse;
• Detailed time including the hour of the day, the day of the week and the day of the month;
• The forecasting weather information including the values of humidity, temperature, and so on;

For reinforcement learning module and optimization method module:

• The key components detailed before;
• The predictions of user load and electricity generation;
• The number of solar generation units in each building;
• The efficiency and capacity of the storage in each building;
• Market prices including the values fo electricity and carbon;

3.2. Deep Learning-based Forecasting Model

As shown in Figure 5 (a), deep learning-based forecasting module generates the corresponding input data for next modules, including optimization method module (or reinforcement learning module). The target variables include user load (denoted as $L_{u,t}$), market prices (denoted as $p_t$) and capacity of solar generation (denoted as $P_{g,t}^{\max }$). The input features of the forecasting models are listed in Feature Engineering part before.

In sequence prediction tasks, deep neural network methods have gradually become state-of-the-art (SOTA). Gated Recurrent Unit (short for GRU) is one of the most commonly-applied types of recurrent neural network with a gating mechanism [16]. We employ recurrent neural network (RNN) with a GRU in our approach. Additionally, our framework can easily adapt to any other neural networks, including CNNs and transformers. Compared to other variants of recurrent networks, RNN shows well performance in small datasets with gated mechanism [17]. Thus, when given the input sequence $x=(x_1,\dots ,x_T)$, the RNN we used is described as:

$$h_t={\varphi }_1\left(h_{t-1},x_t\right),y_t={\varphi }_2\left(h_t\right),t\in \mathcal{T}.$$

where $h_t$ denotes the hidden state of RNN at time t, $y_t$ denotes the corresponding output, ${\varphi }_1$ and ${\varphi }_2$ represent the non-linear functions (active function or the combination with affine transformation). Fitting maximum likelihood on the training data, the model is able to predict $f_{L_u}$, $f_p$ and $f_{P_g}$, corresponding to user load, market prices and capacity of solar generation, respectively. Moreover, since each of our modules is decoupled, it is easy to incorporate the predictions of any other forecasting methods into the framework easily.

3.3. Reinforcement Learning

In most scenarios, reinforcement learning can provide real-time decision-making, but the safety of these decisions cannot be guaranteed. Therefore, reinforcement learning has not been practically applied in LTG. However, SMG serves as a good testing ground for reinforcement learning. Due to the fact that SMG does not require the calculation of power flow in the network, in training process, the interaction between the agent and the simulation environment can be conducted within a limited time. Since its proposal, Proximal Policy Optimization (PPO) [15] has been validated to achieve good results in various fields. Therefore, here we model and adapt the power grid environment based on PPO method.

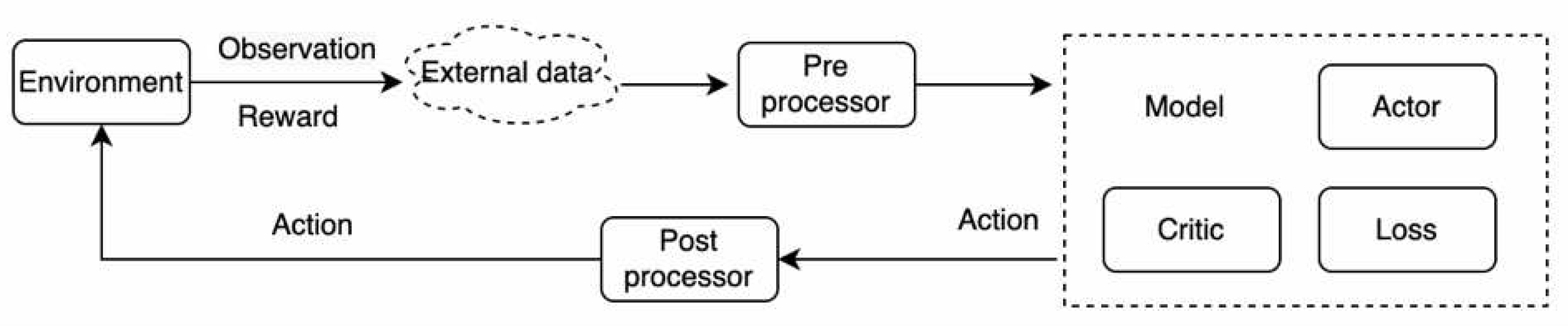
The reinforcement learning framework, as shown in Figure 2, we used for SGM mainly includes several parts: simulation environment module, external data input module, data preprocessor module, model module, and result postprocessor module. The simulation environment simulates and models the microgrid, mainly using past years’ real data for practice simulations. External input data includes real-time climate information obtained from websites. The data preprocessor filters and normalizes the observed data. The model module consists of multi-agent PPO, which includes multiple neural network modules and loss function design. The final result postprocessor module handles the boundaries of the model’s output, such as checking whether the output of the generator exceeds the physical limits.

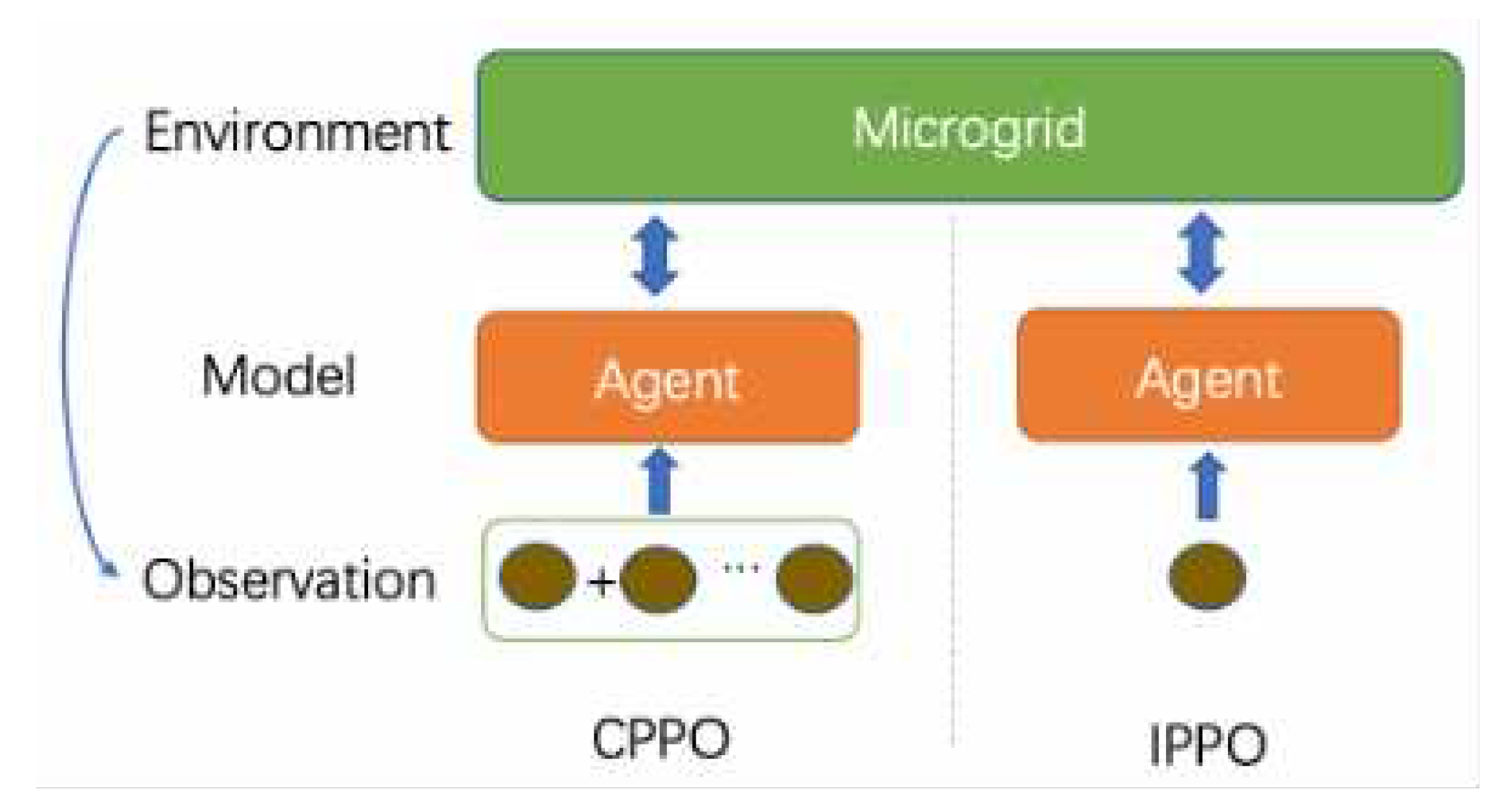
Most existing applications of reinforcement learning focus on single-agent methods, including centralized PPO (short for CPPO) and individual PPO (short for IPPO) [18]. As shown in the Figure 3, CPPO learns the model by consolidating all inputs and interacting with the SMG. On the other hand, IPPO involves independent inputs for multiple learning instances. In the case of a SMG, each input represents a generation or consumption unit, such as a building.

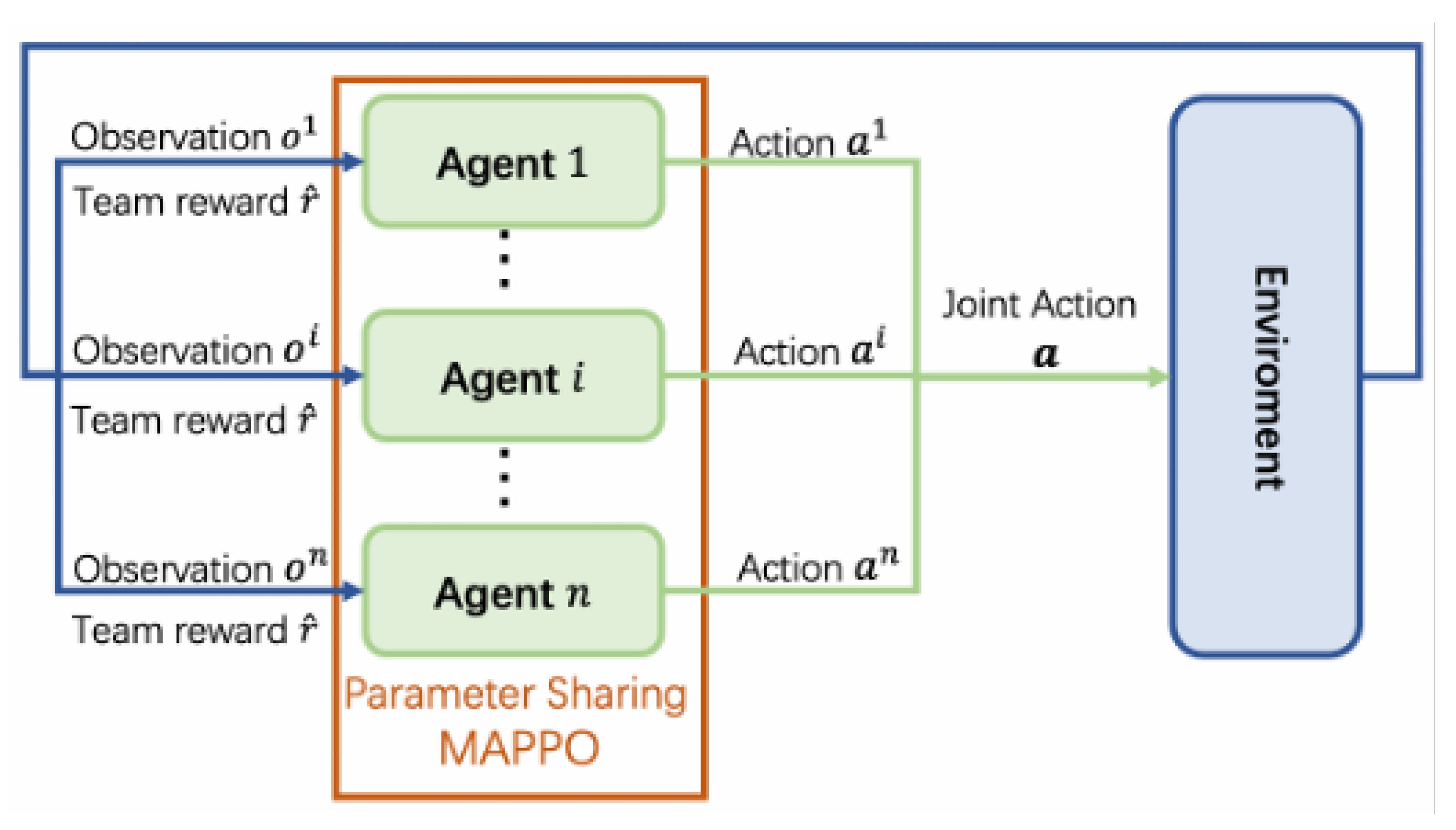
In practical scenarios, there are various types of SMG, including factories, residential communities, schools, hospitals, etc. Therefore, the framework should be able to adapt to different types of SMG. The CPPO method mentioned above concatenates all inputs as one input each time, which cannot be applied to SMG with different inputs. For example, a model trained on a school SMG with 10 teaching buildings cannot be quickly adapted and applied to a school SMG with 20 teaching buildings. To address this issue, the IPPO method is introduced, which allows all teaching buildings to be inputted into the same agent in batches. However, in actual SMG, information sharing among teaching buildings is crucial. For example, the optimal power scheduling plan needs to be achieved through sharing solar energy between teaching buildings in the east and west. Since IPPO only has one agent, it cannot model the information sharing. Based on this, we propose a multi-agent PPO model to address the information sharing problem in SMG.

As shown in the Figure 4, in the MAPPO framework, taking a school microgrid as an example, each agent represents a building, and each building has its own independent input. Additionally, the main model parameters are shared among all the buildings. If set ${\pi }^i\left(a^i\right|{\tau }^i)$ as an agent model, the joint model is: $\pi \left(a\right|s):={\prod }_{i=1}^n{\pi }^i\left(a^i\right|{\tau }^i)$, where n denotes the number of teaching building. The expected discounted accumulated reward is defiend as:

$$J\left(\pi \right)={\mathbb{E}}_{\pi }\left[{\sigma }_{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t,s_{t+1})\right]$$

(4)

where $\gamma$ represents the discount ratio, R is the reward, and $s_t={\left[o_{(}t\right)}^1,\dots ,o_t^n,a_t,{\widehat{r}}_t]$ is current state of the whole system.

3.4. Optimization

3.4.1. Stochastic Optimization

In the deep learning forecasting module, we have trained models that can predict user load (${\widehat{L}}_{u,t}$), market prices (${\widehat{p}}_t$), and the capacity of solar generation (${\widehat{P}}_{g,t}^{\max }$). In the validation dataset, we obtain the deviations of the models for these predictions, and their variances are denoted as $\widehat{\Sigma }{L}_u$, $\widehat{\Sigma }p$, and ${\widehat{\Sigma }}_{P_g}$, respectively. These values represent the level of uncertainty. To mitigate the impact of uncertainty, we propose a stochastic optimization method as shown in Figure 5 (b). We use the predicted values as means and uncertainty as variances, for example, ($\widehat{P}{g,t}^{\max }$, $\widehat{\Sigma }{P}_g$), ($\widehat{L}u,t$, $\widehat{\Sigma }{L}_u$) and ($\widehat{p}t$, $\widehat{\Sigma }p$), to perform Gaussian sampling. Through Gaussian sampling, we can obtain multiple scenarios, which are considered as a multi-scenario optimization problem. Assuming we have N scenarios, the n-th scenario can be represented as ($n\in {\mathcal{S}}_{\mathcal{N}}$):

$$\begin{array}{cc}\hfill {\left({\tilde{P}}_g^{\max }\right)}^n& =\left[{\left({\tilde{P}}_{g,1}^{\max }\right)}^n,{\left({\tilde{P}}_{g,2}^{\max }\right)}^n,\dots ,{\left({\tilde{P}}_{g,T}^{\max }\right)}^n\right],\hfill \\ \hfill {\left({\tilde{L}}_u\right)}^n& =\left[{\left({\tilde{L}}_{u,1}\right)}^n,{\left({\tilde{L}}_{u,2}\right)}^n,\dots ,{\left({\tilde{L}}_{u,T}\right)}^n\right],\hfill \\ \hfill {\left(\tilde{p}\right)}^n& =\left[{\left({\tilde{p}}_1\right)}^n,{\left({\tilde{p}}_2\right)}^n,\dots ,{\left({\tilde{p}}_T\right)}^n\right].\hfill \end{array}$$

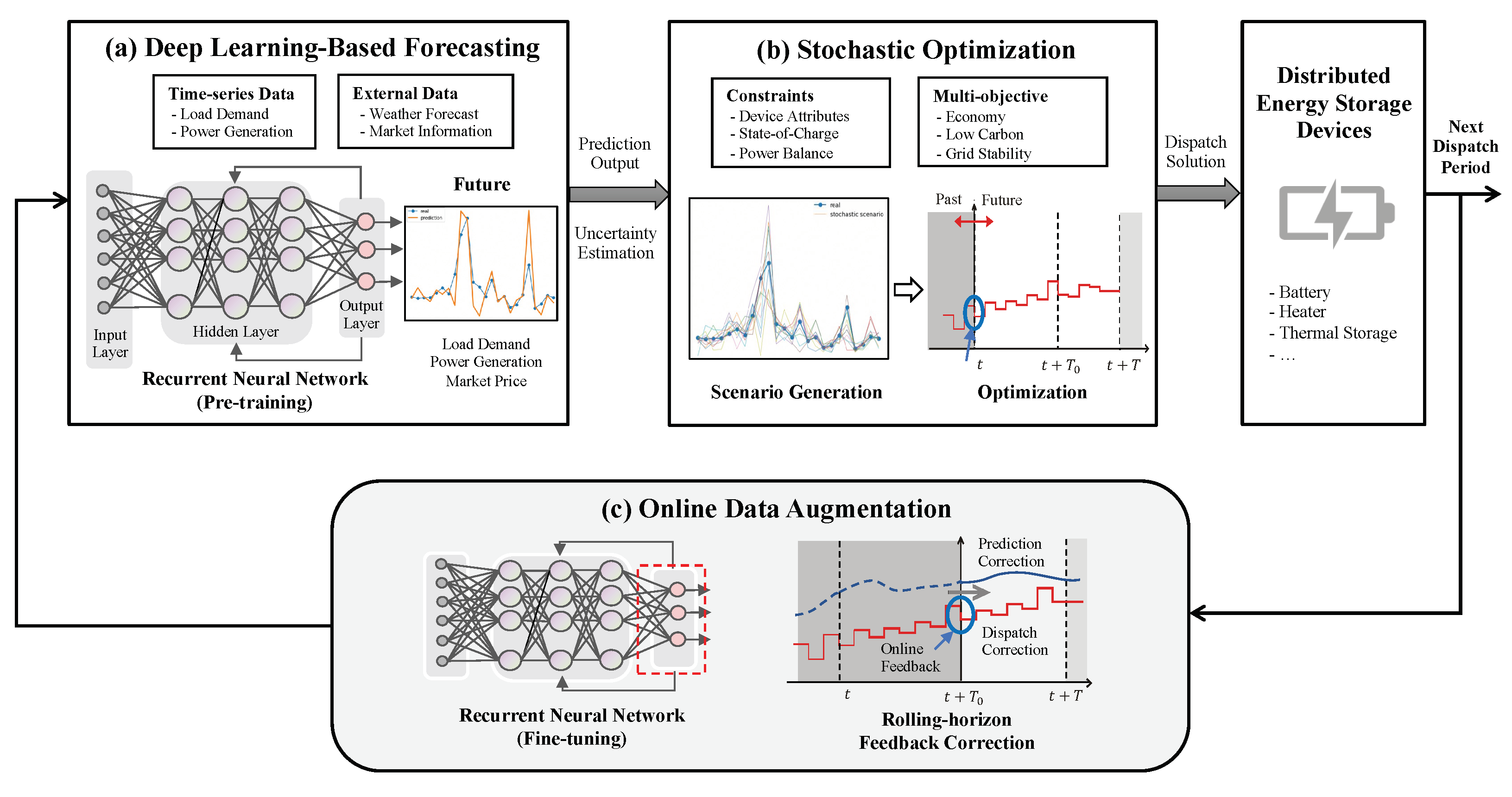
Figure 5. The whole Optimization method framework. The subplot (a) represents the flowchart of prediction based on deep learning. The output of the prediction module serves as the input for the stochastic optimization module, as shown in (b). During the scheduling process, real-time data accumulates over time, and we update the predictions based on the real data, as demonstrated in (c), named the online data augmentation module. This framework enhances the robustness of scheduling under uncertain conditions.

Figure 5. The whole Optimization method framework. The subplot (a) represents the flowchart of prediction based on deep learning. The output of the prediction module serves as the input for the stochastic optimization module, as shown in (b). During the scheduling process, real-time data accumulates over time, and we update the predictions based on the real data, as demonstrated in (c), named the online data augmentation module. This framework enhances the robustness of scheduling under uncertain conditions.

Then, the objective function in our proposed stochastic optimization can be re-defined with:

$$\underset{X}{\mathrm{minimize}}\sum _{t=1}^T{\mathbb{E}}_{n\in {\mathcal{S}}_{\mathcal{N}}}{\left({\tilde{p}}_t\right)}^n·P_{\mathrm{grid},t}.$$

(5)

Constraint (1b) is refined as:

$$P_{g,t}^{\min }\le P_{g,t}\le {\left({\tilde{P}}_{g,t}^{\max }\right)}^{n}n\in {\mathcal{S}}_{\mathcal{N}},g\in \mathcal{G},t\in \mathcal{T}.$$

Constraint (1e) is refined as:

$${\displaystyle P_{\mathrm{grid},t}+\sum _{g\in \mathcal{G}}{P}_{g,t}+\sum _{s\in \mathcal{S}}{P}_{s,t}^{-}=\sum _{s\in \mathcal{S}}{P}_{s,t}^{+}+\sum _{u\in \mathcal{U}}{\left({\tilde{L}}_{u,t}\right)}^{n}n\in {\mathcal{S}}_{\mathcal{N}},t\in \mathcal{T}.}$$

Through solving the stochastic optimization problem (5), we get the scheduling plan: $\dot{X}=\{{\dot{P}}_{\mathrm{grid},t},{\dot{P}}_{g,t},{\dot{P}}_{s,t}^{+},{\dot{P}}_{s,t}^{-},{\dot{E}}_{s,t}\}$ .

3.4.2. Online Data Augmentation

In order to address the data drift problem, we propose the data augmentation method as shown in Figure 5 (c). The module contains two parts: pre-training/fine-tuning Scheme and rolling-horizon feedback correction.

Pre-training/Fine-tuning Scheme

In practice, the real-time energy dispatch processes as a periodic task (e.g., daily dispatch). Considering that the prediction models are trained based on historical data and future data may not necessarily follow the same distribution as the past, we perform online data augmentation. Online data augmentation consists of two parts: pre-training and fine-tuning. Firstly, we pre-train the neural network model using historical data to obtain a model capable of predicting $f_{L_u}$, $f_p$ and $f_{P_g}$. Secondly, we fine-tune the neural network using the accumulated online data. Specifically, in the fine-tuning process, we employ partial parameter fine-tuning to obtain the refined network ${\tilde{f}}_{L_u}$, ${\tilde{f}}_p$ and ${\tilde{f}}_{P_g}$.

Rolling-horizon Feedback Correction

In addition to updating the prediction models online, we also employ the rolling-horizon control technique. In the optimization process, we solve the optimization problem every horizon H (to incorporate the latest prediction models and trade-off computational time). This operation is repeated throughout the scheduling period.

4. Experiments

4.1. Experiment Setup

4.1.1. Dataset

We conducted experiments on building energy management using a real-world dataset from Fontana, California. The dataset includes one year of electricity scheduling for 17 buildings, including their electricity demand, solar power generation, and weather conditions. This dataset was also used for the NIPS 2022 Challenge. With our proposed framework, we achieved the global championship in the competition1.

4.1.2. Metric

We follow the evaluation setup of the competition. The 17 buildings are divided into visible and invisible data. The visible data is used as the training set, while the invisible data includes the validation set and the testing set. The final leaderboard ranking is based on the overall performance of the model on all data sets. The evaluation metrics include carbon emissions, electricity cost, and grid stability. Specifically, the electricity consumption of each building i is calculated as $E_{i,t}=L_{i,t}-P_{i,t}+X_{i,t}$, where $L_{i,t}$ represents the load demand at timestamp t, $P_{i,t}$ represents the solar power generation of the building, and $X_{i,t}$ represents the electricity dispatch value provided by the model. The electricity consumption of the entire district is denoted as $E_t^{\mathrm{dist}}={\sum }_{i=1}^I{E}_{i,t}$.

Using the above notations, three metrics are defined as:

$$\begin{array}{cc}\hfill C_{\mathrm{Emission}}=& \sum _{t=1}^T\left(\sum _{i=1}^{I}max\left(E_{i,t},0\right)\right)·c_t,C_{\mathrm{Price}}=\sum _{t=1}^{T}max\left(E_t^{\mathrm{dist}},0\right)·p_t,\hfill \\ \hfill C_{\mathrm{Grid}}=& \frac{1}{2}\left(C_{\mathrm{Ramping}}+C_{\mathrm{Load}\mathrm{Factor}}\right)\hfill \\ \hfill =& \frac{1}{2}\left(\sum _{t=1}^{T-1}\left|E_{t+1}^{\mathrm{dist}}-E_t^{\mathrm{dist}}\right|+\sum _{m=1}^{\#\mathrm{months}}\frac{{\mathrm{avg}}_{t\in \left[\mathrm{month}m\right]}{E}_t^{\mathrm{dist}}}{{\max }_{t\in \left[\mathrm{month}m\right]}{E}_t^{\mathrm{dist}}}\right).\hfill \end{array}$$

4.1.3. Baseline

To evaluate the proposed MAPPO, Optimization, and their Ensemble method, we compare them with the following baseline methods:

• RBC: Rule-Based Control method. We tested several strategies and selected the best one: charging the battery by 10% of its capacity between 10 a.m. to 2 p.m., followed by discharging it by the same amount between 4 p.m. to 8 p.m..
• MPC [19]: A classical Model-Predictive-Control method. A GBDT-based model [20] is used to predict future features, and a deterministic optimization is used for daily scheduling.

Moreover, after the competition, we compare the proposals of several top-ranked contestants:

• AMPC [19]: An adaptive Model-Predictive-Control mehtod.
• SAC [21]: A Soft Actor-Critic mehtod that uses all agents with decentralization.
• ES [22]: Evolution-Strategy mehtod with adaptive covariance matrix.

4.1.4. Implementations

The environment simulator that reinforcement learning and evaluation process used is provided by the competition organizers [23]. The learning of deep learning networks is implemented using PyTorch. The optimization problem-solving utilizes our self-developed MindOpt [24]. All experiments are conducted on a Nvidia Tesla V100 GPU with 8 cards.

4.2. Results

If only one metric is considered, any of the three metrics can be performed very well singlely. Therefore, the final effect needs to be seen in terms of the average value of the three metrics. Since the performce is compared with no use of storage, a lower value indicates a better performce. Our proposed MAPPO method and Optimization method both achieve better results than other competitors.

As shown in the Table 1, the individual model has limited performance. By combining reinforcement learning and optimization, we can achieve the best results. Through observing the validation dataset, we found that reinforcement learning and optimization perform alternately in different months. By leveraging their advantages, we fuse their results based on the month to create a yearly schedule (named Ensemble), ultimately obtaining the best outcome.

4.3. Ablation Studies

We conducted ablation Studies on some modules to understand their contributions to the overall performance.

4.3.1. Analysis of Online Data Augmentation

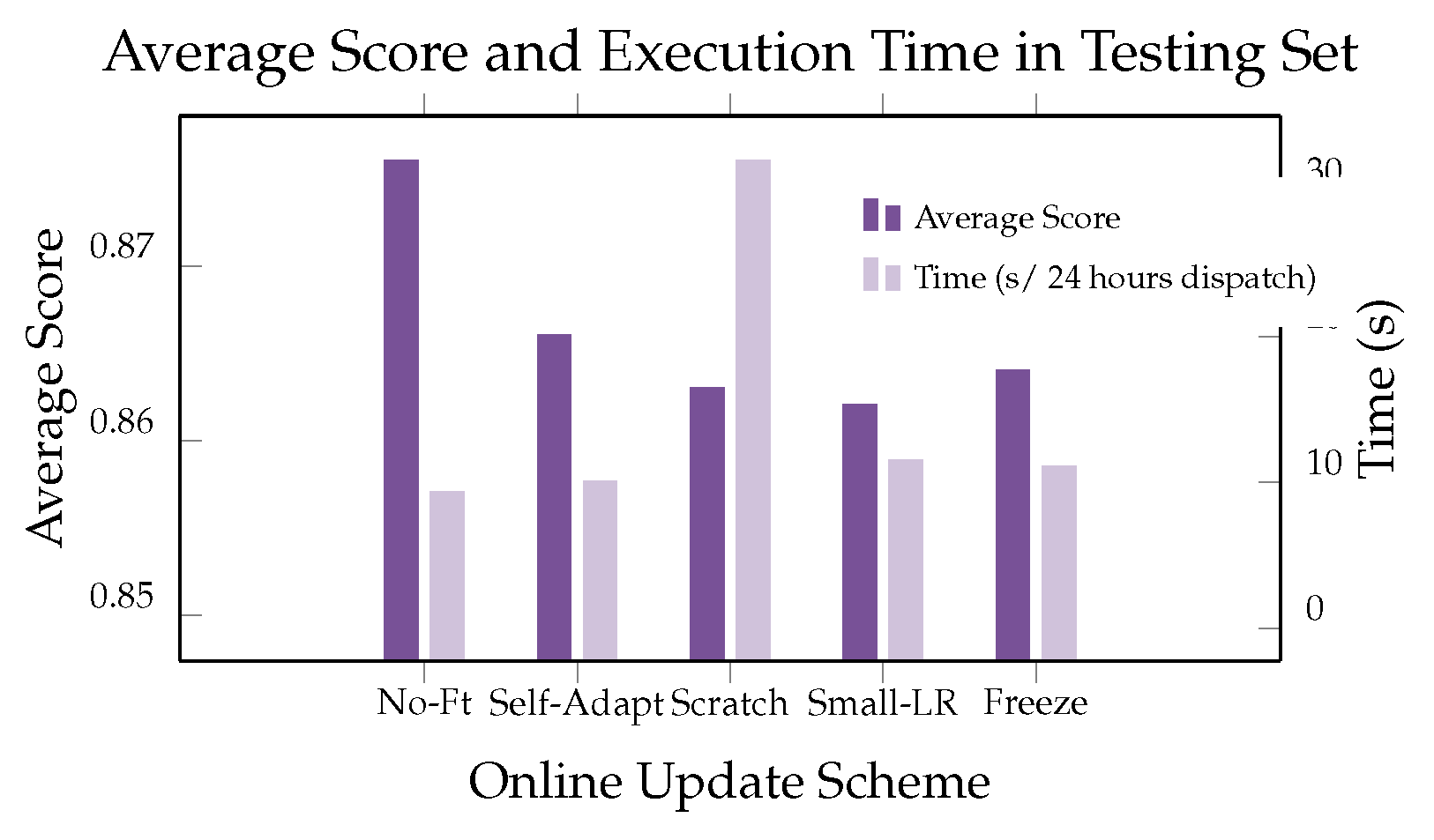
We compare the performances of different online update methods, as shown in Figure 6: No-Ft: No fine-tuning on online data; Self-Adapt: Adaptive linear correction by minimizing the mean squared error between historical value and predicted value; Scratch: Re-learning from scratch; Small-LR: Continuous learning with a smaller learning rate; Freeze: Continuous learning with online data, but freezing the weights of the first few layers and only updating the last layer. To compare the efficiency of the models, we evaluate the average execution time of real-time scheduling within 24 hours.

Results show that fine-tuning with a smaller learning rate has advantages in terms of efficiency and effectiveness.

4.3.2. Analysis of Forecasting Models

As shown in Table 2, we evaluated different forecasting models. The evaluation metrics include overall scheduling performance, execution time, and forecasting performance measured by the weighted mean absolute percentage error (short for WMAPE). The experimental results indicate that the RNN model with online fine-tuning achieves the best performance.

4.3.3. Analysis of Stochastic Optimization

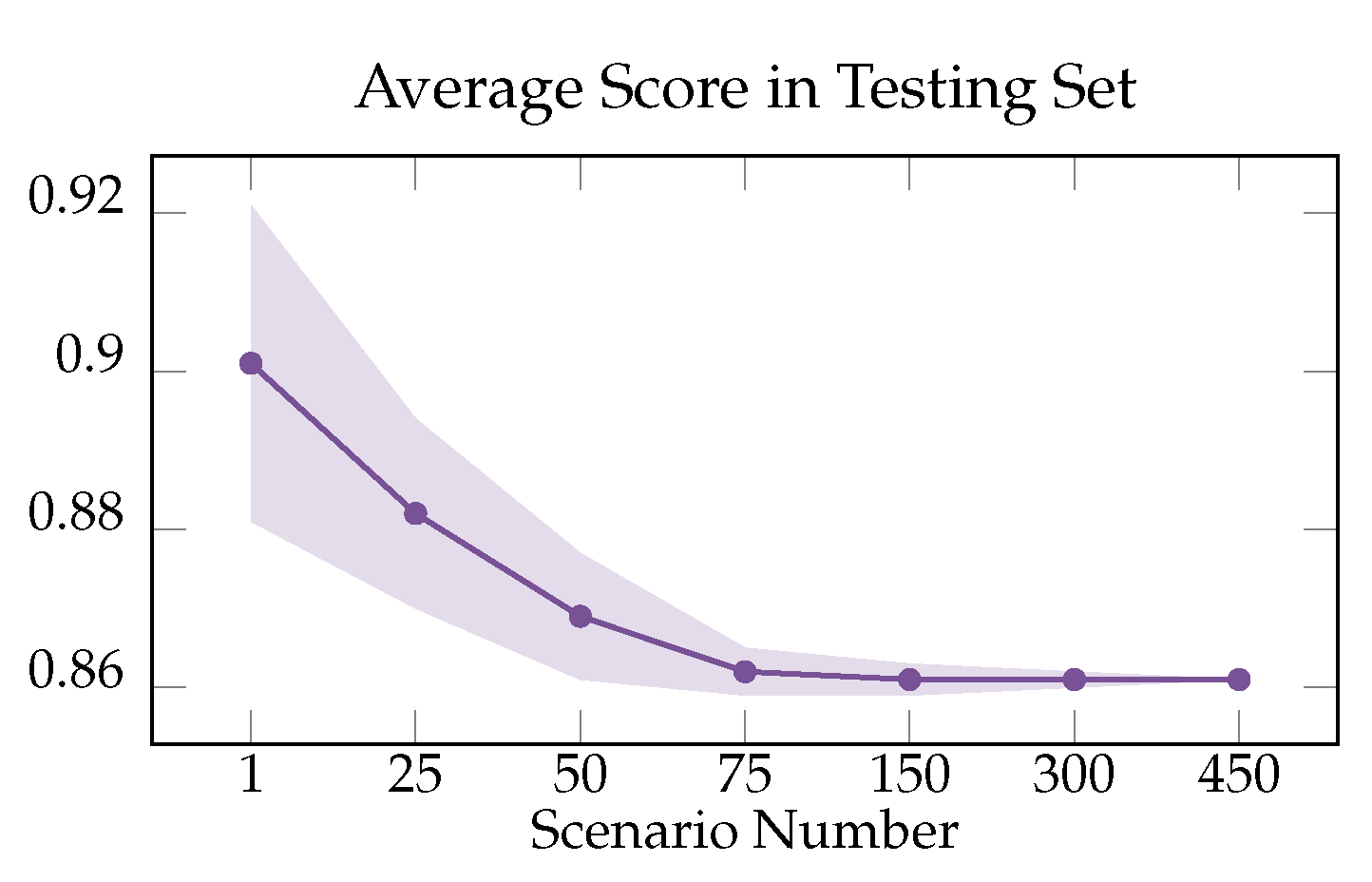
In stochastic optimization, the number of scenarios is a very important parameter. As shown in Figure 7, as the number of scenarios increases, the effectiveness of the model also gradually increases. This is in line with common sense, as a model that can cover more scenarios tends to have better performance.

5. Conclusion

The challenge of power gird scheduling is to handle a complex long-term decision-making task. One of the most important things we learned is that, it is difficult to achieve end-to-end learning with a single strategy for a complex problem. The key information for decision-making is the future load and solar energy generation. We found that using pre-trained auxiliary task to learn representation and prediction ahead of optimization and reinforcement learning, outperforms the way of directly feeding all the data into the decision model. We use optimization and multi-agent reinforcement learning algorithms for decision making. The optimization algorithm can achieve better generalization on unknown dataset through target approximation, data augmentation, and rolling-horizon correction. Multi-agent reinforcement learning can better model the problem and find better solutions on known dataset. In energy management tasks, how to perform data augmentation to improve the generalization ability is a problem worthy of research. We also found that the policies learned by optimization algorithm and reinforcement learning performed differently in different months, which also prompted us to use ensemble learning.