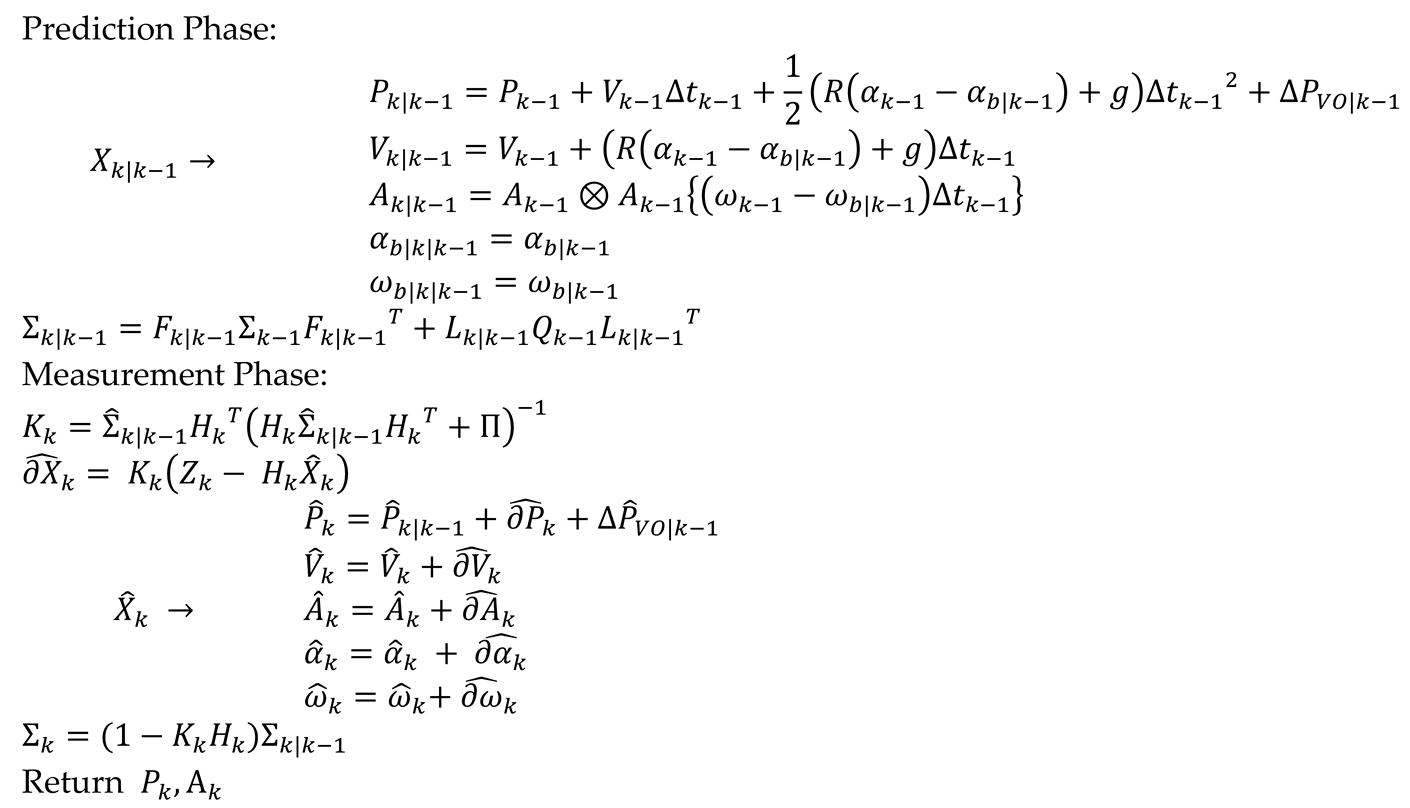Prerpints.org logo
Preprint
Article

Integrating GRU with Kalman Filter to Enhance Visual Inertial Odometry Performance in Complex Environments

Altmetrics

Downloads

153

Views

48

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 September 2023

Posted:

28 September 2023

You are already at the latest version

Alerts
Abstract
To enhance system reliability and mitigate vulnerabilities of the Global Navigation Satellite Systems (GNSS), it is common to fuse the Inertial Measurement Unit (IMU) and visual sensors with the GNSS receiver in the navigation system design, effectively enabling compensations with absolute position and reducing data gaps. To address shortcomings of traditional Kalman Filter (KF) such as sensor error, imperfect nonlinear system model, and KF estimation error, a GRU-aided ESKF architecture is proposed to enhance positioning performance. This study conducts Failure Mode and Effect Analysis (FMEA) to priories and identify the potential faults in the urban environment facilitating the design of improved fault-tolerant system architecture. The identified primary fault events are data association error and navigation environment error during fault conditions of feature mismatch, especially in the presence of multiple failure modes. A hybrid federated navigation system architecture is employed using a Gated Recurrent Unit (GRU) to predict state increments for updating the state vector in the Error Estate Kalman Filter (ESKF) measurement step. The proposed algorithm’s performance is evaluated in a simulation environment in MATLAB under multiple visually degraded conditions. Comparative results provide evidence that the GRU-aided ESKF outperforms standard ESKF and state-of-the-art solutions like VINS-Mono, End-to-End VIO, and Self-Supervised VIO, exhibiting higher efficiency in complex environments.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

In recent years, unmanned aerial vehicles (UAVs) have gained attraction having the evolution of technologies such as artificial intelligence and computer vision which has effectively broadened pathways for diverse applications and services. UAVs have been utilized in many civil applications, such as aerial surveillance, package delivery, precision agriculture, search and rescue operations, traffic monitoring, remote sensing, and post-disaster operations [1]. The increasing demand for commercial UAVs for such applications has highlighted the need for robust, secure, and accurate navigation solutions. However, achieving accurate and reliable UAV positioning in complex environments, including overpasses, urban canyons, illumination variability, etc. has become more challenging.
Although Global Navigation Satellite System (GNSS) has become one of the most popular navigation systems over the past decades, the utilization of GNSS remains suspicious due to its vulnerability to satellite visibility, interference of jamming and spoofing, as well as environmental effects such as multipath, building masks, ionospheric and tropospheric delays. Furthermore, the effects will lead to sharp deteriorations in the positioning precision and GNSS availability [2]. The inertial navigation system (INS) facilitates the provision of high-frequency and continuous position, velocity, and attitude information which makes the integration of INS with GNSS prevalent in most navigation architecture designs. However, the drift error generated from INS accumulates over time which will result in divergent positioning output. The impact of INS drifting on GNSS/INS fusion performance in the case of long-term GNSS outages has been explored widely [3,4,5]. Nevertheless, more variety of sensor types is still in demand to provide higher resilient and accurate positioning resolutions under complex operation scenarios.
The vision-based navigation system is a promising alternative for providing reliable positioning information without radio frequency interference effects during GNSS outages. Visual odometry (VO) is frequently employed as a critical component in the vision-based navigation system due to efficient deployment with low computational complexity in contrast to Visual Simultaneous Localization and Mapping (VSLAM). It is discovered that purely VO-enabled navigation presents performance degradation caused by factors such as illumination, motion blur, field of view, moving objects, and texture environment [6]. Therefore, the advanced navigation solution combined with VO, GNSS, and INS measurements is prominent to reduce the above degradation factors to enhance outdoor positioning performance against satellite scarcity scenarios.
The Visual Inertial Navigation Systems (VINS) have been fully explored by researchers, encompassing notable examples like VINS-Mono [7], MSCKF [8], ORB-SLAM3 [9], and open-VINS [10]. As a common solution for improving navigation performance in terms of accuracy, integrity, update rate, and robustness through adding sensor types with GNSS, the VINS navigation system with multiple sensors integrated presents a higher possibility of existing multiple faults, noise, and sensor failures within the system. As a result, there is a need to explore fault-tolerant designs in the VINS navigation systems to mitigate the fault impact on the visual systems.
For achieving the fault tolerance capability in integrated multi-sensor systems, the decentralized filtering design especially using federated architecture become popular in recent years. Dan et al. [11] proposed an adaptive positioning algorithm based on a federated Kalman filter combined with a robust Error Estate Kalman Filter (ESKF) with adaptive filtering for the UAV-based GNSS/IMU/VO navigation system to eliminate issues of GNSS signal interruption and lack of sufficient feature points while navigating in indoor and outdoor environments. However, most papers using ESKF only measure VO faults by adding position errors whilst faults coming from visual cues like scarcity of features caused by environment complexity and motion dynamics, or high nonlinearity characteristics have not been fully taken into account. Therefore, there is a gap in detecting and identifying faults and threats with consideration of visual cues in the GNSS/IMU/VO navigation system.
Current state-of-the-art fault-tolerant GNSS/IMU/VO navigation systems encounter more difficulties when operating in complex scenarios due to the challenges of identifying visual failure modes and correcting VO errors. As a structured and systematic fault detection, exclusion, and mitigation method, Failure Mode and Effect Analysis (FMEA) is capable of detecting various fault types, defects, and sensor failures based on predicted and measured values as they occur instantly or shortly after they occur. FMEA is commonly used to assess risks to improve the reliability of complex systems using identifying and evaluating potential failures with the provision of occurrence likelihood, severity of impact, and detectability as well as prioritizing high-risk failure modes. However, researchers working on VIO discussed several faults caused by navigation environment or sensor error individually [6,12,13] but the identification of failure modes is a gap. Moreover, for their extracted failure modes, systematic faults have not been discovered with only consideration of single or specific combined faults like motion blur, rapid motion, and illumination variation.
To resolve the inherent non-linearity in the visual navigation system, AI has been employed with the Kalman filter to enhance the ability to model temporal changes in sensor data. Nevertheless, AI has the disadvantages of training time and predicted value inevitability containing errors that can be resolved partly by simplifying the neural network like Gradient Recurrent Unit (GRU) suppressed with ESKF fusion, enabling ESKF to better handle scenarios with verifying level of uncertainty and dynamic sensor conditions.
To implement a fault tolerance navigation system against the visually degraded environment, the paper proposes a GRU-aided ESKF VIO algorithm that conducts FMEA on the VINS system to identify failure modes and then assists the architecture of fault-tolerant multi-sensor system where the AI-aided ESKF VIO integration is used as one of the sub-filters to correct identified visual failure modes. The major contributions of this paper are highlighted as follows:
  • Proposition of a fault detection method on integrated VINS system with facilitation of FMEA. In the FMEA model, a wide range of fault types have been taken into account where the fault events include navigation environment, data association error, sensor model error, and user error.
  • Proposition of GRU to fuse with ESKF for predicting increments of positions to update measurements of ESKF, aiming to correct visual positioning errors leading to more accurate and robust navigation in challenging conditions.
  • Implementation of GRU-aided fault tolerant GNSS/IMU/VO navigation system for evaluating and validating the proposed VIO system performance. The verification is simulated and benchmarked on the Unreal engine where the environment includes complex scenes of sunlight, shadow, motion blur, lens blur, no-texture, light variation, and motion variation. The validation dataset is grouped into multiple zone categories in accordance with single or multiple fault types due to environmental sensitivity and dynamic motion transitions.
  • The performance of the proposed algorithm is compared with the state-of-the-art End-to-End VIO, and Self-supervised VIO by testing similar datasets on the proposed algorithm.
The remaining part of the paper is organized as follows. Section 2 discusses the existing systems designed based on a hybrid approach, Section 3 introduces the proposed GRU-aided KF-based federated GNSS/INS/VO navigation System, Section 4 discusses the experimental setup, Section 5, performs the roast test and result analysis comparison with state-of-the-art systems, and the conclusion is presented in Section 6.

2. Related Works

2.1. Kalman Filter for VIO

Kalman Filter (KF) along with its variations is a traditional method that proves to be efficient in fusing VO and IMU information. Despite its effectiveness, the KF faces certain challenges that can impact its performance. One of the main challenges in navigation applications arising from VO vulnerability is the interruption in updating KF observation, leading to a gradual decline in system performance over time. Moreover, if the error characteristics are non-gaussian and cannot be fully described within the model, the KF may struggle to provide accurate estimation.
Some studies aim to improve the fusion robustness against nonlinear natures from high system dynamics and complex environments, variants of Kalman filter such as Extended Kalman Filter (EKF) [14,15,16,17], Multi-state Constraint Kalman Filter (MSCKF) [18,19,20,21,22], Unscented Kalman Filter (UKF) [23], Cubature Kalman filter (CKF) [24,25], Particle Kalman Filter (PF) [26], have been proposed and evaluated. One challenge in the EKF-based VIO navigation system is handling significant nonlinearity during brightness variations [15,17] and dynamic motion [15] which will cause feature-matching errors and degrade overall performance. When these feature-matching errors occur, the EKF’s assumption about linear system dynamics and Gaussian noise may no longer hold, leading to suboptimal states and even filter divergences. To improve VIO performance under brightness variation and significant nonlinearities, MSCKF was proposed and evaluated in complex environments such as insufficient light [19,20,21,22], texture missing [19,21], and camera jitter [19] specifically characterized by blurry images [22]. However, in the MSCKF algorithm, the visual features are mostly treated as separate states which means that the process is delayed until all visual features are obtained. Another approach is proposed to handle additive noise, VIO uses camera observation to update the filter allowing for avoiding over-parameterization and helping to reduce growth caused by UKF [23]. In most studies like [24,25], researchers have not focused on evaluating their proposed algorithms among complex scenarios such as light variation, rapid motion, motion blur, overexposures, and field of view that deteriorates the accuracy and robustness of the state estimation.
Nevertheless, in GNSS-denied scenarios, UAV navigation predominantly depends on VIO so that the challenges remain unresolved by using KF variations only for VIO applications. Therefore, the use of ESKF-based VIO for performance improvement is highlighted through alleviating challenges by managing parameter constraints, mitigating singularity and gimbal lock concerns, maintaining parameter linearization, and supporting sensor integration in this paper.

2.2. Hybrid Fusion Enhanced by AI

A number of artificial techniques such as neural networks including Deep Neural Networks (DNN), Artificial Neural Networks (ANN), and Reinforcement Learning (RL) have been studied for sensor fusion applications to formulate hybrid fusion solutions. Kim et al [27] conducted a detailed review of KF with AI techniques to enhance the capabilities of the KF and address its specific limitations in various applications. The recent survey [28] summarizes detailed reviews of the GNSS/INS navigation system that utilizes Artificial Neural Networks (ANN) in combination with the Kalman Filter. This survey highlights the advantages of hybrid methods that leverage ANNs to mitigate INS performance degradation during GNSS vulnerability in specific conditions of aerial underwater vehicles [29,30,31], and Doppler underwater navigation [32]. It is found that one advantage of the hybrid fusion scheme is providing the ability to intercorporate a priori knowledge about the level of change in the timer series, enhancing the systems’ adaptability to varying environments and conditions. Additionally, the ANN error predictor proves to be successful in providing extremely precise adjustments to standalone INS when GNSS signals are unavailable, ensuring continuous and accurate navigation. This survey motivates further exploration and development of hybrid fusion-based navigation schemes to maintain robust performance in challenging GNSS-degradation environments.
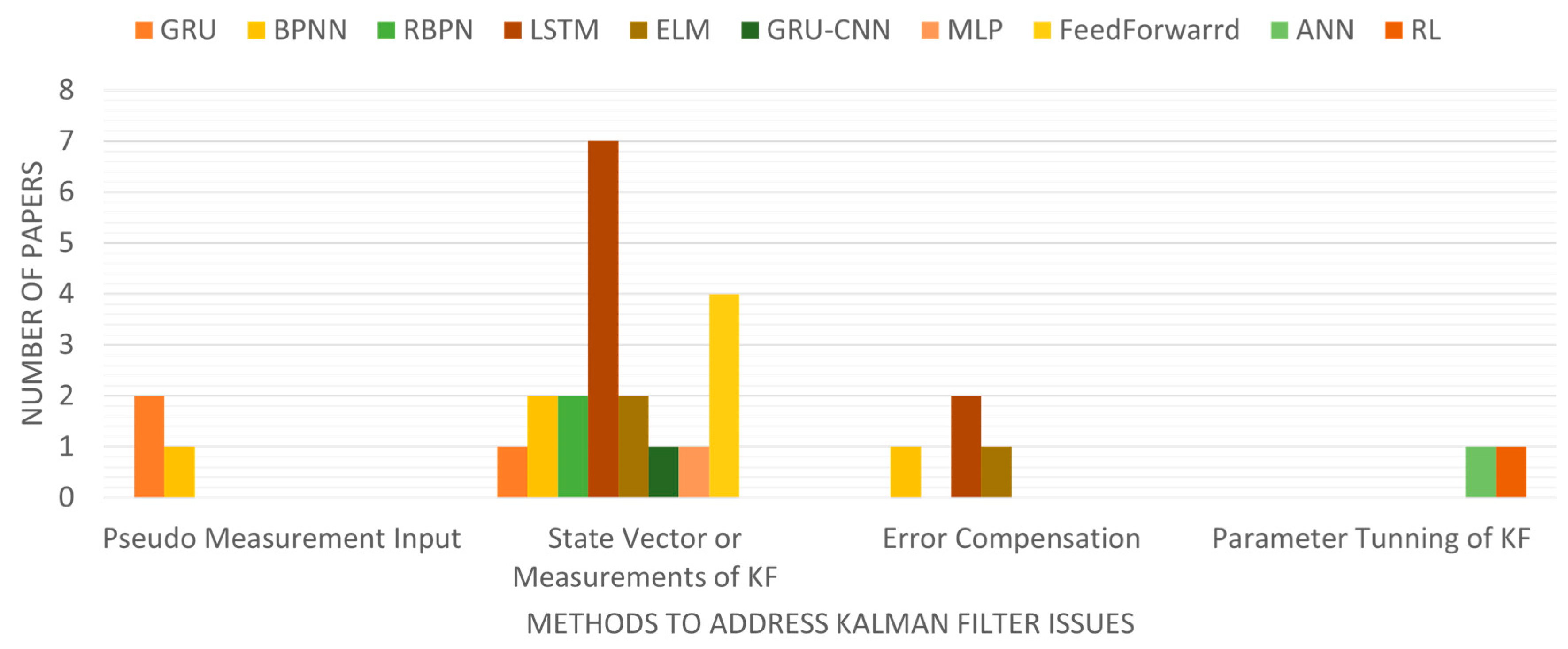
Figure 1 presents an overview of publications on NN-assisted navigation applications over the 2018-2023 period and categorizes them into KF performance degradation following the category rule defined by Kim et al [27]. It is concluded that most studies focus on updating the state vector or measurements of KF ignoring issues arising from imperfect models. Hereby, estimating pseudo-measurements during GNSS outages to update KF measurements using AI is suggested by [27]. In certain scenarios particularly when dealing with high-nonlinear sensors or navigating in complex environments, updating state vectors directly by predicting sensor increments using NN in measurement steps becomes critical regarding the sensor’s complexity and the challenging natures of the environment.
To overcome KF drawbacks in navigation, hybrid methods combining AI approaches especially machine learning (ML) algorithms become promising by accurate prediction of INS and visual sensor errors from diverse training datasets. As depicted in Figure 1, most publications are sourced belonging to the category of ‘State Vector or Measurements of KF’ which means most studies apply ML to predict and compensate state vector error or measurements in KF. For instance, Zhang et al. [33] used RBFN to predict states in the prediction step. However, those studies like [33] predict absolute state vectors instead of vector increments using NN which increases model complexity and requires a more extensive training process. Studies of [29,32,33,34,35,36,37,38,39,40,41,42,43,44,45] adopt vector increments of the sensor observations and predictions during KF prediction whilst most of the work only works on GNSS/INS navigation during GNSS outages aiming for improving INS efficiency INS in urban settings and situations [31,38,39,41,42,46].
Other studies [47,48] corresponding to the error compensation category employ ML to compensate for the navigation performance error with KF but sensor errors such as the nonlinear error model of INS are excluded.
The category named pseudo measurement input applies NN for predicting pseudo-range errors when the occurrence of shortage of satellite numbers so that to update measurement steps in CKF [49] and also the adaptive EKF [46,50].
The category of parameter tuning of KF aims to enhance the performance using RL by predicting the covariance matrix such as using AKF in [50]. However, the prediction of the covariance matrix relies on changeable factors like temperature which is difficult to predict and model. Therefore, using NN for parameter tuning in KF is not considered in this paper.
Regarding the selection of NN types, Radial Basis Factor Neural Networks (RBFN), Backpropagation Neural Networks (BPNN), and Extreme Learning Machines (ELM) are powerful learning algorithms, more suitable for static data or non-sequential problems but neglect the information of historical data. Additionally, navigation applications are indeed inherently time-dependent and dynamic, which makes them challenging to model using these learning algorithms. Authors [30,38] have proved RBFN has less complexity than BPNN and multi-layer backpropagation networks yet haven’t considered any dynamics change over time. Other studies were presented using simple neural networks on SLAM applications by predicting state increments in diverse scenarios. Authors in [35,36] did not account for the temporal variations in features that can significantly impact the performance, given that basic neural networks are sensitive to such changes. Kotov et al. [37] conducted a comparison between NNEKF-MPL and NNEKF-ELM, demonstrating that NNEKF-MPL shows better performance in cases where the vehicle exhibits non-constant systematic error. However, the aforementioned NN methods do not take temporal information contained within historical data into training, which makes those methods insufficient for addressing the dynamic and time-dependent characteristics of navigation applications.
Some studies have proved advantages of using time-dependent recurrent NN architectures like Long Short-Term Memory (LSTM) in VIO. VIIONET [51] used LTSM to process high-rate IMU data that concentrated with feature vectors from images processed through CNN. Although the adoption of IMUs can facilitate the mitigation of IMU dynamic errors, the compensation of visual cues in VIO affected by complex environmental conditions is more critical. DynaNet [52] was the first to apply LSTM-aided EKF to show hybrid mechanism benefits in improving motion prediction performance on VO and VIO without sufficient visual features. Furthermore, this study suggests unresolved challenges of motion estimation tasks, multi-sensor fusion under data absence, and data prediction in visual degradation scenarios. Subsequently, researchers aim to learn VO positions from raw image streams using CNN-LSTM [51,53,54,55]. With the utilization of CNN-LSTM, some of them aim to reduce IMU errors by predicting IMU dynamics in complex lighting conditions [54,55]. Two recent papers attempted to use CNN-LSTM-based EKF VIO [12,45] to evaluate visual observation in dynamic conditions, but the evaluation of the algorithm performance is insufficient due to the lack of sufficient datasets for training the CNN model. One of the common drawbacks of using DL-based visual odometry is the necessity of huge training datasets. DL model requires vast amounts of diverse data to generalize well and provide reliable results in the real world. If the CNN-LSTM model is not trained properly due to the insufficient variety of datasets, it may struggle to capture the complexity of dynamic scenes, leading to subpar performance and unreliable VIO results [12,45]. Thus, by leveraging feature-based techniques, we can simplify the VIO structure where ESKF facilitates the simplification by providing a robust mechanism for handling uncertainty and noise in the data.
In this paper, GRU is chosen due to its efficiency in processing time-varying sequences, offering advantages over other recurrent NNs like LTSM. Some literature has used GRU to predict state increments and update the state vector of KF [41,48] for GNSS/INS systems during GNSS outages. However, the fusion of GRU with GNSS/INS/VIO remains explored yet.

2.3. FMEA in VIO

FMEA could give a detailed description of potential faults in VIO that can affect the whole system, leading to positioning errors in complex environments. In 2007 Bhatti et al. [56] carried out FMEA in INS/GPS integrated systems to categorize potential faults with their causes, characteristics, impact on users, and mitigation methods and discussed how this advanced fault analysis could help to improve positioning performance. Du et al. [57] have reviewed GNSS precise point positioning vulnerability and assisted the researchers in examining failure modes to enhance performance. Current developments in visual navigation research apply conventional fault analysis which has given a reason to adapt the existing GNSS fault analysis approach in order to solve the crucial problems raised by specific characteristics of visual sensors. Zhai et al. [13] have investigated visual faults in visual navigation systems and suggested that identifying potential faults in such systems could prevent users from being threatened by large visual navigation errors. However, the proposed analysis was unable to consider all the potential threats and faults contributing to positioning errors in such systems. A recent work done by Brandon et al. [12] tested their proposed Deep VO aided EKF based VIO on four individual faults by corrupting images of the EUROC dataset [58] with methods like overshot, blur, and image skipping and showed their proposed algorithm performance compared to other state-of-the-art systems. Hence, this study aims to investigate FMEA usage on VIO to give an overview of the faults that occur while navigating complex environments experiencing disruptions in system performance.
Therefore, in order to mitigate failure mode arising from diverse complex scenarios in the urban environment, this paper proposes a GRU-aided ESKF-based VIO, aiming to enhance visual positioning. Later, this proposed system contributes as one of the sub-systems in fault-tolerant federated multi-sensor navigation systems to mitigate overall position errors and increase reliability in multiple fault conditions arising from IMU, GNSS, and VO sensor errors. Ultimately, our proposed fault-tolerant system aims to provide a reliable and effective solution for navigation in complex conditions where VO and GNSS/INS systems may face limitations.

3. Proposed Fault Tolerant Navigation System

In order to correct visual positioning errors that arise from multiple systematic faults when navigating in urban areas, FMEA is executed at the first step to identify and analyse systematic failure modes according to the extracted fault tree model. The failure modes are prioritised based on potential impact and likelihood of occurrence enabling to anticipate and mitigate visual positioning errors. With the FMEA outcome, the hybrid GRU-aided ESKF VIO algorithm is discussed as well as the algorithm implementation following the federated multi-sensor framework.

3.1. Failure Mode and Effect Analysis (FMEA)

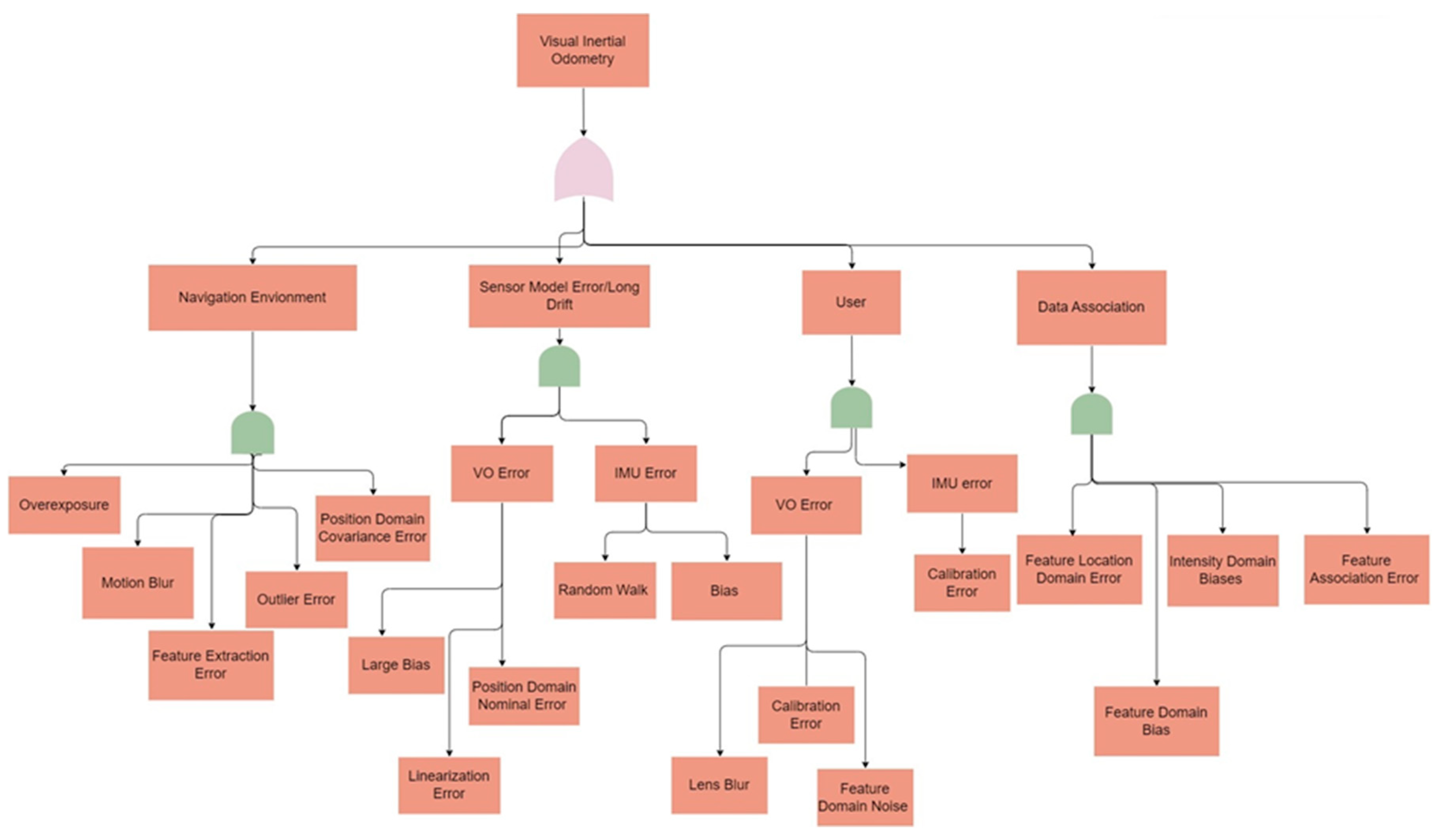
The implementation of FMEA on vision-based navigation systems enables to breaking down of high-level failure events into lower-level events along with allocating risks. Referring to error sources in every domain from the literature review [6], the fault tree model shown in Figure 2 is extracted.
The preliminary conclusion of FMEA is that the error occultation in the camera presents a higher likelihood possibility during feature extraction due to the presence of multiple faults resulting in position errors in the whole system. Specifically, two major fault events, i.e. navigation environment error and data association error [6] show high possibilities of faults in visual systems. Table 1 lists reviews of common error sources over the navigation environment and data association error events along with their visual faults targeted for mitigation in the context of VIO.
  • One common fault in the navigation environment fault event is the feature extraction error that contains deterministic biases leading to position errors frequently.
  • Another common fault in the data association failure event is the feature association error that happens during matching 2D feature location with 3D landmarks.
  • Sensor model error/long drift failure event represents errors generated by sensor dynamics including VO error and IMU error types.
  • User failure event stands for errors created during user operations that are normally relevant to the user calibration mistakes.
With the extension of fault events from the state-of-the-art reviews and proposition of thorough error analysis, i.e. Figure 2, this study aims to mitigate feature extraction errors occurring in failure modes linked to navigation environment and data association events through a fault-tolerant GNSS/IMU/VO navigation system. Hybrid integration of VIO holds great potential for achieving precise and reliable navigation performance in complex conditions.

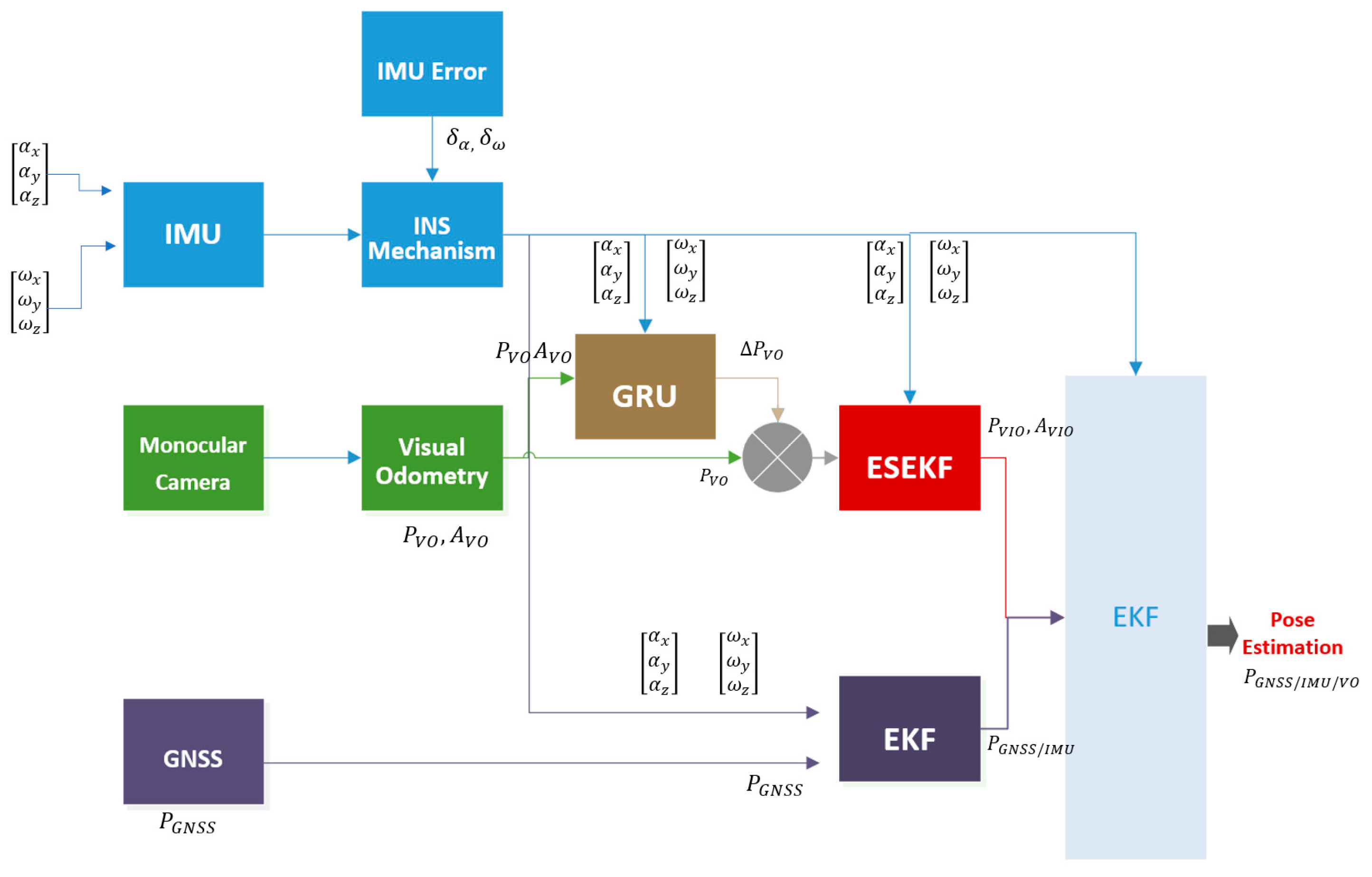
3.2. Fault Tolerant Federated Navigation System Architecture

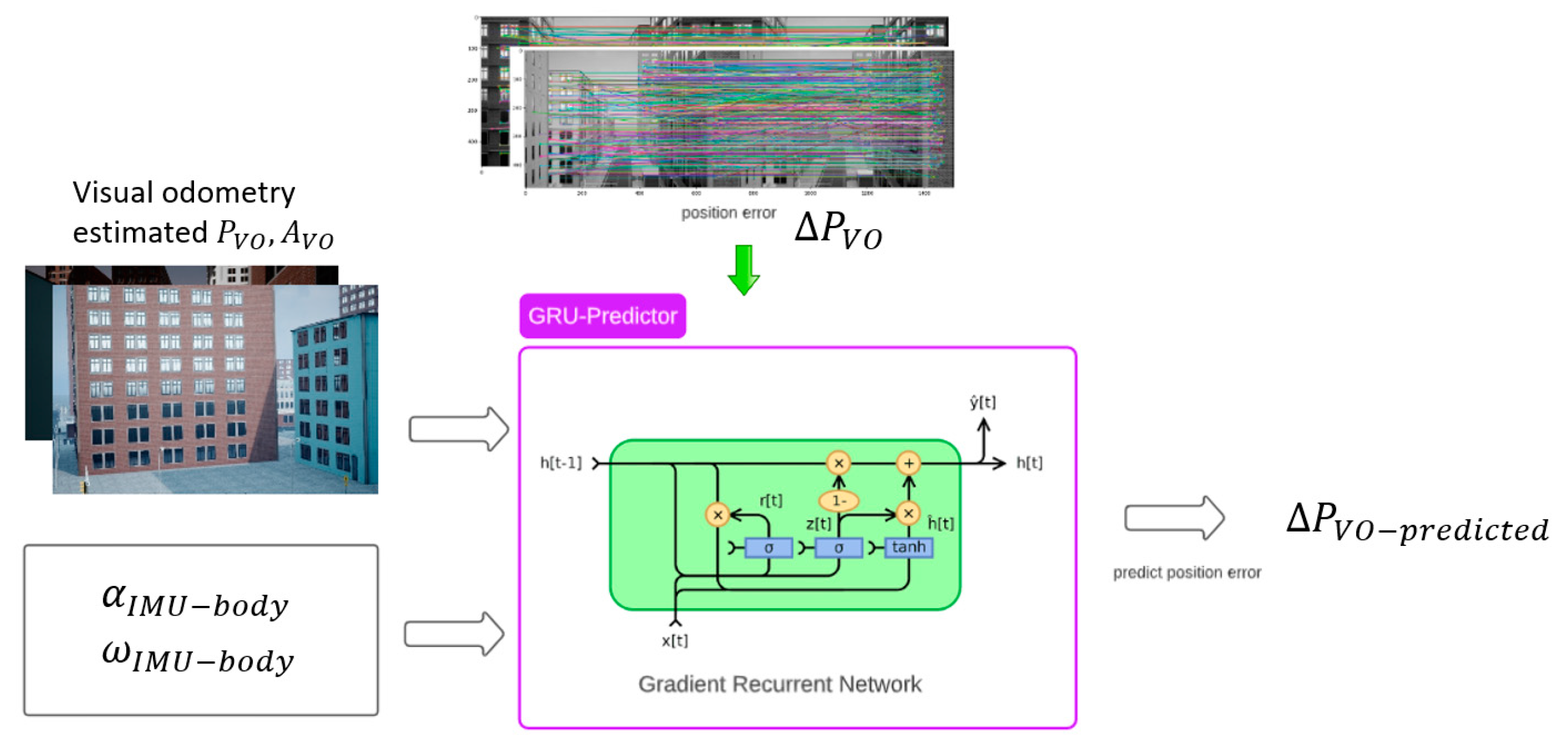
The utilization of a federated architecture proves advantageous in implementing fault tolerant multi-sensor systems, as it is known for its robustness in handling faults. This paper proposes a federated architecture-based integrated multi-sensor fusion scheme that is based on the combination of IMU, VO, and GNSS. The overall architecture of our method is shown in Figure 3. Two sub-filters exist in the proposed architecture that are hybrid GRU-aided ESKF IMU/VO sub-filter, and EKF-based GNSS/IMU integration sub-filter. The output of two sub-filters is merged together with a master EKF to generate the ultimate position estimations. The former sub-filter of hybrid GRU-aided ESKF IMU/VO attempts to compensate for VO and IMU errors, while the latter sub-filter of EKF-based GNSS/IMU integration aims to correct errors from GNSS and IMU.
The state vector of the proposed GRU-aided ESKF IMU/VO sub-filter selects the following states:
X = [ P x , P y , P z , V x , V y , V z , A x , A y , A z , α b x , α b y , α b z , ω b x , ω b y , ω b z ]
where, P x , P y and P z denote the position, V x , V y and V z denote velocity, A x , A y and A z denote attitude, ∆ α x , ∆ α y and ∆ α z denote accelerometer bias and , ∆ ω x , ∆ ω y and , ∆ ω z denote gyroscope bias in x axis, y axis and z axis.
The extraction of visual features by VO is firstly adapted to produce relative pose measurements for ESKF updates [9].
The IMU/VO sub-filter uses proposed ESKF-based tightly coupled integration strategy with a GRU model, which works during GNSS outages. The GRU model is trained with multiple trajectories containing complex scenarios so that it can predict VO error during flight. The GRU output equation is formulated by:
P V O / G R U = P V O − ∆ P V O
where P V O denotes position error from VO, ∆ P V O is position error deviations, and P V O / G R U represents the predicted position increments.
The training phase of the GRU-aided ESKF IMU/VO sub-filter is shown in Figure 4. Two data sources from IMU and VO are generated and used to gather positioning and attitude data for training each trajectory. The GRU structure is adapted from Geragersian et al. [59]. Additionally, VO position P V O and orientation φ V O covering multiple complex environments by UAV and INS measured angular velocity α I N S and linear acceleration ω I N S   are used to calculate inputs of GRU. The output of the GRU model is the positioning error ∆ P V O   generated by VO. When GNSS signal is unavailable, IMU/VO operates to estimate the position of UAV where the GRU module operates in predicting mode that predicts the position error ∆ P V O which is to be updated to measurements vector in the ESKF module. When VO diverges, the GRU block predicts visual errors for error correction.
The pseudo-code of the proposed GRU-aided ESKF fusion algorithm is presented in Algorithm 1.
Algorithm 1: GRU-aided Error Estate Extended Kalman Filter
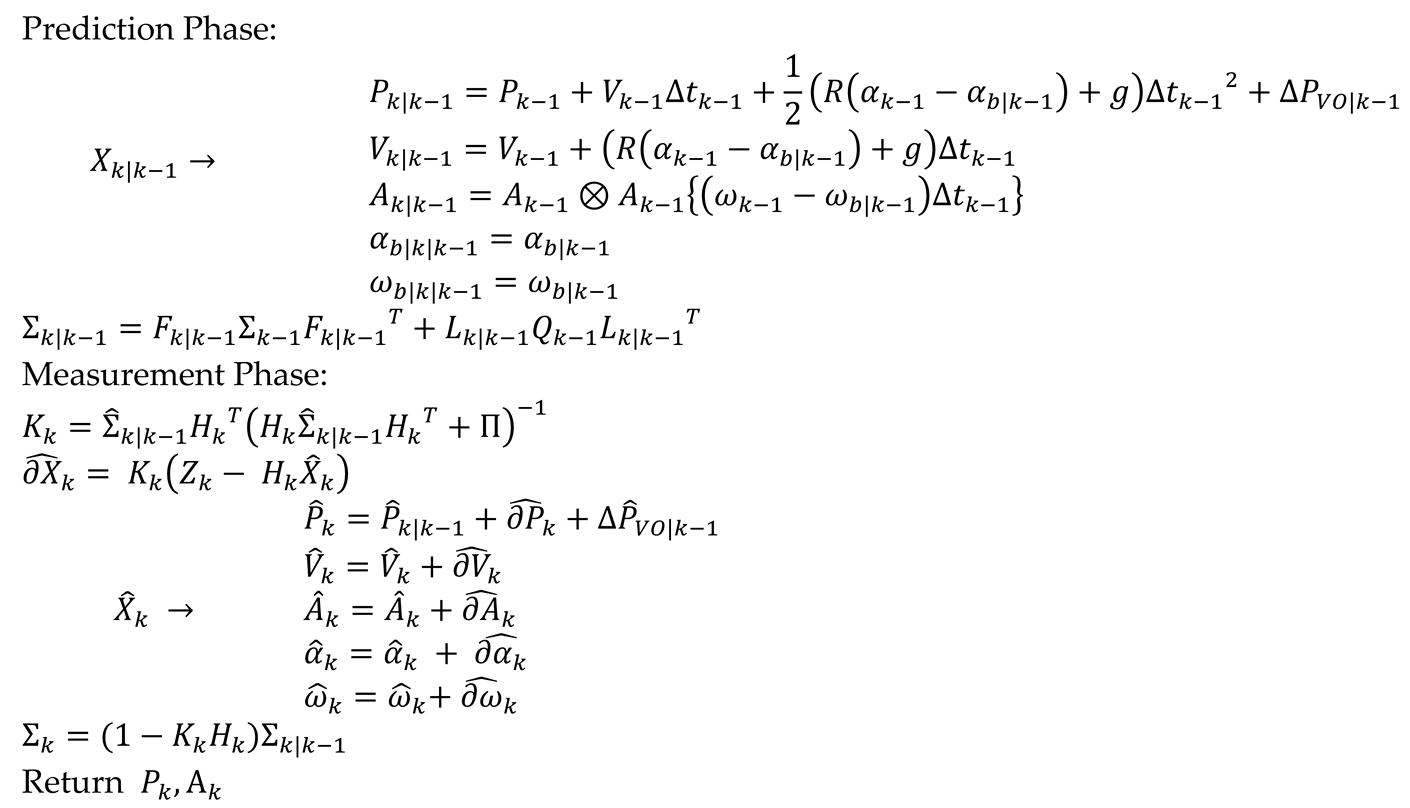Preprints 86379 i001

4. Experimental Setup

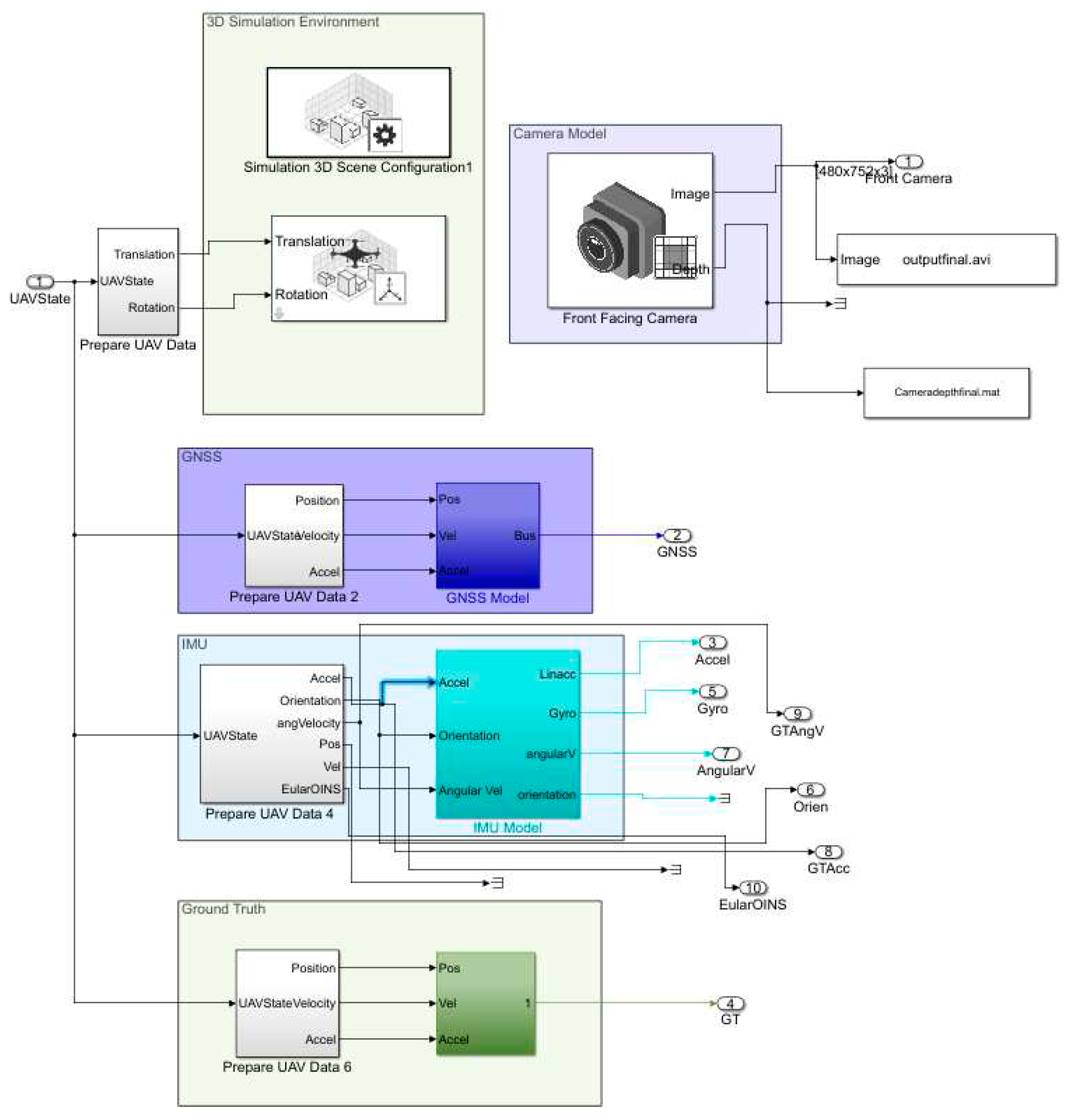
To verify the proposed fault tolerant navigation system performance under complex environments, a GNSS/IMU/VO simulator is built on Unreal Engine with UAV unity dynamic models integrated to urban scenarios in MATLAB 2022a. The sensors implemented in the simulator include IMU block, GNSS receivers, and front-facing monocular camera model generated by the Navigation and UAV toolbox. The dataset is acquired with these sensors mounted on quadrotor shown in Figure 5.
The simulator consists of 4 blocks in total. The 1st block is 3D simulation environment block aims to simulate US city environment with combination of camera and UAV quadrotor models. The 2nd block is GNSS integration with quadrotor consisting of GNSS and the quadrotor dynamics. The 3rd block is IMU block interfaced with the quadrotor block. The 4th block is the ground truth from the quadrotor dynamics to provide true quadrotor trajectories.
The IMU selects ICM 20649 model with specifications provided in Table 2. The experiment data are collected with sampling rate of 10 Hz, 100 Hz, and 100 Hz for camera, IMU and GNSS respectively. The random walk error [0.001, 0.001, 0.001] m / s 2 in IMU accelerometer results a position error growing at a quadratic rate.
The GNSS Model is initialized by injecting two common failure modes of random walk, and step error that will most likely be occurred in urban environment leading to multipath effect.
Regarding the calibration of the camera and extraction of extrinsic and intrinsic parameters of the simulated front-facing camera, the coordinate conversion matrix from world coordination to pixel coordination is denoted by camera instincts matrix k :
k = 1109 0 376 0 1109 240 0 0 0  
For urban operation scenarios surrounded by buildings, visual data of tall buildings is captured by camera for VIO to provide positioning information. Meanwhile, the satellite availability is obstructed by buildings causing GNSS outage. The MATLAB simulator connect to QGroundControl software to generate real-time trajectories for the data collections and save into text file format.
Regarding training GRU models, 10 trajectories covering more than 100,000 samples from each sensor are used for per training.
The general performance evaluation method uses root mean square error (RMSE) formulated by:
R M S E o v e r a l l = ∑ N i = 1 ( P x P r e − P x G T ) 2 + ( P y P r e − P y G T ) 2 + ( P z P r e − P z G T ) 2 2 N

5. Test and results

In order to evaluate the performance of the proposed GRU-aided ESKF-based VIO, two trajectories corresponding to experiment 1 and 2 are selected from the package delivery experiment in urban environment. Both experiments are carried out under sunlight condition, introducing common fault scenario shadows that are consistently present throughout the flight duration. For both experiments, a consistent fault condition is injected, i.e. the shadow of tall buildings on a sunny day during the fight. According to the fault types and number, the flying regions in the experiments are categorized into four distinct zones that encompass single fault, multiple faults, and combined faults. The faults arising from environmental sensitivity and dynamic motion transitions under previously estimated two major failure events in visual systems using FMEA analysis results in Section 3.1 have been discussed.

5.1. Experiment 1 - Dense urban Cynon

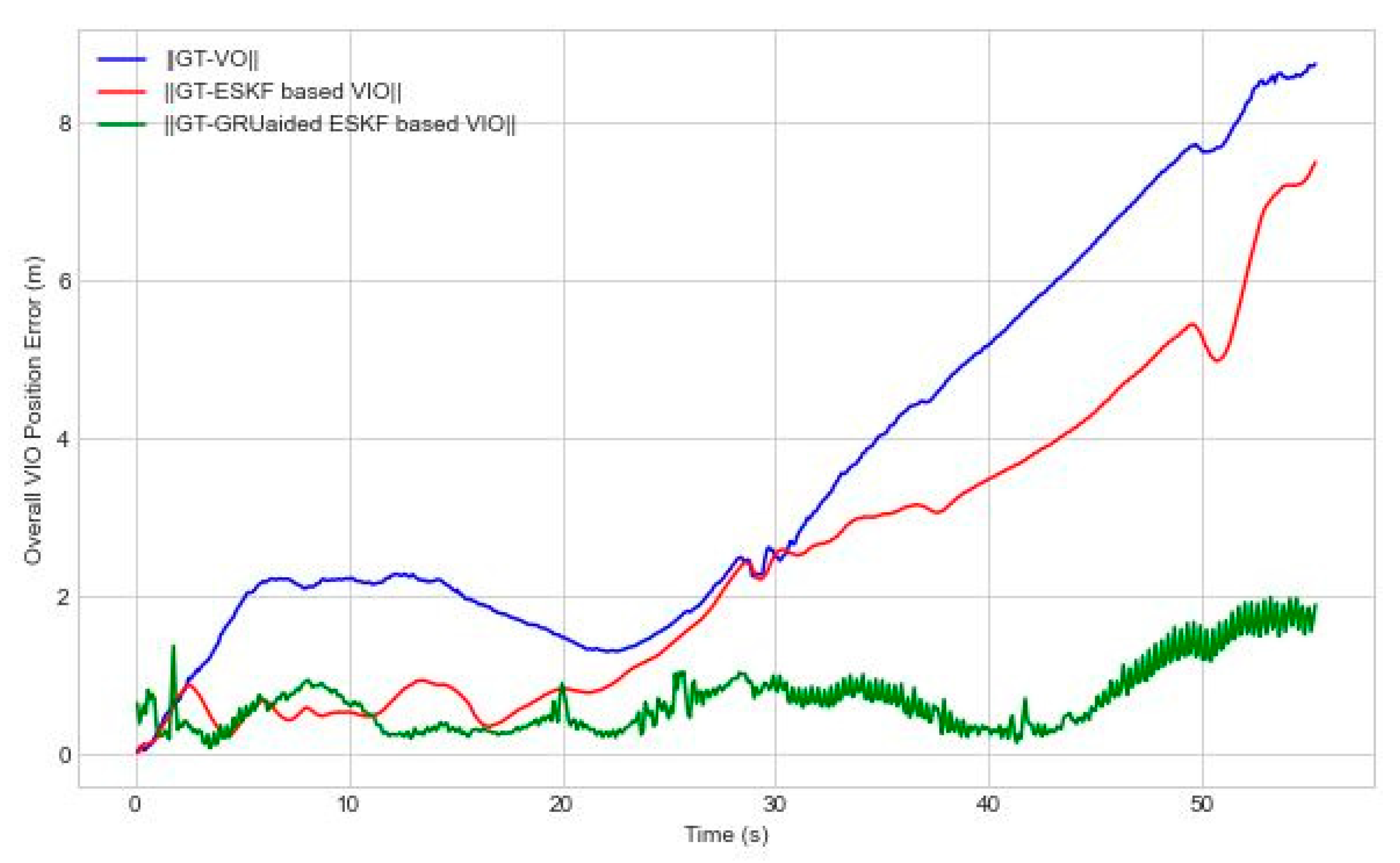
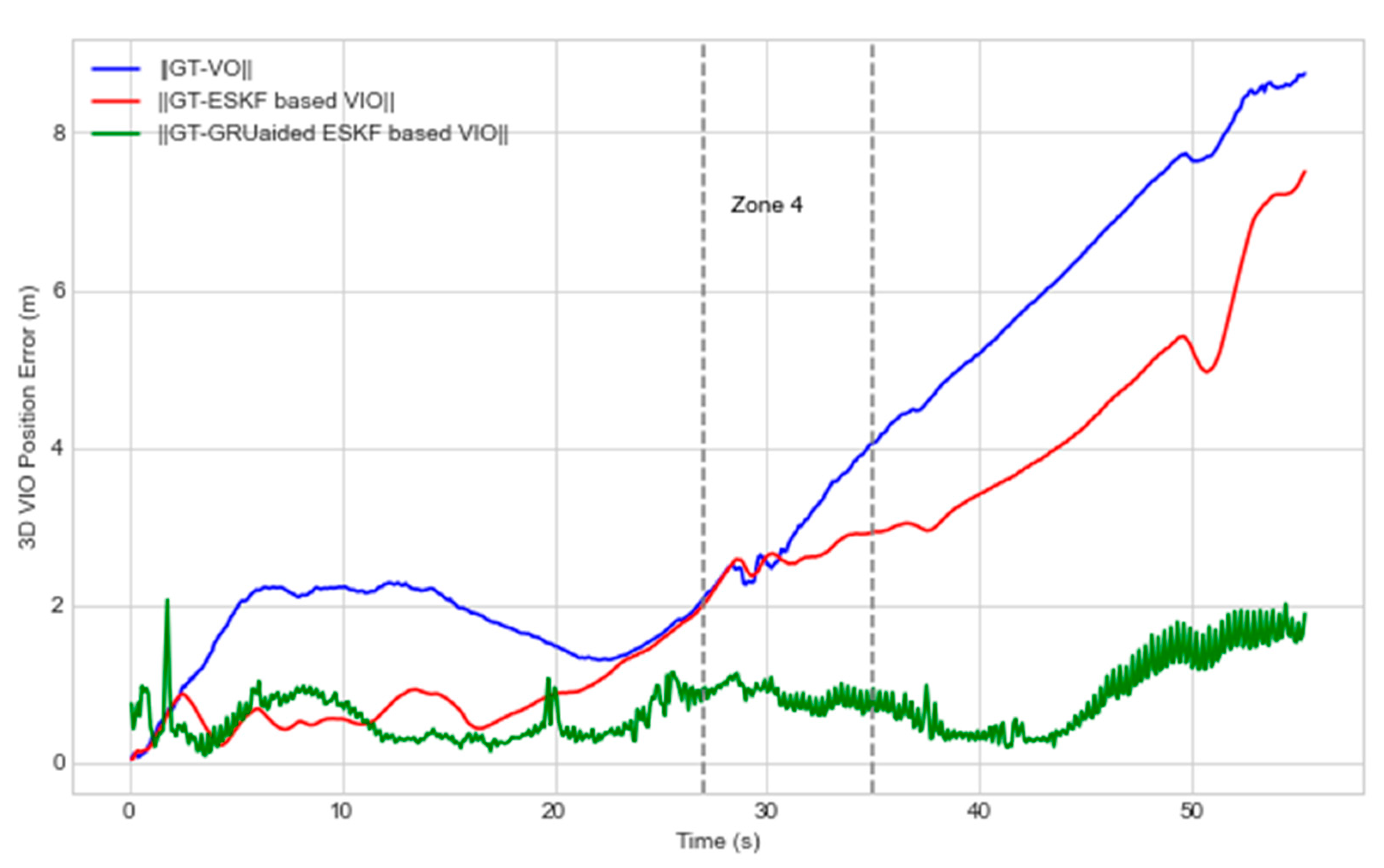
The purpose of this experiment is to validate the effectiveness of the proposed GRU aided VIO in managing specific failure modes in complex conditions. This experiment environment includes combination of tall and short buildings. Figure 6 shows the accumulated 3D visual position error. Our proposed GRU aided VIO is able to reduce position error by 86.6 % compared with ESKF based VIO reference system. The maximum error in Figure 6 reduces from 7.5 m to 1.9 m with the GRU adoption.
When UAV takes off with rapid and sudden change in waypoints, the Dynamic Motion Transitions failure mode occurs under condition of jerking movements that result in feature tracking error and feature association error failure modes in VO consistently. Moreover, the other dynamic motion transition failure mode is incorporated, i.e. turning to replicate complex environmental conditions, thereby emulating real fight scenarios. The UAV takes off speed sets to 20 m/s while its speed will increase up to 50 m/s at 7 sec.
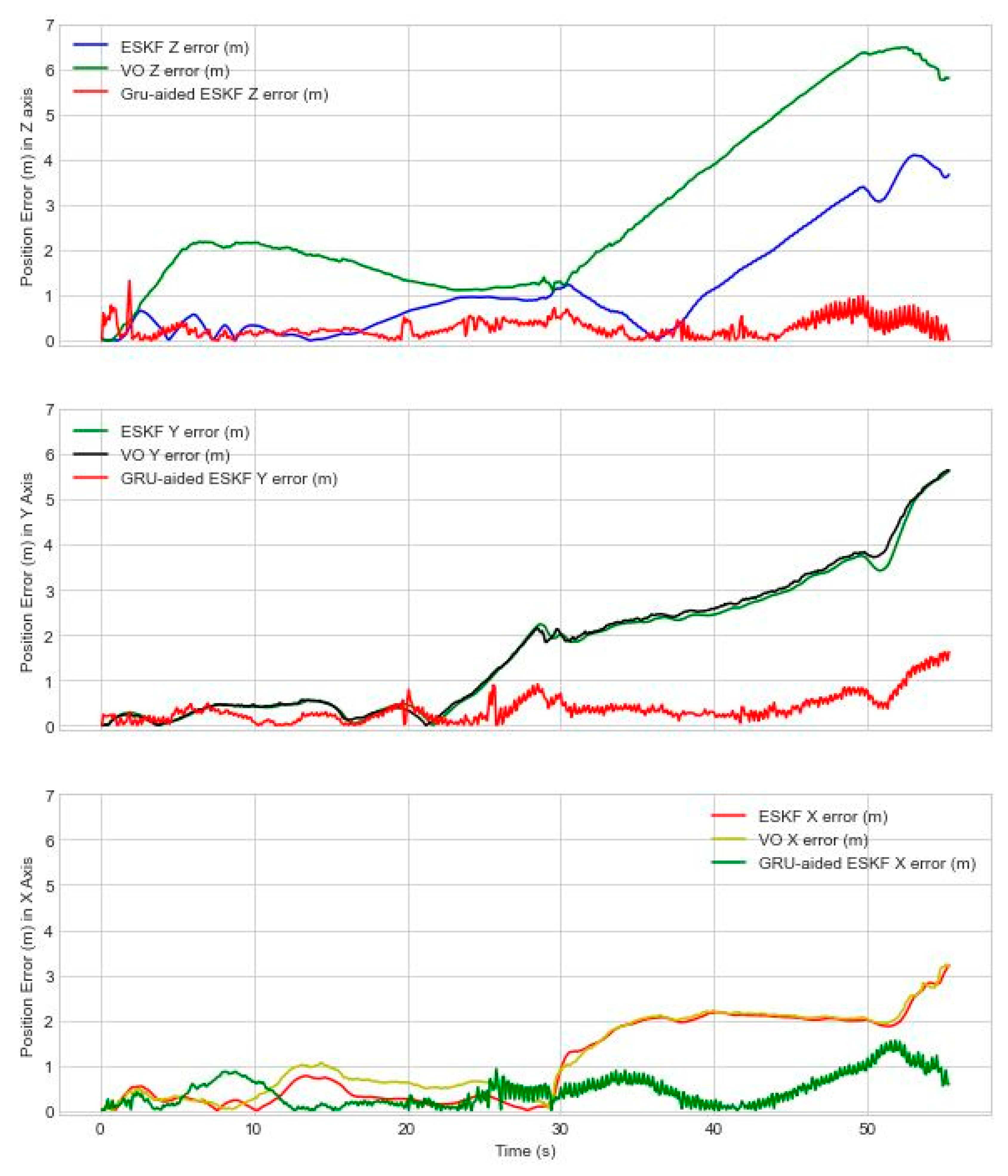
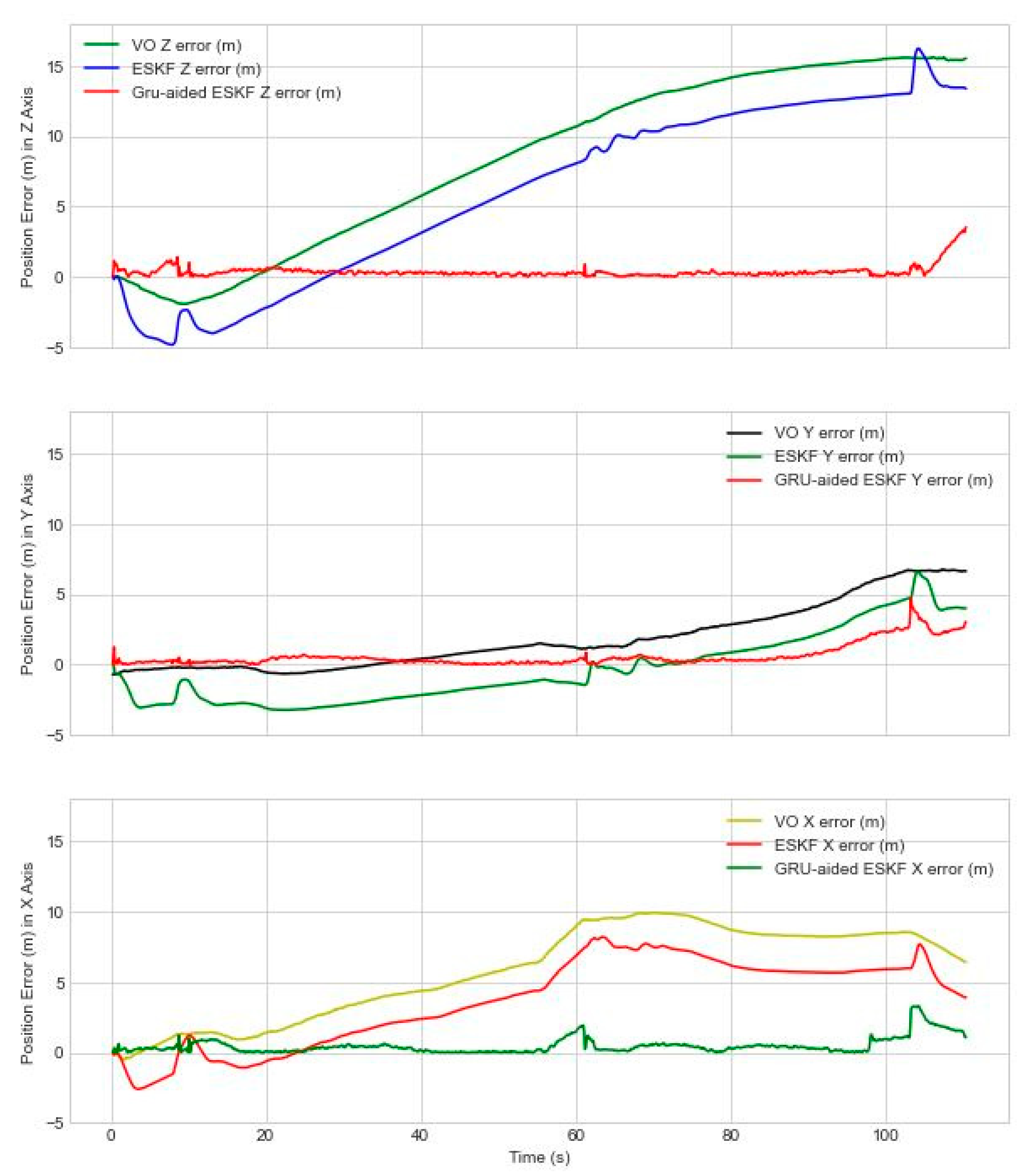
Figure 7 shows the RMSE position error of the proposed GRU aided VIO system, and benchmarked with two references of VO and ESKF based VIO position error. RMSE position error in X axis under NED coordination is relatively lower compared to Y and Z axis. It is noting that the maximum position error of ESKF-based VIO reference system is 3.227 m, 5.6 m and 4.1 m in X, Y, Z axis.
In Y axis, position error axis increases at 22 sec due to the shadow of another building creating variation of light. At 27 sec, UAV encounters a turn facing a plain wall because of lacking textures leading to drift, inaccuracies and failure of visual odometry. ESKF-based VIO showed relatively poor performance along Y axis during diagonal motion due to cross-axis coupling and multiple failure modes due to featureless plain wall, sunlight variation, shadow of tall buildings leading to feature degradation and tracking features. The loss of visual features results in insufficient information for ESKF to estimate the position accurately. In Figure 6 and Figure 7, it is shown that VIO based on ESKF fails to mitigate visual positioning error due to non-linear motion, lack of observable features, non-gaussian noise, uncertain state estimation leading to non-linearization error propagation. However, it is found that our proposed solution is able to mitigate position error by 60.44 %, 78.13 % and 77.13 % in X, Y and Z axis. Additionally, maximum position error is decreased from 1.5 m, 1.6 m and 1.2 m.
When analysing the Z axis performance in Figure 7, around 37 sec ESKF-based VIO position error starts increasing due to a dark wall shadowed from another tall building causing variation of light in the frame leading to feature association error. ESKF performance degrades due to multiple factors presence in the scenario and error accumulates over time. After applying our proposed GRU-aided ESKF VIO fusion method is able to reduce position error at 37 sec from 2.1 m to 0.6 m by predicting VO error that is indicated with details on Table 3.

5.2. Experiment 2 - Semi-structured Urban Environment

This experiment aims to measure GRU-aided ESKF VIO performance under environments of tall buildings with open space parking area. In this experiment UAV encounters 2 turns which means changing of 2 waypoints and at 60 sec, 110 sec leading to variation of motion causes feature association error described as ‘Dynamic Motion Transitions’.
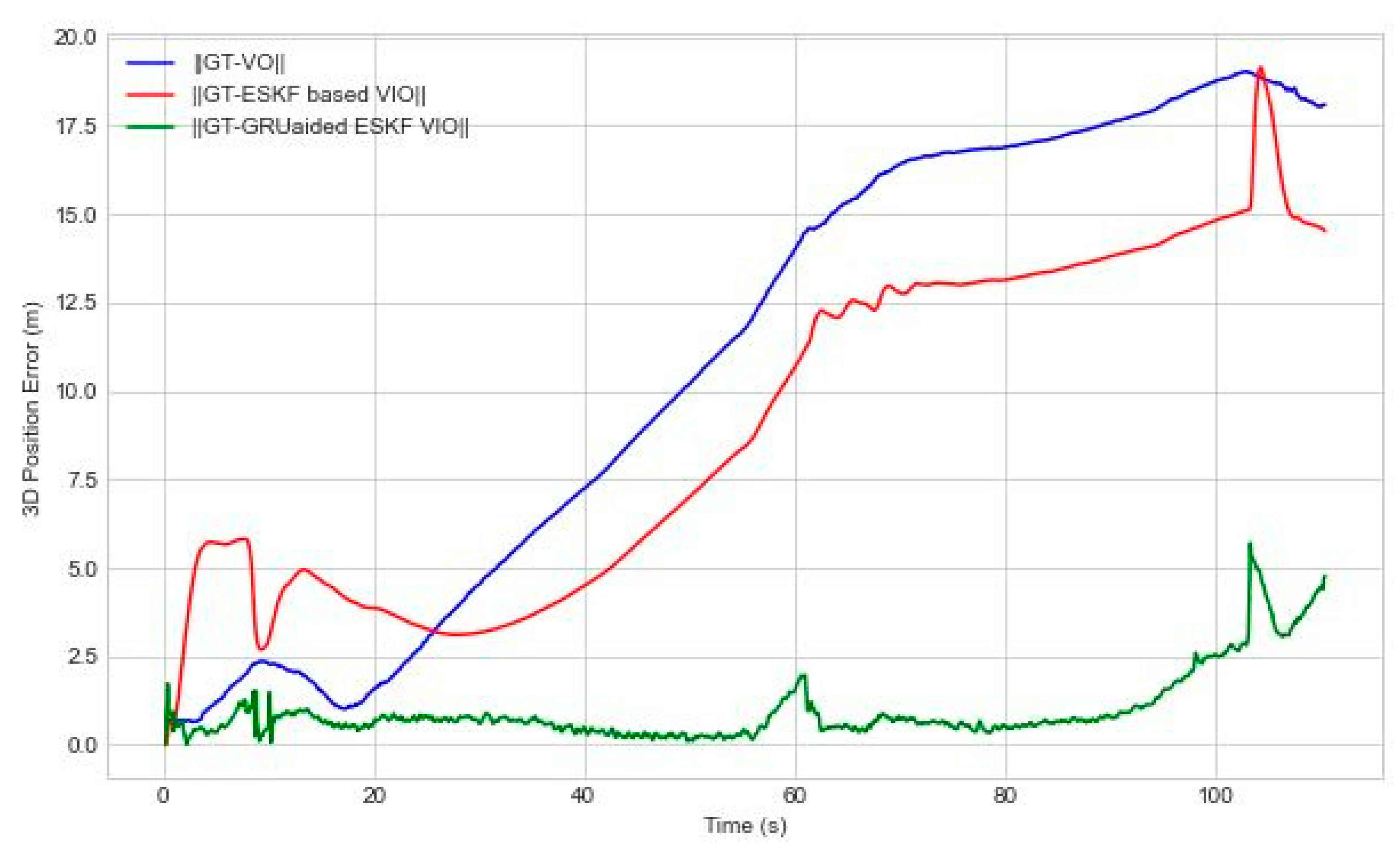
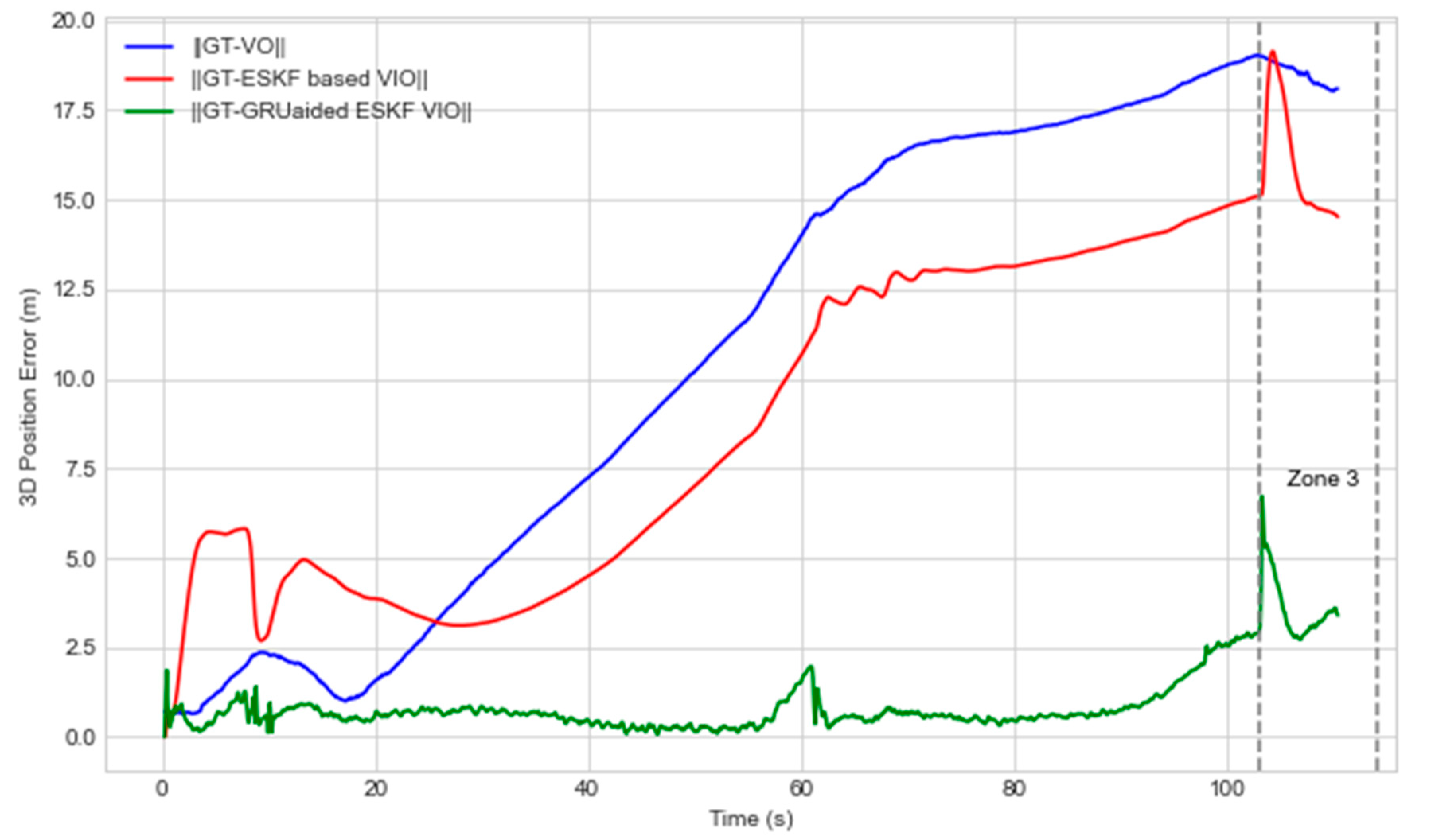
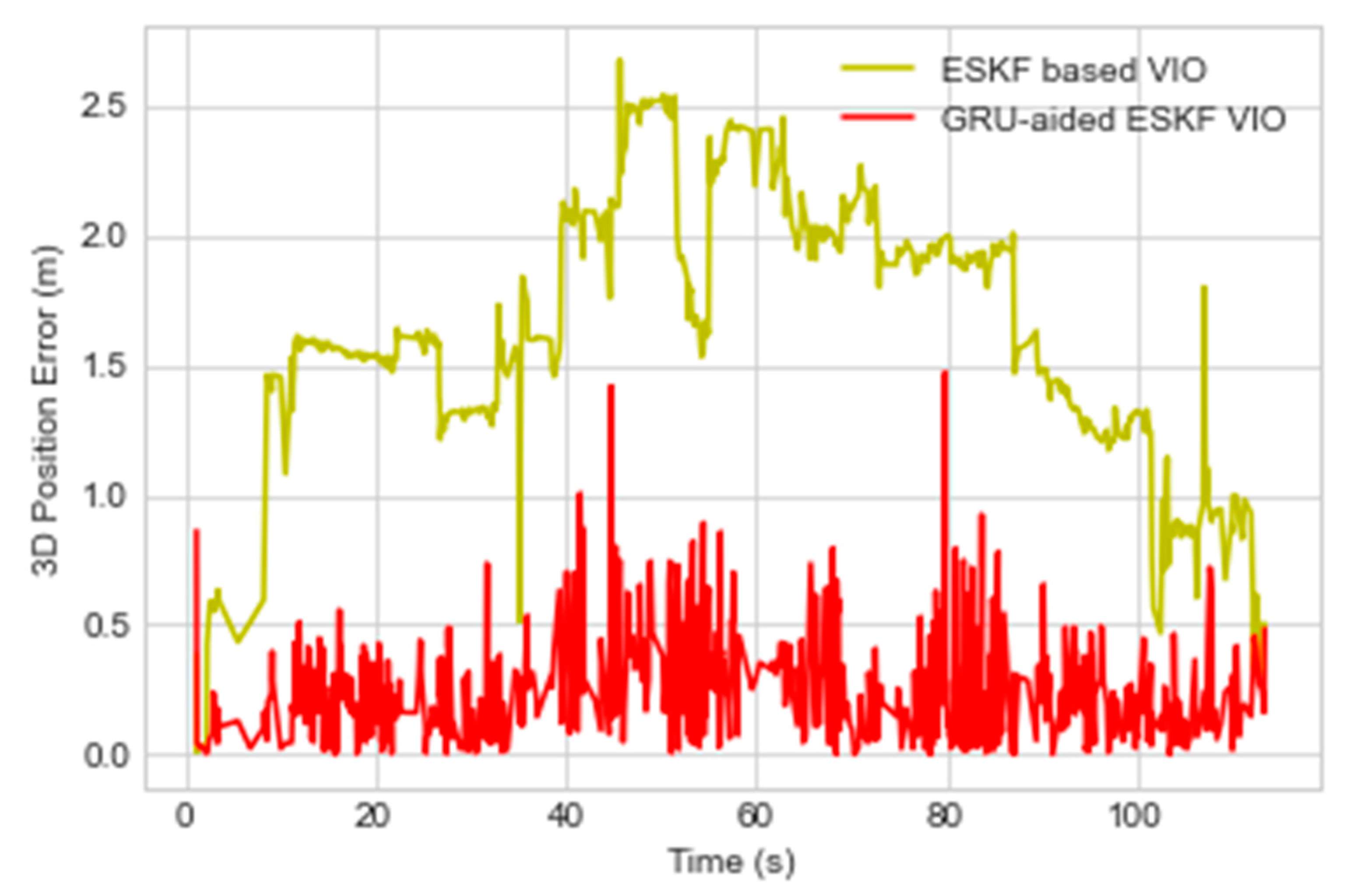
Figure 8 shows accumulated 3D position error of the proposed GRU aided ESKF VIO system and benchmarked with two references of VO and ESKF based VIO position error. In Figure 8, position error in first few seconds is negative due to multiple factors such as shadows of tall buildings, trees on plain surfaces, shadowed building, lighting variations due to sunlight, motion blur, and rapid motion. Maximum position error is 19.1 m at 110 sec due to combinational failure mode such as dark wall, rapid motion and motion blur. The proposed GRU-aided ESKF VIO is able to mitigate 86.62 % of overall position error. Maximum error is reduced from 19.1 m to 6.8 m.
Figure 9 shows VIO position RMSE error in separate X, Y and Z axis. Table 3 indicates that position error RMSE of ESKF is 4.7 m, 2.5 m, 8.6 m in X, Y and Z axis respectively. The proposed GRU-aided ESKF VIO has a remarkable improvement in terms of position error, and the specific values along X, Y and Z axis are 0.8 m, 0.9 m, 0.5 m. Due to cross-axis coupling, Y axis faces larger estimated position error than others. During the time interval of 57 sec-65 sec, UAV takes a turn and passes through a parking area where buildings are under limited field of view. In this case, the features extraction and tracing process encounter challenges and lead to position estimation error. The proposed solution has shown excellent performance improvement in presence of failure modes of feature extraction error and feature tracking error where the position error is decreased by 62.86 % comparing to the reference systems.
When analysing the Z axis performance in Figure 9, the proposed GRU-aided ESKF VIO outperforms the reference ESKF fusion with respect to reduction of the Z axis error by 93.46%. According to Table 3, the reference ESKF has shown the worst performance of 8.6 m RMSE comparing to the proposed method of 0.5 m RMSE. It is noting that at 104 seconds during the landing phase, the UAV turns around and encounters a black wall. This leads to higher performance errors because the VO system struggles to extract enough features in the complex scene with poor lighting [7,9,10]. The GRU-aided ESKF VIO demonstrates improvement compared to the traditional ESKF-based approach resulting in a remarkable reduction of error of 93.45%. The maximum position error in Z axis due to dark scene at 110 sec is reduced from 16.2 m to 3.0 m.
Table 4 indicates maximum position error comparison for two the experiments. By integrating fault-tolerant mechanisms our approach achieves more accurate position estimation, even in challenging situations with limited visual cues. The fault-tolerant GRU-aided ESKF VIO architecture shows robustness over number of realistic visual degradation scenarios.

5.3. Performance Evaluation based on Zone Catogories

To further evaluate successful rate when mitigating failure modes from experiment 1 and 2 as detailed in section 3.1, fault zones are extracted in the above two experiments.
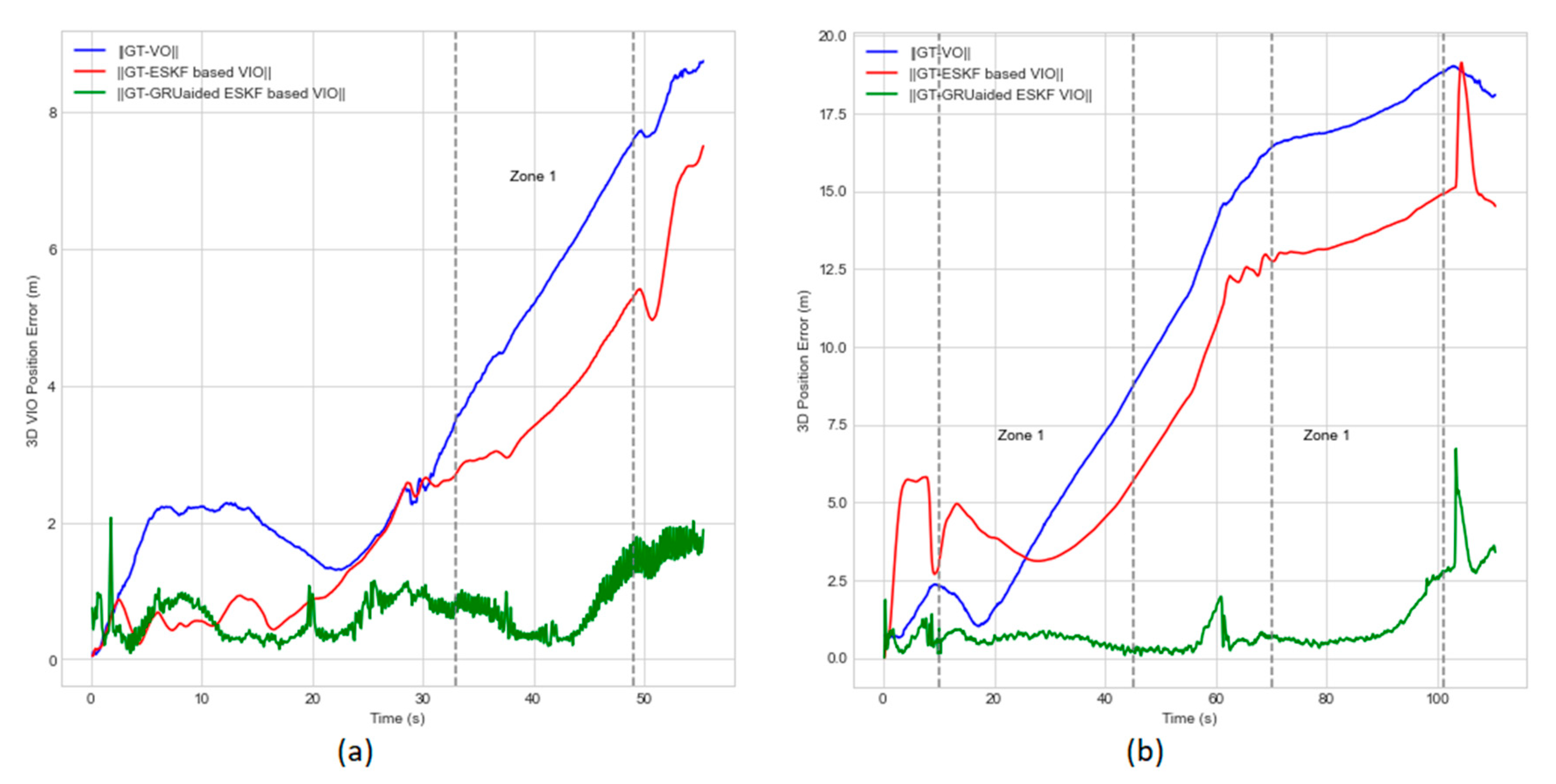
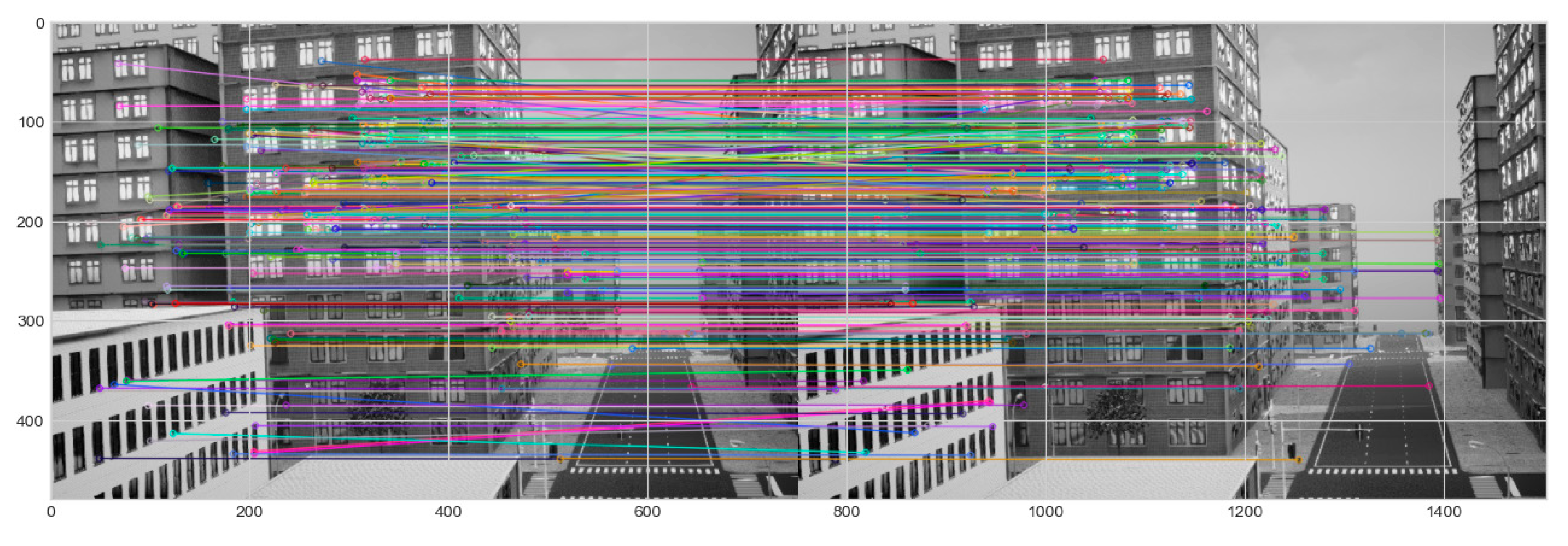
Zone 1 indicates building shadow as the single fault triggering feature matching and feature tracking error failure modes within the time interval. In experiment 1, between the time interval of 33 sec-49 sec, UAV passes through shadows buildings that distort visual features, causing incorrect matches and tracking error when they move into or out of shadows shown on Figure 10. Besides, by introducing sudden change in lighting that may be misinterpreted IMU acceleration and rotation.
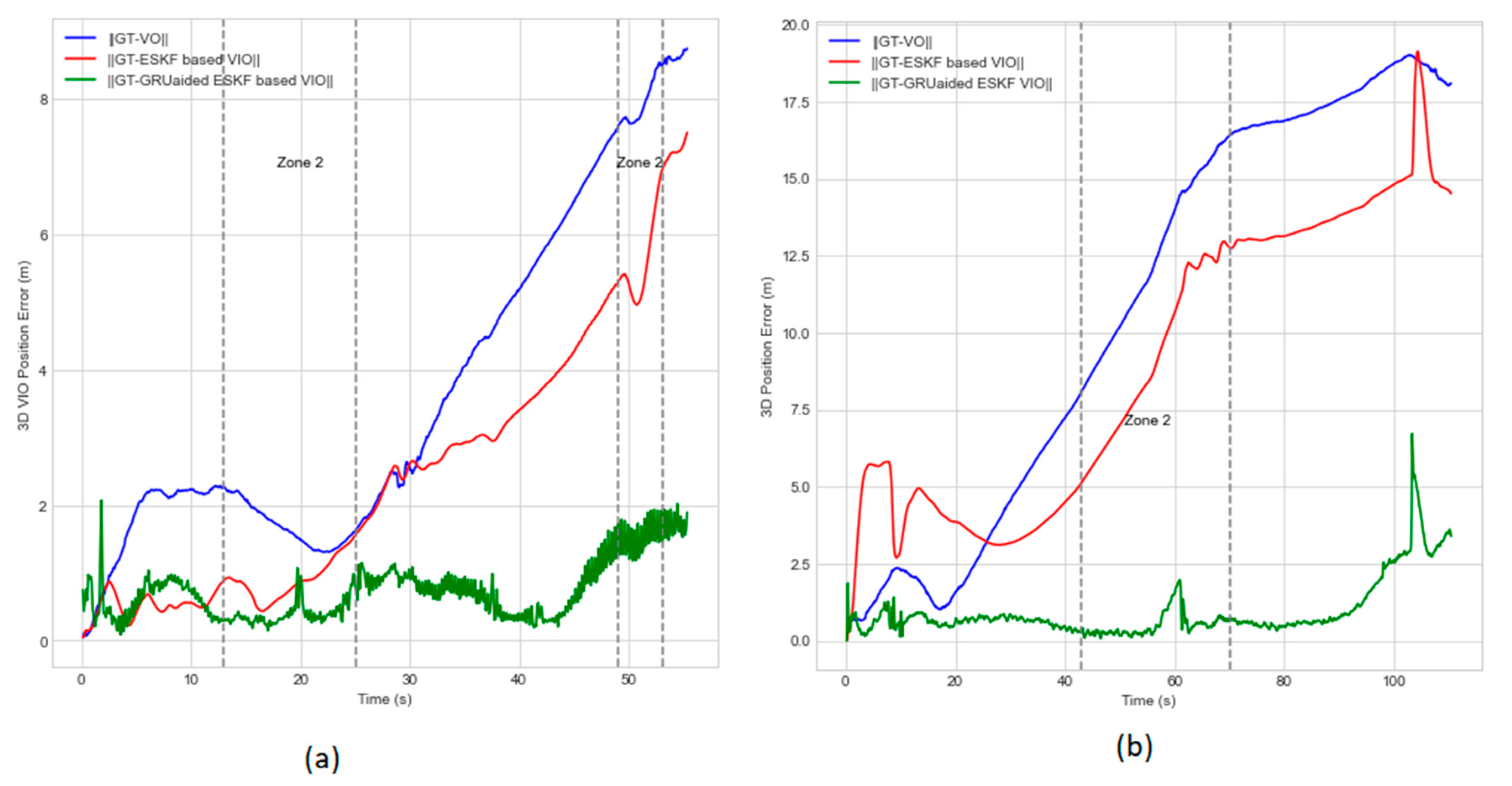
Figure 11 (a) & (b) adds zone 1 region to show performance comparisons of our proposed algorithm with the reference algorithms in presence of two failure modes. Maximum position errors for experiment 1 in the zone 1 along X, Y and Z axis are reduced by 52.38 %, 81.57 %, and 73.17 % respectively. In experiment 2, single fault is encountered twice during the time interval of 13 sec-44 sec and 70 sec-106 sec. Maximum position error in the time interval of 13 sec-44 sec in X, Y and Z axis are reduced by 93.33 %, 75 %, and 85 % respectively. Hence, the proposed solution proves to be robust over two failure modes.
Zone 2 includes multiple faults including turning manoeuvre and shadow of tall buildings that presents in both experiments. When UAV makes a turn, the motion dynamics change rapidly. This leads to challenges in estimating camera motion and orientation estimations causing tracking error. In the meantime, visual distortion also causes feature extraction errors and feature mismatch errors due to inconsistent lighting shown in Figure 12. The combination of both conditions adds complexity to the environment, exacerbating the existing challenges in traditional ESKF-based VIO. Our proposed algorithm is able to mitigate these failure modes and shows robustness in such complex scenes compared with traditional VIO system. The algorithm is able to mitigate motion dynamics and feature extraction error, reducing feature matching error by 20 %, 20 % and 50 % at the time interval of 13 sec-24 sec in experiment 1 and 62.5 %, 40 % and 90 % at the time interval of 45 sec-70 sec with the respect of X, Y, and Z axis shown in Figure 13 (a) and (b).
In Zone 3, multiple faults are combined together including turning manoeuvre, shadow from tall buildings, variation in lighting, areas of darkness and sunlight shadow. Zone 3 only exists as one most complex condition in the experiment 2. As observed in Zone 1 and Zone 2, the turning behaviour and shadow of tall buildings introduce changes in motion dynamics that makes the position estimation and feature tracking challenging for traditional ESKF based VIO. Additionally, the presence of both dark and well-lit areas within the scene created abrupt changes in illumination.
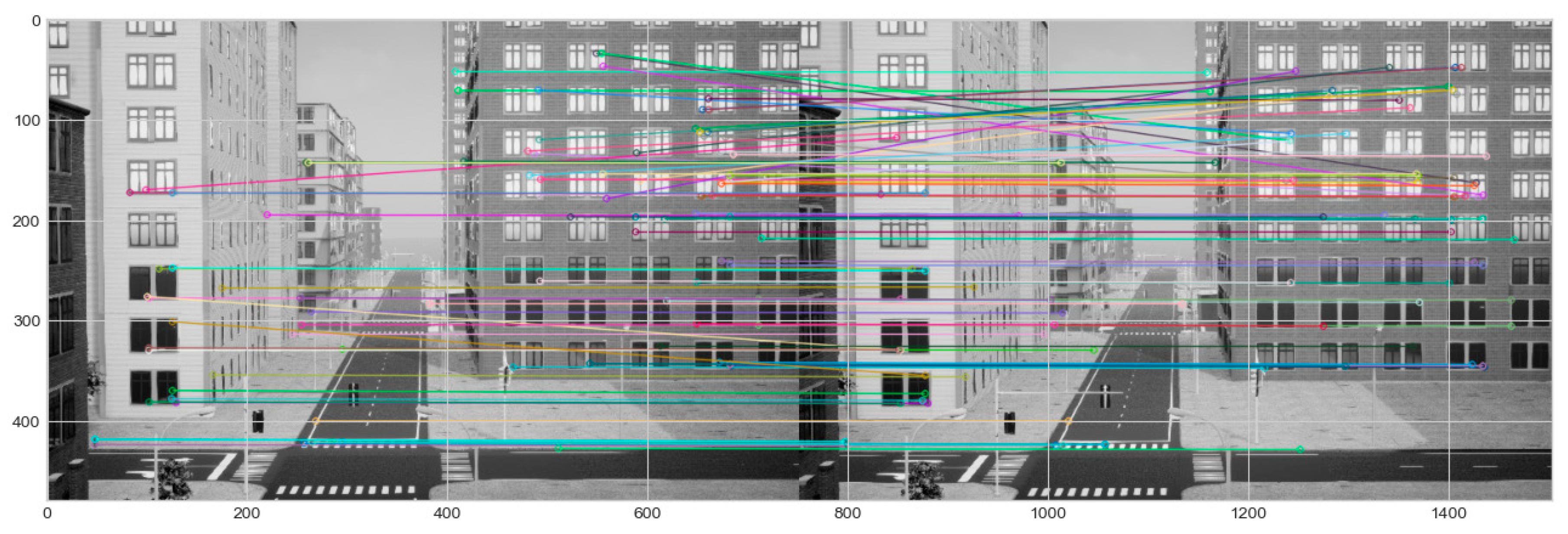
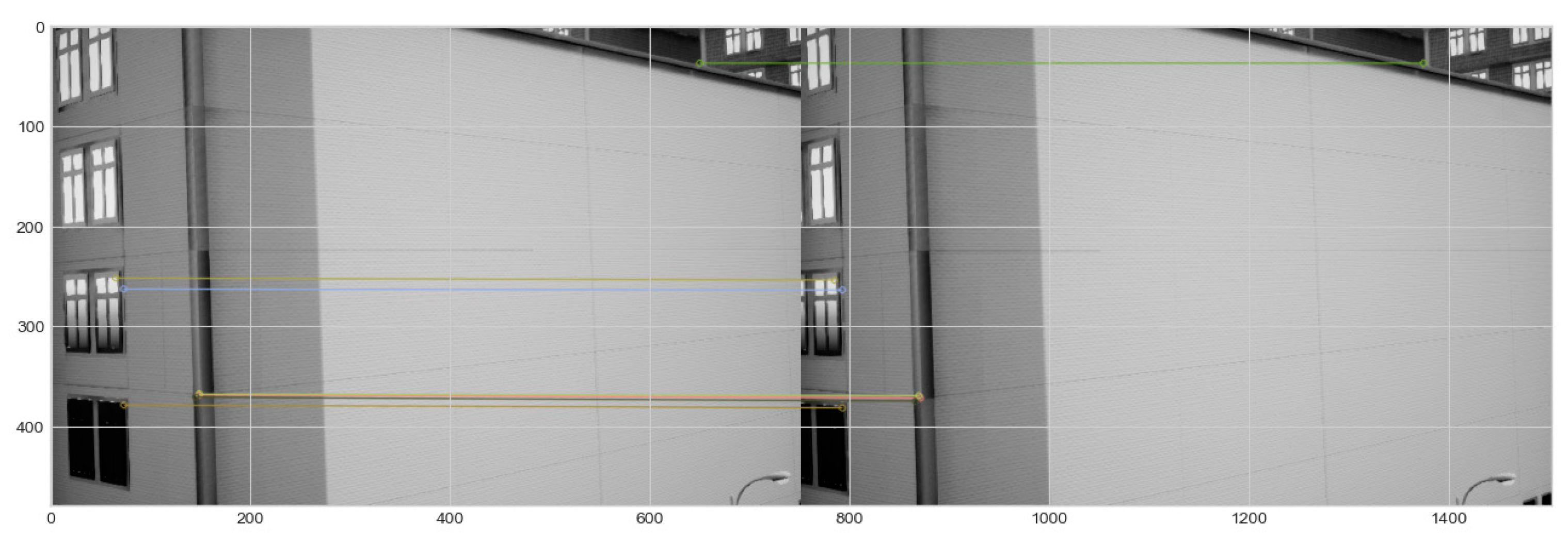
Figure 14 presents one demonstration image from the mounted front-facing camera in UAV when passing through illuminated and shaded area. Shadows caused by direct sunlight also creates sharp pixel contrast between illuminated and shaded areas. These sudden lighting changes and combination of multiple fault conditions amplify the challenges posed by each individual fault, making over all VIO performance more susceptible to tracking error, feature mismatch and feature extraction error failure mode.
Figure 15 shows that GRU-aided ESKF VIO architecture reduces maximum position error in experiment 2 at the time interval of 107 sec-114 sec from 32.6 %, 81.327 % and 64.397 % in X, Y and Z axis. Therefore, the GRU-aided fusion algorithm can perform without interruption when UAV navigates in illuminated and shaded areas and has showed robustness in presence of multiple failure modes and moving features amidst dynamic lightings.
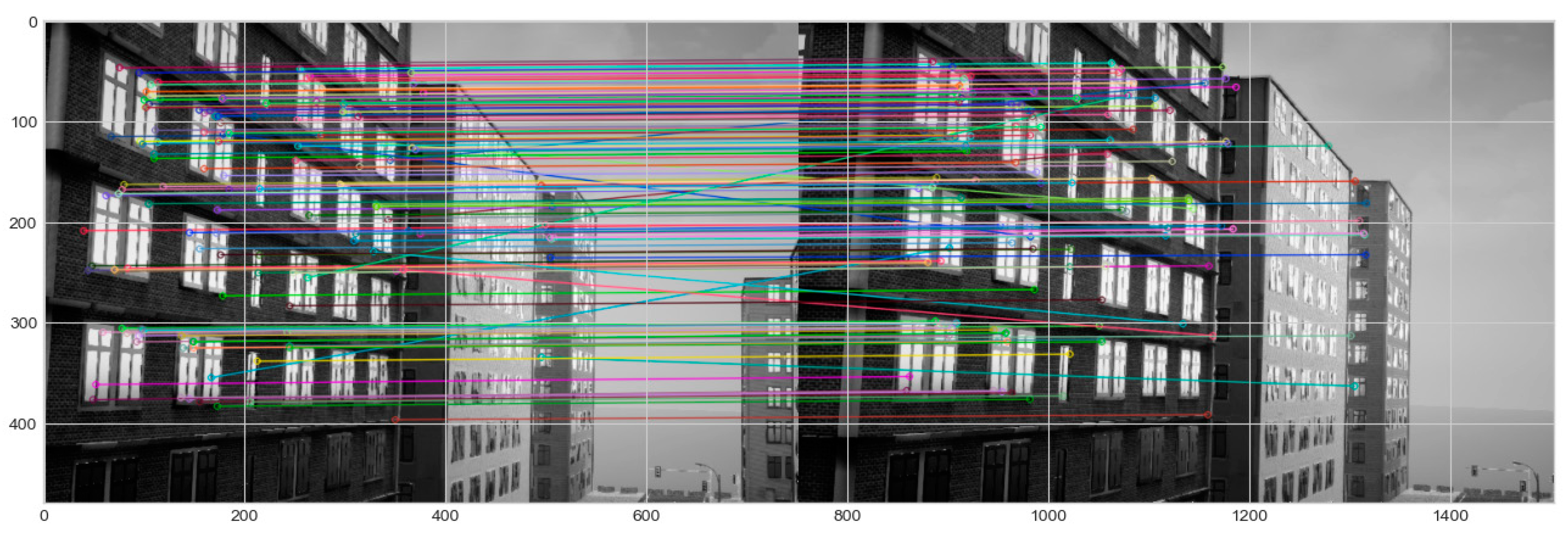
The zone 4 consists of a combination of complex faults including navigation environmental error and data association fault events. The fault events consist of turning manoeuvre, building shadows, presence of featureless blank wall and variation in lighting. In experiment 1, UAV encountered a plain wall at 27 sec -32 sec of its flight, resulting in feature extraction error due to lack of distinctive features on the wall shown on Figure 16. As a result, the feature extraction process failed, leading to lack of identifiable features to track and match in consecutive frames. Such lack of features causes VO to lose its frame-to-frame correspondence, resulting in the inability to accurately estimate the UAV’s motion in this specific time of 27 sec-32 sec. Figure 17 shows increment of position error causing from the mentioned disruption. The ESKF algorithm performance is heavily affected leading to increment in tracking errors and loss of tracking when dealing with featureless wall. Figure 17 shows our algorithm has effectively reduced the maximum position error by 42.1 %, 63.3 % and 60.12 % in X, Y and Z axis respectively.
To evaluate the performance of the proposed fault-tolerant federated multi-sensor navigation system, the experiment is conducted using the Experiment 1 dataset with GNSS condition applied (faulted-GNSS and without fault GNSS) adopted from [60]. Table 5 shows performance comparison results of the proposed GRU-aided ESKF VIO with faulted GNSS and no-fault GNSS. The results indicate that the hybrid approached enables mitigating the overall position error even with faulted GNSS conditions comparing to [11,60] Therefore, it is approved that the FMEA assisted fault-tolerant multi-sensor navigation system facilitates positioning performance in the presence of multiple faults covering all the sensors faults in diverge complex environments.

5.4. Performance Comparison with Other Dataset

This paper selects EUROC dataset specifically MH05_difficult for benchmarking with other algorithms since EUROC is commonly applied by other researchers [12,45]. The EUROC sequence dataset was collected in an indoor machine hall with light variation. MH05_difficult dataset contained black and white images which they referred as dark and shadowed environment and captured with rapid motion. Since, the dataset is captured in customized way that has several limitations including manipulated images, customized blur and brightness.
Figure 18 presents the 3D position error of running our proposed GRU-aided ESKF VIO to process MH05_difficult. The key finding is that the position error in RMSE is reduced by 67.32 %. The maximum error is reduced from 2.81 m to 1.5 m.
Table 6 highlights the comparison results in terms of the accumulated RSME with state-of-the-art-systems, i.e. End-to-End VIO, Self-supervised VIO [12,45]. It worth mentioning that the EUROC dataset doesn’t provide tight synchronization between IMU and images which is primary requirement of using RNN based VIO.
By crossing checking with the reference Brandon et al. [12], the proposed GRU-aided ESKF VIO confirms the robust improvement in the presence of motion blur failure mode.

6. Conclusion

Aiming to provide fault-tolerant VIO navigation solution against complex environments, this study proposed a hybrid federated navigation system framework aided by FMEA for enabling fault tolerance and GRU fused with ESKF-VIO to mitigate visual positioning errors.
Through simulations, the main advantages of the GRU and ESKF hybrid algorithm are summarized as follows- (1) A high efficiency recurrent neural cell with simple architecture, namely the GRU, was chosen to predict position error during visual degradation. Benefiting from the proper selection of the Kalman filter performance enhancement method such as updating state vector with predicting error using AI method, our proposed algorithm possesses superior navigation accuracy under complex conditions. (2) The FMEA analysis helps to prioritise anticipated failure modes such as feature extraction error, feature tracking error, motion dynamics, enabling us to mitigate position error caused by these failure modes before they lead to operation failure. (3) the mitigation of feature extraction failure modes, which can subsequently lead to feature association errors. Via demonstrations, it is found that multiple factors or faults within the navigation environment and the UAV’s dynamics reduce the impact of those failures.
This approach represents a significant step towards improving the robustness and reliability of VIO, particularly in complex and dynamic environments where feature extraction error, feature tracking error, and feature mismatch are critical for accurate navigation. With correction of the VIO, the fault tolerant multi-sensor performance is demonstrated to be improved under diverse complex urban environments in terms of robustness, and accuracy at different time scales, enabling uninterrupted and seamless flight operations.

References

  1. M. Y. Arafat, M. M. Alam, and S. Moh, “Vision-Based Navigation Techniques for Unmanned Aerial Vehicles: Review and Challenges,” Drones, vol. 7, no. 2. MDPI, Feb. 01, 2023. [CrossRef]
  2. Y. Alkendi, L. Seneviratne, and Y. Zweiri, “State of the Art in Vision-Based Localization Techniques for Autonomous Navigation Systems,” IEEE Access, vol. 9, pp. 76847–76874, 2021. [CrossRef]
  3. A. Ben Afia, A.-C. Escher, and C. Macabiau, “A Low-cost GNSS/IMU/Visual monoSLAM/WSS Integration Based on Federated Kalman Filtering for Navigation in Urban Environments A Low-cost GNSS/IMU/Visual monoSLAM/WSS Integration Based on Federated Kalman Filtering for Navigation in Urban A Low-cost GNSS/IMU/Visual monoSLAM/WSS Integration Based on Kalman Filtering for Navigation in Urban Environments,” 2015. [Online]. Available: https://enac.hal.science/hal-01284973.
  4. Y. D. Lee, L. W. Kim, and H. K. Lee, “A tightly-coupled compressed-state constraint Kalman Filter for integrated visual-inertial-Global Navigation Satellite System navigation in GNSS-Degraded environments,” IET Radar, Sonar and Navigation, vol. 16, no. 8, pp. 1344–1363, Aug. 2022. [CrossRef]
  5. J. Liao, X. Li, X. Wang, S. Li, and H. Wang, “Enhancing navigation performance through visual-inertial odometry in GNSS-degraded environment,” GPS Solutions, vol. 25, no. 2, Apr. 2021. [CrossRef]
  6. C. Zhu, M. Meurer, and C. Günther, “Integrity of Visual Navigation—Developments, Challenges, and Prospects,” NAVIGATION: Journal of the Institute of Navigation, vol. 69, no. 2, p. 69, Jun. 2022. [CrossRef]
  7. T. Qin, P. Li, and S. Shen, “VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator,” Aug. 2017. [CrossRef]
  8. A.I. Mourikis and S. I. Roumeliotis, “A multi-state constraint Kalman filter for vision-aided inertial navigation,” Proc IEEE Int Conf Robot Autom, pp. 3565–3572, 2007. [CrossRef]
  9. C. Campos, R. Elvira, J. J. G. Rodriguez, J. M. M. Montiel, and J. D. Tardos, “ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual-Inertial, and Multimap SLAM,” IEEE Transactions on Robotics, vol. 37, no. 6, pp. 1874–1890, Dec. 2021. [CrossRef]
  10. P. Geneva, K. Eckenhoff, W. Lee, Y. Yang, and G. Huang, “OpenVINS: A Research Platform for Visual-Inertial Estimation,” Proc IEEE Int Conf Robot Autom, pp. 4666–4672, May 2020. [CrossRef]
  11. J. Dai, X. Hao, S. Liu, and Z. Ren, “Research on UAV Robust Adaptive Positioning Algorithm Based on IMU/GNSS/VO in Complex Scenes,” Sensors (Basel), vol. 22, no. 8, Apr. 2022. [CrossRef]
  12. B. Wagstaff, E. Wise, and J. Kelly, “A Self-Supervised, Differentiable Kalman Filter for Uncertainty-Aware Visual-Inertial Odometry,” IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM, vol. 2022-July, pp. 1388–1395, 2022. [CrossRef]
  13. Y. Zhai, Y. Fu, S. Wang, and X. Zhan, “Mechanism Analysis and Mitigation of Visual Navigation System Vulnerability,” Lecture Notes in Electrical Engineering, vol. 773 LNEE, pp. 515–524, 2021. [CrossRef]
  14. L. Markovic, M. Kovac, R. Milijas, M. Car, and S. Bogdan, “Error State Extended Kalman Filter Multi-Sensor Fusion for Unmanned Aerial Vehicle Localization in GPS and Magnetometer Denied Indoor Environments,” 2022 International Conference on Unmanned Aircraft Systems, ICUAS 2022, pp. 184–190, Sep. 2021. [CrossRef]
  15. X. Xiong, W. Chen, Z. Liu, and Q. Shen, “DS-VIO: Robust and Efficient Stereo Visual Inertial Odometry based on Dual Stage EKF,” May 2019, [Online]. Available: http://arxiv.org/abs/1905.00684.
  16. F. Fanin and J.-H. Hong, Visual Inertial Navigation for a Small UAV Using Sparse and Dense Optical Flow. 2019. doi: 10.0/Linux-x86_64. [CrossRef]
  17. M. Bloesch, M. Burri, S. Omari, M. Hutter, and R. Siegwart, “Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback,” International Journal of Robotics Research, vol. 36, no. 10, pp. 1053–1072, Sep. 2017. [CrossRef]
  18. K. Sun et al., “Robust Stereo Visual Inertial Odometry for Fast Autonomous Flight,” IEEE Robot Autom Lett, vol. 3, no. 2, pp. 965–972, Apr. 2018. [CrossRef]
  19. G. Li, L. Yu, and S. Fei, “A Binocular MSCKF-Based Visual Inertial Odometry System Using LK Optical Flow,” Journal of Intelligent and Robotic Systems: Theory and Applications, vol. 100, no. 3–4, pp. 1179–1194, Dec. 2020. [CrossRef]
  20. Y. Yang, P. Geneva, K. Eckenhoff, and G. Huang, “Visual-Inertial Odometry with Point and Line Features,” IEEE International Conference on Intelligent Robots and Systems, pp. 2447–2454, Nov. 2019. [CrossRef]
  21. F. Ma, J. Shi, Y. Yang, J. Li, and K. Dai, “ACK-MSCKF: Tightly-coupled ackermann multi-state constraint kalman filter for autonomous vehicle localization,” Sensors (Switzerland), vol. 19, no. 21, Nov. 2019. [CrossRef]
  22. Z. Wang, B. Pang, Y. Song, X. Yuan, Q. Xu, and Y. Li, “Robust Visual-Inertial Odometry Based on a Kalman Filter and Factor Graph,” IEEE Transactions on Intelligent Transportation Systems, Jul. 2023. [CrossRef]
  23. O. Omotuyi and M. Kumar, “UAV Visual-Inertial Dynamics (VI-D) Odometry using Unscented Kalman Filter,” in IFAC-PapersOnLine, Elsevier B.V., Nov. 2021, pp. 814–819. [CrossRef]
  24. X. Sang et al., “Invariant Cubature Kalman Filtering-Based Visual-Inertial Odometry for Robot Pose Estimation,” IEEE Sens J, vol. 22, no. 23, pp. 23413–23422, Dec. 2022. [CrossRef]
  25. J. Xu, H. Yu, and R. Teng, “Visual-inertial odometry using iterated cubature Kalman filter,” Proceedings of the 30th Chinese Control and Decision Conference, CCDC 2018, pp. 3837–3841, Jul. 2018. [CrossRef]
  26. Y. Liu et al., “Stereo Visual-Inertial Odometry with Multiple Kalman Filters Ensemble,” IEEE Transactions on Industrial Electronics, vol. 63, no. 10, pp. 6205–6216, Oct. 2016. [CrossRef]
  27. S. Kim, I. Petrunin, and H. S. Shin, “A Review of Kalman Filter with Artificial Intelligence Techniques,” in Integrated Communications, Navigation and Surveillance Conference, ICNS, Institute of Electrical and Electronics Engineers Inc., 2022. [CrossRef]
  28. D. J. Jwo, A. Biswal, and I. A. Mir, “Artificial Neural Networks for Navigation Systems: A Review of Recent Research,” Applied Sciences 2023, Vol. 13, Page 4475, vol. 13, no. 7, p. 4475, Mar. 2023. [CrossRef]
  29. N. Shaukat, A. Ali, M. Moinuddin, and P. Otero, “Underwater Vehicle Localization by Hybridization of Indirect Kalman Filter and Neural Network,” in 2021 7th International Conference on Mechatronics and Robotics Engineering, ICMRE 2021, Institute of Electrical and Electronics Engineers Inc., Feb. 2021, pp. 111–115. [CrossRef]
  30. N. Shaukat, A. Ali, M. J. Iqbal, M. Moinuddin, and P. Otero, “Multi-sensor fusion for underwater vehicle localization by augmentation of rbf neural network and error-state kalman filter,” Sensors (Switzerland), vol. 21, no. 4, pp. 1–26, Feb. 2021. [CrossRef]
  31. L. Vargas-Meléndez, B. L. Boada, M. J. L. Boada, A. Gauchía, and V. Díaz, “A sensor fusion method based on an integrated neural network and Kalman Filter for vehicle roll angle estimation,” Sensors (Switzerland), vol. 16, no. 9, Sep. 2016. [CrossRef]
  32. Z. Jingsen, Z. Wenjie, H. Bo, and W. Yali, “Integrating Extreme Learning Machine with Kalman Filter to Bridge GPS Outages,” in Proceedings - 2016 3rd International Conference on Information Science and Control Engineering, ICISCE 2016, Institute of Electrical and Electronics Engineers Inc., Oct. 2016, pp. 420–424. [CrossRef]
  33. X. Zhang, X. Mu, H. Liu, B. He, and T. Yan, “Application of Modified EKF Based on Intelligent Data Fusion in AUV Navigation; Application of Modified EKF Based on Intelligent Data Fusion in AUV Navigation,” 2019.
  34. N. Al Bitar and A.I. Gavrilov, “Neural_Networks_Aided_Unscented_Kalman_Filter_for_Integrated_INS_GNSS_Systems,” 27th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), pp. 1–4, 2020.
  35. Z. Miljković, N. Vuković, and M. Mitić, “Neural extended Kalman filter for monocular SLAM in indoor environment,” Proc Inst Mech Eng C J Mech Eng Sci, vol. 230, no. 5, pp. 856–866, Mar. 2016. [CrossRef]
  36. M. Choi, R. Sakthivel, and W. K. Chung, “Neural Network-Aided Extended Kalman Filter for SLAM Problem,” in Proceedings 2007 IEEE International Conference on Robotics and Automation, 2007, pp. 1686–1690.
  37. K. Y. Kotov, A. S. Maltsev, and M. A. Sobolev, “Recurrent neural network and extended Kalman filter in SLAM problem,” in IFAC Proceedings Volumes (IFAC-PapersOnline), IFAC Secretariat, 2013, pp. 23–26. [CrossRef]
  38. L. Chen and J. Fang, “A hybrid prediction method for bridging GPS outages in high-precision POS application,” IEEE Trans Instrum Meas, vol. 63, no. 6, pp. 1656–1665, 2014. [CrossRef]
  39. J. Ki Lee and C. Jekeli, “Neural network aided adaptive filtering and smoothing for an integrated INS/GPS unexploded ordnance geolocation system,” Journal of Navigation, vol. 63, no. 2, pp. 251–267, Apr. 2010. [CrossRef]
  40. S. Bi, L. Ma, T. Shen, Y. Xu, and F. Li, “Neural network assisted Kalman filter for INS/UWB integrated seamless quadrotor localization,” PeerJ Comput Sci, vol. 7, pp. 1–13, 2021. [CrossRef]
  41. C. Jiang et al., “A Novel Method for AI-Assisted INS/GNSS Navigation System Based on CNN-GRU and CKF during GNSS Outage,” Remote Sensing 2022, Vol. 14, Page 4494, vol. 14, no. 18, p. 4494, Sep. 2022. [CrossRef]
  42. D. Xie et al., “A Robust GNSS/PDR Integration Scheme with GRU-Based Zero-Velocity Detection for Mass-Pedestrians,” Remote Sens (Basel), vol. 14, no. 2, Jan. 2022. [CrossRef]
  43. Y. Jiang and X. Nong, “A Radar Filtering Model for Aerial Surveillance Base on Kalman Filter and Neural Network,” in Proceedings of the IEEE International Conference on Software Engineering and Service Sciences, ICSESS, IEEE Computer Society, Oct. 2020, pp. 57–60. [CrossRef]
  44. Z. Miao, H. Shi, Y. Zhang, and F. Xu, “Neural network-aided variational Bayesian adaptive cubature Kalman filtering for nonlinear state estimation,” Meas Sci Technol, vol. 28, no. 10, Sep. 2017. [CrossRef]
  45. C. Li and S. L. Waslander, “Towards End-to-end Learning of Visual Inertial Odometry with an EKF,” Proceedings - 2020 17th Conference on Computer and Robot Vision, CRV 2020, pp. 190–197, May 2020. [CrossRef]
  46. Y. Tang, J. Jiang, J. Liu, P. Yan, Y. Tao, and J. Liu, “A GRU and AKF-Based Hybrid Algorithm for Improving INS/GNSS Navigation Accuracy during GNSS Outage,” Remote Sens (Basel), vol. 14, no. 3, Feb. 2022. [CrossRef]
  47. S. Hosseinyalamdary, “Deep Kalman filter: Simultaneous multi-sensor integration and modelling; A GNSS/IMU case study,” Sensors (Switzerland), vol. 18, no. 5, May 201. [CrossRef]
  48. L. Song, Z. Duan, B. He, and Z. Li, “Application of Federal Kalman Filter with Neural Networks in the Velocity and Attitude Matching of Transfer Alignment,” Complexity, vol. 2018, 2018. [CrossRef]
  49. D. Li, Y. Wu, and J. Zhao, “Novel Hybrid Algorithm of Improved CKF and GRU for GPS/INS,” IEEE Access, vol. 8, pp. 202836–202847, 2020. [CrossRef]
  50. X. Gao et al., “RL-AKF: An adaptive kalman filter navigation algorithm based on reinforcement learning for ground vehicles,” Remote Sens (Basel), vol. 12, no. 11, Jun. 2020. [CrossRef]
  51. M. F. Aslan, A. Durdu, and K. Sabanci, “Visual-Inertial Image-Odometry Network (VIIONet): A Gaussian process regression-based deep architecture proposal for UAV pose estimation,” Measurement, vol. 194, p. 111030, May 2022. [CrossRef]
  52. C. Chen, C. X. Lu, B. Wang, N. Trigoni, and A. Markham, “DynaNet: Neural Kalman Dynamical Model for Motion Estimation and Prediction,” IEEE Trans Neural Netw Learn Syst, vol. 32, no. 12, pp. 5479–5491, Aug. 2019. [CrossRef]
  53. A. Yusefi, A. Durdu, M. F. Aslan, and C. Sungur, “LSTM and filter based comparison analysis for indoor global localization in UAVs,” IEEE Access, vol. 9, pp. 10054–10069, 2021. [CrossRef]
  54. S. Zuo, K. Shen, and J. Zuo, “Robust Visual-Inertial Odometry Based on Deep Learning and Extended Kalman Filter,” Proceeding - 2021 China Automation Congress, CAC 2021, pp. 1173–1178, 2021. [CrossRef]
  55. Y. Luo, J. Hu, and C. Guo, “Right Invariant SE2(3) - EKF for Relative Navigation in Learning-based Visual Inertial Odometry,” 2022 5th International Symposium on Autonomous Systems, ISAS 2022, 2022. [CrossRef]
  56. U. I. Bhatti and W. Y. Ochieng, “Failure Modes and Models for Integrated GPS/INS Systems,” The Journal of Navigation, vol. 60, no. 2, pp. 327–348, May 2007. [CrossRef]
  57. Y. Du, J. Wang, C. Rizos, and A. El-Mowafy, “Vulnerabilities and integrity of precise point positioning for intelligent transport systems: overview and analysis,” Satellite Navigation, vol. 2, no. 1. Springer, Dec. 01, 2021. [CrossRef]
  58. M. Burri et al., “The EuRoC micro aerial vehicle datasets,” International Journal of Robotics Research, vol. 35, no. 10, pp. 1157–1163, Sep. 2016. [CrossRef]
  59. P. Geragersian, I. Petrunin, W. Guo, and R. Grech, “An INS/GNSS fusion architecture in GNSS denied environments using gated recurrent units,” AIAA Science and Technology Forum and Exposition, AIAA SciTech Forum 2022, 2022. [CrossRef]
  60. G. E. Villalobos Hernandez, I. Petrunin, H.-S. Shin, and J. Gilmour, “Robust multi-sensor navigation in GNSS degraded environments,” Jan. 2023. [CrossRef]
Preprints 86379 g001
Figure 1. Published articles on hybrid machine learning usage in KF.
Figure 1. Published articles on hybrid machine learning usage in KF.
Preprints 86379 g001
Preprints 86379 g002
Figure 2. Fault Tree Analysis for feature based VIO.
Figure 2. Fault Tree Analysis for feature based VIO.
Preprints 86379 g002
Preprints 86379 g003
Figure 3. Architecture of the proposed federated fault-tolerant multi-sensor navigation system.
Figure 3. Architecture of the proposed federated fault-tolerant multi-sensor navigation system.
Preprints 86379 g003
Preprints 86379 g004
Figure 4. Illustrative diagram of GRU-aided ESKF IMU/VO sub-filter in training phase.
Figure 4. Illustrative diagram of GRU-aided ESKF IMU/VO sub-filter in training phase.
Preprints 86379 g004
Preprints 86379 g005
Figure 5. Experimental simulation setup in MATLAB.
Figure 5. Experimental simulation setup in MATLAB.
Preprints 86379 g005
Preprints 86379 g006
Figure 6. Overall visual navigation error in the presence of multiple failure modes for Experiment 1.
Figure 6. Overall visual navigation error in the presence of multiple failure modes for Experiment 1.
Preprints 86379 g006
Preprints 86379 g007
Figure 7. Visual navigation error along each axis in the presence of multiple failure modes for Experiment 1.
Figure 7. Visual navigation error along each axis in the presence of multiple failure modes for Experiment 1.
Preprints 86379 g007
Preprints 86379 g008
Figure 8. 3D position error in the presence of multiple failure modes for Experiment 2.
Figure 8. 3D position error in the presence of multiple failure modes for Experiment 2.
Preprints 86379 g008
Preprints 86379 g009
Figure 9. Position error along each axis in the presence of multiple failure modes for Experiment 2.
Figure 9. Position error along each axis in the presence of multiple failure modes for Experiment 2.
Preprints 86379 g009
Preprints 86379 g010
Figure 10. Feature tracking and Feature mismatch error failure modes due to tall-shadowed buildings in experiment 1.
Figure 10. Feature tracking and Feature mismatch error failure modes due to tall-shadowed buildings in experiment 1.
Preprints 86379 g010
Preprints 86379 g011
Figure 11. Position errors of Zone 1 (shadowed building) estimated in each axis for experiment 1 (a). Position errors of Zone 1 (shadowed building) estimated in each axis for experiment 2 (b).
Figure 11. Position errors of Zone 1 (shadowed building) estimated in each axis for experiment 1 (a). Position errors of Zone 1 (shadowed building) estimated in each axis for experiment 2 (b).
Preprints 86379 g011
Preprints 86379 g012
Figure 12. Motion dynamics, Feature tracking and Feature mismatch error failure modes due to tall shadowed buildings in experiment 2.
Figure 12. Motion dynamics, Feature tracking and Feature mismatch error failure modes due to tall shadowed buildings in experiment 2.
Preprints 86379 g012
Preprints 86379 g013
Figure 13. Position errors of Zone 2 (shadowed building and UAV turns) estimated in each axis for experiment 1(a). Position errors of Zone 2 (shadowed building and UAV turn) estimated in each axis for experiment 2 (b).
Figure 13. Position errors of Zone 2 (shadowed building and UAV turns) estimated in each axis for experiment 1(a). Position errors of Zone 2 (shadowed building and UAV turn) estimated in each axis for experiment 2 (b).
Preprints 86379 g013
Preprints 86379 g014
Figure 14. Feature tracking, feature extraction error and feature mismatch failure modes for dark and well-illuminated tall buildings in experiment 2.
Figure 14. Feature tracking, feature extraction error and feature mismatch failure modes for dark and well-illuminated tall buildings in experiment 2.
Preprints 86379 g014
Preprints 86379 g015
Figure 15. Position errors in Zone 3 (UAV turn and illuminated tall buildings) estimated in each axis for experiment 2.
Figure 15. Position errors in Zone 3 (UAV turn and illuminated tall buildings) estimated in each axis for experiment 2.
Preprints 86379 g015
Preprints 86379 g016
Figure 16. Feature extraction error due to plain wall in experiment 1.
Figure 16. Feature extraction error due to plain wall in experiment 1.
Preprints 86379 g016
Preprints 86379 g017
Figure 17. Position errors of Zone 4 (UAV turn, shadowed buildings, and featureless wall buildings) estimated in each axis for experiment 1.
Figure 17. Position errors of Zone 4 (UAV turn, shadowed buildings, and featureless wall buildings) estimated in each axis for experiment 1.
Preprints 86379 g017
Preprints 86379 g018
Figure 18. 3D position error estimated using MH05 seq EUROC Dataset with motion blur failure mode.
Figure 18. 3D position error estimated using MH05 seq EUROC Dataset with motion blur failure mode.
Preprints 86379 g018
Table 1. Common faults in the visual positioning based on a state-of-the-art review.
Table 1. Common faults in the visual positioning based on a state-of-the-art review.
Error Sources Fault event References Error effect
Feature Tracking Error Navigation environment error [45] Motion blur
Outlier Error [52] Overexposure
[12,45] Rapid Motion
Feature Extraction Error [6,12] Overshoot
Feature Mismatch Data Association error
Feature Domain Bias [52] Lighting Variation
Table 2. Specification of the ICM 20649 IMU model.
Table 2. Specification of the ICM 20649 IMU model.
Parameter Value
Accelerometer Bias Stability 0.014 m/s2
Gyroscope Bias Stability 0.0025 rad/s
Angle Random Walk 0.00043633 m/s2 ∗ √Hz
Velocity Random Walk 0.0012356 m/s2 ∗ √Hz
Table 3. RMSE Comparison on the performance of two experiments.
Table 3. RMSE Comparison on the performance of two experiments.
Experiment Method RMSE(m)-X axis RMSE(m)-Y axis RMSE(m)- Z axis RMSE(m)-overall
1 VO 1.4 2.3 3.4 4.3
ESKF VIO 1.3 2.2 1.6 3.1
GRU-aided ESKF VIO 0.5 0.4 0.3 0.7
2 VO 6.6 2.9 10.4 12.6
ESKF VIO 4.7 2.5 8.6 10.1
GRU-aided ESKF VIO 0.8 0.9 0.5 1.3
Table 4. Maximum position error comparison for two experiments.
Table 4. Maximum position error comparison for two experiments.
Experiment Method Maximum Error in X axis (m)- Maximum Error in Y axis (m)- Maximum Error in Z axis (m)- Maximum 3D Error
(m)-
ESKF VIO 3.2 5.6 4.1 7.5
1 GRU-aided ESKF VIO 1.5 1.6 1.2 1.9
ESKF VIO 8.2 6.6 16.2 19.1
2 GRU-aided ESKF VIO 5.0 4.4 3.0 6.8
Table 5. RMSE of 3D position errors of GNSS/faulted-IMU/faulted-VO solution with faulted-GNSS/faulted-IMU/faulted-VO.
Table 5. RMSE of 3D position errors of GNSS/faulted-IMU/faulted-VO solution with faulted-GNSS/faulted-IMU/faulted-VO.
Algorithms 3D RMSE position error (m)
Faulted-VO/GNSS/IMU 1.2
Faulted-VIO-ESKF/ GNSS/IMU 0.7
Faulted-GRU-aided-ESKF-VIO/GNSS/IMU 0.09
Faulted-VO/Faulted-GNSS/IMU 1.5
Faulted-ESKF-VIO/Faulted-GNSS/IMU 1.0
Faulted-GRU-aided-ESKF-VIO/Faulted-GNSS/IMU 0.2
Table 6. Comparison with state-of-the-art methods that used MH_05 seq. EUROC Dataset with motion blur failure mode.
Table 6. Comparison with state-of-the-art methods that used MH_05 seq. EUROC Dataset with motion blur failure mode.
Algorithms RMSE (m)-of MH_05 seq Improvement
End-to-end VIO [45] 1.96 m 66.32%
Self-supervised VIO [12] 1.48 m 55.4%%
Proposed GRU-aided ESKF VIO 0.66 m ---------
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated