Prerpints.org logo
Preprint
Article

Impact of Port Clearance on shipping Safety, Energy Consumption and Green Ports Sustainability

Altmetrics

Downloads

126

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 September 2023

Posted:

28 September 2023

You are already at the latest version

Alerts
Abstract
In many ports, the ship's speed is limited for the safety of navigation. At the same time, ship captains and port pilots choose the speed of the ship, but not higher than the permitted speed of the ship in the port, therefore the speed of the ship also depends on the experience of the ship captains and port pilots and the sailing conditions of the ship in specific conditions. Choosing the optimal speed of ships in port, including the effect of shallow depth, can reduce fuel consumption and ship emissions in ports, which is important for the development of green and sustainable ports. In all cases, shipping safety is the highest priority. The main objectives of the article are determining the optimal speed of ships in ports with low clearance, ensuring navigational safety, reducing fuel consumption and emissions, and at the same time creating a sustainable port. The article presents the methodology of optimal ship speed calculation, minimum ship controllable speed maintenance, fuel consumption and emission reduction methodology and their impact on sustainable and green maritime transport and port development. The developed methodology was tested on real ships and with the help of a calibrated simulator, sailing through harbor channels and harbor waters in low clearance conditions.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

Sustainable and green ports are very important for all regions of the world and it is necessary to achieve this in various possible ways. At the same time, it is necessary to understand that maritime transport is very stagnant, for example, ships are planned to work for 15-20 years and reconstruction or renovation is not always possible to use new types of fuel or new energy sources. At the same time, even small progress in reducing environmental impact is important.
The entry of ships into ports is a daily procedure, but at the same time, the different experience of ship captains and port pilots, different characteristics of ship manoeuvrability, traditions and other elements greatly influence the amount of ship manoeuvres entering and leaving ports, fuel consumption and generated emissions. The analysis of main engine manoeuvres of ships entering ports shows very large differences between ships of the same type and it is mainly related to the knowledge, experience and individual characters of ship captains and port pilots [1-3]. In many ports, port pilots worked for a long time as navigators and captains on relatively small ships before becoming pilots [4, 5]. As pilots become more competent, they receive permits to service larger vessels, but the long working time on smaller vessels greatly affect their working methods.
A very good understanding of the ship's manoeuvrability by the ship's captain and port pilots allows to guarantee the ship's navigational safety when entering ports and other places [2, 6], as well as to optimize the ship's manoeuvres and thereby reduce the ship's fuel consumption and emissions generation [7, 8].
The analysis of accidents and incidents when ships enter the port showed that they are mostly related to the mistakes of ship captains, port pilots or VTS (vessel traffic system) operators, but very rarely ship accidents and incidents are related to the ship’s speed in port channels and port waters [1, 3]. Many ports have speed limits for ships and in most cases these limits are between 6 and 10 knots [3, 9, 10].
In some situations, ship captains and port pilots, due to a lack of information about the ship's manoeuvrability or lack of experience, did not take into account the technical and manoeuvrability parameters of the ships, which affected the ship's behaviour at low clearances (spaces between the ship's keel and the channel bottom), which led to ship manoeuvres errors, especially when ships navigate the bends of navigational channels [3, 11]. It should be noted that in cases where professional training and practical staff training is based on modern knowledge of ship manoeuvrability under various navigational conditions, it can increase the navigational safety of ships entering and leaving ports when ships sail independently and/or with the additional use of external assistance (e.g. port tugs) or without it [12-14].
The optimal of ship’s speed in the ports entrance and internal navigation channels, assessing the manoeuvrability of ships, has not been well studied, so the available experience of ship captains and port pilots is often relied on, but such solutions are not always optimal [15, 16].
The main objective of the paper is to present a developed methodology to determine the optimal ship speed in low clearance conditions, during which the ship is still well controlled, with minimum fuel consumption and minimum ship emissions, which is very important for the development of sustainable and green ports. The novelty of the article is based on the development of a methodology that allows the calculation of the minimum ship's controllable speed, using minimum fuel consumption and generating minimum ship emissions, depending on the size of the clearance (in the case of low clearance).
The research methodology is based on the assessment of external and internal forces and moments acting on the ship while sailing in port channels and port waters, determining the minimum controllable ship’s speed, with small clearances and possible minimum fuel consumption, adapting to specific port conditions and at the same time generating minimum emissions.
The main goal of low-clearance optimization is the safety of navigation in port shipping channels with minimal fuel consumption and minimal ship emissions, which is essential for the development of sustainable and green ports.
The article presents a method for calculating the optimal ship’s speed in port navigation channels and port water areas, which are important for many ports, using the minimum fuel consumption, and its application in specific conditions, which allows guaranteeing navigation safety in ports, optimize fuel consumption, reduce emissions from ships, research results. The article consists of the research analysis of the existing situation, the principles of creating a mathematical model and the mathematical model itself. The application of the developed mathematical model in specific conditions, the results of experiments performed on real ships and using a calibrated visual simulator are presented. It also presents the discussion and conclusions of the calculated and experimentally verified results of optimal ship’s speed in port navigation channels and port waters, using minimal fuel consumption.
The scientific contribution of the conducted research is a new methodology that allows determining the optimal speed of ships in port channels and port waters with minimal fuel consumption and minimal impact on the environment, which is important for the development of sustainable and green ports.

2. Analysis of ships sailing speed and generated emissions in ports situation and literature review

Numerous resources have analysed vessel speed in harbours and inland waterways [2, 10, 17, 18]. Ship speed in ports is limited by the hydrodynamic effect of ship interaction (floating and mooring at quays), as well as waves caused by moving ships, which erode shores and negatively affect (destroy) port infrastructure [15]. . Reduced ship speed also reduces the probability of ship collisions [13, 17, 19 - 22]. For example, in the port of Klaipeda the permitted speed of the ship is up to 8 knots [9], in the access channels of the port of Hamburg (in the Elbe river) up to 13 knots, in the port areas up to 9 knots. (some places have special requirements when approaching individual port locations and individual inland navigation for canal sections) [23]. Vessel speed limits are up to 12 knots in the canals of the port of Rotterdam, up to 8 knots in some sections [24]. Similar permissible ship speeds can be found in other ports of the world [13, 18, 19, 21]. At the same time, the allowed speed of ships in ports is often not optimal in terms of energy (fuel) consumption and emissions of ships [16, 25]. For a sustainable approach, it is very important to find optimal ship speed solutions when entering the port and in the internal shipping channels, as well as approaching individual important points of the port (areas defined by port administrations) [19]. Reduced ship speed is also important in reducing ship energy (fuel) consumption and emissions [25, 26].
After analysing ship accidents and emergency incidents in ports, it became clear that most of them were caused by either too high or too low speed in ports [1, 3, 8, 13, 20], therefore, in determining the optimal but at the same time safe speed of the ship in ports, the minimum possible the speed of ships in ports is very important both from the point of view of the safety of shipping and the impact on the environment [7, 15].
After assessing the main aspects of ship navigation in port channels and port waters (navigation safety is a priority), they can be grouped as follows [20, 27, 28]:
- ship navigation must be safe for the sailing ships themselves;
- the passage of ships must not reduce the safety of other ships sailing in channels or moored at quays;
- ship navigation must meet the general needs of the port (ship sailing schedules, positioning of ships, minimal interaction with other ships entering and leaving the port);
- minimal impact on port infrastructure and superstructure;
- use the minimum fuel consumption;
- emit as little pollutants as possible during navigation.
Navigation of ships in port channels and port waters must be safe for the ship itself, and its speed must allow good controllability of all operations entering the port (navigating through channels, turning in turning basins, stopping, approaching and leaving quays) [21, 29]. In this way, the ship's controllability is very important in the whole process of the ship's entry into the port.
When a ship is sailing through port channels and port water areas, it must not create impact for other ships due to the high hydrodynamic interaction between ships, the impact of create by sailing ship waves on berthing or passing ships as well during sailing clause to other constructions [28, 30]. Ports are sometimes very congested and ships sailing to and from the port must not create additional time wasting for other ships and port operations [13, 17, 19, 31]. In many ports, the harbour approaches and especially the inner navigation channels are not very busy, so ships have the opportunity to sail at minimal but safe speeds, with minimal fuel consumption and at the same time generating minimal emissions.
When sailing through port channels and port water areas, ships must not cause negative consequences or additional risks to the port infrastructure and superstructure due to the waves caused by the sailing ship or the risks of collision with the port infrastructure or superstructure [25, 28, 31, 32].
It is very important for ships to use as little fuel as possible when sailing through port channels and port waters, which is very important for the economic indicators of the ship itself, and at the same time generate minimal emissions in the port area, while positively influencing the creation of green and sustainable ports [15, 33-35].
The above-mentioned factors are very important, but they partially contradict each other, as for example, a very low speed of the ship in the port channels and port waters, as long as the ship is well controlled, increases the safety of the ship, reduces the hydrodynamic impact on other ships, but at the same time requires more time and it worsens port indicators, because other ships have to wait, in some cases they have to stop loading operations for a longer period of time, etc. [25, 33]. Many ports have installed modern navigation systems that allow for high-quality regulation of ship traffic, but they cannot accurately assess the minimum speed of control of ships, which is very important for ensuring the safety of navigation in port channels.
Much attention is paid to the planning of port navigational channels and water areas in order to meet the safety requirements of shipping navigation [33, 36-39], but in old and sometimes newly built ports it is not always possible to fulfil all the requirements (standards and recommendations) due to geographical and other conditions, for example, existing cities, protected historical objects, etc. As, for example, in Helsinki, Haugesund and other ports in similar geographical situations, the navigational channels are located between islands with historical structures and it is very difficult or impossible to implement channel width standards or recommendations [18, 36, 37]. In this case, to guarantee the safety of shipping, restrictions regarding wind speed and direction, requirements for the use of tugboats and the like must be adopted [12, 22], so it is not always possible to use the optimal calculated conditions.
Existing environmental requirements and recommendations, especially for ship emissions [40-42], target ship operators to reduce fuel consumption and emissions at the same time, but this is not always possible to achieve as the priority is navigational safety. In the event that ship captains and harbour pilots, due to insufficient research on the manoeuvrability of the ship in specific conditions or lack of knowledge and practical experience, doubt the possible minimum ships speed, they always choose a speed that seems safe to them and often it is higher than the optimal speed [19, 31].
The minimum speed of the ship at which it can navigate the harbour channels and harbour waters must be such that the ship can be well controlled, especially when braking the ship at turning basins or approaching quays, depending on external forces [22]. In such cases, vessels must use rudder-propeller assemblies and thrusters, if available on board, or use tug(s) to maintain good control of the vessel. The minimum possible ship speed, when the ship is still well controlled, has been analysed in various literature sources [43-45], but the minimum ship speed has been little studied at shallow depths, which are typical for ports. At the same time, the minimum controllable speed of the ship when sailing the ship in the navigation channels of the ports is especially important in extreme hydro meteorological conditions, when it is very difficult to correct even the smallest inaccuracies in the control of the ship.
Many studies deal with the problem of the schedules of ships navigating the harbour channels and harbour waters [31]. Given the uncertainty of the arrival time processes of container ships and other liners at large container ports and other similar ports and terminals, modelling capabilities are often used. Separate works identify the main navigational processes and operations related to the port's marine infrastructure and review and evaluate existing port modelling methods [12, 25]. The indicated studies are for port assessment purposes with a focus on safety and capacity. The evaluation of various similar models focuses on determining the appropriate criteria for ship navigation based on what processes are included in each model and how they have been taken into account in each model, but many models are incompletely related to the optimal ship speed in harbour channels and harbour waters by estimating minimum fuel consumption and minimum emissions [43, 47-49].
The analysis of previous theoretical and experimental works by various authors allows to partially solve the practical problems of shipping safety and reducing environmental impact in ports, but at the same time, new challenges are very important, because ports try to attract ships of the maximum possible sizes, to reduce environmental impact as much as possible, i.e. to become green and sustainable ports, therefore further research is essential.
The literature analysis carried out on the topic analysed in the article showed that a number of studies have been carried out, but at the same time, there is a lack of complex studies related to the minimum ship controllable speed, optimal fuel consumption when ships sail in ports, opportunities to minimize the amount of ship emissions while sailing at an optimal speed, at low clearances in harbour channels and harbour waters, what constitutes the novelty of these studies presented in the article.
In this way, the article analyses the minimum speed at which the ship can be operated using minimum fuel consumption in port conditions, where there is little or in some cases the minimum possible clearance is important both to provide navigational safety and to reduce environmental impact, and this problem has been studied very little in detail.
In this way, there is a need to study the optimal ship’s speed in port channels and water areas in order to optimize the ship’s speed in ports, minimizing fuel consumption and minimizing generated emissions, which is influence on sustainable and green ports development and in same time guaranteeing the necessary navigational safety of ships.

3. Research methodology

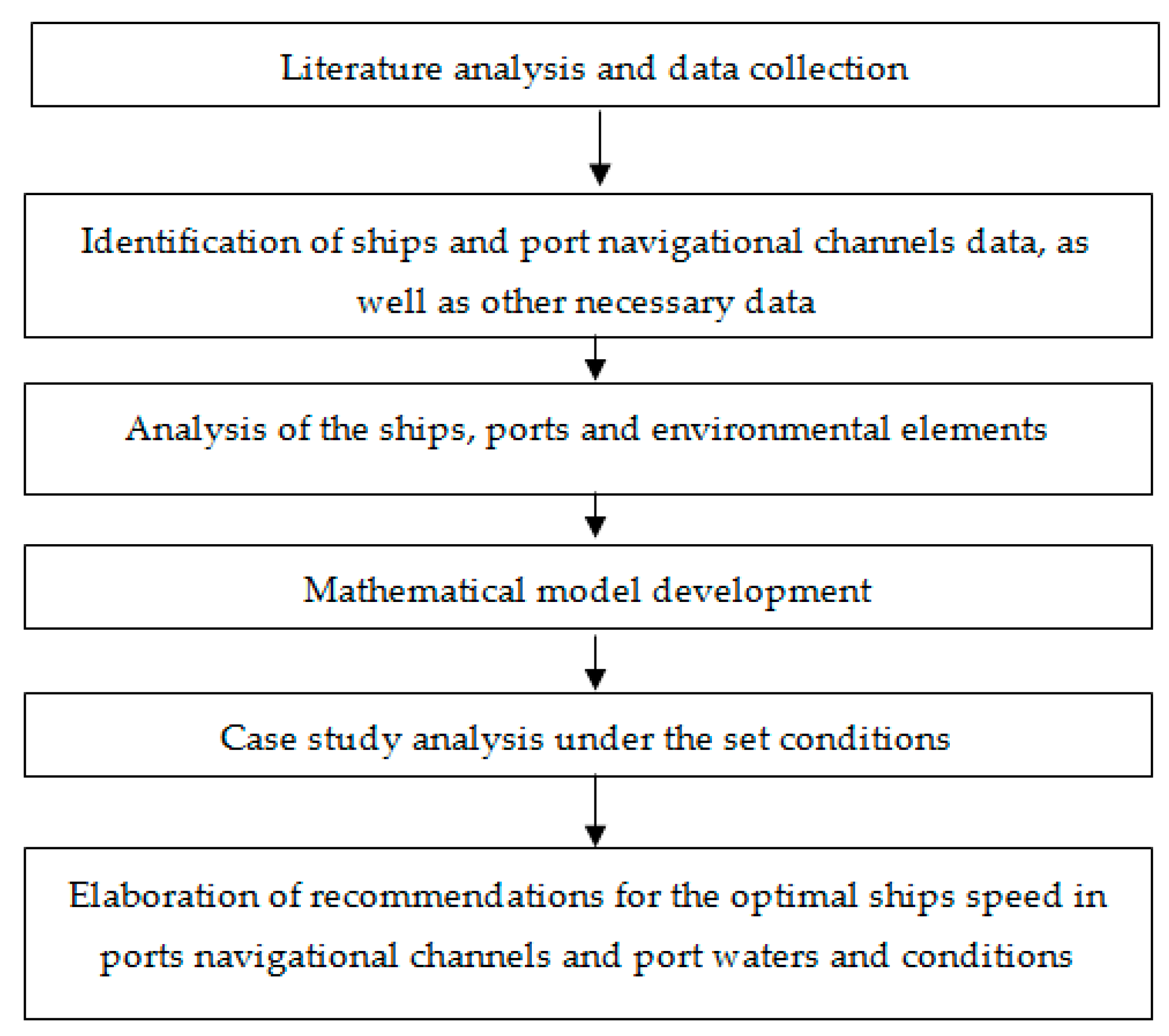
The following steps of research methodology were used to conduct the research (Figure 1). After conducting the situation analysis and literature review, the mathematical model has been developed.

3.1. Research methodology basic ideas

In order to prepare the methodology, first of all, an analysis of the available situation and literature was carried out, which allowed an overview of the situation of ship control of ships entering ports, including navigation safety, using the necessary fuel and the influence of shallow depth on the sailing characteristics of ships. The movement of ships in port channels and port waters, the reduction of emissions from ships in port channels and port waters, etc., were also studied. The necessary data were collected based on literature sources and observations of real ship sailing conditions in port channels and port waters, as well as experimental data obtained from VTS (vessel traffic system) systems operating in ports, shipping companies and using calibrated full-mission simulators.
In this way, the methodology developed in the study must take into account the possible attraction of the largest ships to the ports, the parameters of the port channels and the port water area, the manoeuvrability of ships, fuel consumption, the effect of shallow water, hydrological and hydro metrological conditions in the ports, as well as the possible minimum speed of ships in the port navigation in the channels and in the port areas, guaranteeing the navigational safety of ships (Figure 1).
Hydro-meteorological and hydrological conditions during navigation of ships in port channels and port waters, which must be evaluated when developing research methods, are the following: wind speed, wind course angle, current speed, current course angle, etc.
Additional data needed for research and must be collected and analysed, such as: the width of navigation channels (waterways), depths in port navigation channels and port water areas intended for ship navigation and manoeuvring [50]. In addition, the relevant calibration coefficients of the simulator obtained during theoretical and experimental studies [51-53] were taken into account.
On the basis of theoretical and experimental research, a mathematical model was created that allows to calculate the possible minimum and optimal ships speed in the port channels and in the port water area with the possibility of good control of the ship, the sailing time of the ships, fuel consumption, emissions, as well as evaluating the hydrological and hydro meteorological conditions in the port channels and the port in water areas. This model considers the implementation of the following steps:
- collect and analysis of the aforementioned data,
- plan possible sailing distances in the port,
- calculate the minimum ship’s speed in real harbour conditions, based on the collected necessary data,
- calculate of specific ship sailing parameters: speed, time, costs and fuel consumption;
- calculate and analysis of the total amount of emissions while the ship is sailing in the port channels and in the port water area at optimal speed;
- make conclusions and recommendations on specific conditions.
The boundary conditions of the methodology and the model are as follows: the sizes of ships and their sailing speed in the port channels and in the port water area depend on the infrastructure parameters; the minimum ships speed depends on the external impact forces (wind, current, waves) and clearance in case of good ship controllability; optimal ship speed is due to ship control limitations; tugboat assistance is available to improve vessel handling.
The proposed methodology was verified based on a case study. The possible ships speed which draft to depth ratio was up to 0.92 - 0.96 were analysed in detail, and calculations were made based on the real data. Based on the archived results, recommendations, discussions and conclusions were proposed regarding possible minimum ships speed in harbour channels and harbour waters, with the lowest emission estimates. At the same time, the proposed methodology can be applied in other ports as well.

3.2. Mathematical model

Many ports in the world have long approach and internal navigation channels in which ships can keep optimal speed. External forces and moments acting on the ship sailing by port navigational channels and port waters shall be compensated by ship’s rudder created forces and moments or if use tugs assistance – created by additional tugs forces and moments. Thus, calculation of the forces and moments can be done using the following mathematical model, based on D’Alembert principle [22, 39, 54]:
Bandyti dar kartą
Bandoma iš naujo...
Bandoma iš naujo...
X i n + X k + X β + X p + X N + X a + X c + X b + X s h + X T + X t u g + ... = 0
Y i n + Y k + Y β + Y p + Y N + Y a + Y c + Y b + Y s h + Y T + Y t u g + ... = 0
M i n + M k + M β + M p + M N + M a + M c + M b + M s h + M T + M t u g + ... = 0
Where: X i n , Y i n , M i n - inertia forces and the moment; X k , Y k , M k - forces and moment created by the ship’s hull, could be calculated by using the methodology stated at [51, 53]; X β , Y β , M β - the ship’s hull as the acting “wing” related forces and the moment, could be calculated using the methodology stated at [14]; X p , Y p , M p - forces and the moment created by the ship’s rudder or other steering equipment [51, 53]; X N , Y N , M N - forces and the moment created by thrusters [22, 53]; X a , Y a , M a - aerodynamic forces and the moment, could be calculated using the methodology stated at [51, 53, 54]; X c , X c , M c - forces and the moment created by the current, could be calculated using the methodology stated at [51, 53]; X b , Y b , M b - forces and the moment created by waves, could be calculated using the methodology stated at [51, 53]; X s h , Y s h , M s h - forces and the moment created by shallow water effect [22, 55]; X T , Y T , M T - forces and the moment created by ship’s propeller (propellers), could be calculated using the methodology stated at [51, 56]; X t u g , Y t u g , M t u g - forces and moment created by tugs [22, 51]. Additional forces and moments could be created by anchor or mooring ropes or other factors.
When a ship is moving through port navigation channels and port waters (typical procedures for ships entering ports) and without the assistance of tugboats, the ship's rudder forces and moments must be able to compensate for all external forces and moments to keep the ship on a specific heading. Then equations (1) – (3) could be written as follows:
X i n + X k + X β + X a + X c + X b + X s h + X T + ... = X p
Y i n + Y k + Y β + Y a + Y c + Y b + Y s h + Y T + ... = Y p
M i n + M k + M β + M a + M c + M b + M s h + M T + ... = M p
Forces and moments expressed in equations (4) – (6) could be calculated using methodologies, presented in [14, 51, 53, 55] and others.
When sailing in port navigation channels and port waters, there are often no waves, when a ships speed of 6 knots and more, the ship's control is not affected by tugs and steering devices (thrusters), and only traditional ship steering devices (ship propeller(s) and rudder(s)) are used to control the ship. In such most cases, the ship sails with no or minimal drift angle and the ship's speed does not change significantly (if the power of the ship's main engine(s) does not change), then dependencies (4) - (6) will be written:
X p = X k + X a + X c + X s h + X T + ...
Y p = Y a + Y c + Y T + ...
M p = M a + M c + M T + ...
Equations (7) - (9) are adapted to port conditions when there are no waves and the ship moves straight or in small turns and does not require the use of additional ship control devices: tugs and steering devices, like thrusters. In this case, the equations do not take into account the effects of waves, forces and moments created by tugs and thrusters. In each specific case, equations (4) - (6) must be adapted to the specific situation of the sailing ship (specific port).
Forces and moment created by rudder (rudders) ( X p , Y p , M p ), acting on ship’s steering, could be calculated as follows [22, 51, 53, 56]:
X p = C x ρ 2 S p v 2
Y p = C y ρ 2 S p v 2
M p = Y p l p
Where: C x , C y - rudder hydrodynamic coefficients, could be taken in account until rudder turn angle up to 20 degrees (to have steering reserve) [22, 57, 58]; v - ship’s speed; ρ - water density; S p - the area of projection of the rudder plane into the diametrical plane (area) [39, 53, 57]; l p - rudder’s transverse force shoulder [39, 53, 57].
The lateral (lift) force generated by the ship's steering mechanism, depending on the angle of rotation of the rudder feather on shallow waters, can be calculated using the following formula:
Y p = C y ⋅ ρ 2 ⋅ S p ⋅ v 2 ⋅ k w
Where: k w - turning velocity coefficient as the effect of shallow water factor [22, 54, 55].
In port channels and water areas, the ship will be steered without external help (tug) until the moment created by the rudder (assessing the ship's controllability reserve) is greater than or equal to the moments created by external forces, i.e. [22, 48, 53, 59]:
M p ≥ M a + M c + M T + ...
Aerodynamic forces and the moment ( X a , Y a , M a ), could be calculated using the methodology presented in [51]. Aerodynamic moment could be calculated as follows [51]:
M a = C a ⋅ ρ 1 2 ⋅ S x ⋅ ( x 0 + x a ) ⋅ ( v a ⋅ sin q a ) 2
Where: C a - aerodynamic coefficient, for the calculations could be taken between 1.07 – 1.30 depends of the ships architecture [51, 53]; ρ 1 - air density, for calculations could be taken 1.25 kg/m3;; S x - the space of projection onto diametrical plane (DP) of the wind surface area of the ship [39, 50, 53]; x a - abscissa of centre of gravity of aerodynamic force, can be calculated by methodology, presented in [22, 39, 53, 57]; v a - wind velocity; q a - wind course angle; x 0 - abscissa of the ship’s turning pivot point [57], can be calculate as follows:
x 0 = L ( k x 0 + k x 1 T a − T b L − k x 2 ⋅ α o )
Where: L - ship’s length between perpendiculars; k x 0 - abscissa coefficient, for many type of ships is between 0.3 – 0.4; k x 1 - abscissa coefficient depends of the ship’s draft differences, for many type of ships is between 11.0 – 12.0; k x 2 - abscissa coefficient depends of rudder turn angle, for many type of ships is between 0.004 – 0.0045; T a - ship’s astern draft; T b - ship’s bow draft; α o - ship’s rudder turn angle in degrees.
Current moment could be calculated as follows [51, 53]:
M c = C c ⋅ ρ 2 ⋅ L ⋅ T ⋅ v c 2 ⋅ x 0 ⋅ sin q c
Where: C c - current hydrodynamic coefficient, for many type of ships could be taken between 1.2 – 1.5 (1.5 is for double propeller and ships with bulb); T - ship’s average draft; v c - current velocity; q c - current course angle.
Ship’s propeller(s) creating moment could be calculated as follows [22, 51, 53] (in case of twin propellers with different turning sides, this moment is equal to zero):
M T = K 1 ' ⋅ ρ ⋅ n p r 2 ⋅ D p r 4 ( L 2 + x 0 ) ⋅ sin α p r
Where: K ' 1 - propeller’s coefficient, for many type of conventional propellers could be used for calculations as 0.2 (more accurate coefficient could be taken from propeller’s specification); n p r - rotation frequency of the ship's propeller, s − 1 ; D p r - ship’s propeller diameter; α p r - the deviation angle of the propeller flow, for conventional propellers is from 2 to 4 degrees, about 3 degrees can be accepted in the calculations [22, 39, 53].
Ship’s rudder(s) creating moment could be calculated as follows [22, 51, 53]:
M p = C y ⋅ ρ 2 ⋅ S p ⋅ v 2 ⋅ k w ⋅ ( L 2 + x 0 )
Finally, ship’s minimum steering speed in navigational channel could be calculated as follows:
v = 2 ( M a + M c + M T + ... ) C y ⋅ ρ ⋅ S ⋅ k w ⋅ ( L 2 + x 0 )
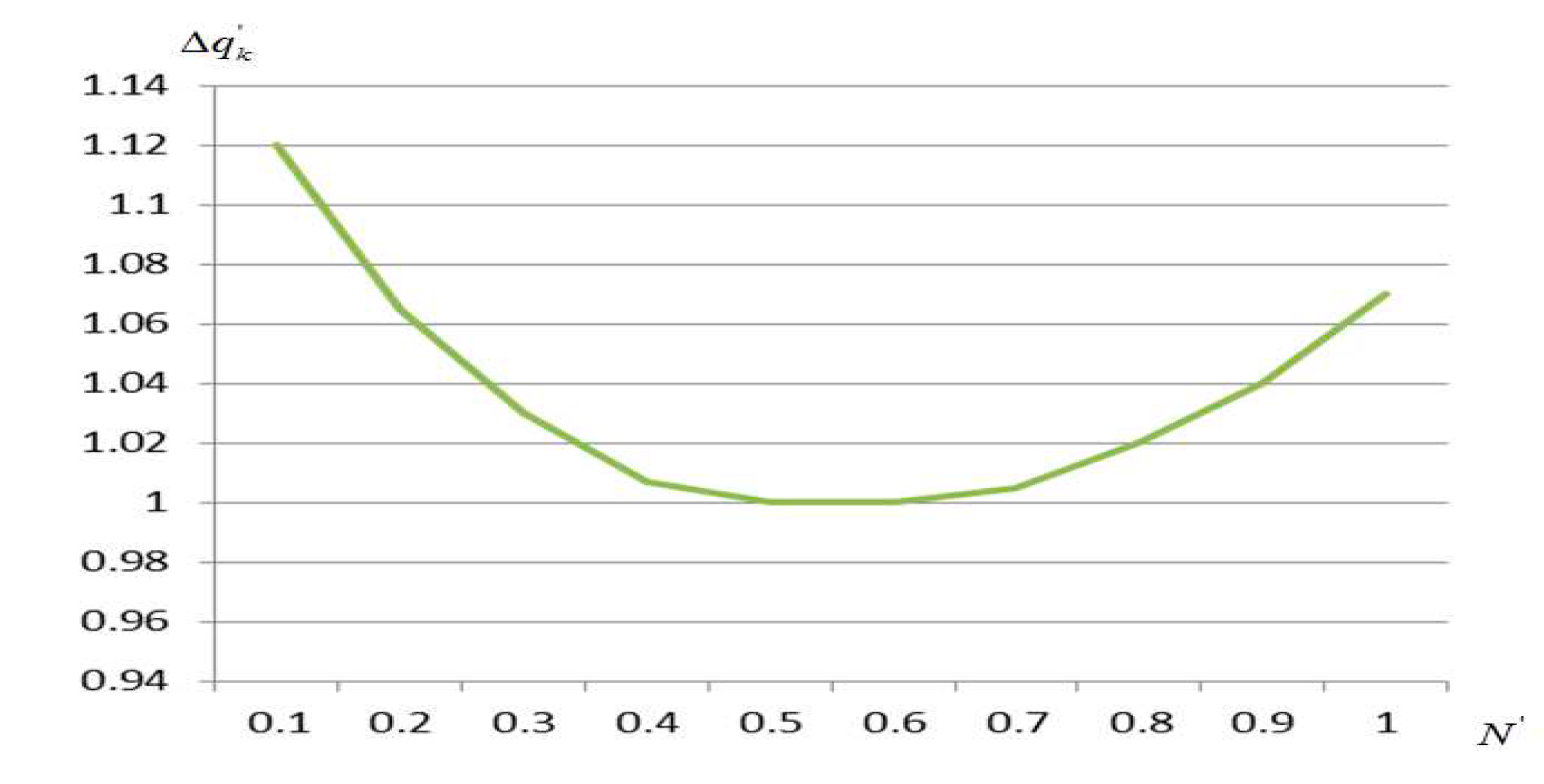
When sailing a ship in port navigational channels and water areas, it is very important that the ship is well controlled and at the same time its speed is such that the fuel consumption is minimal. The power of the ship's main engine and the relative fuel consumption can be expressed in a graph obtained by analysing relevant data from literature sources [60-63] and experimental data obtained on real ships (Figure 2).
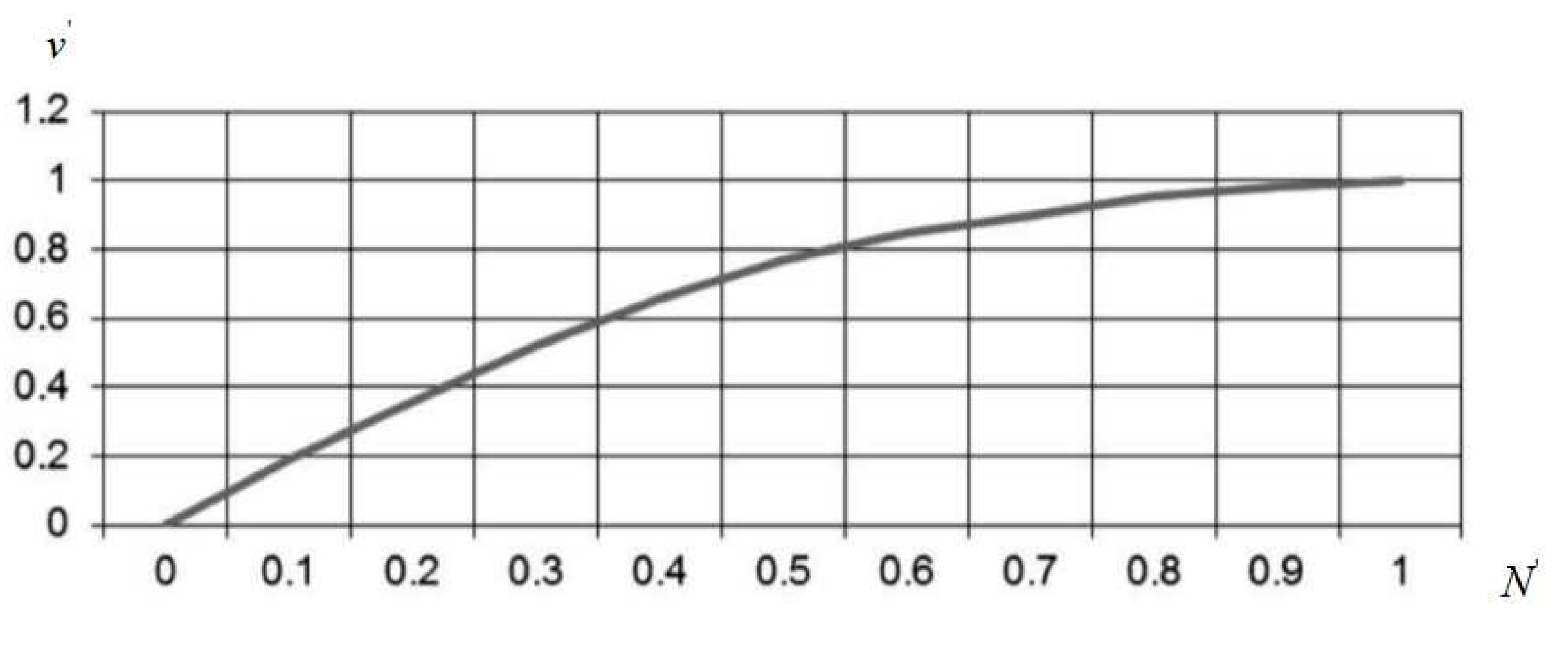
The relative power of the ship's main engine(s) and the ship's relative speed can be expressed by the following expressed on Figure 3 [29, 53, 62, 64]. The power of the engine and the speed of the ship are related by a quadratic relationship [57, 66]. In most cases, the relative power of the ship’s engine(s) and the ship’s speed can be used. For this purpose, a graph based on the experimental results from more than 1000 ship passages can be used [53, 54, 61] (Figure 3).
A limitation of the graph (Figure 3) with a very high overall hull fullness factor (δ) is that with the overall fullness factor of the ship’s hull greater than 0.9, the form resistance parameters of the ship’s hull shape change significantly and the accuracy of the graph is not good enough (error size can reach more than 10 percent) [54].
On Figure 3 is the relative power of the ship's engine(s), could be calculated as follows [14]:
N ' = N N n
Where: N - the current power of the ship's engine, while the ship is sailing at speeds v ; N n - nominal power of the ship's main engine(s).
On Figure 3 the relative ship’s speed v ' is calculated as follows [51]:
v ' = v v 0
Where: v 0 - the ship's speed at the rated power of the ship's engine(s).
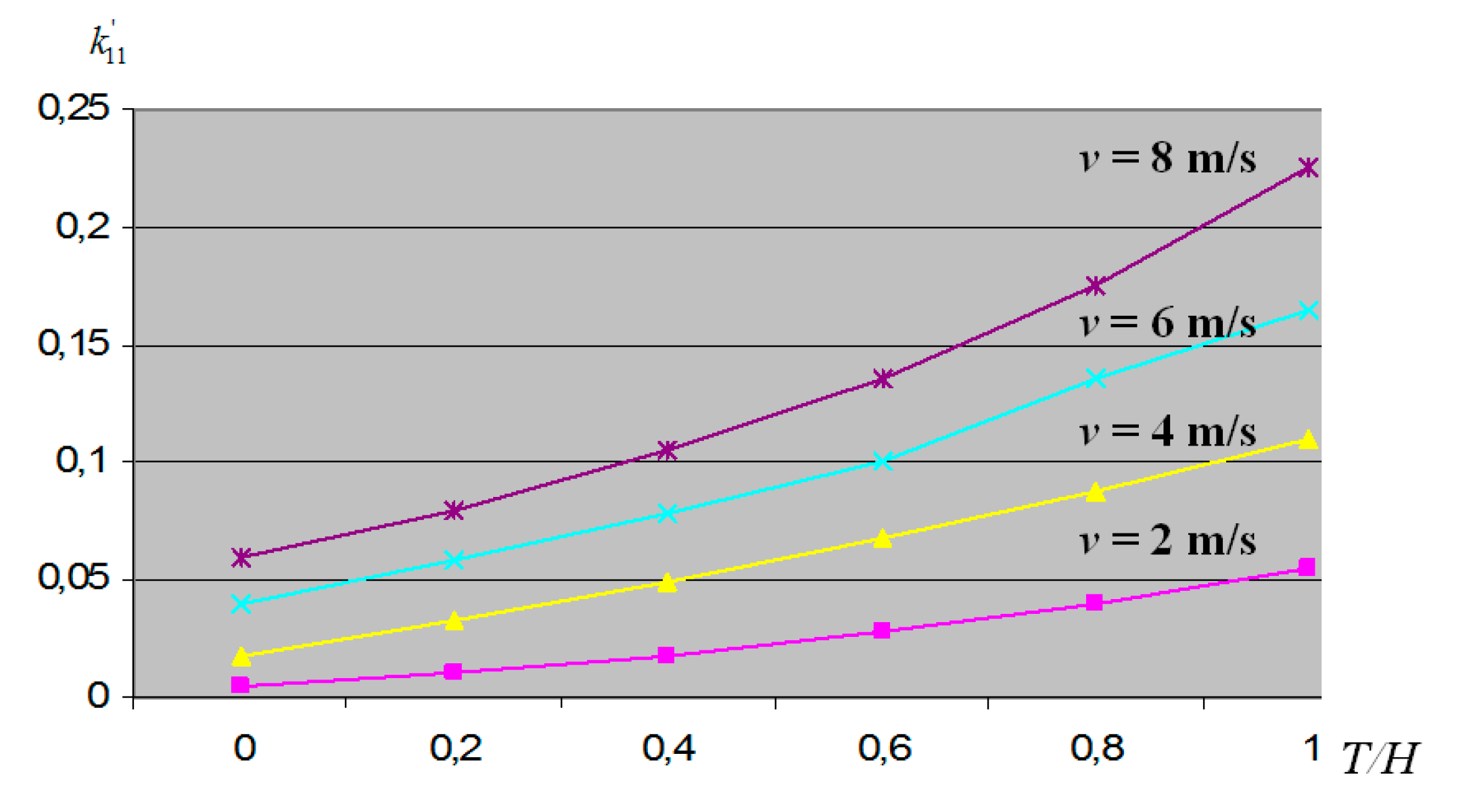
Many harbours have limited depths, and with a small clearance between the ship's hull and the bottom of the navigation channel, the added water mass increases and, at the same time, the resistance of the ship's hull increases. The decrease in ship speed at low depth can be calculated using the following formula [22, 55]:
v S = v ⋅ 1 + k 11 1 + k 11 '
Where: v S - ship’s speed in shallow water; v - ship’s speed in deep water; k 11 ' - attached water mass coefficient in shallow water; k 11 - attached water mass coefficient in deep water.
Added water mass coefficients in deep and shallow waters could be taken from graph (Figure 4) [22].
The added mass of water depends on the speed of the ship and the draft of the ship, as well as on the depth of the navigational channels and port water area, i.e. ratio (T/H). Additional water mass coefficients are usually used for calculation, which are presented in Figure 4, when the ship moves in the longitudinal direction, which corresponds to the navigation of ships in port channels [4,5].
The generation of emissions when a ship navigates port navigation channels and port water areas depends on the amount of fuel consumed, the power used by the engine(s) and the engine(s) working time and can be calculated using the methodologies presented in [7, 35].
The Kalman filter [66] and the maximum distribution method [67] were used for the processing and generalization of the obtained theoretical and experimental results.
The methodology presented in this part allows to determine the optimal speed of the ship in the shipping channels of the port and the water areas of the port, when the ships is still well controlled while sailing through it and at the same time consumes the minimum possible fuel.
By using the lowest possible power of the ship's engine(s) and the lowest possible fuel consumption, the ships produces minimum emissions [62, 64] which is important for the development of sustainable and green ports.
The main tasks of the developed methodology are based on theoretical models that can help to find the optimal navigational parameters of ships in port navigation channels and port water areas, to guarantee navigation safety, to use the safe minimum power of the ship's engine(s) and the possible minimum fuel consumption in order to generate minimal quantities of emissions as possible and minimize the impact on the environment, which is important for the development of sustainable and green ports. The developed methodology can be applied in practice.

4. Case study of the ships sailing in port channels and port water areas

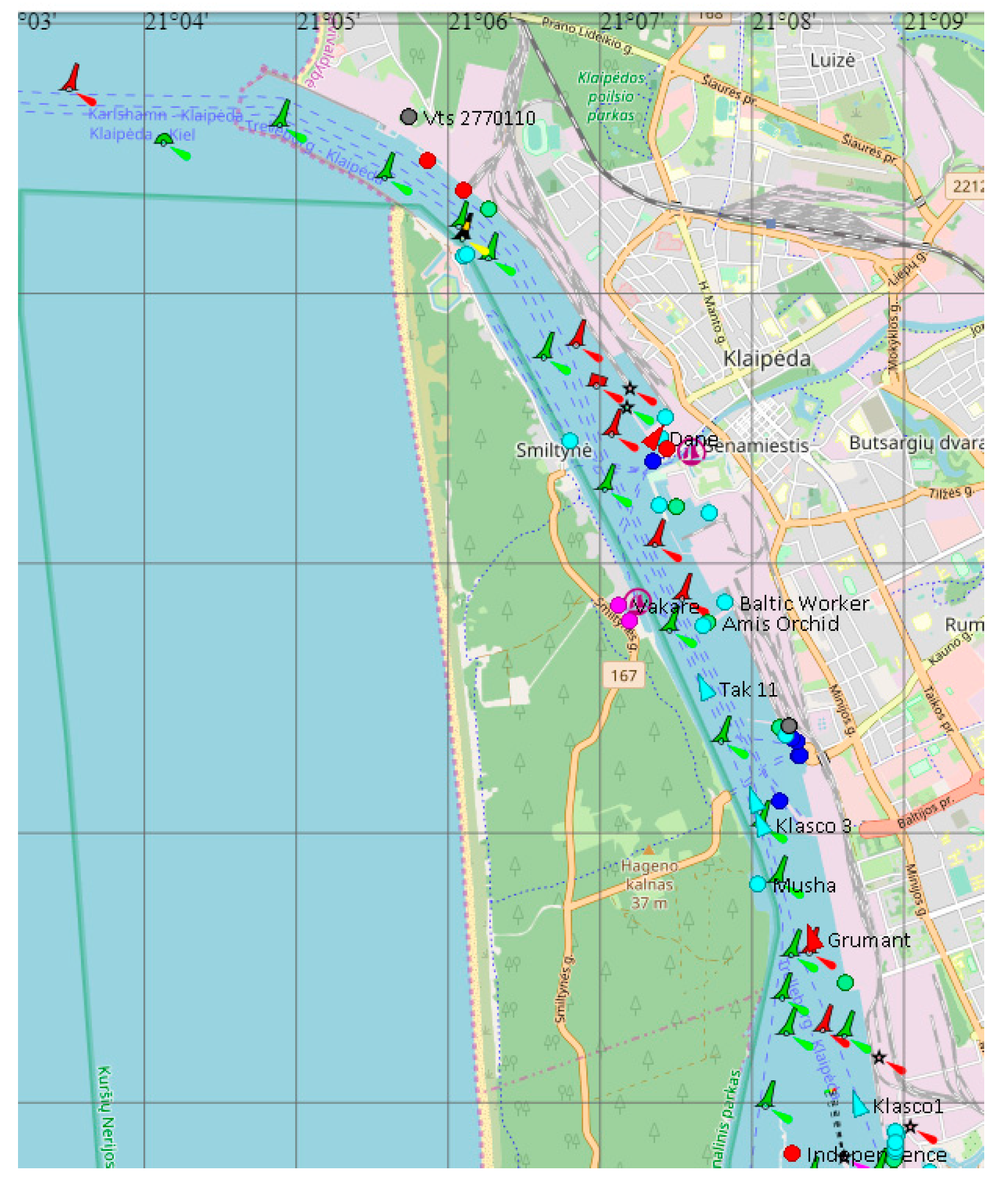
Klaipeda port [9, 68] (Figure 5) and two types of ships are taken as a case study: PANAMAX class container ship and POST PANAMAX class bulk cargo ship.
PANAMAX class container vessel length is about 294 m, length between perpendiculars about 278 m, width about 32.5 m, draft up to 12.5 m (fully loaded), block coefficient about 0.7, engine power about 20 MW, maximum speed about 22 knots, minimum speed about 5 knots, container capacity about 4800 TEU. POST PANAMAX bulk ship length about 235 m, length between perpendiculars about 210 m, width about 36 m, draft about 13.3 m, deadweight about 78000 tons (full loaded), block coefficient about 0.82, engine power about 8 MW, maximum speed about 14.5 knots, minimum speed about 3.5 knots.
For the analysis of the case, the mentioned real ships sailing in the shipping channels of the port and in the port water area and the calibrated simulator "SimFlex Navigator" [69] were used. The experimental data of the mentioned real ships were used for the simulator calibration, and later part of the research was carried out with the help of the mentioned simulator. The obtained simulator results were additionally compared with the results of real ships sailing in analogous conditions. Summarized calculation results obtained using the developed methodology presented in Chapter 3 and experimental results obtained on real ships and with the help of a simulator, as well as using the AIS system for additional comparison [70]. The obtained results were analyzed and the best possible solutions were sought by using the methodologies presented in [64, 65] and other sources and adjusting the developed methodology.
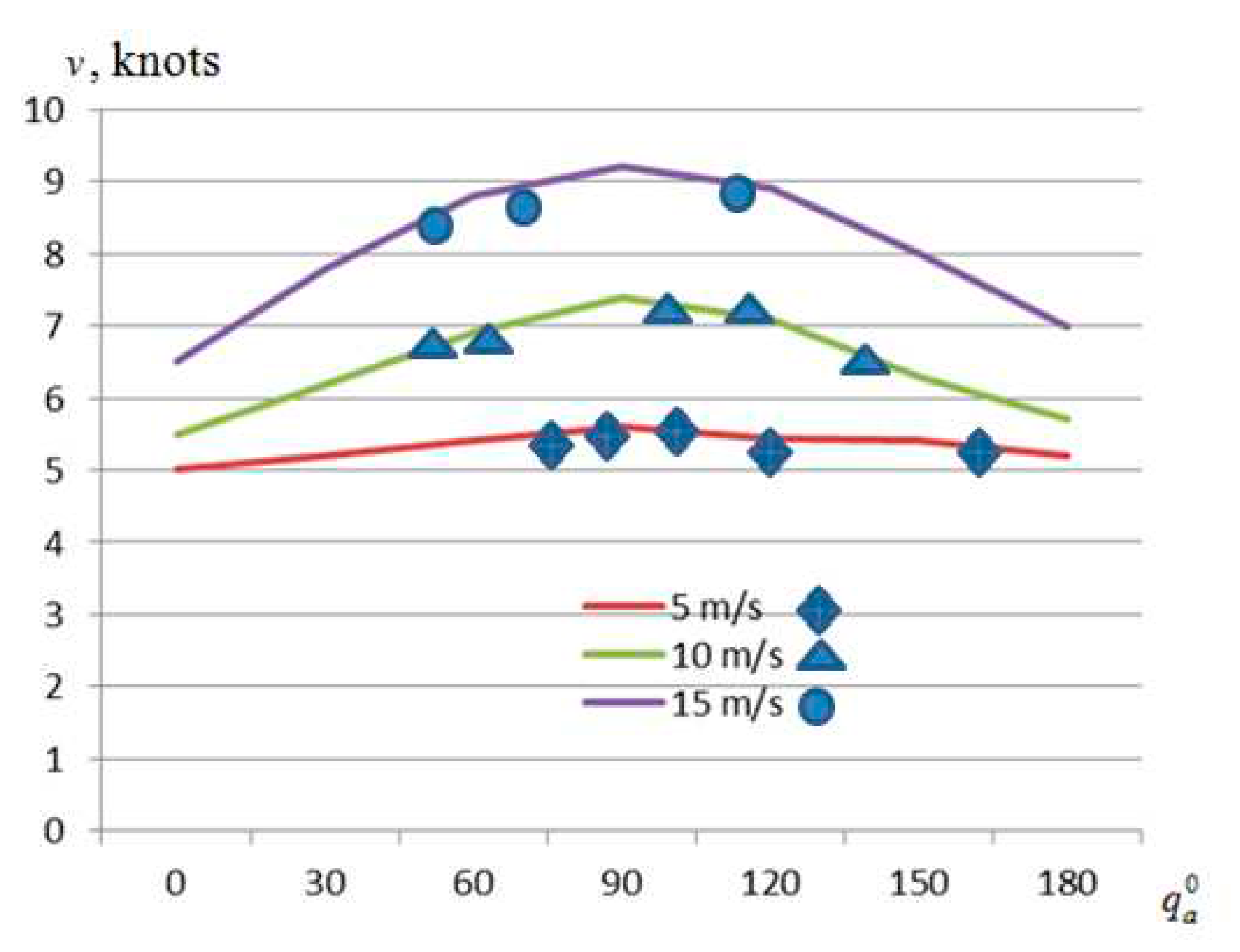
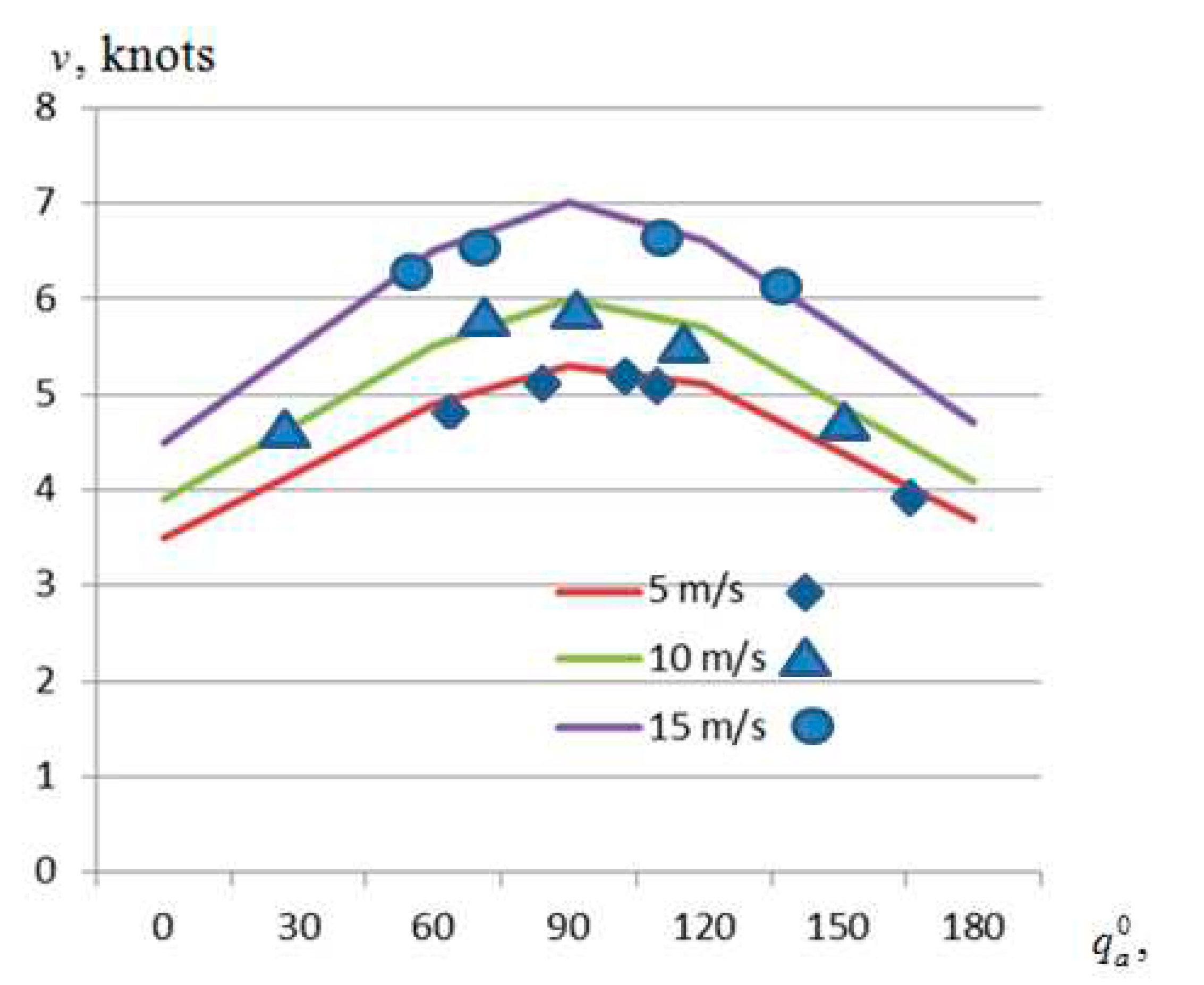
The minimum speed of controllable ships in typical harbour depths, depending on the wind speed and direction, obtained by calculation according to the methodology presented in Chapter 3 and experimentally with real corresponding ships and with the help of a calibrated simulator (the results presented in Figure 6 and Figure 7 were obtained during experiments on real ships and with the help of a calibrated simulator).
According to the obtained optimal solutions, the fuel consumption of the ships' main engines and the resulting emissions were analyzed when the ships sailed from the port entrance to different port terminals: container and bulk cargo terminals, where the total sailing distances was about 5.0 nautical miles.
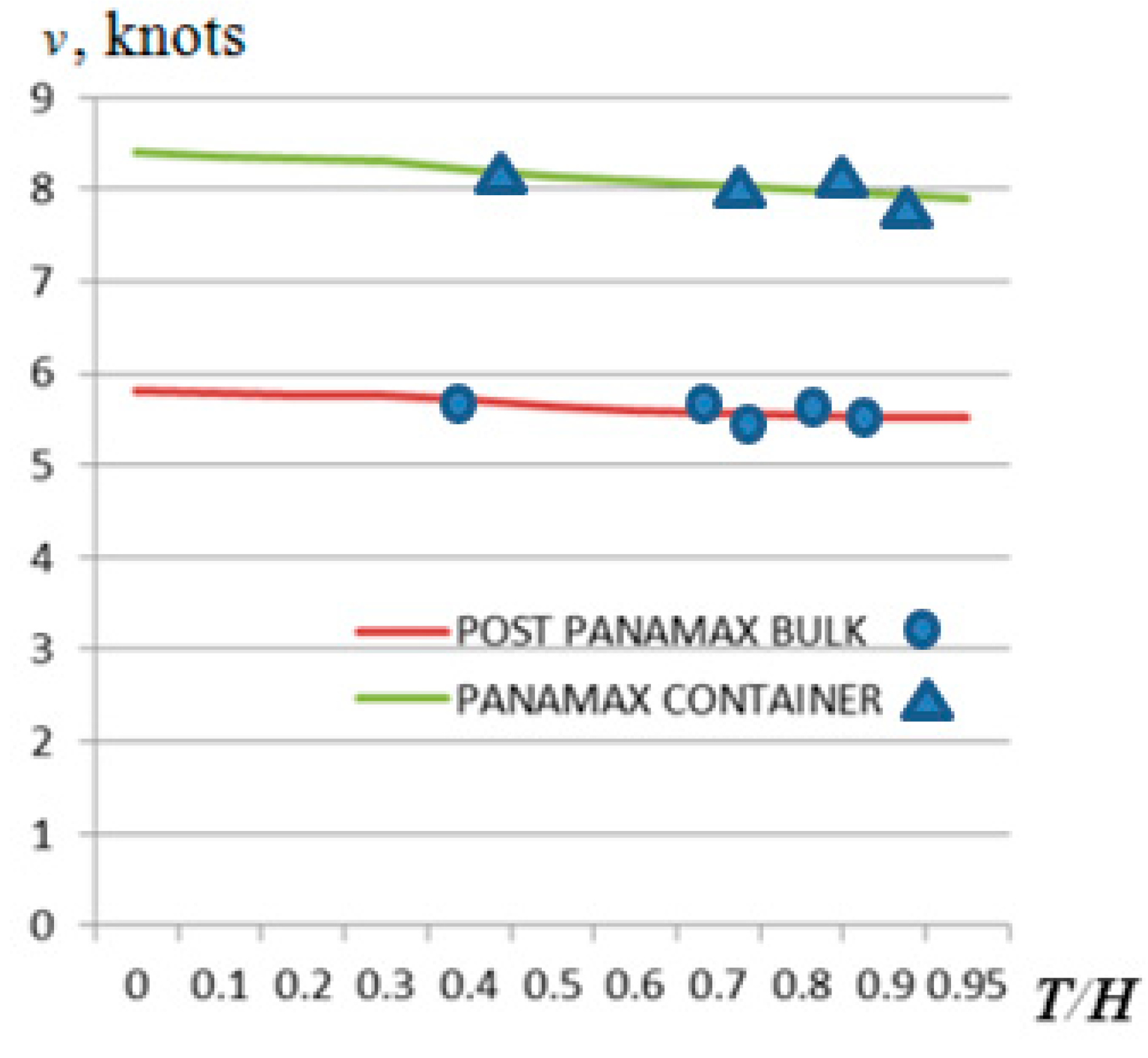
First, the minimum relative fuel consumption of the ships (PANAMAX container ship and POST PANAMAX bulker) was investigated when sailing at great depth (T/H less than 0.2). The study found that the main engine power of the PANAMAX container ship at minimum typical relative fuel consumption was about 5 MW and the corresponding ship speed was about 8.4 knots. The main bulk carrier POST PANAMAX had an engine power of about 2 MW at minimum relative fuel consumption, corresponding to a ship speed of about 5.8 knots.
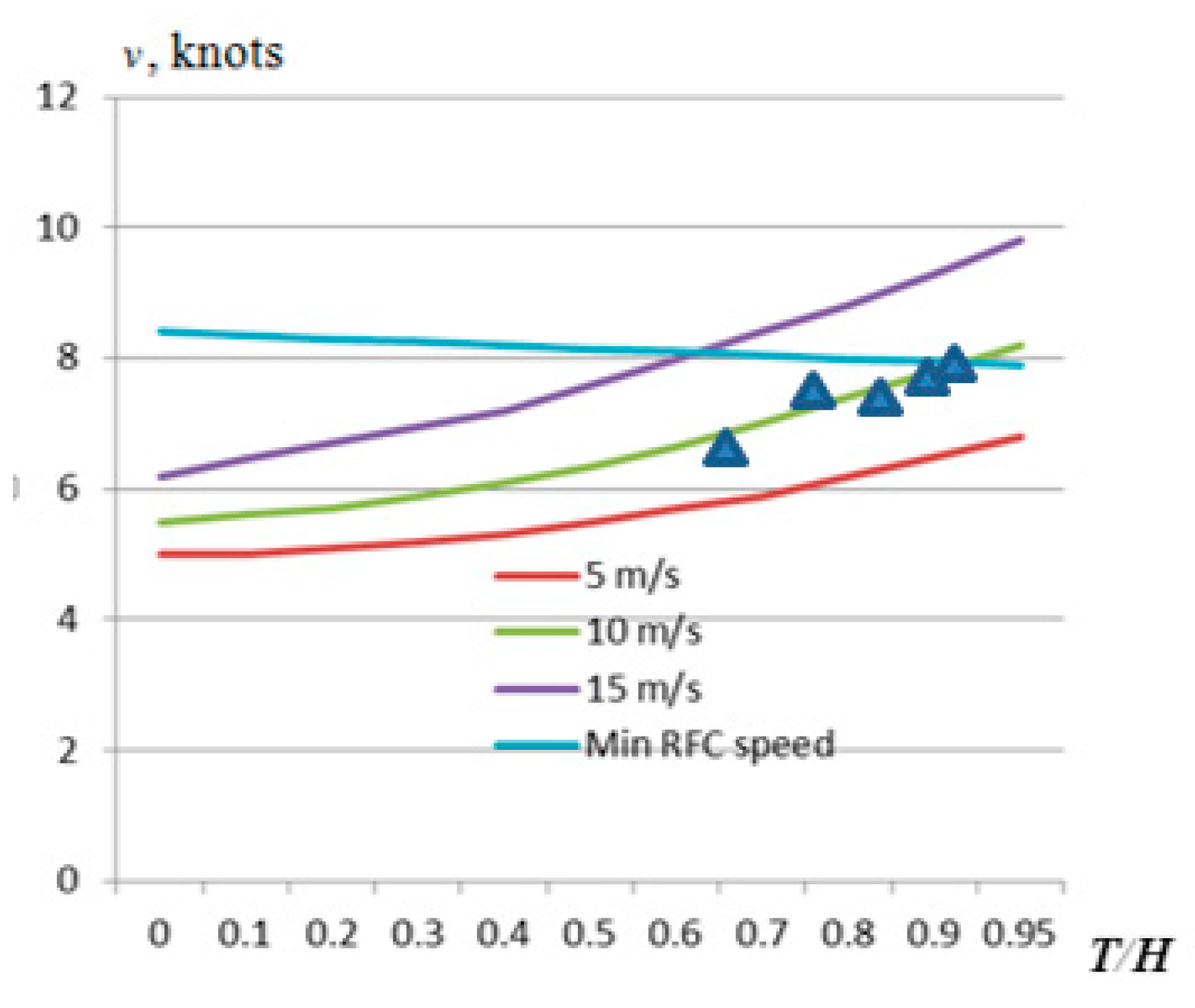
Depending on the ratio of the ship's draft to the depth of the navigation channel (T/H) and as it increases, the resistance of the ship's hull increases. In this way, with increasing T/H ratio and with minimal typical relative fuel consumption, the speeds of PANAMAX containers and POST PANAMAX bulk carriers, calculated according to the methodology presented in Chapter 3 and verified on real ships and with the help of a calibrated simulator, are presented in Figure 8.
The possible optimal speed of the investigated vessels in the harbor navigation channel was investigated, depending on the ratio of the ship's draft to the depth of the channel, as well as the wind speed and the most unfavorable angle of the wind course (the angle of the wind course is about 90°) (underestimated current, because the direction of the current coincides with the direction of the channel). Speed evaluations of PANAMAX containers and POST PANAMAX bulk cargo ships and other ships with similar parameters were performed in the most unfavorable wind directions, after estimating the minimum fuel consumption, calculated according to the methodology presented in Chapter 3 and the results of the evaluation in the SimFlex Navigator simulator [68] and verified by experiments under the same conditions with real ships of the same type are shown in Figure 9 and Figure 10 as an example.
In this way, the optimal speed of the container ship PANAMAX when sailing to the port of Klaipeda would be about 8 knots (permitted speed of ships in the port - up to 8 knots), sailing time about 0.625 hours. At a speed of 8 knots, the main engine of the PANAMAX container ship has a relative fuel consumption of about 0.15 kg/kWh, and during the test voyage (5 miles), this vessel consumed about 470 kg of diesel fuel and generated about 1500 kg of C O 2 . The optimal speed of a bulk cargo POST PANAMAX type ship when sailing to the port of Klaipeda would be about 5.6 knots (the permitted sailing speed in the port is up to 8 knots), the sailing time is about 0.89 hours. Sailing at a speed of 5.6 knots, the bulk carrier POST PANAMAX had a relative main engine fuel consumption of about 0.15 kg/kWh and during the test voyage (5 miles) this vessel consumed about 270 kg of diesel fuel and generated about 860 kg of C O 2 .
When a POST PANAMAX bulk cargo ship enters Klaipeda port at a speed of 8 knots, the sailing time is about 0.625 hours. At 8 knots, the POST PANAMAX bulk carrier has relative main engine fuel consumption of about 0.19 kg/kWh, and during the test voyage (5 miles) this vessel used about 325 kg of diesel fuel and generated about 1040 kg of C O 2 . A POST PANAMAX bulk cargo ship in Klaipeda port consumes about 55 kg less diesel fuel and generates about 180 kg less C O 2 than when sailing at a speed of 8 knots while sailing the same route at a speed of 5.6 knots. About 300 bulk carriers of similar size enter the port of Klaipeda per year, therefore, taking into account the arrival and departure of ships from the port, sailing at the optimal speed (5.6 knots) compared to the permitted speed (8 knots) would allow to reduce about 33,000 kg of diesel of fuel and generate about 106,000 kg less C O 2 .
The results of theoretical and experimental studies obtained in this way allow them to be applied in determining the possible optimal speed of ships in port navigation channels and port water areas. The optimal speed of ships allows to guarantee the safety of navigation in ports, to reduce fuel consumption and at the same time to reduce the generation of emissions when ships navigate the port navigation channels and port water areas, which positively influences the development of sustainable and green ports.
The results of the calculation and experimental research of the case study clearly substantiate that the optimal sailing speed of the PANAMAX container ship in the port channels and in the port water area is about 8 knots, while the optimal sailing speed of the bulk cargo POST PANAMAX type ship is in the port in the shipping channels and the harbor area there is about 5.6 knots (speed allowed in the harbor is 8 knots). When sailing at specified speeds under standard sailing conditions, the tested vessels consume minimal energy (fuel) and generate minimal emissions. At the same time, the tested vessels do not need to use high engine power for braking when entering the turning basin, which also reduces energy (fuel) consumption and generates minimal emissions during this operation.
The results of the experiments on minimum ship controllability speed and minimum fuel consumption obtained on real ships were used to calculate simulator correction factors (simulator calibration). With the help of a calibrated simulator, over 20 tests of ships sailing through port channels at low clearances were performed, which showed that the methodology developed and presented in the article can be used for scientific research and practical use in planning port channels, determining optimal conditions for ships sailing in ports and sustainable and green ports development.
Synthesis of experiments with real ships sailing at minimum controllable speed and minimum fuel consumption and calibration of the simulator based on real experiments and subsequent comparison of the obtained results with calculation results using the developed methodology allowed to assess the reliability of the methodology and the possibility of using the methodology in other ports and waterways.
Similar partial studies were carried out in Polish and other ports [48, 55], the results of which are presented in [7, 22, 28, 55] and other works with different types of ships.
The results of the study also revealed that the qualifications of port pilots, ship captains and tugboat captains are important when maneuvering ships in ports, so their high qualification and good knowledge of ship controllability can help optimize fuel consumption and minimize emissions generated by ships.

5. Discussions

The paper discusses a number of measurements of ship movements in navigable harbour channels, carried out during the case study. Although this number was limited, it is representative of the research topic. Differences in operator behaviour during manoeuvring operations were observed and demonstrated that the skill level of port pilots, vessel and tugboat masters varies and is related to optimal vessel selection speeds. Therefore, it should be noted that the results of the study can be considered satisfactory and allow answering the first research question, i.e. i.e. whether optimization ensures optimal speed in port navigation channels and port water areas.
It should be emphasized that the research results were influenced by external conditions that limited the number of experiments. The interface between real experiments and the use of a calibrated simulator made it possible to expand the research and the conditions of its performance. At the same time, it would be appropriate to continue the experiments, taking into account the external conditions in different seasons, in other ports and compare the results. Based on this, it will be possible to define more precisely the external conditions under which it is especially important to guarantee the navigational safety of shipping, taking into account the qualifications of the personnel, in order to be able to make the right decisions and reduce the power of ship engines when sailing and manoeuvring ships in ports, to reduce fuel consumption when navigating port navigational channels and port water areas and minimize the amount of emissions generated by ships entering and leaving ports, as well should make positive influence on sustainable and green ports development.
Moreover, research results may have managerial implications. Seaports, as well as shipping companies, may change their procedures and introduce strict conditions of skill verification during employee hiring and professional work, in pursuit of optimizing the ships speed in port navigational channels and port waters and as well emissions at seaports. Companies may organize regular trainings and invest in employees’ education aiming at improving staff qualifications in supporting decision-making during sailing and manoeuvre operations in ports. These activities may affect the development of companies’ navigational safety and environmental policy in order to decrease the costs of ships’ energy (fuel) consumption, as well as volume of emissions.
The methodology presented in the article could be successfully used to optimize the ships speed in port navigation channels and port water areas. Port services responsible for navigational safety of shipping should also be made aware of the minimum controllable ships speeds in various situations and evaluate it when organizing shipping in the port.
The obtained results of research on the possible minimum speed of movement of ships in the port, depending on the impact forces and the depth of the navigation channels, using the calculation method presented in the article, showed the possibility of using this method in port conditions and reducing fuel consumption and the amount of emissions in the port. The minimization of fuel costs, using the optimal ship’s speed in the port, which guarantees the safety of navigation, is especially important in ports located within the boundaries of cities, because it is possible to significantly reduce the impact on the environment in the port and improve the living conditions of the city residents due to reduced ship emissions.
At the same time, it is an important scientific contribution of the ongoing research, as a new methodology has been developed that allows determining the optimal ship speeds in port channels and port waters with minimal fuel consumption and minimal impact on the environment, when there is low clearance, which at the same time emphasizes the novelty of these researches and the article.
Detailed studies of the minimum ship handling speed under the influence of external forces and at shallow depths and a good knowledge of these phenomena can increase the safety of ships sailing in harbour channels and water areas.
The developed method provides an opportunity to analyse empirical data of real ships obtained by various modern methods (using high-precision navigation equipment, automatic ship identification systems, use of calibrated simulators) and can be applied in practice. In addition, the presented method can be useful for seaports and shipping companies in reducing fuel consumption and reducing environmental impact as well sustainable and green ports development.
More detailed and complex studies of external factors influencing the optimal manoeuvring of ships in port channels and water areas, fuel consumption of ships and reduction of generated emissions, turning of ships in port turning basins, bringing ships to and from port quays, using ship thrusters and tugs, in the presence of high wind and current velocities, research will be the direction of our further research. In future studies, we will try to expand the number of measurements and include more vessels and operators to participate in similar studies.

6. Conclusions

In this way, based on the research conducted and the results presented in this article, the following conclusions can be drawn:
The developed methodology for calculating the minimum ship-controlled speed at low clearance allows it to be used in port conditions and at the same time improve navigation safety in ports.
Matching the minimum controlled ship speed with minimum fuel consumption when sailing in harbour navigational channels at low clearance allows to reduce not only the ship's fuel consumption, but also to minimize ship emissions.
Conducted experiments with real ships in order to verify the minimum ship controllability speeds and fuel consumption allowed to confirm the correctness of the obtained theoretical models.
The developed methodology for the assessment of minimum ship speed, minimum fuel consumption and minimum emissions from ships can be successfully used for training and research purposes in assessing the safety and environmental impact elements of port navigation.
Ship operators can successfully use the presented methodology to ensure navigational safety, reduce fuel consumption in port canals and port waters, and reduce emissions in case low clearances, what is typical of ports and other waterways.
The use of modern ships and the optimization of fuel consumption for ships navigating the port's navigational channels and port waters have a positive impact on the development of sustainable and green ports.

Author Contributions

This paper was drafted and written by V.P. and all authors worked on the test and simulation results. D.P. contributed to the query, determination, and calculation of the simulation program. V.P., V.S., D.P and MS provided guidance for the overall research ideas and plans. V.P., V.S. and D.P. provided guidance for the formulation and implementation of test methods. All authors have read and agreed to the published version of the manuscript..

Funding

This research received no external funding

Acknowledgments

This article is based on the research conducted in Maritime Engineering Department of the Klaipeda University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Asbjørn Lein AalbergRolf Johan ByePeter Risberg Ellevseth. ,Risk factors and navigation accidents: A historical analysis comparing accident-free and accident-prone vessels using indicators from AIS data and vessel databases 2020. Maritime Transport Research 3 2022, 100062, 17. [Google Scholar] [CrossRef]
  2. Eleftheria, E. , Apostolos, P. and Markos, V. Statistical analysis of ship accidents and review of safety level. Safety science, 2016, 85, 282–292. [Google Scholar] [CrossRef]
  3. Erol, S. , Demir, M., Çetişli, B. and Eyüboğlu, E. Analysis of Ship Accidents in the Istanbul Strait Using Neuro-Fuzzy and Genetically Optimized Fuzzy Classifiers. The Journal of Navigation 2018, 71, 419–436. [Google Scholar] [CrossRef]
  4. Corrigan, S.; Kay, A.; Ryan, M.; Ward, M.E.; Brazil, B. Human factors and safety culture: Challenges and opportunities for the port environment. Saf. Sci. 2019, 119, 252–265. [Google Scholar] [CrossRef]
  5. Chauvin, C. , Lardjane, S., Morel, G., Clostermann, J. P. and Langard, B. Human and organizational factors in maritime accidents: Analysis of collisions at sea using the HFACS. Accident Analysis and Prevention 2013, 59, 26–37. [Google Scholar] [PubMed]
  6. Wu, B.; Yan, X.; Wang, Y.; Soares, C.G. An evidential reasoning-based cream to human reliability analysis in maritime accident process. Risk Anal. 2017, 37, 1936–1957. [Google Scholar] [CrossRef] [PubMed]
  7. Vytautas Paulauskas, Ludmiła Filina-Dawidowicz and Donatas Paulauskas. The Method to Decrease Emissions from Ships in Port Areas. Sustainability 2020, 12, 4374. [Google Scholar] [CrossRef]
  8. Yıldırım, U.; Ba¸sar, E.; U ˘gurlu, Ö. Assessment of collisions and grounding accidents with human factors analysis and classification system (HFACS) and statistical methods. Saf. Sci. 2019, 119, 412–425. [Google Scholar] [CrossRef]
  9. Klaipeda Seaport manual, maps and charts, 2022.
  10. Wawruch R.: Ships’ Routes to Polish Ports of the Gulf of Gdańsk. TransNav, the International Journal on Marine Navigation and Safety of Sea Transportation, 2021, Vol. 15, No. 3. pp. 583–590, 2021. [CrossRef]
  11. Bye Rolf, J. , Gilberg Asbjørn. (2018). Maritime navigation accidents and risk indicators: an exploratory statistical analysis using AIS data and accident reports. Reliab. Eng. Syst. Saf. 2018, 176, 174–186. [Google Scholar]
  12. Zalewski, P; Montewka, J. Navigation safety assessment in an entrance channel, based on real experiments. Guedes-Soares & Kolev Maritime Industry, Ocean Engineering and Coastal Resources, 2007; 1113–1117.
  13. Mou, J.M.; Chen, P.F.; He, Y.X.; Yip, T.L.; Li, W.H.; Tang, J.; Zhang, H.Z. Vessel traffic safety in busy waterways: A case study of accidents in western Shenzhen port. Accid. Anal. Prev. 2019, 123, 461–468. [Google Scholar] [CrossRef]
  14. Paulauskas, V. , Lukauskas V., Plačiene B., Barzdžiukas. Ships leaving a port under emergency conditions. Transport, 2012, 27, 345–350. [Google Scholar] [CrossRef]
  15. Di Vaio, A.; Varriale, L. Management innovation for environmental sustainability in seaports: Managerial accounting instruments and training for competitive green ports beyond the regulations. Sustainability 2018, 10, 783. [Google Scholar] [CrossRef]
  16. Endresen, Ø.; Sørgård, E.; Sundet, J.K.; Dalsøren, S.B.; Isaksen, I.S.A.; Berglen, T.F.; Gravir, G. Emission from international sea transportation and environmental impact. J. Geophys. Res. D Atmos. 2003, 108, ACH 14–1 ACH 14. [Google Scholar] [CrossRef]
  17. Junjie Li, Xinyu Zhang, Bingdong Yang, NannanWang. Vessel traffic scheduling optimization for restricted channel in ports. Computers & Industrial Engineering 2021, 152. [Google Scholar] [CrossRef]
  18. Szlapczynski, R.; Szlapczynska, J. Review of ship safety domains: Models and applications. Ocean Eng. 2017, 145, 277–289. [Google Scholar] [CrossRef]
  19. Bellsolà Olba, X. , Daamen, W., Vellinga, T., Hoogendoorn, S.P.: Risk Assessment Methodology for Vessel Traffic in Ports by Defining the Nautical Port Risk Index. Journal of Marine Science and Engineering 2020, 8, 1. [Google Scholar] [CrossRef]
  20. Bojić F., Bošnjak R., Lušić Z., Gudelj A.: Methodology for the Development of Parameters for the Navigational Safety Risk Assessment Model in Port Approaches. TransNav, the International Journal on Marine Navigation and Safety of Sea Transportation, 2021, Vol. 15, No. 2 365-370. [CrossRef]
  21. Huang, Y. , Chen, L., Chen, P., Negenborn, R.R., van Gelder, P.H.A.J.M. Ship collision avoidance methods: State-of-the-art. Safety Science 2020, 121, 451–473. [Google Scholar] [CrossRef]
  22. Paulauskas V., Paulauskas D. Ship’s steering in port areas. Klaipeda University publish house, Klaipeda, 2009, 256 p. (LT).
  23. Hamburg Seaport manual, maps and charts, 2022.
  24. Rotterdam Seaport manual, maps and charts, 2022.
  25. Jin, L.; Luo, Z.; Gao, S. Visual Analytics Approach to Vessel Behaviour Analysis. J. Navig. 2018, 71, 1195–1209. [Google Scholar] [CrossRef]
  26. Öztürk, Ü.; Boz, H. A.; Balcisoy, S. Visual analytic based ship collision probability modeling for ship navigation safety. Expert Syst. Appl. 2021, 175, 114755. [Google Scholar] [CrossRef]
  27. Haseltalab, A. , Rudy R., Negenborn. Model predictive manoeuvring control and energy management for all-electric autonomous ships. Applied Energy 2020, 251. [Google Scholar] [CrossRef]
  28. Paulauskas, V.; Filina-Dawidowicz, L.; Paulauskas, D. Ships speed limitations for reliable maintenance of the quay walls of navigation channels in ports. Eksploat. I Niezawodn. –Maint. Reliab. 2020, 22, 306–315. [Google Scholar] [CrossRef]
  29. Lack, D.A.; Corbett, J.J. Black carbon from ships: A review of the effects of ship speed, fuel quality and exhaust gas scrubbing. Atmos. Chem. Phys. 2012, 12, 3985–4000. [Google Scholar] [CrossRef]
  30. F. Biehl and E. Lehmann. Collisions of ships with offshore wind turbines: Calculation and risk evaluation, Offshore Wind Energy Res. Environ. Impacts 2006, 281–304.
  31. Coldwell, T.G. Marine traffic behaviour in restricted waters. J. Navig. 1983, 36, 430–444. [Google Scholar] [CrossRef]
  32. Kurowski M., Kockritz O. Korte H. Full-state Manoeuvre Planning System for Marine Vehicles. IFAC Proceedings Volumes, 2013, Volume 46, Issue 33, 144-149. [CrossRef]
  33. Di Vaio, A.; Varriale, L.; Alvino, F. Key performance indicators for developing environmentally sustainable and energy efficient ports: Evidence from Italy. Energy Policy 2018, 122, 229–240. [Google Scholar] [CrossRef]
  34. Heinrich, L.; Koschinsky, A.; Markus, T.; Singh, P. Quantifying the fuel consumption, greenhouse gas emissions and air pollution of a potential commercial manganese nodule mining operation. Mar. Policy, 2020, 114, 103678. [Google Scholar] [CrossRef]
  35. Lion, S.; Vlaskos, I.; Taccani, R. A review of emissions reduction technologies for low and medium speed marine Diesel engines and their potential for waste heat recovery. Energy Convers. Manag. 2020, 207, 112553. [Google Scholar] [CrossRef]
  36. PIANC, 2014. Harbour Approach Channels and Design Guidelines - Report No 121-2014, s.l.: The World Association for Waterborne Transport Infrastructure. Available on-line: http://marineman.ir/wp-content/uploads/2015/04/NAVIGATION-PIANC-Harbour-Approach-Channels-Design-Guidelines-2014.pdf (Accessed: 25 February 2023).
  37. Puertos del Estado. 1999. ROM 3.1-99: Recommendation for Design of the Maritime Configuration of Ports, Approach Channels and Harbour Basins. Puertos del Estado [Ports of the State], Madrid, Spain. 382 p. Available from Internet: http://www. puertos.es/eu-es/BibliotecaV2/ROM%203.1-99%20(EN).pdf.
  38. Wilhelm Ernst & Sohn. Recommendations of the Committee or Waterfront Structures Harbours and Waterways EAU 2012, 9th ed.; Wiley: Hoboken, NJ, USA, 2015; 676p, ISBN 978-3-433-03110-0. [Google Scholar]
  39. Paulauskas V., Ships entering the ports. N.I.M.S. publish house, Riga, 2013, 240 p. ISBN: 9984-679-71-3.
  40. IMO, Amendments to the Annex of the Protocol of 1997 to Amend the International Convention for the Prevention of Pollution from Ships, 1973, as Modified by the Protocol of 1978 Relating thereto (MARPOL Annex VI), 2008. Available online: http://www.imo.org/includes/blastDataOnly.asp/data_id%3D23760/ 176 (accessed on 25 May 2020).
  41. IMO. Marine Engine Regulations; IMO: London, UK, 2015. [Google Scholar]
  42. Cullinane, K.; Bergqvist, R. Emission control areas and their impact on maritime transport. Transp. Res. Part. D Transp. Environ. 2014, 28, 1–5. [Google Scholar] [CrossRef]
  43. Quy, M.N.; Łazuga, K.; Gucma, L.; Vrijling, J.K.; van Gelder, P.H.A.J.M. Towards generalized ship’s maneuver models based on real time simulation results in port approach areas. Ocean Engineering, 2020, 209, 107476. [Google Scholar] [CrossRef]
  44. Zheng, Y. Trajectory data mining: an overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–41. [Google Scholar] [CrossRef]
  45. Zou, Y.; Chen, Y.; He, J.; Pang, G.; Zhang, K. 4D Time Density of Trajectories: Discovering Spatiotemporal Patterns in Movement Data. ISPRS Int. J. Geo-Inf. 2018, 7, 212. [Google Scholar] [CrossRef]
  46. Chun-Ki L, Sam-Goo L. Investigation of ship maneuvering with hydrodynamic effects between ship and bank. Journal of Mechanical Science and Technology, 2008; 22, 1230-1236. [CrossRef]
  47. Fan, S.; Zhang, J.; Blanco-Davis, E.; Yang, Z.; Wang, J.; Yan, X. Effects of seafarers’ emotion on human performance using bridge simulation. Ocean Eng., 2018, 170, 111–119. [Google Scholar] [CrossRef]
  48. Gucma L. The risk assessment of ships manoeuvring on the waterways based on generalized simulation data. Safety and Security Engineering II. WIT Transactions on the Built Environment, 2007, vol. 94, WIT Press. P. 58 – 69.
  49. Theirs, G. F.; Jansses, G. K. A Port Simulation Model as a Performance Decision Instrument. Simulation, 1998, 71, 117–125. [Google Scholar] [CrossRef]
  50. Bitner-Gregerse E., M. , Soares C. G., Vantorre M. Adverse weather conditions for ship manoeuvrability. Transportation Research Procedia, 2016; 14, 1631–1640. [Google Scholar]
  51. Čerka, J. Laivo eigumas. Klaipeda university publish house.2005, 200 p. (In Lithuanian).
  52. Lee, C.-K. , Moon S.-B., Jeong T.-G. The investigation of ship maneuvering with hydrodynamic effects between ships in curved narrow channel. International Journal of Naval Architecture and Ocean Engineering 2016; 8: 102-109. [CrossRef]
  53. Rawson K., J. , Tupper E.C. Basic Ship Theory (Fifth Edition). Elsever 2001, 727 p.
  54. Paulauskas, V.; Paulauskas, D.; Paulauskas, V. Impact of Port Clearance on Ships Safety, Energy Consumption and Emissions. Appl. Sci. 2023, 13, 5582. [Google Scholar] [CrossRef]
  55. Paulauskas, V.; Filina-Dawidowicz, L.; Paulauskas, D. Navigation of Ships in Channel Bends under Special Conditions Using Sensors Systems. Sensors, 2022, 22, 8783. [Google Scholar] [CrossRef]
  56. Nakamura, S. Study on Maneuvering Criteria for Safety Assessment in Shallow Water. TransNav: International Journal on Marine Navigation and Safety of Sea Transportation 2017, 11, 401–407. [Google Scholar] [CrossRef]
  57. Molland, A.F.; Turnock, S.R.; Hudson, D.A. Ship Resistance and Propulsion. Practical Estimation of Propulsive Power. Cambridge University Press 2011, 537 . [CrossRef]
  58. Lisowski, J. Analysis of Methods of Determining the Safe Ship Trajectory. TransNav: International Journal on Marine Navigation and Safety of Sea Transportation, 2016, 10, 223–228. [Google Scholar] [CrossRef]
  59. Mironiuk, W. Model-based investigations on dynamic ship heels in relation to maritime transport safety. Archives of Transport 2015; 33(1): 69-80. [CrossRef]
  60. Pelic, V.; Ozren, B.; Radonja, R.; Degiuli, N. The Impact of Slow Steaming on Fuel Consumption and CO2 Emissions of a Container Ship. Journal of Marine Science and Engineering, 2023, 11, 675–1 -19. [Google Scholar] [CrossRef]
  61. M. A. Kalam, M. Husnawan ∗, H.H. Masjuki. Exhaust emission and combustion evaluation of coconut oil-powered indirect injection diesel engine. Renewable Energy. 2003, 28, 2405–2415. [Google Scholar] [CrossRef]
  62. Tadros M, Ventura M, Guedes Soares. Optimization procedure to minimize fuel consumption of a four-stroke marine turbocharged diesel engine. Energy 168(C),2019, 897–908. [CrossRef]
  63. Operation Manual RT-Flex50DF. Issue 002 2022-07. https:/www. https://www.wingd.com/en/documents/rt-flex50df/engine-operation/operation-manual-(om)/ (Accessed: 25.03.2023).
  64. Clume SF, Belchior CRP, Gutiérrez RHR, Monteiro UA, Vaz LA. Methodology for the validation of fuel consumption in diesel engines installed on board military ships, using diesel oil and biodiesel blends. J Braz Soc Mech Sci Eng 2019, 41, 516. [Google Scholar] [CrossRef]
  65. Le, L.T.; Lee, G.; Kim, H.; Woo, S.-H. Voyage-based statistical fuel consumption models of ocean-going container ships in Korea. Marit. Policy Manag. 2020, 47, 304–331. [Google Scholar] [CrossRef]
  66. Chauhan, S.; Patil, C.; Sinha, M.; Halder, A. Fuzzy state noise-driven Kalman filter for sensor fusion. Proc. Inst. Mech. Eng. Part. G J. Aerosp. Eng. 2009, 223, 8–1091–1097. [Google Scholar] [CrossRef]
  67. Hanqing, J,, Shige, P. Optimal unbiased estimation for maximal distribution. American Institute of Mathematical Science 2021, Volume 6, Issue 3: p. 189-198. [CrossRef]
  68. Openseamap, https://map.openseamap.org/ (Accessed: 25.03.2023).
  69. “SimFlex Navigator” simulator, Force Technology, Denmark, license No 159.
  70. AIS; https://www.marinetraffic.com/en/ais/home/centerx:21.146/centery:55.656/zoom:15 (Accessed: 25.03.2023).
Preprints 86405 g001
Figure 1. The algorithm of the research methodology.
Figure 1. The algorithm of the research methodology.
Preprints 86405 g001
Preprints 86405 g002
Figure 2. The relative fuel consumption coefficient of a ship's engine ( Δ q k ' ), depending on the relative power of the ship's engine(s) ( N ' ).
Figure 2. The relative fuel consumption coefficient of a ship's engine ( Δ q k ' ), depending on the relative power of the ship's engine(s) ( N ' ).
Preprints 86405 g002
Preprints 86405 g003
Figure 3. The relative speed of the ship ( v ' ) as a function of the relative power of the ship's engine(s) ( N ' ).
Figure 3. The relative speed of the ship ( v ' ) as a function of the relative power of the ship's engine(s) ( N ' ).
Preprints 86405 g003
Preprints 86405 g004
Figure 4. Dependences of the added water mass coefficient k 11 ' on the T/H ratio and the ship's sailing speed v .
Figure 4. Dependences of the added water mass coefficient k 11 ' on the T/H ratio and the ship's sailing speed v .
Preprints 86405 g004
Preprints 86405 g005
Figure 5. Klaipeda port navigational channels and port waters [9, 68].
Figure 5. Klaipeda port navigational channels and port waters [9, 68].
Preprints 86405 g005
Preprints 86405 g006
Figure 6. The minimum speed at which the PANAMAX container ships can be controlled depends on the wind speed and the angle of the wind course ( q a o ) in case of T/H = 0.87.
Figure 6. The minimum speed at which the PANAMAX container ships can be controlled depends on the wind speed and the angle of the wind course ( q a o ) in case of T/H = 0.87.
Preprints 86405 g006
Preprints 86405 g007
Figure 7. The minimum speed at which the POST PANAMAX bulk ships can be controlled depends on the wind speed and the angle of the wind course ( q a o ) in case of T/H = 0.9.
Figure 7. The minimum speed at which the POST PANAMAX bulk ships can be controlled depends on the wind speed and the angle of the wind course ( q a o ) in case of T/H = 0.9.
Preprints 86405 g007
Preprints 86405 g008
Figure 8. The speed of ships at minimum relative fuel consumption is calculated according to the methodology presented in Chapter 3 and received on real similar ships and by calibrated simulator.
Figure 8. The speed of ships at minimum relative fuel consumption is calculated according to the methodology presented in Chapter 3 and received on real similar ships and by calibrated simulator.
Preprints 86405 g008
Preprints 86405 g009
Figure 9. Minimum maneuverability and minimum relative fuel consumption (Min RFC) speed of a PANAMAX container ship at various wind speeds and the most unfavorable wind course angle (about 90°) depending on the draft to depth ratio (T/H) of the vessel. The results are obtained according to the methodology presented in Chapter 3 and on real similar ships and a calibrated simulator with a wind speed of 10 m/s (example).
Figure 9. Minimum maneuverability and minimum relative fuel consumption (Min RFC) speed of a PANAMAX container ship at various wind speeds and the most unfavorable wind course angle (about 90°) depending on the draft to depth ratio (T/H) of the vessel. The results are obtained according to the methodology presented in Chapter 3 and on real similar ships and a calibrated simulator with a wind speed of 10 m/s (example).
Preprints 86405 g009
Preprints 86405 g010
Figure 10. The minimum maneuverability and minimum relative fuel consumption (Min RFC speed) speed of a POST PANAMAX bulk ship at various wind speeds and the most unfavorable wind course angle (about 90°) depending on the ship's draft to depth ratio (T/H). Results received by methodology presented in section 3, and on real similar ships and by calibrated simulator in case wind velocity 8 m /s (as example).
Figure 10. The minimum maneuverability and minimum relative fuel consumption (Min RFC speed) speed of a POST PANAMAX bulk ship at various wind speeds and the most unfavorable wind course angle (about 90°) depending on the ship's draft to depth ratio (T/H). Results received by methodology presented in section 3, and on real similar ships and by calibrated simulator in case wind velocity 8 m /s (as example).
Preprints 86405 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated