Prerpints.org logo
Preprint
Article

Scattering of Attosecond Laser Pulses on a DNA Molecule During Its Nicking and Bending

Altmetrics

Downloads

92

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 September 2023

Posted:

29 September 2023

You are already at the latest version

Alerts
Abstract
It is well known that X-ray crystallography is based on X-ray diffraction (XRD) by atoms and molecules. The diffraction pattern arises as a result of scattering of incident radiation, which makes it possible to determine the structure of the scattering substance. With the advent of ultrashort radiation sources, the theory and interpretation of X-ray diffraction analysis remained the same. This work shows that when an attosecond laser pulse is scattered on a DNA molecule, including during its nicking and bending, the pulse duration is an important characteristic of the scattering. In this case, the diffraction pattern changes significantly compared to the previously known scattering theory. The results obtained must be used in XRD theory to study DNA structures, their mutations and damage, since the previously known theory can produce large errors and, therefore, the DNA structure can be “deciphered” incorrectly.
Keywords: 
Subject: Physical Sciences  -   Biophysics

1. Introduction

It is generally believed that when scattering ultrashort laser pulses (USP) in the X-ray frequency range, the results do not depend on the duration of such a pulse τ . As a result, the theory of diffraction analysis of matter (XRD) usually uses a previously known theory based on an infinitely long pulse duration [1,2,3,4]. In this theory, the key quantity in X-ray scattering is the scattering spectrum, related to the Fourier transform of the electron density distribution ρ ( r ) in a substance as follows[5,6]
d ε d Ω = d ε e d Ω ρ ( r ) e i p r d 3 r 2 ,
where d ε e d Ω is the scattering spectrum of a free electron (Thomson scattering), p is the momentum transferred to the electron during scattering (otherwise p = 2 π λ ( n − n 0 ) is the scattering vector, where n is the direction of scattered radiation, n 0 is direction of incident radiation), Ω is the solid angle at which scattering occurs. Using well-known methods [7] based on the inverse Fourier transform, one can determine ρ ( r ) from the X-ray scattering pattern. It is also believed that ultrashort sources of laser pulses are important, primarily for studying the dynamics of processes occurring in various structures [8,9,10,11]. In this case, the interaction time of such pulses τ with the structure under study should be many times less than its characteristic time τ a , i.e. τ ≪ τ a . In other words, to find the electron density varying with time, you need to find ρ ( r , t ) , i.e. in Eq.(1) you need ρ ( r ) → ρ ( r , t ) [6]. This method is well known as time-resolved X-ray diffraction (TR-XRD). In other words the TR-XRD technique uses the same Eq. (1), but the diffraction pattern is "read off" the system being studied over time t and conclusions are drawn about the dynamics of the system from a large set of such patterns. Of course, it is possible to study the structure without resorting to ultrashort pulses, but only in the case of stationary objects. If dynamic structures are to be studied, ultrashort pulses must be used, and the theory of scattering of such pulses for the study of dynamic structures must contain the pulse duration parameter, and it is incorrect to use Eq.(1) directly. One way or another, the problem of interaction of ultrashort pulses with atoms and molecules is an important part of modern physics[6,9,12,13,14,15].
Recently, in works [16,17,18,19] it was shown that Eq.(1) is not correct to use in the case of scattering of attosecond laser pulses on nucleotides and trinucleotides of DNA and RNA. It was shown that the previously known XRD theory can differ greatly from the case of the theory developed in these works, which takes into account the USP duration parameter. Extend similar conclusions to more complex DNA structures, for example, their mutations, breaks, folding, etc. it is not possible directly. This is due to the fact that only direct calculation and analysis of a specific structure using the theory[16,17] can provide information about the effect of pulse duration on scattering spectra. It can only be argued that such pulses should be attosecond and shorter when scattered on biomolecules[16,17,19].
As an object of study we will choose a single-stranded DNA macromolecule with five nitrogenous bases: cytosine-cytosine-guanine-cytosine-cytosine. It is interesting to consider a few states of the molecule that are important in biology, namely the stacking interactions of DNA: Nick - the absence of a single phosphodiester bond,bending DNA, see Figure 1. Nick can be either mutational damage or the result of a directed biochemical reaction [20]. Nick allows DNA to unwind during replication, is a marker for ligase recognition and was detected by XRD, at 2A resolution [21] using Eq.(1). To achieve higher resolution, the results obtained were refined by iterative single isomorphic substitution methods to obtain electron density maps, also by heavy atom methods [22], and indirectly by detecting the embedded ligase in place of Nick [23]. The obtained data do not give a clear understanding of the structure of the studied sample, which is reflected in the search for new ways to find Nick in the DNA structure [24].
This work shows that the previous XRD method gives a large error in the USP scattering spectra in the case of using attosecond pulses on the objects under study, which can lead to incorrect interpretation and “deciphering” of these structures.
Next, we will use the atomic system of units: ℏ = 1; | e | = 1; m e = 1, where ℏ is the Dirac constant, e is the electron charge, m e is the electron mass.

2. Scattering of attosecond laser pulses

Let’s consider the scattering of attosecond laser pulses on single-stranded DNA macromolecules shown in Figure 1. In this work, we study single-stranded DNA macromolecules, since we are interested in comparing and contributing to the scattering spectra of an undamaged DNA chain (Figure 1(a)) with a damaged one ((Figure 1(b) and ( c)). Obviously, if calculations on single-stranded DNA macromolecules differ from the same calculations using the previous theory, then the same will happen for double-stranded structures. We will also carry out calculations on the same structures in the case of using the previous XRD theory, i.e. where the pulse duration is considered infinitely long. Let us consider in more detail the three structures presented above, on which the USP falls, see Figure 2, Figure 3 and Figure 4.
Since we are considering attosecond pulses, we can use the sudden perturbation approximation to find the scattering spectra of ultrashort pulses. In this approximation, the theory of ultrashort pulse scattering was developed in the works [16,17,19,25,26]. In this approximation, it is assumed that the duration of an ultrashort pulse τ is many times shorter than the characteristic atomic time τ a ∼ 1 , i.e. τ ≪ τ a . Let us recall that for sufficiently light atoms τ a ∼ 1 . Also, this theory is also suitable for longer pulses [27], including femtosecond ones. If we consider the USP to be spatially inhomogeneous, i.e. electromagnetic field strength E ( r , t ) = E 0 h ( t − n 0 r / c ) , where E 0 is the field amplitude, h ( t − n 0 r / c ) is an arbitrary function that determines the shape of the USP, c is the speed of light (in a.e. c ≈ 137 ), then the scattering spectra (scattering energy and unit solid angle) of a Gaussian pulse h ˜ ( ω ) = π α e − ( ω − ω 0 ) 2 / 4 α 2 ( α = 1 / τ , h ˜ ( ω ) this is the Fourier transform of h ( x ) , ω 0 is the carrier frequency of the pulse) can be represented as [16,17,25,26]
d ε d Ω k = E 0 n 2 4 c 3 α 2 π ∑ i = 1 s N e , i N A , i ( 1 − | F i ( p 0 ) | 2 ) + ∑ i , j = 1 s γ i , j ( p 0 , p τ ) N e , i N e , j F i ( p 0 ) F j * ( p 0 ) , γ i , j ( p 0 , p τ ) = ∑ A i , A ′ j e − i p 0 ( R A i − R A ′ j ) ) e − 1 2 ( p τ ( R A i − R A ′ j ) ) 2 .
where N A , i is the number of atoms of i type; N e , i is the number of electrons in the atom i type; R A i is a radius vector specifying the position of an atom i of type with number A i ; the summation is carried out over all atoms ( A i , A j ) and over all types of atoms ( i , j ) ; p 0 = ω 0 c ( n − n 0 ) has the meaning of recoil momentum when light with frequency ω 0 is scattered by a bound electron and p τ = 1 c τ ( n − n 0 ) ; F i ( p 0 ) = 1 N e , i ∫ ρ e , i ( r ) e − i p 0 r d 3 r is the form factor of the i atom of the variety with electron density ρ e , i ( r ) . The electron density of the atoms ρ e , i variety i will be chosen in the independent atom model [28]. In this case we get ρ e , i ( r ) = N e , i 4 π r ∑ k = 1 3 A k , i α k , i 2 e − α k , i r , where A k , i , α k , i are constant coefficients defined in [28]. It should be added that Eq.(2) was obtained in the case of multi-cycle pulses, i.e. ω 0 τ ≫ 1 . This case is precisely realized on well-known ultrashort pulse X-ray sources, for example, Free Electron Lasers (XFELs).
Let us add that if in Eq. (2) we increase τ → ∞ , we get the known Eq. (1). Thus, Eq. (2) contains characteristics responsible for the duration of USP τ . Indeed, if τ → ∞ , then the parameter p τ = 1 c τ ( n − n 0 ) → 0 , and Eq. (2) becomes proportional to τ (Fermi’s golden rule), and therefore coincides with Eq. (1). In this case, it is especially interesting to understand the physical meaning of the p τ momentum, since it is precisely this that is responsible for the main difference between Eq.(2) and Eq.(1). Its physical meaning is quite easy to understand if we consider that the incident USP is non-monochromatic, i.e. this pulse has a frequency dispersion proportional to 1 / τ . This means that during USP scattering, a recoil momentum lying in the interval ∼ p 0 ± p τ is transferred to atomic electrons. From Eq.(2), namely the parameter γ i , j ( p 0 , p τ ) it is clear that the momentum ∼ p 0 ± p τ can be transferred not to all electrons in the system under consideration, but only to those where the distance between electrons is of the order of c τ . In other words, due to frequency dispersion, it is not a plane wave of infinite extent that falls, but a wave packet of limited size ∼ c τ ; accordingly, only those electrons that are located inside the region of space ∼ c τ are scattered together. As a result of this analysis, we can say that if we consider a structure whose asymmetrical part dimensions are comparable to or greater than ∼ c τ , then the pulse duration will have a significant contribution to the scattering spectra, i.e. there will be a big difference between Eq.(2) and Eq.(1). If we choose attosecond pulses with τ ∼ 1 and even an order of magnitude more than this, then such systems can be various macromolecules, including DNA, RNA, various proteins, etc. Although the exact quantitative contribution can only be determined as a result of direct calculations.

3. Results

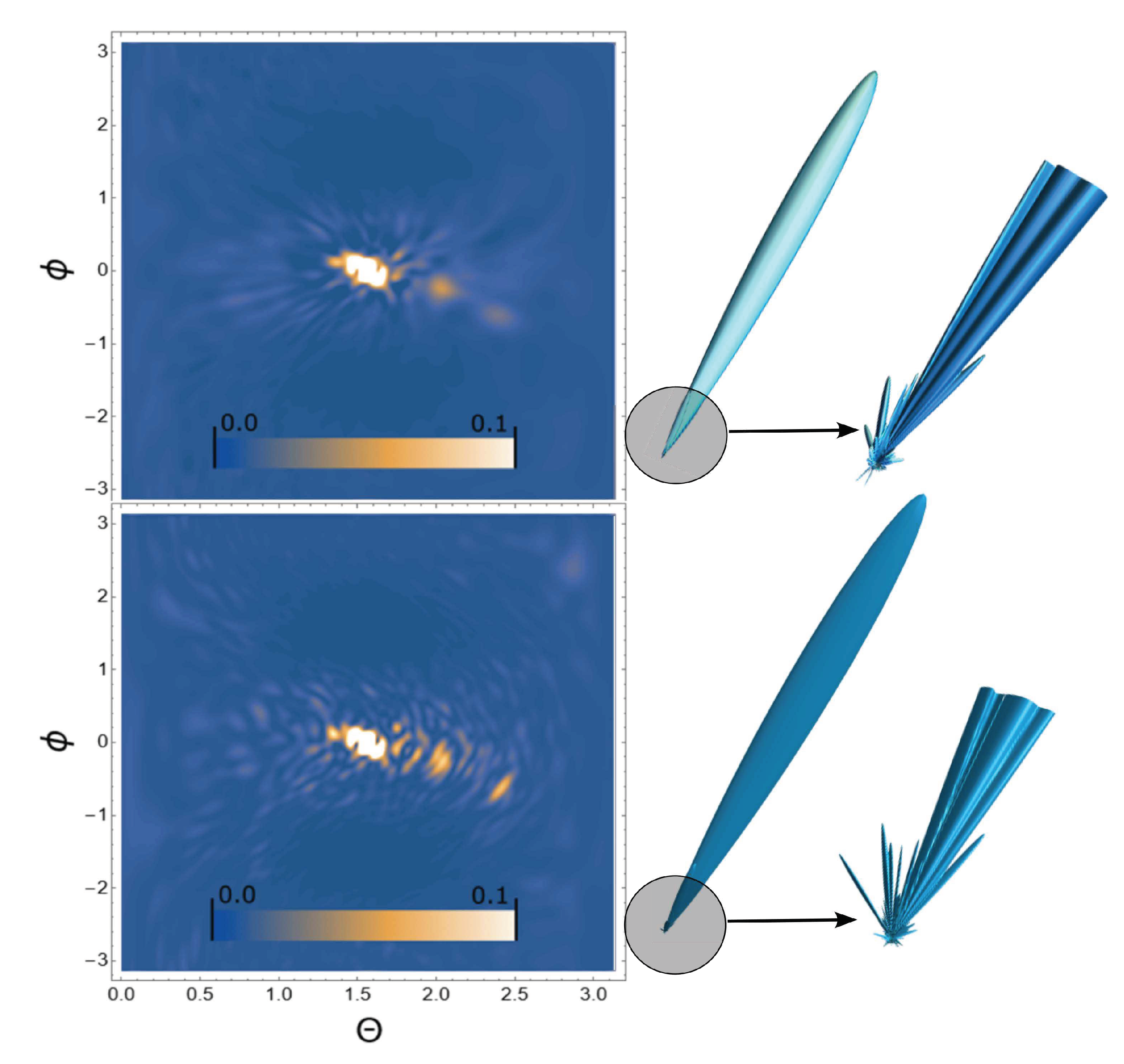
Next, we consider the scattering of USPs on the systems presented in Figure 2, Figure 3 and Figure 4 and show that for such systems the use of Eq. (1) introduces large errors. Results of calculations of scattering spectra using Eq. (2) (top of figures) and using Eq. (1) (lower part of the figures) are shown in Figure 5, Figure 6 and Figure 7. In the presented calculations, the incident USP on the systems under study is presented as shown in Figure 5, Figure 6 and Figure 7 with photon energy ℏ ω 0 = 7.46 k e V , pulse duration τ = 1 as. It should be added that the choice of USP duration is τ = 1 as. purely conditional, in order to better navigate the timeline. We can choose a longer duration in our calculations, about tens of τ ∼ 10 (as), but the results will be close, but more similar to the results of calculations using Eq. (1). It should be added that USP durations of tens of attosecuns have already been implemented [29,30], then our theory and calculations are implementable in practice.
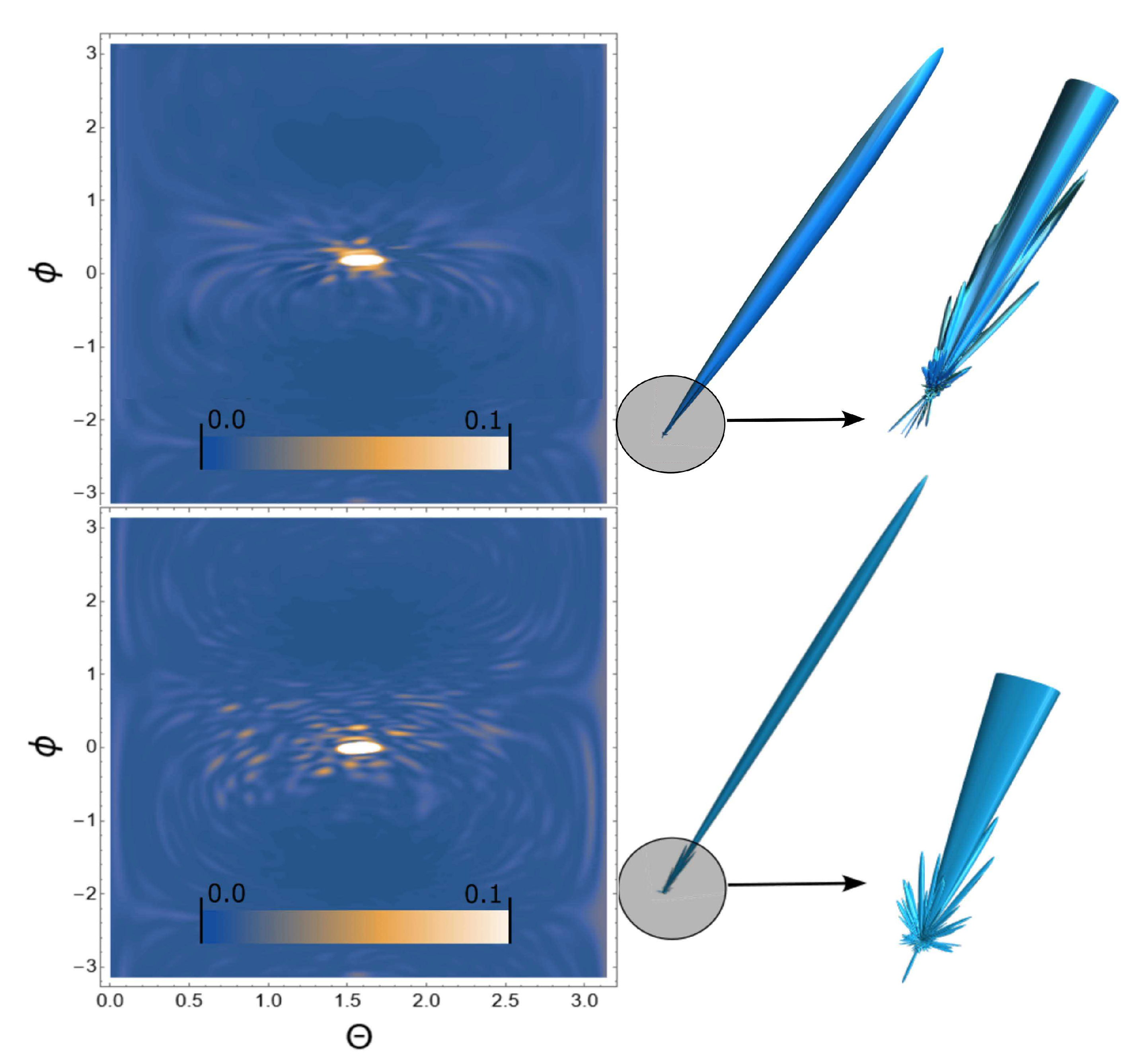
It can be seen from Figure 5, Figure 6 and Figure 7 that the scattering spectra in the case of using Eq. (2) and Eq. (1) are significantly different. There is one basic pattern in the calculations when using Eq. (1) there are more diffraction peaks, especially at large scattering angles. This is easy to explain based on the analysis in the previous section. When using Eq. (1) the pulse duration is not taken into account in the calculations, which means the dimensions of such a pulse are infinitely large, i.e. this is a plane wave. Such a plane wave, incident on the system under study, interacts equally with all the electrons of the polyatomic system, which means there are more scattering centers. When using Eq. (2) the pulse duration is taken into account, and therefore the size of the USP, which is ∼ c τ . The dimensions of our macromolecules are ∼ 100 , which is comparable to the size of USPs. This means that a USP incident on such a system does not interact equally with all electrons of such a structure, which leads to a decrease in scattering centers and, accordingly, diffraction peaks.

4. Conclusion and discussion

The main result obtained in this work is that the use of the previously known and widely used Eq.(1) is unacceptable in the case of scattering of attosecond pulses on the structures under study, see Figure 2, Figure 3 and Figure 4. In this case, it is necessary to use Eq.(2) to calculate the scattering spectra. This output is extremely important for time-resolved X-ray diffraction (TR-XRD). Indeed, to study the dynamics of processes occurring on an atomic and molecular time scale, i.e. where the characteristic time τ a of such systems is comparable to tens of attoseconds, to study the dynamics of such systems it is necessary to use pulses with a duration τ ≪ τ a . When “deciphering” the scattering spectra of such pulses, as shown above, the differences between the old and the presented theory can be very large, which will lead to incorrect determination of the structure and dynamics of the system being studied. Thus, Eq. (2) is more general in XRD (or TR-XRD) theory, where the previous theory is a special case of the theory presented here.
It should be noted that this work studied scattering from spatially oriented structures, which is not the case in the TR-XRD experiment, which uses the pump-probe method. In the pump-probe method, the structures under study are fed randomly oriented relative to the incident USP. To do this, we would need to average the obtained spectra over all possible angles of incident USP. We also carried out similar calculations and all the conclusions are the same as those presented above, i.e. averaging does not qualitatively change the scattering spectra.

Author Contributions

Conceptualization, D.M.; methodology, D.M.; software, D.M. and A.Kh.; validation, D.M. and A.Kh.; formal analysis, D.M. and A.Kh.; writing—original draft preparation, D.M. and A.Kh.; writing—review and editing, D.M.; project administration, D.M. All authors have read and agreed to the published version of the manuscript.

Funding

The study was supported by the Russian Science Foundation No. 23-12-20014; state task of the Russian Federation, No. FSRU-2021-0008.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Request to corresponding author of this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Suryanarayana, C.; Grant, N.M. X-Ray Diffraction: A Practical Approach; Plenum Press, New York and London, 1998.
  2. Jones, N. Crystallography: Atomic secrets. Nature 2018, 505, 602–603. [Google Scholar] [CrossRef]
  3. Pietsch, U.; Holy, V.; Baumbach, T. High-Resolution X-Ray Scattering. Springer Science+Business Media: New York, 2004. [Google Scholar]
  4. Benediktovich, A.; Feranchuk, I.; Ulyanenkov, A. Theoretical Concepts of X-Ray Nanoscale Analysis. Springer-Verlag: Berlin Heidelberg, 2014. [Google Scholar]
  5. James, R. The Optical Principles of the Diffraction of X-rays (Ox Bow); Woodbridge, Conn.: Ox Bow Press, 1982. [Google Scholar]
  6. Dixit, G.; Vendrell, O.; Santra, R. Imaging electronic quantum motion with light. PNAS 2012, 109, 11636–11640. [Google Scholar] [CrossRef] [PubMed]
  7. Hauptman, H.A. The phase problem of x-ray crystallography. Reports on Progress in Physics 1991, 54, 1427–1454. [Google Scholar] [CrossRef]
  8. Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163. [Google Scholar] [CrossRef]
  9. Kraus, P.; Zürch, M.; Cushing, S.K.; Neumark, D.M.; Leone, S.R. The ultrafast X-ray spectroscopic revolution in chemical dynamics. Nature Reviews Chemistry 2018, 2, 82–94. [Google Scholar] [CrossRef]
  10. Peng, P.; Marceau, C.; Villeneuve, D.M. Attosecond imaging of molecules using high harmonic spectroscopy. Nature Reviews Physics 2019, 1, 144–155. [Google Scholar] [CrossRef]
  11. Schoenlein, R.; Elsaesser, T.; Holldack, K.; Huang, Z.; Kapteyn, H.; Murnane, M.; Woerner, M. Recent advances in ultrafast X-ray sources. Philos. Trans. R. Soc. A 2019, 377, 20180384. [Google Scholar] [CrossRef] [PubMed]
  12. Leone, S.R.; McCurdy, C.W.; Burgdörfer, J.; et al. What will it take to observe processes in “real time”? Nature Photonics 2014, 8, 162–166. [Google Scholar] [CrossRef]
  13. Eseev, M.K.; Matveev, V.I.; Makarov, D.N. Diagnostics of Nanosystems with the Use of Ultrashort X-Ray Pulses: Theory and Experiment (Brief Review). JETP Lett. 2021, 114, 387–405. [Google Scholar] [CrossRef]
  14. Astapenko, V.A.; Sakhno, E.V. Excitation of a quantum oscillator by short laser pulses. Applied Physics B 2020, 126, 23. [Google Scholar] [CrossRef]
  15. Rosmej, F.; Astapenko, V.; Lisitsa, V.; Li, X.; Khramov, E. Scattering of ultrashort laser pulses on “ion-sphere” in dense plasmas. Contrib. Plasma Phys. 2019, 59, 189–196. [Google Scholar] [CrossRef]
  16. Makarov, D.; Kharlamova, A. Scattering of X-ray Ultrashort Pulses by Complex Polyatomic Structures. Int. J. Mol. Sci. 2022, 23, 163. [Google Scholar] [CrossRef]
  17. Makarov, D.N.; Makarova, K.A.; Kharlamova, A.A. Specificity of scattering of ultrashort laser pulses by molecules with polyatomic structure. Scientific Reports 2022, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
  18. Eseev, M.; Makarova, K.; Makarov, D. Scattering of Ultrashort X-ray Pulses on Diamonds with NV Centers. Crystals 2022, 12, 1417. [Google Scholar] [CrossRef]
  19. Makarov, D.; Kharlamova, A. Peculiarities of Scattering of Ultrashort Laser Pulses on DNA and RNA Trinucleotides. Int. J. Mol. Sci. 2022, 23, 15417. [Google Scholar] [CrossRef]
  20. Feng, Y.L.; Liu, Q.; Chen, R.D.; et al. DNA nicks induce mutational signatures associated with BRCA1 deficiency. Nature Communications 2022, 13, 4285. [Google Scholar] [CrossRef] [PubMed]
  21. Aymami, J.; Coll, M.; van der Marel, G.A.; et al. Molecular structure of nicked DNA: a substrate for DNA repair enzymes. PNAS 1990, 87, 2526–30. [Google Scholar] [CrossRef] [PubMed]
  22. Odell, M.; Sriskanda, V.; Shuman, S.; Nikolov, D.B. Crystal Structure of Eukaryotic DNA Ligase–Adenylate Illuminates the Mechanism of Nick Sensing and Strand Joining. Molecular Cell 2000, 6, 1183–1193. [Google Scholar] [CrossRef]
  23. Nair, P.; Nandakumar, J.; Smith, P. Structural basis for nick recognition by a minimal pluripotent DNA ligase. Nat Struct Mol Biol 2007, 14, 770–778. [Google Scholar] [CrossRef]
  24. Athreya, N.; Milenkovic, O.; Leburton, J.P. Interaction dynamics and site-specific electronic recognition of DNA-nicks with 2D solid-state nanopores. npj 2D Mater Appl 2020, 4, 32. [Google Scholar] [CrossRef]
  25. Makarov, D. Quantum theory of scattering of ultrashort electromagnetic field pulses by polyatomic structures. Optics Express 2019, 27, 31989–32008. [Google Scholar] [CrossRef] [PubMed]
  26. Eseev, M.; Goshev, A.; Makarova, K.; Makarov, D. X-ray diffraction analysis of matter taking into account the second harmonic in the scattering of powerful ultrashort pulses of an electromagnetic field. Scientific Reports 2021, 11, 3571. [Google Scholar] [CrossRef] [PubMed]
  27. Makarov, D.; Eseev, M.K.; Makarova, K.A. Analytical wave function of an atomic electron under the action of a powerful ultrashort electromagnetic field pulse. Optics Letters 2019, 44, 3042–3045. [Google Scholar] [CrossRef]
  28. Salvat, F.; Martnez, J.; Mayol, R.; Parellada, J. Analytical Dirac-Hartree-Fock-Slater screening function for atoms (Z = 1-92). Phys. Rev. A 1987, 36, 467–474. [Google Scholar] [CrossRef] [PubMed]
  29. Maroju, P.K.; Grazioli, C.; Fraia, M.D.; et al. Attosecond pulse shaping using a seeded free-electron laser. Nature 2020, 578, 386–391. [Google Scholar] [CrossRef] [PubMed]
  30. Duris, J.; Li, S.; Driver, T.; Champenois, E.G.; et al. Tunable isolated attosecond X-ray pulses with gigawatt peak power from a free-electron laser. Nature Photonics 2020, 14, 30–36. [Google Scholar] [CrossRef]
Preprints 86302 g001
Figure 1. (a): a DNA molecule is shown; (b): a DNA molecule is shown with a break in which there is no phosphodiester bond between adjacent nucleotides, i.e. Nick; (c): bending DNA in the Nick molecule.
Figure 1. (a): a DNA molecule is shown; (b): a DNA molecule is shown with a break in which there is no phosphodiester bond between adjacent nucleotides, i.e. Nick; (c): bending DNA in the Nick molecule.
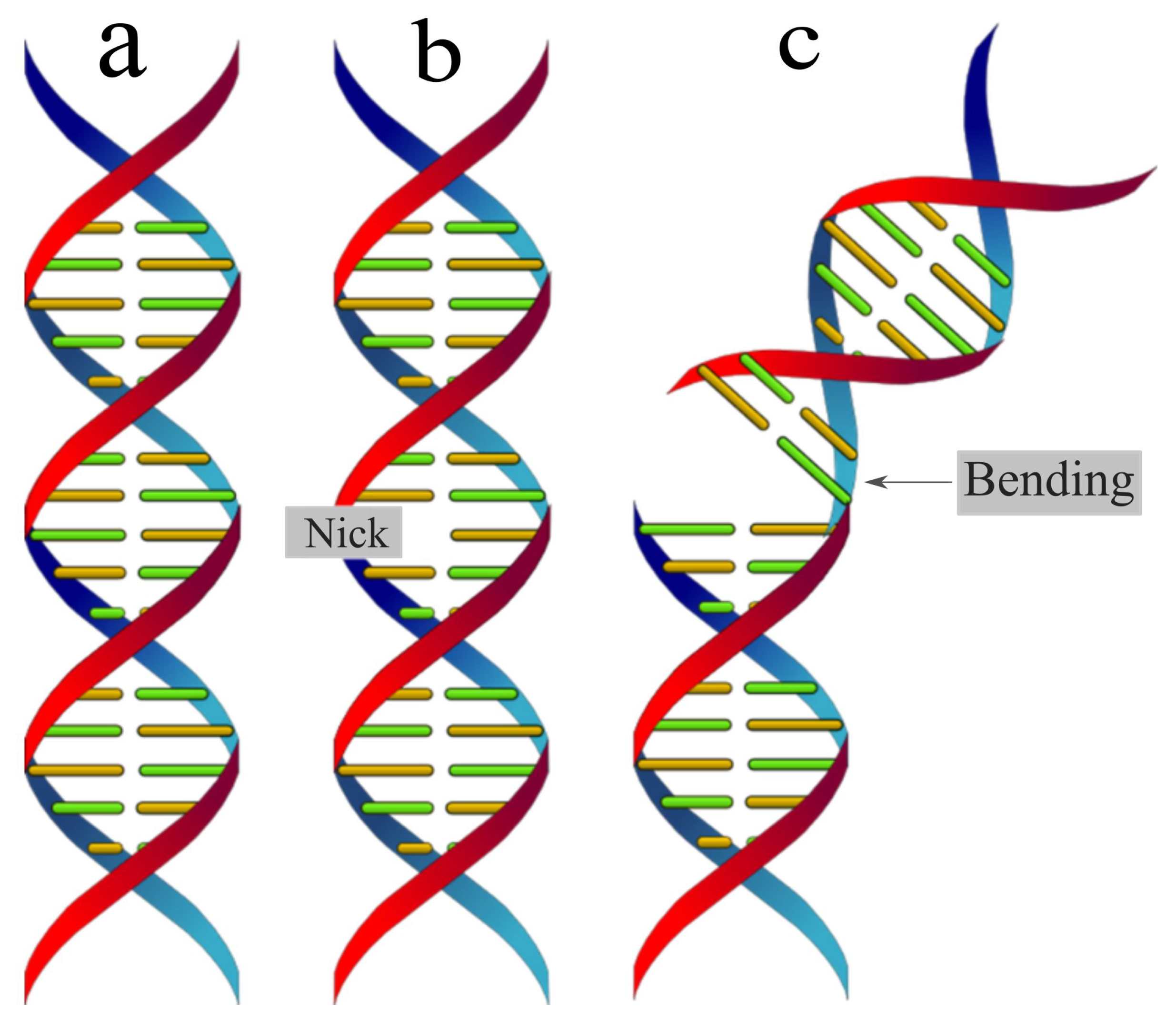
Preprints 86302 g001
Preprints 86302 g002
Figure 2. The USP is shown falling on a section of a single-stranded DNA molecule. The red balls are oxygen atoms (O), the yellow ones are phosphorus (P), the blue ones are nitrogen (N), the light grey ones are hydrogen (H) and the dark grey ones are carbon (C).
Figure 2. The USP is shown falling on a section of a single-stranded DNA molecule. The red balls are oxygen atoms (O), the yellow ones are phosphorus (P), the blue ones are nitrogen (N), the light grey ones are hydrogen (H) and the dark grey ones are carbon (C).
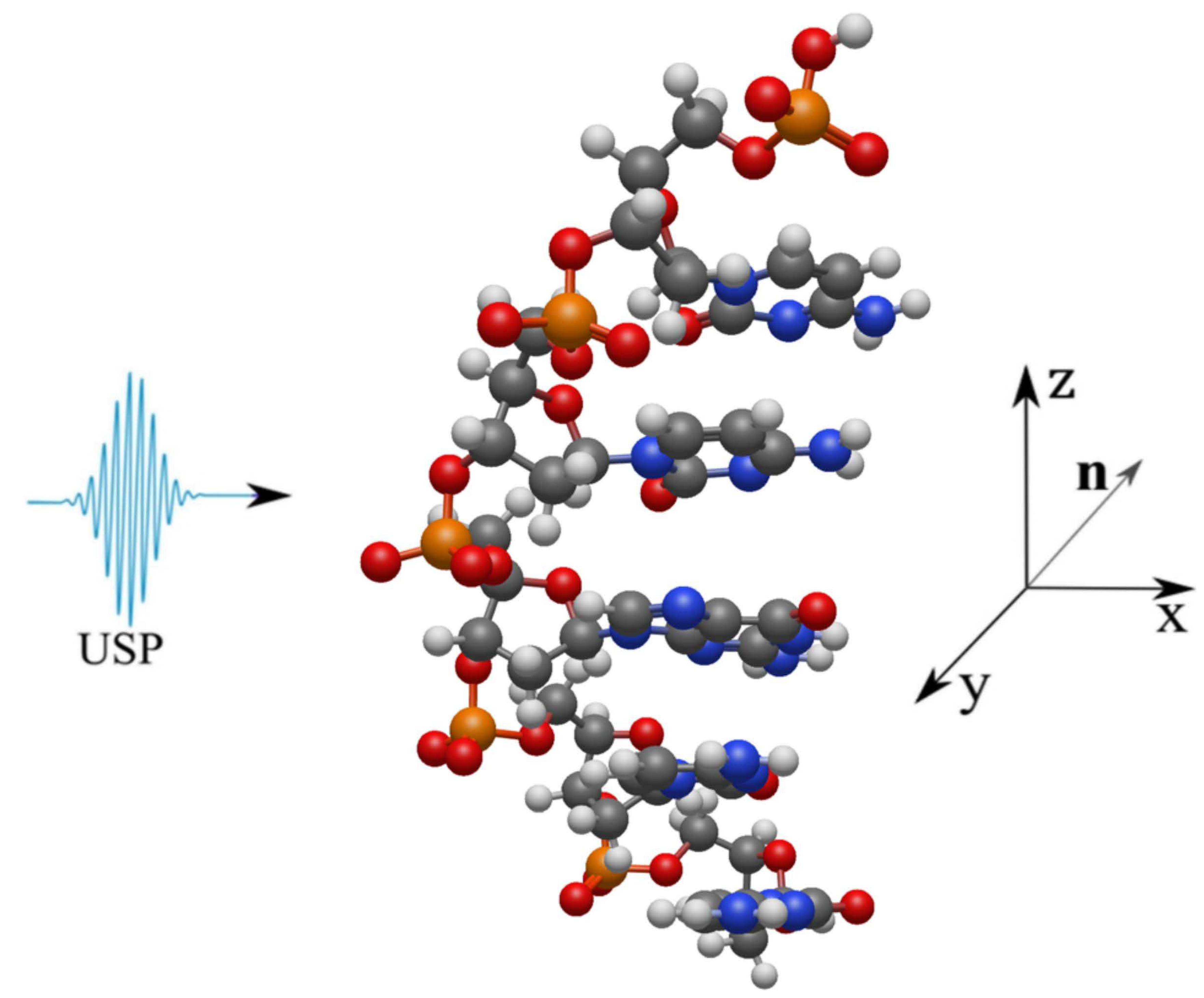
Preprints 86302 g002
Preprints 86302 g003
Figure 3. The USP is shown falling on a section of a single-stranded Nick molecule. The colors of the atoms are the same as in Figure 2.
Figure 3. The USP is shown falling on a section of a single-stranded Nick molecule. The colors of the atoms are the same as in Figure 2.
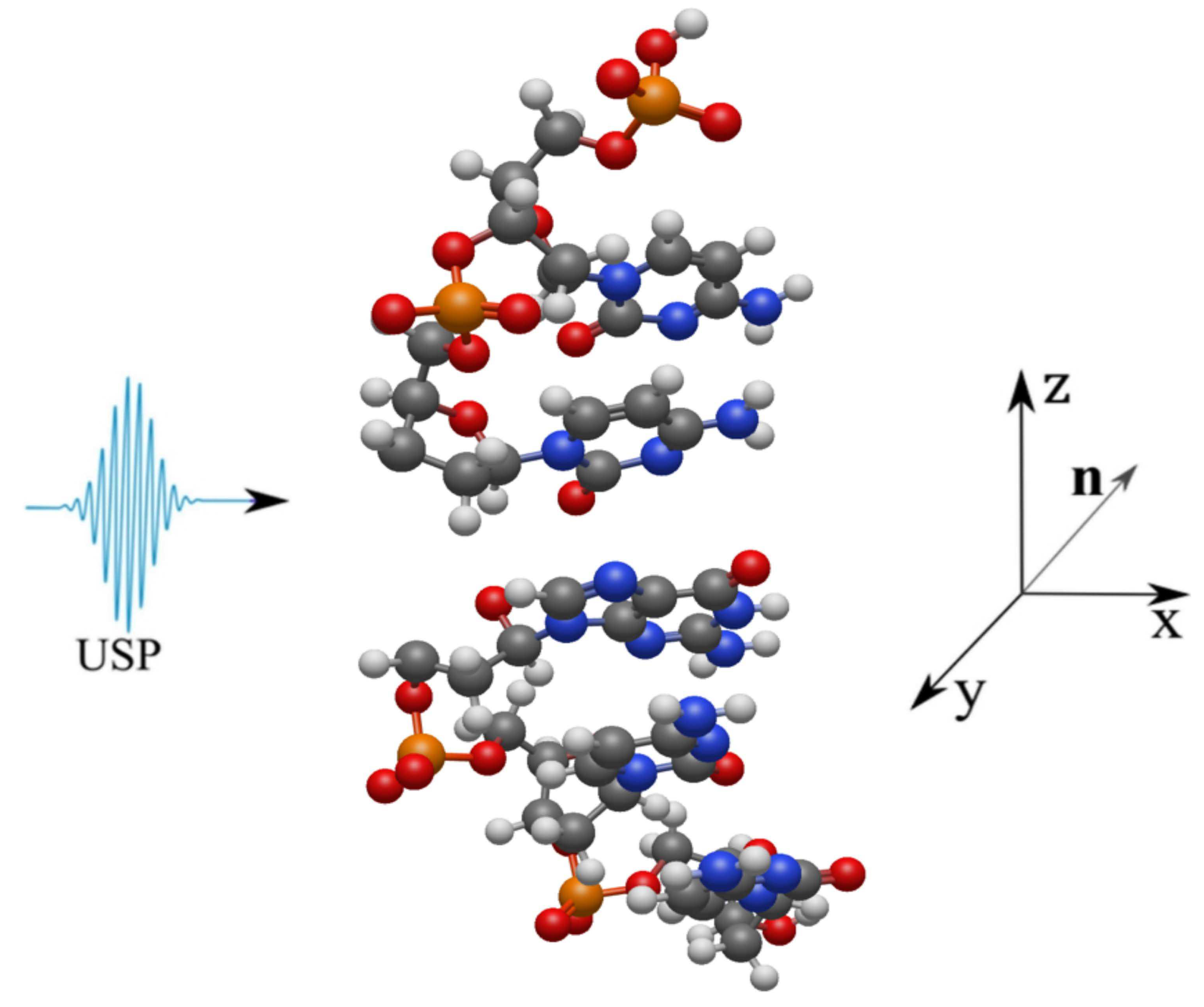
Preprints 86302 g003
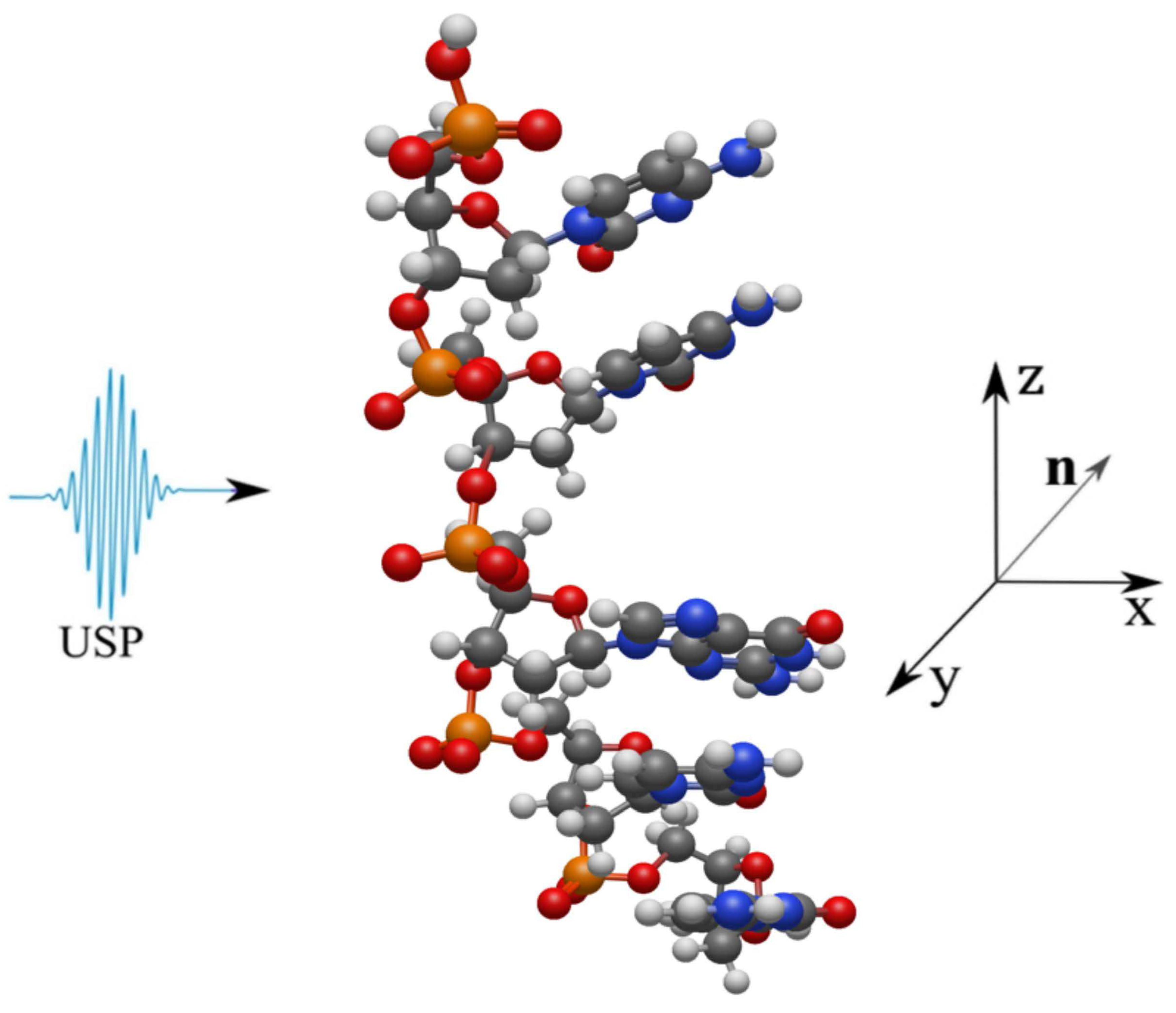
Preprints 86302 g004
Figure 4. The USP is shown falling on a section of a single-stranded bending DNA. The colors of the atoms are the same as in Figure 2.
Figure 4. The USP is shown falling on a section of a single-stranded bending DNA. The colors of the atoms are the same as in Figure 2.
Preprints 86302 g004
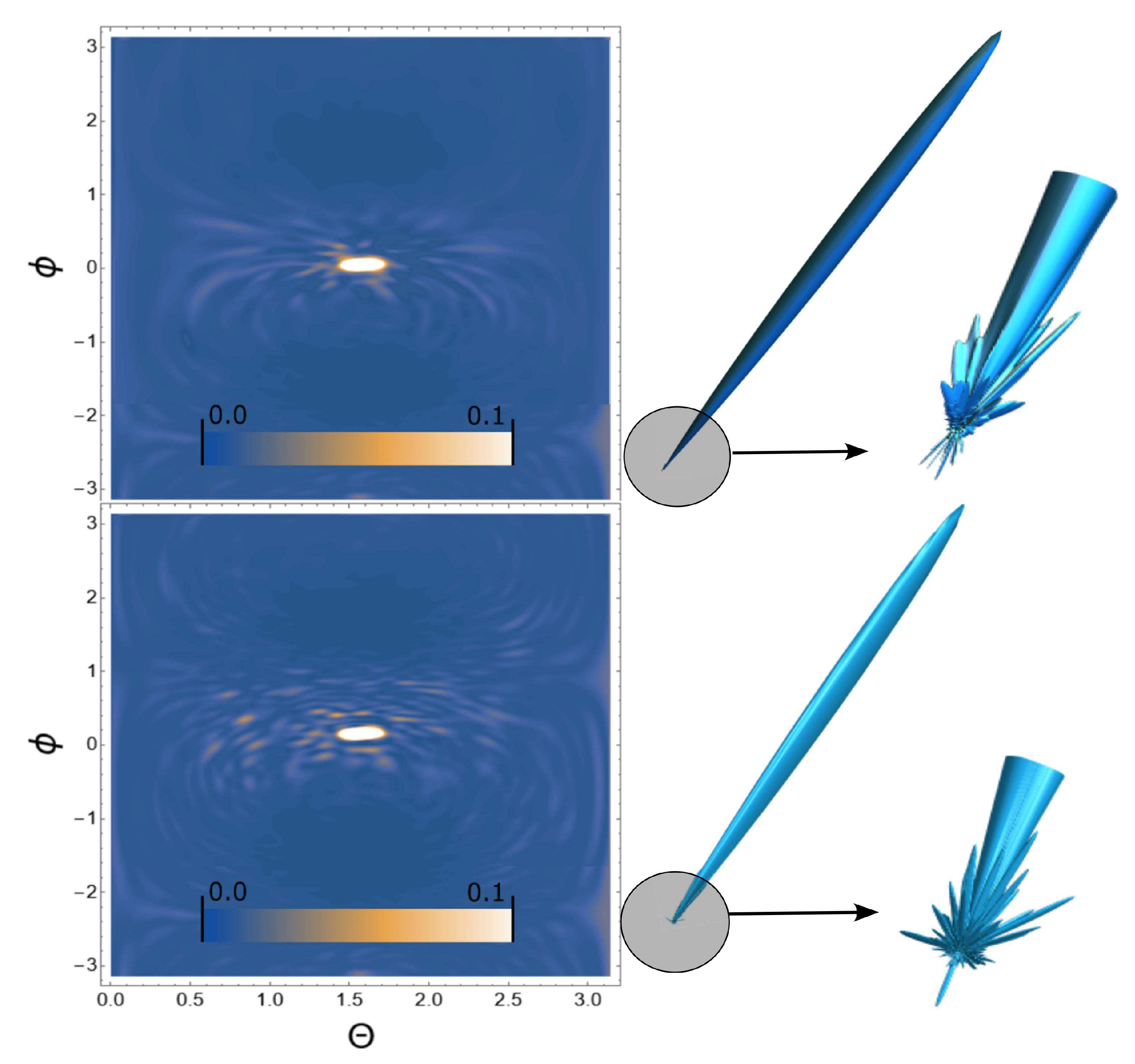
Preprints 86302 g005
Figure 5. Scattering spectra of USP on a region of a single-stranded DNA molecule, see Figure 2: (upper part of the figures) calculated from Eq. (2), (lower part of the figures) calculated from Eq. (1). The spectra are presented as 2D (left) and 3D (right) graphs. 2D plots are presented in dimensionless units and normalized to the maximum value of the spectrum. Angles ϕ , θ are angles in the spherical coordinate system shown in Figure 2.
Figure 5. Scattering spectra of USP on a region of a single-stranded DNA molecule, see Figure 2: (upper part of the figures) calculated from Eq. (2), (lower part of the figures) calculated from Eq. (1). The spectra are presented as 2D (left) and 3D (right) graphs. 2D plots are presented in dimensionless units and normalized to the maximum value of the spectrum. Angles ϕ , θ are angles in the spherical coordinate system shown in Figure 2.
Preprints 86302 g005
Preprints 86302 g006
Figure 6. The same as in Figure 5, but the calculations were carried out for a section of a single-chain Nick molecule, see Figure 3.
Figure 6. The same as in Figure 5, but the calculations were carried out for a section of a single-chain Nick molecule, see Figure 3.
Preprints 86302 g006
Preprints 86302 g007
Figure 7. The same as in Figure 5, but the calculations were carried out for a section of a single-stranded bending DNA, see Figure 4.
Figure 7. The same as in Figure 5, but the calculations were carried out for a section of a single-stranded bending DNA, see Figure 4.
Preprints 86302 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated