Preprint
Article
RC Electrical Modelling of Black Hole. New Method to Calculate the Amount of Dark Matter and the Rotation Speed Curves in Galaxies
Altmetrics
Downloads
273
Views
1113
Comments
1
This version is not peer-reviewed
Submitted:
26 September 2023
Posted:
29 September 2023
You are already at the latest version
Alerts
Abstract
Here we mathematically model black holes following dynamics similar to RC electrical model, focusing on their similarities at the singularity. We use this mathematically modelling to hypothesize the origin and growth of a black Hole. Or model consists of several steps defined by: (1) the formation of a black hole following general relativity equations; (2) growth of the black hole modelled as a resistance-capacitance-like electrical circuit. Based on the mathematical modeling of a black hole following dynamics similar to an RC circuit, for a circular motion with constant acceleration, in which the condition is fulfilled, Vt = ω r, we are going to calculate the amount of dark matter in the Milky Way galaxies and the Andromeda galaxy and subsequently the rotation curve of both galaxies to compare them with observed or measured values.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
Let's remember again the theory of the paper: RLC electrical modelling of black hole and early universe. Generalization of Boltzmann's constant in curved space-time, with which we are going to work to calculate the amount of dark matter in the Milky Way and the Andromeda galaxy M31.
1. RC ELECTRICAL MODEL FOR A BLACK HOLE
If considering electric charge and mass as fundamental properties of matter.
From the point of view of electric charge, we know that a capacitor stores electrical energy and we can represent it as an RC circuit.
Analogously, from the mass point of view, we can consider a black hole as a capacitor that stores gravitational potential energy.
Continuing with the analogy, the space-time that surrounds a black hole can be represented as the inductance L.
from this simple conceptual idea was born RLC electrical modelling of black hole and early universe.
RC electrical model for a Black Hole:
Here we put forward the hypothesis of a black hole growth in analogy to an RC electrical circuit that grows according to a constant Tau being defined as:
First, we will consider the total mass of a black hole to consist of the sum of baryonic mass and dark matter mass (Equation (2)), considering dark matter as an imaginary number.
Where M is the total mass of a black hole, m is the baryonic mass; corresponds to dark matter and I is the irrational number . This equation is in analogy to impedance of an RC circuit.
Where z represents impedance; R represents resistance and Xc represents reactance.
If proper accelerations for the masses are introduced in Equation (2) we obtain the following:
Where F is the total force, f is the force associated to baryonic mass, and i is the force associated to dark mass. In analogy to a phasor diagram for an RC circuit, in which the reactance phasor lags the resistance phasor R by , we can represent the two forces associated to barionic matter and dark matter as two orthogonal vectors (Figure 1).
Vector diagram of forces in a black hole for circular motion with constant acceleration:
taking into account Newton's equation of universal gravitation:
F = - (G M1 M2)/r²
The sign (-) of the equation means that the force Fc is at 180 degrees with respect to the resistance R and the force Ft is also at 180 degrees from the reactance Xc.
It is important to make clear the physical interpretation of the imaginary mass, it is simply telling us that the force Ft due to the mass δ lag the force fc by 90 degrees, that lag is represented by the imaginary number i. Later we will determine that the mass δ, is the result of v > c inside a black hole.
Where v is the speed of a massless particle and c is the speed of light in a vacuum.
Figure 1 is represented for a circular motion with constant acceleration simply because the tangential velocity of a particle is proportional to the radius from the centre of the black hole multiplied by the average angular frequency.
Vt = r ω
The contribution of (Ft, Vt) is what makes the speed of the galaxy remain constant as the radius of the galaxy grows.
Where Vt represents the tangential velocity of a galaxy, r is the radius from the galaxy, and ω is the average angular velocity of the rotation of the galaxy.
Circular motion with constant acceleration tells us that the mass input into a black hole is negligible with respect to the black hole's own mass.
The growth of a black hole according to the tau constant is an intrinsic property of a black hole and is independent of the amount of matter that enters a black hole.
To calculate the total energy associated to the black hole, we can introduce its total mass (Equation (2)) into:
Where E is energy; c represents the speed of light and m represents the mass. This lead to:
We can assume that during the big bang inflation phase baryonic matter was overrepresented compared to dark matter together with an infinitesimal momentum, which would give us from Equation (6) the following:
As expected, this result corresponds to the total energy of the universe at the big bang if we consider it to be made of dark matter represented as a reactance in an RC circuit.
The positive value of E is determined by matter, there is no antimatter inside a black hole.
If we consider charge as a fundamental property of matter, , represents the amount of relativistic dark matter inside the black hole at the time of disintegration.
If we consider mass as a fundamental property of matter, , represents the amount of relativistic dark matter inside a black hole, which exerts a repulsive gravitational force at the moment of disintegration. This repulsive gravitational force is what generates the dark energy after the Big Bang.
At time T0, when the black hole disintegrates and the Big Bang occurs, roughly all matter was dark matter.
We could also consider a universe at infinity proper time in which baryonic matter is dominant over dark matter, which would transform Equation (6) back into Equation (5) but with baryonic matter.
2. RLC ELECTRICAL MODEL OF THE UNIVERSE
We will analyse the Dirac delta function &(t).
&(t) = {∞, t = 0} ^ {0, t ≠ 0}
If we perform the Fourier transform of the function &(t) and analyse the amplitude spectrum, we observe that the frequency content is infinite.
If we perform the Fourier transform of the function &(t) and analyse the phase spectrum, we observe that the phase spectrum is zero for all frequencies.
We say that it is a non-causal zero phase system.
The most important thing to emphasize in this system is that an infinite impulse has an infinite frequency content.
When we work in seismic prospecting looking for gas or oil, using explosives, the detonations produce an energy peak that generates a frequency spectrum that propagates in the layers of the earth. The energy produced in the detonation is not instantly transferred to the ground, a time delay occurs, it is said to be causal system of minimum phase.
In analogy, we are going to suppose that the Big Bang also behaves like a causal system of minimum phase.
Here we put forward the hypothesis that the big bang is the convolution of the energy released by disintegration of the black hole with the space-time surrounding the black hole, being defined as:
Where is the total mass of a black hole, Ɛ is the space-time surrounding the black hole and * is the convolution symbol.
Equation (9) can be simplified and considered analogous to an RLC circuit.
Where RC represents a black hole and L represents the space-time around a black hole
the resolution of the quadratic equation of the RLC circuit will determine how space-time will expand after the Big Bang and the bandwidth of the equation will give us the spectrum of gravitational waves that originated during the Big Bang.
3. COSMIC INFLATION
From the following equation:
We will analyse the Schwarzschild solution for a punctual object in which mass and gravity are introduced.
Where M is the mass of a black hole, c is the speed of light, and G is the gravitational constant.
if we consider dθ = 0; and dφ = 0; that is, we move in the direction of dR.
(14)
R = Rs, ds = 0, let's analyse this specific situation.
(15)
Replacing the conditions given in (13), (14) and (15) in Equation (12), we have:
(dR / dt) ² = v² = c² (1 - (2MG/Rc²) ²
R = Rs, v = 0; ds² = 0; Rs is the Schwarzschild´s radius.
R > Rs, v < c; ds < 0, time type trajectory.
R < Rs, v > c; ds > 0, space type trajectory.
Condition (18) is very important because to the extent that R < Rs, v > c is fulfilled, it is precisely this speed difference that generates the imaginary mass in a black hole given by Planck length equation:
where h is Planck's constant, G is the gravitational constant, and c is the speed of light.
If we consider condition (18) and Equation (19), to the extent that R < Rs and v > c, are fulfilled, we deduce that the Planck length decreases in value.
We define the following:
Lpɛ = Lp = 1.616199 10⁻³⁵ m; electromagnetic Planck length.
Lpɢ = gravitational Planck length.
Always holds:
Lpɢ < Lpɛ
Here we put forward the hypothesis that cosmic inflation is the expansion of space-time that is given by Lpɢ that tends to reach its normal value Lpɛ after a black hole disintegrates.
If we consider the Planck length Lpɛ, the minimum length of space-time, like a spring and due to the action of v > c (300,000 km/s), this length decreases in values of Lpɢ, that is, Lpɢ < Lpɛ, allowing us to imagine the immense forces involved in compressing space-time of length Lpɛ into smaller values of space-time Lpɢ. The immense energy stored and released in the spring of length Lpɢ, to recover its initial length Lpɛ, is the cause of the exponential expansion of space-time in the first moments of the Big Bang.
At time T0, when the black hole disintegrates and the Big Bang occurs, roughly all matter was dark matter, relativistic dark matter.
4. GENERALIZATION OF THE BOLTZMANN´S CONSTANT IN CURVED SPACE-TIME
Equation of state of an ideal gas as a function of the Boltzmann constant.
Where, P is the absolute pressure, V is the volume, N is the number of particles, KB is Boltzmann's constant, and T is the absolute temperature.
Boltzmann's constant is defined for 1 mole of carbon 12 and corresponds to 6.0221 10²³ atoms.
Equation (20) applies for atoms, molecules and for normal conditions of pressure, volume and temperature.
We will analyse what happens with Equation (20) when we work in a degenerate state of matter.
We will consider an ideal neutron star, only for neutrons.
We will analyse the condition:
This condition tells us that the number of particles remains constant, under normal conditions of pressure, volume and temperature
However, in an ideal neutron star, the smallest units of particles are neutrons and not atoms.
This leads us to suppose that number of neutrons would fit in the volume of a carbon 12 atom, this amount can be represented by the symbol Dn.
In an ideal neutron star,
Where Dn represents the number of neutrons in a carbon 12 atom.
However, Equation (22) is not constant, with respect to Equation (21), the number of particles increased by a factor Dn, to make it constant again, I must divide it by the factor Dn.
Where N' = (Dn N), is the new number of particles if we take neutrons into account and not atoms as the fundamental unit.
Where KB' = (KB / Dn), is the new Boltzmann´s constant if we take neutrons into account and not atoms as the fundamental unit.
We can say that Equation (21) is equal to Equation (24), equal to a constant
Generalizing, it is the state in which matter is found that will determine Boltzmann's constant.
A white dwarf star a will have a Boltzmann´s constant KBe, a neutron star will have a Boltzmann´s constant KBn, and a black hole will have a Boltzmann´s constant KBq.
There is a Boltzmann´s constant KB that we all know for normal conditions of pressure, volume and temperature, for a flat space-time.
There is an effective Boltzmann´s constant, which will depend on the state of matter, for curved space-time.
The theory of general relativity tells us that in the presence of mass or energy space-time curves but it does not tell us how to quantify the curvature of space-time.
Here we put forward the hypothesis that there is an effective Boltzmann´ constant that depends on the state of matter and through the value that the Boltzmann´ constant takes we can measure or quantify the curvature of space-time.
Quantifying space-time, considering the variable Boltzmann constant, is also quantizing gravitational waves and, as with the electromagnetic spectrum, we will determine that there is a spectrum of gravitational waves.
These analogies to represent the gravitational and electromagnetic wave equations are achieved thanks to the ADS/CFT correspondence.
We can determine the equations of electromagnetic and gravitational waves as shown below.
Electromagnetic wave spectrum for flat space-time:
Eε = h x fε
Cε = λε x fε
Eε = h x Cε / λε
Eε = Kʙε x Tε
Kʙɛ = 1.38 10⁻²³ J/K
Gravitational wave spectrum for curved spacetime:
Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
Kʙɢ = 1.38 10⁻²³ J/K to 1.78 10⁻⁴³ J/K.
Where the subscript ε means electromagnetic and the subscript ɢ means gravitational.
It can be seen that there is an electromagnetic and a gravitational frequency as well as an electromagnetic and a gravitational temperature.
The maximum curvature of space-time occurs for an effective Boltzmann´s constant of KB = 1.78 10⁻⁴³ J/K, given by the ADS/CFT correspondence in which a black hole is equivalent to the plasma of quarks and gluons to calculate the viscosity of the plasma of quarks and gluons.
Once a black hole is formed and the maximum curvature of space-time is reached, as a black hole grows following the tau growth law analogous to an RC circuit, as v grows fulfilling the relationship v > c, it happens that the gravitational Planck length becomes less than the electromagnetic Planck length, it holds that Lpɢ < Lpɛ.
5. BLACK HOLE´S RADIATION
Equation (2) defines the mass of a black hole, as shown below:
Where M is the total mass of a black hole, m is the baryonic mass; corresponds to dark matter and i is the irrational number .
Also, here we put forward the hypothesis of a black hole growth in analogy to an RC electrical circuit that grows according to a constant Tau being defined as:
If we consider the black hole´s radiation that produces pairs of particles and antiparticles at the event horizon.
Here we put forward the hypothesis:
the HR (matter) particle, with frequency ω and energy hω, falls into the black hole and adds to m and δ increasing the mass of the black hole, that is, it adds mass.
This is defined with the assumption that a black hole grows according to the tau constant just like an RC circuit.
The P particle (antimatter), with frequency ω and energy -hω, moves away from the black hole in the form of a gravitational wave.
According to the proposed hypothesis, a black hole always grows, following the curve of the tau constant in analogy to an RC electrical circuit.
For a black hole of 3 solar masses, the stationary frequency would be approximately 2.6 10³ Hz.
6. APPLICATION OF THE MODEL AND RESULTS
6.1. Additional calculations. Growth of a black hole in analogy to the tau growth curve of an RC circuit
In the ADS/CFT correspondence to calculate the viscosity of quark-gluon plasma, the following assumption is used, a black hole is equivalent to quark-gluon plasma.
We consider the temperature of a black hole equal to the temperature of the quark-gluon plasma, equal to T = 10¹³ K.
Another way of interpreting it is as follows:
When a star collapses, a white dwarf star, a neutron star, or a black hole is formed.
A white dwarf star has a temperature of about 10⁶ K, a neutron star has a temperature of about 10¹¹ K. If we consider that a black hole is a plasma of quarks and gluons, its temperature is expected to be higher than 10¹¹ K.
Hypothesis: the temperature of a black hole is 10¹³ K.
We will make the following approximation:
T = 0.0000000000001τ, T = 10⁻¹³τ
τ = 10²⁶ K
Cɢ(T) = Cɢmax (1 - e⁻(ᵀ/τ))
Cɢ(T) = Cɢmax (1 - e ⁻ ⁰·⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰¹(τ/τ))
Cɢ(T) = Cɢmax (1 - e ⁻ ⁰·⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰⁰¹)
Cɢ(T) = Cɢmax (1 - e ⁻ (¹ / 10¹³)
Cɢ(T) = Cɢmax (1 - 1 / e (¹/ 10¹³))
Cɢ(T) = Cɢmax (1 – 0.9999999999999)
Cɢ(T) = Cɢmax x 10⁻¹³
Cɢmax = Cɢ(T) / 10⁻¹³ = 3 10⁸ m/s x 10¹³
Cɢmax ≡ 3 10²¹ m/s.
Where T is the absolute temperature, τ represents the growth constant tau, Cɢ = v represents the speed of a massless particle greater than the speed of light and Cɢmax represents the maximum speed that Cɢ can take.
Parametric equations:
Cɢ (T) = Cɢmax (1 – e ⁻(ᵀ/τ)
T (kelvin) = {(ɦ c³) / (8 x ᴨ x Kʙ x G x M)}, Hawking's equation for the temperature of a black hole.
Rs = (2 x G x M) / c², Schwarzschild´s radius.
IMI = K ImI, where K is a constant.
IMI = I δ I
Kʙq = 1.78 10⁻⁴³ J/K, Boltzmann ´s constant for black hole.
- a)
- In item 1 of the Table 1, for the following parameters, T = 10¹³ K, Cɢ = C = 310⁸ m/s, calculating we get the following values:
m = 6 10³⁰ kg, baryonic mass.
δ = 0, dark matter mass.
M = m = 6 10³⁰ kg
Rs = 8,89 10³ m, Schwarzschild radius.
- b)
- In item 9 of the Table 1, for the following parameters, T = 5 10²⁶ K, Cɢ = 3 10²¹ m/s, C = 310⁸ m/s, calculating we get the following values:
m = 1.20 10⁵⁶ kg, baryonic mass.
δ = 1.20 10⁸² kg, dark matter mass.
M = δ = 1.20 10⁸² kg
Rs = 1.77 10²⁹ m, Schwarzschild radius.
- c)
- It is important to emphasize, for the time t equal to 5τ, at the moment the disintegration of the black hole occurs, the big bang originates, the total baryonic mass of the universe corresponds to m = 10⁵⁶ kg.
- d)
- Figure 2 shows the growth of the tau (τ) constant, as a function of speed vs. temperature.
6.2. Calculation of the amount of dark matter that exists in the Milky Way
Mass and Schwarzschild´s radius of the Sagittarius A* black hole:
m = 4.5 10⁶ Ms = 4.5 x 10⁶ x 1.98 10³⁰ kg
Where Ms is the mass of the sun.
m = 8.1 x 10³⁶ kg
Rs = 6 million kilometres
Where Rs is the Schwarzschild´s radius of the Sagittarius A*.
Rs = 6 x 10⁹ m
If we look at Figure 2, for m = 8.1 x 10³⁶ kg and Rs = 6 x 10⁹ m, extrapolating we have approximately that T = 3 10¹⁴ K.
To calculate the speed Cɢ we are going to use the Hawking temperature equation:
T = hc³ / (8ᴨ x KB x G x M)
Where h is Boltzmann's constant, c is the speed inside a black hole, KB is Boltzmann's constant, G is the universal constant of gravity, and M is the mass of the black hole.
Substituting the values and calculating the value of C we have:
Cɢ = 10.30 10¹⁰ m/s
If we look at Figure 3, we see that this value corresponds approximately to the calculated value.
With the value of Cɢ we calculate δ and M:
E = m C²
Where E is energy, m is mass, and C is the speed of light.
Eɢ = M Cɢ
Eɢ = K m C²
Eɢ = k E
Where K is a constant.
Calculation of the constant K:
C = 3 10⁸ m/s,
Cɢ = 10.30 10¹⁰ m/s,
m = 8.1 10³⁶ kg
E = 8.1 10³⁶ kg x 9 10¹⁶ m²/s²
E = 72.9 10⁵² J
Eɢ = 8.1 10³⁶ x (10.30 10¹⁰) ² = 8.1 10³⁶ x 106 10²⁰
Eɢ = 858.6 10⁵⁶ J
Eɢ = (106 / 9) 10⁴ x 8.1 10³⁶ x 9 10¹⁶
Eɢ = K E
K = 11.77 10⁴
Calculation of the total mass M:
M = K m
M = (11.77 10⁴) x (8.1 10³⁶ kg)
M = 9.54 10⁴¹ kg, Total mass of black hole Sagittarius A*
m = 8.1 x 10³⁶ kg, total baryonic mass inside the black hole Sagittarius A*
Calculation of the mass of dark matter δ:
M = δ
δ = 9.54 10⁴¹ kg, total dark matter inside the black hole Sagittarius A*
Calculation of the ratio of the mass of dark matter and the mass of the Milky Way
Mvl = 1.7 10⁴¹ kg
Mvl, mass of the milky way
δ = 9.54 10⁴¹ kg
δ, dark matter inside the black hole Sagittarius A*
δ / Mvl = (9.54 10⁴¹ kg / 1.7 10⁴¹ kg)
δ / Mvl = 5.61, ratio of the mass of dark matter and the mass of the Milky Way
δ = 5.61 Mvl
The total dark matter δ is 5.61 times greater than the measured amount of baryonic mass of the Milky Way Mvl.
Circular motion with constant acceleration.
Let's consider, for a black hole, circular motion with constant acceleration.
Circular motion with constant acceleration tells us that the mass input into a black hole is negligible with respect to the black hole's own mass.
Figure 1, is represented for a circular motion with constant acceleration simply because the tangential velocity of a particle is proportional to the radius from the centre of the black hole multiplied by the average angular frequency.
Vt = ω r
Equation (29) is very important, based on this equation we are going to work.
Let's consider the Figure 4, provided by the Federal University of Rio Grande do Sul UFRS:
In Figure 3, we observe that there is a difference between the observed or measured rotation speed of the Milky Way and the rotation speed considering only visible matter.
This difference is attributed to the existence of an invisible matter that we call dark matter, because we do not know its origin.
However, if we look at Figure 3, as the black hole grows, a tangent force Ft appears, as a consequence of v > c inside a black hole, which generates additional mass. This tangential force Ft delays the force Fc by 90 degrees. Both forces are gravitational forces.
Taking as reference (29) and the distance r in Kpc to the centre of the Milky Way; We are going to generate the Table 2:
Let's calculate ω:
To calculate ω, we are going to consider Figure 4.
ω = (187 km/s) / (7 Kpc)
ω = 187 / 10 x 21 10¹⁶ = 8.9 10ˉ¹⁶
ωt = 8.9 10ˉ¹⁶ rad/s
ωt, constant angular velocity of the Milky Way.
ωt is theoretical omega ou proposed omega.
We are going to carry out the calculations of the angular rotation speed considering the data provided by the University of São Paulo, USP [3].
For the position of the sun, we have:
r = 8.5 Kpc
Vt = 224.4 km/s
Vt = ω x r
ω = Vt / r
ω = 224.4 km/s / 8.5 Kpc = 224.4 /8.5 x 3 10¹⁶
ωc = 8.8 10ˉ¹⁶ rad/s
ωc, calculated value given by USP university.
We observe that the angular velocity ωt, given by (31), is approximately equal to the value calculated ωc, in (30)
If we look at Figure 4, starting at 7 Kpc, we see that the speed begins to decrease gently, therefore, we are going to consider r = 7 Kpc
Taking all this data into consideration, we are going to make the following table:
If we analyse Figure 5, we observe that the relationship Vt = ω r, is fulfilled up to 7 Kpc, from 7 Kpc onwards, we observe that the tangency speed does not comply with the relationship Vt = ω r. From 7 Kpc onwards, the tangent velocity due to the contribution of dark matter decreases parallel to the rotation velocity curve of the Milky Way, measured or observed.
Considering the graph of the rotation speed of only the visible matter and the graph in red, of the rotation speed of the dark matter, we are going to calculate the vector sum of both speeds to obtain a total speed and compare it with the graph of the observed or measured rotation speed.
In the following table we represent the calculations:
Table 3.
We represent Vdm, tangential rotation speed due to dark matter in red; Vm, tangential rotation speed due only to visible matter, Vc, calculated tangential rotation speed that results from the sum of Vdm + Vm and Vo, is the observed or measured tangential speed.
Table 3.
We represent Vdm, tangential rotation speed due to dark matter in red; Vm, tangential rotation speed due only to visible matter, Vc, calculated tangential rotation speed that results from the sum of Vdm + Vm and Vo, is the observed or measured tangential speed.
 |
It is important to remember that the tangential rotation speeds are vectors, therefore, the sum of speeds is vector and for this we use Pythagoras.
If we look at Figure 6, we see that the observed tangential speed Vo is approximately coincident with the calculated tangential rotation speed Vc, in orange.
Vc is the vector sum of the velocity Vdm plus the velocity Vm, Vdm + Vm.
Finally, we have shown that using the theory of RLC electrical modeling of a black hole and the primitive universe and the theory of the generalization of the Boltzmann constant in curved space-time, we can determine the tangential rotation curve of the Milky Way, in coincidence with the observed or calculated values. This is another method that we can use to calculate the tangential rotation speeds of galaxies.
6.2. Calculation of the amount of dark matter existing in the Andromeda galaxy M31
We will consider the mass of the black hole at the centre of the Andromeda galaxy equal to:
Let's assume m the following value [1]:
m = 1.5 10⁷ Ms = 1.5 x 10⁷ x 2 10³⁰ kg
Where Ms is the mass of the sun.
m = 3 x 10³⁷ kg
m, mass of the black hole at the centre of the Andromeda galaxy
Let's assume ML the following value [2]:
ML = 3 10⁴² kg
Where ML is the luminous mass of the Andromeda galaxy
If we look at Figure 2, for m = 4 x 10³⁷ kg, extrapolating we have approximately that:
T = 4 10¹⁵ K and c = 5 10¹¹ m/s.
T = 4 10¹⁵ K
Cɢ = 3 10¹¹ m/s
We are going to verify if these extrapolated values are correct or within the order of error.
MBH = hc³ / (8ᴨ x KB x G x T)
Where h is Boltzmann's constant, c is the speed inside a black hole, KB is Boltzmann's constant, G is the universal constant of gravity, and M is the mass of the black hole.
Substituting (32) and (33) into (34), we have:
MBH = 1.5 10³⁷ kg
We see that m = 3 10³⁷ kg, is approximately equal to MBH = 1.5 10³⁷ kg
If we look at Figure 3, we see that this value corresponds approximately to the calculated value.
We will take m = 1.5 10³⁷ kg, as true.
With the value of Cɢ we calculate δ and M:
E = m C²
Where E is energy, M is mass, and C is the speed of light.
Eɢ = m Cɢ²
Eɢ = K m C²
Where K is a constant.
Calculation of the constant K:
C = 3 10⁸ m/s
Cɢ = 3 10¹¹ m/s
m = 1.5 10³⁷ kg
E = 1.5 10³⁷ kg x 9 10¹⁶ m²/s² = 13.5 10⁵³
E = 13.5 10⁵³ J
Eɢ = 1.5 10³⁷ x (3 10¹¹) ² = 1.5 10³⁷ x 9 10²²
Eɢ = 13.5 10⁵⁹ J
Eɢ = K E
K = Eɢ / E = 13.5 10⁵⁹ / 13.5 10⁵³ = 10⁶
K = 10⁶
Calculation of the total mass of the black hole of the Andromeda M31 galaxy:
M = K m
M = (10⁶) x (1.5 10³⁷ kg)
M = 1.5 10⁴³ kg
Where M is the total mass of the central black hole of the Andromeda Galaxy.
m = 1.5 x 10³⁷ kg, total baryonic mass inside the black hole of the Andromeda Galaxy.
Calculation of the mass of dark matter δ:
M = δ
δ = 1.5 10⁴³ kg,
Where δ, is total dark matter inside the black hole.
Calculation of the ratio of the mass of dark matter and the mass of the andromeda galaxy.
ML= 3 10⁴² kg
Where ML is the luminous mass of the Andromeda M31 galaxy.
δ = 1.5 10⁴³ kg
δ / ML= (1.5 10⁴³ kg / 3 10⁴² kg)
δ / Mvl = 5
δ = 5 ML
The total dark matter δ is 5 times greater than the measured amount of baryonic mass of the andromeda galaxy.
Let's consider circular motion with constant acceleration.
Circular motion with constant acceleration tells us that the mass input into a black hole is negligible with respect to the black hole's own mass.
Vector diagram of forces in a black hole for circular motion with constant acceleration:
Figure 3, is represented for a circular motion with constant acceleration simply because the tangential velocity of a particle is proportional to the radius from the centre of the black hole multiplied by the average angular frequency.
Vt = ω r
Equation (37) is very important, based on this equation we are going to work.
From now on, I inform you that the data and graphs with which we are going to work were provided in the Cosmology 1 course, taught by Dr Alexander Sabot, from the federal university of Santa Catarina, UFSC. The graphs were made in Python with real astronomical data.
We are going to carry out the calculations of the angular rotation speed considering the data provided by [4].
r = 33,000 Ly; Vt = 250 km km/s
1 Ly = 9.46 10¹⁵ m
ω = Vt / r
ω = 250 10³ / 308 10³ 10¹⁵
r = 80,000 Ly; Vt = 200 km/s
ωa = 8.11 10ˉ¹⁶ rad/s
ω = Vt / r
ω = 200 10³ / 752 10³ 10¹⁵
ωb = 2.6 10ˉ¹⁶ rad/s
We observe that the angular velocity ωa, given by (38), is approximately equal to the value calculated ωb, in (39)
THEORETICAL ANALYSIS - CALCULATION OF DARK MATTER IN THE COSMOLOGY 1 COURSE, UFSC:
The Python program, developed by Dr Alexander Zabot, from the Cosmology I course, is used to calculate the rotation curves of the Andromeda galaxy due to dark matter, the galactic nucleus and the galactic disk.
Value of parameters used in Python.
Figure 7. Parameter values used in the Python program to generate the graph in Figure 8.
We observe in Figure 8, how the calculated rotation curve values, in purple, are close to the measured or observed values, in blue.
THEORETICAL ANALYSIS - WE CONSIDER THAT THE BLACK HOLE IS COMPOSED OF THE MASS M = m - i δ, THAT IS, THAT THERE IS A TANGENTIAL FORCE Ft. WE ASSUME THAT THE RELATIONSHIP, Vt = ω r, IS FULFILLED.
The Python program, developed by Dr Alexander Zabot, from the Cosmology I course, is used to calculate the rotation curves of the Andromeda galaxy due to dark matter, the galactic nucleus and the galactic disk.
Value of parameters used in Python.
Figure 9. Parameter values used in the Python program to generate the graph in Figure 10.
Taking into account Figure 11, we are going to perform the following calculations:
Vt = ω r
ω = Vt / r
ω = 250 km/s / 700 Kpc = (250 10³ m/s) / 700 10³ 3 10¹⁶
ω = 250 / 2100 10¹⁶ = 0.119 10ˉ¹⁶ = 1.19 10ˉ¹⁷ rad/s
ω = 1.19 10ˉ¹⁷ rad/s
With the value of ω, we do the following and fill out the following table:
Table 4.
Represents the values of the tangential velocity Vt, angular velocity ω, , as a function of the radius r.
Table 4.
Represents the values of the tangential velocity Vt, angular velocity ω, , as a function of the radius r.
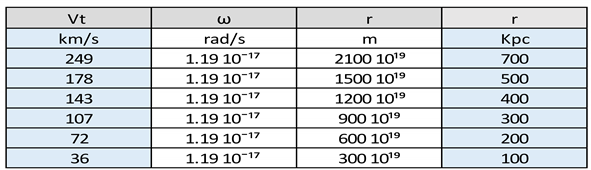 |
If we analyse Figure 11, we observe that the relationship Vt = ω r, is fulfilled up to 700 Kpc, from 700 Kpc onwards, we observe that the tangency speed does not comply with the relationship Vt = ω r; from 700 Kpc onwards, the tangent velocity due to the contribution of dark matter decreases parallel to the rotation velocity curve of the Galaxy M31, measured or observed.
Considering the graph of the rotation speed of only the visible matter and the graph in red, of the rotation speed of the dark matter, we are going to calculate the vector sum of both speeds to obtain a total speed and compare it with the graph of the observed or measured rotation speed.
In the following table we represent the calculations:
Table 5.
We represent Vdm, tangential rotation speed due to dark matter; Vm, tangential rotation speed due only to visible matter; Vc, calculated tangential rotation speed that results from the sum of Vdm + Vm and Vo, is the observed or measured tangential speed.
Table 5.
We represent Vdm, tangential rotation speed due to dark matter; Vm, tangential rotation speed due only to visible matter; Vc, calculated tangential rotation speed that results from the sum of Vdm + Vm and Vo, is the observed or measured tangential speed.
 |
As seen in Figure 11, from 400 Kpc onwards, the influence of dark matter is predominant.
It is important to remember that the tangential rotation speeds are vectors, therefore, the sum of speeds is vector and for this we use Pythagoras.
If we look at Figure 12, we see that the observed tangential speed Vo is approximately coincident with the calculated tangential rotation speed Vc, in yellow.
Vc is the vector sum of the velocity Vdm plus the velocity Vm, Vdm + Vm.
Let's compare the following figures:
If we look at Figure 13, it corresponds to the theoretical model that we used in the cosmology course 1 and compare with Figure 13, it corresponds to the RC model of a black hole that has mass M = m - i δ and that satisfies the equation Vt = ω r; We conclude that the rotation curve calculated in Figure 13 fits the observed or measured data of the Andromeda galaxy.
To improve, you could combine both methods, below 400 Kpc, we use the theoretical analysis applied in Cosmology 1, above 400 Kpc, we apply the RC model of a black hole, in which the mass is M = m - i δ and it holds that Vt = ω r.
Finally, we have shown that using the theory of RLC electrical modelling of a black hole and the primitive universe and the theory of the generalization of the Boltzmann constant in curved space-time, we can determine the tangential rotation curve of the galaxy M31, in coincidence with the observed or calculated values. This is another method that we can use to calculate the tangential rotation speeds of galaxies.
6.3. We will describe the contribution of all the forces involved in determining the rotation speed of a galaxy using the RC electrical model of a black hole.
Let us remember that all forces and velocity are vector magnitudes. We are also going to remember that in the RC electrical model of a black hole it is true that M = m - i δ and Vt = ω r.
Ḟв + Ḟᴅ + Ḟdm = (m / r) x (Vв² + Vᴅ²) + (δ / r) Vdm ²
Ḟв + Ḟᴅ + Ḟdm = (m / r) x (Vв² + Vᴅ²) + (δ/ r) x (ω r) ²
Ḟв + Ḟᴅ + Ḟdm = (m / r) x (Vв² + Vᴅ²) + δ ω² r
Equation (40), (41) y (42); represents the contribution of all the forces that intervene in the rotation curve of a galaxy.
Where m, is baryonic matter; δ, it's dark matter.
Where Ḟв, force of the bojo or galactic nucleus; Ḟᴅ, force of the galactic disk; Ḟdm, force of the imaginary mass or dark matter inside a black hole and r, radius of the galaxy.
Where Vв, is the rotation speed due to the bojo or galactic nucleus; Vᴅ, is the rotation speed due to the galactic disk; Vdm, is the rotation speed due to dark matter.
m >> δ, r near the black hole, we have:
V, the rotation speed of the galaxy will be the vector sum of the speed of the disk Vᴅ plus the rotation speed of the galactic nucleus Vв, that is:
V, is vector sum of velocity.
Ḟв + Ḟᴅ + Ḟdm ≈ (m / r) x (Vв² + Vᴅ²)
δ >> m, r far from the galactic centre, we have:
The speed of the rotation curve of the galaxy will be approximately Vdm, due to the contribution of dark matter.
V = Vdm
Ḟв + Ḟᴅ + Ḟdm ≈ (δ / r) Vdm ²
m ≈ δ, baryon mass of the order of the mass of dark matter.
V = Vв + Vᴅ + Vdm
V, is vector sum of velocity.
Ḟв + Ḟᴅ + Ḟdm = (m / r) x (Vв² + Vᴅ²) + (δ / r) Vdm ²
Ḟв + Ḟᴅ + Ḟdm ≈ (m / r) x (Vв² + Vᴅ² + Vdm²)
The speed of the rotation curve of the galaxy will be the vector sum of the rotation speed of the galactic nucleus plus the rotation speed of the galactic disk and plus the rotation speed due to dark matter.
Vm = Vв + Vᴅ
Where Vm represents the rotation curve of visible matter and is the vector sum of the velocity due to the galactic nucleus plus the velocity due to the galactic disk.
Using the criteria described here, a), b) y c), the mentioned approaches, we perform calculations to determine the speed of the rotation curve of a galaxy, Vc, calculated speed represented in the tables, which we compare with Vo, which is the observed or measured speed.
7. Conclusions
Using the theory of RC electrical modelling of a black hole, we have demonstrated how to calculate the amount of dark matter contained in a galaxy and its rotation speed curve. We have shown that if the matter entering a black hole is negligible in relation to the mass of the black hole, the tangential force Ft is constant, therefore, the tangential velocity due to the dark matter is also constant, the angular velocity It is also constant, that is, Ft produces a circular movement with constant acceleration, for this condition is fulfilled that Vt = ω r, very important for our calculations.
In the first instance, we have calculated the dark matter existing in the Milky Way and by applying RC electrical modelling of a black hole, we calculated the theoretical rotation curve of the Milky Way and saw how it approaches the values of the rotation curve measured or observed of the Milky Way. Figure 6.
In a second instance, we have calculated the dark matter existing in the Andromeda galaxy M31, using Python and through this theoretical procedure we calculated the rotation curve of the Andromeda galaxy M31 and compared it with the rotation curve of the measured or observed values. Figure 13. In a second procedure, we calculate the amount of dark matter in the Andromeda galaxy M31, applying RC electrical modelling of a black hole, we calculate the rotation curve of Andromeda M31 and show how it approximates the rotation curve from the measured values and observed, Figure 13.
Finally, we have shown that using the theory of RLC electrical modelling of a black hole and the primitive universe and the theory of the generalization of the Boltzmann constant in curved space-time, we can determine the tangential rotation curve of the galaxies. This is another method that we can use to calculate the tangential rotation speeds of galaxies.
About the authors
HECTOR GERARDO FLORES (ARGENTINA, 1971). I studied Electrical Engineering with an electronic orientation at UNT (Argentina); I worked and continue to work in oil companies looking for gas and oil for more than 25 years, as a maintenance engineer for seismic equipment in companies such as Western Atlas, Baker Hughes, Schlumberger, Geokinetics, etc.
Since 2010, I study theoretical physics in a self-taught way.
In the years 2020 and 2021, during the pandemic, I participated in the course and watched all the online videos of Cosmology I and Cosmology II taught by the Federal University of Santa Catarina UFSC (graduate level).
MARIA ISABEL GONÇALVEZ DE SOUZA (Brazil, 1983). I studied professor of Portuguese language at the Federal University of Campina Grande and professor of pedagogy at UNOPAR University, later I did postgraduate, specialization. I am currently a qualified teacher and I work for the São Joao do Rio do Peixe Prefecture, Paraiba. I am Hector's wife and my studies served to collaborate in the formatting of his articles, corrections, etc; basically, help in the administrative part with a small emphasis in the technical part analyzing and sharing ideas.
Conflicts of Interests
The authors declares that there are no conflicts of interest.
References
- Ismaeel, A. Al-Baidhany; Sami S. Chiad; Wasmaa A. Jabbar; Ahmed K. Al-kadumi; Nadir F. Habubi ; Hazim L. Mansour. Determine the mass of supermassive black hole in the centre of M31 in different methods. [CrossRef]
- Sunshun Yuan, Ling Zhu, Cheng Liu, Han Qu, and Zhou Fan. Constraining Mass of M31 Combing Kinematics of Stars, Planetary Nebulae and Globular clusters. [CrossRef]
- Ronaldo, E. de Souza. Via Láctea: a nossa galáxia, Universidad de São Paulo, USP. http://www.astro.iag.usp.br/~ronaldo/extragal/Cap2.
- Wikipedia. Andromeda Galaxy. https://en.wikipedia.
- Tamm, E. Tempel, P. Tenjes, O. Tihhonova, and T. Tuvikene. Stellar mass map and dark matter distribution in M 31. https://arxiv.org/abs/1208. 5712. [Google Scholar]
- Yoshiaki SOFUE. Rotation and Mass in the Milky Way and Spiral Galaxies. Institute of Astronomy, The University of Tokyo, Mitaka, 181-0015 Tokyo. https://arxiv.org/abs/1608. 0835.
- Dr Alexander Zabot - Curso de Cosmologia 1. Astrofisica para todos, Universidad Federal de Santa Catarina - UFSC, Brazil. https://astrofisica.ufsc.
- Flores, H. G; Preprints 2023, 2023052246. Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time. [CrossRef]
- Curva de rotação do nossa galaxia. Instituto de fisica da Universidad Federal de Rio Grande do Sul, UFRGS. https://www.if.ufrgs.br/oei/cgu/galstru/galstru.
- Eisberg Resnick, Física Cuántica.
- Eyvind, H. Wichmann. Física cuántica.
- Sears – Zemansky. Física Universitaria con Física Moderna Vol II.
- Kostas kokkotas, Field Theory.
- James, B. Hartle, Gravity and introduction to Einstein´s General Relativity.
- Charles, W. Misner, Kip S. Thorne and Jhon Archibald Wheelher, Gravitation.
Figure 1.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential force that retards Fc by 90 degrees, generated by the mass δ.
Figure 1.
Vector representation of the forces in a black hole. Fc = f, represents the force towards the interior of the black hole generated by the mass m and Ft = -iφ, is a tangential force that retards Fc by 90 degrees, generated by the mass δ.

Figure 2.
Represents the variation of speed Cɢ, as a function of temperature T, inside a black hole.
Figure 2.
Represents the variation of speed Cɢ, as a function of temperature T, inside a black hole.
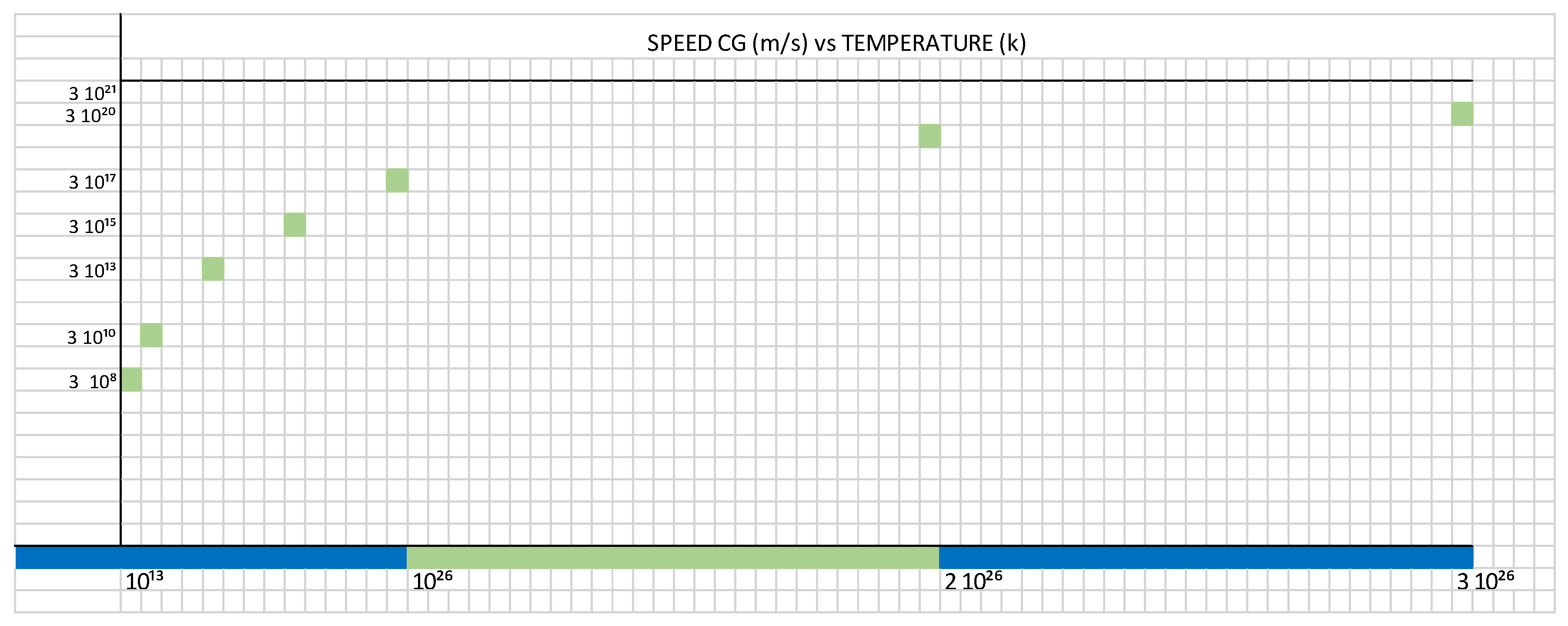
Figure 3.
It represents the observed rotation speed of the Milky Way versus the rotation speed of visible matter, ref [1].
Figure 3.
It represents the observed rotation speed of the Milky Way versus the rotation speed of visible matter, ref [1].
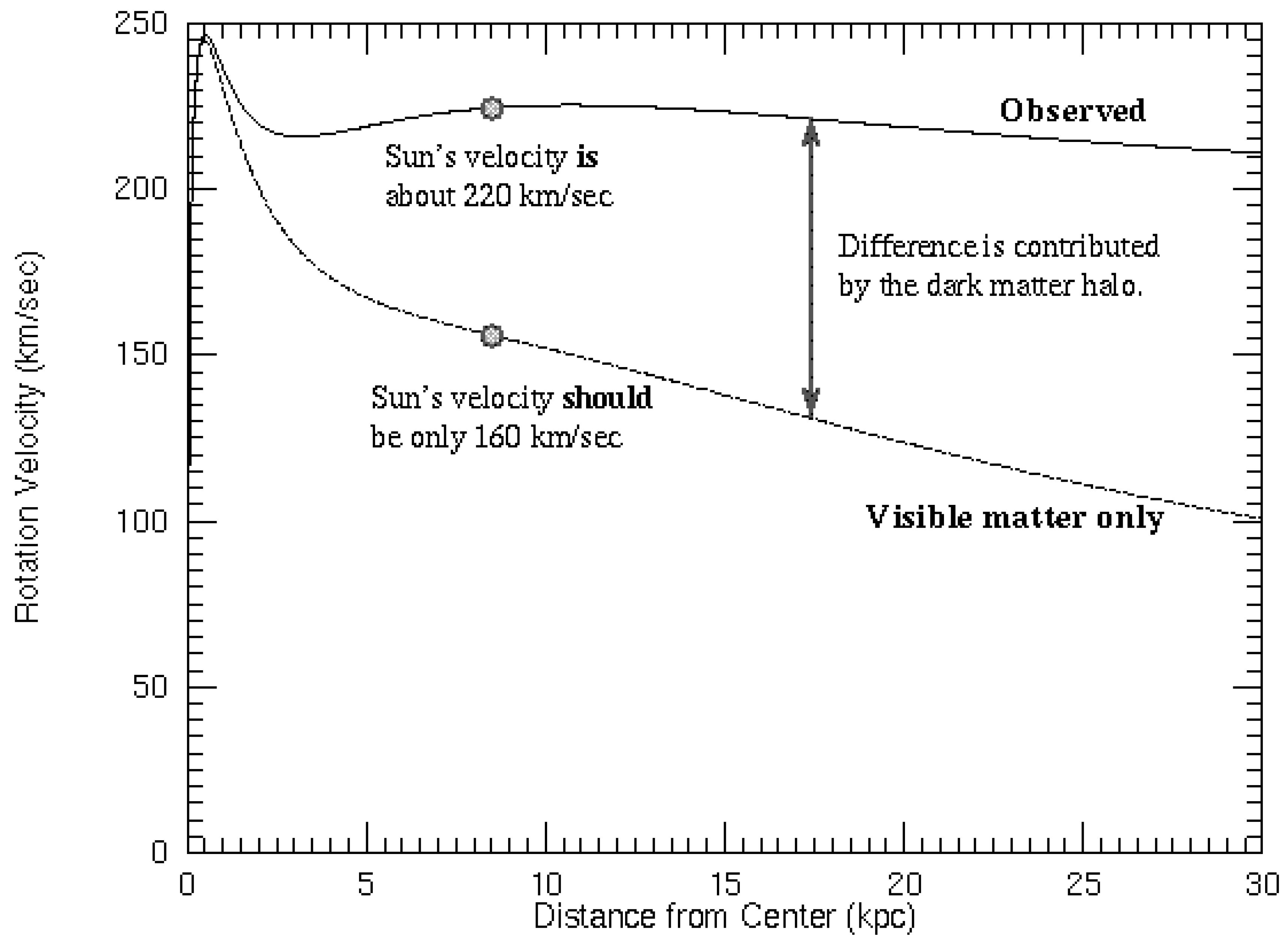
Figure 4.
In red you can see the tangential velocity Vt that results from the contribution of dark matter.
Figure 4.
In red you can see the tangential velocity Vt that results from the contribution of dark matter.

Figure 5.
In red is represented the tangential rotation speed Vdm, due to the contribution of dark matter, in orange is represented the sum of the tangential speed due to dark matter plus the tangential speed due only to visible matter, Vdm + Vm.
Figure 5.
In red is represented the tangential rotation speed Vdm, due to the contribution of dark matter, in orange is represented the sum of the tangential speed due to dark matter plus the tangential speed due only to visible matter, Vdm + Vm.

Figure 6.
- Parameter values used in the Python program to generate the graph in Figure 8.

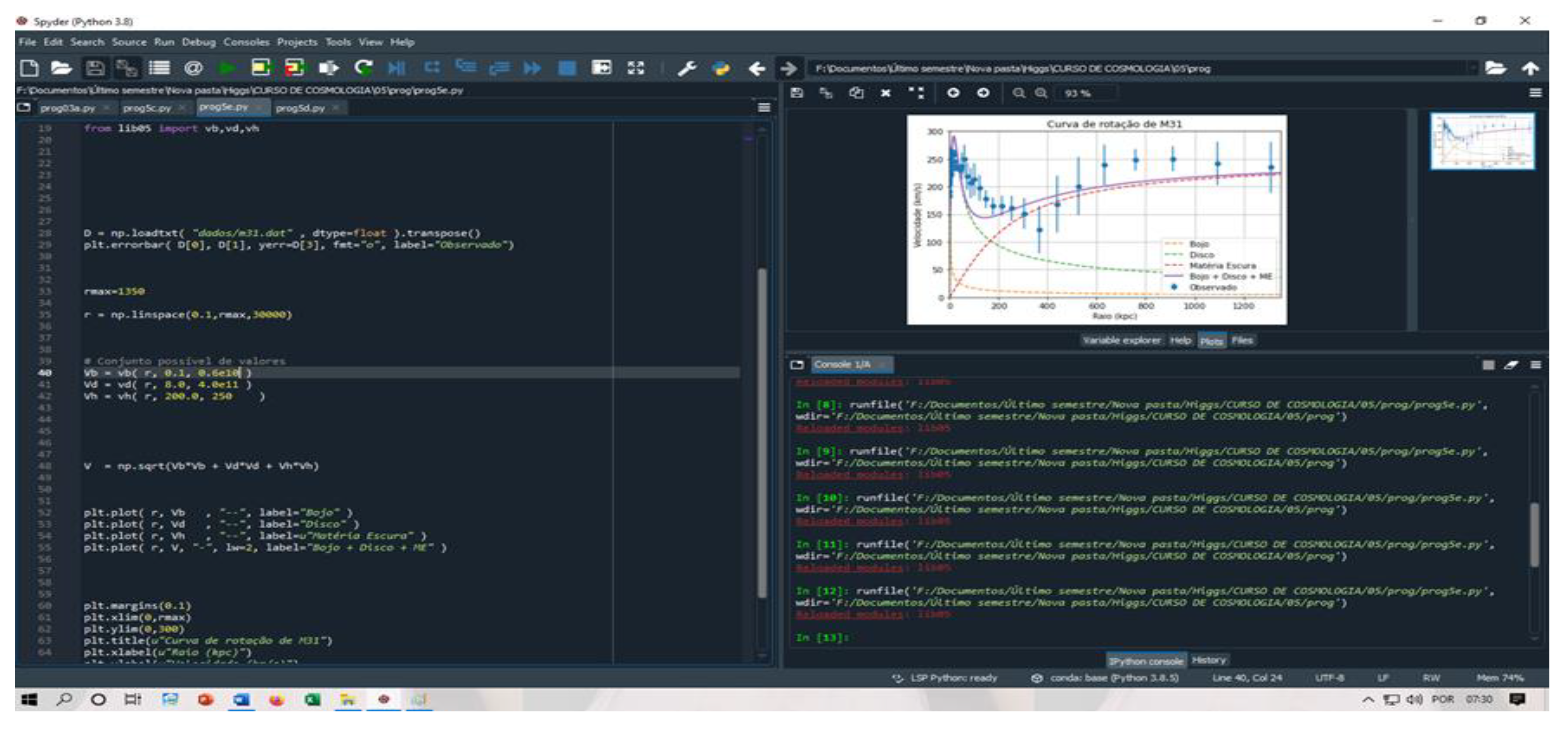
Figure 7.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; green, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; red, represents the rotation speed due to dark matter; purple, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 7.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; green, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; red, represents the rotation speed due to dark matter; purple, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
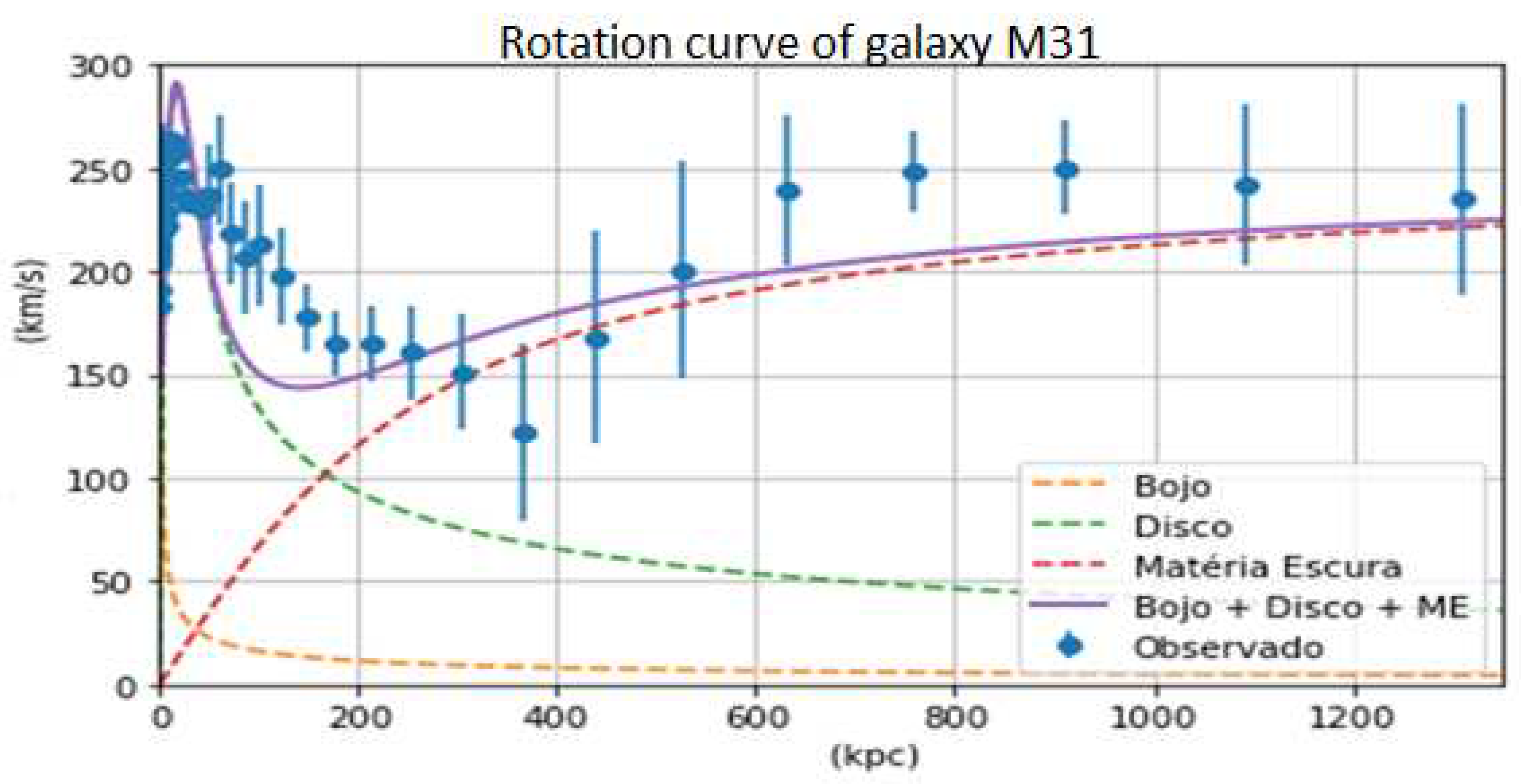
Figure 8.
Parameter values used in the Python program to generate the graph in Figure 9.
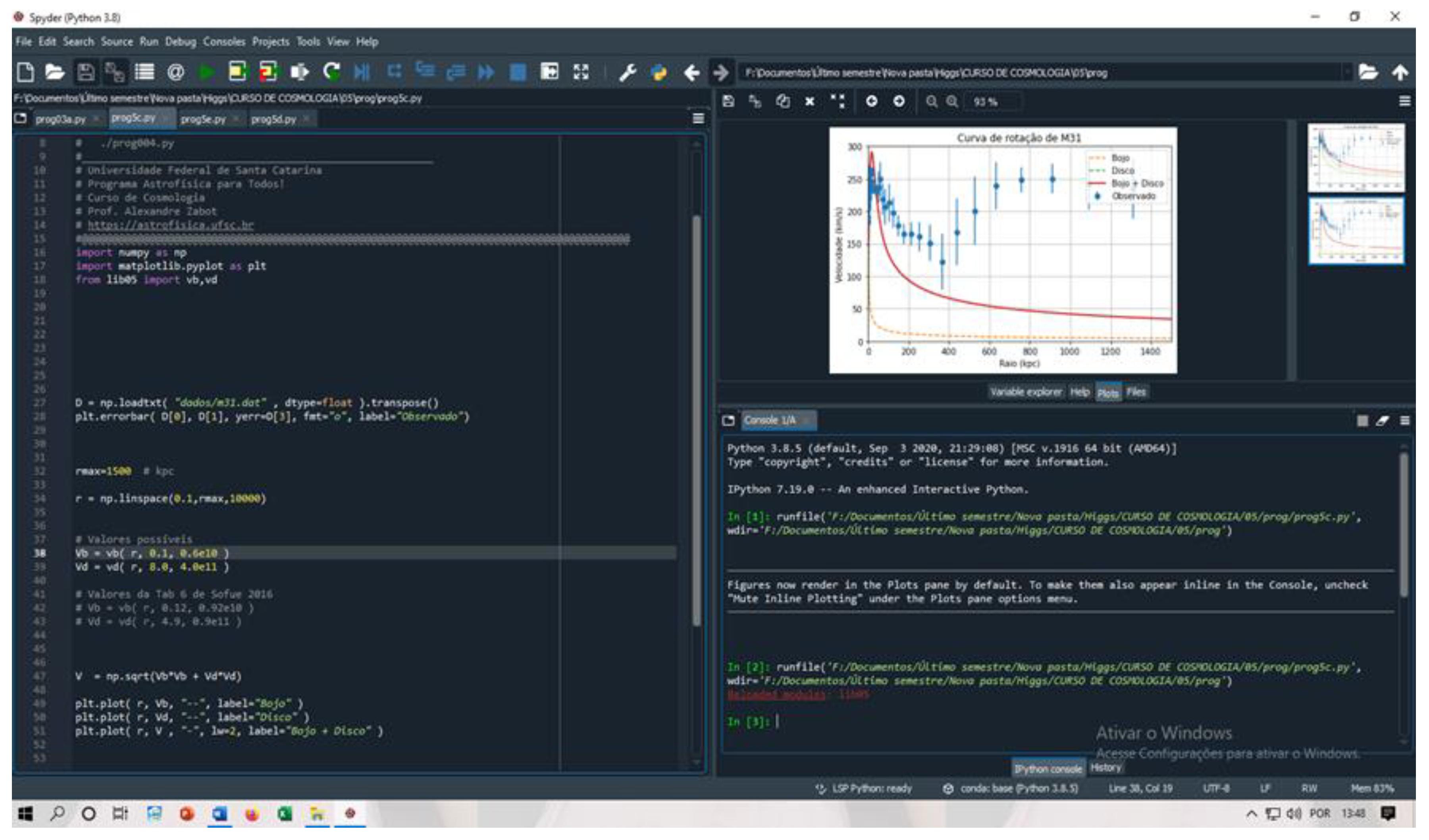
Figure 9.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre.
Figure 9.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre.

Figure 10.
The rotation speed due to dark matter is represented in purple.

Figure 11.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; purple, represents the rotation speed due to dark matter; yellow, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 11.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; purple, represents the rotation speed due to dark matter; yellow, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
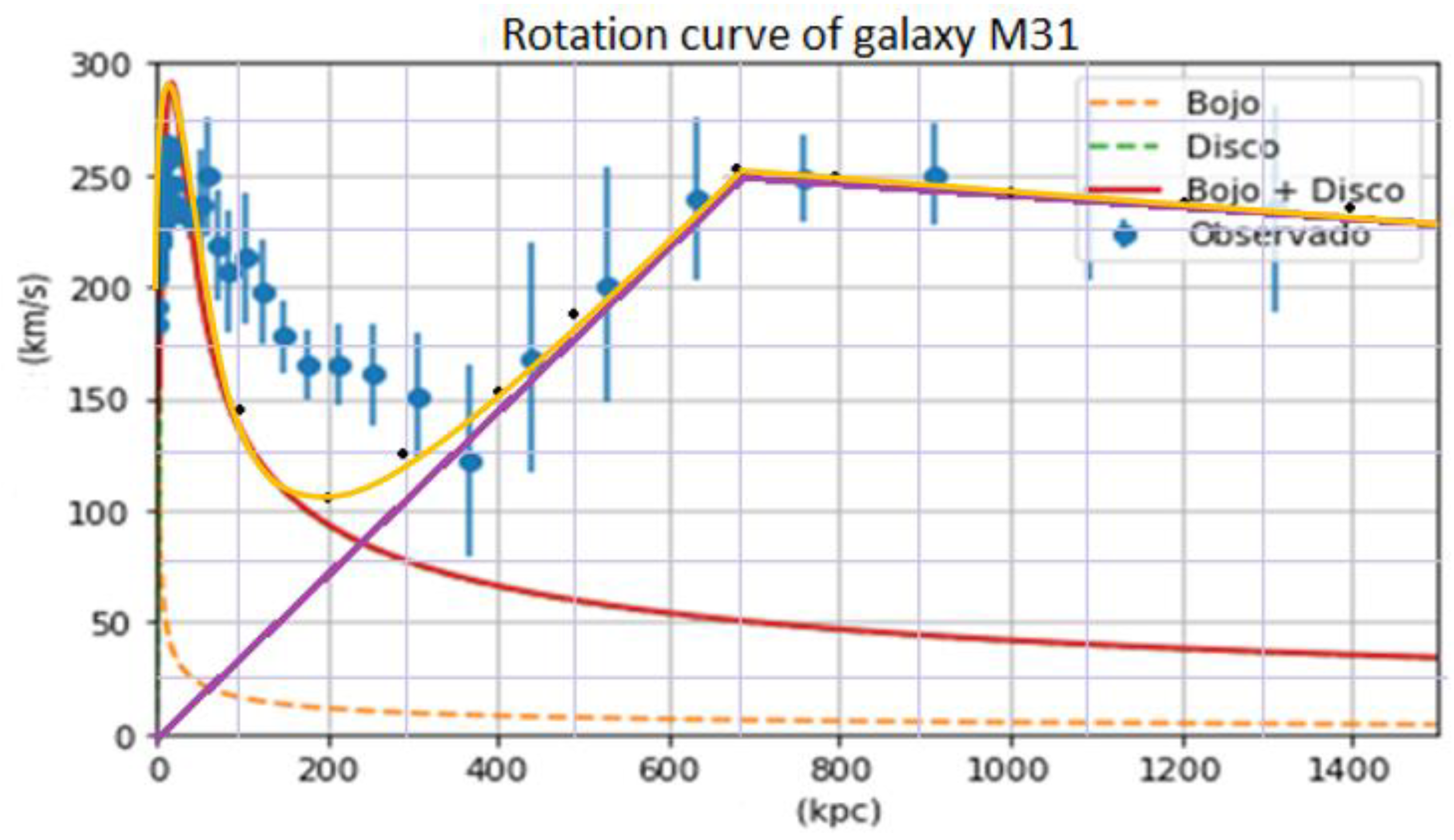
Figure 12.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; green, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; red, represents the rotation speed due to dark matter; purple, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 12.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; green, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; red, represents the rotation speed due to dark matter; purple, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
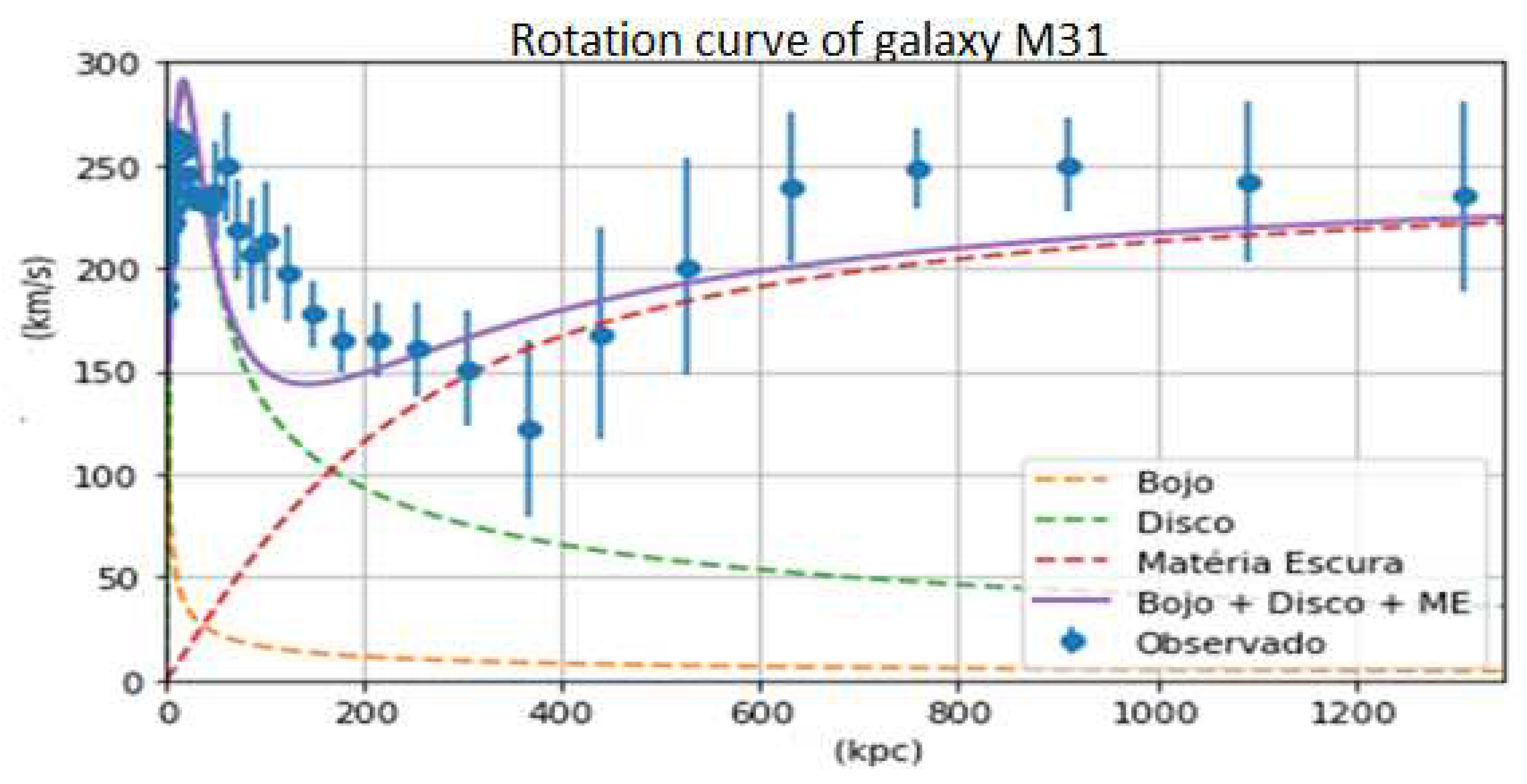
Figure 13.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; purple, represents the rotation speed due to dark matter; yellow, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
Figure 13.
M31 rotation curve, blue, represents the measured or observed values of the rotation speed of M31; red, represents the values of the rotation speed due to the galactic disk; orange, represents the values of the rotation speed due to the galactic centre; purple, represents the rotation speed due to dark matter; yellow, represents the vector sum of the rotation speed that corresponds to the galactic centre, galactic disk and dark matter.
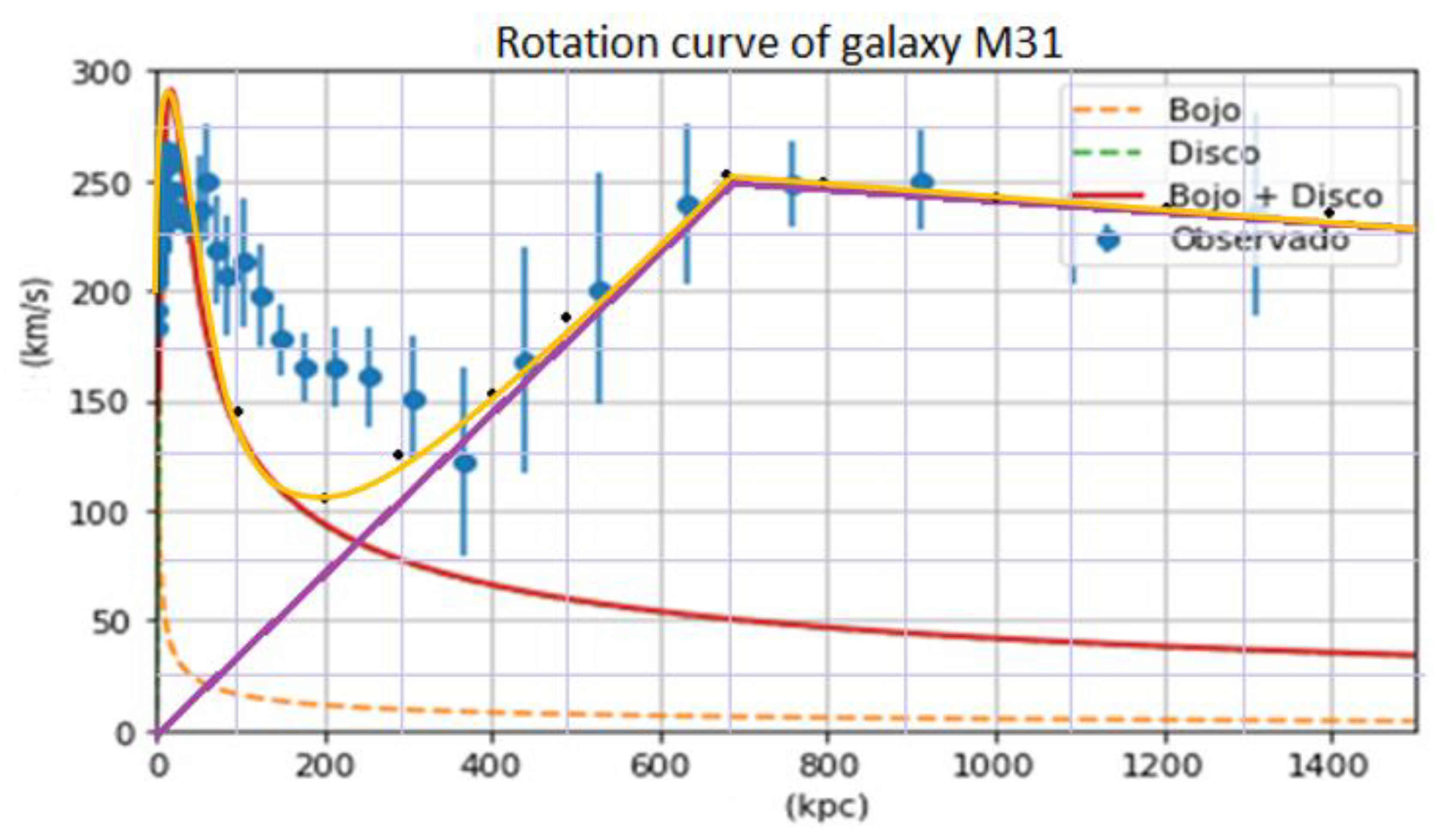
Table 1.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.
Table 1.
Represents values of ImI, baryonic mass; IδI, dark matter mass; IMI, mass of baryonic matter plus the mass of dark matter; IEmI, energy of baryonic matter; IEδI, dark matter energy; IEI, Sum of the energy of baryonic matter plus the energy of dark matter and Rs, Schwarzschild´s radius, as a function of, c, speed of light; Cɢ, speed greater than the speed of light; T, temperature in Kelvin; using the parametric equations.
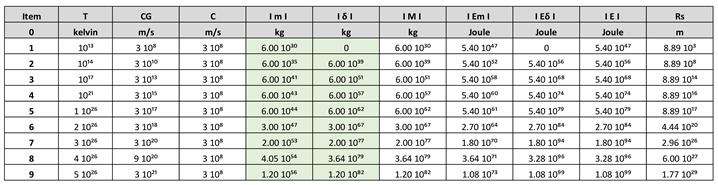 |
Table 2.
Represents the values of the tangential velocity Vt, angular velocity ω, as a function of the radius r.
Table 2.
Represents the values of the tangential velocity Vt, angular velocity ω, as a function of the radius r.
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






