Fault Recovery Methods for a Converged System Comprised of Power Grids, Transportation Networks and Information Networks

Preprint

Article

Fault Recovery Methods for a Converged System Comprised of Power Grids, Transportation Networks and Information Networks

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Geng Zhang,

Chenxu Liu,

Hao Jiang^*,Jiye Wang

Geng Zhang,

Chenxu Liu,

Hao Jiang^*,Jiye Wang

This version is not peer-reviewed

Submitted:

28 September 2023

Posted:

29 September 2023

You are already at the latest version

Alerts

Abstract

Recently, the triple-network convergence system (TNCS) has emerged from the deep integration of the power grid, transportation network, and information network. Fault recovery research in the TNCS is important since this system's complexity and interactivity can expand the faults scale and increase faults impact. Currently, fault recovery focuses primarily on single power grids and cyber-physical systems, but there are certain shortcomings, such as ignoring uncertainties including generator start-up failures and the occurrence of new faults during recovery, energy supply-demand imbalances leading to system security issues and communication delay caused by network attacks. In this study, we propose a recovery method based on the improved TD3 algorithm, factoring in shortcomings of the existing research. Specifically, we establish a TNCS model to analyze interaction mechanisms and design a state matrix to represent the uncertainty changes in the TNCS, a negative reward to reflect the impact of unit start-up failures, a special reward to reflect the impact of communication delay and an improved Actor network update mechanism. Experimental results show that our method obtains the optimal recovery decisions, maximizes restoration benefit in power grid failure scenarios and demonstrates a strong resilience against communication delay caused by DoS attacks.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

In recent years, the TNCS has emerged due to the rapid development and deep integration of power grids, transportation networks, and information networks, caused by the widespread adoption of electric vehicles. This convergence system enables efficient coordination among energy flow, traffic flow, and information flow [1,2]. However, the increasing complexity and interdependence of the system has also created favorable conditions for fault propagation, in which local disturbances can easily initiate cascading failures across networks, resulting in severe system risks such as wide-scale power outages [3,4,5,6,7]. Therefore, research on fault recovery method for the TNCS is essential.

The development of a recovery method for the TNCS necessitates a clear understanding of its interaction mechanisms. However, there is a paucity of explicit domestic and international research on modelling the interaction mechanisms of such systems, which adds to the complexity of the study. Furthermore, there is a paucity of research on fault recovery method related to the TNCS. Despite this, a body of research exists on fault recovery for power grids and power cyber-physical systems. In reference [8], for instance, cascading fault recovery model based on the SRG was suggested for power transmission networks and proven by simulations. In reference [9], an optimization model for the entire black start restoration process in gearbox systems was formulated and solved using a linearized hybrid integer linear programming model and the L-shaped algorithm, taking into consideration the uncertainty of wind power output. Reference [10] analyzed the potential delays caused by information system failures on power system generation, transmission line operation, and load restoration. In these studies, however, the impact of generator start-up failures on restoration decisions is not considered. Reference [11] proposed a parallel recovery method for power systems. Although this method considered uncertainties during the restoration process, it did not consider the possibility of new faults occurring in power systems during component restoration.

The recovery of power system components can result in alterations to the power system's topology, power flow, and power levels, which may cause problems such as line overloads, imbalances in energy supply and demand in certain regions, and system instability. However, existing research lacks studies on the risks of new faults or system instability that may arise from component recovery. For instance, in reference [12], a two-stage recovery strategy was proposed for power facility restoration after hurricanes, focusing on the design of distributed generation and maintenance personnel scheduling, but excluding the analysis of new faults that might occur from power system component recovery. References [13,14,15] also ignored the occurrence of new faults.

It is evident that existing research typically establishes optimization models for different fault scenarios and solves them using various optimization algorithms, but lacks consideration of uncertainties that may occur during the actual restoration process, such as generator start-up failures and faults triggered by recovery actions, and their impact on recovery decisions. Consequently, these uncertainties should be considered, when studying fault recovery methods for TNCS. Such research methods would be more applicable to real-world circumstances.

Moreover, due to the high complexity and interactivity of the TNCS, network attacks can exploit intricate network interaction mechanisms and exacerbate the hazards of faults with relative ease. By manipulating power grid data and injecting false information, for instance, the assessment of the system's operational status may deviate, resulting in erroneous decisions by administrators and potentially triggering large-scale cascading failures [16,17,18,19]. By injecting a large number of useless requests and obstructing communication channels, DoS attacks can cause an increase in communication delay and thus initiate or exacerbate power outages [20,21,22,23,24]. An example of this is the DoS attack launched by a hacker group against a power company in the western United States in 2019, which resulted in communication disruption between the control center and various site devices [25]. There is limited research on restoration decisions for power cyber-physical systems that take network attacks into account at present. While the optimization strategy proposed in [26] considered the impact of information system failures caused by DoS attacks on the restoration process, but the solving algorithm lacks flexibility to handle uncertainty factors and becomes less efficient as the system scale increases.

The TD3 algorithm from the discipline of deep reinforcement learning can be used to address this issue [27]. By designing the state space and reward function appropriately, uncertainties can be accounted for, and the neural network can effectively address the curse of dimensionality problem caused by the large scale of the TNCS [28,29]. In addition, compared to DQN, AC, and DDPG algorithms [30,31,32], the TD3 algorithm exhibits better capability to suppress network overestimation and provides more stable network training. Consequently, the utilization of the TD3 algorithm is more suitable for solving the model. However, the optimization objective of the TD3 algorithm is to find actions that maximize the action-value function in different states, without considering the specific role and impact of recovery actions in particular scenarios, such as system security. Therefore, improvements to the TD3 algorithm are necessary to ensure system security.

Based on the above analysis, this study makes the following main contributions to the research on fault recovery methods in TNCS:

Focusing on the charging behavior of electric vehicles, a TNCS model is established to reveal the underlying interaction mechanisms.
An efficient fault recovery method for TNCS is proposed, incorporating an improved TD3 algorithm and considering communication delays. By designing and improving the TD3 algorithm, the uncertainties and security issues in the restoration process are considered, leading to the design of an effective recovery algorithm. In addition, the resilience of the algorithm is evaluated by introducing DoS attacks in the context of power grid faults. Lastly, the efficacy of the proposed recovery method is demonstrated through simulation experiments.

2. Methods

2.1. Modeling

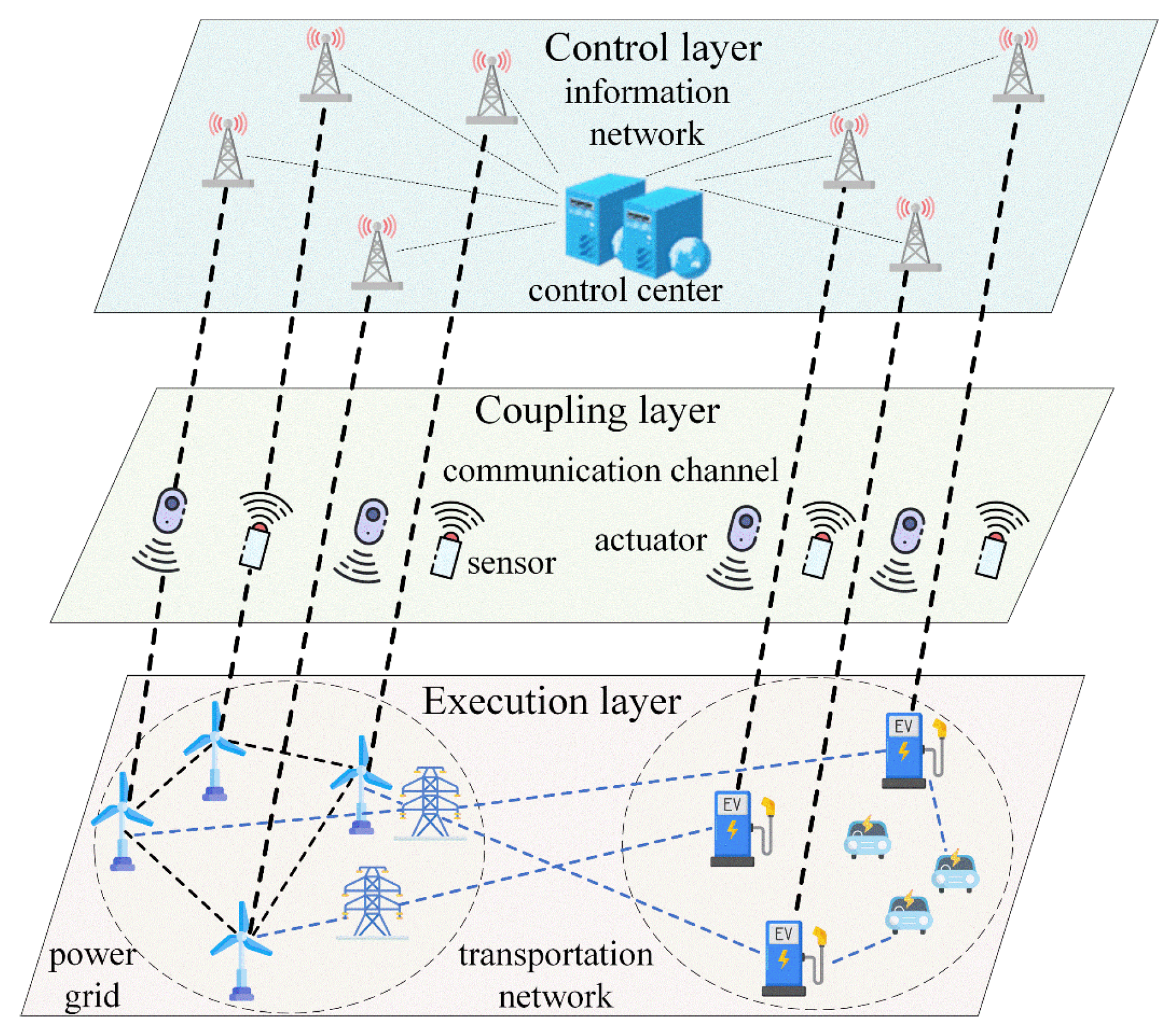
2.1.1. Overall Framework

As shown in Figure 1, the TNCS in this study consists of three layers: the execution layer, the coupling layer, and the control layer. The execution layer consists of the actual power grid and transportation network, responsible for the reliable operation of energy interactions. The coupling layer mainly consists of power collection and control devices, as well as communication channels, responsible for information acquisition, execution of control commands, and information data transmission. The control layer, primarily based on the information network, is responsible for state monitoring and dispatch control.

2.1.2. Execution Layer

The power grid topology is a directed graph

G_{P} = (V_{P}, E_{P})

, where

V_{P}

represents power nodes including generators, loads, and circuit breakers, and

E_{P}

represents transmission lines. The topological information of the power grid is represented by a matrix

T^{P}

whose elements

T_{i j}^{P}

adhere to the following rule:

T_{i j}^{P} = 1

denotes the presence of a line between nodes i and j, while

T_{i j}^{P} = 0

denotes the absence of a line. The nodal admittance matrix

B

, nodal injection power vector

P

, line power flow vector

f

, and nodal phase angle vector

θ

are established. Based on the DC power flow model, the power flow information matrix

P F

of the power grid can be obtained from the following equations.

P F = d i a g (P) + f

(1)

B θ = P

(2)

(θ Q - Q^{T} θ^{T}) \circ B = f

(3)

where the value of

Q

[1, 1, 1, \dots, 1]

, and

d i a g (P)

represents a diagonal matrix with vector

P

as its diagonal elements.

The road topology of the transportation network is an undirected graph

G_{T} = (V_{T}, E_{T})

, where

V_{T}

represents road nodes (including charging stations) and

E_{T}

represents paths between them. A matrix

A_{T}

is established to represent the topological information of the transportation network, with matrix elements

A_{i j}^{T}

following the following rule:

A_{i j}^{T} = 1

indicates the presence of a connected road between road nodes i and j, while

A_{i j}^{T} = 0

indicates the absence of a connected road. A decision vector

S E

is used to assess whether each road node has a charging station, where

S E_{i} = 1

indicates the presence of a charging station in road node i and

S E_{i} = 0

indicates its absence. A charging station load vector

P^{c}

is introduced for the transportation network, where

P_{i}^{c}

represents the load at the charging station located on road node i and can be obtained from the following equations.

P_{i}^{c'} = \sum_{j = 1}^{N_{i}^{S}} C S O_{i j} \circ C S W_{i j} \circ C S P_{i j}

(4)

P_{i}^{c} = S E_{i} \circ P_{i}^{c'}

(5)

where

N_{i}^{S}

represents the number of charging piles in the charging station located at road node i.

C S O_{i j}

indicates the operational status of the j-th charging pile in the charging station at road node i, with a value of 1 indicating that it is operational and 0 indicating that it is not.

C S W_{i j}

represents the operational status of the j-th charging pile in the charging station at road node i, with 1 indicating operation and 0 indicating inactivity.

C S P_{i j}

represents the charging power of the j-th charging pile at the road node i charging station.

To assure the safety of charging services, the maximum charging power for each charging pile must be specified. Establishing a maximum power vector

C S M

, where

C S M_{i j}

represents the maximum charging power of the j-th charging pile in the charging station at road node i.

2.1.3. Coupling Layer

The matrices

S^{P}

and

S^{T}

are respectively defined to represent sensor deployment in the power grid and transportation network. In

S^{P}

, diagonal elements denote sensors on the nodes of the power grid, while off-diagonal elements represent sensors on the power lines. In

S^{T}

, the diagonal elements represent sensors on the road node charging stations. The elements of both matrices are assigned the value 1 to denote the presence of a sensor and the value 0 to denote the absence of a sensor. The actuator matrices

A^{P}

and

A^{T}

are defined in the same way as the sensor matrices.

The uplink data communication channel matrix contains

U C^{P}

for the power grid and

U C^{T}

for the transportation network. The matrix elements,

U C_{i j}

, satisfy

U C_{i j} \in \{0, 1\}

. In

U C^{P}

U C_{i i}^{P} = 1

indicates the presence of an uplink data communication channel between the sensor on the power grid node and the information network control center, transmitting node power information.

U C_{i j}^{P} = 1

indicates the existence of an uplink data communication channel between sensors on power grid lines i-j and the information network control center, transmitting current flow information and circuit breaker status. In

U C^{T}

U C_{i}^{T} = 1

denotes the presence of an uplink data communication channel between the sensors in the charging station at road node i and the information network control center, transmitting charging station operational information. The downlink data communication channel matrix is defined in the same way as

U C^{P}

and

U C^{T}

, with different transmitted content. It carries commands for the charging station's circuit breaker open or close, node power adjustment, charging pile open or close, and maximal charging power adjustment.

2.1.4. Control Layer

The information network topology is defined as a directed graph

G_{C} = (V_{C}, E_{C})

, where

V_{C}

represents the information nodes and

E_{C}

represents the communication links between nodes. The connectivity status of the communication links is represented by the link status matrix

C

, with matrix elements

C_{i j} (i \neq j) = \{0, 1\}

. A value of

C_{i j} = 1

indicates that an effective connection has been established between information nodes i and j. The control center in the information network adjusts the operational status of the power grid and transportation network based on the received data. The storage of received information includes

P M^{f}

and

P M^{t}

for power flow information (

P F

) and power grid topology information (

T^{P}

), respectively, while

T M^{S}

represents the storage of received charging station information. Utilizing this information, the reduction in output of generator nodes and the reduction in load of load nodes are calculated, thereby calculating the decrease in power at the charging stations in the transportation network, as illustrated below.

\sum_{i}^{N} P_{i}^{a} \sum_{j = 1}^{N_{i}^{S}} C S O_{i j}^{'} = \sum_{i = 1}^{N} P_{i}^{C} - P_{i}^{S}

(6)

|P^{C} - P^{S}| \leq |L S|

(7)

where

L S

satisfies equations (1) to (3), it is used to represent the reduction in output of power nodes or the reduction in load of load nodes.

P^{S}

is the drop value in charging power at road node i, while

P_{i}^{a}

is the adjusted average charging power of charging piles in charging stations.

C S O_{i j}^{'}

refers to the adjusted operational state of the j-th charging pile in the i-th road node. N represents the number of road nodes in the transportation network. We assume that the charging stations will bear the maximum extent of power grid load variations.

The control center then generates and distributes decision instructions to the executive layer.

2.2. Fault Recovery Method

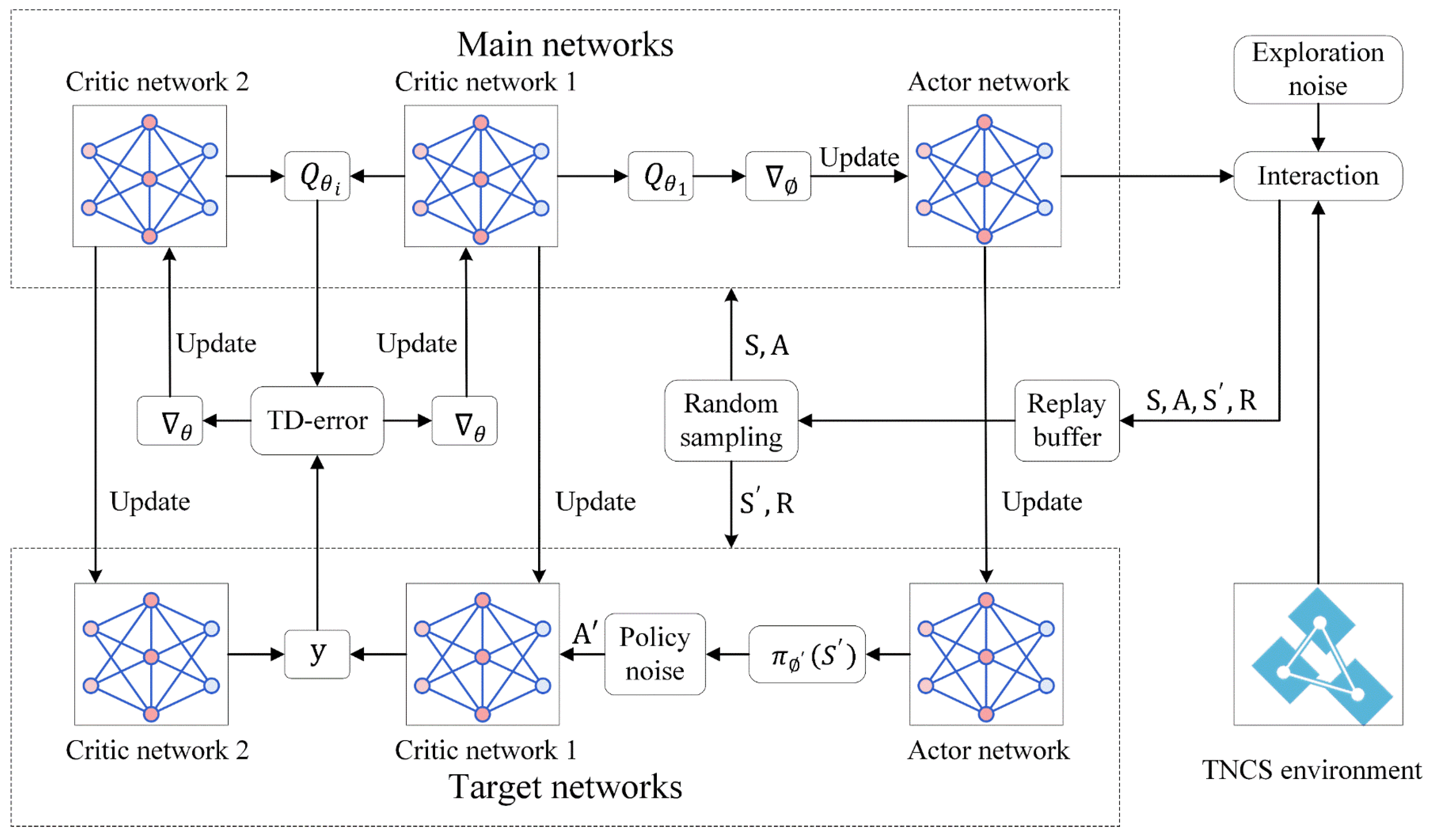
2.2.1. Design of Restoration Model

In this section, we define importance indicators for power grid faults in the context of the TNCS, assessing the importance of fault power lines. With the objective of maximizing restoration benefits, a restoration model is established.

We assume that power grid faults in the TNCS result from the overload-induced disconnection of power lines, leading to redistribution of power flow, reduction in output of generator nodes, and load shedding at load nodes. Concurrently, adjustments are made to the charging power of charging stations in the transportation network corresponding to the affected power nodes, which may impact the travel of EV users. The importance of power lines,

η

, is determined by the importance of its connected power nodes (

η_{P}

) and the importance of the charging stations on the corresponding coupled road nodes (

η_{S}

), as shown below.

η = λ_{1} \cdot ω η_{P} + λ_{2} \cdot (1 - ω) η_{S}, η > 0, η_{P} > 0, η_{S} > 0, 0 < ω < 1

(8)

where

ω

represents the weight coefficient.

λ_{1}

and

λ_{2}

are binary variables that indicate the existence of the respective item, taking a value of 1 if it exists and 0 otherwise.

η_{P}

consists of the degree, generation capacity, and load of the power nodes, and

η_{S}

consists of the degree of the road nodes and the number of electric vehicles affected, as shown below.

η_{P} = λ_{3} \frac{P_{g}}{\sum_{i \in g e n} P_{i}^{g}} + λ_{4} \frac{γ_{d}}{\sum_{i \in |V_{P}|} γ_{i}} + λ_{5} \frac{P_{l}}{\sum_{i \in l o a d} P_{i}^{l}}

(9)

η_{S} = λ_{6} \frac{γ_{t}}{\sum_{i \in |V_{T}|} γ_{i}} + λ_{7} \frac{χ_{t}}{\sum_{i \in |V_{T}|} χ_{i}^{t}}

(10)

χ_{t} = χ_{t 1} + χ_{t 2}

(11)

χ_{t 1} = χ_{t 1} + 1, \sum_{i = 1}^{K} \sum_{j = 1}^{|V_{T}|} \sum_{k = 1}^{N^{S}} \begin{matrix} I F (|T S_{i}^{p} (j, k)| > 0 \\ A N D C S N_{i} (j, k) \neq 0, 1, 0) \end{matrix}

(12)

χ_{t 2} = χ_{t 2} + 1, \sum_{i = 1}^{K} \sum_{j = 1}^{|V_{T}|} \sum_{k = 1}^{N^{S}} \begin{matrix} I F (|T S_{i}^{p} (j, k)| > 0 \\ A N D C S Q_{i} (j, k) \neq 0, 1, 0) \end{matrix}

(13)

where

λ_{3}

λ_{4}

λ_{5}

λ_{6}

, and

λ_{7}

are binary variables indicating the existence of the respective items.

P_{g}

represents the power output of generator nodes, and

\sum_{i \in g e n} P_{i}^{g}

represents the total power output of generator nodes.

γ_{d}

represents the degree of nodes in the power grid, while

\sum_{i \in |V_{P}|} γ_{i}

represents the sum of degree of power nodes.

γ_{t}

represents the degree of road nodes in the transportation network, while

\sum_{i \in |V_{T}|} γ_{i}^{t}

is the sum of degree of road nodes.

P_{l}

represents the power load of load nodes in the power grid, while

\sum_{i \in l o a d}^{m} P_{i}^{l}

denotes the total power load of load nodes in the power grid.

χ_{t}

obtained by equations (11), (12), and (13) represents the number of EVs impacted during travel, while

\sum_{i \in |V_{T}|} χ_{i}^{t}

represents the total number of EVs impacted during travel. Equation (12) calculates the adjusted number of charging station users

χ_{t 1}

, while equation (13) calculates the adjusted number of charging station electric vehicles

χ_{t 2}

T S_{i}^{p}

represents the power adjustment matrix for the i-th charging station,

C S N_{i}

represents the identifier of the current charging station users, and

C S Q_{i}

represents the identifier of the current charging station reservation users.

After calculating the importance of each power line, they are sorted in descending order to determine the restoration priority.

Γ

is defined as the quantified priority value, and

e_{p}

represents the number of restoration steps. The optimization objective is to maximize the restoration benefit which consists of the recovery power from the power grid and transportation network, based on the importance of power lines.

\max \sum_{m}^{e_{p}} Γ (L S_{r m} + P_{r m}^{S})

(14)

s . t . Γ = 1 - 0.02 (e_{p} - 1), e_{p} \geq 1

(15)

\min (L S) \leq L S_{r m} \leq \max (L S)

(16)

\min (P^{S}) \leq P_{r m}^{S} \leq \max (P^{S})

(17)

P_{m i n}^{G} \leq P^{G} \leq P_{m a x}^{G}

(18)

V_{m i n} \leq V \leq V_{m a x}

(19)

f_{m i n} < f < f_{m a x}

(20)

0 < T^{u p} < T^{h}

(21)

\sum_{i \in g e n} P_{i}^{g} = \sum_{i \in l o a d} P_{i}^{l}

(22)

where

Γ (L S_{r m} + P_{r m}^{S})

represents the restoration benefit obtained from restoring the fault at step m.

P^{G}

is the active power of the generator, and

V

is the voltage at the terminals of the power system. Equation (20) represents the line flow constraint, where power flow varies with the restoration of the faults. Exceeding the limits of line flow,

f_{m i n}

f_{m a x}

, may result in overload issues, leading to the disconnection or damage of the concerned line or other lines. In Equation (21),

T^{u p}

represents the unit start-up time, while

T^{h}

represents the maximum start-up time of the unit, ensuring the required time for thermal start-up. Equation (22) represents the energy supply-demand balance constraint in the power grid, ensuring the balance between actual supply and demand. Imbalances can lead to voltage fluctuations, frequency deviations, and overloaded operation, causing power equipment failures or system security issues such as power grid collapse. In this study, we assume that energy imbalance can cause line overloads and disconnection so that fault recovery should avoid energy supply-demand imbalances.

2.2.2. Design of Restoration Algorithm

In the context of fault recovery in the power grid of TNCS, the restoration sequence of each faulty line significantly influences the restoration benefit, giving rise to a decision-making problem. In this section, we focus on the design and improvement of the TD3 algorithm in the field of deep reinforcement learning with the aim of determining the optimal restoration strategy. Figure 2 illustrates the restoration algorithm structure based on the TNCS.

Specifically, we consider the control center as the agent and define the action space as the set of all available restoration actions from which the control center can choose in the TNCS environment, denoted as

A c

, and action

A

belongs to

A c

. In the restoration model, the recovery of faults can cause new faults. To address this uncertainty, we employ a state matrix

S

to represent the state space, reflecting the changes in the state of the TNCS. As shown in Figure 3, each row of the state matrix represents a power node or line, and each column represents a fault type. The arrangement follows the order of power node and line numbering, as well as fault type. Based on the rows and columns, the location and type of faults can be determined. An element value of 1 indicates no fault, while 0 indicates that a fault exists. Consequently, the changes in the state of the TNCS caused by fault recovery and occurrence can be reflected through the variation of element values.

The design of the reward function is as follows.

R = \{\begin{matrix} I_{d} + I_{b} + I_{m}, (μ = 1, ε = 1) \\ I_{d} + I_{c}, (μ = 0) \\ I_{d} - 1, (μ = 1, ε = 0) \end{matrix}

(23)

I_{m} = \frac{L S_{r m} + P_{r m}^{S}}{\max (L S) + \max (P^{S})}

(24)

I_{c} = (1 + β \frac{h_{t}}{H}) Γ + α \frac{e_{c}}{E}

(25)

The control center conducts a status check on the TNCS at the beginning of each restoration step, and when the check is complete, the reward

I_{d}

is obtained. If no data information is received from a node or line in the execution layer within time

T_{l}

, it is considered communication delays,

μ = 0

is set, and the reward

I_{c}

is obtained. Equation (25) represents the impact of communication delays on restoration decisions, where

β

and

α

are proportional coefficients with respective ranges of [0,1] and (0,1).

H

represents the total number of restoration stages, indicating the duration of the entire restoration process, while

h_{t}

represents the restoration stage at which the communication delay occurs. The restoration stage

E

represents the maximum number of restoration steps required to address communication faults (with a single stage consisting of multiple consecutive restoration steps), and

e_{c}

represents the actual number of restoration steps required for communication fault recovery.

μ = 1

denotes normal communication, with

ε = 1

indicating the effectiveness of the restoration action, resulting in the reward

I_{b}

, and the restoration benefit

I_{m}

calculated from equation (24). When

ε

equals zero, the restoration action is ineffective, resulting in a negative reward of -1.

The effectiveness of a restoration action refers to its objective of targeting the faulty lines without causing any additional faults. Restoring a power node requires at least one connected power line to be operational (excluding black-start nodes). For a power generation node, equation (21) must be satisfied, and if not, it is considered a failed unit start-up, which is uncertain and may be caused by unpredictable factors. In the case of a failed unit start-up, the reward function returns -1, reflecting the impact of this uncertainty on restoration decisions, and we can enhance the practicality of our method by employing this approach.

In response to potential system security issues caused by an imbalance between energy supply and demand during the restoration process, the TD3 algorithm is improved as follows.

ρ = λ_{8} η

(26)

{q = Q_{θ_{1}} (S, A)|}_{A = π_{ϕ} (S)} \cdot (1 - ρ_{a})

(27)

Equation (27) adds a multiplicative term,

(1 - ρ_{a})

in the original estimated value,

Q_{θ_{1}} (S, A) |_{A = π_{\emptyset} (S)}

used for updating the Actor network, where

q

represents the improved estimated value and

ρ_{a}

belongs to the set

ρ

ρ

represents the set of line importance, as determined by equation (26).

λ_{8}

is a binary variable with values of 0 and 1, and it is set to 1 if the restoration action causes an energy supply-demand imbalance in the system, and 0 otherwise.

The addition of the multiplicative term can affect the original estimated value after the improvement. When high-priority lines are disconnected due to an energy supply-demand imbalance, the multiplicative term becomes smaller, resulting in a decrease in estimated value, and indicating that the restoration actions under the current state pose a security risk to the system. Therefore, the Actor network can conclude that the chosen restoration action is not optimal.

Lastly, the neural networks used in the algorithm consist of an input layer, fully connected hidden layers, and an output layer. The specific parameter setting depends on the simulation experimental scenarios.

3. Experiments and Results

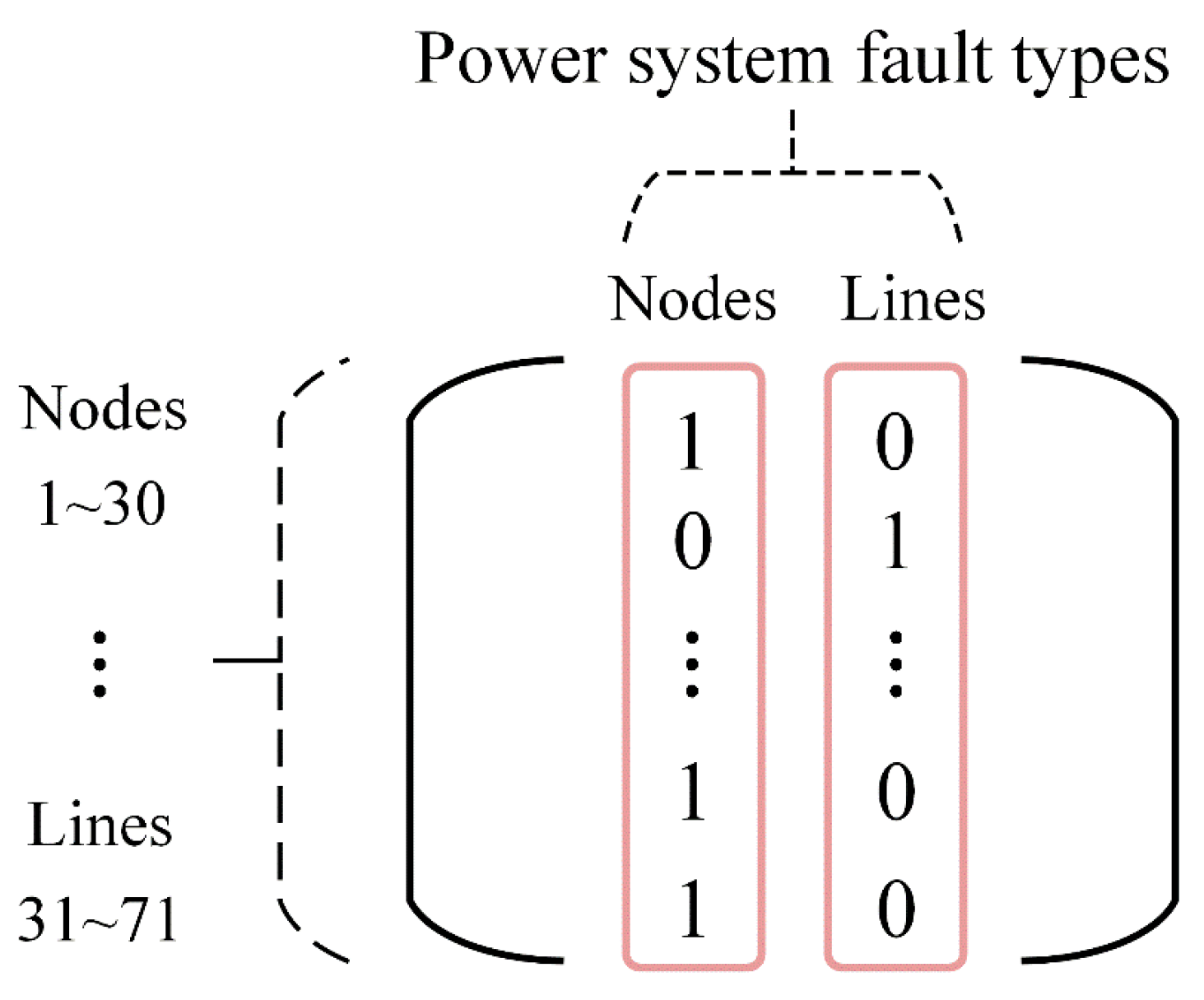
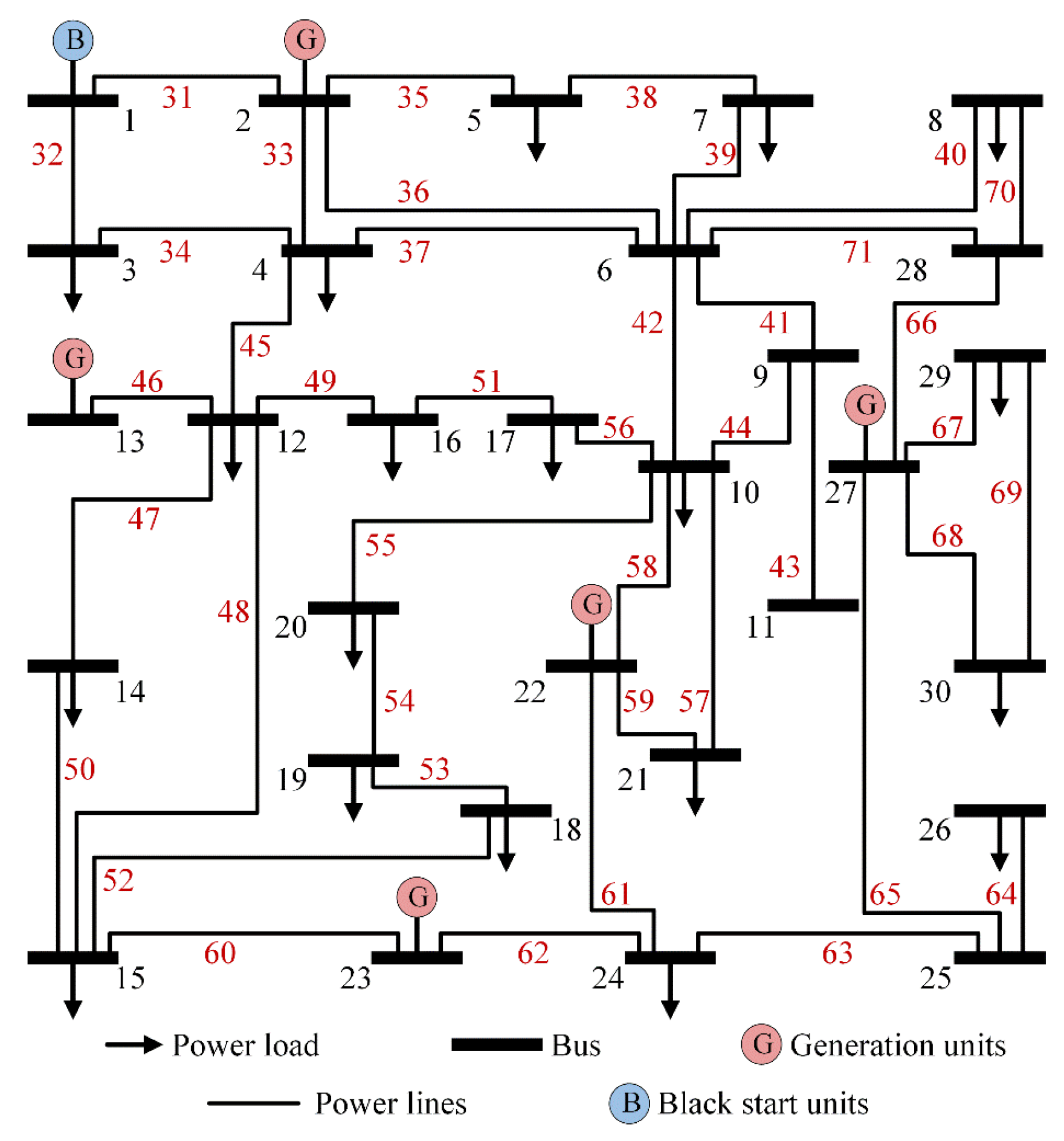
3.1. Experimental Settings

Based on the TNCS model, a simulation experimental scenario is constructed as follows.

The power grid uses the IEEE 30-bus power system [33], as shown in Figure 4. The transportation network has 5000 EVs and 30 nodes with 50 charging piles at each road node. Each charging pile has a maximal output of 20 kW. The nodes of the transportation network and the power grid with the same number are coupled. The information network consists of 101 information nodes, where the first 30 nodes correspond to the power grid nodes, with node 10 serving as the control center. Nodes 31 to 71 correspond to the power lines, while the remaining nodes correspond to the transportation network nodes. The simulation experiments are implemented using MATLAB programming without GPU acceleration techniques.

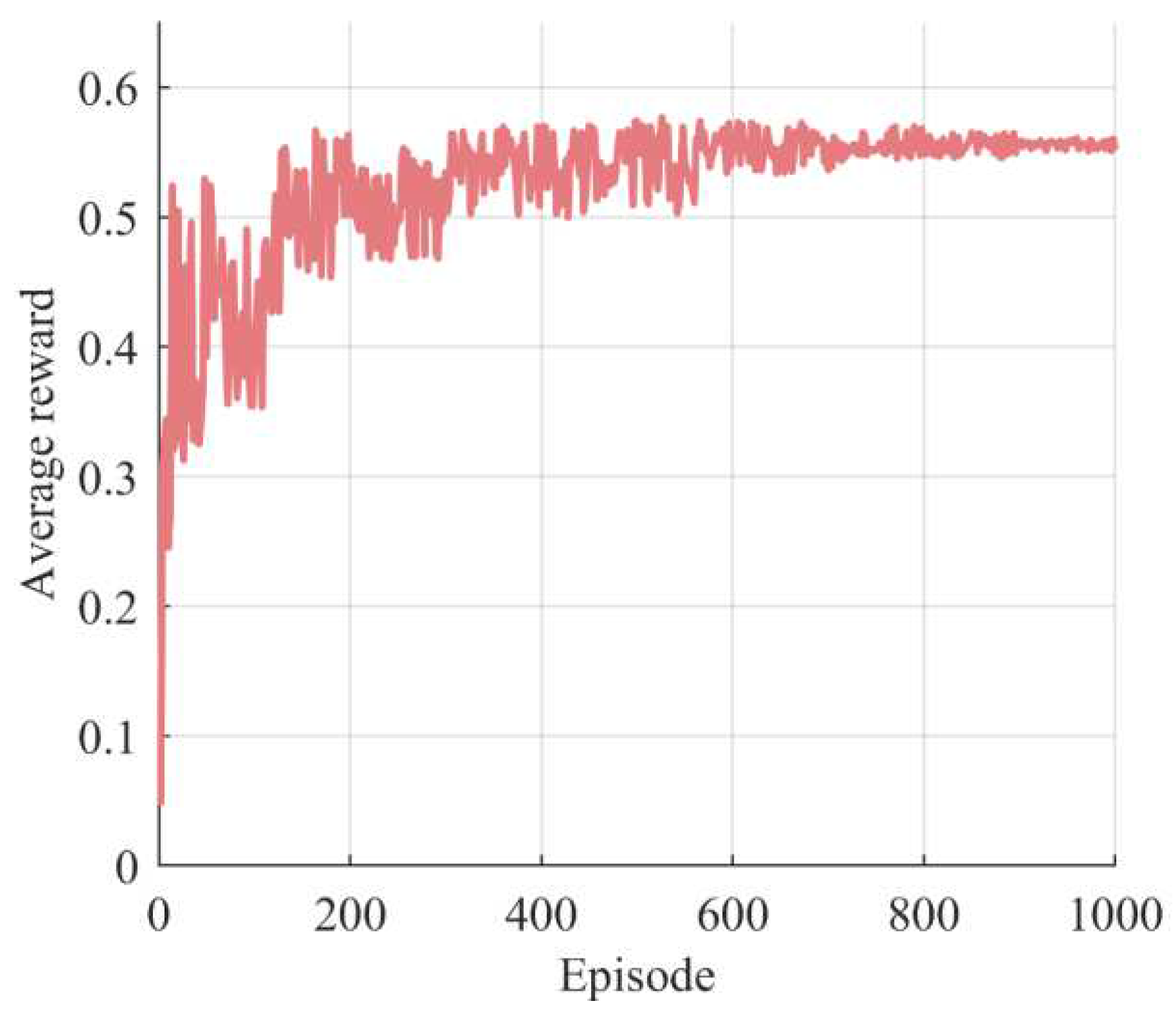
3.2. Small-scale Power Grid Faults

In this section, we simulated small-scale faults in the power grid of the TNCS. Specifically, we induce faults in the power lines with the line numbers 31, 32, 33, 34, 36, and 37, and these lines are placed in an open-circuit state. The specific experimental parameter settings are as follows.

The Actor network consists of an input layer with 142 neurons, a first hidden layer with 256 neurons, a second hidden layer with 128 neurons, and an output layer with 6 neurons. The target Actor network is updated once after every five updates of the Actor network.

The Critic network consists of an input layer with 142 neurons, a first hidden layer with 256 neurons, a second hidden layer with 256 neurons, and an output layer with 1 neurons. The target Critic network is updated once after every five updates of the Critic network.

The ReLU function is used as the activation function in the hidden layers of all networks. The Actor network is updated once after every three updates of the Critic network. Set the discount factor to 0.99, the exploration noise standard deviation to 0.15, the policy noise standard deviation to 0.3, the batch size to 64, the total number of episodes to 1000, and the

ω

I_{d}

I_{b}

, and

τ

values to 0.5, 0.1, 0.1, and 0.005, respectively. The parameter

τ

, specifically, is used in the soft update.

The simulation experimental results are as follows.

The result in Figure 5 indicates that the Actor network is well-trained and able to make accurate and effective decisions.

The obtained restoration scheme is shown in Table 1. The restoration sequence is primarily determined by the order of line restoration; once a line is restored, the connected nodes automatically begin their restoration process (except for black-start nodes). The restoration sequence refers specifically to the order of initiating restoration. As a result, the restoration processes for multiple faults can proceed simultaneously. For example, the restoration of line 36 can be initiated during the restoration of node 1.

To validate the optimality of the restoration sequence, we compared it with several backup schemes based on the restoration benefit criterion. As shown in Table 2, the restoration benefit obtained by our proposed scheme, denoted

F_{1}

, is 15.36% to 25.52% greater than that of the other schemes, indicating that our scheme is optimal in terms of restoration benefit.

Additionally, Figure 6 shows the improvement effect of the TD3 algorithm.

It can be observed that the occurrence number of

λ_{8} = 1

is lower in the improved algorithm compared to the unimproved version. This indicates that the evaluation of restoration actions in the improved algorithm is not solely based on maximizing

Q (S, A)

, but also considers system security issues caused by energy supply-demand imbalances, as represented by the inclusion of a multiplicative term. Using this method, it is possible to lower the original estimated values

Q_{θ_{1}} (S, A) |_{A = π_{\emptyset} (S)}

, as shown by the lower values of the line in the figure for the improved TD3 algorithm compared to the unimproved TD3 algorithm. When the chosen restoration action leads to an energy supply-demand imbalance,

λ_{8}

equals 1, the estimated value decreases, and the Actor network receives feedback indicating that the chosen restoration action is not optimal. As the number of episodes increases, the Actor network gradually learns to avoid restoration actions that may cause energy supply-demand imbalances. Consequently, in the figure, we can observe that the frequency of

λ_{8} = 1

decreases over time, with only three occurrences between episodes 800 and 1000, representing a probability of 1.5%. This is a 66.67% reduction compared to the unimproved TD3 algorithm, and demonstrates the effectiveness of our improvements to the TD3 algorithm in reducing the probability of system security issues caused by energy supply-demand imbalances during the restoration process.

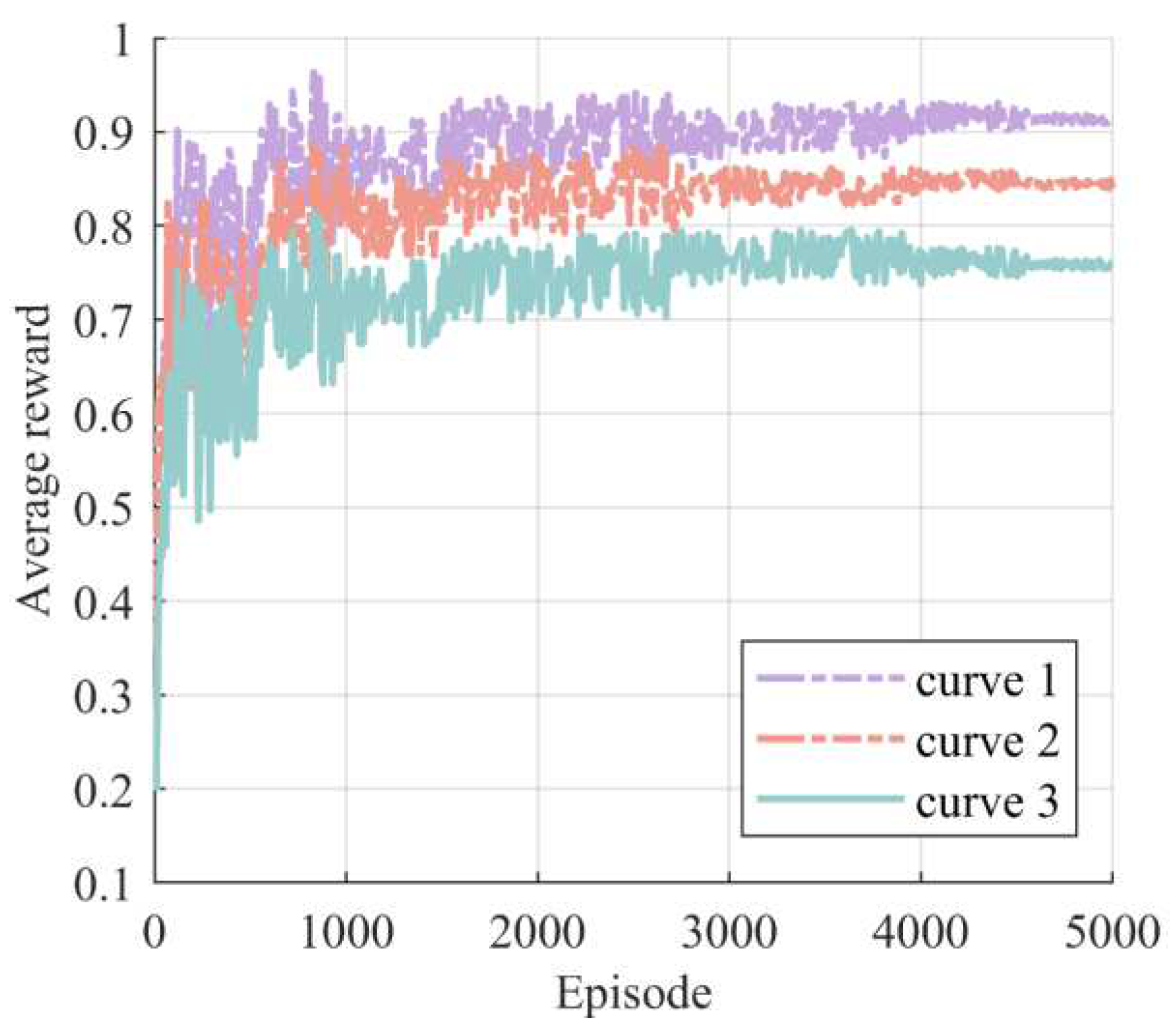
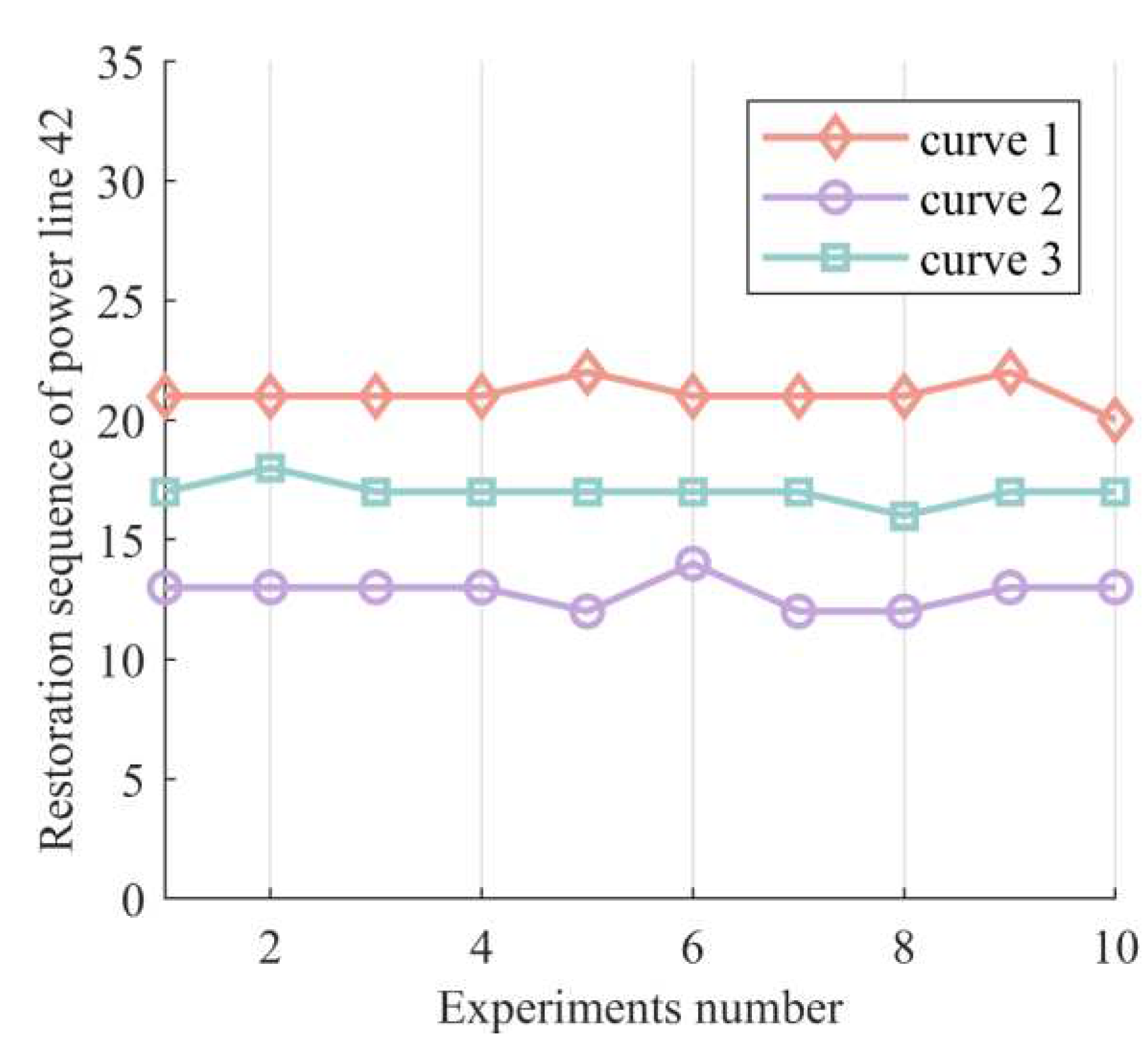
3.3. Large-scale Power Grid Faults

We set all power lines to an open-circuit state, paralyzing the power grid in TNCS. In this scenario, the impact of uncertainties such as failed unit start-up and the occurrence of new faults caused by the restoration process is analyzed, and algorithm proposed in this study is compared with other algorithms to evaluate the performance and efficacy.

Set the batch size to 128 and the total number of episodes to 5000, while the settings of the remaining experimental parameters are identical to those in the small-scale fault scenario. The simulation results are shown below.

We can observe that curve 3 gradually converges to a stable value in Figure 7, which indicates that the Actor network is well-trained and able to make accurate and effective decisions in the scenario of large-scale power grid faults. Furthermore, curve 3 exhibits the lowest average reward, and both curve 3 and curve 1 show significantly higher fluctuations compared to curve 2. This is due to the fact that both generator start-up failures and new faults occurring during the restoration process result in a reward value of -1. Consequently, curve 3 exhibits lower values than the other two curves. The presence of new faults increases the uncertain change of

S

and the difficulty of convergence, leading to higher fluctuations in curve 3 and curve 1.

To validate the impact of uncertainties on restoration sequence, we take the restoration sequence of power line 42 as an example to observe the change of its restoration sequence, and the results are shown in Figure 8. We can observe that in the case corresponding to curve 3, the restoration sequence of power line 42 in 10 experiments is approximately the 17th step, which differs from the cases corresponding to curves 1 and 2. This indicates that uncertainties during the restoration process can alter the restoration sequence, and should not be ignored in practical restoration process.

At the end of this section, we also compare the proposed algorithm with other intelligent algorithms to verify the superiority of the proposed algorithm in solving the fault recovery problem of the TNCS. The results are shown in Table 3. We can observe that Ours outperforms other algorithms by 0.3% to 20.96% in terms of restoration benefit, and in terms of convergence time, there exists a reduction of 2.82% to 14.39% compared to other algorithms except for the PSO algorithm, with only a marginal increase of 1.2% compared to the PSO algorithm. The aforementioned comparative results demonstrate that ours has distinct advantages in terms of both restoration benefit and convergence time, indicating its superiority in an overall assessment. Moreover, compared to the TD3 algorithm, although the restoration benefit is very close, ours exhibits an 8.93% reduction in time. This is due to improvement made to the TD3 algorithm, which reduces the occurrence of new faults during the restoration process and effectively reduce the uncertain change of

S

, thereby reducing convergence difficulties during training.

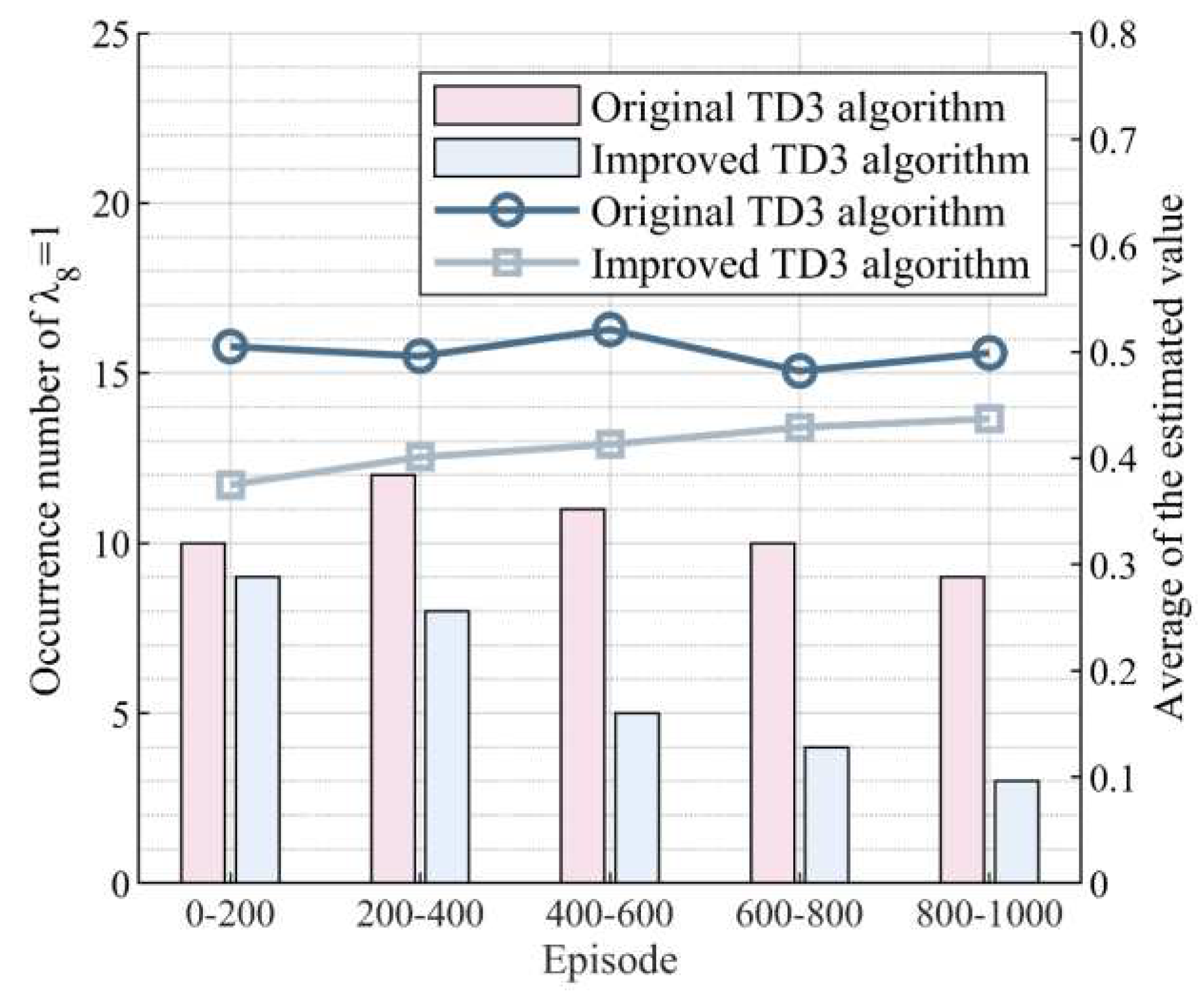
3.4. Communication Faults

In this section, we add the simulation of communication faults on the basis of large-scale power grid faults to validate the resilience of algorithm proposed in this study.

Specifically, we assume that DoS attackers send a significant volume of disguised packets to information nodes 31, 32, 33, and 34, resulting in their infection. As a result, the communication channels within the coupling layer connected to the information nodes and the communication links within the information network of the control layer become blocked. When communication delays are detected, the technical staff at the control center suspends the restoration of power grid faults and initiate the deployment of firewalls and intrusion detection systems to restore communication faults. Equation (25) demonstrates that the impact of communication delays on restoration benefit depends on its occurrence timing and restoration speed. To facilitate statistical analysis, the occurrence time of communication delays is divided into six stages: stage 1: 1 to 6 steps, stage 2: 7 to 12 steps, stage 3: 13 to 18 steps, stage 4: 19 to 24 steps, stage 5: 25 to 30 steps, and stage 6: More than 30 steps. We set

H = 6

, with

h_{t} = 1

corresponding to the first stage,

h_{t} = 2

corresponding to the second stage, etc. There are five levels of restoration speed: level 1:

e_{c} = 1

, level 2:

e_{c} = 2

, level 3:

e_{c} = 3

, level 4:

e_{c} = 4

, and level 5:

e_{c} = 5

. Among them,

e_{c} = 1

indicates that the restoration of communication delay requires one step,

e_{c} = 2

requires two steps, etc. We set

E = 5

and

α = 0.1

. The remaining experimental parameters are maintained in accordance with the previous section. The simulation results are shown as follows.

As shown in Figure 9, the restoration benefit of the communication delay curves is less than that of the normal communication curve, which is due to communication delay causes a reduction in

Γ

value of certain power lines, illustrated in Figure 10.

Figure 9 also illustrates two additional aspects: first is the impact of the occurrence time of DoS attacks on restoration and second is the impact of restoration speed of communication delay on restoration.

The timing of DoS attacks is characterized by uncertainty, while the reduction in restoration benefit caused by DoS attacks can be mitigated by adjusting the value of

β

. According to Table 4, when communication delay occurs in stage 1, stage 2, and stage 3, setting

β

to its maximum value of 1 minimizes the reduction in restoration benefit by 9.23%, 4.22 %, and 0.68%, respectively, compared to the normal communication benefit of 12.3968 MW. However, in stage 4, setting

β

to 1 leads to a restoration benefit of 12.510 MW, which is higher than the normal benefit and unrealistic. Therefore,

β

cannot be set to 1, and

β = 0.75

results in a restoration benefit of 12,267 MW, which is marginally less than 12,3968 MW. Thus, the valid range for

β

in stage 4 is

0.75 \leq β < 1

. Similarly, in stage 5 and stage 6, the valid range for

β

0.75 \leq β < 1

and

0.5 \leq β < 0.75

, respectively.

For the second aspect, it can be observed that the restoration benefit of the communication delay curve corresponding to

e_{c} = 1

is greater than that of the curves corresponding to other restoration speed in all restoration stages. This is due to restoring communication delay leads to obtain the reward

I_{c}

. If the restoration speed is fast, such as completing the restoration in a single step, one

I_{c}

is obtained. Alternatively, multiple

I_{c}

can be obtained if the restoration speed is slow and requires multiple stages to complete. However,

I_{c}

and

I_{b} + I_{m}

are not equivalent, and a difference exists between them. Obtaining multiple

I_{c}

can lead to overestimation or underestimation of

Q (S, A)

, which may result in policy bias and affect restoration decision-making. To solve this issue, we can adjust the values of

β

and

α

to reduce the difference between

I_{c}

and

I_{b} + I_{m}

. It is important to note that we cannot directly control the restoration speed due to its uncertainty and dependence on the defensive deployment level of the information network. When the occurrence time of DoS attacks is fixed, we can adjust the value of

α

to mitigate the policy bias caused by restoration speed. Figure 11 illustrates the impact of different values of

α

on policy bias when

β = 0.5

It can be observed from the Figure 11 that as the value of

α

reduces, the occurrence number of

I_{c}

reduces regardless of the restoration speed. First, this indicates that when

β = 0.5

, the value of

I_{c}

is greater than

I_{b} + I_{m}

, resulting in a

Q (S, A)

overestimation. To solve this, the value of

β

can be appropriately reduced with considering the occurrence time of DoS attacks. Second, the minimum occurrence number of

I_{c}

reduces by 60.26% to 80.12% compared to the maximum occurrence number for the five restoration speed by adjusting the value of

α

, demonstrating that adjusting the value of

α

effectively resolves the policy bias issue caused by restoration speed.

The average occurrence number of

I_{c}

for the five restoration speed under each

α

value in Figure 11 is calculated to represent the actual policy bias under normal restoration speed. The results are shown in Table 5, where the difference ratio indicates the percentage reduction in the average occurrence number of

I_{c}

for the next

α

value compared to the current

α

value. For instance, when the value of

α

changes from 1 to 0.9, the average occurrence number of

I_{c}

reduces by 11.29%, resulting in a difference ratio of 11.29%. We can observe that as the value of

α

reduces from 1, the difference ratio increases continuously. When the value of

α

changes from 0.4 to 0.3, the difference ratio reaches its maximum value of 24.38%, and as the value of

α

continues to reduce, the difference ratio also reduces. This indicates that under the condition of

β = 0.5

, the optimal range of

α

value for minimizing the difference between

I_{c}

and

I_{b} + I_{m}

is around 0.3, leading to a more effective improvement in solving the problem of policy bias.

Based on the aforementioned analysis, it is evident that for uncertainties that cannot be directly controlled, such as the occurrence time of DoS attack and the restoration speed of communication delay，we can adjust the value of

β

to mitigate the extent of restoration loss under various occurrence time of DoS attack. Additionally, we can improve the issue of policy bias caused by restoration speed by adjusting the value of

α

. The experimental results demonstrate that the proposed algorithm exhibits strong adaptability and resilience in the presence of communication delay caused by DoS attack.

4. Conclusions

In addressing the issue of fault recovery in TNCS, we propose a recovery method based on improved TD3 algorithm. In the design of this method, we have particularly considered the uncertainties, system security issues and communication faults. Experimental results indicate that the proposed method can obtain the optimal recovery decisions and accomplish the maximum restoration benefit when faults occur in the power grid of the TNCS. Furthermore, the improvement to the TD3 algorithm effectively reduces the occurrence of energy supply-demand imbalance and the uncertainties are able to impact the restoration sequence so that they should not be ignored during actual restoration process. The results also show that communication delay caused by DoS attacks can reduce the restoration benefit and lead to the policy bias. By adjusting the values of

β

and

α

, the proposed algorithm can effectively mitigate the extent of restoration loss under various occurrence time of DoS attack and improve the issue of policy bias caused by restoration speed, thereby demonstrating strong resilience. Lastly, regarding future research directions, several avenues can be explored, such as studying the impact of transportation network faults on restoration process, designing recovery method when confronted with various types of network attacks, and employing other intelligent algorithms to solve the fault recovery problem in TNCS.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, Geng Zhang and Jiye Wang; methodology, Geng Zhang and Hao Jiang; software, Geng Zhang and Chenxu Liu; validation, Geng Zhang、Hao Jiang and Chenxu Liu; formal analysis, Geng Zhang; investigation, Geng Zhang; resources, Geng Zhang and Jiye Wang; data curation, Jiye Wang; writing—original draft preparation, Geng Zhang and Chenxu Liu; writing—review and editing, Geng Zhang and Chenxu Liu; visualization, Chenxu Liu; supervision, Hao Jiang and Jiye Wang; project administration, Jiye Wang.

Acknowledgments

This paper was supported by National Natural Science Foundation of China: “Theory and analysis method of morphological evolution of electric power information Physical system (U216620068)”.

Conflicts of Interest

The authors declare no conflict of interest.

References

Yang, T.; Guo, Q.; Sheng, Y. Urban integrated electric-traffic network collaboration from perspective of system coordination. Automation of Electric Power Systems 2020, 44, 1–9. [Google Scholar]
He, Z.; Xiang, Y.; Liao, K. Demand, form and key technologies of integrated development of energy-transport-information networks. Automation of Electric Power Systems 2021, 45, 73–86. [Google Scholar]
Hu, Q.; Ding, H.; Chen, X. Analysis on rotating power outage in California, USA in 2020 and its enlightenment to power grid of China. Automation of Electric Power Systems 2020, 44, 11–18. [Google Scholar]
Sun, H.; Xu, T.; Guo, Q. Analysis on blackout in Great Britain power grid on August 9th, 2019 and its enlightenment to power grid in China. Proceedings of the CSEE 2019, 39, 6183–6192. [Google Scholar]
Zhang, Y.; Xie, G.; Zhang, Q. Analysis of 2·15 power outage in Texas and its implications for the power sector of China. Electric Power 2021, 54, 192–198. [Google Scholar]
Yan, D.; Wen, J.; Du, Z. Analysis of Texas blackout in 2021 and its enlightenment to power system planning management. Power System Protection and Control 2021, 49, 121–128. [Google Scholar]
Hu, Y.; Xue, S.; Zhang, H. Cause analysis and enlightenment of global blackouts in the past 30 years. Electric Power 2021, 54, 204–210. [Google Scholar]
Wu, J.; Chen, Z.; Zhang, Y. Sequential recovery of complex networks suffering from cascading failure blackouts. IEEE Transactions on Network Science and Engineering 2020, 7, 2997–3007. [Google Scholar] [CrossRef]
Han, O.; Chen, Z.; Ding, T. Power system black-start restoration model considering wind power uncertainties[J/OL]. Power System Technology 2022, 1–15. [Google Scholar]
Pang, K.; Wang, Y.; Wen, F. Cyberphysical collaborative restoration strategy for power transmission system with communication failures. Automation of Electric Power Systems 2021, 45, 58–67. [Google Scholar]
Li, Z.; Xue, Y.; Wang, H. A dynamic partitioning method for power system parallel restoration considering restoration-related uncertainties. Energy Reports 2020, 6, 352–361. [Google Scholar] [CrossRef]
Arif, A.; Wang, Z.; Wang, J. Power distribution system outage management with co-optimization of repairs, reconfiguration, and DG dispatch. IEEE Transactions on Smart Grid 2017, 9, 4109–4118. [Google Scholar] [CrossRef]
Liu, T.; Zhu, Y.; Sun, R. Resilience-enhanced-strategy for cyber-physical power system under extreme natural disasters. Automation of Electric Power Systems 2021, 45, 40–48. [Google Scholar]
Sun, L.; Liu, W.; Chung, C. Improving the restorability of bulk power systems with the implementation of a WF-BESS system. IEEE Transactions on Power Systems 2018, 34, 2366–2377. [Google Scholar] [CrossRef]
Yang, Z.; Sun, L.; Ding, M. Optimization strategy for start-up sequence of generation units considering critical restoration paths. Electric Power Construction 2019, 40, 28–35. [Google Scholar]
Xiang, Y.; Ding, Z.; Zhang, Y. Power system reliability evaluation considering load redistribution attacks. IEEE Transactions on Smart Grid 2016, 8, 889–901. [Google Scholar] [CrossRef]
Che, L.; Liu, X.; Shuai, Z. Cyber cascades screening considering the impacts of false data injection attacks. IEEE Transactions on Power Systems 2018, 33, 6545–6556. [Google Scholar] [CrossRef]
Che, L.; Liu, X.; Li, Z. False data injection attacks induced sequential outages in power systems. IEEE Transactions on Power Systems 2018, 34, 1513–1523. [Google Scholar] [CrossRef]
Wang, Q.; Pipattanasomporn, M.; Kuzlu, M. Framework for vulnerability assessment of communication systems for electric power grids. IET Generation, Transmission & Distribution 2016, 10, 477–486. [Google Scholar]
Huseinović, A.; Mrdović, S.; Bicakci, K. A survey of denial-of-service attacks and solutions in the smart grid. IEEE Access 2020, 8, 177447–177470. [Google Scholar] [CrossRef]
Tan, S.; Sun, J.; Wan, L. A DoS attack intensity-aware adaptive critic design of frequency regulation for EV-integrated power grids. International Journal of Electrical Power & Energy Systems 2023, 145, 108656. [Google Scholar]
Li, X.; Jiang, C.; Du, D. A Novel State Estimation Method for Smart Grid Under Consecutive Denial of Service Attacks. IEEE Systems Journal 2022, 17, 513–524. [Google Scholar] [CrossRef]
Zhang, B.; Dou, C.; Yue, D. Attack-defense evolutionary game strategy for uploading channel in consensus-based secondary control of islanded microgrid considering DoS attack. IEEE Transactions on Circuits and Systems I: Regular Papers 2021, 69, 821–834. [Google Scholar] [CrossRef]
Gao, Q.; Du, Z.; Gi, Y. Resilient load frequency control for multi-area interconnected power system under denial-of-service attacks. Electric Power Construction 2023, 44, 54–62. [Google Scholar]
An, X.; Sun, H.; Zhang, X. Analysis and lessons of Texas power outage event on February 15, 2021. Proceedings of the CSEE 2021, 41, 3407–3415. [Google Scholar]
Li, M.; Sun, L.; Ma, Y. An optimization strategy for generator start-up sequence after blackouts considering the cyber system fault. Electric Power 2022, 55, 146–155. [Google Scholar]
Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods[C]//International conference on machine learning. PMLR, 2018: 1587-1596.
Xie, S.; Girshick, R.; Dollár, P. Aggregated residual transformations for deep neural networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 1492-1500.
Wang, Q.; Wu, B.; Zhu, P. ECA-Net: Efficient channel attention for deep convolutional neural networks[C]//Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020: 11534-11542.
Mnih, V.; Kavukcuoglu, K.; Silver, D. Human-level control through deep reinforcement learning. nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
Sutton, R.S.; McAllester, D.; Singh, S. Policy gradient methods for reinforcement learning with function approximation. Advances in neural information processing systems 1999, 12. [Google Scholar]
Lillicrap, T.P.; Hunt, J.J.; Pritzel, A. Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971, 2015.
Liu, Y.; Gu, X. Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization. IEEE Transactions on Power Systems 2007, 22, 1267–1274. [Google Scholar] [CrossRef]

Figure 1. TNCS model.

Figure 2. Structure of the restoration algorithm. First, the TNCS environment interacts with the Actor network in the Main networks, incorporating exploration noise. Specifically, this interaction indicates the state matrix

S

, as the input to the Actor network, and the Actor network chooses an action based on

S

. Then, the action can change the state matrix, resulting in a certain reward. Second, the obtained transitions from the interaction (transitions primarily include

S

A

S'

and

R

) are preserved in the replay buffer via experience replay. To train and update the Actor network and Critic network in the Main networks, a batch-sized transition sample is selected at random. During the update of the Critic network, TD-error is generated and gradient descent is performed with introducing policy noise into the process. The Actor network is updated using gradient ascent to maximize

Q_{θ_{1}}

. The Target networks are updated after a certain number of updates to the Main networks.

S

, as the input to the Actor network, and the Actor network chooses an action based on

S

. Then, the action can change the state matrix, resulting in a certain reward. Second, the obtained transitions from the interaction (transitions primarily include

S

A

S'

and

R

Q_{θ_{1}}

. The Target networks are updated after a certain number of updates to the Main networks.

Figure 3. State matrix. We assume the presence of 30 power nodes, 41 lines, and fault types including faults at power nodes and lines.

Figure 4. IEEE 30-bus power system diagram. The power lines are numbered from 31 to 71.

Figure 5. Learning curve. We can observe that the learning curve exhibits significant fluctuations during the first 300 or so episodes. Approximately between 300 and 700 episodes, the fluctuations decrease. After roughly 700 episodes, the average reward converges on a stable value.

Figure 6. Improvement effect of the TD3 algorithm. The values of the bar indicate the number of occurrence of

λ_{8} = 1

per 200 episodes, while the values of the line indicate the average of the estimated value every 200 episodes.

Figure 6. Improvement effect of the TD3 algorithm. The values of the bar indicate the number of occurrence of

λ_{8} = 1

per 200 episodes, while the values of the line indicate the average of the estimated value every 200 episodes.

Figure 7. The impact of uncertainty factors on fault recovery. curve 1 represents the scenario without considering the possibility of unit start-up failures during the restoration process. curve 2 represents the scenario without considering the possibility of fault recovery causing new faults. curve 3 represents the scenario that considers both unit startup failures and the occurrence of new faults during the restoration process.

Figure 8. Impact of uncertainties on restoration sequence. The curves labeled as curve1, curve2, and curve3 in this figure correspond to curve2, curve1, and curve3 in Figure 7, respectively. The restoration sequence of power line 42 refers to the step at which this line is recovered.

Figure 9. Impact of communication delay on restoration benefit. There is one curve representing normal communication, the value of which remains constant at 12,3968 MW, and five curves representing communication delay.

Figure 10. Mechanism of

Γ

value reduction. We assume that a DoS attack is launched against the information node at step 2. It can be observed that the DoS attack has no impact on the restoration of steps 2 and 1. As the restoration process reaches step 3, the control center performs a status check and detects the communication delay, initiating its restoration. Power line 42 cannot be restored in step 3, and its recovery order is changed from step 3 to step 4. The reason it is changed to step 4, rather than step 5, step 6, etc. is because

e_{c} = 1

. Similarly, the restoration step for power line 45 transitions from step 4 to step 5, etc. At step 4, regardless of whether power lines 45 or 42 are restored, the

Γ

value corresponding to step 4 remains unchanged. When power line 42 is restored at step 4, the

Γ

value reduces from 0.96 (corresponding to step 3) to 0.94. The above analysis explains the reduction of the

Γ

value.For the first aspect, we can observe that when the restoration speed remains constant, the later the occurrence of communication delay caused by DoS attacks, the less the restoration benefit is reduced. This is due to the fact that a delayed occurrence of communication delay results in fewer affected power lines, resulting in a less reduction in the

\sum_{m}^{e_{p}} Γ

value of the objective function (as explained by the mechanism for

Γ

value reduction), while the

\sum_{m}^{e_{p}} L S_{r m} + P_{r m}^{S}

value remains unchanged. Consequently, the communication delay curve exhibits an increasing trend as the restoration process progresses.

Figure 10. Mechanism of

Γ

e_{c} = 1

. Similarly, the restoration step for power line 45 transitions from step 4 to step 5, etc. At step 4, regardless of whether power lines 45 or 42 are restored, the

Γ

value corresponding to step 4 remains unchanged. When power line 42 is restored at step 4, the

Γ

value reduces from 0.96 (corresponding to step 3) to 0.94. The above analysis explains the reduction of the

Γ

\sum_{m}^{e_{p}} Γ

value of the objective function (as explained by the mechanism for

Γ

value reduction), while the

\sum_{m}^{e_{p}} L S_{r m} + P_{r m}^{S}

value remains unchanged. Consequently, the communication delay curve exhibits an increasing trend as the restoration process progresses.

Figure 11. The impact of

α

on policy bias. The various colored bars represent various

α

values.

Figure 11. The impact of

α

on policy bias. The various colored bars represent various

α

values.

Table 1. Restoration sequence.

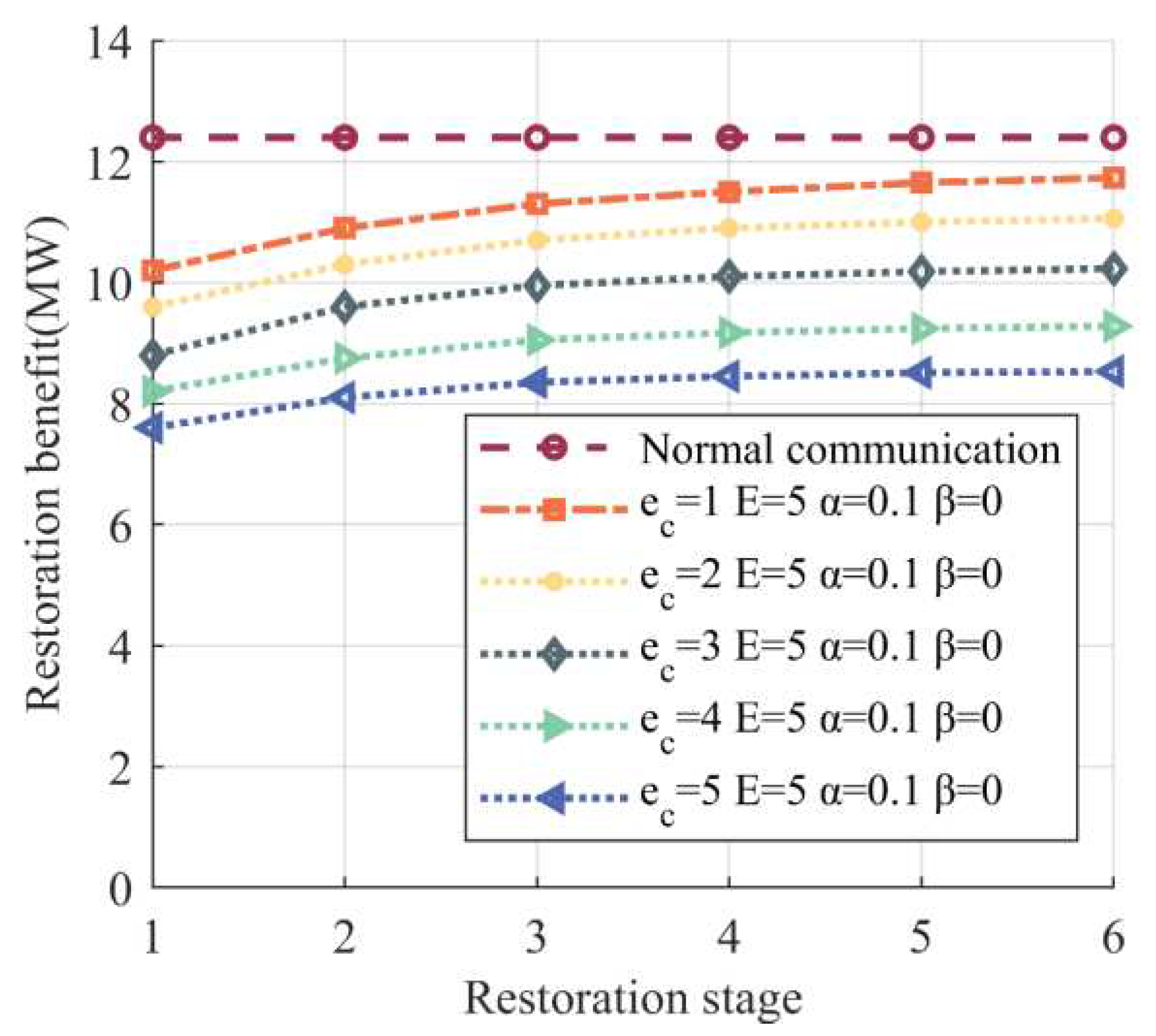
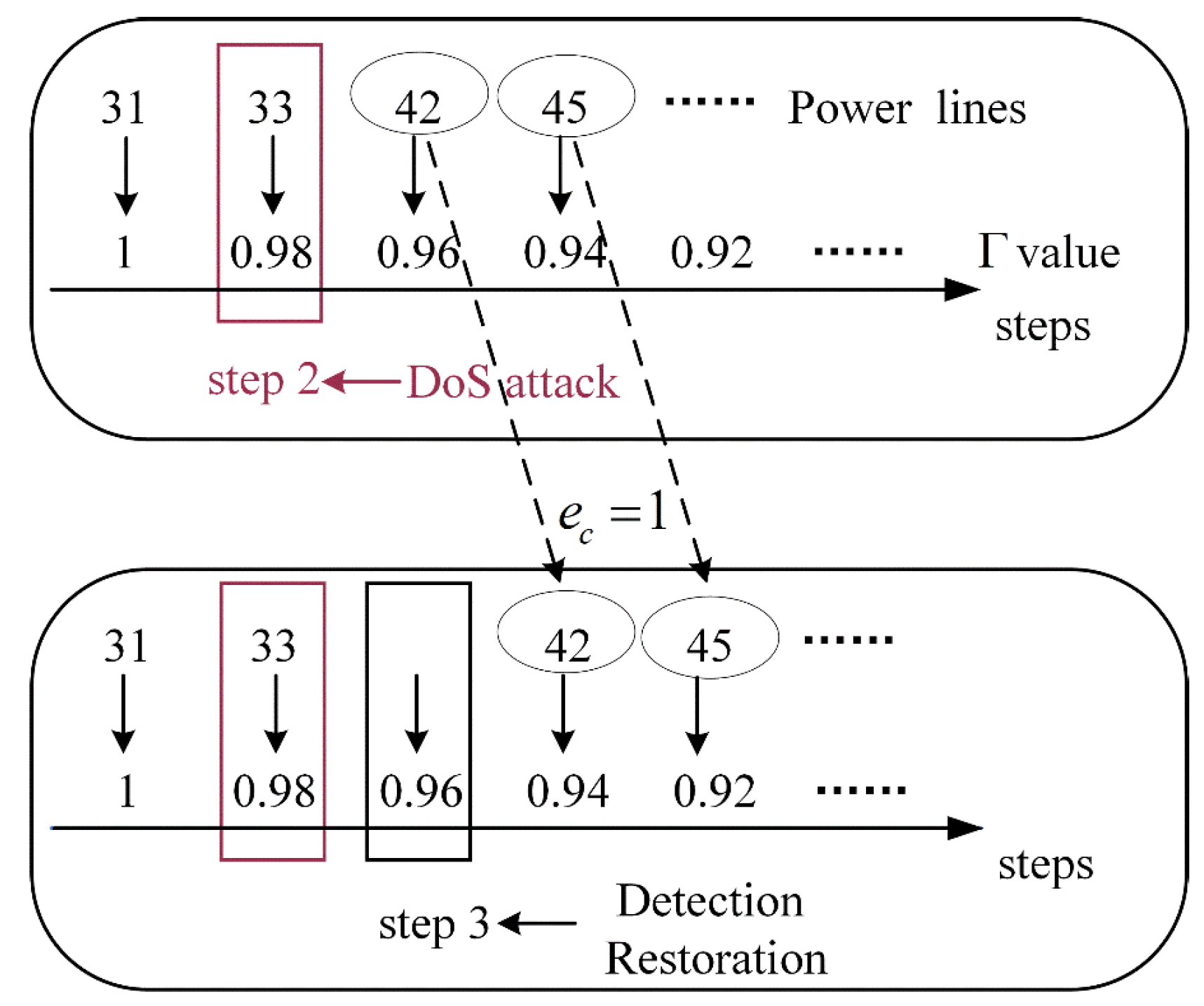
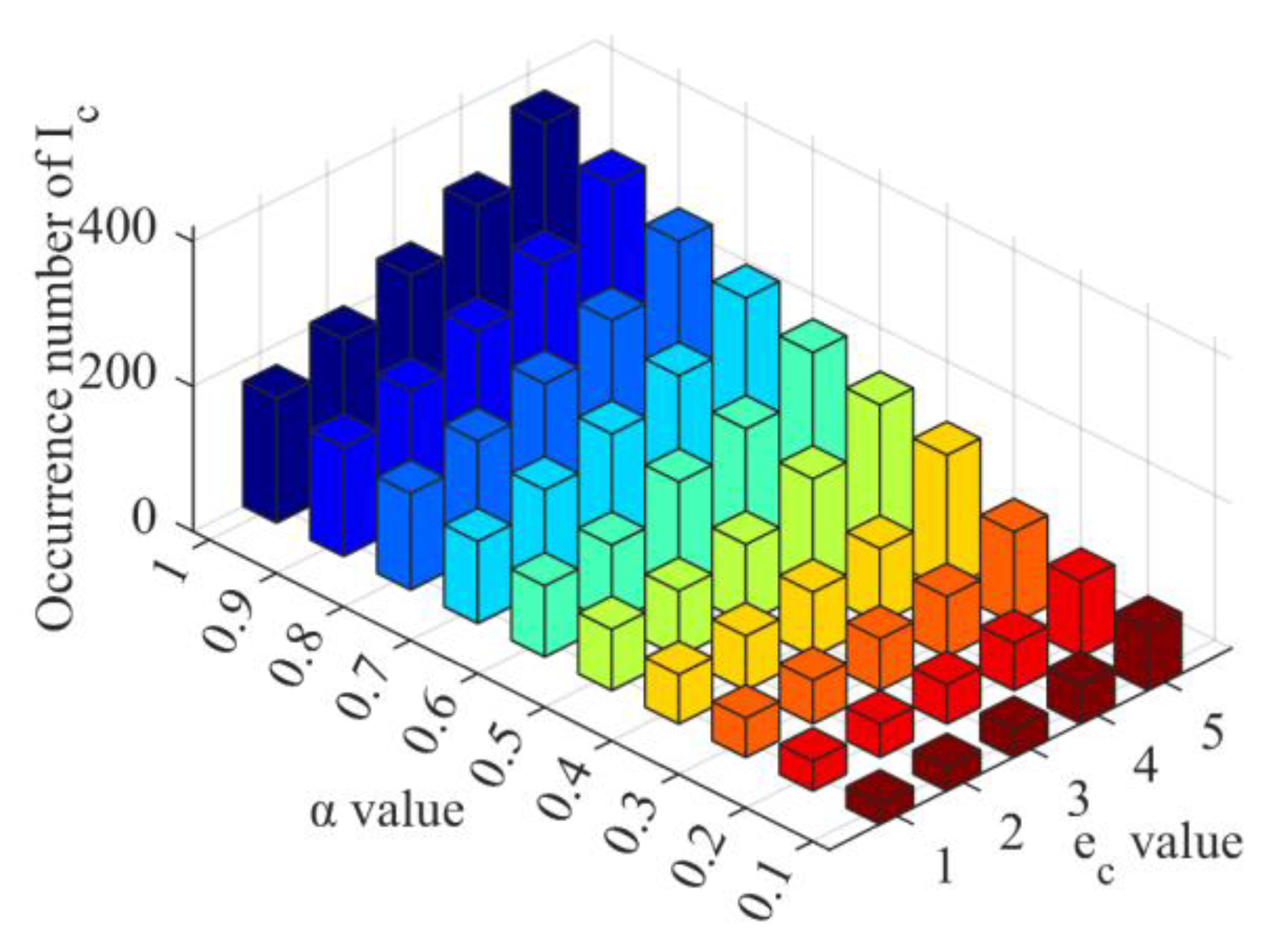
Steps		Power grid lines and nodes
1		1、31、2
2		36、6
3		33、4
4		37
5		32
6		34

Table 2. Comparison of schemes.

Scheme	Restoration sequence	Restoration benefit(MW)
$F_{1}$	31、36、33、37、32、34	2.8239
$F_{2}$	33、36、37、32、31、34	2.2689
$F_{3}$	31、32、34、37、36、33	2.3564
$F_{4}$	36、32、34、31、33、37	2.3901
$F_{5}$	34、33、36、32、31、37	2.1032
$F_{6}$	31、37、32、34、36、33	2.2946

Table 3. Comparison of different algorithms.

Algorithm	Performance metrics
Algorithm	Restoration benefit (MW)	Convergence time (s)
Ours	12.3968	14763
GA	10.4519	15192
PSO	9.7987	14580
DQN	10.4832	17244
AC	10.8751	16848
DDPG	11.7285	16416
TD3	12.3812	16211

Table 4. The impact of

β

on restoration benefit.

Table 4. The impact of

β

on restoration benefit.

$h_{t}$	$Restoration benefit (MW) (e_{c} = 1$ )
$h_{t}$	$β = 1$	$β = 0.75$	$β = 0.5$	$β = 0.25$	$β = 0$
1	11.252	10.955	10.705	10.457	10.207
2	11.873	11.590	11.401	11.159	10.915
3	12.312	12.065	11.823	11.577	11.321
4	12.510	12.267	12.030	11.780	11.531
5	12.627	12.371	12.120	11.878	11.652
6	12.800	12.550	12.231	11.990	11.730

Table 5. The impact of

α

on policy bias.

Table 5. The impact of

α

on policy bias.

$α$ value	$I_{c}$ average occurrence number	Difference ratio
1	258.6	0
0.9	229.4	11.29%
0.8	202.6	11.68%
0.7	177.4	12.44%
0.6	153.2	13.64%
0.5	129.2	15.67%
0.4	104.2	19.35%
0.3	78.8	24.38%
0.2	65.0	17.51%
0.1	55.5	14.62%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Fault Recovery Methods for a Converged System Comprised of Power Grids, Transportation Networks and Information Networks

Abstract

1. Introduction

2. Methods

2.1. Modeling

2.1.1. Overall Framework

2.1.2. Execution Layer

2.1.3. Coupling Layer

2.1.4. Control Layer

2.2. Fault Recovery Method

2.2.1. Design of Restoration Model

2.2.2. Design of Restoration Algorithm

3. Experiments and Results

3.1. Experimental Settings

3.2. Small-scale Power Grid Faults

3.3. Large-scale Power Grid Faults

3.4. Communication Faults

4. Conclusions

Author Contributions

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe