Prerpints.org logo
Preprint
Article

Impact of Nd Doping on Electronic, Optical, and Magnetic Properties of ZnO: A GGA+U Study

Altmetrics

Downloads

90

Views

13

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 September 2023

Posted:

30 September 2023

You are already at the latest version

Alerts
Abstract
The electronic, optical, and magnetic properties of Nd-doped ZnO systems were calculated using the DFT/GGA+U method. According to the results, the Nd dopant causes lattice parameter expansion, negative formation energy, and bandgap narrowing, resulting in the formation of an n-type degenerate semiconductor. Overlapping of the generated impurity and Fermi levels results in a significant trap effect that prevents electron-hole recombination. The absorption spectrum demonstrates a redshift in the visible region and improved intensity, leading to enhanced photocatalytic performance. The Nd-doped ZnO system displays ferromagnetic, with FM coupling due to strong spd-f hybridization through magnetic exchange interaction between the Nd-4f state and O-2p, Zn-4s, and Zn-3p states. These findings imply that Nd-doped ZnO may be a promising material for DMS spintronic devices.
Keywords: 
Subject: Physical Sciences  -   Atomic and Molecular Physics

1. Introduction

The incorporation of magnetic ions in a non-magnetic semiconductor can make it acquire many unique physical properties such as the hysteresis phenomenon, magneto-optical effect, abnormal Hall effect, negative giant magnetoresistive effect, etc. Therefore, it can be made into spin diodes, spin field effect transistors, and other devices, having broad potential applications in information storage, transmission, and processing [1, 2]. In 2000, Dietl’s research team found that manganese-doped ZnO and GaN can obtain room-temperature ferromagnetism according to their calculations [3], and predicted that transition metal-doped ZnO semiconductors are dilute magnetic semiconductors with room-temperature ferromagnetism, which laid the foundation for the research of oxide-based dilute magnetic semiconductors. ZnO, a semiconductor with high exciton binding energy (60 eV) and wide band gap (3.37 eV), is magnetic owing to intrinsic defects, as well as the doping effect of rare earth elements and 3d transition metals and other magnetic ions [4, 5] and shows significant application value in the fields of information storage and processing. However, there are drawbacks such as a low Curie temperature. Additionally, the understanding of magnetic sources and magnetic coupling mechanisms are still inconsistent. The valence electrons of rare earth elements are positioned in the 4f orbital, which is surrounded by the 5s orbital and the 5p orbital, and they have a distinct electronic structure and luminescence properties. Because of the shielding effect between the outer orbitals and lack of compensation effect, the influence of crystal field, temperature, and carriers on the 4f orbital electron transition is minimal, and even under conditions of elevated temperature or powerful outer electric fields, the rare earth elements’ optical transition is stable [6]. Thus, the researchers have given a lot of attention to the rare earth-doped ZnO’s physical properties. Xu et al. prepared flower-like nano-ZnO and its La- and Nd-doped modified composites by using a hydrothermal method and studied their photocatalytic properties on reactive dyes. The results showed that the excitation wavelength of 3%La-3%Nd/ZnO was extended to the visible region, and the degradation rate of reactive yellow 145 and reactive red 24 reached more than 80%. In the UV-Vis region, ZnO composites significantly reduced the COD and TOC of printing and dyeing wastewater, indicating that 3%La-3%Nd/ZnO is an excellent photocatalyst. Sharma et al. synthesized Ce-doped ZnO by using chemical precipitation and studied its magnetic and optical properties. Their results showed a significantly reduced bandgap and obvious ferromagnetism after the doping of Ce ions in ZnO, which was caused by the higher orbital momentum of localized 4f electrons in Ce. Wen et al. investigated the Ce-doped ZnO’s magnetic and optical properties employing first-principles calculation and discovered that the doped system’s magnetic properties were related to its configuration. Ag/Co co-doped ZnO’s optoelectronic and ferromagnetic (FM) properties were studied by Liu et al. who discovered that both Ag/Co co-doped ZnO and Ag-doped ZnO exhibited FM properties, while Co-doped ZnO presented antiferromagnetic (AFM) properties. Mka et al. performed density functional theory (DFT) calculation on the electronic, optical, and magnetic properties of rare earth (RE = Tm, Yb, Ce) doped with ZnO, and according to the findings, REE doping in ZnO had a considerable effect on its magnetic and photoelectric properties, primarily owing to the presence of 4f electrons and the greatly improved conductivity following doping. Zhang et al. carried out first-principles calculations to predicate the electronic structure and magnetism of rare earth doped ZnO, and the findings presented that La doping in ZnO can result in a diamagnetic ground state, the La and Ce doping had more stability in contrast with Pr, Nd, and Eu doping, the ground state of Pr, Nd, and Eu dopants at Zn sites were weak AFM, but the ground state of Ce dopants is FM.
Based on the above research results, ZnO’s electronic, optical, and magnetic properties can be altered by structural design, impurity doping, and co-doping. The dilute magnetic semiconductors’ magnetic properties are primarily determined by the competition of double- and hyper-exchange interactions, which are mainly affected by the doping geometry. However, it is a challenge to experimentally study doping geometry. DFT is an important tool to reveal the relationship between magnetic properties and doping geometry of dilute magnetic semiconductors [13]. This study utilizes the GGA+U method for calculating the rare earth Nd-doped ZnO’s electronic, optical, and magnetic properties in order to shed some light on electronic device-related research and development with outstanding magnetic and optical properties.

2. Computational Methodology and Models

The energy band structure, electronic states’ density, optical properties, differential charge density (DCD), Mulliken charge population, bond population, and magnetic properties were computed through the CASTEP module of Material Studio 2020. CASTEP is utilizing the first-principles calculation method under the framework of DFT. The norm-conserving pseudopetential method was utilized for describing the interaction between atomic real and valence electrons, with the generalized gradient approximation Perdew–Burke–Ernzerhof (GGA-PBE) exchange-correlation potential and screened Coulomb potential. The outer valence electrons chosen for the calculation were from configurations of Zn-3d104s2, O-2s22p4, and Nd-4f45s25p66s2, and we treated the rest of the orbital electrons as core electrons. When calculating energy, electrons were treated using spin polarization. The following computational parameters were set for ensuring convergence: the energy tolerance of 5×10−6 eV/atom, and the convergence criteria of 0.01 eV/Å maximum force, 5×10−4 Å displacement, and 0.02 GPa stress. To balance calculation speed and accuracy, an energy cut-off of 800 eV and a k-point mesh of 4×4×2 were chosen. Since the geometrical configuration of Nd plays a substantial role in investigating the magnetic behaviors of Zn15Nd1O16 and Zn14Nd2O16, it is important to grasp the realistic geometries of the doped structures. By using the linear response method [16], we calculated the value of U and verified its validity. When Ud-Zn = 10.0 eV, Up-O = 7.0 eV, and Uf-Nd = 6.0 eV, the computed lattice parameters of a = 3.269 Å, c = 5.272 Å, and bandgap = 3.34 eV have consistency with the experimental ones (a = 3.248 Å, c = 5.220 Å [17], and bandgap = 3.37 eV [18]). In the present work, the super-cellular models used in our calculation are presented in Figure 1, wherein a Zn16O16 (2×2×2) supercell comprises 16 O and 16 Zn, a Zn15Nd1O16 (2×2×2) supercell has 16 O, 15 Zn, and 1 Nd, and a Zn14Nd2O16 (2×2×2) supercell consists of 16 O, 14 Zn, and 2 Nd.

3. Results and Discussion

3.1. Analysis of system structure and stability

The geometric structural optimizations were carried out for the intrinsic Zn16O16 supercell model, as well as doped Zn15Nd1O16 and Zn14Nd2O16 supercell models, and Table 1 lists the intrinsic ZnO (i-ZnO) and doped ZnO system’s cell parameters. According to the analysis, as the concentration of Nd doping increased, the cell parameters of the doped system became larger and the volume also increased, indicating a lattice mismatch between Nd3+ and ZnO. In accordance with the theory of quantum chemistry, the ionic radius of Nd3+ (0.0983 nm) is bigger in contrast with that of Zn2+ (0.074 nm), the system will have a greater volume after replacing Zn2+ with Nd3+. In addition, after doping, the repulsion between the excess positive charges of Nd3+ is improved. Due to these two factors, the system volume after impurity doping will become greater and the lattice distortion will occur.
To further verify the doping system’s stability and the intricacy of Nd doping, the formation energy Ef of the Nd-doped ZnO system was computed with the following equations [19, 20]:
E f = E ( ZnO + Nd ) − E ZnO − n Nd μ Nd + n Zn μ Zn
where, E ( ZnO + Nd ) and E ZnO are the total energy of the doped and i-ZnO system, containing the same numbers of atoms, n Nd is the number of Nd atoms, n Zn is the number of replaced Zn atom, μ N d and μ Z n are the chemical potentials of Nd and Zn (at T = 0 K), respectively. The calculated formation energies are also summarized in Table 1. The formation energy Ef of the Nd-doped ZnO system was negative and reduced with the rise of doping concentration, indicating easier doping.

3.2. Analysis of energy band structure

Under spin polarization conditions, the structure of the spin-up (SU) and spin-down (SD) energy band in i-ZnO and Nd-doped ZnO systems are illustrated in Figure 2, and Fermi level of 0 eV is represented by the dotted line Ef. The high symmetry points of the band structure were located at G(0.0, 0.0, 0.0), A(0.0, 0.0, 0.5), H(-0.333, 0.667, 0.5), K(-0.333, 0.667, 0.0), M(0.0, 0.5, 0.0), and L(0.0, 0.5, 0.5). The i-ZnO’s band structure diagram is depicted in Figure 2(a). Employing the modified GGA+U method, the calculated bandgap value for i-ZnO was 3.34 eV, which is essentially consisten with the experimental finding of 3.37 eV [18]. Therefore, the selected U parameter was reliable. Furthermore, the top of the valence band (VB) and the bottom of the conduction band (CB) were positioned at the G points, and the transition type was G-G, indicating that i-ZnO is a direct bandgap semiconductor. Besides, the SU and SD bands of the i-ZnO system have the same structure, and there was no occurrence of a spin-splitting phenomenon, demonstrating that the i-ZnO material does not reveal magnetic characteristics.
Figure 2(b) and (c) are the diagrams of the SU and SD band structure of Nd-doped ZnO systems under spin polarization conditions. The bandgap values of Zn15Nd1O16 and Zn14Nd2O16 were 3.25 eV and 3.08 eV, respectively, indicating that the bandgap decreases with the increase of Nd doping concentration. This will be conducive to improving the doped system’s optical and electronic transport properties. The VB’s top and the CB’s bottom of Zn15Nd1O16 and Zn14Nd2O16 were positioned at point G, and the transition type was G-G, indicating that Nd-doped ZnO is a direct bandgap semiconductor. In the energy bands of Zn15Nd1O16, a deep donor impurity energy level) was generated at 1.69 eV from the CB, and the ionization energy was large. From the density of states (DOS) in Figure 3(b) and (c), the impurity energy level had a primary contribution from Nd-4f state electrons, some of the impurity energy levels coincided with the Fermi level, and the trapping effect was significant. The trap effect has the effect leads to the accumulation of non-equilibrium carriers on the impurity energy level [21], which reduces the electron-hole recombination velocity and increases luminous efficiency concurrently. The impurity energy level shifted to lower energy with the increase of Nd doping concentration. In the energy band of Zn14Nd2O16, a shallow main impurity energy level was produced at the VB’s top, and the number of impurity energy levels increased, meaning that the number of electrons that underwent level transitions increased. The photoexcited electrons absorbed lower energy and were transferred from the VB to the impurity energy level, and then absorbed lower energy again and further transferred from the impurity energy level to the CB’s bottom, resulting in an increased photocatalytic activity and realized the redshift of the absorption spectrum. The Fermi level in the band structure of Zn15Nd1O16 and Zn14Nd2O16 systems entered the CB, because the Nd atom lost 3 valence electrons of its 5d and 6s states, whereas the valence state of Zn in ZnO was +2. Nd introduced excess carriers (electrons) that occupied the CB energy level below the Fermi level. These carriers were degenerated and the doped system became n-type degenerate semiconductors, indicating that the conductivity and the metallicity of the Nd-doped ZnO system are enhanced. In addition, the structures for the SU and SD energy bands of the Nd-doped ZnO system were different, resulting in spin splitting, demonstrating that Nd-doped ZnO is magnetic and possesses electromagnetic transport properties.

3.3. Analysis of density of states

Under spin polarization conditions, the total (TDOS) and partial (DOS) of i-ZnO and Nd-doped ZnO are shown in Figure 3. The GGA+U method corrected the interaction between electrons in atomic orbitals. The DOS distributions of the Zn-3d state and O-2p state in the VB near the Fermi level were noticeably divided, leading to the broadening of the VB, the weakening of p-d hybridization, and the moving of the O-2p state energy band in the direction of low energy. Therefore, the bandgap was widened and consistent with the experimental results. The deep VB (-15.8 eV, -14.3 eV) had a contribution from O-2s states, and it is strongly localized. The VB (-10.3 eV, -6.9 eV) had a contribution from the Zn-3d state and some O-2p state. Since Zn-3d state and O-2p state were strongly hybridized, strong Zn-O bonds were created. The upper VB (-6.3 eV, 0 eV) had a contribution from O-2p state electrons, while the CB had a contribution from Zn-4s and 3p state electrons. Additionally, it was discovered that the Zn-4s state determined the bottom position of the i-ZnO’s CB, and the O-2p state determined the top position of the i-ZnO’s VB. Thus, when the Zn and O atoms combined, electrons of these two states interacted to form a chemical bond, and the O-2p state contributed the majority. Furthermore, the total DOS of SU and SD orbitals were completely symmetric for i-ZnO, and the net spin DOS was zero, indicating that i-ZnO material does not exhibit magnetic characteristics.
Figure 3(b) and (c) illustrate the TDOS and PDOS of Nd-doped ZnO. At the top of VB, the repulsion of the anti-bonding Zn-3d state and O-2p state caused the shift of the VB towards the high-energy direction, while the interaction between the bonding Zn-3p state and O-2p state led to the shift of the VB in the direction of low energy. Because the bonding effect was greater in contrast with the anti-bonding effect, the VB moved in the direction of low energy. Concurrently, the CB experiences a more significant reduction, resulting in a narrower bandgap for the Nd-doped ZnO system. Moreover, the Fermi level entered the CB, leading to a band-tail effect, which is conducive to improving the doped system’s optical and electronic transport properties. The doping of Nd introduced strongly localized states in the CB, which were separately contributed by Nd-5d and Nd-4f electrons. The concentration of CB carriers increased, and electrons underwent degeneracy, showing n-type degenerate semiconductor characteristics. The doping of Nd primarily involved the hybridization of Nd-5d and Nd-4f states, which had a significant impact on the DOS at the VB top, forbidden band, and CB bottom of the doped system. The energy region (20 eV, -17.7 eV) had a primary contribution from O-2s, Zn-3d, and Nd-5p state electrons, (-14.2 eV, -10.9 eV) had a primary contribution from Zn-3d and O-2p state electrons, and (9.6 eV, -3.7 eV) had a primary contribution from Zn-3d, and O-2p state electrons. The impurity energy level of forbidden band had a primary contribution from Nd-4f state electrons. The CB’s localized state had a primary contribution from the hybridization of Nd-5d and Nd-4f state electrons. For Zn15Nd1O16 and Zn14Nd2O16 systems, the TDOS curves of the SU and SD orbitals were asymmetric, so the net spin density of states was not zero. The SU state of the Nd-4f state was completely occupied, while the SD state has empty below the Fermi level. The spin splitting was obvious. The Nd-4f state electrons had a net magnetic moment (MM), and the SU and SD orbitals of the O-2p state electrons were asymmetric, indicating that Nd-doped ZnO has obvious magnetic characteristics and electromagnetic transport capability.

3.4. Analysis of orbital charges

The Mulliken population analysis was used to describe the transfer of charge after bonding between atoms[22]. Under spin polarization conditions, the Mulliken charge distribution of i-ZnO and Nd-doped ZnO systems are depicted in Table 2. From the table, in i-ZnO, the Zn atom had a strong capacity to release electrons, resulting in a +0.93 positive charge, while the O atom had a strong capacity to gain electrons, resulting in -0.93 negative charge, primarily owing to the electronic transfer from Zn-4s state to O-2p state. Besides, in i-ZnO, the number of SU and SD electrons in each orbital of Zn was the same as that of O, indicating that i-ZnO was not magnetic, which is consistent with the band structure analysis finding in section 3.2 and the state density analysis finding in section 3.3.
In the Nd-doped ZnO system, the doped atom transforms into a center that is positively charged and has properties of donor impurities as a result of losing electrons. For the Zn15Nd1O16 system, the Nd atom lost electrons, resulting in a +1.05 positive charge, the Zn atom lost electrons, resulting in a +0.88 positive charge, while the O atom gained electrons, resulting in a -0.99 negative charge, due to the electronic transfer from Nd-6s and Nd-4f states to Zn-3p and O-2p states. For the Zn14Nd2O16 system, the number of electrons lost by two Nd atoms decreased, resulting in +1.01 and +0.87 positive charge in total, the number of electrons lost by Zn atoms increased, resulting in +0.92 positive charge, and the number of electrons obtained by O atoms correspondingly decreased, resulting in -0.88 negative charge. The distribution of O-2s and 2p electrons remained almost unchanged after Nd doping, indicating that the Nd-O chemical bond was relatively stable. The Nd atom has a higher number of positive charge, indicating that the Nd atom contributed more electrons due to the difference between the valence electron of Nd and that of Zn. Furthermore, the findings revealed that the charge numbers of spin-up and spin-down orbitals of Zn15Nd1O16 and Zn14Nd2O16 systems were different, demonstrating that Nd-doped ZnO materials were magnetic, which is in line with the band structure analysis finding in section 3.2 and state density analysis finding in section 3.3.

3.5. Analysis of population value and bond length

The population value and bond length (BL) of i-ZnO and Nd-doped ZnO systems were computed in this section for the purpose of more clearly illustrating the charge distribution, and Table 3 lists the calculation findings[23,24]. In contrast with the population value of i-ZnO’s Zn-O bond, the population values of Zn-Omax bonds between Zn and O atoms that are not directly connected to the Nd atom in Nd-doped ZnO system were smaller, and the BL was larger, demonstrating that the covalence was weaker. With the rise of doping concentration, the population value of Zn-Omax bonds decreased, and the BL increased, which weakened the covalence. The population value of Zn-Omin bonds was almost unchanged, the population values of Nd-O bonds parallel and perpendicular to the c-axis increased, and the BLs decreased, which weakened the covalence. This is consistent with the analysis outcomes of the lattice constant of the doped system in section 3.1 and indicates that the doped system’s lattice had distortion, and the centers of positive and negative charge were destroyed to produce a local potential difference that hindered hole-electron pair recombination and improved the photocatalytic performance of ZnO materials. This can be attributed to the fact that the doping of Nd atoms intensified the overlapping of electron shells between atoms, which accelerated electron transfer and enhanced the covalence. Further analysis shows that since the electronegativity of the doped Nd atom is lower than that of the Zn atom, and it is easier for the O atom to obtain electrons from the Nd atom, therefore the population of Nd-O bond in the doped system is lower, and the polarity of the Nd-O bond is stronger, compared with Zn-O bond.

3.6. Analysis of differential charge density

Under the spin polarization condition, the DCD distribution of Zn16O16, Zn15Nd1O16, and Zn14Nd2O16 on the plane of the doped Nd atom was calculated, and Figure 4 depicts the findings. The electron transfer between each atom is crystal clear. The pink electron cloud in the figure denotes electron dissipation, whereas the green electron cloud signifies electron aggregation. The scale bar’s red and blue colors represent electron gain and loss, respectively. More electrons are transferred, as shown by the darker color. The doping atoms had a greater effect on the surrounding O atoms’ electron cloud density in contrast to the electron cloud between the Zn atom and the O atom in i-ZnO, which improved the interaction. The electron cloud displayed a significant directionality since electrons lost by Nd gathered between Nd-O bonds. With the rise of Nd doping concentration, the Nd-O bond region’s electron transfer density increased, reflecting their chemical bond. The covalence of the Nd-O bond was weakened while the ionic property was enhanced. This is because of the weakening of the electron cloud overlap between Nd atoms and the surrounding O atoms in the doped system, which indicated that all the chemical bond of doped systems was primarily covalent, but with ionic bond components as well. Rare earth-doped ZnO was a semiconductor material with hybrid bonds, which is consistent the population value and BL analysis findings in section 3.5.

3.7. Optical properties

The semiconductors’ optical properties have a strong link to the electronic structure. The bulk materials’ optical properties are typically examined in the linear response region employing the dielectric functions (DFs). Thus, the DFs, absorption coefficients, reflectivities, and energy loss functions (ELFs) were calculated to systematically analyze the influence of the doping of Nd on the optical properties of ZnO. In accordance with the description of direct transition probability and Kramers-Kronig dispersion relation, the imaginary part ε 2 ( ω ) and real part ε 1 ( ω ) of the crystal DF, absorption coefficient, reflectivity, and ELF can be derived and the results are presented below (See Refs. [25-27] for detailed derivation process):
ε ( ω ) = ε 1 ( ω ) + i ε 2 ( ω )
ε 2 ( ω ) = π ε 0 ( e m ω ) 2 ⋅ ∑ V , C { ∫ B Z 2 d K → ( 2 π ) 3 | a → ⋅ M → V , C | 2 δ [ E C ( K → ) − E V ( K → ) − ℏ ω ] }
ε 1 （ ω ） = 1 + 2 e ε 0 m 2 ⋅ ∑ V , C ∫ B Z 2 d K → ( 2 π ) 3 | a → ⋅ M → V , C ( K → ) | 2 [ E C ( K → ) − E V ( K → ) ] / ℏ ⋅ 1 [ E C ( K → ) − E V ( K → ) ] 2 / ℏ 2 − ω 2
R ( ω ) = ( n − 1 ) 2 + k 2 ( n + 1 ) 2 + k 2
α ≡ 2 ω κ c = 4 π κ λ 0
L ( ω ) = I m ( − 1 ε ( ω ) ) − ε 2 2 ( ω ) ε 1 2 ( ω ) + ε 2 2 ( ω )
where, ε 0 is the vacuum’s dielectric constant, λ 0 is the vacuum’s wavelength, ℏ is the Planck constant, C and V are the CB and VB, respectively, BZ denotes the first Brillouin zone, K → is the electron wave vector, a is the unit direction vector of the vector potential A , M V , C is the transition matrix’s element, ω is the electromagnetic frequency, R ( ω ) is the reflectivity, E C ( K ) and E V ( K ) are the intrinsic energy level of the CBs and VBs, respectively, L ( ω ) is the ELF and α is the absorption coefficient.
The DF curves of i-ZnO and Nd-doped ZnO systems are depicted in Figure 5. Figure 5 (a) presents the curves of the DF’s real part. The average static dielectric constant of i-ZnO, Zn15Nd1O16, and Zn14Nd2O16 were 3.21, 5.58, and 10.70, respectively. in contrast with i-ZnO, the dielectric constants of these doped systems all increased, indicating that Nd doping enhanced the polarization of the system and prolonged the lifetime of photoelectrons in the CB, indicating that Nd doping improved the photocatalytic performance of the system. With the rise of the doping concentration, the photocatalytic performance was enhanced. The average static dielectric constant of the Zn14Nd2O16 system was the largest, demonstrating that its photocatalytic activity was the best.
The curves of the DF’s imaginary part are depicted in Figure 5 (b). Four dielectric peaks were visible in the imaginary part of the i-ZnO’s DF. The first peak positioned at 5.82 eV was primarily caused by electronic transitions from the O-2p state at the VB’s top to the Zn-4s state at the CB’s bottom. The second peak positioned at 9.15 eV was primarily owing to electronic transitions from Zn-3d and O-2s states in the VB far away from the Fermi surface to O-2p and Zn-3d states at the VB’s top. The third peak positioned at 13.33 eV was primarily derived from the electronic transitions from the Zn-3d, O-2s, and O-2p states in the VB away from the Fermi surface to the Zn-4s state at the CB’s bottom. The fourth peak positioned at 15.71 eV was primarily attributed to the electronic transitions from O-2s, Zn-3d, and Zn-4s states in the VB far away from the Fermi surface to the O-2p state at the VB’s top. After Nd doping, a new peak near 0.7 eV emerged, primarily owing to the electronic transitions from the impurity levels in the bandgap to the CB’s bottom. According to the PDOS in Figure 3, in the Nd-doped ZnO system, the first peak was primarily produced by the electronic transitions from the impurity level of the Nd-4f state coinciding with the Fermi surface to the Zn-4s state at the CB’s bottom. With the increase in doping concentration, the peak value and the transition probability increased. Compared to i-ZnO, the peaks around 5.82 eV and 9.15 eV of Nd-doped ZnO systems were shifted towards the high energy direction (blueshift), with an increased peak value. The peaks near 13.33 eV and 15.71 eV were shifted towards the low energy direction (redshift), with a decreased peak value.
The absorption and reflection spectra of i-ZnO and Nd-doped ZnO systems are presented in Figure 6. Figure 6(a) displays the absorption spectra that were calculated using equations (6). The absorption coefficient was 105 cm-1, and the absorption edge of i-ZnO located around 3.30 eV denoted the onset of intrinsic absorption, which investigates the important ZnO’s optical properties. The absorption coefficient undergoes a sharp enhancement in the order of 105 with the rise of photon energy, meaning strong optical absorption occurred. The direct transition began, and the absorption edge of Nd-doped ZnO moved towards the high energy direction, resulting in a blueshift. This was induced by the introduction of several carriers (electrons) by donor atoms of Nd. In addition, the Fermi level entered the CB, leading to the Burstein-Moss effect [28, 29]. In the visible region (1.63 eV-3.10 eV), the i-ZnO’s optical absorption was extremely marginal and almost non-existent, while the Nd-doped ZnO system’s optical absorption was significantly enhanced. This was ascribed to the formation of a deep impurity energy level partially coinciding with the Fermi level in the forbidden band after doping, which significantly improved the photocatalytic performance of ZnO. The optical absorption intensity of Zn14Nd2O16 was the greatest, signifying that the photocatalytic activity of this system was the best. The maximum optical absorption intensity was achieved at around 16.7 eV. Compared with i-ZnO, the maximum light absorption peak was shifted towards the low energy direction, resulting in an obvious redshift. As the doping concentration increased, the redshift phenomenon became more pronounced, expanding the infrared absorption range of ZnO. On the basis of the PDOS diagram in Figure 3, the maximum absorption peak was produced by electronic transitions from the O-2s state in the deep VB to the CB’s bottom.
Figure 6 (b) shows the curves for the reflectivity of i-ZnO and Nd-doped ZnO systems, which were determined using equations (5). The static reflectivity R (0) of i-ZnO was 0.08, while R (0) of Zn15Nd1O16 and Zn14Nd2O16 were 0.17 and 0.29, respectively. In the range of 16 eV to 20 eV, the reflectivity was high. For i-ZnO, the highest reflectivity of 0.24 was reached at 17.2 eV. The highest reflectivity was 0.25 at 17.4 eV for Zn15Nd1O16 and 0.22 at 16.5 eV for Zn14Nd2O16. The maximum reflectivity of i-ZnO and Nd-doped ZnO systems appeared in the ultraviolet region, and the magnitude was approximately 0.2. With the rise of Nd doping concentration, the reflectivity peak decreased; the reflectivity peak of the single-Nd-doped ZnO system was larger than that of i-ZnO, and the peak underwent a blueshift; and the reflectivity peak of dual-Nd-doped ZnO system was less than that of i-ZnO, and the peak underwent a redshift. In the low-energy region, the reflectivity of the Nd-doped system was higher than that of i-ZnO. Some photons are reflected, some are absorbed, and the remaining portion is transmitted through the substance as they travel through it. Therefore, , the absorption coefficient and reflectivity increased in the region of low energy for Nd doped ZnO, and decreased the transmittance. However, the absorption coefficient and reflectivity decreased in the high-energy region, while the transmittance increased in the ultraviolet region.
Figure 7 (a) shows the PC for i-ZnO and Nd-doped ZnO systems, corresponding to the imaginary part ε 2 ( ω ) of DFs (Figure 5 (b)). In the range of 10 eV to 20 eV, i-ZnO and Nd-doped ZnO systems showed high conductivity, and the PC reached its maximum value near 15 eV. The peak values of i-ZnO, Zn15Nd1O16 and Zn14Nd2O16 were 7.71 fs-1, 6.47 fs-1, and 5.72 fs-1, respectively. In the visible region, the PC of i-ZnO and Nd-doped ZnO systems increased with the rise of the energy of incident photons. Comparing the peak PC of all systems in the low energy region, the PC of the Nd-doped ZnO system was larger compared to that of i-ZnO, which was owing to the increase of the electron density of Nd-4f state at the doped system’s Fermi level, resulting in the increase of the PC in the region of low energy. However, the PC of all systems was small, and as the number of Nd atoms increased, the peak was shifted to the left, indicating that Nd doping improved the PC of ZnO semiconductors in the visible region.
Figure 7(b) displays the ELF of i-ZnO and Nd-doped ZnO systems. The plasma frequencies of i-ZnO, Zn15Nd1O16, and Zn14Nd2O16 were 40.29 eV, 39.10 eV, and 36.08 eV, respectively. With the rise of Nd doping concentration, the peak value was redshifted, and the intensity was weaker than that of the i-ZnO system.

3.8. Magnetic. properties

Rare earth elements have large MM and strong orbital anisotropy, and can possibly improve the magnetic properties of doped ZnO semiconductors. According to Dhar et al. [30], Gd-doped GaN has a huge MM, and it is envisaged that the coupling between the 4f state electrons of rare earth ions and the host’s electrons can produce stable ferromagnetism, which was conducive to the study of ZnO magnetism. ZnO consists of a large number of s electrons and presents n-type conductivity. By using the spin polarization computational method, we calculated the magnetic coupling and total MM of the intrinsic and Nd-doped ZnO systems (Table 4), as well as the atomic MM and orbital MM (Table 5). Analysis shows that the total MM of i-ZnO was equal to 0 μB, indicating that the Zn16O16 system was non-magnetic, which has consistency with the band structure analysis finding in section 3.2 and the state density analysis result in section 3.3. The sum of the absolute values of MM of the Nd-doped ZnO system was not equal to zero, demonstrating that the doped system was magnetic. The total MM of Zn15Nd1O16 and Zn14Nd2O16 systems were 3.75 μB and 5.97 μB, respectively, and with the rise of concentration of Nd doping, the total MM of the doped system increased, showing obvious ferromagnetism.
From Table 5 and referring to Figure 1(b) and (c) for the atomic positions, in Zn15Nd1O16, the atomic MM of the Nd atom was 3.79 µB, the orbital MM of Nd-4f, Nd-4d, and Nd-5s orbitals were 3.67 µB, 0.07 µB, and 0.06 µB, respectively, the atomic MM of surrounding Zn atoms was about 0.01 µB, the orbital MM of Zn-4s orbital was about 0.01 µB, the atomic MM of surrounding O atoms was about -0.03 µB, the orbital MM of O-2s and O-2p orbitals was about -0.01 µB and -0.02 µB, respectively; in Zn14Nd2O16, the atomic MM of two Nd atoms were 3.06 µB and 3.08 µB, respectively, the orbital MM of Nd-4f and Nd-4d orbitals were 2.96 µB, 0.07 µB, respectively, the atomic MM with a single surrounding Zn atom was about -0.01 µB, the orbital MM of Zn-4s orbital was about -0.01 µB, the atomic MM of O atom was about -0.02 µB, the orbital MM of O-2s and O-2p orbitals were about -0.01 µB and -0.01 µB, respectively. We concluded that the total MM of Zn15Nd1O16 had a primary contribution from Nd-4f, Nd-4d, and Nd-5s orbitals, as well as O-2s, O-2p, and Zn-4s orbitals near Nd atoms, while the magnetism of Zn14Nd2O16 primarily came from the coupling between two Nd atoms and O atoms, wherein Nd-4f orbital contributed the most. Additionally, it was found that the coupling between Nd and Zn was FM, and the coupling between Nd and O was AFM.
The above conclusions indicate that the magnetism of the Nd-doped ZnO system originated from the double exchange mechanism caused by orbital-spin interaction[31-33], that is, the anisotropic exchange of Nd atoms. In addition, according to the Goodenough-Kanamori rule, since Nd-4f orbital is in a semi-full state, its ferromagnetism is significant [34, 35], and the electrons of Nd-4f orbital are localized electrons that contribute to magnetism, and these localized electrons couple with the conductive electrons in surrounding orbitals such as Zn-3p, O-2s, and O-2p orbitals, and conductive electrons are spin-polarized, resulting in different densities of the SU and SD electrons, thus the spin polarization direction of electrons in Nd-4f orbital is determined and spin transport is realized. Therefore, Nd-doped ZnO systems show FM characteristics, which can be further verified by the partial-wave density analysis of the doped system.
To reveal the Nd doping effect on the ZnO’s magnetic properties more intuitively, the diagram of TDOS in Figure 3 was analyzed. Figure 3 (a) shows that the value of the net DOS of i-ZnO was 0, and the curves of the SU and SD TDOS of i-ZnO are absolutely symmetrical, demonstrating that i-ZnO is non-magnetic. Figure 3(b) and (c) present that the values of the DOS of Zn15Nd1O16 and Zn14Nd2O16 systems were not zero, indicating that the curves of the SU and SD TDOS of the Nd-doped ZnO systems were not completely symmetrical. There was a variation in the number of electrons in the SU and SD directions, demonstrating that the doped system had a net MM, which is consistent with the analysis findings of the total MM. Further analysis of the PDOS in Figure 8 shows that the magnetism of Zn15Nd1O16 and Zn14Nd2O16 was derived from the spin exchange of Nd-4f, Nd-4d, Zn-4s, and Zn-3p states at the CB’s bottom, and the spin exchange of Nd-4f, Nd-4d, and O-2p states at the VB’s top and was caused by the strong hybridization of Nd-4f, Nd-4d, O-2p, Zn-4s, and Zn-3p states near Fermi surface. Among them, the Nd-4f state showed the most notable spin-splitting phenomenon. With the increase of Nd doping concentration, the spd-f hybridization became more intense, and the spin polarization phenomenon became more pronounced, indicating that the net MM was larger.
Since Zn15Nd1O16 and Zn14Nd2O16 systems all exhibited ferromagnetism, indicating that the electrons in such systems underwent spin polarization. Spin polarizability p is generally considered the variation between the DOS of majority carriers ( N ↑ ) and the normalized DOS of minority carriers ( N ↓ ) at the Fermi surface [36].
p = N ↑ − N ↓ N ↑ + N ↓
The spin polarizability and the magnetization strength M have the following relationship,
M = μ B ∫ ( N ↑ − N ↓ ) d E
where µB is the Bohr magneton.
Then, we have
p ∝ M
Further the TDOS near the Fermi surface in Figure 8, the number of majority carriers N ↑ at the Fermi surface in Zn15Nd1O16 and Zn14Nd2O16 > 0, while that of minority carriers N ↓ was almost 0, so the spin polarizability was close to 100%. The number of majority carriers N ↑ above the Fermi surface in Zn14Nd2O16 > 0, while that of minority carriers N ↓ was close to 0, so the spin polarizability was less than 100%, indicating that Nd-doped ZnO systems had dilute magnetic semiconductor (DMS) properties.
The net spin density distributions of Zn15Nd1O16 and Zn14Nd2O16 systems were computed, and the findings are presented in Figure 9. The blue signifies the positive spin-charge density, and the yellow signifies the negative spin-charge density, with a unit of ± 0.008 e/Å. Nd atom and its nearby O atoms were AFM coupled, while the Nd atom and its nearby Zn atoms were FM coupled, indicating that the total MM of the doped system had primary contribution from spin-polarized Nd atom(s) and surrounding spin-polarized Zn and O atoms, which has consistency with the findings of atomic and orbital MM analysis.

4. Conclusion

Based on DFT, the electronic, optical, and magnetic properties of Nd-doped ZnO were investigated by the GGA+U method with spin polarization conditions. The findings of the electronic structure revealed that the cell parameters of Nd-doped ZnO systems became larger, the volume became larger, the formation energy was less than zero, and the Nd atoms were more easily doping into the ZnO materials. But the bandgap of Nd-doped ZnO decreased, and the impurity energy level introduced high-concentration carriers and degenerates. Fermi level entered the CB, presenting the features of n-type degenerate semiconductors. The calculation findings of optical properties showed that the impurity energy level and Fermi level generated in the forbidden band of Nd-doped ZnO partially overlapped, and the trap effect was significant, which effectively prevented the recombination of electron-hole pairs. The photogenerated electron transition was completed in a multistage process. In the visible region, the absorption spectrum was obviously redshifted and its intensity was significantly enhanced, which effectively improved the photocatalytic performance. In the strongest absorption region, with the rise of doping concentration, the absorption spectrum underwent a redshift, expanding the infrared absorption range. The calculation results of magnetic properties indicated that Nd-doped ZnO systems were FM, and the coupling was FM. Magnetism was primarily caused by strong spd-f hybridization due to the magnetic exchange between the Nd-4f state and O-2p, Zn-4s, and Zn-3p states. Therefore it could be a preferred material for DMS spintronic devices.

Author Contributions

Fuchun Zhang and Suqin Xue provided funding for the study, supervised the research team, reviewed and approved the manuscript prior to submission. Qiao Wu conceived and designed the study, caculated and analyzed the data, wrote the original manuscript. Gaihui Liu, Huihui Shi, Bohang Zhang, Jing Ning and Tingting Shao collected and analyzed the data, and revised manuscript. All authors were involved in the study design, data analysis and interpretation, and manuscript revision.

Funding

This research was funded by the National Natural Science Foundation of China (No.62264015).

Institutional Review Board Statement

This work is not involving humans or animals.

Data Availability Statement

All data are presented in the form of charts in the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Liu, C.; Yun, F.; Morkoc, H.; et al. Ferromagnetism of ZnO and GaN: A Review. Science: Materials in Electronics. 2005, 16, 555–597. [Google Scholar] [CrossRef]
  2. Zutic, I.; Fabian, J.; Sarma, S.D. Spintronics: fundamentals and applications. Reviews of Modern Physics. 2004, 76, 323–410. [Google Scholar] [CrossRef]
  3. Dietl, T.; Ohno, H.; Matsukura, F.; et al. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors. Science. 2000, 287, 1019–1022. [Google Scholar] [CrossRef] [PubMed]
  4. Larabi, A.; Mebarki, M.; Sari, A.; et al. Chromium and hydrogen doping effects on magnetic and electronic properties of ZnO. Journal of Magnetism and Magnetic Materials. 2018, 446, 192–199. [Google Scholar] [CrossRef]
  5. Foster, G.M.; Faber, G.; Yao, Y.F.; et al. Direct measurement of defect and dopant abruptness at high electron mobility ZnO homojunctions. Applied Physics Letters. 2016, 109, 143506. [Google Scholar] [CrossRef]
  6. Wang, Y.R.; Piao, J.Y.; Lu, Y.H.; et al. Intrinsic ferromagnetism in Sm doped ZnO. Materials Research Bulletin. 2016, 83, 408–413. [Google Scholar] [CrossRef]
  7. Xu, X.Y.; Wang, L.M.; Fu, J.J.; et al. Preparation and doping of flower-like nano ZnO and its photocatalytic degradation of reactive dye. China Dyeing & Finishing. 2021, 47, 47–51. [Google Scholar]
  8. Sharma, D.K.; Sharma, K.K.; Kumar, V.; et al. Effect of Ce doping on the structural, optical and magnetic properties of ZnO nanoparticles. Journal of Materials Science: Materials in Electronics. 2016, 27, 10330–10335. [Google Scholar] [CrossRef]
  9. Wen, J.Q.; Zhang, J.M.; Qiu, Z.G.; et al. The investigation of Ce doped ZnO crystal: The electronic, optical and magnetic properties. Physica B: Condensed Matter. 2018, 534, 44–50. [Google Scholar] [CrossRef]
  10. Liu, Y.; Hou, Q.; Sha, S.; Xu, Z. Electronic structure, optical and ferromagnetic properties of ZnO co-doped with Ag and Co according to First-principles calculations. Vacuum. 2020, 173, 109127. [Google Scholar] [CrossRef]
  11. Mka, B.; Nfb, D.; Haem, C.; et al. First-principles calculations of rare earth (RE=Tm, Yb, Ce) doped ZnO: structural, optoelectronic, magnetic, and electrical properties. Vacuum. 2020, 181, 109603. [Google Scholar] [CrossRef]
  12. Zhang X. J., B W, et al. First-principles prediction of electronic structure and magnetic ordering of rare-earth metals doped ZnO. Journal of Alloys and Compounds. 2014, 617, 828–833. [CrossRef]
  13. Pham, A.; Assadi MH, N.; Yu, A.B.; et al. Critical role of Fock exchange in characterizing dopant geometry and magnetic interaction in magnetic semiconductors. Physical Review B. 2014, 89, 155110. [Google Scholar] [CrossRef]
  14. Segall, M.D.; Lindan PJ, D.; Probert, M.J.; et al. First-principles simulation: ideas, illustrations and the CASTEP code. Phys Condens Matter. 2002, 14, 2717. [Google Scholar] [CrossRef]
  15. Hamann, D.R.; Schlüter, M.; Chiang, C. Norm-Conserving Pseudopotentials. Physical Review Letters. 1979, 43, 1494–1497. [Google Scholar] [CrossRef]
  16. Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Physical Review B. 2005, 71, 035105. [Google Scholar] [CrossRef]
  17. Reeber, R.R. Lattice parameters of ZnO from 4.2°to 296°K. Journal of Applied Physics. 1970, 41, 5063. [Google Scholar] [CrossRef]
  18. Li, F.; Zhang, C.W.; Zhao, M.W. Magnetic and optical properties of Cu-doped ZnO nanosheet: First-principles calculations. Physica E: Low-dimensional Systems and Nanostructures. 2013, 53, 101–105. [Google Scholar] [CrossRef]
  19. Ma, X.; Miao, L.; Bie, S.; et al. Synergistic effect of V/N-codoped anatase TiO2 photocatalysts. Solid State Communications. 2010, 150, 689–692. [Google Scholar] [CrossRef]
  20. Long, R.; English, N.J. First-principles calculation of nitrogen-tungsten codoping effects on the band structure of anatase-titania. Applied Phresics Letters. 2009, 94, 132102. [Google Scholar] [CrossRef]
  21. Hou, Q.Y.; Guo, S.Q.; Zhao, C.W. First-principle study of the effects of oxygen vacancy on the electronic structure and the absorption spectrum of ZnO. Acta Physica Sinica. 2014, 63, 1–6. [Google Scholar] [CrossRef]
  22. Wu, H.C.; Chen, H.H.; Zhu, R. Effects of Al-impurity type on formation energy, crystal structure, electronic structure, and optical properties of ZnO by using density functional theory and the hubbard-U method. Materials. 2016, 9, 647. [Google Scholar] [CrossRef] [PubMed]
  23. Sun, C.Q. Oxidation electronics: bond-band-barrier correlation and its applications. Progress in Materials Science. 2003, 48, 521–685. [Google Scholar] [CrossRef]
  24. Segall, M.D.; Pickard, C.J.; Shah, R.; et al. Population analysis in plane wave electronic structure calculations. Molecular Physics. 1996, 2, 571–577. [Google Scholar] [CrossRef]
  25. Huang, K. Solid physics; Higher Education Press: Beijing, 2002. (in Chinese) [Google Scholar]
  26. Fang, R.C. Solid State spectroscopy; University of Science and Technology of China Press: Hefei, 2001. (in Chinese) [Google Scholar]
  27. Shen, X.C. Spectra and optical properties of semiconductors second edition; Science Press: Beijing, 2002. (in Chinese) [Google Scholar]
  28. Fang, R.C. Solid state spectroscopy; University of Science and Technology of China Press: He fei, 2001; p. 68. [Google Scholar]
  29. Shen, X.C. Semiconductor spectroscopy and optical properties. Science Press: Beijing, 2002; pp. 140–141. [Google Scholar]
  30. Dhar, S.; Brandt, O.; et al. Colossal magnetic moment of Gd in GaN. Physical Review Letters. 2005, 94, 037205. [Google Scholar] [CrossRef] [PubMed]
  31. Ruderman, M.A. KittelC Indirect exchange coupling of nuclear magnetic moments by conduction electrons. Physical Review. 1954, 96, 99–102. [Google Scholar] [CrossRef]
  32. Kasuya, T. A theory of metallic ferro- and antiferromagnetism on Zener’s model. Progress of Theoretical Physics. 1956, 16, 45–57. [Google Scholar] [CrossRef]
  33. Miyazaki, M.; Sato, K.; Mitsui, A.; et al. Properties of Ga-doped ZnO films. Journal of Non-Crystalline Solids. 1997, 218, 323–328. [Google Scholar] [CrossRef]
  34. Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. Journal of Physics and Chemistry of Solids. 1959, 10, 87–98. [Google Scholar] [CrossRef]
  35. Goodenough, J.B. An interpretation of the magnetic properties of the erovskite-type mixed crystals La1−xSrxCoO3−λ. Journal of Physics and chemistry of Solids. 1958, 6, 287–297. [Google Scholar] [CrossRef]
  36. Sun, Z.; Wang, Q.; Douglas, J.F.; et al. Minority-spin t2g states and the degree of spin polarization in ferromagnetic metallic La2-2xSr1+2xMn2O7 (x=0. 38). Scientific Reports. 2013, 3, 3167. [Google Scholar] [CrossRef] [PubMed]
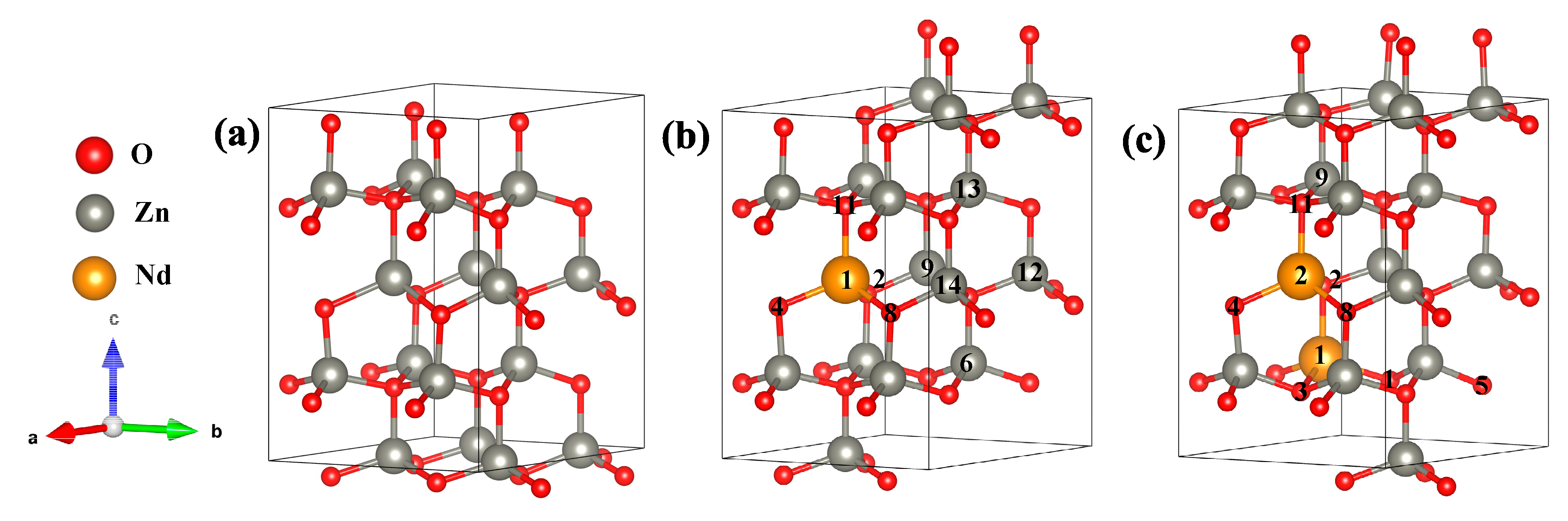
Preprints 86428 g001
Figure 1. Calculation model of (a) Zn16O16, (b) Zn15Nd1O16, and (c) Zn14Nd2O16.
Figure 1. Calculation model of (a) Zn16O16, (b) Zn15Nd1O16, and (c) Zn14Nd2O16.
Preprints 86428 g001
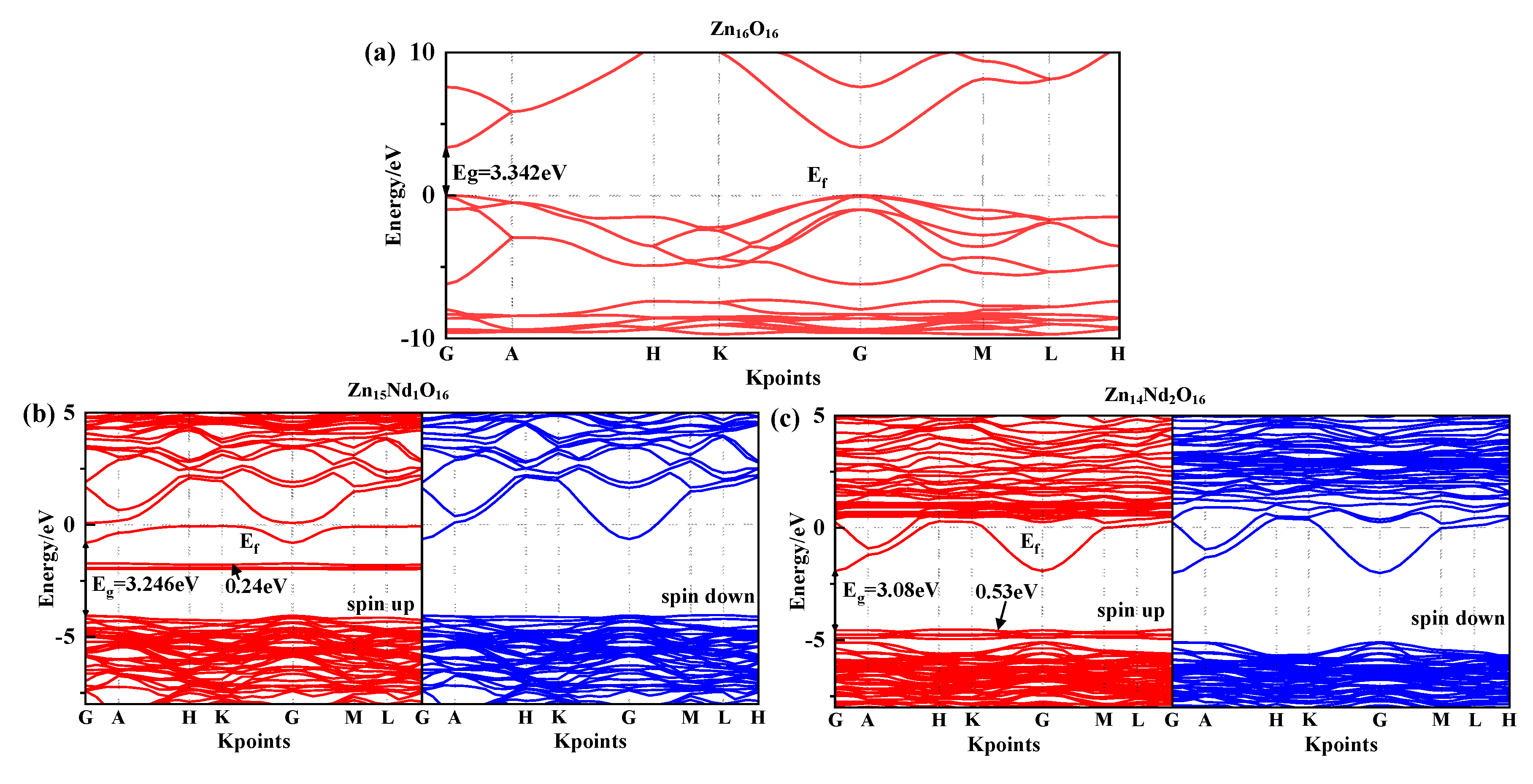
Preprints 86428 g002
Figure 2. Energy band structure near Fermi surface of (a) Zn16O16, (b) Zn15Nd1O16, and (c) Zn14Nd2O16.
Figure 2. Energy band structure near Fermi surface of (a) Zn16O16, (b) Zn15Nd1O16, and (c) Zn14Nd2O16.
Preprints 86428 g002
Preprints 86428 g003
Figure 3. Density of states (DOS) of (a) Zn16O16, (b) Zn15Nd1O16, and (c) Zn14Nd2O16.
Figure 3. Density of states (DOS) of (a) Zn16O16, (b) Zn15Nd1O16, and (c) Zn14Nd2O16.
Preprints 86428 g003
Preprints 86428 g004
Figure 4. Differential charge density diagrams of (a) Zn16O16, (b) Zn15Nd1O16, and (c) Zn14Nd2O16.
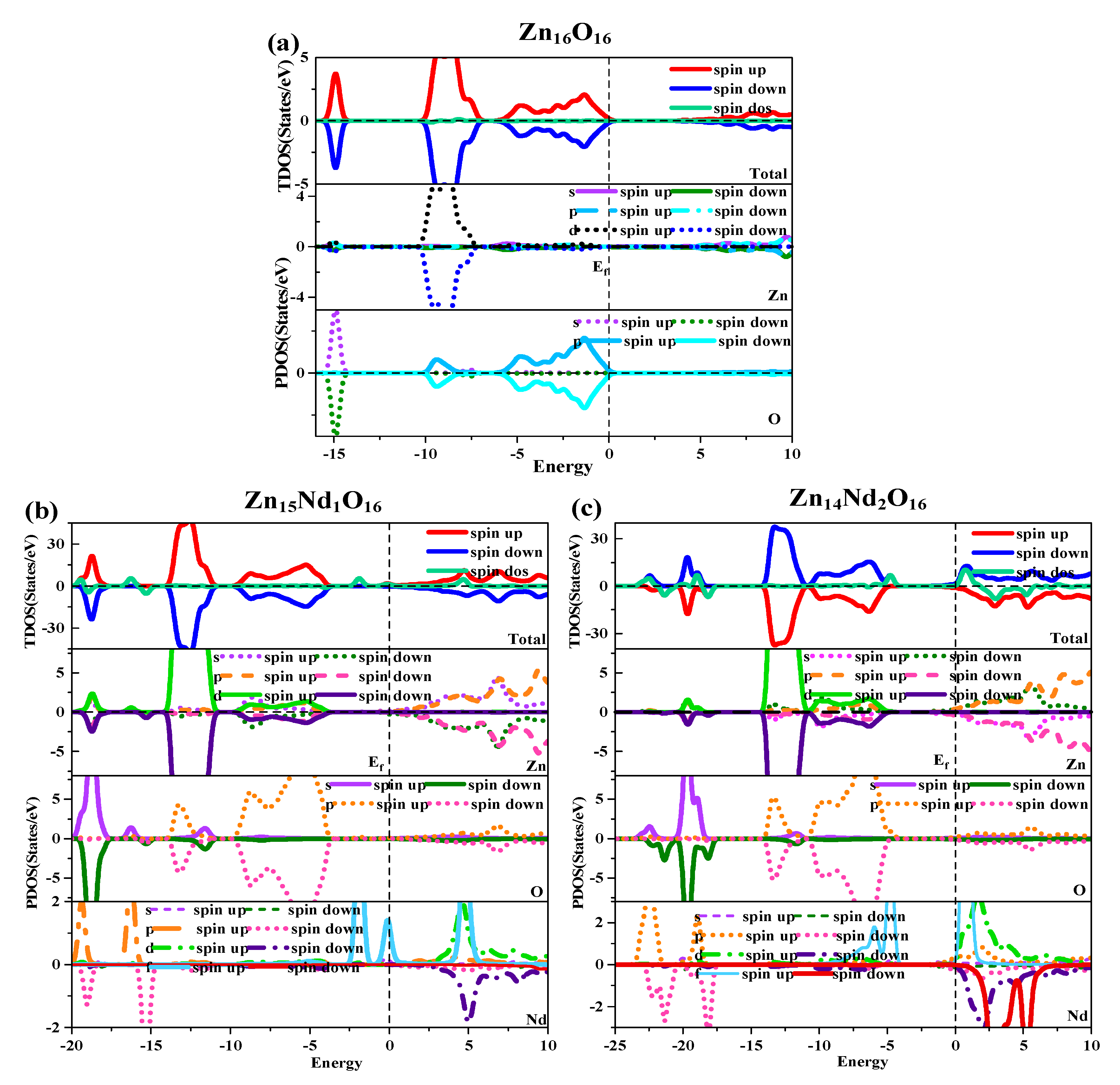
Figure 4. Differential charge density diagrams of (a) Zn16O16, (b) Zn15Nd1O16, and (c) Zn14Nd2O16.
Preprints 86428 g004
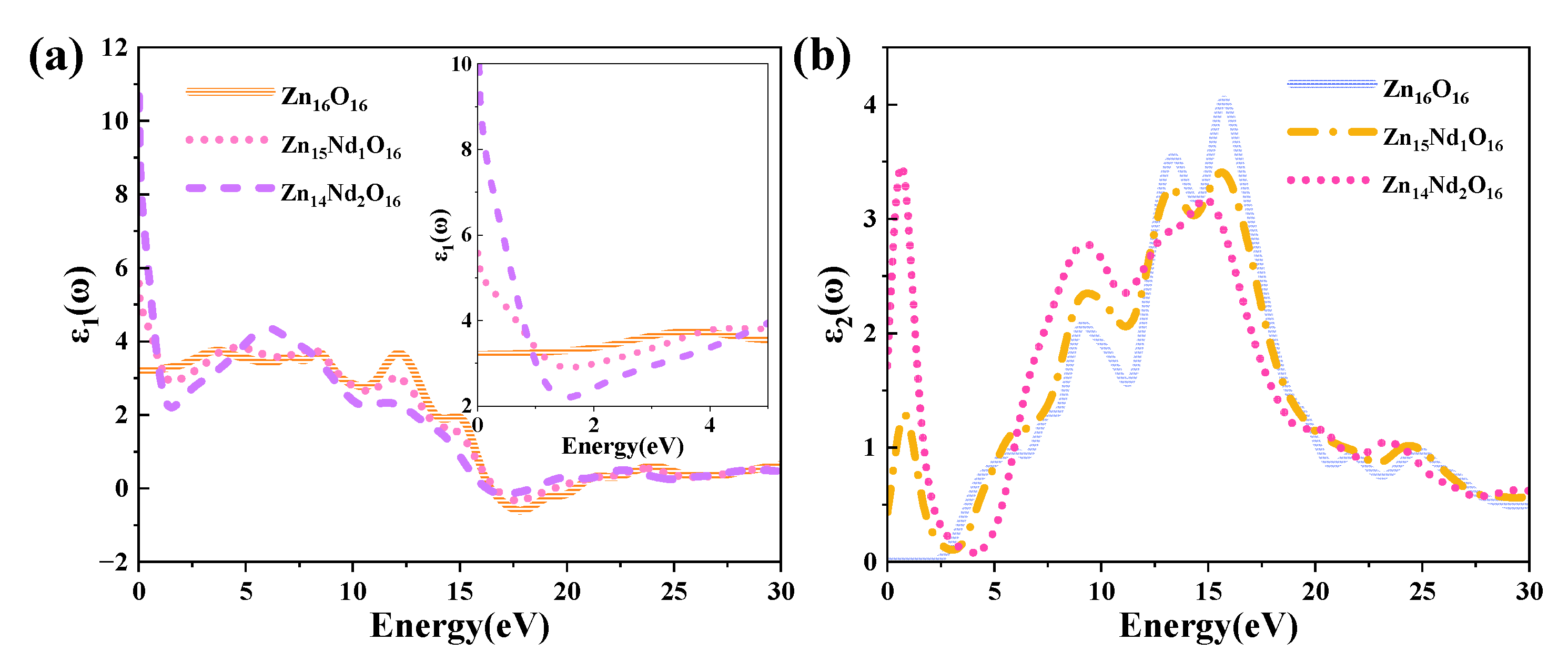
Preprints 86428 g005
Figure 5. (a) Real part, and (b) Imaginary part of the dielectric function.
Figure 5. (a) Real part, and (b) Imaginary part of the dielectric function.
Preprints 86428 g005
Preprints 86428 g006
Figure 6. (a) Absorption spectrum, (b) Reflectivity.
Figure 6. (a) Absorption spectrum, (b) Reflectivity.
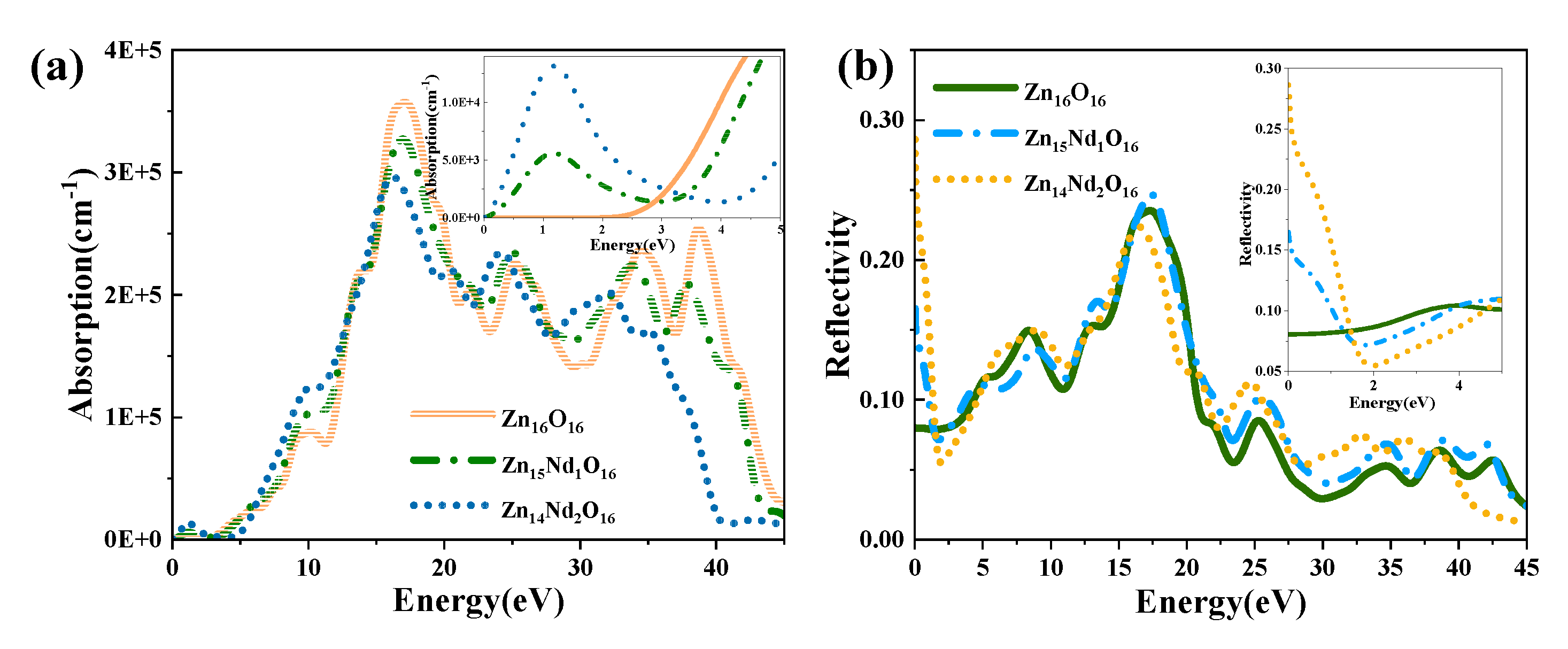
Preprints 86428 g006
Preprints 86428 g007
Figure 7. (a) Photoconductivity. (b) Energy loss function.
Figure 7. (a) Photoconductivity. (b) Energy loss function.
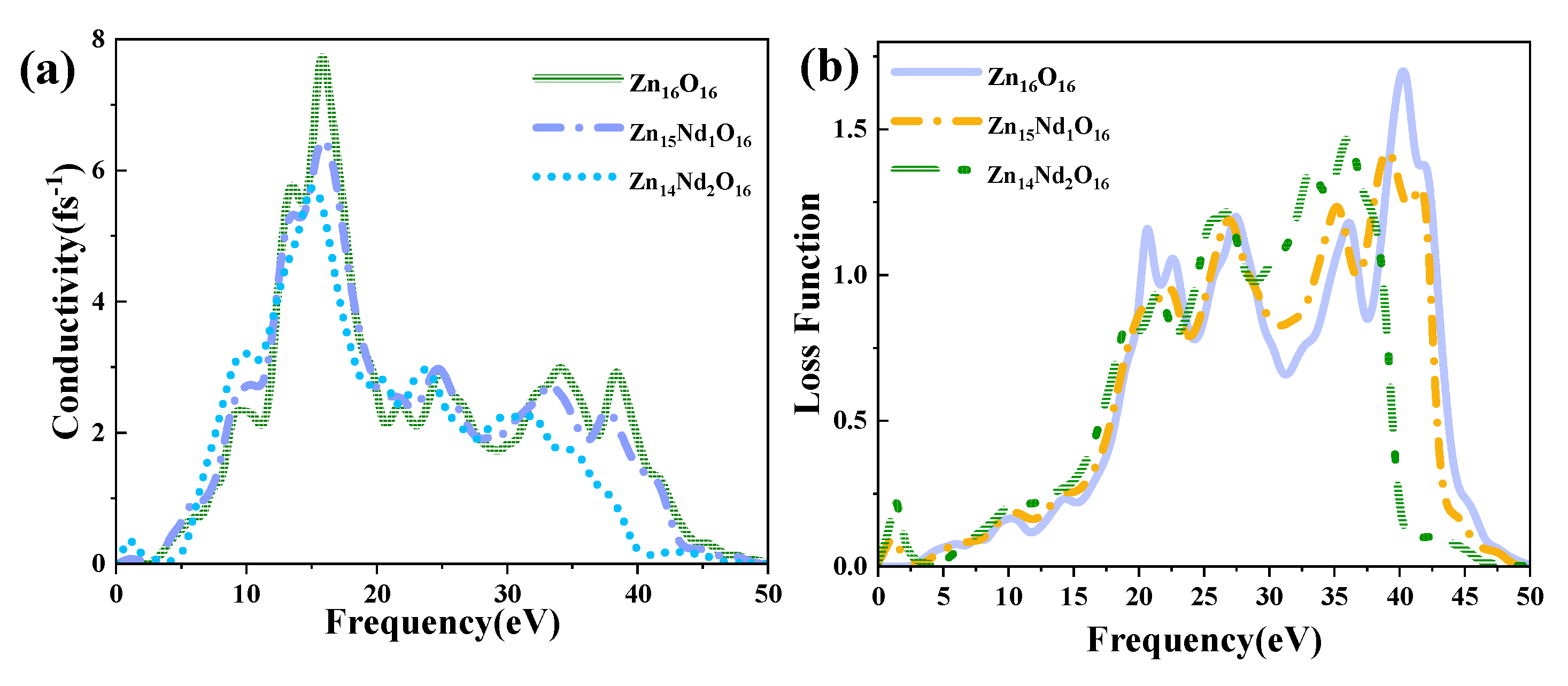
Preprints 86428 g007
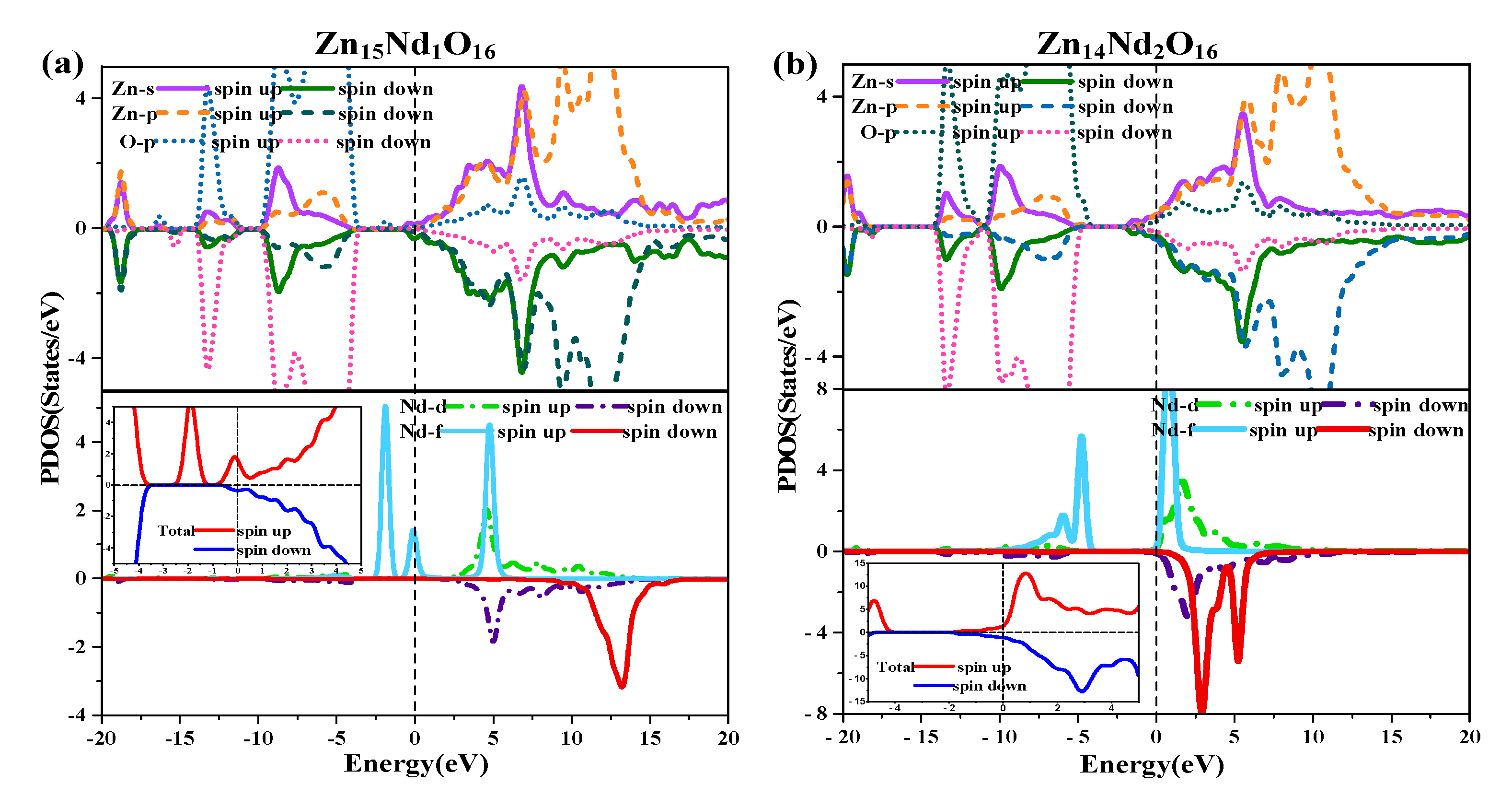
Preprints 86428 g008
Figure 8. Spin wave state densities of (a) Zn15Nd1O16, and (b) Zn14Nd2O16.
Figure 8. Spin wave state densities of (a) Zn15Nd1O16, and (b) Zn14Nd2O16.
Preprints 86428 g008
Preprints 86428 g009
Figure 9. Net spin density distributions of (a) Zn15Nd1O16, and (b) Zn14Nd2O16.
Figure 9. Net spin density distributions of (a) Zn15Nd1O16, and (b) Zn14Nd2O16.
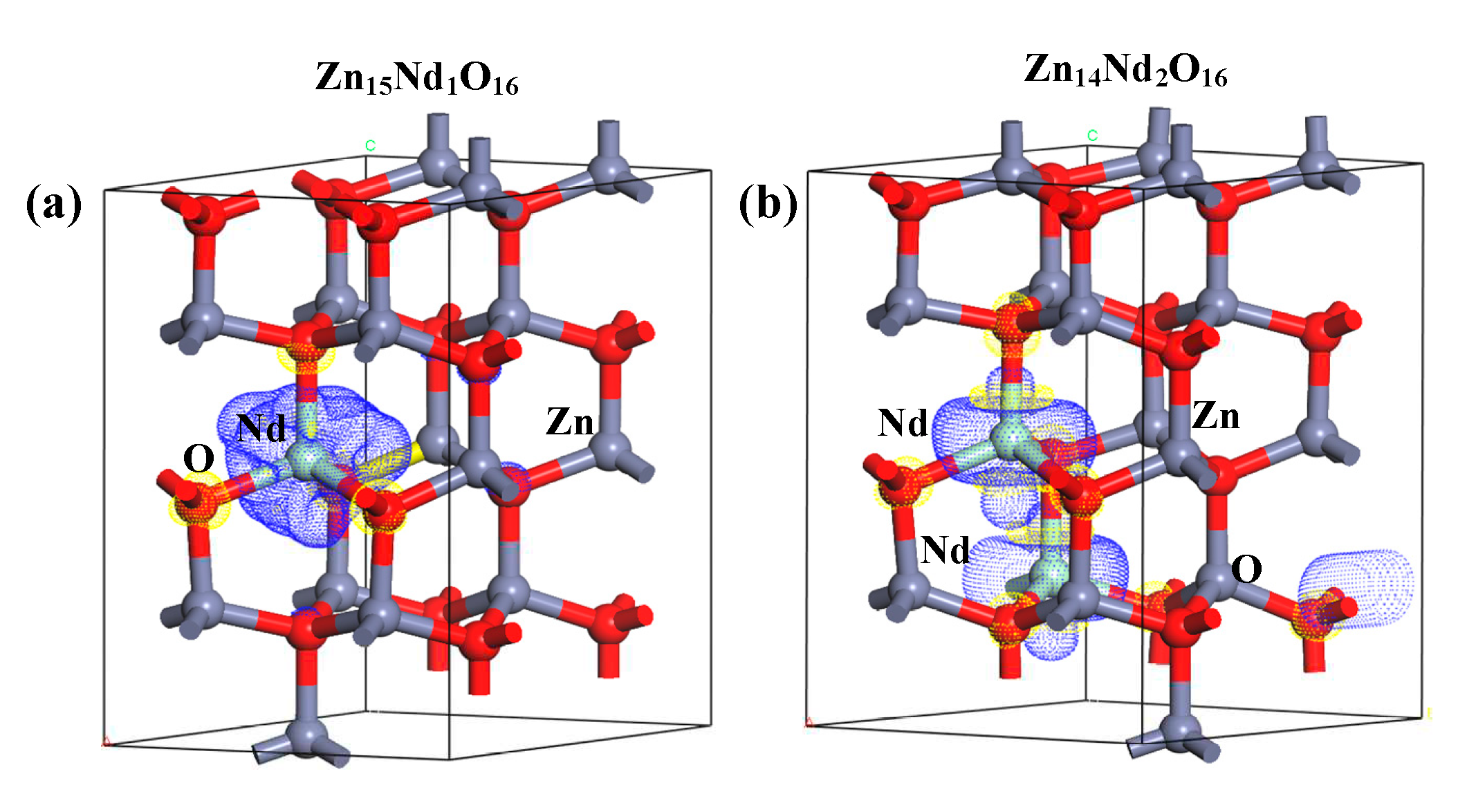
Preprints 86428 g009
Table 1. Cell parameters and formation energies of intrinsic and Nd-doped ZnO systems after structural optimization.
Table 1. Cell parameters and formation energies of intrinsic and Nd-doped ZnO systems after structural optimization.
Model a/Å b/Å c/Å V/ Å3 Ef/eV
Zn16O16 6.538 6.454 10.544 390.305 -
Zn15Nd1O16 6.553 6.552 10.558 392.537 -0.78
Zn14Nd2O16 6.612 6.630 10.674 404.854 -0.8
Table 2. Mulliken charge distribution of intrinsic ZnO and Nd-doped ZnO systems.
Table 2. Mulliken charge distribution of intrinsic ZnO and Nd-doped ZnO systems.
Model Atom S p d f Total /eV Net charge/e
Zn16O16 Zn(SU) 0.20 0.34 4.99 0.00 5.54 0.93
Zn(SD) 0.20 0.34 4.99 0.00 5.54 -
O(SU) 0.92 2.55 0.00 0.00 3.46 -0.93
O(SD) 0.92 2.55 0.00 0.00 3.46 -
Zn15Nd1O16 Zn(SU) 0.20 0.38 4.99 0.00 5.57 0.88
Zn(SD) 0.20 0.37 4.99 0.00 5.55 -
O(SU) 0.90 2.54 0.00 0.00 3.44 -0.91
O(SD) 0.91 2.56 0.00 0.00 3.46 -
Nd(SU) 1.21 2.90 0.56 3.70 8.37 1.05
Nd(SD) 1.14 2.90 0.50 0.03 4.58 -
Zn14Nd2O16 Zn(SU) 0.19 0.35 4.99 0.00 5.53 0.92
Zn(SD) 0.20 0.35 4.99 0.00 5.54 -
O(SU) 0.91 2.51 0.00 0.00 3.42 -0.88
O(SD) 0.91 2.54 0.00 0.00 3.46 -
Nd1(SU) 1.29 3.02 0.71 3.01 8.03 1.01
Nd1(SD) 1.26 3.01 0.64 0.05 4.97 -
Nd2(SU) 1.31 3.05 0.72 3.01 8.10 0.87
Nd2(SD) 1.29 3.04 0.64 0.05 5.03 -
Table 3. Population value and bond length of inherent ZnO and Nd-doped ZnO systems.
Table 3. Population value and bond length of inherent ZnO and Nd-doped ZnO systems.
Model Bond Population value Bond length/Å
Zn16O16 Zn-Omax 1.08 1.966
Zn-Omin 0.12 1.975
Zn15Nd1O16 Zn-Omax 0.35 1.985
Zn-Omin 0.40 1.967
Nd-O(//c) 0.22 2.238
Nd-O(⊥c) 0.34 2.191
Zn14Nd2O16 Zn-Omax 0.33 1.982
Zn-Omin 0.41 1.985
Nd1-O(//c) 0.27 2.260
Nd1-O(⊥c) 0.43 2.195
Nd2-O(//c) 0.35 2.230
Nd2-O(⊥c) 0.46 2.223
Table 4. Magnetic coupling modes and total magnetic moment of intrinsic and Nd-doped ZnO systems.
Table 4. Magnetic coupling modes and total magnetic moment of intrinsic and Nd-doped ZnO systems.
Model ∑ M ∑ | M | Coupling mode Total magnetic moment (µB)
Zn15Nd1O16 3.75 3.92 FM 3.75
Zn14Nd2O16 5.97 6.29 FM 5.97
Annotation: ∑ M represents the result of spin-polarized DOS integration. ∑ | M | denotes the total absolute value of the spin-polarized DOS integral.
Table 5. Atomic magnetic moment and orbital magnetic moment of Nd-doped ZnO systems.
Table 5. Atomic magnetic moment and orbital magnetic moment of Nd-doped ZnO systems.
Model Atoms Magnetic moment (µB) Orbital magnetic moment (µB)
s p d f
Zn15Nd1O16 O2 -0.03 -0.01 -0.02 - -
O4 -0.03 -0.01 -0.02 - -
O8 -0.03 -0.01 -0.02 - -
O11 -0.01 0.00 -0.01 - -
Zn6 -0.02 -0.02 0.00 0.00 -
Zn9 0.01 0.00 0.01 0.00 -
Zn12 0.01 0.00 0.01 0.00 -
Zn13 -0.01 -0.01 0.00 0.00 -
Zn14 0.01 0.00 0.01 0.00 -
Nd 3.79 0.07 0.00 0.06 3.67
Zn14Nd2O16 O1 -0.02 0.00 -0.02 - -
O2 -0.03 0.00 -0.03 - -
O3 -0.02 -0.01 -0.01 - -
O4 -0.02 -0.01 -0.01 - -
O5 -0.02 0.00 -0.02 - -
O8 -0.02 -0.01 -0.01 - -
O11 -0.02 0.00 -0.02 - -
Zn9 -0.01 -0.01 0.00 0.00 -
Nd1 3.06 0.03 0.01 0.07 2.96
Nd2 3.08 0.02 0.01 0.08 2.96
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated