Preprint
Article
Soft End Effector using Spring Roll Dielectric Elastomer Actuators
Altmetrics
Downloads
111
Views
28
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
28 September 2023
Posted:
29 September 2023
You are already at the latest version
Alerts
Abstract
Dielectric elastomer actuators (DEAs) offer robust, high energy density solutions for soft robotics. The proposed end effector consists of three spring roll configuration DEAs, each acting as a robotic finger, using a 3M VHB-F9473PC adhesive membrane. The lateral force, bending angle and response time of the actuator are measured experimentally and compared with the predictions of an analytical model. The cylindrical actuator measures 70 mm in length and 15 mm in diameter and achieved a lateral force of 30 mN, a bending angle of 6.8 ° and a response time of ≈ 1 s. Spring roll configuration DEAs are shown to reduce the effects of viscoelasticity seen in the membrane, making the actuator more controllable at higher voltages. The dielectric constant of the membrane is shown to be a limiting factor of actuation, with a decrease in dielectric constant resulting in larger actuation. The end effector successfully gripped numerous light objects for extended periods, showing the applicability of spring roll DEAs for soft end effectors.
Keywords:
Subject: Engineering - Mechanical Engineering
1 s. Spring roll configuration DEAs are shown to reduce the effects of viscoelasticity seen in the membrane, making the actuator more controllable at higher voltages. The dielectric constant of the membrane is shown to be a limiting factor of actuation, with a decrease in dielectric constant resulting in larger actuation. The end effector successfully gripped numerous light objects for extended periods, showing the applicability of spring roll DEAs for soft end effectors.
1. Introduction
Dielectric elastomer actuators (DEAs) consist of an elastic dielectric membrane sandwiched between two compliant electrodes (Figure 1). DEAs have a very high energy density allowing them to outperform other actuators when weight is constrained [1]. Actuating the bulk material allows for smaller form factors (subgram) and more resilient actuators due to their low inertia [2]. DEAs are promising because of their large strains, fast response, long lifetime and high efficiency [3,4]. Currently, one of the most popular dielectric elastomer (DE) materials used is the very high bond (VHB) polyacrylate film because of the large strains achievable and low cost. Another benefit to this material is that it can be pre-stretched, which offers substantial actuation performance including higher efficiency and dielectric breakdown voltages, and reduces the probability of pull-in instability [5]. The thickness of the compliant electrode used also affects the performance of the actuator with thinner electrode generally being favoured over thicker provided the electrode maintains its conductivity for the expected strains [6]. When a voltage is applied to the DEA, it becomes part of the circuit, i.e., a compliant capacitor. The physical changes the membrane experiences once the voltage is applied can be modelled using circuit components [7].
Creating a dynamic model allows the performance of the actuator to be assessed across all scales, especially subgram actuators/robotics where performance is shown to be highest when compared with other actuation methods [2]. DEAs can be modelled statically using an appropriate hyperelastic energy function and viscoelastic relaxation model [8]. The frequency response can also be modelled in a similar way to predict the amplitude of oscillation [9,10]. The dynamic response of a spring roll actuator during aperiodic actuation is not as well documented. As viscoelasticity causes a non-linear response in both the time and frequency domains [5], developing a complete model which can predict the behaviour of the actuator when gripping an object is essential to better understand the potential applications of spring roll DEAs.
When a voltage is applied to the electrodes, the membrane is compressed in the thickness direction due to the opposing stored charges, resulting in in-plane expansion and hence actuation [11]. Spring roll DEAs (shown in Figure 2a) consist of a compressed spring rolled in a dielectric elastomer (DE) membrane, with electrode applied, and offer structural rigidity and some membrane pre-stretching. The response of the spring roll actuator highly depends on the properties of the spring with the bending angle, decreasing with spring diameter, and rate, . This study proposes a soft gripper using spring roll DEAs. The gripper consists of three spring roll DEAs attached to a polymer base creating a soft gripper, as shown in Figure 2b.
Voltages of 0.5 to 10 kV are typically seen to achieve large strains [8]. Elastomers are composed of long entangled polymer chains, bound by weak intermolecular bonds. DEs are similar except when placed in an electric field, the distribution of charges within the polymer chains is disrupted, causing the chains to become polarised [12]. The chains then acquire an electric dipole moment resulting in a rotation due to the electric field (Figure 3a) with each pole being attracted to the oppositely charged electrode. Under large deformation, the polarisation of the chains is impeded (Figure 3b) [13]. The electromechanical response of the DEA can be uncoupled, i.e., investigated electrically and mechanically, and modelled computationally [8]. The DEs used are hyperplastic materials and behave highly non-linearly due to the complex phenomena dictating the resulting in-plane expansion due to the conditions imposed upon the elastomer.
Numerous spring roll DEAs have been studied [5,14,15,16,17]; however, they are yet to be used for a soft gripper. DEAs may also be used as sensors, as when compressed, a predictable voltage is produced. DEAs have been developed for applications such as soft end effectors, energy harvesting and lightweight crawling and flying robots [2,18,19]. An analytical model is first constructed and tested to predict the mechanical behaviour and response of the actuator. Actuator samples and a soft gripper are fabricated and compared with the analytical model to demonstrate the applicability of spring roll DEAs for use as soft end effectors.
2. Modelling and Experiment
Dynamic modelling is essential for accurate analysis of the actuator behaviour. It allows parameters such as spring rate, diameter and length to be chosen so the response can be optimised for a given task. It also allows the effect of the material properties on the response to be analysed which can improve the design of the actuator.
2.1. Equations of State for DEAs
To model the DEA, a 1D planar model is constructed and then used to predict the in-plane expansion and the curvature of the spring roll. The membrane has original dimensions , and . The membrane is subject to forces from the electric field generated by the voltage across the electrodes, and mechanical forces , and , acting on the membrane, such as a pre-stretch, and cause original dimensions of the membrane to become , and , as shown in Figure 4. Each element of the actuated membrane is modelled as shown in Figure 4b. The accumulated charge on each opposing electrode is represented by and the resulting stretch of the membrane can be represented by the principal stretches, = , = , = . Deformation of the membrane is shown by the curvature of the actuator and is assumed entropic [20].
The resulting work done on the membrane (mechanical and charge from the applied voltage) can be represented using the Helmholtz free energy, taken to be a function of four independent variables, . Equation (1) is the free energy of the thermodynamic system, using the potential energy from the forces, compressed massless spring, [5] and the applied voltage [11].
This is a measure of the useful work of a closed system and states that energy is conserved, therefore represents the maximum amount of work the system can perform. Assuming the forces and voltage are fixed, the free energy of the system, can be defined as a function of four independent variables. Minimising this function represents an equilibrium state, i.e., the free energy has been minimised with respect to the variables. It can be assumed the membrane undergoes homogeneous deformation therefore the nominal density of the Helmholtz free energy, = can now be defined using: the stresses, = , = , = , the electric field, = and the electric displacement, = . The volume of an elastomer undergoing a large deformation can be assumed to be constant, as the change in shape of an elastomer is typically much more significant. Equation (2) represents the constant volume, and one of the equations of state of the membrane [20]:
Prior to the incompressibility assumption, each stretch was independent, however only two are required now to fully represent the deformation, along with the electrical displacement, . Setting = [8] and assuming is a function of the three independent variables:
The free energy of the system can be represented using equations (1) and (3) [20]:
Fixing the forces and voltage, an equilibrium state is achieved when equation (4) is true. Setting the partial derivative of with respect to each independent variable = 0, i.e., = 0 gives the other three equations of state:
The forces and voltage can now be determined given a suitable energy function, for the incompressible DE [8]. Setting = , where is the relative permittivity of the membrane, and integrating equation (7) with respect to gives:
This integration leaves two independent terms, the constant of integration, which represents the Helmholtz free energy from the deformation of the elastomer and the term representing the Helmholtz free energy associated with the membrane polarisation. Note that represents the free energy due to elastic stretching [20] or the strain energy density function used to model the deformation of the membrane. The electromechanical coupling is therefore a geometric effect given the expression, = . Equation (8) is known as the model of ideal dielectric elastomers [20] and can now be combined with the free energy of the system (equation (4)):
Note that the free energy of the system, , is now a function of only two planar stretches as the voltage is fixed. Again, a state of equilibrium is reached at the minimum value of i.e., = 0. Equivalents to equations (5) & (6) can now be written as [8]:
Where represents the Maxwell stress [21]. Acrylic membranes, especially the VHB series, suffer from viscoelastic effects. This results in long-term relaxations (hundreds of seconds [10]) and slower response times which makes precisely modelling and controlling the actuator difficult. Additionally, any forces acting on the membrane, represented by , and in equation (9) will change the characteristics of the actuator and thus the response. Pre-stretching the film reduces the creep strain behaviour due to viscoelasticity and, therefore may be an effective method to combat the difficulties with modelling and controlling the viscoelastic effects. The effect of the degree of pre-stretching on the performance of the actuator can be investigated [10].
The viscoelasticity was modelled using the nonlinear viscoelastic DE model developed by Yang et al [22] as it was developed using the same DE membrane. The model combines two parallel springs (one elastic and one inelastic with a viscous dashpot). Figure 5 shows the viscoelastic model composed of two parallel units. The upper unit consists of a spring, with shear modulus, and the lower unit consists of a spring, with shear modulus, and a dashpot, with viscosity, . The spring and dashpot represent the nonlinear time-dependent deviation from the equilibrium state, described by equation (17). The deformations in the spring , spring and dashpot are characterised by & , & , and & respectively. The stretch of the parallel units is equal therefore, = & = . Limiting stretch parameters and are used to represent the finite contour length of the membrane.
As the dashpot relaxes with time, the stored energy is dissipated, reducing the deformation capacity [10]. The strain energy density function, can now be written as the sum of the contributions from the two units, & :
The axial pre-stress of the film, due to the compression of the spring may be represented by:
The pre-stretch, is a result of the spring’s extension, is assumed = 1 as the spring restricts any lateral expansion of the membrane. A lower value for increases the bending angle, and therefore as is low, the pre-stress from the spring can be assumed = 0 [5]. Maintaining the incompressibility assumption sets = . The nonlinearities in the deformation of the film are now represented and the deformation may be predicted and compared with experimental results. Therefore, setting = = 0 [23] and = 1 gives:
Written in full using the Gent energy function:
Where and are material constant and represent the limiting stretches of spring, and spring, respectively. Only the membrane regions with electrode will be subjected to the Maxwell stress. The viscoelastic relaxation time, is set = = 50 s [10]. Equation (15) can be solved for as a function of time, allowing the dynamic behavior of the actuator to be assessed. Model specific material parameters are seen in Table 1.
The bending angle of the 2-DOF roll, is assumed to have constant curvature and estimated using [17]:
Where is the stroke of the actuator and is the radius of the spring. The viscoelastic relaxation of the membrane can be represented by the deformation rate, and viscosity, of the dashpot, shown using the Gent model [24]:
2.2. Charge-control & leakage current
The membrane cannot be assumed to be a perfect insulator, and therefore part of the charge which accumulates on the electrodes, leaks through, as shown in Figure 6. This leakage current consists of electronic and ionic conduction, where charged particles within the material complete the circuit due to the applied field [7,24].
The process of charging and discharging the capacitor is not instant and can be represented by:
Where is the charge moving in the wire. Dividing equation (18) by gives the change in current with time:
Where = represents the current in the wire, represents the rate of change of the charge on the electrodes and = represents the leakage current through the membrane [25]. The capacitor and resistor circuit transfer function is then generated and used to create the first-order lag response of the capacitor charging with leakage current. Equation (20) shows the resulting transfer function:
Where is the voltage across the capacitor, is the resistance used to limit the current from the power supply, is the leakage current equivalent resistance, is the capacitance of the DEA and is the complex parameter from the Laplace transform. The charge on the capacitor was then converted to an equivalent field, where the leakage current is modelled using a resistor, [24,25]:
Where is the breakdown voltage of the membrane, and the membrane conductivity, = 2.159 10-14 [24]. The discharging process is equivalent and inverse.
3. Method
3.1. Fabrication of Spring Rolls
The membrane used is 3M VHB F9473PC ( = 250 μm) and is cut into sheets and sprayed with Kontakt Chemie Graphit 33 Conductive Lacquer using an MDF stencil. Copper foil tape is added so that the voltage is applied to alternating electrodes as seen in Figure 7a. The spring is first compressed, then the membrane is rolled around the spring. To ensure no air is trapped between the layers, the membrane is pressed against the spring as it is rolled. The spring roll DEA is then released and left to relax until the spring and membrane are in equilibrium. The axial pre-stress of the membrane can be determined using the length of the relaxed spring. Multiple samples are fabricated and tested to ensure the reliability of the fabrication process.
This process can be automated using an electric motor and jig however, as the membrane did not require constant tension when rolling as is required when pre-stretching, this is not necessary for coherent rolling.
3.2. Experimental Setup
The actuator is fixed at the base, placed in front of a grid of known size and actuated in increments of 1 kV from 0 to 6 kV (Figure 8b). The response is captured using a camera and then calibrated and analysed using motion capture software Kinovea. To measure the lateral force, the actuator is fixed horizontally and allowed to relax. The end cap was then fastened to a cantilever beam and actuated in increments of 1 kV from 0 to 6 kV. Multiple measurements for each voltage increment are taken. Bending angle and lateral force are measured multiple times per second whilst the voltage is applied to generate time series data, allowing dynamic response to be analysed and assessed across the entire stroke of the actuator. Standard insulated wires could not be used to connect the actuators to the power supply as their inertia affected the response of the actuator.
The gripper was fabricated using polymer sheets and copper foil tape, as shown in Figure 8a. A membrane layer is placed over the foil tape at the effecting end of the actuator. Gaps between the edges of the membrane and electrodes were left to ensure no arcing occurred between or within the membrane layers. The electrode regions are sized and spaced to maintain alignment when rolled, increasing with roll diameter.
4. Results
The total mass of the gripper was 36 g and was able to hold objects, with masses of up to 35 g as shown in Figure 8a. The fingers were angled perpendicular to the base of the gripper and were arranged radially with a radius of 35 mm. The fingers were directed towards the centre, with the actuated spans facing outwards such that the gripper closes when actuated. To test the performance of the gripper, the cup was located within the grasp of the gripper, the gripper was then actuated and lifted. When the voltage was removed, the cup fell after 2 s because of the viscoelastic effects of the membrane. The gripper showed repeatable actuation with a predictable response.
4.1. Static Response
The voltage-controlled actuation is shown in Figure 9. The bending angle and lateral force increase quadratically with voltage and fit to the predictions of the model. The voltage was applied for = 10 s before measurements were taken to assess the dynamic elastic and viscoelastic predictions of the Simulink model. Small deviations were seen from the trend line across all experimental data points. The bending angle at 5 to 6 kV is lower than the model predictions and is likely due to defects in the membrane and imperfections in the fabrication process.
Dielectric breakdown occurs at the breakdown voltage, and below given sufficient time for the viscoelastic effects to reduce the membrane thickness according to the relationship:
Where is the dielectric strength. When actuated, the gripper is more vulnerable to external forces causing dielectric breakdown as a slight decrease in the membrane thickness is able to reduce below the supplied voltage.
The model accurately predicted the lateral force of the actuator at lower voltages, becoming less accurate at higher voltages due to membrane defects. Another likely cause is that only forces with components normal to the beam are represented correctly by the experimental data. As the actuator has a constant curvature, there will be some component of force not acting normal to the beam, which is not measured. This effect becomes more apparent at 4 kV and above (Figure 9).
4.2. Dielectric properties of membrane
From Figure 10, a lower value of dielectric constant results in a larger breakdown voltage and thus allows for a much larger stretch before breakdown occurs. This is due to the breakdown strength of the material being inversely proportional to the dielectric constant and agrees with the literature [26,27]. The increase in from = 4 to = 2 is significant and would result in an increase in bend angle proportional to the additional stretch. The theoretical maximum was plotted, = 1, resulting in a much larger actuation. The lowest dielectric constant of polymers is usually around 2 [27], which would suggest that the membrane chosen is not optimal in terms of dielectric constant, and the performance of the DEA would see a significant increase by reducing the dielectric constant, assuming the material properties are similar.
The breakdown line for each voltage is not at a constant voltage as the thickness of the membrane reduces with actuation, and therefore the maximum voltage the membrane can withstand before breakdown decreases with as shown.
4.3. Dynamic Response
A predictable dynamic response was observed as shown in Figure 11a with the viscoelasticity effects being represented by the configuration shown in Figure 5. A voltage of 3 kV was used as this is the highest voltage accurately predicted by the model. The discrepancy between the magnitude of the responses is likely due to efficiency losses in the membrane from defects, air bubbles, miss aligned electrode spans and non-actuated electrode regions near the ends of the actuator visible in Figure 7b. The initial sharp increase seen in Figure 11a is also dictated by the current from the power supply and can be adjusted to alter the power of the actuator with a larger current increasing the speed of the response.
Figure 11b shows the viscoelastic relaxation time after actuation is held for 50 seconds. The actuator cannot hold a 6 kV voltage for 50 s as dielectric breakdown will occur due to the membrane thickness reducing. Once the voltage is removed, the time taken to reach is roughly five times longer than the initial actuation period (left of the blue dashed line). This limits the period of actuation for continuous operation required for good performance and controllability.
5. Discussion
The actuators display a predictable and reliable response for short term actuations, where the dashpot is not fully extended and is responsible for a small portion of the total actuation. Should the voltage be applied for longer periods, shown in Figure 11b, the membrane must be allowed to relax before accurate actuation can be performed again. The controllability of the actuator reduces significantly for multiple long term actuations because of the this. Incorporating the spring into the actuator design improves the controllability by forcing the membrane to adopt its shape allowing for the bend angle to be calculated easily with a constant curvature assumption. This also limits the stretch seen in the membrane once the spring is fully extended, allowing for actuations to be held indefinitely with a fixed and predictable relaxation period. The spring increases the relaxation period as the spring is re-compressed, decreasing the shear modulus of the upper unit of the viscoelastic model, . The spring can be replaced with any elastic material allowing the actuator to be scaled down. As the electrode pattern on the membrane allows for multiple degrees of freedom, on subgram scales it is possible for a single membrane to carry out multiple functions with appropriate supporting structure and electrode patterning.
Each sample tested gave repeatable results and demonstrates the reliability of the fabrication process and experimental setup. Samples where the dielectric breakdown occurred were no longer able to actuate. Samples which were punctured or damaged often displayed arcing. Given the voltage used for actuation, and the large membrane area required for actuation the current design requires altering to improve the safety of the actuator such that puncture or defects do not result in arcing or damage to the surrounding environment. Samples showed resilience to wear, dropping, bending to = 180 ° and tightly gripping caused no visible damage or detectable performance losses. Soldering directly to the copper foil tape did not damage the membrane.
The Gent model values, specifically , and are likely inaccurate because they are generated from a similar but different membrane (VHB 4910). The main difference between the membranes is the thickness with VHB 4910 being 1 mm thick, opposed to 0.25 mm. Material tests must be carried out on VHB F9473PC for the values to be accurate. The effects of the pre-stretch on the membrane were assumed negligible as a ratio of 1.03 was applied. The performance of the actuator is compared with previous works in Table 2.
The values obtained from previous works represent the actuation achieved once the dashpot has been fully extended. However, this can take hundreds of seconds, as shown in Figure 11b and only partially represents the performance of the gripper. The actuation expected is therefore lower if the dashpot is not allowed to fully extend.
6. Conclusions
The actuation of a helical spring based DEA was modelled and compared with experimental data. The analytical model predicted the behaviour of the actuator with discrepancies identified. Methods of mitigating the viscoelastic effects of the membrane were identified. The dielectric constant and the breakdown strength of the membrane limited the performance of the actuator. The model may be used to identify materials and assess actuator designs with desired parameters. Spring roll DEAs may be used for collision resistant, lightweight grippers. The spring can be substituted for a lightweight, elastic structural support. Multiple regions of a single membrane can be supported and patterned with electrode for specific tasks including locomotion or as a soft gripper, especially for subgram robots.
Author Contributions
Conceptualization, H.L. and M.P.; methodology, H.L. and M.P.; formal analysis, H.L.; investigation, H.L.; data curation, H.L.; writing—original draft preparation, H.L.; writing—review and editing, M.P.; supervision, M.P.; funding acquisition, M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of Bath Alumni Fund, grant number F1920A-RS02.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank Dr. Runan Zhang for supporting the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brochu, P.; Pei, Q. Advances in Dielectric Elastomers for Actuators and Artificial Muscles. Macromol. Rapid Commun. 2009, 31, 10–36. [CrossRef]
- Chen, Y.; Xu, S.; Ren, Z.; Chirarattananon, P. Collision Resilient Insect-Scale Soft-Actuated Aerial Robots With High Agility. IEEE Trans. Robot. 2021, 37, 1752–1764. [CrossRef]
- Pelrine, R.; Kornbluh, R.; Pei, Q.; Joseph, J. High-Speed Electrically Actuated Elastomers with Strain Greater Than 100%. Science 2000, 287, 836–839. [CrossRef]
- Pelrine, R.; Kornbluh, R.; Kofod, G. High-Strain Actuator Materials Based on Dielectric Elastomers. Adv. Mater. 2000, 12, 1223–1225. [CrossRef]
- Zhang, J.; Chen, H.; Tang, L.; Li, B.; Sheng, J.; Liu, L. Modelling of spring roll actuators based on viscoelastic dielectric elastomers. Appl. Phys. A 2015, 119, 825–835. [CrossRef]
- Lau, G.-K.; Shiau, L.-L.; Chua, S.-L. Effects of Thinner Compliant Electrodes on Self-Clearability of Dielectric Elastomer Actuators. Actuators 2020, 9, 121. [CrossRef]
- Lochmatter, P.; Kovacs, G.; Wissler, M. Characterization of dielectric elastomer actuators based on a visco-hyperelastic film model. Smart Mater. Struct. 2007, 16, 477–486. [CrossRef]
- F.-b. Zhu, C.-l. Zhang, J. Qian and W.-q. Chen, “Mechanics of dielectric elastomers: materials, structures, and devices,” Journal of Zhejiang University-SCIENCE A (Applied Physics & Engineering), vol. 17, no. 1, pp. 1-21, 2016. [CrossRef]
- Zhang, J.; Chen, H.; Li, B.; McCoul, D.; Pei, Q. Coupled nonlinear oscillation and stability evolution of viscoelastic dielectric elastomers. 2015, 11, 7483–7493. [CrossRef]
- D. Q. Tran, J. Li, F. Xuan and T. Xiao, “Viscoelastic effects on the actuation performance of a dielectric elastomer actuator under different equal, un-equal biaxial pre-stretches,” Materials Research Express, vol. 5, no. 1, pp. 1-12, 2018. [CrossRef]
- W. Lai, “Characteristics of dielectric elastomers and fabrication of dielectric elastomer actuators for artificial muscle application,” Iowa State University, Ames, 2011.
- Britannica, “Dielectrics, polarization, and electric dipole moment,” Britannica, 2023. [Online]. Available: https://www.britannica.com/science/electricity/Dielectrics-polarization-and-electric-dipole-moment. [Accessed 7 2 2023].
- Britannica, “Molecular structure and charge distribution,” Britannica, 2023. [Online]. Available: https://www.britannica.com/science/liquid-state-of-matter/Molecular-structure-and-charge-distribution. [Accessed 7 2 2023].
- Löwe, C.; Zhang, X.; Kovacs, G. Dielectric Elastomers in Actuator Technology. Adv. Eng. Mater. 2005, 7, 361–367. [CrossRef]
- Wang, H.; Li, L.; Zhu, Y.; Yang, W. Analysis and application of a rolled dielectric elastomer actuator with two degrees of freedom. Smart Mater. Struct. 2016, 25. [CrossRef]
- Li, L.; Godaba, H.; Ren, H.; Zhu, J. Bioinspired Soft Actuators for Eyeball Motions in Humanoid Robots. IEEE/ASME Trans. Mechatronics 2018, 24, 100–108. [CrossRef]
- Pei, Q.; Rosenthal, M.; Stanford, S.; Prahlad, H.; Pelrine, R. Multiple-degrees-of-freedom electroelastomer roll actuators. Smart Mater. Struct. 2004, 13, N86–N92. [CrossRef]
- Heng, K.-R.; Ahmed, A.S.; Shrestha, M.; Lau, G.-K. Strong dielectric-elastomer grippers with tension arch flexures. SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring; pp. 101631Z–101631Z-8. [CrossRef]
- van Kessel, R.; Bauer, P.; A Ferreira, J. Electrical modeling of cylindrical dielectric elastomer transducers. Smart Mater. Struct. 2021, 30, 035021. [CrossRef]
- Huang, R.; Suo, Z. Electromechanical phase transition in dielectric elastomers. Proceedings of the Royal Society 2011, 468, 1014–1040. [CrossRef]
- Goulbourne, N.; Mockensturm, E.; Frecker, M. A Nonlinear Model for Dielectric Elastomer Membranes. J. Appl. Mech. 2005, 72, 899–906. [CrossRef]
- E. Yang, M. Frecker and E. Mockensturm, “Viscoelastics model of dielectric elasmtomer membranes,” Proc. SPIE 5759, Smart Structures and Materials, vol. 5759, no. 1, pp. 82-92, 2005. [CrossRef]
- T. Lu, J. Huang, C. Jordi, G. Kovacs, R. Huang, D. R. Clarkeb and Z. Suo, “Dielectric elastomer actuators under equal-biaxial forces, uniaxial forces, and uniaxial constraint of stiff fibers,” Soft Matter, vol. 8, no. 1, pp. 6167-6173, 2012. [CrossRef]
- Foo, C.C.; Cai, S.; Koh, S.J.A.; Bauer, S.; Suo, Z. Model of dissipative dielectric elastomers. J. Appl. Phys. 2012, 111. [CrossRef]
- J. Zhang, H. Chen, J. Sheng, L. Liu and B. Li, “Leakage current of a charge-controlled dielectric elastomer,” Proceedings of SPIE, vol. 9056, no. 1, pp. 1-10, 2014. [CrossRef]
- J. McPherson, A. S. J. Kim, H. Mogul and J. Rodriguez, “Proposed universal relationship between dielectric breakdown and dielectric constant,” Digest. International Electron Devices Meeting, vol. 1, no. 1, pp. 633-636, 2002. [CrossRef]
- Q. Tan, P. Irwin and Y. Cao, “Advanced Dielectrics for Capacitors,” Transactions on Fundamentals and Materials, vol. 126, no. 11, pp. 1153-1159, 2006. [CrossRef]
- Teh, Y.S.; Koh, S.J.A. Giant continuously-tunable actuation of a dielectric elastomer ring actuator. Extreme Mech. Lett. 2016, 9, 195–203. [CrossRef]
- Romasanta, L.; Lopez-Manchado, M.; Verdejo, R. Increasing the performance of dielectric elastomer actuators: A review from the materials perspective. Prog. Polym. Sci. 2015, 51, 188–211. [CrossRef]
- Zhao, X.; Suo, Z. Electrostriction in elastic dielectrics undergoing large deformation. J. Appl. Phys. 2008, 104, 123530. [CrossRef]
Figure 1.
Working principle of DEA schematic.
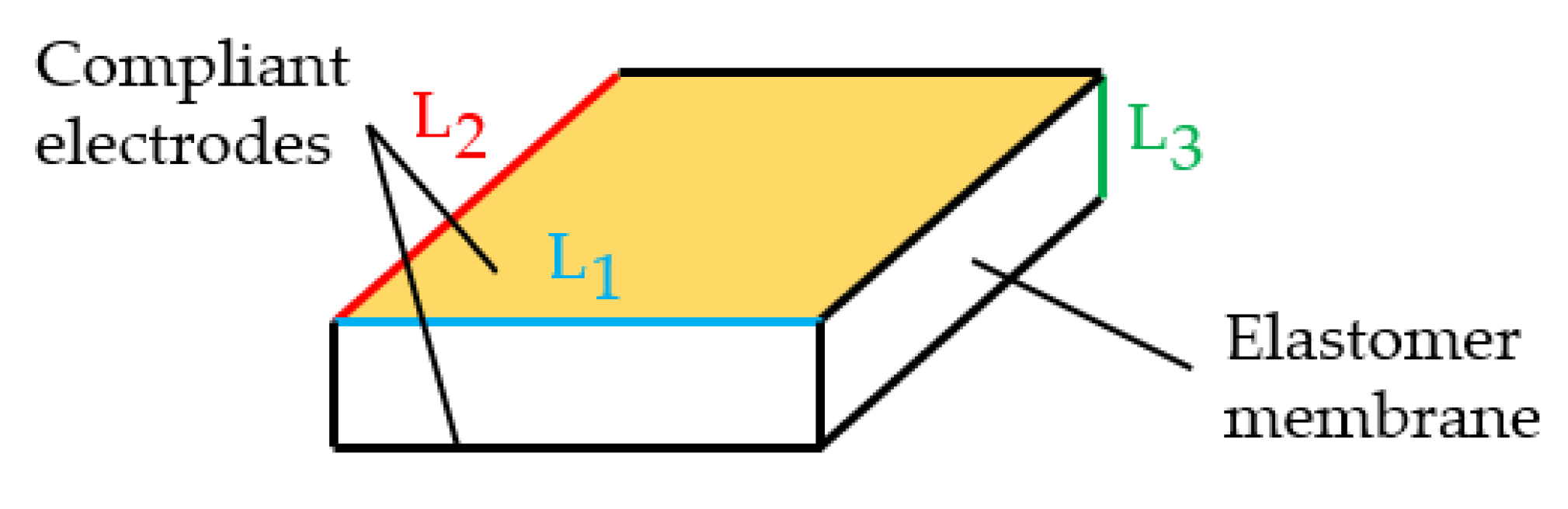
Figure 2.
(a) 2-DOF Bending spring roll. For bending, only one span is actuated. For 1-DOF both sides are actuated simultaneously resulting in a linear strain; (b) Spring roll DEA gripper concept schematic.
Figure 2.
(a) 2-DOF Bending spring roll. For bending, only one span is actuated. For 1-DOF both sides are actuated simultaneously resulting in a linear strain; (b) Spring roll DEA gripper concept schematic.
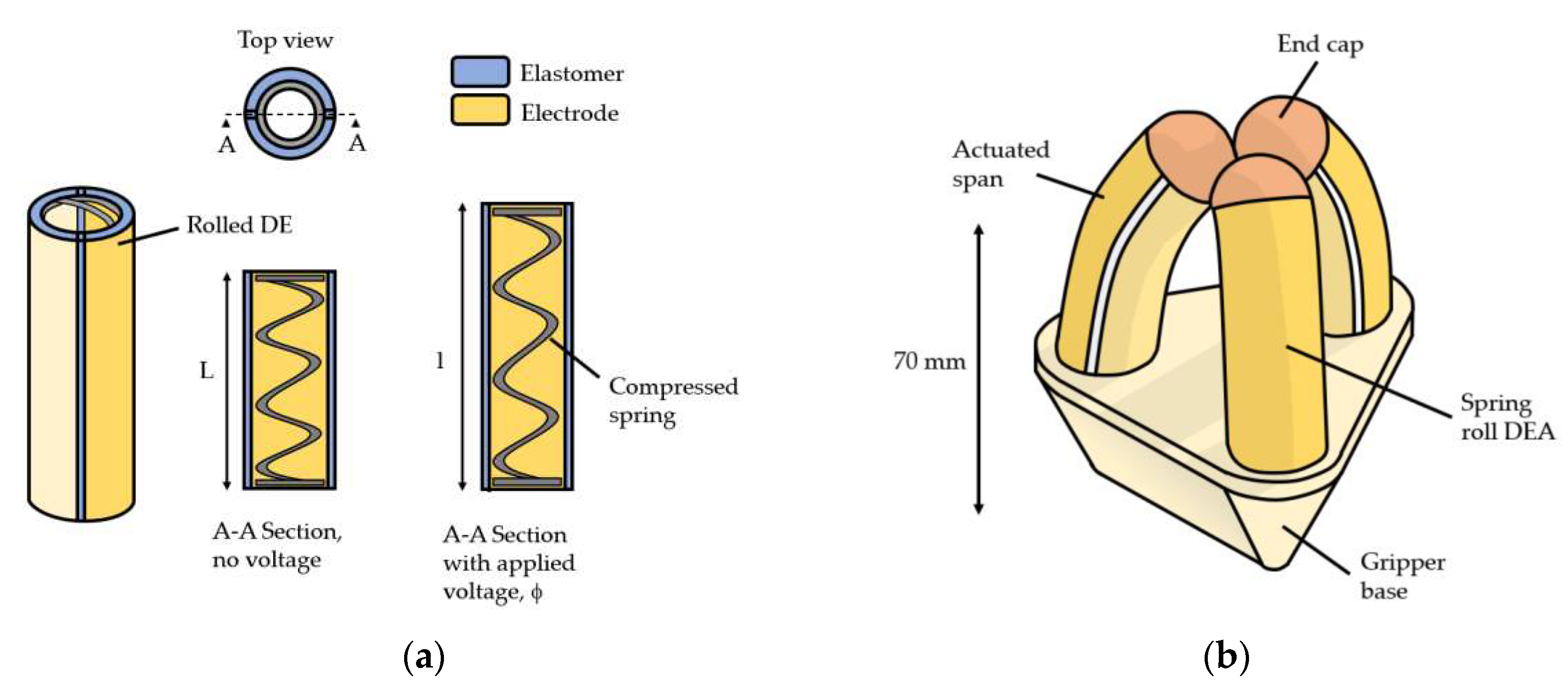
Figure 3.
(a) Electric dipole moment, rotation of polymer chains in the direction of the applied voltage; (b) Electric dipole moment with deformation from applied voltage.
Figure 3.
(a) Electric dipole moment, rotation of polymer chains in the direction of the applied voltage; (b) Electric dipole moment with deformation from applied voltage.
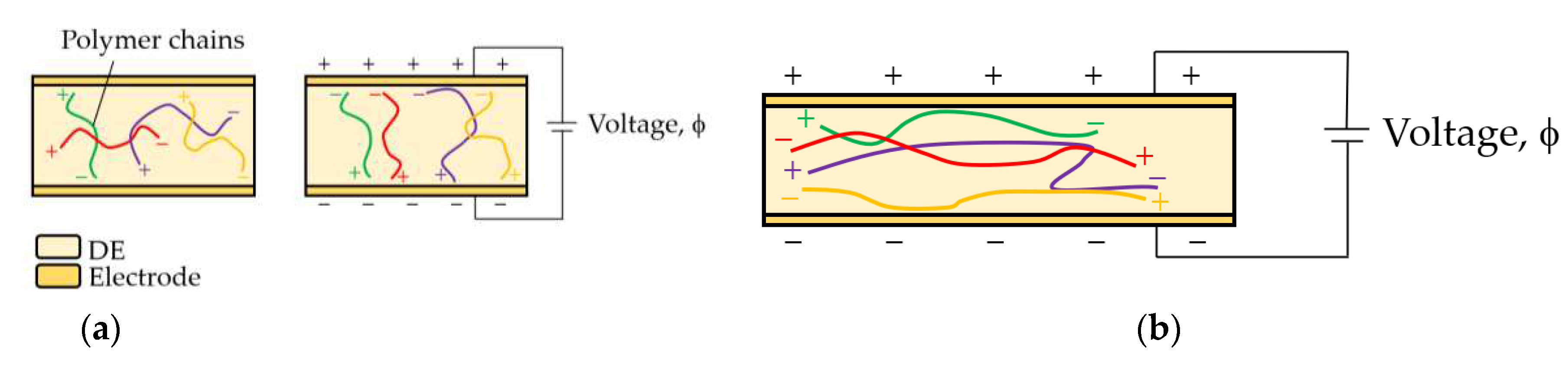
Figure 4.
(a) Spring roll bending configuration with the right side actuated (shown in darker hue) resulting in a curvature of angle, and radius, . An element of the actuated membrane is subjected to stresses when the voltage is applied, and for any forces acting on the membrane. Red surface represents the fixed end, blue surface represents the free end of the actuator and orange represents the massless spring; (b) Schematic of DE membrane element from (a).
Figure 4.
(a) Spring roll bending configuration with the right side actuated (shown in darker hue) resulting in a curvature of angle, and radius, . An element of the actuated membrane is subjected to stresses when the voltage is applied, and for any forces acting on the membrane. Red surface represents the fixed end, blue surface represents the free end of the actuator and orange represents the massless spring; (b) Schematic of DE membrane element from (a).
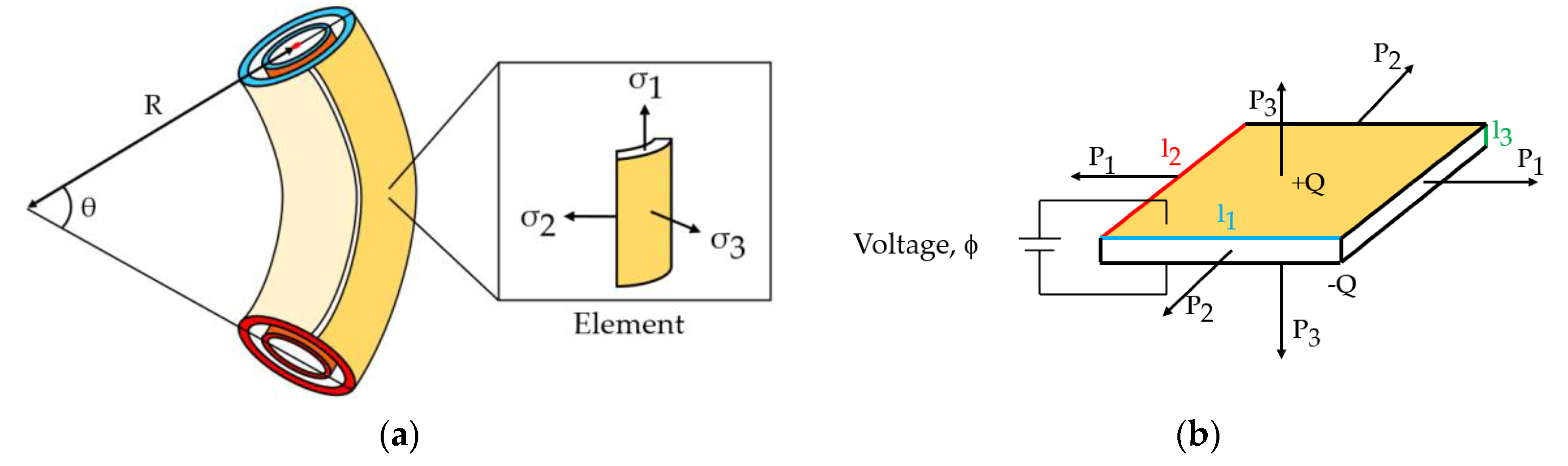
Figure 5.
Standard linear solid viscoelastic model of dielectric elastomer using two parallel springs and a viscous dashpot.
Figure 5.
Standard linear solid viscoelastic model of dielectric elastomer using two parallel springs and a viscous dashpot.
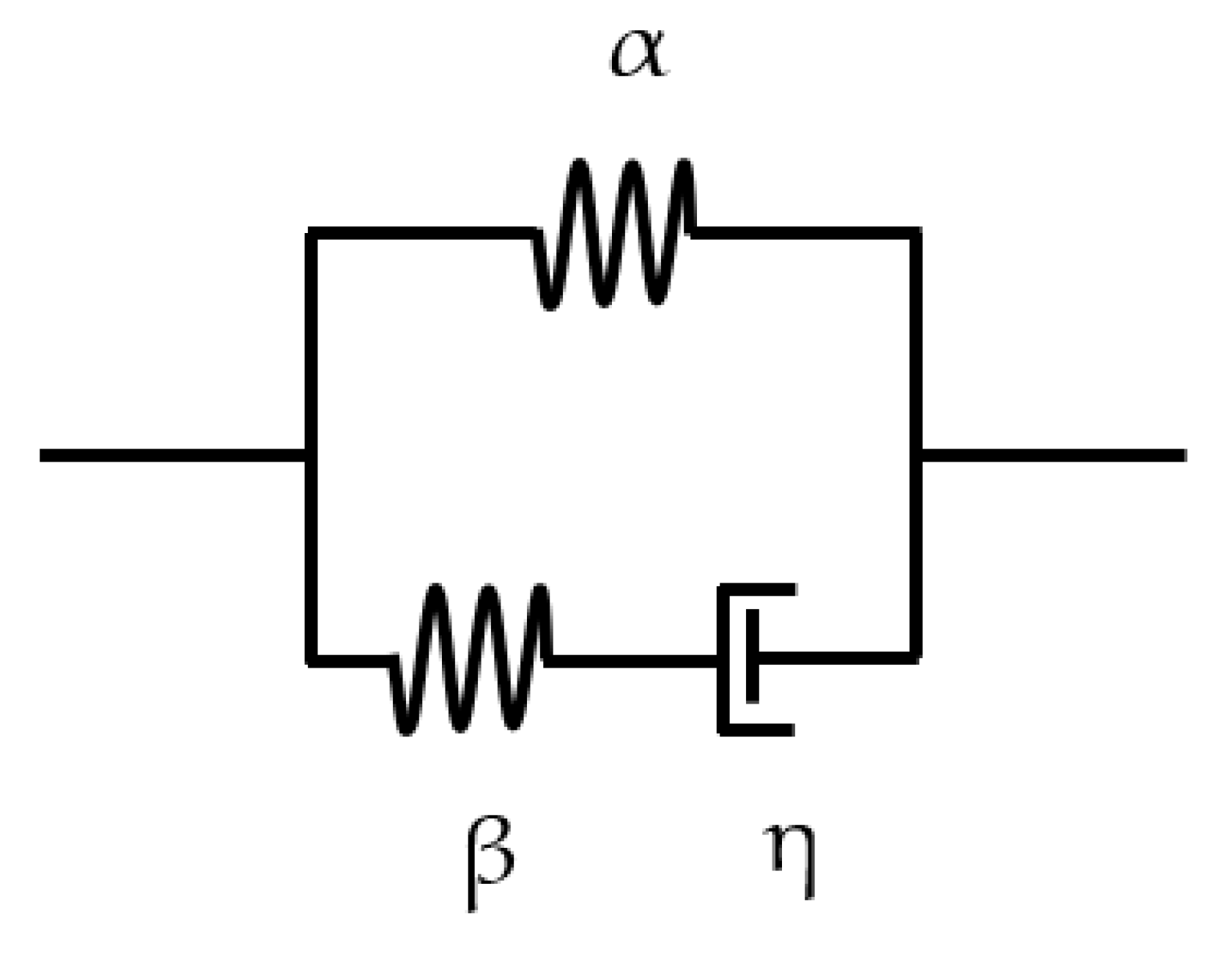
Figure 6.
Leakage current model.
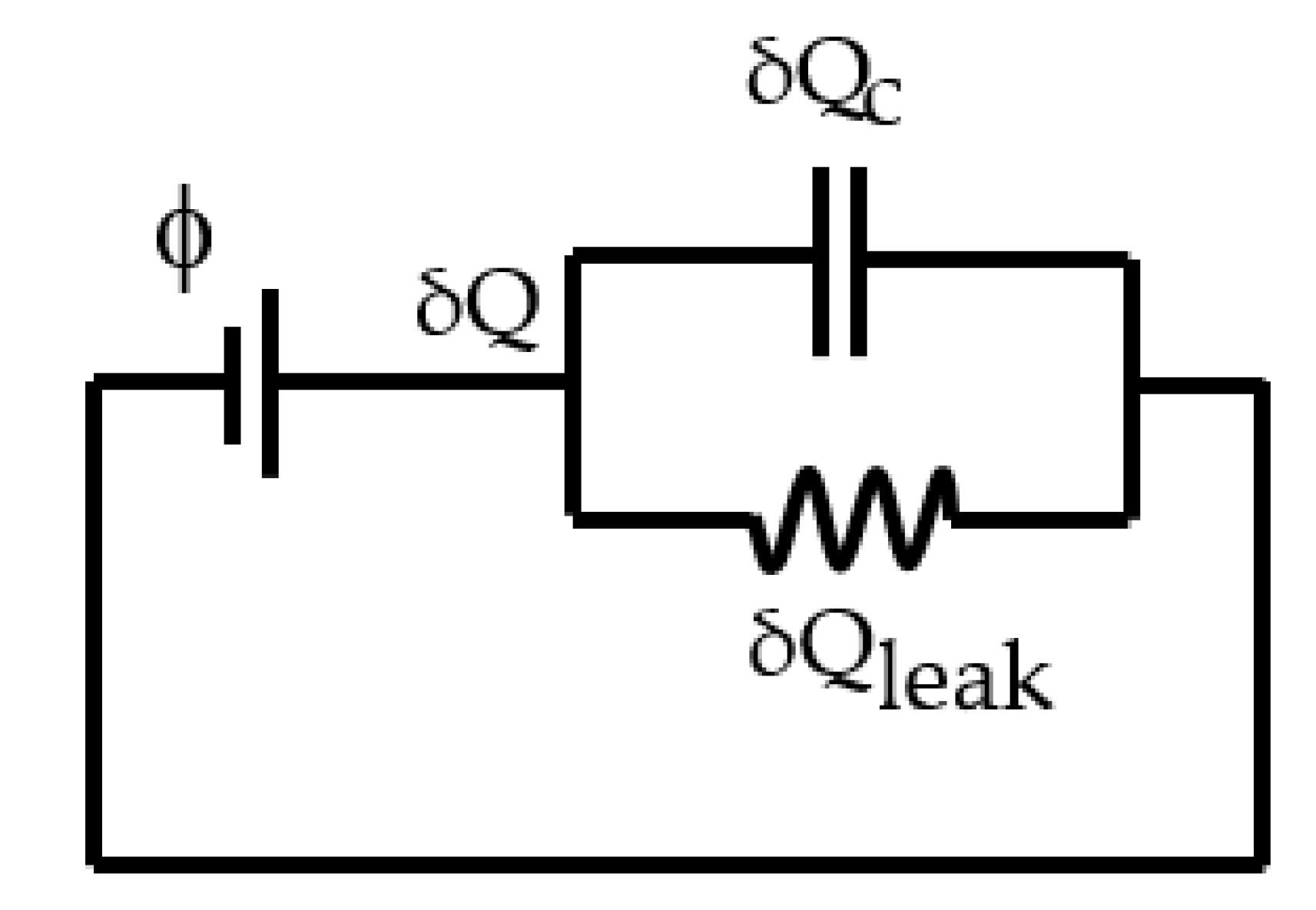
Figure 7.
(a) Fabrication process components; (b) Completed spring roll actuator.

Figure 8.
(a) Gripper holding a 35 g mass in a cup. The gripper consists of three single actuators arranged radially; (b) Single actuator bending test, shown in an actuated state. A lateral deflection of 5 mm was achieved for the actuator design used.
Figure 8.
(a) Gripper holding a 35 g mass in a cup. The gripper consists of three single actuators arranged radially; (b) Single actuator bending test, shown in an actuated state. A lateral deflection of 5 mm was achieved for the actuator design used.
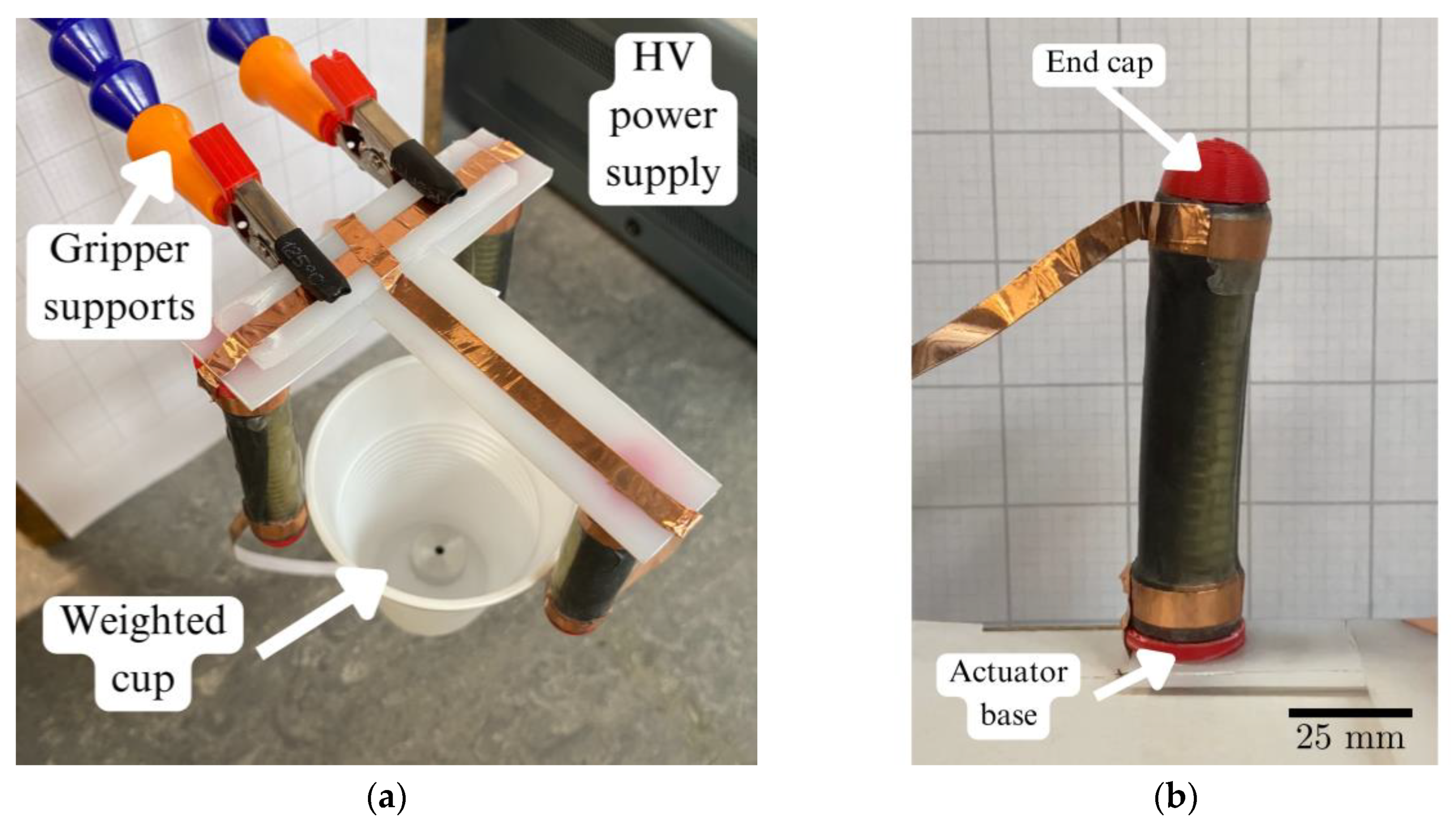
Figure 9.
(a) Voltage-controlled bend angle for = 10 s or ; (b) Maximum lateral force generated for = 10 s.
Figure 9.
(a) Voltage-controlled bend angle for = 10 s or ; (b) Maximum lateral force generated for = 10 s.
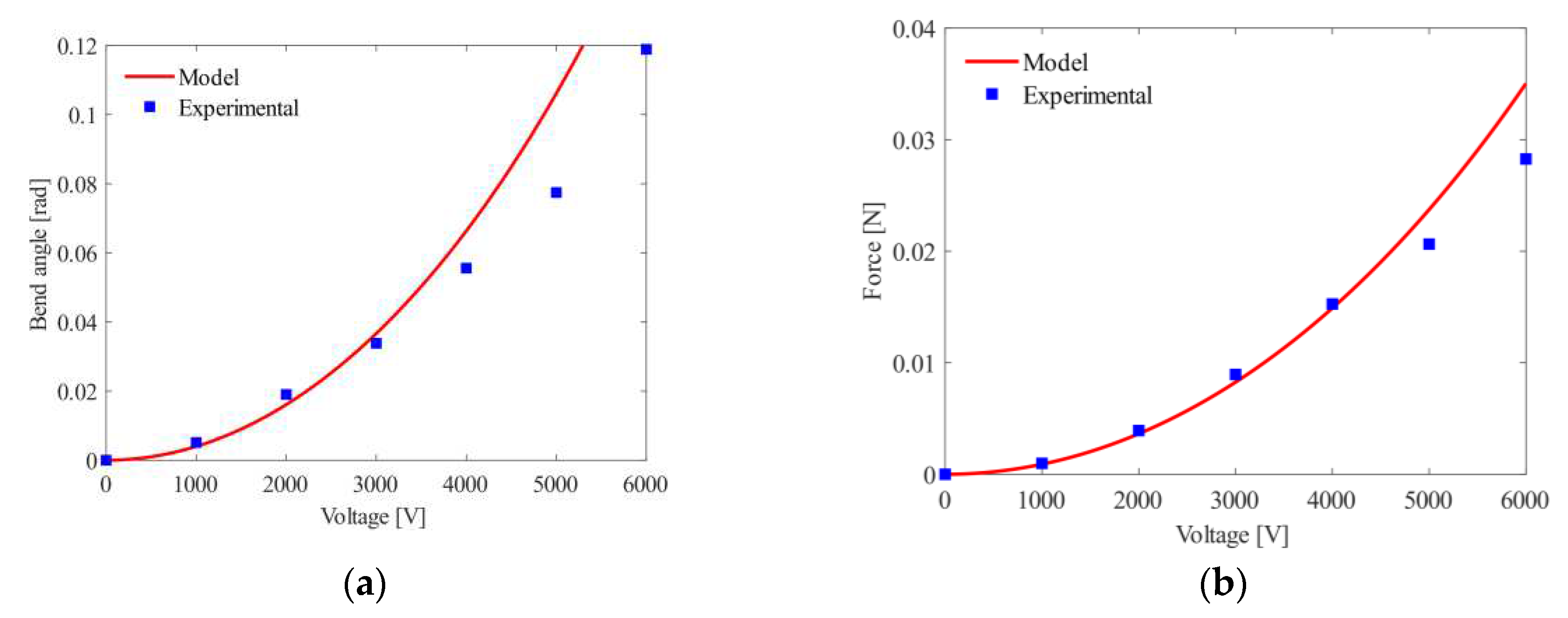
Figure 10.
Membrane actuation for varying dielectric constant, . Breakdown line for each value shown by red dashed line, with the intersection point (maximum stretch of the membrane, ) shown by red circles for each dielectric constant. = 3 for VHB-F9473PC.
Figure 10.
Membrane actuation for varying dielectric constant, . Breakdown line for each value shown by red dashed line, with the intersection point (maximum stretch of the membrane, ) shown by red circles for each dielectric constant. = 3 for VHB-F9473PC.
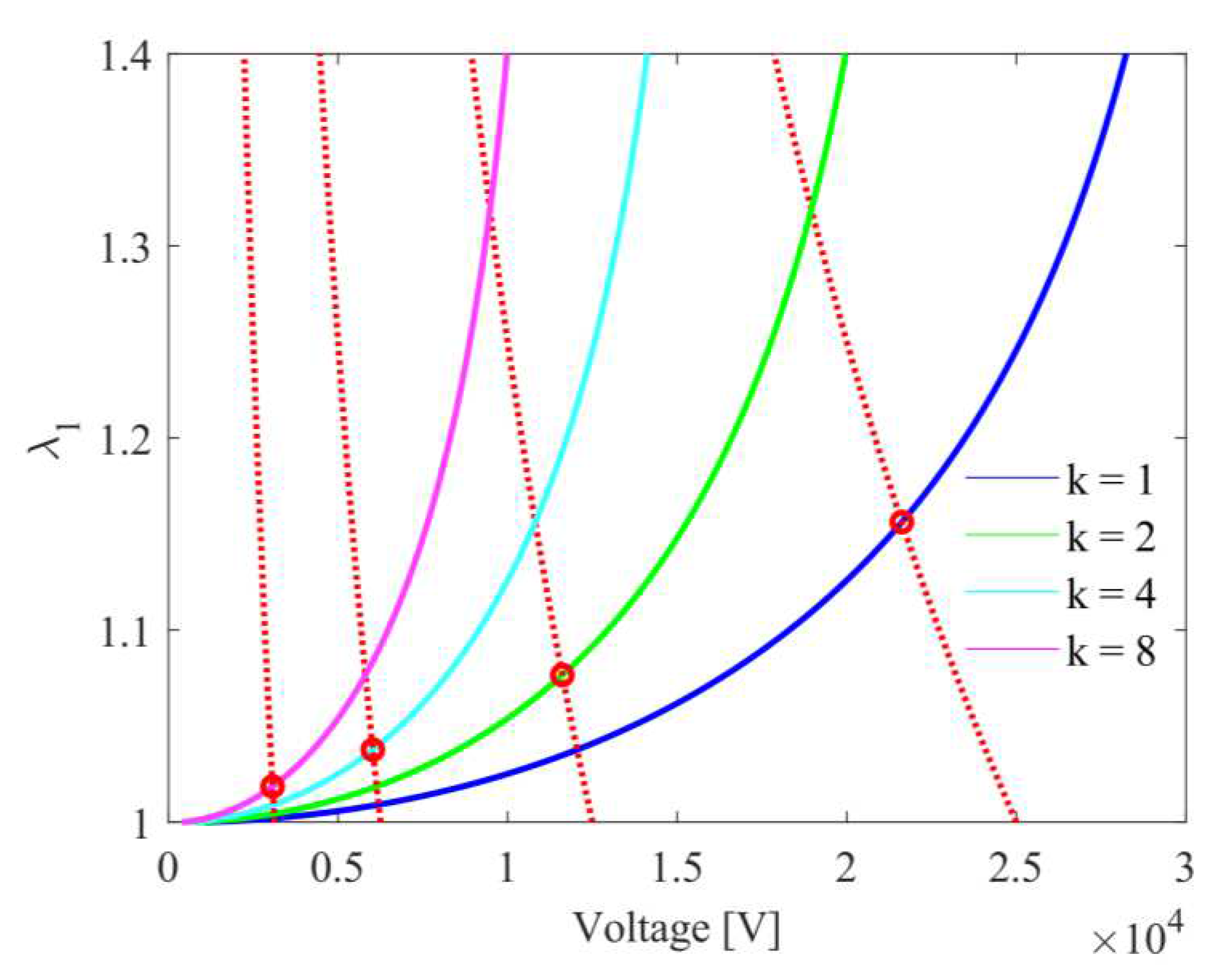
Figure 11.
(a) Effect of spring on controllability of actuator for 3 kV; (b) Viscoelastic relaxation time of actuator when actuated for 50 seconds at 5 kV.
Figure 11.
(a) Effect of spring on controllability of actuator for 3 kV; (b) Viscoelastic relaxation time of actuator when actuated for 50 seconds at 5 kV.
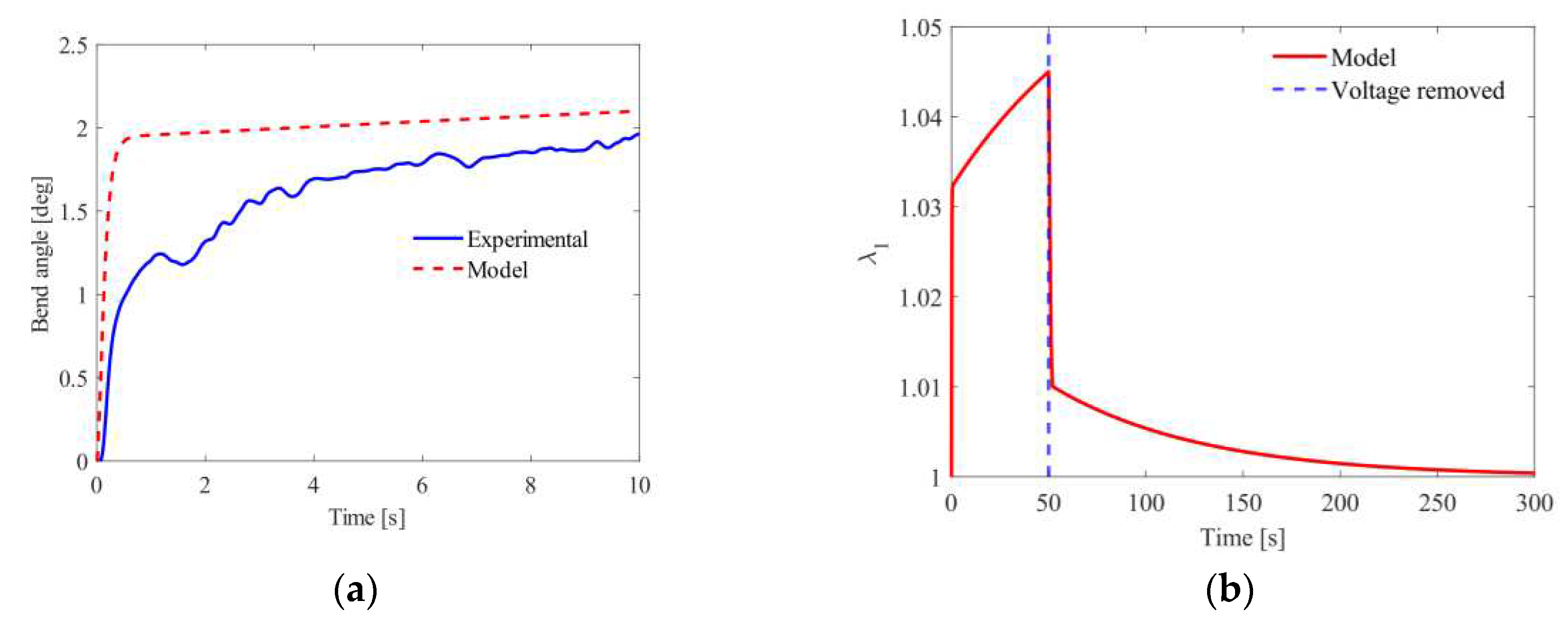
Table 1.
Gent energy function model parameters [24].
Table 1.
Gent energy function model parameters [24].
| Material parameter | Value |
|---|---|
| 115 | |
| 70 | |
| 16000 | |
| 45000 | |
| 6 |
Table 2.
Comparison of actuator performance with pervious works.
| Parameter | 2-DOF roll (Version 1), 2004 [17] | 2-DOF roll, 2016 [15] | This work |
| Actuator mass | 29 g | - | 10 g |
| Actuator length | 68 mm | 40 mm | 70 mm |
| Dielectric elastomer (pre-stretch ratio) | VHB-4910 | VHB-4910 (3, 5) | VHB-F9473PC (1.03, 1) |
| Maximum operating voltage | 5.5 kV | 5 kV | 6 kV |
| Maximum stroke | - | 8.4 mm | - |
| Maximum bending angle | 60 ° | 75.3 ° | 6.8 ° |
| Maximum force | 1.68 N | 0.7 N | 0.03 N |
| No. of rolls | 20 | 14 | 10 |
| Dashpot fully extended | Yes | Yes | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







