Preprint
Review
Qualitative Comparative Analysis of Medical and Epidemiological Data
Altmetrics
Downloads
108
Views
100
Comments
0
This version is not peer-reviewed
Analytics and Modelling Clinical Data Using Advanced Biostatistical Methods
Submitted:
29 September 2023
Posted:
29 September 2023
You are already at the latest version
Alerts
Abstract
Qualitative comparative analysis (QCA) was developed by Charles Ragin in 1987 for the comparative analysis of small data sets. The method has become widespread in sociological and economic research. There are examples of successful use of QCA in the field of medicine and epidemiology. The purpose of this review is to describe the key stages of QCA with a discussion the application of this method to the analysis of medical and epidemiological data.
Keywords:
Subject: Medicine and Pharmacology - Other
Introduction
Clinical and epidemiological studies primarily use quantitative data analysis methods based on probability theory and mathematical statistics. Such methods require data to fit a limited set of distribution types and often require a large, representative sample. The complexity of interpreting the results of quantitative methods inevitably increases with the number of variables studied, which usually requires the use of additional labor-intensive methods of multivariate analysis. In turn, it is known that medical research is one of the most complex and expensive studies in which the amount of data collected is limited by economic and ethical considerations, and the representativeness of the sample can usually only be guaranteed for a small population that meets certain conditions. In addition, the prevalence of phenomena (conditions) studied in medicine can be very low, which significantly complicates data collection. In the case of epidemiological studies, the sample elements are often observations from the past and it is not possible to obtain new, clarifying estimates. All of the above often leads to situations where the sample size or its pronounced imbalance do not allow traditional statistical analysis of the data and the use of other alternative approaches can help achieve the research goals.
Qualitative comparative analysis (QCA) is a method of data analysis based on studying the relationship between conditions and results from the perspective of set theory. This method was first proposed by the American sociologist Charles Ragin in 1987 for the comparative analysis of small data sets (from 10 to 50 observations) [1]. In subsequent years, QCA became widespread in sociological and economic research, and the development of computer technology made it possible to analyze large data sets. Today there are examples of the successful use of QCA in biomedical research [16,17,18,19,20,21], and their number, according to open analytics PubMed, has increased sharply over the past few years.
The purpose of this review is to describe the key stages of QCA with a discussion the application of this method to the analysis of medical and epidemiological data.
Calibration
QCA requires data to be presented in a specific format, where all independent and dependent variables are converted into indicators of membership in a certain set. This process of data transformation is called calibration and is the fundamental operation of the method. When using crisp sets, the variable is calibrated to one of two values: 0 or 1 (FALSE or TRUE), which is a simple logical judgment and reflects the presence of some attribute, for example, a patient either belongs to the set of male patients (1) or does not belong ( 0). In the case of fuzzy sets, the variable is calibrated into one of a continuum of values on a numerical range from 0 to 1, which is only possible for variables measured on an interval and ratio scale. This value is a simple judgment in fuzzy logic and reflects the degree of inclusion (presence) of some attribute, for example, a patient belongs more to the set of overweight patients than thin ones. It is worth noting that in this case, fat and thin are two separate sets, and not two ends of the same numerical segment from 0 to 1. Each set has its own continuum of degrees of inclusion, so that the patient can be either fat or thin, to varying degrees, and the sum of the degrees of inclusion does not have to be equal to one. This approach allows us to take into account the presence of asymmetries in real data when analyzing them. In addition, it should be noted that the degree of inclusion is not the probability of the presence of a certain sign, for example, any small probability of a patient being overweight does not exclude its presence, which is interpreted differently if the patient belongs to some fuzzy set.
Data calibration is not data normalization or standardization. The main difference is that calibration is not carried out automatically and necessarily requires the participation of a researcher to determine threshold values. Such additional information necessary for the formation of qualitative conclusions, as a rule, cannot be obtained from the data themselves and is external, theoretical and often subjective. Despite the fact that this fact describes one of the most significant shortcomings of the method, the use of abstract, intuitive concepts to form qualitative conclusions can significantly simplify the interpretation of the results obtained, and in some cases is a prerequisite and is included in the purpose of the study. In practical medicine and epidemiology, such abstract and often subjective concepts are used everywhere, for example, some diagnosis, syndrome, symptom or standard definition of an epidemiological case. It is not always possible to clearly determine their “boundaries”, as well as the degree of severity, for example, how much the throat hurts or the nose is stuffy. In this regard, it can be said that many medical and epidemiological indicators require qualitative assessment, often using subjective or theoretically based thresholds. In practice, with a sufficient number of observations, threshold values can also be determined using quantitative data analysis methods such as cluster analysis, ROC analysis, regression analysis, decision trees and others.
To convert a variable into an indicator of membership in a crisp set, simple recoding of values below a given threshold is used to 0, and above — to 1. To obtain a fuzzy set membership indicator from a variable, there are several most common and recommended approaches [2,3,4,5,6] (Table 1). It is worth noting that for the subsequent conversion of fuzzy estimates into crisp estimates at the calibration stage, it is necessary to avoid ambiguous values of degrees of inclusion equal to 0.5.
Analysis of Necessity and Sufficiency
QCA allows you to study under what conditions the desired result occurs. Researchers can come up with various hypotheses about how the phenomena under study arise and test them using QCA, but in most cases it is not possible to accurately establish cause-and-effect relationships.
A condition or reason in QCA is a variable proposition (predicate) with one or more arguments that take the values of calibrated independent variables. In the case of several arguments, the predicate is constructed using the conjunction or disjunction of simple logical judgments with their participation. In other words, the condition allows you to select from a data set the set of all observations with the presence or absence of specific characteristics based on independent variables in all their possible combinations. In turn, a result or consequence in QCA is a predicate, usually with one argument, taking the value of a calibrated dependent variable. Such a predicate allows you to select from a data set the set of all observations with the phenomenon (outcome) being studied.
Different conditions affect the result differently, but some of them are so important that the result will not occur in their absence. If the set of observations corresponding to a certain condition includes many observations of the phenomenon being studied, then such a condition is said to be necessary for the result to occur (Figure 1A). In turn, if a set of observations corresponding to a certain condition is included in the set of observations with the phenomenon being studied, then such a condition is said to be sufficient for the occurrence of the result (Figure 1B). In other words, a condition is necessary if it is always present when the phenomenon being studied occurs, and sufficient if the result always occurs when the given condition is present. It is worth noting that since QCA allows us to take into account the presence of asymmetry in the data, the absence of a necessary or sufficient condition is not necessarily a necessary or sufficient condition, respectively, for the absence of a result.
Analysis of sufficient conditions for the occurrence of a result is the most intuitive and popular from a practical point of view. Indeed, the researcher first of all wants to find exactly those conditions that guarantee the presence or development of the phenomenon being studied, for example, the presence of a certain diagnosis or exceeding the morbidity threshold. As a rule, one sufficient condition cannot explain the entire result, but only part of it. A complete explanation usually requires a combination of several sufficient conditions, which must be selected from a list of all possible combinations based on knowledge of the subject area and intermediate results of the analysis. In turn, necessity analysis provides additional important information that can be used to select the most promising independent variables and potentially the most stable and reproducible (robust) sufficient conditions derived from them.
Complete inclusion of one set of observations within another is rare in practice. In most cases, one set is partially (to a greater or lesser extent) included in another set (Figure 1C,D). Indeed, not all patients with influenza will experience muscle and joint aches in the first days of the disease, however, many will. QCA uses special metrics that make it possible to more accurately describe the relationship of necessary and sufficient conditions with the result. All of them can take one of a continuum of values on the interval from 0 to 1.
The inclusion rate reflects the degree of inclusion and is defined as the proportion of elements of a subset that also belong to the superset. In necessity analysis (1), the elements of the subset are observations with the result being studied, and the elements of the superset are observations that satisfy the condition. In sufficiency analysis (2), the opposite is true.
The coverage rate is defined as the proportion of elements of a superset that also belong to the subset. In necessity analysis (3), coverage reflects the triviality or relevance of a condition. The necessary condition becomes less trivial and more relevant (relevant) as the indicator values approach one [7]. In sufficiency analysis, original coverage (4) shows what part of the result is explained by a given condition, and unique coverage (5) shows what part of the result is explained only by this condition and no other. Any sufficient condition is redundant if its use does not improve the explanation of the result, or, conversely, if it is excluded, the explanation of the result does not worsen. For example, one of the conditions, such as fever, headache, or muscle and joint aches, might be expected to be redundant for early symptomatic diagnosis of influenza. All three of these symptoms are manifestations of intoxication syndrome with influenza and are often observed simultaneously.
The relevance of the need (6) is an additional parameter that reflects the relevance of the necessary condition. The lower the value of this indicator, the more trivial the condition, and the higher, the higher the relevance (relevance, importance) of the condition as necessary [8].
The proportional reduction of inconsistency (7) metric allows you to make the right decision in the case of identifying simultaneous relations of subsets, when, within the framework of fuzzy logic, the same condition is sufficient for both the presence of a result and its absence. Simultaneous subset relationships occur when there is at least one logically inconsistent case in the data for at least one of the relationships with the presence or absence of the phenomenon being studied [8,9]. For example, a patient may have catarrhal symptoms both with influenza and in cases where the diagnosis of influenza was not laboratory confirmed, and the symptoms are a manifestation of another acute respiratory viral infection.
Truth Table
The truth table is the main analytical tool required to perform the minimization process in QCA. Calibrated data allows you to construct a truth table with a number of columns equal to the number of independent variables included in the analysis and a number of rows equal to the number of all conditions involving all these variables simultaneously. The number of such conditions in the case of binary features is equal to the number of all placements with repetitions of two (0 and 1) by k, where k is the number of independent variables, or the Boolean of a set of k elements (2k). The next step is to distribute the individual observations to the appropriate rows of the truth table, counting the total number of observations that match each condition. When using fuzzy sets, to distribute observations it is necessary to transform fuzzy estimates into crisp ones. The procedure for such a transformation was proposed by Charles Ragin [4,10] and is based on a fundamental property: if none of the individual fuzzy estimates is equal to 0.5, each observation has at most one suitable condition from the truth table. This correspondence can be established using the membership index, which in only one case can be greater than 0.5, and is defined as the minimum of specially transformed values of all independent variables. If a condition presupposes the presence of a certain attribute, then the value of the corresponding independent variable remains the same. If the condition assumes the absence of some attribute, then the value of the corresponding variable is converted to its logically inverse or, which is the same thing, subtracted from unity. For example, if the condition assumes the absence of high body temperature, the presence of a sore throat and headache, and the sequence of fuzzy estimates of some observation has the form (0.7, 0.4, 0.8), then the membership index is defined as min((1–0.7), 0.4, 0.8) = 0.3, which is less than 0.5, therefore the observation does not meet this condition.
At the next stage, when the distribution of observations by conditions is known, special indicators are calculated for all rows of the truth table, characterizing the relationship of necessary and sufficient conditions with the result, first of all, the inclusion rate, with the help of which the key column of the truth table (output value) is encoded. This column contains generalized information about the presence or absence of the phenomenon being studied under various conditions, and its values are determined by comparing the inclusion rate with one or two thresholds specified by the researcher. If the rate value is greater than the upper threshold, then the output value is coded one, if it is less than the lower threshold, then it is zero, and if the rate value is between two thresholds, then the output value is coded as a contradiction. Another common option is uncertainty, when not a single observation matches the condition from the truth table and it is impossible to assess the cause-and-effect relationship. As a rule, such conditions are the majority in the truth table; they are called residuals (unobservable configurations) and can be used in logical minimization algorithms to find a simpler solution. However, it is advisable to leave not all residuals, as well as not all empirically observed configurations, in the truth table and use them in the minimization process. Many condition configurations may turn out to be invalid assumptions that must be excluded from the truth table [11,12]. First, special care must be taken to exclude impossible residuals — combinations of causative factors that could never occur, such as a pregnant male patient. Secondly, contradictory assumptions (simultaneous relations of subsets) should be excluded, when the same condition is sufficient for both the presence of a result and its absence. Thirdly, it is worth eliminating all sufficient conditions and remainders, which include the negation of a necessary condition. Indeed, if a superset includes some subset, then the logical negation of the superset should not include elements of this subset. A special way to additionally exclude residuals is the expected effect method, when the researcher expects the development of a result if certain conditions are met, then residuals with the negation of these conditions can also be excluded from the truth table.
Logical Minimization
Combining all the sufficient conditions from the truth table produces perfect disjunctive normal form. Such a logical expression is redundant and can be reduced (minimized) to a much simpler form that also explains the result well and can be interpreted by the researcher. It is worth noting that the input data for the minimization procedure is the truth table, and not the original data set. There are various approaches to minimizing logical functions from the method of direct transformations and minimizing maps to analytical and heuristic methods: the classic Quine-McCluskey algorithm (QMC), eQMC, CCubes and Espresso. The most interesting from the point of view of qualitative comparative analysis are analytical and heuristic methods, which, taking into account modern computing capabilities, make it possible to analyze large data sets including several dozen independent variables. These methods differ in their approach to optimizing calculations, and therefore in the efficiency of using computing power and computer memory. For example, the classic QMC method reaches its limit when including 11–12 explanatory variables (while consuming a lot of memory), while the CCubes algorithm can easily handle up to 30 causal conditions without the need for additional memory.
The classic minimization process uses only positive rows and residuals from the truth table. Residuals are viewed as conditions with a potentially positive outcome, even if not observed in the data. Meanwhile, the algorithm includes in the final expression only those remainders that contribute to obtaining a simpler and more economical solution. The idea of classical minimization is simple and is based on the rule of reducing a sequence of logical operations through gluing. If two logical propositions differ by exactly one literal, this literal can be minimized (8).
In turn, in the process of minimizing the eQMC [13] and CCubes [14,15] algorithms, both rows with a positive result and a negative one (output value is 0), as well as residuals excluded from the truth table, are used as conditions which should not lead to the occurrence of the phenomenon being studied. Unlike, for example, regression analysis, QCA does not focus on cause-effect pairs with the goal of averaging quantification of effect sizes, but attempts to first group causes into complex judgments conjunctively, and then into even more complex judgments disjunctively. As a result, a model in QCA is a logical expression made up of alternative conjunctions that can lead to a result independently of each other.
Conclusions
QCA allows to study the relationship between conditions and outcome in both small and large samples, taking into account the presence of data asymmetry. The method requires a qualitative assessment of all independent and dependent variables using a special and necessary data transformation procedure called calibration. A two-dimensional table that represents various conditions and their corresponding output values is called a truth table. If some condition configurations do not occur in the data, then they are residuals and can be useful during the logical minimization stage of the process. Data calibration and the process of eliminating invalid conditions from the truth table are key steps in the analysis that can significantly affect the outcome of the study. At the same time, these stages require the direct participation of the researcher and the use of external (not present in the data) theoretical information, often with a subjective approach to making certain decisions. Logical minimization produces a simpler and more interpretable solution, which is a set of alternative solutions that satisfy the result independently of each other. In addition to classical minimization methods, faster and more optimized algorithms have been developed (eQMC, CCubes, Espresso), which make it possible to analyze large volumes of data using several dozen independent variables in a reasonable time.
Medical and epidemiological studies are some of the most complex and expensive studies, often challenging to obtain large, representative, balanced samples and often involving abstract concepts and subjective assessments. Undoubtedly, the process of formalization of knowledge in many areas of medicine contributes to a significant reduction in the share of subjective assessments in clinical practice. However, in order to successfully formalize new knowledge, it is necessary to conduct new research, including using subjective and theoretically based assessments. In addition, from this point of view, QCA does not limit the researcher in any way, because threshold values for calibration can be selected both subjectively and on the basis of empirical experience and formalized knowledge. Summarizing all of the above, we can conclude that QCA is a promising method for analyzing medical and epidemiological data, which is an alternative to traditional quantitative methods, has its own advantages and disadvantages, and allows you to expand the set of algorithms and approaches to data analysis used in scientific research.
Author Contributions
Conceptualization, Tsvetkov V.V.; Investigation, all authors; Resources, all authors; Writing – Original Draft Preparation, Tsvetkov V.V.; Writing – Review & Editing, Tsvetkov V.V.; Visualization, Tsvetkov V.V.; Supervision, Tokin I.I.
Conflicts of Interest
All authors declared no conflict of interest.
References
- Ragin, C.C. The Comparative Method. Moving Beyond Qualitative and Quantitative Strategies. Berkeley, Los Angeles & London: University Of California Press 1987.
- Box-Steffensmeier J, Brady HE and Collier D. Measurement Versus Calibration: A Set Theoretic Approach. Oxford: Oxford University Press 2008.
- Ragin, C.C. Redesigning Social Inquiry. Fuzzy Sets and Beyond. Chicago; London: University of Chicago Press 2008.
- Alrik Thiem. Membership Function Sensitivity of Descriptive Statistics in Fuzzy-Set Relations. International Journal of Social Research Methodology 2014;17(6):625–642.
- Alrik Thiem and Adrian Dușa. Qualitative Comparative Analysis with R. A User’s Guide. New York; Heidelberg; Dordrecht 2013.
- Verkuilen, J. Assigning Membership in a Fuzzy Set Analysis. Sociological Methods & Research 2005;33(4):462–496. [CrossRef]
- Goertz, G. Assessing the Trivialness, Relevance, and Relative Importance of Necessary or Sufficient Conditions in Social Science. St Comp Int Dev 2006;41:88–109. [CrossRef]
- Schneider, C.Q.; Wagemann, C. Set-Theoretic Methods for the Social Sciences. A Guide to Qualitative Comparative Analysis. Cambridge: Cambridge University Press 2012. [CrossRef]
- Ragin CC, Drass KA, Davey S. Fuzzy-set/qualitative comparative analysis 2.0. Tucson, Arizona: Department of Sociology, University of Arizona 2006;23(6):1949-55.
- From Fuzzy Sets to Crisp Truth Tables. http://www.compasss.org/wpseries/Ragin2004.pdf.
- Schneider CQ, Rohlfing I. Combining QCA and Process Tracing in Set-Theoretic Multi-Method Research. Sociological Methods & Research 2013;42(4):559–597. [CrossRef]
- Schneider CQ, Wagemann C. Doing Justice to Logical Remainders in QCA: Moving Beyond the Standard Analysis. Political Research Quarterly 2013;66(1):211–220. http://www.jstor.org/stable/23563605.
- Duşa A, Thiem A. Enhancing the Minimization of Boolean and Multivalue Output Functions With eQMC, The Journal of Mathematical Sociology 2015;39(2):92–108. [CrossRef]
- Ragin, C.C. Fuzzy Set Social Science. Chicago; London: University of Chicago Press 2000.
- Dușa, A. Consistency Cubes: A Fast, Efficient Method for Boolean Minimization. The R Journal 2017;10(2):357–370. [CrossRef]
- Blackman, T. Exploring Explanations for Local Reductions in Teenage Pregnancy Rates in England: An Approach Using Qualitative Comparative Analysis. Social policy and society 2013;12(1):61–72. [CrossRef]
- Vanden Broeke L, Grillon M, Yeung AWK, Wu W, Tanaka R, Vardhanabhuti V. Feasibility of photon-counting spectral CT in dental applications-a comparative qualitative analysis. BDJ Open 2021;7(1):4. [CrossRef]
- Beifus K, Breitbart E, Köberlein-Neu J. Effects of complex interventions in 'skin cancer prevention and treatment': protocol for a mixed-method systematic review with qualitative comparative analysis. BMJ Open 2017;7(9):e017196. [CrossRef]
- Rodrigues NCP, de Noronha Andrade MK, Netto JT, Monteiro DLM, Lino VTS, Almeida EGR. Applying fuzzy qualitative comparative analysis to identify typical symptoms of COVID-19 infection in a primary care unit, Rio de Janeiro, Brazil. Sci Rep 2022;12(1):22319. [CrossRef]
- Eng S, Woodside AG. Configural analysis of the drinking man: fuzzy-set qualitative comparative analyses. Addict Behav 2012;37(4):541-543. [CrossRef]
- Davis A, Javernick-Will A, Cook SM. The use of qualitative comparative analysis to identify pathways to successful and failed sanitation systems. Sci Total Environ 2019;663:507-517. [CrossRef]
Figure 1.
A – a necessary condition: the set of observations (X) corresponding to the condition includes the set of observations (Y) with the result being studied; B – a sufficient condition: the set of observations (X) corresponding to the condition is included in the set of observations (Y) with the result being studied; C – a necessary condition (fuzzy sets); D – a sufficient condition (fuzzy sets).
Figure 1.
A – a necessary condition: the set of observations (X) corresponding to the condition includes the set of observations (Y) with the result being studied; B – a sufficient condition: the set of observations (X) corresponding to the condition is included in the set of observations (Y) with the result being studied; C – a necessary condition (fuzzy sets); D – a sufficient condition (fuzzy sets).
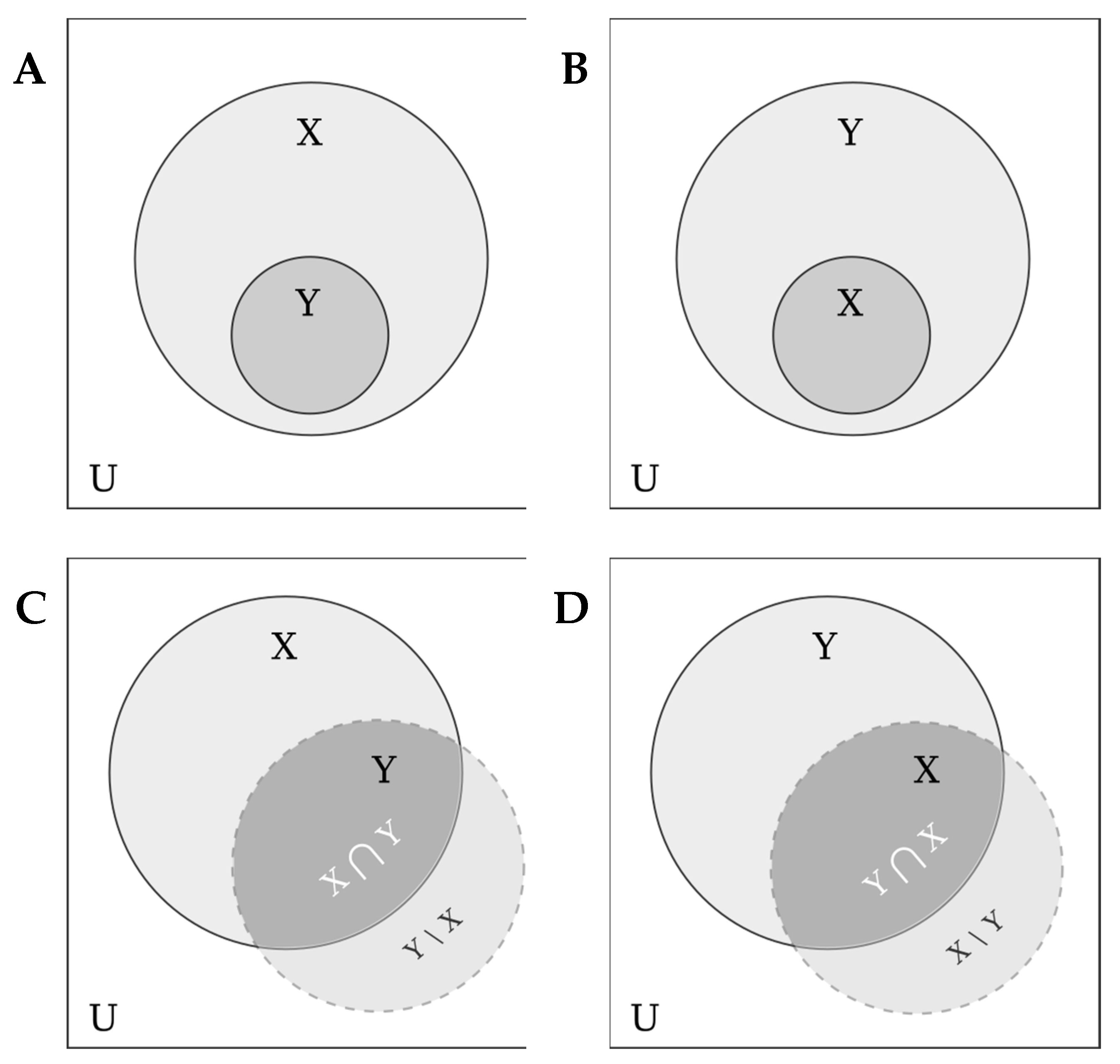
Table 1.
Methods for calibrating data into fuzzy set membership indicators.
| Methods | Description |
|---|---|
| Direct | |
| Monotonic function | A monotonic s-shaped function (linear or logistic) is used for calibration. Inclusion corresponds to observations at the edges of the data distribution. |
| Non-monotonic function | A non-monotonic bell-shaped function (triangular or trapezoidal) is used for calibration. Inclusion corresponds to observations in the middle of the data distribution. |
| Indirect | It is based on simple recoding of data followed by analytical prediction of encodings specified by the researcher based on the initial values of the variable, for example, using regression analysis. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






