Blockchain-enabled Pharmaceutical Supply Chain under Uncertain Demand: Cost Prediction through the Tuning of Evolutionary Supervised Learning

Preprint

Article

Blockchain-enabled Pharmaceutical Supply Chain under Uncertain Demand: Cost Prediction through the Tuning of Evolutionary Supervised Learning

Altmetrics

Downloads

107

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 September 2023

Posted:

01 October 2023

You are already at the latest version

Alerts

Abstract

This paper provides a new multi-function Blockchain Technology-enabled Pharmaceutical Supply Chain (BT-enabled PSC) mathematical cost model, including PSC costs, BT costs, and uncertain demand fluctuations. The purpose of this study is to find the most appropriate algorithm(s) with minimum prediction errors to predict the costs of the BT-enabled PSC model. This paper also aims to determine the importance and cost of each component of the multi-function model. To reach these goals, we combined four Supervised Learning algorithms (KNN, DT, SVM, and NB) with two Evolutionary Computation algorithms (HS and PSO) after data generation. Each component of the multi-function model has its own importance, and we applied the Feature Weighting approach to analyse their importance. Next, four performance metrics evaluated the multi-function model, and the Total Ranking Score determined predictive algorithms with high reliability. The results indicate the HS-NB and PSO-NB algorithms perform better than the other six algorithms in predicting the costs of the multi-function model with small errors. The findings also show that the Raw Materials cost has a stronger influence on the model than the other components. This study also introduces the components of the multi-function BT-enabled PSC model.

Keywords:

Subject: Engineering - Other

1. Introduction

The multi-function Blockchain Technology-enabled Pharmaceutical Supply Chain (BT-enabled PSC) may positively affect medication quality, ultimate patient outcomes, the tracking of medical records/sources, the distribution of drugs, stability of information, and information safety. The PSC performs reasonably well in society’s healthcare system and manages a considerable part of healthcare expenditures. However, in a Supply Chain System (SCS), there is no information sharing between systems, and manufacturers have difficulty tracking products. The regulations for the stability and safety of medical records, medical devices, and supplies are among the highest standards in the pharmaceutical industry, and Blockchain Technology (BT) can monitor PSC safely and transparently. Therefore, BT-enabled PSC can improve the safety and security of the system and significantly reduce delays and human errors. Generally, access to medical records is difficult because they are distributed in many different healthcare centers. Already, BT significantly impacts the healthcare industry, and its use has increased remarkably in the healthcare domain. BT shifts a centralized healthcare network into a decentralized one, and number of institutions, including hospitals, diagnostic laboratories, pharmaceutical companies, and physicians, utilize BT’s services to preserve and exchange patients’ information. One of the important advantages of using BT in the PSC is to detect fake medicines with appropriate control over the supply and demand of drugs [11]. Another advantage of BT-enabled PSC is to improve the interoperability of patient health data between healthcare providers while maintaining the privacy and security of their data [9]. Using BT-enabled PSC has also enhanced the transparency and communications between healthcare organisations and patients [8]. The PSC also deals with demand uncertainty, in which the demand for each medicine is uncertain and changeable.

As BT has been used in PSC in the past, several studies have discussed its advantages and disadvantages [8]; the present study, however, seeks to predict the cost of a PSC system utilizing BT and managing uncertain demand. A manager controls how financial resources are utilized in a system’s performance, determines whether a new system will benefit the organization, monitors the organization’s financial health, reduces expenses, stays within budget, and analyses information to identify unnecessary costs and business opportunities [27].

Another significant contribution of this study is to provide a PSC system with BT that considers the demand uncertainty. Examples of pharma companies using BT in PSC are Pfizer, Amgen, and Sanofi [32]. BT in a PSC could improve safety, performance, and medical information transparency while reducing the data transformation cost and time. The multi-function BT-enabled PSC BT-enabled PSC has two objectives: to manage system costs and deal with uncertain demand. Demand uncertainty in a PSC may affect product demand, product prices, raw material availability, regulatory changes, investment risk, unit manufacturing, costs of transportation, etc.

In this study, we aim to estimate the costs of the multi-function BT-enabled PSC BT-enabled PSC model, which includes demand uncertainty, and identify which SL algorithms have the lowest prediction errors and component costs. Determining the model’s cost components is essential, which helps managers make the most appropriate decisions. Additionally, this study aims to evaluate the significance of each cost component in the multi-function model or the degree to which each feature is relevant to the model. In this study, three research questions are sought to be answered: (i) What are the components of a multi-function BT-enabled PSCBT-enabled PSC model, including uncertain demand? What is the mathematical model? (ii) Which algorithms perform better in minimising the prediction errors of the multi-function BT-enabled PSCBT-enabled PSC model among eight algorithms? (iii) What are the most important cost components of a multi-function model? The procedure to determine the responses to these questions is as follows. We first identified the cost components of BT-enabled PSC, paying particular attention to demand uncertainty, and then designed a multi-function BT-enabled PSC mathematical cost model. We utilized four Supervised Learning (SL) algorithms after data generation, namely Naive Bayes (NB), Support Vector Machine (SVM), Decision Tree (DT), and K-Nearest-Neighbors (KNN), in conjunction with two Evolutionary Computation (EC) algorithms: Harmony Search (HS) and Particle Swarm Optimization (PSO), resulting in an overall set of eight algorithms. We utilized the EC algorithms to optimize the hyperparameters of the SL algorithms and enhance the multi-function model. We chose these widely recognized algorithms because they provide effective solutions for engineering issues and help us examine their behaviors within the new cost multi-function model. Finally, we evaluated the multifunctional model using four performance metrics and identified the most reliable prediction algorithms using a point-based ranking system, Total Ranking Score (TRS).

The remainder of the paper is structured as follows.

We start by giving a general review of the literature regarding BT-enabled PSCBT-enabled PSC. SL optimized by EC, and uncertain demand in Section 2. Then, in Section 3, we go through the methodology and data generation, and in Section 4, we talk about the design of the mathematical model for the multi-function BT-enabled PSC BT-enabled PSC model. In Section 5, the experiments and the results are presented. We address the findings, limitations, and directions for further study in section 6 before summarizing our findings in section 7.

2. Literature Review

2.1. Introduction to PSC (Pharmaceutical Supply Chain)

PSC management is essential for tracking materials sourced for manufacturing and distributing pharmaceuticals, while SCS seems necessary for industries moving materials and goods [1]. PSC is a considerable part of healthcare expenditures and plays an essential role in healthcare [2], and the PSC process significantly influences ultimate patient outcomes and medication quality [3]. Uthayakumar and Priyan define PSC as ‘‘the integration of all activities associated with the flow and transformation of drugs from raw materials to the end-user, as well as the associated information flows, through improved SC relationships to achieve a sustainable competitive advantage’’ [4]. Haq and Muselemu Esuka [12] stress that PSC systems protect patient data privacy. Finally, several stakeholders participate in the movement of a product in the PSC system, including Primary manufacturers, Secondary manufacturers, Distribution centers/wholesalers, and Retailers (such as pharmacies and hospitals), each with their specifications, obligations, and priorities [5].

2.2. Introduction to BT (Blockchain Technology)

BT is a cutting-edge technology with various applications such as cryptocurrency, financial services, risk management, and public and social services [6]. Hosseini Bamakan et al. [7] introduce three categories of BT: public, private, and consortium, according to the type of access for their users. In public BT, all data and transactions are recorded in a chain of blocks, and normally, medical organisations do not participate in networks that anyone can access and join because clinical institutes deal with highly classified and sensitive data [7]. BT is currently being explored for the following areas in healthcare: securing patient and provider identities, managing supply chains in pharmaceuticals and medical devices, medical fraud detection, public health surveillance, and sharing public health data to help public health workers respond faster to a crisis [1]. Decentralization is the main aspect of BT, as all information is stored permanently and securely without requiring a centralized authority to monitor the transactions [8].

2.3. Key Features and Benefits of BT in PSC

BT can improve healthcare data sharing and storage systems thanks to its decentralization, immutability, transparency, and traceability features [9]. PSC has four main elements: the suppliers, the pharmacy, the hospital, and the patients. The suppliers manufacture or distribute the medicines; a pharmacy orders medicines from the suppliers, keeps the medicines safe, manages the inventory, and distributes the medicines to the hospital; a hospital provides medicines to patients and places orders from the pharmacy; and the patients require treatment and medicines [10]. The key features of BT ensure the traceability of medical products by providing a transparent, decentralized tracking system [8]. Mansur Hussien et al. state that the immutability and timestamps of BT transactions allow the accurate tracking of products and ensure that the information inside a block cannot be altered. Mansur Hussien et al. also found that the data transparency feature in BT can detect the full path of counterfeit medication. The key BT attributes that allow it to meet the requirements of many applications in the healthcare industry are decentralisation, transparency, security and privacy, and scalability and storage capacity [8]. Decentralisation prevents a single point of security failures, as BT distributes medical data across the network rather than from a single central point [8]. BT uses transactions and multilateral relationships that have been made more accurate, stable, and efficient by using smart contracts, and BT’s transparency allows different healthcare providers to access patients’ medical data, thereby overcoming the lack of transparency in the healthcare industry [8]. BT can allow patients to have secure access to their medical history records and professionals involved in their treatment [6]. Security and privacy are especially crucial as the volume of medical data continues to grow, requiring creative processing and storage methods. BT’s methods serve to safeguard healthcare storage and data transfer. Scalability and storage capacity are directly linked to confidentiality and scalability issues [8].

2.4. Enabling BT in PSC

BT in the pharmaceutical industry plays a significant role in safeguarding and optimizing the SC [11]. The present pharmaceutical SCS is out-of-date and unable to fend against 21st-century cyber-security threats because it does not provide visibility and control or regulatory power over medication distribution [12]. Haq and Muselemu Esuka note that a BT-enabled PSC BT-enabled PSC will examine the products without knowing the manufacturer’s trade secrets; however, patients’ medical records will be accessible to certified network participants – without revealing any patient’s private data [12]. BT-enabled PSC BT-enabled PSC improves the security and trust of the system, prevents any single person from modifying the data and transactions, and eliminates the biases found in traditional SCSs [12]. BT can maintain the PSC’s monitoring system, track medication responsibilities, store individual patient information, and analyze the effects of a particular procedure [13]. Another advantage of BT is maintaining hospital financial statements and minimizing the data transformation time and cost [13]. Kumar Badhotiya et al. (2021) believe that the concept of BT in the PSC can be utilized to detect fake medicines with proper control oversupply and demand of the drugs, allowing pharmaceutical companies to unmask fake and unregistered medicines [11].

2.5. Uncertain Demand in PSC

Uncertainty in a PSC may arise in product demand, price, clinical trials, raw material availability, regulatory changes, investment risk, unit manufacturing, transportation costs, etc. [14]. Ahmadi et al. observe that uncertainty may also arise because of the required data’s unavailability and the dynamic and imprecise nature of this data. PSCs deal with uncertainty, which makes them different from other SCs; for example, the demand for each medicine is uncertain and can be influenced by seasonal changes [10]. Moreover, [10]. Ahmadi et al. (2017) classify uncertainty into two categories: (a) uncertainty in data (which is the most common uncertainty faced in SCs) and (b) flexibility in constraints and goals. There are typically two forms of uncertainty in data: (a) randomness, which originates from the random nature of the data, and (b) epistemic uncertainty, which is due to the unavailability or insufficiency of required data, leading to imprecise data being extracted from the experts’ subjective opinions [14].

2.6. SL optimized by EC

An intelligent optimization algorithm is applied to optimize the hyperparameters of the machine learning or deep learning model to build a modified model [15]. During the evolutionary progress, the EC algorithm explores possible combinations of parameters [16]. The deep learning model generally has a long training time, and its parameters are not optimal [17]. Therefore, Li et al. state that improving the deep learning model and optimizing the hyperparameters would make a notable difference. Li et al. also mention that the parameters of deep learning neural network models are usually set empirically, which means that finding the best predictive performance of the model takes a considerable amount of time. Neural network model training usually faces some problems, such as local optimization or overfitting, and it is difficult to determine many network parameters. An intelligent optimization algorithm that constantly improves the neural network model or optimizes the parameters is an important addition [18]. For example, the improved Sparrow Search Algorithm used by Tian and Chen [18] optimizes the hyperparameters of the Long Short-Term Memory model. Shu et al. [19] apply Bayesian optimization to search the hyperparameter space of label propagation and spreading using the default random Forest Algorithm [19]. Another approach is to use the swarm intelligence optimization algorithm to find a model’s optimal parameters according to the dataset’s characteristics [17].

3. Research Method and Data Generation

This section provides the research method and data generation process that evaluates, optimizes, and estimates the cost of the multi-function BT-enabled PS BT-enabled PSC C model. In the first step, Python software helps us generate raw data for our multi-function BT-enabled PSCBT-enabled PSC model. As a built-in function of the random module, we used randint(), one of the most well-known tools for generating random data in Python. Once a pair of parameters are given, this module provides a random integer number from the inclusive range between the lower and upper bounds (including both limits). The generated dataset includes six features as the components of the model (C_{raw_materials}, C_{finished_products}, C_{shortage_surplus}, C_{BT_Installation}, C_{BT_Transaction}, and D_{i,uncertainty}) and the total cost for objective 1 (C_Total) as the label in the regression process. 5000 series of the produced raw data were uploaded to https://data.mendeley.com/datasets/sfc7hst95m, including six components and the total costs of the multi-function BT-enabled PSCBT-enabled PSC model. In this paper, we combine EC and SL approaches to evaluate the multi-function BT-enabled PSCBT-enabled PSC model.

The HS and PSO algorithms are applied for the EC approach, and the KNN, DT, SVM, and NB algorithms are applied for SL. The HS and PSO algorithms improve the hyperparameters of the KNN, DT, SVM, and NB algorithms and minimize the model prediction errors. EC combined with four algorithms (KNN, DT, SVM, and NB) reduces prediction errors and thus plays a significant role in improving the SL algorithms’ performance. 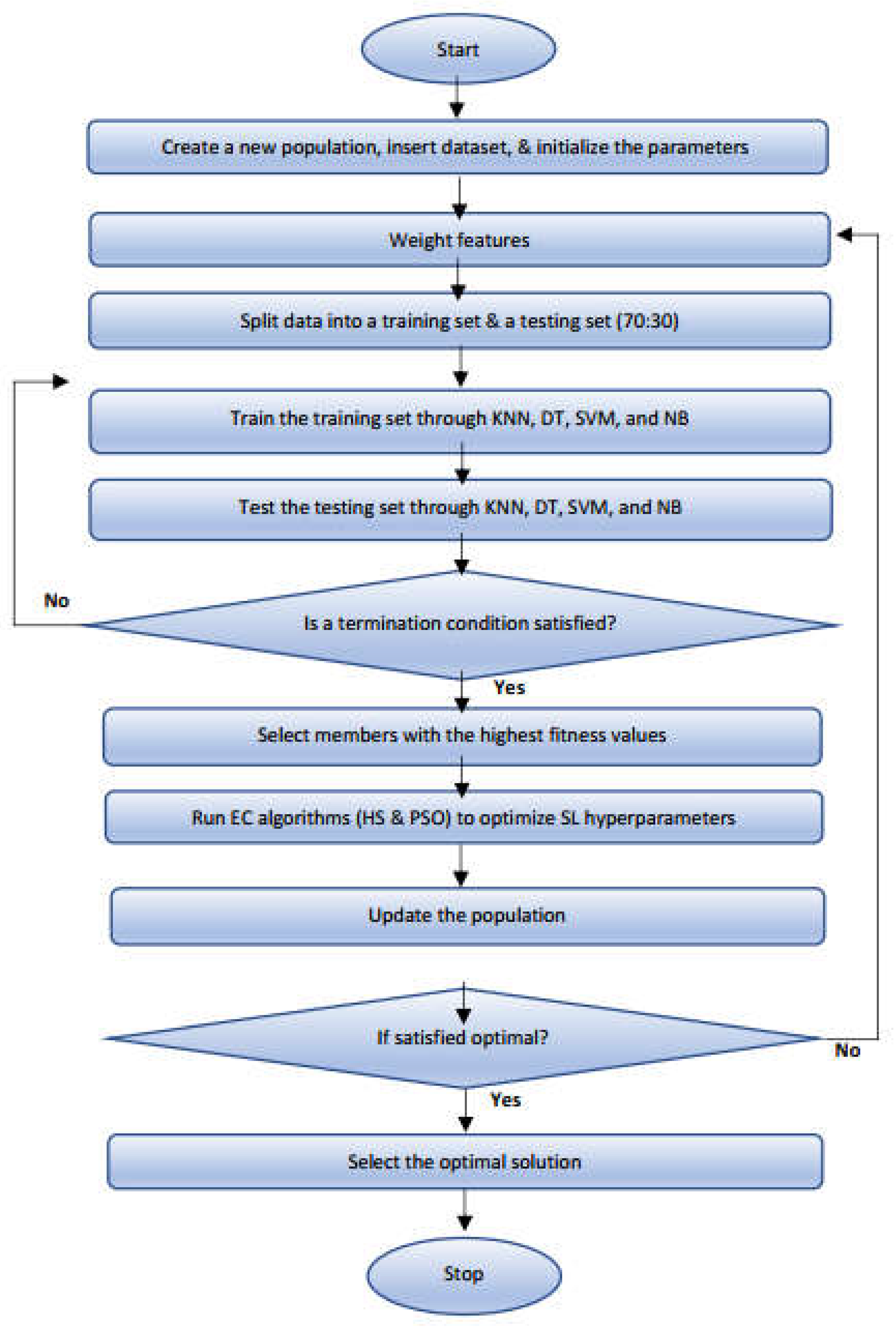Figure 1 illustrates the research method’s flowchart and the algorithm’s implementation in MATLAB. This flowchart includes the following steps: creating the population using four SL algorithms (KNN, DT, SVM, and NB) combined with two EC algorithms (HS and PSO), incorporating the Feature Weighting approach and using four performance metrics (MSE, RMES, MAE, and R²), and each method (SL combined with EC algorithms) received a score with a Total Ranking Score technique. Initializing the parameters and generating a new population are the first steps in the flowchart. Next, we use the Feature Weighting (FW) method to assess each feature’s significance, give it a suitable weight, and calculate how relevant it is to the model as a whole. Every feature instance’s value is multiplied throughout the FW process, and the feature instances are then sorted by their values [20]. The chosen features are often equally significant for predicting the outcome.

However, some features with a more significant weight might affect the performance and accuracy of the entire algorithm and the outcomes. We then split the data into two parts: 70% of the dataset for training and 30% for testing. We applied four different SL algorithms (KNN, DT, SVM, and NB) to predict the costs of the model and then select the precise algorithms for the model. Two EC algorithms (HS and PSO) are then utilized to improve the hyperparameters of the SL algorithms and enhance the SL algorithms’ performance. Next, we use four performance metrics to access the model: the Mean Square Error (MSE), the Root Mean Square Error (RMSE), the Mean absolute error (MAE), and the correlation coefficient (R²). This method produced the following outputs: five FWs (one weight for each feature) for objective 1 and four performance metrics for objectives 1 and 2.

The Total Ranking Score (TRS), a score-based ranking methodology, was utilized to identify which prediction algorithms were the most reliable. Based on the estimated MSE, RMES, MAE, and R2 values, the TRS assigned a score to each approach and five feature weight values in objectives 1 and 2. After that, each method’s ranking position was determined by adding all the scores.

4. Proposed Optimization Multi-Function BT-enabled PSC Model

This section defines the nonlinear BT-enabled PSC cost model with two objectives. The proposed model is a nonlinear multi-function approach to evaluate Pharmaceutical Supply Chains with their uncertainties in demand parameters. The model is designed to estimate the total costs of BT-enabled PSCs, including considering the unmet demand in the pharmaceutical system. The mathematical model with two objectives includes the Raw Materials cost, Finished Products cost, Shortage-Surplus cost, Blockchain Installation cost, Blockchain Transaction cost, and the Unsatisfied Demand of product families. Eq. (1) expresses the multi-function BT-enabled PSC model.

{Obj}_{1} = [C_{PCS}] + [C_{Blockchain}] {Obj}_{1} = [C_{raw_materials} + C_{finished_products} + C_{s h o r t a g e_s u r p l u s}] + [C_{BT_Installation} + C_{BT_Transaction}] Min {Obj}_{1} = M i n (\sum_{i = 1}^{M} [C_{i, r a w_m a t e r i a l s} + C_{i, f i n i s h e d_p r o d u c t s} + C_{i, s h o r t a g e_s u r p l u s} + C_{i, B T_I n s t a l l a t i o n} {+ C}_{i, B T_T r a n s a c t i o n}]) Min {Obj}_{2} = M i n (Max \sum_{i = 1}^{M} [D_{i, uncertainty}])

(1)

Table 1 lists the parameters and constraints for the BT-enabled PSC cost model in the pharmaceutical system, including the parts of the mathematical model.

A list of the assumptions is provided below, along with additional notations and assumptions as required [4].

The PSC comprises a single pharmaceutical system with multiple (M) pharmaceutical products. For the i^th product, the pharmaceutical system produces nq_i units at a finite production rate of p_i per unit time in one production cycle.
For the i^th raw material, all orders are delivered to the pharmaceutical system in one shipment by an external supplier. In other words, the quantity of the i^th raw material required for production in each production cycle is instantaneous.
All expired pharmaceutical products held in inventory by the pharmaceutical system are a constant fraction of the accumulated inventory.
The pharmaceutical system offers a certain trade credit period (permissible payment delay) for all products to cooperate with clients (like a hospital or a pharmacy) in an integrated strategy. Thus, the customers do not have to pay immediately on receipt of products.
The credit period T_c is less than the reorder interval for each product, meaning the credit period cannot be longer than when another order is placed. This agrees with the usual practice in healthcare industries.
Products are all packed, and the number of products is an integer.
It is assumed the model uses the available Public Blockchain platform in the market as a hosting platform.
Node hosting space (cloud storage) stores data; the node number is the copy number of data. We assigned one node in this research (A Blockchain node’s primary job is to confirm the legality of each subsequent batch of network transactions, known as blocks).
Unsatisfied demand is positive; otherwise, it is zero.

4.1. Cost elements of a PSC

4.1.1. Raw Materials cost elements

The following function, Eq. (2), represents the Raw Materials cost in the pharmaceutical system, including the Ordering cost, Holding cost for perfect raw materials, Holding cost for imperfect raw materials, Labor cost for order handling and receipts, and Transportation cost. Eq. (2) shows the Cost Order (

\frac{a_{w i} d_{i}}{n q_{i}}

), the Holding cost for perfect raw materials (

\frac{d_{i} (1 - β_{i}) q_{w i} h_{w i}}{n_{} q_{i}}

), the Holding cost for imperfect raw materials (

\frac{h_{w i} β_{i} q_{w i} {q_{w i} d_{i}}_{}}{r_{s i} n_{} q_{i}}

), the Labor cost for order handling and receipt (

\frac{d_{i} {q_{w i} v_{w i}}_{}}{n q_{i}}

), and the Transportation cost (

\frac{F_{w} d_{i}}{n q_{i}}

) (Uthayakumar & Priyan, 2013; Havaeji, Dao, & Wong, 2022). It is assumed that each quantity q_w_i contains defective raw materials at a rate of

β

_i, which is a random variable.

\sum_{i = 1}^{M} [\frac{a_{w i} d_{i}}{n q_{i}} + \frac{d_{i} (1 - β_{i}) q_{w i} h_{w i}}{n_{} q_{i}} + \frac{h_{w i} β_{i} q_{w i} {q_{w i} d_{i}}_{}}{r_{s i} n_{} q_{i}} + \frac{d_{i} {q_{w i} v_{w i}}_{}}{n q_{i}} + \frac{F_{w} d_{i}}{n q_{i}}]

(2)

4.1.1. Finished Products cost elements

Finished Product i for the pharmaceutical system, which equals the sum of the Set-up cost, Holding cost, Production cost, Expected opportunity interest, and Expiry cost. Equation (3) shows the cost elements of the Finished Products in the pharmaceutical system: the Set-up cost (

\frac{s_{i} d_{i}}{n q_{i}}

), the Holding cost (

\frac{h_{v i} q_{i}}{2} [n (1 - \frac{d_{i}}{p_{i}}

)

-

+

\frac{2 d_{i}}{p_{i}}]

), the Production cost (

{d_{i} p}_{c i} q_{i}

), the Expected opportunity interest loss per unit time for the product i is I_vb_iT_cd_i, and the Expiry cost (

{q_{i} d}_{c i} c_{d c i} [(\frac{d_{i}}{p_{i}} + (n - 1)) - \frac{{n d}_{i}}{2 p_{i}}]

) (Uthayakumar & Priyan, 2013; Havaeji, Dao, & Wong, 2022).

\sum_{i = 1}^{M} [\frac{s_{i} d_{i}}{n q_{i}} + \frac{h_{v i} q_{i}}{2} [n (1 - \frac{d_{i}}{p_{i}}) - 1 + \frac{2 d_{i}}{p_{i}}] + {d_{i} p}_{c i} q_{i} + I_{v} T_{c} d_{i} + {q_{i} d}_{c i} c_{d c i} [(\frac{d_{i}}{p_{i}} + (n - 1)) - \frac{{n d}_{i}}{2 p_{i}}]]

(3)

4.1.1. Shortage-Surplus cost elements

It should be noted that medicine and drug shortages are serious issues in any society, and they are a worldwide problem that governments face because of demand uncertainty and other factors [21]. Eq. (4) expresses the shortage-surplus cost equation, including Shortage and Surplus costs.

\sum_{i = 1}^{M} [{z^{1}}_{i} \times c o s t S U_{i} + {z^{2}}_{i} \times τ_{i} \times c o s t S U_{i}]

(4)

In Table 1, z¹_i ≥ p_i

-

d_i and z²_i ≤ d_i

-

p_i represent a lower bound for the surplus and an upper bound for the shortage of a product, respectively.

4.1. Blockchain Implementation cost elements

According to Havaeji, Dao, and Wong (2022), Blockchain Implementation cost (C_Blockchain) consists of two components: Blockchain Transaction cost (C_{BT_Transaction}) and Blockchain Installation cost (C_{BT_Installation}) (Eq. (5)). As an alternative for designing and developing a Blockchain platform, it is assumed the model uses the available public Blockchain platform in the market as a hosting platform.

C_Blockchain = C_{BT_Transaction} + C_{BT_Installation}

(5)

Havaeji, Dao, and Wong (2022) introduced the C_{BT_ Transaction} calculation to pay miners in Eq. (6): Total Transaction cost = Gas cost (gasUsed × gasPrice) + Storage cost (Longo, Nicoletti, Padovano, d’Atri, & Forte, 2019; Jabbar & Dani, 2020; Wood, 2020).

G_u × g_p × 365 + s × C_s

(6)

G_u × g_p is the Gas cost per day, and s × C_s is the storage cost per year, with a secured cloud-based warehouse storing the actual data off-chain. The IBM Cloud website calculates the storage cost portion [22]. Table 1 also presents the parameters and constraints for the BT Transaction costs.

Wood (2020) mentions Ethereum as a fee for all programmable computation and a kind of currency called Ether (ETH). Proof-of-Work (PoW), like Bitcoin and Ethereum, is the most popular consensus protocol in a public blockchain system [23]. There are two parts to the cost of a typical transaction: gasLimit and gasPrice. Longo et al. (2019) state that this calculation must be performed based on the gas used by a transaction to calculate the cost of the Ethereum blockchain. The gasLimit (purchased from the sender’s account balance) is the maximum gas amount that should be used to execute any transaction; any unused gas at the end of a transaction is refunded (at the same rate of purchase) to the sender’s account (Wood, 2020; Havaeji, Dao, & Wong, 2022). Wood clarifies that the number of W_ei units to be paid for per unit of gas is the gasPrice (a scalar value), which comprises all computation costs incurred due to the transaction’s execution. After submitting a transaction, a given amount of gas is associated with that transaction [24].

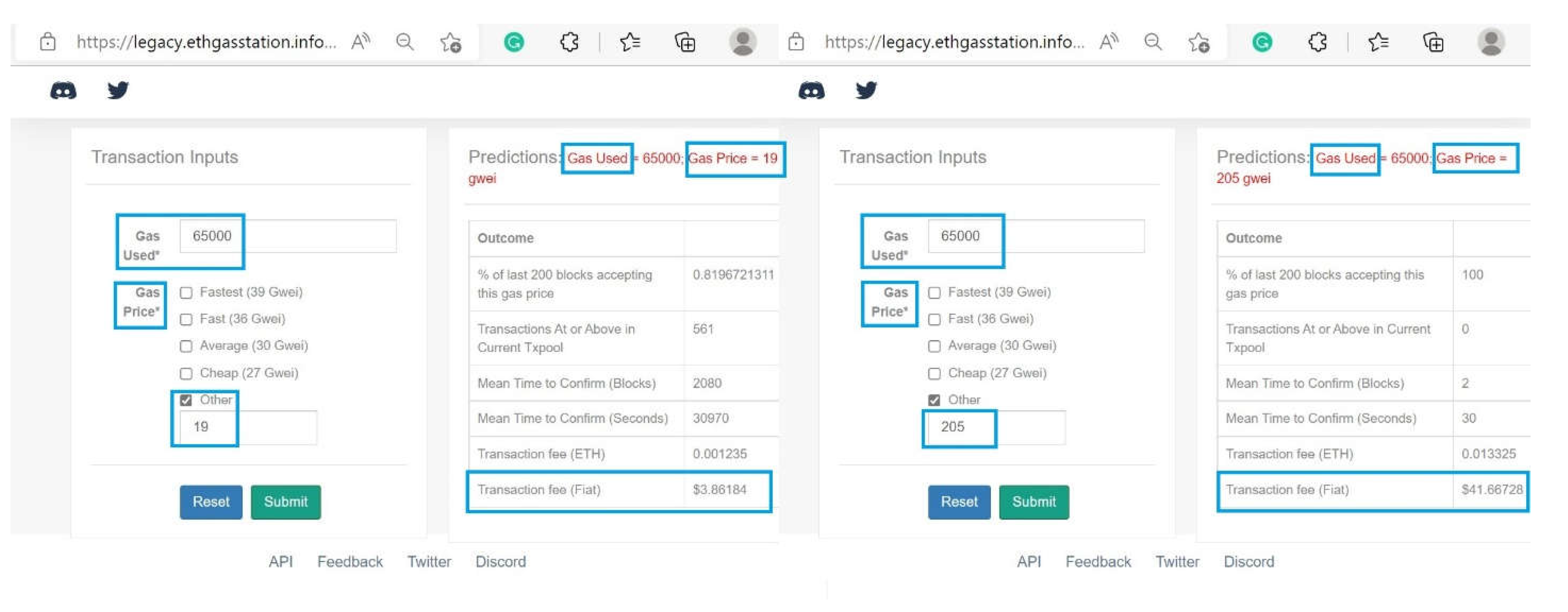
ETH Gas Station calculates G_u × g_p and incentivizes computation within the network (Jabbar & Dani, 2020; ETH Gas Station, 2022). The gW_ei is the cost paid to the transaction validators (or the network) for conducting a transaction on the Ethereum Blockchain. The most important aspect is how gW_ei is converted to USD based on the current price of Ethereum by using the ETH Gas Station website [25]. The gasUsed (a scalar value) is the total gas used in transactions. The amount 65000 as the amount of gasUsed and the range of 19 gW_ei to 205 gWei as the gasPrice were selected to calculate the G_u × g_p cost and convert the gW_ei cost to USD via the ETH Gas Station website (Figure 2).

The Blockchain Installation cost (C_{BT_Installation}), or the cost of utilizing BT for PSC, has four cost elements (Eq. (7)), including a Fixed cost (c_fixed), Onboarding cost (c_onboarding), Maintenance cost (c_mc), and Monitoring cost (c_mo) (Gopalakrishnan, Hall, & Behdad, 2021; Havaeji, Dao, & Wong, 2022).

\sum_{i = 1}^{M} [c_{f i x e d} + (c_{onboarding} \times U + c_{m c} + c_{m o}) \times q_{i}]

(7)

The Onboarding cost (such as onboarding and training) is the cost involved in training suppliers and clients into active users of a product or service and includes any expenses and costs, which was about integrating new employees into a system so they could learn about and be trained in BT. The c_mc and c_mo costs occur yearly and contribute to 15–25 percent of a project’s value (Takyar, 2021a; Gopalakrishnan, Hall, & Behdad, 2021). Other parameters, including the parameters and constraints for the Blockchain Installation cost, are also shown in Table 1.

4.1. Uncertain Demand elements

The PSC deals with uncertainty, given that the demand for each product of medicine is uncertain and can be influenced by various factors, such as seasonal changes. The uncertain demand occurs when the amount of demand exceeds the available stock. For instance, if a drug price is too low, the demand for that product will be increased, and customers will purchase it from suppliers that can accommodate their demand. This process leads to drug shortages, and so producers should raise their prices and output until supply equals demand and equilibrium is reached. The uncertainty imposes many challenges for modeling and determining optimal solutions. Our model represents the demand uncertainty as shown in Eq. (8), with the input parameters considered under uncertainty [26, 5, 21, 14].

Min {Obj}_{2} = Min ({Max}_{} \sum_{i = 1}^{M} [τ_{i} [d_{i} - p_{i}]])

(8)

In Eq. (1), the second objective function (Obj₂) aims to reduce the maximum unsatisfied demand of product families, implying an upper constraint for overall unsatisfied demand.

Since the unit unfulfilled demand of a low-priority product family is not as important as that of a high-priority product family, this objective is empowered by incorporating the importance parameters π_p to take a balanced attitude towards different product families. To better explain Eq. (1), D_i,u_ncertainty is equal to τ_i[d_i

-

p_i] and should be positive; otherwise, it is zero (D_{i,uncertainty} ≥ 0).

4.1. Optimization Multi-Function for BT-enabled PSC

The integrated expected total cost for the multi-function BT-enabled PSC model for products in a pharmaceutical system can be expressed in Eq. (9) as the sum of the expected total costs of the following components: Raw Materials cost (Ordering cost, Holding cost for perfect raw materials, Holding cost for imperfect raw materials, Labor cost for order handling and receipt, and Transportation cost) (Eq. (2)), Finished Products cost (Set-up cost, Holding cost, Production cost, Expected opportunity interest, and Expiry cost) (Eq. (3)), Shortage-Surplus cost (Shortage cost and Surplus cost) (Eq. (4)), Blockchain Installation cost (Fixed cost, Onboarding cost, Maintenance cost, and Monitoring cost (Eq. (7)), and Blockchain Transaction cost (Gas cost and Storage cost) (Eq. (6)). The second objective is the Unsatisfied Demand, given by Eq. (8).

Min {Obj}_{1} = \sum_{i = 1}^{M} [\frac{a_{w i} d_{i}}{n q_{i}} + \frac{d_{i} (1 - β_{i}) q_{w i} h_{w i}}{n_{} q_{i}} + \frac{h_{w i} β_{i} q_{w i} {q_{w i} d_{i}}_{}}{r_{s i} n_{} q_{i}} + \frac{d_{i} {q_{w i} v_{w i}}_{}}{n q_{i}} + \frac{F_{w} d_{i}}{n q_{i}} + \frac{s_{i} d_{i}}{n q_{i}} + \frac{h_{v i} q_{i}}{2} [n (1 - \frac{d_{i}}{p_{i}}) - 1 + \frac{2 d_{i}}{p_{i}}] + {d_{i} p}_{c i} q_{i} + I_{v} T_{c} d_{i} + {q_{i} d}_{c i} c_{d c i} [(\frac{d_{i}}{p_{i}} + (n - 1)) - \frac{{n d}_{i}}{2 p_{i}}] + {z^{1}}_{i} \times {costSU}_{i} + {z^{2}}_{i} \times τ_{i} \times {costS}_{i} + c_{fixed} + (c_{onboarding} \times U + c_{mc} + c_{mo}) \times q_{i}] + G_{u} \times G_{p} \times 365 + s \times C_{s} Min {Obj}_{2} Min ({Max}_{} \sum_{i = 1}^{M} [τ_{i} [d_{i} - p_{i}]])

(9)

5. Results

The numerical examples considered in this study validate the proposed multi-function BT-enabled PSC model in this section. The model is designed to minimize the total costs of BT-enabled PSC, or objective 1, and the unmet demand in the pharmaceutical company, objective 2. This section displays the findings, the performance metrics of eight algorithms on the produced datasets in objectives 1 and 2, and the weights of the objective 1 cost features. The numerical dataset examined here validates the multi-function model and demonstrates the performance of our research method. We used HS and PSO (EC algorithms) to enhance the outputs and to optimize the hyperparameters of the KNN, DT, SVM, and NB SL algorithms. This combination provides eight algorithms to reduce prediction errors: HS-KNN, HS-DT, HS-SVM, HS-NB, PSO-KNN, PSO-DT, PSO-SVM, and PSO-NB. To evaluate the efficiency of the proposed algorithms, four performance metrics were used: the MSE, RMSE, MAE, and R². In objective 1, the FW technique was also employed to determine the influencing features for the produced dataset. There was no need to use FW for objective 2 because it only has one component. Without affecting the basic data content, FW plays a key role in analysis. After data generation, we designed the model, executed the proposed methodology, and used MATLAB software to evaluate the multi-function BT-enabled PSC model. In eighty runs (410 + 410), we examined the ‘‘average’’ of the four performance metrics in objectives 1 and 2 and the ‘‘average’’ of the weight of the cost features in objective 1. We used averages to analyze the results since the runs have different outputs, and the average provides us with stability and dependability in behavioral data. Each run had a maximum of 1000 iterations. Next, rather than assessing the predictions of the multi-function BT-enabled PSC model in each run, we compared the average of every ten runs. Lastly, the TRS technique was utilized to identify the most reliable forecasting algorithms for the multi-function BT-enabled PSC model. Tables 2 through 9 show all of the findings.

5.1. HS combined with four SLs

Four performance metrics and the FW method (the weights of five cost features) assessed the multi-function BT-enabled PSC model which has two objectives. MATLAB was applied to run HS together with four SL algorithms (HS-KNN, HS-DT, HS-SVM, and HS-NB) 40 times (each algorithm was run 10 times) in 1000 iterations.

Table 2 presents the four performance metrics for four algorithms in objectives 1 and 2, the five weights of the cost features in objective 1, each performance metric’s average value, and the average values for each cost feature in 40 runs. Table 3 and Table 4 are derived from Table 2.

The average of four performance evaluation criteria for each approach in objectives 1 and 2 is summarized and compared in Table 3. In Table 3, HS-NB demonstrates robust behaviour in both objectives, with a minimum average of MSE, RMSE, and MAE and the best average R² of 1 for objective 1 among the four methods. Objective 2 is realized well in both HS-SVM and HS-NB, with R² values of 0.64 and 0.61, respectively. The weakest results in all performance metrics are for HS-KNN in objective 1 and HS-DT in objective 2. Table 3 shows that the HS-NB algorithm performs better at realizing objectives 1 and 2 for the multi-function BT-enabled PSC model in comparison to the other suggested algorithms.

Table 4 focuses on the average of the weights of each cost feature using the FW technique for the HS-KNN, HS-DT, HS-SVM, and HS-NB algorithms in objective 1. Objective 2 has just one element, and the FW approach does not work. HS-NB has the most significant average weight for the Raw Materials cost feature (0.86) and the lowest average weight for Finished Products and BT Installation (0.00) among these four approaches. The BT Installation cost feature via the HS-DT algorithm has the second-highest average weight (0.77), and next is the BT Transaction cost feature via the HS-KNN algorithm (0.73). With HS-DT (0.02), the BT Transaction cost feature has the second-lowest average weight. Furthermore, features like the BT Transaction cost and BT Installation fluctuate because the algorithms have different behavior.

5.2. PSO linked with four SL algorithms

In the next step, a PSO linked with four SL algorithms (PSO -KNN, PSO -DT, PSO -SVM, and PSO -NB) was run forty times (ten runs for each) (see Table 5). Next, we used the four performance metrics for the four algorithms in objectives 1 and 2, and the weights of the five cost features in objective 1 to evaluate the multi-function BT-enabled PSC model in these 40 runs (10 runs for each algorithm). In addition, Table 5 shows the average values of the performance metrics and the average values of the weights of the cost features. Table 6 and Table 7 are derived from the data presented in Table 5.

Table 6, from Table 5, displays the average values of four performance indicators used in assessing the PSO algorithm linked with four SL algorithms in objectives 1 and 2. In this table, PSO-NB performs better than the others, with an average R² of 1 and a minimum of Ave-MSE = 106765.19, Ave-RMSE = 170.34, and Ave-MAE = 133.07 in objective 1. On the other hand, In objective 1, PSO-DT has the lowest score of any performance indicator. In objective 2, PSO-NB also behaves well with all performance metrics among the four methods. As a result, we believe that the PSO-NB findings are more trustworthy than the results produced by the other offered approaches in both objectives.

Table 7 illustrates the average weights of five cost features through the FW method in the PSO-KNN, PSO-DT, PSO-SVM, and PSO-NB algorithms in objective 1. Objective 2 has only one element, which is why the FW approach does not work. PSO-NB provides the minimum and maximum average weights among all cost features. The Shortage Surplus cost feature receives the highest average weight of 0.98, while the Finished Products and BT Installation cost features have the lowest average weight of 0.16 for the PSO-NB algorithm. The PSO-DT method produced the second-highest average weight for the Finished Products cost feature (0.48). A variation in the average weight of some features in this table is observed, such as Shortage Surplus with 0.98 and 0.45 by PSO-NB and PSO-KNN, respectively. The reason for this variation is explained by the algorithms’ varying behavior.

For multi-function BT-enabled PSC

Table 8 displays the TRS of eight algorithms according to the values acquired in objectives 1 and 2 for Ave-MSE, Ave-RMSE, Ave-MAE, and Ave-R2. To compute the TRS, we allocated the highest scores to the lowest Ave-MSE, Ave-RMSE, and Ave-MAE values, and the highest scores to the highest Ave-R2 values (and inversely). Generally, with a TRS of 63, the HS-NB algorithm performed better than other algorithms, followed by PSO-NB with a TRS of 51, HS-SVM with a TRS of 47, and HS-DT with a TRS of 37. TRS scores of 23 (rank 8th) and 27 (rank 7th) were obtained by HS-KNN and PSO-KNN, respectively.

Table 9 indicates the average weights ranking of the five cost features in objective 1: Raw Materials, Finished Products, Shortage Surplus, BT Installation, and BT Transaction for the HS-KNN, HS-DT, HS-SVM, HS-NB, PSO-KNN, PSO-DT, PSO-SVM, and PSO-NB algorithms. This table provides a suitable average weight and a TRS to demonstrate the significance of each cost feature. In the TRS procedure, the average weight with a higher TRS obtains a more significant priority (and inversely). In general, the Raw Materials cost in objective 1 has the best TRS of 30 for the average weight, second by the Shortage Surplus cost, which has a TRS of 26, and the Finished Products cost, which has a TRS of 25. The minimal TRS for average weight is assigned to the BT Installation and BT Transaction cost features; both rank fourth with TRS = 22.

6. Discussion

This section presents the outcomes of the suggested eight strategies for minimizing the prediction errors of the multi-function BT-enabled PSC model. In this section, respond to three of the research questions listed in the introduction and discuss the results. As mentioned before, the multi-function BT-enabled PSC model has six components: Raw Materials cost, Finished Products cost, Shortage-Surplus cost, Blockchain Installation cost, Blockchain Transaction cost, and Unsatisfied Demand of product families. Our model has two objectives. The first includes Raw Materials cost (Ordering cost, Holding cost for perfect raw materials, Holding cost for imperfect raw materials, Labor cost for order handling and receipt, and Transportation cost), Finished Products cost (Set-up cost, Holding cost, Production cost, Expected opportunity interest, and Expiry cost), Shortage-Surplus cost (Shortage cost and Surplus cost), Blockchain Installation cost (Fixed cost, Onboarding cost, Maintenance cost, and Monitoring cost, and Blockchain Transaction cost (Gas cost and Storage cost). The second objective covers the Unsatisfied Demand. This explanation answers our first research question. Concerning the second study question, we chose those algorithms (among the eight considered here) that performed better in terms of reducing the prediction errors of the multi-function BT-enabled PSC model. 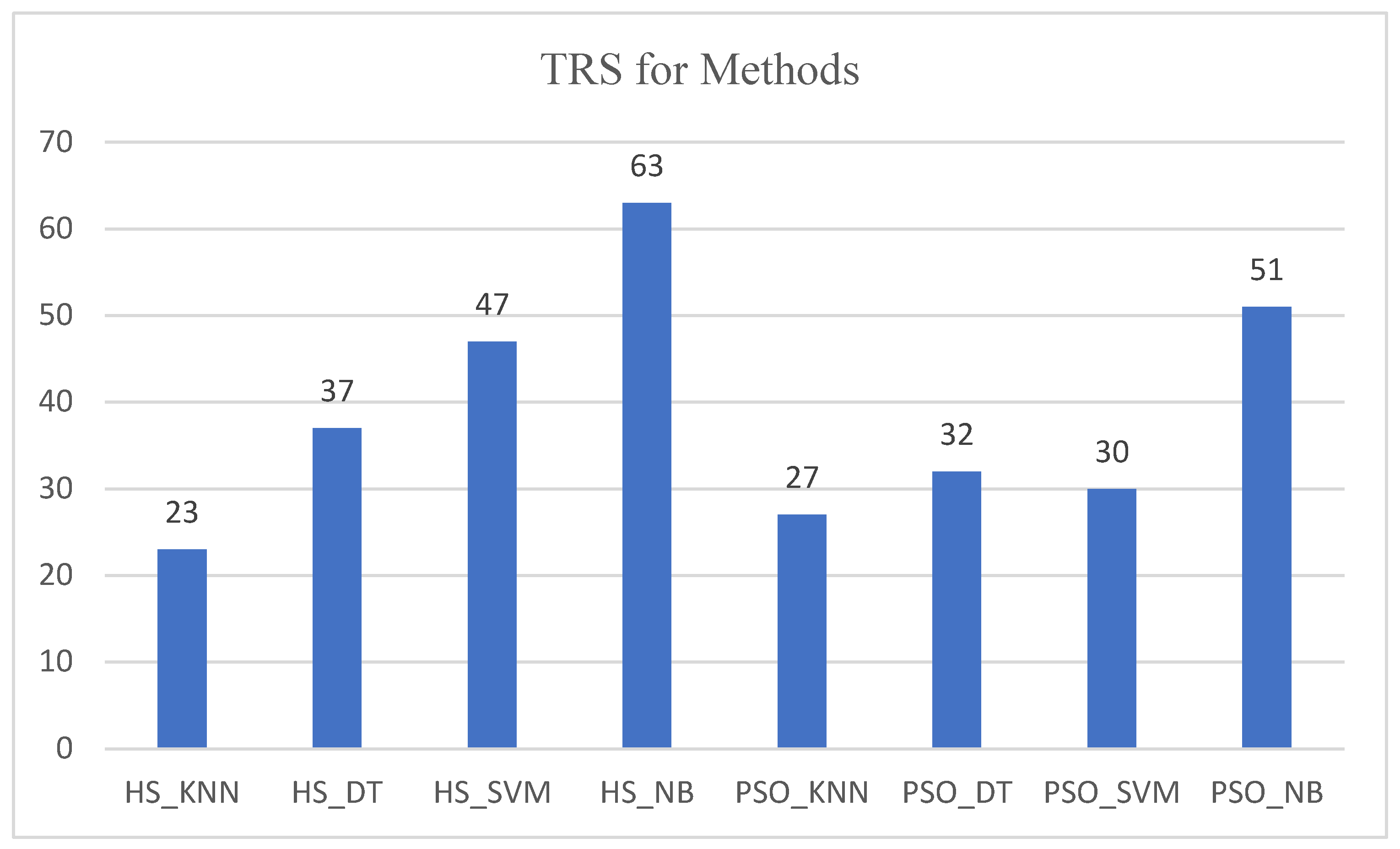Figure 3 displays the TRS for all eight algorithms tested (HS-KNN, HS-DT, HS-SVM, HS-NB, PSO-KNN, PSO-DT, PSO-SVM, and PSO-NB) based on the data reported in Table 8. The efficiency of the eight methods is assessed using four performance indicators (MSE, RMSE, MAE, and R2). The findings of this study suggest that the HS-NB (first position) and PSO-NB (second position) algorithms perform better than the other examined algorithms in terms of reducing model prediction errors. This indicates that NB, when linked with either HS or PSO, is thought to be the most efficient regression method. The EC algorithms (HS and PSO) are also important in enhancing the hyperparameters of the eight SL algorithms. Moreover, according to the performance metrics’ values and the TRS scores, the SVM, DT, and KNN algorithms, combined with HS and PSO, cannot adequately estimate the costs of the multi-function BT-enabled PSC model. As a result, in response to the second question, we determined that the NB algorithm, when linked with HS and PSO, is the most reliable forecasting algorithm for our multi-function model based on TRS and four performance indicators.

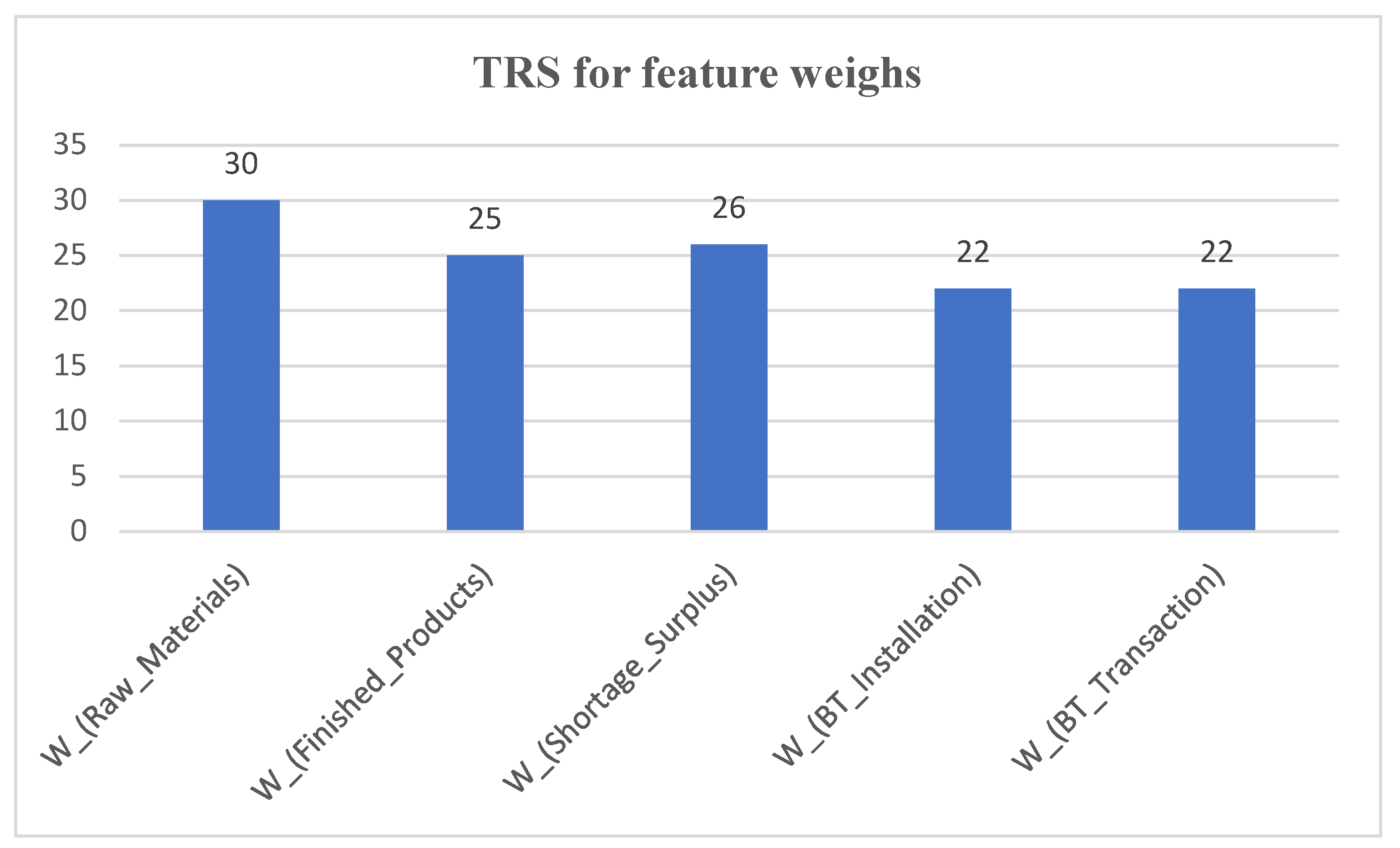
The third research question is to determine the significant components of the model. The only component of objective 2 in the model is the Unsatisfied Demand of product families. On the other hand, objective 1 includes five cost components, and the FW approach measures the importance of the cost features and assigns an appropriate weight to each feature. Figure 4 is derived from Table 9 and shows the TRS for the weights of all the cost components (features) of the multi-function BT-enabled PSC model in objective 1. These weights estimate the degree of relevance that each feature has for extracting the cost prediction. The results show the Raw Materials cost strongly influences the cost model. The remaining four cost features in objective 1 have relatively the same weight (Shortage-Surplus cost, Finished Products cost, Blockchain Installation cost, and Blockchain Transaction cost).

As a result, in response to the second question, we determined that the NB algorithm, when linked with HS and PSO, is the most reliable forecasting algorithm for our multi-function model based on TRS and four performance indicators. Researchers in various domains can utilize BT cost formulation (BT Transaction cost and BT Installation cost) in their mathematical models to evaluate the SC costs combined with BT. Another significant contribution of this study is to provide a BT-enabled PSC system with uncertain demand, which occurs when the demand exceeds the available stock. The study is useful because it gives the most reliable prediction algorithms for the multi-function BT-enabled PSC model, the model’s cost components, the degree of relevance of each model component, and the BT components in the PSC model.

Similar to other studies, there are some limitations in this research. Because the use of BT in PSC is a new area of study, our first constraint is the lack of real data. As a result, raw data was collected to validate the suggested multi-function BT-enabled PSC model. Using produced data instead of real data may have an impact on the research’s findings and conclusions. The second constraint pertains to the model’s components, as this research may not include some of the cost components of a real instance.

At last, further study might lead to developing a multi-function BT-enabled Pharmaceutical Cold Supply Chain model. Pharmaceutical Cold Supply Chain utilizes advanced technology to control the temperature inside cargo containers and storage units. Another idea for future study is to use other EC algorithms to improve the performance of SL algorithms or assess alternative SL algorithms to estimate expenses. Lastly, future studies may quantify the cost components of private BT and, therefore, formulate private BT rather than the public BT employed in the present paper.

7. Conclusion

The BT-enabled PSC allows for traceability and transparency in the distribution of pharmaceuticals and stakeholders across the supply chain, which can impact medication quality and end patient results. This work proposes a mathematical multi-function model for a BT-enabled PSC system to determine the model’s costs. This research is significant because it gives a PSC system with BT costs (BT Transaction cost and BT Installation cost) that may enhance the safety, efficiency, and transparency of medical information exchange in a healthcare system. The research also provides six components of the multi-function model: Raw Materials cost (Ordering cost, Holding cost for perfect raw materials, Holding cost for imperfect raw materials, Labor cost for order handling and receipt, and Transportation cost), Finished Products cost (Set-up cost, Holding cost, Production cost, Expected opportunity interest, and Expiry cost), Shortage-Surplus cost (Shortage cost and Surplus cost), Blockchain Installation cost (Fixed cost, Onboarding cost, Maintenance cost, and Monitoring cost), Blockchain Transaction cost (Gas cost and Storage cost), and Unsatisfied Demand. The combination of two EC algorithms and four SL algorithms yields eight methods for reducing prediction errors, improving the SL algorithms’ hyperparameters, and enhancing the multi-function model. The results show that the HS-NB and PSO-NB algorithms beat the other six algorithms in predicting the costs of the multi-function model with reduced errors. This means that the NB algorithm can estimate the costs of the BT-enabled PSC system better than the KNN, DT, and SVM algorithms. The other six algorithms perform similarly for this comparison, except HS-SVM, which acts better, demonstrating that these algorithms are not a suitable forecasting method for the existing cost model. The results also reveal the Raw Materials cost strongly influences the cost model, more so than the remaining four cost features: Shortage-Surplus cost, Finished Products cost, Blockchain Installation cost, and Blockchain Transaction cost. Therefore, the statistical findings on the provided dataset demonstrate that the NB algorithm can produce acceptable results and assign suitable feature weights. These results can assist healthcare service managers in making the correct decisions, regulating financial resources, remaining within budget, evaluating data, and detecting wasteful costs, especially if they decide to apply BT into the system. This research also provides a PSC system with BT that includes demand uncertainty. Managers may utilize the chosen SL algorithms to predict costs with the fewest forecast errors and then evaluate if the new system is beneficial to their organization. Using this approach will also allow managers to know how to determine and measure each cost component of the multi-function BT-enabled PSC model to make the best decision before installing the new system.

Data Availability Statement

The data supporting this study’s findings are openly available at https://data.mendeley.com/datasets/sfc7hst95m.

References

M. N. Kamel Boulos, J. T. Wilson and K. A. Clauson, “Geospatial blockchain: promises, challenges, and scenarios in health and healthcare,” International Journal of Health Geographics, vol. 17, 2018.
R. Jafar Heydari and M. Rabbani, “A mathematical model for pharmaceutical supply chain coordination: Reselling medicines in an alternative market,” Journal of Cleaner Production, vol. 268, 2020.
A. Chircu, E. Sultanow and S. P. Saraswat, “Healthcare RFID In Germany: An Integrated Pharmaceutical Supply Chain Perspective,” Journal of Applied Business Research, vol. 30, no. 3, 2014.
R. Uthayakumar and S. Priyan, “Pharmaceutical supply chain and inventory management strategies: Optimization for a pharmaceutical company and a hospital,” Operations Research for Health Care, p. 52–64, 2013.
B. Zahiri, P. Jula and R. Tavakkoli-Moghaddam, “Design of a pharmaceutical supply chain network under uncertainty considering perishability and substitutability of products,” Information Sciences, vol. 423, pp. 257-283, 2018.
S. M. Hosseini Bamakan, S. Ghasemzadeh Moghaddam and S. Dehghan Manshadi, “Blockchain-enabled pharmaceutical cold chain: Applications, key challenges, and future trends,” Journal of Cleaner Production, vol. 302, 2021.
Q. Mamun, “Blockchain technology in the future of healthcare,” Smart Health, vol. 23, 2022.
H. Mansur Hussien, S. Md Yasin, N. Izura Udzir, M. I. Hafez Ninggal and S. Salman, “Blockchain technology in the healthcare industry: Trends and opportunities,” Journal of Industrial Information Integration, vol. 22, 2021.
I. Abu-elezz, A. Hassan, A. Nazeemudeen, M. Househ and A. Abd-alrazaq, “The benefits and threats of blockchain technology in healthcare: A scoping review,” International Journal of Medical Informatics, vol. 142, 2020.
C. Franco and E. Alfonso-Lizarazo, “Optimization under uncertainty of the pharmaceutical supply chain in hospitals,” Computers & Chemical Engineering, vol. 135, 2020.
G. Kumar Badhotiya, V. Prakash Sharma, S. Prakash, V. Kalluri and R. Singh, “Investigation and assessment of blockchain technology adoption in the pharmaceutical supply chain,” Materials Today: Proceedings, vol. 46, no. 20, pp. 10776-10780, 2021.
I. Haq and O. Muselemu Esuka, “Blockchain Technology in Pharmaceutical Industry to Prevent Counterfeit Drugs,” International Journal of Computer Applications, vol. 180, no. 25, 2018.
A. Haleem, M. Javaid, R. Pratap Singh, R. Suman and S. Rab, “Blockchain technology applications in healthcare: An overview,” International Journal of Intelligent Networks, vol. 2, pp. 130-139, 2021.
A. Ahmadi, M. Mousazadeh, S. Ali Torabi and M. S. Pishvaee, “OR Applications in Pharmaceutical Supply Chain Management,” in Operations Research Applications in Health Care Management, vol. 262, Springer, Cham, 2017, pp. 461-491.
H. Hu, X. Xia, Y. Luo, C. Zhang, M. S. Nazir and T. Peng, “Development and application of an evolutionary deep learning framework of LSTM based on improved grasshopper optimization algorithm for short-term load forecasting,” Journal of Building Engineering, vol. 57, 2022.
F. Zhang, C. Deb, S. E. Lee, J. Yang and K. W. Shah, “Time series forecasting for building energy consumption using weighted Support Vector Regression with differential evolution optimization,” Energy and Buildings, vol. 126, pp. 94-103, 2016.
Y. Li, T. Peng, L. Hua, C. Ji, H. Ma, M. S. Nazir and C. Zhang, “Research and application of an evolutionary deep learning model based on improved grey wolf optimization algorithm and DBN-ELM for AQI prediction,” Sustainable Cities and Society, vol. 87, 2022.
Z. Tian and H. Chen, “A novel decomposition-ensemble prediction model for ultra-short-term wind speed,” Energy Conversion and Management, vol. 248, 2021.
R. Shu, T. Xia, H. Tu, L. Williams and T. Menzies, “Reducing the Cost of Training Security Classifier (via Optimized Semi-Supervised Learning),” arXiv, 2022.
A. M. Al-Zoubi, M. A. Hassonah, A. A. Heidari, H. Faris, M. Mafarja and I. Aljarah, “Evolutionary competitive swarm exploring optimal support vector machines and feature weighting,” Methodologies and Application, vol. 25, p. 3335–3352, 2021.
M. Roshan, R. Tavakkoli-Moghaddam and Y. Rahimi, “A two-stage approach to agile pharmaceutical supply chain management with product substitutability in crises,” Computers and Chemical Engineering, vol. 127, p. 200–217, 2019.
IBM, “IBM Cloud,” 2022. [Online]. Available: https://cloud.ibm.com/objectstorage/create#pricing.
X. Wang, W. iNi, X. Zha, G. Yu, R. P. Liu, N. Georgalas and A. Reeves, “Capacity analysis of public blockchain,” Computer Communications, vol. 177, pp. 112-124, 2021.
F. Longo, L. Nicoletti, A. Padovano, G. d’Atri and M. Forte, “Blockchain-enabled supply chain: An experimental study,” Computers & Industrial Engineering, vol. 136, p. 57–69, 2019.
“ETH Gas Station,” 2022. [Online]. Available: https://ethgasstation.info/.
M. Mousazadeh, S. Torabi and B. Zahiri, “A robust possibilistic programming approach for pharmaceutical supply chain network design,” Computers & Chemical Engineering, vol. 82, pp. 115-128, 2015.
H. Havaeji, T.-M. Dao and T. Wong, “Cost Optimization of Blockchain Technology-enabled Supply Chain System using Evolutionary Computation Approaches: A Healthcare Case Study,” World Wide Journal of Multidisciplinary Research and Development, 2022.
G. Wood, “Ethereum: A Secure Decentralised Generalised Transaction Ledger,” Ethereum project yellow paper, 2020.
A. Jabbar and S. Dani, “Investigating the link between transaction and computational costs in a blockchain environment,” International Journal of Production Research, vol. 58, no. 11, p. 3423–3436, 2020.
P. K. Gopalakrishnan, J. Hall and S. Behdad, “Cost analysis and optimization of Blockchain-based solid waste management traceability system,” Waste Management, vol. 120, pp. 594-607, 2021.
A. Takyar, “HOW TO DETERMINE THE COST OF BLOCKCHAIN IMPLEMENTATION?,” 2021a. [Online]. Available: https://www.leewayhertz.com/cost-of-blockchain-implementation/.
P. Ram, “Top 5 Blockchain Use Cases in Pharma and Healthcare — that you should know about!,” 2018. [Online]. Available: https://medium.com/blockchainbistro/top-5-use-cases-of-blockchain-in-pharma-and-healthcare-that-you-should-know-about-77ccdd76369b#:~:text=and%20its%20revocation.-,Industry%20Proof%2Dof%2DConcept,ultimately%20lowering%20drug%20development%20costs.

Figure 1. Flowchart of the research method.

Figure 2. Transaction cost by ETH Gas Station [25].

Figure 3. TRS of all algorithms in objectives 1 and 2.

Figure 4. TRS for feature weighs in objective 1.

Table 1. Parameters and constraints for all parts of the BT-enabled PSC cost model.

Parameters	Explanation	Constraints
M	Number of products controlled in the PSC variables	`3`5
q_i	Order quantity for the i^th product per year (i = 1, 2, 3, . . . , M)	50 ≤ q_i ≤ 100 (integer)
d_i	The average demand for the i^th product per year	45 ≤ d_i ≤ 115 (integer)
n	Total number of lots of M products delivered by the pharmaceutical system to the client per year	50 ≤ n ≤ 100 (integer)
I_v	The interest rate for calculating the opportunity interest loss for the pharmaceutical system due to delayed payment per year	I_v = 0.02
T_c	Common trade credit period for all products offered by the pharmaceutical system in years	0.1
h_v_i	Holding cost for the i^th finished product per year	20 ≤ h_v_i ≤ 40
s_i	Set-up cost for the i^th finished product per year	12 ≤ s_i ≤ 25
p_i	The production rate for the i^th finished product	45 ≤ p_i ≤ 115 (integer)
bi	The purchase price per unit for the i^th product	80 ≤ bi ≤ 150
p_ci	Production cost for a product i per year	25 ≤ p_ci ≤ 50
d_ci	Expiration rate for the i^th finished product	6% ≤ d_ci ≤ 15%
c_dci	Cost of expiry for the i^th finished product	25 ≤ c_dci ≤ 55
q_w_i	Replenishment quantity for the i^th raw material for the production	20 ≤ q_w_i ≤ 27
a_w_i	Ordering cost for the i^th raw material	15 ≤ a_w_i ≤ 25
h_w_i	Holding cost per year for the i^th raw material	10 ≤ h_w_i ≤ 15
F_w	Fixed transportation cost for all raw materials per year	3500
v_w_i	Labor cost for order handling and receipt for the i^th raw material per year	16 ≤ v_w_i ≤ 28
$β$ _i	Defect rate for the i^th raw material in an order lot, $β$ _i $\in$ [0, 1], a random variable	0 ≤ $β$ _i ≤ 1
r_si	Screening rate per year for the i^th raw material	1.04% ≤ r_si ≤ 7.2%
costSi	Shortage cost of unit product type i	10≤ costSi ≤ 20
costSUi	Surplus cost of unit product type i	15 ≤ costSUi ≤ 25
z¹_i	Surplus amount of product i	0 ≤ z¹_i ≤ 70 (integer) z¹_i ≥ p_i $-$ d_i
z²_i	Shortage amount of product i	0 ≤ z²_i ≤ 70 / (integer) z²_i ≤ d_i $-$ p_i
τ_i	Comparative importance of product i	1 ≤ τ_i ≤ 5 (integer)
gWei	The cost paid to the transaction validators and the network (Wei is the unit of ETH)	---
G_u	The amount of Ether as gasUsed per day	$3.86 ≤ G_u × g_p ≤ $41.66
g_p	Number of gWei to be paid for gasUsed per day	$3.86 ≤ G_u × g_p ≤ $41.66
s	The data storage size to store the data	51 TB/yr ≤ s ≤ 99 TB/yr
C_s	Cost storage per year (USD/TB) for Public outbound bandwidth service [22]	$110×12 = 1320 $/yr
c_fixed	The initial fixed cost per year	860 ≤ c_fixed ≤ 1160
c_onboarding	The Onboarding cost	$180 ≤ c_onboarding ≤ $260
c_mc	The unit Maintenance cost; c_mc + c_mo is 15%–25% of the project value	$230 ≤ c_mc + c_mo ≤ $550
c_mo	The unit Monitoring cost; c_mc + c_mo is 15%–25% of the project value
U	The number of Blockchain users	4
d_i - p_i	The demand uncertainty	≥ 0

Table 2. Examining objectives 1 and 2 in 10 runs using feature weighting and performance indicators for HS linked with four SL algorithms.

		Objective 1									Objective 2
HS_KNN	Run	Feature weighting					Performance metrics				Performance metrics
	Run	W_(Raw_Materials)	W_(Finished_Products)	W_(Shortage_Surplus)	W_(BT_Installation)	W_(BT_Transaction)	MSE	RMSE	MAE	R^2	MSE	RMSE	MAE	R^2
	1	0.31	1	0.83	1	1	447578659.37	21156.05	15225.04	0.99	24710.22	157.19	122.09	0.006
	2	0.321	0.978	0.911	0.874	0.568	12216876173.60	110529.97	83903.98	0.991	24508.02	156.55	120.55	0.003
	3	0.493	0	0.797	0	0.253	2584577237772.87	1607662.04	1428615.72	0.033	23231.68	152.41	117.72	0.006
	4	0.855	0	0.239	0	0.067	2559565339629.15	1599864.16	1316755.65	0.082	8411.63	91.71	59.56	0.132
	5	0.513	0.332	0.087	0.358	0.892	24544114160.46	156665.61	112810.15	0.983	4820.3	69.42	39.76	0.474
	6	0.068	0.974	1	1	0.938	592467081.45	24340.64	16459.35	0.999	3021.13	54.96	34.6	0.554
	7	0.0989	0.994	1	1	1	558779878.15	23638.52	16243.51	0.999	13822.96	117.57	88.13	0.195
	8	1	0.934	0.695	0.848	1	517518033.07	22749.0227	16312.7089	0.999	23441.02	153.10	117.82	0.004
	9	1	0.940	0.685	0.915	1	18935746767.50	137607.21	101185.10	0.986	13012.55	114.07	85.42	0.205
	10	0	0.548	0.479	0.584	0.672	414695195.67	20364.0663	15134.7278	0.999	7351.13	85.73	59	0.0302
Average		0.46	0.67	0.67	0.65	0.73	520237035335.13	283604.18	227843.03	0.86	14633.06	115.27	84.47	0.16
		Objective 1									Objective 2
HS_DT	Run	Feature weighting					Performance metrics				Performance metrics
	Run	W_(Raw_Materials)	W_(Finished_Products)	W_(Shortage_Surplus)	W_(BT_Installation)	W_(BT_Transaction)	MSE	RMSE	MAE	R^2	MSE	RMSE	MAE	R^2
	1	0.194	0.257	0.838	0.271	0.248	487814443.56	22086.52	16297.92	0.999	22777.09	150.92	114.31	0.010
	2	0	0.898	0	1	0	2499618098.92	49996.18	35512.63	0.998	19404.58	139.30	106.21	0.004
	3	0	0.866	0	0.691	0	2008075275.94	44811.55	32162.61	0.998	19118.08	138.26	105.64	0.004
	4	0	1	0	0.572	0	2222526522.60	47143.67	34027.37	.998	18782.17	137.04	106.68	0.010
	5	0.878	0.299	0.714	1	0	2124057520.85	46087.49	33848.02	0.998	10892.02	104.36	77.62	0.313
	6	0	0.154	0	1	0	2407898995.12	49070.34	35782.17	0.998	19876.76	140.98	106.38	0.002
	7	0	0.406	0	0.896	0	2268558510.16	47629.38	34306.15	0.998	19171.03	138.45	105.52	0.006
	8	0.356	0.012	0.957	1	0	2121641968.13	46061.28	34345.41	0.998	9716.27	98.57	73.83	0.341
	9	1	0.108	1	0.500	0	2425609238.87	49250.47	35790.56	0.998	10676.44	103.32	77.43	0.304
	10	0.166	0.044	0.392	0.784	0	2760284205.16	52538.40	36269.32	0.998	10342.51	101.69	74.97	0.324
Average		0.26	0.40	0.39	0.77	0.02	2132608477.93	45467.53	32834.22	1.00	16075.70	125.29	94.86	0.13
		Objective 1									Objective 2
HS_SVM	Run	Feature weighting					Performance metrics				Performance metrics
	Run	W_(Raw_Materials)	W_(Finished_Products)	W_(Shortage_Surplus)	W_(BT_Installation)	W_(BT_Transaction)	MSE	RMSE	MAE	R^2	MSE	RMSE	MAE	R^2
	1	0.231	0.981	0.642	0.076	0.744	8216337569.52	90644.01	78810.96	0.999	1343.01	36.64	27.23	0.713
	2	0.679	0	0.020	0.003	0.153	6757738172.25	82205.46	70810.95	0.997	2076.14	45.56	33.16	0.588
	3	0.126	0.504	0.799	0.198	0.0431	4785591120.97	69177.96	63238.64	0.999	2076.14	45.56	33.16	0.588
	4	0.001	0.599	0.818	0.208	0.115	5539994619.11	74431.14	63613.45	0.999	1764.26	42.00	33.29	0.727
	5	0.993	0.287	1	0.243	0.174	6618206320.17	81352.35	64946.07	0.995	2887.11	53.73	45.25	0.579
	6	0.689	0.725	0.533	0.104	0.126	6964170744.91	83451.60	72470.90	0.999	1764.26	42.00	33.29	0.727
	7	0.064	0.172	1	0.027	0.68	6600773868.49	81245.14	68273.45	0.999	8108.04	90.04	73.82	0.346
	8	0.750	0.016	0.035	0.007	0.534	6002777653.01	77477.59	68913.88	0.999	2155.18	46.42	37.33	0.814
	9	0.460	0.031	0.787	0.031	0.432	4877903687.16	69841.99	57241.79	0.996	5128.06	71.61	53.09	0.535
	10	0.679	0	0.020	0.003	0.153	6757738172.25	82205.46	70810.95	0.997	2934.60	54.17	36.95	0.773
Average		0.47	0.33	0.57	0.09	0.32	6312123192.78	79203.27	67913.10	1.00	3023.68	52.77	40.66	0.64
		Objective 1									Objective 2
HS_NB	Run	Feature weighting					Performance metrics				Performance metrics
	Run	W_(Raw_Materials)	W_(Finished_Products)	W_(Shortage_Surplus)	W_(BT_Installation)	W_(BT_Transaction)	MSE	RMSE	MAE	R^2	MSE	RMSE	MAE	R^2
	1	0.968	0.001	0.987	0	0.047	757.59	27.52	20.52	1	2618.22	51.16	34.57	0.809
	2	0.576	0.008	0.966	0.001	0.403	115.42	10.74	9.53	1	1713.43	41.39	34.15	0.634
	3	1	0.002	0.982	0	0.146	193.52	13.91	11.66	1	2256.35	47.50	36.31	0.551
	4	0.986	0.001	0.905	0	0.169	197.89	14.06	11.57	1	2141.78	46.27	31.92	0.655
	5	0.761	0.002	0.650	0	0.039	164.36	12.82	10.43	1	1959.94	44.27	33.18	0.649
	6	0.871	0.003	0.924	0	0.955	162.34	12.74	10.87	1	2918.73	54.02	44.42	0.584
	7	0.926	0.006	0.920	0.001	0.728	185.71	13.62	11.60	1	4111.33	64.11	47.80	0.402
	8	0.950	0.003	0.527	0	0.080	217.95	14.76	12.86	1	2566.81	50.66	41.41	0.447
	9	0.990	0.002	0.355	0	0.034	130.74	11.43	8.04	1	2451.95	49.51	37.18	0.704
	10	0.576	0.008	0.966	0.001	0.403	115.42	10.74	9.53	1	1323.14	36.37	29.23	0.694
Average		0.86	0.00	0.82	0.00	0.30	224.09	14.23	11.66	1.00	2406.17	48.53	37.02	0.61

Table 3. Performance indicators for HS linked with four SL algorithms were utilized to assess objectives 1 and 2.

	Objective 1				Objective 2
	Performance metrics				Performance metrics
Methods	Ave_MSE	Ave_RMSE	Ave_ MAE	Ave_R^2	Ave_MSE	Ave_RMSE	Ave_ MAE	Ave_R^2
HS_KNN	520237035335.13	283604.18	227843.03	0.86	14633.06	115.27	84.47	0.16
HS_DT	2132608477.93	45467.53	32834.22	1.00	16075.70	125.29	94.86	0.13
HS_SVM	6312123192.78	79203.27	67913.10	1.00	3023.68	52.77	40.66	0.64
HS_NB	224.09	14.23	11.66	1.00	2406.17	48.53	37.02	0.61

Table 4. FW criteria for four SL algorithms optimized by HS in objective 1.

	Feature weighting
Methods	Max_Ave_Weighting	Min_ Ave_Weighting
HS_KNN	W_(BT_Transaction) = 0.73	W_(Raw_Materials) = 0.46
HS_DT	W_(BT_Installation) = 0.77	W_(BT_Transaction) = 0.02
HS_SVM	W_(Shortage_Surplus) = 0.57	W_(BT_Installation) = 0.09
HS_NB	W_(Raw_Materials) = 0.86	W_(Finished_Products) & W_(BT_Installation) = 0.00

Table 5. Evaluation of objectives 1 and 2 using feature weighting and performance indicators for PSO linked with four SL algorithms across ten runs.

		Objective 1									Objective 2
PSO_KNN	Run	Feature weighting					Performance metrics				Performance metrics
	Run	W_(Raw_Materials)	W_(Finished_Products)	W_(Shortage_Surplus)	W_(BT_Installation)	W_(BT_Transaction)	MSE	RMSE	MAE	R^2	MSE	RMSE	MAE	R^2
	1	0	0.825	0	1	1	549741219.89	23446.5609	16634.91	0.999	23806.25	154.29	117.60	0.011
	2	0.533	0.744	0.322	0.817	0.884	491607040.75	22172.21	15688.57	0.999	22455.19	149.85	114.24	0.009
	3	0.767	0.007	0.102	0.018	0.786	61527504303.02	248047.38	185904.62	0.959	19758.51	140.56	106.62	0.042
	4	0.676	0.049	0.794	0.045	0	525110440.86	22915.28	17221.68	0.999	23954.87	154.77	118.47	0.009
	5	0.516	0.560	0.111	0.907	0.281	550748692.11	23468.03	17092.62	0.999	24544.10	156.66	122.29	0.0079
	6	1	1	0.617	1	0.627	454654767.36	21322.63	15340.97	0.999	24004.42	154.93	118.78	0.006
	7	1	0.186	0	0.080	0.942	10745095521.78	103658.55	79592.31	0.987	12554.8	112.04	79.13	0.103
	8	0	0.554	1	0.702	0.470	431096960.34	20762.87	15099.64	0.999	6669	81.66	59.33	0.226
	9	1	1	0.543	1	0.616	454972132.96	21330.07	15345.73	0.999	24561.92	156.72	122.34	0.007
	10	0.886	0.047	1	0.152	0	742284495.02	27244.89	20085.31	0.999	20796.63	144.21	109.21	0.020
Average		0.64	0.50	0.45	0.57	0.56	7647281557.41	53436.85	39800.64	0.99	20310.57	140.57	106.80	0.04
		Objective 1									Objective 2
PSO_DT	Run	Feature weighting					Performance metrics				Performance metrics
	Run	W_(Raw_Materials)	W_(Finished_Products)	W_(Shortage_Surplus)	W_(BT_Installation)	W_(BT_Transaction)	MSE	RMSE	MAE	R^2	MSE	RMSE	MAE	R^2
	1	0.074	0.453	0.252	0.142	0	2124057520.85	46087.49	33848.02	0.998	10892.02	104.36	77.62	0.313
	2	0.333	0.322	0.811	0.069	0.406	66808063437.00	258472.55	196228.98	0.952	10643.44	103.16	77.68	0.337
	3	0.232	0.304	0.073	0.088	0	2222537815.15	47143.79	34199.82	0.998	9340.04	96.64	72.67	0.351
	4	0.917	0.778	0.670	0.210	0	68611472474.87	261937.91	202530.73	0.953	2361.72	48.59	29.84	0.694
	5	0.225	1	0.277	1	0	2464171102.89	49640.41	35610.29	0.998	3199.95	56.56	34.61	0.409
	6	0	0.145	0.627	0.285	0	50446994254.48	224604.08	166066.93	0.957	2678.00	51.74	35.21	0.654
	7	0	1	0.169	0.315	0	68200434557.48	261152.12	201638.36	0.925	2920.60	54.04	40.28	0.552
	8	0.602	0.248	0.020	0.947	0.061	65259550220.65	255459.48	194744.85	0.946	3266.07	57.14	41.86	0.537
	9	0.789	0.134	0.134	0.751	0	2331651357.13	48287.17	35532.25	0.998	10094.09	100.46	74.92	0.313
	10	0.428	0.428	0.208	0.011	0.948	2353131810.38	48509.09	35571.26	0.998	10475.52	102.35	76.50	0.325
Average		0.36	0.48	0.32	0.38	0.14	33082206455.09	150129.41	113597.15	0.97	6587.15	77.50	56.12	0.45
		Objective 1									Objective 2
PSO_SVM	Run	Feature weighting					Performance metrics				Performance metrics
	Run	W_(Raw_Materials)	W_(Finished_Products)	W_(Shortage_Surplus)	W_(BT_Installation)	W_(BT_Transaction)	MSE	RMSE	MAE	R^2	MSE	RMSE	MAE	R^2
	1	0.834	0.994	0.999	0.340	0.535	6481651810.93	80508.70	72188.64	0.999	293747.64	541.98	437.60	0.136
	2	1	0.527	0.283	0.184	0.966	5547584998.00	74482.11	69169.55	0.999	3507.26	59.22	48.12	0.745
	3	0.935	1	0.481	0.347	1	3605444643.76	60045.35	55331.24	0.999	3373.98	58.08	48.39	0.572
	4	0.916	1	0.680	0.351	1	4514645983.04	67191.11	61008.17	0.999	3715.10	60.95	51.35	0.354
	5	0.783	0.832	0.080	0.181	0.862	5844285150.30	76447.92	68615.39	0.999	1644.43	40.55	31.86	0.699
	6	0.530	0.340	1	0.134	0	5986270734.82	77370.99	66270.24	0.999	3927.42	62.66	52.17	0.651
	7	0.490	0.305	0.999	0.106	1	4348863443.90	65945.91	57060.60	0.999	2011.16	44.84	34.05	0.650
	8	0.679	0.107	0.392	0.037	0.313	4509807347.28	67155.09	58613.10	0.999	3655.66	60.46	47.21	0.504
	9	1	0.281	0.282	0.108	0.617	6022445081.15	77604.41	66322.34	0.999	1170745.01	1082.00	919.48	0.0669
	10	0.895	0.624	0.413	0.245	0.753	4374513944.83	66140.10	57651.87	0.999	1149307.12	1072.05	753.85	0.174
Average		0.81	0.60	0.56	0.20	0.70	5123551313.80	71289.17	63223.11	1.00	263563.48	308.28	242.41	0.46
		Objective 1									Objective 2
PSO_NB	Run	Feature weighting					Performance metrics				Performance metrics
	Run	W_(Raw_Materials)	W_(Finished_Products)	W_(Shortage_Surplus)	W_(BT_Installation)	W_(BT_Transaction)	MSE	RMSE	MAE	R^2	MSE	RMSE	MAE	R^2
	1	0.019	0.091	0.883	0.244	0.335	27165.54	164.81	139.53	1	4374.03	66.13	54.98	0.438
	2	1	0.004	1	0.001	1	241.74	15.54	13.24	1	2335.18	48.32	40.55	0.60
	3	1	0.029	0.995	0	0.999	158.73	12.59	10.48	1	1622.74	40.28	33.03	0.679
	4	0.336	0.472	1	0.377	0.582	385352.01	620.76	517.70	1	4244.30	65.14	55.06	0.255
	5	1	0.529	0.990	0.965	1	653210.23	808.21	583.32	1	9377.69	96.83	69.14	0.243
	6	1	0.005	1	0.001	0.085	80.76	8.98	7.00	1	1874.46	43.29	36.17	0.560
	7	0.992	0.464	0.989	0.026	0.650	754.26	27.46	22.41	1	3180.67	56.39	52.21	0.116
	8	0.558	0	0.942	0	1	147.15	12.13	9.87	1	2392.15	48.90	35.94	0.554
	9	0.992	0.001	0.984	0	0.157	277.38	16.65	13.96	1	1929.62	43.92	34.37	0.638
	10	0.750	0.015	0.999	0	0.656	264.05	16.24	13.20	1	5488.47	74.08	59.06	0.310
Average		0.76	0.16	0.98	0.16	0.65	106765.19	170.34	133.07	1.00	3681.93	58.33	47.05	0.44

Table 6. Performance indicators for PSO linked with four SL algorithms for assessing objectives 1 and 2.

	Objective 1				Objective 2
	Performance metrics				Performance metrics
Methods	Ave_MSE	Ave_RMSE	Ave_ MAE	Ave_R^2	Ave_MSE	Ave_RMSE	Ave_ MAE	Ave_R^2
PSO_KNN	7647281557.41	53436.85	39800.64	0.99	20310.57	140.57	106.80	0.04
PSO_DT	33082206455.09	150129.41	113597.15	0.97	6587.15	77.50	56.12	0.45
PSO_SVM	5123551313.80	71289.17	63223.11	1.00	263563.48	308.28	242.41	0.46
PSO_NB	106765.19	170.34	133.07	1.00	3681.93	58.33	47.05	0.44

Table 7. In objective 1, the FW criteria for PSO were linked with four SL algorithms.

	Feature weighting
Methods	Max_ Ave_Weighting	Min_ Ave_Weighting
PSO_KNN	W_(Raw_Materials) = 0.64	W_(Shortage_Surplus) = 0.45
PSO_DT	W_(Finished_Products) = 0.48	W_(BT_Transaction) = 0.14
PSO_SVM	W_(Raw_Materials) = 0.81	W_(BT_Installation) = 0.20
PSO_NB	W_(Shortage_Surplus) = 0.98	W_(Finished_Products) & W_(BT_Installation) = 0.16

Table 8. Using the performance indicators in objectives 1 and 2 to rank eight chosen algorithms based on their TRS ratings.

		Objective 1				Objective 2
		Performance metrics				Performance metrics				TRS	Rank
Method		Ave_MSE	Ave_RMSE	Ave_ MAE	Ave_R^2	Ave_MSE	Ave_RMSE	Ave_MAE	Ave_R^2
HS_KNN		520237035335.13	283604.18	227843.03	0.86	14633.06	115.27	84.47	0.16
HS_DT		2132608477.93	45467.53	32834.22	1.00	16075.70	125.29	94.86	0.13
HS_SVM		6312123192.78	79203.27	67913.10	1.00	3023.68	52.77	40.66	0.64
HS_NB		224.09	14.23	11.66	1.00	2406.17	48.53	37.02	0.61
PSO_KNN		7647281557.41	53436.85	39800.64	0.99	20310.57	140.57	106.80	0.04
PSO_DT		33082206455.09	150129.41	113597.15	0.97	6587.15	77.50	56.12	0.45
PSO_SVM		5123551313.80	71289.17	63223.11	1.00	263563.48	308.28	242.41	0.46
PSO_NB		106765.19	170.34	133.07	1.00	3681.93	58.33	47.05	0.44
Ranking Score	HS_KNN	1	1	1	5	4	4	4	3	23.00	8
	HS_DT	6	6	6	8	3	3	3	2	37.00	4
	HS_SVM	4	3	3	8	7	7	7	8	47.00	3
	HS_NB	8	8	8	8	8	8	8	7	63.00	1
	PSO_KNN	3	5	5	7	2	2	2	1	27.00	7
	PSO_DT	2	2	2	6	5	5	5	5	32.00	5
	PSO_SVM	5	4	4	8	1	1	1	6	30.00	6
	PSO_NB	7	7	7	8	6	6	6	4	51.00	2

Table 9. FW Ranking based on TRS ratings for five algorithms chosen algorithms in objective 1.

		Objective 1
		Methods								TRS	Rank
Ave_FW		HS_KNN	HS_DT	HS_SVM	HS_NB	PSO_KNN	PSO_DT	PSO_SVM	PSO_NB
W_(Raw_Materials)		0.46	0.26	0.47	0.86	0.64	0.36	0.81	0.76
W_(Finished_Products)		0.67	0.40	0.33	0.00	0.50	0.48	0.60	0.16
W_(Shortage_Surplus)		0.67	0.39	0.57	0.82	0.45	0.32	0.56	0.98
W_(BT_Installation)		0.65	0.77	0.09	0.00	0.57	0.38	0.20	0.16
W_(BT_Transaction)		0.73	0.02	0.32	0.30	0.56	0.14	0.70	0.65
Ranking Score	W_(Raw_Materials)	2	2	4	5	5	3	5	4	30	1
	W_(Finished_Products)	4	4	3	2	2	5	3	2	25	3
	W_(Shortage_Surplus)	4	3	5	4	1	2	2	5	26	2
	W_(BT_Installation)	3	5	1	2	4	4	1	2	22	4
	W_(BT_Transaction)	5	1	2	3	3	1	4	3	22	4

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Blockchain-enabled Pharmaceutical Supply Chain under Uncertain Demand: Cost Prediction through the Tuning of Evolutionary Supervised Learning

Abstract

1. Introduction

2. Literature Review

2.1. Introduction to PSC (Pharmaceutical Supply Chain)

2.2. Introduction to BT (Blockchain Technology)

2.3. Key Features and Benefits of BT in PSC

2.4. Enabling BT in PSC

2.5. Uncertain Demand in PSC

2.6. SL optimized by EC

3. Research Method and Data Generation

4. Proposed Optimization Multi-Function BT-enabled PSC Model

4.1. Cost elements of a PSC

4.1.1. Raw Materials cost elements

4.1.1. Finished Products cost elements

4.1.1. Shortage-Surplus cost elements

4.1. Blockchain Implementation cost elements

4.1. Uncertain Demand elements

4.1. Optimization Multi-Function for BT-enabled PSC

5. Results

5.1. HS combined with four SLs

5.2. PSO linked with four SL algorithms

For multi-function BT-enabled PSC

6. Discussion

7. Conclusion

Data Availability Statement

References

MDPI Initiatives

Important Links

Subscribe