Embedding Some Classes of Signed Graphs in the Line

Preprint

Article

Embedding Some Classes of Signed Graphs in the Line

Altmetrics

Downloads

Views

Comments

Sattar Sattari^*

This version is not peer-reviewed

Submitted:

29 September 2023

Posted:

01 October 2023

You are already at the latest version

Alerts

Abstract

A signed graph is an undirected graph such that all of its edges are labeled positive or negative. Let D be an embedding of a signed graph G in the Euclidean line. If in D for all of the vertices their positive neighbors are closer than the negative neighbors, then D is called a valid drawing of G. In this paper we show that signed trees, unicyclic graphs, and ladder graphs have a valid drawing in the Euclidean line.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction

Let

G (V, E)

be a simple and undirected graph with vertex set V and edge set E. The graph G is called a signed graph when there is a function

σ : E \mapsto {\pm 1}

which labels each edge in E as positive or negative. We denote by

E^{+}

the set of edges with positive sign, and by

E^{-}

the set of edges with negative sign. Signed graphs were defined by Harary [1].

Kermarrec and Thraves [2,3] define drawing a graph

G (V, E)

R^{l}

as an injection of V in

R^{l}

. They define valid graph drawing in

R^{l}

as follows:

Definition 1.(Valid drawing in

R^{l}

) Let

G = (V, E^{+} \cup E^{-})

be a signed graph, and

D (G)

be a drawing of G in

R^{l}

. We say that

D (.)

is valid if and only if

d (D (v); D (u)) < d (D (v); D (w))

for all pair of incident edges

(v, w)

(v, u)

such that

(v, u) \in E^{+}

and

(v, w) \in E^{-}

, where

d (., .)

denotes the Euclidean distance between two elements in

R^{l}

Kermarrec and Thraves [2,3] provided a polynomial time algorithm that can decide if there is a valid drawing of a complete signed graph in the Euclidean line. This algorithm also gives the drawing if the answer is yes. They also provided examples of graphs without valid drawings in the Euclidean line and Euclidean plane.

Cygan et al. [4,5] proved that in general case deciding whether a signed graph has a valid drawing in the Euclidean line is an NP-complete problem. They also provided a dynamic programming algorithm that has single-exponential running time. They proved that the existence of a subexponential time algorithm would violate the Exponential Time Hypothesis.

Benítez et al. [6] studied embedding complete signed graphs in the circumference. Becerra and Thraves [7] explored the problem of embedding complete signed graphs in the real tree metric space. Aracena and Thraves [8] considered weighted graphs and defined valid drawing of them in the line. Pardo et al. [9] gave an experimental study of an optimization version of the problem in the Euclidean line.

In this paper, we focus on the 1-dimensional case i.e.

R

, where drawing is done in a Euclidean line. We will show how to provide a valid drawing for signed trees, signed unicyclic graphs, and signed ladder graphs in

R

2. Preliminaries

Let

σ : E \mapsto {\pm 1}

be the function that determines signs of the edges in a signed graph

G (V, E)

. When

σ ((v, w)) = 1

, we have

(v, w) \in E^{+}

and we call w a positive neighbor of v, and vice versa. Similarly,

σ ((v, u)) = - 1

implies

(v, w) \in E^{-}

and we say v and u are negative neighbors of each other. For any vertex v in V, we denote the set of its positive and the set of its negative neighbors by

N^{+} (v)

and

N^{-} (v)

, respectively.

It is clear that drawing a graph

G (V, E)

R

implies an ordering of the vertices V. According to Theorem 1 which is adopted from Pardo et al. [9], the existence of a valid graph drawing in

R

is equivalent to finding an ordering of the vertices that satisfies two conditions.

Theorem 1.

For a given signed graph

G = (V, E^{+} \cup E^{-})

, there exists a valid drawing in

R

, if and only if there exists an ordering

π : V \mapsto {1, 2, \dots, | V |}

of the set of vertices V such that:

label=(): $(v, w) \in E^{-} \land π (w) < π (v) \Rightarrow \forall u$ such that $π (u) < π (w), (v, u) \notin E^{+}$
lbbel=(): $(v, w) \in E^{-} \land π (v) < π (w) \Rightarrow \forall u$ such that $π (w) < π (u), (v, u) \notin E^{+}$

From now on, when we use the term valid drawing of a signed graph

G (V, E)

, we mean a function

π : V \mapsto {1, 2, \dots, | V |}

that satisfies Theorem 1. The following definition is adopted from Pardo et al. [9]:

Definition 2. (Error in a vertex) Given a signed graph

G = (V, E^{+} \cup E^{-})

and a drawing π of V, an error in vertex v produced by a pair of vertices w and u in V occurs when

(v, u) \in E^{+}

(v, w) \in E^{-}

and

π (u) < π (w) < π (v)

π (v) < π (w) < π (u)

Note that a drawing without any error is a valid drawing. We define a special kind of valid drawing to help us in the proofs:

Definition 3. (v-valid drawing) Let

G (V, E)

be a signed graph and

v \in V

. We say a drawing π of G, is v-valid if and only if π is a valid drawing of G and

π (v) = 1 .

In order to prove that a drawing is valid, we show that for every vertex, no pair of its neighbors make an error for it. The following propositions follow from Theorem 1:

_{\overset{+ +}{=}}

Let

π

be a drawing of a signed graph G in

R

. If vertices w and u are neighbors of a vertex v such that

π (w) < π (v) < π (u)

π (u) < π (v) < π (w)

, then w and u do not make an error for v.

_{\overset{+ +}{=}}

Let

π

be a drawing of a signed graph G in

R

. If vertices w and u are neighbors of a vertex v such that

π (v) < π (u) < π (w)

π (w) < π (u) < π (v)

, and we have

(v, u) \in E^{+}

, then w and u do not make an error for v.

_{\overset{+ +}{=}}

Let

π

be a drawing of a signed graph G in

R

. If vertices w and u are neighbors of a vertex v such that

π (v) < π (u) < π (w)

π (w) < π (u) < π (v)

, and we have

(v, w) \in E^{-}

, then w and u do not make an error for v.

_{\overset{+ +}{=}}

Let

G (V, E)

be a signed graph and

V = {v_{1}, v_{2}, \dots, v_{n}}

where

n = | V |

. Let

π

be a valid drawing of G in

R

. The function

π^{'} : V \mapsto {1, 2, \dots, n}

defined by

π^{'} (v) = n + 1 - π (v) (v \in V)

is also a valid drawing of G in

R

To illustrate and describe a drawing in the Euclidean line, we use a horizontal line. We assume the leftmost vertex is a vertex v for which

π (v) = 1

. If for any two vertices w and u we have

π (w) < π (u)

, then we say w is to the left of u or w is before u, and u is to the right of w or u is after w.

3. Valid drawing of trees and unicyclic graphs

In this section we show that signed trees and signed unicyclic graphs have a valid drawing in the Euclidean line.

Theorem 2.

G (V, E)

is a signed tree, then it has a valid drawing in

R

Proof.

We show that for all

v \in V

, the tree G has a v-valid drawing in

R

. We use induction on

n = | V |

. The case

n \leq 2

is trivial. Let

n \geq 3

and assume the theorem is true for all

n^{'} < n

. Let v be an arbitrary vertex in V. Let

N^{+} (v) = {w_{1}, w_{2}, \dots, w_{k}}

and

N^{-} (v) = {w_{k + 1}, w_{k + 2}, \dots, w_{l}}

. If we remove v and its edges from G, we will have l signed trees. We name them

H_{i} (V_{i}, E_{i}) (1 \leq i \leq l)

where

w_{i} \in V_{i}

. Each

H_{i}

is a tree with less than n vertices and thus the induction hypothesis guarantees that it has a

w_{i}

-valid drawing in

R

say

ϕ_{i}

. We define

π

as follows:

π (u) = \{\begin{matrix} 1, & if u = v \\ 1 + \sum_{j = 1}^{i - 1} | V_{j} | + ϕ_{i} (u), & if u \in V_{i} (1 \leq i \leq l) \end{matrix}

Vertex v is the only neighbor of

w_{i} (1 \leq i \leq l)

to its left, thus by Proposition 1, v does not cause an error with any vertices of

H_{i}

for

w_{i}

. Also, since members of

N^{+} (v)

are placed before members of

N^{-} (v)

, no error is produced for v. Hence,

π

is a v-valid drawing of G. □

Lemma 1.

G (V, E)

is a signed cycle graph, then it has a valid drawing in

R

Proof.

Let assume

V = {v_{1}, v_{2}, \dots, v_{n}}

and

E = {(v_{1}, v_{2}), \dots, (v_{n - 1}, v_{n}), (v_{n}, v_{1})}

. If

E^{-} = \emptyset

, then any

π : V \mapsto {1, 2, . . ., n}

is a valid drawing. If

E^{-} \neq \emptyset

, w.l.o.g let

(v_{n}, v_{1}) \in E^{-}

. We define

π (v_{i}) = i (1 \leq i \leq n)

. Since

(v_{n}, v_{1}) \in E^{-}

, Proposition 3 applies to

v_{1}

and its neighbors

v_{n}

and

v_{2}

. Also Proposition 3 applies to

v_{n}

and its neighbors

v_{1}

and

v_{n - 1}

. Each vertex in

V - {v_{1}, v_{n}}

has two neighbors on different sides, thus by Proposition 1, no error occurs for it. □

Theorem 3.

G (V, E)

is a signed unicyclic graph, then it has a valid drawing in

R

Proof.

Let

C (V_{C}, E_{C})

be the cycle subgraph of G. By Lemma 1, there exist a valid drawing

ϕ

for it. Assume

V_{c} = {v_{1}, v_{2}, . . ., v_{p}}

E_{c} = {(v_{1}, v_{2}), \dots, (v_{p - 1}, v_{p}), (v_{p}, v_{1})}

, and

ϕ (v_{i}) = i (1 \leq i \leq p)

Let H be the forest which is obtained by removing cycle C from G. For each

v_{i} \in V_{C}

, let

N_{H}^{+} (v_{i}) = {w_{i 1}, w_{i 2}, \dots, w_{i k_{i}}}

be the set of its positive neighbors in H, and

N_{H}^{-} (v_{i}) = {w_{i k_{i} + 1}, w_{i k_{i} + 2}, \dots, u_{i l_{i}}}

be the set of its negative neighbors in H. Each vertex

w_{i j}

belongs to some tree

T_{i j} (V_{i j}, E_{i j})

in H. Let

ϕ_{i j}

be the

w_{i j}

-valid drawing of

T_{i j}

that Theorem 2 gives.

1 \leq j \leq k_{i}

, we call members of

T_{i j}

in the ordering

ϕ_{i j}

, the positive trees of

v_{i}

. If

k_{i} < j \leq l_{i}

, we call members of

T_{i j}

in the ordering

ϕ_{i j}

, the negative trees of

v_{i}

. Let define:

f (i, a, j) = \sum_{b = a}^{j} | V_{i b} |

The function

f (i, a, j)

gives sum of the sizes of the trees

T_{i a}

T_{i j}

π

, first we put the negative trees of

v_{1}

, then the positive trees of

v_{1}

. Next we put

v_{1}

and

v_{2}

. This means that:

π (u) = \{\begin{matrix} 1 + f (1, 1, l_{1}), & if u = v_{1} \\ 2 + f (1, 1, l_{1}), & if u = v_{2} \\ f (1, k_{i} + 1, j - 1) + ϕ_{1 j} (u), & if u \in V_{1 j} \land j > k_{i} \\ f (1, k_{i} + 1, l_{i}) + f (i, 1, j - 1) + ϕ_{1 j} (u), & if u \in V_{1 j} \land j \leq k_{i} \end{matrix}

For

i \geq 2

, after

v_{i}

we put its positive trees, next we put

v_{i + 1}

, and then the negative trees of

v_{i}

. For

v_{p}

, after its positive trees, we put its negative trees. Thus, we have:

π (u) = \{\begin{matrix} π (v_{i - 1}) + f (i - 1, 1, k_{i}) + 1, & if u = v_{i} \land i > 2 \\ π (v_{i}) + f (i, 1, j - 1) + ϕ_{i j} (u), & if u \in V_{i j} \land j \leq k_{i} \land 2 \leq i < p \\ π (v_{i}) + f (i, 1, j - 1) + 1 + ϕ_{i j} (u), & if u \in V_{i j} \land j > k_{i} \land 2 \leq i < p \\ π (v_{p}) + f (p, 1, j - 1) + ϕ_{p j} (u), & if u \in V_{p j} \end{matrix}

Since, for all

u \in N_{H}^{+} (v_{1})

and all

w \in N_{H}^{-} (v_{1})

, we have

π (w) < π (u) < π (v_{1})

, they do not make any error for

v_{1}

. For all

w \in N_{H}^{+} (v_{1}) \cup N_{H}^{-} (v_{1})

, we have

π (w) < π (v_{1}) < π (v_{2}) < π (v_{p})

. Thus, because of Proposition 1, no error is made for

v_{1}

v_{2}

and

v_{p}

with any of its trees. Similarly, no error is made for

v_{p}

because for all

u \in N_{H}^{+} (v_{p})

and all

w \in N_{H}^{-} (v_{p})

, we have

π (v_{1}) < π (v_{p - 1}) < π (v_{p}) < π (u) < π (w)

Let

2 \leq i < p

. For all

u \in N_{H}^{+} (v_{i})

and all

w \in N_{H}^{-} (v_{i})

, we have

π (v_{i}) < π (u) < π (v_{i + 1}) < π (w)

. Hence, whatever the sign of

(v_{i}, v_{i + 1})

, no error is made for

v_{i}

For each

w_{i j}

, vertex

v_{i}

is placed in different side from the other neighbors of

w_{i j}

T_{i j}

, thus, by Proposition 1 no error is produced for

w_{i j}

. □

4. Valid drawing of ladder graphs

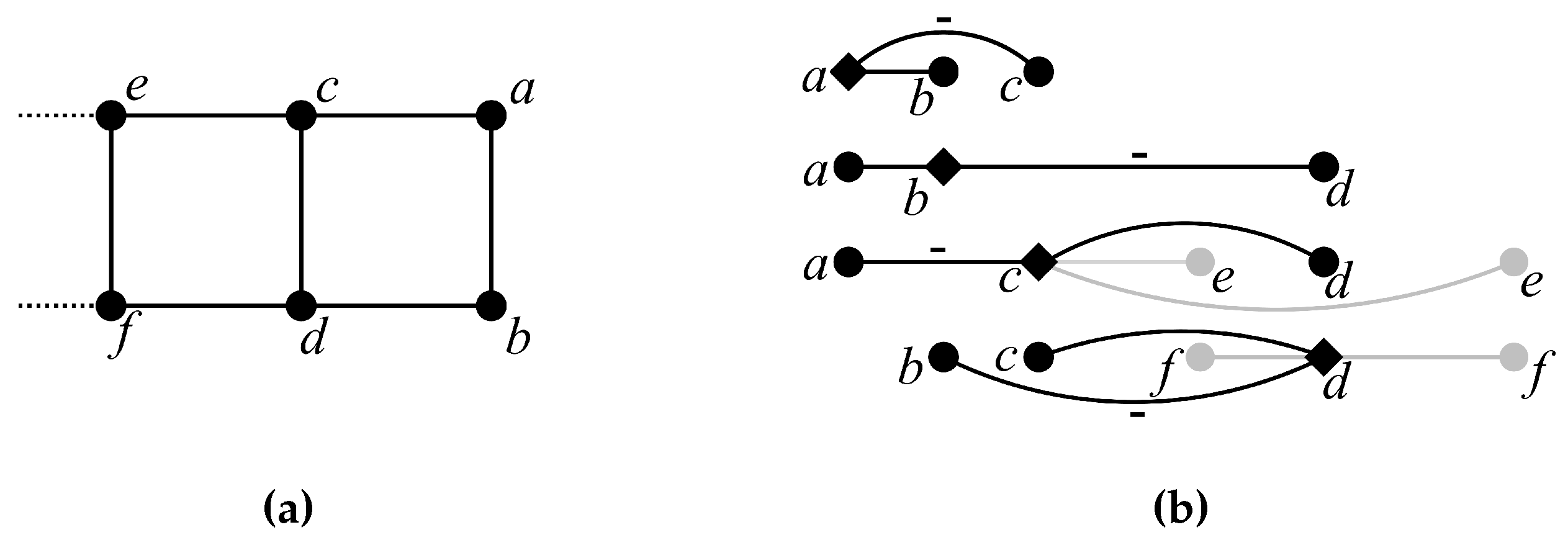
In this section, we show that signed ladder graphs have a valid drawing in the Euclidean line. If we denote a path graph of order k by

P_{k}

, then a ladder graph

L_{n}

is defined as

P_{n} □ P_{2}

We draw

L_{n}

such that it consists of two path graphs drawn horizontally. We label the leftmost vertices at bottom and top as

v_{1}

and

v_{2}

, respectively. Moreover, for each vertical edge that

L_{n}

adds to

L_{n - 1}

, the bottom and top vertices are labeled

v_{2 n - 1}

and

v_{2 n}

, respectively.

Theorem 4.

G (V, E)

is a signed ladder graph, then G has a valid drawing in

R

Proof.

We prove that a signed ladder graph

L_{n}

that its vertices are labeled as described above has a

v_{2 n}

-valid drawing. We argue by induction on the number of vertices. For

n = 1

the result is trivial.

To simplify the notation, we set

a = v_{2 n}

b = v_{2 n - 1}

c = v_{2 n - 2}

, d=

v_{2 n - 3}

e = v_{2 n - 4}

f = v_{2 n - 5}

, and

V (L_{n - 1}) = {v_{1}, v_{2}, \dots, v_{2 n - 2}}

(See Figure 1a). For the induction step, assume there exists a c-valid drawing

ϕ : V (L_{n - 1}) \mapsto {1, 2, \dots, 2 n - 2}

for

L_{n - 1}

. We provide a a-valid drawing

π : V (L_{n}) \mapsto {1, 2, \dots, 2 n}

for

L_{n}

To obtain

L_{n}

from

L_{n - 1}

, vertices a and b are added to

L_{n - 1}

, and neighbors of the vertices

v_{1}, v_{2}, \dots, v_{2 n - 4}

do not change. Thus, we only need to verify that no error occurs for the vertices a, b, c, and d.

We study different cases based on the signs of the edges that

L_{n}

adds to

L_{n - 1}

. For

n = 2

, vertices e and f do not exist, which will simplify the discussion in the following cases. Note that since

ϕ

is a c-valid drawing, we know

ϕ (c) = 1

Case 1.

(a, c) \in E^{-}

and

(b, d) \in E^{-}

In this case for all

w \in V (L_{n - 1})

, we set

π (w) = ϕ (w) + 2

. Also, we set

π (a) = 1

and

π (b) = 2

(See Figure 1b).

Proposition 3 applies to a and its neighbors c and b.
Proposition 1 applies to b and its neighbors a and d.
Proposition 1 applies to c and its neighbors a and d, and also to its neighbors a and e.
Proposition 3 applies to d and its neighbors b and c. If f is on the left of d, then it must be between c and d, thus Proposition 1 applies to d and its neighbors b and f. If f is on the right of d, then Proposition 3 applies to d and its neighbors b and f.

Case 2.

(a, c) \in E^{+}

and

(b, d) \in E^{+}

Let

x = ϕ (d)

. For all

w \in V (L_{n - 1})

, if

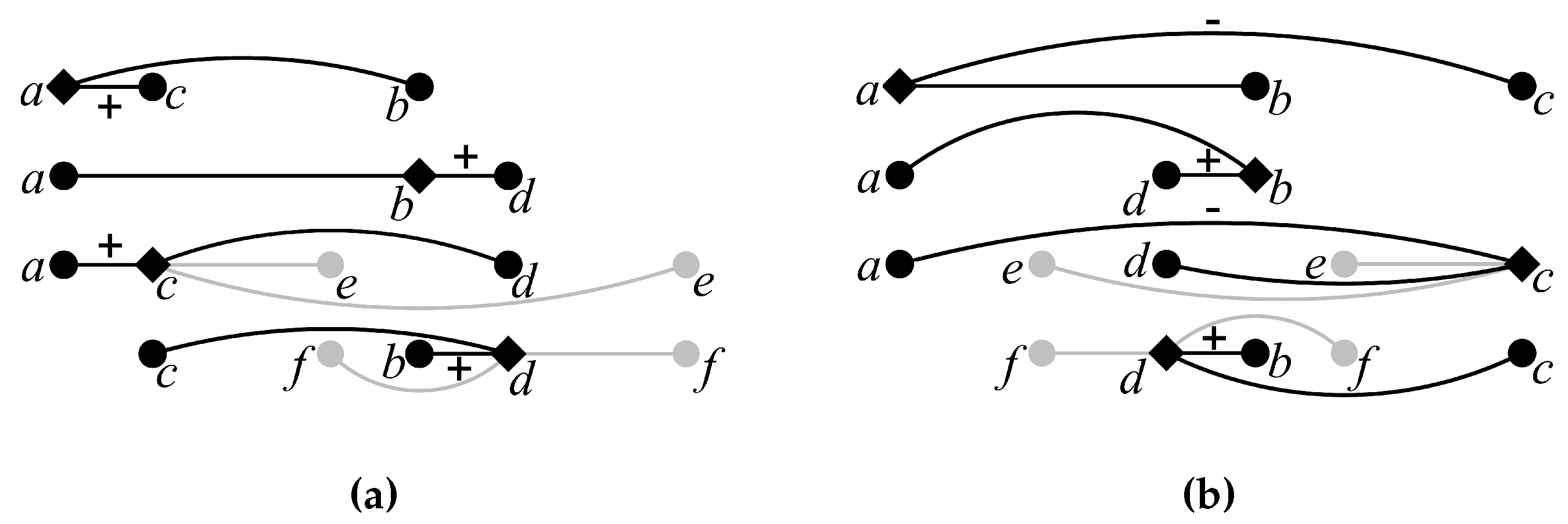
ϕ (w) < x

, we set

π (w) = ϕ (w) + 1

and if

ϕ (w) \geq x

, we set

π (w) = ϕ (w) + 2

. Also, we set

π (a) = 1

and

π (b) = x + 1

(See Figure 2a).

Proposition 2 applies to a and its neighbors b and c.
Proposition 1 applies to b and its neighbors a and d.
Proposition 1 applies to c and its neighbors a and d, and also to its neighbors a and e.
Proposition 2 applies to d and its neighbors c and b. If f is on the left of d, then it must be between c and b, thus Proposition 2 applies to d and its neighbors f and b. If f is on the right of d, then Proposition 1 applies to d and its neighbors b and f.

Case 3.

(a, c) \in E^{-}

and

(b, d) \in E^{+}

Let

x = ϕ (d)

. For all

w \in V (L_{n - 1})

, if

ϕ (w) < x

, we set

π (w) = 2 n + 1 - ϕ (w)

and if

ϕ (w) \geq x

, we set

π (w) = 2 n - ϕ (w)

. Also, we set

π (a) = 1

and

π (b) = 2 n + 1 - x

(See Figure 2b).

Since we have reversed the order of vertices in $V (L_{n - 1})$ , Proposition 4 applies to them.
Proposition 3 applies to a and its neighbors c and b.
Proposition 2 applies to b and its neighbors a and d.
Proposition 3 applies to c and its neighbors a and d, and also to its neighbors a and e.
Proposition 2 applies to d and its neighbors c and b. If f is on the left of d, then Proposition 1 applies to d and its neighbors f and b. If f is on the right of d, then it must be between b and c, thus Proposition 2 applies to d and its neighbors f and b.

Case 4.

(a, c) \in E^{+}

(b, d) \in E^{-}

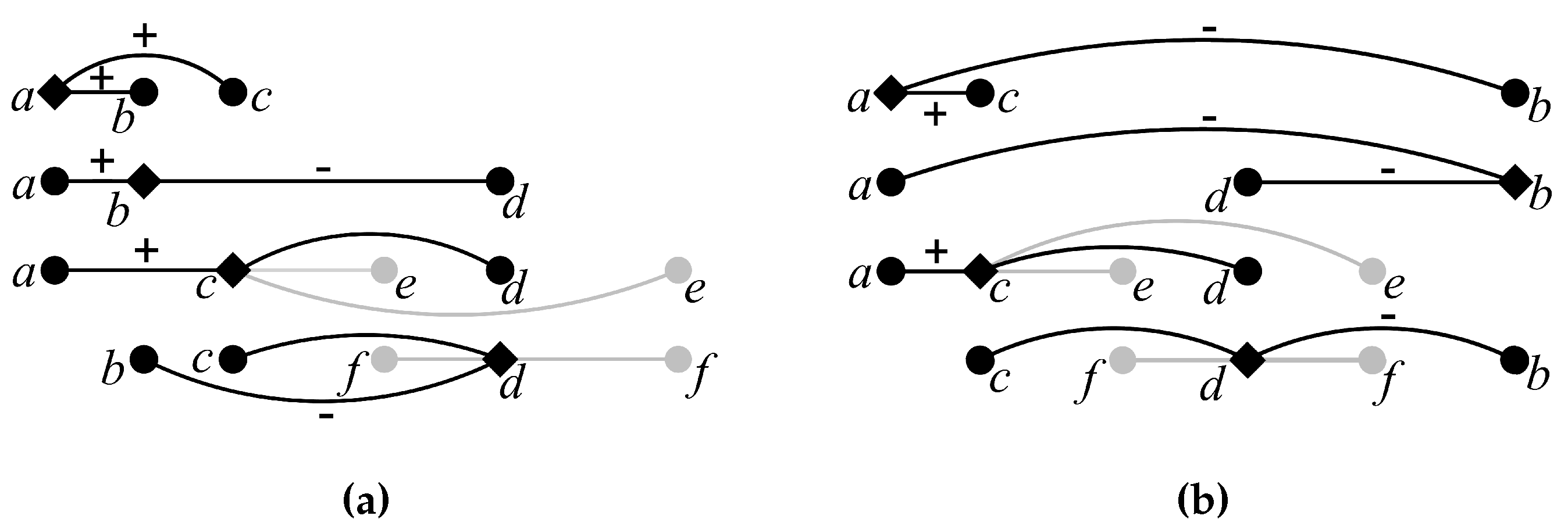
, and

(a, b) \in E^{+}

In this case for all

w \in V (L_{n - 1})

, we set

π (w) = ϕ (w) + 2

. Also, we set

π (a) = 1

and

π (b) = 2

(See Figure 3a).

Since ${b, c} \subset N^{+} (a)$ , vertices b and c do not make an error for a.
Proposition 1 applies to b and its neighbors a and d.
Proposition 1 applies to c and its neighbors a and d, and also to its neighbors a and e.
Proposition 3 applies to d and its neighbors b and c. If f is on the left of d, then it must be between c and d, thus Proposition 3 applies to d and its neighbors b and f. If f is on the right of d, then Proposition 1 applies to d and its neighbors b and f.

Case 5.

(a, c) \in E^{+}

(b, d) \in E^{-}

, and

(a, b) \in E^{-}

In this case for all

w \in V (L_{n - 1})

, we set

π (w) = ϕ (w) + 1

. Also, we set

π (a) = 1

and

π (b) = 2 n

(See Figure 3b).

We have $(a, c) \in E^{+}$ , $(a, b) \in E^{-}$ , and $π (a) < π (c) < π (b)$ . Thus, vertices b and c do not make an error for a.
Since ${a, d} \subset N^{-} (b)$ , vertices a and d do not make an error for b.
Proposition 1 applies to c and its neighbors a and d, and also to its neighbors a and e.
Proposition 1 applies to d and its neighbors c and b. If f is on the left of d, then Proposition 1 applies to d and its neighbors f and b. If f is on the right of d, then it must be between d and b, thus Proposition 3 applies to d and its neighbors b and f.

By cases 1 to 5 and the induction hypothesis, the proof is complete. □

5. Conclusion

In this paper, we proved that if a signed graph is a tree, a unicyclic graph, or a ladder graph, then it has a valid drawing in

R

. Our proofs are based on induction and they can be used to construct a drawing. For future work, one can consider other graph classes such as fan graphs and cactus graphs. Another possible direction of research is to study valid drawing in

R^{2}

References

Harary, F. On the notion of balance of a signed graph. Michigan Mathematical Journal 1953, 2, 143–146. [Google Scholar] [CrossRef]
Kermarrec, A.M.; Thraves, C. Can everybody sit closer to their friends than their enemies? Mathematical Foundations of Computer Science 2011: 36th International Symposium. MFCS 2011, Warsaw, Poland, 2011. Springer, 2011, Vol. 6907, pp. 388–399. [CrossRef]
Kermarrec, A.M.; Thraves, C. Signed graph embedding: when everybody can sit closer to friends than enemies. arXiv 2014, arXiv:1405.5023 2014. [Google Scholar]
Cygan, M.; Pilipczuk, M.; Pilipczuk, M.; Wojtaszczyk, J.O. Sitting closer to friends than enemies, revisited. Mathematical Foundations of Computer Science 2012: 37th International Symposium. MFCS 2012, Bratislava, Slovakia, 2012. Springer, 2012, pp. 296–307. [CrossRef]
Cygan, M.; Pilipczuk, M.; Pilipczuk, M.; Wojtaszczyk, J.O. Sitting Closer to Friends than Enemies, Revisited. Theory of Computing Systems 2015, 56, 394. [Google Scholar] [CrossRef] [PubMed]
Benítez, F.; Aracena, J.; Caro, C.T. The sitting closer to friends than enemies problem in the circumference. arXiv 2018, arXiv:1811.02699 2018. [Google Scholar]
Becerra, R.; Caro, C.T. The Sitting Closer to Friends than Enemies Problem in Trees. arXiv 2019, arXiv:1911.11494 2019. [Google Scholar]
Aracena, J.; Thraves Caro, C. The weighted sitting closer to friends than enemies problem in the line. Journal of Combinatorial Optimization 2023, 45, 1–21. [Google Scholar] [CrossRef]
Pardo, E.G.; Soto, M.; Thraves, C. Embedding signed graphs in the line: heuristics to solve MinSA problem. Journal of Combinatorial Optimization 2015, 29, 451–471. [Google Scholar] [CrossRef]

Figure 1. (a) Naming the last six vertices of

L_{n}

(b) Case 1 of Theorem 4.

Figure 1. (a) Naming the last six vertices of

L_{n}

(b) Case 1 of Theorem 4.

Figure 2. (a) Case 2 of Theorem 4 (b) Case 3 of Theorem 4.

Figure 3. (a) Case 4 of Theorem 4 (b) Case 5 of Theorem 4.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Embedding Some Classes of Signed Graphs in the Line

Abstract

1. Introduction

2. Preliminaries

3. Valid drawing of trees and unicyclic graphs

4. Valid drawing of ladder graphs

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe