Prerpints.org logo
Preprint
Article

Energy Efficient Power Allocation in Massive MIMO based on Parameterized Deep DQN

Altmetrics

Downloads

73

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 October 2023

Posted:

03 October 2023

You are already at the latest version

Alerts
Abstract
Machine learning offers advanced tools for efficient management of radio resources in modern wireless networks. In this study, we leverage a multi-agent deep reinforcement learning (DRL) approach, specifically the Parameterized Deep Q-Network (DQN), to address the challenging problem of power allocation and user association in massive multiple-input multiple-output (M-MIMO) communication networks. Our approach tackles a multi-objective optimization problem aiming to maximize network utility while meeting stringent quality of service requirements in M-MIMO networks. To address the non-convex and nonlinear nature of this problem, we introduce a novel multi-agent DQN framework. This framework defines a large action space, state space, and reward functions, enabling us to learn a near-optimal policy. Simulation results demonstrate the superiority of our Parameterized Deep DQN (PD-DQN) approach when compared to traditional DQN and RL methods. Specifically, we show that our approach outperforms traditional DQN methods in terms of convergence speed and final performance. Additionally, our approach shows 72.2 % and 108.5 % improvement over DQN methods and RL method respectively in handling large-scale multi-agent problems in M-MIMO networks.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

With the increasing demand for mobile communications and Internet of Things technologies, wireless networks are facing increased data traffic and resource management issues owing to the rapid growth of wireless applications. Fifth-generation cellular networks have gained considerable attention for achieving spectrum efficiency and storage capacity. Massive multiple-input multiple-output (M-MIMO) networks are a reliable option to overcome data storage and capacity issues to satisfy diverse user requirements. The main concept in M-MIMO technology is to equip the base stations (BSs) with a large number (i.e., 100 or more) of wireless antennas to simultaneously serve numerous users, enabling significant improvement in spectrum efficiency [1,2].
The presence of a huge number of antennas in M-MIMO, data multiplexing and management would make MIMO transceiver optimization more challenging compared to single-antenna networks. The multi-objective nature of M-MIMO transceivers have resulted in various optimization strategies being performed in the past, including user association [3], power allocation [4], and user scheduling [5]. A joint user association and the resource allocation problem was investigated in [7, 8]. Given the non-convex multiple objective function in the M-MIMO problem, achieving the Pareto optimal solution set in multi-objective environment becomes more challenging. Recently proposed methods to solve multi-objective problems include approaches based on linear programming [9], game-theory [10], and Markov approximation [11, 12]. Success of these methods requires complete knowledge of the system, which is rarely available.
Thus, emerging machine learning (ML) is an efficient tool to solve such complex multi-objective problems. In this ML field, Reinforcement Learning (RL) is the most appropriate branch to solve a non-convex problem. In RL-based optimization methods, three major elements (i.e., agents, reward, and action) of the proposed solution enable the self-learning abilities from the environment.
The Q-learning algorithm is one of the widely used RL methods because it requires a minimum computation. It can be expressed by single equations and, does not need to know the state transition probability The RL agents maximize the long-term rewards over the current optimal reward function [13-14] using a Q-learning algorithm [14,15,16]. The agents are free to change their actions independently in a single-agent RL method, leading to a fluctuation in the overall action space, as well as action and rewards of the different agents in the process [16]. Q-learning methods have been used for power and resource allocation in heterogeneous and cellular networks [17]. However, it may be considerably difficult to handle such large state and action spaces in M-MIMO systems using Q-learning methods. To handle these issues of RL methods, deep reinforcement learning (DRL) methods are coupled with deep learning and RL to enhance the performance of RL for large scale scenario problems. Nowadays, DRL methods [18] are promising to handle these complicated objective functions. DRL methods have already been applied to several tasks, such as resource allocation, fog radio access networks, dynamic channel, access, and mobile computing [19-21].
In DRL, deep Q-network (DQN) method is mostly employed to train the agents to achieve an optimal scheme from a large state and action space. In [23], Rahimi et al. gave an algorithm of DQN which was based on deep neural networks and has been previously used in past literature data. In [23], Zhao et al. used the DRL method for the efficient management of user association and resource allocation for maximizing the network utility and maintains the quality of service (QoS) requirements. In [25-27], the authors proposed a DQN algorithm to allocate power using a multi-agent DRL method. Recent advancements DRL, particularly techniques like Deep Q-Networks (DQN), have opened up new avenues for addressing resource allocation challenges in wireless networks. However, when it comes to applying DQN to solve the combined problem of power allocation and user association, a critical step involves converting the continuous action space for power allocation into a discrete action space. This quantization process can potentially result in suboptimal power allocation decisions, limiting the overall performance. Additionally, the complexity of DQN grows significantly as the dimension of the action space increases. This exponential complexity can lead to high power consumption and slow convergence rates, which are highly undesirable in practical applications. To address these challenges, our paper introduces the use of Parameterized Deep Q-Network (PD-DQN) techniques which deal with parameterized state spaces. However, it falls short in terms of estimation capabilities and tends to produce sub-optimal policies due to its tendency to overestimate Q-values [28]. PD-DQN is well-suited for solving problems involving hybrid action spaces, making it a more efficient choice for the joint power allocation and user association problem, which uses discrete and continuous action space [25]. This hybrid approach is designed to address the challenges posed by a mixed discrete-continuous action space.
In this study, we introduced a novel approach PD-DQN algorithm [25]. The main contributions of this paper are listed in the following:
  • This paper proposes a user association and power allocation problem with objective of maximizing EE in a massive MIMO network.
  • To solve the power allocation problems, the action space, the state space, and the reward function have been considered. We apply the model-free DQN framework and PD-DQN to update policies in action space. We also employ the novel PD-DQN framework that is able to updating policies in a hybrid discrete-continuous action space.
  • The simulation results show that the proposed user association and power allocation method based on PD-DQN perform better than DRL and RL method.

2. System Model

In this study, we considered single cell massive MIMO network which consists of N remote radio heads (RRHs) and single antenna users. Here, RRHs are connected to a baseband unit via backhaul connections. Each RRH is equipped with M m a x antennas. There are U single-antenna users served by N RRHs together operating in the same time frequency domain. It is assumed that M m a x > U. In this network, we associate each user with a single RRH [7]. The set of users is denoted by U. Figure 1 shows the network architecture based on a DRL.
It is assumed that the channel between the uth users and the nth RRH is given by
h n , u = β n , u g n , u
where β n , u signifies the large-scale fading coefficient, and g n , u signifies the small-scale fading coefficient. g n , u is also known as Rayleigh fading and the elements are independent and identically distributed (i.i.d) random variables having zero mean and unit variance[8].
The received signal of the uth user on the nth RRH can be given by [7]
Y n , u = p u h n , u w n , u s n , u + ∑ j = 1 , j ≠ u U p j h n , u w n , u s n , j + z n , u
where p u is power transmitted through uth user, s n , u is the N r × 1 data symbol of the uth user on the nth RRH, w n , u is the N t × N r beamforming vector of the uth user on the nth RRH which is given by w n , u = h n , u E h ^ n , u 2 and h n , u is the channel matrix of the uth user on the nth RRH. z n , u is the noise vector of independent identically distributed (i.i.d.) additive complex Gaussian noise having zero mean and variance of σ .
Without loss of generality, we set
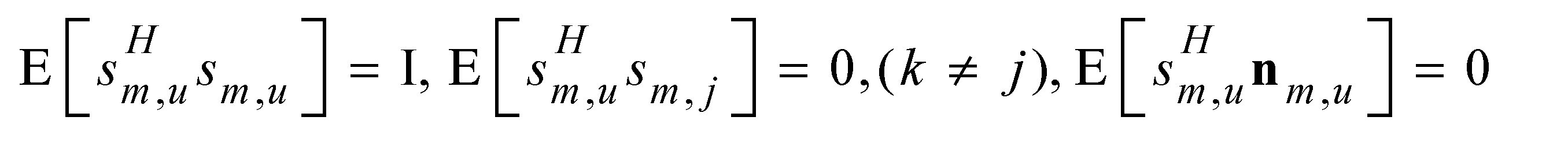
Preprints 86680 i001

2.1. Power consumption

We considered the downlink phase for power consumption. The overall P c is expressed as the sum of the transmit power and fixed power consumption of the RRHs and base units denoted as P F I X and the power consumed by the components of the active antennas [5]. The total P c can then be given by
P c = P F i x + P a ∑ n = 1 N M n + ∑ n = 1 N ∑ u = 1 U 1 ν P n , u
where P a denotes power assumed for active antenna and ν power amplifier efficiency, ν ∈ 0,1 .

3. Problem formulation

According to the system model, the ergodic achievable rate of the uth user is given by[10]
R n , u = log 2 ⁡ 1 + Γ u , n
where Γ u , n is signal-to-interference-plus-noise ratio of uth and nth RRH and given by
R n , u = M n p n Γ n , u ∑ j = 1 N ∑ q = 1 U p j , q β j , u + σ 2
To deal with the above problem, the association between uth users and nth RRH is given by
x n , u = 1 , u ∈ L l 0 , u ∈ U L l l = 1 , . . . L
The system energy efficiency (EE) can be expressed as
m a x X , P η = ∑ u = 1 U R u P F I X + p a ∑ n = 1 N M n + ∑ n = 1 N ∑ u = 1 U 1 v p n , u
The optimization problem maximizing the system EE can be formulated as
P 1 : m a x X , P η = ∑ u = 1 U R u ( X , P ) P c X , P ,
s . t     C 1 : 0 < P u , m ≤ P u m a x
C 2 : a u , m ∈ 0,1
C 3 : ∑ m a u , m = 1
C 4 : R u ≥ R min
In the above problem, C1 denotes that the transmitted power consumption is smaller than the transmit power limit of each RRH. Constraints C2 and C3 indicate that one user can only be associated with one RRH. C4 maintains the QoS requirement of each user and signifies the lower limit of the required transmit rate of users. Problem (8) is NP-hard and is usually difficult to find a feasible solution [22]. Therefore, a multi-agent DRL approach was used to solve this problem, as described in the next section.

4. Multi-Agent DRL Optimization Scheme

The problem P1 is a non-convex problem where user association as well as power allocation approaches are involved. To solve this tractable problem, a multi-agent DQN-based RL technique was applied. The major component of the RL approach is based on the Markov decision-making process (MDP), which is a new proposed reward function, prior to the application of the multi-agent DQN approach.

4.1. Overview of RL method

In this section, we present the overview of RL. In RL the aim is to find optimal policy. The problem P1 is converted into a MDP (s, a, r, P s s n e w ) similar to the existing work [26-27], where s, a, and r represent the set of state, set of action, and reward functions, respectively. P s s n e w is the transition probability from state s to s n e w with reward r. In the DRL, these state variables are defined as follows:
State space: In problem P1, the users as agents select the BSs for communication at time t. The network consists of U agents. The state space can be expressed as
s ( t ) = s 1 ( t ) , s 2 ( t ) , . . . s u ( t ) , . . . , s U ( t )
Action space: At time t, the action of the agent is to control the transmit power level between the user association and BS. The action space consisting of each user can be defined as
a ( t ) = a 1 ( t ) , a 2 ( t ) , . . a s u ( t ) , . . . , a U ( t )
Reward function: The energy efficiency of all users can be expressed as a system reward function
r ( t ) = ∑ u U r u ( t ) = ∑ u = 1 U η u ( t )
where is r ( t ) the reward function, which is maximized to achieve the optimal policy with interaction with the outer environment.
Therefore, within the RL framework, the problem P1 can be transformed into problem P2, as follows:
P 1 :   max X , P , M r n
where X represents the user association matrix and P denotes the power allocation vector. The agent identifies its state s(t) at time t and follows a policy π to perform an action a(t) that is, a ( t ) = π ( s ( t ) ) . Following this, the users communicate with the BSs and the reward function becomes r t = r t | s = s ( t ) , a = a ( t ) . Therefore, the future cumulative discounted reward at time t can be given by
R ( t ) = ∑ τ = t T γ τ − t r ( τ )
where γ ∈ [0, 1] denotes the discount factor for the upcoming rewards. To solve the P2, a value function for policy π u is defined as
V u π u = Ε ∑ τ = t T γ τ − t r u ( τ ) | s u τ , a u ( τ )
where E[·] denotes the expectation operator. By Markov property, the value function is defined as
V u π u = r ( s u τ , π u ) + γ ∑ s n e w ∈ S P s s n e w ( π u ) V u π u ( s u τ n e w )
The Q-function when performing action a u ( τ ) in state s u τ with policy π u can be expressed as [24], that is,
Q π s τ , a ( τ ) = Ε R τ | s τ , a ( τ )
The optimal Q-value function satisfies the Bellman equation [29-30] derived as
Q π * s τ , a ( τ ) = r s τ , a ( τ ) + γ ∑ s ′ ∈ S P s s ′ a ( τ ) V π * ( s τ ′ )
Accordingly, the Bellman optimality equation (17) [24], V u π u * ( s u τ n e w ) can be obtained as
V u π u * ( s u τ n e w ) = m a x a ′ u Q π u * s u τ n e w , a u τ n e w ( τ )
Adding Eq (17) and (18), we get
Q π * s τ , a ( τ ) = r s τ , a ( τ ) + γ ∑ s ′ ∈ S P s s ′ a ( τ ) m a x a ′ u Q π u * s u τ n e w , a u τ n e w ( τ )
The update of the Q-value function is given by [14] as
Q π * s τ , a ( τ ) = ( 1 − α ) Q π s τ , a ( τ ) + α r s τ , a ( τ ) + γ m a x a ′ Q π ′ s τ , a ′ ( τ ′ )
where α is learning rate scaled between 0 and 1 and updating speed of Q π u s u τ , a u ( τ ) The RL algorithm shows good performance if size of states is small. In case of high dimensional state space, classical RL approaches fail to perform. Some states are not sampled because of the high dimensional state space and require several restrictions. First, the convergence rate might become slow and storage of lookup table becomes impractical. Thus, the use of the DRL method was explored to solve the problem with the large space.

4.2. Multi-agent DQN frameworks

In contrast to the classical Q-learning approach, the author in [ 23 ] proposed the DQN method which was basically DRL method. This DQN method relies on two components, e.g., replay memory and target network. The agent stores transitions s u τ , a u ( τ ) , r u ( τ ) , s u τ n e w in a replay memory D. Then extract this transition from memory D by using random sampling to compute Q-value function. The agent uses the memory D in a part of mini-batch to train the Q-network and then a gradient descent method is applied to update the weight parameter θ of behavior network.
π u = max ⁡ Q π u * s u τ , a u n e w ( τ ) a ′
In the DQN method, the types of networks are included, that is, DQN sets the θ target target networks. The learning model calculates the target value y j with a weight parameter θ target for a certain time t, which can mitigate the volatility of the learning scheme. During the learning process, after several iterations H the weight parameter θ is synchronized with the target network θ → θ target . The agent utilizes a greedy random policy means that the agent randomly selects an action a u ( τ ) parameter θ for the behavior network. Consequently, a ( τ ) value and θ are updated iteratively using the minimum loss function [31]:
L ( θ ) = ∑ y j − Q π u ( s u , a u ; θ ) ,
where y j = r j + γ m a x a u n e w ( j ) Q π u ( s u j n e w , a u n e w ( j ) ; θ target ) The proposed DQN algorithm for user association and power allocation is shown in Algorithm 1.
Preprints 86680 i002

4.3. Parameterized Deep Q-Network Algorithm

The combined user association and power allocation procedure in a hybrid action space can be solved via parameterization, but it still has generalization problems. In order to solve this problem, we used the epsilon greedy exploration method, which enables the DQN to explore a wide variety of states and actions and improves generalization. In a hybrid action space, the Q-value is recast as Q ( s , a ) = Q ( a , β , χ ) where β denotes a discrete action and χ denotes a continuous action. The reward is defined as parameterized double DQN with replay buffer EE. Whether UE is associated with BS or not, the user association will only have the two discrete values β = 0 and 1. On the other hand, χ is a matrix that represents various levels of power distribution. PD-DQN for user association and power allocation algorithm is presented in Algorithm 2.
Preprints 86680 i003

5. Simulation Result

In this section, the results of the simulation with the DRL algorithms are presented. We considered a distributed M-MIMO with three RRHs equipped with 300 antennas in the cell with diameter of 2000 m. We consider K= 20 randomly distributed users within the cell. The PC of each RRH is set to 10000 mW.
The power consumed by component of active antennas is 200 mW, and the power ampli fier efficiency, ν is 0.25. We assumed a transmission bandwidth of 10 MHz [7]. The other parameters are given in Table 1. We consider the Hata-COST231 propagation model [8]. The large-scale-fading β in eq (1) borrowed from literature [8] which is given by 10 log 10 ⁡ β n , u = P L n , u + Ω where PL is path loss and Ω represents standard deviation. Here, dn,u is the distance between uth users and nth RRH.
Figure 2 shows the energy efficiency of the proposed DRL algorithm and RL algorithm. Figure 2 gives two observations indicate that the EE achieved by the DRL method outperforms the RL methods. As the number of episodes increases up to 50, the system EE increases and tends to converge after 250 episodes for both schemes. Additionally, the learning speed of the Q-learning method is lower than that of the multi-agent DQN algorithm. For the Q-learning method, there is a slight improvement in the system EE at episode 120, whereas in DRL approach, the system EE tends to be stable at episode 257. The EE is unstable at the beginning as seen in the DRL scheme, and the stability increases as the episodes increase, and thereafter increases slowly. This is because the agent selects actions in a random manner and stores the transition information in D.
Figure 3 shows the EE versus the number of user fix M= 20. From the figure we can see that, the EE generally first increases with K from 5 to 45 and then decreases flatten. This is due to the fact that when scheduling more users, more RRHs are activated to serve users creating more interference noise. Furthermore, proposed DRL algorithm performs superior to QL.
Figure 4 compares the EE performance at different discounted factors, γ = {0.1, 0.5, and 0.8}. It can be observed that a lower discount factor results in higher EE through different discount factors. Figure 4 illustrates that the PD-DQN methods optimize the user association and power allocation. Moreover, when the number of epochs increases, the EE performance of each user is better at a different discount factor.
From the figure, we can observe that PDQN consistently outperforms both DQN and RL in terms of energy efficiency. The EE values achieved by PDQN show a steady increase, starting from 1.5 and reaching 5.25, indicating significant improvement. DQN and RL also exhibit improvements, but their EE values remain below that of PDQN. In terms of percentage improvement, PDQN surpasses DQN by an average of around 35%, while PDQN outperforms RL by approximately 40%. Additionally, DQN exhibits a slight advantage over RL, with an average improvement of about 5%.

5. Conclusion

In this paper, we have studied the user association and power allocation problem in a massive MIMO based on PD-DQN framework. The numerical results indicate that the PD-DQN approach performs better than the DQN and classical Q-learning scheme. The main motivation of this paper is to study resource allocation scheme in M-MIMO. In addition, for the simulation results in this study, we considered DQN approach to tackle the problem of user association and power allocation in M-MIMO. The aforedescribed optimization problem was formulated to maximize the EE in the downlink network, and the convergence of the multi-agent DRL (DQN) algorithm was studied. Furthermore, convergence analyses confirmed that the proposed methods perform better in terms of EE than the RL method. The convergence rate indicates that the proposed algorithm excels in terms of energy efficiency. Furthermore, additional simulation outcomes demonstrate superior energy efficiency across varying user counts, number of antennas, and diverse learning rates. The enhancement of the proposed PD-DQN on average may reach 72.2% and 108.5 % over the traditional DQN and RL respectively.

Acknowledgments

This research was funded by the National Research Foundation of Korea (NRF), Ministry of Education, Science and Technology (Grant No. 2016R1A2B4012752).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hao L, Zhigang W, & Houjun W. (2021). An energy-efficient power allocation scheme for Massive MIMO systems with imperfect CSI, Digital Signal Processing, 112. 1029. [CrossRef]
  2. Rajoria, S. , Trivedi, A., Godfrey, W. W., & Pawar, P. (2019). Resource Allocation and User Association in Massive MIMO Enabled Wireless Backhaul Network. IEEE 89th Vehicular Technology Conference (VTC2019-Spring), (pp. 1-6). [CrossRef]
  3. Ge, X. , Li, X., Jin, H., Cheng, J., Leung, V.C.M., (2018). Joint user association and user scheduling for load balancing in heterogeneous networks, IEEE Trans. Wireless Commun. 17 (5), 3211–3225. [CrossRef]
  4. Liang, L. , and Kim, J., and Jha, S. C., and Sivanesan, K., and Li, G. Y. (2017). Spectrum and power allocation for vehicular communications with delayed CSI feedback, IEEE Wireless Communications Letters, 6, 458–461. [CrossRef]
  5. Bu, G. , and Jiang, J. (2019). Reinforcement Learning-Based User Scheduling and Resource Allocation for Massive MU-MIMO System, 2019 IEEE/CIC International Conference on Communications in China (ICCC), Changchun, China, 2019, pp. 641-646. [CrossRef]
  6. Yang, K., Wang, L., Wang, S, Zhang, X. (2017). Optimization of resource allocation and user association for energy efficiency in future wireless networks, IEEE Access., 5, 16469-16477. 5, 16469–16477. [CrossRef]
  7. Dong, G. , Zhang, H., Jin, S., and Yuan, D. (2019). Energy-Efficiency-Oriented Joint User Association and Power Allocation in Distributed Massive MIMO Systems, in IEEE Transactions on Vehicular Technology, vol. 68 (6), 5794-5808. [CrossRef]
  8. Ngo, H. Q. et al. (2017). Cell-free massive MIMO versus small cells. IEEE Transaction on Wireless Communication, 16, 1834–1850. [CrossRef]
  9. Elsherif, A. R, Chen, W.-P., Ito, A. and Ding, Z. (2015). Resource Allocation And Inter-Cell Interference Management For Dual-Access Small Cells. IEEE Journal of Selected Areas In Communication. 33 (6), 1082-1096. [CrossRef]
  10. Sheng, J. , Tang, Z., Wu, C., Ai, B. and Wang, Y. (2020). Game Theory-Based Multi-Objective Optimization Interference Alignment Algorithm for HSR 5G Heterogeneous Ultra-Dense Network. in IEEE Transactions on Vehicular Technology, 69(11), 13371-13382. [CrossRef]
  11. Zhang, X. , Sun, S. (2018). Dynamic scheduling for wireless multicast in massive MIMO HetNet, Physical Communication, 27, 1-6. [CrossRef]
  12. Nassar, A. , Yilmaz, Y. (2019). Reinforcement Learning for Adaptive Resource Allocation in Fog RAN for IoT with Heterogeneous Latency Requirements. in IEEE Access, 7, 128014-128025. [CrossRef]
  13. Sun, Y. , Feng, G., Qin, S, Liang, Y.-C, and Yum. T. P. (2018). The Smart Handoff Policy For Millimeter Wave Heterogeneous Cellular Networks, IEEE Trans. Mobile Comput., 17 (6), 1456-1468, 2018. [CrossRef]
  14. Watkins, C. J. , and Dayan, P. (1992). Q-Learning, Machine Learning, 8 (3-4), 279-292. [CrossRef]
  15. Zhai, Q. , Bolić, M., Li, Y., Cheng, W. and Liu, C. (2021). A Q-Learning-Based Resource Allocation for Downlink Non-Orthogonal Multiple Access Systems Considering QoS. in IEEE Access, 9, 72702-72711. [CrossRef]
  16. AMIRI, R., et al. (2018). A machine learning approach for power allocation in HetNets considering QoS. In The Proceedings of 2018 IEEE International Conference on Communications (ICC). Kansas City (MO, USA), 2018, p. 1–7. pp. 20181–7. [CrossRef]
  17. Ghadimi, E. , Calabrese, F. D. Peters, G. and Soldati, P. (2017). A reinforcement learning approach to power control and rate adaptation in cellular networks, in Proc. IEEE Int. Conf. Commun. (ICC), 2017, pp. 1-7. [CrossRef]
  18. F. Meng, P. F. Meng, P. Chen, and L. Wu, Power allocation in multi-user cellular networks with deep Q learning approach, in Proc. IEEE Int. Conf. Commun (ICC), 2019, pp. 1–7. [CrossRef]
  19. Ye, H., Li, G.Y., Juang, B.F. (2019). Deep reinforcement learning based resource allocation for v2v communications, IEEE Trans. Veh. Technol. 68 (4), 3163–3173. [CrossRef]
  20. Wei, Y. , Yu, F.R., Song, M., Han, Z. (2019). Joint optimization of caching, computing, and radio resources for fog-enabled IOT using natural actor critic deep reinforcement learning. IEEE Internet Things J. 6 (22), 2061–2073. [CrossRef]
  21. Sun, Y. , Peng, M., Mao,S. (2019). Deep reinforcement learning-based mode selection and resource management for green fog radio access networks. IEEE Internet Things J., 6 (2), 960–1971. [CrossRef]
  22. Rahimi, A. , Ziaeddini, A. & Gonglee, S. (2021) A novel approach to efficient resource allocation in load-balanced cellular networks using hierarchical DRL. J Ambient Intell Human Comput. doi: 1007/s12652-021-03174-0.
  23. Zhao, N. , Liang, Y.-C., Niyato, D., Pei, Y., Wu, M. and Jiang, Y(2018). Deep reinforcement learning for user association and resource allocation in heterogeneous networks. in IEEE Globecom, Abu Dhabi, UAE, Dec. 2018, pp. 1–6. [CrossRef]
  24. Nasi, Y. S. and Guo, D. (2019), Multi-Agent Deep Reinforcement Learning for Dynamic Power Allocation in Wireless Networks, in IEEE J. Sel. Areas in Commun, 37 (10), 2239-2250. [CrossRef]
  25. Xu, Y. , Yu, J., and William C. H. and Buehrer, R (2018). Deep Reinforcement Learning for Dynamic Spectrum Access in Wireless Networks, 2018 IEEE Military Communications Conference (MILCOM), pp. 207-212. [CrossRef]
  26. Li, M. , Zhao, X., Liang, H., Hu. F., (2019). Deep reinforcement learning optimal transmis- sion policy for communication systems with energy harvesting and adaptive mqam, IEEE Trans. Veh. Technol. 68 (6), 5782–5793. [CrossRef]
  27. Su, Y. Lu, X. Zhao, Y. Huang, L., Du, X. (2019). Cooperative communications with relay selection basedon deep reinforcement learning in wireless sensor networks. IEEE Sensors Journal, 19(20), 9561-9569. [CrossRef]
  28. Xiong, J.; Wang, Q.; Yang, Z.; Sun, P.; Han, L.; Zheng, Y.; Fu, H.; Zhang, T.; Liu, J.; Liu, H. Parametrized deep q-networks learning: Reinforcement learning with discrete-continuous hybrid action space. arXiv arXiv:1810.06394, 2018.
  29. Hsieh C-K, Chan K-L, Chien F-T. Energy-Efficient Power Allocation and User Association in Heterogeneous Networks with Deep Reinforcement Learning. Applied Sciences. 2021; 11(9):4135. [CrossRef]
  30. R. S. Sutton and A. G. Barto, Reinforcement learning: An introduction. MIT Press Cambridge, 1998.
  31. Mnih, V. et al. (2015). Human-level control through deep reinforcement learning. Nature, 518 (7540), 529–533. [CrossRef]
Preprints 86680 g001
Figure 1. System Model based on DRL.
Figure 1. System Model based on DRL.
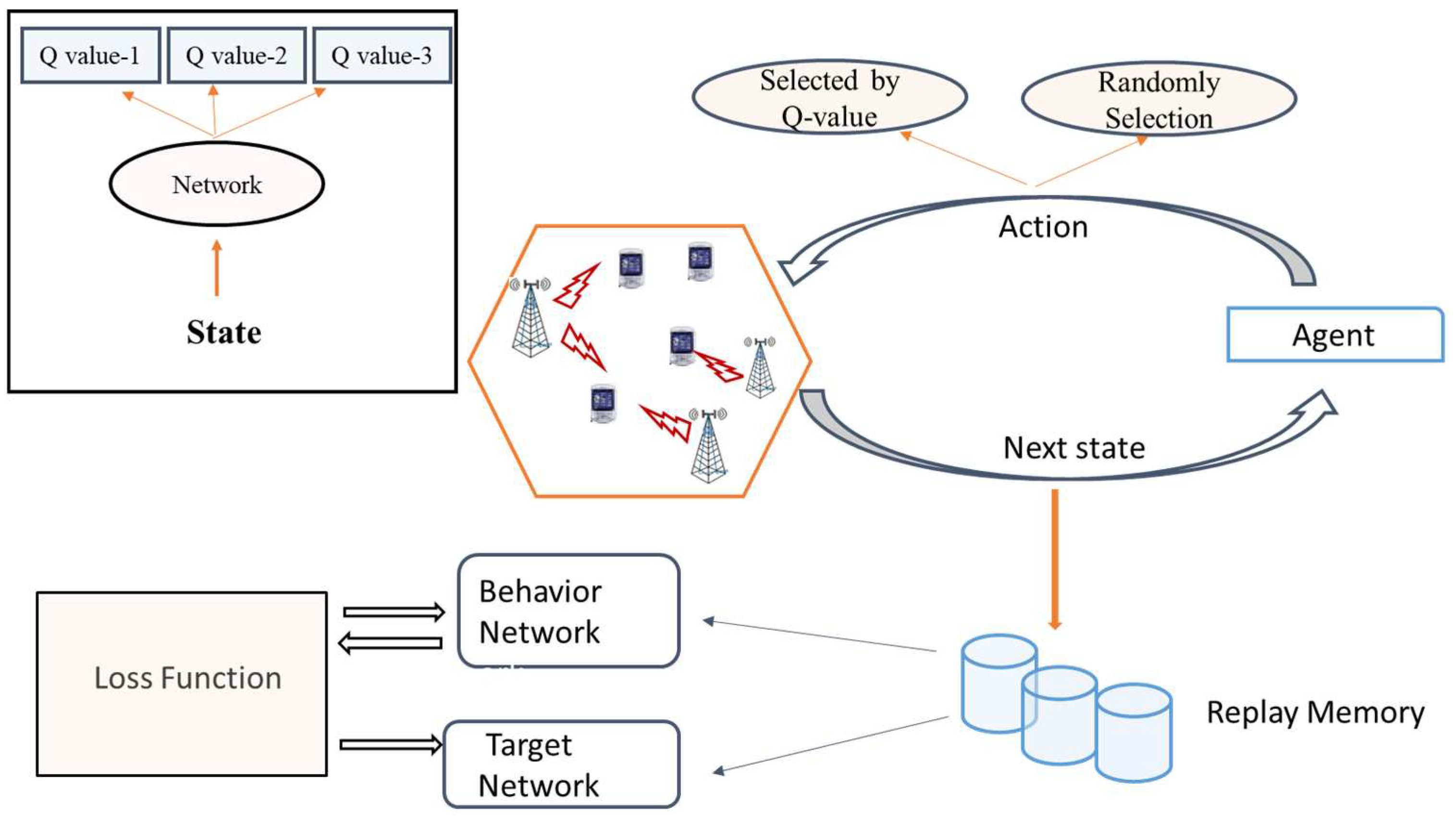
Preprints 86680 g001
Preprints 86680 g002
Figure 2. Convergence of energy efficiency values.
Figure 2. Convergence of energy efficiency values.
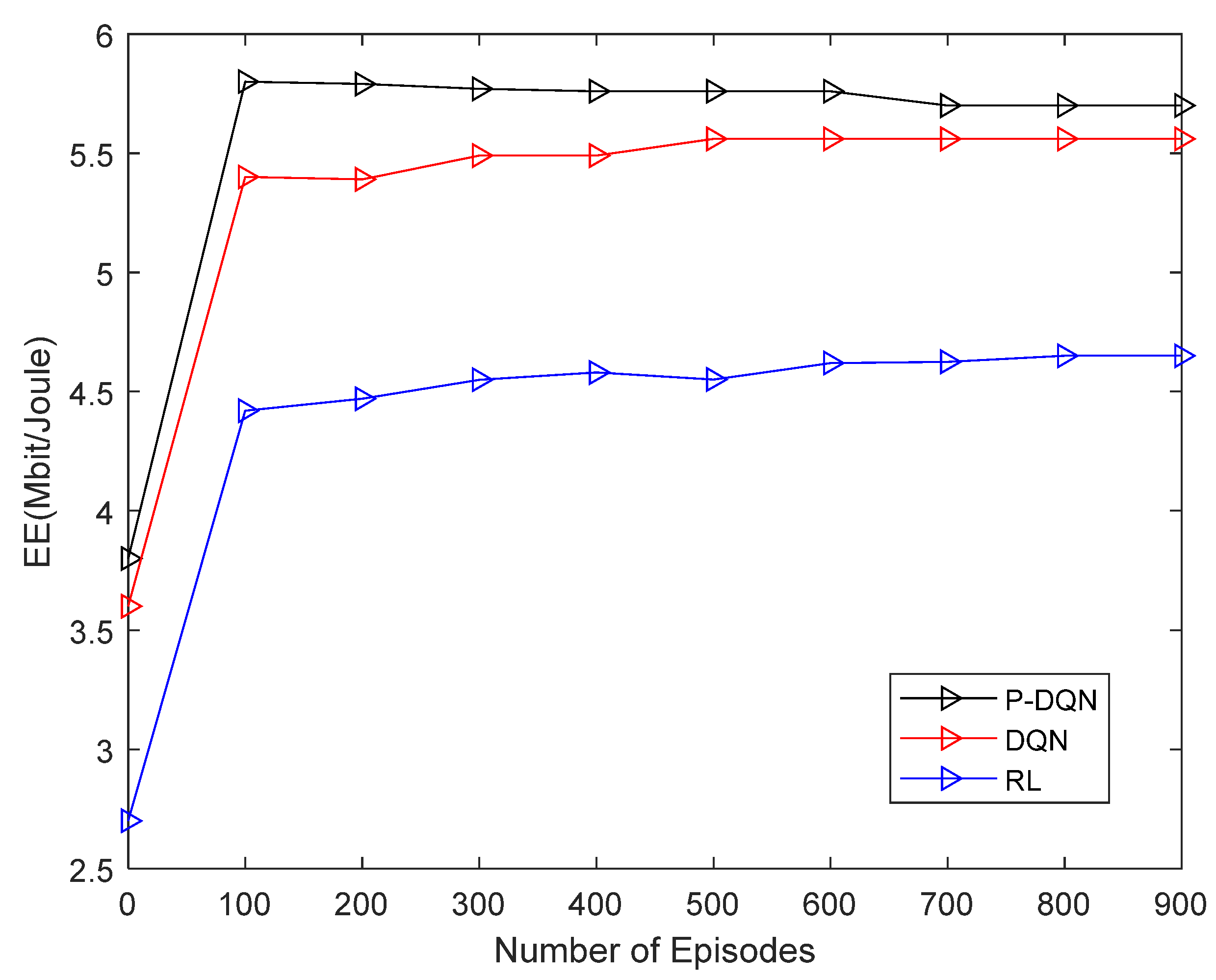
Preprints 86680 g002
Preprints 86680 g003
Figure 3. EE versus Number of user.
Figure 3. EE versus Number of user.
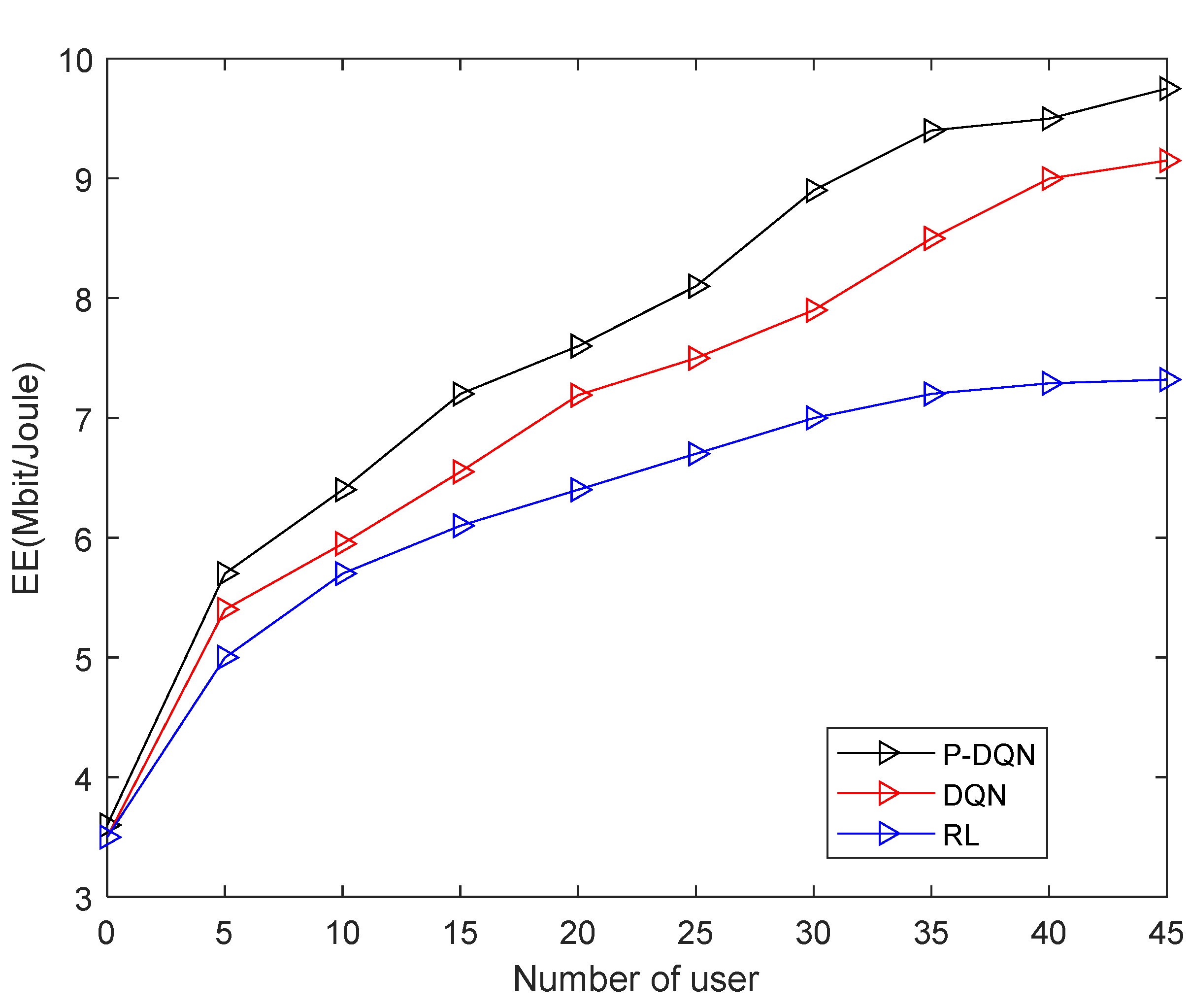
Preprints 86680 g003
Preprints 86680 g004
Figure 4. EE versus Number of users.
Figure 4. EE versus Number of users.
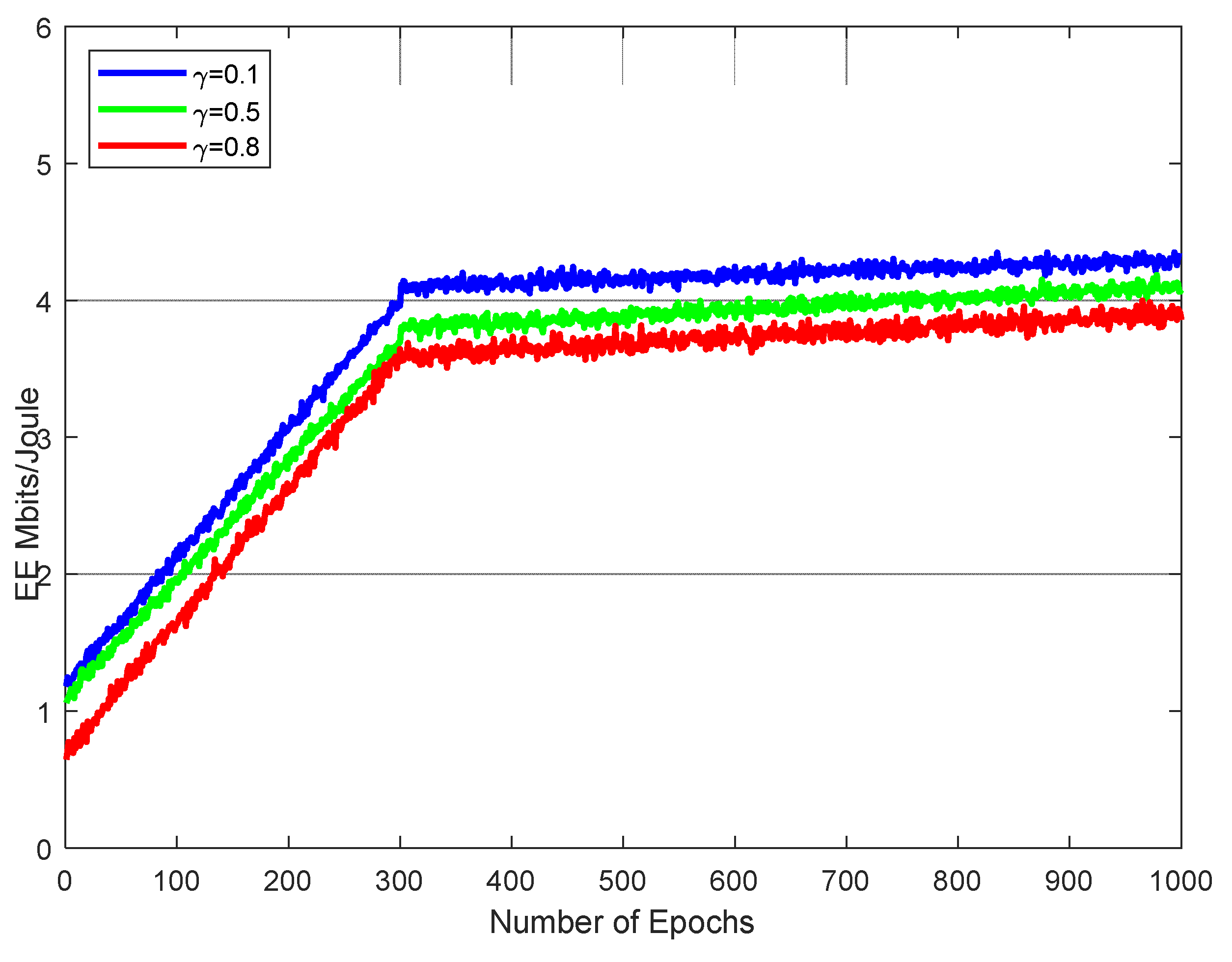
Preprints 86680 g004
Preprints 86680 g005
Figure 5. EE versus number of antennas.
Figure 5. EE versus number of antennas.
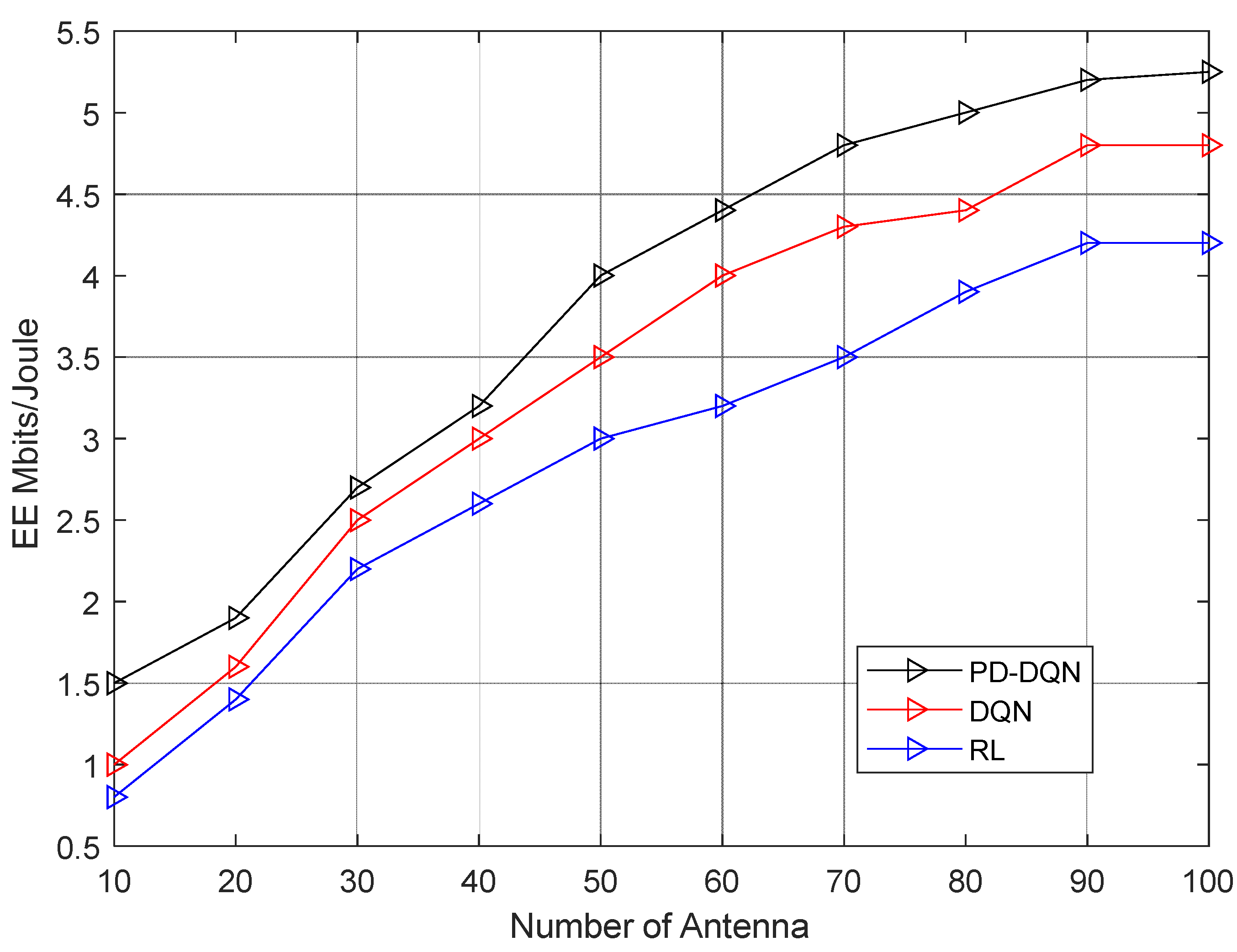
Preprints 86680 g005
Table 1. Simulation parameters.
Table 1. Simulation parameters.
Parameter Values
Standard Deviation 8 dB
Path loss model PL PL=−140.6−35log10(d)
Episodes 500
Steps T 500
Discount rate γ 0.9
Mini-batch size b 8
Learning Rate 0.01
Replay Memory size D 5000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated