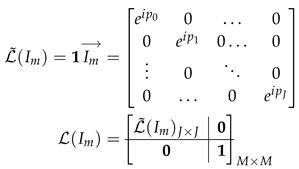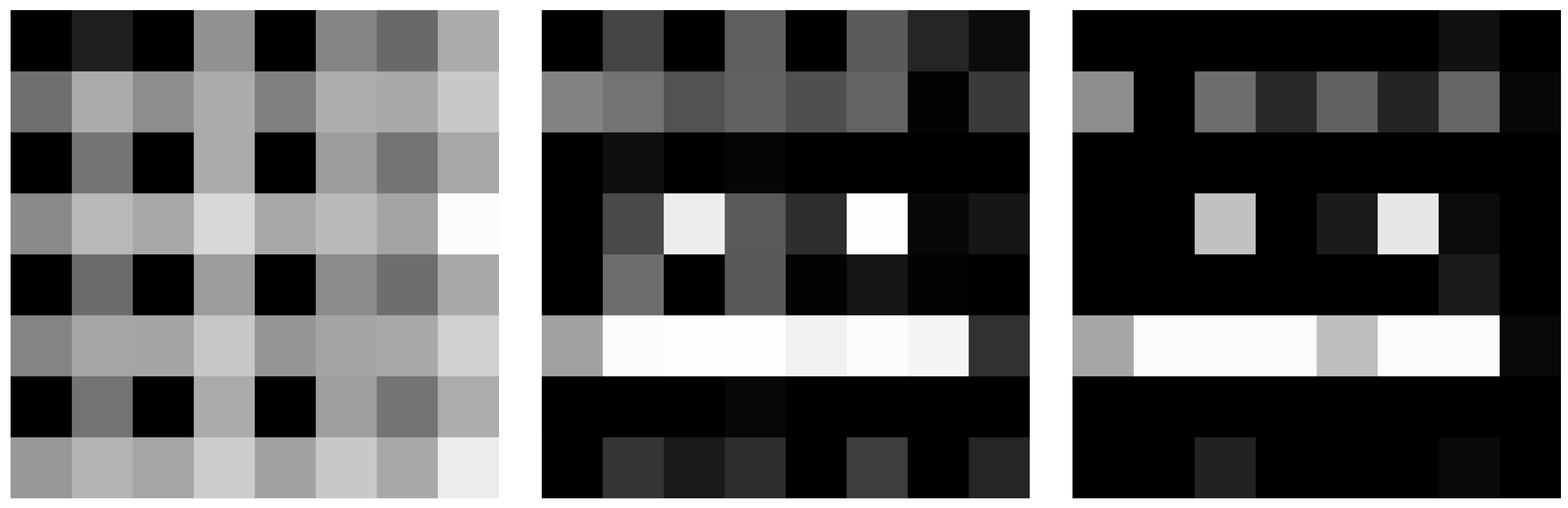Deep learning as a tool of quantum error reduction in quantum image processing

Preprint

Article

Deep learning as a tool of quantum error reduction in quantum image processing

Altmetrics

Downloads

131

Views

Comments

Krzysztof Werner^*

Kamil Wereszczyński^*,Rafał Potempa,

Krzysztof A Cyran

Krzysztof Werner^*

Kamil Wereszczyński^*,Rafał Potempa,

Krzysztof A Cyran

This version is not peer-reviewed

Submitted:

30 September 2023

Posted:

03 October 2023

You are already at the latest version

Alerts

Abstract

Quantum image representation is a widely researched area of quantum computing. Currently developed methods use angle parameter of the rotation gate (e.g., the FRQI method), sequences of qubits (ex. NEQR method) or phase shift (ex. LPIQE method) for storing color information of pixels. All of those methods are affected by decoherence and other classical and quantum noise, which is an inseparable part of quantum computing in a NISQ (Noisy Intermediate Scale Quantum) era. These all phenomenons influence the measurements, its probability distribution over the measurement basis and, as the result, makes the extracted images not even similar to those, which was stored in quantum computers. Since this process is, in its foundation, quantum as well, the computational reversal of this process is possible. There are a lot of methods for error correction, mitigation and reduction, but all of them use quantum computer time, or additional qubits to achieve desired result. We report a successful use of the Generative Adversarial Network tuned for image-to-image translation in conjunction with PDU method, for error reduction in images encoded using LIPQE (Local Phase Image Quantum Encoding) method.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

We propose a use of GAN (Generative Adversarial Network) for error reduction, as a new way of error reduction in image processing, where the quantum computer is used to handle all calculations, and the classical computer is used for error reduction. In the future, we plan to implement the error reduction method on the quantum computer as well.

This method is intended for use in quantum object detection of aviation instruments, on images taken on Microsoft HoloLens 2 device inside the flight simulator cockpit.

GAN, is a class of deep learning algorithm proposed in 2014 by Goodfellow et al. [1]. In this approach, two neural networks compete against each other in a zero-sum game as follows.

Generator, produces candidates for output, using input, original data,
Discriminator, evaluates candidates provided by the generator, recognizing if the generated output is artificial or original. So it is trained to distinguish generated output from the original samples.

Such game force the generator to produce the output similar to desired one. After the network is trained it can be used for generation of images, or to evaluate image correctness. Such networks was used e.g., for generating painting in the desired style from images. The GAN networks can be implemented using wide variety of programming libraries, e.g., TensorFlow [2] and Keras [3], pygan or torchgan [4]. In our experiment, after training we have used the model for generation of images with reduced error, based on the images reconstructed from the quantum computers.

LPIQE method of quantum image encoding was proposed in 2020 [5]. It was meant to be implemented in photonic quantum computers (which are the computers that uses photons as the source of qubits. Computers like this are currently in operation and are being offered for researchers. The most known photonic processor from Xanadu, described by Somhorst et al. in [6] or Madsen et al. in [7] uses the squeezed states and measurement-based quantum computation model. QuiX Quantum from Netherlands, e.g., Taballione et al. [8] or de Goede et al. [9] uses other sources like single photons or quantum dots as the supply of the quantum systems.

LPIQE method uses controlled phase shift gates, for color representation. Such configurations are very natural for optic based system, in contrary to other methods, that needs to be implemented with the usage of significantly more optical devices, which certainly has

For image representation this method uses

⌈ l o g_{2} X ⌉ + ⌈ l o g_{2} Y ⌉ + 1

qubits, where X and Y references X and Y dimensions of encoded image, while the additional qubit is used for storing color information (in 1 channel mode). For storing images represented in RGB spectrum additional 2 qubits are needed for R, G or B channel selection. Encoding color information in local phase allows the method to be combined with PDU error reduction.

Quantum error correction and reduction is also a widely researched area. Currently existing implementations of quantum computers are heavily affected by the impact of the decoherence. They require the temperatures of

0.015 K

(which is the consequence of the lack of the room temperature superconductors) and perfect vacuum. These conditions are nearly impossible to achieve on earth, which make quantum systems volatile to the slightest changes of the surrounding environment. The decoherence, is the term, that encompasses every interaction, between quantum computer, and other particles, that are not expected there by their operators, and which destroys the quantum nature of the system [10].

Some types of quantum error correction, which aims to protect the qubit or a quantum system against the decoherence and quantum noise, are ex. quantum redundancy and measurement stabilizer which uses multidimensional Hilbert space on which the quantum states are mapped [11], quantum surface codes, which are implemented on 2D qubit latices, and comprehensively tackle the error of the whole quantum system [12]. These methods of course have their shortcomings, like using additional qubits, or severely restricting the architecture of quantum circuits. Either way they are always implemented on a quantum computer alongside the algorithm.

Quantum error reduction focuses on minimising the error. The methods that are the part of this family are implemented on classical machines, quantum computers on as a hybrid - classical-quantum systems. Some of the methods are: Richardson extrapolation error mitigation [13] which performs measurement with artificially increased noise levels and than uses Richardson extrapolation to approximate no noise in the system, or the quasi-probability method [14,15], which tries to probabilistically inverse the noise process that occurred in the system.

PDU method of error reduction was proposed in 2022 [16]. It was made to be use in conjunction with quantum circuits using phase shift gates for calculations. Error reduction is then conducted fully on classical computer. PDU method is based on PDU functions. These are interpolated functions for the set of points

(x_{d}, ε_{d})

, where

x_{d}

is value for which the function was measured, and

ε_{d}

is the recorded error. The method is then applied on the result acquired from the quantum computer.

Considered the current state of quantum hardware, the goal of our research is to overcome the quantum volume (QV), and Noisy Intermediate-Scale Quantum (NISQ) era limitations, and to allow researchers to reach meaningful conclusions, even with not perfect systems. This work shows experimentally, that generative artificial intelligence could be used in error reduction in NISQ era. In the area of quantum computing its usefulness can be conserved even beyond NISQ, since the expectations of transmitted state are that their fidelity will be on the much lower level than inside the quantum computers, e.g., Tann [17].

2. Materials and Methods

2.1. LPIQE Method

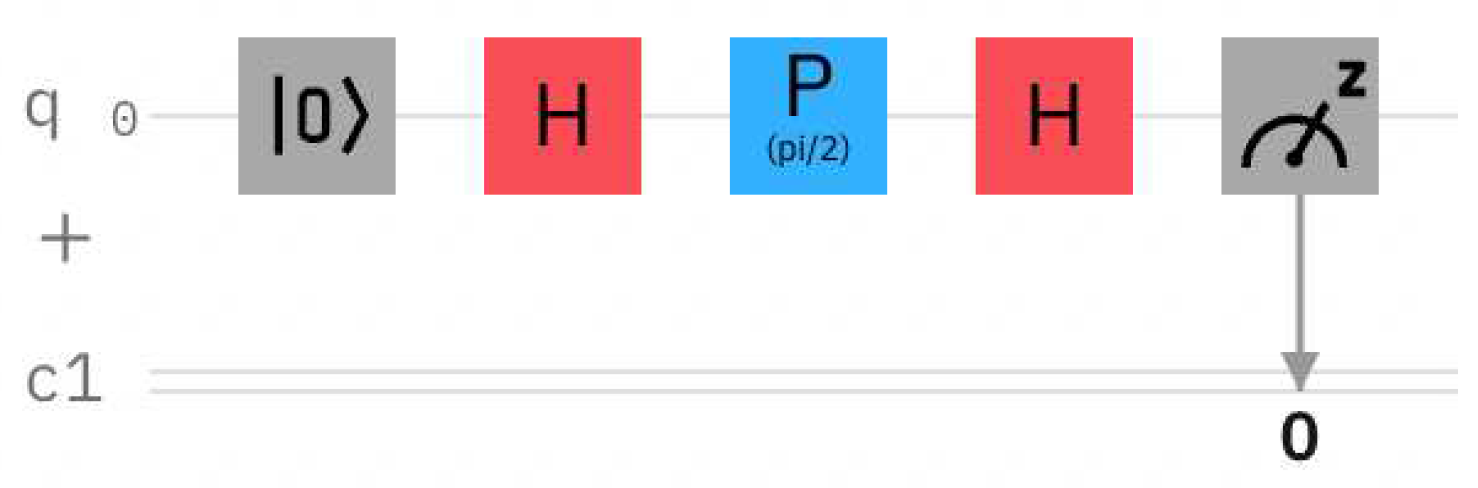
LPIQE is the method of quantum image representation, which uses angle parameter of the controlled phase gate. It was developed for implementation on the quantum computers. The basic building block of the method is QCoSamp (Quantum Cosine Sampling) operator can seen on Figure 1.

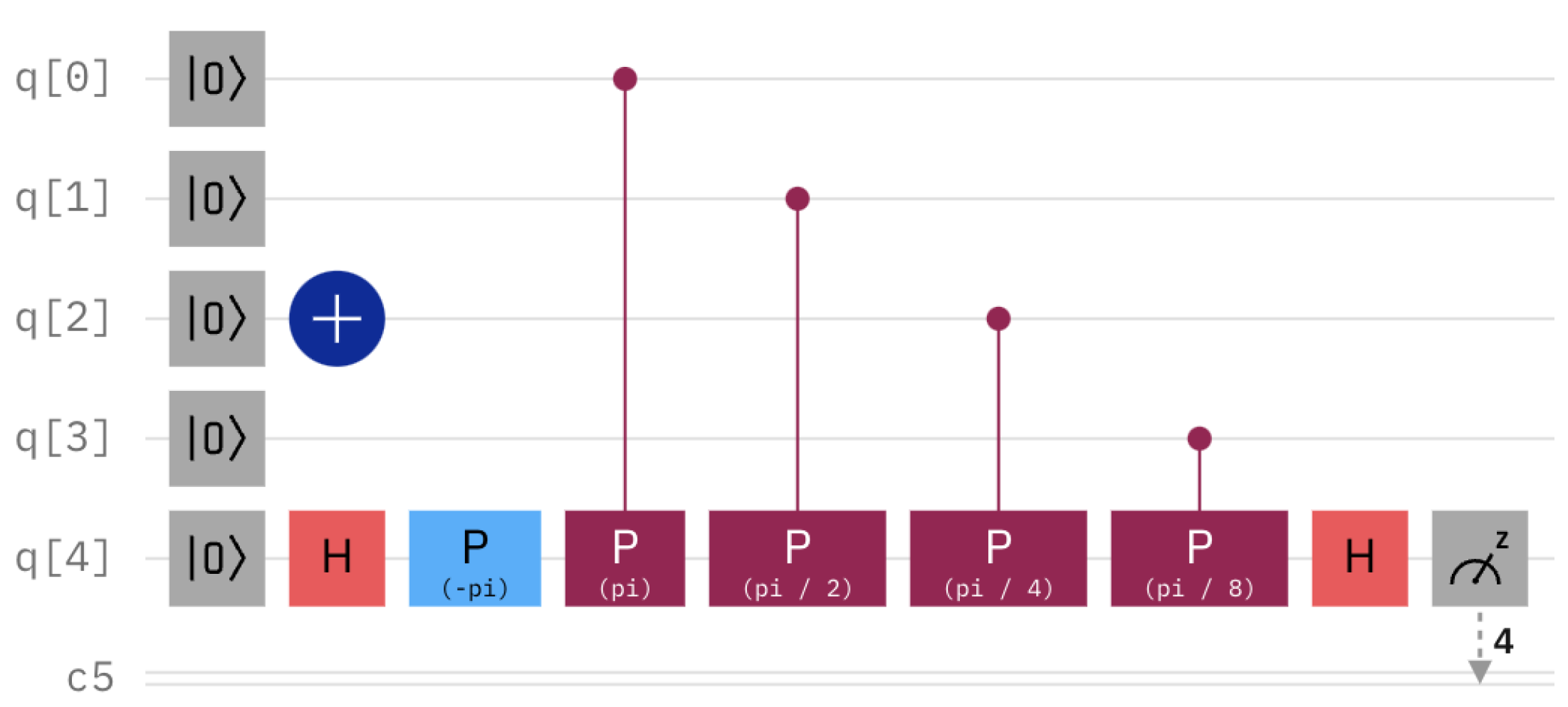
The encoding circuit is composed of a base of computation, and controlled phase shift gates. The simplified version could be seen on Figure 2.

For the image encoding using this method, let’s take the image of size H × W pixels. It could be represented as a matrix

I_{m} = {[{\hat{p}}_{r, c}]}_{H \times W}

, where

{\hat{p}}_{r, c}

is the intensity of pixel placed in r-th row and c-th column. Image then can be flatten to a single vector using vertical vectorization and obtain:

\overset{⟶}{I_{m}} = {[p_{j}]}^{T}, s . t . : j = r W + c .

(1)

Then, it could be represented in the form of the state:

\begin{matrix} I_{m} = [e^{i p_{0}} \dots e^{i p_{J}}, 0^{M - J}] = \sum_{j = 0}^{J} e^{i p_{j}} j, \\ J = W H - 1, M = 2^{⌈ l o g_{2} (W H) ⌉} \end{matrix}

(2)

where the first part of the above state is the vector of

W H

exponential functions of pixels intensities, and the second part is a complement to quantum state’s requirement of having the power of two coefficients.

The final state can be then obtained by an operator defined by the matrix:

(3)

where

1

is an identity matrix/operator. At this point it can be easily encoded using unitary gate from matrix function present in most modern libraries.

2.2. Error Reduction with PDU Method

PDU method is the hybrid classical-quantum error reduction method. It comprises of the set of PDU (Phase Distortion Unraveling) functions, that are calibrated for the quantum computer and circuit, and than interpolated between calibrated values. The correlations between qubits are important for achieving the desired level of correction.

The calibration consists of running the function on quantum computer, and recording the differences between the expected values

\tilde{γ} (x)

and values received from the quantum computer

γ (x)

ε (x) = \tilde{γ} (x) - γ (x),

(4)

where x is the arbitrary value. The function is interpolated for the set of those. These arguments are the probabilities following from local phases of qubits, extracted using phase-kickback technique. It can be generalized in a way, that x can be any object, which is described as follows:

Definition 2.1.

Let

{| ψ 〉}_{x}

be the the local phase

e^{i x}

of the eigen state

| ψ 〉 \in E

(

E

is a measurement basis) in a subspace of a n-qubit state, and the

p {| ψ 〉}_{x_{k}}

is, experimentally designated probability amplitude for state |ψ〉 with phase

x_{k}

. In that case the function

ε : E \times [- π, π] \cap R ⟶ R

isGeneral PDU functionif and only if its each projection on the eigen-state is smooth due to phase and fulfills following:

\begin{matrix} \forall k : ε (| ψ 〉, x_{k}) = p {| ψ 〉}_{x_{k}} - {〈 ψ 〉}_{x_{k}} \\ \forall | ψ 〉 \neg \exists \tilde{ε} (| ψ 〉, x) : \int_{- π}^{π} d x \tilde{ε} (| ψ 〉, x) < \int_{- π}^{π} d x ε (| ψ 〉, x) \end{matrix}

(5)

2.3. GAN pix2pix Network

Generative Adversarial Networks [1], or GANs, are a class of artificial intelligence algorithms. In this architecture exist networks two competing with each other in a zero-sum game of two players - the generator G and the discriminator D. Given a random noise vector z and ground truth y, the generator learns to produce artificial outputs similar to ground truth:

G : z \to y .

(6)

The PatchGAN (or pix2pix) model designed by Isola et al. [18] used for the experiments in this work, belongs to group of conditional GANs proposed by Mirza et al. [19]. This means, that except the random noise z, the GAN takes a side input x, e.g., an outline of an object, used to generate its outputs:

G : {x, z} \to y .

(7)

Generally the GAN’s zero-sum game has an objective, also known as the value function:

G^{*} = arg min_{G} max_{D} V (G, D),

(8)

V (D, G) = E_{x \sim p_{data}} log [D (x)] + E_{x \sim p_{model}} log [1 - D (G (z))],

(9)

where V is the value function, x denotes the data, z is the input noise for the generator.

D (x)

represents the probability that x came from the ground truth data, rather than from the model. For a conditional GAN, e.g., pix2pix model, the value Function (9) takes the form of

V (D, G) = E_{x \sim p_{data}} log [D (x, y)] + E_{x \sim p_{model}} log [1 - D (x, G (x, z))] .

(10)

From the Equations (9) and (10) comes the conclusion, that the goal of generator is to minimize the objective, while the goal of the discriminator is to maximize it. Namely, the two models compete with each other, where discriminator tries to catch the generator’s output, while generator tries to outsmart it. The only difference is that the conditional GAN has a side input x which is used by both the generator and discriminator. During training the two models compete, while at the convergence the generator’s outputs are indistinguishable from the ground truth by the discriminator, i.e.,

D (x) \approx 0.5

. The discriminator can be discarded during the model’s inference phase. [20]

2.4. Experimental Protocol

In the experiments we explored the usage of pix2pix GAN neural networks for error correction in quantum image processing.

We devised the following experiments:

Reducing error in $16 \times 16$ images encoded with a quantum computer simulator, using images corrected with PDU function as a reference,
Reducing error in $8 \times 8$ images encoded on real quantum computers, using images corrected with PDU function as a reference,
Reducing error in $16 \times 16$ images encoded with a quantum computer simulator and corrected using PDU function, with original images as a reference,
Reducing error in $8 \times 8$ images encoded on real quantum computers and corrected using PDU function, with original images as a reference.

Experiments (1) and (3) were done with the usage of the same initial dataset of 631 encoded and reconstructed images, and experiments (2) and (4) were done using the initial dataset of 61 encoded and reconstructed images.

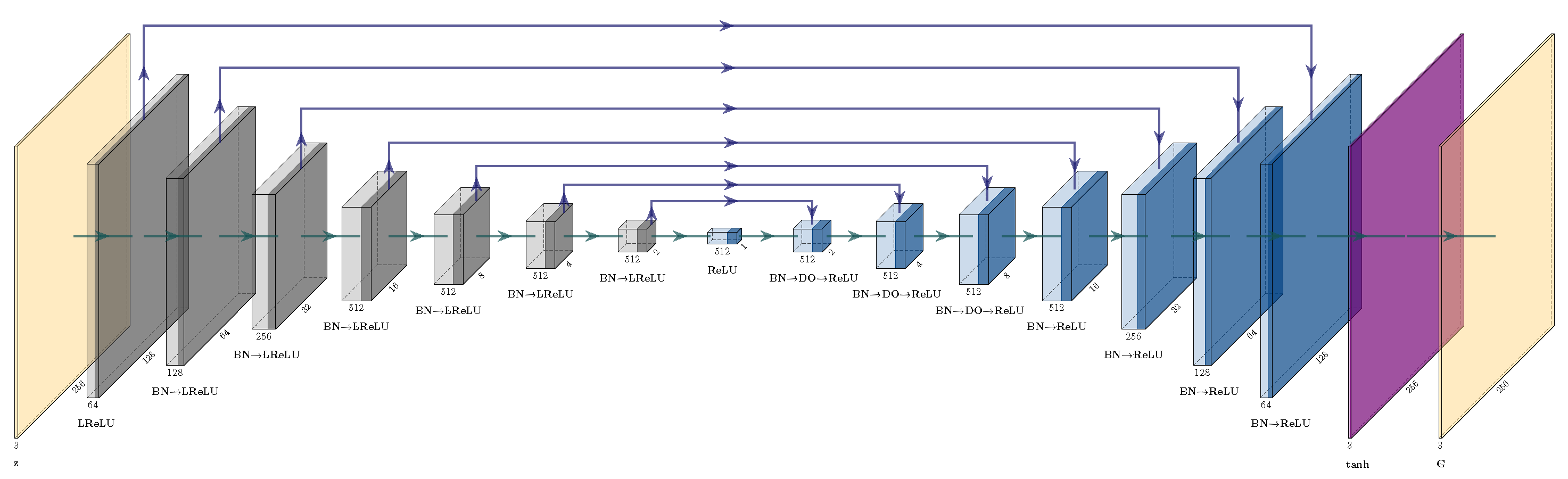
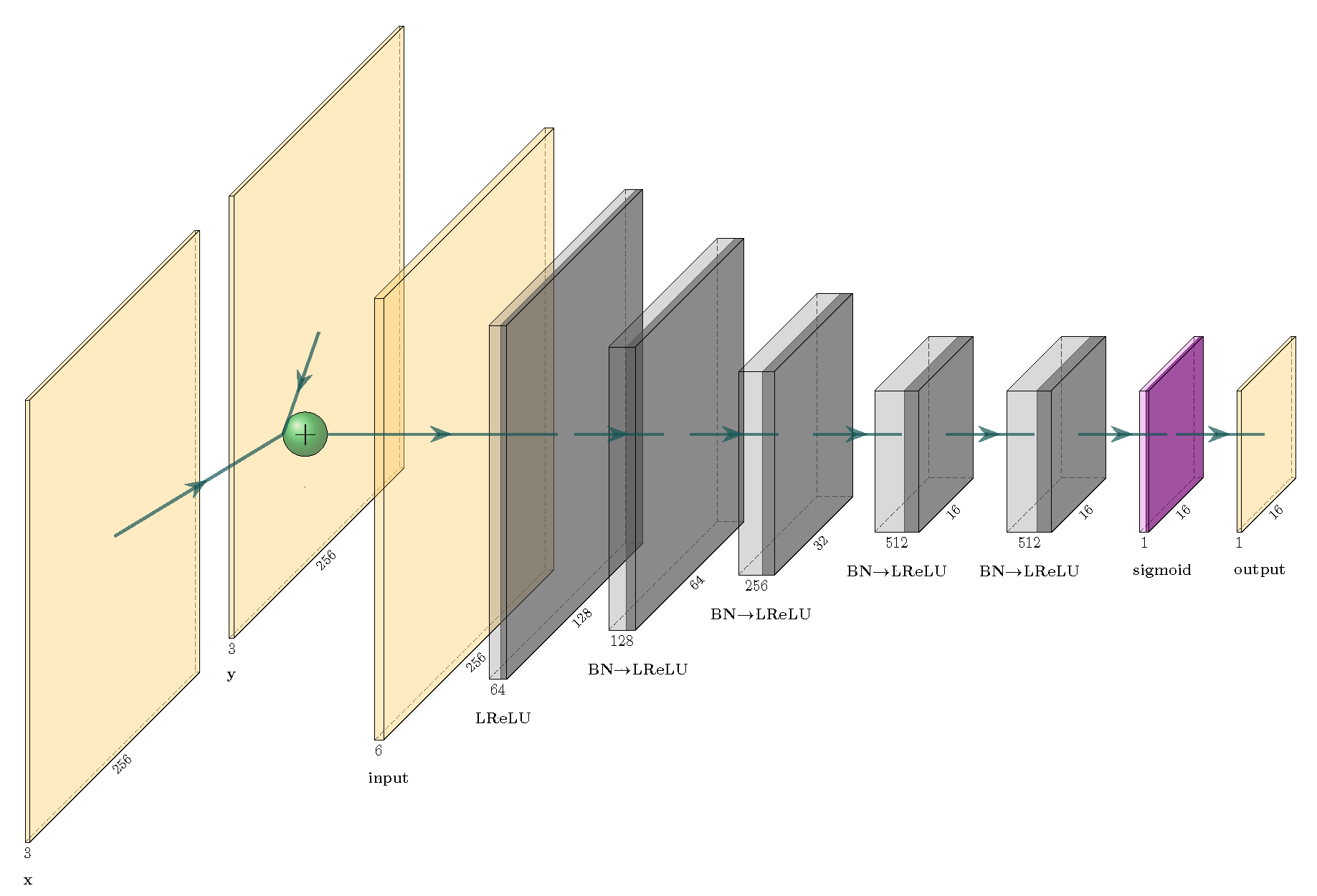
For the experiments, the GAN network was implemented using TensorFlow and Keras libraries for Python. Both generator and discriminator were designed to accept

256 \times 256

pixel images, to increase the networks’ learning capacities. The generator was implemented as the U-Net model with the total of 54,429,315 training parameters, 15 convolutional layers with LeakyReLU in the initial 7 encoding blocks. The bottleneck and decoding blocks used ReLU as activation function. Between each of the consecutive encoding and decoding blocks there was also a batch normalization operation. The three first decoding blocks additionally had a dropout with the value of 0.5. The network contains skip connections from encoders to corresponding decoders. The overview of the generator can be seen on Figure 3.

The discriminator was defined as a model with 6 convolutional layers, resulting in 6,968,257 training parameters. All the encoding blocks used LeakyReLU as the activation layers and between all of them there was performed the batch normalization operation. Output block used sigmoid function as activation layer. The overview of the generator can be seen on Figure 4.

Each up- or down-scaling layer used stride of

2 \times 2

. Convolutional and transpose convolutional layers used kernel of size

4 \times 4

. For all LeakyReLU the alpha parameter was set to 0.2.

The training was performed using Adam optimizer [21] with learning rate of

2 \cdot 10^{- 4}

and exponential decay rate for the first moment estimates

β_{1} = 0.5

. The loss function was a weighted combination of binary cross-entropy defined as

H (y, \hat{y}) = - y log \hat{y} - (1 - y) log (1 - \hat{y}),

(11)

and mean absolute error (MAE) defined as

MAE (y, \hat{y}) = \frac{1}{N} | y - \hat{y} |,

(12)

where y denotes the true output and

\hat{y}

its estimate, N is the total number of performed estimations. The corresponding weights are equal to 1 and 100, respectively.

2.4.1. Steps for the Experiments

Steps to reproduce the experiments are as follows:

1.

Obtain images:

(a): Implement the PDU function for the experiment, with desired granularity of measurements (for the experiment the granularity used was 5),
(b): Calibrate the PDU function,
(c): Generate black and white images (sizes for the experiment were $16 \times 16$ and $8 \times$ pixels) with 256 shades of gray,
(d): Implement the quantum circuits for the generated images with LPIQE method,
(e): Implement the quantum circuits for the generated images with LPIQE method,
(f): Encode the images by running the circuits (for experiments (1) and (3) statevector_simulator was used, and for (2) and (4) - IBMQ Nairobi was used),
(g): Reconstruct the images, and save the results alongside original images,
(h): Use calibrated PDU function on results to perform error reduction, and save the resulting image with previous ones,

2.

Create and train GAN network:

(a): Create GAN neural network for picture to picture translation,
(b): Upscale the images to $256 \times 256$ pixels,
(c): Load training data appropriate for the experiment (for (1) it’s reconstructed images and original ones from quantum simulator, for (2) it’s the same but from quantum computer, for (3) it’s images after error reduction and original ones from quantum simulator and for (4) it’s images after error reduction and original ones from a quantum computer),
(d): Divide the data into training and testing set, and train the network on training set (for experiments 1 and 3 250 epochs were performed, and for (2) and (4) - 1000 epochs were performed in training),

3.

Evaluate the data:

(a): For the testing set, collect the results from the generator,
(b): Descale resulting images into original resolution,
(c): Compare the resulting pictures with original ones.

3. Results

3.1. Reducing Error in $16 \times 16$ Images Encoded Using Quantum Simulator, Using Original Images as a Reference

For the experiment we collected 631 distinct images reconstructed after encoding on a quantum simulator.

An example of the correction performed could be seen on Figure (Figure 5). For that particular example the Pearson’s correlation increased from -0.01935 to 0.99962 after using generator from the GAN network.

Detailed statistics can be seen on Figure 6 and in Table 1.

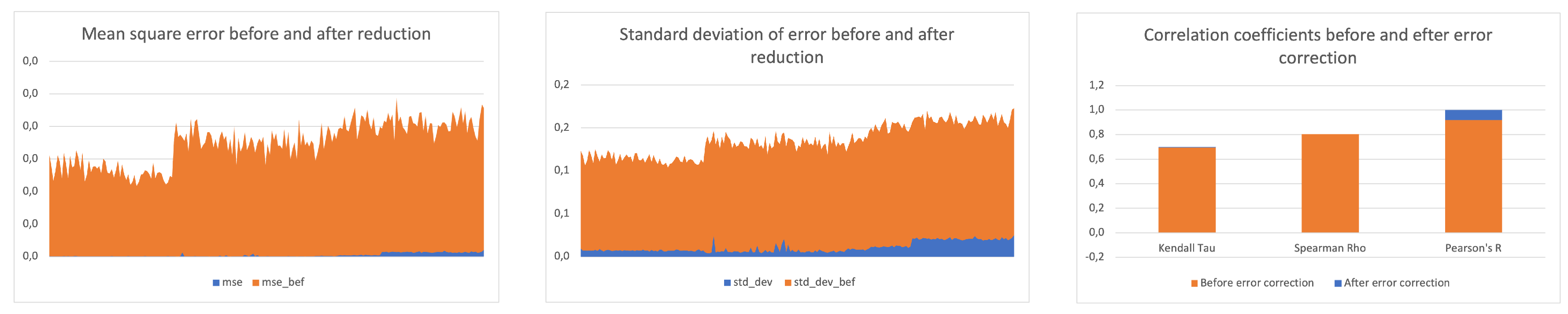
For this experiment we observed numerical improvement in all measured statistics. Standard deviation of error dropped on average 7.4 times, mean square error dropped on average 25.1 times. Also Pearson’s R rose by 0,954.

3.2. Reducing Error in $8 \times 8$ Images Encoded on Real Quantum Computers, Using Images Corrected with PDU Function as a Reference

For the experiment we collected 61 distinct images reconstructed after encoding on a quantum computer, and feed them to the neural network to obtain imgaes with reduced error.

An example of that could be seen on Figure 7. For that particular example the Pearson’s correlation increased from 0,24326 to 0,89631.

Statistics for all collected samples could be seen in Table 2, and on Figure 8.

For this experiment we still observed numerical improvement in all measured statistics, although the level of correction was much lower. Standard deviation of error dropped on average 1.45 times, while mean square error dropped on average 1.26 times, also Pearson’s R rose by 0,392

3.3. Educing Error in $16 \times 16$ Images Encoded with a Quantum Computer Simulator and Corrected Using PDU Function, with Original Images as a Reference

In this experiment we used images encoded onto a quantum simulator, decoded than corrected with PDU function, which were feed to the GAN network. An exmaple could be shown on Figure 9.

Detailed statistics can be seen on Figure 10 and in Table 3.

In this experiment we observed numerical improvement in Pearson’s R test which rose by 0,0818. Meanwhile mean square error dropped 270,14 times, while standard deviation of error dropped 16,46 times.

For the collected mean square error data, we have also calculated standard deviation for mean square error (

σ

), and calculated statistics, about the percentage of data, that fit into the equation

m s e \pm n * σ

. We found that for

n = 1

, 75.71% of data fallen into this category, for

n = 2

it was 97.62%, and for

n = 3

it was 99.52%. We have also calculated that for the 95% of data to meet the criteria of the equation, n should be equal to 1.845, for 90%, n should be equal to 1.716, for 75% n should be equal to 0.756 and for 50% n should be 0.679.

3.4. Reducing Error in $8 \times 8$ Images Encoded on Real Quantum Computers and Corrected Using PDU Function, with Original Images as a Reference

In this experiment, to reduce error after encoding and decoding the image on a quantum computer, first the PDU method was used and than trained GAN network was used to reduce the error further. Example of such correction could be seen on Figure 11.

Statistics for all collected samples could be seen in Table 4, and on Figure 12.

In terms of measured statistics we observed further improvement noticed mostly in drop of mean square error, which was 226 times smaller after using neural network for error reduction. Also standard deviation of error dropped by 15,9 times, and average Pearson’s R have rose by 0,117.

For the collected mean square error data, we have also calculated standard deviation for mean square error (

σ

), and calculated statistics, about the percentage of data, that fit into the equation

m s e \pm n * σ

. We found that for

n = 1

85.71% of data fallen into this category, for

n = 2

it was 95.23%, and for

n = 3

it was 100%. We have also calculated that for the 95% of data to meet the criteria of the equation, n should be equal to 1.168, for 90%, n should be equal to 1.001, for 75% n should be equal to 0,975 and for 50% n should be 0,877.

We suspect, that this noticeable error reduction was possible, because PDU function already corrected a bulk of error induced by quantum noise, leaving result less random (comparing to original), and easier for the neural network to observe patterns.

Also the observed statistics for the standard deviation of the combined mean square error seems to be higher than for ones obtained in experiment (3). We suspect, that the reason for that could be the different quantum computer architecture for which the simulator was constructed. The simulator was made for simulating ion trap computers, and phase elements of qubits seems to be simulated in less precise way.

4. Discussion & Conclusions

In this paper we presented that Generative Adversarial Networks can be used to further reduce the error, stemming from quantum noise in quantum calculations, that uses quantum sampling. Existing error reduction methods (like PDU presented in this paper) are now able to bring the quantum error down to a point, where neural networks can be effectively used to further reduce it even with the use of the computing power of normal personal computer, with Intel i7-13700K processor and 16GB of RAM. We have also proved, that GAN networks are able to reduce the quantum noise error of images, but are much less effective especially on normal computers. Maybe with the use of supercomputers this method would be able to reduce the quantum error in similar fashion, but as researchers we didn’t have an access to such machine. The combined PDU and GAN error reduction was statistically significant, which is confirmed by visual similarity between the expected result, and one produced by the neural network. The Pearson coefficients are on the level of

0.99

with p-value near zero, which proves very high linear correlation between original and corrected images. We are especially happy with the results obtained from the real quantum computers in experiment 4. The mean square error of 0,00014 and standard deviation of error of 0,00993 shows, that this method could be use with existing, imperfect quantum computers from the NISQ era and produce results, that - at least for us - are visually indistinguishable from the original images. Also results obtained from experiments 1 and 3 shows, that these networks can be used beyond NISQ era, for quantum error reduction. We would like to develop this method further, for it to be used as a part of a quantum image processing pipeline, where images will be not only encoded onto a quantum computer, and then measured and decoded, but also to perform image transformations int he encoded state. We focused of quantum image processing, because we are interested in developing methods in this are, however those methods could be used for other types of data. Concluding, in this paper we have presented how neural networks can enhance the existing PDU error reduction method for quantum encoded images. It will be utilized in the image processing in photonic quantum solutions and for quantum communication in the term of faster-then-light communication. The results also allows us to pursue the goal, of quantum object detection using this method, which will be used for detecting aviation instruments on the pictures taken inside flight simulator cockpit, that could be than used for pilot training.

Author Contributions

Conceptualization, Krz.W. and Kam.W.; methodology, R.P. and Krz.W; validation, Kam.W.; formal analysis, R.P., Krz.W.; investigation, R.P. and Krz.W.; writing—original draft preparation, R.P. and Krz.W.; writing—review and editing, Krz.W.; visualization, R.P. and Krz.W.; supervision, Kam.W and K.C.; project administration, K.C.; funding acquisition, K.C. and Kam.W. All authors have read and agreed to the published version of the manuscript.

Funding

The authors would like to acknowledge that this paper has been written based on the results achieved within the WrightBroS project. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 822483. Supplementarily, this research work has been co-financed from Polish financial resources for science in 2019-2023 conferred for implementation of the co-financed international project. Disclaimer. The paper reflects only the author’s view and the Research Executive Agency (REA) is not responsible for any use that may be made of the information it contains.

Conflicts of Interest

The authors declare no conflict of interest.

References

Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27.
Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Goodfellow, I.; Harp, A.; Irving, G.; Isard, M.; Jia, Y.; Jozefowicz, R.; Kaiser, L.; Kudlur, M.; Levenberg, J.; Mané, D.; Monga, R.; Moore, S.; Murray, D.; Olah, C.; Schuster, M.; Shlens, J.; Steiner, B.; Sutskever, I.; Talwar, K.; Tucker, P.; Vanhoucke, V.; Vasudevan, V.; Viégas, F.; Vinyals, O.; Warden, P.; Wattenberg, M.; Wicke, M.; Yu, Y.; Zheng, X. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. https://github.com/tensorflow/tensorflow, 2015. Software available from tensorflow.org.
Chollet, F.; others. Keras. https://github.com/fchollet/keras, 2015.
Pal, A.; Das, A. TorchGAN: A Flexible Framework for GAN Training and Evaluation. J. Open Source Softw. 2021, 6, 2606. [CrossRef]
Wereszczyński, K.; Michalczuk, A.; Pęszor, D.; Paszkuta, M.; Cyran, K.; Polański, A. Cosine series quantum sampling method with applications in signal and image processing. arXiv 2020. arXiv: 2011.12738.
Somhorst, F.H.B.; van der Meer, R.; Anguita, M.C.; Schadow, R.; Snijders, H.J.; de Goede, M.; Kassenberg, B.; Venderbosch, P.; Taballione, C.; Epping, J.P.; Vlekkert, H.H.v.d.; Bulmer, J.F.F.; Lugani, J.; Walmsley, I.A.; Pinkse, P.W.H.; Eisert, J.; Walk, N.; Renema, J.J. Quantum photo-thermodynamics on a programmable photonic quantum processor. arXiv preprint arXiv:2201.00049 v1 2022. Publisher: arXiv Version Number: 1. [CrossRef]
Madsen, L.S.; Laudenbach, F.; Askarani, M.F.; Rortais, F.; Vincent, T.; Bulmer, J.F.F.; Miatto, F.M.; Neuhaus, L.; Helt, L.G.; Collins, M.J.; Lita, A.E.; Gerrits, T.; Nam, S.W.; Vaidya, V.D.; Menotti, M.; Dhand, I.; Vernon, Z.; Quesada, N.; Lavoie, J. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75–81. [CrossRef]
Taballione, C.; Anguita, M.C.; de Goede, M.; Venderbosch, P.; Kassenberg, B.; Snijders, H.; Kannan, N.; Smith, D.; Epping, J.P.; van der Meer, R.; Pinkse, P.W.H.; Vlekkert, H.v.d.; Renema, J.J. 20-Mode Universal Quantum Photonic Processor. Quantum 2022. Publisher: arXiv Version Number: 3. [CrossRef]
de Goede, M.; Snijders, H.; Venderbosch, P.; Kassenberg, B.; Kannan, N.; Smith, D.H.; Taballione, C.; Epping, J.P.; Vlekkert, H.v.d.; Renema, J.J. High Fidelity 12-Mode Quantum Photonic Processor Operating at InGaAs Quantum Dot Wavelength, 2022. arXiv:2204.05768 [physics, physics:quant-ph].
Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. arXiv: quant-ph/0105127. [CrossRef]
Laflamme, R.; Miquel, C.; Paz, J.P.; Zurek, W. Perfect Quantum Error Correction Code. Phys. Rev. Lett. 1996, 77.
Bravyi, S.; Englbrecht, M.; König, R.; Peard, N. Correcting coherent errors with surface codes. NPJ Quantum Inf. 2018, 4, 55.
Li, Y.; Benjamin, S.C. Efficient Variational Quantum Simulator Incorporating Active Error Minimization. Phys. Rev. X 2017, 7, 021050. [CrossRef]
Temme, K.; Bravyi, S.; Gambetta, J.M. Error Mitigation for Short-Depth Quantum Circuits. Phys. Rev. Lett. 2017, 119, 180509. [CrossRef]
Endo, S.; Benjamin, S.C.; Li, Y. Practical Quantum Error Mitigation for Near-Future Applications. Phys. Rev. X 2018, 8, 031027. [CrossRef]
Werner, K.; Wereszczyński, K.; Michalczuk, A. Experiment-Driven Quantum Error Reduction. Computational Science – ICCS 2022: 22nd International Conference, London, UK, June 21–23, 2022, Proceedings, Part IV 2022, p. 195–201. [CrossRef]
Tann, W.J.W. Quantum Remote Entanglement for Medium-Free Secure Communication? arXiv 2022, arXiv:2202.00830. Publisher: arXiv Version Number: 1. [CrossRef]
Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. Proceedings of the IEEE conference on computer vision and pattern recognition, 2017, pp. 1125–1134.
Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784.
Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT press, 2016.
Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980.

Figure 1. QCoSamp operator base of computation, source: IBM’s quantum composer

Figure 2. QCoSamp operator encoding the angle of

- \frac{3}{4} π

(1), source: IBM’s quantum composer.

Figure 2. QCoSamp operator encoding the angle of

- \frac{3}{4} π

(1), source: IBM’s quantum composer.

Figure 3. Overview of the generator network in form of U-Net used for experimental part. All encoding layers’ blocks consist of convolutional layer (not shown), batch normalization (BN) and LeakyReLU (LReLU) activation. Decoding layers’ blocks consist of transposed convolutional layer (not shown), batch normalization (BN), dropout (DO) and ReLU activation. Output block is a transpose convolutional layer with tanh function activation layer. Thickness dimension of each block corresponds to the number of it’s output channels, while its width corresponds to the edge of resulting square image, source: own compilation.

Figure 4. Overview of the discriminator network of pix2pix GAN used for experimental part. All encoding layers’ blocks consist of convolutional layer (not shown), batch normalization (BN) and LeakyReLU (LReLU) activation. Output block is convolutional layer with sigmoid function activation layer. Thickness dimension of each block corresponds to the number of it’s output channels, while its width corresponds to the edge of resulting square image, source: own compilation.

Figure 5. Example result for the image encoded using statevector simulator. The figure represents - image after encoding on a simulator, and reconstruction (left), image generated by the neural network (middle) and expected original image (right).

Figure 6. The charts shows the difference of mean square error (left), standard deviation of error (center) and change in measured correlation coefficients (right) before and after reduction.

Figure 7. Example result for the image encoded using IBMQ Nairobi, 7 qubit quantum computer. The figure represents - image after encoding and reconstruction (left), image generated by the neural network (middle) and expected original image (right).

Figure 8. The charts shows the difference of mean square error (left), standard deviation of error (center) and change in measured correlation coefficients (right) before and after reduction for experiment performed on a real quantum device.

Figure 9. Example result for the image encoded using statevector simulator. The figure represents - image after encoding on a simulator, reconstruction and error reduction with PDU method (left), image generated by the neural network (middle) and expected original image (right).

Figure 10. The charts shows the difference of mean square error (left), standard deviation of error (center) and change in measured correlation coefficients (right) before and after error reduction.

Figure 11. Example result for the image encoded using IBMQ Nairobi, 7 qubit quantum computer. The figure represents - image after encoding, decoding and correction with PDU method, (left), image generated by the neural network (middle) and expected original image (right).

Figure 12. The charts shows the difference of mean square error (left), standard deviation of error (center) and change in measured correlation coefficients (right) before and after reduction for experiment performed on a real quantum computer.

Table 1. Minimal, maximal and mean correlation coefficients values, MSE and STDEV of error for experiment (1).

	Value before error reduction			Value after error reduction
	min	mean	max	min	mean	max
Pearson’s R	-0,15957	0,00708	0,16703	0,72075	0,96135	0,99993
Mean square error	0,17357	0,22277	0,28308	0,00003	0,00885	0,06843
Std dev for error	0,29144	0,32861	0,38558	0,00484	0,04444	0,24108

Table 2. Minimal, maximal and mean correlation coefficients values, mean square error and standard deviation of error for experiment (2).

	Value before error reduction			Value after error reduction
	min	mean	max	min	mean	max
Pearson’s R	0,01121	0,17262	0,31465	-0,32539	0,56511	0,98399
Mean square error	0,12317	0,21375	0,35261	0,00410	0,10783	0,34393
Std dev for error	0,32898	0,37183	0,42898	0,05883	0,26588	0,55277

Table 3. Minimal, maximal and mean correlation coefficients values, mean square error and standard deviation of error for experiment (3).

	Value before error reduction			Value after error reduction
	min	mean	max	min	mean	max
Pearson’s R	0,87700	0,91805	0,94214	0,99639	0,99983	0,99993
Mean square error	0,01077	0,01779	0,02378	0,000014	0,00007	0,00106
Std dev for error	0,09665	0,12655	0,14971	0,00371	0,00769	0,02574

Table 4. Minimal, maximal and mean correlation coefficients values, MSE, and STDEV of error for experiment (4).

	Value before error reduction			Value after error reduction
	min	mean	max	min	mean	max
Pearson’s R	0,79338	0,88266	0,96455	0,99805	0,99970	1,00000
Mean square error	0,00906	0,03122	0,04825	0,0000006	0,00016	0,00065
Std dev for error	0,09512	0,15817	0,19945	0,00069	0,00993	0,02175

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Deep learning as a tool of quantum error reduction in quantum image processing

Abstract

1. Introduction

2. Materials and Methods

2.1. LPIQE Method

2.2. Error Reduction with PDU Method

2.3. GAN pix2pix Network

2.4. Experimental Protocol

2.4.1. Steps for the Experiments

3. Results

3.1. Reducing Error in 16 × 16 Images Encoded Using Quantum Simulator, Using Original Images as a Reference

3.2. Reducing Error in 8 × 8 Images Encoded on Real Quantum Computers, Using Images Corrected with PDU Function as a Reference

3.3. Educing Error in 16 × 16 Images Encoded with a Quantum Computer Simulator and Corrected Using PDU Function, with Original Images as a Reference

3.4. Reducing Error in 8 × 8 Images Encoded on Real Quantum Computers and Corrected Using PDU Function, with Original Images as a Reference

4. Discussion & Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.1. Reducing Error in $16 \times 16$ Images Encoded Using Quantum Simulator, Using Original Images as a Reference

3.2. Reducing Error in $8 \times 8$ Images Encoded on Real Quantum Computers, Using Images Corrected with PDU Function as a Reference

3.3. Educing Error in $16 \times 16$ Images Encoded with a Quantum Computer Simulator and Corrected Using PDU Function, with Original Images as a Reference

3.4. Reducing Error in $8 \times 8$ Images Encoded on Real Quantum Computers and Corrected Using PDU Function, with Original Images as a Reference