Prerpints.org logo
Preprint
Article

Assisted Requirements Selection by Clustering using Analytical Hierarchical Process

Altmetrics

Downloads

150

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 October 2023

Posted:

05 October 2023

You are already at the latest version

Alerts
Abstract
Keywords: Requirements prioritization, Next release plan, Software product planning, Decision support, MoSCoW, AHP, K-Menas, GMM, BIRCH, PAM, Hierarchical, Clustering, Clusters Evaluation
Keywords: 
Subject: Computer Science and Mathematics  -   Software

1. Introduction

Software engineering is built on several pillars and involves more than just programming. It contains every piece of supporting information, design principle, or idea required to make these programmes function as intended. Software requirements prioritisation (SRP) is one of the design principles that enables software that is being considered for development to function as intended (Achimugu et al., 2014).
A subfield of requirements engineering called requirements prioritisation assists in selecting requirements based on the interests of stakeholders. Giving each requirement a priority to decide the order in which they should be implemented is a step in the software engineering process. A requirement engineering decision process is used to decide which features or requirements will be developed in the upcoming release while considering technical, resource, risk, and budget constraints (Franch & Ruhe, 2016). Choosing the order in which requirements should be addressed is a crucial step in the software development process. This process aids in managing the priority and urgency of software requirements while considering stakeholders’ interest, cost, resource, and time issues. Numerous academics have provided definitions for the ranking of software demands in order of importance. Software requirement prioritisation is a process that determines the order in which needs will be implemented (Azzolini & Passoni, 2013). The process of selecting the best set of requirements from several conflicting and competing expectations gathered from various stakeholders participating in a software development project, according to Karlsson and Ryan (Olaronke et al., 2018).
The success or failure of a project is largely dependent on the software requirements specification in general and the prioritisation of software requirements in particular. Almost 80% of software projects fail to achieve the Standish Group's definitions of success based on time, cost, and scope criteria each year (Emam & Koru, 2008). The failure is often due to shifting requirements, as requirements are often documented and rarely changed. This suggests that software projects fail due to their inability to evolve efficiently to match shifting requirements or accommodate new ones. This highlights the importance of releases management and the need for proper decision-making about the functionality of a software product's release. A well-selected release will minimize problems with shifting requirements in future releases.
As a remedy to this issue, many requirements prioritisation techniques have been put forth. These techniques aim to reduce the length and cost of software development projects by supporting developers in identifying the most important and urgent requirements. Each method has limitations and makes both explicit and implicit assumptions about the project context during requirements prioritisation (A. Ahmad et al., 2010). These presumptions must be considered while experimentally assessing a requirement prioritisation approach for usefulness, utility, application, or effectiveness.
One technique for ranking software requirements is to use clustering techniques. Similar observations, data points, or feature vectors can be clustered together based on shared characteristics using the clustering technique (Govender & Sivakumar, 2020). Clustering algorithms are used in the prioritising process to group and categorise requirements based on similarity or relatedness. This enables effective requirements prioritisation based on the characteristics of each cluster and the discovery of patterns and relationships between them. Clustering algorithms can assist in managing the complexity of prioritising various requirements by organising requirements into meaningful clusters that can then be prioritised more successfully.
This study thoroughly explores an innovative and promising method for requirement prioritisation that combines the Analytic Hierarchy Process (AHP) and clustering techniques. With the use of the data mining approach known as clustering, it may be possible to group together requirements that are similar, making it easier to handle them and improving the decision-making process. AHP, on the other hand, is a structured method for making decisions based on several factors and enables the creation of priorities based on both qualitative and quantitative judgements.
As we seek to assess the accuracy of quantitative records, it is crucial to assign requirements the proper level of importance to determine the core set of requirements. To do this, the MoSCoW technique, a tried-and-true framework for prioritising requirements, is used that divides each into Must-haves, Should-haves, Could-haves, and Won't-haves categories based on how important and consequential they are. A robust evaluation framework is also developed using metrics like the Dunn Index, Silhouette Index, and Calinski Harabaz Index. These metrics provide quantitative insights into the quality and cohesion of clusters, aiding decision-making processes.
Our overarching objective in this research is to evaluate the results of combining clustering methods with the Analytic Hierarchy Process (AHP). Our view of this integration's potential impact will be greatly influenced by the outcomes of this integration, which are expected to provide a distinctive perspective on requirement prioritisation and project management. In keeping with this goal, we have developed two key research questions that will direct our empirical studies and provide the information required to make well-informed decisions.
RQ1: Is a semi-automated approach to SRP processes possible with the incorporation of clustering techniques?
RQ2: Does the fusion of AHP and clustering generate better results?
The remainder of the paper is structured as follows: It commences with the state of art for clustering algorithms and prioritisation techniques in Section 2. Following this, Section 3 gives an overview of established techniques for clustering and requirements prioritisation. In Section 4, we elaborate the methodology proposed for clustering requirements using AHP including how to determine the number of clusters, evaluate clusters and associate MoSCoW categories with them. Section 5 presents and analyzes the results of an effectiveness study conducted on two different datasets. Section 6 is dedicated to address the effectiveness of the proposed method. Lastly, Section 7 encapsulates the conclusions drawn from the research.

2. Literature Review

Table 1. Literature Review.
Table 1. Literature Review.
Year
Of
Pub		 Title Techniques Used Results Ref.
2015 Applying analytical hierarchy process to system quality requirements prioritisation
 AHP The AHP technique effectively removes discrepancies between stakeholders’ interests and the business goals. (Kassab & Kilicay-Ergin, 2015)
2015 Comparison of Requirement Prioritisation Techniques to Find Best Prioritisation Technique binary search tree, AHP, hierarchy AHP, spanning tree matrix, priority group/Numerical Analysis, bubble sort, MoSoW, simple ranking and Planning Game AHP is the best requirements prioritisation technique amongst all the requirements prioritisation techniques (Ali Khan et al., 2015)
2016 An Evaluation of Requirement Prioritisation Techniques with ANP ANP, binary search tree, AHP, hierarchy AHP, spanning tree matrix, priority group and bubble sort ANP is the best technique among the seven techniques, though it consumes time (Khan et al., 2016)
2016 An approach to estimation of degree of customization for ERP projects using prioritised requirements Framework using AHP AHP framework gave better results (Parthasarathy & Daneva, 2016)
2017 Fuzzy_MoSCoW: A fuzzy based MoSCoW method for the prioritisation of software requirements
 Fuzzy MoSCoW This technique incorporates uncertainty and allocates resource effectively. (K. S. Ahmad et al., 2017)
2020 A Novel Approach for Software Requirement Prioritisation
 MAHP, a combination of AHP and MoSCoW MAHP reduces the number of comparisons and hence saves time (Jahan et al., 2019)
2020 Prioritisation of Software Functional Requirements from Developers Perspective
 Spanning Tree and AHP There was less dependency among requirements hence less waiting time for developers because of spanning tree (Yaseen et al., 2020)
2022 E-AHP: An Enhanced Analytical Hierarchy Process Algorithm for Prioritising Large Software Requirements Numbers Enhanced AHP E-AHP gives better results for large projects (Mohamed et al., 2022)
2015 Efficient agglomerative hierarchical clustering Efficient agglomerative hierarchical clustering Experimental results show consistent performance across various settings, proving efficient AHP to be reliable. (Bouguettaya et al., 2015a)
2016 A hierarchical clustering method for multivariate geostatistical data Aglomerative hierarchical clustering Proposed clustering method yields satisfactory results compared to other geostatistical methods. (Fouedjio, 2016)
2017 Milling tool wear state recognition based on partitioning around medoids (PAM) clustering PAM PAM outperforms k-means and fuzzy c-means in Ti-6Al-4V alloy end milling experiments. (Li et al., 2017)
2017 Malware family identification with BIRCH clustering BIRCH BIRCH excels in malware family identification with high accuracy and low clustering time. (Pitolli et al., 2017)
2020 Unsupervised K-Means Clustering Algorithm Unsupervised K-Means The U-k-means algorithm is robust to data structure and performs better than existing algorithms. (Sinaga & Yang, 2020a)
2020 Applications of Clustering Techniques in Data Mining: A Comparative Study K-Means, Hierarchical Clustering, DB Scan, OPTICS, Density-Based Clustering, EM Algorithm The paper emphasises the value of K-means clustering in consumer data analysis and business decision-making (Faizan et al., 2020)
2020 A Comparative Study on K-Means Clustering and Agglomerative Hierarchical Clustering K-Means and Agglomerative Hierarchy K-means performs faster for large datasets and agglomerative hierarchical is better for smaller ones. (B, 2020)
2021 Gaussian Mixture Model Clustering with Incomplete Data GMM Experiments validate the effectiveness of the proposed algorithm. (Y. Zhang et al., 2021a)
2022 Bayesian Inference-Based Gaussian Mixture Models with Optimal Components Estimation Towards Large-Scale Synthetic Data Generation for In Silico Clinical Trials BGMM-OCE BGMM-OCE outperforms other synthetic data generators in terms of computational efficiency and unbiasedness (Pezoulas et al., 2022)
2022 Design and Implementation of an Improved K-Means Clustering Algorithm Improved K-Means Enhanced algorithm works better than conventional K-Means. (Zhao, 2022)
2022 Gaussian mixture model clustering algorithms for the analysis of high-precision mass measurements
 GMM Results from GMMs were closely congruent with values that had previously been published. (Weber et al., 2022)
This section carefully extensively evaluates several works on algorithms for clustering and requirements prioritisation. Notably, a wide range of techniques were investigated within the state of the art, including Binary Search Tree, Analytic Network Process, Spanning Tree, Numerical Analysis, Bubble Sort, MoSCoW, and Analytical Hierarchical Process. Remarkably, the Analytical Hierarchical Process (AHP) was the method of choice among researchers due to its constant production of superior results. The section also discusses several clustering techniques, such as K-Means, Partition Around Medoids, BIRCH, Agglomerative Hierarchical Clustering, and Gaussian Mixture Model (GMM). This review of the literature provides an overview of the field and paves the way for the creation of an original and useful framework, laying the groundwork for succeeding research phases.
Research Gap:
The limited investigation of the Analytical Hierarchy Process (AHP) as a technique for clustering requirements in the context of planning a project's next release is the area of research that will be be addressed in this research. Although most of the literature now in existence focuses on the use of AHP in requirements prioritisation and decision-making, there is a striking paucity of study that explores its potential utility in grouping or clustering requirements to speed up the release planning process. In the context of release planning, AHP in integration with clustering can be used to enhance how requirements are organised, classified, and prioritised. This will ultimately result in more effective and efficient project management.

3. Techniques Used in the Study

3.1. Requirements Prioritisation Techniques

Software engineering professionals utilise a collection of methodologies called software requirements prioritisation techniques to rank the importance or priority of various software project requirements. Because not all requirements can be addressed at the same time during software development due to restricted resources (such as time and money), prioritising requirements is essential. To ensure the successful delivery of a software product, it is crucial to identify and concentrate on the most important and significant needs. The two techniques that we will be using in this study are AHP and MoSCoW.

3.1.1. Analytical Hierarchical Process

The Analytical Hierarchy Process (AHP) is a systematic decision-making technique (Regnell et al., 2001) proposed by Thomas L. Saaty in the 1970s. It was developed for complex decision-making so that the decision-maker could set priorities and get to the best option possible (Bruce L. Golden et al., 1989). AHP starts by modeling the decision issue as a hierarchical structure and breaks it into three parts: a goal or aim, criteria that help achieve the goal, and alternatives or possibilities that need to be examined. In the next step, experts or decision-makers are requested to compare the criteria and options at each level of the hierarchy in pairs. They utilise a scale to indicate the relative importance of things, often ranging from 1 (equal importance) to 9 (much more essential). Then a consistency check is done to make sure the comparisons are reliable. To determine if decision-makers' judgements are consistent, the AHP technique uses mathematical calculations. It may be necessary for decision-makers to reevaluate their conclusions if contradictions are found.
AHP uses pairwise comparison data to determine the relative weights or priorities of the criteria and alternatives. These weights reflect the preference for each choice relative to the criteria and the significance of each criterion in reaching the overall aim. The scores of the options for each criterion are then combined using the estimated weights. Depending on the decision context, different aggregation techniques, such as weighted sum or weighted average, might be used. To rank and evaluate the options based on their overall desirability or performance in relation to the goal, AHP aggregates the aggregated scores. Lastly, decision-makers can use the prioritised rankings and scores to take decisions. Based on the established criteria and their relative relevance, AHP offers an organised and clear way to assess and choose the best alternative.

3.1.2. MoSCoW

The Dynamic Software Development Method (DSDM) provides the foundation for the MoSCoW method (Hatton, n.d.). It is a common strategy for prioritising requirements. As a matter of fact, it is one of the easiest techniques (Hudaib et al., 2018). The acronym stands for must have, should have, could have, and won't have. The importance or priority of a certain feature within a project is represented by each category. The core project scope is made up of must-haves, which are important and non-negotiable components necessary for project success. Should-haves are crucial characteristics that greatly enhance the value of the project and ought to be applied whenever practical. Could-haves offer flexibility for prospective improvements because they are desired but not necessary. To manage scope and avoid feature creep, won't-haves are expressly left out of the current phase or project. MoSCoW supports resource allocation and project planning by assisting project teams and stakeholders in prioritising requirements, ensuring that critical components are addressed first while providing clarity on what may be postponed or excluded.

3.2. Clustering Algorithms

The need to find knowledge in multidimensional data is growing since massive volumes of data are being continuously collected today. One of the crucial steps in mining or extracting massive information is data miming. Clustering is the most intriguing area of data mining, which seeks to identify underlying patterns in data and identify some useful subgroups for additional investigation. Each group, or cluster, is made up of things that are dissimilar from those in other groups yet like one another (Pradeep Rai & Shubha Singh, 2010).
A total of five clustering algorithms have been used in this paper and each algorithm is briefly discussed in this section.

3.2.1. K-Means

In machine learning and data mining, the clustering algorithm K-Means is very famous and frequently employed (Hartigan & Wong, 1979). It requires the number of clusters to be specified prior to the operation (Sinaga & Yang, 2020b). It seeks to divide a given dataset into the specified number of clusters (K) according to how similar the data points are to one another to maximise certain clustering criteria. K-Means is an iterative technique that minimises the sum of squared distances between data points and the centroids of each cluster to give results. The k-means algorithm is a well-liked clustering technique that minimises clustering error (Likas et al., 2003).

3.2.2. Partition Around Medoids (PAM)

The PAM method partitions a distance matrix into a predetermined number of clusters (L Kaufman & PJ Rousseeuw, 2009). The goal of PAM is to divide a dataset into a predetermined number of clusters by choosing actual data points, known as medoids, as representatives of the clusters. PAM is meant to work with dissimilarity or distance matrices. Like centroids, medoids are chosen from the actual data points, which makes PAM more resistant to noise and outliers.

3.2.3. Agglomerative Hierarchical Clustering

The process of clustering data points into a hierarchical structure of clusters is called agglomerative hierarchical clustering. Due to the exponential rise of real-world data, hierarchical clustering is crucial for data analytics (Bouguettaya et al., 2015b). In this type of clustering, each item at first represents a separate cluster. The appropriate cluster structure is then created by repeatedly merging clusters until all data points are members of a single cluster, or until a stopping requirement is satisfied. A dendrogram, which is a tree-like structure created because of this procedure, shows the clustering hierarchy visually.

3.2.4. Gaussian Mixture Models (GMM)

Gaussian Mixture Models (GMMs) are probabilistic models used for modelling complicated data distributions in statistical analysis and machine learning. Much research has been done on it due to its usefulness and efficiency (Y. Zhang et al., 2021b). They presume that a variety of Gaussian (normal) distributions, each with its own mean and covariance, were combined to produce the data. These parameters are intended to be learned, and GMMs estimate the likelihood that data points will belong to each Gaussian component. They are frequently used for tasks like clustering, density estimation, and data generation.

3.2.5. BIRCH

Balanced Iterative Reducing and Clustering Using Hierarchies is an effective hierarchical clustering algorithm made for grouping huge datasets. Its key characteristic is to employ low memory resources for high-quality clustering of large-scale data datasets and to only scan datasets once to reduce I/O overhead (Peng et al., 2018). A comparable B + tree structure known as a Clustering Feature Tree (CF Tree) is used by Birch to perform clustering (T. Zhang et al., 1996).

4. Proposed Methodology

Preprints 86709 g001
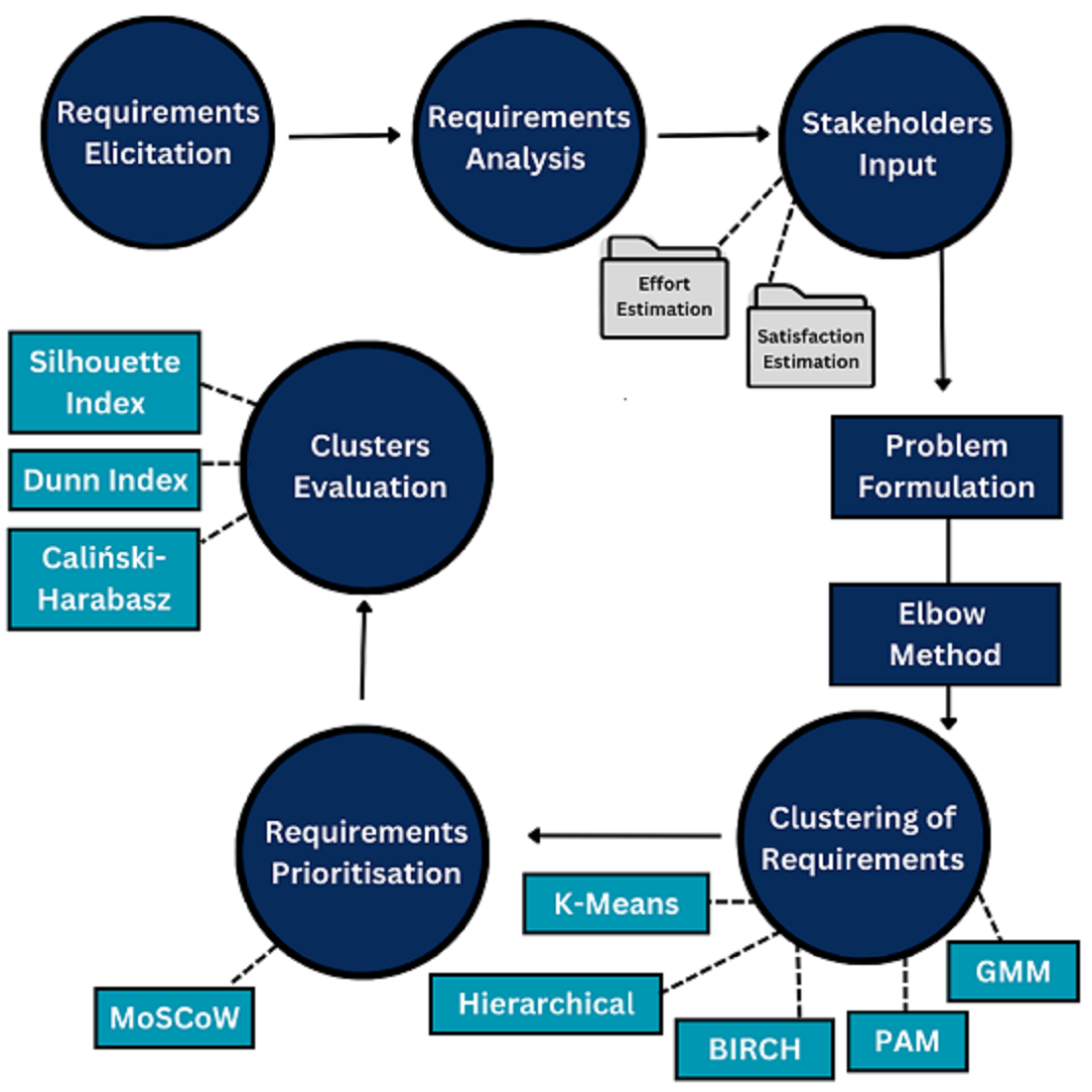
Figure 1. Proposed Methodology.
Figure 1. Proposed Methodology.
Preprints 86709 g001
This study presents a method for prioritizing requirements for the next release using requirements prioritisation methods. It considers the effort required for implementing a requirement and its satisfaction with stakeholders. Clustering algorithms are applied to cluster requirements, and the technique is used to extract a group of requirements for the next release. The validity of clusters is evaluated. In the end MoSCoW is applied to assign importance to the clusters. The figure provides a bird's eye view of the process.

4.1. Requirements Elicitation

Requirement elicitation is a crucial step in requirement engineering, gathering stakeholders' needs and expectations for a software project through discussions, interviews, and surveys, ensuring comprehensive documented requirements.

4.2. Requirements Analysis

Requirements Analysis involves thorough examination of requirements to eliminate ambiguity, address inconsistencies, and evaluate feasibility. It aims to create a refined representation of the software's functionalities.

4.3. Stakeholders’ Input

Stakeholders actively contribute to the decision-making process by offering critical input on two important factors: the amount of work necessary to accomplish the project and the expected degree of satisfaction. Their insights cover both effort (resource allocation, time commitments, and potential obstacles) and satisfaction (alignment with organisational goals and client needs). Through the careful balancing of resource optimisation and stakeholder satisfaction throughout project planning, this dual input enables informed decision-making.

4.4. Problem Formulation

4.4.1. Quantitative Data

Consider a situation where we have a list of requirements, R = r1, r2,...,rn, that reflect the new features that various customers have recommended for a forthcoming software version. Each stakeholder i is given a weight wi to indicate their significance. This implies that some stakeholders' preferences will be taken into consideration more so than others when deciding what issues need to be solved in a software version. The set of customer weights is denoted by the notation W = w1, w2,..., wn.
Each requirement rj in the set R has a corresponding development effort value ej that calculates the resources or cost necessary for its implementation. The notation for this collection of effort values is E = e1, e2,..., en. This is measured by a value vij, which expresses the significance of need rj for customer i. In essence, higher vij values indicate that stakeholder i is given more priority.
Summing up a requirement's importance ratings across all stakeholders yields the total value of including it in the upcoming software release, or its global satisfaction, abbreviated as sj (sj = m i=1 wi vij). By considering each stakeholder's own priorities and weights, this indicates the overall satisfaction that the addition of requirement rj would offer to all stakeholders. The set of requirement satisfactions that result is denoted by S = s1, s2,..., sn (del Sagrado & del Águila, 2021).

4.4.2. AHP Dataset

For the pairwise comparisons of each criterion in this study, the quantitative data set is used. As a result, the AHP data set for our requirements generated. Following the collection of pairwise comparison judgements, the eigenvector approach is used to determine the respective weights of the two criteria, effort, and satisfaction. Then, a square matrix known as the comparison matrix is formed, with elements cij standing in for the weighting of the criteria effort (ci) and satisfaction (cj). By dividing each column by its sum, the matrix is normalised, producing a matrix of normalised values. To determine the priority vector for each level, the normalised values in each row are averaged. The consistency ratio (CR), which assesses whether the judgements line coherently, is used in a consistency check to ensure consistent pairwise comparisons. Adjustments are made if the CR exceeds a predetermined limit, which is commonly set at 0.1. The priority vectors show the relative weights of the requirements after the consistency check has been successful.

4.5. Elbow Method

The elbow method is a heuristic in data science and machine learning for determining the optimal number of clusters in a dataset. It involves considering a range of potential cluster numbers and computing the sum of squared distances between data points and cluster centers. The study applies the elbow method to the requirements dataset, calculating the within-cluster sum of squares (WCSS) for varying cluster numbers and plotting these values.

4.6. Clusters Formation

In this phase clusters of requirements are formed. It involves organizing and grouping similar requirements into clusters using techniques like similarity analysis or domain categorization. This process enhances manageability and provides a structured approach for analysis. Five distinct clustering algorithms will be employed: K-Means, Agglomerative Hierarchical Clustering, Partitioning Around Medoids (PAM), Gaussian Mixture Model (GMM), and BIRCH. These algorithms help extract meaningful patterns and structures from requirements, aiding in informed decision-making during the prioritization process.

4.7. Clusters Evaluation

The evaluation of clusters is crucial for assessing the quality and validity of data analysis or machine learning algorithms. Three mechanisms are used: Dunn Index, Silhouette Index, and Caliński-Harabasz Index, which are calculated after cluster formation and used to rate them.

4.7.1. Dunn Index

The Dunn Index is a clustering validation statistic that unsupervised machine learning researchers use to rate the accuracy of their clustering findings. It gauges the separation between clusters, or how far away various clusters are, in relation to the compactness of clusters, or how near the data points inside a cluster are to one another. Better clustering with smaller within-cluster distances and larger between-cluster distances is indicated by a higher Dunn Index.
Dunn Index = min_intercluster_distance / max_intracluster_distance
Where:
Min_intercluster_distance: The minimal distance between any two centroids that belong to separate clusters.
Max_intracluster_distance: The maximum distance between any two data points within the same cluster.

4.7.2. Silhouette Index

The Silhouette Index is a tool for clustering evaluation that assesses how cohesive and well-separated clusters are. Higher values denote better clustering quality; the range is -1 to 1. (b(i) - a(i)) / maxa(i), b(i) is the formula for calculating the silhouette score for a single data point, where a(i) is the average distance inside the same cluster and b(i) is the smallest average distance to another cluster. Greater clustering is suggested by average silhouette scores that are higher across all data points.
S(i) = (b(i) - a(i)) / max{a(i), b(i)}
Where:
S(i): The silhouette score for data point i.
a(i): The average distance between data points i and all other data points in the same cluster.
b(i): The shortest average distance between data point i and all other data points in a distinct cluster.

4.7.3. Caliński-Harabasz Index

The Calinski-Harabasz Index, commonly referred to as the Variance Ratio Criterion, is a clustering evaluation metric used in unsupervised machine learning to rate the calibre of clusters. It calculates the difference between the variances within and between clusters. Better-defined and more distinct clusters are indicated by higher Calinski-Harabasz Index values.
CH= B/W{(N-K)/(K-1)}
Where:
B: Between-cluster variance, which measures the variance between different clusters.
W: Within-cluster variance, which measures the variance within individual clusters.
N: Total number of data points.
K: Number of clusters.

4.8 Requirements Prioritisation

The MoSCoW approach is used in this study as a useful tool to prioritise requirements clusters. Requirements clusters are systematically classified and ranked using MoSCoW based on their importance and criticality to the project. This will help in improving efficiency and efficacy of the project planning and resource allocation and will make sure that the development efforts are concentrated on the most important and impactful clusters of needs.

5. Methodology Implementation

5.1. Formulation of Problem

5.1.1. 20 Requirements Problem

There are twenty requirements and five stakeholders in this dataset, and it was drawn from (Greer & Ruhe, 2004). The level of priority or value assigned by each stakeholder to each requirement is shown in Table 2 along with the development effort connected to each requirement. The stakeholder weights are offered in the range of 1 to 5. These values might be thought of as linguistic terms like "without importance" (1), "less important" (2), "important" (3), "very important" (4), and "extremely important" (5). They also line up with the relative importance of each need. There is an estimated effort score that corresponds to each requirement, ranging from 1 to 10.
Table 2. 20 Requirements Problem.
Table 2. 20 Requirements Problem.
C1 C2 C3 C4 C5 Effort
R1 4 4 5 4 5 1
R2 2 4 3 5 4 4
R3 1 2 3 2 2 2
R4 2 2 3 3 4 3
R5 5 4 4 3 5 4
R6 5 5 5 4 4 7
R7 2 1 2 2 2 10
R8 4 4 4 4 4 2
R9 4 4 4 2 5 1
R10 4 5 4 3 2 3
R11 2 2 2 5 4 2
R12 3 3 4 2 5 5
R13 4 2 1 3 3 8
R14 2 4 5 2 4 2
R15 4 4 4 4 4 1
R16 4 2 1 3 1 4
R17 4 3 2 5 1 10
R18 1 2 3 4 2 4
R19 3 3 3 3 4 8
R20 2 1 2 2 1 4
Table 1. Customers’ Weights for 20 Req. Problem.
Table 1. Customers’ Weights for 20 Req. Problem.
Customers' Weights C1 C2 C3 C4 C5
1 4 2 3 4

5.1.2. 20 Requirements Problem using Quantitative Approach

To convert the data into two dimensions to apply clustering on it, we considered section 4.4.1. Here:
R = {r1, r2, ……., r20},
E = {1, 4, 2, …….,4},
W = {1, 4, 2, ……., 4}.
This is how ‘S’ (Satisfaction) was calculated for r1.
S = ∑ (Vij * Wi)
S= {(4*1) + (4*4) + (5*2) + (4*3) + (5*4)}
S= 62
So, satisfaction for r1 was calculated to be 62 whereas the effort is 1. The rest was also calculated similarly, and this table was generated as a result.
Table 2. Quantitative Dataset for 20 Req. Problem.
Table 2. Quantitative Dataset for 20 Req. Problem.
ID Effort Satisfaction ID Effort Satisfaction
R1 1 62 R11 2 45
R2 4 55 R12 5 49
R3 2 29 R13 8 35
R4 3 41 R14 2 50
R5 4 58 R15 1 56
R6 7 63 R16 4 27
R7 10 24 R17 10 39
R8 2 56 R18 4 35
R9 1 54 R19 4 46
R10 3 49 R20 4 20

5.1.3. 20 Requirements Problem using AHP

This table was created by using the same data set to get the AHP values for effort and satisfaction.
Table 3. AHP Dataset for 20 Req. Problem.
Table 3. AHP Dataset for 20 Req. Problem.
ID Effort Satisfaction
R1 12.7640176 3.24660865
R2 3.19100441 3.65981339
R3 6.38200881 6.9410254
R4 4.25467254 4.90950577
R5 3.19100441 3.4705127
R6 1.82343109 3.19507518
R7 1.27640176 8.38707236
R8 6.38200881 3.59445958
R9 12.7640176 3.72758771
R10 4.25467254 4.10795381
R11 6.38200881 4.47310526
R12 2.55280353 4.10795381
R13 1.5955022 5.75113533
R14 6.38200881 4.02579473
R15 12.7640176 3.59445958
R16 3.19100441 7.45517543
R17 1.27640176 5.1612753
R18 3.19100441 5.75113533
R19 3.19100441 4.37586384
R20 3.19100441 10.0644868

5.1.4. 100 Requirements Problem

There are 5 stakeholders in this data set as well, but there are 100 requirements this time and it was obtained from (del Sagrado et al., 2015).The difficulty of selecting requirements from a bigger set in the early timeboxes of establishing true agile software projects led to the selection of this dataset. Because of this, we now have 100 requirements rather than simply 20. For the development effort, each requirement has a value that runs from 1 to 20. The maximum development effort in this case is 20 units, or 4 weeks, which roughly corresponds to the timescale set by agile approaches (such as Scrum's proposed iteration length of 2 to 4 weeks). Stakeholders rate the significance of criteria on a scale of 1 to 3. Here, the digits 1-3 stand for (1) not necessary, (2) preferable, or (3) required (Simmons, 2004).
The Effort and Satisfaction for each requirement was calculated in the similar way as it was calculated for 20 Requirements problem. The Quantitative and AHP datasets for 100 requirements problem is given below.
Table 4. Quantitative Dataset (left) and AHP Dataset (right) for 100 Req. Problem.
Table 4. Quantitative Dataset (left) and AHP Dataset (right) for 100 Req. Problem.
ID Effort Satisfaction ID Effort Satisfaction
R1 16 29 R1 0.35245612 0.87906114
R2 19 23 R2 0.29680515 1.10838143
R3 16 18 R3 0.35245612 1.41626516
R4 7 21 R4 0.80561398 1.21394157
R5 19 22 R5 0.29680515 1.15876241
R6 15 20 R6 0.37595319 1.27463865
R7 8 22 R7 0.70491224 1.15876241
R8 10 29 R8 0.56392979 0.87906114
R9 6 27 R9 0.93988298 0.94417678
R10 18 21 R10 0.31329433 1.21394157
R11 15 31 R11 0.37595319 0.82234751
R12 12 33 R12 0.46994149 0.77250827
R13 16 33 R13 0.35245612 0.77250827
R14 20 25 R14 0.28196489 1.01971092
R15 9 25 R15 0.62658865 1.01971092
R16 4 30 R16 1.40982447 0.8497591
R17 16 25 R17 0.35245612 1.01971092
R18 2 28 R18 2.81964894 0.91045618
R19 9 35 R19 0.62658865 0.72836494
R20 3 29 R20 1.87976596 0.87906114
R21 2 27 R21 2.81964894 0.94417678
R22 10 23 R22 0.56392979 1.10838143
R23 4 28 R23 1.40982447 0.91045618
R24 2 29 R24 2.81964894 0.87906114
R25 7 36 R25 0.80561398 0.70813258
R26 15 28 R26 0.37595319 0.91045618
R27 8 30 R27 0.70491224 0.8497591
R28 20 22 R28 0.28196489 1.15876241
R29 9 30 R29 0.62658865 0.8497591
R30 11 32 R30 0.51266344 0.79664915
R31 5 20 R31 1.12785958 1.27463865
R32 1 31 R32 5.63929788 0.82234751
R33 17 24 R33 0.3317234 1.06219887
R34 6 26 R34 0.93988298 0.98049127
R35 2 24 R35 2.81964894 1.06219887
R36 16 23 R36 0.35245612 1.10838143
R37 8 26 R37 0.70491224 0.98049127
R38 12 32 R38 0.46994149 0.79664915
R39 18 26 R39 0.31329433 0.98049127
R40 5 27 R40 1.12785958 0.94417678
R41 6 32 R41 0.93988298 0.79664915
R42 14 30 R42 0.40280699 0.8497591
R43 15 15 R43 0.37595319 1.6995182
R44 20 26 R44 0.28196489 0.98049127
R45 14 29 R45 0.40280699 0.87906114
R46 9 28 R46 0.62658865 0.91045618
R47 16 27 R47 0.35245612 0.94417678
R48 6 21 R48 0.93988298 1.21394157
R49 6 28 R49 0.93988298 0.91045618
R50 6 32 R50 0.93988298 0.79664915
R51 6 34 R51 0.93988298 0.74978744
R52 2 27 R52 2.81964894 0.94417678
R53 17 24 R53 0.3317234 1.06219887
R54 18 30 R54 0.31329433 0.8497591
R55 1 24 R55 5.63929788 1.06219887
R56 3 35 R56 1.87976596 0.72836494
R57 14 35 R57 0.40280699 0.72836494
R58 16 18 R58 0.35245612 1.41626516
R59 18 23 R59 0.31329433 1.10838143
R60 7 26 R60 0.80561398 0.98049127
R61 10 18 R61 0.56392979 1.41626516
R62 7 28 R62 0.80561398 0.91045618
R63 16 29 R63 0.35245612 0.87906114
R64 19 38 R64 0.29680515 0.67086245
R65 17 25 R65 0.3317234 1.01971092
R66 15 22 R66 0.37595319 1.15876241
R67 11 23 R67 0.51266344 1.10838143
R68 8 26 R68 0.70491224 0.98049127
R69 20 34 R69 0.28196489 0.74978744
R70 1 15 R70 5.63929788 1.6995182
R71 5 23 R71 1.12785958 1.10838143
R72 8 32 R72 0.70491224 0.79664915
R73 3 28 R73 1.87976596 0.91045618
R74 15 29 R74 0.37595319 0.87906114
R75 4 21 R75 1.40982447 1.21394157
R76 20 21 R76 0.28196489 1.21394157
R77 10 31 R77 0.56392979 0.82234751
R78 20 39 R78 0.28196489 0.65366084
R79 3 21 R79 1.87976596 1.21394157
R80 20 23 R80 0.28196489 1.10838143
R81 10 22 R81 0.56392979 1.15876241
R82 16 22 R82 0.35245612 1.15876241
R83 19 24 R83 0.29680515 1.06219887
R84 3 25 R84 1.87976596 1.01971092
R85 12 29 R85 0.46994149 0.87906114
R86 16 15 R86 0.35245612 1.6995182
R87 15 28 R87 0.37595319 0.91045618
R88 1 21 R88 5.63929788 1.21394157
R89 6 34 R89 0.93988298 0.74978744
R90 7 32 R90 0.80561398 0.79664915
R91 15 27 R91 0.37595319 0.94417678
R92 18 32 R92 0.31329433 0.79664915
R93 4 27 R93 1.40982447 0.94417678
R94 7 25 R94 0.80561398 1.01971092
R95 2 21 R95 2.81964894 1.21394157
R96 7 24 R96 0.80561398 1.06219887
R97 8 24 R97 0.70491224 1.06219887
R98 7 39 R98 0.80561398 0.65366084
R99 7 18 R99 0.80561398 1.41626516
R100 3 27 R100 1.87976596 0.94417678

5.2. Determining No. of Clusters

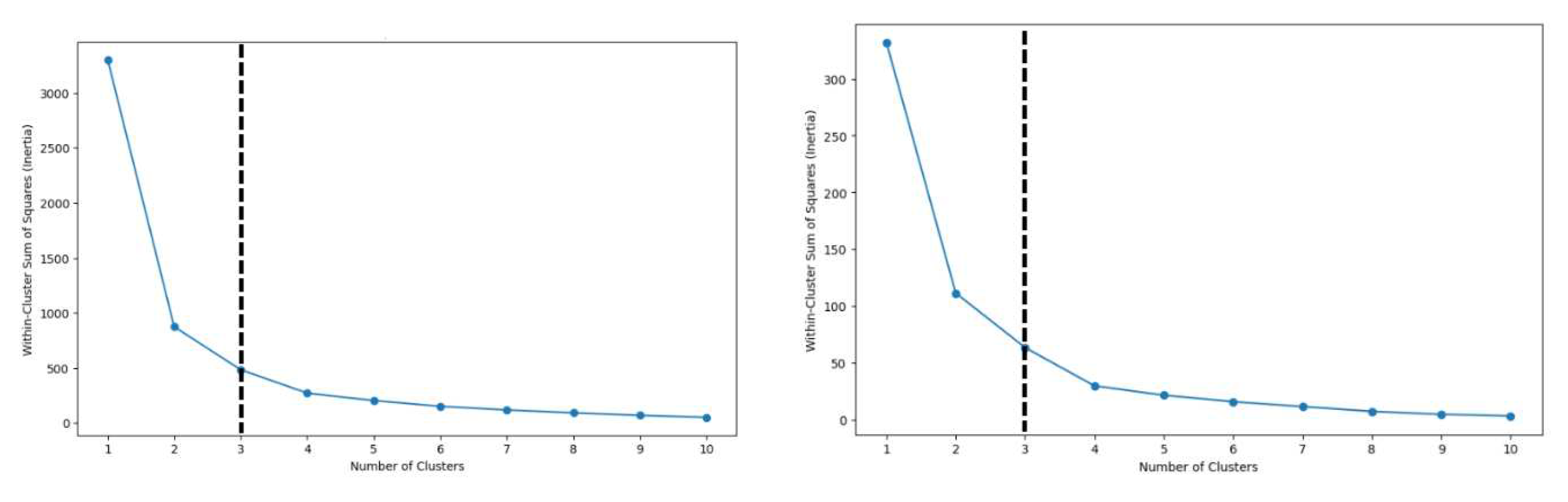
To determine the ideal number of clusters, the elbow approach was used on data sets from the 20 and 100 Requirements Problem. The ideal number of clusters is depicted in the graphs below.
Preprints 86709 g002
Graph 1. Optimum no. of Clusters using AHP (left) and Quantitative (right) dataset for 20 Req. Problem.
Graph 1. Optimum no. of Clusters using AHP (left) and Quantitative (right) dataset for 20 Req. Problem.
Preprints 86709 g002

5.3. Clusters Formation and Evaluation

The elbow method's findings show that three clusters are the ideal number for both the 20 and 100 Requirements Problems. We made 3 and 4 clusters because we are employing MoSCoW in addition to AHP for requirement prioritising. This is because MoSCoW has four characteristics.
In the publication (del Sagrado & del Águila, 2021), quantitative dataset was used to evaluate three clustering algorithms: K-means, Hierarchical Clustering, and Partition Around Medoids (PAM). In this research, we compare the values acquired by the Analytic Hierarchy Process (AHP) approach to the values of quantitative dataset. The benefits and drawbacks of various techniques are better understood through holistic comparison, which also advances knowledge of efficient clustering methodologies and their real-world applications.
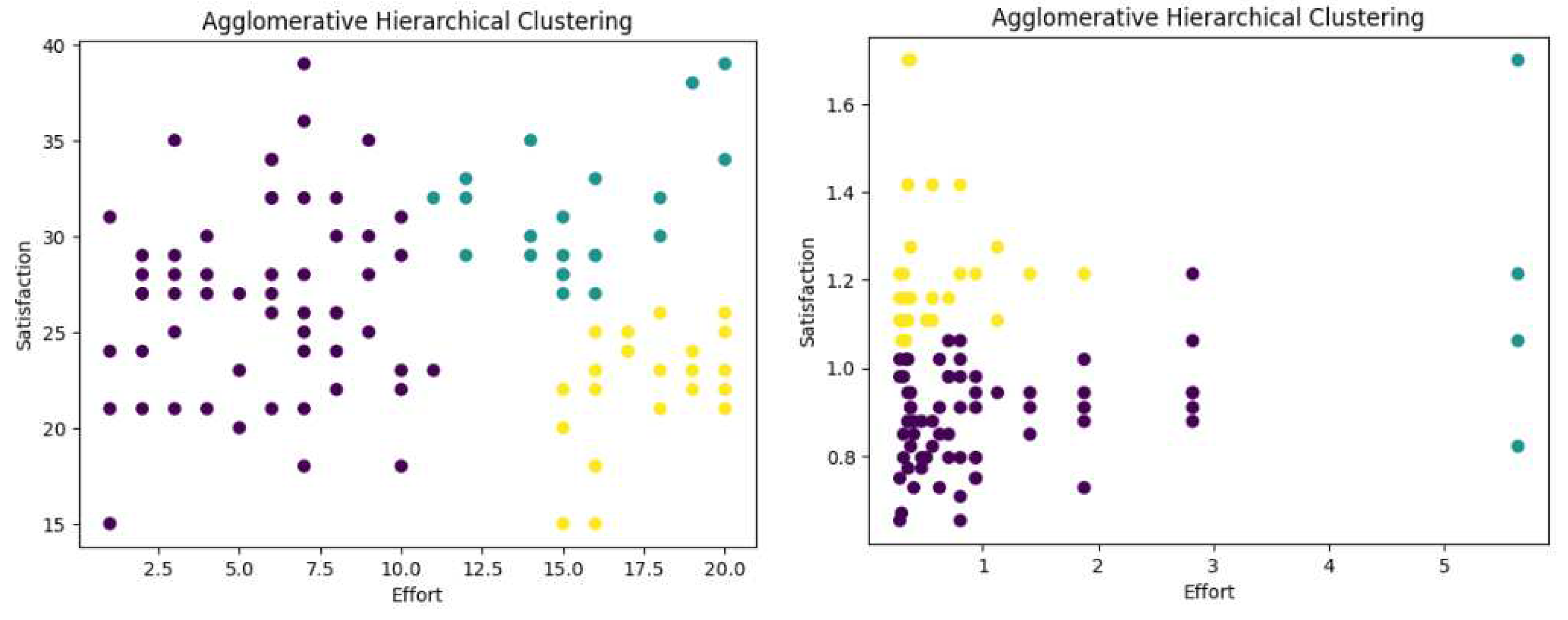
Preprints 86709 g003
Figure 1. Hierarchical Clustering for 100 Req. Problem using Quantitative (left) and AHP (right) dataset.
Figure 1. Hierarchical Clustering for 100 Req. Problem using Quantitative (left) and AHP (right) dataset.
Preprints 86709 g003
To gain a deeper knowledge of how the proposed technique interacts with various clustering algorithms, evaluation indices for both types of data sets, namely Quantitative and AHP, are also calculated using Gaussian Mixture Models (GMM) and BIRCH.
Preprints 86709 g004
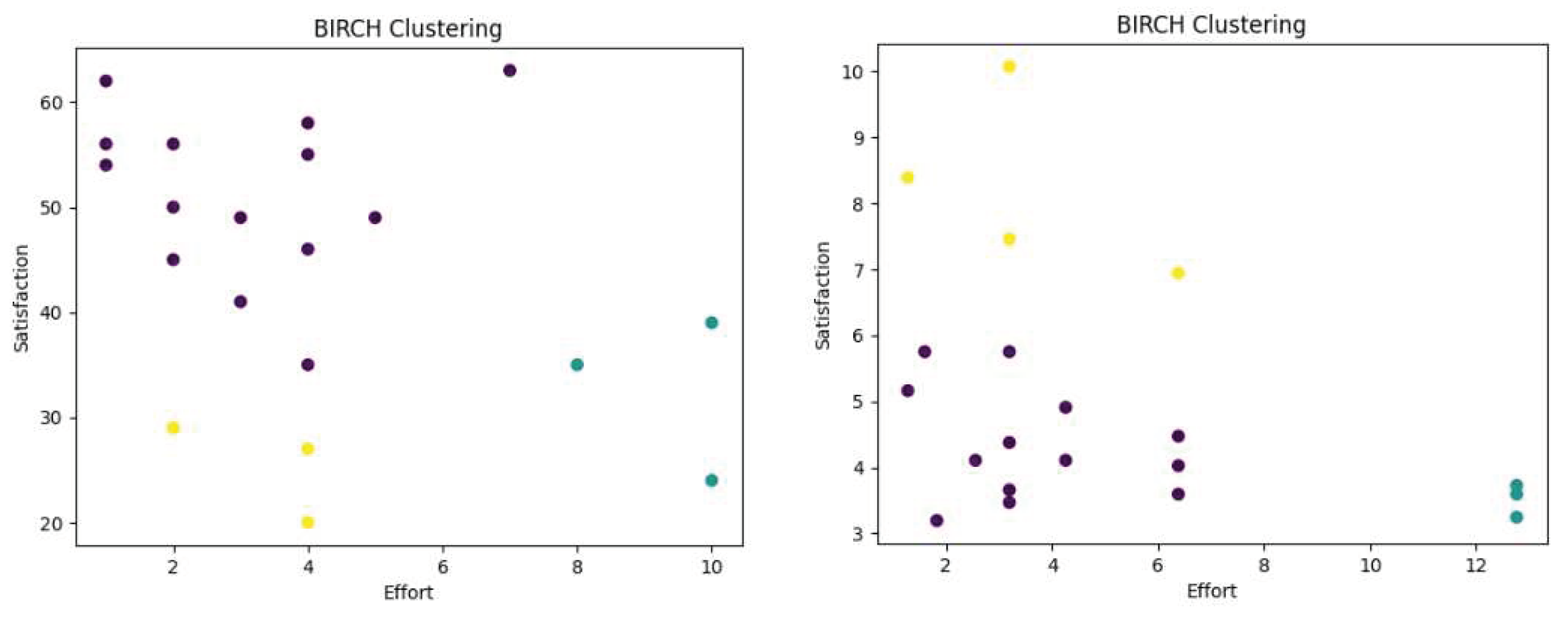
Figure 3. BIRCH Clustering for 20 Req. Problem using Quantitative Dataset (left) and AHP (right) dataset.
Figure 3. BIRCH Clustering for 20 Req. Problem using Quantitative Dataset (left) and AHP (right) dataset.
Preprints 86709 g004
All in all, five clustering algorithms: K-Means, Partition Around Medoids, Agglomerative Hierarchical Clustering, Gaussian Mixture Models, and BIRCH and 3 three evaluation metrics: the Dunn Index, the Silhouette Index, and the Calinski-Harabasz Index are used in this research.
The outcomes of each clustering algorithm for cluster evaluation metrics are provided below.

5.3.1. K-Means

Table 5. Evaluation Metrics for 20 Req. Problem.
Table 5. Evaluation Metrics for 20 Req. Problem.
20 Requirements Problem
Clusters Quantitative AHP
Dunn 3 0.209 0.4336
Silhouette 3 0.4666 0.5690
CH 3 22.9273 33.7443
Dunn 4 0.2527 0.2417
Silhouette 4 0.4176 0.4863
CH 4 24.3832 34.1044
Table 6. Evaluation Metrics for 100 Req. Problem.
Table 6. Evaluation Metrics for 100 Req. Problem.
100 Requirements Problem
Clusters Quantitative AHP
Dunn 3 0.0548 0.2364
Silhouette 3 0.4283 0.4632
CH 3 89.5132 89.7174
Dunn 4 0.0783 0.2377
Silhouette 4 0.3993 0.4766
CH 4 90.9959 96.8018

5.3.2. PAM

Table 7. Evaluation Metrics for 20 Req. Problem.
Table 7. Evaluation Metrics for 20 Req. Problem.
20 Requirements Problem
Clusters Quantitative AHP
Dunn 3 0.2607 2.7100
Silhouette 3 0.4843 0.5208
CH 3 22.6144 31.1727
Dunn 4 0.3151 1.5103
Silhouette 4 0.4116 0.4374
CH 4 24.0329 31.2174
Table 8. Evaluation Metrics for 100 Req. Problem.
Table 8. Evaluation Metrics for 100 Req. Problem.
100 Requirements Problem
Clusters Quantitative AHP
Dunn 3 0.0831 0.3396
Silhouette 3 0.4308 0.3943
CH 3 89.5132 46.9101
Dunn 4 0.0696 0.3024
Silhouette 4 0.3993 0.3998
CH 4 88.7641 64.6714

5.3.3. Hierarchical

Table 9. Evaluation Metrics for 20 Req. Problem.
Table 9. Evaluation Metrics for 20 Req. Problem.
20 Requirements Problem
Clusters Quantitative AHP
Dunn 3 0.2576 2.9804
Silhouette 3 0.4549 0.5690
CH 3 18.6832 33.7443
Dunn 4 0.2482 2.7427
Silhouette 4 0.3561 0.4863
CH 4 18.7909 34.1044
Table 10. Evaluation Metrics for 100 Req. Problem.
Table 10. Evaluation Metrics for 100 Req. Problem.
100 Requirements Problem
Clusters Quantitative AHP
Dunn 3 0.1096 0.3472
Silhouette 3 0.4278 0.4327
CH 3 88.0933 82.8722
Dunn 4 0.1096 0.2518
Silhouette 4 0.3964 0.4576
CH 4 82.5902 95.1834

5.3.4. GMM

Table 11. Evaluation Metrics for 20 Req. Problem.
Table 11. Evaluation Metrics for 20 Req. Problem.
20 Requirements Problem
Clusters Quantitative AHP
Dunn 3 0.2739 0.3723
Silhouette 3 0.4568 0.5690
CH 3 22.5821 33.744
Dunn 4 0.1796 0.310
Silhouette 4 0.3839 0.4905
CH 4 22.0866 33.633
Table 12. Evaluation Metrics for 100 Req. Problem.
Table 12. Evaluation Metrics for 100 Req. Problem.
100 Requirements Problem
Clusters Quantitative AHP
Dunn 3 0.7259 0.1706
Silhouette 3 0.4285 0.0743
CH 3 90.674 26.5032
Dunn 4 0.5557 0.077
Silhouette 4 0.3721 0.1082
CH 4 90.7001 36.2847

5.3.5. BIRCH

Table 13. Evaluation Metrics for 20 Req. Problem.
Table 13. Evaluation Metrics for 20 Req. Problem.
20 Requirements Problem
Clusters Quantitative AHP
Dunn 3 12.9526 7.249
Silhouette 3 0.4672 0.5690
CH 3 18.9442 33.744
Table 14. Evaluation Metrics for 100 Req. Problem.
Table 14. Evaluation Metrics for 100 Req. Problem.
100 Requirements Problem
Clusters Quantitative AHP
Dunn 3 8.9139 0.665
Silhouette 3 0.4384 0.4053
CH 3 96.1607 79.1779

5.4. Prioritisation of Requirements

The MoSCoW method is used to prioritize requirements clusters. Clusters with higher satisfaction and minimal effort were given the highest priority and are designated as "MUST" fulfillments. Clusters with higher satisfaction and minimal effort are designated as "SHOULD" requirements. Clusters in the "COULD" category are considered for enhancement due to their higher effort cost. Clusters in the "WON'T" category are intentionally deferred due to higher effort requirements. This dynamic prioritization methodology offers a nuanced perspective for optimizing software requirements in line with project goals.

6. RESULTS

The Analytic Hierarchy Process (AHP) and the quantitative datasets were compared 54 times in total using evaluation metrics. The purpose of these comparisons was to assess the efficiency and performance of the AHP approach in comparison to the quantitative data representation.39 of these 54 comparisons revealed that the AHP technique performed better than other approaches. This indicates that, in contrast to the quantitative data technique, AHP typically produced more favourable outcomes or results.
This finding's relevance stems from the AHP approach's consistent propensity to outperform the quantitative data representation over a sizable majority of the comparisons. This series of outcomes highlights the possible advantages of applying the AHP approach to cluster or analyse the provided dataset, suggesting that it might be a more efficient and reliable method for producing valuable insights or groups.

7. CONCLUSION AND FUTURE WORK

The importance of using data mining techniques to efficiently prioritise requirements in software engineering is shown by this study. It also emphasises the extraordinary excellence of the Analytic Hierarchy Process (AHP) in the context of software engineering for prioritising software requirements. Based on a detailed analysis of five clustering algorithms and three cluster assessment indices, our results consistently demonstrate that AHP outperforms traditional quantitative data representations in the majority of the 54 comparisons conducted. Furthermore, the combination of AHP with the MoSCoW need prioritisation framework not only led to better results but also enhanced resource allocation, flexible planning, and increased stakeholder satisfaction. This study recommends using AHP, data mining techniques, and the MoSCoW framework as the suggested methodology for prospective projects.
Since the data sets were generated manually with the help of stakeholders in this research. In the future, we can use machine learning algorithms. These algorithms can be trained on historical project data to learn the underlying patterns and characteristics of similar projects. By improving the overall efficiency of requirements prioritisation techniques, this integration could pave the way for more sophisticated and context-sensitive approaches to managing software requirements.

References

  1. Achimugu, P., Selamat, A., Ibrahim, R., & Mahrin, M. N. (2014). A systematic literature review of software requirements prioritization research. Information and Software Technology, 56(6), 568–585. [CrossRef]
  2. Ahmad, A., Goransson, M., & Shahzad, A. (2010). Limitations of the Analytic Hierarchy Process Technique with Respect to Geographically Distributed Stakeholders . World Academy of Science, Engineering and Technology, 111–116.
  3. Ahmad, K. S., Ahmad, N., Tahir, H., & Khan, S. (2017). Fuzzy_MoSCoW: A fuzzy based MoSCoW method for the prioritization of software requirements. 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), 433–437. [CrossRef]
  4. Ali Khan, J., Ur Rehman, I., Hayat Khan, Y., Javed Khan, I., & Rashid, S. (2015). Comparison of Requirement Prioritization Techniques to Find Best Prioritization Technique. International Journal of Modern Education and Computer Science, 7(11), 53–59. [CrossRef]
  5. Azzolini, M., & Passoni, L. I. (2013). Prioritization of Software Requirements: a Cognitive Approach. Procedings of the Fourth International Workshop on Knowledge Discovery, Knowledge Management and Decision Support. [CrossRef]
  6. B, K. (2020). A Comparative Study on K-Means Clustering and Agglomerative Hierarchical Clustering. International Journal of Emerging Trends in Engineering Research, 8(5), 1600–1604. [CrossRef]
  7. Bouguettaya, A., Yu, Q., Liu, X., Zhou, X., & Song, A. (2015a). Efficient agglomerative hierarchical clustering. Expert Systems with Applications, 42(5), 2785–2797. [CrossRef]
  8. Bouguettaya, A., Yu, Q., Liu, X., Zhou, X., & Song, A. (2015b). Efficient agglomerative hierarchical clustering. Expert Systems with Applications, 42(5), 2785–2797. [CrossRef]
  9. Bruce L. Golden, Edward A. Wasil, & Patrick T. Harker (Eds.). (1989). “The analytic hierarchy process.” Applications and Studies.
  10. del Sagrado, J., & del Águila, I. M. (2021). Assisted requirements selection by clustering. Requirements Engineering, 26(2), 167–184. [CrossRef]
  11. del Sagrado, J., del Águila, I. M., & Orellana, F. J. (2015). Multi-objective ant colony optimization for requirements selection. Empirical Software Engineering, 20(3), 577–610. [CrossRef]
  12. Emam, K. El, & Koru, A. G. (2008). A Replicated Survey of IT Software Project Failures. IEEE Software, 25(5), 84–90. [CrossRef]
  13. Faizan, M., F., M., Ismail, S., & Sultan, S. (2020). Applications of Clustering Techniques in Data Mining: A Comparative Study. International Journal of Advanced Computer Science and Applications, 11(12). [CrossRef]
  14. Fouedjio, F. (2016). A hierarchical clustering method for multivariate geostatistical data. Spatial Statistics, 18, 333–351. [CrossRef]
  15. Franch, X., & Ruhe, G. (2016). Software release planning. Proceedings of the 38th International Conference on Software Engineering Companion, 894–895. [CrossRef]
  16. Govender, P., & Sivakumar, V. (2020). Application of k-means and hierarchical clustering techniques for analysis of air pollution: A review (1980–2019). Atmospheric Pollution Research, 11(1), 40–56. [CrossRef]
  17. Greer, D., & Ruhe, G. (2004). Software release planning: an evolutionary and iterative approach. Information and Software Technology, 46(4), 243–253. [CrossRef]
  18. Hartigan, J. A., & Wong, M. A. (1979). Algorithm AS 136: A K-Means Clustering Algorithm. Applied Statistics, 28(1), 100. [CrossRef]
  19. Hatton, S. (n.d.). Early Prioritisation of Goals. In Advances in Conceptual Modeling – Foundations and Applications (pp. 235–244). Springer Berlin Heidelberg. [CrossRef]
  20. Hudaib, A., Masadeh, R., Qasem, M. H., & Alzaqebah, A. (2018). Requirements Prioritization Techniques Comparison. Modern Applied Science, 12(2), 62. [CrossRef]
  21. Jahan, M. S., Azam, F., Anwar, M. W., Amjad, A., & Ayub, K. (2019). A Novel Approach for Software Requirement Prioritization. 2019 7th International Conference in Software Engineering Research and Innovation (CONISOFT), 1–7. [CrossRef]
  22. Kassab, M., & Kilicay-Ergin, N. (2015). Applying analytical hierarchy process to system quality requirements prioritization. Innovations in Systems and Software Engineering, 11(4), 303–312. [CrossRef]
  23. Khan, J. A., Izaz-ur-Rehman, Khan, S. P., Qasim, I., & Khan, Y. H. (2016). An Evaluation of Requirement Prioritization Techniques with ANP. International Journal of Advanced Computer Science and Applications, 7(7).
  24. L Kaufman, & PJ Rousseeuw. (2009). Finding Groups in Data: An Introduction to Cluster Analysis. John Wiley & Sons.
  25. Li, Z., Wang, G., & He, G. (2017). Milling tool wear state recognition based on partitioning around medoids (PAM) clustering. The International Journal of Advanced Manufacturing Technology, 88(5–8), 1203–1213. [CrossRef]
  26. Likas, A., Vlassis, N., & J. Verbeek, J. (2003). The global k-means clustering algorithm. Pattern Recognition, 36(2), 451–461. [CrossRef]
  27. Mohamed, N., Mazen, S., & Helmy, W. (2022). E-AHP: An Enhanced Analytical Hierarchy Process Algorithm for Priotrizing Large Software Requirements Numbers. International Journal of Advanced Computer Science and Applications, 13(7). [CrossRef]
  28. Olaronke, I., Rhoda, I., & Ishaya, G. (2018). An Appraisal of Software Requirement Prioritization Techniques. Asian Journal of Research in Computer Science, 1–16. [CrossRef]
  29. Parthasarathy, S., & Daneva, M. (2016). An approach to estimation of degree of customization for ERP projects using prioritized requirements. Journal of Systems and Software, 117, 471–487. [CrossRef]
  30. Peng, K., Zheng, L., Xu, X., Lin, T., & Leung, V. C. M. (2018). Balanced Iterative Reducing and Clustering Using Hierarchies with Principal Component Analysis (PBirch) for Intrusion Detection over Big Data in Mobile Cloud Environment (pp. 166–177). [CrossRef]
  31. Pezoulas, V. C., Tachos, N. S., Gkois, G., Olivotto, I., Barlocco, F., & Fotiadis, D. I. (2022). Bayesian Inference-Based Gaussian Mixture Models With Optimal Components Estimation Towards Large-Scale Synthetic Data Generation for In Silico Clinical Trials. IEEE Open Journal of Engineering in Medicine and Biology, 3, 108–114. [CrossRef]
  32. Pitolli, G., Aniello, L., Laurenza, G., Querzoni, L., & Baldoni, R. (2017). Malware family identification with BIRCH clustering. 2017 International Carnahan Conference on Security Technology (ICCST), 1–6. [CrossRef]
  33. Pradeep Rai, & Shubha Singh. (2010). A Survey of Clustering Techniques. International Journal of Computer Applications, 7.
  34. Regnell, B., Höst, M., och Dag, J. N., Beremark, P., & Hjelm, T. (2001). An Industrial Case Study on Distributed Prioritisation in Market-Driven Requirements Engineering for Packaged Software. Requirements Engineering, 6(1), 51–62. [CrossRef]
  35. Simmons, E. (2004). Requirements triage: what can we learn from a “medical” approach? IEEE Software, 21(4), 86–88. [CrossRef]
  36. Sinaga, K. P., & Yang, M.-S. (2020a). Unsupervised K-Means Clustering Algorithm. IEEE Access, 8, 80716–80727. [CrossRef]
  37. Sinaga, K. P., & Yang, M.-S. (2020b). Unsupervised K-Means Clustering Algorithm. IEEE Access, 8, 80716–80727. [CrossRef]
  38. Weber, C. M., Ray, D., Valverde, A. A., Clark, J. A., & Sharma, K. S. (2022). Gaussian mixture model clustering algorithms for the analysis of high-precision mass measurements. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 1027, 166299. [CrossRef]
  39. Yaseen, M., Mustapha, A., & Ibrahim, N. (2020). Prioritization of Software Functional Requirements from Developers Perspective. International Journal of Advanced Computer Science and Applications, 11(9).
  40. Zhang, T., Ramakrishnan, R., & Livny, M. (1996). BIRCH. ACM SIGMOD Record, 25(2), 103–114. [CrossRef]
  41. Zhang, Y., Li, M., Wang, S., Dai, S., Luo, L., Zhu, E., Xu, H., Zhu, X., Yao, C., & Zhou, H. (2021a). Gaussian Mixture Model Clustering with Incomplete Data. ACM Transactions on Multimedia Computing, Communications, and Applications, 17(1s), 1–14. [CrossRef]
  42. Zhang, Y., Li, M., Wang, S., Dai, S., Luo, L., Zhu, E., Xu, H., Zhu, X., Yao, C., & Zhou, H. (2021b). Gaussian Mixture Model Clustering with Incomplete Data. ACM Transactions on Multimedia Computing, Communications, and Applications, 17(1s), 1–14. [CrossRef]
  43. Zhao, H. (2022). Design and Implementation of an Improved K-Means Clustering Algorithm. Mobile Information Systems, 2022, 1–10. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated