Prerpints.org logo
Preprint
Article

Impact of Financial Development Shocks on Renewable Energy Consumption in Saudi Arabia

Altmetrics

Downloads

165

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 October 2023

Posted:

03 October 2023

You are already at the latest version

Alerts
Abstract
The demand for renewable energy is increasing globally due to concerns about climate change, pollution, and the finite nature of fossil fuel resources, as renewable energy has been recognized as a significant factor in realizing sustainable development. The government of Saudi Arabia adopted the reduction of fossil fuel subsidies policy as a financial motivation for supporting both the production and consumption of fossil fuels. Therefore, this study aims to investigate the influence and shocks of Saudi’s financial development indicators on renewable energy consumption (REC). And to examine the track of causality between financial development indicators and REC. The study covers the annual data period of 1990-2021 and applies the Basic Vector Autoregressive model (VAR), Granger causality test, forecast error variance decomposition (FEVD), and impulse response function (IRF). The results imply that the financial development indicators have a significant positive impact on REC. The results of causality between REC and financial development indicators were conflicting. The results reveal that REC variation is explained by its innovative shocks and has a positive response to shocks in financial development. Authorities can encourage investment in renewable energy consumption by providing financial incentives also the governments can foster national and international partnerships between investors, policymakers, and industry stakeholders. Employing different determinants of financial development indicators and incorporating population factors in the REC function will be highly recommended for forming the renewable energy demand in Saudi Arabia.
Keywords: 
Subject: Social Sciences  -   Area Studies

1. Introduction

Globally in the last decades, renewable energies have been the major focus of investment, specifically solar photovoltaic, and wind, and now they account for more than 80% of total investment in renewable energies globally [1]). Whereas the global investment in clean energy is estimated at USD 1.6 trillion in 2022. On average, USD 339 billion per year was committed globally for renewable power generation, compared to USD 135 billion, for fossil fuel power generation [2]. More than 60% of investment in renewables is derived from the private sector [3]. The demand for renewable energy usage has been increasing frequently in the world, as renewable energy has been recognized as a significant factor in realizing sustainable development [4]. The last decades have been described by global crises, involving food, finance, and energy prices, and in link to disastrous climate change [5]. In the context of the global finance crisis, financial development can exert both positive and negative consequences on the economy. On the one hand, it can improve economic growth by providing capital for investment and facilitating the efficient allocation of resources [6]. On a similar line financial development can raise access to financial services for low-income families and promote entrepreneurship by reducing poverty [7]. Likewise, financial development can also contribute to financial instability and systemic risk if financial institutions and markets are not properly controlled and regulated, further, this can result in financial crises and economic deterioration ([8]; [9]).
Meanwhile, understanding the role of financial development is crucial for renewable energy consumption for several reasons because, financial development can provide incentives for the adoption of renewable energy, such as tax credits, subsidies, and other financial incentives ([10]; [11]. These incentives can assist in decreasing the cost of renewable energy projects and make them more competitive with traditional energy sources [12]. Besides, [13] stated that the initial cost of installation is considered the key barrier to the approval of renewable energy. Financial development can afford access to capital and financing opportunities that can help overcome this barrier and increase investment in renewable energy projects [14], also, renewable energy projects can involve significant risks, such as technological risk [15]. Financial development can provide risk management tools such as insurance and hedging products [16], which can help mitigate these risks and encourage investment in renewable energy projects.
Globally since REC has increased continuously, the nexus between REC and financial development has garnered significant attention from researchers and policymakers alike over the past decades ([17]; [4]). The relationship between REC and financial development has been examined by several investigators using different datasets and applying different mathematical and econometric methods in dissimilar regions. The study investigates the relationship between REC and the financial development index in Nigeria, utilizes times series data, and uses financial institutions and financial markets indicators by Applying the fixed effects model, finding that financial development is significant for renewable energy consumption [18]. A similar study considering the impact of financial development index using the mixes of econometrics models, fully modified ordinary least square (FMOLS), Dynamic ordinary least squares (DOLS), and canonical cointegrating regression (CCR), Bayer and Hanck cointegration and frequency-domain causality tests for investigating the long-run interaction among the impact of financial development index on REC and environmental sustainability from a global perspective. The results show that financial development negatively influences CO2 emissions. Also, renewable energy usage boosts environmental quality in the world [19].
Also, another study conducted in the USA using the novel Fourier causality test with wavelet transforms finds that financial development encourages renewable energy consumption at high quantiles in the medium- and long run [20]. While [21] applied the ARDL co-integration indicated that financial sector intermediation had a significant positive effect on energy demand in the Nigerian economy in the long-term.
[22] investigate the long-run effect of the financial development level of developing countries on renewable energy consumption by using the FMOLS approach. The observed findings indicate the existence of a long-run connection between renewable energy consumption and financial development; besides, financial development increases the demand for renewable energy.
[23] evaluate the relationship between REC and financial development by employing panel nonlinear Autoregressive Distributed Lag (ARDL) and find that the non-linear estimation approves the long-run asymmetric relationships between financial development, trade openness, capital flows, and renewable energy consumption, also under the vector error correction estimation (VECM), they observed a long-run causality of financial development for REC. In the same manner, [24] examined the relationship between energy consumption, private credit indicator as a proxy for financial development, and economic growth in Azerbaijan, employing mixed cointegration techniques (Johansen tests, Pesaran’s Bounds test, and Gregory-Hansen test) for times series data. The Johansen and Pesaran’s Bounds test showed the existence of a significant change relationship. In contrast, the Gregory–Hansen test results showed no statistically significant change in the long-run relationship.
Most of the above-mentioned studies have confirmed the appositive relation between financial development and REC, however, some studies of REC and financial development nexus did not gain consistent findings for instance, [25] investigated the impact of financial development and economic growth on REC in India using the annual data and performed DOLS model and Granger causality test under VECM model environment. Their studies argue that significant and positive influences of economic growth and financial development on renewable energy consumption. In contrast same study performed in China [26] used a combination of ARDL, pooled mean group (PMG) model, and Granger causality based on the panel data and found that in the long run economic growth stimulates REC whereas financial development negatively affects REC. But in the short-run inverse result is noted, financial development has a positive effect on REC, while economic growth negatively affects REC. Also, the study observes unidirectional causal relationships between financial development and REC [26]. Compared with other panel data methods, [27] used VECM and Granger causality test to explore the relationship between REC and foreign direct investment, their empirical results indicate that there is a long-term and stable equilibrium relationship between foreign direct investment and renewable energy consumption, however, in the short term, foreign direct investment does not significantly cause renewable energy consumption.
[28] investigated the long-run relationship between the financial development index, REC, and environment in Asia Pacific Economic Cooperation (APEC) countries, applying the econometric approaches namely feasible generalized least square (FGLS), Augmented Mean Group (AMG), and Correlated Effect Mean Group (CCEMG), their outcomes reveal that financial development and renewable energy consumption significantly accelerate the environmental quality. Based on a system Generalized Method of Moments (GMM) estimator, [29] found that financial development had positive influences on REC in emerging economies.
In the context of Saudi Arabia, most of the studies in Saudi Arabia search for the effect of renewable energy on ecological footprints, carbon dioxide emissions, economic growth, and renewable energy systems and types ([30]; [31]; [32] and [33]). The studies examining the connection between renewable energy consumption and financial development are limited in Saudi Arabia. The study examines the causal relationship between renewable energy consumption, and financial development with real GDP and trade, in the Gulf Cooperation Council (GCC) countries employing the multivariate Granger causality and panel error correction model (ECM), which indicates no evidence of causality in the short run between exports and REC. However, a negative impact of financial development on economic growth is observed [34]. Another study conducted in Saudi Arabia investigates the impact of financial development factors (using real domestic credit to the private sector and real capital use) on total energy consumption, using the ARDL model. It is found that in the long run, financial development improves energy demand in Saudi Arabia [35].
While considering these studies, it observed that different econometric approaches such as vector error correction model (VECM), ARDL bounds testing, ordinary least squares (DOLS), Granger Causality, Generalized Method of Moments (GMM), etc., were used in these investigations. Therefore, a few studies investigate the impact of financial development on REC by applying vector autoregressive models (VAR). [36] used time-series data applying VAR to investigate how much financial development indicators (stock market development, credit market growth, and the growth of international investment) have contributed to the growth of renewable energy in China, and found that the financial sector contributes significantly to shifting the structure of energy in China. [37] performed a study in the European Union using a GMM panel VAR, finding that the banking sector, bond market, and capital market have a positive effect on the share of renewable energy consumption.
In conclusion, the contradictory findings obtained from the mentioned review are generated by the period and variables selected, different econometric techniques [38], and different zones [39]. From the cited literature review some gaps were observed: Firstly, the study applies the Basic VAR for investigation of the connection between financial development indicators and REC is neglectable. Secondly, no studies have been carried out in Saudi Arabia to examine the relationship between the financial development indicators (such as stock price volatility, private credit by deposit money banks to GDP, and liquid liabilities to GDP) and total renewable energy consumption. Hence, this paper increases the existing literature to supply the observed gaps.
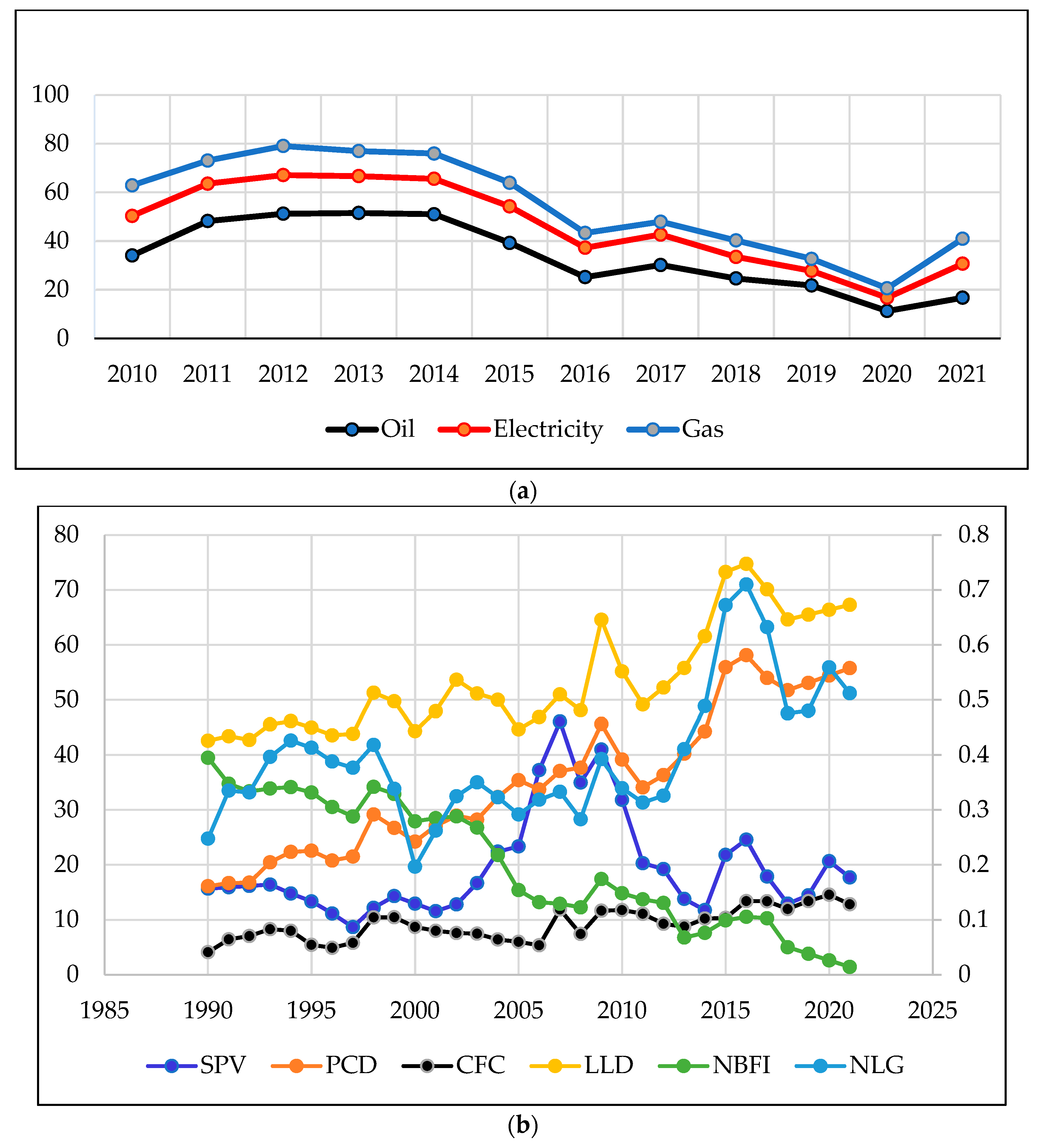
In the context of Saudi Arabia over the last years, the government of Saudi Arabia adopted the reduction of fossil fuel subsidies policy as a financial motivation for supporting both the production and consumption of fossil fuels, oil, coal, and gas. A further target of this policy, the country has been making efforts to enhance its utilization of renewable energy sources, particularly solar and wind energy by reducing its requirement on fossil fuels and reducing its subsidies. Fig 1a displays the trend of subsidy reduction in oil, electricity, and gas. Recently, Saudi Arabia has pointed to producing 50% of its electrical energy from renewable sources by 2030, which includes a mix of wind, solar, and other sources [40]. Across 2021, the contribution of the final REC by sector accounted for 66%, 31%,2%, and 1% for residential, commercial, and industry; respectively, while the contribution of the final REC by technology accounted for 84%, 9%, 5%,1% and < 1% for charcoal, concentrated solar power, solid biofuels, solar photovoltaic and wind; respectively [3]
Preprints 86728 g001
Figure 1. (a) Fossil fuel subsidies in Suadi Arabia (1000 millions USD). Source: [41]) and author design (2023). (b) Financial Developement Indicators in Saudi Arabia (1990-2021). Source: [44] and author design (2023). Note: (1) Right axis represents, SPV, PCD, CFC, LLD, and NBFI values, (2) Left axis represents NLG.
Figure 1. (a) Fossil fuel subsidies in Suadi Arabia (1000 millions USD). Source: [41]) and author design (2023). (b) Financial Developement Indicators in Saudi Arabia (1990-2021). Source: [44] and author design (2023). Note: (1) Right axis represents, SPV, PCD, CFC, LLD, and NBFI values, (2) Left axis represents NLG.
Preprints 86728 g001
To raise and boost the renewables share in Saudi Arabia, the Ministry of Energy in Saudi Arabia launched the National Renewable Energy Program (NREP) in 2019 intending to generate 27.3 GW of renewable energy by 2024 and up to 60 GW by 2030 [40]. The program aims to develop solar, wind, and other renewable energy projects and work on raising the renewable energy sector by establishing a competitive national market that contributes to the development of private sector investments and promotes a combination of public and private sector investments [42].
Generally, the financial sector in Saudi Arabia is dominated by the banks, the Saudi Central Bank (SCB) is a regulator of the financial sector. In recent years Saudi Arabia has made significant progress in financial development and has undergone significant reforms to become more advanced and integrated with the global financial system. The Financial Sector Development Program's partners have made continuous and boosted attempts to keep in step with the main transformations in the Kingdom since the launch of Vision 2030 [43]. SCB has launched several initiatives planned for promoting financial inclusion, involving the establishment of a credit bureau and the introduction of regulations to promote microfinance. However, despite these developments, there are still challenges facing the financial sector in Saudi Arabia, including the need for further reforms to improve the regulatory framework, enhance corporate governance, and promote competition in the sector [43]. In addition, the financial sector system has defeated many challenges considering the consequences of the (Covid-19) pandemic.
The trend of the annual data of some important financial development indicators namely stock price volatility (SPV), private credit by deposit money banks to GDP (PCD) in (%), consolidated foreign claims of BIS reporting banks to GDP (CFC), liquid liabilities to GDP (LLD) in (%), nonbank financial institutions’ assets to GDP (NBFI) in (%) and non-life insurance premium volume to GDP (NLG) in (%) can be seen from Figure 1b. We find that most financial development indicators have steadily declining trends in recent years with relatively fluctuating trends across the period 1990-2021.
Despite the reduction in carbon dioxide (CO2) emission in the last decades, which accounted for 15.1, 14. 7 and 14.3 tonnes per capita, in 2018, 2019, and 2020, correspondingly Saudi Arabia still faces serious issues from fuel ignition [45], therefore, [46] works on emerging the renewable energy sector by creating a competitive local market that contributes to the development of private sector investments and promotes partnerships between the public and private sectors. However, Saudi Arabia is still heavily reliant on fossil fuels, particularly oil, for its energy needs. However, the government's drive towards renewable energy is viewed as a step for diversifying the country's energy mix and lowering its carbon footprint. In comeback to these problems, this paper aims to explore the influence and shocks of Saudi’s financial development indicators on REC. And to establish the direction of causality between financial development indicators and REC.
The contribution of this paper to the recent literature is threefold; first, is based on the BVAR forecasting for testing a theoretical linkage between financial development indicators and REC . Second, it enrichment the generalizability of the literature review through more appropriate outcomes of the two concepts (financial development indicators and REC), as well as the researchers can gain a better understanding of the mechanisms through which financial development can contribute to the progress of the renewable energy sector. Third, the empirical results may be more reliable for policymakers by providing them with further comprehensive knowledge to plan policies.
The study is organized as follows. An introduction has been argued in Section 1. Section 2 displays the review of empirical studies related to financial development and REC concepts. Section 3 presents data, variables description, and methodological framework. Empirical results are presented in Section 4, and Section 5 concludes the study.

2. Materials and Methods

2.1. Data and Descriptive Statistics

The current study examines the impact of financial development indicators on renewable energy consumption in Saudi Arabia. We chose Saudi Arabia as a case study on the justification that it is one of the wealthiest countries in the world in terms of total GDP ([47] and [48]), the total GDP is estimated as USD 1010589.333 million in 2022, increased by 12% in contrast to 2021, therefore the country can invest the utmost in renewable energy. Due to data viability, the annual time series (1990-2021) have been collected from the World Bank, Sustainable Energy for all database [21], World Bank, global financial development database [22], and [49]. The selected variables involve total renewable energy consumption (REC) in (TJ), as a proxy of sustainable development factors (including solar, wind, hydropower, biofuels, and others). Stock price volatility (SPV), private credit by deposit money banks to GDP (PCD) in (%), and liquid liabilities to GDP (LLD) in (%) are selected as financial development indicators (FDI).
In this study, the reason for choosing the REC variable is that Saudi Arabia is greatly dependent on fossil fuels, particularly oil, for its energy needs. The reason for choosing the financial development indicators is related to their significance in economic growth, attracting foreign investment, and generating income through renewable energy consumption which can similarly play a vital role in investing in renewable energy technology in Saudi Arabia. Furthermore, the advanced financial system in Saudi Arabia can sustain credits to the renewable energy industry in an effective way, since the REC requires high startup costs, and long-term debt repayment [32]. The variables definitions and the descriptive statistics of the selected variables are provided in Table 1.

2.2. Econometrics Methods

As an initial step in the present study and before implementing the study models some relevant pre-test analyses, such as normality, and unit roots are analyzed.

2.2.1. Unit-Root Test

For testing the stationarity level of the time series variables, first, we applied the proposed developed version of Phillips and Perron -PP (1988), which is employed by [47] based on generalized least square (GLS) detrended data, ∆ydt. We apply the Ng- perron test because it is more suitable than the traditional tests [48] and it is also more efficient for large negative errors than the PP test [49]. We analyze the properties of four Ng-Perron tests involving modifications of the subsequent four-unit root tests: Phillips-Perron Zα and Zt, Bhargava R1, and ERS which is considered a feasible optimal point test, collectively referred to as the M tests. These properties testes are taking the formulas as follows:
1 M Z α d = ( T − 1 ( y T d ) 2 − f 0 ) / 2 k
2 M S B d = ( k / f 0 ) 1 2
3 M Z t d = M Z α d x M S B d
4 M P T T d = ( ( c ) ¯ 2 k + ( 1 − c ) ¯ T − 1 ) y T d 2 / f 0
Whereas: the statistics M Z α d and M Z t d are efficient versions of the PP test and:
5 k = ∑ t − 2 T ( y t − 1 ) d 2 / T 2
6 f 0 = ∑ j = − ( T − 1 ) T − 1 ∅ j . k ( j / l )
Where, c ¯ =-13.5, l is a bandwidth parameter (which acts as a truncation lag in the covariance weighting), and ∅ j is the jth sample auto covariance of residuals.
Second, we used the Zivot–Andrews unit-root test proposed by [50] to capture a single structural break in the times series data. The Zivot–Andrew test not only tests the unit-root properties of each variable but also considers one structural break. The [50] test applied the sequential Augmented Dickey-Fuller, ADF (Dickey and Fuller, 1981) test to find the break corresponding to the model A, B, and C models and takes the equations formed as follows:
7 ∆ Y t = K + α Y t − j + β t + γ i U D t + ∑ j = 1 k d j ∆ Y t − j + ε i Model (A)
8 ∆ Y t = K + α Y t − j + β t + θ U D t + ∑ j = 1 k d j ∆ Y t − j + ε i Model (B)
(9) ∆ Y t = K + α Y t − j + β t + θ U D t + γ i D T t + ∑ j = 1 k d j ∆ Y t − j + ε i Model (C)
Whereas: ∆ is the first difference, Y t denotes variables series contains unit root refer to existing study are REC, SPV, PCD, and LLD. The Y t − j terms on the right-hand side of the three equations allow the serial correlation and prove that the disturbance term is white noise with variance σ2, and t = 1….., T which represents to index of time. U D t is an indicator dummy variable for a mean shift appearing at each possible time break date (TBD) while D T t is the corresponding trend variable, whereas:
(10) U D t = 1       i f   t > T B     0   o t h e r w i s e and
(11) T D t = 1 − T B D     i f   t > T B   0       o t h e r w i s e
The null hypothesis of the three models is α = 0, which implies that the existence of a unit root in a series ( Y t ) with drift that rejects any structural break, whereas the alternative hypothesis α < 0 implies the series is trend stationary. Model (A) permits a change in the intercept of the series, Model (B) permits a change in the trend of a series, while Model (C) permits changes in both intercept and trend. Most of the scholars ([51]; [52]), applied Model A and/ or C. In this study model A is applied for the analysis of unit root because it is more comprehensive than model B, as it allows for a break in intercept.

2.2.2. Basic VAR Model

After testing the unit root problem in the time-series variables, the multivariate Basic VAR approach is used. The reasoning for using this method is as follows: it has the possibility for both REC and financial development to be endogenous and can capture the dynamic relationships between multiple variables, making them a flexible tool for analysing complex systems. Second Basic VAR models can be used for forecasting, allowing us to make predictions about future values of the variables in the system and examine the causality [53].
The VAR model is principally suggested by Sims (1980) and recently has been broadly applied in macroeconomics analysis of energy and financial development ([54]; [55] and [56]). Given the M times series variables Y t = ( Y 1 t , … … . , Y M t ) , following [57], the Basic VAR model takes a reduced-simultaneous form as follows:
12 Y t = v + A 1 y t − 1 + … + A ρ y t − ρ + u t = v + A Y t − 1 t − ρ + u t
where Y t is the vector of endogenous variables, in our study represented as REC, SPV, PCD, and LLD which are being forecasted, the only deterministic component is a constant term which denotes by v is a constant term (Mx1), a vector of the intercept. A is the matrix of coefficients for the ith lag (M x n) polynomial matrix in the backshift operator with lag length p, and u t (n x 1) vector of white-noise error terms, i.e., the vector comprising the reduced form residuals, which in general will have non-zero correlations. Equation (12) For a given VAR order p, an estimation can be conveniently done by equation-wise ordinary least squares (OLS) including 2 lags. We applied the lag length selection criteria for selecting the number of lags according to an explicit statistical information criterion.

The Lag Length Selection Criteria

After we performed the Basic VAR analysis the selection of the length lag is essential for determining the lag length for the VAR(p) model by using the optimum model selection criteria We utilized the lag length selection criteria to determine the appropriate lag length according to [58] which involves the Akaike Information Criterion (AIC), Schwartz-Bayesian (SBIC) criterion, Hannan-Quinn (HQIC) criteria, Likelihood Ratio, sequential modified (LR) criteria and Final Prediction Error (FPE). The following formulas for each lag length criterion take the equation:
13 A I C p = − n 2 1 + l o g 2 π − n 2 l o g δ 2 − p
14 S B I C p = l o g ( δ 2 ) + l o g n n p
15 H Q I C = l o g δ + 2 l o g l o g n n p
(16) LR = n ( log ⁡ Σ P − log ⁡ Σ P )
(17) FPE = n [ ( n + p ) ( n − p ) log ⁡ Σ P )
Whereas: δ 2 represents the Maximum Likelihood (ML) estimator of the variance of the regression disturbances, ∑p represents the estimated sum of squared residuals, and 𝑛 is the number of estimated parameters, p=0,1,2……P, where P is the optimum order of the model selected. The HQ and SC criteria are both consistent [59], that is, under general conditions, the order considered with these criteria converges in probability or almost surely to the true VAR order p if pmax is at least as large as the true lag order [60]. We approved the model selection fitting to the lowest AIC or SBIC value.

Granger causality test

The next stage of analysis test used in this study is the Granger causality in the VAR environment. The Granger-causality test proposed by [61] can be tested in a VAR multivariate model to test for the simultaneousness of all integrated variables [62]. We suggest the Granger causality test for the case of LogFDI and LogREC, which is involved as a first step in the estimation of the following VAR models:
18 l o g F D I t = ∝ 1 + ∑ i = 1 n β i l o g R E C t − 1 + ∑ j = 1 m δ j l o g F D I t − j + μ t
19 l o g R E C t = θ + ∑ i = 1 n ∅ i l o g F D I t − 1 + ∑ j = 1 m φ j l o g R E C t − j + ω t
Whereas: FDI are financial development indicators, could be SPV, PCD, or LLD; α and θ are intercepts of the two equations, respectively; β i a n d ∅ i , represent the coefficients of the equations, μ t and ω t are error terms for the two equations; respectively. The symbols m and n represent the maximum number of lags for each of the variables.
Based on the estimated OLS coefficients for equations (18) and (19) and following [63], four different hypotheses about the relationship between REC and financial development indicators can be clarified:
  • Unidirectional Granger-causality from FDIs to REC. In this condition, FDIs increase the prediction of the REC but not vice versa.
  • Unidirectional Granger-causality from REC to FDIs. In this condition, the REC increases the prediction of FDIs but not vice versa.
  • Bidirectional Granger-causality from FDIs to REC. In this condition FDIs increase the prediction of the REC and vice versa.
  • Independence between FDIs and REC. In this condition, there is no Granger causality in any direction.

Impulse response functions and forecast-error variance decompositions tests

For examining the dynamics of the VAR model for estimating the progress of variable shocks we focus on impulse response functions (IRFs) and forecast-error variance decompositions (FEVDs). The VAR analysis frequently involves the estimation of IRFs and FEVDs which are the fundamental elements of the VAR method. Finally, we follow [64] and [65] for setting the IRFs and FEVDs for a 10-year forecast horizon (h).
The orthogonalized impulse response function is employed to evaluate the sensitivity of the dependent variable to changes (shocks) in each of the variables, i.e., the shock of financial development indicators on REC. The impulse response at horizon h of the variables to an exogenous shock to variable y can be easily displayed with Cholesky decomposition proposed by Sims (1980) as follows:
20 y t = ∑ i = 0 ∞ ϑ i ν t − i [ ϑ 0 = I k i s t h e K x K i d e n t i t y m a t r i x ]
Whereas ϑ i
21 ϑ i = ∑ j = 1 i ϑ i − j A j [ i = 1,2 , 3 , … . . ]
where ϑ i are explained as impulse responses of the model; Aj =0 for j >p (for a k dimensional VAR (p) process); ν t represents the orthogonal residuals [53]. The IRFs do not imply causation, but they clarify the probability of a shock on one variable affecting the other variables [66]. Additionally, the decomposition is not exclusive but is affected by the ordering of the variables [67]. Variance decomposition provides a rationale for the percentage of changes in the dependent variable explained by its shocks, and it is used to forecast exogenous shocks of the variables [68].
Follows [67], the h-step ahead predictor vector error equation used in this study is written as:
22 Y i t + h = E Y i t + h = ∑ M = 0 h − 1 A j [ e i ( t + h − i ) ϑ i
Where Y i t + h is observed vector at time t+h, E Y i t + h is the h-step ahead forecast vector error made at time t; or the orthogonalized shocks E Y i t + h is the h-step ahead predictor is the g-step ahead predictor vector made at time t; the orthogonalized shocks e i t M − 1 (with M matrix) have a covariance matrix I M .

3. Discussion of Outcomes and Results

In this section, we view the results of pre-test analyses and Basic VAR results based on the standard approaches defined in Section 3.

3.1. Preliminary Results

From Table 2 the selected variables for REC and SPV are positively skewed with P< 0.05, which indicates that this variable is non-normally distributed and vice versa for the PCD and LLD which have a normal distribution. Further, the [69] test confirms the results obtained from the skewness and kurtosis test. The results of the heteroskedasticity test show a serial correlation of the series. To ensure the reliability and consistency of empirical results by reducing non-linearity or heteroscedasticity in the time series data set and modeling purposes, all variables are transferred in logarithms form.
For examining cointegration between the selected variables, testing the stationarity of the selected variables is a crucial condition. For this point, we apply the new unit root test of [70] unit root test. It is noted that the selected variable is non-stationary at levels. However, REC, SPV, and PCD take the stationary nature at the first difference, whereas the LLD takes the stationary nature at the second difference with intercept (Table 3). However, the Ng-Perron unit root test has a limitation that the Ng-Perron test has limited power, i.e., provides ambiguous and spurious results in some time series data, even if unit roots exist. Also, the Ng-Perron test assumes that the data is stationary over the entire time being analyzed and may not be able to detect unit roots if there are structural breaks originating from the series which further declines the stationarity hypothesis [71]. To overcome these limitations, we applied the [72] unit root test with single structural breaks in intercept to get more robust results. The structural break date (SBD) test considers the probability of exhibiting single structural breaks that are assumed to be endogenously determined. The results of the Zivot-Andrews structural break(s) unit root test show that all the selected variables are found to be non-stationary, but we note that all the variables became stationary after their first difference despite having the presence of structural break(s) found to be stationary. In the intercept condition result, the structural break dates are 1999, 2010, and 2014 observed in REC, SPV, and PCD; respectively. However significant break date has been identified as 2009 for LLD. Whereas in the trend condition result, the breaks are 2007 for REC, 2005 for SPV, 1997 for the PCD, and 2016 for LLD.

3.2. Estimation of the Basic VAR Model Results

The VAR model implies an equation for each variable describing its evolution with its lags and the lags of other variables, therefore, all the variables are symmetrically treated as endogenous. We estimate the VAR system using REC, SPV, PCD, and LLD as endogenous variables and constant as exogenous. From Table 4, the estimated model of REC indicates that REC reacts positively to a short-run change in SPV (-2) and PCD (-2) in Saudi Arabia.
So, a unit increase in REC (1-), SPV (-2), and PCD (-2) causes REC to improve by 0.471, 0.441, and 1.15 per unit increase in REC; respectively. while a unit increase in REC (-2) cause REC to reduce by 0.27 unit. A unit increase in SPV (-1) and PCD (-1) causes a significant increase in SPV by 0.937 and 1.126, respectively, and vice versa a unit increase in SPV (-2) and LLD (-1) causes a decrease in SPV by 0.376 and 1.676; respectively. This means that PCD (-1) positively impacts the SPV, while LLD (-1) exerts a negative impact on SPV. This finding can be justified by the increase in liquid liabilities can generate and increase the risk associated with investing in renewable energy companies, which can lead to higher stock price volatility and a decline in the company's stock price.
Also, a unit increase in PCD (-2) significantly increased the REC by 1.15. Likewise, PCD (-1) has a significantly positive impact the PCD and LLD. Finally, SPV (-1) causes a significant reduction in LLD. This can justify the unwillingness of the stockholders to invest in institutions with volatile stock prices, as the stock price volatility reduces an institution’s liquid assets.
Overall, the Root Mean Squared Forecast Errors (RMSFE) of all equations are dramatically lower (less than one) which indicates better fit and more precise predictions of the selected variables. In comparing our results with other studies, we agreed with [73], indicating that, the stock price volatility (national market stock) in the short-term is significant with renewable energy. Moreover, [74] find that stock market value affects renewable energy in the long run. Also, [75] finds that financial development promotes renewable energy use, however, [76] argue that REC does not react to a short-run change in bank-based financial development (stock price volatility).

3.3. Var Diagnostic Results

We perform diagnostic tests on a VAR model to assess its reliability and validity in succeeding accurate predictions about the connections between the selected variables. In this study it is assumed that the optimal lag length for the BVAR model is one (1) because it has many more (3) stars (*) in pre-estimation and has the much more (4) stars in the post-estimation than the other lags which will make it possible to employ the BVAR model (Table 5).
The Wald lag exclusion test has been achieved to examine the possibility of lag elimination of any variable in the VAR system. The Wald test is a safety test for the number of lags chosen from the selection criteria [77]. Based on the results of the Wald test attained from Table 6, we find that the selected variables used in the VAR are significant (p-value < 0.05). Thus, the VAR model will be estimated by using the lag in order number one which is determined by selection criteria in Table 5.
For more model reliability, the study also has applied the Lagrange Multiplier (LM) test, which is a multivariate test statistic for autocorrelation in residuals up to the specified lag order. The null hypothesis of the LM test is the non-existence of serial correlation versus the alternative of autocorrelated residuals. Our result from Table 6 shows that both the lag lengths accept the null hypothesis of no serial correlation indicating that the error terms of the equations are not correlated, this suggests that the fitted VAR system is reasonable.
Further, we applied the VAR eigenvalue stability condition to check the stability of the VAR model. It is based on the eigenvalues of the matrix of coefficients in the VAR model (equation 12). In particular, the situation requires that all the eigenvalues of the coefficient matrix lie inside the unit circle in the complex plane, which means that they have a modulus or absolute value of less than one [78]. Table 7 and Figure 2 illustrate that no root lies outside the unit circle, as each modulus value in the table and figure is lower than 1, this assessment implies that the VAR model fits the stability condition.

3.4. Pairwise Granger Causality Approach for Robustness Check

For investigating the possibility of causal relationships between logarithms for the time series of the selected variables and their direction, we used the Granger causality in the VAR environment analysis. This is a useful approach that can assist in recognizing which variables are significant in our model that have a causal influence on other variables. All outcomes from asymmetric Granger-causality analysis are reported in Table 8. The results propose that there is significant causality running from LogSPV and LogPCD to LogREC. The result also shows a significant causality running from LogPCD and LogLLD to LogSPV. However, the results indicate that logREC, LogSPV, and LogLLD do not Granger cause the Log PCD, i.e., there are independence conditions between these variables. Meanwhile, the logREC is not sensitive to the Log LLD, though LogSPV and LogPCD do Granger cause the Log LLD.
From the findings, it is possible to draw a hypothesis that an increase in the SPV and PCD leads to an increase in REC, i.e., there are unidirectional runs from SPV and PCD to REC. Also, bidirectional runs between SPV and PCD. Also, an increase in PCD leads to an increase in LLD, which implies Unidirectional runs from PCD to LLD. From our Granger findings, we concluded that the results of causality between REC and financial development indicators were conflicting. We concluded that from our Granger causality results all four different hypotheses derived from equations (18) and (19) exist. In comparing our results with other studies, [79] argue that renewable energy sources do not have a statistically significant impact on financial development. However, [28] realize the bidirectional causality relationship between financial development and REC.

3.5. Forecast Error Variance Decomposition Results

Furthermore, in the present study, we have analyzed FEVD using the Choleskey orthogonalization technique to detect the strength horizons beyond the selected time, in our study we chose 10 periods/horizons. We analyzed the FEVD to quantify the extent to which forecast error variance in a variable can be explained by innovations or impulses originating from that variable and the other variables in the system. Therefore, this approach estimates the simultaneous shock effects. In this study, we take, for example, 3 years represent the short run and 10- years for the long run. Table 9 shows that 65.69% of the variation in REC was caused by itself, while SPV and PCD caused increasing variation in REC contributed with 14.82% and 13.44%: respectively in the last duration (10). At the same time, LLD causes a decreasing variation of forecast error in REC throughout the 10 years, ending with 6.15%; respectively in the last period (10). This indicates that REC is shocked by itself with larger percentages of forecast error than the selected financial development indicators of forecast error throughout the 10 years. The empirical evidence from Table 10 indicates that 63.82% of SPV is contributed by its shocks and REC contributes by innovative shock for SPV with 5.76% in the long run. The contribution of PCD and LLD to SPV is minimal, 2.82% and 2.76%; respectively. Also, it’s noted that the shock of SPV by itself estimates the largest percentages of forecast error in the short run and long run than other selected financial development indicators of forecast error. Nearly 8641 % portion of PCD is significantly contributed by its innovative shock. The innovative shocks of REC, SPV, and LLD are enhanced in PCD by 4.32%, 4.37%, and 4.90%; respectively. The contribution of REC, and PCD is negligible in LLD, estimated at 6.15% and 6.80%; respectively. While the innovative shocks of SPV contribute to LLD by 63.82%. Whereas 13.84 % portion of LLD is contributed by its innovative shock. This portion of the empirical proof resounds with the findings of ([43,83,84]).

3.6. Impulse Response Function Analyses

Finally, the impulse response function analyses are analyzed to illustrate the response in one variable due to shocks originating from other variables. Figure 3 plots the dynamic impact of one standard deviation of financial development indicators shock on Saudi Arabia’s renewable energy consumption over a range of a horizon of 10 years, in Figure 3 the steady blue line symbolizes the impulse response of one variable (for instance REC) to a one standard deviation shock to a different variable (for instance PCD), whereas the dashed lines symbolize the upper and lower bounds of the 95% confidence intervals. Notably, REC shows positive responses to PCD, LLD, and SPV shock in the short run. Also, it observes that the impulse response function (IRF) is close to the zero line for the response of PCD on REC and LLD, which means that the system being analyzed does not respond to unexpected shocks or impulse in the PCD.

4. Conclusions and Policy Implications

During the last decades, the government of Saudi Arabia adopted the reduction of fossil fuel subsidies policy as a financial motivation for supporting both the production and consumption of fossil fuels. The country launched, the National Renewable Energy Program (NREP) plans to develop renewable energy projects and works on developing the renewable energy sector through a partnership of public and private investments sector. Therefore, this paper aims to explore the influence and shocks of Saudi’s financial development indicators on renewable energy consumption. And to establish the direction of causality between financial development indicators and renewable energy consumption.
This study uses the total renewable energy consumption in (TJ) as a proxy of sustainable development indicators, thus other three proxies of financial development indicators are incorporated in the study: stock price volatility, private credit by deposit money banks to GDP in (%), and liquid liabilities to GDP in (%) as financial development indicators. The study covers the annual data period of 1990-2021 and applies some quantitative methodologies, the Basic Vector Autoregressive model (VAR), Granger causality test, forecast error variance decomposition (FEVD) test, and impulse response function (IRF) test.
The empirical results of this study reveal that dissimilar findings of the normality test for the selected variables were observed, so all variables transformed to logarithm form, also the selected variables became stationary after their first differences. The results show significant structural breaks and single dates are spotted in renewable energy consumption and financial development indicators variables.
The VAR results concluded that in the short run, stock price volatility and private credit significantly positively influence the REC. Private credit impacts the stock price volatility while liquid liabilities exert a negative impact on stock price volatility. Likewise, private credit has a significantly positive influence on its changes and liquid liabilities.
The results from the asymmetric Granger-causality test propose a significant causality running from stock price volatility and private credit to REC. The result also shows a positive significant causality running from private credit and liquid liabilities to stock price volatility. The feedback of the hypotheses assumes that there exists unidirectional Granger casualty runs from stock price volatility and private credit to REC and bi-directional Granger causality between stock price volatility and private credit. From our Granger findings, we concluded that the results of causality between REC and financial development indicators were conflicting.
Further, the results of FEVD discover that more than half the percentage of the variation in REC was caused by itself, while liquid liabilities caused increasing variation in REC throughout 10 years. At the same time stock price volatility and private credit cause decreasing variation of forecast error in REC throughout 10 years. This indicates that REC is shocked by its own with the largest percentages of forecast error than the selected financial development indicators of forecast error throughout the 10 years. The empirical evidence indicates that stock price volatility is contributed by its shocks and REC contributes to price volatility shock. The contribution of private credit and liquid liabilities to the price volatility stock is minimal. Also, it’s noted that the shock of price volatility by itself estimates the largest percentages of forecast error than other selected financial development indicators of forecast error throughout the 10 years. We also find that REC and stock price volatility contribute to innovation shocks of private credit. A nearly high portion of private credit is significantly contributed by its innovative shock. The contribution of REC private credit is negligible in liquid liabilities shocks, while the innovative shocks of price volatility contribute to liquid liabilities change. Also, a low portion of liquid liabilities is contributed by its innovative shocks.
The IRF results concluded that the REC is a positive response to shock on private credit, liquid liabilities, and stock price volatility. Also, it notes that the impulse response function (IRF) is close to the zero line for the response of private credit on REC and liquid liabilities, which means that the system being analyzed does not respond to an unexpected shock (changes) or "impulse" in the private credit.
The policy implications of renewable energy consumption and financial development indicators are vital. Authorities can encourage investment in renewable energy consumption by providing financial incentives and motivations such as tax, and subsidies, facilitating access to financing for renewable energy projects, and establishing frameworks that will support the development of renewable energy markets. Financial policies for enhancing innovation in the renewable energy sector are significant for offering support and funds for research and supporting the development of new technologies. Adding the government can foster national partnerships between investors (financial institutions and companies), policymakers, and industry stakeholders. Besides attracting international cooperation that can assist in accelerating the transition to a low-carbon economy and encourage sustainable economic growth.
Further studies are suggested by employing different determinants of financial development indicators, such as nonbank financial institutions’ assets to GDP, Bank deposits to GDP (%), state-owned enterprises to GDP (%), and so on. Also, incorporating population growth in the REC function will be highly recommended for forming the renewable energy demand in Saudi Arabia.

Funding

This research was funded by the Deanship of Scientific Research, King Faisal University, Al-Ahsa, Saudi Arabia for financial support under the Ambitious Researcher Track.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. IEA (2022a) “World Energy Investment 2022”, International Energy Agency, Paris, World Energy Investment 2022 – Analysis - IEA.
  2. IEA (2022b) World Energy Investment 2022 Datafile – Data Product”, International Energy Agency,.
  3. IRENA (2023) International Renewable Energy Agency. Final Renewable Energy Consumption.
  4. Khan, H.; Khan, I.; Binh, T.T. The Heterogeneity of Renewable Energy Consumption, Carbon Emission and Financial Development in the Globe: A Panel Quantile Regression Approach. Energy Reports 2020, 6, 859–867. [Google Scholar] [CrossRef]
  5. UNDP (2018). Financing the 2030 Agenda for Sustainable Development. United Nations Development Programme. Retrieved from: Financing_the_2030_Agenda_CO_Guidebook.pdf. at 21, J. 2023. UNDP (2018). Financing the 2030 Agenda for Sustainable Development. United Nations Development Programme. Retrieved from: Financing_the_2030_Agenda_CO_Guidebook.Pdf. at 21, July 2023. 20 July.
  6. Erdoğan, S.; Yıldırım, D.Ç.; Gedikli, A. Natural Resource Abundance, Financial Development and Economic Growth: An Investigation on Next-11 Countries. Resources Policy 2020, 65, 101559. [Google Scholar] [CrossRef]
  7. Boukhatem, J. Assessing the Direct Effect of Financial Development on Poverty Reduction in a Panel of Low- and Middle-Income Countries. Res Int Bus Finance 2016, 37, 214–230. [Google Scholar] [CrossRef]
  8. Batuo, M.; Mlambo, K.; Asongu, S. Linkages between Financial Development, Financial Instability, Financial Liberalisation and Economic Growth in Africa. Res Int Bus Finance 2018, 45, 168–179. [Google Scholar] [CrossRef]
  9. Cincinelli, P.; Pellini, E.; Urga, G. Systemic Risk in the Chinese Financial System: A Panel Granger Causality Analysis. International Review of Financial Analysis 2022, 82, 102179. [Google Scholar] [CrossRef]
  10. Sarzynski, A.; Larrieu, J.; Shrimali, G. The Impact of State Financial Incentives on Market Deployment of Solar Technology. Energy Policy 2012, 46, 550–557. [Google Scholar] [CrossRef]
  11. Rana, A.; Sadiq, R.; Alam, M.S.; Karunathilake, H.; Hewage, K. Evaluation of Financial Incentives for Green Buildings in Canadian Landscape. Renewable and Sustainable Energy Reviews 2021, 135, 110199. [Google Scholar] [CrossRef]
  12. Miller, L.; Carriveau, R. A Review of Energy Storage Financing—Learning from and Partnering with the Renewable Energy Industry. J Energy Storage 2018, 19, 311–319. [Google Scholar] [CrossRef]
  13. Nguyen, P.A.; Abbott, M.; Nguyen, T.L.T. The Development and Cost of Renewable Energy Resources in Vietnam. Util Policy 2019, 57, 59–66. [Google Scholar] [CrossRef]
  14. Anton, S.G.; Afloarei Nucu, A.E. The Effect of Financial Development on Renewable Energy Consumption. A Panel Data Approach. Renew Energy 2020, 147, 330–338. [Google Scholar] [CrossRef]
  15. Ioannou, A.; Angus, A.; Brennan, F. Risk-Based Methods for Sustainable Energy System Planning: A Review. Renewable and Sustainable Energy Reviews 2017, 74, 602–615. [Google Scholar] [CrossRef]
  16. Mihaylov, G. , & Z.R. The Relationship between Financial Risk Management and Succession Planning in Family Businesses. International Journal of Managerial Finance 2021, 17, 438–454. [Google Scholar]
  17. Saudi Vision 2030 Kingdom of Saudi Arabia. National Transformation Program 2020. Saudi Vis. 2030. 2016.
  18. IEA (2023) International Energy Agency. Data and Statistics.
  19. SMoE (2023a). The Ministry of Energy, R.S.Arbia. The Ministry of Energy, Riyadh, Saudi Arbia.
  20. SCB (2022). Saudi Central Bank. Annual report, T. financial sector development program. R. from: F.-2021-EN. pdf (sama. gov. sa), at 22 J. 2023. Saudi Central Bank. Annual Report, The Financial Sector Development Program.2022.
  21. WB (2023a). World Bank Development Indicators, G.F.I.| D. (worldbank. org). World Bank Development Indicators, Global Financial Inclusion | DataBank (Worldbank.Org).
  22. WB (2023b).World Bank, G.F. WB (2023b).World Bank, G.F.Development.R. from: https://databank. worldbank. org/reports. aspx?source=global-financial-development, at 13, J. 2023.
  23. SMoE (2023b). Minisitry of Energy, S.A.R. from: S. (moenergy. gov. sa), at 22, J. 2023 SMoE (2023b). Minisitry of Energy, Sadui Arabia, Retrieved from: Scope (Moenergy.Gov.Sa), at 22, July, 2023.
  24. Razmi, S.F.; Ramezanian Bajgiran, B.; Behname, M.; Salari, T.E.; Razmi, S.M.J. The Relationship of Renewable Energy Consumption to Stock Market Development and Economic Growth in Iran. Renew Energy 2020, 145, 2019–2024. [Google Scholar] [CrossRef]
  25. Dimnwobi, S.K.; Madichie, C. V.; Ekesiobi, C.; Asongu, S.A. Financial Development and Renewable Energy Consumption in Nigeria. Renew Energy 2022, 192, 668–677. [Google Scholar] [CrossRef]
  26. Kirikkaleli, D.; Adebayo, T.S. Do Renewable Energy Consumption and Financial Development Matter for Environmental Sustainability? New Global Evidence. Sustainable Development 2021, 29, 583–594. [Google Scholar] [CrossRef]
  27. Pata, U.K.; Yilanci, V.; Zhang, Q.; Shah, S.A.R. Does Financial Development Promote Renewable Energy Consumption in the USA? Evidence from the Fourier-Wavelet Quantile Causality Test. Renew Energy 2022, 196, 432–443. [Google Scholar] [CrossRef]
  28. Fasheyitan, O.D.; Omankhanlen, A.E.; Okpalaoka, C.I. Effects of Renewable Energy Consumption and Financial Development: Using Nigeria’s Economy as a Case Study. Energy Conversion and Management: X 2022, 16, 100329. [Google Scholar] [CrossRef]
  29. Shahbaz, M.; Van Hoang, T.H.; Mahalik, M.K.; Roubaud, D. Energy Consumption, Financial Development and Economic Growth in India: New Evidence from a Nonlinear and Asymmetric Analysis. Energy Econ 2017, 63, 199–212. [Google Scholar] [CrossRef]
  30. Qamruzzaman, M.; Jianguo, W. The Asymmetric Relationship between Financial Development, Trade Openness, Foreign Capital Flows, and Renewable Energy Consumption: Fresh Evidence from Panel NARDL Investigation. Renew Energy 2020, 159, 827–842. [Google Scholar] [CrossRef]
  31. Mukhtarov, S.; Mikayilov, J.; Mammadov, J.; Mammadov, E. The Impact of Financial Development on Energy Consumption: Evidence from an Oil-Rich Economy. Energies (Basel) 2018, 11, 1536. [Google Scholar] [CrossRef]
  32. Eren, B.M.; Taspinar, N.; Gokmenoglu, K.K. The Impact of Financial Development and Economic Growth on Renewable Energy Consumption: Empirical Analysis of India. Science of The Total Environment 2019, 663, 189–197. [Google Scholar] [CrossRef]
  33. Wang, J.; Zhang, S.; Zhang, Q. The Relationship of Renewable Energy Consumption to Financial Development and Economic Growth in China. Renew Energy 2021, 170, 897–904. [Google Scholar] [CrossRef]
  34. Fan, W.; Hao, Y. An Empirical Research on the Relationship amongst Renewable Energy Consumption, Economic Growth and Foreign Direct Investment in China. Renew Energy 2020, 146, 598–609. [Google Scholar] [CrossRef]
  35. Usman, M.; Hammar, N. Dynamic Relationship between Technological Innovations, Financial Development, Renewable Energy, and Ecological Footprint: Fresh Insights Based on the STIRPAT Model for Asia Pacific Economic Cooperation Countries. Environmental Science and Pollution Research 2021, 28, 15519–15536. [Google Scholar] [CrossRef]
  36. Wu, L.; Broadstock, D.C. Does Economic, Financial and Institutional Development Matter for Renewable Energy Consumption? Evidence from Emerging Economies. International Journal of Economic Policy in Emerging Economies 2015, 8, 20. [Google Scholar] [CrossRef]
  37. Abid, M.; sakrafi, H.; Gheraia, Z.; Abdelli, H. Does Renewable Energy Consumption Affect Ecological Footprints in Saudi Arabia? A Bootstrap Causality Test. Renew Energy 2022, 189, 813–821. [Google Scholar] [CrossRef]
  38. AlNemer, H.A.; Hkiri, B.; Tissaoui, K. Dynamic Impact of Renewable and Non-Renewable Energy Consumption on CO2 Emission and Economic Growth in Saudi Arabia: Fresh Evidence from Wavelet Coherence Analysis. Renew Energy 2023, 209, 340–356. [Google Scholar] [CrossRef]
  39. Barhoumi, E.M.; Okonkwo, P.C.; Zghaibeh, M.; Belgacem, I. Ben; Alkanhal, T.A.; Abo-Khalil, A.G.; Tlili, I. Renewable Energy Resources and Workforce Case Study Saudi Arabia: Review and Recommendations. J Therm Anal Calorim 2020, 141, 221–230. [Google Scholar] [CrossRef]
  40. Almasoud, A.H.; Gandayh, H.M. Future of Solar Energy in Saudi Arabia. Journal of King Saud University - Engineering Sciences 2015, 27, 153–157. [Google Scholar] [CrossRef]
  41. Hassine, M.B. & H.N. The Causal Links between Economic Growth, Renewable Energy, Financial Development and Foreign Trade in Gulf Cooperation Council Countries. International Journal of Energy Economics and Policy 2017, 7, 76–85. [Google Scholar]
  42. Mahalik, M.K.; Babu, M.S.; Loganathan, N.; Shahbaz, M. Does Financial Development Intensify Energy Consumption in Saudi Arabia? Renewable and Sustainable Energy Reviews 2017, 75, 1022–1034. [Google Scholar] [CrossRef]
  43. Ji, Q.; Zhang, D. How Much Does Financial Development Contribute to Renewable Energy Growth and Upgrading of Energy Structure in China? Energy Policy 2019, 128, 114–124. [Google Scholar] [CrossRef]
  44. Anton, S.G.; Afloarei Nucu, A.E. The Effect of Financial Development on Renewable Energy Consumption. A Panel Data Approach. Renew Energy 2020, 147, 330–338. [Google Scholar] [CrossRef]
  45. Mutascu, M. A Bootstrap Panel Granger Causality Analysis of Energy Consumption and Economic Growth in the G7 Countries. Renewable and Sustainable Energy Reviews 2016, 63, 166–171. [Google Scholar] [CrossRef]
  46. Bao, C.; Xu, M. Cause and Effect of Renewable Energy Consumption on Urbanization and Economic Growth in China’s Provinces and Regions. J Clean Prod 2019, 231, 483–493. [Google Scholar] [CrossRef]
  47. FAO Food and Agriculture Organization of the United Nations. Macro Indicators Databases.. 2023.
  48. GASTAT (2023a) General Authority for Statistics. King of Saudi Arabia.
  49. GASTAT (2023b) General Authority for Statistics. King of Saudi Arabia.
  50. Ng, S.; Perron, P. LAG Length Selection and the Construction of Unit Root Tests with Good Size and Power. Econometrica 2001, 69, 1519–1554. [Google Scholar] [CrossRef]
  51. Adnan Hye, Q.M.; Ali Khan, R.E. Tourism-Led Growth Hypothesis: A Case Study of Pakistan. Asia Pacific Journal of Tourism Research 2013, 18, 303–313. [Google Scholar] [CrossRef]
  52. Kirikkaleli, D.; Athari, S.A.; Ertugrul, H.M. The Real Estate Industry in Turkey: A Time Series Analysis. The Service Industries Journal 2021, 41, 427–439. [Google Scholar] [CrossRef]
  53. Zivot, E.; Andrews, D.W.K. Further Evidence on the Great Crash, the Oil-Price Shock, and the Unit-Root Hypothesis. Journal of Business & Economic Statistics 1992, 10, 251. [Google Scholar] [CrossRef]
  54. Rjoub, H.; Odugbesan, J.A.; Adebayo, T.S.; Wong, W.-K. Sustainability of the Moderating Role of Financial Development in the Determinants of Environmental Degradation: Evidence from Turkey. Sustainability 2021, 13, 1844. [Google Scholar] [CrossRef]
  55. Narayan, P.K.; Smyth, R. Random Walk versus Multiple Trend Breaks in Stock Prices: Evidence from 15 European Markets. Applied Financial Economics Letters 2006, 2, 1–7. [Google Scholar] [CrossRef]
  56. Lütkepohl, H. A Note on the Asymptotic Distribution of Impulse Response Functions of Estimated Var Models with Orthogonal Residuals. J Econom 1989, 42, 371–376. [Google Scholar] [CrossRef]
  57. Shokoohi, Z.; Saghaian, S. Nexus of Energy and Food Nutrition Prices in Oil Importing and Exporting Countries: A Panel VAR Model. Energy 2022, 255, 124416. [Google Scholar] [CrossRef]
  58. Kousar, S.; Sabir, S.A.; Ahmed, F.; Bojnec, Š. Climate Change, Exchange Rate, Twin Deficit, and Energy Inflation: Application of VAR Model. Energies (Basel) 2022, 15, 7663. [Google Scholar] [CrossRef]
  59. Usman, O.; Alola, A.A.; Akadiri, S. Saint Effects of Domestic Material Consumption, Renewable Energy, and Financial Development on Environmental Sustainability in the EU-28: Evidence from a GMM Panel-VAR. Renew Energy 2022, 184, 239–251. [Google Scholar] [CrossRef]
  60. Cong, R.-G.; Wei, Y.-M.; Jiao, J.-L.; Fan, Y. Relationships between Oil Price Shocks and Stock Market: An Empirical Analysis from China. Energy Policy 2008, 36, 3544–3553. [Google Scholar] [CrossRef]
  61. Akaike, H. Fitting Autoregressive Models for Prediction. Ann Inst Stat Math 1969, 21, 243–247. [Google Scholar] [CrossRef]
  62. Hashimzade, N., & T.M.A. (Eds. ) Handbook of Research Methods and Applications in Empirical Microeconomics; Edward Elgar Publishing., 2021.
  63. Paulsen, J. ORDER DETERMINATION OF MULTIVARIATE AUTOREGRESSIVE TIME SERIES WITH UNIT ROOTS. J Time Ser Anal 1984, 5, 115–127. [Google Scholar] [CrossRef]
  64. Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 1969, 37, 424. [Google Scholar] [CrossRef]
  65. Turlach, B.A.; Venables, W.N.; Wright, S.J. Simultaneous Variable Selection. Technometrics 2005, 47, 349–363. [Google Scholar] [CrossRef]
  66. Aluko, O.A.; Adeyeye, P.O. Imports and Economic Growth in Africa: Testing for Granger Causality in the Frequency Domain. J Int Trade Econ Dev 2020, 29, 850–864. [Google Scholar] [CrossRef]
  67. Hessler, A. Unobserved Components Model Estimates of Credit Cycles: Tests and Predictions. Journal of Financial Stability 2023, 66, 101120. [Google Scholar] [CrossRef]
  68. Vo, L.H.; Le, T.-H. Eatery, Energy, Environment and Economic System, 1970–2017: Understanding Volatility Spillover Patterns in a Global Sample. Energy Econ 2021, 100, 105391. [Google Scholar] [CrossRef]
  69. Rana, R.H.; Alam, K.; Gow, J. Health Expenditure and Gross Domestic Product: Causality Analysis by Income Level. Int J Health Econ Manag 2020, 20, 55–77. [Google Scholar] [CrossRef] [PubMed]
  70. Abrigo, M.R.M.; Love, I. Estimation of Panel Vector Autoregression in Stata. The Stata Journal: Promoting communications on statistics and Stata 2016, 16, 778–804. [Google Scholar] [CrossRef]
  71. Sehrawat, M.; Giri, A.K.; Mohapatra, G. The Impact of Financial Development, Economic Growth and Energy Consumption on Environmental Degradation. Management of Environmental Quality: An International Journal 2015, 26, 666–682. [Google Scholar] [CrossRef]
  72. Bera, A.K.; Jarque, C.M. Efficient Tests for Normality, Homoscedasticity and Serial Independence of Regression Residuals. Econ Lett 1981, 7, 313–318. [Google Scholar] [CrossRef]
  73. Ng, S.; Perron, P. LAG Length Selection and the Construction of Unit Root Tests with Good Size and Power. Econometrica 2001, 69, 1519–1554. [Google Scholar] [CrossRef]
  74. Mahalik, M.K.; Babu, M.S.; Loganathan, N.; Shahbaz, M. Does Financial Development Intensify Energy Consumption in Saudi Arabia? Renewable and Sustainable Energy Reviews 2017, 75, 1022–1034. [Google Scholar] [CrossRef]
  75. Zivot, E.; Andrews, D.W.K. Further Evidence on the Great Crash, the Oil-Price Shock, and the Unit-Root Hypothesis. Journal of Business & Economic Statistics 1992, 10, 251. [Google Scholar] [CrossRef]
  76. Saculsan& Kanamura, T. Examining Risk and Return Profiles of Renewable Energy Investment in Developing Countries: The Case of the Philippines. 2019.
  77. Razmi, S.F.; Ramezanian Bajgiran, B.; Behname, M.; Salari, T.E.; Razmi, S.M.J. The Relationship of Renewable Energy Consumption to Stock Market Development and Economic Growth in Iran. Renew Energy 2020, 145, 2019–2024. [Google Scholar] [CrossRef]
  78. Prempeh, K.B. The Impact of Financial Development on Renewable Energy Consumption: New Insights from Ghana. Future Business Journal 2023, 9, 6. [Google Scholar] [CrossRef]
  79. Lahiani, A.; Mefteh-Wali, S.; Shahbaz, M.; Vo, X.V. Does Financial Development Influence Renewable Energy Consumption to Achieve Carbon Neutrality in the USA? Energy Policy 2021, 158, 112524. [Google Scholar] [CrossRef]
  80. Daniela, V.A.; Liliana, D.; Gabriela, D. Investments, Economic Growth and Employment: VAR Method for Romania. Studies in Business and Economics 2019, 14, 231–244. [Google Scholar] [CrossRef]
  81. Akbar, M.; Hussain, A.; Akbar, A.; Ullah, I. The Dynamic Association between Healthcare Spending, CO2 Emissions, and Human Development Index in OECD Countries: Evidence from Panel VAR Model. Environ Dev Sustain 2021, 23, 10470–10489. [Google Scholar] [CrossRef]
  82. Lahiani, A.; Mefteh-Wali, S.; Shahbaz, M.; Vo, X.V. Does Financial Development Influence Renewable Energy Consumption to Achieve Carbon Neutrality in the USA? Energy Policy 2021, 158, 112524. [Google Scholar] [CrossRef]
  83. Nurgazina, Z.; Ullah, A.; Ali, U.; Koondhar, M.A.; Lu, Q. The Impact of Economic Growth, Energy Consumption, Trade Openness, and Financial Development on Carbon Emissions: Empirical Evidence from Malaysia. Environmental Science and Pollution Research 2021, 28, 60195–60208. [Google Scholar] [CrossRef]
  84. Qudrat-Ullah, H.; Nevo, C.M. Analysis of the Dynamic Relationships among Renewable Energy Consumption, Economic Growth, Financial Development, and Carbon Dioxide Emission in Five Sub-Saharan African Countries. Energies (Basel) 2022, 15, 5953. [Google Scholar] [CrossRef]
Preprints 86728 g002
Figure 2. Roots of the complanion matrix.
Figure 2. Roots of the complanion matrix.
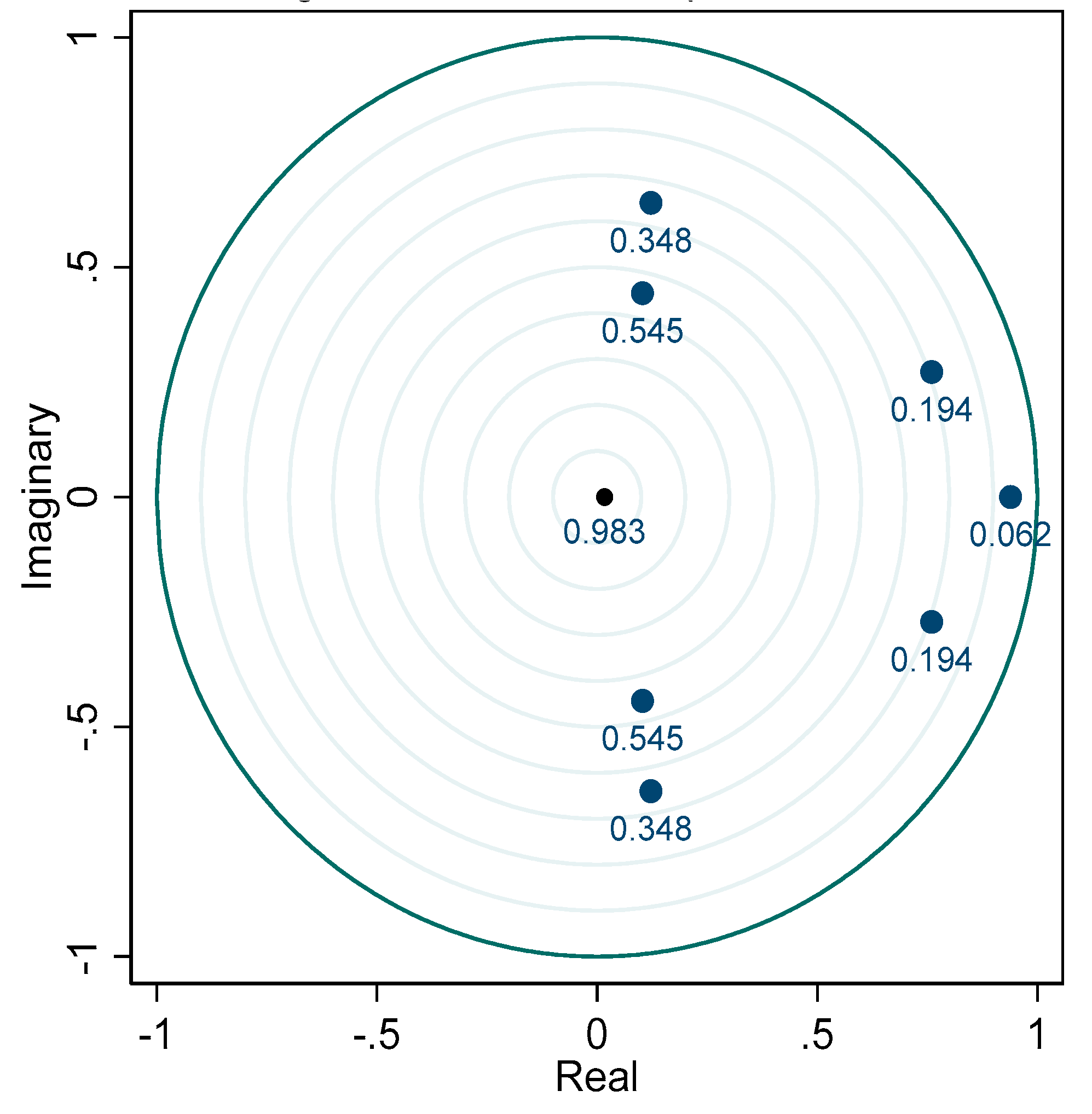
Preprints 86728 g002
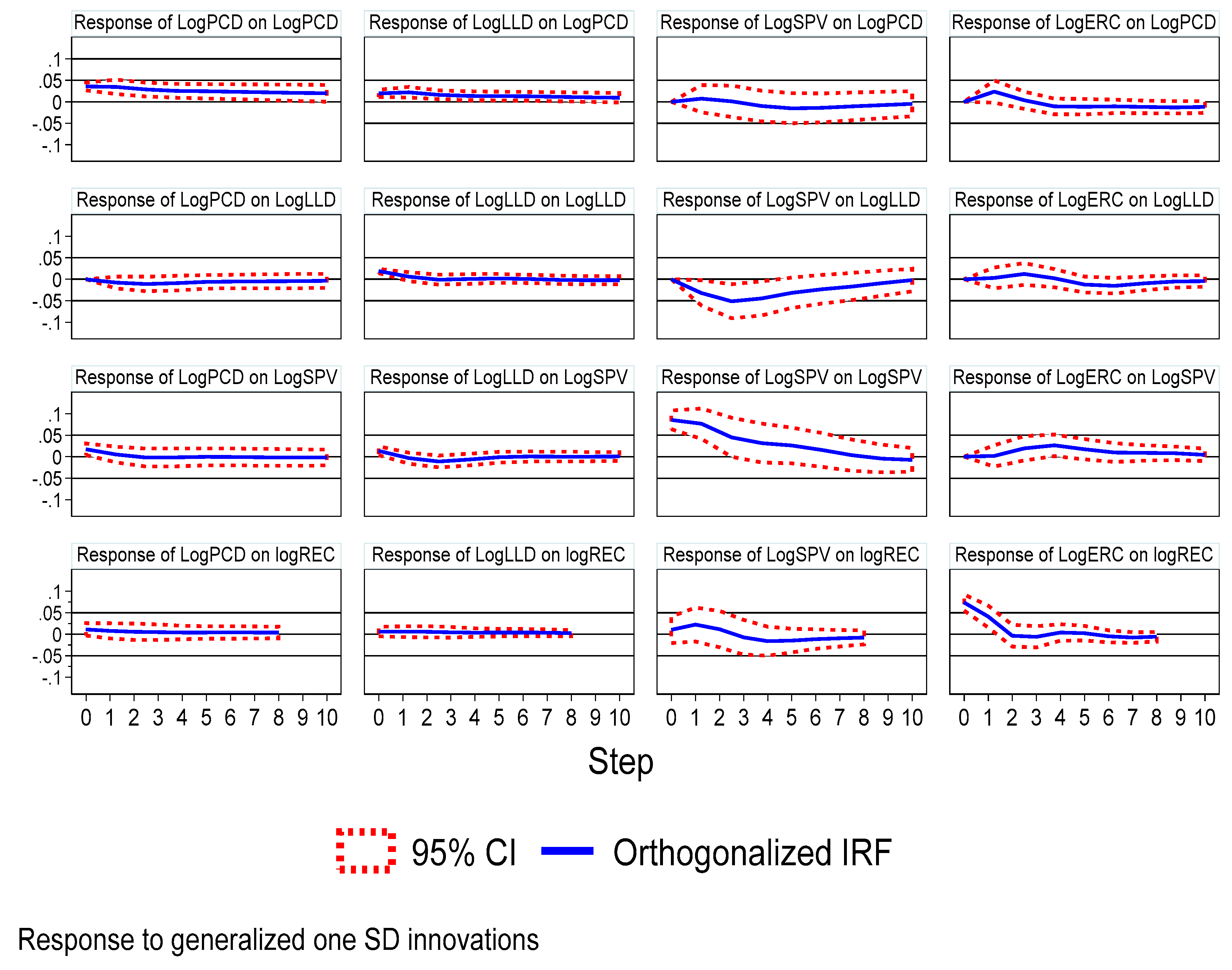
Preprints 86728 g003
Figure 3. Impulse response functions analysis.
Figure 3. Impulse response functions analysis.
Preprints 86728 g003
Table 1. Descriptive statistics of the selected variables.
Table 1. Descriptive statistics of the selected variables.
Variable Variable explanation and units Mean Std. dev. Min Max Obs
REC (This indicator is derived from energy balances statistics and is equivalent to total final consumption ignoring non-energy use [21].) * Renewable energy consumption (TJ). Is the total final energy consumption. 263.22 100.28 161.90 536.58 32
SPV **Stock price volatility refers to
the average of the 360-day volatility of the national stock market index.		 19.52 9.21 8.68 46.06 32
PCD (Domestic money banks comprise commercial banks and other financial institutions that accept transferable deposits, such as demand deposits [22].) ** Private credit by deposit money banks to GDP (%), is the financial resources provided to the private sector by domestic money banks as a share of GDP. 35.02 13.09 16.11 58.11 32
LLD (Liquid liabilities are also known as broad money, which is regonized as M3. M3= deposits in the central bank (M0) + transferable deposits and electronic currency (M1) + time and savings deposits, foreign currency transferable deposits, certificates of deposit, and securities repurchase agreements (M2)+ travellers’ checks, foreign currency time deposits, commercial paper, and shares of mutual funds or market funds held by residents [22].) ** Liquid liabilities to GDP (%) is the ratio of liquid liabilities to GDP. 53.50 9.81 42.60 74.73 32
Source: * = Data derived from WB (2023a) and GASTAT (2023b). ** data derived from WB (2023b).
Table 2. Normality and residual diagnostic tests.
Table 2. Normality and residual diagnostic tests.
Variable Obs Pr(skewness) Pr(kurtosis) Joint Test Normality Status
Adj X2 (2) Prob> X2
REC 32 0.0003 0.0316 13.46*** 0.00 Non-normal
SPV 32 0.0012 0.0740 10.97*** 0.00 Non-normal
PCD 32 0.3786 0.0487 4.68 0.10 Normal
LLD 32 0.0522 0.4191 4.50 0.11 Normal
JB tests Heteroskedasticity: Breusch–Pagan’s test****
Variable X2 Prob> X2 Normality status X2 Prob> X2 Description
REC 19.66 *** (0.00) Non-normal 16.51*** (0.00) Serial correlation
SPV 13.58*** (0.00) Non-normal 4.85*** (0.02) Serial correlation
PCD 2.17 (0.34) Normal 15.35*** (0.00) Serial correlation
LLD 3.89 (0.14) Normal 10.34*** (0.00) Serial correlation
Note: ***, **, * Levels of significance at 1%, 5% and 10%; respectively. X2= Pearson’s chi-square tests, ****H0: No serial correlation, Durbin–Watson d-statistic (7, 32) = 1.217352.
Table 3. Unit root test results.
Table 3. Unit root test results.
Variable Ng-Perron Test Statistics with Intercept
MZα MZt MSB MPT
Log REC (-1) -14.9877 -2.73746 0.18265 1.63477
Log SPV (-1) -51.3672 -5.01774 0.09768 0.60084
Log PCD (-1) -36.6042 -4.27765 0.11686 0.6706
Log LLD (-2) -29.0409 -3.81041 0.13121 0.84415
Asymptotic critical values for Ng -Perron test
1% -13.8 -2.58 0.174 1.78
5% -8.1 -1.98 0.233 3.17
10% -5.7 -1.62 0.275 4.45
Zivot–Andrew Unit test results
Intercept* Trend**
t-Stat SBD t-Stat SBD
Log REC -9.380 1999 -8.113 2007
Log SPV -6.571 2010 -4.793 2005
Log PCD -6.076 2014 -5.846 1997
Log LLD -5.261 2009 -5.215 2016
* The critical values for the Zivot and Andrews test are -5.34, -4.80, and -4.58 at 1 %, 5 %, and 10% levels of significance: respectively.
** The critical values for Zivot and Andrews test are -4.93, -4.42, and -4.11, at 1 %, 5 %, and 10% levels of significance; respectively.
Source: Authors' calculations (2023).
Table 4. Basic VAR model results.
Table 4. Basic VAR model results.
Independent Variable Dependent Variable (Equations)
Log REC Log SPV Log PCD Log LLD
Log REC (-1) 0.471 [.0.15]
(3.12) ***		 0.139 [0.176]
(0.079)		 -0.029 [0.084]
(-0.35)		 0.010 [0.064]
(0.17)
Log REC (-2) -0.27 [0.14]
(-1.87) *		 -0.86 [0.172]
(-0.50)		 0.043 [0.083]
(0.53)		 0.064 [0.062]
(1.03)
Log SPV (-1) -.119 [0.148]
(-0.80)		 0.937 [0.174]
(5.38) ***		 -0.116 [0.083]
(-1.40)		 -0.179 [0.063]
(-2.84) ***
Log SPV (-2) 0.441 [0.163]
(2.71) ***		 -0.376[0.19]
(-1.98) **		 0.019 [0.091]
(0.21)		 0.060[0.069]
(0.87)
Log PCD (-1) 0.579 [0.52]
(1.11)		 1.126 [0.611]
(1.84) *		 1.193 [0.292]
(4.08) ***		 0.443[0.221]
(2.00) **
Log PCD (-2) 1.15 [0.507]
(2.28) ***		 -0.230 [0.59]
(-0.39)		 0.018 [0.284]
(0.05)		 0.109[0.215]
(0.05)
Log LLD (-1) 0.161 [0.65]
(0.25)		 -1.676 [0.76]
(-2.21) ***		 -0.398 [0.362]
(-1.10)		 -0.32 [0.27]
(1.17)
Log LLD (-2) 0.545 [0.59]
(0.91)		 -0.147 [0.70]
(-0.21)		 -0.165 [0.336]
(-0.49)		 0.279[0.255]
(-1.10)
RMSFE 0.088338 0.103461 0.049465 0.037482
R-squared 0.5706 0.7660 0.9260 0.8180
Chi2 39.86597*** 98.18493*** 375.264*** 134.8692***
Note: The test statistic (z) is in parentheses, [Std. err.] in square brackets.
RMSFE: It means that the forecast errors (the difference between the predicted values and the actual values) are relatively small compared to the scale of the data.
***,**, * Levels of significance at 1%, 5% and 10%; respectively.
Source: Authors' calculations (2023).
Table 5. Optimal Lag Selection Criteria.
Table 5. Optimal Lag Selection Criteria.
Pre-estimation Lag Order Statistics
Sample: 1994 Thru 2021       Number of Obs = 28
Lag LogL LR FPE AIC HQIC SBIC df P-value
0 113.886 6.0e-09 -7.57835 -7.51928 7.38976
1 179.188 130.6 2.0e-10* -10.9785 -10.6832* 10.0355* 16 0.000
2 192.636 26.895 2.6e-10 -10.8025 -10.2709 9.10516 16 0.043
3 214.397 43.522* 2.1e-10 -11.1998* -10.4319 8.74809 16 0.000
Postestimation lag order statistics
Sample: 1992 thru 2021       Number of obs = 30
Lag LogL LR FPE AIC HQIC SBIC df P-value
0 115.395 -7.36654 -7.4263 -7.36654 -7.23948
1 186.545 142.3 1.8e-10* -11.103* -10.8041* -10.1689* 16 0.000
2 200.051 27.012* 2.3e-10 -10.9367 -10.3988 -9.25527 16 0.041
* Indicates lag order selected by the criterion (optimal lag), endogenous: exogenous: constant.
LR: Likelihood Ratio, sequential modified LR test statistic (each test at 5% level).
FPE: Final prediction error.
AIC: Akaike information criterion.
HQIC: Hannan-Quinn information criterion
SBIC: Schwarz information criterion.
Source: Authors' calculations (2023).
Table 6. Wald statistics and Lagrange multiplier test.
Table 6. Wald statistics and Lagrange multiplier test.
Lag VAR Lag Exclusion Wald Tests for Equations
Log REC Log SPV Log PCD Log LLD All
1 16.52674
(0.002) ***		 39.26219
(0.00) ***		 24.63254
(0.00) ***		 21.13896
(0.00) ***		 115.1125
(0.00) ***
2 12.75615
(0.013) ***		 9.42758
(0.05) **		 .6563887
(0.96)		 3.509985
(0.78)		 32.61345
(0.00) ***
Lagrange Multiplier test
Lag Chi2 Prob > chi2 Df Decision
1 23.9736 (0.09) * 16 Accept
2 21.4786 (0.16) 16 Accept
Ho: No autocorrelation at lag order
Note: The test statistic X2, P-value is in parentheses.
***, **, * Levels of significance at 1%, 5% and 10%; respectively.
Source: Authors' calculations (2023).
Table 7. The eigenvalue stability condition of the VAR model.
Table 7. The eigenvalue stability condition of the VAR model.
Eigenvalue Modulus
.9384261
.7592049 + .2719225i
7592049 - .2719225i
.1220844 + .6400749i
.1220844 - .6400749i
.1028066 + .443515i
.1028066 - .443515i
.01691226		 .938426
.806433
.806433
.651614
.651614
.455274
.455274
.016912
Statement: All the eigenvalues lie inside the unit circle which proves that VAR satisfies stability conditions.
Source: Authors’ calculations (2023).
Table 8. Granger causality Wald tests.
Table 8. Granger causality Wald tests.
Equation Excluded X2 Prob > chi2 The results of causality run Direction
Log REC LogSPV 10.533 0.005** SPV → REC Unidirectional
LogPCD 6.906 0.032** PCD → REC Unidirectional
LogLLD 1.6073 0.448 No causality Independence
ALL 14.163 0.028** REC←→FDI Bi-directional
LogSPV logREC .63461 0.728 No causality Independence
LogPCD 7.224 0.027** PCD→ SPV Unidirectional
LogLLD 7.6933 0.021** LLD→SPV Bi-directional
ALL 11.343 0.078 No causality Independence
Log PCD logREC .28536 0.867 No causality Independence
LogSPV 3.4615 0.177 No causality Independence
LogLLD 2.8823 0.237 No causality Independence
ALL 5.3268 0.503 No causality Independence
Log LLD logREC 1.7124 0.425 No causality Independence
LogSPV 11.399 0.003** SPV →LLD Bi-directional
LogPCD 12.677 0.002** PCD→LLD Unidirectional
ALL 18.06 0.006** LLD←→REC Bi-directional
Table 9. Forecast error variance decomposition for the selected variables.
Table 9. Forecast error variance decomposition for the selected variables.
Period FEVD for Log REC FEVD for Log SPV
Log REC Log SPV Log PCD Log LLD Log REC Log SPV Log PCD Log LLD
1 1 0 0 0 .013642 .986358 0 0
2 .924296 .000498 .07398 .001227 .040248 .887699 .003523 .06853
3 .863166 .046957 .070524 .019353 .037419 .775254 .002723 .184604
4 .785503 .119789 .076491 .018217 .034481 .713203 .006573 .245744
5 .738403 .143864 .085208 .032526 .04195 .679115 .015031 .263905
6 .707133 .146983 .092498 .053386 .048467 .657358 .021901 .272274
7 .68696 .149686 .103244 .06011 .05229 .644544 .025787 .277378
8 .672218 .151272 .115632 .060878 .055068 .639355 .027628 .27795
9 .662303 .149972 .126397 .061328 .056946 .638118 .028259 .276677
10 .655949 .148189 .134397 .061465 .057613 .638201 .028275 .275911
Period FEVD for Log PCD FEVD for Log LLD
Log REC Log SPV Log PCD Log LLD Log REC Log SPV Log PCD Log LLD
1 .075479 .174743 .749778 0 .037532 .1937 .396734 .372034
2 .061696 .1058 .81364 .018863 .04636 .129101 .566059 .258481
3 .054756 .081188 .819653 .044403 .05217 .163554 .580642 .203635
4 .050658 .06896 .826832 .05355 .055497 .16417 .600129 .180204
5 .047545 .060771 .837663 .054021 .056583 .151216 .624903 .167298
6 .04553 .054911 .846448 .053112 .058388 .140951 .644608 .156054
7 .044506 .050803 .852323 .052369 .060864 .133082 .658039 .148015
8 .043919 .047892 .856767 .051423 .062063 .127266 .667348 .143324
9 .043479 .045605 .860704 .050212 .061966 .123196 .674501 .140337
10 .043211 .043715 .864053 .049021 .061462 .120215 .67994 .138383
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated