Preprint
Article
Analysis and Optimal Control Measures of a Typhoid Fever Mathematical Model for a Multiple Socio-Economic Population
Altmetrics
Downloads
150
Views
42
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
01 October 2023
Posted:
03 October 2023
You are already at the latest version
Alerts
Abstract
Typhoid fever is an infectious disease that affects humanity worldwide particularly in the lower socio-economic communities where many individuals are exposed to a dirty environment and unclean food. A mathematical model is formulated to analyze the impact of control measures such as vaccination of susceptible humans, treatment of infected humans and sanitation in the different socio-economic communities. The model assumed that the population comprises of two socio-economic classes. The essential dynamical system analysis of our model was appropriately carried out. The impact of the control measures was analyzed, and the optimal control theory was applied on the control model to explore the impact of the different control measures. Numerical simulation of the models and the optimal controls were carried out and results obtained indicates that the overall combination of the control measures eradicates Typhoid fever in the population but the controls are more optimal in the higher socio-economic communities.
Keywords:
Subject: Computer Science and Mathematics - Mathematical and Computational Biology
1. Introduction
Typhoid fever is a life-threatening infection that originated from the bacterium Salmonella Typhi and is a major cause of illness and mortality in regions of the world with limited access to treated water and sanitation [1,2]. Recent statistics show that an average of 15 million cases and 145 000 typhoid-related deaths occur annually worldwide and its more endemic in many developing countries, and despite recent interventions in sanitation coverage, the disease remains a significant public health problem [1,3]. People who are infected with Salmonella Typhi, often referred to as "typhoid carriers," shed the bacteria in their feces (stool) and, to a lesser extent, in their urine. These individuals may have symptoms of typhoid fever or be asymptomatic carriers. The transmission of the disease is primarily a result of poor sanitation and lack of clean drinking water, but can also be transmitted via person-to-person on unclean surfaces [1]. Symptoms of typhoid fever include headache, weakness, loss of appetite, prolonged fever, nausea and constipation, or sometimes diarrhea [1].
In developing countries, the public health goal of preventing and controlling typhoid disease through sanitation and adequate medical care is challenging. Besides that, delays in diagnosis and treatment occur due to barriers to medical care, such as difficulty accessing medical facilities caused by delayed referral, the distance to hospital, and the cost of getting healthcare. The socio-economic class (SEC) of individuals has been shown to influence the dynamics of some infectious diseases [4,5,6,17]. Since typhoid fever is linked with poor sanitation and unclean water, individuals in the SEC are expected to be more exposed to typhoid fever compared to the individuals in a higher SEC [17]. In this work, we analyze the influence of control measures on the dynamics of typhoid fever disease for multiple socio-community. Specifically, we look at a case when the community consists of two socio-economic classes (i.e, lower SEC and higher SEC).
Several control measures have been implemented in fighting typhoid fever. Some of the effective ones include sanitation, vaccination, and treatment [1]. Medically, each of these three control measures (sanitation, vaccination, and treatment) are independent and hence can be applied simultaneously. Others include accurate diagnosis at the right time and treatment of typhoid disease in the community to prevent hospitalization complications. Prevention of the disease through improving sanitation and accessibility to safe water and food, health education to increase public awareness and induce healthy behavioral changes [3,7,8,9].
A mathematical model is a powerful approach to learning how disease spreads among both human and animal populations. Mathematical models help us to understand the transmission dynamics quantitatively and allow us to check hypotheses to understand their importance [10]. Interpreting a mathematical model for an infectious disease requires some assumptions about the spreading infection mechanism [11]. The basic compartmental mathematical models to describe the spread of disease are introduced [12,13]. This approach may test and compare different disease interventions as a strategy to prevent and control the disease. The origin of a mathematical model for typhoid disease could be related to Branko Cvjetanovi´c, an assistant professor at the Zagreb School of Medicine, who implemented the medical trial of the first typhoid vaccine that was funded by the US Public Health Service and WHO in the 1950s [16]. He was involved in research about the vaccines for diphtheria, pertussis, tetanus, cholera, and typhoid. In the 1973s, Cvjetanovi´c noted that no controlled trials had been run to demonstrate the extent to which typhoid transmission can control the spread through various sanitation strategies. Moreover, some researchers developed a non-autonomous mathematical model [14,15] to study typhoid transmission by considering the effect of seasonal conditions and some time-dependent parameters.
2. Model formulation
A multiple socio-economic community with total human inhabitant N is considered. We assume that the community is made up of two socio-economic classes whose sub-population is . Suppose there is a typhoid fever outbreak within the two socio-economic classes of the community. Assumed that each of these socio-economic community () engages three control measures (vaccination, treatment, and sanitation) in fighting the disease. Based on these assumptions, the formulation of mathematical model requires that the total population () for each socio-economic class is partitioned into susceptible population , vaccinated population , infected population , treated population and recovered population . The variable represented the pathogen in the environment for each SEC i. Epidemiologically, the transmission of typhoid fever disease is either through contact with infected humans or through exposure to the bacteria causing the illness. Recruitment of individuals into each of the susceptible class occur at a rate . Individuals in each moves to as they get vaccinated at a rate . Direct transmission from to and occur at a rate while the indirect transmission from to and occur at a rate . Note that the vaccinated individuals have less chances of being infected because they are vaccinated. This is captured in the model by assuming that the efficacy of the vaccine is for SEC i. Each infected class get treated at a rate . The treated class recovers at a rate . The who did not get treatment can recover naturally at a rate . Note that we discourage not getting treatment because typhoid fever can be very fatal and there are available treatment for the disease. Natural death occur at each of the SEC at a rate . Each of the recovered class can loss immunity and become susceptible again at a rate . Susceptible individuals move from to at a rate whereas infected individuals move from to at a rate . Infected individuals shed pathogens into the environment at a rate and the pathogen decay at a rate . Sanitation enhances pathogens decay at a rate . Based on these explanations, we obtained the typhoid fever control model given by
The variables and parameters meanings can be found in Table 1 and Table 2 respectively.
Let the initial conditions of the multiple control model be assumed as:
3. Model analysis
In this section, we present the dynamical system analysis of the multiple control model 1. The analysis will improve our understanding of typhoid fever disease dynamics. Mathematically, there exists a unique disease-free equilibrium (DFE) for the multiple control model 1
where and .
The basic reproduction number for the multiple control model 1 can be referred to as the expected number of new infections of typhoid fever produced when an infected individual is brought into contact with the population susceptible to typhoid fever in the presence of vaccination and sanitation. Mathematically, the basic reproduction number of model 1, using the next generation matrix approach [20] is
where , , ,
, , , and .
Epidemiologically, when , the disease can be eradicated from the two socio-economic classes. This can be shown by proving that the disease free equilibrium is stable when [20,21,22]. This implies that the control measures ensure that the basic reproduction number is less than unity so that the disease will not be established in any of the socio-economic class in the community. On the contrary, if the control measures are not effectual in decreasing below unity, a typhoid fever outbreak is likely to occur. The outbreak may persist or remain endemic in either or both socio-economic classes of the population [18,20,21,22]. Further investigation on the influence of the control measures on typhoid fever disease dynamics is considered via numerical illustrations in the subsequent section.
4. Numerical illustrations
Numerical illustrations are presented here to analyze the influence of the control measures on typhoid fever disease dynamics for the diverse socio-economic community. The parameter values used in the numerical illustrations are given in Table 3.
Vaccination is one of the effective control measures for minimizing typhoid fever [1]. Figure 1 illustrates the influence of vaccination rate in the population. We observe from the figure that increasing vaccination rates lead to a decrease in infected humans in both socio-economic classes. We observe that the infected populace is greater in the lower SEC 1 in the presence of vaccination. Hence, to achieve disease eradication, this lower SEC 1 should be the main target of vaccination.
Vaccine efficacy is a major factor in vaccination that determines the percentage reduction of the disease in a vaccinated group. Figure 2 illustrates the impact of vaccine efficacy on the dynamics of typhoid fever. The figure shows that an increase in vaccine efficacy decreases typhoid fever infected humans in the entire community. Hence, considering a vaccination with a very high efficacy (say 99% as we have in Figure 2) will results in faster disease eradication in the two socio-economic classes if the vaccine is applied uniformly in the entire populace.
Typhoid fever can be treated with appropriate antibiotic medicine [1]. Treatment of infected individuals is one of the effective control measures for reducing typhoid fever infections. Figure 3 is a graphical illustration of the effect of treatment rate in decreasing typhoid fever. The figure illustrates that an increase in treatment rate results in to decrease in typhoid fever in both socio-economic classes. Based on this, effective treatment of infected humans is recommended in the entire population.
Contaminated food and environment are one of the major routes of contracting typhoid fever [1]. So, to reduce typhoid fever infections, sanitation should be maintained in society. Figure 4 is a graphical representation of the impact of sanitation on the dynamics of typhoid fever. From the figure, we observe that an increase in sanitation results in a decrease in typhoid fever infected humans. The effects of sanitation are less in the higher SEC 2. A possible explanation for this could be because the higher SEC 2 have a certain level of sanitation in their environment, so introducing what is already in existence in their environment will not lead to major results unlike in the lower SEC 1 that have limited access to sanitation. Based on these, the lower SEC 1 should be the target of sanitation for maximum results.
Multiple control measures in this study are the situation when different possible control measures are introduced simultaneously in fighting a particular disease. In this study, we have discussed three possible control measures that can be used in fighting typhoid fever outbreaks. Figure 5 describes the effects of introducing these three control measures in fighting typhoid fever. The figure shows that using multiple control measures has maximum influence in decreasing the infected population (in both socio-economic classes) when compared with any of the single control measures. Therefore, whenever a typhoid fever outbreak occurs, multiple control measures should be considered for the faster eradication of the disease.
5. Optimal control analysis
Qualitative and numerical analysis of our model showed that implementing multiple control measures as aforementioned plays major roles in reducing the influence of Typhoid fever among humanity. Here, we intend to carryout optimal control analysis to determine the most effective control strategy for minimizing the number of humans affected by Typhoid fever along different socioeconomic classes. To minimize the cost of implementing the controls. we assume that the control parameters , and denoting vaccination, treatment and sanitation, respectively are measurable functions of time and then we formulate an appropriate optimal control function that minimizes the cost of implementing the controls subject to the model (1). For simplicity, we write the control strategies as control functions given as , and which are bounded, lebesgue integrable functions. Given the above, we now write the optimal control model as
subject to the initial conditions , , , , , , , , , .
This implies that the optimal control model is said to be optimal if it minimizes the objective functional
subject to the model (5), where the coefficients , , , , and are cost balancing coefficients that transform the integral into money expended over time T. Here, , is the direct cost associated with reducing the number of susceptibility to disease in each SEC, is the direct cost associated with reducing the number of infected humans in each SEC and is the direct cost associated with reducing the number of bacteria in the environment, while , and are relative costs for enforcing the control strategies , , . The goal is to minimise the number of humans susceptible to Typhoid fever among different SECs, minimize the infectious humans in all SECs and minimize the bacteria that causes Typhoid. In doing this, we anticipate nonlinear costs arising from these controls and so we consider quadratic functions for measuring the control costs [19,27,28,29,30,31].
The goal is to determine an optimal control , and such that
where are measurable}.
The Pontryagins Maximum Principle [36] introduces adjoint functions that enable us to combine the state system to the objective functional. With the Pontryagins principle we can convert the problem of minimizing the objective functional to the state system into a problem that involves minimizing a Hamiltonian H, with respect to , and . From the idea above we now have the Hamiltonian for the objective functional and the state system given as
where , , , , , , , , , , , and are associated adjoint for the states , , , , and , respectively. Given an optimal control triple (, , ) together with corresponding states (, , , , , ) that minimizes over , there exits adjoint variables , , , , , and that satisfies
together with the transversality conditions , for and .
Note that we get the differential equation (8) which governs the adjoint variables by differentiating the appropriate Hamiltonian function (8) with respect to the corresponding state as follows:
Now, consider the optimality conditions
So for the control triplet , and to satisfy the optimality condition we have;
For we have
The solving for using the optimality condition (10), we have
and subsequently taking bounds into consideration, we have
Solving for using the optimality condition, we have
and subsequently taking bounds into consideration, we have
Similarly for , we have
The results obtained above, shows that the optimal triple has the tendency of reducing the impact of typhoid fever in any human population, if there is application of the disease control measures at a minimum cost. The optimal control triple is parameter dependent, hence further analysis is to be carried out to determine the exact effect of these optimal control parameters in eradicating these diseases and its magnitude of reduction taking into consideration cost of application. This is done using numerical simulation to give pictorial view of this impact using published data in similar peer reviewed works.
5.1. Existence of the optimal control
Let and . Hence, a reduced function corresponding to (6) is given by
Lemma 1.
Set Ω is convex and closed.
Proof.
To prove that is a closed set, assume that in for but , i.e., or on a set of positive measure. Then taking , from lebesgue measure methods there exists and a positive measure set such that on [37]. This implies that
a contradiction. Thus, set is closed.
To prove convexity of set , it suffices to show that if is a convex set and , then any convex combination of any of (say ) for , is also contained in .
The proof is by induction. For , since then . For , since ,
and
Thus, . This also relates to and . This can also be extended to the nth socioeconomic class.
For , suppose that . By the inductive hypothesis,
For ,
Since it follows that the RHS of (24) is a convex combination of two points of . Thus, , so, is and hence, is convex. □
Theorem 1.
There exists an optimal control pair to the optimization problem (7).
Proof.
Set
This implies, for any , there exists so that
As set is a bounded subset of , it follows from Bolzano-Weierstrass theorem, that there exists a subsequence such that
weakly in . From (2) we have that all non-negative initial conditions are bounded. Thus, there exists a subsequence such that
From (25),
5.2. Uniqueness of the optimal control system
The optimality system of our optimal control problem is the combination of model (5) and the adjoint variables (8). So we have
where , , , and , , , , , .
Theorem 2.
For sufficiently small , the solution to the optimality system (30) of the optimal control problem is unique.
Proof.
Suppose , and
are two solutions of the optimality system (30). Let , , , , , , , , , , , , , , , , , , , , , , , , where is chosen arbitrarily. We now let
Now lets consider the first equation of (30), we have
For simplicity, we assume that there is no movement between and in this prove.
By subtracting and integrating from to for the above two equations, we have
Note that
where depends on the bounds of , depends on the bounds of , depends on the bounds of . So, by (31), we have
where is an appropriate upper-bound. Similarly, we can get the following inequalities for and , :
where , , and depend on the coefficients and the bounds of the state variables and co-state variables. Adding up equations (32) to (41), we have
From equation (42), we can see clearly that the coefficients of the integrals and non-negative anytime we choose a large is chosen and in turn choosing a small value of . For instance, if we take and also , then we see that the coefficient ( in relation to the integral . This is also application to the various relative to different x and y’s, which shows that each integral of (42) is non negative.
To this effect, we can see that , , , , , , , , , , and , , , , , . We can conclude that the solution of (42) is unique for small time t. □
The unique optimal control triple ( is characterised in terms of the unique solution of the optimal system. Therefore, the optimal triple gives us the optimal control strategy that is effective in preventing the incidence of Typhoid fever in any human population.
6. Numerical illustration of optimal control
Here we present the numerical solution of the optimal control problem. We first consider the effect of the controls on different socio-economic status independently as seen in Figure 6 and then systematically show the effects of the optimal controls over the controls on the different classes as illustrated in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. To illustrate this we use the parameter values as given in Table 3 with the following assigned cost factors: , , , , , , , , , , , . We carried out iterative technique by employing the forward-backward algorithm postulated by Lenhart and Workman [33] to obtain the optimal control functions () and ( as shown in Figure 6. The figure shows that it is most appropriate or optimal to commence treatment early and to make it readily available to affected victims of Typhoid fever and also to ensure that vaccination is adequately provided across all socio-economic communities and lastly adherence to good sanitation. This result is realistic, since it agrees with disease epidemiology in human, that supports good treatment and introduction of vaccination at early stage before the onset of an epidemic while ensuring adequate treatment of individuals throughout the endemic period.
Figure 6 illustrates the optimal control profiles of the two socioeconomic profiles. Here vaccination is denoted by red thick line on SEC 1 and red dashed line on SEC 2. From Figure 6(a), it is seen that the vaccination is very effective at the onset but weans out with time on SEC 1. Also we have that for SEC 2 vaccination also thrives at the onset but waens out over a period of time but when compared with vaccination on SEC 1, we have that vaccination in SEC 1 weans faster than that of SEC 2 and this could be attributed to the healthy or unhealthy activities carried out in either of the classes. Treatment on the other hand denoted by blue thick line on SEC 1 and blue dashed line on SEC 2 weans out almost the same time on both socio-economics classes and this agrees with real life intuition as treatment may be helpful but if the epidemic is not controlled, does requiring treatment may outnumber available medical equipment’s and practitioners. This also shows that treatment when properly administered has same effect on both socioeconomic classes. Finally, we have sanitation denoted by black thick line in SEC 1 and black dashed line in SEC 2. It is seen that sanitation plays a major role in reducing the impact of Typhoid fever but it is more active on SEC 2 than SEC 1 and this readily agrees with real life scenario as high socio-economics class individuals tends to reside more in an environment that is hygienic and they obey sanitation regulations.
Figure 7 illustrates the impact of control and optimal control on susceptible humans in both socioeconomic classes. The optimal control of vaccination reduces completely susceptibility to typhoid fever in both socioeconomic class population. Alternatively just combining the controls have more impact on SEC 1 than on SEC 2 and this may be consequent on the fact that vaccination maybe more targeted on SEC 1 population than SEC 2.
Figure 8 illustrates the effect of optimal control and controls on the vaccinated class. The vaccinated class in SEC 1 increases when vaccination is applied optimally but the impact of vaccination quickly reduces rather than in SEC 2 where there is more impact of optimal vaccination as shown in Figure 8(b). Also, even without optimal control we have that the control by vaccination weans out more in SEC 1 when compared to SEC 2 even though we have more reduction in susceptibility in SEC 1 (Figure 7a). This agrees with our earlier prediction that vaccination weans out faster in SEC 1 population due to unhealthy practices and due to poor living standard has less immunity to diseases than those in SEC 2.
Figure 9 also illustrates the impact of optimal control and controls on the infected class of the two socioeconomic classes. Optimal control has same effect on the two classes but the controls are more effective on SEC 2 than SEC 1. There is more reduction in the population of infected class in SEC 2 (see Figure 9b) than in SEC 1 (Figure 9a) when the controls are not optimal. This agrees with real life intuition as those in higher socio-economic status tend to benefit more from disease control strategies than those in lower socio-economic status. But when either or all the controls are optimally used in both communities it yields the same result.
From Figure 10 it is shown that with either controls or optimal control there is higher number of recovered humans in SEC 2 (Figure 10b) than in SEC 1 (Figure 10a) and this is attributed to good medical practices, good sanitation and early exposure to vaccination and generally good standard of living which boosts their immune system to enable them recover faster even when infected.
Finally, Figure 11 illustrates the impact of optimal control of sanitation on the pathogens in the two socioeconomic classes. Analogous to other cases discussed, optimal sanitation reduces pathogens in both classes but just applying sanitation in relation to what is obtainable in the different socioeconomic classes. It is seen that it is more effective in SEC 2 than in SEC 1.
7. Discussion
Typhoid fever is a fatal illness affecting humans especially those in the lower socio-economic community with limited access to clean food and a neat environment. The disease can be prevented or controlled by adopting effective control intervention measures. Some of the effective control measures for decreasing typhoid fever infections in some affected communities include vaccination, treatment, and sanitation. Many countries/communities are comprised of individuals in different socio-economic classes. For more accurate results on the dynamics of typhoid fever, the socio-economic classes of individuals in the community must be taken into consideration. This study used a mathematical epidemiological model to analyze the influence of control measures (vaccination, treatment, and sanitation) in decreasing typhoid fever in multiple socio-economic communities. By developing and analyzing a mathematical epidemiological model for typhoid fever for multiple socio-economic community, the dynamics of the disease were explored. The results of our analysis showed that the disease can be eradicated from the two socio-economic classes using the control measures provided that the basic reproduction number remained below unity. In contrast, when no control measure is introduced, the disease remains endemic in the community, especially in the lower socio-economic community. Further analysis revealed that under uniform movement rates, the lower SEC have a greater infected population, so control measures should be the focus on this class for faster disease eradication.
Next, the influence of each of the control measures was investigated numerically. Each of the control measures was found to have some influence in reducing typhoid fever. The combined effects of the multiple control measures yield better results when compared with the no-control measure and single control measure. Based on these findings, multiple control measures are highly recommended for controlling typhoid fever. However, if it is not available, any of the single control measures can be used because each of them is shown to have some positive influence in reducing infections in the two socio-economic communities.
Finally, we carried out optimal control analysis on our control model and it was observed that optimal control has effect on both socio-economic classes but optimizing treatment has more effect on SEC 2 than SEC 1 followed by vaccination and then sanitation. We also compared optimal control and controls on each of the classes in the two socioeconomic classes. Our analysis showed that optimal control has good effect on both classes even though it may wean out with time rather than using the controls collectively or independently. In all our analysis showed that more attention should be paid on communities of low socio-economic status in the event of typhoid fever epidemic.
Author Contributions
Obiora Collins conceived the project and provided the conceptual framework and early mathematical model and analysis. Ifeanyi Onah further developed and refined the model to add optimal control analysis and Stephen Aniaku contributed in the analysis and wrote the manuscript with assistance of Obiora Collins and Ifeanyi Onah.
Funding
This research received no external funding.
Informed Consent Statement
This research is a deterministic mathematical model which provides postulations on Typhoid disease epidemic in any human population but no real data was used in the study.
Data Availability Statement
Data sharing not applicable in this research article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Health Organisation (WHO) (August, 2020).
- Wain J, Hendriksen, R. S., Mikoleit, M. L., Keddy, K. H., Ochiai, R. L. Typhoid fever, Lancet: 2015; 385:1136–45. [CrossRef]
- Edward, S. A deterministic mathematical model for direct and indirect transmission dynamics of typhoid fever, Open Access Library Journal: 4(05), 1. [CrossRef]
- Moyer, C. A., Johnson, C., Kaselitz, E., Aborigo, R. Using social autopsy to understand maternal, newborn, and child mortality in low-resource settings: a systematic review of the literature, Global health action: 10(1); 1413917. [CrossRef]
- Snavely, M. E., Maze, M. J., Muiruri, C., Ngowi, L., Mboya, F., Beamesderfer, J., Rubach, M. P. Sociocultural and health system factors associated with mortality among febrile inpatients in Tanzania: a prospective social biopsy cohort study, BMJ global health: 3(1), e000507. [CrossRef]
- Snavely, M. E., Oshosen, M., Msoka, E. F., Karia, F. P., Maze, M. J., Blum, L. S., Muiruri, C. If You Have No Money, You Might Die: A Qualitative Study of Sociocultural and Health System Barriers to Care for Decedent Febrile Inpatients in Northern Tanzania, The American Journal of Tropical Medicine and Hygiene: 103(1); 494. [CrossRef]
- Crump, J. A. Progress in typhoid fever epidemiology, Clinical Infectious Diseases: 68(Supplement1); S4-S9. [CrossRef]
- Crump, J. A., Sjölund-Karlsson, M., Gordon, M. A., Parry, C. M. Epidemiology, clinical presentation, laboratory diagnosis, antimicrobial resistance, and antimicrobial management of invasive Salmonella infections, Clinical microbiology reviews: 28(4); 901-937. [CrossRef]
- Pitzer, V. E., Feasey, N. A., Msefula, C., Mallewa, J., Kennedy, N., Dube, Q., Heyderman, R. S. Mathematical modeling to assess the drivers of the recent emergence of typhoid fever in Blantyre, Malawi, Clinical Infectious Diseases: 61(suppl4); S251-S258. [CrossRef]
- Bakach, I., Just, M. R., Gambhir, M., Fung, I. C. H. Typhoid transmission: a historical perspective on mathematical model development, Transactions of The Royal Society of Tropical Medicine and Hygiene: 109(11); 679-689. [CrossRef]
- Brauer, F. Mathematical epidemiology: Past, present, and future, Infectious Disease Modelling: 2(2); 113-127. [CrossRef]
- Kermack, W. O., McKendrick, A. G. Contributions to the mathematical theory of epidemics. III.—Further studies of the problem of endemicity, Proceedings of the Royal Society of London. Series A, Containing papers of a mathematical and physical character: 141(843); 94-122.
- Kermack, W. O., McKendrick, A. G. A contribution to the mathematical theory of epidemics, Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character: 115(772); 700-721. [CrossRef]
- Matsebula, L., Nyabadza, F., Mushanyu, J. Mathematical analysis of typhoid fever transmission dynamics with seasonality and fear, Commun. Math. Biol. Neurosci.: 2021; Article-ID.
- Irena, T. K., Gakkhar, S. Modelling the dynamics of antimicrobial-resistant typhoid infection with environmental transmission, Applied Mathematics and Computation: 401; 126081. [CrossRef]
- Cvjetanovic, B. B. Field trial of typhoid vaccines, American Journal of Public Health and the Nations Health: 47(5); 578-581. [CrossRef]
- Collins O. C., Robertson, S. L., Govinder, K. S. Analysis of a waterborne disease model with socioeconomic classes Mathematical Biosciences: 269; 86–93. [CrossRef]
- Collins O. C., Govinder, K. S. Stability analysis and optimal vaccination of a waterborne disease model with multiple water sources, Natural Resource Model: 29; 426–447. [CrossRef]
- Onah, I. S., Collins, O. C., Madueme, P. G. U., Mbah, G. C. E. Dynamical System Analysis and Optimal Control Measures of Lassa Fever Disease Model, International Journal of Mathematics and Mathematical Sciences: 2020. [CrossRef]
- Van den Driessche, P., Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences: 180; 29–48. [CrossRef]
- Tien, J. H., Earn, D. J. D. Multiple Transmission Pathways and Disease Dynamics in a Waterborne Pathogen Model, Bull. Math. Biol.: 72; 1506–-1533. [CrossRef]
- Castillo-Chavez, C. Feng, Z. Huang, W. On the Computation of R0 and Its Role on Global Stability, in Mathematical Approaches for Emerging and Reemerging Infectious Diseases, An Introduction, IMA: 125; Springer-Verlag, New York.
- Robertson, S. L., Eisenberg, M. C., Tien, J. H. Heterogeneity in Multiple Transmission Pathways: Modelling the Spread of Cholera and Other Waterborne Disease in Networks with a Common Water Source, J. Biol. Dyn.: 7; 254-–275. [CrossRef]
- Onah, I. S., Collins, O. C. Dynamical system analysis of a Lassa fever model with varying socioeconomic classes, Journal of Applied Mathematics: 2020; 1-12. [CrossRef]
- Collins, O. C., Okeke, J. E. Analysis and control measures for Lassa fever model under socio-economic conditions, In Journal of Physics: Conference Series: 1734;(1) p. 012049). IOP Publishing. [CrossRef]
- Collins, O. C., Okeke, J. E, Analysis and multiple control measures for a typhoid fever disease model, In Journal of Physics: Conference Series: 1734; (1) p. 012053). IOP Publishing. [CrossRef]
- Miller Neilan, R. L., Schaefer, E., Gaff, H., Fister, K. R., Lenhart, S. Modeling optimal intervention strategies for cholera, Bulletin of mathematical biology: 72(8): 2004-2018. [CrossRef]
- Kar, T. K., Batabyal, A. Stability analysis and optimal control of an SIR epidemic model with vaccination, Biosystems: 104(2-3); 127-135. [CrossRef]
- Agusto, F. B. Optimal chemoprophylaxis and treatment control strategies of a tuberculosis transmission model, World journal of modelling and simulation: 5(3); 163-173.
- Joshi, H. R. Optimal control of an HIV immunology model, Optimal control applications and methods: 23(4); 199-213. [CrossRef]
- Onah, I. S., Aniaku, S. E., Ezugorie, O. M. Analysis and optimal control measures of diseases in cassava population, Optimal Control Applications and Methods: 43(5); 1450-1478. [CrossRef]
- King, A. A., Lonides, E. L., Pascual, M., Bouma, M. J. Inapparent Infections and Cholera Dynamics, Nature: 454; 877-–881. [CrossRef]
- Lenhart, S., Workman, J. T. Optimal control applied to biological models, CRC press.
- Lucas, M. E. S., Deen, J. L., Seidlein, L., Wang, X., Ampuero, J., Puri, M., Ali, M., Ansaruzzaman, M., Amos, J., Macuamule, A., Cavailler, P., Guerin, P. J., Mahoudeau, C., Kahozi-Sangwa, P., Chaignat, C., Barreto, A., Songane, F. F., Clemens, J. D. Effectiveness of Mass Oral Cholera Vaccination in Beira, Mozambique, N. Engl. J. Med.: 352; 757–767. [CrossRef]
- Mukandavire, Z, Garira, W. HIV/AIDS model for assessing the effects of prophylactic sterilizing vaccines, condoms and treatment with amelioration, J. Biol. Syst.: 14(3); 323–355. [CrossRef]
- Pontryagin, L.S. Mathematical theory of optimal processes, CRC Press: Boca Raton.
- Mugabi, F., Mugisha, J., Nannyonga, B., Kasumba, H., Tusiime, M. Parameter-dependent transmission dynamics and optimal control of foot and mouth disease in a contaminated environment, Journal of the Egyptian Mathematical Society: 27(1); 1-21. [CrossRef]
Figure 1.
Plot illustrating the effects of vaccination rate on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
Figure 1.
Plot illustrating the effects of vaccination rate on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
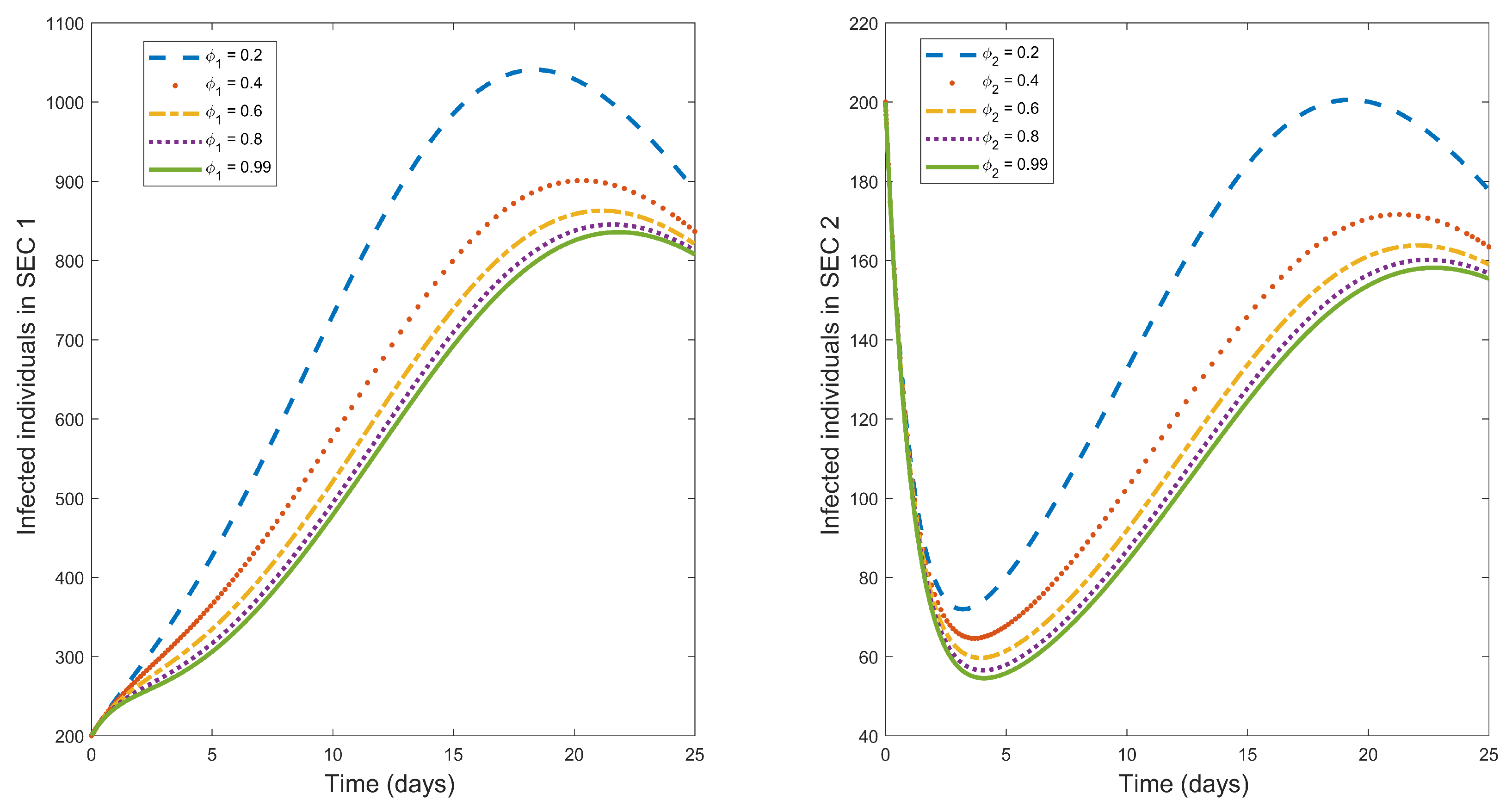
Figure 2.
Plot illustrating the impact of vaccine efficacy on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
Figure 2.
Plot illustrating the impact of vaccine efficacy on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
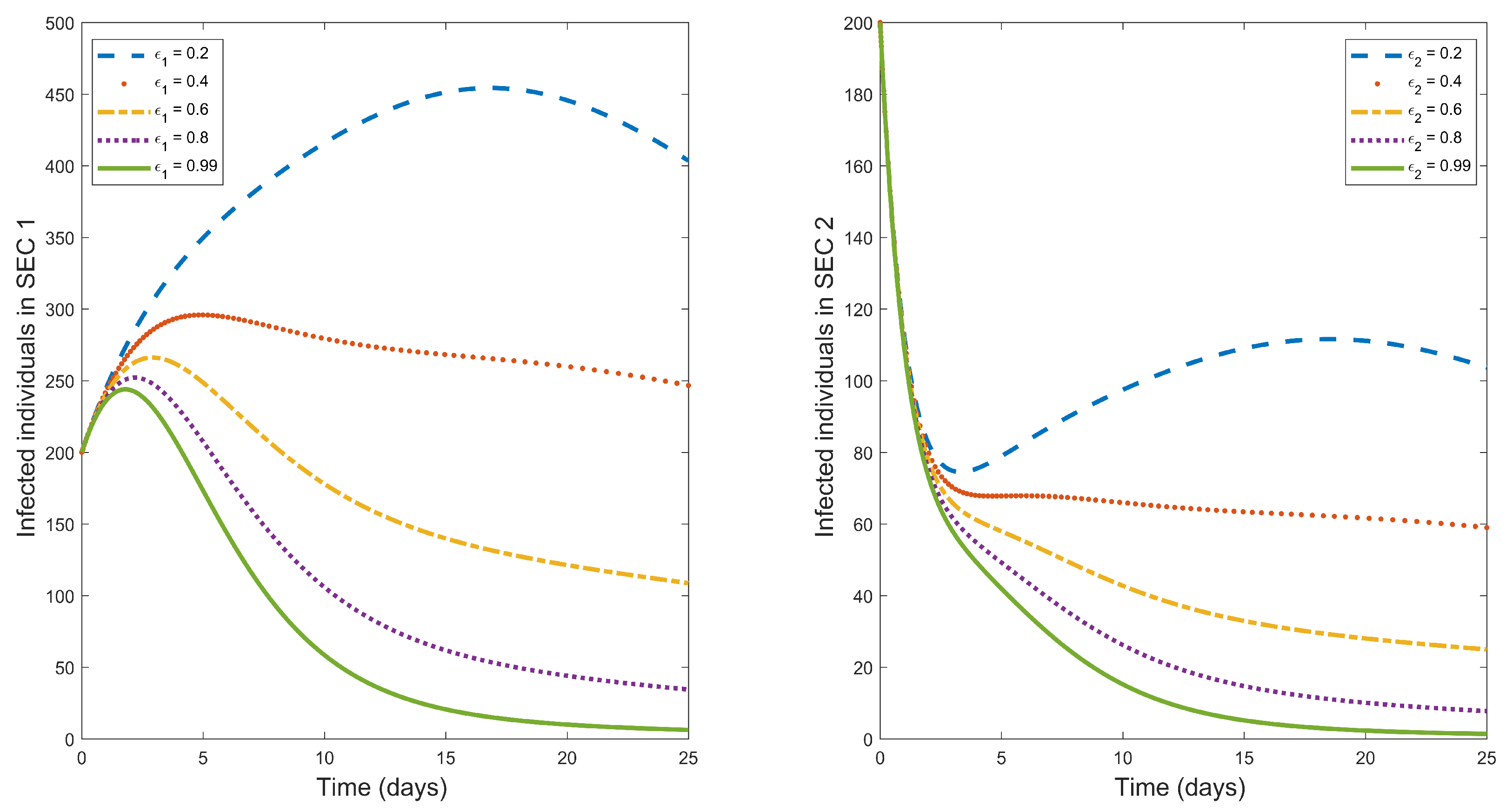
Figure 3.
Plot illustrating the influence of treatment on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
Figure 3.
Plot illustrating the influence of treatment on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
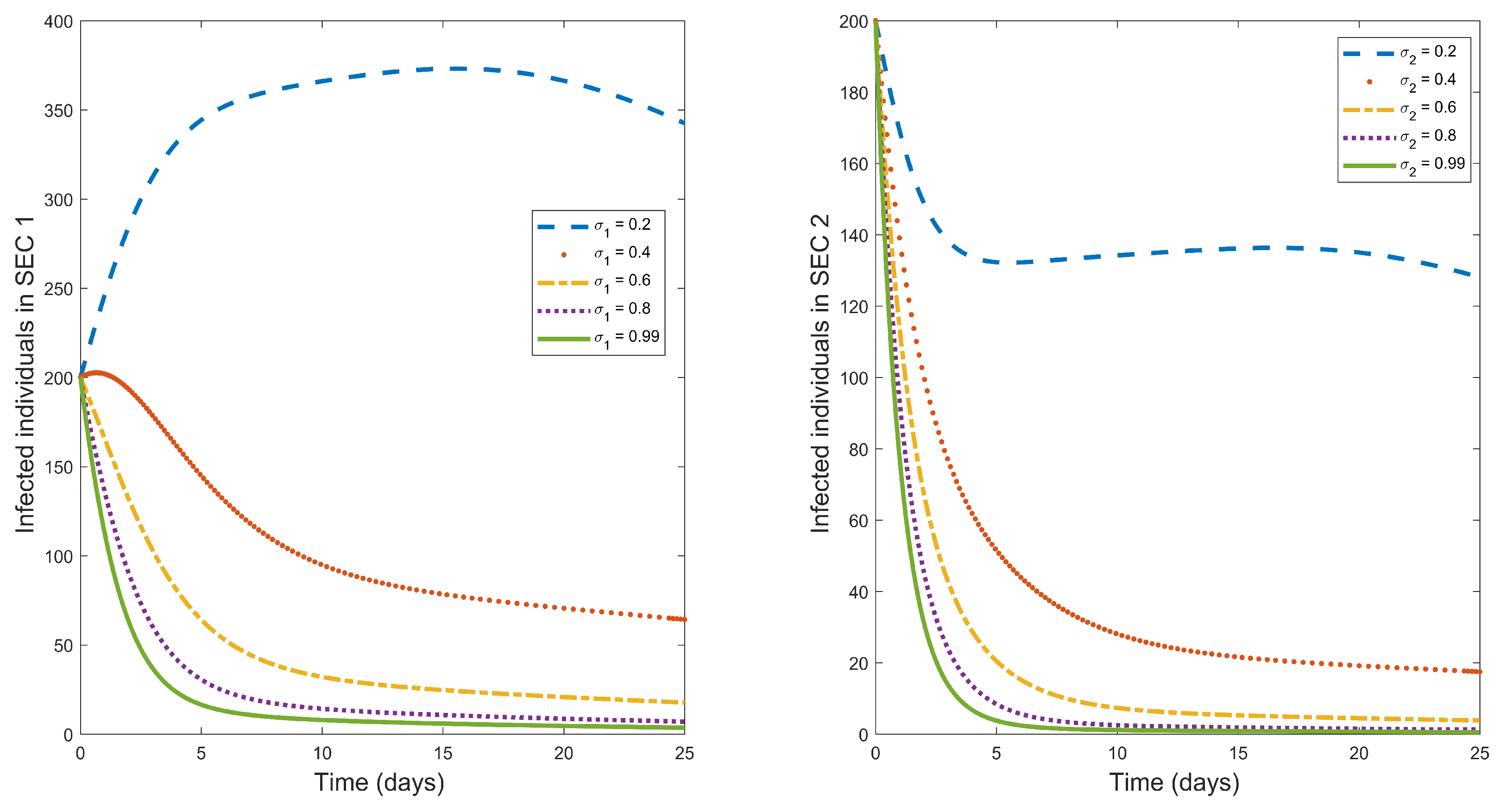
Figure 4.
Plot illustrating the influence of sanitation on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
Figure 4.
Plot illustrating the influence of sanitation on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
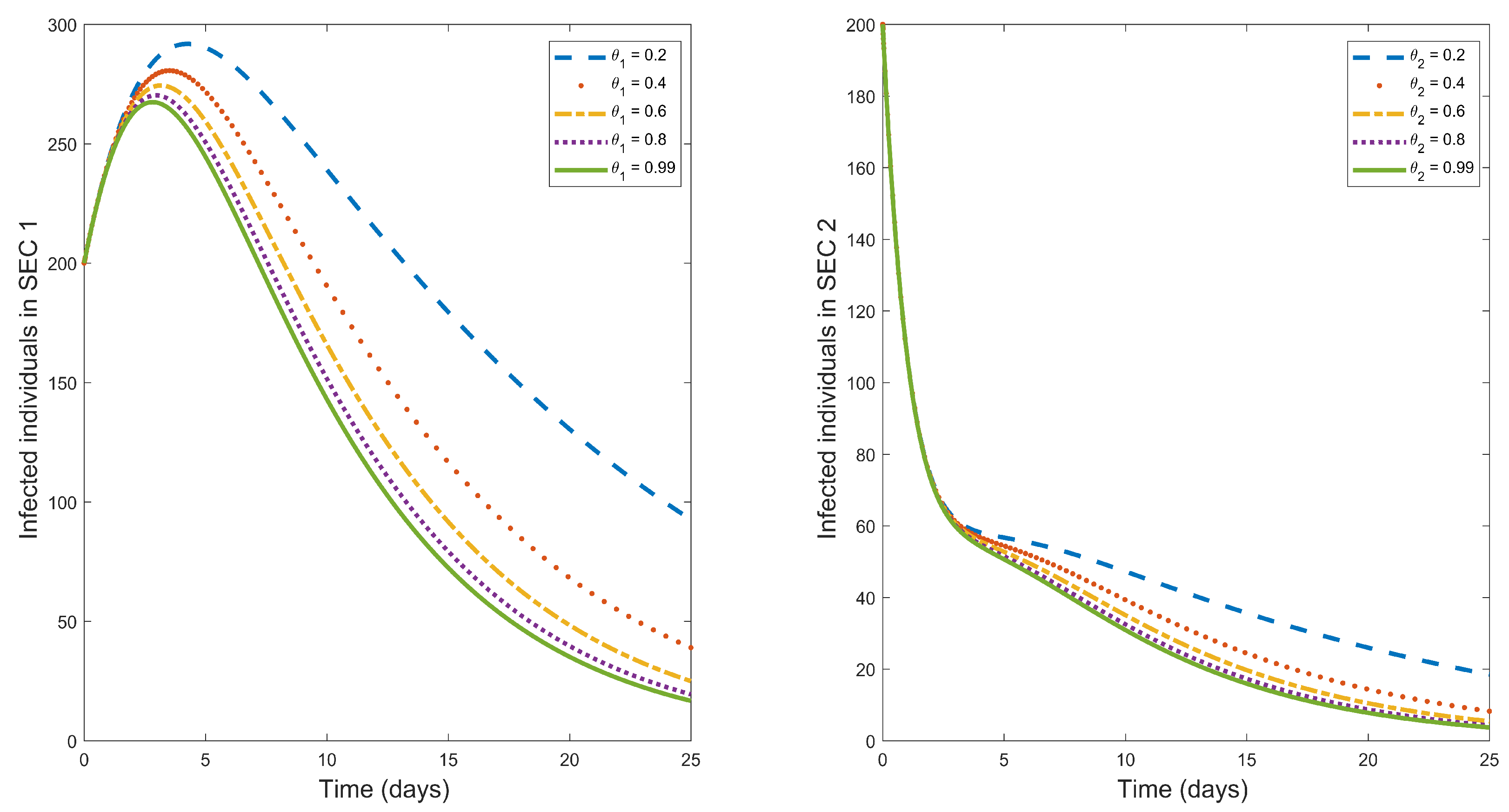
Figure 5.
Plot illustrating the impact of multiple control measures on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
Figure 5.
Plot illustrating the impact of multiple control measures on the dynamics of typhoid fever infections in SEC 1 and SEC 2.
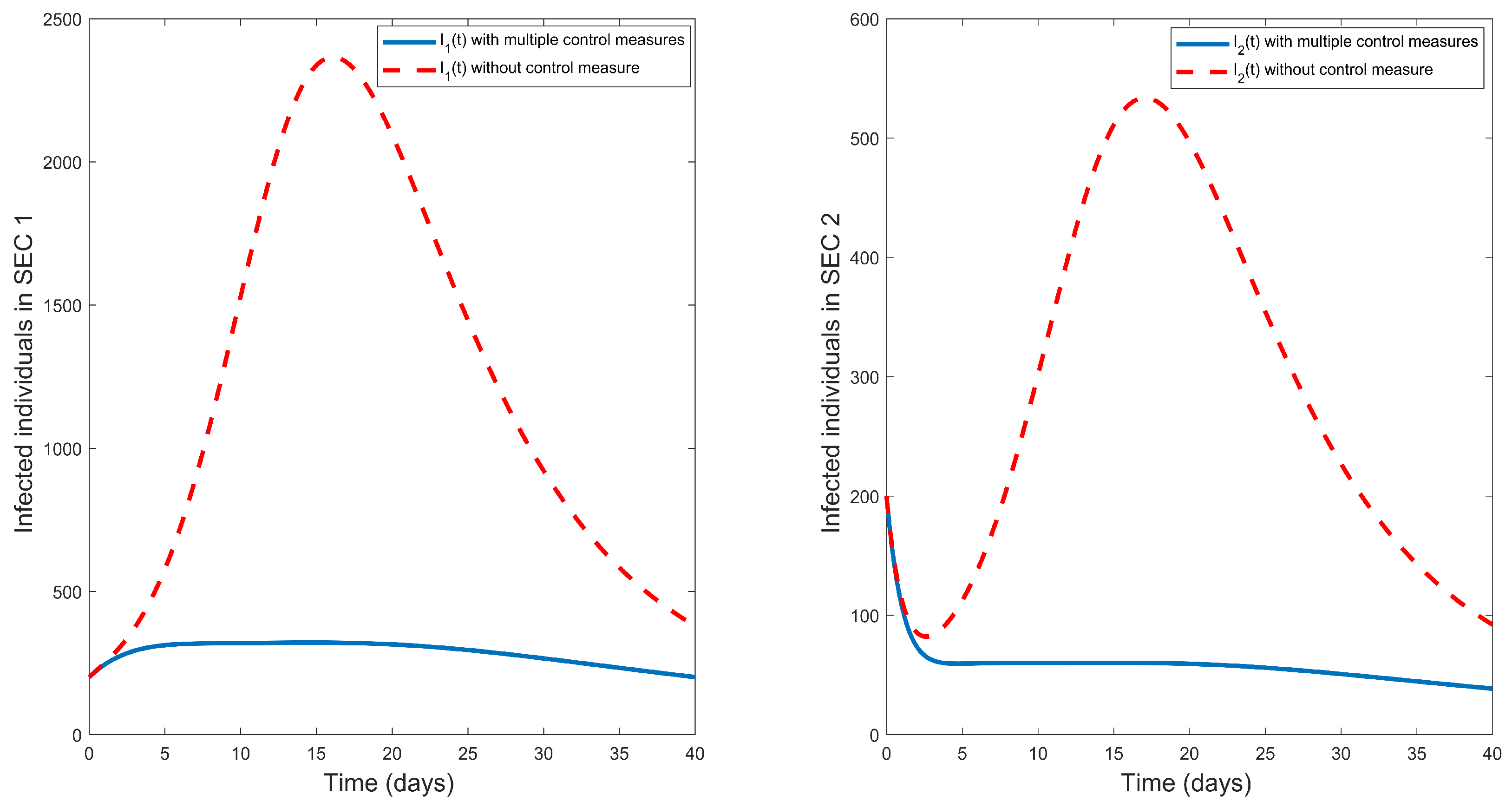
Figure 6.
Plot illustrating the control profiles of the two socioeconomic classes. Figure 6(a) illustrates the control profiles for SEC 1 while Figure 6(b) illustrates control profiles for SEC 2.
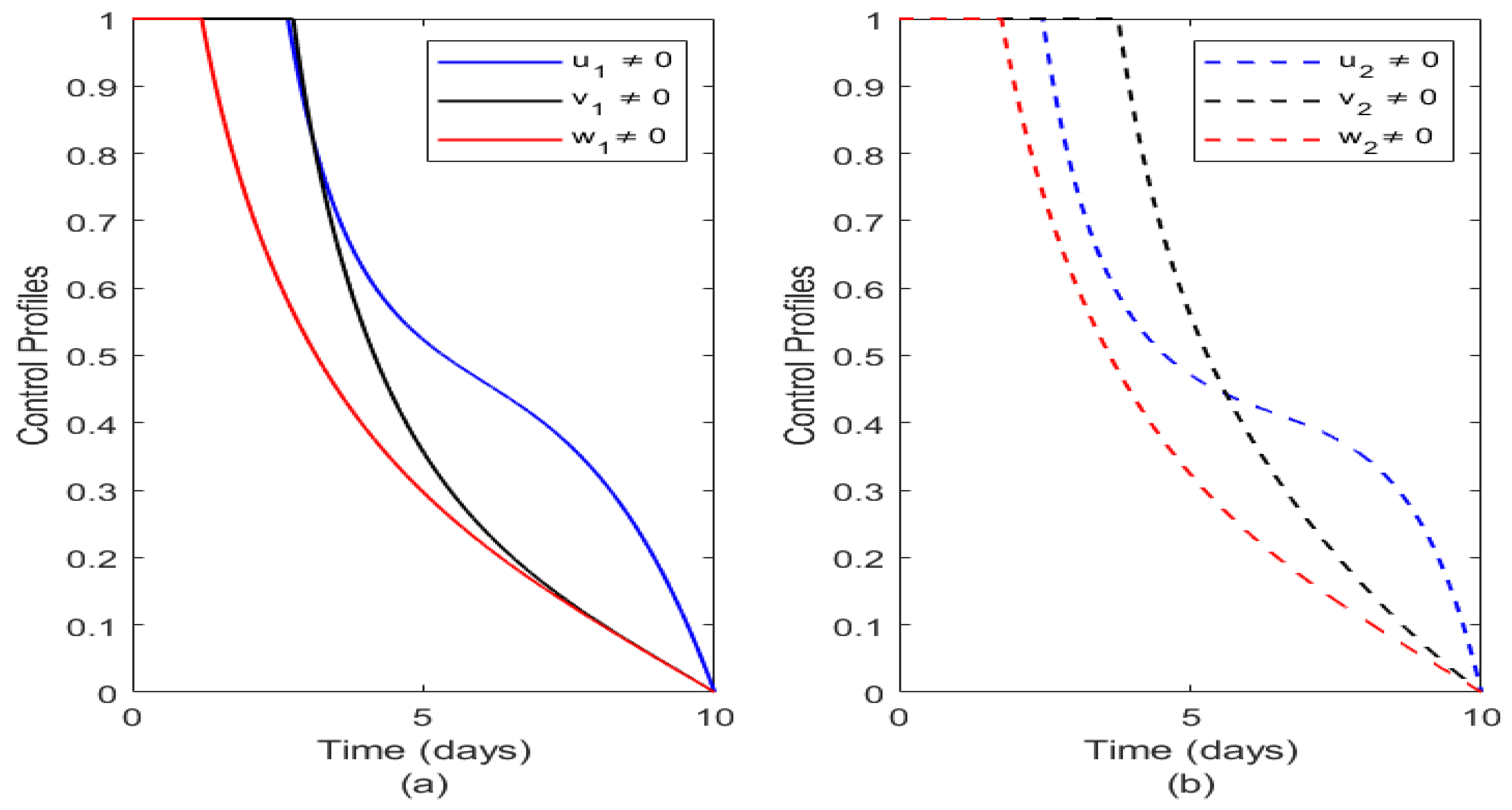
Figure 7.
Plot illustrating effect of optimal control and controls on the two socioeconomic classes. Figure 7(a) illustrates the effect of optimal control and controls on susceptible class of SEC 1 while Figure 7(b) illustrates the effect of optimal control and controls on susceptible class of SEC 2.
Figure 7.
Plot illustrating effect of optimal control and controls on the two socioeconomic classes. Figure 7(a) illustrates the effect of optimal control and controls on susceptible class of SEC 1 while Figure 7(b) illustrates the effect of optimal control and controls on susceptible class of SEC 2.
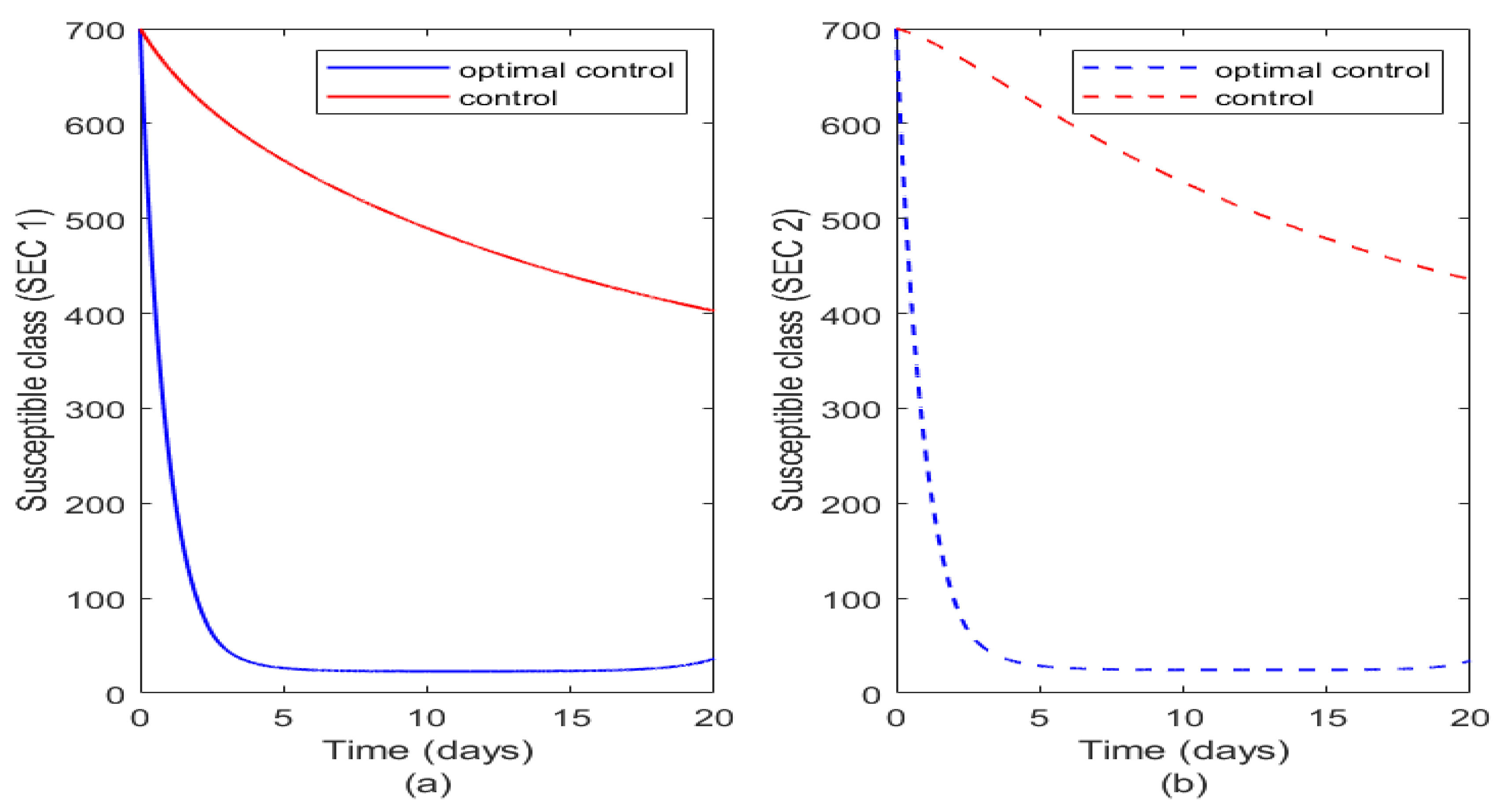
Figure 8.
Plot illustrating effect of optimal control and controls on the two socioeconomic classes. Figure 8(a) illustrates the effect of optimal control and controls on vaccinated class of SEC 1 while Figure 8(b) illustrates the effect of optimal control and controls on vaccinated class of SEC 2.
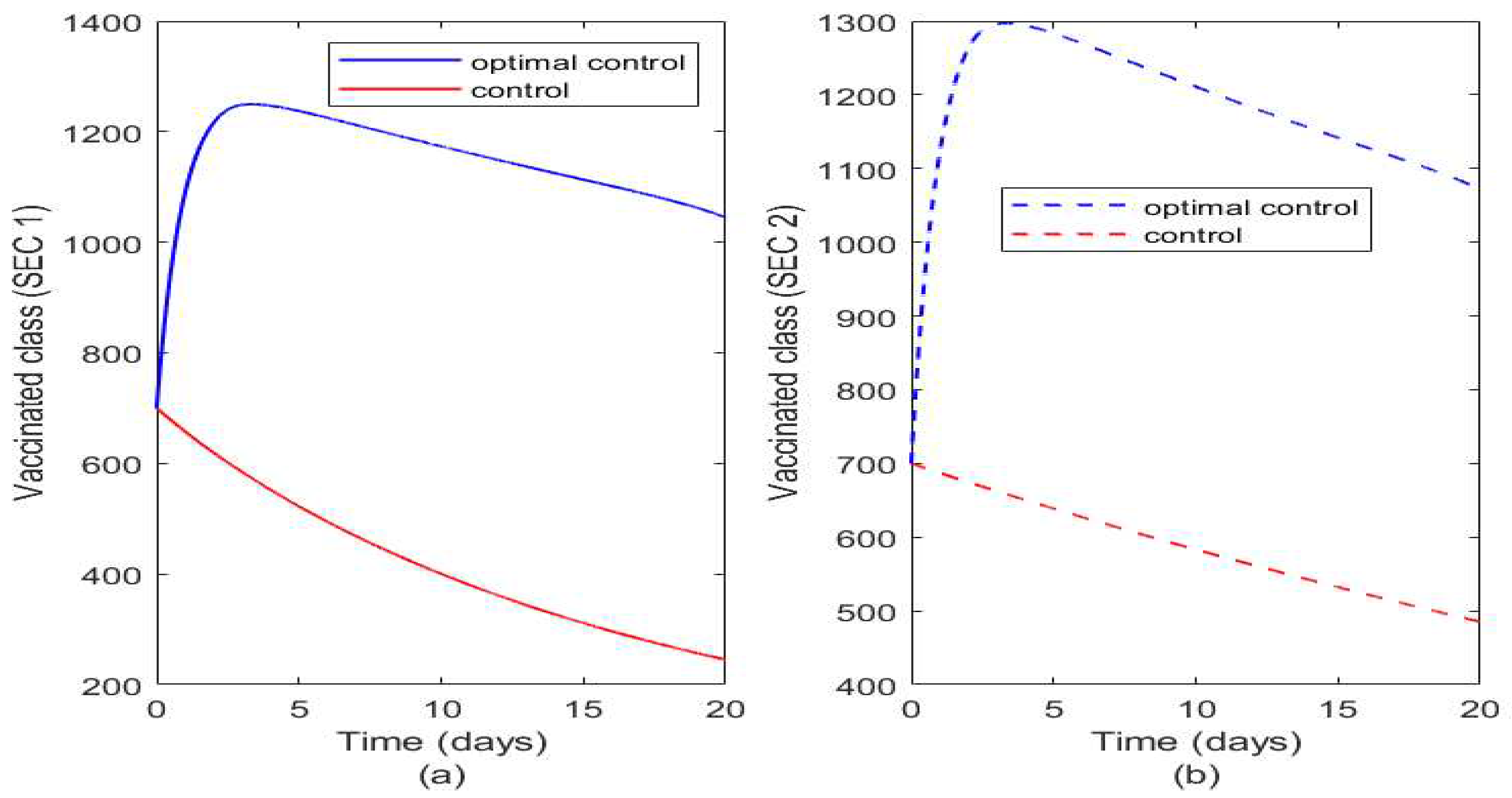
Figure 9.
Plot illustrating effect of optimal control and controls on the two socioeconomic classes. Figure 9(a) illustrates the effect of optimal control and controls on infected class of SEC 1 while Figure 9(b) illustrates the effect of optimal control and controls on infected class of SEC 2.
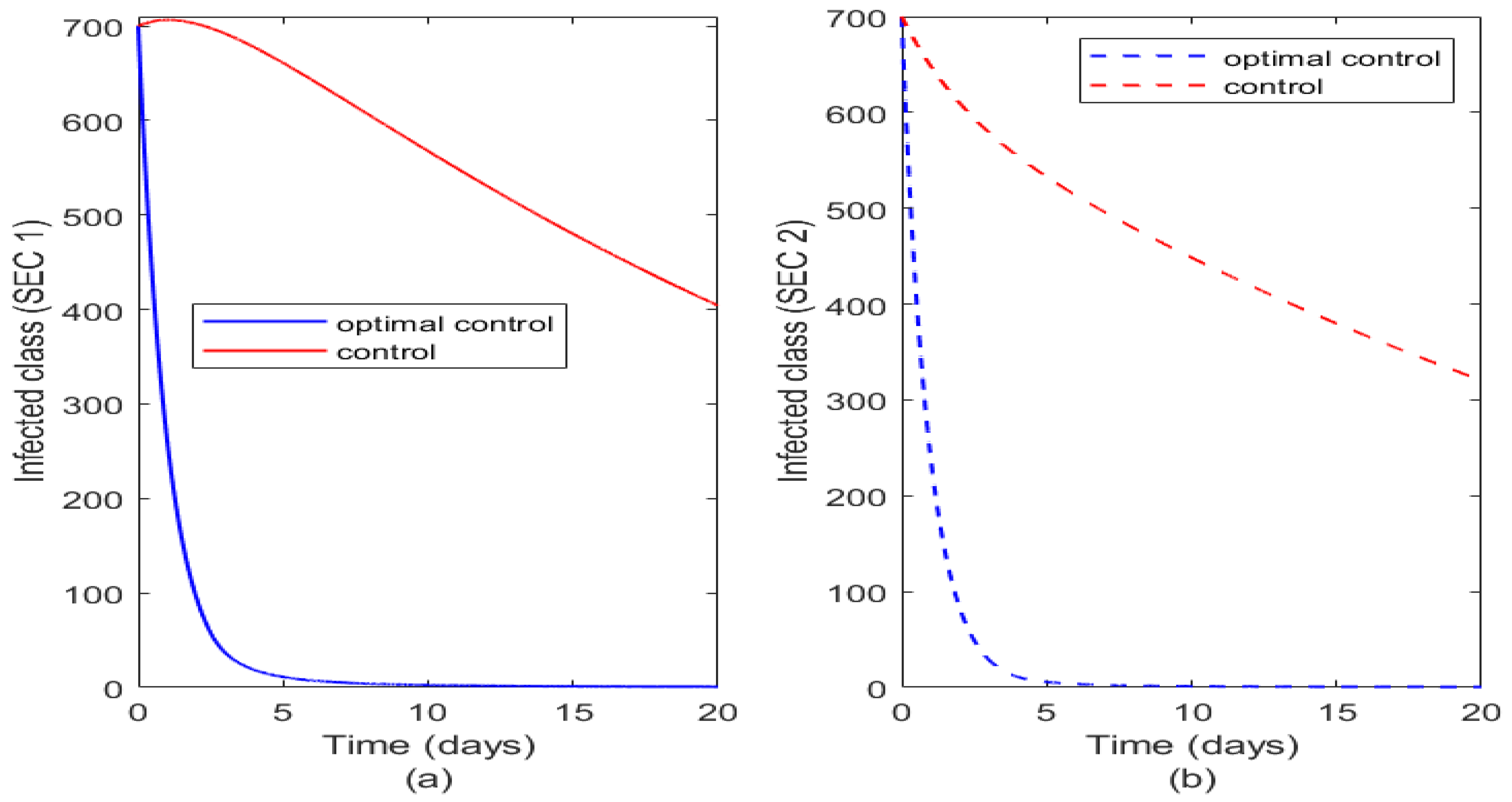
Figure 10.
Plot illustrating effect of optimal control and controls on the two socioeconomic classes. Figure 10(a) illustrates the effect of optimal control and controls on recovered class of SEC 1 while Figure 10(b) illustrates the effect of optimal control and controls on recovered class of SEC 2.
Figure 10.
Plot illustrating effect of optimal control and controls on the two socioeconomic classes. Figure 10(a) illustrates the effect of optimal control and controls on recovered class of SEC 1 while Figure 10(b) illustrates the effect of optimal control and controls on recovered class of SEC 2.
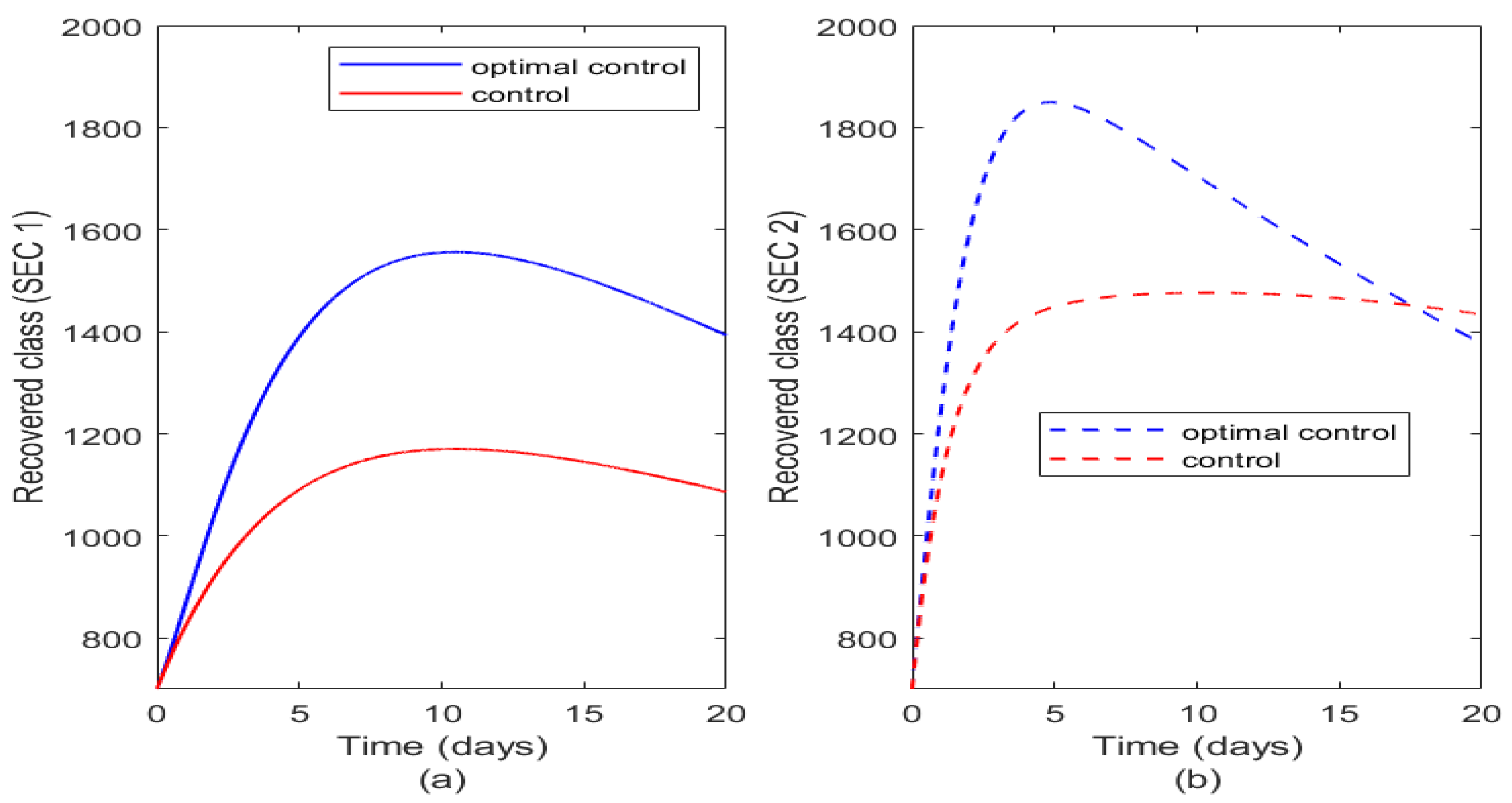
Figure 11.
Plot illustrating effect of optimal control and controls on the two socioeconomic classes. Figure 11(a) illustrates the effect of optimal control and controls on pathogens in the environment of SEC 1 while Figure 11(b) illustrates the effect of optimal control and controls on pathogens in the environment of SEC 2.
Figure 11.
Plot illustrating effect of optimal control and controls on the two socioeconomic classes. Figure 11(a) illustrates the effect of optimal control and controls on pathogens in the environment of SEC 1 while Figure 11(b) illustrates the effect of optimal control and controls on pathogens in the environment of SEC 2.
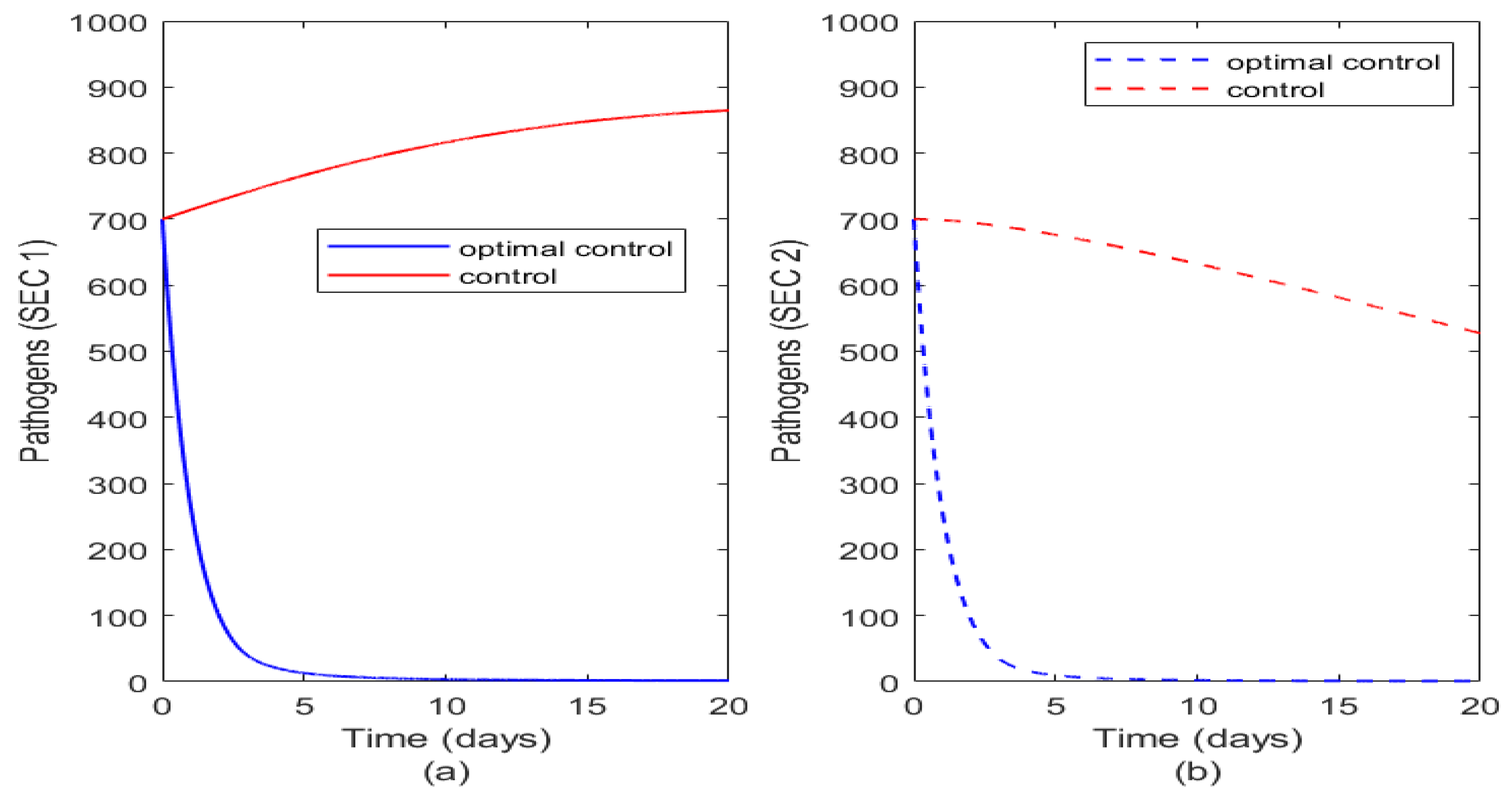
Table 1.
Meaning of variables in model 1
Table 1.
Meaning of variables in model 1
| Variable | Meaning |
| Total population of individuals in SEC i | |
| Susceptible population in SEC i | |
| Vaccinated population in SEC i | |
| Infected population in SEC i | |
| Treated population in SEC i | |
| Recovered population in SEC i | |
| Pathogens in the environment in SEC i |
Table 2.
Meaning of parameters used in model 1
Table 2.
Meaning of parameters used in model 1
| Parameter | Meaning |
| Contact rate of susceptible with infected population in SEC i | |
| Contact rate of susceptible population with pathogens in SEC i | |
| Natural mortality rate of humans in the SEC i | |
| Vaccination rate of individuals in the SEC i | |
| Efficacy of vaccination in the SEC i | |
| Natural recovery rate of infected population in SEC i | |
| Recovery rate of infected population due to treatment in SEC i | |
| Treatment rate of infected population in SEC i | |
| Rate at which recovered population becomes susceptible in SEC i | |
| Shedding rate of by the infected population in SEC i | |
| Natural death rate of pathogens in the environment | |
| Decay rate of due to sanitation | |
| Movement rate of susceptible population from to | |
| Movement rate of infected population from to |
Table 3.
Parameter values used for the numerical illustrations
| Symbol of the parameters | Parameter values | Source |
|---|---|---|
| 0.0200 | [18,23] | |
| 0.00002 | Estimated | |
| 1.6 | Estimated | |
| 0.4 | Estimated | |
| 0.00001 | Estimated | |
| 1.6 | Estimated | |
| 0.4 | Estimated | |
| 0.001 | Estimated | |
| 0.4 | Estimated | |
| 1.6 | Estimated | |
| 0.0445 | [21] | |
| 0.4 | Estimated | |
| 1.6 | Estimated | |
| 0.0333 | [18,21] | |
| 0.20 | [17] | |
| 0.20 | [17] | |
| 0.20 | [17] | |
| 0.20 | [17] | |
| 0.78 | [34] | |
| 0.4 | Estimated | |
| 1.6 | Estimated | |
| 0.20 | Estimated | |
| 0.80 | Estimated | |
| 0.04 | Estimated | |
| 0.16 | Estimated | |
| 0.18 | Estimated | |
| 0.72 | Estimated | |
| [21] | ||
| 1.6 | Estimated | |
| 0.4 | Estimated |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





