Preprint
Review
From Shallow to Deep Bioprocess Hybrid Modeling: Advances and Future Perspectives
Altmetrics
Downloads
172
Views
152
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.docx (1.99MB )
This version is not peer-reviewed
Submitted:
29 September 2023
Posted:
04 October 2023
You are already at the latest version
Alerts
Abstract
Deep learning is emerging in many industrial sectors in hand with big data analytics to streamline production. In the biomanufacturing sector, big data infrastructure is lagging comparatively to other industries. A promising approach is to combine Deep Neural Networks (DNN) with prior knowledge in Hybrid Neural Network (HNN) workflows that are less dependent on the quality and quantity of data. This paper reviews published articles over the past 30 years on the topic of HNN applications to bioprocesses. It revealed that HNNs were applied to various bioprocesses, including microbial cultures, animal cells cultures, mixed microbial cultures, and enzyme biocatalysis. HNNs were mainly applied for process analysis, process monitoring, development of software sensors, open- and closed-loop control, batch-to-batch control, model predictive control, intensified design of experiments, quality-by-design, and recently for the development of digital twins. Most previous HNN studies combined shallow Feedforward Neural Networks (FFNNs) with physical laws, such as macroscopic material balance equations, following the semiparametric design principle. Only recently, deep HNNs based on deep FFNNs, Convolution Neural Networks (CNN), Long Short-Term Memory (LSTM) networks and Physics Informed Neural Networks (PINNs) have been reported. The biopharma sector is currently a major driver but applications to biologics quality attributes, new modalities, and downstream processing are significant research gaps.
Keywords:
Subject: Engineering - Bioengineering
1. Introduction
The use of mathematical models for bioprocess monitoring, optimization and control has a long history in tandem with the progress in computation power and process analytical technology (Noll & Henkel, 2020). As early as mid-70s, Cooney et al. reported an unstructured bioprocess model (elemental material balances combined with macroscopic material balances and off-gas analysis) for computer-based bioprocess monitoring and control (Cooney et al., 1977). Over the years, bioprocess models became more detailed and computationally intensive with the emergence of e.g. genome-scale models (GEMs) and Computational Fluid Dynamics (CFD) (Noll & Henkel, 2020). With the advent of Industry 4.0, mathematical modeling is taking a prominent role in biomanufacturing more than ever before (A. Udugama et al., 2021). Companies are investing on bioprocess Digital Twins (DT) that rely on high-fidelity mathematical models with different levels of integration with the physical process. Machine Learning (ML) techniques are being applied on large collections of biological and process data to extract valuable process insights (Yang et al., 2023). Historically, bioprocess modeling has been hindered by the lack of fundamental knowledge compared to other engineering fields. Due to its intrinsic mechanistic complexity, ML techniques are gaining popularity for bioprocess digitalization (e.g. (Helleckes et al., 2023; Mowbray et al., 2021, 2022).
ML is a subfield of Artificial Intelligence (AI) dedicated to data-based modeling methods and algorithms that are able to learn with experience (Mitchell, 1997). The “learning with experience” feature is at the heart of the Industry 4.0 smart factories vision. Within ML, Artificial Neural Networks (ANNs) are currently the most popular technique in bioprocess, followed by ensemble learning, multivariate data analysis, support vector machines and gaussian processes (Mowbray et al., 2021). The emergence of deep learning with the publication of the adaptive moment estimation method (ADAM) method (Kingma & Ba, 2015), which allowed to effectively train DNNs, has significantly contributed to their growing interest for process digitalization (Kor et al., 2023). Despite their growing popularity, DNNs have several disadvantages in relation to mechanistic modeling. Due to the typically large number of parameters, they require large data sets (big data) for training. DNNs trained on sparse and noisy data are prone to overfitting and poor generalization (Bejani & Ghatee, 2021). They are less transparent as their structure and parameters have no physical meaning. Moreover, they often violate first principles, such as mass or energy conservation laws, due to their loose structure and their overfitting propensity.
In the case of bioprocess modeling, it is rarely the case that prior knowledge or process data are sufficient per se to develop a reliable process model. To overcome this limitation, some authors have proposed methods to combine ANNs with prior knowledge in HNN modeling workflows. Psichogios and Ungar (1992) proposed the combination of ANNs with First Principles equations to model a fed-batch bioreactor. The HNN model consisted of a shallow feedforward neural network (FFNN) (with a single hidden layer) connected in series with a system of ordinary differential equations (ODEs) derived from macroscopic material balances. The authors compared HNN modeling, Kalman filtering, non-linear programming (NLP), and fully ANN for predictive modeling and state estimation in a fed-batch bioreactor. The indirect training method using the sensitivity equations was introduced in this study, which allowed to train the FFNN by error backpropagation in a similar fashion to a fully FFNN. The authors concluded that extended Kalman filtering and NLP estimation performed better than the hybrid approach when a detailed mechanistic model is available. When, however, the mechanistic model was incomplete or unreliable, then the hybrid model outperformed the Kalman filtering and NLP estimation. The key messages of this pioneering study were: 1) effective indirect training of the FFNN using the sensitivity method, 2) hybrid models are more flexible (better interpolation) than standalone mechanistic models, and 3) hybrid models have better generalization properties and are easier to interpret than standalone neural network models.
Shortly after, Thompson and Kramer (1994) conducted a study in which they applied a hybrid model to a fed-batch penicillin fermentation. The hybrid model consisted of a Radial Basis Function Network (RBFN) connected in parallel with a mechanistic kinetic model to calculate specific kinetic rates. The RBFN worked as residual model to correct the output of the fundamental kinetic model. The kinetic rates were then fed to the bioreactor material balance equations (connected in series with the kinetic models). This pioneering study has framed hybrid models as parallel and/or serial semiparametric mathematical structures that may grow in complexity depending on prior knowledge. They also concluded that less data is required for parameter estimation, and more accurate and consistent prediction of the hybrid model are obtained in comparison to the standalone mechanistic or standalone ANN models (Thompson & Kramer, 1994).
Schubert and co-authors studied the application of hybrid models for state and parameter estimation, feed rate optimization (open-loop control problem), and closed-loop control of a fed-batch baker's yeast process (Schubert et al., 1994a; Schubert et al., 1994b). While Psichogios and Ungar (1992) and Thompson and Kramer (1994) used synthetic data, Schubert et al. (1994a,b) addressed a real-life problem. The hybrid model consisted of a simultaneously serial and parallel structure composed of a FFNN (with 12 inputs, single hidden layer with 10 nodes and 3 outputs), dynamical ODEs and a fuzzy expert system to decide on which process conditions the FFNN predictions are reliable. This pioneering study pointed out for the first time to the need of reliability monitoring of the neural network outputs outside the training domain and to adjust the model accordingly. A simple rule-based expert system was adopted for this purpose. It was concluded that process optimization and control based on hybrid models have a higher benefit/cost ratio than other methodologies.
Since these pioneering studies, a large number of bioprocess HNN modeling studies have been reported, highlighting its potential for bioprocess digitalization. In this paper, we present a systematic literature review and meta-analyses focused on the application of HNNs to bioprocesses. The remaining of this paper is organized as follows. In Section 2, basic hybrid modeling methods are overviewed. In Section 3, the methodology adopted in this review is briefly presented and further detailed as supplementary information. In Section 4, the application of HNNs to bioprocesses is overviewed. Finally, in Section 5 and Section 6 future perspectives are discussed and final conclusions are withdrawn.
2. What is hybrid neural network modeling?
HNN modeling may be defined as the combination of ANNs with prior knowledge in a common mathematical structure. According to Thompson and Kramer (Thompson & Kramer, 1994), there are two main approaches to embody prior knowledge in neural network models, namely design and training approaches. In design approaches the prior knowledge dictates the structure of the model. Prior knowledge is used to define the ANN topology (e.g., number of layers, types of layers, types of nodes), for modularization of the network, or to include nonnetwork mathematical equations (e.g., physical laws) in tandem with the ANN model. In training approaches, the prior knowledge dictates the parameter estimation problem either in the form of variable constraints, network weights constraints or in the definition of the loss function. In both the design and training approaches, the inclusion of prior knowledge reduces the data dependency. In design approaches, the dimension of the parameter space is reduced (i.e., the ANN is smaller and the number of weights is lower) whereas in training approaches the feasible region of the parameter space is reduced. In both cases the training becomes less sensitive to sparce and noisy data and the final model improves its descriptive and predictive power in relation to a standalone ANN model.
2.1. Design approaches
In design approaches the prior knowledge shapes the structure of the HNN model. Design approaches may be further subdivided into modular and semiparametric design. In modular design, the overall model is decoupled into smaller interconnected modules. A biochemical process typically comprehends several interconnected unit operations. Instead of a large ANN to describe the full process, smaller ANNs may be interconnected to match process topology (prior knowledge). Whereas in a single ANN all input nodes are connected to all output nodes, in modular ANNs the connectivity is sparser, the number of parameters is reduced and therefore the data requirements are also reduced. The modular ANN model is also more transparent as the input/outputs variables of the modules have physical meaning. The hierarchical neural network model proposed by Mavrovouniotis and Chang (1992) is an example of modular ANN design (Mavrovouniotis & Chang, 1992). A more recent example is the knowledge-based ANN concept proposed by (Nagarajan et al., 2019).
The most frequently reported approach is semiparametric design (Figure 1A,B), in which physical laws are directly incorporated in the model structure. Instead of a large ANN, a smaller one is combined with physical laws in the form of a semiparametric model. Semiparametric models combine parametric and nonparametric functions in the same model structure. Parametric functions are derived from prior knowledge of First-Principles, well-established mechanisms and/or empirical correlations. They have a fixed mathematical structure and a fixed number of parameters with physical interpretation. On the contrary, the ANNs are nonparametric functions entirely derived from process data. They have a loose structure without physical interpretation. Both model components are trained together.
Semiparametric HNN models may be classified as serial or parallel (Figure 1A,B). In serial structures (Figure 1A), the parametric equations (prior knowledge) cover only some parts of the process. The ANN has the job of learning from data the cause-effect relationships of those process parts lacking prior knowledge. One example of a serial semiparametric structure is the bioreactor model proposed by (Psichogios & Ungar, 1992), where a FFNN (nonparametric model that calculates bioreaction kinetics) is connected in series with macroscopic material balance equations (parametric model). Other examples are the general bioreactor hybrid model (Oliveira, 2004) and the Neural Ordinary Differential Equations (Neural ODEs) structure (Chen et al., 2018), (Rackauckas et al., 2020).
In the case of parallel semiparametric structures (Figure 1B), a full parametric model stemming from prior knowledge exists that, however, is not sufficiently accurate to describe the process. The ANN runs in parallel to compensate for the parametric model inaccuracies. The parametric model takes priority in describing the process. Firstly, the parametric model parameters are estimated to minimize the model-process mismatch. Then the residuals of the parametric model are calculated over the data input space. If the residuals contain relevant information beyond the noise level, an ANN is trained to extract cause-effect relationship from the parametric model residuals. The size of the ANN compensator is inversely proportional to the explained data variance by the parametric model. In limit, if the explained variance is sufficiently high then the ANN compensator is not needed. If the explained variance is negative, then the parametric model should be removed since a standalone ANN will perform better than the hybrid structure. Examples of parallel semiparametric hybrid models are provided by e.g. Côté et al. (1995), (Piron et al., 1997) and (Peres et al., 2001). The bioreactor model proposed by Thompson and Kramer (1994) is simultaneously parallel and serial. The biologic kinetics are described by a Monod type kinetic model (parametric) connected in parallel with a RBFN (nonparametric) compensator. The RBFN performs an additive correction of the Monod type kinetic model outputs. The corrected kinetics are then connected in series with macroscopic material balances (parametric) in a similar way to the model reported by (Psichogios and Ungar, 1992).
2.2. Training approaches
Prior knowledge may also be incorporated in HNN models through the training method. Prior knowledge may dictate constraints on process variables, e.g. concentrations or reaction rates of irreversible reactions must be positive. Variable inequality constraints, network weights inequality constraints and loss function regularizers may be introduced in the training method to enforce such desired output behavior (Thompson & Kramer, 1994). Several methods have been developed to enforce ANN output behavior such as monotonicity, convexity, concavity or smoothness by adding parameter constraints and loss function regularizers (Richman & Wuthrich, 2023), (Rosca et al., 2020). More recently, Physics Informed Neural Networks (PINNs) have emerged for modeling CFD problems based on the Navier Stokes equations (Raissi et al., 2019) or Partial Differential Equations (PDEs) in general. The innovative aspect of PINNs is that exact physical equations are embodied in a pure ANN structure via the training approach (Figure 1C). PINNs apply a DNN to parameterize state variables over independent variables (time and spatial coordinates). Automatic Differentiation (AD) is applied to obtain partial derivatives of the state variables in time and spatial coordinates and to calculate a PDEs agreement error. Two different sets of residuals are minimized during the training process: (i) the residuals between calculated and measured state variables are minimized, (ii) simultaneously, the Navier Stokes PDEs agreement residuals are minimized. PINNs were shown to converge to PDEs solutions obtained by numerical discretization methods. Moreover, PINNs were shown to seamlessly integrate data and mathematical models in flow problems in a straightforward way (Jin et al., 2021). A key advantage of PINNs in relation to semiparametric HNNs is that numerical integration, or any other numerical method inherent to the parametric model, are avoided. This may be a substantial advantage in the case of PDEs and stiff systems of ODEs. A possible disadvantage is however that the exact mapping of the physical laws to the ANN structure is not guaranteed nor that the physical laws will still be obeyed in case of extrapolation.
2.3. General bioreactor hybrid model
Since the pioneering works by (Psichogios & Ungar, 1992), (Thompson & Kramer, 1994), (Schubert, Simutis, et al., 1994; Schubert, SIMUTIS, et al., 1994), attempts were made to propose a bioreactor HNN structure that covers a wide range of problems (Oliveira, 2004; Teixeira et al., 2007; von Stosch et al., 2011, Pinto et al., 2019, 2022). The general bioreactor hybrid model (Figure 2) is a serial semiparametric structure that combines an ANN with a system of ODEs with information feedback. Prior knowledge is represented by a system of ODEs derived from macroscopic material balances and/or intracellular material balances. These may be divided in a state-space model and a measurement model that computes observable process outputs. The ANN is used to model cell properties lacking fundamental knowledge as function of the process state and exogenous inputs. The model outputs are compared with training examples for supervised learning.
As reviewed in the next section, most of previous studies have adopted a shallow HNN configuration based on 3-layered FFNNs with a single hidden layer with tanh activation function connected in series with material balance equations. Shallow HNNs are typically trained in a least squares sense employing the Levenberg-Marquardt optimization algorithm. The computation of gradients follows the indirect sensitivity method originally proposed by (Psichogios & Ungar, 1992) and detailed by (Oliveira, 2004). The sensitivity equations are required because the observable model outputs are not directly linked to the ANN outputs. Cross-validation is adopted to prevent overfitting. Recently, the general bioreactor HNN has been extended to deep multilayered FFNNs and deep learning (Pinto et al., 2022, Pinto et al., 2023a, Pinto et al 2023b). Multiple hidden layers with rectified linear unit (ReLU) activation functions were adopted connected in series with material balance equations. The deep learning ADAM algorithm (Kingma & Ba, 2015) was applied to train the HNN in a weighted least squares sense. The objective function gradients were computed by modified semidirect sensitivity equations, which were shown to reduce the CPU time (Pinto et al., 2022). Stochastic regularization based on random training examples and ANN weights dropout was adopted for avoiding overfitting. Deep HNN was shown to generalize better than shallow HNN modeling.
3. Systematic literature review
The Preferred Reporting Items for Systematic reviews and Meta-Analyses (PRISMA) methodology was adopted in order to have a more structured vision of the literature produced on the application of HNNs to bioprocesses. The articles were selected based on a selection algorithm and the PRISMA flow diagram instructions (Page et al., 2021), which are divided in four categories:
- Scopus: The algorithm initially retrieved 481 publications from the Scopus database and after screening 94 relevant cases were obtained.
- Web of Science (WoS): The algorithm initially retrieved 251 publications from the WoS database, and after screening 84 relevant cases were obtained.
- From the well-known authors’ search, 825 publications were extracted, and after screening 66 relevant cases were obtained.
- From the backward citation, 74 relevant cases were obtained.
After merging the articles and deletion of duplicates, 185 publications were selected for keyword analysis, covering journal and conference papers published before September 2023. Figure 3 shows the evolution of the number of papers over time. The first paper was in 1992 (Psichogios & Ungar, 1992), followed by consistent growth, a peak in 2004 (15 papers) and a decline until 2015-16. The number of papers is surging again.
Among the 185 papers, the ten most cited papers listed in Table 1. Keyword analysis showed that HNNs were first applied to microbial cultures for the production of bakers’ yeast, bioethanol and antibiotics. In the last decade, keywords such as “design of experiments”, “critical process parameters”, “process analytical technology”, “digital twins”, and “big data” have appeared. These are now hot topics for the application of HNNs to bioprocesses, especially in the biopharma sector. Only recently the “deep learning” keyword has appeared explicitly or implicitly in connection with hybrid modeling (Bangi et al., 2022; Cheng et al., 2021; Merkelbach et al., 2022; Pinto et al., 2023a, Pinto et al 2023b; Pinto et al., 2022; Pinto et al., 2023c; Shah et al., 2022). Further details of the PRISMA analysis are provided as supplementary material. In what follows, the produced literature is critically overviewed.
4. Applications of HNNs for bioprocess modeling
4.1. Microbial culture
In the early years, hybrid models were mainly applied to traditional microbial processes such as Baker’s yeast (Schubert, Simutis, et al., 1994; Schubert, SIMUTIS, et al., 1994), antibiotics production (Preusting et al., 1996) and beer/bioethanol production (Costa et al., 1998, 1999; Da Silva Henriques et al., 1999; Harada et al., 2002; Meleiro & Maciel Filho, 2000). Preusting et al. (1996) addressed the historical penicillin process at the production scale (Preusting et al., 1996). The hybrid model structure was similar to Schubert et al. (1994) (Schubert, Simutis, et al., 1994), using an expert system to weight the outputs of the neural network and fundamental kinetic model depending on the reliability of the FFNN. This model was used to optimize (open-loop control problem) the large-scale production of penicillin using the HYBNET software.
Simutis et al. (1998) developed a simple hybrid model of S. cerevisiae showing successful predictive modeling of Diacetyl formation during beer production in a production plant (Simutis et al., 1997). In the study by da Silva Henriques et al (1999) a hybrid model for the alcoholic Zymomonas mobilis fermentation was developed (Da Silva Henriques et al., 1999). The model consisted of a 3-layers FFNN (describing the kinetic rates) connected in series with macroscopic mass balance equations. Meleiro et al. (2000) applied a hybrid model for dynamic modeling and control of an industrial-scale S. cerevisiae fermentation process for bioethanol production. They combined a 3-layers FFNN with macroscopic material balances and simple Monod-type kinetics. The hybrid model provided online estimations of key process state variables and kinetic parameters based on reliable and easily accessible measurements. It enabled the implementation of efficient automatic control strategies (Meleiro & Maciel Filho, 2000). Recently, hybrid modeling of bioethanol production was revisited by Da Silva Pereira et al. (2021) (da Silva Pereira et al., 2021). Bioethanol was produced by a flocculating yeast grown on cashew apple juice. A hybrid model was built consisting of three shallow FFNN combined with mass balance equations (biomass, substrate, and product). Particle swarm optimization (PSO) was adopted to optimize bioethanol production (open-loop/dynamic optimization problem) at aid of the hybrid model, thereby achieving high yield and productivity.
Hybrid modeling of the Pichia pastoris yeast for recombinant protein production was first addressed by Ferreira et al. (2014). The authors applied a serial hybrid model (3-layers FFNN combined with material balance equations in series) for dynamic modeling of P. pastoris GS115 expressing scFv in a pilot 50L bioreactor. The hybrid model was subsequently employed for iterative batch-to-batch control showing a fourfold titer improvement after 4 optimization cycles. Batch-to-batch control using hybrid models and evolutionary programming was addressed in a simulation study by Teixeira et al. (2006) (A. P. Teixeira et al., 2006). Constraining the optimization design space depending on the reliability of the FFNN was shown to be essential to ensure stable convergence to the global optimum. Another important finding was that the hybrid model should not include “wrong” mechanisms or otherwise an off-set to the global optimum is observed. Recently, hybrid modeling of P. pastoris was revisited by Pinto et al. (2022) using state-of-the-art deep learning methods (Pinto et al., 2022). FFNN networks with varying depths and ReLU nodes were combined with material balance equations in the form of deep hybrid models. Deep learning techniques, namely the ADAM, stochastic regularization and depth-dependent weights initialization were evaluated in a hybrid modeling context. The semi-direct training method was proposed to reduce the CPU time of the sensitivity equations, which then become independent of the size and depth of the neural network. The CPU time for training deep HNN models was significantly reduced.
Recombinant E. coli was addressed by von Stoch et al. (2016, 2017), who introduced the methodology of intensified design of experiments (iDoE) coupled with dynamic hybrid modeling (von Stosch et al., 2016b; von Stosch & Willis, 2017). This approach was applied to an industrial E. coli process expressing a therapeutic protein. iDoE is a dynamic design of experiments based on intraexperiment step changes of design factors (such as pH, temperature and feed rates) and dynamic modeling. Contrary to standard DoE, different combinations of process conditions are explored step-wise in the same experiment. A serial hybrid dynamic model (FFNN + Material balance equations) was adopted to capture the dynamic relationship between step-wise variations of design factors and process response variables. The authors concluded that intraexperimental variations of process conditions could reduce the number of experiments by a factor, which in limit would be equivalent to the number of intraexperimental variations per experiment. Bayer et al. (2020) further explored the iDoE methodology in a 20L fed-batch E. coli process expressing hSOD. The hybrid model could accurately predict the endpoint biomass concentration and product titer as well as the respective time-resolved trajectories (Bayer, von Stosch, et al., 2020). These studies emphasized the potential of hybrid modeling to address the challenges of Process Analytical Technology (PAT) and Quality by Design (QbD) in the biopharma sector.
Hybrid modeling of biopolymers production by bacteria has been addressed in several studies (Morabito et al., 2021; Novak et al., 2015; Patnaik, 2010; Peres et al., 2004). One of the first studies addressing Polyhydroxyalkanoates (PHA) production by bacteria was reported by Peres et al. (2004). A competitive hybrid structure was applied where a gating system was trained with the expectation maximization (EM) algorithm to learn in which regions of the input space the FFNN performs better than the competing mechanistic model. This hybrid approach was further detailed in a follow-on paper applied to baker’s yeast (Peres et al., 2008). Production of Poly-β-hydroxybutyrate (PHB) by Ralstonia Eutropha has been addressed by Patnaik et al. (2008). The authors demonstrated the superiority of the hybrid model (H-model) to the neural-cum-dispersion model (D model) and to the neural network model (N-model). Recently, Luna et al. developed a HNN model with four layers of five nodes to describe the continuous production of PHA by Pseudomonas Putida GPo1(Luna et al., 2021). The hybrid model was shown to describe the process in a wide range of operating conditions, including single and dual nutrient-limited growth conditions.
4.2. Animal cell culture
Animal cells are ubiquitous in the biopharmaceutical industry and are getting momentum in the hybrid modeling community (Bayer, Striedner, et al., 2020; Bayer, von Stosch, et al., 2020; Krippl et al., 2020; Narayanan, Behle, et al., 2020; Pirrung et al., 2017; von Stosch, Davy, et al., 2014; von Stosch et al., 2016a). One of the first hybrid modeling studies of mammalian cell culture was reported by Dors et al. (1995) (Dors et al., 1995). Fu and Barford (1996) reported one the first consistent HNN model applications to animal cells' monoclonal antibody production. The HNN model predicted substrate consumption, toxic byproduct accumulation, cell growth, cell composition, and metabolic product formation (Fu & Barford, 1996). The HNN produced better result compared to the standalone mechanistic model or artificial neural network model. Teixeira et al. (2005) developed a hybrid model for BHK-21 cultures expressing the fusion glycoprotein IgG1-IL2 (A. Teixeira et al., 2005). The model consisted of a simultaneously serial and parallel structure for dynamic predictive modeling. A shallow FFNN was connected in parallel with a fundamental kinetic model. The experience measure technique was adopted to automatically switch between the fundamental model and FFNN predictions depending on the reliability of the latter. The hybrid model was used to optimize the feeding strategy (dynamic optimization / open-loop control problem) of glucose and glutamine. Later, Teixeira et al. (2007) extended the hybrid model to incorporate knowledge of the metabolic network using the concept of elementary flux modes (A. P. Teixeira, Alves, et al., 2007). The resulting hybrid model predicted simultaneously extracellular concentrations and intracellular fluxes. The model was adopted for on-line optimizing control, which delivered a 10% titer increase in relation to the control experiment. This was one of the first attempts to include metabolic detail in hybrid models. Recently, Maton et al. (2022) applied a similar elementary flux modes hybrid model to a hybridoma HB-58 cell line (Maton et al., 2022). Aehle et al. (2010) developed a serial hybrid model for on-line estimation of viable cell concentration in fed-batch CHO cultures (Aehle et al., 2010). The authors concluded that the hybrid model outperformed other data-based and model-based techniques. Narayanan et al. (2019) developed a serial hybrid model (FFNN with one hidden layer connected to material balances) for a CHO fed-batch process (81 batches in a 3.5-liter bioreactor) (Narayanan et al., 2019). They used the mass balance equation as the mechanistic part of the hybrid model to predict the process variables (substrate and metabolite concentration, cell density, and product concentration). The hybrid model showed high predictive power of CHO dynamics using only the initial and process conditions as inputs, in comparison to other statistical modeling methods. Kotidis et al. (2020) developed a complex serial hybrid model to describe N-glycosylation of recombinant proteins in CHO cultures (Kotidis & Kontoravdi, 2020). The hybrid model utilized the extracellular concentration of metabolites and certain amino acids as inputs. A metabolic module calculated the specific growth rate and the specific antibody production rate. These rates were then fed to a nucleotide sugar donors module that calculated the respective intracellular concentration. The nucleotide sugar donors concentrations were then inputted to a 4-layers FFNN, which calculated glycans distribution. The overall hybrid model simulated the glycoforms distribution of four different proteins (two IgGs and two fusion proteins, EPO-Fc and Fc-DAO) expressed in three CHO cell lines (GS-CHO, CHO–K1, CHO–S). This study was one of the first addressing hybrid modeling of glycosylation. As follow up of the previous E. coli study, Bayer et al (2021) applied the same iDoE/hybrid modeling approach to reduce the validation burden of CHO cultures in a PAT and QbD context (Bayer et al., 2021). They also investigated the transferability of hybrid modeling along process scales (300 mL shaker-scale and 15 L bioreactor). The authors concluded that the hybrid model trained on 300 mL bolus feeding shake flask DoE could be used to correctly estimate the cell behavior and product formation in a 15 L stirred-tank bioreactor.
4.3. Mixed Microbial Cultures
Mixed microbial cultures (MMC) are of widespread use in waste treatment plants commonly termed as activated sludge. Reducing wastewater treatment costs has long been of interest, and modeling has proven an essential tool to optimize wastewater treatment plants (WWTP). Due to the intrinsic complexity of WWTP, some researchers combined a hybrid artificial neural network with other methods or models to estimate and/or control process parameters. Côté et al (1995) reported one of the first studies where a hybrid model was applied to a WWTP (Côté et al., 1995). A mechanistic model was combined with a three-layer FFNN in parallel. The FFNN was used to extract cause-effect patterns from the mechanistic model residuals, thereby correcting its outputs (residual modeling strategy). The parallel coupling of the mechanistic model with the FFNN provided more accurate simulations of five key variables of the activate sludge process. Zhao et al. (1997) developed a hybrid dynamic model of a Sequencing Batch Reactor (SBR) consisting of a simplified mechanistic model and a FFNN connected in parallel also following the residual modeling approach (Zhao et al., 1997). Anderson et al. (2000) applied different hybrid mechanistic/FFNN models for dynamic modeling of WWTPs and process control (Anderson et al., 2000). They concluded that hybrid models do not necessarily produce superior control results. Sung Lee et al. (2002) applied a parallel hybrid model to a full-scale WWTP (Lee et al., 2002). The authors reported more accurate predictions with good extrapolation properties of the hybrid model compared with other modeling approaches. Fang and Dai (2003) developed a simple hybrid model for chemical oxygen demand (COD) prediction (Fang & Dai, 2003). Azwar et al. (2006) proposed a hybrid FFNN/Proportional Integral controller of dissolved oxygen concentration in a SBR (Azwar et al., 2006). The hybrid control scheme consisted of a basic FFNN controller in parallel with a proportional integral (PI) controller. This approach was shown to outperform other nonhybrid control schemes. Peres et al. (2006) reported a hybrid modular model applied to a phosphorous removal WWTP (Peres et al., 2006). The hybrid model consisted of a mixture of experts (ME) network and a gating system connected in series with material balance equations. This serial/parallel hybrid structure with competing expert networks was trained with the EM algorithm. The final ME network was shown to better represent the cellular kinetics structure, which resulted in higher accuracy and generalization capacity of the hybrid model. Xiao et al. (2020) developed a hybrid model of dark fermentation for biohydrogen production. A NARX-BP hybrid neural network consisting of a two-stage model was developed, which combined NARX (nonlinear autoregressive exogenous) and BP-NN (Back propagation neural networks). The model could predict biogas production with high accuracy (Xiao et al., 2021). Cheng et al. (2021) proposed a complex hybrid model that combined the Activated Sludge model (ASM) (knowledge-based model) and deep neural networks (data-based model) (Cheng et al., 2021). For the latter, a convolutional neural network (CNN) was combined with a long short-term memory network (LSTM). The CNN was used to extract data spatial features whereas the LSTM was used to extract temporal features. The integration of knowledge- and data-based models in parallel was achieved with a FFNN model connected in series. This complex hybrid model was applied to a sewage treatment plant. It showed an improvement in the prediction accuracy in comparison with the typical existing models. The authors could also prove the hybrid model's stability by applying it to different datasets. This paper is one of the first hybrid modeling studies incorporating state-of-the-art deep neural networks and the ADAM training method.
4.4. Enzymatic bio-catalysis
Enzyme reaction mechanism can be quite complex and difficult to model mechanistically. A few studies applied HNNs to enzymatic conversion processes. van Can et al. (1998, 1999) addressed the problem of enzymatic conversion of penicillin G to 6-ami-nopenicillanic acid (6APA) and phenyl acetic acid (PhAH) by the enzyme penicillin acylase (Van Can et al., 1998, 1999). The extrapolation properties of hybrid models combining FFNNs, white-box kinetics and macroscopic material balance equations were investigated. It was concluded that when the macroscopic material balances are correctly formulated, the identification data only cover the amplitude domain of the rate terms without taking into account the future frequency domain of the complete model. Silva et al. (2008) developed a hybrid model of penicillin G acylase immobilized in chitosan for the production of amoxicillin (Silva et al., 2008). Three kinetic models were compared, namely a mechanistic, a semi-empiric, and a hybrid–neural model. It was shown that the hybrid model could accurately predict the reaction rates for conditions where the semi-empiric model failed (e.g. at low substrate concentrations occurring at the end of the fed-batch industrial process). This study did not explicitly consider the reaction-diffusion problem typically occurring in immobilized catalysis.
4.5. Downstream applications
The keyword analysis in this review clearly shows that only a few hybrid modeling publications have addressed downstream unit operations. One of the early studies was that by Piron et al. (1997), who applied a parallel hybrid model to cross-flow microfiltration in a baker’s yeast process (Piron et al., 1997). The hybrid model consisted of a static FFNN connected in parallel with a dynamic material balance equation. They concluded that a recurrent neural network provided better approximation of process dynamics than the hybrid model and questioned the validity of the material balance equation. Santos et al. (2007) developed a similar parallel HNN model to describe the transport of solvents through nanofiltration membranes. The authors concluded that most used mechanistic models are not sufficiently general to cover a wide range of membrane–solvent systems. To overcome this limitation, membrane and solvent molecular descriptors were incorporated in a parallel semiparametric HNN, where a statistic FFNN corrected the outputs of a mechanistic solution-diffusion model (Santos et al., 2007). Rajabzadeh et al. (2012) estimated the filtration time and total solid concentration in the biomass leachate in permeate flux during reverse osmosis (Rajabzadeh et al., 2012). They applied a FFNN with four neurons in a single hidden layer. The standard Levenberg−Marquardt algorithm was chosen to train the FFNN. The model predicted more than 80% rejection efficiency of calcium, magnesium, phosphorus, and silica (for three types of biomass leachate samples) in the reverse osmosis permeate. Nagrath et al. (2004) applied hybrid models to represent complex preparative chromatographic systems, thereby significantly reducing the computational time required for simulation and optimization (Nagrath et al., 2004). Other recent applications of hybrid models in chromatography are optimization, cleaning, and resin aging (Krippl et al., 2020; Pirrung et al., 2017; G. Wang et al., 2017). Narayanan et al. (2021) compared a HNN model with a mechanistic lumped kinetic model. They applied these models to in-silico data, and the results showed a higher prediction accuracy of the HNN model (Narayanan, Seidler, et al., 2021).
5. Future perspectives
5.1. From shallow to deep hybrid modeling
As discussed previously, the number of HNN publications showed a first peak in 2004 followed by a decline and is growing again (Figure 3). Neural networks applications to bioprocesses have shown similar publication trends, with a first explosion in the 80s/early 90s followed by a prolonged decline. The resurgence of neural networks was triggered by advances in deep learning, particularly the publication of the ADAM method in 2014, which enabled the efficient training of complex multi-layered topologies such as CNNs and LSTMs.
Most of the hybrid semiparametric studies published so far applied very simple shallow neural networks, namely 3-layered (shallow) FFNNs. With a delay, hybrid modeling is now incorporating more complex neural network topologies and deep learning. Cheng and co-authors reported a multilayered hybrid modeling workflow for a wastewater treatment process that combined a mechanistic model, a convolutional neural network (CNN), a LSTM and a FFNN (Cheng et al., 2021). Shah et al. (2022) proposed a serial semiparametric deep hybrid model for an industrial fermentation process. The model applied multilayered FFNN but was trained with the traditional Levenberg Marquardt algorithm (Shah et al., 2022). Bangi et al. (2022) recently proposed the Universal Differential Equations (UDE) method based on deep FFNNs and applied it to a Saccharomyces cerevisiae batch fermentation process. The UDE approach is however similar to a serial semiparametric HNN modeling problem (Bangi et al., 2022). Merkelbach (2022) developed a software package called HybridML that uses TensorFlow for artificial neural network deep learning and Casadi to integrate ODEs (Merkelbach et al., 2022). Pinto et al. (2022, 2023) recently compared traditional shallow hybrid modeling (using the Levenberg-Marquardt training coupled with the indirect sensitivities, cross-validation and tanh activation function) with a deep hybrid modeling approach based on ADAM, semidirect sensitivities, stochastic regularization, multiple hidden layers and ReLU activation functions (Pinto et al., 2022, 2023c). The deep hybrid models systematically outperformed the shallow hybrid models both in terms of predictive power and computational cost. A significant result was that for the same problem the deep hybrid model systematically generalized better than the shallow hybrid model. Given the clear advantages, an “explosion” of deep hybrid modeling bioprocess applications will likely follow in the near future, incorporating state-of-the-art deep neural network topologies and deep learning algorithms hybridized with physical laws.
5.2. Narrowing the gap between hybrid modeling and systems biology
With the emergence of systems biology in the early 2000s (Kitano, 2002), several GEnome-scale Models (GEM) have been reconstructed for industrially relevant cell factories. GEMs represent the most complete set of metabolic reactions and metabolites reconstructed from the full set of annotated gene-to-protein relationships. This explosion in mechanistic detail is hardly present in the hybrid modeling field. Hybrid model topologies embodying detailed mechanistic models are almost absent in the literature. The penetration of systems biology tools in routine bioprocess operations will likely challenge novel hybrid modeling methods and applications that incorporate more mechanistic detail (A. P. Teixeira, Carinhas, et al., 2007). GEMs represent a major progress in the understanding of the reaction structure of a given organism, but they are incomplete and difficult to deploy in practice. Recently, the combination of ML and constraint-based modeling (mechanistic) has been proposed to fill this gap (Zampieri et al., 2019), (Bai et al., 2023), (Rana et al., 2020), (Ramos et al., 2022). Faure and co-authors have proposed a hybrid ANN method that combines mechanistic layers, based on Flux Balance Analysis (FBA), and ANN layers, trained on experimental data and/or FBA generated data (Faure et al., 2023). The proposed method improved the prediction of the growth rate of Escherichia coli and Pseudomonas putida in different culture media. An important tool to facilitate the widespread use of hybrid genome-scale models will be the encoding in Systems Biology Markup Language (SBML). Pinto and co-authors recently developed a standalone Python tool that greatly facilitates the hybridization of mechanistic SBML models and ANNs (Pinto et al., 2023). This tool uses symbolic mathematics for the conversion of existing mechanistic models in SBML into hybrid models that combine mechanistic functions with ANNs. It applies symbolic differentiation to automatically generate sensitivity equations for the computation of gradients during the training. Furthermore, after training, such hybrid models can be stored in public databases in SBML format. The upgrade of SBML models into hybrid models was illustrated with three well-known literature case studies: the Escherichia coli threonine synthesis model, the P58IPK signal transduction model, and the Yeast glycolytic oscillations model (Pinto et al., 2023).
5.3. Physics-Informed Neural Networks (PINNs)
The integration of deep ANNs and the Navier Stokes equations (or systems of Partial Differential Equations in general) has evolved to a subfield coined as Physics Informed Neural Networks (PINNs) (Raissi et al., 2019), (Jin et al., 2021), (Mao et al., 2020). The simulation of fluid flow using numerical discretization requires complex mesh-generation methods that are cost-prohibitive for high-dimensional problems. PINNs apply an ANN to parameterize state variables over independent variables (time and spatial coordinates). Automatic Differentiation (AD) is applied to obtain partial derivatives of the state variables in time and spatial coordinates. Two different sets of residuals are minimized during the training: (i) the residuals between calculated and measured state variables are minimized, (ii) the Navier Stokes equations residuals are also minimized. PINNs can thus be trained on experimental data and on additional information of the underlying physical laws, for example, at random points in the continuous space-time domain. Such physics-informed learning allows integrating seamlessly data and PDEs in complex flow problems in a straightforward way (Karniadakis et al., 2021). Moreover, specialized network topologies may be designed that automatically satisfy some of the physical constraints for better accuracy, faster training and improved generalization. This is in contrast with ANN models that typically allow good fitting of a system, but their prediction may be inconsistent when performing extrapolation (Mahanty, 2023).
Given their potential, PINNs are a growing research field and new applications are being developed in material science, medicine, geography and also bioprocessing (Karniadakis et al., 2021), (Zhao et al., 1997), (Hao et al., 2022). Recently, Cui and co-authors developed a PINN model to describe a fed-batch cultivation of Chinese Hamster Ovary (CHO) cells (Cui et al., 2023). The authors used a mechanistic kinetic model to train a PINN to capture the dynamics of a CHO cultivation. Mowbray and co-authors proposed a physics-informed hybrid modeling and reinforcement learning (RL) framework for bioprocess kinetics identification (Mowbray et al., 2021). The authors trained the model on a synthetic data set of a fermentation process under the constraint of physical bound of kinetic parameters. The RL served to identify the best suited model structure. This approach correctly identified the underlying kinetic structures and showed high prediction accuracy (average error of 1.3%). Rogers and co-authors proposed a PINN framework to infer time-varying kinetic parameters (Rogers et al., 2023). The framework was used to investigate known kinetics and its time-varying trajectories while simultaneously identified the optimal hybrid model structure. The performance of this PINN framework was tested on several in-silico bioprocess simulations.
Lagergren and co-authors also proposed an extension of the PINNs to include biological information coined as Biologically-Informed Neural Networks (BINNs) (Lagergren et al., 2020). The authors used BINN to approximate in vitro biologic experiments (Lagergren et al., 2020). The BINN was trained on sparse data with varying initial cell densities and the knowledge of the governing reaction-diffusion partial differential equations were used as constraints. The authors were able to use the model to discover a previously unconsidered biological mechanism that describes delayed population responses.
5.4. HNNs for biopharma 4.0
HNN applications in the biopharma sector are currently boosting particularly for process monitoring and control (Gargalo et al., 2020; Mandenius & Gustavsson, 2015; A. P. Teixeira et al., 2009; Von Stosch et al., 2012) and QbD (Bayer, von Stosch, et al., 2020; von Stosch, Davy, et al., 2014; von Stosch et al., 2016a, 2016b) within the PAT framework. Significant achievements have been reported on process validation using HNNs and iDOE for E. coli and CHO culture (Bayer, Striedner, et al., 2020; von Stosch & Willis, 2017). There is however a clear gap in the application to new modalities such as cell-based therapies and nucleotide-based therapies. Most of published studies are still focused on yield and productivity of upstream processes. Very few studies incorporate critical quality attributes (CQAs) of biotherapeutics related to molecular properties such as glycosylation patterns (Kotidis & Kontoravdi, 2020), charge variants and aggregates.
Industry 4.0 (Gargalo et al., 2020; Sansana et al., 2021), big data (Gargalo et al., 2020; D. Wang et al., 2021), and digital twin (Krippl et al., 2020; Zhang et al., 2020) are recently added subjects that introduce new concepts that challenge the application of HNN modeling to the digitalization of biopharmaceutical processes. A digital twin is a virtual replica of the physical process that combines real-time data from sensors and other sources with advanced analytics to create a digital counterpart that mirrors the behavior and characteristics of the physical process. Digital twins allow for monitoring, analysis, and optimization of the physical process, enabling better decision-making, predictive maintenance, and improved performance. Deep HNNs are very promising for the development of high-fidelity digital twins as they seamlessly combine the learning from experience feature with constant physical laws. This allows in principle to reduce the parameter dimension space, to decrease the data dependency, and to implement a more focused learning of those process parts that are more variable.
A major future challenge is the implementation of “platform HNNs”. Platform HNNs should bear the capacity to learn from experience across different molecules and/or therapies. For platform models, a multi-scale vision is needed that links the molecular properties of the target biologic, the host cell biology and the macroscopic scale of the production equipment. HNN modeling is in principle a strong candidate to address such complex modeling problems.
5.5. Downstream processing
The present literature review shows that most applications of HNN models are found in upstream operation steps and just a few in downstream operation steps. This could be explained by the availability of well-established mechanistic models of many downstream unit operations, which are generally less complex than bioreaction unit operations. However, many critical process parameters, such as mass and energy transfer coefficients, are directly linked with material properties at the molecular level that are difficult to model in the continuum mechanics macroscopic world. Deep ANNs could be a valuable tool to deploy micro-physics informed transport flux representations applicable to continuum mechanics (Miniati & Gregori, 2022). There is thus a significant potential in applying HNNs for filtration, adsorption, chromatography, membrane separation, lyophilization, supercritical CO2 extraction and many more downstream unit operations.
In the case of chromatography processes, Narayanan et al. (2020) noted that the lack of accurate knowledge of adsorption isotherms and mass transfer kinetics may limit the applicability of mechanistic modeling (Narayanan et al., 2020). The authors compared a hybrid semiparametric model (ANNs + material balance equations) with the Lumped Kinetic Model approach in a chromatography process of industrial relevance. Both methods were compared using an in-silico generated data set and an experimental data set. The authors concluded that the hybrid model had 2 to 3-fold lower prediction error than the mechanistic model. Learning complex adsorption isotherms from breakthrough data has been successfully achieved using the proposed HNN approach (Narayanan, Luna, et al., 2021), (Narayanan, et al., 2021).
Subraveti et al. (2023) have recently applied the concept of PINNs to model chromatography seps. The authors concluded that PINNs can effectively predict elution curves of complex nonlinear, binary chromatography with minimal data requirements. Particularly, no isotherm information was required to train the models (Subraveti et al., 2023). PINNs are likely to take a prominent role in the scale-up of many downstream steps in the near future. Process scale-up is nontrivial in many downstream steps (e.g., (Bourlès et al., 2019)). Smyth et al. emphasized the difficulties to collect informative data sets in production facilities due to regulatory constraints (Smyth et al., 2019). Lab or pilot scale data is more easily accessible but not necessarily representative of the production-scale. Building computational fluid dynamics models based on PINNs could greatly facilitate the scale up of such downstream unit operations.
As for upstream steps, HNNs are being considered for the development of digital twins of downstream unit operations. Krippl et al. (2020) applied a HNN model to predict the flux evolution and duration in cross-flow ultrafiltration processes for various proteins, membrane types, input parameters, and filtration modes. The prediction accuracy of the hybrid model was shown to be higher than the mechanistic film theory model. The authors concluded that this HNN model could be used as a high-fidelity digital twin with the ability to predict the physical process under varying input parameters and different operation modes (Krippl et al., 2020).
6. Conclusions
In this paper, a systematic literature review on the application of HNN models to biological processes is presented using the PRISMA method, which shows a structured vision of the research developed on the subject. Statistical analysis regarding the number of articles, subject area of interest, and keywords occurrence in the last 30 years was performed. HNN modeling has covered a wide range of microbial, animal cells, mixed microbial, and enzyme biocatalysis in different industries such as wastewater treatment, clean energy, biopolymers, and biopharmaceutical manufacturing. HNN models were mainly applied for process analysis, process monitoring, open- and closed-loop control, batch-to-batch control, model predictive control, intensified design of experiments, and quality-by-design. Some recent “hot” topics such as big data, deep learning, industry 4.0, and digital twins are major drivers of HNN applications mainly in the biopharma sector. These topics will likely drive hybrid models to incorporate deep neural networks, deep learning methods, and systems biology models in the near future. The majority of HNN studies followed the semiparametric design approach where physical laws are directly incorporated in the model structure. Recently, the PINNs framework has been proposed that maps physical laws to the ANN structure during the training process. Both approaches will likely merge in a common framework whereby both methods are used simultaneously to incorporate prior knowledge in ANN models. A significant research gap is the application of HNNs to downstream operations. Some recent publications have addressed membrane processes and chromatographic processes. There is significant potential for research in applying hybrid models to filtration, adsorption, chromatography, membrane separation, lyophilization, and many more. Closing this gap will likely enable HNNs to evolve towards plant-wide digitalization platforms integrating multiple up- and down-stream operations as the next big step in the future.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
Author Contributions
Conceptualization, methodology, software, data curation, investigation, writing original draft preparation, visualization, and resources, RA; writing review and editing, RA, JRCR and RO; supervision, JMM and RO; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Associate Laboratory for Green Chemistry - LAQV which is financed by national funds from FCT/MCTES (UIDB/50006/2020 and UIDP/50006/2020). This work received funding from the European Union’s Horizon 2020 research and innovation program under the grant agreement no. 101099487- BioLaMer-HORIZON-EIC-2022-PATHFINDEROPEN-01 (BioLaMer).
Data Availability Statement
The data that support the findings of this study are openly available in “Mendeley Data” at http://doi.org/10.17632/gng5bdjbmr.1[82].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Hybrid neural network | HNN) |
| Genome-scale Models | GEM) |
| Monoclonal antibody | mAb) |
| Design of experiments | DOE) |
| Preferred Reporting Items for Systematic Reviews and Meta-Analyses | PRISMA) |
| Radial Basis Function Network | RBFN) |
| Non-linear programming | NLP) |
| Chinese hamster ovary | CHO) |
| Proportional–integral–derivative controller | PID controller) |
| Process analytical technology | PAT) |
| Chemical oxygen demand | COD) |
| Artificial neural network | ANN) |
| Genetic algorithm | GA) |
| Feedforward neural networks | FFNN) |
| Activated Sludge model | ASM) |
| Convolutional neural network | CNN) |
| Long short-term memory neural networks | LSTM) |
| Particle swarm optimization | PSO) |
| Nonlinear autoregressive exogenous | NARX) |
| Backpropagation neural networks | BP-NN) |
| Quality by design | QbD) |
| Poly(3-hydroxy alkanoates) | PHA) |
| Poly-β-hydroxybutyrate | PHB) |
| Adaptive Moment Estimation Method | ADAM) |
| Rectified Linear Unit | ReLU) |
| Hyperbolic tangent | tanh) |
| Physics-Informed Neural Networks | PINNs) |
| Universal differential equations | UDEs) |
| Biologically-Informed Neural Networks | BINNs) |
References
- Udugama, I., Öner, M., Lopez, P. C., Beenfeldt, C., Bayer, C., Huusom, J. K., Gernaey, K. V., & Sin, G. (2021). Towards Digitalization in Bio-Manufacturing Operations: A Survey on Application of Big Data and Digital Twin Concepts in Denmark. Frontiers in Chemical Engineering, 3. [CrossRef]
- Aehle, M., Simutis, R., & Lübbert, A. (2010). Comparison of viable cell concentration estimation methods for a mammalian cell cultivation process. Cytotechnology, 62(5), 413–422. [CrossRef]
- Anderson, J. S., McAvoy, T. J., & Hao, O. J. (2000). Use of hybrid models in wastewater systems. Industrial and Engineering Chemistry Research, 39(6), 1694–1704. [CrossRef]
- Azwar, Hussain, M. A., & Ramachandran, K. B. (2006). The study of neural network-based controller for controlling dissolved oxygen concentration in a sequencing batch reactor. Bioprocess and Biosystems Engineering, 28(4), 251–265. [CrossRef]
- Bai, L., You, Q., Zhang, C., Sun, J., Liu, L., Lu, H., & Chen, Q. (2023). Advances and applications of machine learning and intelligent optimization algorithms in genome-scale metabolic network models. In Systems Microbiology and Biomanufacturing (Vol. 3, Issue 2). [CrossRef]
- Bangi, M. S. F., Kao, K., & Kwon, J. S. Il. (2022). Physics-informed neural networks for hybrid modeling of lab-scale batch fermentation for β-carotene production using Saccharomyces cerevisiae. Chemical Engineering Research and Design, 179. [CrossRef]
- Bayer, B., Duerkop, M., Striedner, G., & Sissolak, B. (2021). Model Transferability and Reduced Experimental Burden in Cell Culture Process Development Facilitated by Hybrid Modeling and Intensified Design of Experiments. Frontiers in Bioengineering and Biotechnology, 9. [CrossRef]
- Bayer, B., Striedner, G., & Duerkop, M. (2020). Hybrid Modeling and Intensified DoE: An Approach to Accelerate Upstream Process Characterization. Biotechnology Journal, 15(9). [CrossRef]
- Bayer, B., von Stosch, M., Striedner, G., & Duerkop, M. (2020). Comparison of Modeling Methods for DoE-Based Holistic Upstream Process Characterization. Biotechnology Journal, 15(5). [CrossRef]
- Bejani, M. M., & Ghatee, M. (2021). A systematic review on overfitting control in shallow and deep neural networks. Artificial Intelligence Review, 54(8). [CrossRef]
- Bourlès, E., de Lannoy, G., Scutellà, B., Fonseca, F., Trelea, I. C., & Passot, S. (2019). Scale-up of freeze-drying cycles, the use of process analytical technology (PAT), and Statistical Analysis. In Methods in Pharmacology and Toxicology. [CrossRef]
- Chen, R. T. Q., Rubanova, Y., Bettencourt, J., & Duvenaud, D. K. (2018). Neural ordinary differential equations. Advances in Neural Information Processing Systems, 31.
- Cheng, X., Guo, Z., Shen, Y., Yu, K., & Gao, X. (2021). Knowledge and data-driven hybrid system for modeling fuzzy wastewater treatment process. Neural Computing and Applications. [CrossRef]
- Cooney, C. L., Wang, H. Y., & Wang, D. I. C. (1977). Computer-aided material balancing for prediction of fermentation parameters. Biotechnology and Bioengineering, 19(1). [CrossRef]
- Costa, A. C., Alves, T. L. M., Henriques, A. W. S., Maciel Filho, R., & Lima, E. L. (1998). An adaptive optimal control scheme based on hybrid neural modelling. Computers and Chemical Engineering, 22(SUPPL.1). [CrossRef]
- Costa, A. C., Henriques, A. S. W., Alves, T. L. M., Maciel Filho, R., & Lima, E. L. (1999). Hybrid neural model for the optimization of fed-batch fermentations. Brazilian Journal of Chemical Engineering, 16(1), 53–63. [CrossRef]
- Côté, M., Grandjean, B. P. A., Lessard, P., & Thibault, J. (1995). Dynamic modelling of the activated sludge process: Improving prediction using neural networks. Water Research, 29(4), 995–1004. [CrossRef]
- Cui, T., Bertalan, T. S., Ndahiro, N., Khare, P., Betenbaugh, M., Maranas, C., & Kevrekidis, I. G. (2023). Data-driven and Physics Informed Modelling of Chinese Hamster Ovary Cell Bioreactors. ArXiv Preprint ArXiv:2305.03257.
- Da Silva Henriques, A. W., Da Costa, A. C. C., Alves, T. L. M. L. M., Lima, E. L. L., Henriques, A. W. D., Da Costa, A. C. C., Alves, T. L. M. L. M., Lima, E. L. L., Da Silva Henriques, A. W., Da Costa, A. C. C., Alves, T. L. M. L. M., & Lima, E. L. L. (1999). A hybrid neural model of ethanol production by Zymomonas mobilis. APPLIED BIOCHEMISTRY AND BIOTECHNOLOGY, 77–9(20th Symposium on biotechnology for Fuels and Chemicals), 277–291. [CrossRef]
- da Silva Pereira, A., Pinheiro, Á. D. T., Rocha, M. V. P. V. P., Gonçalves, L. R. B., Cartaxo, S. J. M. J. M., Pereira, A. D., Pinheiro, A. D. T., Rocha, M. V. P. V. P., Goncalves, L. R. B., Cartaxo, S. J. M. J. M., da Silva Pereira, A., Pinheiro, Á. D. T., Rocha, M. V. P. V. P., Gonçalves, L. R. B., & Cartaxo, S. J. M. J. M. (2021). Hybrid neural network modeling and particle swarm optimization for improved ethanol production from cashew apple juice. BIOPROCESS AND BIOSYSTEMS ENGINEERING, 44(2), 329–342. [CrossRef]
- Dors, M., Simutis, R., & Lübbert, A. (1995). Advanced Supervision of Mammalian Cell Cultures Using Hybrid Process Models. IFAC Proceedings Volumes, 28(3), 72–77. [CrossRef]
- Fang, J., & Dai, L.-K. (2003). Prediction method for wastewater COD based on hybrid neural network model. Zhongguo Jishui Paishui/China Water and Wastewater, 19(12), 6.
- Faure, L., Mollet, B., Liebermeister, W., & Faulon, J.-L. (2023). A neural-mechanistic hybrid approach improving the predictive power of genome-scale metabolic models. BioRxiv.
- Ferreira, A. R., Dias, J. M. L., Von Stosch, M., Clemente, J., Cunha, A. E., & Oliveira, R. (2014). Fast development of Pichia pastoris GS115 Mut+ cultures employing batch-to-batch control and hybrid semi-parametric modeling. Bioprocess and Biosystems Engineering, 37(4), 629–639. [CrossRef]
- Fu, P.-C., & Barford, J. P. (1996). A hybrid neural network - First principles approach for modelling of cell metabolism. Computers and Chemical Engineering, 20(6–7), 951–958. [CrossRef]
- Gargalo, C. L., Udugama, I., Pontius, K., Lopez, P. C., Nielsen, R. F., Hasanzadeh, A., Mansouri, S. S., Bayer, C., Junicke, H., & Gernaey, K. V. (2020). Towards smart biomanufacturing: a perspective on recent developments in industrial measurement and monitoring technologies for bio-based production processes. Journal of Industrial Microbiology and Biotechnology, 47(11), 947–964. [CrossRef]
- Guo, B., Tang, S. T., Lu, Z. A., Li, D. K., & Shen, Y. T. (2001). Simulation of biomass gasification with a hybrid neural network model. Taiyangneng Xuebao/Acta Energiae Solaris Sinica, 22(1), 77–83.
- Hao, Z., Liu, S., Zhang, Y., Ying, C., Feng, Y., Su, H., & Zhu, J. (2022). Physics-informed machine learning: A survey on problems, methods and applications. ArXiv Preprint ArXiv:2211.08064.
- Harada, L. H. P., Da Costa, A. C., & Maciel Filho, R. (2002). Hybrid neural modeling of bioprocesses using functional link networks. Applied Biochemistry and Biotechnology - Part A Enzyme Engineering and Biotechnology, 98–100, 1009–1023. [CrossRef]
- Helleckes, L. M., Hemmerich, J., Wiechert, W., von Lieres, E., & Grünberger, A. (2023). Machine learning in bioprocess development: from promise to practice. In Trends in Biotechnology (Vol. 41, Issue 6). [CrossRef]
- Jin, X., Cai, S., Li, H., & Karniadakis, G. E. (2021). NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. Journal of Computational Physics, 426. [CrossRef]
- Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris, P., Wang, S., & Yang, L. (2021). Physics-informed machine learning. In Nature Reviews Physics (Vol. 3, Issue 6). [CrossRef]
- Kingma, D. P., & Ba, J. L. (2015). Adam: A method for stochastic optimization. 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings.
- Kitano, H. (2002). Systems biology: A brief overview. In Science (Vol. 295, Issue 5560). [CrossRef]
- Kor, M., Yitmen, I., & Alizadehsalehi, S. (2023). An investigation for integration of deep learning and digital twins towards Construction 4.0. Smart and Sustainable Built Environment, 12(3). [CrossRef]
- Kotidis, P., & Kontoravdi, C. (2020). Harnessing the potential of artificial neural networks for predicting protein glycosylation. Metabolic Engineering Communications, 10. [CrossRef]
- Krippl, M., Dürauer, A., & Duerkop, M. (2020). Hybrid modeling of cross-flow filtration: Predicting the flux evolution and duration of ultrafiltration processes. Separation and Purification Technology, 248. [CrossRef]
- Lagergren, J. H., Nardini, J. T., Baker, R. E., Simpson, M. J., & Flores, K. B. (2020). Biologically-informed neural networks guide mechanistic modeling from sparse experimental data. PLoS Computational Biology, 16(11). [CrossRef]
- Lee, D. S., Jeon, C. O., Park, J. M., & Chang, K. S. (2002). Hybrid neural network modeling of a full-scale industrial wastewater treatment process. Biotechnology and Bioengineering, 78(6), 670–682. [CrossRef]
- Luna, M. F., Ochsner, A. M., Amstutz, V., von Blarer, D., Sokolov, M., Arosio, P., & Zinn, M. (2021). Modeling of continuous PHA production by a hybrid approach based on first principles and machine learning. Processes, 9(9). [CrossRef]
- Mahanty, B. (2023). Hybrid modeling in bioprocess dynamics: Structural variabilities, implementation strategies, and practical challenges. In Biotechnology and Bioengineering. [CrossRef]
- Mandenius, C.-F., & Gustavsson, R. (2015). Mini-review: Soft sensors as means for PAT in the manufacture of bio-therapeutics. Journal of Chemical Technology and Biotechnology, 90(2), 215–227. [CrossRef]
- Mao, Z., Jagtap, A. D., & Karniadakis, G. E. (2020). Physics-informed neural networks for high-speed flows. Computer Methods in Applied Mechanics and Engineering, 360. [CrossRef]
- Maton, M., Bogaerts, P., & Vande Wouwer, A. (2022). Hybrid Dynamic Models of Bioprocesses Based on Elementary Flux Modes and Multilayer Perceptrons. Processes, 10(10). [CrossRef]
- Mavrovouniotis, M. L., & Chang, S. (1992). Hierarchical neural networks. Computers & Chemical Engineering, 16(4), 347–369. [CrossRef]
- Meleiro, L. A. C., & Maciel Filho, R. (2000). State and parameter estimation based on a nonlinear filter applied to an industrial process control of ethanol production. Brazilian Journal of Chemical Engineering, 17(4), 991–1001. [CrossRef]
- Merkelbach, K., Schweidtmann, A. M., Müller, Y., Schwoebel, P., Mhamdi, A., Mitsos, A., Schuppert, A., Mrziglod, T., & Schneckener, S. (2022). HybridML: Open source platform for hybrid modeling. Computers and Chemical Engineering, 160. [CrossRef]
- Miniati, F., & Gregori, G. (2022). Learning transport processes with machine intelligence. Scientific Reports, 12(1). [CrossRef]
- Mitchell, T. M. (1997). Machine learning.
- Morabito, B., Pohlodek, J., Matschek, J., Savchenko, A., Carius, L., & Findeisen, R. (2021). Towards Risk-aware Machine Learning Supported Model Predictive Control and Open-loop Optimization for Repetitive Processes. IFAC-PapersOnLine, 54(6), 321–328. [CrossRef]
- Mowbray, M., Savage, T., Wu, C., Song, Z., Cho, B. A., Del Rio-Chanona, E. A., & Zhang, D. (2021). Machine learning for biochemical engineering: A review. Biochemical Engineering Journal, 172. [CrossRef]
- Mowbray, M., Vallerio, M., Perez-Galvan, C., Zhang, D., Del Rio Chanona, A., & Navarro-Brull, F. J. (2022). Industrial data science - a review of machine learning applications for chemical and process industries. In Reaction Chemistry and Engineering (Vol. 7, Issue 7). [CrossRef]
- Nagarajan, H. P. N., Mokhtarian, H., Jafarian, H., Dimassi, S., Bakrani-Balani, S., Hamedi, A., Coatanéa, E., Gary Wang, G., & Haapala, K. R. (2019). Knowledge-based design of artificial neural network topology for additive manufacturing process modeling: A new approach and case study for fused deposition modeling. Journal of Mechanical Design, Transactions of the ASME, 141(2). [CrossRef]
- Nagrath, D., Messac, A., Bequette, B. W., & Cramer, S. M. (2004). A Hybrid Model Framework for the Optimization of Preparative Chromatographic Processes. Biotechnology Progress, 20(1), 162–178. [CrossRef]
- Narayanan, H., Behle, L., Luna, M. F., Sokolov, M., Guillén-Gosálbez, G., Morbidelli, M., & Butté, A. (2020). Hybrid-EKF: Hybrid model coupled with extended Kalman filter for real-time monitoring and control of mammalian cell culture. Biotechnology and Bioengineering, 117(9), 2703–2714. [CrossRef]
- Narayanan, H., Luna, M. F., von Stosch, M., Cruz Bournazou, M. N., Polotti, G., Morbidelli, M., Butté, A., & Sokolov, M. (2020). Bioprocessing in the Digital Age: The Role of Process Models. Biotechnology Journal, 15(1). [CrossRef]
- Narayanan, H., Luna, M., Sokolov, M., Arosio, P., Butté, A., & Morbidelli, M. (2021). Hybrid Models Based on Machine Learning and an Increasing Degree of Process Knowledge: Application to Capture Chromatographic Step. Industrial and Engineering Chemistry Research, 60(29). [CrossRef]
- Narayanan, H., Seidler, T., Luna, M. F., Sokolov, M., Morbidelli, M., & Butté, A. (2021). Hybrid Models for the simulation and prediction of chromatographic processes for protein capture. Journal of Chromatography A, 1650. [CrossRef]
- Narayanan, H., Sokolov, M., Morbidelli, M., & Butté, A. (2019). A new generation of predictive models: The added value of hybrid models for manufacturing processes of therapeutic proteins. Biotechnology and Bioengineering, 116(10), 2540–2549. [CrossRef]
- Noll, P., & Henkel, M. (2020). History and Evolution of Modeling in Biotechnology: Modeling & Simulation, Application and Hardware Performance. Computational and Structural Biotechnology Journal, 18, 3309–3323. [CrossRef]
- Novak, M., Koller, M., Braunegg, G., & Horvat, P. (2015). Mathematical modelling as a tool for optimized PHA production. Chemical and Biochemical Engineering Quarterly, 29(2), 183–220. [CrossRef]
- Oliveira, R. (2004). Combining first principles modelling and artificial neural networks: A general framework. Computers and Chemical Engineering, 28(5), 755–766. [CrossRef]
- Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., Shamseer, L., Tetzlaff, J. M., Akl, E. A., Brennan, S. E., Chou, R., Glanville, J., Grimshaw, J. M., Hróbjartsson, A., Lalu, M. M., Li, T., Loder, E. W., Mayo-Wilson, E., McDonald, S., … Moher, D. (2021). The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. In The BMJ (Vol. 372). [CrossRef]
- Patnaik, P. R. (2008). Neural and hybrid optimizations of the fed-batch synthesis of poly-β-hydroxybutyrate by ralstonia eutropha in a nonideal bioreactor. Bioremediation Journal, 12(3), 117–130. [CrossRef]
- Patnaik, P. R. (2010). Design considerations in hybrid neural optimization of fed-batch fermentation for PHB production by Ralstonia eutropha. Food and Bioprocess Technology, 3(2), 213–225. [CrossRef]
- Peres, J., Freitas, F., Reis, M., Feyo de Azevedo, S., & Oliveira, R. (2006). Hybrid modular mechanistic/ANN modelling of a wastewater phosphorus removal process. In Computer Aided Chemical Engineering (Vol. 21, Issue C). [CrossRef]
- Peres, J., Oliveira, R., & de Azevedo, S. F. (2008). Bioprocess hybrid parametric/nonparametric modelling based on the concept of mixture of experts. Biochemical Engineering Journal, 39(1), 190–206. [CrossRef]
- Peres, J., Oliveira, R., & Feyo De Azevedo, S. (2001). Knowledge based modular networks for process modelling and control. Computers and Chemical Engineering, 25(4–6), 783–791. [CrossRef]
- Peres, J., Oliveira, R., Serafim, L. S., Lemos, P., Reis, M. A., & Feyo de Azevedo, S. (2004). Hybrid Modelling of a PHA Production Process Using Modular Neural Networks. In Computer Aided Chemical Engineering (Vol. 18, Issue C). [CrossRef]
- Pinto, J., Costa, R. S., Alexandre, L., Ramos, J., & Oliveira, R. (2023). SBML2HYB: a Python interface for SBML compatible hybrid modeling. Bioinformatics (Oxford, England), 39(1). [CrossRef]
- Pinto, J., de Azevedo, C. R., Oliveira, R., & von Stosch, M. (2019). A bootstrap-aggregated hybrid semi-parametric modeling framework for bioprocess development. Bioprocess and Biosystems Engineering, 42(11), 1853–1865. [CrossRef]
- Pinto, J., Mestre, M., Ramos, J., Costa, R. S., Striedner, G., & Oliveira, R. (2022). A general deep hybrid model for bioreactor systems: Combining first principles with deep neural networks. Computers and Chemical Engineering, 165. [CrossRef]
- Pinto, J., Ramos, J. R. C., Costa, R. S., & Oliveira, R. (2023). A General Hybrid Modeling Framework for Systems Biology Applications: Combining Mechanistic Knowledge with Deep Neural Networks under the SBML Standard. AI, 4(1). [CrossRef]
- Pinto, J., Ramos, J. R. C., Costa, R. S., Rossell, S., Dumas, P., & Oliveira, R. (2023). Hybrid deep modeling of a CHO-K1 fed-batch process: combining First-Principles with deep neural networks. Frontiers in Bioengineering and Biotechnology, 11, 1237963.
- Piron, E., Latrille, E., & René, F. (1997). Application of artificial neural networks for crossflow microfiltration modelling: “black-box” and semi-physical approaches. Computers and Chemical Engineering, 21(9), 1021–1030. [CrossRef]
- Pirrung, S. M., van der Wielen, L. A. M., van Beckhoven, R. F. W. C., van de Sandt, E. J. A. X., Eppink, M. H. M., & Ottens, M. (2017). Optimization of biopharmaceutical downstream processes supported by mechanistic models and artificial neural networks. Biotechnology Progress, 33(3), 696–707. [CrossRef]
- Preusting, H., Noordover, J., Simutis, R., & Lübbert, A. (1996). The Use of Hybrid Modelling for the Optimization of the Penicillin Fermentation Process. CHIMIA, 50(9), 416. [CrossRef]
- Psichogios, D. C., & Ungar, L. H. (1992). A hybrid neural network-first principles approach to process modeling. AIChE Journal, 38(10), 1499–1511. [CrossRef]
- Rackauckas, C., Ma, Y., Martensen, J., Warner, C., Zubov, K., Supekar, R., Skinner, D., Ramadhan, A., & Edelman, A. (2020). Universal differential equations for scientific machine learning. ArXiv Preprint ArXiv:2001.04385.
- Raissi, M., Perdikaris, P., & Karniadakis, G. E. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378. [CrossRef]
- Rajabzadeh, A. R., Ruzich, N., Zendehboudi, S., & Rahbari, M. (2012). Biomass leachate treatment and nutrient recovery using reverse osmosis: Experimental study and hybrid artificial neural network modeling. Energy and Fuels, 26(12), 7155–7163. [CrossRef]
- Ramos, J. R. C., Oliveira, G. P., Dumas, P., & Oliveira, R. (2022). Genome-scale modeling of Chinese hamster ovary cells by hybrid semi-parametric flux balance analysis. Bioprocess and Biosystems Engineering, 45(11), 1889–1904. [CrossRef]
- Rana, P., Berry, C., Ghosh, P., & Fong, S. S. (2020). Recent advances on constraint-based models by integrating machine learning. In Current Opinion in Biotechnology (Vol. 64). [CrossRef]
- Richman, R., & Wuthrich, M. V. (2023). Smoothness and Monotonicity Constraints for Neural Networks Using ICEnet. SSRN Electronic Journal. [CrossRef]
- Rogers, A. W., Cardenas, I. O. S., Del Rio-Chanona, E. A., & Zhang, D. (2023). Investigating physics-informed neural networks for bioprocess hybrid model construction. In Computer Aided Chemical Engineering (Vol. 52, pp. 83–88). Elsevier.
- Rosca, M., Weber, T., Gretton, A., & Mohamed, S. (2020). A case for new neural network smoothness constraints.
- Sansana, J., Joswiak, M. N., Castillo, I., Wang, Z., Rendall, R., Chiang, L. H., & Reis, M. S. (2021). Recent trends on hybrid modeling for Industry 4.0. Computers and Chemical Engineering, 151. [CrossRef]
- Santos, J. L. C., Hidalgo, A. M., Oliveira, R., Velizarov, S., & Crespo, J. G. (2007). Analysis of solvent flux through nanofiltration membranes by mechanistic, chemometric and hybrid modelling. Journal of Membrane Science, 300(1–2). [CrossRef]
- Schubert, J., Simutis, R., Dors, M., Havlík, I., & Lübbert, A. (1994). Hybrid modelling of yeast production processes – combination of a priori knowledge on different levels of sophistication. Chemical Engineering & Technology, 17(1), 10–20. [CrossRef]
- Schubert, J., SIMUTIS, R., Dors, M., Havlik, I., Lübbert, A., LUBBERT, A., Lübbert, A., & LUBBERT, A. (1994). Bioprocess optimization and control: Application of hybrid modelling. Journal of Biotechnology, 35(1), 51–68. [CrossRef]
- Shah, P., Sheriff, M. Z., Bangi, M. S. F., Kravaris, C., Kwon, J. S.-I., Botre, C., & Hirota, J. (2022). Deep neural network-based hybrid modeling and experimental validation for an industry-scale fermentation process: Identification of time-varying dependencies among parameters. Chemical Engineering Journal, 441. [CrossRef]
- Silva, J. A., Costa Neto, E. H., Adriano, W. S., Ferreira, A. L. O., & Gonçalves, L. R. B. (2008). Use of neural networks in the mathematical modelling of the enzymic synthesis of amoxicillin catalysed by penicillin G acylase immobilized in chitosan. World Journal of Microbiology and Biotechnology, 24(9), 1761–1767. [CrossRef]
- Simutis, R., Oliveira, R., Manikowski, M., de Azevedo, S. F., & Lübbert, A. (1997). How to increase the performance of models for process optimization and control. Journal of Biotechnology, 59(1–2), 73–89. [CrossRef]
- Smyth, P., de Lannoy, G., Von Stosch, M., Pysik, A., & Khan, A. (2019). Machine learning in research and development of new vaccines products: Opportunities and challenges. ESANN 2019 - Proceedings, 27th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, 215–220.
- Subraveti, S. G., Li, Z., Prasad, V., & Rajendran, A. (2023). Can a Computer “Learn” Nonlinear Chromatography?: Experimental Validation of Physics-Based Deep Neural Networks for the Simulation of Chromatographic Processes. Industrial and Engineering Chemistry Research, 62(14). [CrossRef]
- Teixeira, A., Cunha, A. E., Clemente, J. J., Moreira, J. L., Cruz, H. J., Alves, P. M., Carrondo, M. J. T., & Oliveira, R. (2005). Modelling and optimization of a recombinant BHK-21 cultivation process using hybrid grey-box systems. Journal of Biotechnology, 118(3), 290–303. [CrossRef]
- Teixeira, A. P., Alves, C., Alves, P. M., Carrondo, M. J. T., & Oliveira, R. (2007). Hybrid elementary flux analysis/nonparametric modeling: Application for bioprocess control. BMC Bioinformatics, 8. [CrossRef]
- Teixeira, A. P., Carinhas, N., Dias, J. M. L., Cruz, P., Alves, P. M., Carrondo, M. J. T., & Oliveira, R. (2007). Hybrid semi-parametric mathematical systems: Bridging the gap between systems biology and process engineering. Journal of Biotechnology, 132(4), 418–425. [CrossRef]
- Teixeira, A. P., Clemente, J. J., Cunha, A. E., Carrondo, M. J. T., & Oliveira, R. (2006). Bioprocess iterative batch-to-batch optimization based on hybrid parametric/nonparametric models. Biotechnology Progress, 22(1), 247–258. [CrossRef]
- Teixeira, A. P., Oliveira, R., Alves, P. M., & Carrondo, M. J. T. (2009). Advances in on-line monitoring and control of mammalian cell cultures: Supporting the PAT initiative. Biotechnology Advances, 27(6), 726–732. [CrossRef]
- Thompson, M. L., & Kramer, M. A. (1994). Modeling chemical processes using prior knowledge and neural networks. AIChE Journal, 40(8), 1328–1340. [CrossRef]
- Van Can, H. J. L., Te Braake, H. A. B., Bijman, A., Hellinga, C., Luyben, K. Ch. A. M., & Heijnen, J. J. (1999). An efficient model development strategy for bioprocesses based on neural networks in macroscopic balances: Part II. Biotechnology and Bioengineering, 62(6), 666–680. [CrossRef]
- Van Can, H. J. L., Te Braake, H. A. B., Dubbclman, S., Hellinga, C., Luyben, K. Ch. . A. M., & Heijnen, J. J. (1998). Understanding and applying the extrapolation properties of serial gray-box models. AIChE Journal, 44(5), 1071–1089. [CrossRef]
- von Stosch, M., Davy, S., Francois, K., Galvanauskas, V., Hamelink, J.-M., Luebbert, A., Mayer, M., Oliveira, R., O’Kennedy, R., Rice, P., Rice, P., & Glassey, J. (2014). Hybrid modeling for quality by design and PAT-benefits and challenges of applications in biopharmaceutical industry. Biotechnology Journal, 9(6), 719–726. [CrossRef]
- von Stosch, M., Hamelink, J.-M., & Oliveira, R. (2016a). Hybrid modeling as a QbD/PAT tool in process development: an industrial E. coli case study. Bioprocess and Biosystems Engineering, 39(5), 773–784. [CrossRef]
- von Stosch, M., Hamelink, J.-M., & Oliveira, R. (2016b). Toward intensifying design of experiments in upstream bioprocess development: An industrial Escherichia coli feasibility study. Biotechnology Progress, 32(5), 1343–1352. [CrossRef]
- Von Stosch, M., Oliveira, R., Peres, J., & Feyo De Azevedo, S. (2011). A novel identification method for hybrid (N)PLS dynamical systems with application to bioprocesses. Expert Systems with Applications, 38(9), 10862–10874. [CrossRef]
- von Stosch, M., Oliveira, R., Peres, J., & Feyo de Azevedo, S. (2014). Hybrid semi-parametric modeling in process systems engineering: Past, present and future. Computers and Chemical Engineering, 60, 86–101. [CrossRef]
- Von Stosch, M., Oliveria, R., Peres, J., & De Azevedo, S. F. (2012). Hybrid modeling framework for process analytical technology: Application to Bordetella pertussis cultures. Biotechnology Progress, 28(1), 284–291. [CrossRef]
- von Stosch, M., & Willis, M. J. (2017). Intensified design of experiments for upstream bioreactors. Engineering in Life Sciences, 17(11), 1173–1184. [CrossRef]
- Wang, D., Thunéll, S., Lindberg, U., Jiang, L. L., Trygg, J., Tysklind, M., Souihi, N., Thunell, S., Lindberg, U., Jiang, L. L., Trygg, J., Tysklind, M., & Souihi, N. (2021). A machine learning framework to improve effluent quality control in wastewater treatment plants. Science of the total environment, 784. [CrossRef]
- Wang, G., Briskot, T., Hahn, T., Baumann, P., & Hubbuch, J. (2017). Root cause investigation of deviations in protein chromatography based on mechanistic models and artificial neural networks. Journal of Chromatography A, 1515, 146–153. [CrossRef]
- Wu, Z., & Shi, X. (2007). Optimization for high-density cultivation of heterotrophic Chlorella based on a hybrid neural network model. Letters in Applied Microbiology, 44(1), 13–18. [CrossRef]
- Xiao, J., Liu, C., Ju, B., Xu, H., Sun, D., & Dang, Y. (2021). Estimation of in-situ biogas upgrading in microbial electrolysis cells via direct electron transfer: Two-stage machine learning modeling based on a NARX-BP hybrid neural network. Bioresource Technology, 330. [CrossRef]
- Yang, C. T., Kristiani, E., Leong, Y. K., & Chang, J. S. (2023). Big data and machine learning driven bioprocessing – Recent trends and critical analysis. Bioresource Technology, 372. [CrossRef]
- Zampieri, G., Vijayakumar, S., Yaneske, E., & Angione, C. (2019). Machine and deep learning meet genome-scale metabolic modeling. In PLoS Computational Biology (Vol. 15, Issue 7). [CrossRef]
- Zhang, D., Savage, T. R., & Cho, B. A. (2020). Combining model structure identification and hybrid modelling for photo-production process predictive simulation and optimisation. Biotechnology and Bioengineering, 117(11), 3356–3367. [CrossRef]
- Zhao, H., Hao, O. J., McAvoy, T. J., & Chang, C.-H. (1997). Modeling nutrient dynamics in sequencing batch reactor. Journal of Environmental Engineering, 123(4), 311–318. [CrossRef]
Figure 1.
Different methods to embody prior knowledge in HNN models. (A) Serial semiparametric hybrid structure. (B) Parallel semiparametric hybrid structure. (C) Physics-Informed Neural Network structure.
Figure 1.
Different methods to embody prior knowledge in HNN models. (A) Serial semiparametric hybrid structure. (B) Parallel semiparametric hybrid structure. (C) Physics-Informed Neural Network structure.
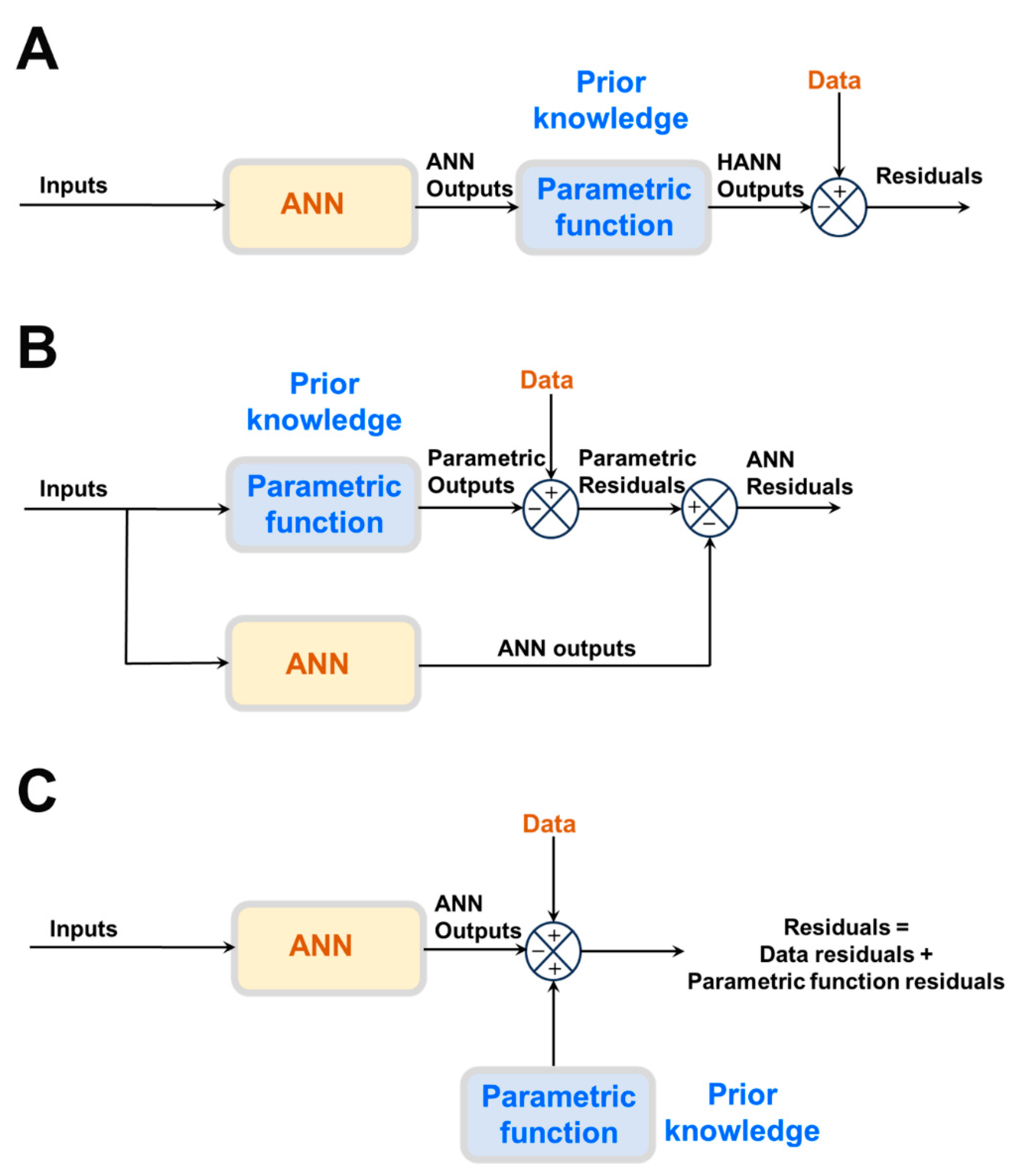
Figure 2.
General deep hybrid model for bioreactor systems. The model has parametric functions (functions f(.) and h(.)) with fixed mathematical structure (typically material/energy balance equations). Some process properties lacking mechanistic explanation are modelled by a feedforward neural network (FFNN) as function of the process state, x, exogenous inputs, u, and time, t. FFNN is a nonparametric function with loose structure that must be identified from process data given the absence of explanatory mechanisms for that particular part of the model. The model is dynamic in nature with state vector, x, and observable outputs, y.
Figure 2.
General deep hybrid model for bioreactor systems. The model has parametric functions (functions f(.) and h(.)) with fixed mathematical structure (typically material/energy balance equations). Some process properties lacking mechanistic explanation are modelled by a feedforward neural network (FFNN) as function of the process state, x, exogenous inputs, u, and time, t. FFNN is a nonparametric function with loose structure that must be identified from process data given the absence of explanatory mechanisms for that particular part of the model. The model is dynamic in nature with state vector, x, and observable outputs, y.
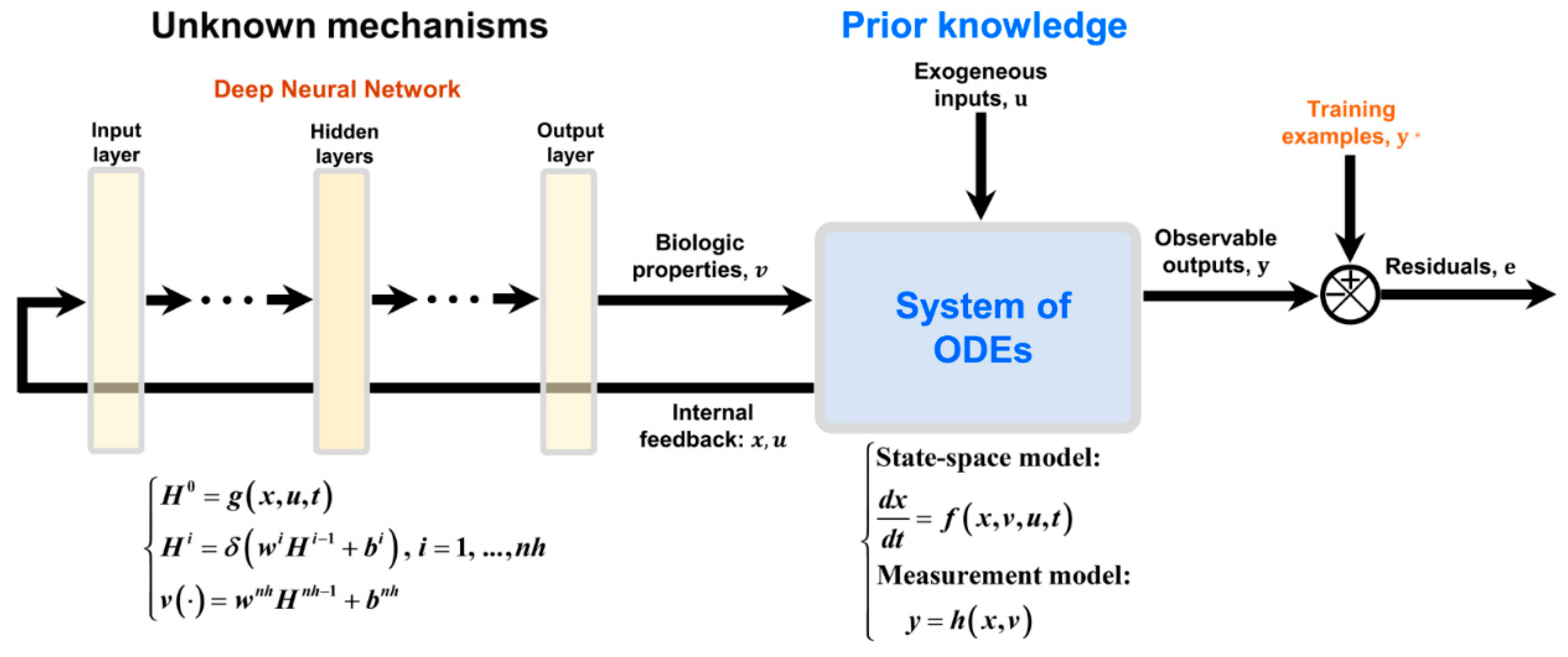
Figure 3.
Number of HNN bioprocess modeling publications from January 1992 until September 2023.
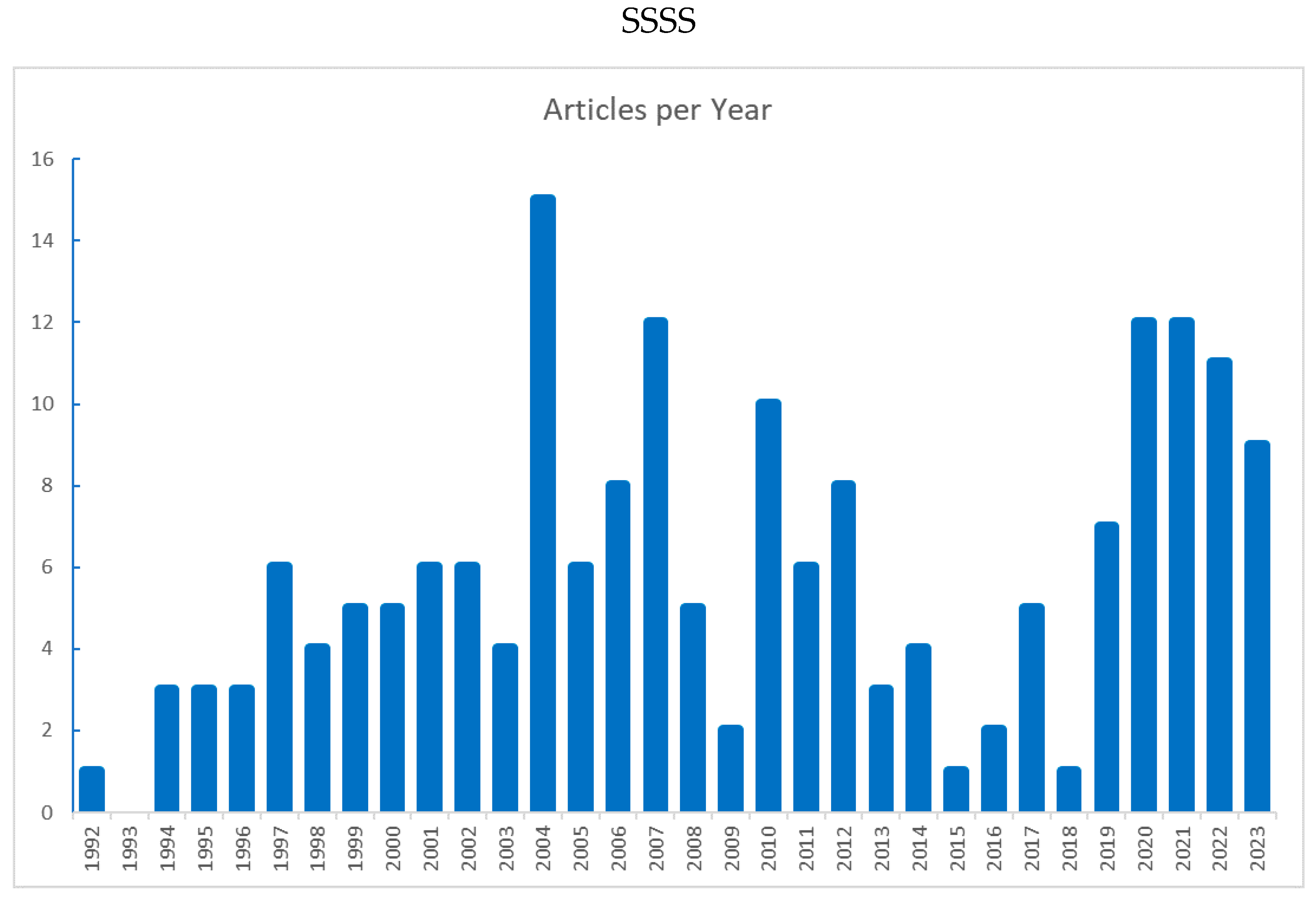
Table 1.
Ten most cited HNN bioprocess modeling publications.
| No | Authors | Title | Source title | Cited by |
|---|---|---|---|---|
| 1 | (Psichogios & Ungar, 1992) | A hybrid neural network-first principles approach to process modeling | AIChE Journal | 637 |
| 2 | (Thompson & Kramer, 1994) | Modeling chemical processes using prior knowledge and neural networks | AIChE Journal | 435 |
| 3 | (von Stosch, Oliveira, et al., 2014) | Hybrid semi-parametric modeling in process systems engineering: Past, present and future | Computers and Chemical Engineering | 234 |
| 4 | (Côté et al., 1995) | Dynamic modelling of the activated sludge process: Improving prediction using neural networks | Water Research | 151 |
| 5 | (Schubert, SIMUTIS, et al., 1994) | Bioprocess optimization and control: Application of hybrid modelling | Journal of Biotechnology | 147 |
| 6 | (Oliveira, 2004) | Combining first principles modelling and artificial neural networks: A general framework | Computers and Chemical Engineering | 126 |
| 7 | (Lee et al., 2002) | Hybrid neural network modeling of a full-scale industrial wastewater treatment process | Biotechnology and Bioengineering | 118 |
| 8 | (Guo et al., 2001) | Simulation of biomass gasification with a hybrid neural network model | Bioresource Technology | 97 |
| 9 | (Wu & Shi, 2007) | Optimization for high-density cultivation of heterotrophic Chlorella based on a hybrid neural network model | Letters in Applied Microbiology | 93 |
| 10 | (A. P. Teixeira, Alves, et al., 2007) | Hybrid elementary flux analysis/nonparametric modeling: Application for bioprocess control | BMC Bioinformatics | 75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







