Prerpints.org logo
Preprint
Article

Guided Direct Time-of-Flight Lidar using Stereo Cameras for Enhanced Laser Power Efficiency

Altmetrics

Downloads

148

Views

81

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 October 2023

Posted:

03 October 2023

You are already at the latest version

Alerts
Abstract
Self-driving vehicles demand efficient and reliable depth sensing technologies. Lidar, with its capacity for long-distance, high-precision measurement, is a crucial component in this pursuit. However, conventional mechanical scanning implementations suffer from reliability, cost, and frame rate limitations. Solid-state lidar solutions have emerged as a promising alternative, but the vast amount of photon data processed and stored using conventional direct time-of-flight (dToF) prevents long-distance sensing unless power-intensive partial histogram approaches are used. In this paper, we introduce a groundbreaking ‘guided’ dToF approach, harnessing external guidance from other onboard sensors to narrow down the depth search space for a power and data-efficient solution. This approach centers around a dToF sensor in-which the exposed time widow of independent pixels can be dynamically adjusted. We utilize a 64-by-32 macropixel dToF sensor and a pair of vision cameras to provide the guiding depth estimates. Our demonstrator captures a dynamic outdoor scene at 3 fps with distances up 75 m. Compared to a conventional full histogram approach, on-chip data is reduced by over 25 times, while the total laser cycles in each frame are reduced by at least 6 times compared to any partial histogram approach. The capability of guided dToF to mitigate multipath reflections is also demonstrated. For self-driving vehicles where a wealth of sensor data is already available, guided dToF opens new possibilities for efficient solid-state lidar.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

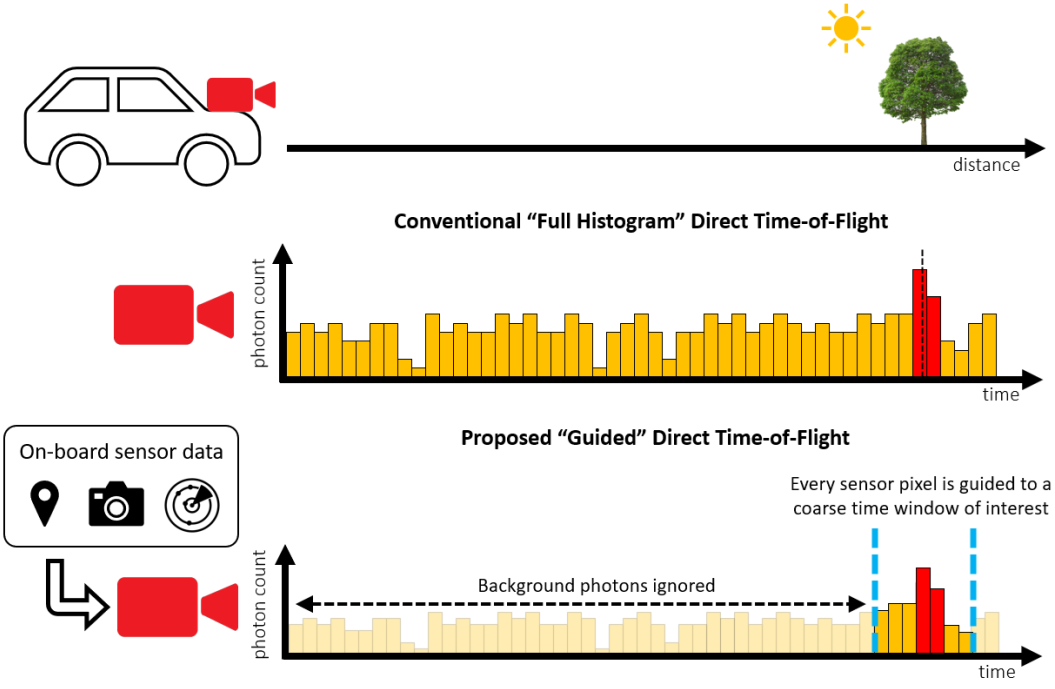
Self-driving vehicles require a diverse range of depth sensors to ensure safety and reliability [1,2]. This is the consensus among vehicle manufacturers such as Audi, BMW, Ford, and many more, as outlined in their automated driving safety frameworks [3,4]. Sensor types include ultrasound, radar, vision cameras and lidar. Of these, lidar can provide long distance sensing over hundreds of meters with centimeter precision [5]. Direct time-of-flight (dToF), illustrated in Figure 1a, is performed by measuring the roundtrip time of a short laser pulse and is currently the most suited lidar approach for these distances [6]. However, traditional mechanical scanning implementations introduce reliability issue, frame rate limitations and high cost [7]. For widespread adoption of self-driving vehicles, a more practical and cost-effective lidar solution is required.
Contrastingly, new solid-state lidar solutions including flash lidar, are made using established and economical semiconductor processes with no moving parts. Many solid-state lidar solutions center around a chip containing a 2D array of dToF sensor pixels to time the returning laser from each point in the scene. However, ambient background photons are also present, so the detected arrival times of all photons must be accumulated over multiple laser cycles to distinguish the laser arrival time, as illustrated in Figure 1b. This presents a significant challenge, as each pixel in the dToF sensor must accommodate enough area to detect, process, and time the arrival of photons, as well as store the resulting data. Histogramming, the process of sorting detected photon arrival times into coarse time bins illustrated in Figure 1c, mitigates the challenge of storing large volumes of photon data [8]. However, the requirement to process and store such large volumes of photon data inevitably limits the achievable maximum distance and/or resolution.
The increased adoption of expensive 3D chip stacking processes (Figure 2) to add more histogram bin storage in-pixel demonstrates the value in overcoming this challenge. This is further highlighted by the increased adoption of novel ‘partial histogram’ dToF sensors which concede a limited bin capacity at the cost of greatly increasing lidar laser power consumption (discussed further in Section 2.3).
To overcome the unmanageable volume of photon data, without using power-hungry partial histogram methods, we propose a new ‘guided’ direct time-of-flight approach. Illustrated in Figure 1d, this approach centers around a dToF sensor where the observed time window of each individual pixel can be externally programmed on-the-fly. By allowing the diverse range of sensors already on the vehicle to guide the sensor, each pixel can efficiently gather the returning laser photons with a reduced set of bins.
This paper is organized as follows: in Section 2 we discuss related work to highlight the value of the proposed guided dToF approach; in Section 3 the technical details of the implemented guided ToF system are documented; Section 4 presents the achieved performance of the system; and finally a discussion and conclusion of the work is given in Section 5, respectively.

2. Related Work

Two techniques have so far played a critical role in enabling 2D arrays of dToF pixels for long range solid-state lidar: 3D chip stacking and partial histogram techniques.

2.1. 3D Stacked DToF Sensors

While 3D chip stacking has been long established in image sensors, dToF sensors which rely on the high sensitivity and fine time-resolution of single photon avalanche diodes (SPADs) have only been made possible through more recent advancements. The first 3D stacked dToF sensor chip was developed in 2018 by Ximenes et. al [9]. An infinite impulse response (IIR) filter is used, instead of histogramming, to average successive photon arrival times and narrow in on the laser arrival time. However, this technique suffers under ambient conditions, making it impractical for automotive lidar. In 2019, Henderson et. al [10] showcased a stacked dToF sensor with capacity for 16 histogram bins. The demonstrated ranging outdoors as far as 50 m within tens of centimeter accuracy while running at 30 fps was a significant step towards automotive grade depth sensing performance. In 2021, Padmanabhan et al. [11] highlighted the value of using programmable time windows to achieve long distance ranging outdoors. The stacked sensor presented achieved a maximum distance of 100 m with 0.7 m error under low ambient light conditions (10 klux), although this is only given for a single-point measurement and at an undisclosed frame rate.

2.2. Partial Histogram DToF Sensors

Partial histogram sensors aim to achieve the same maximum range and precision of a full histogram approach (Figure 1c) with a reduced number of histogram bins. They can be grouped into two categories: ‘zooming’ and ‘sliding’.
Zooming, as illustrated in Figure 3a, spreads the reduced histogram initially across the full distance range. After multiple laser cycles, the peak (signal) bin is identified, and the histogram is zoomed in to a new, narrower time window. Multiple zoom steps can be performed until the required precision is achieved. Zhang et al. [13] published the first dToF sensor capable of independent per-pixel histogram zooming in 2019. Each pixel contained an 8×10-bit histogram which zoomed in 3 steps to achieve a maximum range of 50 m with 8.8 cm accuracy using a 60% reflective target, albeit for a single point measurement. An updated iteration [14] built on a stacked process, enabled an increased histogram bin capacity of 32 bins, allowing zooming to be reduced to a 2-step approach. In 2021, Kim et al. [15] reduced the required histogram capacity even further to only 2 bins using 8 zooming steps. The impact of using many zoom steps on frame rate was acknowledged and prompted a follow-up publication by Park et al. [16]. This reduced the number of zoom steps from 8 down to 4 to range up to 33 m at 1.5 fps.
Sliding, as illustrated in Figure 3b, achieves a partial histogram solution by spreading the reduced histogram across only a subset of the full distance range. After sufficient laser cycles have been accumulated, the time window slides to a new time range and the process repeats until the full the distance range has been covered. Stoppa et al. [17], published the first sliding histogram sensor in 2021. Using 3D chip stacking, each pixel has capacity for 32 histogram bins which slide over 16 windows. 6 bins of overlap between each slide step is used to cover edge-cases. The sensor was upgraded the following year [18] using 22 nm technology on the bottom tier (previously 40 nm), to further increased to the histogram bin capacity to 59 bins per pixel.

2.3. Summary of DToF Histogram Approaches

The conventional full histogram dToF approach efficiently collects returning laser photons, but limited on-chip area makes long-range, outdoor performance impractical. Even if a full histogram solution could be implemented, the large amount of data output from potentially millions of pixels would only compound the problem of high data volume that self-driving vehicles already face [19].
On the other hand, partial histogram dToF sensors are more feasible. However, these introduce a severe laser power penalty. This occurs in zooming because each step adds an additional set of laser cycles on top of what is required for a full histogram approach, while in sliding the penalty is a result of most steps not containing the laser return time. This is particularly problematic for flash lidar architectures where a high peak laser power is typically required. The laser power introduced by partial histogram approaches has been extensively studied in [20], showing a minimum 5× laser power penalty is required to meet a typical automotive lidar specification.
In addition to increased laser power, partial histogram approaches introduce other limitations. Sliding does not solve the issue of high data volume and can introduce motion artefacts if the target moves between slide windows within a frame. Zooming can also introduce image artefacts if multiple peaks occur in the same line-of-sight as a result of transparent objects for example.
In contrast, if the complexity of integrating multiple on-board data sources can be overcome, a guided dToF system would be able to achieve long distance outdoor depth sensing with a reduced set of histogram bins and without a laser power penalty. Exploring the feasibility, implementation and performance of such a system is therefore of significant value in the context of self-driving vehicles, where an abundance of sensor data is already available. A summary of the merits of different dToF histogram alongside the proposed guided dToF approach is provided in Table 1.

3. Materials & Methods

3.1. Guided Lidar Sensor

The sensor used to demonstrate this approach (Figure 4) was fabricated in a standard 40 nm CMOS technology and features 32×64 dToF pixels. Each pixel contains 4×4 SPADs alongside processing and storage of photon events into a histogram of 8×12-bit bins. Originally presented in [21], each dToF pixel is able to independently slide its histogram time window and automatically lock on to a peak when detected. To use the chip as guided dToF sensor for this work, the tracking feature is been disabled and configured such that the time window allocated to each pixel can dynamically programmed.

3.2. Guiding Source: Stereo Camera Vision

The variety of sensors available on-board self-driving vehicles, including ultrasound, radar, vision cameras, and geolocation, provide ample data for a guided lidar system. In this work, we use a pair of vision cameras and perform stereo depth processing to provide the required guiding depth estimates. The foundation of stereo depth estimation is to match each point in the image of one (principal) camera to that in the image of another (secondary) camera. The number of pixels any point has shifted by, termed disparity d , gives the distance z to that point according to Equation (1) assuming both cameras are separated by a baseline distance B and share the same focal length f .
z = f   B d
Quantization as a result of discrete pixel disparity values limits the achievable depth accuracy, although sub-pixel estimation can enable resolving disparity to less than a single pixel value [22]. Stereo depth accuracy ∆ z is derived in Equation (2) revealing the squared increase in error with distance characteristic of stereo depth.
∆ z ∆ d = − f   B d 2 ⇒ ∆ z = z 2   ∆ d f   B
In reality, the achieved accuracy is limited by the point matching ability of the chosen stereo processing algorithm [23]. Although state-of-the-art machine learning algorithms now outperform traditional computer vision algorithms for stereo depth estimation [24], the aim of this work is to prove the concept of guided lidar. Therefore, we adopt the established semi-global matching (SGM) algorithm for simplicity [25].
Figure 5 shows the process used to acquire stereo depth estimates in our guided dToF system. Prior to running, the cameras must be carefully calibrated by imaging a checkerboard in various poses [26]. This allows the intrinsic (focal length and optical center) and extrinsic (relative separation and rotation) camera parameters to be extracted. These are used during runtime for both rectification and conversion of disparity to distance. Rectification allows the stereo matching search space to be dramatically reduced by aligning all points in both images along the same horizontal plane.

3.3. Pixel Mapping

Once depth estimates of the scene have been acquired, they must be mapped onto each individual pixel of the lidar sensor to guide it to the appropriate depth window. The process of mapping a depth estimate from the principal (left) stereo camera to a lidar pixel is illustrated in Figure 6. Camera calibration is once again adopted to determine the translation of the lidar sensor with respect to the principal stereo camera. Capturing checkerboard images using the lidar sensor is achieved by configuring it for photon counting using intensity data. After calibration, the parameters required for pixel mapping are established: the intrinsic matrix of the principal stereo camera K s , the intrinsic matrix of the lidar K l and the extrinsic parameters of the lidar with respect to the principal camera position, composed of rotation matrix R l and translation matrix T l .
The pixel mapping process is achieved in two steps: (a) map each pixel coordinate in the stereo depth image ( x s , y s ) to its corresponding world coordinate ( X , Y , Z ) and then (b) map each world coordinate to the corresponding lidar camera pixel coordinate ( x l , y l ).
The first step is achieved by multiplying the inverse intrinsic matrix of the principal stereo camera K s by the camera coordinate to give a normalized world coordinate. The world coordinate can then be scaled appropriately by multiplying by the distance Z to that point (which has already been estimated by the stereo depth algorithm).
K s − 1 × x s y s 1 = X ~ Y ~ 1
Z · X ~ Y ~ 1 = X Y Z
The second step is achieved by multiplying the lidar camera’s extrinsic matrix P l by the prior calculated world coordinated, giving the corresponding lidar camera coordinate.
P l × X Y Z 1 = x l y l 1 where   P l = K l × R l   T l
In the case where multiple camera pixels map to one lidar pixel, the modal pixel value can be taken. Alternatively, duplicates may be discarded to save processing time.

3.4. Process Optimization

The stereo depth and pixel matching processes can be greatly optimized by reducing the total data processed in the pipeline. Figure 7a shows a full 1080 × 1440 resolution image produced by one of the stereo vision cameras. Figure 7b shows the total processing time required to rectify and run the SGM algorithm in our setup is approximately 0.4 s, equivalent to a maximum frame rate of around 2 fps. However, the projected lidar field-of-view overlaps only a small portion of the camera image. In addition, multiple pixels of the stereo vision camera occupy a single projected lidar pixel. By acquire images cropped to half height and enabling pixel binning in 2 × 2, the total amount of data is reduced by 8 times, reducing the stereo depth processing time to 50 ms without degrading the guiding depth estimates. Moreover, this also reduces number of coordinates that need to be point matched to the lidar sensor.

3.5. Process Flow

An overview of each process step in the implemented guided dToF lidar system is illustrated in Figure 8. After acquiring images from the stereo cameras, the stereo algorithm creates depth estimate image from the perspective of the chosen principal (left) camera. Depth estimates are then mapped to each pixel of the lidar sensor as described in Section 3.3. The exposure time window of each lidar pixel is then programmed to the interval corresponding to the provided depth estimate. Finally, the lidar acquisition period begins, with each pixel building a histogram of photon returns within its allocated time window to converge on a precise measured distance, producing a depth map.

3.6. Setup

Details of the guided dToF lidar demonstrator are presented in Table 2. The lidar sensor bin widths are configured to 0.375 m (2.5 ns) as an optimum ratio to the laser pulse width as recommended in [27]. While many solid-state lidar architectures utilize dToF sensors, a flash lidar architecture is adopted here for proof-of-concept.
The entire setup runs off a 1.9 GHz Intel Core i7 8th generation laptop with a Bosch GLM250VF rangefinder used to provide ground truth distance information for benchmarking. An image of the working demonstrator is shown in in Figure 9.

4. Results

4.1. Scenes

To assess the guided lidar demonstrator, multiple challenging scenes have been captured in real time running at 3 fps.

4.1.1. Outdoor Clear Conditions

The first scene is conducted under daylight conditions of 15 klux and captures a van driving away from the guided lidar setup. The constituent parts in one frame of guided lidar data from this scene are shown in Figure 10. By configuring the lidar sensor histogram window step size (1.875 m) to be less than the window size (3 m), the depth map across the van is continuous even though it spans multiple time windows.
Figure 11 shows the subsequent frames captured from the same scene. The histogram and guided time window of a sample lidar pixel are provided to validate that the pixel is correctly updated as the van drives away. The guided lidar setup continues to track and resolve the distance to the van all the way out to 75 m.

4.1.2. Outdoor Foggy Conditions

Fog presents adverse weather conditions for lidar. Not only does it reduce the intensity of the returning laser, but it also produces early laser returns reflecting from the fog itself [28]. The scene presented in Figure 12 is captured under foggy conditions with both a moving pedestrian and car. The figure shows the time window of a lidar pixel looking at the pedestrian being correctly updated independently of the pixel looking at the car, with the car distance resolved as far as 60 m under these challenging conditions.

4.1.3. Transparent Obstacles

Transparent objects such as glass present additional challenges to lidar due to the multipath reflections they introduce [29]. This is particularly problematic for approaches such as partial histogram zooming which favor the first signal peak. The point cloud in Figure 13b shows the result of evaluating only the first peak when presented with a scene through a glass door Figure 13a. Using a guided dToF approach, each lidar pixel can be correctly guided to the human figure behind the glass door, as shown in Figure 13c.

4.2. Performance

4.2.1. Measurement Error

To quantitively evaluate the performance of the guided dToF demonstrator, the measured distance to a human target is compared to ground truth distance from the rangefinder. A window of 3×3 pixels across 9 frames are assessed to provide a total 81 sample points at each distance step. The experiment was conducted outdoors under daylight conditions of 72 klux. As before, the setup is configured to run at 3 fps (no frame averaging). The results are presented in Figure 14, showing the guided lidar maintains a root-mean squared (RMS) error less than 20 cm as far 50 m. The error of the stereo depth guiding source is also evaluated, showing the squared increase in distance error characteristic of this approach.

4.2.2. Processing Time

The time consumed by each step within a single frame of our guided lidar system is shown in Figure 15. Aside from the lidar acquisition period, the main processes consume a total of 150 ms running on the 1.9 GHz Intel Core i7 processor, limiting the maximum achievable frame rate of this demonstrator to just over 6 fps.

4.3. Laser Power Efficiency

To further benchmark the presented guided dToF lidar system, the lidar sensor’s photon budget (signal and background photon arrival rate) are characterized. This allows established models [20,27] to be applied and determine the additional laser power consumed by equivalent partial histogram approaches.

4.3.1. Lidar Characterisation

To characterize the photon budget of our lidar system, a 1 m2 Lambertian target calibrated to 10% reflectivity is positioned at various distance intervals and captured. Characterization was performed under ambient daylight conditions of 60 klux. A photograph of the scene during characterization is shown in Figure 16a.
For the signal (laser) photon budget, the lidar exposure time is optimized to ensure a high signal count without clipping. For the background photon budget, the laser is disabled. A total of 100 frames are averaged and a window of 3×3 pixels are sampled. The results are shown in Figure 16b. The observed background return rate is independent of distance, in keeping with literature [30], and is measured to be 4.8 Mcounts/s, equivalent to 8 Mcounts/s at 100 klux. While the observed signal photon return rate varies with distance, it can be considered to follow an inverse square law. Fitting a trendline to this relationship allows the expected signal photons per laser cycle for any target distance ( z ) for this lidar system to be approximated as 89 z -2.

4.3.2. Laser Power Penalty of Partial Histogram Equivalent

Having characterized the lidar photon budget, the required number of laser cycles as a function of distance for equivalent partial histogram approaches can be quantified. The Thompson model presented in [27] calculates the minimum number of laser cycles for a dToF lidar system to achieve a specified precision. Using attribute of our lidar sensor (laser pulse and histogram bin width) in Table 2, and measured photon return rate in Figure 16b, the minimum laser cycles required to achieve 10 cm precision using a full histogram approach as given by the Thompson model is shown in Figure 17a.
An equivalent sliding partial histogram approach (8×0.375 m bins sliding in intervals of 3 m) would require the same number of laser cycles for distances up to the width of the first slide window. Past this distance, the total laser cycles required to measure any given distance with 10 cm precision is the sum of the full histogram laser cycle value for each additional 3 m slide window. The resulting increase in laser cycles for an equivalent sliding partial histogram approach is shown in Figure 17a.
An equivalent zooming partial histogram approach would require an additional zoom step to measure distances greater than 3 m by configuring each bin to 3 m wide. Past 27 m, yet another zoom step would be required, configuring each bin to 27 m wide. At each zoom step, the laser must be cycled enough times to detect the peak bin within a specified probability of detection for a given distance. Using the probability of detection model for histogram-based dToF published in [20] and specifying a minimum 99.7% detection rate (3σ rule), the minimum number of laser cycles for each step of an equivalent zooming dToF sensor is given in Figure 17b. The total laser cycles required to zoom to a given distance is therefore sum of laser cycles required at each zoom step for a given distance, shown in Figure 17a.
The required increase in total laser cycles for each equivalent partial histogram approach compared to a full histogram/guided approach, is shown in Figure 17c. At the maximum distance of 75 m achieved by our guided dToF system, a minimum 6× laser power is saved compared to adopting an equivalent partial histogram approach. It should be noted that the sliding approach modelled here assumes no overlapping of windows between steps which would further increase its laser power penalty.

5. Discussion

A summary of the presented guided dToF demonstrator performance alongside state-of-the-art dToF lidar sensors is presented in Table 3. The table shows that, while the implemented system uses a single-tier sensor chip with a relatively small number of histogram bins in each macropixel, the combined range and frame rate achieved in bright ambient conditions through a guided dToF approach is amongst the top performing. Using only 8 histogram bins per macropixel, the guided dToF demonstrator achieves a maximum distance of 75 m. A conventional full histogram approach with equivalent 0.375 m bin width would require over 200 histogram bins per macropixel. This is much more than any state-of-the-art sensor is yet to achieve and equivalent to a 25× increase in pixel histogram area for our sensor.
The ability to correctly guide lidar under multipath conditions is also of unique value. In addition to the glass obstruction tested in Figure 15, many other real-world conditions can create multiple signal peaks which can be incorrectly interpreted by a standalone lidar. These include obstructions from smoke [33] and retroreflectors such as road signs [34].
Various enhancements are proposed to enable the preliminary guided dToF demonstrator presented here to achieve the performance required for automotive lidar of 200 m range at 25 fps [35]. Firstly, by adopting the increased sensitivity of state-of-the-art SPAD processes [32,36], the maximum range of the system can be extended while reducing the required lidar exposure time. Figure 15 shows the stereo depth processing algorithm to be the next most time-dominant process after the lidar exposure time. A guided dToF solutions with a greater capacity for histogram bins would tolerate larger error from the stereo depth estimates, allowing for less accurate but faster stereo algorithms [37]. Parallel execution of the various guided processes and adoption of GPU processing will also enable further acceleration. Finally, the use of different depth estimate sources (radar, ultrasound) should be explored, as well as processing methods such as Kalman filters to extrapolate previous depth frames.
For the practical realization of guided dToF in self-driving vehicle using the specific implementation presented here, the main practical challenge is camera alignment. Any variation in the extrinsic properties of the cameras due to vehicle movement or vibrations not only worsen the accuracy of stereo depth accuracy, but also impact pixel mapping of depth estimates to the lidar sensor. While continuous camera self-calibration techniques have been developed [38], these need to be explored in the context of a stereo camera guided dToF lidar system.

Author Contributions

Conceptualization, F.T., T.A. and R.H.; methodology, F.T., I.G., T.A. and R.H.; software, F.T. and I.G.; validation, F.T.; formal analysis, F.T.; investigation, F.T.; writing—original draft preparation, F.T.; writing—review and editing, F.T, T.A. and R.H.; supervision, I.G., T.A. and R.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Ouster Inc.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to thank Robert Fisher from the University of Edinburgh for guidance on stereo depth and all the staff at Ouster Inc. for their continued support throughout this project.

Open Access

For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) license to any Author Accepted Manuscript version arising from this submission.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rangwala, S. Automotive LiDAR Has Arrived. In Forbes: 2022.
  2. Wang, Z.; Wu, Y.; Niu, Q. Multi-Sensor Fusion in Automated Driving: A Survey. IEEE Access 2020, 8, 2847–2868. [Google Scholar] [CrossRef]
  3. Aptiv; Audi; Baidu; BMW; Continental; Daimler; Group, F.; Here; Intel; Volkswagen Safety First For Automated Driving [White Paper]; 2019.
  4. Ford, A Matter of Trust: Ford’s Approach to Developing Self-driving Vehicles. In 2018.
  5. Lambert, J.; Carballo, A.; Cano, A. M.; Narksri, P.; Wong, D.; Takeuchi, E.; Takeda, K. Performance Analysis of 10 Models of 3D LiDARs for Automated Driving. IEEE Access 2020, 8, 131699–131722. [Google Scholar] [CrossRef]
  6. Villa, F.; Severini, F.; Madonini, F.; Zappa, F. , SPADs and SiPMs Arrays for Long-Range High-Speed Light Detection and Ranging (LiDAR). Sensors (Basel) 2021, 21. [Google Scholar] [CrossRef] [PubMed]
  7. Rangwala, S., Lidar Miniaturization. In ADAS & Autonomous Vehicle International: 2023; Vol. April, pp 34-38.
  8. Niclass, C.; Soga, M.; Matsubara, H.; Ogawa, M.; Kagami, M. In A 0.18µm CMOS SoC for a 100m-range 10fps 200×96-pixel time-of-flight depth sensor, 2013 IEEE International Solid-State Circuits Conference Digest of Technical Papers, 17-21 Feb. 2013, 2013; 2013; pp 488-489.
  9. Ximenes, A. R.; Padmanabhan, P.; Lee, M. J.; Yamashita, Y.; Yaung, D. N.; Charbon, E. In A 256×256 45/65nm 3D-stacked SPAD-based direct TOF image sensor for LiDAR applications with optical polar modulation for up to 18.6dB interference suppression, 2018 IEEE International Solid - State Circuits Conference - (ISSCC), 11-15 Feb. 2018, 2018; 2018; pp 96-98.
  10. Henderson, R. K.; Johnston, N.; Hutchings, S. W.; Gyongy, I.; Abbas, T. A.; Dutton, N.; Tyler, M.; Chan, S.; Leach, J. In 5.7 A 256×256 40nm/90nm CMOS 3D-Stacked 120dB Dynamic-Range Reconfigurable Time-Resolved SPAD Imager, 2019 IEEE International Solid- State Circuits Conference - (ISSCC), 17-21 Feb. 2019, 2019; 2019; pp 106-108.
  11. Padmanabhan, P.; Zhang, C.; Cazzaniga, M.; Efe, B.; Ximenes, A. R.; Lee, M. J.; Charbon, E. In 7.4 A 256×128 3D-Stacked (45nm) SPAD FLASH LiDAR with 7-Level Coincidence Detection and Progressive Gating for 100m Range and 10klux Background Light, 2021 IEEE International Solid- State Circuits Conference (ISSCC), 13-22 Feb. 2021, 2021; 2021; pp 111-113.
  12. Taneski, F.; Gyongy, I.; Abbas, T. A.; Henderson, R. , Guided Flash Lidar: A Laser Power Efficient Approach for Long-Range Lidar. In International Image Sensor Workshop, Crieff, Scotland, 2023.
  13. Zhang, C.; Lindner, S.; Antolović, I. M.; Pavia, J. M.; Wolf, M.; Charbon, E. , A 30-frames/s, 252 x 144 SPAD Flash LiDAR With 1728 Dual-Clock 48.8-ps TDCs, and Pixel-Wise Integrated Histogramming. IEEE Journal of Solid-State Circuits, 2019; 54, 1137–1151. [Google Scholar]
  14. Zhang, C.; Zhang, N.; Ma, Z.; Wang, L.; Qin, Y.; Jia, J.; Zang, K. , A 240 x 160 3D Stacked SPAD dToF Image Sensor with Rolling Shutter and In Pixel Histogram for Mobile Devices. IEEE Open Journal of the Solid-State Circuits Society, 2021; 2, 3–11. [Google Scholar]
  15. Kim, B.; Park, S.; Chun, J. H.; Choi, J.; Kim, S. J.; Kim, S. J.; Kim, S. J.; Kim, S. J. In 7.2 A 48×40 13.5mm Depth Resolution Flash LiDAR Sensor with In-Pixel Zoom Histogramming Time-to-Digital Converter, 2021 IEEE International Solid- State Circuits Conference (ISSCC), 13-22 Feb. 2021, 2021; 2021; pp 108-110.
  16. Park, S.; Kim, B.; Cho, J.; Chun, J.; Choi, J.; Kim, S.; Kim, S.; Kim, S.; Kim, S.; Kim, S. In 5.3 An 80×60 Flash LiDAR Sensor with In-Pixel Histogramming TDC Based on Quaternary Search and Time-Gated Δ-Intensity Phase Detection for 45m Detectable Range and Background Light Cancellation, 2022 IEEE International Solid- State Circuits Conference (ISSCC), 2022; 2022.
  17. Stoppa, D.; Abovyan, S.; Furrer, D.; Gancarz, R.; Jessenig, T.; Kappel, R.; Lueger, M.; Mautner, C.; Mills, I.; Perenzoni, D.; Roehrer, G.; Taloud, P.-Y. In A Reconfigurable QVGA/Q3VGA Direct Time-of-Flight 3D Imaging System with On-chip Depth-map Computation in 45/40nm 3D-stacked BSI SPAD CMOS, International Image Sensor Workshop 2021, 2021; 2021.
  18. Taloud, P.-Y.; Bernhard, S.; Biber, A.; Boehm, M.; Chelvam, P.; Cruz, A.; Chele, A. D.; Gancarz, R.; Ishizaki, K.; Jantscher, P.; Jessenig, T.; Kappel, R.; Lin, L.; Lindner, S.; Mahmoudi, H.; Makkaoui, A.; Miguel, J.; Padmanabhan, P.; Perruchoud, L.; Perenzoni, D.; Roehrer, G.; Srowig, A.; Vaello, B.; Stoppa, D. , A 1.2K dots dToF 3D Imaging System in 45/22nm 3D-stacked BSI SPAD CMOS. In International SPAD Sensor Workshop, 2022.
  19. Sudhakar, S.; Sze, V.; Karaman, S. Data Centers on Wheels: Emissions From Computing Onboard Autonomous Vehicles. IEEE Micro 2023, 43, 29–39. [Google Scholar] [CrossRef]
  20. Taneski, F.; Abbas, T. A.; Henderson, R. K. Laser Power Efficiency of Partial Histogram Direct Time-of-Flight LiDAR Sensors. Journal of Lightwave Technology 2022, 40, 5884–5893. [Google Scholar] [CrossRef]
  21. Gyongy, I.; Erdogan, A. T.; Dutton, N. A.; Mai, H.; Rocca, F. M. D.; Henderson, R. K. In A 200kFPS, 256×128 SPAD dToF sensor with peak tracking and smart readout, International Image Sensor Workshop 2021, 2021; 2021.
  22. Fisher, R. , Subpixel Estimation. In 2021; pp 1217-1220.
  23. Geiger, A.; Lenz, P.; Urtasun, R. In Are we ready for autonomous driving? The KITTI vision benchmark suite, 2012 IEEE Conference on Computer Vision and Pattern Recognition, 16-21 June 2012; 2012; pp 3354-3361. 21 June.
  24. Laga, H.; Jospin, L. V.; Boussaid, F.; Bennamoun, M. , A Survey on Deep Learning Techniques for Stereo-Based Depth Estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence 2022, 44, 1738–1764. [Google Scholar] [CrossRef] [PubMed]
  25. Hirschmuller, H. , Stereo Processing by Semiglobal Matching and Mutual Information. IEEE Transactions on Pattern Analysis and Machine Intelligence 2008, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
  26. Zhang, Z. , A flexible new technique for camera calibration. IEEE Transactions on Pattern Analysis and Machine Intelligence 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
  27. Koerner, L. J. , Models of Direct Time-of-Flight Sensor Precision That Enable Optimal Design and Dynamic Configuration. IEEE Transactions on Instrumentation and Measurement 2021, 70, 1–9. [Google Scholar] [CrossRef]
  28. Bijelic, M.; Gruber, T.; Ritter, W. In A Benchmark for Lidar Sensors in Fog: Is Detection Breaking Down?, 2018 IEEE Intelligent Vehicles Symposium (IV), 26-30 June 2018; 2018; pp 760-767. 30 June.
  29. Gyongy, I.; Dutton, N. A.; Henderson, R. K. , Direct Time-of-Flight Single-Photon Imaging. IEEE Transactions on Electron Devices 2022, 1–12. [Google Scholar] [CrossRef]
  30. Tontini, A.; Gasparini, L.; Perenzoni, M. , Numerical Model of SPAD-Based Direct Time-of-Flight Flash LIDAR CMOS Image Sensors. Sensors (Basel) 2020, 20. [Google Scholar] [CrossRef] [PubMed]
  31. Okino, T.; Yamada, S.; Sakata, Y.; Kasuga, S.; Takemoto, M.; Nose, Y.; Koshida, H.; Tamaru, M.; Sugiura, Y.; Saito, S.; Koyama, S.; Mori, M.; Hirose, Y.; Sawada, M.; Odagawa, A.; Tanaka, T. In 5.2 A 1200×900 6µm 450fps Geiger-Mode Vertical Avalanche Photodiodes CMOS Image Sensor for a 250m Time-of-Flight Ranging System Using Direct-Indirect-Mixed Frame Synthesis with Configurable-Depth-Resolution Down to 10cm, 2020 IEEE International Solid- State Circuits Conference - (ISSCC), 16-20 Feb. 2020, 2020; 2020; pp 96-98.
  32. Kumagai, O.; Ohmachi, J.; Matsumura, M.; Yagi, S.; Tayu, K.; Amagawa, K.; Matsukawa, T.; Ozawa, O.; Hirono, D.; Shinozuka, Y.; et al. In 7.3 A 189×600 Back-Illuminated Stacked SPAD Direct Time-of-Flight Depth Sensor for Automotive LiDAR Systems, 2021 IEEE International Solid- State Circuits Conference (ISSCC), 13-22 Feb. 2021, 2021; 2021; pp 110-112.
  33. Wallace, A. M.; Halimi, A.; Buller, G. S. , Full Waveform LiDAR for Adverse Weather Conditions. IEEE Transactions on Vehicular Technology 2020, 69, 7064–7077. [Google Scholar] [CrossRef]
  34. Schönlieb, A.; Lugitsch, D.; Steger, C.; Holweg, G.; Druml, N. In Multi-Depth Sensing for Applications With Indirect Solid-State LiDAR, 2020 IEEE Intelligent Vehicles Symposium (IV), 19 Oct.-13 Nov. 2020, 2020; 2020; pp 919-925.
  35. Warren, M. E. In Automotive LIDAR Technology, 2019 Symposium on VLSI Circuits, 9-14 June 2019; 2019; pp C254-C255. 14 June.
  36. Morimoto, K.; Iwata, J.; Shinohara, M.; Sekine, H.; Abdelghafar, A.; Tsuchiya, H.; Kuroda, Y.; Tojima, K.; Endo, W.; Maehashi, Y.; et al. In 3.2 Megapixel 3D-Stacked Charge Focusing SPAD for Low-Light Imaging and Depth Sensing, 2021 IEEE International Electron Devices Meeting (IEDM), 11-16 Dec. 2021, 2021; 2021; pp 20.2.1-20.2.4.
  37. Abhishek Badki; Alejandro Troccoli; Kihwan Kim; Jan Kautz; Pradeep Sen; Gallo, O., Bi3D: Stereo Depth Estimation via Binary Classifications. Computer Vision and Pattern Recognition CVPR 2020, 2020.
  38. Dang, T.; Hoffmann, C.; Stiller, C. , Continuous Stereo Self-Calibration by Camera Parameter Tracking. IEEE Transactions on Image Processing 2009, 18, 1536–1550. [Google Scholar] [CrossRef] [PubMed]
Preprints 86722 g001
Figure 1. Direct time-of-flight (a) ideal case with no ambient background photons (b) accumulating photons over multiple laser cycles to average out background (c) compressing photon data into a histogram (d) proposed ‘guided’ approach.
Figure 1. Direct time-of-flight (a) ideal case with no ambient background photons (b) accumulating photons over multiple laser cycles to average out background (c) compressing photon data into a histogram (d) proposed ‘guided’ approach.
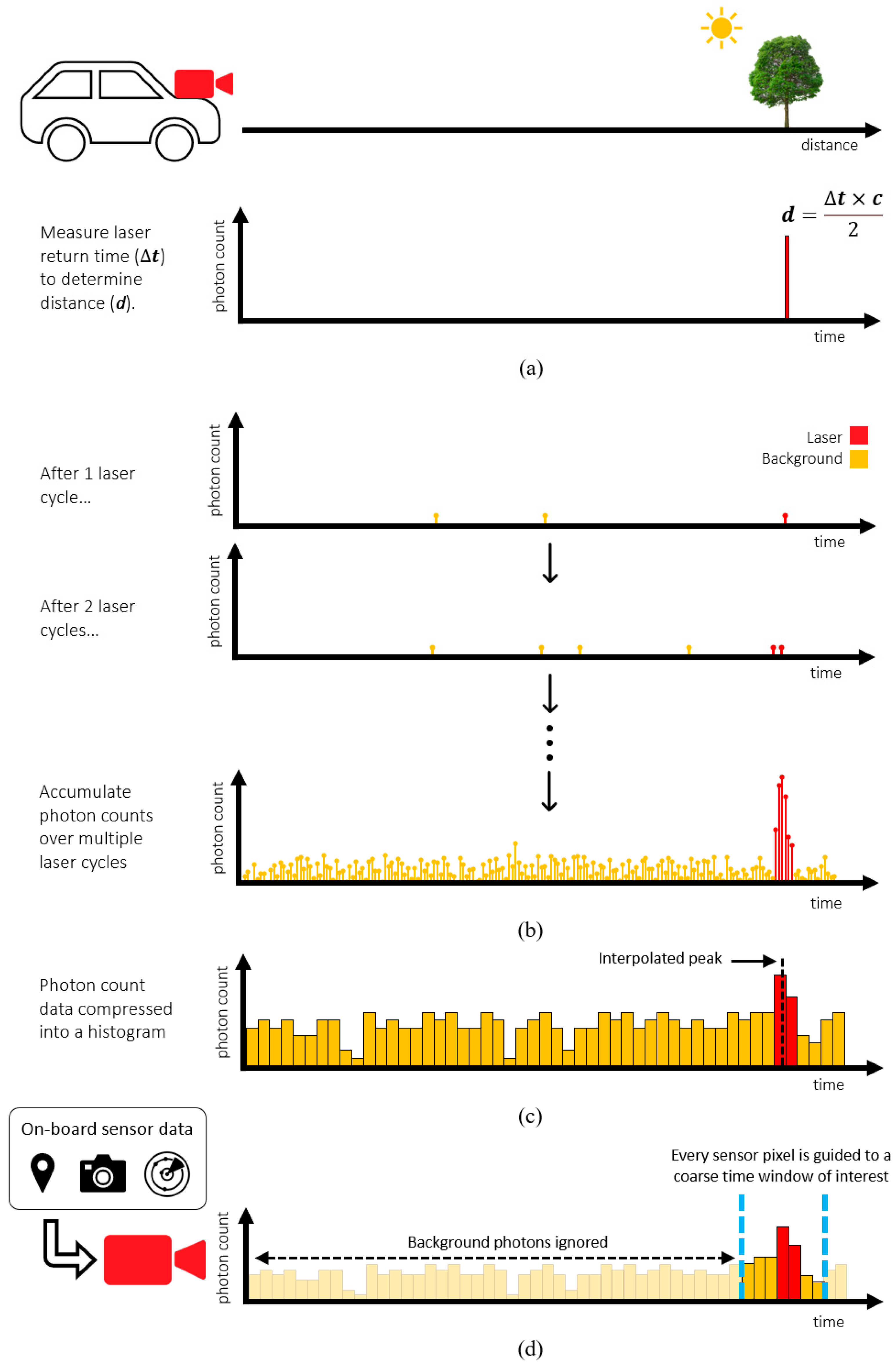
Preprints 86722 g001
Preprints 86722 g002
Figure 2. Bin capacity per ToF pixel of published dToF sensor arrays.
Figure 2. Bin capacity per ToF pixel of published dToF sensor arrays.
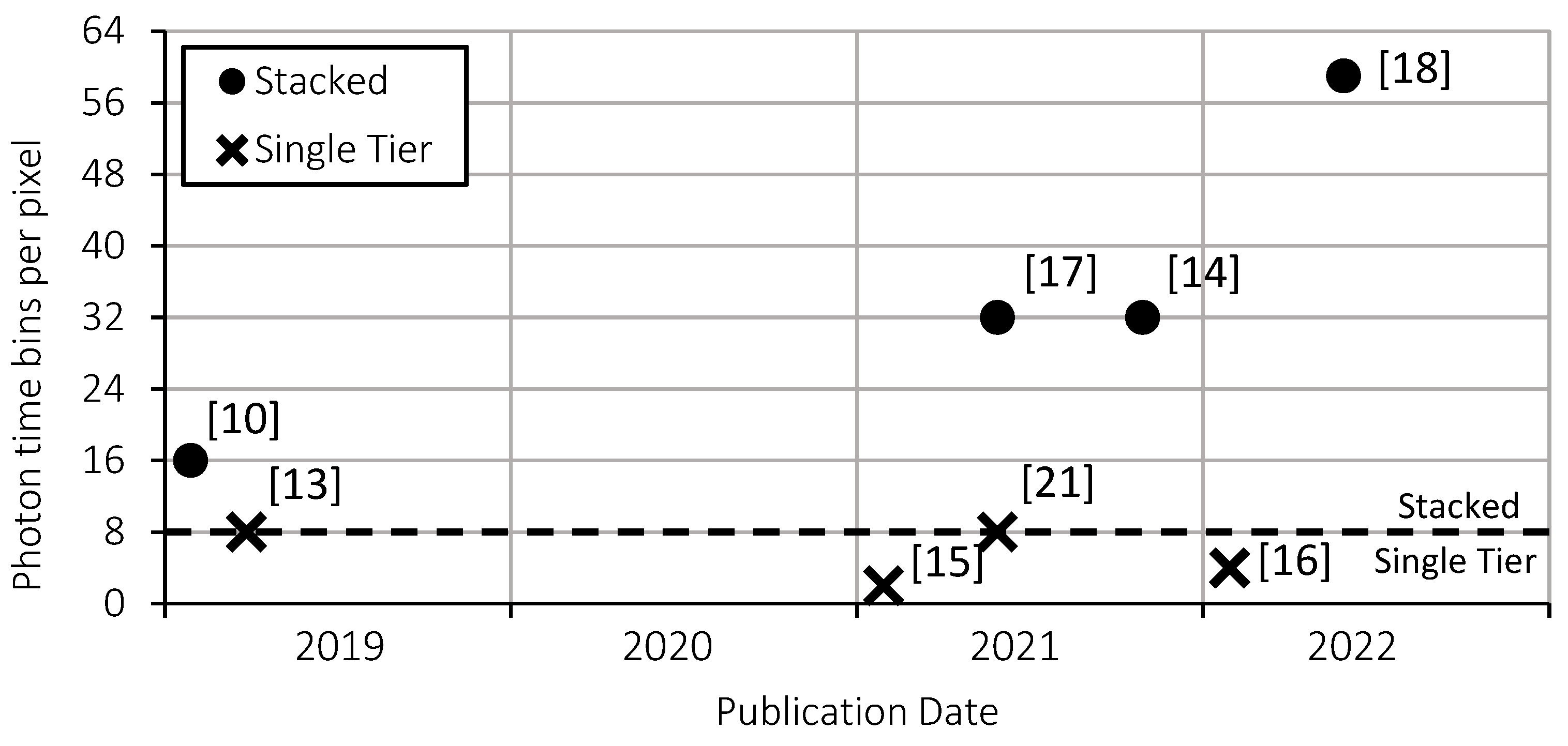
Preprints 86722 g002
Preprints 86722 g003
Figure 3. Illustration of partial histogram approaches (a) zooming and (b) sliding. Reproduced from [12].
Figure 3. Illustration of partial histogram approaches (a) zooming and (b) sliding. Reproduced from [12].
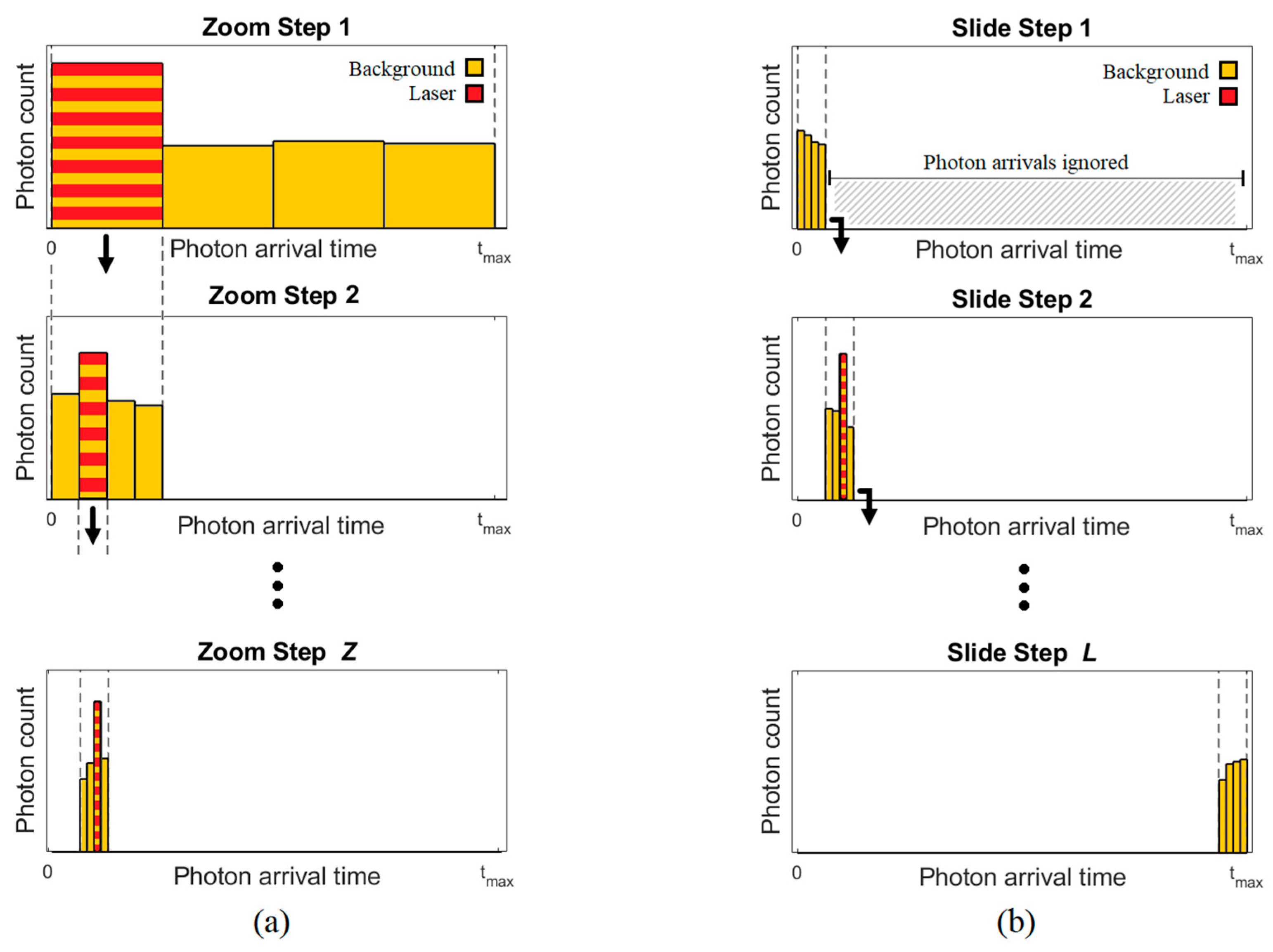
Preprints 86722 g003
Preprints 86722 g004
Figure 4. Micrograph of the guided dToF sensor. Reproduced from [21] with author's permission.
Figure 4. Micrograph of the guided dToF sensor. Reproduced from [21] with author's permission.
Preprints 86722 g004
Preprints 86722 g005
Figure 5. Process flow diagram of acquiring stereo depth estimates for the guided lidar system.
Figure 5. Process flow diagram of acquiring stereo depth estimates for the guided lidar system.
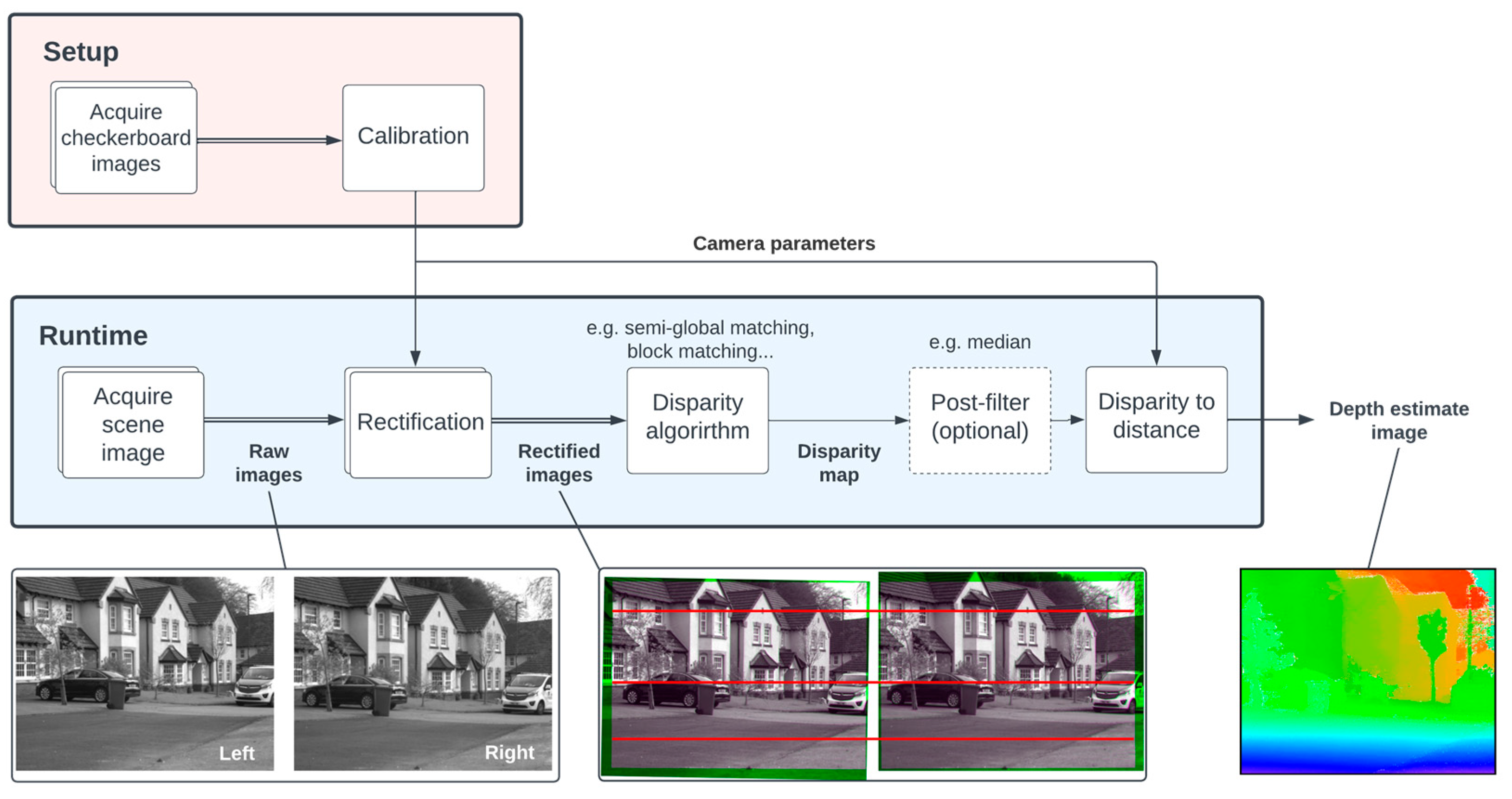
Preprints 86722 g005
Preprints 86722 g006
Figure 6. Pixel mapping a point from one stereo camera to the corresponding lidar sensor pixel.
Figure 6. Pixel mapping a point from one stereo camera to the corresponding lidar sensor pixel.
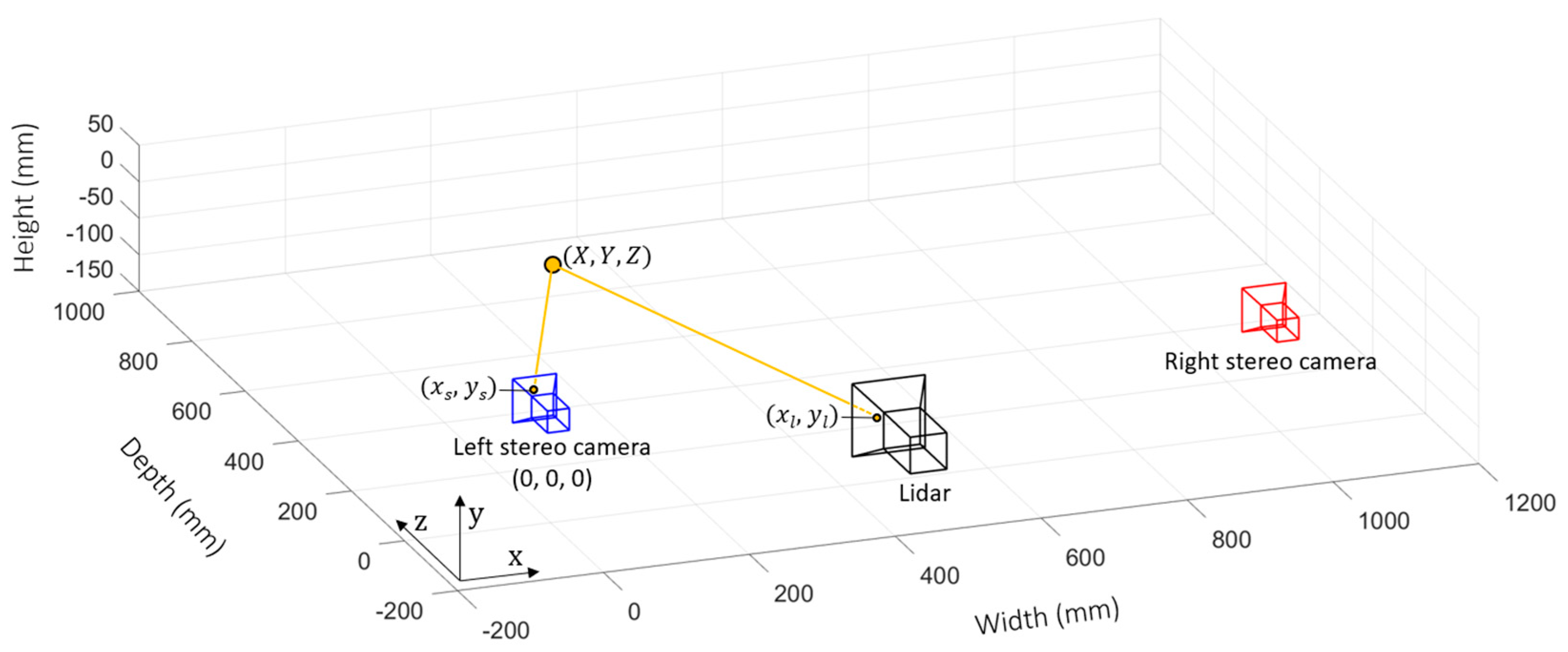
Preprints 86722 g006
Preprints 86722 g007
Figure 7. (a) Full resolution stereo camera image compared to the projected lidar FOV (b) processing time for rectification and SGM stereo depth processing in MATLAB using the current setup.
Figure 7. (a) Full resolution stereo camera image compared to the projected lidar FOV (b) processing time for rectification and SGM stereo depth processing in MATLAB using the current setup.
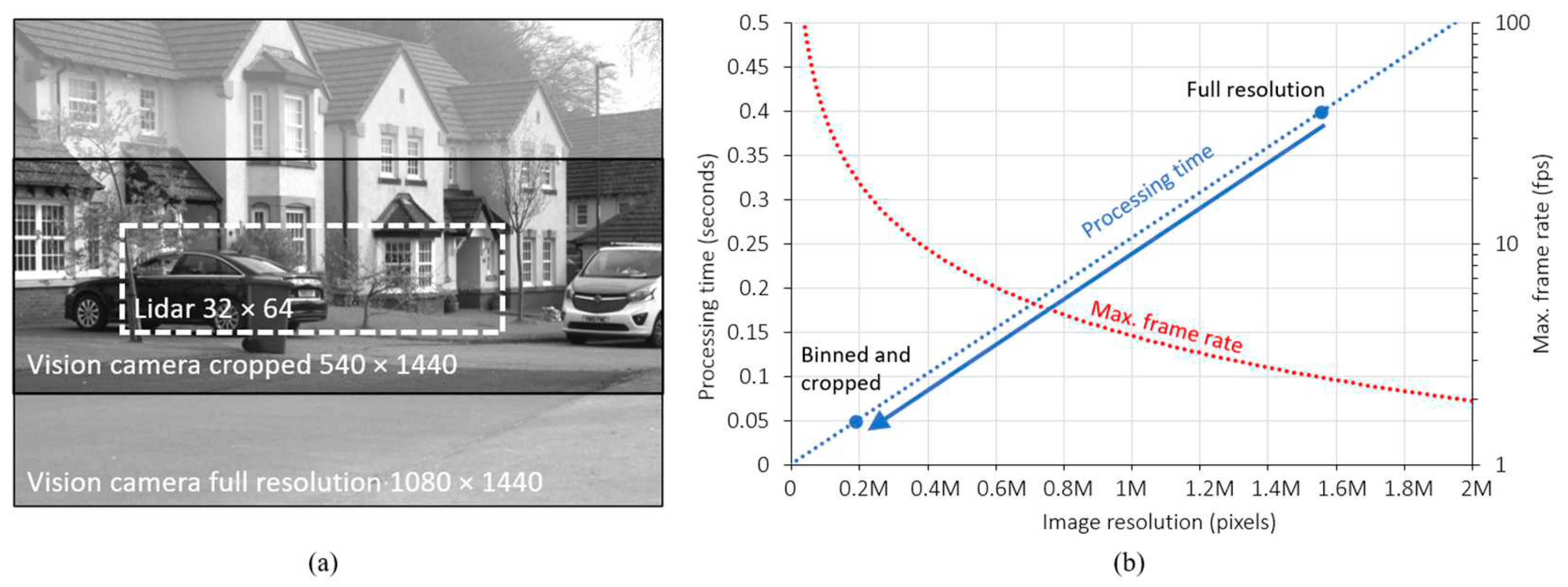
Preprints 86722 g007
Preprints 86722 g008
Figure 8. The main steps in the guided dToF lidar process. Adapted from [12].
Figure 8. The main steps in the guided dToF lidar process. Adapted from [12].
Preprints 86722 g008
Preprints 86722 g009
Figure 9. The guided dToF lidar demonstrator described in this publication. Adapted from [12].
Figure 9. The guided dToF lidar demonstrator described in this publication. Adapted from [12].
Preprints 86722 g009
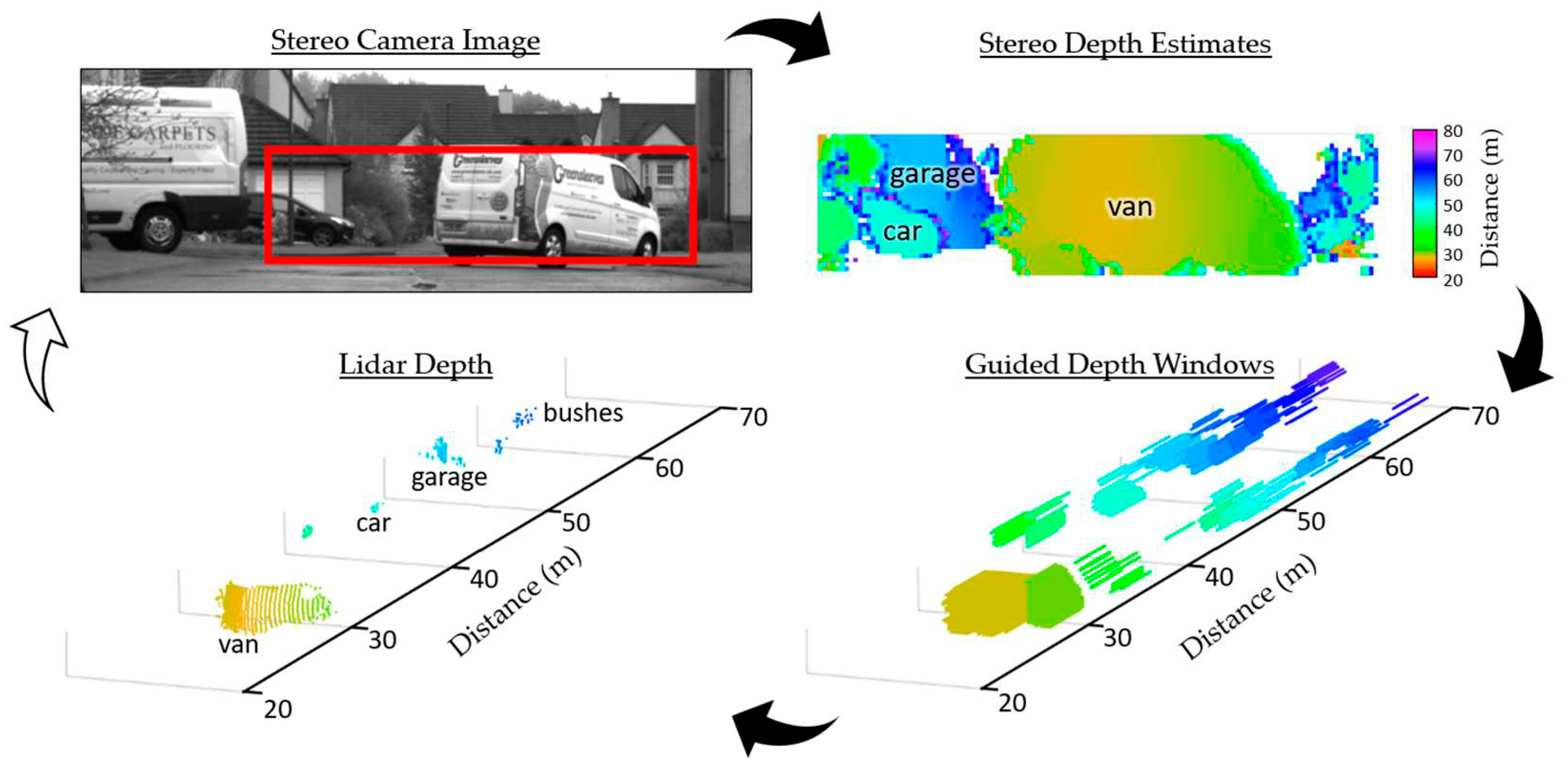
Preprints 86722 g010
Figure 10. One frame of guided lidar data showing each of the constituent parts of the process as outlined in Figure 8. Adapted from [12].
Figure 10. One frame of guided lidar data showing each of the constituent parts of the process as outlined in Figure 8. Adapted from [12].
Preprints 86722 g010
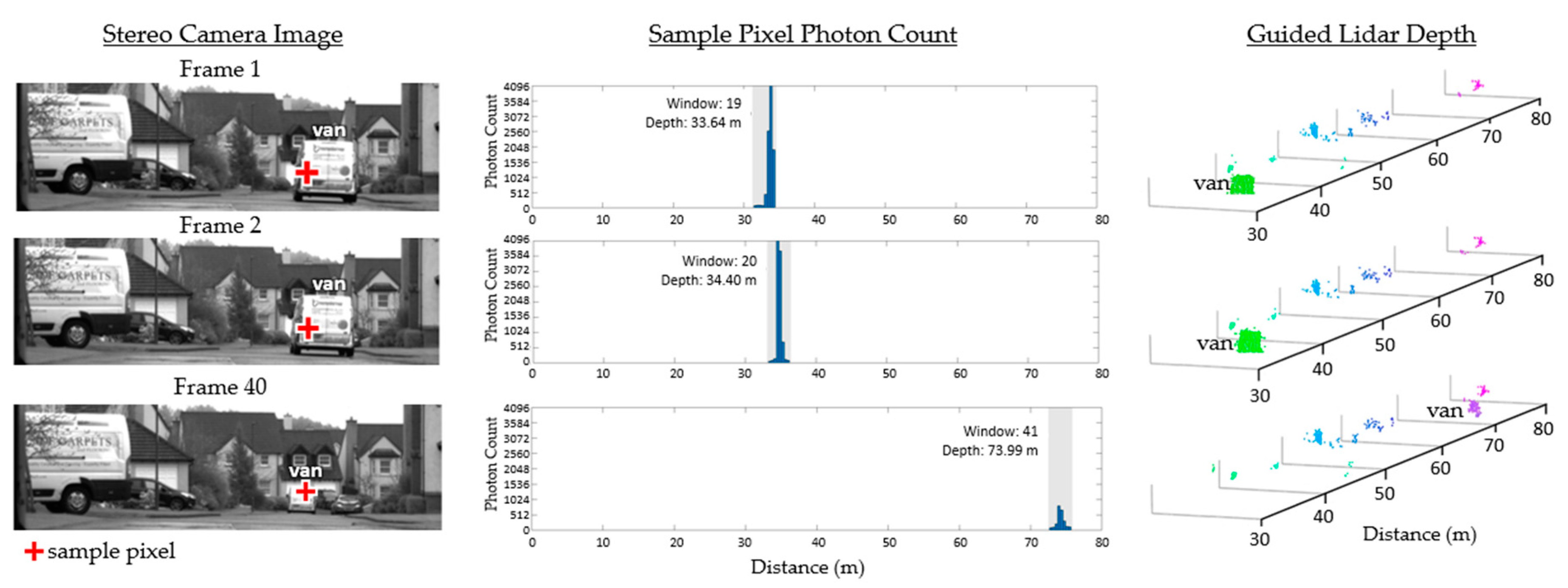
Preprints 86722 g011
Figure 11. Three further frames of the outdoor scene in Figure 10 on a clear day. A sample pixel of the lidar sensor shows the time window it is configured to and the resulting histogram produced. Reproduced from [12].
Figure 11. Three further frames of the outdoor scene in Figure 10 on a clear day. A sample pixel of the lidar sensor shows the time window it is configured to and the resulting histogram produced. Reproduced from [12].
Preprints 86722 g011
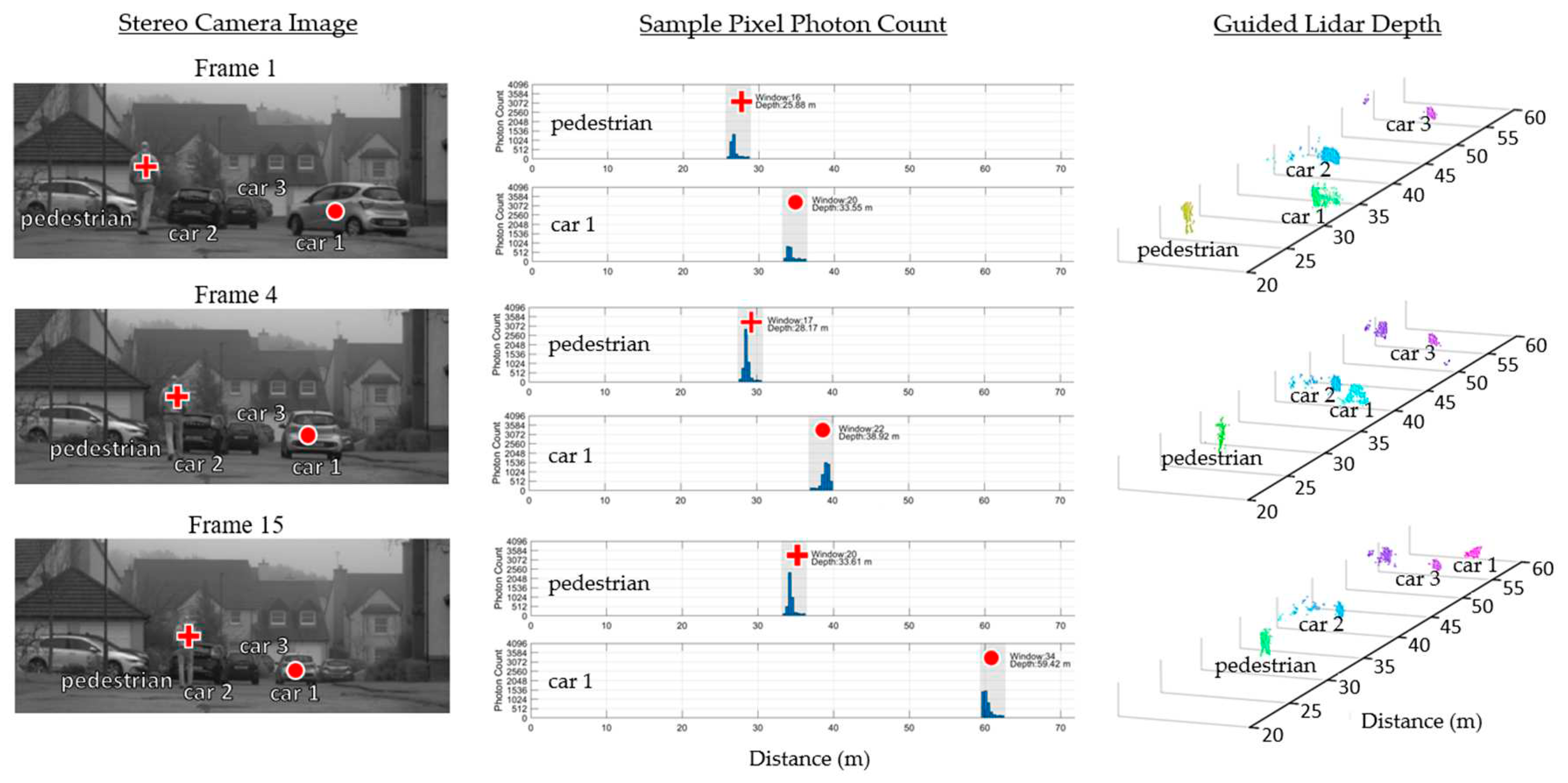
Preprints 86722 g012
Figure 12. Three frames of an outdoor scene on a foggy day. Sample pixels of the lidar sensor show the time windows they are configured to and the resulting histogram produced.
Figure 12. Three frames of an outdoor scene on a foggy day. Sample pixels of the lidar sensor show the time windows they are configured to and the resulting histogram produced.
Preprints 86722 g012
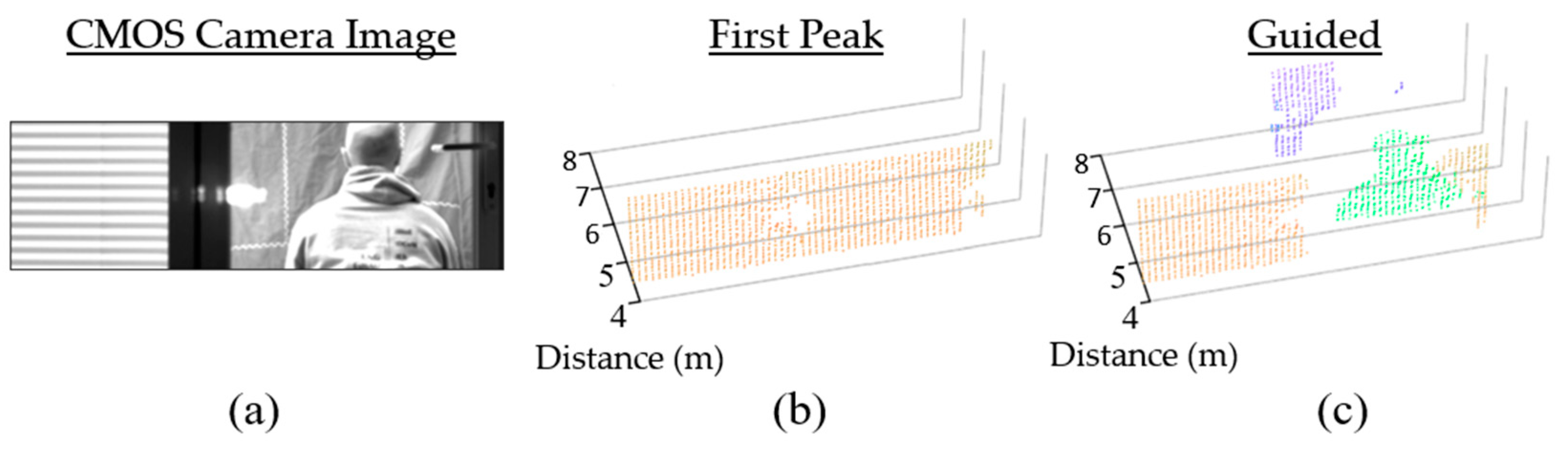
Preprints 86722 g013
Figure 13. (a) a scene through a glass door (b) human figure obscured if only the first lidar peak is used (c) human figure resolved using guided dToF lidar. Reproduced from [12].
Figure 13. (a) a scene through a glass door (b) human figure obscured if only the first lidar peak is used (c) human figure resolved using guided dToF lidar. Reproduced from [12].
Preprints 86722 g013
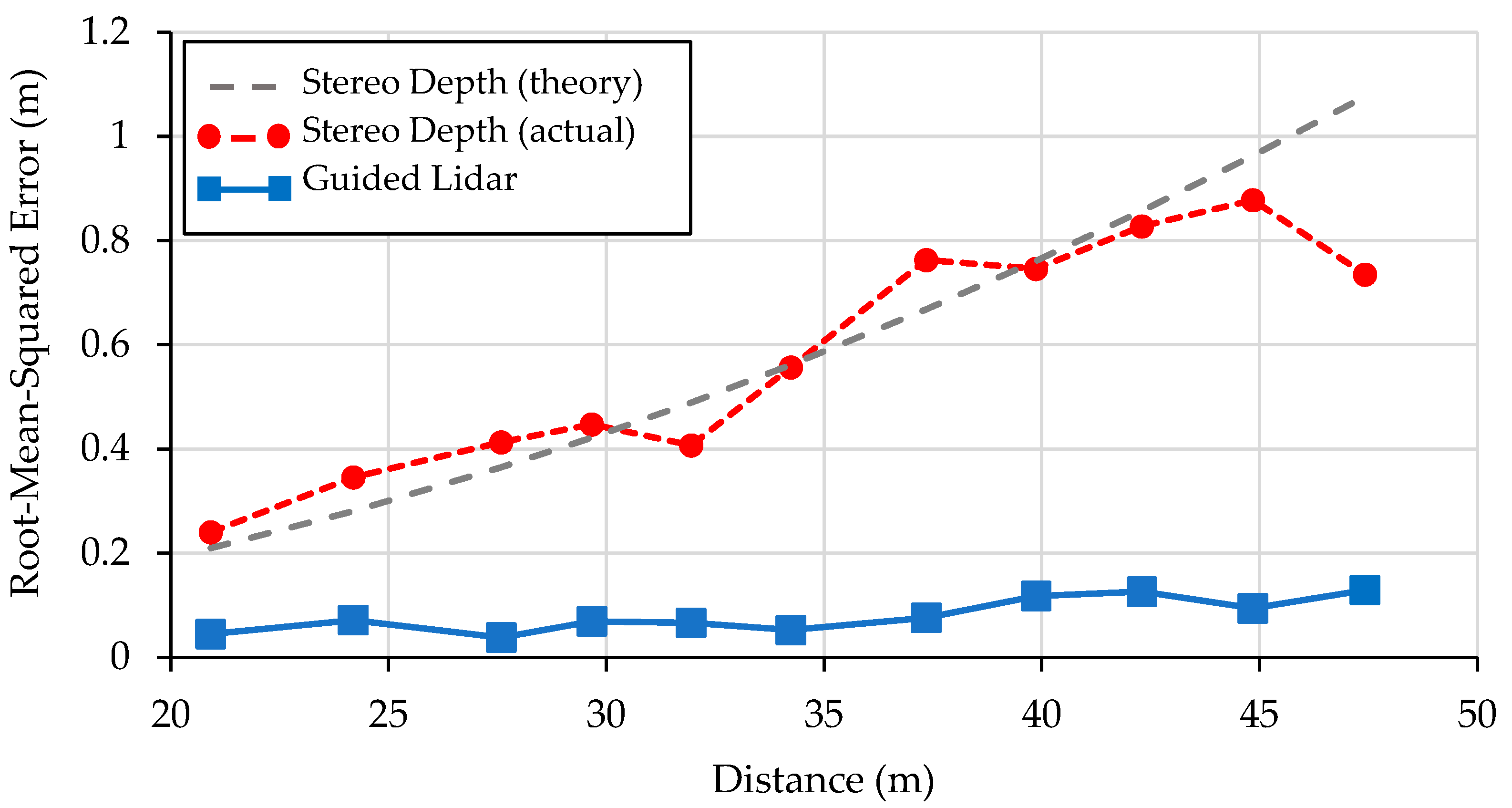
Preprints 86722 g014
Figure 14. Distance measurement error operating at 3 fps under 72 klux ambient intensity. Theoretical stereo depth accuracy based on to Equation (2) assuming a sub-pixel disparity resolution of 0.25 pixels. Reproduced from [12].
Figure 14. Distance measurement error operating at 3 fps under 72 klux ambient intensity. Theoretical stereo depth accuracy based on to Equation (2) assuming a sub-pixel disparity resolution of 0.25 pixels. Reproduced from [12].
Preprints 86722 g014
Preprints 86722 g015
Figure 15. Execution time of each main process in one frame of our guided dToF demonstrator.
Figure 15. Execution time of each main process in one frame of our guided dToF demonstrator.
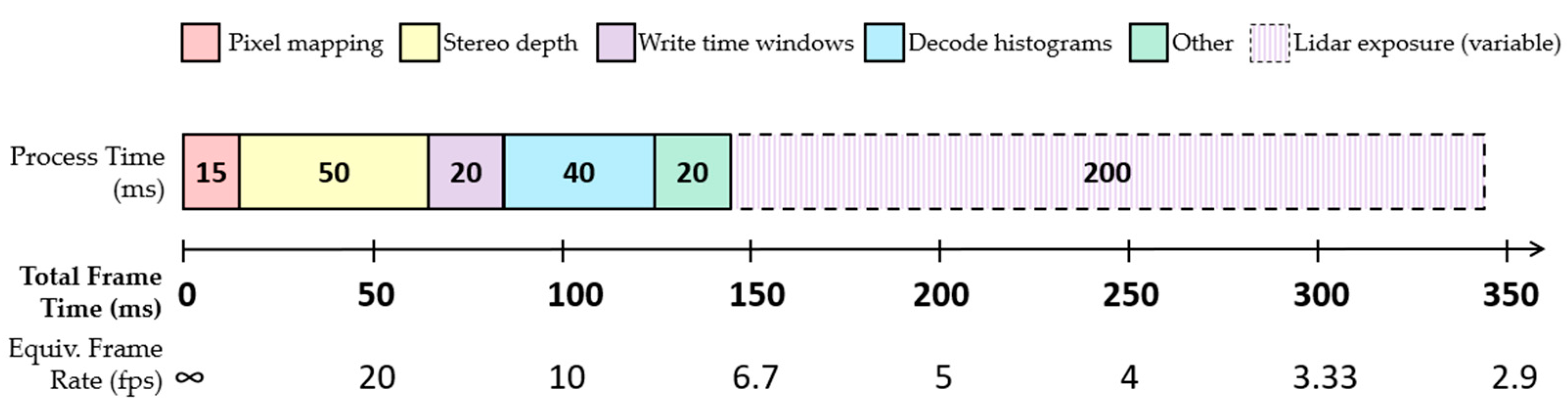
Preprints 86722 g015
Preprints 86722 g016
Figure 16. (a) Setup during characterization using a 10% reflectivity target under ambient conditions of 60 klux (b) measured and extrapolated photon return rate during characterization. .
Figure 16. (a) Setup during characterization using a 10% reflectivity target under ambient conditions of 60 klux (b) measured and extrapolated photon return rate during characterization. .
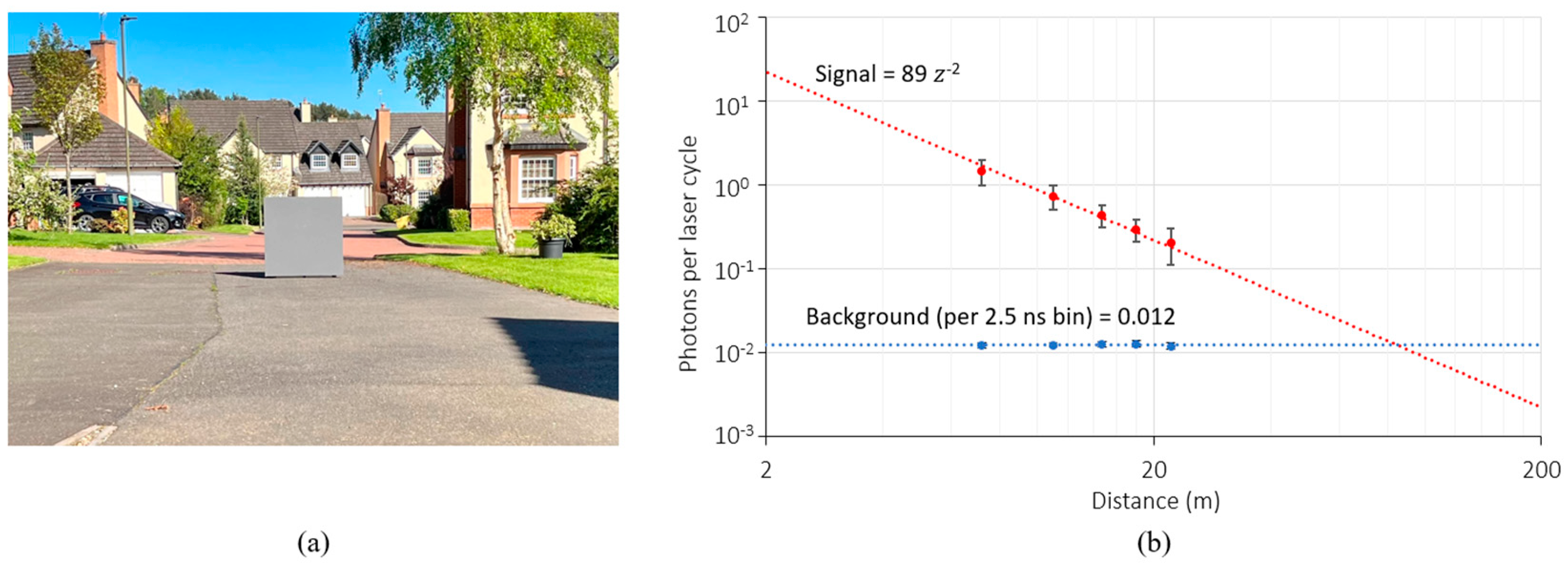
Preprints 86722 g016
Preprints 86722 g017
Figure 17. (a) Minimum laser cycles required to achieve 10 cm depth precision using the presented guided lidar configuration and equivalent sliding and zooming partial histogram approaches (b) minimum laser cycles required for each step of an equivalent zooming partial histogram approach (c) laser power penalty of equivalent sliding and zooming partial histogram approaches.
Figure 17. (a) Minimum laser cycles required to achieve 10 cm depth precision using the presented guided lidar configuration and equivalent sliding and zooming partial histogram approaches (b) minimum laser cycles required for each step of an equivalent zooming partial histogram approach (c) laser power penalty of equivalent sliding and zooming partial histogram approaches.
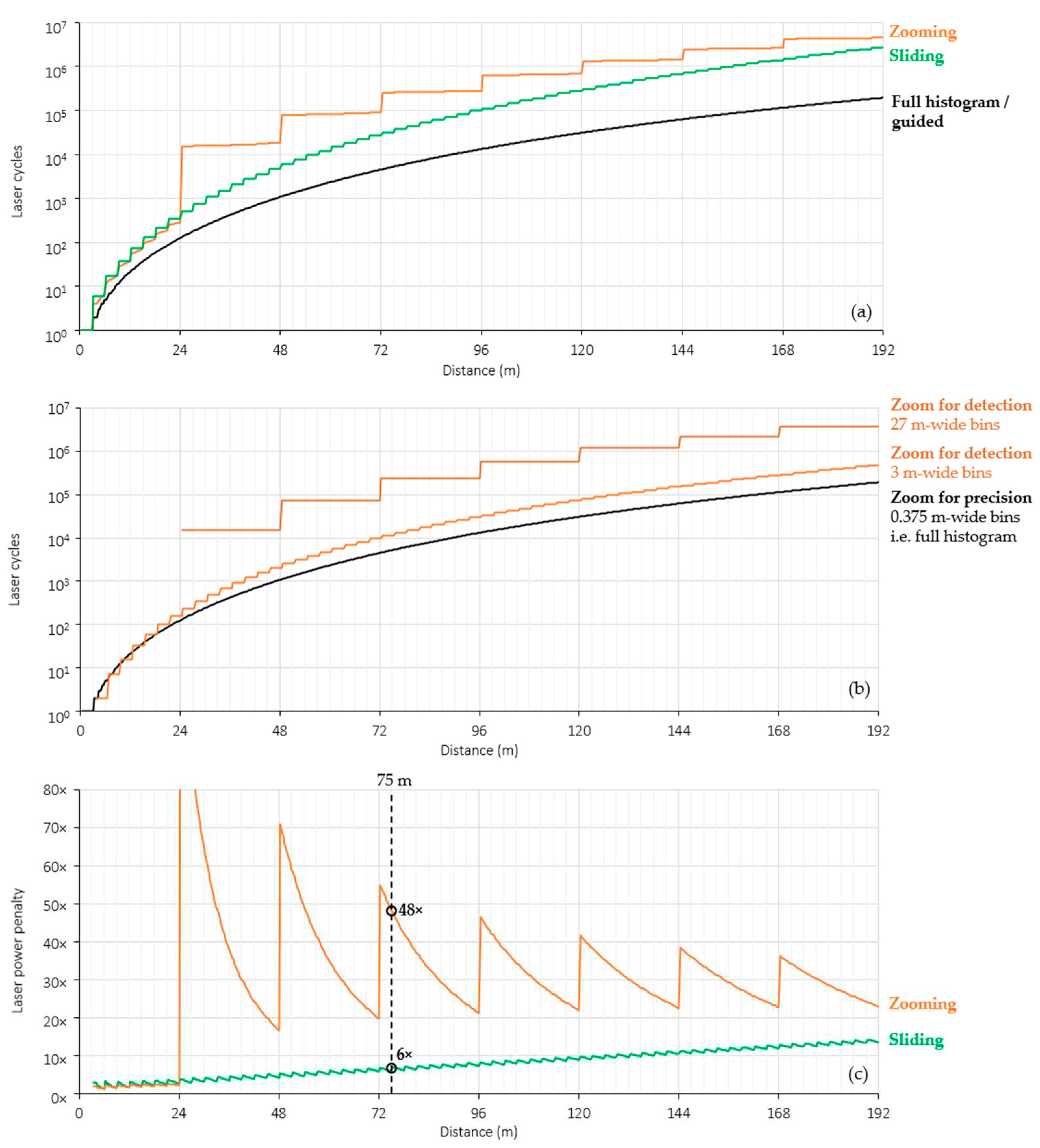
Preprints 86722 g017
Table 1. Merits of different dToF histogram approaches alongside the proposed guided approach.
Table 1. Merits of different dToF histogram approaches alongside the proposed guided approach.
Parameter Full Histogram Partial Histogram Guided
Zooming Sliding
Laser power penalty Low High High Low
Area requirement High Low Low Low
Data volume High Low High Low
Multipath reflection artefacts Low Medium Low Low
Motion artefacts Low Medium Medium Medium
System complexity Low Low Low High
Table 2. Component and attributes for the presented guided dToF lidar system.
Table 2. Component and attributes for the presented guided dToF lidar system.
Component Parameter Value
Stereo Rig Baseline 1 m
Camera type BFS-U3-16S2M-CS
Maximum resolution 1080×1440
Focal length 12 mm
Lidar Laser pulse width 4.5 ns FWHM
Laser repetition rate 80 kHz
Wavelength 940 nm
Filter bandwidth 10 nm FWHM
Focal length 25 mm
Field of view (H×V) 16°×4°
Histogram bins 8×12-bit
Histogram bin width 0.375 m (2.5 ns)
Histogram window step 1.875 m (1.25 ns)
Table 3. Performance overview of state-of-the-art direct time-of-flight lidar sensors.
Table 3. Performance overview of state-of-the-art direct time-of-flight lidar sensors.
Author Ref Resolution (ToF pixels) Max. Range (m) Ambient Intensity (klux) Precision / Accuracy (m) Frame Rate (Hz) Histogram Bins Stacked Partial Histogram
Ximenes [9] 64 × 128 300 1 - 0.47 / 0.8 30 2 - Yes No
Henderson [10] 64 × 64 50 - - / 0.17 30 16 Yes No
Zhang [13] 144 × 252 50 - 0.0014 / 0.88 30 2 8 No Zooming
Okino [31] 900 × 1200 250 - 1.5 / - - - No No
Kim [15] 40 × 48 45 - 0.014 / 0.023 - 2 No Zooming
Kumagai [32] 63 × 168 200 117 - / 0.3 20 - Yes No
Padmanabhan [11] 128 × 256 100 1 10 - / 0.07 - - Yes No
Stoppa [17] 60 × 80 4.4 50 0.007 / 0.04 30 32 Yes Sliding
Zhang [14] 160 × 240 9.5 10 0.01 / 0.02 20 32 Yes Zooming
Park [16] 60 × 80 45 30 0.015 / 0.025 1.5 2 4 No Zooming
Taloud [18] 32 × 42 8.2 1 0.007 / 0.03 30 59 Yes Sliding
This work - 32 × 64 75 70 0.2 3 8 No No
1. Single point measurement. 2. Frame rate not specified at maximum distance.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated