Prerpints.org logo
Preprint
Article

Polarimetric SAR Image Classification Based on Double-Channel Convolution Network and Edge-preserving Markov Random Field

Altmetrics

Downloads

107

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 October 2023

Posted:

03 October 2023

You are already at the latest version

Alerts
Abstract
Deep learning methods have been widely used in PolSAR image classification. To learn the polarimetric information, many deep learning methods expect to learn high-level semantic features from original PolSAR data. However, only original data cannot learn multiple scattering features and complex structures for extremely heterogeneous terrain objects. In addition, deep learning methods always cause edge confusion due to the high-level features. To overcome these shortages, we propose a double-channel CNN network combined with an edge-preserving MRF model(DCCNN-MRF) for PolSAR image classification. Firstly, to combine complex matrix data and multiple scattering features together, a double-channel convolution network(DCCNN) is developed, which consists of a Wishart-based complex matrix and multi-feature subnetworks. The Wishart-based complex matrix network can learn the statistical characteristics and channel correlation well, and the multi-feature network can learn high-level semantic features well. Then, a unified network framework is designed to fuse two kinds of features to enhance advantageous features and reduce redundant ones. Finally, an edge preserving MRF model is designed to combine with the DCCNN network. In the MRF model, a sketch map-based edge energy function is designed by defining adaptive weighted neighborhood for edge pixels. Experiments are conducted on four real PolSAR data sets with different sensors and bands. Experimental results demonstrate the effectiveness of the proposed DCCNN-MRF method.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Polarimetric Synthetic Aperture Radar (PolSAR) is an active radar imaging system by emitting and receiving electromagnetic waves in multiple polarimetric directions [1]. In comparison to single polarimetric SAR systems, a full polarimetric SAR system can capture more scattering information of ground objects by four polarimetric modes, which can produce a 2 × 2 scattering matrix instead of a complex-valued data. The advantages of PolSAR systems have led to their widespread applications in various fields such as military monitoring [2], object detection [3], crop growth prediction [4], and terrain classification [5] etc. One particular task related to PolSAR is image classification by assigning a class label to each pixel. This step is fundamental and essential for further automatic image interpretation. For decades years, various PolSAR image classification methods have been proposed, which mainly include traditional scattering mechanism-based methods and more recent deep learning-based methods.
Traditional scattering mechanism-based methods primarily focus on exploiting the scattering features and designing classifier, which can be categorized into three main groups. The first category comprises statistical distribution-based methods that leverage the statistical characteristics of PolSAR complex matrix data, such as Wishart [6,7,8,9], mixed Wishart [10,11,12,13], G 0 [14], Kummer [15] distributions. These methods try to exploit various non-Gaussian distribution models for heterogeneous PolSAR images. However, parameter estimation is complicated for non-Gaussian models. The second category is the target decomposition-based methods that extract scattering features from target decomposition to differentiate various terrain objects. Some commonly employed methods include Cloude and Pottier decomposition [16,17], Freeman decomposition [18], four-component decomposition [19], m − δ decomposition [20], eigenvalue decomposition [21], and others. These methods can extract various target scattering information to distinguish different objects. Nevertheless, it is important to note that these pixel-wise methods easily produce noisy classes by speckle. Further, some researchers have explored the combination of statistical distribution and scattering features, including W G − Γ [22], K-Wishart [23], Γ − W M M [24] and other similar approaches. The initial classification result is obtained by utilizing the scattering features in these methods, and they are further optimized using a statistical distribution model. However, these methods based on scattering mechanisms tend to overlook the incorporation of high-level semantic information. Additionally, they face challenges in effectively learning the complicated textural structures associated with heterogeneous terrain types, including buildings, forests, and so on.
Recently, deep learning models have achieved remarkable performance in learning high-level semantic features, making them extensively utilized in the domain of PolSAR image classification. In light of the valuable information contained within PolSAR original data, numerous deep learning methods have been developed for PolSAR image classification. Deng et al. [21] proposed a deep belief network for PolSAR image classification. Jiao et al. [25] introduced the Wishart deep stacking network for fast PolSAR image classification. Later, Dong et al. [26] applied the neural structure searching to PolSAR images and produced good performance. In a separate study, Xie et al. [27] developed a semi-supervised recurrent complex-valued CNN model that could effectively learn the complex data to improve the classification accuracy. Liu et al. [28] derived an active assemble deep learning method that incorporates active learning into the deep network, which made a significant reduction in training samples required for PolSAR image classification. Additionally, Liu et al. [29] further constructed an adaptive graph model to decrease computational complexity and enhance the classification performance. Luo et al. [30] proposed a novel approach by combining the stacking auto-encoder network with the CNN model for multi-temporal PolSAR image classification. These deep learning methods tried to learn the polarimetric and scattering high-level features to enhance the performance of classification algorithms. However, these methods only utilize the original data information,which may lead to misclassification of extremely heterogeneous terrain objects, such as buildings, forests, and mountains. It is because there are significant scattering variations and textural structures within the heterogeneous object, which makes it difficult to extract high-level semantic features using complex matrix learning alone.
Nowadays, it has many advantages in the field of PolSAR image classification with the multiple scattering feature-based deep learning methods. It is widely recognized that the utilization of various target decomposition-based and textural features can greatly improve the accuracy of PolSAR image classification. However, feature selection is an essential issue in improving the classification performance. In order to tackle this issue, Yang et al. [31] proposed a CNN-based polarimetric feature selection model. This model incorporates the use of the Kullback-Leibler distance to select feature subsets and employs a Convolutional Neural Network (CNN) to identify the optimal features that can enhance classification accuracy. Bi et al. [32] proposed a method that combined the low-rank feature extraction, convolutional neural network (CNN), and Markov random field (MRF) together for classification. Dong et al. [33] introduced an end-to-end feature learning and classification method for PolSAR images. They input high-dimensional polarimetric features directly into a CNN, allowing the network to learn discriminating representation for classification. Furthermore, Wu et al. [34] proposed the statistical-spatial feature learning network, which not only joint learned both statistical and spatial features from the PolSAR data, but also reduced the speckle noises. Shi et al. [35] proposed a multi-feature sparse representation model that enabled learning joint sparse features for classification. Besides, Liang et al. [36] introduced a multi-scale deep feature fusion and covariance pooling manifold network (MFFN-CPMN) for high-resolution SAR image classification. This network combines the benefits of local spatial features and global statistical properties to enhance classification performance. These multi-feature learning methods have the capability to automatically fuse and select multiple polarimetric and scattering features in order to enhance classification performance. However, they ignore the statistical distribution of original complex matrix and consequently lose the channel correlation.
The aforementioned deep learning methods solely focus on either the original complex matrix data or multiple scattering features. However, it is important to note that these two types of data can offer complementary information to each other. Unfortunately, few methods can utilize both types of data simultaneously. It is because they have different data structures and distributions, which cannot be employed to the same data space directly. To combine them, Shi et al. [35] proposed complex matrix and multi-feature joint learning method, which constructed a complex matrix dictionary in the Riemannian space and a multi-feature dictionary in the Euclidean space respectively, and further jointly learned the sparse features for classification. However, it has been observed that this method is unable to effectively learn high-level semantic features, particularly for heterogeneous terrain objects. In this paper, we construct a double-channel convolution network (DCCNN) that aims to effectively learn both the complex matrix and multiple features. Additionally, a unified fusion module is designed to combine both of them.
Furthermore, deep learning-based methods demonstrate a strong capability to effectively learn semantic features for heterogeneous PolSAR images. However, it is important to note that the utilization of high-level features often leads to the loss of edge details. This phenomenon can be attributed to the fact that two neighboring pixels across the edge have similar high-level semantic features, which are extracted from large-scale contextual information. Therefore, high-level features cannot identify the edge details, as a result of edge confusion. In order to address this issue and mitigate the impact of speckle noises, the Markov Random Field (MRF) [37] has emerged as a valuable tool in remote sensing image classification. For example, Song et al. [22] combine the MRF with WGt mixed model, which can capture both the statistical distribution and contextual information simultaneously. It is considered that traditional MRF with the fixed square neighborhood window can remove speckle noises well, while it will blur the edge pixels. It is because, for edge pixels, its neighbors should be along the edge instead of the square box. Consider the edge direction, Liu. et al. [38] proposed the polarimetric sketch map to describe the edges and structure of PolSAR images. In this paper, we define an adaptive weighted neighborhood for edge pixels with the favor of polarimetric sketch map. Then, an edge preserving prior term is designed to optimize the edges. Therefore, by implementing appropriate contextual design, the MRF has the capability to modify the edge details. It can not only smooth the classification map to reduce speckles, but also preserve edges through designing suitable adaptive neighborhood prior term.
To preserve edge details, we combine the proposed DCCNN model and MRF together. By leveraging the strengths of both semantic features and edge preservation, this approach aims to achieve optimal results. Furthermore, we have developed an edge-preserving prior term that specifically addresses the issue of confused edges. Therefore, the main contribution of our proposed method can be concluded into three aspects as follows.
(1)
A novel double-channel CNN (DCCNN) network is proposed to joint learn both the complex matrix and multiple features. Firstly, a Wishart-based complex matrix subnetwork is designed to learn the statistical distribution of complex matrix. In addition, a multi-feature subnetwork is developed to learn the high-level semantic features for multiple scattering information, especially for extremely heterogeneous terrain objects.
(2)
In this paper, the Wishart-based complex matrix and multi-feature subnetworks are integrated into a unified framework, and a fusion module is utilized to combine both the valuable features and reduce redundant features for improving the classification performance.
(3)
A novel DCCNN-MRF method is proposed by combining edge-preserving MRF with the DCCNN model, which can reduce speckle noises as well as revising the edges. In this model, sketch map-based adaptive weighted neighborhood is developed and an edge-preserving prior term is designed to refine the edge pixels.
The rest of this paper is organized as follows. Related works are introduced in Section 2. Section 3 explains the proposed method in detail. The experimental result and analysis are given in Section 4, and the conclusion is summarized in Section 5.

2. Related Work

2.1. PolSAR Data

PolSAR data is the back-scattering echo waves by electromagnetic wave under the horizontal and vertical polarization basis. The scattering matrix S is obtained by
S = S h h S h v S v h S v v
where S h h is the scattering waves by horizontal emitting and vertical receiving. It is similar in concept to S h v , S v h and S v v . Under the Pauli base, the scattering matrix can be vectored as k = 1 2 [ S h h + S v v , S h h − S v v , 2 S h v ] T . After multi-look processing, the coherency matrix T is expressed as
T = k i k j H = T 11 T 12 T 13 T 21 T 22 T 23 T 31 T 32 T 33
Where ( · ) H is the conjugate transpose operation. The coherency matrix T is a Himeinn symmetry matrix, in which the diagonal elements are real numbers while the others are complex numbers, and T 12 = T 21 H . In addition, another PolSAR data representation, such as the covariance matrix C, can be converted from T through linear transformation.

2.2. Polarimetric Sketch Map

The polarimetric sketch map [39] is a powerful tool for analyzing PolSAR images, which can provide a comprehensive overview of the basic structure for PolSAR images. Moreover, it can effectively represent inner structures of complex heterogonies terrain types. Liu et al. [38] proposed a hierarchical semantic model (HSM) that combines the CFAR detector and weighted gradient-based detector to obtain a polarimetric sketch map for object detection.
The extracting procedure of the polarimetric sketch map is illustrated as follows. Firstly, the polarimetric edge-line detection technique is applied to obtain the polsarimetric energy map. Non-maximum suppression is then utilized to obtain the edge map. Finally, the hypothesis-testing method is employed to select the sketch lines, resulting in the polarimetric sketch maps. Figure 1 shows the polarimetric sketch maps on Xi’an and Flevoland data sets respectively. The Pauli RGB images of Xi’an and Flevoland are shown in Figures 1(a) and (b) respectively. Figures 1(c) and (d) are the corresponding polarimetric sketch maps. It can be seen that the polarimetric sketch map is the sparse structure representation of the PolSAR image. It can describe both the edges and the object structures well. The sketch map consist of sketch segments with certain orientation and length.

3. Proposed method

In this paper, a novel MRF-based double-channel convolution network (DCCNN-MRF) is proposed for PolSAR image classification, of which the framework is illustrated in Figure 2. Firstly, a double-channel convolution network is developed to jointly learn the complex matrix and multiple features. On the one hand, a Wishart-based convolutional network is designed, which utilizes the complex matrix as the input, and defines the Wishart measurement as the first convolution layer. The Wishart convolution network effectively measures the similarity of complex matrices, followed by a CNN to learn deeper features. On the other hand, a multi-feature subnetwork is specifically designed to acquire various polarimetric scattering features. These features serve the purpose of providing supplementary information for the Wishart convolution network. Subsequently, a unified framework is developed to merge the outputs of the two subnetworks. To accomplish this fusion, multiple layer convolutions are employed to effectively combine the two types of features. Secondly, to suppress speckle and revise the edges, a MRF model is incorporated with the DCCNN network. This integration can also improve the overall performance of image classification. The data term in MRF model is defined as the class probability obtained from the DCCNN model, and the prior term is designed using an edge penalty function. The purpose of this edge penalty function is to reduce the confusion related to edges that may arise due to the high-level features of the deep model.

3.1. Double-channel convolution network

In this paper, a double-channel convolution network (DCCNN) is developed to jointly learn the complex matrix and various scattering features from PolSAR data, as shown in Figure 2. The DCCNN network consists of two subnetworks: Wishart-based complex matrix and multi-feature subnetworks, which can learn complex matrix relationships and various polarimetric features, respectively. Then, an unified feature fusion module is designed to combine different features dynamically for enhancing the classification performance. This method provides a unified framework for integrating complex matrix and multi-feature learning. The incorporation of complementary information further enhances the classification performance.
1) Wishart-based complex matrix subnetwork
Traditional deep learning methods commonly convert the polarimetric complex matrix into a column vector. However, this conversion process results in the loss of both the matrix structure and data distribution of PolSAR data. In order to capture the characteristics of the complex matrix effectively, a Wishart-based complex matrix network is designed. This network aims to learn the statistical distribution of PolSAR complex matrix. The first layer in the neural network architecture is the Wishart convolution layer. This layer is responsible for converting the Wishart metric into a linear transformation, which corresponds to the convolution operation. To be specific, the coherency matrix T, which is widely known to follow the Wishart distribution, is processed by this layer. For example, the distance between the jth pixel T m and the ith class center W i can be measured by the Wishart distance, defined as
d T j , W i = ln W i + T r ( W i − 1 T j )
where ln · is the log operation. T r · is the the trace operation of a matrix. · is the determinant operation of a matrix. However, the Wishart metric is not directly applicable to the convolution network due to its reliance on complex matrices. In [25], Jiao et al. proposed a method to convert the Wishart distance into a linear operation. Firstly, the T matrix is converted into a vector as follows
T ¯ = [ T 11 , T 22 , T 33 , r e a l ( T 12 ) , i m a g ( T 12 ) , r e a l ( T 13 ) , i m a g ( T 13 ) , r e a l ( T 23 ) , i m a g ( T 23 ) ]
where r e a l ( · ) and i m a g ( · ) are used to extract the real and imagery parts of a complex number respectively. This allows for the conversion of a complex matrix into a real-valued vector, where each element is a real value. Then, the Wishart convolution can be defined as
h ( I i ) = W ¯ T T i ¯ + b
where W ¯ is the convolution kernel, and T i ¯ is the ith pixel value. b is the bias vector defined as b = ln T 1 , ln T 2 , … , ln T C . h ( · ) is the output of Wishart convolution layer. Although it is a linear operation on vector T i ¯ , it is equal to the Wishart distance between pixel T i and class center W.
In addition, to learn the statistical characteristics of complex matrices, we initialize the convolution kernel as the class center. Thus, the Wishart convolution is interpretable, which can learn the distance between each pixel and the class centers. By doing so, it overcomes the non-interpretability of traditional networks. The number of kernel is set equal to the number of classes, and the initial convolution kernel is calculated by averaging complex matrices of labeled samples for each class. After the first Wishart convolution layer, a complex matrix is transformed into a real value for each pixel. Subsequently, several CNN convolution layers are utilized to learn the contextual high-level features.
2) multi-feature subnetwork
The Wishart subnetwork is capable of effectively learning the statistical characteristic of complex matrix. However, when it comes to heterogeneous areas, the individual complex matrices cannot learn the high-level semantic features. It’s because the heterogeneous structure results in neighboring pixels having significantly different scattering matrices, even though they belong to the same class. To learn high-level semantic in heterogeneous areas, it is necessary to employ multiple features that offer complementary information to the original data. In this paper, 57-dimension features are extracted, containing both the original data and various polarimetric decomposition-based features. These features include Cloude decomposition, Freeman decomposition, Yamaguki decomposition, and others. The detailed feature extraction can be found in Ref. [40] as shown in Table 1. The feature vector is defined as F = { f 1 , f 2 , … , f 57 } , which describes each pixel from several aspects. Due to greatly various ranges of different features, the normalization process is employed initially. Subsequently, several layers of convolutions are applied to facilitate the learning of high-level features.
In addition, the network structure is designed as follows. a three-layer convolution is utilized to achieve multi-scale feature learning. The convolution kernel size is 3 × 3 , and the moving step size is set to 1. Besides, the maximum pooling is selected to conduct the down-sampling, which effectively reduces both parameters and computational complexity while maintaining the same receptive field.
3) The proposed DCCNN fusion network
To enhance the benefits derived from both complex matrix and multiple features, a unified framework is designed to fuse these two subnetworks. To be specific, the complex matrix features H 0 is extracted from Wishart subnetwork and the multi-feature vector H 1 is achieved from the multi-feature subnetwork. Then, they are connected to construct the combined feature X. Later, several CNN convolution layers are utilized to fuse them. By multiple layer convolution, all the features are fused to capture global feature information effectively. After fully connected layer, discriminating features are extracted and useless features are suppressed. The classification accuracy of the target object can be improved by focusing on useful features. Therefore, the feature transformation of the proposed DCCNN network can be described as
H f = D C C N N ( W i s h a r t ( T ) ⊕ M u l t i − f e a t u r e ( F ) )
where W i s h a r t ( T ) means the extracted feature H 0 from the Wishart subnetwork based on T matrix, M u l t i − f e a t u r e ( F ) means the extracted feature H 1 from the multi-feature subnetwork based on multi-feature F. ⊕ is the connection operation of H 0 and H 1 . That is, features from two networks are connected, and then, the DCCNN network is utilized to generate the high-level feature H f .Finally, the softmax layer is utilized for classification.

3.2. Combining edge-preserving MRF and DCCNN model

The proposed DCCNN model can effectively learn both the statistical characteristics and multiple features for PolSAR data. The learned high-level semantic features can improve the classification performance especially for heterogeneous areas. However, it contains a larger-scale contextual information with the increasing number of convolution layers, which is unfavourable for edge pixels, since the high-level features are difficult to identify neighboring pixels crossing the edge with different classes. So, the deep learning methods always blur edge details with high-level features. In order to learn the contextual relationships for heterogeneous terrain object and identify edge features accurately simultaneously, we combines the proposed DCCNN network with MRF to optimize the pixel level classification results.
Markov random field (MRF) is a widely used probability model which can learn contextual relationship by designing the energy function. The MRF can learn the pixel feature effectively, as well as incorporating the contextual information. In this paper, we design an edge penalty function to revise the edge pixels and suppress the speckle. In MRF, an energy function is defined, which consists of data and prior terms. The data term represents the probability of each pixel belonging to a certain class, while the prior term is the class prior probability. The energy function is defined as
U ( Y | X ) = ∑ S U 1 ( x s | y s ) + ∑ s U 2 y s | y r , r ∈ η s
where U 1 ( x s | y s ) is the data term, which stands for the probability of data x s belonging to class y s for pixel s. In this paper, we define the data term as the probability learned from the DCCNN model. U 2 y s | y r , r ∈ η s is the prior term, which is the prior probability of class y s . In MRF, the spatial contextual relationship is involved to learn the prior probability. η s is neighboring set of pixel s, and r is the neighboring pixel of s. When neighboring pixel r has the same class label as pixel s, the probability increases, otherwise decreases. When none of the neighboring pixels belong to class y s , it indicates that pixel s may likely be a noisy point. In such cases, it is advisable to revise the classification of pixel s to match the majority class of its neighboring pixels. In addition,the neighborhood set is essential for the prior term. If pixel s belongs to non-edge regions, a 3 × 3 square neighbor is suitable for suppressing speckle noises. If pixel s is nearing the edges, its neighbors should be pixels along the edges instead of pixels in a square box. Furthermore, it’s not fair that all the neighbors contribute to the pixel with the same probability especially for edge pixels. Pixels in the same side of the edge are similar to the central pixel, which should have higher probability than totally different ones crossing the edge, even though they are also close to the central pixel. Neighboring pixels crossing the edge with a completely different class are unfavorable for estimating the probability of pixel s, and can even lead to erroneous estimation.
In this paper, we firstly define the edge and non-edge regions for a PoLSAR image by utilizing the polarimetric sketch map [39]. Firstly, the polarimetric sketch map is calculated by polarimetric edge detection and sketch pursuit methods. For each sketch segment, there are direction and length to characterize it. Then, edge regions are extracted by using a geometric structure block to expand a certain width along the sketch segments, such as five-pixel width. Figure 3 illustrates an example of edge and non-edge regions. Figure 3(a) is the PolSAR PauliRGB images. Figure 3(b) are the extracted polarimetric sketch map from (a). Figure 3(c) shows the geometric structure block. By expanding the sketch segments with (c), the edge and non-edge regions are shown in Figure 3(d). Pixels in white are edge regions, while pixels in black are non-edge regions. For edge pixels, their directions are assigned as the direction of sketch segments.
In addition, we designed the adaptive neighborhood sets for edge and non-edge regions respectively. For non-edge regions, a 3 × 3 box is utilized as the neighbors. For edge regions, adaptive weighted neighborhood window is adopted to obtain the adaptive neighbors. That is, pixels along the edges have higher probability than other pixels. The weight of pixel r to central pixel s is measured by the revised Wishart distance, defined as
D w = 1 2 ln C r + ln C s + T r C r − 1 C s + C s − 1 C r
where C r and C s are the covariance matrices of neighboring and central pixels respectively. According to Wishart measurement, the weight of neighboring pixel r to central pixel s is defined as
W r s = exp − D w
The adaptive weighted neighboring window is shown in Figure 4. Figure 4(a) is the PauliRGB subimage of Xi’an area, in which pixel A is in the non-edge region, while pixels B and C belong to edge regions. Figure 4(b) is the class label map of (a). We select 3 × 3 neighborhood window for pixel A in non-edge region as shown in Figures 4(c). Figure 4(d) and (e) are the adaptive weighted neighbors for point B and C respectively. In addition, for edge pixels, varying weights are assigned to the neighboring pixels. It is evident that the neighborhood pixels are always located along the edges. The black pixels that are distant from the center pixel no longer qualify as neighborhood pixels. Furthermore, neighborhood pixels with lighter colors are assigned higher weights, while pixels with darker colors have lower weights. From Figures 4(c) and (d), we can see that pixels in the same side of edge have higher weights than ones in the other side, which can avoid the confusion by the neighboring pixels crossing the edge.
According to the adaptive weighted neighborhood, we develop an edge-preserved prior term that effectively integrates the contextual relationship while simultaneously minimizing the impact of neighboring pixels that traverse the edge. The prior term is built as
U 2 y s | y r , r ∈ η s = − β ∑ r ∈ η s ω r s δ y s , y r
where β is the balance factor between data and prior terms. y s and y r are the class labels of pixel s and r respectively. ω r s is the neighborhood weight of pixel r to central pixel s. δ y s , y r is the Kronecker delta function, defined as:
δ y s , y r = 1 , y s = y r 0 , y s ≠ y r
where δ y s , y r takes 1 when y s and y r are equal, otherwise 0. It is used to describe class relationship between the central point and its neighbor pixels.
After MRF optimization, the proposed method can obtain the final classification map with both better region homogeneity in heterogeneous regions and edge preservation. The proposed DCCNN-MRF algorithm procedure is given in Algorithm 1.
Algorithm 1 Algorithm procedure of the proposed DCCNN-MRF method
Input: PolSAR coherency matrix T, PolSAR multiple features F, class label map L . Balance factor β and class number C
Step 1: Extract multiple of scattering features F from PolSAR images by Table 1.
Step 2: Learn the complex matrix features H 0 from original data T by the Wishart subnetwork.
Step 3: Learn the high-level features H 1 from multiple features F by the multi-feature subnetwork.
Step 4: Combine the H 0 and H 1 into the DCCNN model, and learn the fused feature H f .
Step 5: Obtain the class probability P and estimated class label map Y by the DCCNN model.
Step 6: Obtain the sketch map of the PolSAR image, and compute the adaptive weighted neighbors for edge pixels by Equation (8).
Step 7:Optimize the estimated class label Y using Equation (6) by the edge-preserved MRF model.
Output: class label estimation map Y.

4. Experimental Results and Analysis

4.1. Experimental data and settings

In this section, four sets of PolSAR images with different bands and sensors are used to validate the effectiveness of the proposed method. The overview of four PolSAR datasets is summarized in Table 2. The detailed descriptions are given as follows.
A)Xi’an data set: The first image is a full-polarization subset acquired by the RADARSAT-2 system over the Xi’an area with a size of 512 × 512 pixels. The Pauli RGB image and its ground truth map are shown in Figures 5(a) and (b) respectively. In this PolSAR image, there are mainly three kinds of land covers, including water, grass, and building areas.
B)Flevoland data set 1: The other data set is acquired from the Flevoland area, which is a four-look L band fully polarimetric SAR data from the AIRSAR system with a spatial resolution of 12 . 1 × 6 . 7 m. The image size is 750 × 1024 pixels. The Pauli RGB image and its ground truth map are illustrated in Figures 7(a) and (b) respectively. In this image, there are 15 types of crops, including the stembean, peas, forest, lucerne, beat, wheat, potatoes, baresoil, grasses, rapeseed, barley, wheat2, wheat3, water and buildings area. We name it the Flevoland 1 data set.
C)San Francisco data set: This is a four-look C band full polarimetric SAR data covering the Francisco area from RADARSAT-2 sensor. The spatial resolution is 10 × 5 m and the image size is 1800 × 1380 pixels. Figures 9(a) and (b) give its Pauli RGB image and ground truth map respectively. There are five terrain types in this image, including ocean, vegetation, low-density, high-density and developed urban areas.
D)Flevoland data set 2: This is another Flevoland data set acquired by RADARSAT-2, which is C-Band over Flevoland in the Netherlands, with an image size of 1400 × 1200 pixels. The Pauli RGB image and its ground truth map are presented in Figures 11(a) and (b) respectively. In this image, there are four kinds of land covers, including water, urban, woodland, and cropland area. We name it the Flevoland 2 data set.
In addition, some evaluation indicators are calculated to testify the performance of the proposed method, such as class accuracy, overall accuracy (OA), average accuracy (AA), Kappa coefficient, and confusion matrix.
To verify the proposed method, four classification algorithms are used, namely: Super-RF [41], DBDA [42], S3ANet [43], and CV-CNN [44]. The first method is the superpixel and polarimetric features-based classification method (shorted by `"super-RF"), in which the random forest algorithm and superpixels are combined to reduce the influence of speckle and misclassification. The second method is the double-branch dual-attention mechanism network (shorted by `"DBDA"), in which two branches are designed to capture spectral and spatial features, and then construct the channel and spatial attention blocks to optimize the feature maps. The third method is the spatial-scattering separated attention network(shorted by `"S3ANet"), in which the spatial and scattering channel information are fused to acquire the feature, and then a squeeze and fusion attention unit is used to enhance the network. The last one is a complex-valued convolutional neural network (shorted by `"CV-CNN"), in which this method applies CNN to PolSAR data, making full use of amplitude and phase information presented in PolSAR images.
The parameter settings include a patch size of 9 × 9 , a learning rate of 0.001, and the batchsize is 128 with 50 training epochs. The sample proportions of training and testing are set to 10% and 90% respectively. To ensure fairness, the four comparative experiments also maintain a 10% training ratio, and all the experimental results are the average accuracies of running ten times. Moreover, the experimental environment is the Windows 10 operating system with an Intel(R) Core (TM) i7-10700 CPU, 64GB RAM, and an NVIDIA GeForce RTX 3060 GPU. The deep learning platform is Python 3.7 and PyTorch GPU 1.12.1.

4.2. Experimental results on Xi’an data set

The experimental results by four compared and our methods are illustrated in Figures 5(c)-(h) respectively. The super-RF method is the superpixels-based method, which can effectively reduce speckle noise. However, The classification map in Figure 5(c) produces some misclassifications in the edge regions of water and building due to the low-level features. In contrast, the DBDA approach shown in (d) effectively preserves edge details, while it also produces some misclassifications in the building area due to the missing of global information. The S3ANet in (e) is capable of effectively eliminating noisy points by integrating spectral, spatial, and multi-scale features. However, there are some misclassifications at the edges of water and building classes. The CV-CNN in (f) exhibits numerous small misclassified areas as a result of solely relying on the matrix information. In contrast, the proposed DCCNN method, as depicted in Figure 5(g), demonstrates superior performance by fully exploiting multiple scattering information. Furthermore, Figure 5(h) showcases the outcome of combining the DCCNN with the Markov Random Field. It is evident that this approach acquires a more precise water boundary and effectively reduces speckle noise through the incorporation of the MRF energy function. The experimental results further validate the effectiveness of the proposed DCCNN-MRF method.
Moreover, Table 3 presents the classification accuracy of compared and proposed methods on the Xi’an data set. It is evident that the proposed DCCNN-MRF and DCCNN outperform the other methods in terms of overall accuracy (OA), average accuracy (AA), and Kappa coefficients. Specifically, the proposed DCCNN method achieves a significantly higher OA compared to the four compared methods, with an improvement of 7.45%, 5.3%, 3.88%, and 5.58% respectively. In addition, the performance is further enhanced by the DCCNN-MRF method, which combines the DCCNN and MRF to effectively suppress noise and optimize edges. To be specific, the Super-RF algorithm tends to produce misclassifications, particularly in the water class, since it does not fully utilize the pixel information of the edges. Similarly, both the DBDA and S3ANet algorithms also encounter misclassification issues in the water class due to their pixel-wise classification approach. Although the CV-CNN method achieves high classification accuracy in the water area, it still generates noticeable false classes, particularly in the grass class. In contrast, the proposed method achieves the best classification accuracy in multiple classes, which contributes to the full use of scattering characteristics and boundary information. In addition, the confusion matrix is given in Figure 6. Analyzing the values in the first row of the matrix, we can see that in the water classification results, a total of 1681 pixels are inaccurately predicted as grass. Within the grass category, there are 1385 pixels misclassified as water and 1359 pixels misclassified as building. Furthermore, the building category contains 1214 pixels that are mistakenly classified as grass, indicating that there is a tendency for confusion between grass and water.

4.3. Experimental results on Flevoland 1 data set

The experimental results obtained from four different methods and our proposed methods are depicted in Figures 7(c)-(h) respectively. Upon observation, it is evident that our proposed method outperforms the other methods in terms of classification performance. Specifically, all comparison methods yield excellent classification results in the areas of steambean, potatoes, wheat, peas, and wheat3. However, the Super-RF method in Figure 7(c) exhibits low classification performance in areas such as rapeseed, buildings, and wheat2 due to a lack of high-level features. The DBDA method produces some noisy classes in the water, rapeseed, and barley areas as the absence of matrix features On the other hand, by combining spatial and scattering features, the S3ANet method can obtain better classification effects in water area. However, the pixel-wise S3ANet makes it difficult to classify the beet and wheat2 accurately. The CV-CNN still misclassifies rapeseed as wheat2. Additionally, there is some speckle noise presented in beet, wheat2, and wheat3 areas in Figure 7(f) due to the lack of global information. In comparison to these four methods, the proposed DCCNN method extracts deep features to enhance classification accuracy. Moreover, the proposed DCCNN method, with the incorporation of MRF, can reduce isolated points by utilizing contextual information.
Moreover, to test the classification performance quantitatively, the classification indicators of compared and our methods are given in Table 4. It can be seen that the proposed method can achieve better results than other approaches in terms of OA, AA, and Kappa coefficient. The overall accuracy (OA) of the proposed method is improved by 7.8%, 5.67%, 4.97%, 1.02%, and 0.01% compared with the three compared methods and the DCCNN method respectively. According to Table 4, we can see that the entire building area is misclassified by the Super-RF method due to the low-level features. The DBDA method primarily misclassifies the rapeseed class because of its reliance on vectorized features as input. The S3ANet method achieves the highest classification accuracy in the baresoil area, yet it still shows low performance in the grasses and building areas. The CV-CNN method exceeds other compared methods in terms of OA, because it can exploit the phase information. However, the CV-CNN struggles to accurately classify rapeseed, with a classification accuracy rate of 94.18%. Besides, Figure 8 presents the confusion matrix of the proposed DCCNN-MRF method. From the analysis of the confusion matrix, it can be observed that there are only a few pixels misclassified across all classes. Furthermore, the proposed method achieves 100% accuracy in forest, lucerne, wheat, potatoes, bare soil, barely, wheat2, and water classes, which further validates the effectiveness of the proposed method. The 18 pixels belonging to the beat class and the 3 pixels belonging to the building class are incorrectly classified as potatoes, while the potatoes class does not have any misclassified pixels.
Preprints 86827 g007
Figure 7. Classification results of the Flevoland 1 data set. (a) PauliRGB image of Flevoland 1 area; (b) The label map of (a); (c) The classification map by the Super-RF method; (d) The classification map by the DBDA method; (e) The classification map by the S3ANet method; (f) The classification map by the CV-CNN method; (g) The classification map by the proposed DCCNN method; (h) The classification map by the proposed DCCNN-MRF method; (i) The corresponding classes for different colors.
Figure 7. Classification results of the Flevoland 1 data set. (a) PauliRGB image of Flevoland 1 area; (b) The label map of (a); (c) The classification map by the Super-RF method; (d) The classification map by the DBDA method; (e) The classification map by the S3ANet method; (f) The classification map by the CV-CNN method; (g) The classification map by the proposed DCCNN method; (h) The classification map by the proposed DCCNN-MRF method; (i) The corresponding classes for different colors.
Preprints 86827 g007

4.4. Experimental results on San Francisco data set

Figures 9 (c)—(h) show the experimental results of the four comparison methods and the proposed method respectively. The Super-RF method in (c) leads to confusion between high density urban and low density urban classes due to the use of low-level polarimetric features. Additionally, in (c), some edges between vegetation and low density urban areas are either lost or misclassified due to the absence of boundary information. On the contrary, the pixel-wise DBDA method exhibits better performance at boundary areas, but it tends to generate many noisy classes in vegetation areas. The S3ANet method addresses the issue of speckle noise by capturing both the scattering and the phase information, while it still results in misclassified pixels along the edges. It is noteworthy that the classification results of the CV-CNN method exhibit a smoother outcome, whereas some speckles present in both low density urban and high density urban areas in (f) due to the utilization of low-level features. Compared to the four comparison methods, the proposed DCCNN method in (f) effectively strengthens classification accuracy by fully exploiting scattering features. Furthermore, by incorporating Markov Random Field (MRF), the proposed DCCNN-MRF method can acquire superior performance, which attaches to suppressing noise and optimizing edges.
More importantly, Table 5 provides the OA, AA, and Kappa metrics of various methods applied to the San Francisco data set. It is evident from the table that the proposed DCCNN method surpasses four other compared methods in terms of overall accuracy (OA) by achieving a 5.45%, 4.39%, 0.64%, and 2.07% higher OA. Additionally, by incorporating the MRF, the proposed DCCNN-MRF method indicates a further improvement of 0.08% compared to the proposed DCCNN method. For the Super-RF method, the classification accuracy in high density urban areas is only 77.76%. This is because the method fails to effectively distinguish homogeneous regions. The DBDA method cannot classify the vegetation and develop, which is consistent with the experimental result in Figure 9(d). Conversely, The S3ANet and CV-CNN models have demonstrated exceptional performance, achieving an accuracy rate of over 95% across all indicators. Lastly, the CV-CNN technique produces false classes, particularly in low density urban areas, as it solely relies on the T matrix as input. By fusing complex matrix and multiple features, the proposed DCCNN and DCCNN-MRF can obtain the highest classification accuracy on ocean class compared to the other methods. Furthermore, the proposed DCCNN achieves 99.94% in develop, which is 0.5% higher than that of the comparison method. Additionally, the confusion matrix of the DCCNN-MRF method is demonstrated in Figure 10. Analyzing the first row of the matrix, it can be observed that only 2 pixels are misclassified as low density urban in the ocean category, accounting for almost 0% of the total. However, a significant number of mispredictions occur in other categories. Specifically, 801 pixels are incorrectly predicted as low density urban in the vegetation category, and 555 pixels are misclassified as vegetation in the low density urban category. These results indicate that the main source of confusion is between the vegetation and low density urban areas.
Preprints 86827 g009
Figure 9. Classification results of different methods in the San Francisco area. (a) PauliRGB image of San Francisco area; (b) The label map of (a); (c) The classification map by the Super-RF method; (d) The classification map by the DBDA method; (e) The classification map by the S3ANet method; (f) The classification map by the CV-CNN method; (g)The classification map by the proposed DCCNN method; (h) The classification map by the proposed DCCNN-MRF method.
Figure 9. Classification results of different methods in the San Francisco area. (a) PauliRGB image of San Francisco area; (b) The label map of (a); (c) The classification map by the Super-RF method; (d) The classification map by the DBDA method; (e) The classification map by the S3ANet method; (f) The classification map by the CV-CNN method; (g)The classification map by the proposed DCCNN method; (h) The classification map by the proposed DCCNN-MRF method.
Preprints 86827 g009

4.5. Experimental results on Flevoland 2 data set

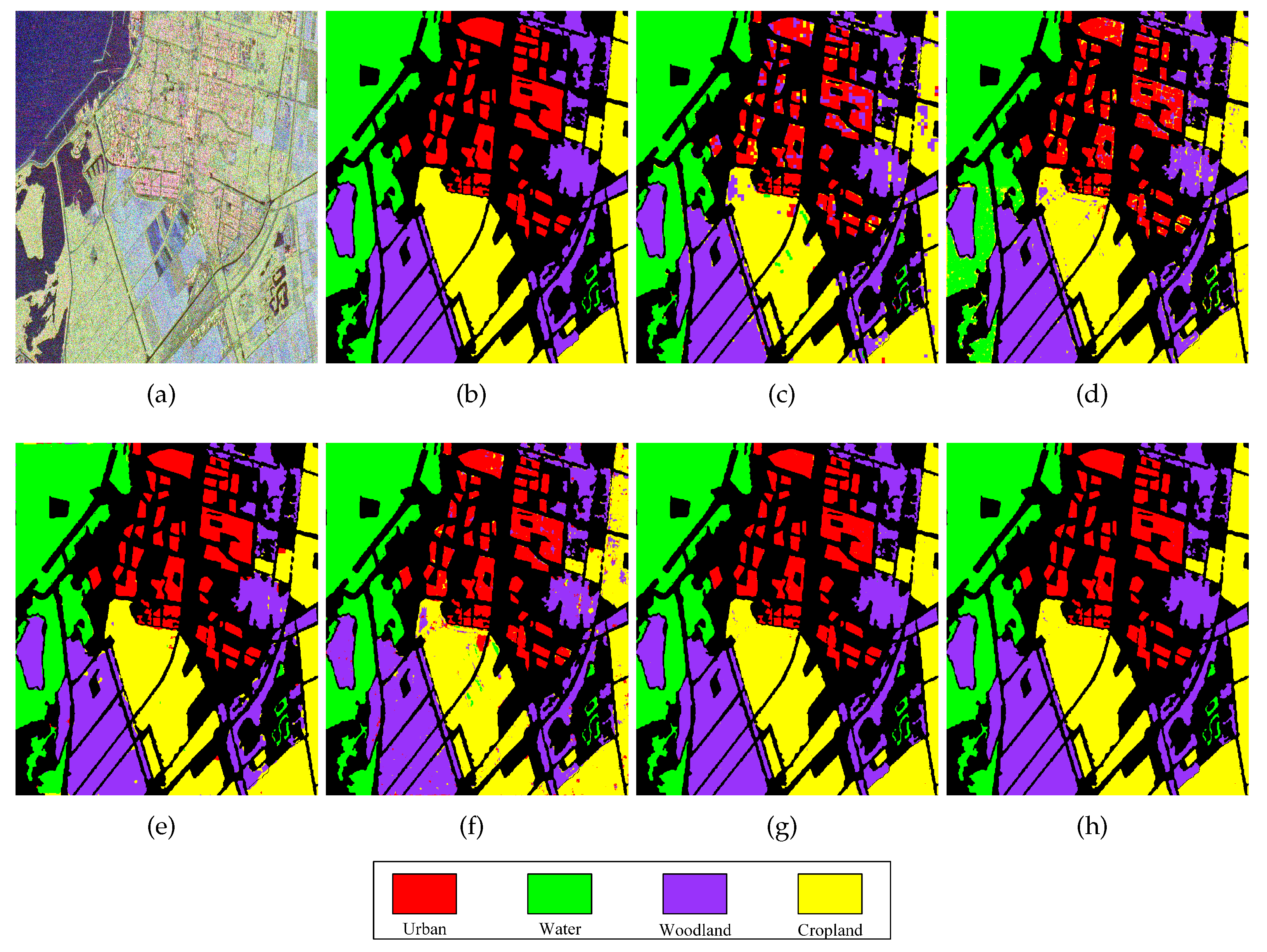
As depicted in Figure s11(c)-(h), the visualized classification results demonstrate that the method we proposed outperforms other methods. When comparing the label in Figure 11(b), it becomes evident that the Super-RF method fails to correctly classify urban and cropland areas due to its reliance on low-level features. In addition, both the DBDA and CV-CNN methods in Figures 11 (d) and (f) generate a significant amount of speckle, disregarding global information. By contrast, the S3ANet method in Figure 11(e) exhibits effective classification results in cropland and urban areas due to the addition of attention mechanisms. Nevertheless, it produces isolated points in vegetation and cropland areas. The effectiveness of the proposed DCCNN method in reducing misclassification caused by learning high-level features can be readily observed. Moreover, the proposed DCCNN-MRF can enhance the classification result by using the MRF to suppress noise and optimize edges.
Moreover, per-class accuracy, OA, AA, and Kappa coefficient for the methods mentioned above are compared to what we proposed in Table 6. The analysis reveals that both the Super-RF method and the DBDA method have lower accuracy within the urban class of 81.84% and 89.37% respectively, primarily due to the presence of strong heterogeneous areas. This observation highlights the inherent difficulty in accurately classifying urban regions. Compared to these two methods, the S3ANet demonstrates the greatest classification accuracy rate of 99.91% in urban areas but exhibits lower performance in woodland areas. The CV-CNN method primarily results in misclassification in the cropland class. However, the proposed DCCNN method offers significant improvements in the classification of all four classes. This is achieved by leveraging its capability to extract scattering features and incorporating neighboring pixels’ information. Furthermore, the proposed DCCNN-MRF method demonstrates superior classification performance, achieving an Overall Accuracy (OA) of 99.86%, an Average Accuracy (AA) of 99.84%, and a Kappa coefficient of 99.81%. Meanwhile, three of the existing four classes, including water, woodland, and cropland, obtained their maximum OA using the proposed DCCNN-MRF. Additionally, the confusion matrix of we proposed DCCNN-MRF method is displayed in Figure 12. Upon analyzing the confusion matrix, it becomes apparent that within the urban area, there exists a total of 242 pixels that are erroneously classified as woodland. Conversely, there are relatively few misclassified pixels in the water region. Furthermore, the confusion matrix reveals that 428 pixels are mispredicted as cropland in woodland. Similarly, 221 pixels are misclassified as woodland in cropland. The presence of a significant number of misclassifications between woodland and cropland highlights a main source of confusion in the classification result.
Preprints 86827 g011
Figure 11. Classification results of different methods in the Flevoland 2 area. (a) PauliRGB image of Flevoland 2 area; (b) The label map of (a); (c) The classification map by the Super-RF method; (d) The classification map by the DBDA method; (e) The classification map by the S3ANet method; (f) The classification map by the CV-CNN method; (g)The classification map by the proposed DCCNN method; (h) The classification map by the proposed DCCNN-MRF method.
Figure 11. Classification results of different methods in the Flevoland 2 area. (a) PauliRGB image of Flevoland 2 area; (b) The label map of (a); (c) The classification map by the Super-RF method; (d) The classification map by the DBDA method; (e) The classification map by the S3ANet method; (f) The classification map by the CV-CNN method; (g)The classification map by the proposed DCCNN method; (h) The classification map by the proposed DCCNN-MRF method.
Preprints 86827 g011

4.6. Discussion

1)Effect of each subnetwork
The proposed DCCNN contains two critical parts for fully exploiting scattering features, that is the Wishart complex matrix subnetwork (shorted by `"Wishart") and the multi-feature subnetwork (shorted by `"Multi-feature"). To assess the contributions of these two components, we present the classification results of Wishart, Multi-feature, and the complete DCCNN model on four different datasets. The classification accuracies are presented in Table 7. According to the data in Table 7, it is evident that the proposed DCCNN method consistently achieves higher overall accuracy (OA) on all four datasets compared to both Wishart and Multi-feature subnetworks, with improvements of at least 1.62%, 0.06%, 0.03%, and 0.02% respectively than multi-feature subnetwork. In addition, in most cases, the Multi-feature method outperforms the Wishart subnetwork due to exploiting more scattering features. The fused DCCNN method can obtain higher classification accuracy than both subnetworks. It can be observed that each subnetwork is indispensable for the proposed DCCNN method.
2)Effect of MRF
The MRF is a crucial component of the proposed DCCNN-MRF method. To vary the effect of the component, we report the classification results of Wishart subnework, Wishart+MRF, Multi-feature subnetwork, Multi-feature+MRF, DCCNN, and DCCNN+MRF on the four data sets. In addition, the classification accuracy is summarized in Table 8. It can be seen that all the Wishart, Multi-feature, and proposed DCCNN can obviously improve the classification accuracy by combining the MRF. Furthermore, the proposed DCCNN-MRF method can achieve 0.17%, 0.01%, 0.08%, and 0.08% on the four data sets higher than the DCCNN. It proves the effectiveness of the MRF component in enhancing classification outcomes.
3)Effect of patch size
In this experiment, the influence of the patch size of the proposed method on the Overall Accuracy (OA) is investigated (as seen Figure 13). To be specific, we vary the patch size from 7 × 7 to 15 × 15 with an interval of 2. It can be observed that as the patch size increases, there is fluctuation in OA for the Xi’an data set. However, the OA gradually improves for the other datasets. Another interesting observation is that after reaching a patch size of 9 × 9 , the OA does not show a significant increase. However, as the patch size increases, the required training and testing times also significantly increase. Therefore, we select 9 × 9 as the patch size in the experiment.
4)Effect of training sample ratio
We discuss the classification performance of the proposed method with different training sample ratio (see Figure 14). Specifically, we vary the training sample ratio from 5% to 30% with an interval of 5%. It’s evident that as the training sample ratio increases, the OA gradually improves for all four datasets. However, the magnitude of improvement gradually diminishes. In addition, when the training proportion reaches 10%, the proposed DCCNN-MRF method on the Xi’an data set shows an improvement of 0.62% to 1.4%, while it improves 0.13% on the other three datasets most. To balance the trade-off between time expenditure and classification accuracy, a training sample ratio of 10% is selected.
5)Analysis of running time
In Table 9, we give the running time of compared methods and the proposed DCCNN-MRF on Xi’an data set. The Super-RF method uses the random forest algorithm to obtain the initial classification result, and then combines the obtained superpixel information for optimization. This makes the method of the training time and test time relatively short. It can be seen that the main time is costed in the training stage. The proposed DCCNN-MRF takes less training time than the DBDA, the S3ANet, and the CV-CNN methods. In addition, the DCCNN-MRF takes less test time than the DBDA, and CV-CNN. Although the proposed DCCNN-MRF is not the best in terms of running time, it can achieve the best classification accuracy.

5. Conclusion

In this paper, a novel DCCNN-MRF method was proposed for PolSAR image classification, which combined the proposed double-channel convolution network and edge-preserving MRF together to improve classification performance. Firstly, a novel double-channel convolution network(DCCNN) was developed, which consisted of Wishart-based complex matrix and multi-feature subnetworks. The Wishart-based complex matrix subnetwork was designed to learn the statistical characteristics of original data. The multi-feature subnetwork was designed to learn more high-level scattering features especially for extremely heterogenous areas. Then, a unified framework was given to combine the two subnetworks to fuse both the advantageous features. Finally, the DCCNN model was combined with an edge-preserving MRF to alleviate the issue of edge confusion caused by deep network. In this model, the adaptive weighted edge penalty function was developed to optimize the edges. Experiments was conducted on four real PolSAR data sets, and quantitative evaluation indicators were given, including the OA, AA and kappa coefficient. All the experimental results verified the effectiveness of the proposed method. In addition, the ground truth is difficult to acquire for PolSAR images. The proposed method need 10% of the training samples, which is a little high for deep learning methods. To reduce the requirement of training samples, we try to exploit the few-shot deep learning method in the further work.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grant 62006186,62272383, the Science and Technology Program of Beilin District in Xi’an under Grant GX2105, in part by the Open fund of National Key Laboratory of Geographic Information Engineering under Grant SKLGIE2019-M-3-2.

References

  1. Kim, H.; Hirose, A. Unsupervised Fine Land Classification Using Quaternion Autoencoder-Based Polarization Feature Extraction and Self-Organizing Mapping. IEEE Transactions on Geoscience and Remote Sensing 2017, 56, 1839–1851. [Google Scholar] [CrossRef]
  2. Shi, J. Image processing model and method of full-polarization synthetic aperture radar; Publishing House of Electronics Industry: Beijing, 2021. [Google Scholar]
  3. Susaki, J.; Kishimoto, M. Urban Area Extraction Using X-Band Fully Polarimetric SAR Imagery. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2016. [Google Scholar] [CrossRef]
  4. Zhang, W.T.; Wang, M.; Guo, J. A Novel Multi-Scale CNN Model for Crop Classification with Time-Series Fully Polarization SAR Images. In Proceedings of the 2021 2nd China International SAR Symposium (CISS). [CrossRef]
  5. Wang, Y.; Chen, W.; Mao, X.; Lei, W. Terrain classification of polarimetric SAR images based on optimal polarization features. 2022 International Conference on Computer Engineering and Artificial Intelligence (ICCEAI). IEEE, pp. 400–403. [CrossRef]
  6. Gadhiya, T.; Roy, A.K. Classification of Polarimetrie Synthetic Aperture Radar Images Using Revised Wishart Distance. 2018 15th IEEE India Council International Conference (INDICON). IEEE, pp. 1–6. [CrossRef]
  7. Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. International Journal of Remote Sensing 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
  8. Luo, S.; Tong, L. A Fast Algorithm for the Sample of PolSAR Data Generation Based on the Wishart Distribution and Chaotic Map. IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE, pp. 389–392. [CrossRef]
  9. Xie, W.; Xie, Z.; Zhao, F.; Ren, B. POLSAR image classification via clustering-WAE classification model. IEEE Access 2018, 6, 40041–40049. [Google Scholar] [CrossRef]
  10. Huang, Y.; Zhang, Y.; Shi, P.; Chambers, J. Variational adaptive Kalman filter with Gaussian-inverse-Wishart mixture distribution. IEEE Transactions on Automatic Control 2020, 66, 1786–1793. [Google Scholar] [CrossRef]
  11. Liu, C.; Liao, W.; Li, H.C.; Fu, K.; Philips, W. Unsupervised classification of multilook polarimetric SAR data using spatially variant wishart mixture model with double constraints. IEEE Transactions on Geoscience and Remote Sensing 2018, 56, 5600–5613. [Google Scholar] [CrossRef]
  12. Liu, M.; Deng, Y.; Wang, D.; Liu, X.; Wang, C. Unified Classification Framework for Multipolarization and Dual-Frequency SAR. IEEE Transactions on Geoscience and Remote Sensing 2023, 61, 1–13. [Google Scholar] [CrossRef]
  13. Wu, Q.; Hou, B.; Wen, Z.; Jiao, L. Variational learning of mixture wishart model for PolSAR image classification. IEEE Transactions on Geoscience and Remote Sensing 2018, 57, 141–154. [Google Scholar] [CrossRef]
  14. Li, M.; Shen, Q.; Xiao, Y.; Liu, X.; Chen, Q. PolSAR Image Building Extraction with G0 Statistical Texture Using Convolutional Neural Network and Superpixel. Remote Sensing 2023, 15, 1451. [Google Scholar] [CrossRef]
  15. Zou, P.; Li. Zhen.; Tian, B. High-resolution polarized SAR image level set segmentation. Journal of Image and Graphics 2014, 19, 1829–1835. [Google Scholar]
  16. Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE transactions on geoscience and remote sensing 1996, 34, 498–518. [Google Scholar] [CrossRef]
  17. Fang, C.; Wen, H.; Yirong, W. An improved Cloude-Pottier decomposition using H-α-span and complex Wishart classifier for polarimetric SAR classification. 2006 CIE international conference on radar. IEEE, pp. 1–4. [CrossRef]
  18. Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE transactions on geoscience and remote sensing 1998, 36, 963–973. [Google Scholar] [CrossRef]
  19. An, W.; Xie, C.; Yuan, X.; Cui, Y.; Yang, J. Four-component decomposition of polarimetric SAR images with deorientation. IEEE Geoscience and Remote Sensing Letters 2011, 8, 1090–1094. [Google Scholar] [CrossRef]
  20. Zhang, W.; Ye, H. Unsupervised classification for Mini-RF SAR using m-δ decomposition and Wishart classification. 2019 International Applied Computational Electromagnetics Society Symposium-China (ACES). IEEE, Vol. 1, pp. 1–2. [CrossRef]
  21. Deng, J.W.; Li, H.L.; Cui, X.C.; Chen, S.W. Multi-Temporal PolSAR Image Classification Based on Polarimetric Scattering Tensor Eigenvalue Decomposition and Deep CNN Model. 2022 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). IEEE, pp. 1–6. [CrossRef]
  22. Song, W.; Li, M.; Zhang, P.; Wu, Y.; Tan, X.; An, L. Mixture WG Γ-MRF Model for PolSAR Image Classification. IEEE Transactions on Geoscience and Remote Sensing 2017, 56, 905–920. [Google Scholar] [CrossRef]
  23. Qu, J.; Qiu, X.; Ding, C.; Lei, B. Unsupervised classification of polarimetric SAR image based on geodesic distance and non-Gaussian distribution feature. Sensors 2021, 21, 1317. [Google Scholar] [CrossRef]
  24. Li, Z.C.; Li, H.C.; Hu, W.S.; Pan, L. Spatially Variant Gamma-WMM with Extended Variational Inference for Unsupervised PolSAR Classification. IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE, pp. 2550–2553. [CrossRef]
  25. Jiao, L.; Liu, F. Wishart deep stacking network for fast POLSAR image classification. IEEE Transactions on Image Processing 2016, 25, 3273–3286. [Google Scholar] [CrossRef] [PubMed]
  26. Dong, H.; Zou, B.; Zhang, L.; Zhang, S. Automatic design of CNNs via differentiable neural architecture search for PolSAR image classification. IEEE Transactions on Geoscience and Remote Sensing 2020, 58, 6362–6375. [Google Scholar] [CrossRef]
  27. Xie, W.; Ma, G.; Zhao, F.; Liu, H.; Zhang, L. PolSAR image classification via a novel semi-supervised recurrent complex-valued convolution neural network. Neurocomputing 2020, 388, 255–268. [Google Scholar] [CrossRef]
  28. Liu, S.J.; Luo, H.; Shi, Q. Active ensemble deep learning for polarimetric synthetic aperture radar image classification. IEEE Geoscience and Remote Sensing Letters 2020, 18, 1580–1584. [Google Scholar] [CrossRef]
  29. Liu, F.; Wang, J.; Tang, X.; Liu, J.; Zhang, X.; Xiao, L. Adaptive graph convolutional network for PolSAR image classification. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–14. [Google Scholar] [CrossRef]
  30. Luo, J.; Lv, Y.; Guo, J. Multi-temporal PolSAR Image Classification Using F-SAE-CNN. 2022 3rd China International SAR Symposium (CISS). IEEE, pp. 1–5. [CrossRef]
  31. Yang, C.; Hou, B.; Ren, B.; Hu, Y.; Jiao, L. CNN-based polarimetric decomposition feature selection for PolSAR image classification. IEEE Transactions on Geoscience and Remote Sensing 2019, 57, 8796–8812. [Google Scholar] [CrossRef]
  32. Bi, H.; Santos-Rodriguez, R.; Flach, P. Polsar Image Classification via Robust Low-Rank Feature Extraction and Markov Random Field. IGARSS 2020-2020 IEEE International Geoscience and Remote Sensing Symposium. IEEE, pp. 708–711. [CrossRef]
  33. Dong, H.; Zhang, L.; Lu, D.; Zou, B. Attention-based polarimetric feature selection convolutional network for PolSAR image classification. IEEE Geoscience and Remote Sensing Letters 2020, 19, 1–5. [Google Scholar] [CrossRef]
  34. Wu, Q.; Wen, Z.; Wang, Y.; Luo, Y.; Li, H.; Chen, Q. A Statistical-Spatial Feature Learning Network for PolSAR Image Classification. IEEE Geoscience and Remote Sensing Letters 2021, 19, 1–5. [Google Scholar] [CrossRef]
  35. Shi, J.; Jin, H. Complex Matrix And Polarimetric Feature Joint Learning For Polarimetric Sar Image Classification. IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE, pp. 2714–2717. [CrossRef]
  36. Liang, W.; Wu, Y.; Li, M.; Cao, Y.; Hu, X. High-resolution SAR image classification using multi-scale deep feature fusion and covariance pooling manifold network. Remote Sensing 2021, 13, 328. [Google Scholar] [CrossRef]
  37. Ni, L.; Zhang, B.; Shen, Q.; Gao, L.; Sun, X.; Li, S.; Wu, H. Edge constrained MRF method for classification of hyperspectral imagery. 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS). IEEE, pp. 1–4. [CrossRef]
  38. Shi, J.; Li, L.; Liu, F.; Jiao, L.; Liu, H.; Yang, S.; Liu, L.; Hao, H. Unsupervised polarimetric synthetic aperture radar image classification based on sketch map and adaptive Markov random field. Journal of Applied Remote Sensing 2016, 10, 025008. [Google Scholar] [CrossRef]
  39. Fang Liu; Junfei Shi; Licheng Jiao; Hongying Liu; Shuyuan Yang. Hierarchical semantic model and scattering mechanism based PolSAR image classification. Pattern Recognition 2016.
  40. Shi, J.; Jin, H.; Li, X. A Novel Multi-feature Joint Learning Method for Fast Polarimetric SAR Terrain Classification. IEEE Access 2020. [Google Scholar] [CrossRef]
  41. Chen, Q.; Cao, W.; Shang, J.; Liu, J.; Liu, X. Superpixel-based Cropland Classification of SAR Image with Statistical Texture and Polarization Features. IEEE Geoscience and Remote Sensing Letters 2021. [Google Scholar] [CrossRef]
  42. Li, R., Zheng, S., Duan, C., Yang, Y., & Wang, X. Classification of Hyperspectral Image Based on Double-Branch Dual-Attention Mechanism Network. Remote Sensing 2020, 12, 582.
  43. Fan, Z.; Ji, Z.; Fu, P.; Wang, T.; Sun, Q. Complex-Valued Spatial-Scattering Separated Attention Network for Polsar Image Classification. IGARSS 2020 - 2020 IEEE International Geoscience and Remote Sensing Symposium. [CrossRef]
  44. Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Transactions on Geoscience and Remote Sensing 2017. [Google Scholar] [CrossRef]
  45. Deng, J.W.; Li, H.L.; Cui, X.C.; Chen, S.W. Multi-Temporal PolSAR Image Classification Based on Polarimetric Scattering Tensor Eigenvalue Decomposition and Deep CNN Model. 2022 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). IEEE, pp. 1–6. [CrossRef]
  46. Liu, X.; Jiao, L.; Tang, X.; Sun, Q.; Zhang, D. Polarimetric Convolutional Network for PolSAR Image Classification. IEEE Transactions on Geoscience and Remote Sensing 2019, 57, 3040–3054. [Google Scholar] [CrossRef]
Preprints 86827 g001
Figure 1. Examples of polarimetric sketch maps. (a) PauliRGB PolSAR image on Xi’an data set; (b) PauliRGB PolSAR image on Flevoland data set; (c) Corresponding polarimetric sketch map on Xi’an data set; (d) Corresponding polarimetric sketch map on Flevoland data set.
Figure 1. Examples of polarimetric sketch maps. (a) PauliRGB PolSAR image on Xi’an data set; (b) PauliRGB PolSAR image on Flevoland data set; (c) Corresponding polarimetric sketch map on Xi’an data set; (d) Corresponding polarimetric sketch map on Flevoland data set.
Preprints 86827 g001
Preprints 86827 g002
Figure 2. Framework of the proposed double-channel CNN and MRF model for PolSAR image classification.
Figure 2. Framework of the proposed double-channel CNN and MRF model for PolSAR image classification.
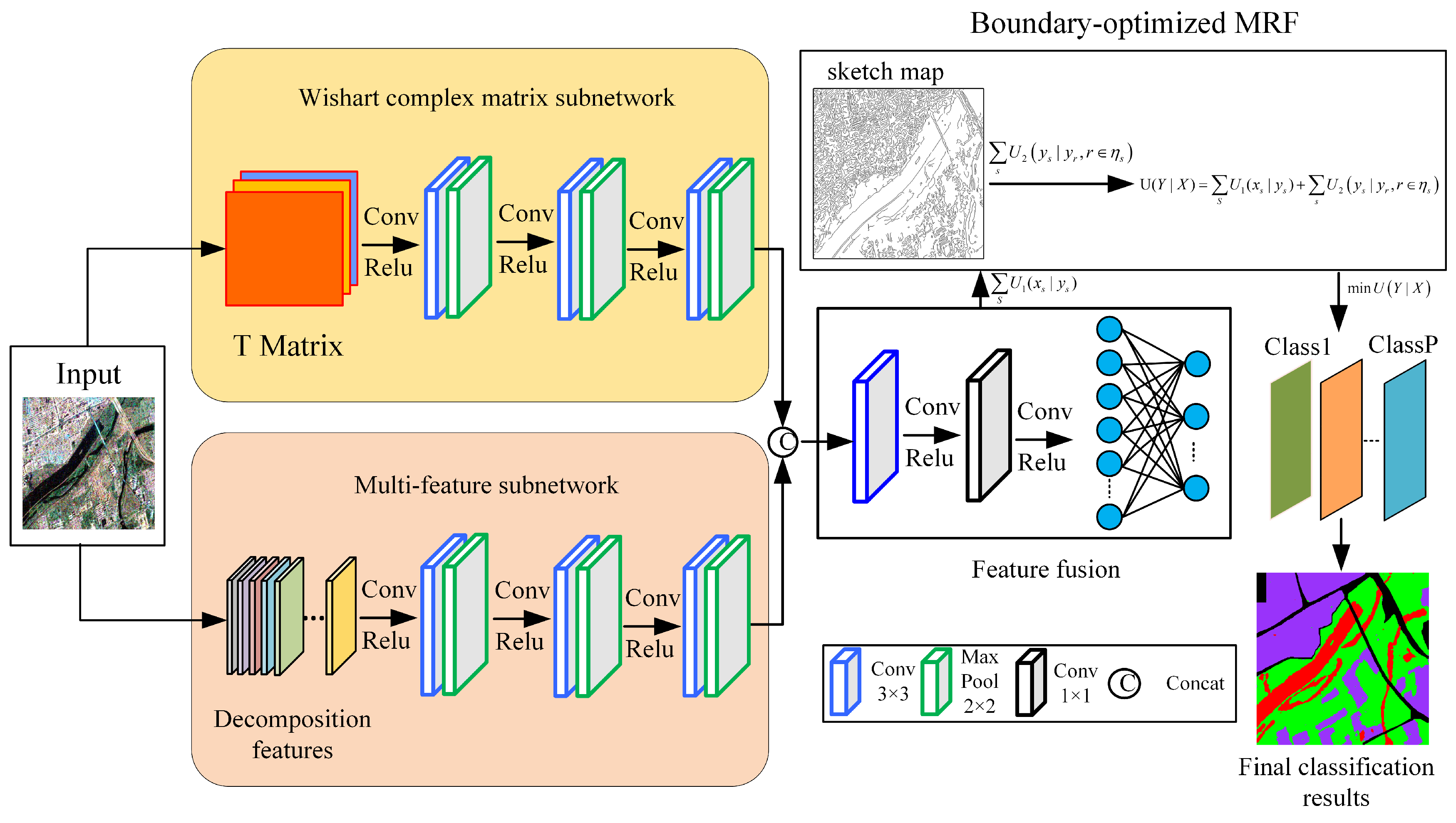
Preprints 86827 g002
Preprints 86827 g003
Figure 3. Example of edge and non-edge regions. (a) PauliRGB image of Ottawa; (b) The corresponding polarimetric sketch map; (c) Geometric structural block; (d) The white area is edge regions and the black area is the non-edge regions.
Figure 3. Example of edge and non-edge regions. (a) PauliRGB image of Ottawa; (b) The corresponding polarimetric sketch map; (c) Geometric structural block; (d) The white area is edge regions and the black area is the non-edge regions.
Preprints 86827 g003
Preprints 86827 g004
Figure 4. Example of adaptive neighbor structures. (a) the PauliRGB image of Xi’an area, the point A is in the non-edge region, and point B and point C are in the edge region; (b) The label map of (a); (c) 3 × 3 fixed neighborhood for point A; (d) weighted neighborhood structure for point B; (e)weighted neighborhood structure for point C.
Figure 4. Example of adaptive neighbor structures. (a) the PauliRGB image of Xi’an area, the point A is in the non-edge region, and point B and point C are in the edge region; (b) The label map of (a); (c) 3 × 3 fixed neighborhood for point A; (d) weighted neighborhood structure for point B; (e)weighted neighborhood structure for point C.
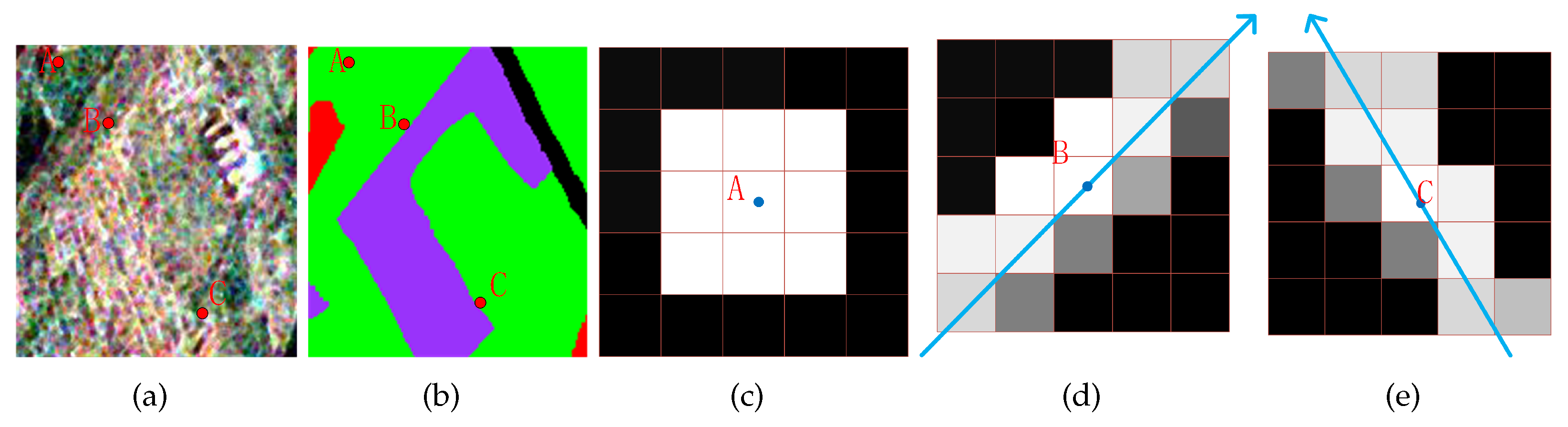
Preprints 86827 g004
Preprints 86827 g005
Figure 5. Classification results of different methods in the Xi’an area. (a) PauliRGB image of Xi’an area; (b) The label map of (a); (c) The classification map by the Super-RF method; (d) The classification map by the DBDA method; (e) The classification map by the S3ANet method; (f) The classification map by the CV-CNN method; (g)The classification map by the proposed DCCNN method; (h) The classification map by the proposed DCCNN-MRF method.
Figure 5. Classification results of different methods in the Xi’an area. (a) PauliRGB image of Xi’an area; (b) The label map of (a); (c) The classification map by the Super-RF method; (d) The classification map by the DBDA method; (e) The classification map by the S3ANet method; (f) The classification map by the CV-CNN method; (g)The classification map by the proposed DCCNN method; (h) The classification map by the proposed DCCNN-MRF method.
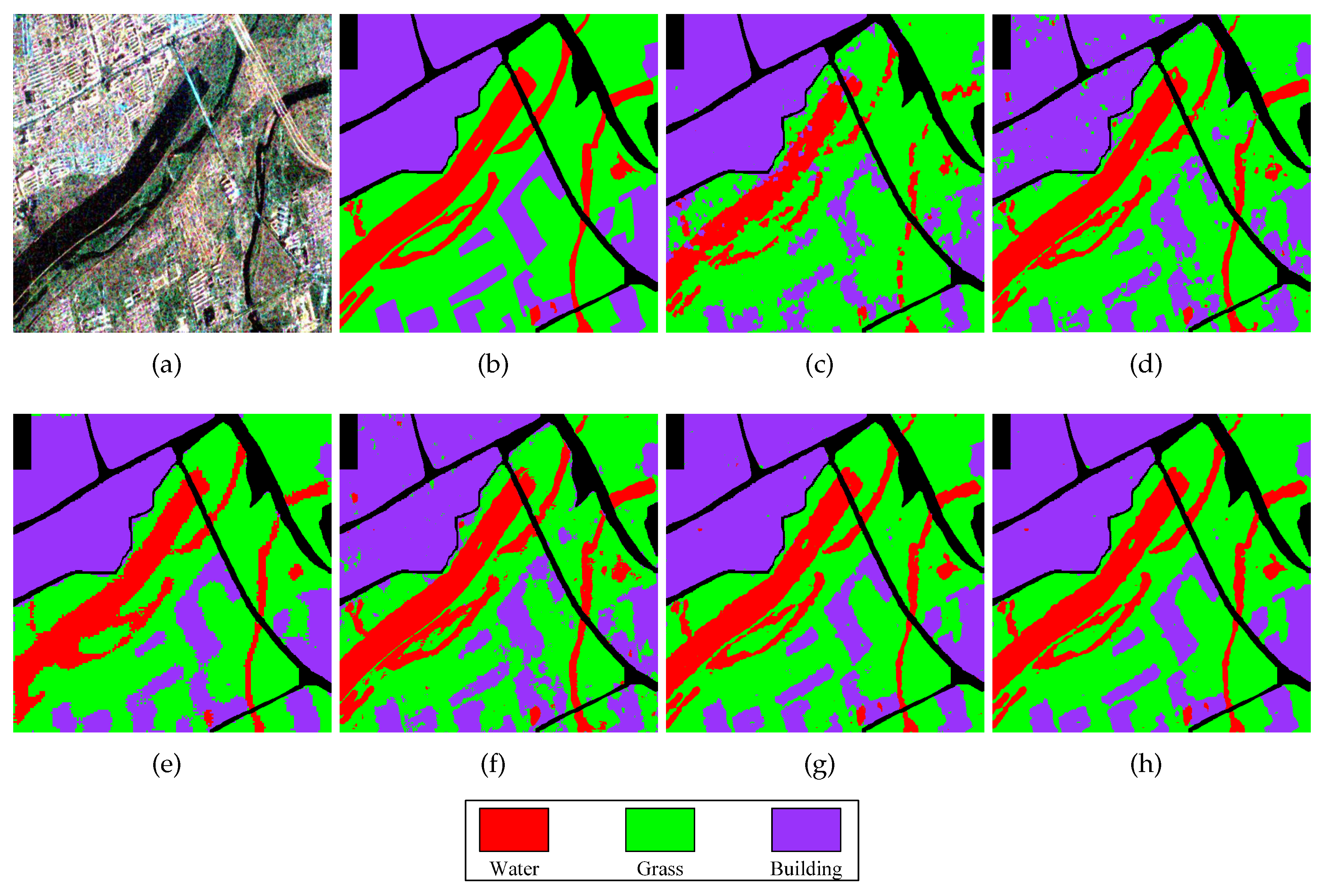
Preprints 86827 g005
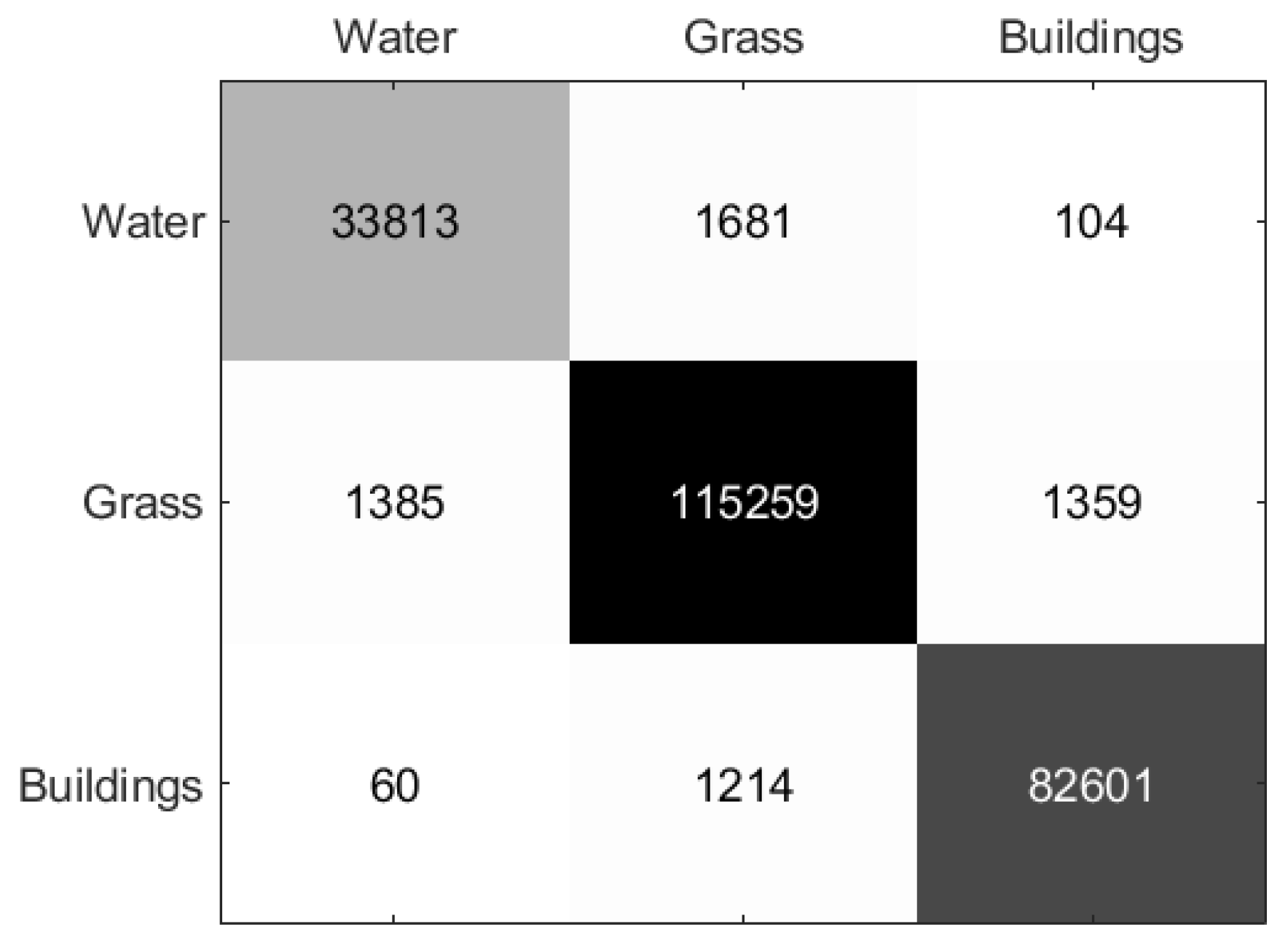
Preprints 86827 g006
Figure 6. Confusion matrix of the proposed method on Xi’an Data Set.
Figure 6. Confusion matrix of the proposed method on Xi’an Data Set.
Preprints 86827 g006
Preprints 86827 g008
Figure 8. Confusion matrix of the proposed method on Flevoland 1 Data Set.
Figure 8. Confusion matrix of the proposed method on Flevoland 1 Data Set.
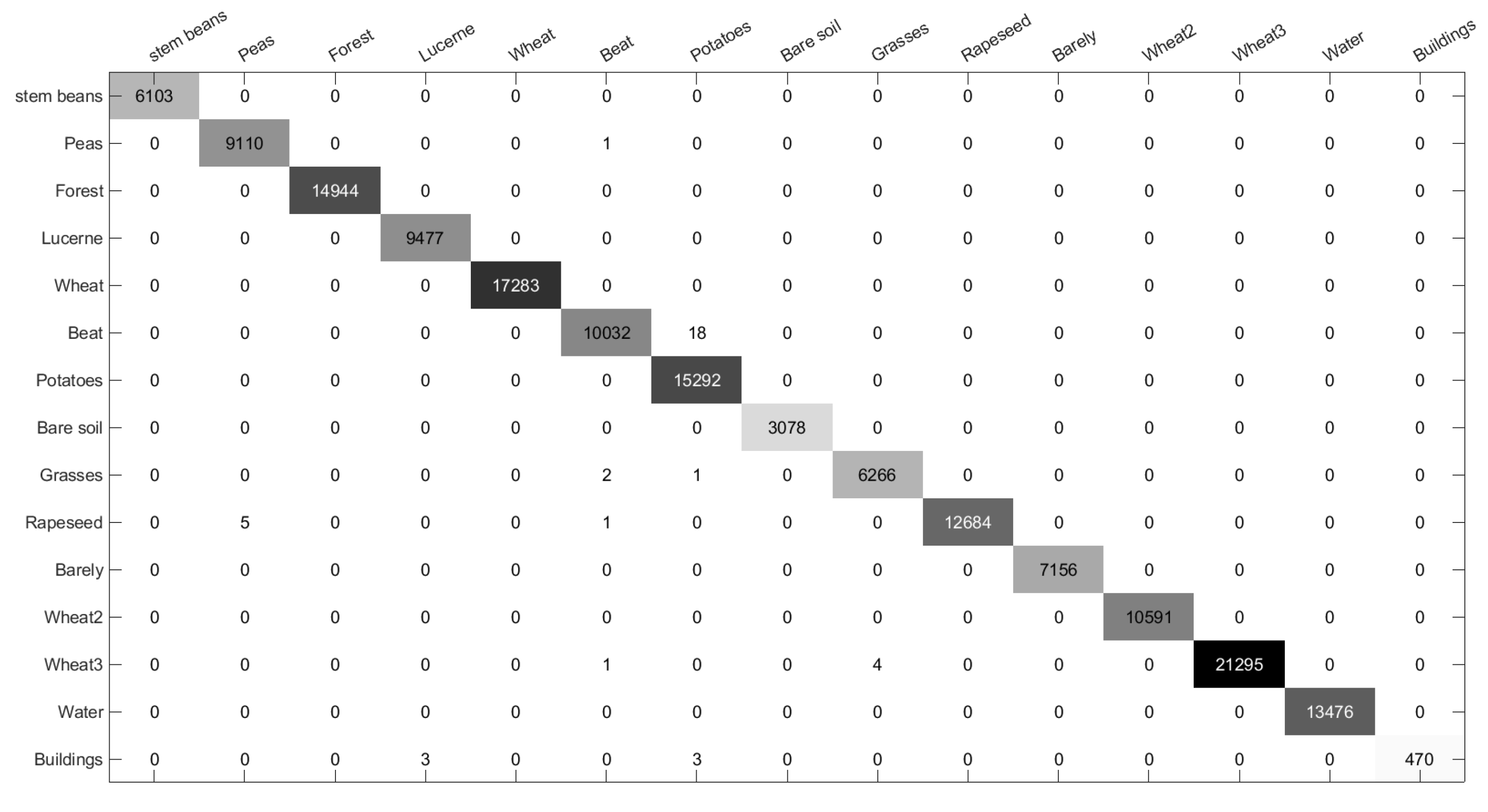
Preprints 86827 g008
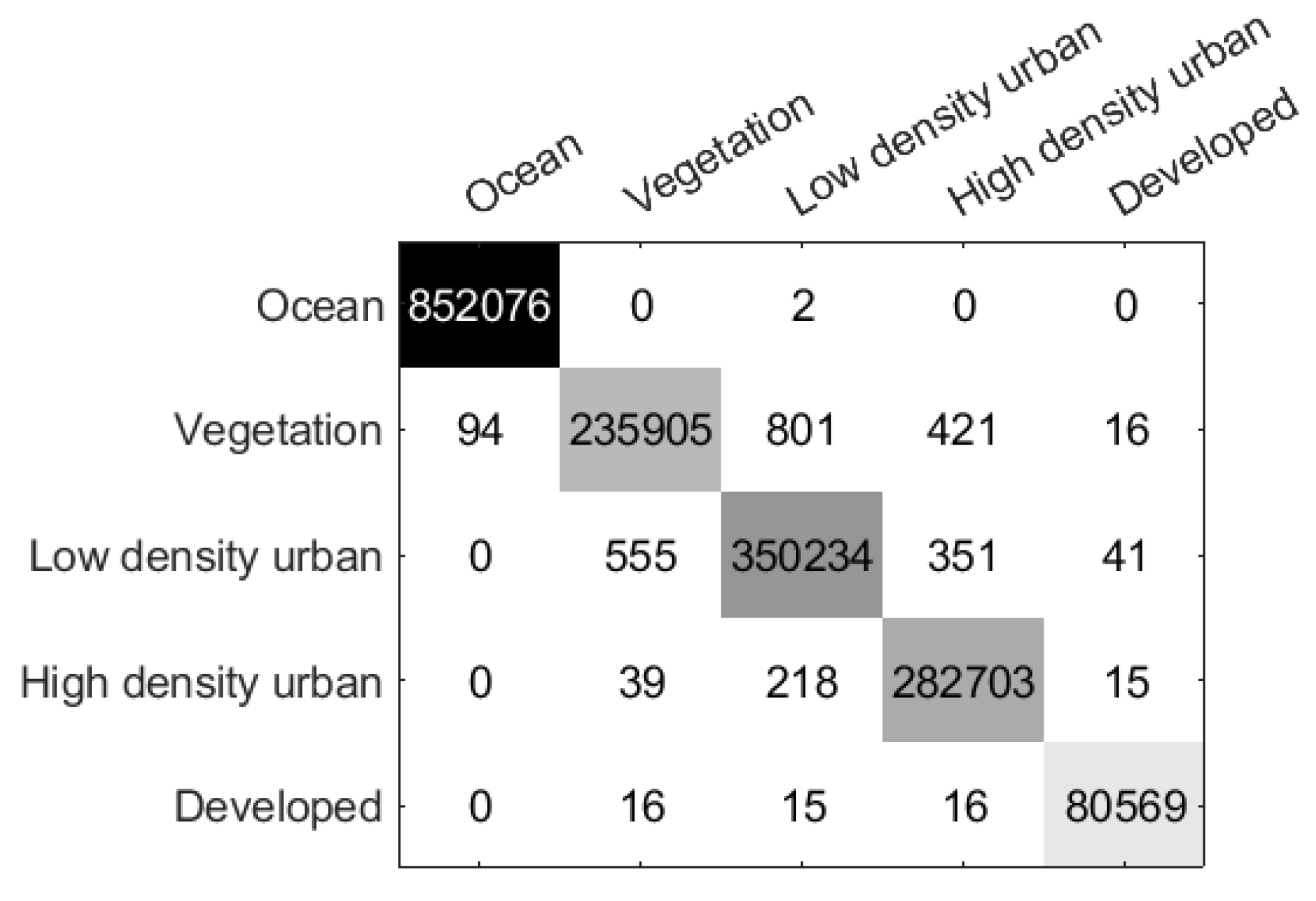
Preprints 86827 g010
Figure 10. Confusion matrix of the proposed method on San Francisco Data Set.
Figure 10. Confusion matrix of the proposed method on San Francisco Data Set.
Preprints 86827 g010
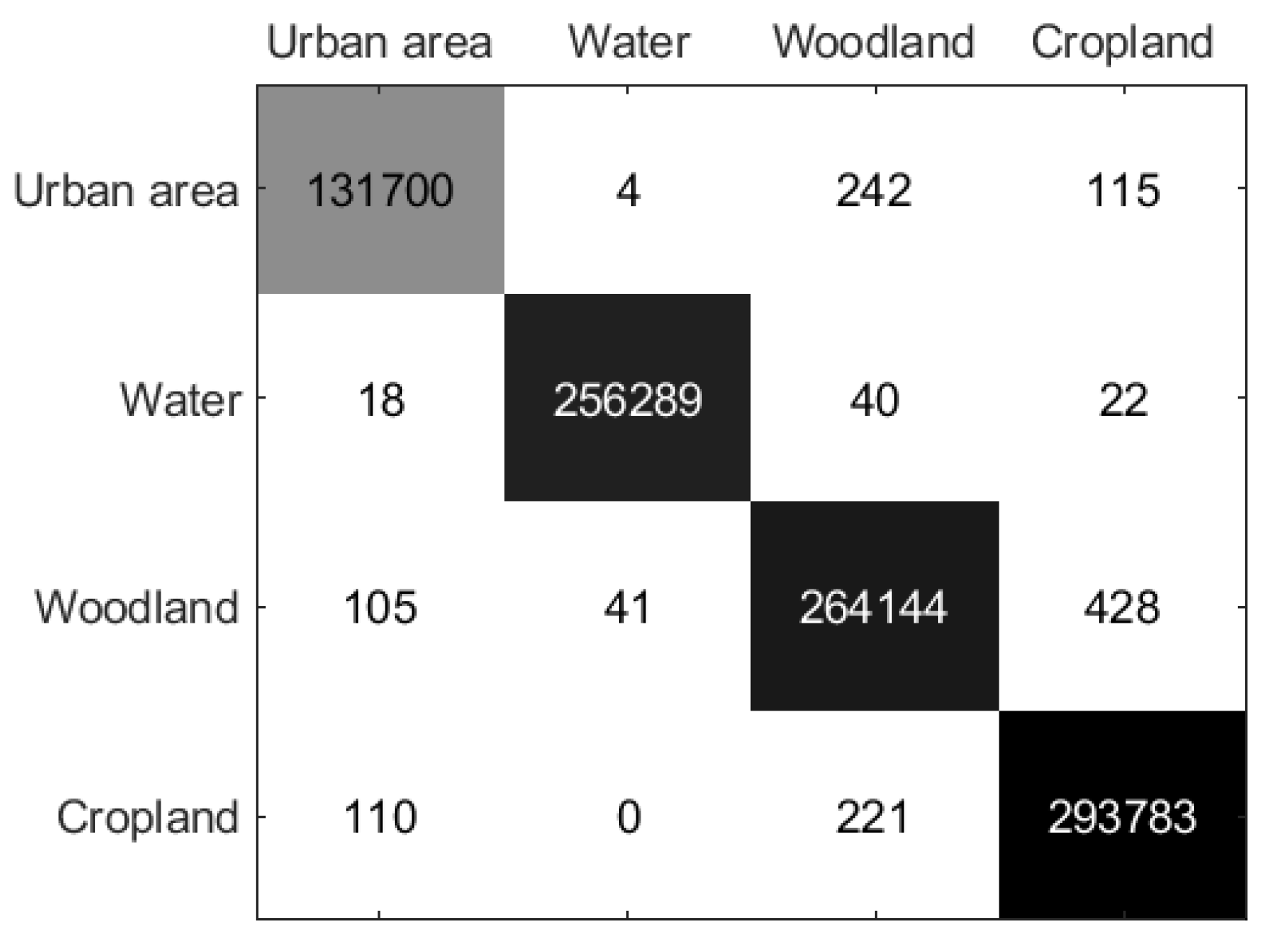
Preprints 86827 g012
Figure 12. Confusion matrix of the proposed method on Flevoland 2 Data Set.
Figure 12. Confusion matrix of the proposed method on Flevoland 2 Data Set.
Preprints 86827 g012
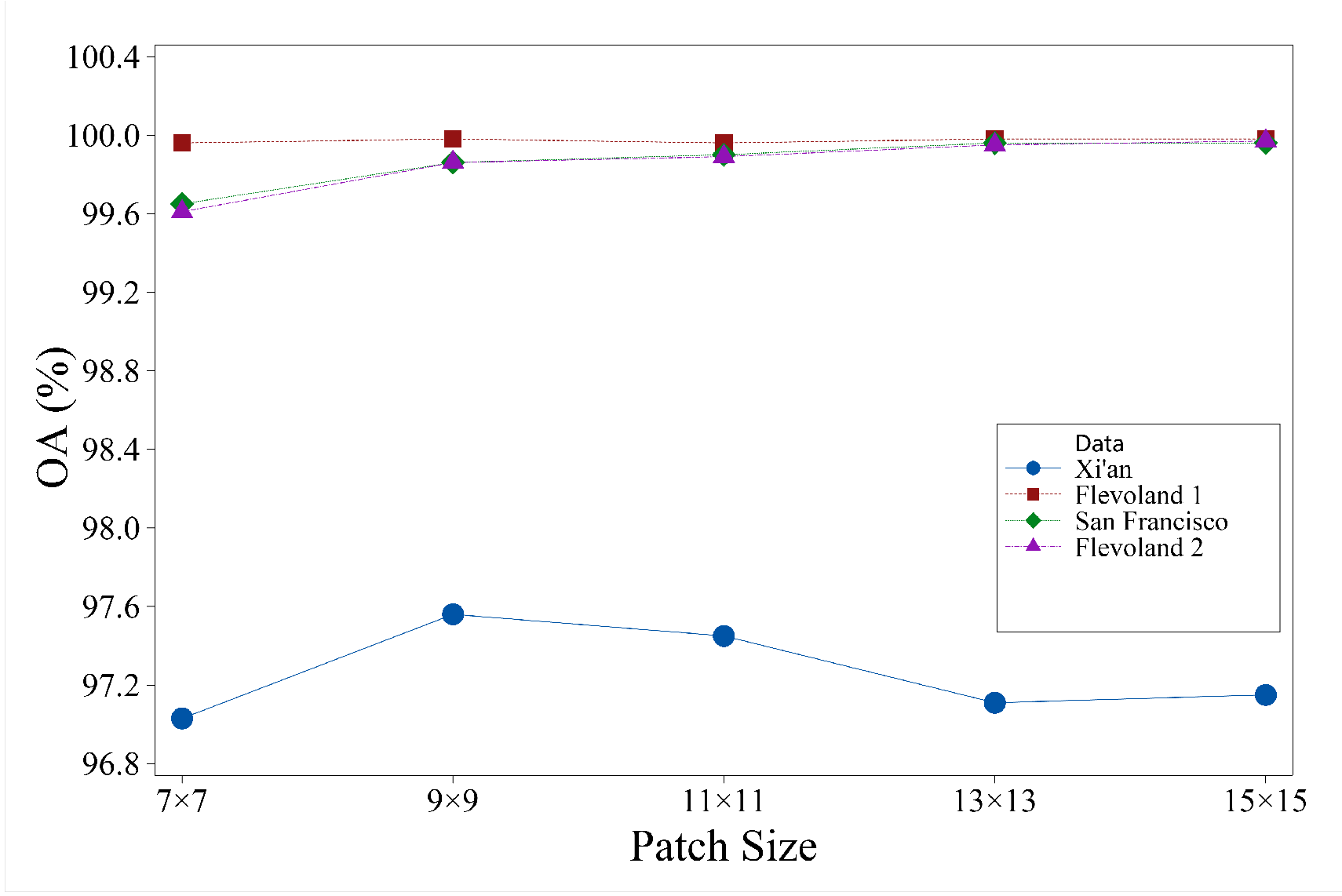
Preprints 86827 g013
Figure 13. The effect of patch size on classification accuracy.
Figure 13. The effect of patch size on classification accuracy.
Preprints 86827 g013
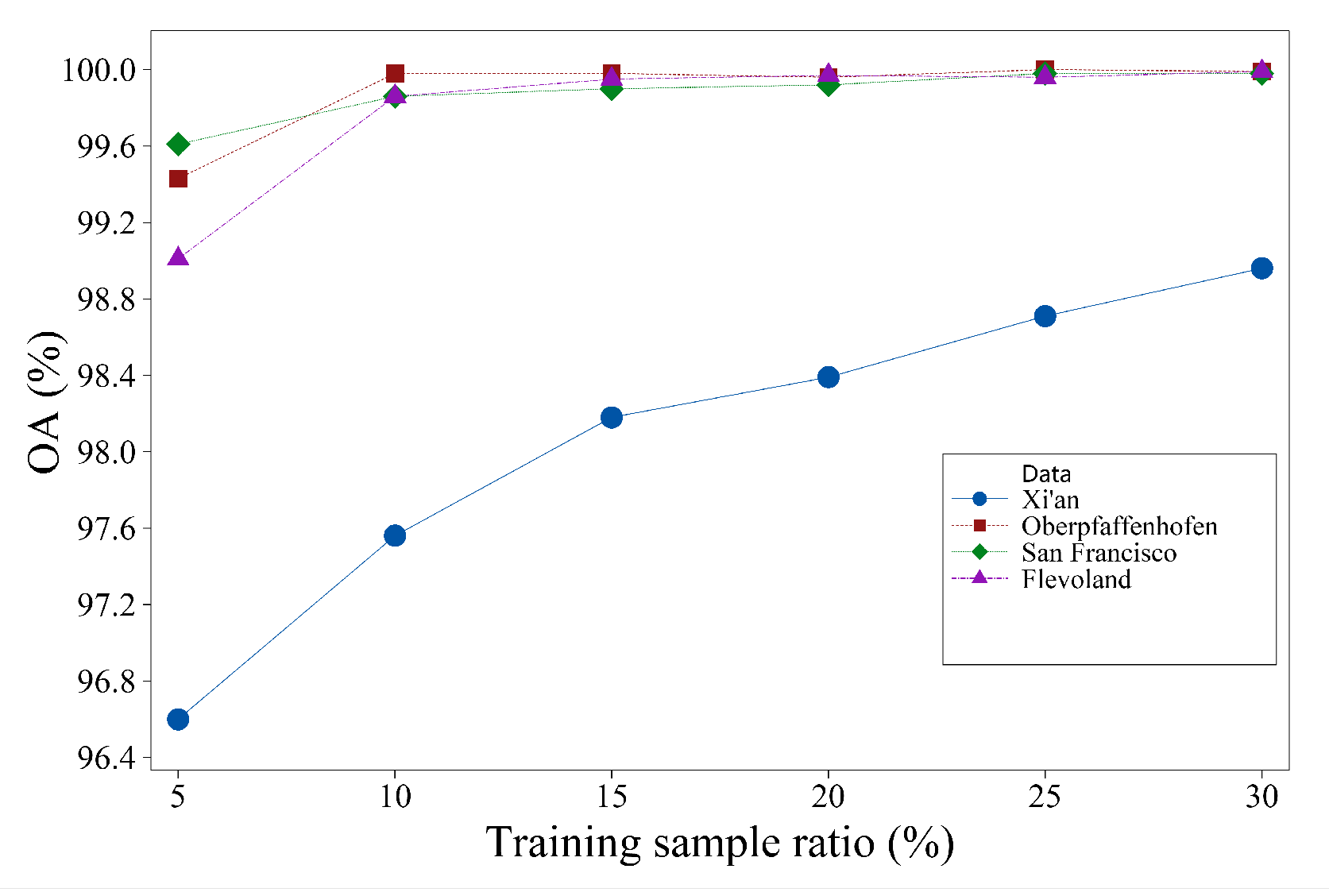
Preprints 86827 g014
Figure 14. The effect of training sample ratio on classification accuracy.
Figure 14. The effect of training sample ratio on classification accuracy.
Preprints 86827 g014
Table 1. Multiple Feature Extraction of PolSAR images.
Table 1. Multiple Feature Extraction of PolSAR images.
Preprints 86827 i001
Table 2. PolSAR data set used within the experiments.
Table 2. PolSAR data set used within the experiments.
Name System Band Dimensions Resolution Class
Xi’an RADARSAT-2 C 8 × 8 m 512 × 512 3
Flevoland1 AIRSAR L 12 . 1 × 6 . 7 m 750 × 1024 15
San Francisco RADARSAT-2 C 10 × 5 m 1800 × 1380 5
Flevoland2 AIRSAR C 12 × 8 m 1400 × 1200 4
Table 3. Classification accuracy of different methods on Xi’an Data Set. (%)
Table 3. Classification accuracy of different methods on Xi’an Data Set. (%)
class Super-RF DBDA S3ANet CV-CNN DCCNN DCCNN-MRF
water 70.91 89.88 84.39 95.30 94.88 94.99
grass 94.97 93.13 93.99 88.25 97.49 97.67
building 90.94 91.56 96.72 95.34 98.31 98.48
OA 89.94 92.09 93.51 91.81 97.39 97.56
AA 85.61 91.53 91.70 92.96 96.90 97.05
Kappa 83.02 86.91 89.24 86.67 95.69 95.96
Table 4. Classification accuracy of different methods on Flevoland 1 Data Set (%).
Table 4. Classification accuracy of different methods on Flevoland 1 Data Set (%).
class Super-RF DBDA S3ANet CV-CNN DCCNN DCCNN-MRF
stembeans 96.77 99.97 93.79 99.72 100 100
peas 98.64 99.53 96.63 99.99 99.98 99.99
forest 95.88 99.37 96.01 99.82 100 100
lucerne 96.63 100 96.86 98.17 99.97 100
wheat 99.05 98.69 99.86 98.66 100 100
beat 95.70 99.83 98.09 99.22 99.82 99.82
potatoes 96.04 99.59 95.21 99.14 100 100
baresoil 94.57 83.11 100 100 100 100
grasses 84.03 85.12 68.19 99.94 99.94 99.95
rapeseed 53.13 65.23 81.60 94.18 99.94 99.95
barely 100 85.52 95.11 99.58 100 100
wheat2 79.93 99.48 96.83 99.41 100 100
wheat3 99.39 99.23 99.79 99.37 99.97 99.98
water 100 89.93 99.27 99.99 100 100
building 0 95.17 66.39 100 98.95 98.74
OA 92.18 94.31 95.01 98.96 99.97 99.98
AA 85.98 93.32 92.24 99.15 99.90 99.90
Kappa 91.44 93.79 94.55 98.87 99.97 99.97
Table 5. Classification accuracy of different methods on San Francisco Data Set (%).
Table 5. Classification accuracy of different methods on San Francisco Data Set (%).
class Super-RF DBDA S3ANet CV-CNN DCCNN DCCNN-MRF
ocean 99.98 99.32 99.73 99.99 100 100
vegetation 93.89 88.20 97.40 96.42 99.31 99.44
low-density urban 97.31 98.33 98.27 94.51 99.51 99.73
high-density urban 77.76 90.00 99.82 96.37 99.80 99.90
develop 81.00 81.15 99.47 95.92 99.87 99.94
OA 94.33 95.39 99.14 97.71 99.78 99.86
AA 89.99 91.40 98.93 96.64 99.70 99.80
Kappa 91.81 93.36 98.76 96.70 99.68 99.79
Table 6. Classification accuracy of different methods on Flevoland 2 Data Set (%).
Table 6. Classification accuracy of different methods on Flevoland 2 Data Set (%).
class Super-RF DBDA S3ANet CV-CNN DCCNN DCCNN-MRF
urban 81.84 89.37 99.91 96.26 99.57 99.73
water 98.69 95.83 98.86 99.85 99.96 99.97
woodland 94.92 95.82 97.11 96.48 99.70 99.78
cropland 94.16 97.69 99.17 93.94 99.78 99.89
OA 93.88 95.50 98.61 96.57 99.78 99.86
AA 92.40 94.68 98.76 96.63 99.76 99.84
Kappa 91.61 93.84 98.11 95.33 99.70 99.81
Table 7. Classification accuracy of different subnetworks on four data sets (%).
Table 7. Classification accuracy of different subnetworks on four data sets (%).
Data set Xi’an Flevoland 1 San Francisco Flevoland 2
Accuracy OA Kappa OA Kappa OA Kappa OA Kappa
Wishart 88.58 81.12 95.49 95.08 92.36 89.00 94.37 92.31
Multi-feature 95.77 92.98 99.91 99.90 99.75 99.64 99.76 99.68
DCCNN 97.39 95.69 99.97 99.97 99.78 99.68 99.78 99.70
Table 8. Classification accuracy of different model settings on data sets (%).
Table 8. Classification accuracy of different model settings on data sets (%).
Data set Xi’an Flevoland 1 San Francisco Flevoland 2
Accuracy OA Kappa OA Kappa OA Kappa OA Kappa
Wishart 88.58 81.12 95.49 95.08 92.36 89.00 94.37 92.31
Wishart+MRF 89.25 82.24 95.93 95.55 93.00 89.92 95.84 94.33
Multi-feature 95.77 92.98 99.91 99.90 99.75 99.64 99.76 99.68
Multi-feature+MRF 95.98 93.33 99.94 99.93 99.83 99.76 99.85 99.79
DCCNN 97.39 95.69 99.97 99.97 99.78 99.68 99.78 99.70
DCCNN+MRF 97.56 95.96 99.98 99.97 99.86 99.79 99.86 99.81
Table 9. Running time of different methods on Xi’an data set (s).
Table 9. Running time of different methods on Xi’an data set (s).
Super-RF DBDA S3ANet CV-CNN DCCNN-MRF
training time 59.22 239.35 461.33 7872.68 121.99
test time 1.85 32.50 1.43 19.88 13.24
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated