Preprint
Article
An automatic pixel-wise multi-penalty approach to image restoration
Altmetrics
Downloads
62
Views
20
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
02 October 2023
Posted:
04 October 2023
You are already at the latest version
Alerts
Abstract
This work tackles the problem of image restoration, a crucial task in many fields of applied sciences, focusing on removing degradation caused by blur and noise during the acquisition process. Drawing inspiration from the multi-penalty approach based on the Uniform Penalty principle introduced in [Bortolotti et al. arXiv.math.NA/2309.14163], we develop here a new image restoration model and an iterative algorithm for its effective solution.
The model incorporates pixel-wise regularization terms and establishes a rule for parameters selection, aiming to restore images through the solution of a sequence of constrained optimization problems. To achieve this, we present a modified version of the Newton Projection method, adapted to multi-penalty scenarios, and prove its convergence. Numerical experiments demonstrate the efficacy of the method in eliminating noise and blur while preserving the image edges.
Keywords:
Subject: Computer Science and Mathematics - Computer Vision and Graphics
1. Introduction
Image restoration is an important task in many areas of applied sciences since digital images are frequently degraded by blur and noise during the acquisition process. Image restoration can be mathematically formulated as the linear inverse problem [1]
where and respectively are vectorized forms of the observed image and the exact image to be restored, is the linear operator modeling the imaging system and represents Gaussian white noise with mean zero and standard deviation . The image restoration problem (1) is inherently ill-posed and regularization strategies, based on the prior information on the unknown image, are usually employed in order to effectively restore the image from .
In a variational framework, image restoration can be reformulated as a constrained optimization problem of the form
whose objective function contains a -based term, imposing consistency of the model with the data, and a regularization term , forcing the solution to satisfy some a priori properties. Here and henceforth, the symbol denotes the Euclidean norm. The constraint imposes some characteristics on the solution which are often given by the physics underlying the data acquisition process. Since image pixels are known to be nonnegative, a typical choice for is the positive orthant.
The quality of the restored images strongly depends on the choice of the regularization term which, in a very general framework, can be expressed as
where the positive scalars are regularization parameters and the are regularization functions for . The multi-penalty approach (3) allows to impose several regularity properties on the desired solution, however a crucial issue with its realization is the need to define reliable strategies for the choice of the regularization parameters , .
Therefore, in the literature, the most common and famous regularization approach is single-penalty regularization, also known as Tikhonov-like regularization, which corresponds to the choice :
In image restoration, smooth functions based on the -norm or convex nonsmooth functions like the Total Variation, the norm or the Total Generalized Variation are usually used for in (4) [2,3]. Even in the case , the development of suitable parameter choice criteria is still an open question. The recent literature has demonstrated a growing interest in multi-penalty regularization, with a significant number of researchers focusing on scenarios involving two penalty terms. Notably, the widely-used elastic regression in Statistics serves as an example of a multi-penalty regularization technique, integrating the and penalties from the Lasso and Ridge methods. However, the majority of the literature primarily addresses the development of suitable rules for parameter selection.
Lu, Pereverzev et al. [4,5] have extensively investigated two -based terms, introducing a refined discrepancy principle to compute dual regularization parameters, along with its numerical implementation.
The issue of parameter selection is further discussed in [6], where a generalized multi-parameter version of the L-curve criterion is proposed, and in [7], which suggests a methodology based on the GCV method.
Reichel and Gazzola [8] propose regularization terms of the form
where are suitable regularization matrices. They present a method to determine the regularization parameters utilizing the discrepancy principle, with a special emphasis on the case . Fornasier et al. [9] propose a modified discrepancy principle for multi-penalty regularization and provide theoretical background for this a posteriori rule.
Works such as [10,11,12,13,14] also explore multi-penalty regularization for unmixing problems, employing two penalty terms based on and norms, and . The latter specifically concentrates on the and norms.
The study [15] assesses two-penalty regularization, incorporating and penalty terms, to tackle nonlinear ill-posed problems and analyzes its regularizing characteristics.
In [16], an automated spatially adaptive regularization model combining harmonic and Total Variation (TV) terms is introduced. This model is dependent on two regularization parameters and two edge information matrices. Despite the dynamic update of the edge information matrix during iterations, the model necessitates fixed values for the regularization parameters.
Calatroni et al. [17] present a space-variant generalized Gaussian regularization approach for image restoration, emphasizing its applicative potential.
In [18], a multipenalty point-wise approach based on the Uniform Penalty principle is considered and analyzed for general linear inverse problems, introducing two iterative methods, UpenMM and GUpenMM, and analyzing their convergence.
Here we focus on image restoration and, following [18], we propose to find an estimate of satisfying
where is a positive scalar and is the discrete Laplacian operator. This model, named MULTI, is specifically tailored for the image restoration problem. Observe that MULTI incorporates a pixel-wise regularization term and includes a rule for choosing the parameters. Building upon UPenMM and GUpenMM methods analyzed in [18], we formulate an iterative algorithm for computing the solution of (6), where . In every inner iteration, once the regularization parameters are set, the constrained minimization subproblem is efficiently solved by a customized version of the Newton Projection (NP) method. Here, the Hessian matrix is approximated by a Block Circulant with Circulant Blocks (BCCB) matrix, which is easily invertible in the Fourier space. This modified version of NP was designed in [19] for single-penalty image restoration under Poisson noise and it is adapted here to the context of multi-penalty regularization. Consequently, the convergence of the modified NP method can be established.
The principal contributions of this work are summarized as follows:
- We propose a novel variational pixel-wise regularization model for image restoration.
- We devise an algorithm capable of effectively and efficiently solving the proposed model.
- Through numerical experiments, we demonstrate that the proposed approach can proficiently eliminate noise and blur in smooth areas of an image while preserving its edges.
2. Materials and Methods
In this section we present the iterative algorithm that generates the sequence converging to the solution in (6).
Starting from an initial guess taken as the observed image , the correspondent initial guess of the regularization parameters is computed as:
where
and is a neighborhood of size , (with R odd and ) of the th pixel with coordinates .
The successive terms are obtained by the update formulas reported in steps 3-5 of Algorithm 1. The iterations are stopped when the relative distance between two successive regularization vectors is smaller than a fixed tolerance .
| Algorithm 1 Input: , , , Output: |
|
Algorithm 1 is well defined, and it is possible to prove its convergence. Let’s assume for now that the maximum value of in the neighborhood of the th pixel is exactly in the center of with coordinates . In this case, Algorithm 1 corresponds to UPenMM and, using Theorem 3.4 in [18] we can prove that the sequence converges to in (6). In the general case, when , it is possible to preserve convergence through a correction obtained from a convex combination between and . This approach is presented as Generalized Uniform Penalty method (GUPenMM) [18].
However, such algorithmic correction is not necessary in image restoration problems where it is not essential to compute solutions with a high level of accuracy. Indeed the human eye cannot distinguish the difference smaller than a few gray levels.
At each inner iteration, the constrained minimization subproblem (step 3 in Algorithm 1) is solved efficiently by a tailored version of the NP method where the Hessian matrix is approximated by a BCCB matrix easily invertible in the Fourier space.
Let us denote by the function to be minimized at step 3 in Algorithm 1:
and by its gradient where the iteration index k has been omitted for easier notation. Moreover, let denote the reduced gradient:
where is the set of indices [20]:
with
and is a small positive parameter.
The Hessian matrix has the form
where is the diagonal matrix with diagonal elements .
A general iteration of the proposed NP-like method has the form:
where is the search direction, is the steplength and denotes the projection on the positive orthant.
At each iteration ℓ, the computation of requires the solution of the linear system
where is the following approximation to
Under periodic boundary conditions, is a BCCB matrix and system (11) can be efficiently solved in the Fourier space by using Fast Fourier Transforms. Hence, despite its simplicity, the BCCB approximation is efficient, since it allows to solve the linear system in operations, and effective as it is shown by the numerical results. Finally, given the solution of (11), the search direction is obtained as
The step length is computed with the variation of the Armijo rule discussed in [20] as the first number of the sequence , , such that
where and .
We observe that the approximated Hessian is constant for each inner iteration ℓ and it is positive definite, then it satisfies
Then, the results given in [19] for single-penalty image restoration under Poisson noise, can be applied here to prove the convergence of the NL-like iterations to critical points.
The stopping criteria for the NP-like method are based on the relative distance between two successive iterates and the relative projected gradient norm. In addition, a maximum number of NP iterations have been fixed.
3. Numerical Experiments
All the experiments are performed under Windows 10 and MATLAB R2021a running on a desktop (Intel(R) Core(TM) i5-8250CPU@1.60 GHz). Quantitatively, we evaluate the quality of image restoration by the relative error (RE), improved signal to noise ratio (ISNR) and mean structural similarity index (MSSIM) measures. The MSSIM is defined by Wang et al. [21] and ISNR is calculated as:
where is the restored image, is the reference image and is the blurred, noisy image.
Four reference images were used in the experiments: galaxy, mri, leopard and elaine, shown in Figure 1, Figure 2, Figure 3 and Figure 4. The first three images have size , while the elaine image is . In order to define the test problems, each reference image was convolved with two PSFs corrsponding to a Gaussian blur with variance 2, generated by the psfGauss function from the MATLAB toolbox Restore-Tool [1], and an out-of-focus blur with radius 5, obtained with the function fspecial from the MATLAB Image Processing Toolbox. The resulting blurred image was then corrupted by Gaussian noise with different values of the noise level . The values were used.
We compare the proposed pixel-wise multi-penalty regularization model (MULTI) with Tikhonov (TIKH), Total Variation (TV) and Total Generalized Variation (TGV) regularization with nonnegative constraints. The regularization parameter values for TIKH, TV and TGV have been chosen heuristically by minimizing the relative error values. The Alternating Direction Method of Multipliers (ADMM) was used for the solution of the TV-based minimization problem, while for TIKH, we used the Scaled Gradient Projection (SGP) method with Barzilai and Borwein rules for the step length selection. Regarding the TGV regularization, the RESPOND method [22] has been used. We remark that RESPOND has been originally proposed for the restoration of images corrupted by Poisson noise, by using Directional Total Generalized Variation regularization. It has been adapted here to deal with TGV-based restoration of images under Gaussian noise. The MATLAB implementation for Poisson noise is available on GitHub.
The tolerance in the outer loop of MULTI in Algorithm 1 step 7 was , while the maximum number of iterations was 20. Regarding the NP method, a tolerance of was used and the maximum number of iterations was 1000.
The size of the neighborhood in (8) was pixels for all tests except for Galaxy, where a neighborhood was used.
The values of the parameter in (6), used in the various tests, are in the range . In order to compare all the algorithms at their best performance, the values used in each test are reported in Table 1, where we observe that the value of is proportional to the noise level. The parameter represents a threshold and, in general, should have a small value when compared to the non null values of . We note that at the cost of adjusting a single parameter , it is possible to achieve point-wise optimal regularization.
Table 2, Table 3, Table 4 and Table 5 report the numerical results for all the test problems. The last column of the tables shows the used values of the regularization parameter for TIKH, TV and TGV while, for MULTI, it reports the norm of the regularization parameters vector computed by Algorithm 1. Column 7 shows the number of RESPOND, ADMM and SGP iterations for TGV, TV and TIKH, respectively. For the MULTI algorithm, Column 7 shows the number of outer iterations and NP iterations in parenthesis.
In Table 2, Table 3, Table 4 and Table 5, we observe that TGV always outperforms TIKH and TV in terms of accuracy, since it has greater MSSIM and ISNR values and smaller values of RE. Therefore, in Figure 1, Figure 2, Figure 3 and Figure 4 we represent the images obtained by MULTI and TGV in the out-of-focus case, with as this is a very challenging case.
Moreover, from the images provided in Figure 5, it can be observed that MULTI method better preserves the local characteristics of the image, avoiding flattening the shooth areas and optimally preserving the sharp contours. We observe that a smooth area like the cheek is better represented by MULTI, avoiding the presence of the staircasing effect. Moreover, an area with strong contours, such as the teeth and the eyes, is better depicted.
The regularization parameters computed by MULTI are represented in Figure 6, the adherence of the regularization parameters’ values to the image content is clear, showing larger values in areas where the image is flat and smaller values where there are pronounced gradients (edges). The parameters range automatically adjusts according to the different test types.
Finally we show in Figure 7 an example of the algorithm behaviour, reporting the history of regularization parameter norm, relative error and residual norm in the case of leopard test with out-of-focus blur and noise level . The relative error flattens after a few iterations, and the same behaviour can be observed in all the other test. Therefore we used a large tolerance value () in the outer loop of Algorithm 1.
4. Conclusions
Our work is inspired by the uniform multi-penalty approach developed in [18] and proposes the pixel-wise regularization model to tackle the significant task of image restoration, concentrating on the elimination of degradation originating from blur and noise. The iterative method analized in [18] is adapted an made efficient for image restoration problems, by introducing a modified version of the Newton Projection method, tailored for multi-penalty scenarios.
The numerical results confirm the algorithm’s proficiency in eliminating noise and blur while concurrently preserving the edges of the image. These outcomes encourage us to extend the application of this algorithm to various imaging problems.
Acknowledgments
This research was partially supported by the Istituto Nazionale di Alta Matematica, Gruppo Nazionale per il Calcolo Scientifico (INdAM-GNCS).
References
- Hansen, P.C.; Nagy, J.G.; O’leary, D.P. Deblurring Images: Matrices, Spectra, and Filtering; SIAM: 2006.
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Bredies, K.; Kunisch, K.; Pock, T. Total generalized variation. SIAM J. Imaging Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Lu, S.; Pereverzev, S.V. Multi-parameter regularization and its numerical realization. Numer. Math. 2011, 118, 1–31. [Google Scholar] [CrossRef]
- Lu, S.; Pereverzev, S.V.; Shao, Y.; Tautenhahn, U. Discrepancy Curves for Multi-Parameter Regularization; 2010. [Google Scholar]
- Belge, M.; Kilmer, M.E.; Miller, E.L. Efficient determination of multiple regularization parameters in a generalized L-curve framework. Inverse Probl. 2002, 18, 1161. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo-Zaglia, M.; Rodriguez, G.; Seatzu, S. Multi-parameter regularization techniques for ill-conditioned linear systems. Numer. Math. 2003, 94, 203–228. [Google Scholar] [CrossRef]
- Gazzola, S.; Reichel, L. A new framework for multi-parameter regularization. BIT Numer. Math. 2016, 56, 919–949. [Google Scholar] [CrossRef]
- Fornasier, M.; Naumova, V.; Pereverzyev, S.V. Parameter choice strategies for multipenalty regularization. SIAM J. Numer. Anal. 2014, 52, 1770–1794. [Google Scholar] [CrossRef]
- Kereta, Z.; Maly, J.; Naumova, V. Linear convergence and support recovery for non-convex multi-penalty regularization. CoRR 2019. [Google Scholar]
- Naumova, V.; Peter, S. Minimization of multi-penalty functionals by alternating iterative thresholding and optimal parameter choices. Inverse Probl. 2014, 30, 125003. [Google Scholar] [CrossRef]
- Kereta, Ž.; Maly, J.; Naumova, V. Computational approaches to non-convex, sparsity-inducing multi-penalty regularization. Inverse Probl. 2021, 37, 055008. [Google Scholar] [CrossRef]
- Naumova, V.; Pereverzyev, S.V. Multi-penalty regularization with a component-wise penalization. Inverse Probl. 2013, 29, 075002. [Google Scholar] [CrossRef]
- Grasmair, M.; Klock, T.; Naumova, V. Adaptive multi-penalty regularization based on a generalized lasso path. Appl. Comput. Harmon. Anal. 2020, 49, 30–55. [Google Scholar] [CrossRef]
- Wang, W.; Lu, S.; Mao, H.; Cheng, J. Multi-parameter Tikhonov regularization with the ℓ0 sparsity constraint. Inverse Probl. 2013, 29, 065018. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, J.; Wu, C.; He, Z.; Zeng, T.; Jin, Q. Edge adaptive hybrid regularization model for image deblurring. Inverse Probl. 2022, 38, 065010. [Google Scholar] [CrossRef]
- Calatroni, L.; Lanza, A.; Pragliola, M.; Sgallari, F. A flexible space-variant anisotropic regularization for image restoration with automated parameter selection. SIAM J. Imaging Sci. 2019, 12, 1001–1037. [Google Scholar] [CrossRef]
- Bortolotti, V.; Landi, G.; Zama, F. Uniform multi-penalty regularization for linear ill-posed inverse problems. arXiv 2023, arXiv:2309.14163. [Google Scholar]
- Landi, G.; Loli Piccolomini, E. An improved Newton projection method for nonnegative deblurring of Poisson-corrupted images with Tikhonov regularization. Numer. Algorithms 2012, 60, 169–188. [Google Scholar] [CrossRef]
- Bertsekas, D.P. Projected Newton methods for optimization problems with simple constraints. SIAM J. Control. Optim. 1982, 20, 221–246. [Google Scholar] [CrossRef]
- Wang, S.; Rehman, A.; Wang, Z.; Ma, S.; Gao, W. SSIM-motivated rate-distortion optimization for video coding. IEEE Trans. Circuits Syst. Video Technol. 2011, 22, 516–529. [Google Scholar] [CrossRef]
- di Serafino, D.; Landi, G.; Viola, M. Directional TGV-based image restoration under Poisson noise. J. Imaging 2021, 7, 99. [Google Scholar] [CrossRef]
Figure 1.
galaxy test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.
Figure 1.
galaxy test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.

Figure 2.
mri test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.
Figure 2.
mri test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.
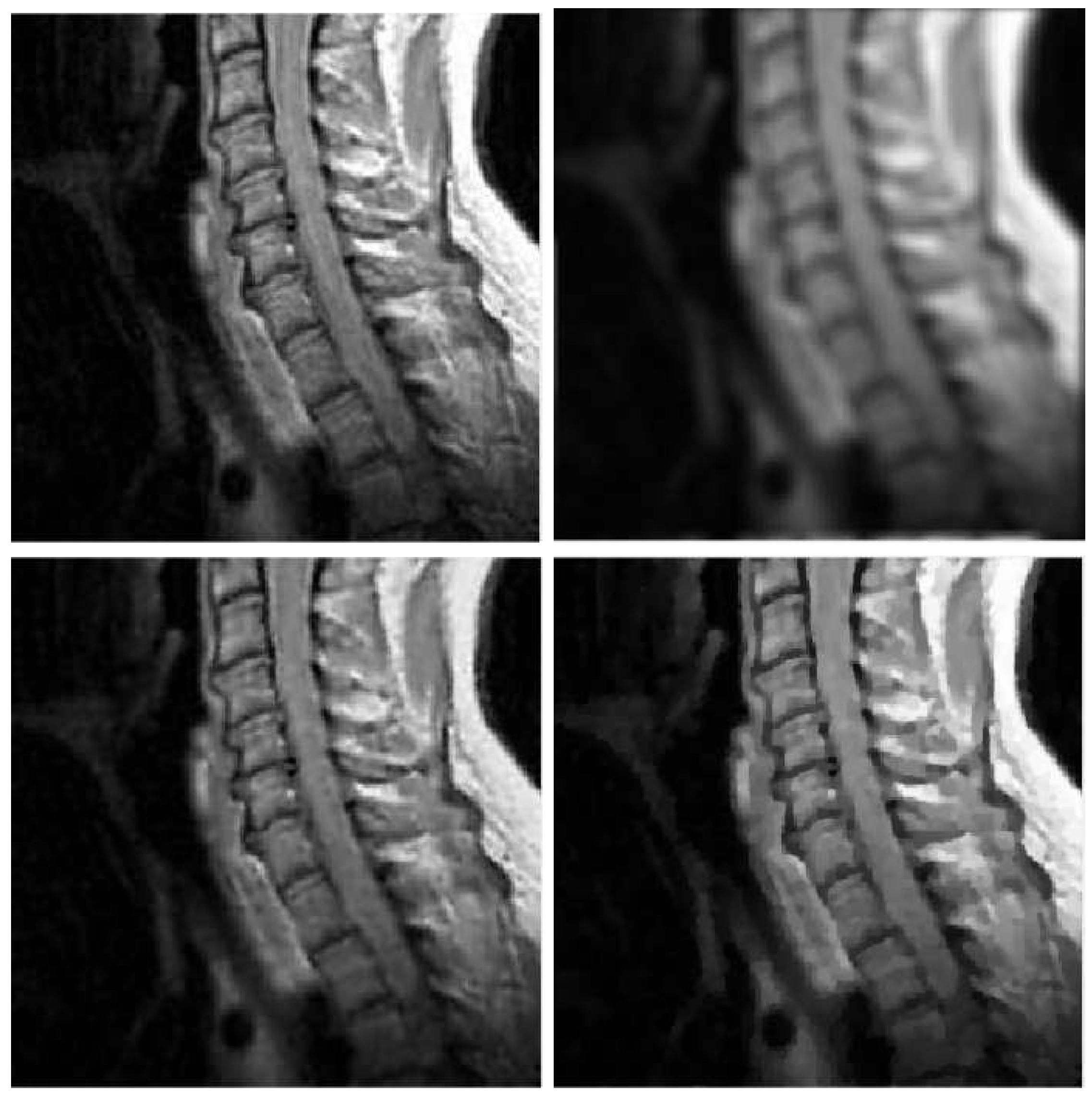
Figure 3.
leopard test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.
Figure 3.
leopard test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.

Figure 4.
elaine test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.
Figure 4.
elaine test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.

Figure 5.
elaine test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.
Figure 5.
elaine test problem: out-of-focus blur; . Top row: original (left) and blurred (right) images. Bottom row: MULTI (left) and TGV (right) restorations.

Figure 6.
Computed regularization parameters: out-of-focus blur, .

Figure 7.
leopard test problem (out-of-focus blur, ): regularization parameters norm (left), relative error (middle) and residual norm (right) history for the multi-penalty model.
Figure 7.
leopard test problem (out-of-focus blur, ): regularization parameters norm (left), relative error (middle) and residual norm (right) history for the multi-penalty model.
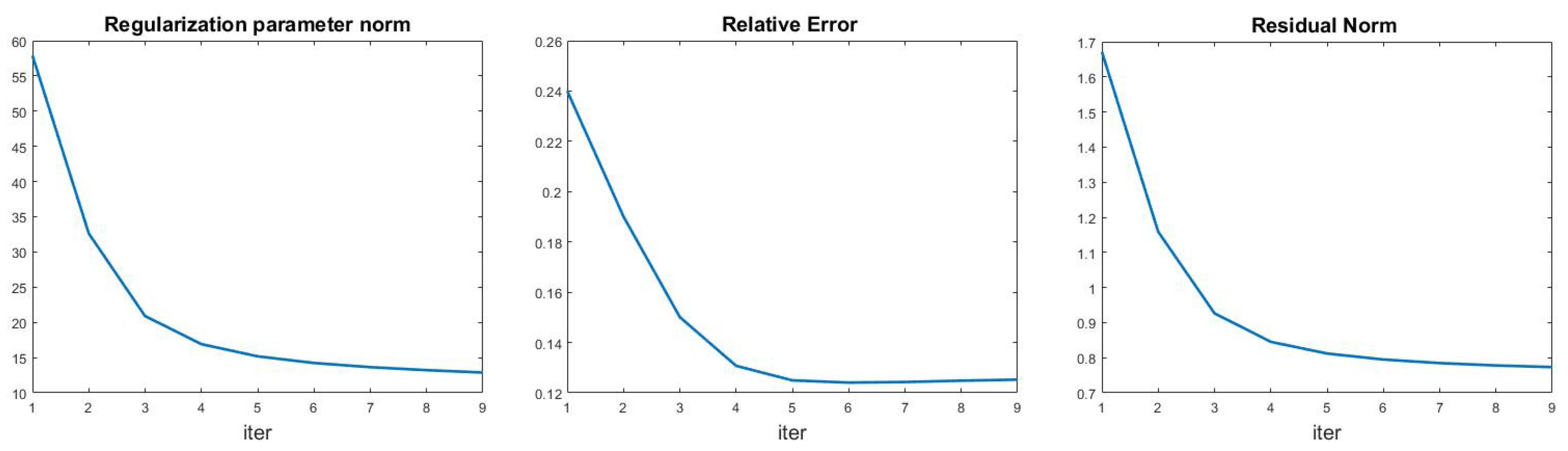
Table 1.
Values for the parameter .
| Test Problem | Blur | |||
|---|---|---|---|---|
| Galaxy | Out-of-focus | 0.5e-3 | 0.25e-3 | 0.1e-3 |
| Gaussian | 0.5e-3 | 0.25e-3 | 0.1e-3 | |
| mri | Out-of-focus | 1.5e-3 | 1e-3 | 0.5e-3 |
| Gaussian | 1.5e-3 | 1e-3 | 0.5e-3 | |
| leopard | Out-of-focus | 2.5e-3 | 1.5e-3 | 1.e-3 |
| Gaussian | 2.5e-3 | 0.1e-3 | 0.5e-4 | |
| Elaine | Out-of-focus | 1e-3 | 1e-3 | 1e-3 |
| Gaussian | 1e-3 | 0.5e-3 | 0.5e-3 |
Table 2.
Numerical results for the galaxy test problem.
| Blur | Model | RE | ISNR | MSSIM | Iters | ||
|---|---|---|---|---|---|---|---|
| Out-of-focus | TGV | 9.5953e-02 | 7.2175e+00 | 9.1418e-01 | 226 | 3.0000e+02 | |
| TV | 1.0268e-01 | 6.6291e+00 | 8.7089e-01 | 278 | 1.0000e-04 | ||
| TIKH | 1.3864e-01 | 4.0211e+00 | 8.3486e-01 | 200 | 1.1000e-02 | ||
| MULTI | 8.2096e-02 | 8.5722e+00 | 9.3431e-01 | 4(857) | 8.4116e+00 | ||
| TGV | 7.1519e-02 | 9.7292e+00 | 9.5015e-01 | 302 | 7.5000e+02 | ||
| TV | 6.7196e-02 | 1.0271e+01 | 9.4744e-01 | 259 | 5.0000e-05 | ||
| TIKH | 1.0943e-01 | 6.0351e+00 | 8.5965e-01 | 200 | 3.0000e-03 | ||
| MULTI | 6.2660e-02 | 1.0878e+01 | 9.5843e-01 | 7(1061) | 2.1493e+00 | ||
| TGV | 6.1028e-02 | 1.1102e+01 | 9.6274e-01 | 323 | 1.0000e+03 | ||
| TV | 6.3776e-02 | 1.0719e+01 | 9.4229e-01 | 303 | 1.0000e-05 | ||
| TIKH | 9.1181e-02 | 7.6143e+00 | 8.7665e-01 | 200 | 1.0000e-03 | ||
| MULTI | 4.8955e-02 | 1.3017e+01 | 9.7150e-01 | 9(1013) | 1.0491e+00 | ||
| Gaussian | TGV | 9.6150e-02 | 4.5854e+00 | 9.3328e-01 | 198 | 2.5000e+02 | |
| TV | 8.8306e-02 | 5.3246e+00 | 9.2702e-01 | 224 | 1.0000e-04 | ||
| TIKH | 1.0047e-01 | 4.2032e+00 | 9.0136e-01 | 200 | 5.0000e-03 | ||
| MULTI | 7.3686e-02 | 6.8966e+00 | 9.5114e-01 | 4(699) | 8.3317e+00 | ||
| TGV | 8.5737e-02 | 5.5019e+00 | 9.4922e-01 | 246 | 1.0000e+03 | ||
| TV | 7.7929e-02 | 6.3312e+00 | 9.3945e-01 | 223 | 1.0000e-05 | ||
| TIKH | 8.4284e-02 | 5.6503e+00 | 9.2110e-01 | 200 | 1.0000e-03 | ||
| MULTI | 6.0402e-02 | 8.5442e+00 | 9.6606e-01 | 5(437) | 2.3968e+00 | ||
| TGV | 8.0734e-02 | 6.0131e+00 | 9.5637e-01 | 280 | 2.5000e+03 | ||
| TV | 7.3912e-02 | 6.7800e+00 | 9.5186e-01 | 214 | 1.0000e-06 | ||
| TIKH | 7.3620e-02 | 6.8143e+00 | 9.4621e-01 | 200 | 5.0000e-04 | ||
| MULTI | 5.7592e-02 | 8.9471e+00 | 9.7129e-01 | 6(383) | 1.3106e+00 |
Table 3.
Numerical results for the mri test problem.
| Blur | Model | RE | ISNR | MSSIM | Iters | ||
|---|---|---|---|---|---|---|---|
| Out-of-focus | TGV | 8.6404e-02 | 6.8531e+00 | 8.3691e-01 | 185 | 9.0000e+01 | |
| TV | 8.7052e-02 | 6.7882e+00 | 8.3805e-01 | 212 | 5.0000e-04 | ||
| TIKH | 1.1476e-01 | 4.3882e+00 | 7.4472e-01 | 200 | 1.0000e-02 | ||
| MULTI | 7.9139e-02 | 7.6160e+00 | 8.5073e-01 | 4(1403) | 1.0098e+01 | ||
| TGV | 6.6508e-02 | 9.0670e+00 | 8.9245e-01 | 180 | 2.5000e+02 | ||
| TV | 6.7875e-02 | 8.8903e+00 | 8.9272e-01 | 232 | 1.0000e-04 | ||
| TIKH | 9.4934e-02 | 5.9760e+00 | 8.2645e-01 | 200 | 5.0000e-03 | ||
| MULTI | 5.4634e-02 | 1.0775e+01 | 9.1681e-01 | 5(1456) | 1.7962e+00 | ||
| TGV | 5.3582e-02 | 1.0936e+01 | 9.2644e-01 | 292 | 1.0000e+03 | ||
| TV | 6.2557e-02 | 9.5905e+00 | 8.9043e-01 | 283 | 1.0000e-05 | ||
| TIKH | 7.8021e-02 | 7.6717e+00 | 8.2844e-01 | 200 | 1.0000e-03 | ||
| MULTI | 4.6590e-02 | 1.2150e+01 | 9.4086e-01 | 7(2483) | 5.8348e-01 | ||
| Gaussian | TGV | 7.4295e-02 | 5.1521e+00 | 8.8489e-01 | 212 | 5.0000e+01 | |
| TV | 7.2950e-02 | 5.3107e+00 | 8.9032e-01 | 214 | 5.0000e-04 | ||
| TIKH | 8.0602e-02 | 4.4444e+00 | 8.6998e-01 | 200 | 7.5000e-03 | ||
| MULTI | 5.8445e-02 | 7.2363e+00 | 9.0902e-01 | 4(650) | 9.6213e+00 | ||
| TGV | 6.3055e-02 | 6.4566e+00 | 9.1791e-01 | 204 | 1.7500e+02 | ||
| TV | 6.1079e-02 | 6.7331e+00 | 9.3336e-01 | 173 | 8.0000e-05 | ||
| TIKH | 6.7156e-02 | 5.9092e+00 | 9.1910e-01 | 200 | 2.5000e-03 | ||
| MULTI | 4.6651e-02 | 9.0737e+00 | 9.4174e-01 | 3(462) | 1.9888e+00 | ||
| TGV | 5.6288e-02 | 7.4254e+00 | 9.3696e-01 | 222 | 1.0000e+03 | ||
| TV | 5.7295e-02 | 7.2713e+00 | 9.5196e-01 | 155 | 5.0000e-05 | ||
| TIKH | 5.8965e-02 | 7.0219e+00 | 9.3828e-01 | 200 | 7.5000e-04 | ||
| MULTI | 4.0354e-02 | 1.0316e+01 | 9.5758e-01 | 4(1075) | 8.1542e-01 |
Table 4.
Numerical results for the leopard test problem.
| Blur | Model | RE | ISNR | MSSIM | Iters | ||
|---|---|---|---|---|---|---|---|
| Out-of-focus | TGV | 1.6971e-01 | 6.0610e+00 | 7.5515e-01 | 221 | 1.2500e+02 | |
| TV | 1.7345e-01 | 5.8714e+00 | 7.5114e-01 | 276 | 5.0000e-04 | ||
| TIKH | 2.0715e-01 | 4.3292e+00 | 5.8731e-01 | 200 | 5.0000e-03 | ||
| MULTI | 1.6854e-01 | 6.1211e+00 | 7.4807e-01 | 3(325) | 4.4885e+00 | ||
| TGV | 1.3874e-01 | 7.7949e+00 | 8.0408e-01 | 250 | 3.0000e+02 | ||
| TV | 1.3360e-01 | 8.1228e+00 | 8.0757e-01 | 371 | 1.0000e-04 | ||
| TIKH | 1.6784e-01 | 6.1411e+00 | 6.6137e-01 | 200 | 1.5000e-03 | ||
| MULTI | 1.2572e-01 | 8.6512e+00 | 8.1534e-01 | 10(9141) | 1.2627e+01 | ||
| TGV | 1.1579e-01 | 9.3633e+00 | 8.3657e-01 | 353 | 7.5000e+02 | ||
| TV | 1.1976e-01 | 9.0706e+00 | 8.2166e-01 | 411 | 2.5000e-05 | ||
| TIKH | 1.3891e-01 | 7.7821e+00 | 7.1537e-01 | 200 | 5.0000e-04 | ||
| MULTI | 1.1057e-01 | 9.7643e+00 | 8.1755e-01 | 19(18607) | 2.7656e+00 | ||
| Gaussian | TGV | 1.6936e-01 | 3.7549e+00 | 7.7259e-01 | 261 | 1.0000e+02 | |
| TV | 1.6515e-01 | 3.9736e+00 | 7.7529e-01 | 314 | 4.0000e-04 | ||
| TIKH | 1.7150e-01 | 3.6456e+00 | 6.8620e-01 | 200 | 2.5000e-03 | ||
| MULTI | 1.6298e-01 | 4.0884e+00 | 7.7539e-01 | 3(241) | 4.5599e+00 | ||
| TGV | 1.5058e-01 | 4.7470e+00 | 8.0108e-01 | 339 | 1.0000e+03 | ||
| TV | 1.4747e-01 | 4.9279e+00 | 8.0458e-01 | 281 | 5.0000e-05 | ||
| TIKH | 1.5280e-01 | 4.6194e+00 | 7.2992e-01 | 200 | 5.0000e-04 | ||
| MULTI | 1.4385e-01 | 5.1440e+00 | 8.0937e-01 | 4(375) | 1.0924e+00 | ||
| TGV | 1.4220e-01 | 5.2400e+00 | 8.1688e-01 | 500 | 1.0000e+04 | ||
| TV | 1.4489e-01 | 5.0775e+00 | 8.0509e-01 | 309 | 1.0000e-06 | ||
| TIKH | 1.4156e-01 | 5.2795e+00 | 7.7128e-01 | 200 | 1.0000e-04 | ||
| MULTI | 1.3314e-01 | 5.8118e+00 | 8.2728e-01 | 5(513) | 3.6611e-01 |
Table 5.
Numerical results for the elaine test problem.
| Blur | Model | RE | ISNR | MSSIM | Iters | ||
|---|---|---|---|---|---|---|---|
| Out-of-focus | TGV | 5.2937e-02 | 4.2620e+00 | 7.0502e-01 | 117 | 2.5000e+01 | |
| TV | 5.3390e-02 | 4.1879e+00 | 7.0068e-01 | 79 | 2.5000e-03 | ||
| TIKH | 6.7772e-02 | 2.1162e+00 | 6.4440e-01 | 200 | 2.5000e-02 | ||
| MULTI | 5.2967e-02 | 4.2571e+00 | 7.0941e-01 | 6(789) | 9.2884e+01 | ||
| TGV | 4.7522e-02 | 4.8898e+00 | 7.2933e-01 | 111 | 1.0000e+02 | ||
| TV | 4.7884e-02 | 4.8238e+00 | 7.3036e-01 | 86 | 5.0000e-04 | ||
| TIKH | 5.6612e-02 | 3.3695e+00 | 6.9381e-01 | 200 | 1.0000e-02 | ||
| MULTI | 4.6498e-02 | 5.0791e+00 | 7.3630e-01 | 4(426) | 2.6005e+01 | ||
| TGV | 4.4345e-02 | 5.4451e+00 | 7.4655e-01 | 123 | 2.0000e+02 | ||
| TV | 4.6262e-02 | 5.0776e+00 | 7.4001e-01 | 80 | 5.0000e-04 | ||
| TIKH | 5.0669e-02 | 4.2873e+00 | 7.3213e-01 | 200 | 5.0000e-03 | ||
| MULTI | 4.3129e-02 | 5.6867e+00 | 7.5707e-01 | 4(201) | 5.5324e+00 >> | ||
| Gaussian | TGV | 4.8945e-02 | 2.5540e+00 | 7.2618e-01 | 98 | 1.5000e+01 | |
| TV | 4.8877e-02 | 2.5660e+00 | 7.2428e-01 | 78 | 2.5000e-03 | ||
| TIKH | 6.0527e-02 | 7.0909e-01 | 7.1350e-01 | 200 | 3.0000e-02 | ||
| MULTI | 4.7693e-02 | 2.7791e+00 | 7.3403e-01 | 5(537) | 8.6631e+01 | ||
| TGV | 4.5610e-02 | 2.6121e+00 | 7.4550e-01 | 100 | 1.0000e+02 | ||
| TV | 4.5903e-02 | 2.5566e+00 | 7.4522e-01 | 75 | 8.0000e-04 | ||
| TIKH | 4.9219e-02 | 1.9508e+00 | 7.3947e-01 | 200 | 7.5000e-03 | ||
| MULTI | 4.4332e-02 | 2.8590e+00 | 7.5318e-01 | 3(135) | 1.2558e+01 | ||
| TGV | 4.3903e-02 | 2.8586e+00 | 7.5594e-01 | 112 | 2.5000e+02 | ||
| TV | 4.4699e-02 | 2.7025e+00 | 7.5904e-01 | 68 | 2.5000e-04 | ||
| TIKH | 4.6376e-02 | 2.3826e+00 | 7.5546e-01 | 200 | 2.5000e-03 | ||
| MULTI | 4.2950e-02 | 3.0493e+00 | 7.6433e-01 | 2(56) | 2.9785e+00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







