Method for theoretical Assessment of Safety against Wagon Derailment

Preprint

Article

Method for theoretical Assessment of Safety against Wagon Derailment

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Valeri Stoilov,

Sanel Purgic^*,

Svetoslav Slavchev,Vladislav Maznichki

Valeri Stoilov,

Sanel Purgic^*,

Svetoslav Slavchev,Vladislav Maznichki

This version is not peer-reviewed

Submitted:

03 October 2023

Posted:

04 October 2023

You are already at the latest version

Alerts

Abstract

The assessment of safety against freight wagons derailment is a mandatory element of the documents provided to the EU notifying authorities for the entry into service of new freight wagons. The assessment methodology is presented in EN 14363:2016. It is mainly aimed at experimental measurement of certain parameters and the data are used to calculate the safety criterion. The practical implementation of the tests is accompanied by many difficulties: finding a track with a proper radius, ensuring free access to the railway infrastructure for a long period of time, waiting for suitable metrological conditions, preparation of the curve and the test wagon etc. These difficulties are well known to the European legislators, and as a solution they propose a large set of reference wagons that have undergone real tests. It is sufficient to demonstrate that the parameters of the new wagon relate to some of reference wagon parameters to avoid such a requirement. Proving the "convergence" of the parameters of the new and the reference wagons is a lengthy, complex and, in many cases, subjective process. To introduce an objective assessment, the authors set themselves the task of developing a theoretical method for assessment of safety against derailment.

Keywords:

Subject: Engineering - Transportation Science and Technology

1. Introduction

There are many methods used for evaluating safety against derailments worldwide. A good overview of these methods is given in [1]. The methods for assessment of safety against derailment for new vehicle acceptance are mostly done by using some combination of testing and theoretical mathematical calculations or simulations. Most of these methods are based on dynamic tests which can be performed as controlled tests in a laboratory, or as long runs under representative service conditions, or under described test conditions using exactly defined track characteristics and statistical assessment methods. All three test types have their advantages and disadvantages as well described in [1].

Theoretical mathematical calculations have a long tradition since the first attempts from Hertz [2], Klingel [3] and Nadal [4] to describe mathematically the processes occurring in the wheel-rail interface. Namely Nadal criterion [4] sets the basics for further development of theoretical methods for assessment of safety against derailment [5,6,7,8] and today is applied in different international and European normative documents [9,10].

In the last 70 years the development of computers has allowed their very intense use in numerical and multibody simulations as well as in testing and analysis techniques. Many simulations methods have their advantages but also problems [1,11,12]. Main issue for simulations in last decades is that a vehicle model must be validated in tests and is still unclear what can be determined as validated model. In [10] computer simulations were introduced to supplement or replace testing and to be used as an alternative assessment method. Same happened in the last version of [9], but with some restrictions regarding the validation procedure: in Europe, for every new freight wagon which should enter the service across European railways mandatory document provided to EU notifying authorities is the assessment of safety against derailment. The required evidence and procedure for acceptance is well defined in European standard EN 14363:2016 [9]. It is also possible to compare resulting parameters from theoretical calculations or simulations of safety against derailment with parameters of reference wagons that have undergone real tests. This approach is allowed by clause 6.1.5.2.6 of EN 14363:2016 [9] when using Method 2 for the assessment. This method is described in detail in Section 2 of this paper.

According to this approach, it is sufficient to demonstrate that the parameters of the new wagon relate to some of reference wagon parameters to avoid such a requirement. Proving the “convergence” of the parameters of the new and the reference wagons is a lengthy, complex and, in many cases, subjective process. In this work we introduce an objective theoretical method for assessment of safety against derailment. In this way it is possible to shorten the time and the costs for the approval procedure. To achieve a high degree of validation, the results obtained from theoretical analyses as described in Section 3 of this work were compared and validated with results from experimental tests carried out on real objects.

2. Method for assessment of theoretical safety against freight wagon derailment

In accordance with EN 14363:2016 [9], section 6.1, Method 2 (paragraph 6.1.5.2) the safety criterion against derailment is determined by the Equation (1):

{(\frac{Y}{Q})}_{j a} = \frac{Y_{j a}}{Q_{j k, \min} {+ ∆ Q}_{j H}} {\leq (\frac{Y}{Q})}_{\lim} = 1.2

(1)

where Y_ja is total reaction of the rail at its contact with the attacking wheel, Q_jk,_min is the lowest value of the vertical reaction of the wheel calculated when the frame of the wagon is twisted and ΔQ_jH is load on the wheel from the moment of the forces acting on the 2 wheels of the examined wheel axle (Figure 1).

The component ΔQ_jH is determined by Equation (2):

Δ Q_{j H} = (Y_{j a} + Y_{j i}) . \frac{h}{2 b_{0}}

(2)

where Y_ja is total reaction of the rail at its contact with the attacking (outer) wheel, h is effective height above the rail of the journal box suspension (for most common used bogie Y25, h = 365 mm is assumed), Y_ji is horizontal load force between the inner (non-attacking) wheel of the examined axle and the inner rail (Figure 1), 2b₀ is the nominal transverse distance between the contact points of the wheels (2b₀ = 1500 mm is assumed), j is index (number) of the examined axle, a is index (number) of the outer wheel and i is index of the inner wheel.

For the purposes of the theoretical assessment of criterion from Equation (1), it is necessary to apply appropriate methods for the theoretical determination of the following parameters:

Y_ja – the total reaction of the rail in contact with the attacking (outer) wheel. The parameter is involved in equations (1) and (2);
Y_ji – horizontal load force between the inner (non-attacking) wheel of the examined track axle and the inner rail. The parameter is involved in equation (2);
Q_jk_,min – the lowest value of the vertical reaction of the wheel calculated when the frame of the wagon is twisted. The parameter is involved in Equation (1).

The methods for determining these three important parameters are given in the next three subsections.

2.1. Methodology for theoretical determination of leading forces Y_a on axles of railway vehicles with bogies

In [4] a theoretical method for determining the total reaction of the rail on the wheels of bogie is proposed. Briefly, the method consists of the following: when moving on a curved section of the rail track, the wagon performs two movements - translational and rotational. The rotation occurs around the instantaneous center of rotation M (Figure 2), characterized by the pole distance x, which can be determined by the Equation (3):

x = l + \frac{R {. σ}_{b}}{2 . l}

(3)

where 2.l is the distance between wheelsets of the bogie (for compliance with European standards, it should be noted that 2.l = 2a⁺), R is radius of the calculation curve and σ_b is current coordinate.

The current coordinate σ_b depends on the position of the bogie when passing a curved section of the track. In Figure 3, the bogie is represented by section AB (AB’ or AB”). For this purpose, the transverse dimensions of the track with gauge 2s and of the bogie are reduced by the constant amount 2d, defining the transverse distance between the bases of the wheel flanges of the same axle. In this way the bases of the flanges of the two wheels merge and are represented in Figure 3 by points A and B (B’ and B”). The same points depict the attacking (A) and the non-attacking (B) axle, respectively.

The reduced gauge is determined by Equation (4):

σ = 2 s - 2 d = ∆ + δ

(4)

where Δ is the total clearance between the flange and the rail, equal to 0,01 m and δ is additional expansion of the rail track in a curved section depending on radius of calculation curve as determined with data from Table 1 [13].

In this way calculated value represents maximum total clearance between the rails and the axle in a curved section of rail track. In Figure 3 the attacking axle (point A) always contacts the outer rail. Depending on the movement speed and the radius of the curve, the second axle (point B or B’ or B”) can take one of the following positions:

АB – maximum crossing (σ_b = σ = Δ + δ);
AB’ – free settling (0 ≤ σ_b ≤ δ);
AB’’– maximum displacement (σ_b = 0).

When moving in a curve, the following forces act on the bogie (Figure 4):

The transverse force H is induced by the centrifugal (Н_c) and wind (Н_w) forces. It is applied at the mass center of the wagon and is determined by the equation (5):

H = H_{c} + H_{w}

(5)

2.: The centrifugal force is defined by the Equation (6):

H_{c} = P . (\frac{v^{2}}{R . g} - \frac{h}{2 . s})

(6)

where P (in [N]) is force from the mass of the wagon, v (in [m/s]) is movement speed, g (in [m/s²]) is ground acceleration, R (in [m]) is curve radius, 2.s (in [mm]) is distance between wheels rolling circles (for normal track width 2.s = 1500 mm) and h (in [mm]) is overhang of the outer rail and is determined from table in Figure 5 [13].

3.: The wind force is determined by Equation (7):

H_{w} = F . W

(7)

where F is the surface of the wagon on which the wind is acting (in [m²]) and W is the wind pressure (in [N/m²]).

4.: The frictional forces Ф obtained because of the rotation around the pole M are determined by the Equation (8):

Φ = μ . N_{s t}

(8)

where µ is the coefficient of friction between the wheel and the rail and N_st is static vertical load on one wheel determined by equation (9):

N_{s t} = \frac{P}{N}

(9)

where N is the number of wheels. For compliance with European standards, it should be noted that N_st = Q_nom.

5.: The total reactions Y_i from rails on the wheelset i are obtained from the equilibrium conditions ΣY=0 and ΣМ_М=0, according to equations system (10):

|\begin{array}{l} Y_{1} - Y_{2} - H - 2 . Φ . c o s α_{1} + 2 Φ \cos α_{2} = 0 \\ Y_{1} x + Y_{2} (2 l - x) - H (x - l) - 2 Φ . r_{1} - 2 Φ . r_{2} = 0 \end{array}

(10)

where Ф_yi is the component of force Ф along the y-axis and r_i is the distance from pole M to the corresponding contact point between the rail and wheel of the i-th wheel axle.

In the equations system (10) there are four unknown terms: Y1, Y2, x and speed v implicitly set by the centrifugal forces. Therefore, the total reactions Y1 and Y2 are determined according to the following methodology and graphical representation is shown in Figure 6:

Step 1. It is assumed that the bogie is in the limit state between “maximum overshoot” and “free settling”. It is possible at a precisely determined but unknown speed v₁. From the condition for the considered boundary condition, it follows that the distance from pole M according to Equation (11) is:

x = x_{m a x} = l + \frac{R {. σ}_{b}}{2 . l}

(11)

which is typical for the “maximum overshoot” position. It also follows that the total reaction of the second wheel axle is zero, e.g.

Y_{2} = 0

(12)

which is typical for the “free settling” position.

This allows the equations system (10) to be solved and to obtain specific values for Y₁ and for v₁ that are typical for the limit state. When solving equation system (10), it is possible for Y₁ or for v₁ to obtain negative values. This indicates that the boundary condition is not valid for the specified track and bogie parameters. In this case, it is necessary to go to step 3 of the current methodology.

Step 2. When the bogie is in the “maximum overshoot” state, it will move with a speed in the interval from 0 to v₁, and the pole distance will be x = x_max. Therefore, the system of equations (10) can be solved with respect to Y₁ and Y₂ by setting discrete movement speed values in the specified interval.

Step 3. It is assumed that the bogie is in a limit state between free settling and maximum displacement. From this follow next conditions (13):

x = x_{m i n} = l a n d Y_{2} = 0

(13)

Movement speed v₂ and force Y₁ in this case can be found by solving the equation system (10) under conditions (13).

Step 4. If the bogie is freely fixed (Y₂ = 0), then in the system (10) there are three unknowns - Y₁, v and x. In this case, condition (14) is relevant:

{v_{1} < v < v_{2} a n d x}_{m i n} < x < x_{m a x}

(14)

Therefore, by setting discrete values of v or x in equation system (10), it is possible to obtain the remaining two unknowns. The calculation process is greatly simplified when setting values of the parameter x.

Step 5. If the design speed of the wagon v_k is higher than v₂, it is necessary to build the third zone of the horizontal dynamic calculations, i.e., the zone of maximum displacement. In this case, condition (15) is valid:

x = x_{m i n} = l

(15)

Therefore, setting movement speed values in the interval between v₂ and v_k, the full reaction forces Y₁ and Y₂ can be determined.

The methodology proposed above allows to determine the full reactions Y₁ and Y₂ of the first- and second-wheel axles of each bogie at different speeds, curve radii, specific track parameters, different wheel loads, different bogie wheel axles distances and other parameters.

2.2. Methodology for theoretical determination of the horizontal load force between the inner (non-attacking) wheel Y_ji of the investigated wheel axle and the inner rail

The inner wheel of the examined wheel axle does not contact its flange with the corresponding rail. Therefore, the horizontal force acting between them arises from the frictional forces, which are determined by the Equation (16):

Y_{j i} = μ . Q_{j i} = μ . (2 . Q_{n o m} - Q_{j a, m i n})

(16)

where μ is the coefficient of friction between the wheel and the rail, assumed to be equal to 0,4 for clean rails, Q_ji is vertical load force of the inner wheel (index i) on axle j, Q_nom is nominal vertical load force of the wagon wheels and Q_ja,min is the minimum vertical force acting on the outer (attacking) wheel of axle j. It is determined in accordance with the methodology given in Section 2.3. of this paper. Q_nom is determined by the ratio of the force from the weight of the wagon Q and the number of wheels of the vehicle N as given in equation (17):

Q_{n o m} = \frac{Q}{N}

(17)

2.3. Methodology for theoretical determination of the smallest value of the vertical reaction of the wheel Q_jk,,min calculated during torsion of the wagon frame

The proposed methodology for the theoretical determination of the minimum value of the vertical reaction of the wheels Q_jk,,min allows obtaining the corresponding maximum value of this parameter Q_jk,,max. Calculations are carried out in the following sequence:

The frame of the wagon is loaded with an arbitrary force ΔF_p (Figure 7) according to UIC Leaflet 432 [14] and the deflection of the frame Δz_p in the area around the lateral supports is determined (Figure 8).

2.: In accordance with EN 14363 [9], the minimum deflection of the frame Δz* is determined, which should be reached during real (in-situ) testing of the wagon. It is determined by Equation (18) subject to requirement (19). 2a* in this case is valid for wagon frames with pivot distance between 4 and 30 meters.

∆ z^{*} = g^{*} . 2 a^{*}

(18)

g^{*} = \frac{15}{2 a^{*}} + 2

(19)

3.: Recalculation of the force ΔF_p from step 1 for loading the wagon frame to achieve the minimum deflection Δz* according to the Equation (20):

∆ F_{z *} = \frac{∆ F_{p} . ∆ z^{*}}{∆ z_{p}}

(20)

The result of Equation (20) gives the force that acts on one side of the bogie in the area around the lateral support in Figure 8. This means that force ΔF_z* significantly loads the two unilaterally located wheels and significantly less the other two.

4.: The force ΔF_z* is than transmitted from the lateral support to the side beams of the bogie with a value of ΔF`_z*max and ΔF`_z*min according to Equations (21) and (22). The corresponding distances b_1F and b_s are shown in Figure 9.

∆ {F'}_{z *, m a x} = \frac{∆ F_{z *} . (b_{1 F} + b_{s})}{2 b_{1 F}}

(21)

∆ {F'}_{z *, m i n} = ∆ F_{z *} - ∆ {F'}_{z *, m a x}

(22)

From the side beam, the forces ΔF`_z*max and ΔF`_z*min are distributed between the two axle journals of the overloaded and the two axle journals of the unloaded wheels, with the forces ΔF`_z*max and ΔF`_z*min acting on the first (attacking) wheel axle, defined by equations (22) and (23):

∆ {F'}_{1 z *, m a x} = \frac{∆ {F'}_{z *, m a x}}{2}

(23)

∆ {F'}_{1 z *, m i n} = \frac{∆ {F'}_{z *, m i n}}{2}

(24)

From the corresponding axle journal, the forces from (23) and (24) cause additional reactions in the two wheels with values defined in equations (25) and (26):

∆ Q_{1, m a x} = \frac{∆ {F^{'}}_{1 z *, m a x .} (b_{1 F} + b_{0}) - ∆ {F^{'}}_{1 z *, m i n} . (b_{1 F} - b_{0})}{2 b_{0}}

(25)

∆ Q_{1, m i n} = ∆ {F'}_{1 z *, m a x} + ∆ {F'}_{1 z *, m i n} - ∆ Q_{1, m a x}

(26)

5.: The minimum value of the wheel reaction Q_jk,,min is determined by the Equation (27) and the maximum value by the Equation (28) respectively:

Q_{j k, m i n} = Q_{n o m} + ∆ Q_{1, m i n}

(27)

Q_{j k, m a x} = Q_{n o m} + ∆ Q_{1, m a x}

(28)

where the force Q_nom is determined by the Equation (17).

3. Results from the theoretical derailment safety assessment

The study was done only for the first bogie axle of a Sggmrss series wagon (90 feet) in unloaded condition. The reason for this is that theoretical analyzes categorically state that the first wheel axle of an unloaded wagon is most at risk of derailment. This conclusion is also confirmed by the test results of all wagons from the reference list given in UIC Leaflet 530-2 [15]. It was also found during field tests of the same wagon [16]. The initial data used in the theoretical study are:

Tare weight of the wagon: 27,5 t;
Curve radius: R = 150 m;
Clearance between flanges and rail threads in a straight section of the track, equal to δ = 0,01 m;
Additional tracks widening in a curved section δ = 0,002 m (in accordance with the test data of the wagon [16]);
Coefficient of friction between the rail and the wheel μ = 0,4;
Wheel axle distance a⁺ = 1,8 m;
Pivot distance (for one wagon section only) a* = 11,995 m;
Speed of passing through the curve v = 7 km/h (in accordance with the test data of the wagon [16]);
Wind pressure W = 0 N/m² (in accordance with the test data of the wagon [16]);
Distance between the rolling circles of the two wheels of the same axle 2b₀ =1,5 m;
Transverse distance between the axle journals 2b_jF = 2,0 m;
Distance between the side supports on the bogie 2b_s = 1,7 m;
Overhang of the outer rail h = 0,15 m;
Earth acceleration g = 9,81 m/s².

For the theoretical determination of the safety criterion against derailment of a Sggmrss wagon (90 feet), the methods described in detail in Section 2 of this paper were applied. The results from the calculations conducted with the mentioned methodology are given in Table 2.

With the data from Table 2 the final assessment of safety against derailment can be conducted. This is done by using the Equation (1) and the calculated value is equal to 1,017. According to [9], when using the theoretical assessment methods, the limit value 1,2 is reduced by 10%, which means that the limit value of Nadal’s criterion should be set to 1,08 and compared with calculated value as done in Equation (29).

{(\frac{Y}{Q})}_{j a} = \frac{Y_{j a}}{Q_{j k, \min} {+ ∆ Q}_{j H}} = 1,017 {\leq (\frac{Y}{Q})}_{\lim} = 1, 08

(29)

The obtained value of safety criterion 1,017 is lower than limit value 1,08 which means that for wagon series Sggmrss the requirement for safety against derailment is fulfilled. The results from the experimental study (test) [16] also confirm that the safety against derailment for this wagon is fulfilling the requirements. The value obtained in tests equals to 1,03 and it should be mentioned that the limit value in this case is set to 1,2. For the final assessment in tests not all parameters from Table 2 were determined, but only few of them, which are necessary for the assessment. These parameters are Y_1, Y_1i, g*, Δz*, Q_nom and Q_{jk, min.} Values of these parameters are close enough (in order of ±10%), which gives reason to claim that the proposed theoretical safety assessment method is delivering very good results and can be used for safety assessment of similar wagons.

4. Discussion

By using resulting parameters from theoretical calculations of safety against derailment with proposed method and by comparing them with parameters of reference wagons that have undergone real tests, it is possible to make savings of costs and time for acceptance procedure. This approach is allowed by clause 6.1.5.2.6 of EN 14363:2016 [9]. In this paper we show that proposed methodology for calculation of safety against derailment gives good results and is verified in test on real object, wagon Sggmrss series. This gives reason to claim that the proposed theoretical safety assessment method can be used to study other wagons and railway vehicles.

The advantages of our method compared to similar methods are mainly the use of fewer input parameters, simplicity, and no need for complex simulations. On the other hand, the proposed method uses some initial parameters for which assumptions are made (the value of coefficient of friction µ) or for which their values are determined in tests (additional tracks widening in a curved section δ or wind pressure W). With other values for these parameters safety against derailment would have other than calculated values and the final fulfillment maybe would be questionable. This is reason why for future research it would be necessary to conduct more assessments using the proposed method and on different wagon series. This would help to additionally verify the results from calculations.

Author Contributions

Conceptualization, V.S. and S.P.; methodology, V.S. and S.P.; software, S.S. and V.M.; validation, V.S. and S.P.; formal analysis, S.S. and V.M.; investigation, S.S.; resources, S.S. and S.P.; data curation, S.S. and V.M.; writing—original draft preparation, V.S. and S.P.; writing—review and editing, V.S. and S.P.; visualization, V.M.; supervision, V.S.; project administration, V.S.; funding acquisition, V.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the European Regional Development Fund within the Operational Programme “Science and Education for Smart Growth 2014 - 2020” under the Project CoE “National center of mechatronics and clean technologies” under Grant BG05M2OP001-1.001-0008-С01.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article and references [16] and [17].

Acknowledgments

The authors would like to thank the Research and Development Sector at the Technical University of Sofia for the financial and technical support.

Conflicts of Interest

The authors declare no conflict of interest.

References

Wilson, N.; Fries, R.; Wittea, M.; Haigermoser, A.; Wrang, M.; Evans, J.; Orlova, A. Assessment of safety against derailment using simulations and vehicle acceptance tests: A worldwide comparison of state-of-the-art assessment methods. Veh. Syst. Dyn. 2011, 49, 1113–1157. [Google Scholar] [CrossRef]
Hertz, H. Über die Berührung fester elastischer Körper. Jour. reine angew. Math. 1881, 92, 156–171. [Google Scholar]
Klingel, W. Über den Lauf Eisenbahnwagen auf Gerarder Bahn. Organ Fortscr. Eisenbahnwesens, 1883, 20, 113–123. [Google Scholar]
Nadal, M. J. , Locomotives a Vapeur, 1st ed; Collection Encyclopedie Scientifique: Paris, France, 1908. [Google Scholar]
Kardas-Cinal, E. Selected problems in railway vehicle dynamics related to running safety. Arch. of Trans., 2014, 31, 37–45. [Google Scholar] [CrossRef]
Zeng, J.; Guan, Q. Study on flange climb derailment criteria of a railway wheelset. Veh. Syst. Dyn., 2008, 46, 239–251. [Google Scholar] [CrossRef]
Zeng, J.; Wu, P. Study on the wheel/rail interaction and derailment safety. Wear, 2008, 265, 1452–1459. [Google Scholar] [CrossRef]
Konowrocki, R.; Chojnacki, A. Analysis of rail vehicles’ operational reliability in the aspect of safety against derailment based on various methods of determining the assessment criterion. Maint. and Reliab 2020, 22(1), 73–85. [Google Scholar] [CrossRef]
EN 14363:2016; Railway applications – Testing and Simulation for the acceptance of running characteristics of railway vehicles – Running Behaviour and stationary tests. European Committee for Standardization: Brussels, Belgium, 2016.
UIC CODE 518: Testing and approval of railway vehicles from the point of view of their dynamic behaviour – Safety - Track fatigue - Running behaviour. 5th edition, Paris, September 2009.
Boronenko, Y.; Orlova, A.; Iofan, A.; Galperin, S. Effects that appear during the derailment of one wheelset in the freight wagon: simulation and testing, Veh. Syst. Dyn., 2006, 44, 663–668. [Google Scholar] [CrossRef]
Evans, J.; Berg, M. Challenges in simulation of rail vehicle dynamics, Int. Jour. Veh. Mech. Mob., 2009, 47, 1023–1048. [Google Scholar]
Stoliov, V.; Slavchev, S. Wagons (in Bulgarian), 1st ed; ; Technical University Sofia: Sofia, Bulgaria, 2014; pp. 150–156. ISBN 978-619-167-135-9. [Google Scholar]
UIC CODE 432: Wagons. Running speeds. Technical conditions to be observed. 12th ed. Paris, October 2008.
UIC CODE 530-2: Wagons - Running safety. 7th ed., Paris, December 2011.
Test report of safety against derailment of Sggmrss wagon. No: LSV 6/19 14.04.2019. Laboratory of rail vehicles, University of Belgrade, 2019.
Report “Strength analysis of wagon series Sggmrss”. Project-VS Ltd., Sofia, October 2017.

Figure 1. Forces acting in wheel-rail contact.

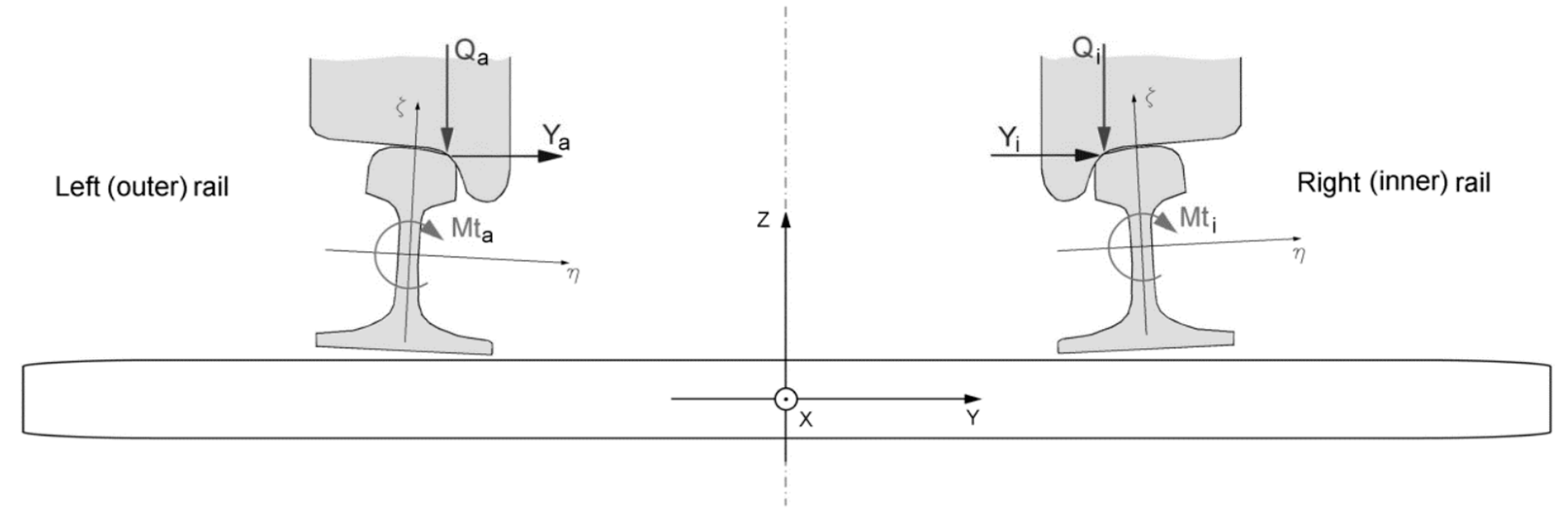
Figure 2. Movement of bogie in curved section of the track.

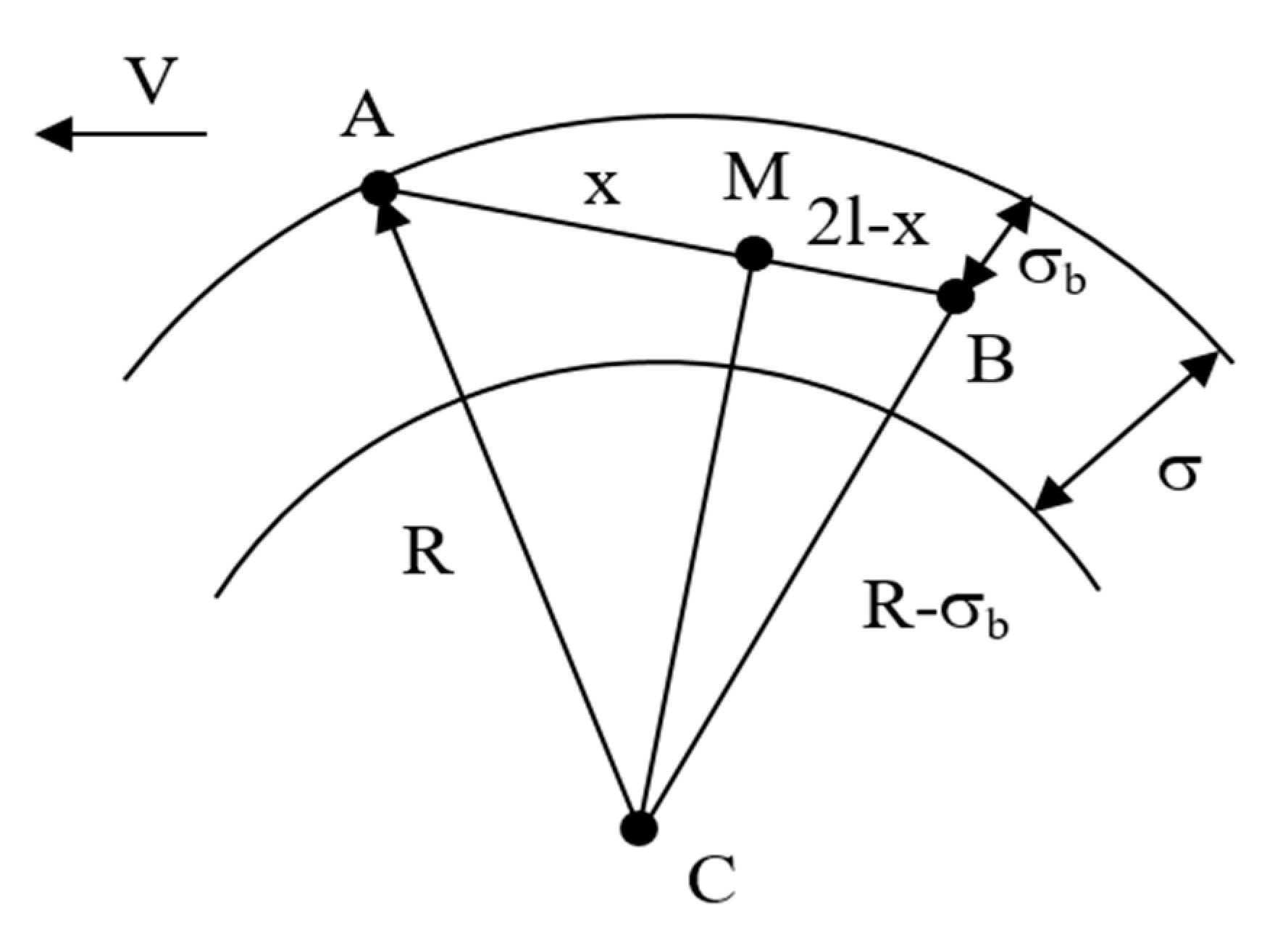
Figure 3. Representation of bogie moving in curved section of the track.

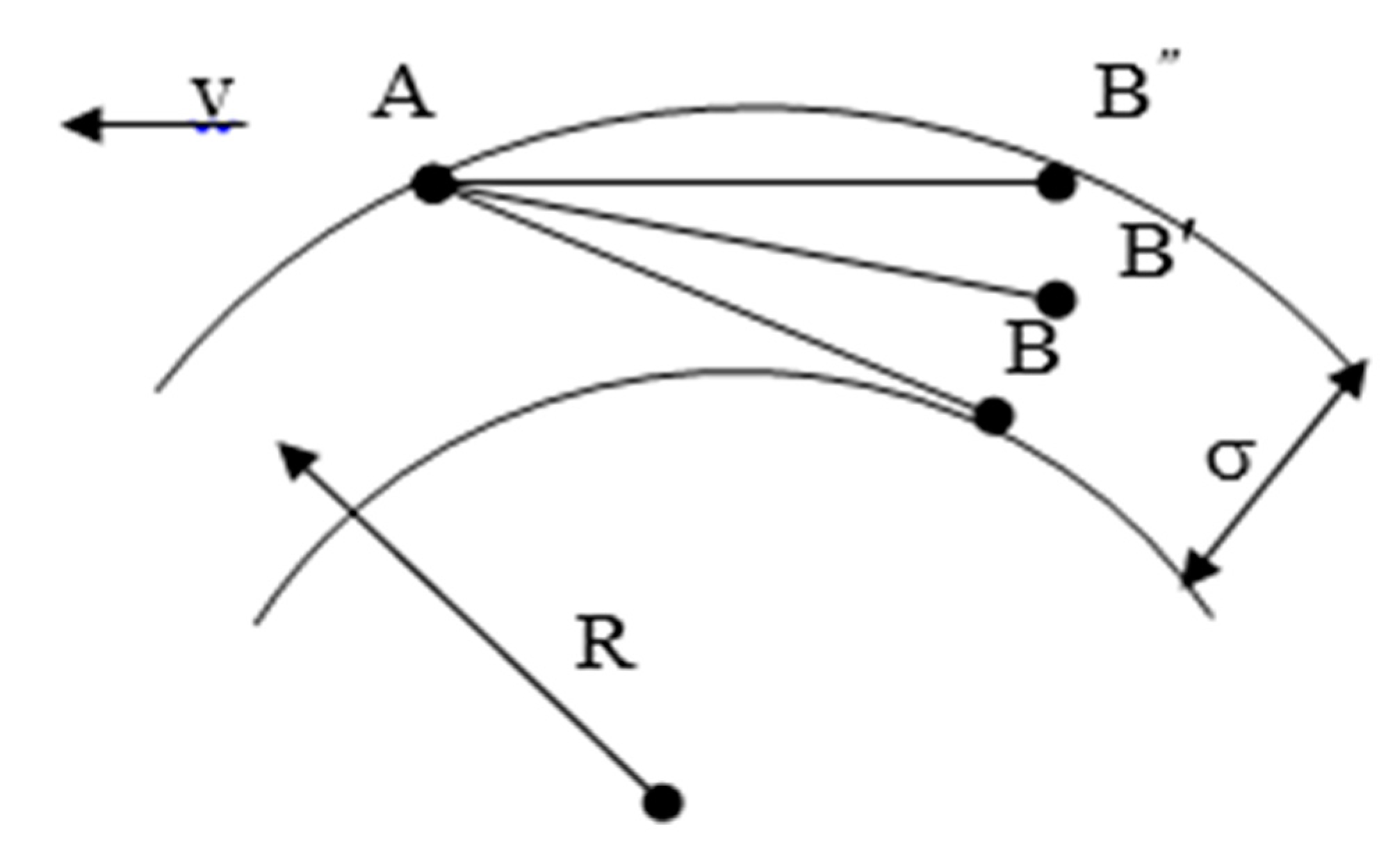
Figure 4. Forces acting on the bogie while moving in a curve.

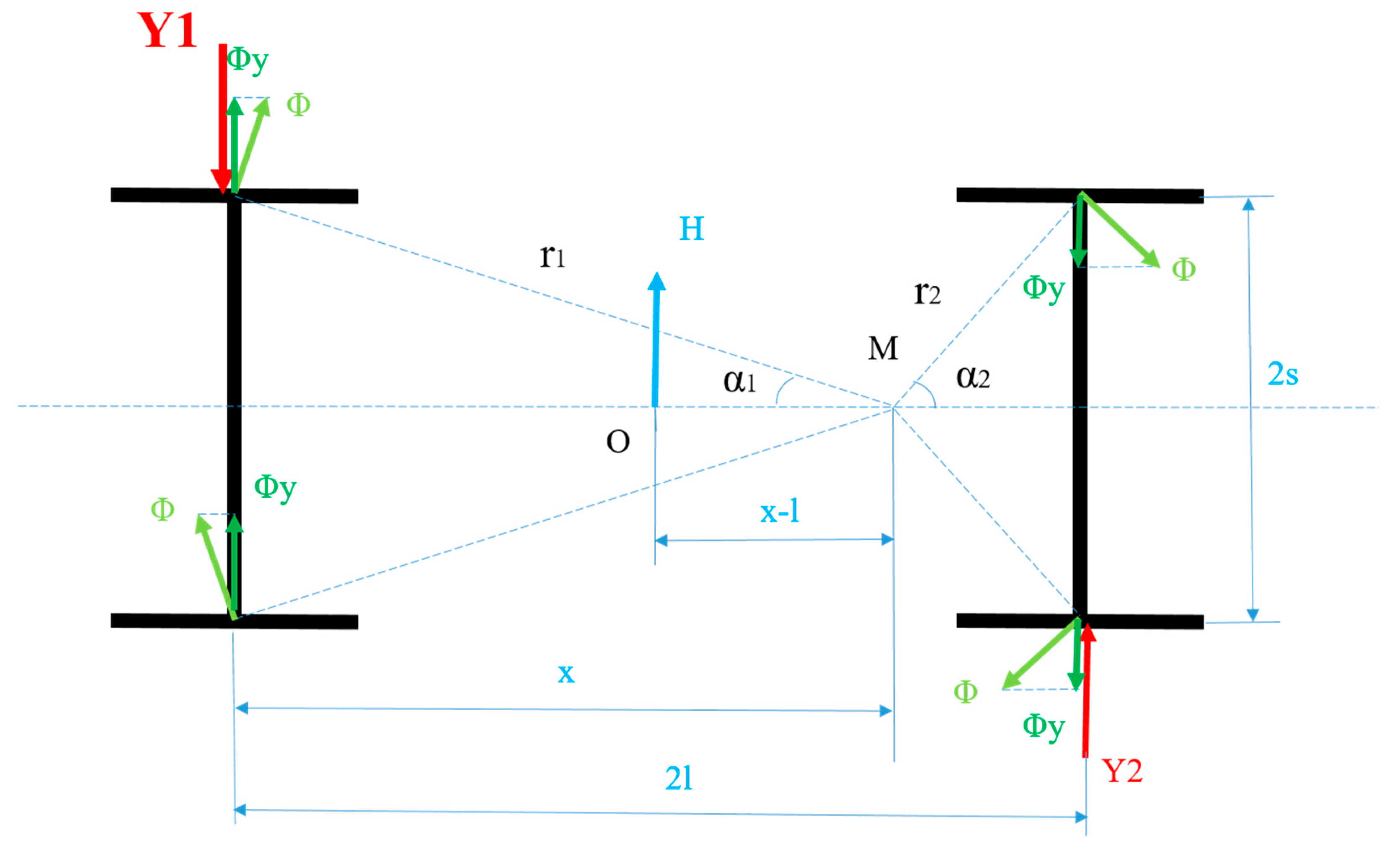
Figure 5. Overhang of the outer rail depending on radius of curve and movement speed [13].

Figure 6. Graphical representation of dependencies Y₁ = Y₁(v) and Y₂= Y₂(v) [13].

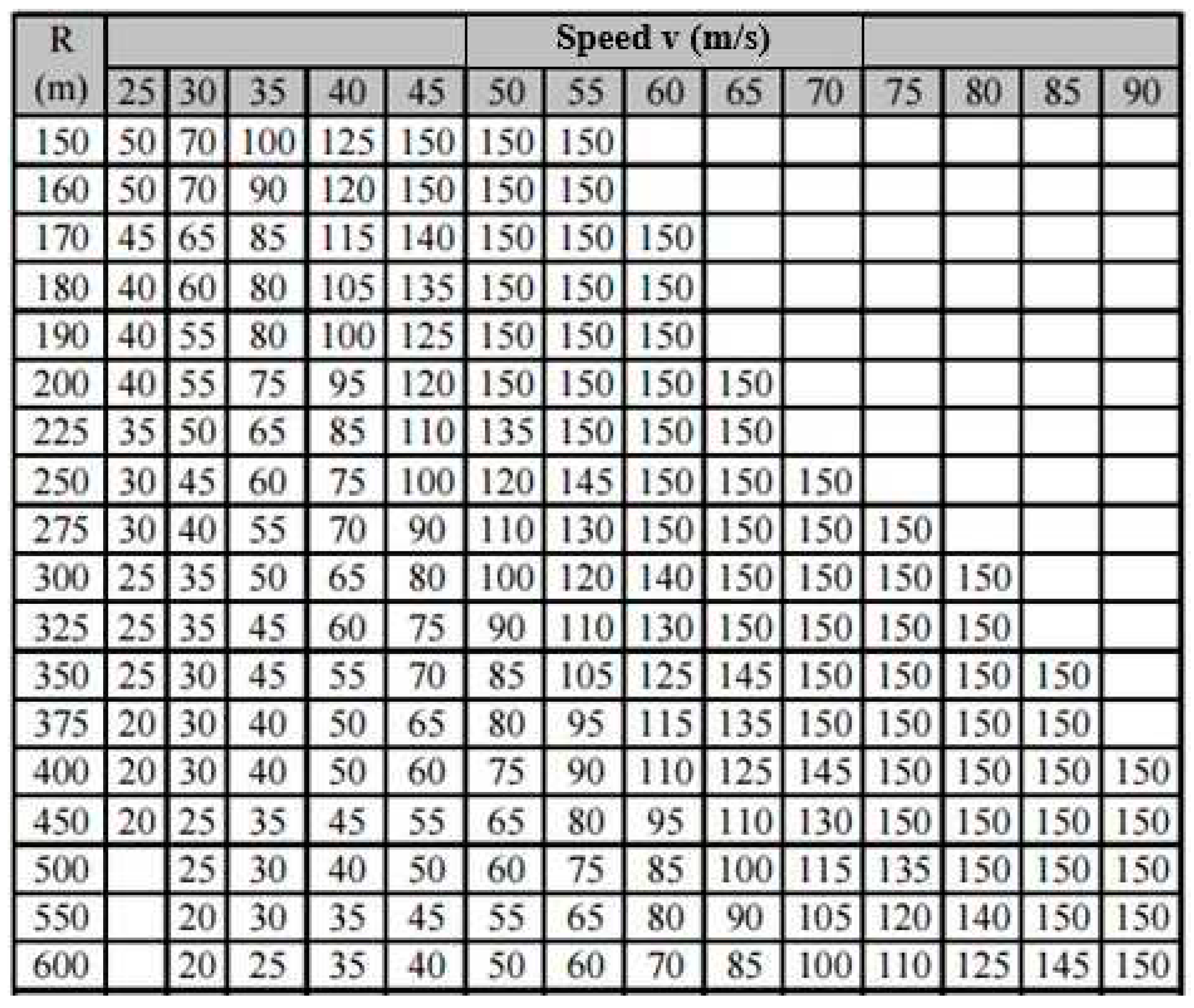
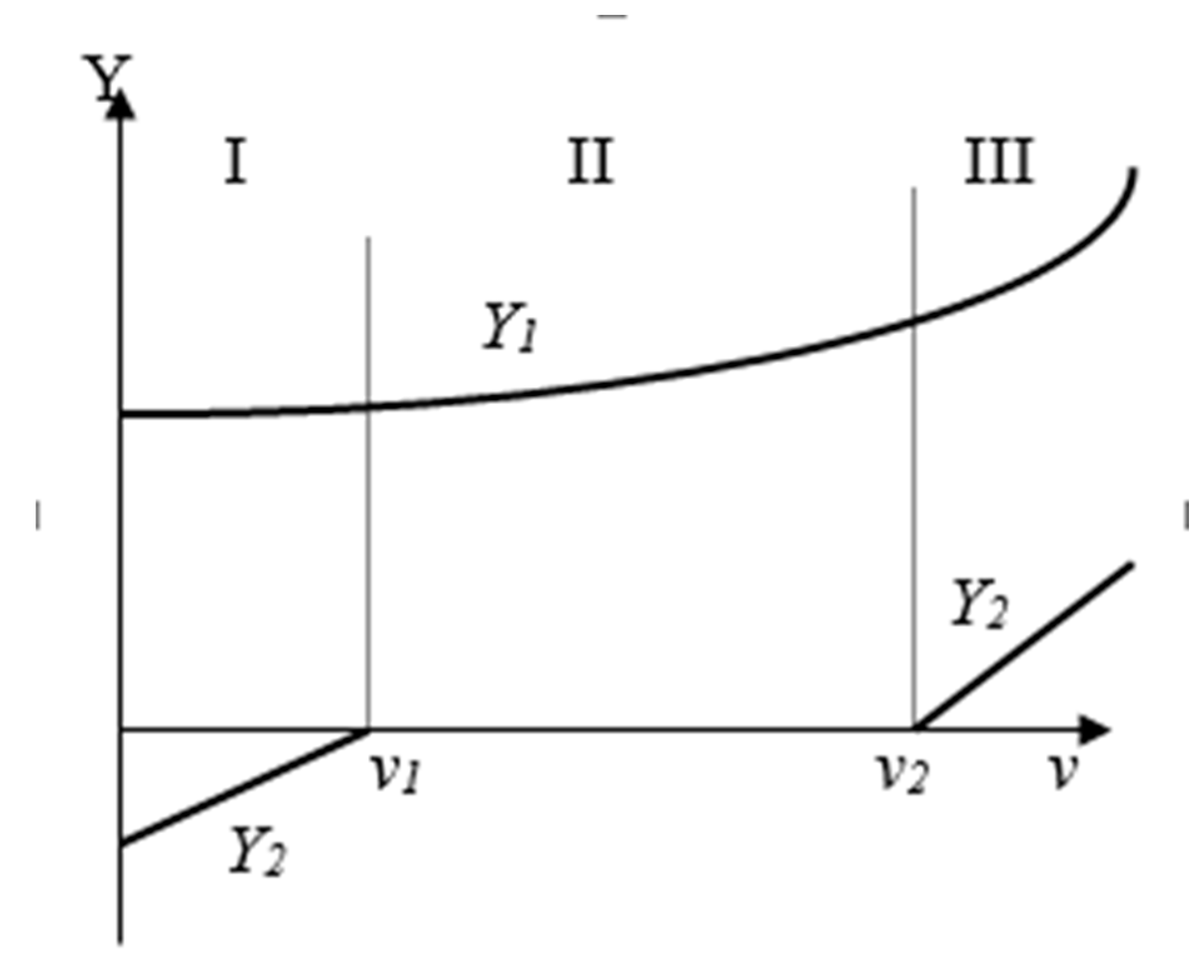
Figure 7. Forces acting on wagon frame during torsion tests.

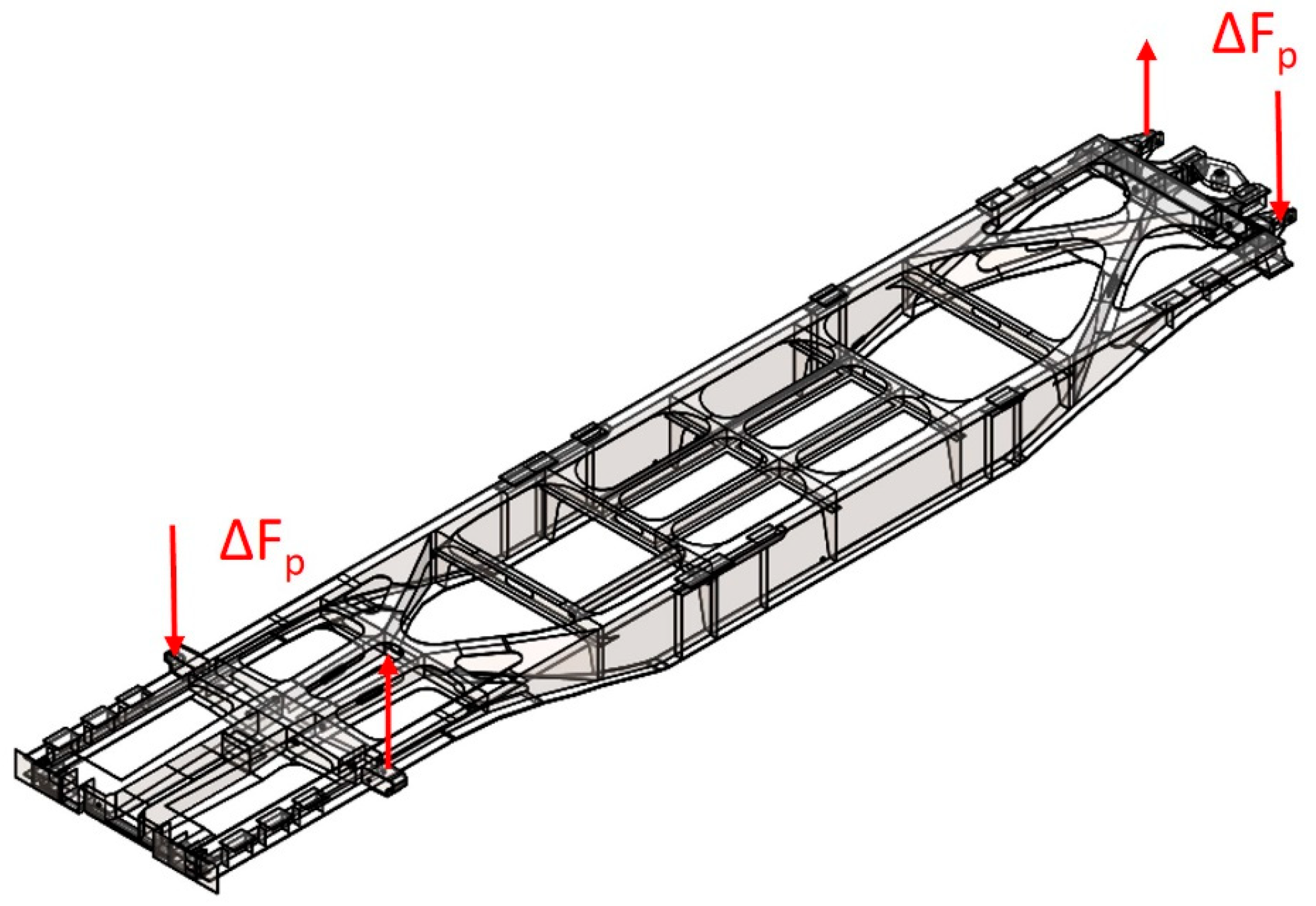
Figure 8. Area of lateral support in which the deflection of the frame is measured.

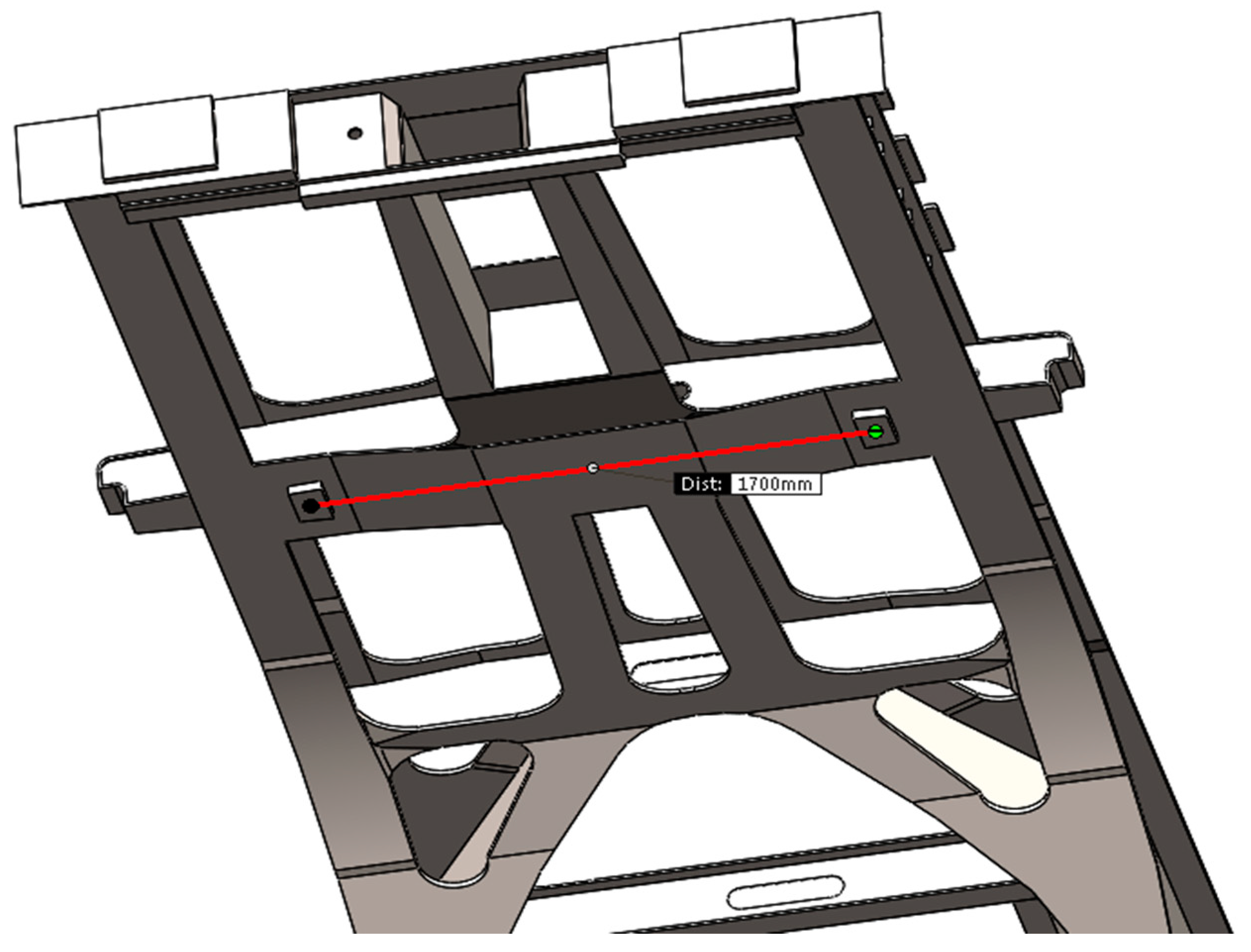
Figure 9. Forces acting on the bogie with distances used for calculations.

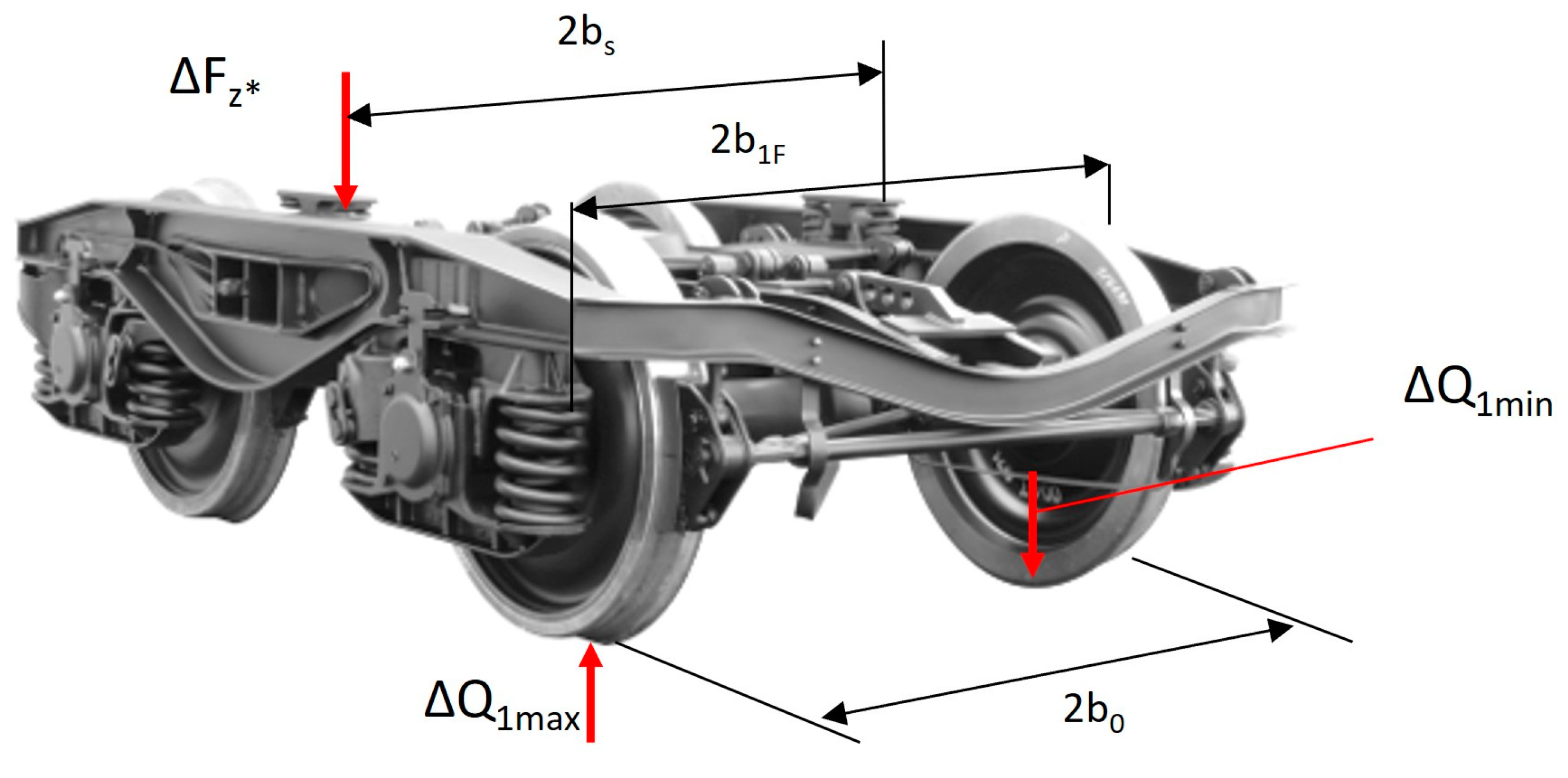
Table 1. Additional expansion of the rail track in a curved section depending on radius of calculation curve [13].

Radius R (m)	δ (mm)
125 ÷ 150	20
150 ÷ 180	15
180 ÷ 250	10
250 ÷ 300	5
Over 300	0

Table 2. Results from the calculation needed for determination of safety against derailment.

Parameter	Value	Remark
v₁	58,3 km/h	Methodology from Section 2.1.
Y₁=Y_1a Y_1i g* Δz* ΔF_p Δz_p ΔF_z* ΔF’_{z, max} ΔF’_{z, min} ΔF’_{1z, max} ΔF’_{1z, min} ΔQ_{1, max} ΔQ_{1, min} Q_nom Q_{jk, min} Q_{jk, max}	24,718 kN -14,024 kN 3,251 ‰ 39 mm 50 kN 0,08265 mm 23,59 kN 21,82 kN 1,769 kN 10,909 kN 0,885 kN 12,58 kN -0,7862 kN 22,48 kN 21,695 kN 35,061 kN	Methodology from Section 2.1. Methodology from Section 2.2. Equation (19) Equation (18) The selected load value for the torsional stiffness test [17] Deflection of the frame under the load ΔF_p, determined in [17] Equation (20) Equation (21) Equation (22) Equation (23) Equation (24) Equation (25) Equation (26) Equation (17) Equation (27) Equation (28)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Method for theoretical Assessment of Safety against Wagon Derailment

Abstract

1. Introduction

2. Method for assessment of theoretical safety against freight wagon derailment

2.1. Methodology for theoretical determination of leading forces Ya on axles of railway vehicles with bogies

2.2. Methodology for theoretical determination of the horizontal load force between the inner (non-attacking) wheel Yji of the investigated wheel axle and the inner rail

2.3. Methodology for theoretical determination of the smallest value of the vertical reaction of the wheel Qjk,,min calculated during torsion of the wagon frame

3. Results from the theoretical derailment safety assessment

4. Discussion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.1. Methodology for theoretical determination of leading forces Y_a on axles of railway vehicles with bogies

2.2. Methodology for theoretical determination of the horizontal load force between the inner (non-attacking) wheel Y_ji of the investigated wheel axle and the inner rail

2.3. Methodology for theoretical determination of the smallest value of the vertical reaction of the wheel Q_jk,,min calculated during torsion of the wagon frame