Preprint
Article
Weighted Generalized Group Inverse in Banach *-Algebras
Altmetrics
Downloads
105
Views
26
Comments
0
This version is not peer-reviewed
Submitted:
03 October 2023
Posted:
04 October 2023
You are already at the latest version
Alerts
Abstract
In this paper, we introduce the notion of weighted generalized group inverse in a Banach algebra with proper involution. This is a natural generalization of weighted weak group inverse for a complex matrix and Hilbert space operator. We present several characterizations and representations of this generalized inverse. In addition, a new partial order on elements in a Banach *-algebra is investigated by using the weighted generalized group inverse and some known results are thus generalized.
Keywords:
Subject: Computer Science and Mathematics - Algebra and Number Theory
1. Introduction
Let be a complex matrix. The group inverse of A is defined as the matrix satisfies the equations:
Such X is unique if exists, denoted by . As is well known, a square complex matrix A has group inverse if and only if .
In [18], Wang and Chen introduced and studied a weak group inverse for square complex matrices. A square complex matrix A has weak group inverse X if it satisfies the equations:
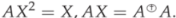 Here,
Here, 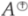 is the core-EP inverse of A (see [11,13,14]). Weak group inverse was also generalized to a rectangular matrix and Hilbert space operator (see [5,15]). We refer the reader to [16,19,20] for more results on weak group inverse.
is the core-EP inverse of A (see [11,13,14]). Weak group inverse was also generalized to a rectangular matrix and Hilbert space operator (see [5,15]). We refer the reader to [16,19,20] for more results on weak group inverse.
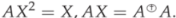
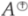 is the core-EP inverse of A (see [11,13,14]). Weak group inverse was also generalized to a rectangular matrix and Hilbert space operator (see [5,15]). We refer the reader to [16,19,20] for more results on weak group inverse.
is the core-EP inverse of A (see [11,13,14]). Weak group inverse was also generalized to a rectangular matrix and Hilbert space operator (see [5,15]). We refer the reader to [16,19,20] for more results on weak group inverse.Let be the set of all bounded linear operators from X to Y, where X and Y are infinite-dimensional complex Hilbert spaces. Very recently, Mosić and D. Zheng introduced and studied weighted weak group inverse for Hilbert space operators. Let and . The W-weighted weak group inverse of A is defined as
Here, is the weighted core-EP inverse of A (see [10,12,15]).
A Banach algebra is called a Banach *-algebra if there exists an involution satisfying . The involution ∗ is proper if for any . The algebra of all complex matrices is a Banach algebra with conjugate transpose ∗ as its proper involution. If X is a Hilbert space then the algebra of all bounded linear operators from on X, with the usual operations and norm, is a Banach algebra with the adjoint operation as its proper involution. The goal of this paper is to generalize (weighted) weak group inverse for complex matrices and Hilbert space operators to elements in a Banach algebra with proper involution. Some known results are thus generalized wider cases.
Let be a Banach algebra with proper involution ∗. An element has g-Drazin inverse (i.e., generalized Drazin inverse) if there exists such that Such x is unique, if exists, and denote it by . Here, Evidently, As a generalization of weak group inverse mentioned above, the author introduced and studied generalized group inverse (see [2]). An element has generalized group inverse if there exists such that
Such x is unique, if exists, and denote it by . Here, we list several characterizations of generalized group inverse.
Theorem 1.
(see [2] Theorem 2.2, Theorem 4.1 and Theorem 5.1) Letbe a Banach *-algebra, and let. Then the following are equivalent:
- (1)
- .
- (2)
- There exist such that
- (3)
- and there exists such that
- (4)
- There exists an idempotent such that
- (5)
-
andfor an idempotent .
In Section 2, we extend the definition of weighted weak group inverse for a Hilbert space operator to an elements in a Banach algebra. We obtain some characterizations of weighted generalized group inverse, in particular, the representations of weighted generalized group inverse in terms of generalized group inverses. Recall that an element has generalized w-core-EP inverse if there exist such that
The preceding x is unique if exists, and we denote it by (see [3]). An element has generalized core-EP inverse if the w mentioned above is 1, and denote its weighted generalized core-EP inverse by (see [1]). In Section 3, we establish the representations of weighted generalized group inverse as a subclass of weighted generalized core-EP inverses. In Section 4, we characterize the weighted generalized group inverse in terms of involved images and kernels. A new property of weighted group inverse is presented by using three systems of equations. Finally, in the last Section, we investigate constrained binary relations and some properties of weighted generalized group orders are derived by using weighted generalized group inverses.
Throughout the paper, all Banach algebras are complex with a proper involution ∗. We use and to denote the sets of all invertible, group invertible, g-Drazin invertible, weak group invertible, generalized core-EP invertible and generalized group invertible elements in , respectively. An element has -inverse x if it satisfies the equations and and denote x by .
2. Weighted Generalized GROUP Inverse
The purpose of this section is to introduce a new generalized inverse which is a natural generalization of group inverse in a *-Banach algebra. Our starting points is the following.
Theorem 2.
Let . Then the following are equivalent:
- (1)
- There exists such that
- (2)
- .
In this case,
Proof.
By hypothesis, we can find such that
Then
Furthermore, we have
Therefore
Hence,
Accordingly,
as desired.
Let Then we verify that
We easily check that
Hence, we have
Therefore
the result follows. □
Corollary 1.
Let . Then the following are equivalent:
- (1)
- The system of conditionsis consistent and it has the unique solution given by
- (2)
- .
Proof. This is obvious by Theorem 2.1.
Since , by the argument above, satisfies the preceding equations. If x satisfies the system of conditions mentioned above, then . Therefore , as asserted. □
The preceding unique solution x is called the generalized w-group inverse of a, and denote it by . That is, We use to denote the set of all generalized w-group invertible elements in . By the argument above, we now derive
Corollary 2.
Let . Then
- (1)
- .
- (2)
- and .
An element has generalized w-Drazin inverse if there exist such that
Such x is unique, if exists, and denote it by . Evidently, (see [4]). Let be the set of all generalized w-Drazin invertible elements in .
Theorem 3.
Let . Then if and only if
- (1)
- ;
- (2)
- there exists such that
Proof.
⟹ In view of Theorem 2.1, . By virtue of ([2] Theorem 2.2), . Hence . Set . Then
Since , it follows by ([2] Theorem 2.2) that , as required.
⟸ Since , . By hypothesis, there exists such that
Then . Moreover, we see that
Thus, we have
In light of ([2] Theorem 2.2), . Therefore we complete the proof by Theorem 2.1. □
Corollary 3.
Let and . Then if and only if
- (1)
- ;
- (2)
- there exists such that
Proof.
⟹ Let . In view of Theorem 2.1, we have
We have shown that . That is, , as desired.
⟸ By hypothesis, there exists such that
Then . Therefore , This completes the proof by Theorem 2.4. □
Corollary 4.
Let and . Then if and only if
- (1)
- ;
- (2)
- there exists such that
Proof.
This is obvious by choosing in Corollary 2.5. □
3. Representations by Weighted Generalized Core-EP Inverses
Every square complex has core-EP inverse, and so has weighted generalized core-EP inverse (see [17]). Every weighted g-Drazin invertible bounded linear Hilbert operator has weighted generalized core-EP inverse (see [15]). In view of ([2] Theorem 6.1), . Thus, weighted generalized core-EP invertible elements form a rich subclass of weighted generalized group inverse. Let . The aim of this section is to present the representations of weighted generalized group inverse as a subclass of weighted generalized core-EP inverse.
Theorem 4.
Let . Then
Proof.
In [15], Mosić and Zhang introduced and studied the weighted weak group inverse for Hilbert space operators. Evidently, weighted weak group inverse and weighted generalized group inverse coincide with each other for a Hilbert space operator as the following shows.
Corollary 5.
Let X be a Hilbert space, and . Then
Proof.
This is obvious by Theorem 3.1. □
We are ready to prove:
Theorem 5.
Let . Then if and only if
Proof.
⟹ In view of Theorem 3.1, . Since and , we check that
as desired.
⟸ By hypothesis, we have
Then we see that
In light of Theorem 3.1, , as asserted. □
Corollary 6.
Let . Then if and only if
Proof.
This is obvious by choosing in Theorem 3.3. □
In [18], Wang and Chen introduced and studied the weighted weak group inverse for complex matrices. As an immediate consequence of Corollary 3.4, the weak group inverse and generalized group inverse coincide with each other for a square complex matrix.
Corollary 7.
Let . Then if and only if X satisfies the system of equations
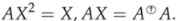
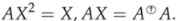
We are ready to prove:
Theorem 6.
Let . Then the following are equivalent:
- (1)
- .
- (2)
- (3)
Proof.
In view of Theorem 3.3,
By virtue of ([2] Theorem 3.1), . Applying Theorem 3.1, we have
Then
In light of Theorem 3.1, we have , as desired.
By hypothesis, we have
as required.
By hypothesis, Then . In view of Theorem 3.3, ; hence the result. □
Corollary 8.
Let . Then the following are equivalent:
- (1)
- .
- (2)
- (3)
Proof.
This is obvious by choosing in Theorem 3.6. □
4. Characterizations Involving Images and Kernels
Let and . The notation denotes the idempotent such that and . We easily check that the preceding idempotent p is uniquely determined by . The goal of this section is to characterize the weighted generalized group inverse by using involved images and kernels.
Theorem 7.
Let . Then the following are equivalent:
- (1)
- .
- (2)
- .
Proof.
In view of Theorem 3.1, . Then
Let . Then . Since , we have
hence, . On the other hand, we have
whence, . Thus . Likewise, Moreover, we verify that
This implies that as required.
By the preceding discussion, satisfies
Assume that . Then , and so . On the other hand, . Therefore , and so , thus yielding the result. □
Corollary 9.
Let . Then the following are equivalent:
- (1)
- .
- (2)
- .
Proof.
We easily obtain the result by choosing in Theorem 4.1. □
Theorem 8.
Let . Then
- (1)
- .
- (2)
- .
- (3)
- is group invertible and
Proof.
In view of Theorem 3.6, we have . Set . By using Theorem 4.1, , as required.
By virtue of Theorem 3.1, we have
In light of Theorem 3.6, ; whence, . It follows by Theorem 4.1 that . Therefore .
Clearly, . By virtue of Theorem 3.3., we derive
and so the result is proved. □
As an immediate consequence, we derive
Corollary 10.
Let . Then. Then
- (1)
- .
- (2)
- .
- (2)
- is group invertible and
Let . We say that A is simply equivalent to B if A is equivalent to B by a column and a row transformations, i.e.,
We denote it by
Theorem 9.
Let . Then
- (1)
- there exists a unique such that
- (2)
- there exists a unique such that
- (3)
- there exists a unique such that
In this case,
Proof.
Let and . One directly checks that equalities in and hold. In view of Theorem 3.6, . Then we verify that
Therefore
Claim 1. Assume that there exists such that Then . By using ([2] Theorem 3.4), we have . Then by Corollary 2.3. Since , we have . Thus,
Since and are idempotents, we have
In view of Theorem 2.1 and [2, Theorem 6.1], , and so
Hence,
Therefore , and so . The uniqueness of x is proved.
Claim 2. Assume that there exists such that Then . Since , we see that . In view of ([2] Theorem 3.4), we have By using Theorem 3.1 and ([1] Theorem 1.2), we directly check that
and so Therefore
Since and are idempotents, we get
As in the argument above, we see that
This implies that
Accordingly, ; hence, . The uniqueness of y is proved.
Claim 3. Assume that there exists such that
Then
By the argument above, and . Then
Obviously, we have
Then
Since we see that
Accordingly, , and then , thus yielding the result. □
Corollary 11.
Let . Then
- (1)
- there exists a unique such that
- (2)
- there exists a unique such that
- (3)
- there exists a unique such that
In this case,
Proof.
This is an immediate consequence of Theorem 4.5. □
Let and represent the null space and range space of a complex matrix X, respectively. As an immediate consequence, we improve ([6] Theorem 4.2) and ([7] Theorem 2.1) as follows.
Corollary 12.
Let and . Then
- (1)
- there exists a unique matrix X such that
- (2)
- there exists a unique matrix Y such that
- (3)
- there exists a unique matrix Z such that
In this case,
Proof.
Since very rectangular matrix can be regarded as a subblock of a square matrix by adding some zero entries, the result is true by Theorem 4.5. □
5. weighted Generalized Group Orders
Our main concern in this section is to describe the relations between two elements in a Banach *-algebra by means of weighted generalized group inverses. Let and . Our starting point is the following:
Definition 1.
if
if
if and .
Lemma 1.
Let and . Then
- (1)
- if and only if .
- (2)
- if and only if
Proof.
⟹ Since , we have In view of Theorem 2.1,
Then we derive
Since , we obtain
In light of ([2] Theorem 6.1), Then we have
By virtue of ([15] Theorem 1.2), , and then . Therefore
⟸ Since , we have . As , we get . This implies that
Therefore .
Analogously to the preceding discussion, the result follows. □
Lemma 2.
Let and . Then
- (1)
- if and only if .
- (2)
- if and only if .
Proof.
Assume that . As in the proof of Lemma 5.2, we have . Conversely, assume that . In view of ([15] Theorem 1.2), we have . Therefore , as required.
This is proved in the similar way to the above. □
We are ready to prove:
Theorem 10.
Let and . Then
- (1)
- .
- (2)
- and
- (3)
- and
Proof.
This is obvious by combing and in Lemma 5.2.
Since , we have . The implication is obtained by Lemma 5.3.
Since , by virtue of Lemma 5.3, . According to Lemma 5.2, . On the other hand, . Since we have . Then . So the theorem is true. □
The relation is a pre-order as the following shows.
Corollary 13.
If and , then .
Proof.
In view of Theorem 5.4, we have
Then
Since and
we see that
Therefore By a similar route, we check that Therefore , the corollary is true. □
Let . Then and We are now ready to prove the main result of this section.
Theorem 11.
Let . Then the following statements are equivalent:
- (1)
- if and only if .
- (2)
- if and only if .
- (3)
- if and only if and .
Proof.
Since , we have
In view of Theorem 2.1, Hence
Furthermore, we check that
Therefore . Analogously, we show that , as required.
Let be projections and . Then . We write x as in the matrix form:
Theorem 12.
Let . Then the following statements are equivalent:
- (1)
- .
- (2)
- and b are represented aswhere
Proof.
Let and . Then we have
Moreover, we verify that
Write Then we have
Thus,
and so
Furthermore, we have
Then
Moreover, we have
By Lemma 5.2 and Lemma 5.3, we have hence, , and so . Since is invertible, we obtain . Since , we see that , and so . On the other hand, we have . This implies that
Hence,
Accordingly,
By direct computations, we have
Likewise, we check that Therefore , as asserted. □
Corollary 14.
Let. Then the following are equivalent:
- (1)
- .
- (2)
- and B are represented aswhere
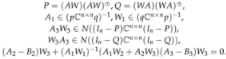
Proof.
This is obvious by Theorem 5.7. □
Analogously, we now derive
Theorem 13.
Let . Then the following statements are equivalent:
- (1)
- .
- (2)
- and b are represented aswhere
References
- H. Chen and M. Sheibani, On generalized core-EP invertibility in a Banach algebraa, arXiv:2309.09862 [math.FA]. arXiv:2309.09862 [math.FA]. [CrossRef]
- H. Chen and M. Sheibani, Generalized group inverse in a Banach *-algebra, preprint, 2023. [CrossRef]
- H. Chen and M. Sheibani, Weighted generalized core-EP inverse in Banach *-algebras, preprint, 2023. [CrossRef]
- A. Dajić and J.J. Koliha, The weighted g-Drazin inverse for operators, J. Australian Math. Soc., 82(2007), 163–181.
- D.E. Ferreyra; V. Orquera and N. Thome, A weak group inverse for rectangular matrices, RACSAM. 2019. [CrossRef]
- D.E. Ferreyra; V. Orquera and N. Thome, Representation s of weighted WG inverse and a rank equation’s solution, Linear and Multilinear Algebra, 71(2023), 226–241.
- J. Marovt and Mosic, On some orders in *-rings based on the core-EP decompositions, J. Algebra Appl. 2022. [CrossRef]
- D. Mosić, Weighted binary relations for operators on Banach spaces, Aequat. Math., 90(2016), 787–798.
- D. Mosić, Core-EP pre-order of Hilbert space operators, Quaest. Math., 41(2018), 585–600.
- D. Mosić, Weighted core-EP inverse of an operator between Hilbert spaces, Linear Multilinear Algebra, 67(2019), 278–298.
- D. Mosić, Core-EP inverse in ring with involution, Publ. Math. Debrecen, 96(2020), 427–443.
- D. Mosić, Weighted core-EP inverse and weighted core-EP pre-orders in a C*-algebra, J. Aust. Math. Soc., 111(2021), 76–110.
- D. Mosic, Core-EP inverses in Banach algebras, Linear Multilinear Algebra, 69(2021), 2976–2989.
- D. Mosic and D.S. Djordjevic, The gDMP inverse of Hilbert space operators, J. Spectral Theory, 8(2018), 555–573.
- D. Mosic and Z. Daochang, Weighted weak group inverse for Hilbert space operators, Front. Math. China, 15(2020), 709–726.
- D. Mosic; P.S. Stanimirovic, Representations for the weak group inverse, Appl. Math. Comput., 397(2021), Article ID 125957, 19 p.
- H. Wang, Core-EP decomposition and its applications, Linear Algebra Appl., 508(2016), 289–300.
- H. Wang; J. Chen, Weak group inverse, Open Math., 16(2018), 1218–1232.
- M. Zhou; J. Chen and Y. Zhou, Weak group inverses in proper *-rings, J. Algebra Appl. 2020; 19. [CrossRef]
- M. Zhou; J. Chen; Y. Zhou and N. Thome, Weak group inverses and partial isometries in proper *-rings, Linear and Multilinear Algebra, 70(2021), 1–16.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




