Prerpints.org logo
Preprint
Article

Development of Slope Detection ASIC for On-Chip Current Sensing in Voltage Converters

Altmetrics

Downloads

117

Views

33

Comments

0

Submitted:

03 October 2023

Posted:

04 October 2023

You are already at the latest version

Alerts
Abstract
This article introduces the design and analysis of a slope detection circuit tailored for on-chip sensing of the load current in DC-DC converters. The novel indirect sensing approach is grounded in measuring the output voltage slope across the filtering capacitor during discharge phases. Consequently, this slope data can be effectively harnessed to control the converter switches. The slope detector circuit was designed in standard 65 nm CMOS technology using the nominal supply voltage of 1.2 V and can be used for current sensing within the range from one to hundreds of mA. Since the proposed circuit has mainly digital character, the robustness to process, temperature and supply voltage variations can be ensured rather conveniently.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

In the present era, achieving low power consumption has become a paramount requirement in design of integrated circuits (ICs) and complex system-on-chip (SoC) configurations. Contemporary advancements and research in the realm of portable electronic devices predominantly concentrate on design principles towards energy savings, operation under reduced voltage conditions, and integration of different mixed-signal circuits and/or systems into a singe monolithic chip. Generally, analog circuits tend to be the most power-hungry subsystems within SoCs. As a result, in the majority of instances, having knowledge regarding the specific load or current consumption can provide an efficient method for lowering the power dissipation of the entire system. Furthermore, advances in IC manufacturing are welcome but leads to sophisticated technologies with notable deviations in process characteristics. As a consequence, ensuring the IC performance with resilience to process-voltage-temperature (PVT) variations becomes one of the most demanding endeavors for both IC designers and researchers. This concern becomes particularly critical when addressing circuits requiring a high degree of precision.
The established measure of electric current coursing through a specific circuit could be highly advantageous in controlling other components within a system. An example of a system, where electric current can be used as a control signal is controller in DC-DC converters. A flyback DC-DC converter is categorized as a straightforward configuration of an isolated converter, extensively employed as the power supply circuit in cellphones, laptops, PCs, LCD TVs, and various other portable gadgets [1].
Within on-chip current sensing techniques, the typical approach involves a direct method of current measurement utilizing a sensing element. This often includes components like a shunt resistor, a MOS transistor configured as a resistor, or a sensing transistor connected in parallel with the power MOS device [2,3,4,5,6,7]. The main properties and features of such techniques are described in more detail in [4]. However, the main disadvantages of direct measurement approaches include low accuracy and rather high power losses across the sensing element. Conversely, indirect methodologies provide the opportunity to detect current without requiring an extra sensing element connected in series. In this way, they present lossless options for on-chip measurement of electric current. These techniques leverage alternative electrical parameters that are directly correlated with the sensed current. Thus, indirect methods do not influence performance of a measured circuit through additional measurement hardware.
In this paper, we present the slope detector circuit designed in 65nm CMOS technology, which can be used for indirect on-chip current measurement and then, controlling the flyback DC-DC converter. Section 2 elaborates on the fundamental concept underpinning the devised slope detector. The simulation-derived outcomes are displayed in Section 3, while the actual measured results are exhibited in Section 4. The utilization of the indirect measurement approach is outlined in Section 5, and the paper culminates with the drawn conclusions in Section 6.

2. Background and Motivation

As mentioned above, many portable electronic devices use Flyback DC-DC coverter as a power source due to its electrical isolation and simple topology. Under light-load conditions or standby mode, Flyback converter usually works in so-called “burst” mode [8]. In order to regulate the converter output voltage and control the voltage ripple, the output current and voltage of converter need to be estimated. For this purpose, direct sensing approaches using auxiliary winding of the transformer are usually employed. However, the typical Flyback converter topology includes an output bypass capacitor to reduce voltage ripple at the converter output. The output current can therefore, be estimated indirectly just by sensing a voltage drop across the capacitor. This is the main idea behind such an indirect method of measuring the output current of Flyback DC-DC converter working in the burst mode. The basic topology of Flyback converter and typical waveform of the signals are shown in Figure 1 and Figure 2, respectively. It can be observed that the burst mode contains two phases: burst-on and burst-off periods. During the burst-on time, the output voltage is boosted to the requested value. On the other hand, during the burst-off time, the converter output voltage decreases due to current flow from the output capacitor to the load. Hence, the output current of converter can be sensed during this phase indirectly by sensing the output voltage. The proposed sensing approach presented in this paper is based on the idea described above.
This operational concept outlines the fundamental operation of the BUCK-BOOST converter. When the power transistor switch is turned on, it collects energy from the power source and stores it within the primary winding of the transformer. Subsequently, while the transistor is turned off, the stored energy is transferred to the secondary winding of the transformer and eventually delivered as the output voltage by the converter [9,10]. Enhancing the energy conversion efficiency of the converter can be achieved by sensing the load current and strategic control of the power MOS switch, which is performed by the controller (see Figure 1). Thus, it is rather evident that the output current sensing needs to be performed within the integrated circuit of DC-DC converter [11,12,13].
The waveforms depicted in Figure 2 illustrate the signal sequence in context of the implemented current measurement approach. The diagram displays the following signals (waveforms from top to bottom): DC-DC flyback converter output voltage (blue curve), the input references such as VREF_H and VREF_L (orange and red curves), the outcome from the pulse generator responsible for driving the power transistor switch, outputs from comparators COMP_L and COMP_H, the actual state of the counter denoted as C o u n t (an internal signal), the output stemming from the measurement method referred to as C o u t o u t , and finally, the CLK signal. Following the global reset activation, C o u n t value returns to its default value, which in turn configures the default waveform of P u l s e o u t . As the converter output becomes charged, it ascends until it reaches the predefined upper voltage limit (VREF_H). Amid the discharge phase, the measurement process is initiated. With each rising edge of the clock signal, the value of C o u t is incremented. Once the designated measurement time window has elapsed, the value of C o u t is written to the output register C o u n t o u t . This value is then utilized to select the appropriate waveform for the P u l s e o u t signal from a Look-Up Table. Upon the VREF_H threshold being achieved by the output signal, a counter reset is triggered, returning the internal counter value to zero.
As introduced earlier, the proposed load current measurement technique relies on an indirect approach involving voltage drop sensed across the external capacitor on the DC-DC flyback converter output. The designed measurement system was implemented though a controller circuit to ensure the controlled switching of the power NMOS transistor on the primary side of transformer. The comprehensive block diagram of the developed controller is illustrated in Figure 3. The controller consists of three main components: the proposed indirect measurement method of the output current, a lookup table (LUT), and a pulse generator. The pulse generator is a sequential circuit that was described at the RTL (Register Transfer Level) using Verilog language. It generates the control signal named P u l s e o u t , which drives the power NMOS switch. The control signal is determined by the input parameters t o n and t o f f . The input signals for the pulse generator are fed from the LUT block that can be programmed externally using a digital logic. An instance of LUT configurations is shown in Figure 3, where the left-side table (within the LUT) illustrates configuration of the parameters t o n and t o f f based on the measured current value. These values were obtained by simulation, and with these parameters, the converter achieved optimum efficiency. The right-side table presents the conversion table that correlates the finite counter values with the corresponding currents. The input applied to the LUT, which is a 10-bit value, is obtained by the designed current measurement method.

3. Proposed Slope Detector Circuit

Basic principle of the proposed slope detector (SD) circuit is depicted in Figure 4. Since the designed SD is intended to be used in the presented controller for DC-DC converter, the output voltage representing the output load current can be sensed through the external capacitor (converting the output load current to voltage value). This approach is based on an assumption of using a large bypass capacitor that is an existing component of the converter. In such a case, during the discharging phase of capacitor C O , the output voltage will vary linearly in time. The sensed load current I s e n s can be expressed as follows:
I s e n s = V s e n s R L · e − t R L C O ≈ V s e n s R L ,
where V s e n s is the output voltage, R L is the load resistor and C O is the output capacitor (see Figure 1). The output voltage will vary linearly in time if we considered that t / R L C O → 0 . This condition is ensured only if either the current sensing is carried out in a short time interval or the capacitor discharging time constant t / R L C O will be large. Thus, if one of these two conditions is fulfilled, the electric current can be conveniently sensed in the indirect manner by measuring the slope of voltage across the capacitor C O within its discharging phase.
The measured time window is given by two voltage reference V R E F _ H and V R E F _ L (denoted as the voltage window Δ V in Figure 4). In such a case, the respective electric current will be given as:
I s e n s = C O · Δ V Δ T = V R E F _ L − V R E F _ H t L − t H ,
It is important to note that accuracy of the proposed current measurement approach can be influenced by process, temperature and supply voltage variations. Such fluctuations are not considered in Equation (5) but these will be further investigated in the following part of the paper.
The circuit block diagram of the designed slope detector is depicted in Figure 5. The output voltage denoted as V s e n s across the capacitor C O is sensed by a window comparator (forming by comparators K1 and K2). Both comparators are based on a common topology with hysteresis introduced to protect the circuit from unwanted glitches at the comparator output. Digital outputs of comparators K1 and K2 control the start/stop switching of the counter, which is driven by c l k signal with frequency of 500 kHz (considering the external input frequency of 1 MHz and multiplexer output being transferred from input i n 1 ). In order to extend the range of possible slope that can be detected, the input frequency is decreased and multiplexed to the input of counter. This simple feature brings possibility of sensing a wider range of currents but on the other hand decreasing switching frequency of counter reduce accuracy of measurement system. After the counter stops counting, its value can be easily compared to the reference value stored in a Look-Up-Table (LUT), and the measured current is evaluated.
The slope value of the output sensed voltage ranges from 10 to 150, and the counter switching frequencies are set to 500 KHz, 250 KHz, 125 KHz, and 62.5 KHz. The achieved calculated results represent the ideal finite counter value without any measurement errors considered. These calculation results, obtained using Equations (3) and (4), are shown in Table 1. In calculations, we take into account the specified time window length Δ t , the change in output voltage Δ V (set to 60 mV), and the counter switching frequency f s t a r t .
Δ t = Δ V S L O P E
C o u n t = Δ t 1 f s t a r t
Due to the window comparator circuit being employed to sense the voltage at capacitor C O , the detection can be sensitive to process variations, including the input offset voltage of comparators. As a result, the delay of both comparators might influence the overall accuracy of proposed measurement method. For this reason, Equation (5) needs to be extended as follows:
I s e n s = C O · Δ V Δ T = V R E F _ L − V R E F _ H ± Δ V o f f t L − t H ± Δ t d ,
where Δ V o f f and Δ t d is difference of the input offset voltage and transition delay of comparators (K1 and K2), respectively. In the proposed SD circuit, differences in the parameters will be mainly influenced by mismatch of devices forming the comparators. This mismatch caused by variations in manufacturing process, can lead to discrepancies in the performance of individual components. As a result, the input offset voltage and delay of the comparators can vary, affecting the accuracy and reliability of the measurement method.
The waveforms shown in Figure 6 illustrate the sequence of signals in measurement system (from top to bottom): comparator reference voltage inputs (VREF_H and VREF_L), outputs of the window comparator circuit (COMP_H and COMP_L), and finally, clock signal (CLK) and the counter output (Count). The counter output is set to zero by the external global reset and then, its value is incremented by each rising edge of the clock signal CLK. The middle graph displays the comparator outputs (K1 indicated by green color and K2 indicated by red) using continuous lines, without considering hysteresis and transition delays. Because the comparator circuits work asynchronously and their outputs are not synchronized with the clock signal, an error denoted as Δ t c l k might occur. In this scenario, the maximum delay error between the initial rising edge of the clock signal within the measurement window and the falling edge of comparator K1 output COMP_H may be less than one clock period. Likewise, a comparable measurement error can occur at the end of the measurement time window due to the lack of synchronization between the rising edge of comparator K2 output COMP_L and the rising edge of the clock signal. The hysteresis of comparators K1 and K2, denoted as Δ V 1 and Δ V 2 , respectively, and both comparators share the same hysteresis value. As a result of this hysteresis effect, delays named Δ t 1 and Δ t 2 will be present in the output signals of comparators K1 and K2, respectively. The comparator outputs and the counter values, with their delays, are depicted using dashed lines in middle and bottom graphs, respectively. The variances between Δ t 1 of comparator K1 and Δ t 2 of comparator K2 are consistently kept within a nanosecond range, even across different process corners. This slight difference is considered acceptable as it does not significantly affect the measurement time window.

4. Simulation Results

This section presents results obtained from simulation of the proposed slope detector circuit. The simulations took into account variations caused by fabrication process, and the designed circuit was analyzed using Corner and Monte Carlo (MC) analyses. The temperature range considered in all simulations was from − 20 ∘ C to + 85 ∘ C.
The relationship between the counter finite value and the sensed voltage slope is shown in Figure 7. These results were obtained from both Corner Analysis and Monte Carlo. As the proposed slope detector operates by counting clock pulses within a specific time window, it exhibits robustness against variations caused by fabrication process fluctuation. The concept is primarily sensitive to any mismatch between the devices forming comparators K1 and K2.
Results shown in Figure 7 and Figure 8 indicate that device mismatch introduces variations in the finite counter value, with a standard deviation of ±6 pulses counted by the counter. Counting for ± 3 σ variations, the accounted pulses can range from 138 to 172, with a mean value of 159. This parameter represents the overall error of the proposed approach, considering the mismatch of all devices used in the slope detector circuit.
The second part of the measurement error is caused by Δ t c l k (see Figure 6) and explained in the previous section. In Figure 9, Δ t c l k error over the process corners for slope of 150 V/s is shown. It can be observed that Δ t c l k can exhibit variations across different process corners, leading to a measurement error of approximately 2 μ s . For the input frequency of 1 MHz, this implies that in a process corner, Δ t c l k can have an undesirable impact on the finite counter value, resulting in the addition of 1 to 2 extra pulses counted by the counter. It is essential to highlight that Δ t c l k was examined for various slope values, and in most cases, the maximum measurement error of 2 μ s was observed. Figure 10 illustrates the results of Monte Carlo analysis for the Δ t c l k error at a slope of 150 V/s. Considering variations of ± 3 σ , the value of Δ t c l k can vary within the range from 1.512 μ s to 2.506 μ s , with a mean value of 1.955 μ s.
The maximum current error caused by the Δ t c l k effect was determined using Equations (6) and (7). In these equations, I e r r represents the calculated current error, C O is the value of the external capacitor, Δ V denotes the change in the sensed output voltage, Δ t is the duration of the time window, and Δ t c l k represents the maximum error caused by the asynchronous operation of comparators K1 and K2. If the counter switching frequency remains constant during the measurement process, Δ t c l k can be calculated as 2 ( 1 f s t a r t ) , where f s t a r t is the counter switching frequency. The calculated measurement current error I [ m A ] with a constant switching frequency is illustrated in Figure 11. The lowest measurement current error was achieved with the maximum switching frequency of 500 kHz, which corresponds to 1 MHz input frequency of the measurement system.
I e r r = C O Δ V Δ t + 2 Δ t c l k
I e r r = C O Δ V Δ t + 2 ( 1 f s t a r t )
The measurement current error when the counter switching frequency is changed is calculated using Equation (8), where f S t a r t represents the initial switching frequency of 500 k H z , and f S t o p is the changed switching frequency that depends on the SLOPE of sensed output voltage and it is set to determine the range corresponding to the switching frequency. The most favorable results were obtained with the switching frequency changed from 500 kHz to 250 kHz, as shown in Figure 12.
I = C O Δ V Δ t + ( 1 f S t a r t + 1 f E n d )
To further examine robustness of the proposed slope detector, variations of the time window were analyzed across all process corners and the entire temperature range. Figure 13 shows the time window variation for different slope values. As one can observe, the absolute value of the time window differs for various slope values, but it remains consistent across different process corners. However, device mismatch within K1 and K2 can introduce additional measurement errors, necessitating the use of sophisticated layout techniques. Monte Carlo analysis of the time window variation for a slope of 150V/s is depicted in Figure 14. The time window value can fluctuate within the range from 369.1 μ s to 424.7 μ s , with a mean value of 398.041 μ s . For this analysis, variations of ± 3 σ was considered.
Figure 15 presents physical layout of the developed slope detector circuit. The implemented layout has dimensions of 62 μ m x 265 μ m, resulting in an occupied chip area of 0.016 mm 2 . Both comparators essentially contribute to the total area. On the other hand, they also incorporate additional functionalities, such as hysteresis tuning and calibration features, necessary for testing the fabricated chip samples.

5. ASIC Evaluation and Measurement Results

The slope detector circuit was designed using the hardware description language (HDL) Verilog. An experimental ASIC was fabricated using a general-purpose 65 nm CMOS process. The required measurement circuits were integrated onto the same chip alongside the ASIC system. Vital and significant points of the ASIC were linked to external measurement circuits that were implemented on the test board. A developed digital logic unit controls the entire system on the chip and the measurement process. The presence of this control logic facilitates the experimental verification process and also reduces the number of required package pins, resulting in greater efficiency. Additionally, the control logic has the capability to adjust specific parameters of the circuit, such as hysteresis in comparators K1 and K2.
The block diagram of the entire measurement setup is depicted in Figure 16. For this setup, the following equipment was used: Keysight InfiniVision DSOX2054 4-channel digital storage oscilloscope with 5 GSPS and 500 MHz of bandwidth, Keysight 33600A Series Waveform Generator, and Rohde & Schwarz HMC 8043 3-channel power supply.
Table 2 displays the measured conversion table, which shows the relationship between slope of the output sensed voltage, the input switching frequency of the counter, and the corresponding finite counter value. The input conditions used for measurements were identical to those used in simulations. The slope was varied from 10 to 150, and the switching frequency was set to 500 kHz, 250 kHz, and 125 kHz. Additionally, an adaptive frequency was used, depending on the set range corresponding to the specific slope value. When comparing the results obtained from simulation to the measured results, some differences can be observed in the counter values. These differences may caused by various factors, such as process tolerances, noise, and other influences. The main source of error within the measurement is likely to be the mismatch between comparators K1 and K2, as this can affect the accuracy of SD circuit.
To identify the underlying reasons for the error, conducting a comprehensive investigation of the implemented comparators in the SD circuit through precise measurements of delay and hysteresis characteristics is of utmost importance. To verify the results, we performed the measurement for five different chip samples.
The measured time delays of comparators K1 and K2 are depicted in Table 3. The error of time window, caused by the time delay of comparators, was calculated by determining the time difference between the rising edge of comparator K1 and the falling edge of comparator K2. This time difference represents the delay of time window, and can impact the overall accuracy of measurement. The worst case is observed in chip 3, where the time difference between the rising edge of comparator K1 and the falling edge of comparator K2 results in the largest error in the time window of 994 ns. Such a value of delay have only a negligible impact on measurement results, especially when the input frequency of 500 kHz is used. In such cases, the delay is relatively small compared to the period of input signal, and its influence on the measurement accuracy can be neglected.
In Table 4 and Table 5, one can find the measurement results of hysteresis for comparators COM_L (K1) and COMP_H (K2), respectively. Hysteresis was measured for the slope values of 10 and 150, encompassing both the rising and falling edges of the comparators. The total error in the finite counter value, taking into account the switching frequency and the slope, is presented in Table 6. These errors represent variations in the width of time window due to the differences in hysteresis between rising edge COM_L and falling edge of COMP_H. The best outcomes were attained in the case of SLOPE 10 for Chip1 and Chip5, and SLOPE 150 for Chip4 and Chip5. As can be observed, reducing the switching frequency leads to a decrease in the total measurement error. However, it is important to note that this reduction in error comes at the cost of diminished measurement accuracy.

6. Conclusions

A novel indirect strategy for on-chip current sensing, utilizing measurement of the output voltage slope, is introduced. However, it is essential to guarantee a high degree of device matching to minimize discrepancies leading to the measurement error and enhance the overall precision of current measurement. Thus, further improvement can be reached by employing calibration/trimming of the input voltage offset of the comparator circuits used in SD. The time delay of comparator suggests that this delay has no significant influence on the measurement accuracy and can be considered negligible. Nevertheless, the varying hysteresis values of comparators may lead to differences in the width of time window, which becomes the cause of notable measurement inaccuracies. The dissimilarities in comparator hysteresis could be caused by inadequate device matching or result from variations in the manufacturing process. The proposed measurement method and the designed SD circuit have the potential to find utility within a DC-DC converter system, providing the measurement of load current or helping approximate the output current. This application can significantly enhance control of the entire converter and improve its conversion efficiency. As for the future, our primary goal will include enhancing the design of K1 and K2 comparators, aiming to the improvement of durability and precision of the applied indirect technique for electric current measurement.

Acknowledgments

This work was supported in part by grants VEGA 1/0731/20 and VEGA 1/0760/21, and the Slovak Research and Development Agency under grant APVV-19-0392. This work has also received funding from the Electronic Components and Systems for European Leadership Joint Undertaking under grant agreement No 876868. This Joint Undertaking receives support from the European Union’s Horizon 2020 research and innovation programme and Germany, Slovakia, Netherlands, Spain, Italy.

References

  1. Coruh, N.; Urgun, S.; Erfidan, T. Design and implementation of flyback converters. In Proceedings of the 2010 5th IEEE conference on industrial electronics and applications. IEEE, 2010, pp. 1189–1193.
  2. Forghani-Zadeh, H.P.; Rincon-Mora, G.A. Current-sensing techniques for DC-DC converters. In Proceedings of the The 2002 45th Midwest Symposium on Circuits and Systems, 2002. MWSCAS-2002. IEEE, 2002, Volume 2, pp. II–II.
  3. Arar, S. Using Single-Ended Amplifiers in Low-Side Current Sensing: Error Sources and Layout Tips - Technical Articles, 2021.
  4. Lee, C.F.; Mok, P.K. A monolithic current-mode CMOS DC-DC converter with on-chip current-sensing technique. IEEE J. -Solid-State Circuits 2004, 39, 3–14. [Google Scholar] [CrossRef]
  5. Kim, Y.S.; No, B.M.; Min, J.S.; Al-Sarawi, S.; Abbott, D. On-chip current sensing circuit for current-limited minimum off-time PFM boost converter. In Proceedings of the 2009 International SoC Design Conference (ISOCC). IEEE, 2009, pp. 544–547.
  6. Xiao, Y.; Cao, J.; Chen, J.; Spring, K. Current sensing trench power MOSFET for automotive applications. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, 2005. APEC 2005. IEEE, 2005, Volume 2, pp. 766–770.
  7. Takaya, H.; Miyagi, K.; Hamada, K. Current-sensing power MOSFETs with excellent temperature characteristics. In Proceedings of the 2009 21st International Symposium on Power Semiconductor Devices & IC’s. IEEE, 2009, pp. 73–76.
  8. Huang, C.Y.; Liang, T.J.; Chen, K.H.; Li, C.Y. Primary-side feedback control IC design for flyback converter with energy saving burst mode. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), 2018, pp. 2054–2061. [CrossRef]
  9. Wu, K.C. Switch-Mode Power Converters: Design and Analysis; Elsevier, 2005.
  10. Maniktala, S. Switching Power Supplies A-Z; Elsevier, 2012.
  11. Billings, K.; Morey, T. Switchmode Power Supply Handbook; McGraw-Hill Education, 2011.
  12. Taneri, M.C.; Genc, N.; Mamizadeh, A. Analyzing and comparing of variable and constant switching frequency flyback DC-DC converter. In Proceedings of the 2019 4th International Conference on Power Electronics and their Applications (ICPEA). IEEE, 2019, pp. 1–5.
  13. Mohammed, A.A.; Nafie, S.M. Flyback converter design for low power application. In Proceedings of the 2015 International conference on computing, control, networking, electronics and embedded systems engineering (ICCNEEE). IEEE, 2015, pp. 447–450.
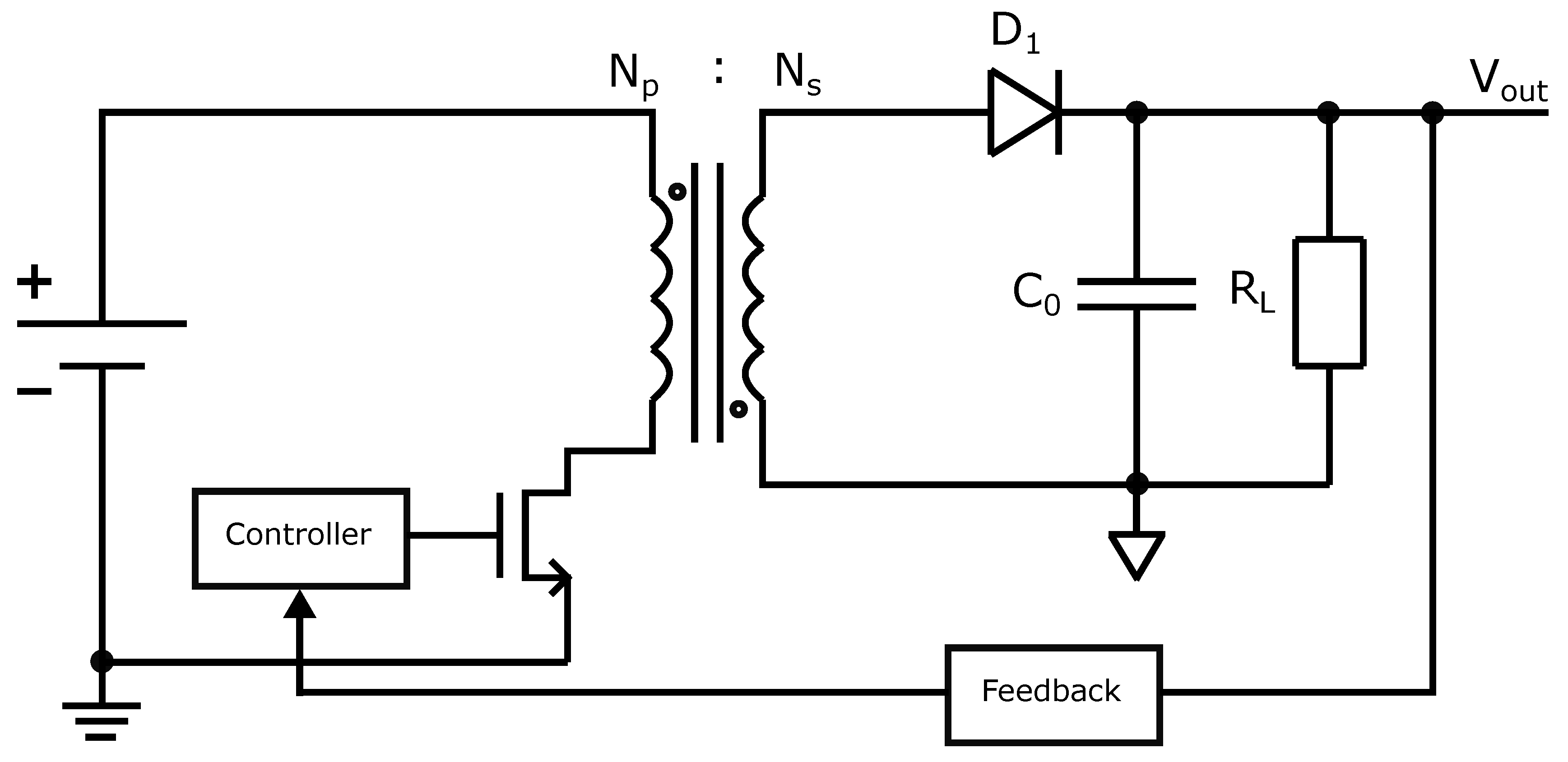
Preprints 86859 g001
Figure 1. Typical topology of Flyback converter
Figure 1. Typical topology of Flyback converter
Preprints 86859 g001
Preprints 86859 g002
Figure 2. Principle of the proposed approach to converter load current sensing
Figure 2. Principle of the proposed approach to converter load current sensing
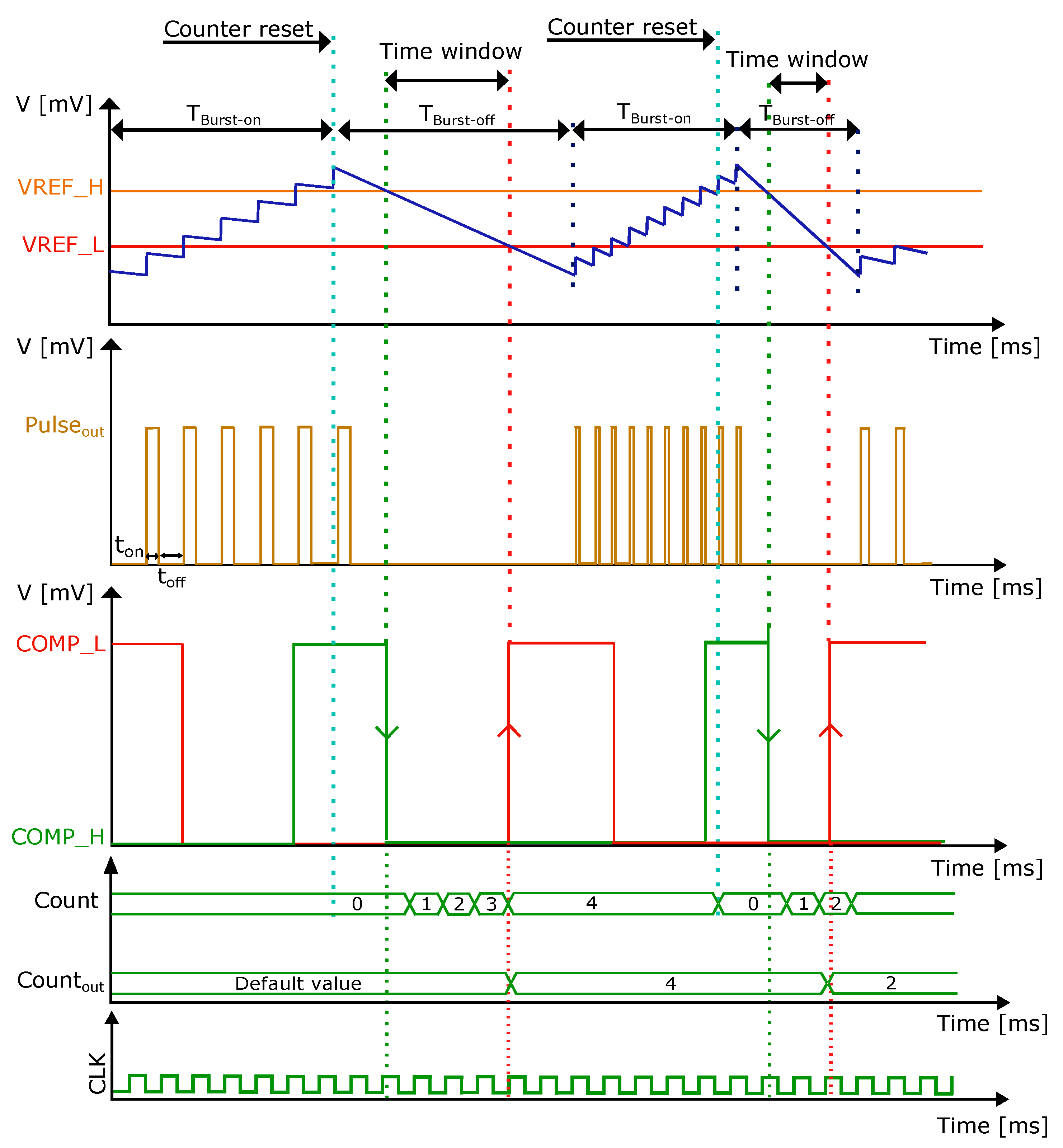
Preprints 86859 g002
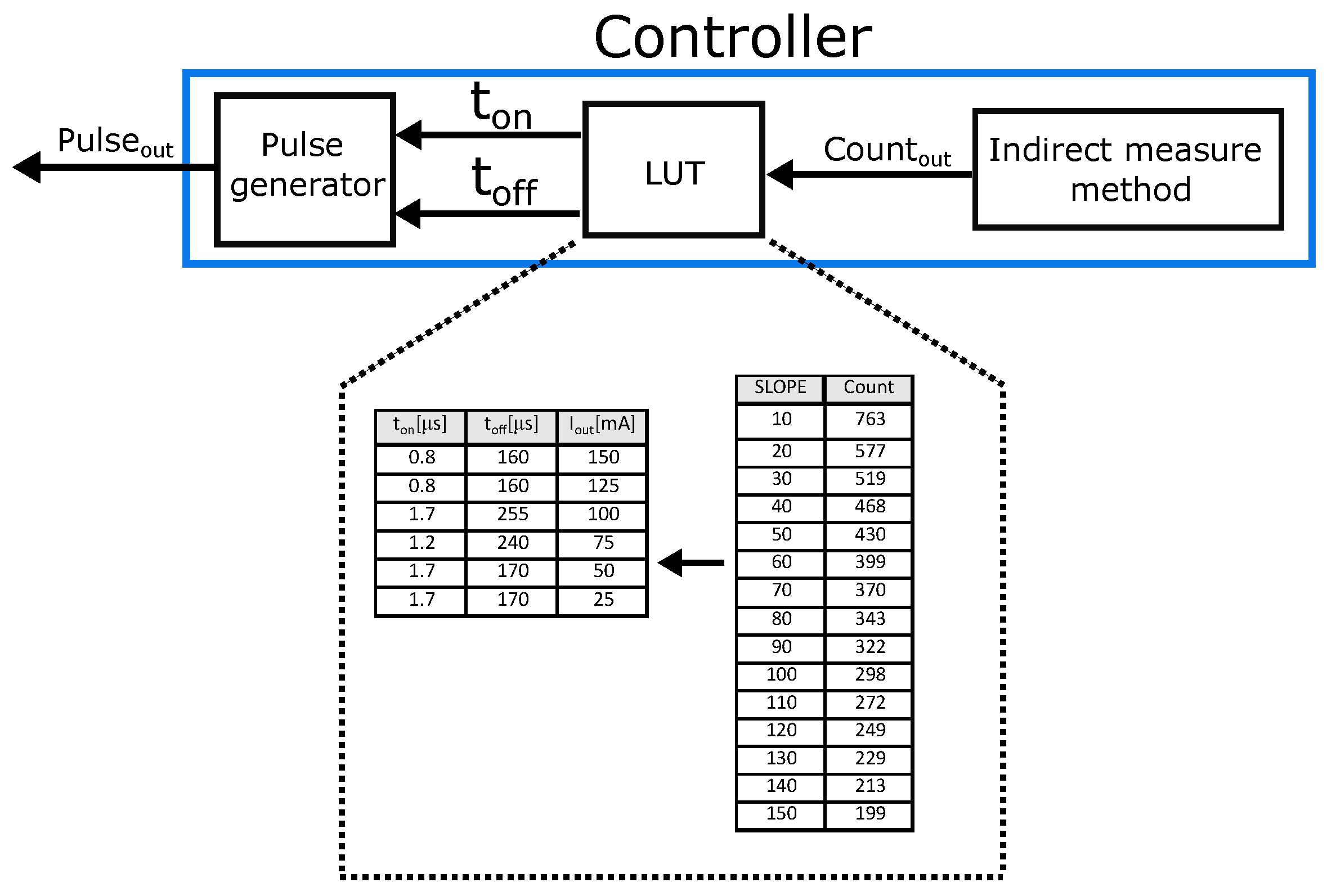
Preprints 86859 g003
Figure 3. Block diagram of the controller in Flyback converter
Figure 3. Block diagram of the controller in Flyback converter
Preprints 86859 g003
Preprints 86859 g004
Figure 4. Output voltage slope detection principle
Figure 4. Output voltage slope detection principle
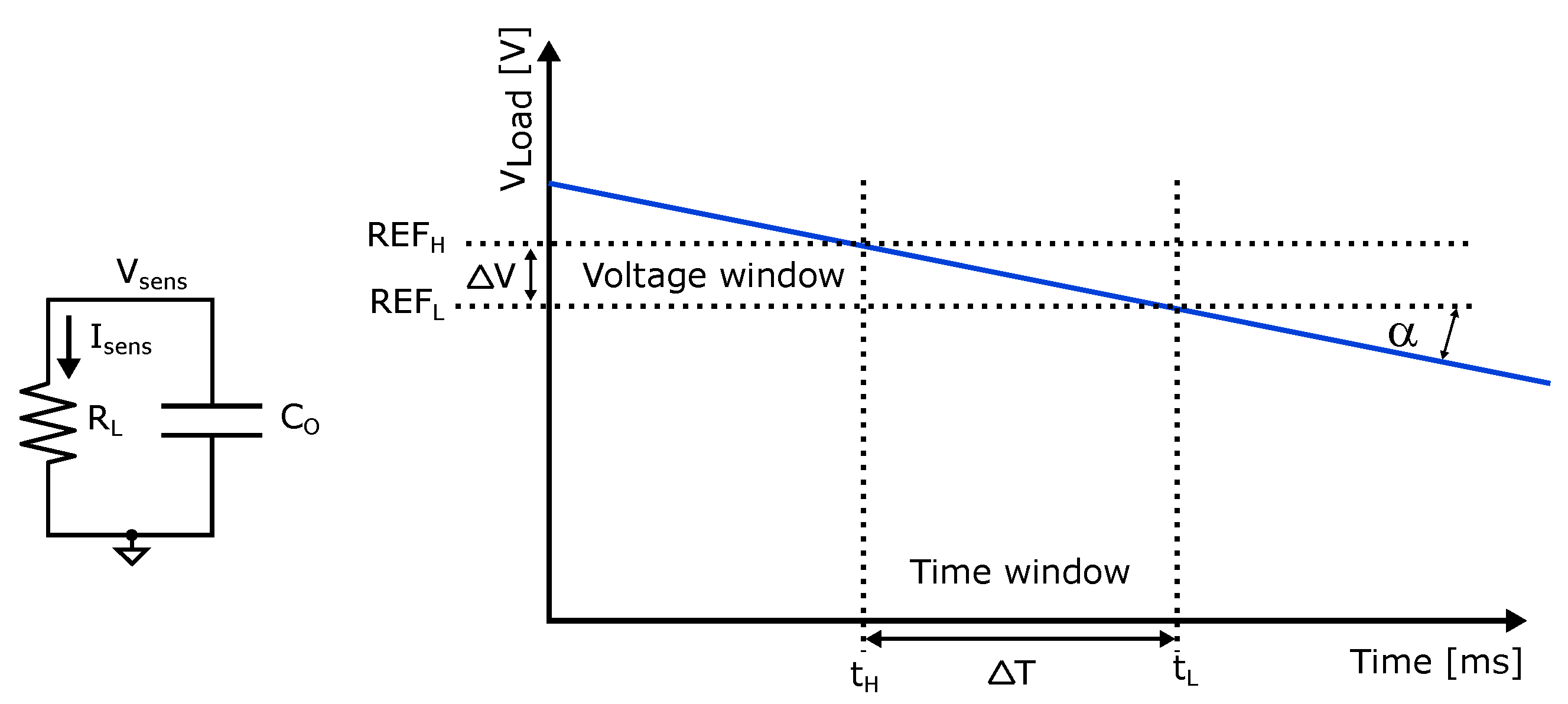
Preprints 86859 g004
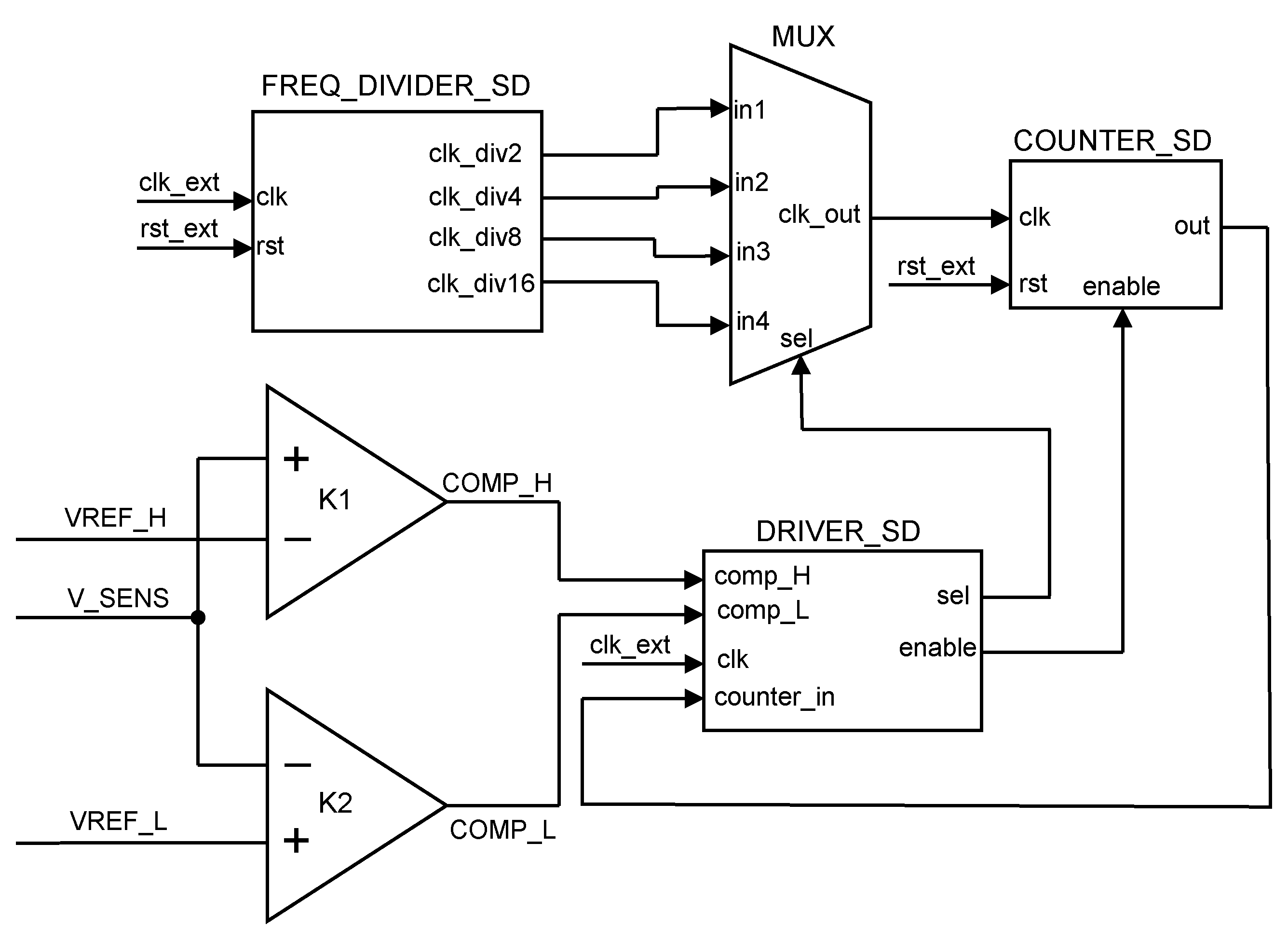
Preprints 86859 g005
Figure 5. Block diagram of the slope detector circuit
Figure 5. Block diagram of the slope detector circuit
Preprints 86859 g005
Preprints 86859 g006
Figure 6. Operation of the SD circuit
Figure 6. Operation of the SD circuit
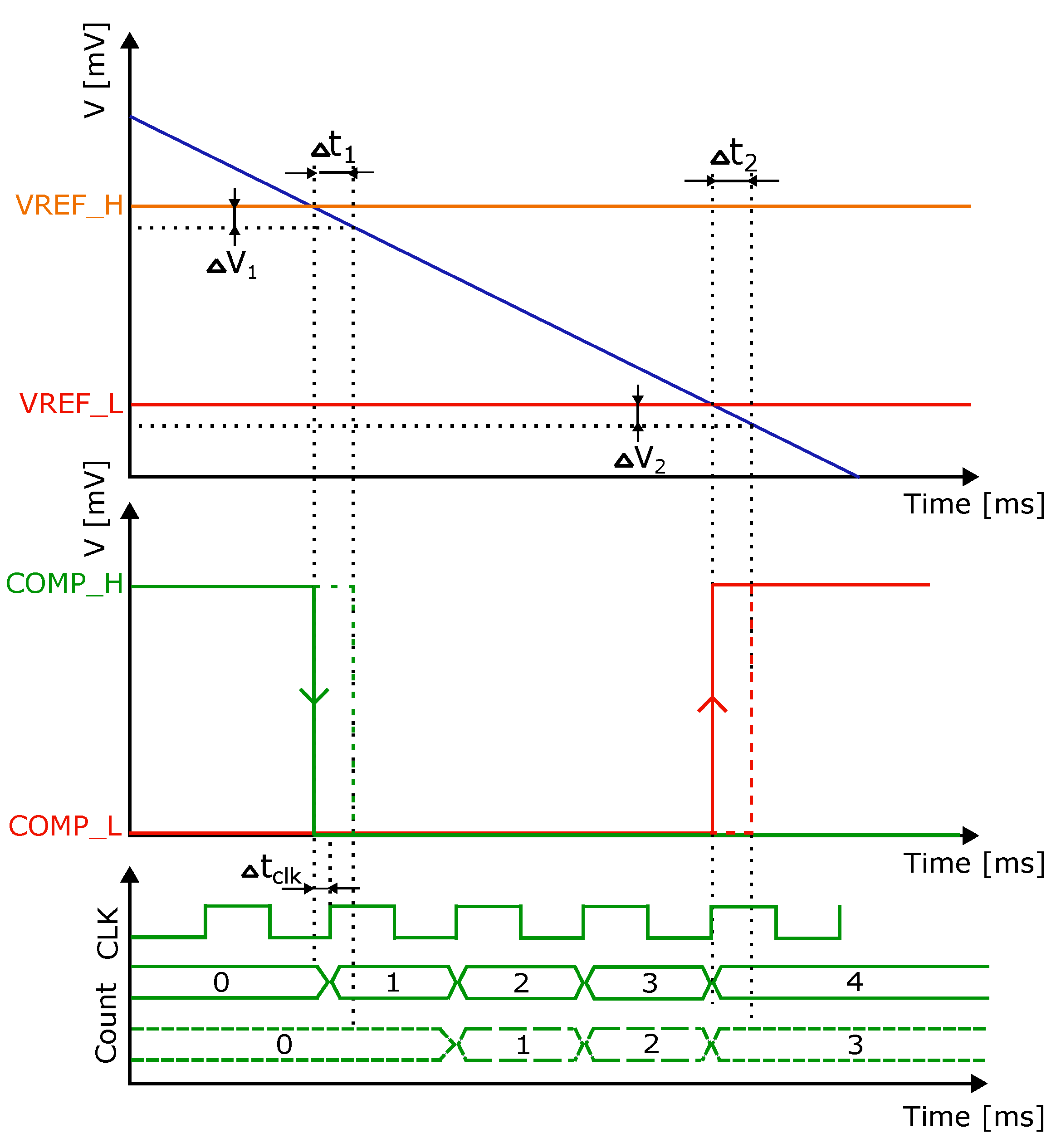
Preprints 86859 g006
Preprints 86859 g007
Figure 7. Dependence of the counter finite value on the sensed voltage slope
Figure 7. Dependence of the counter finite value on the sensed voltage slope
Preprints 86859 g007
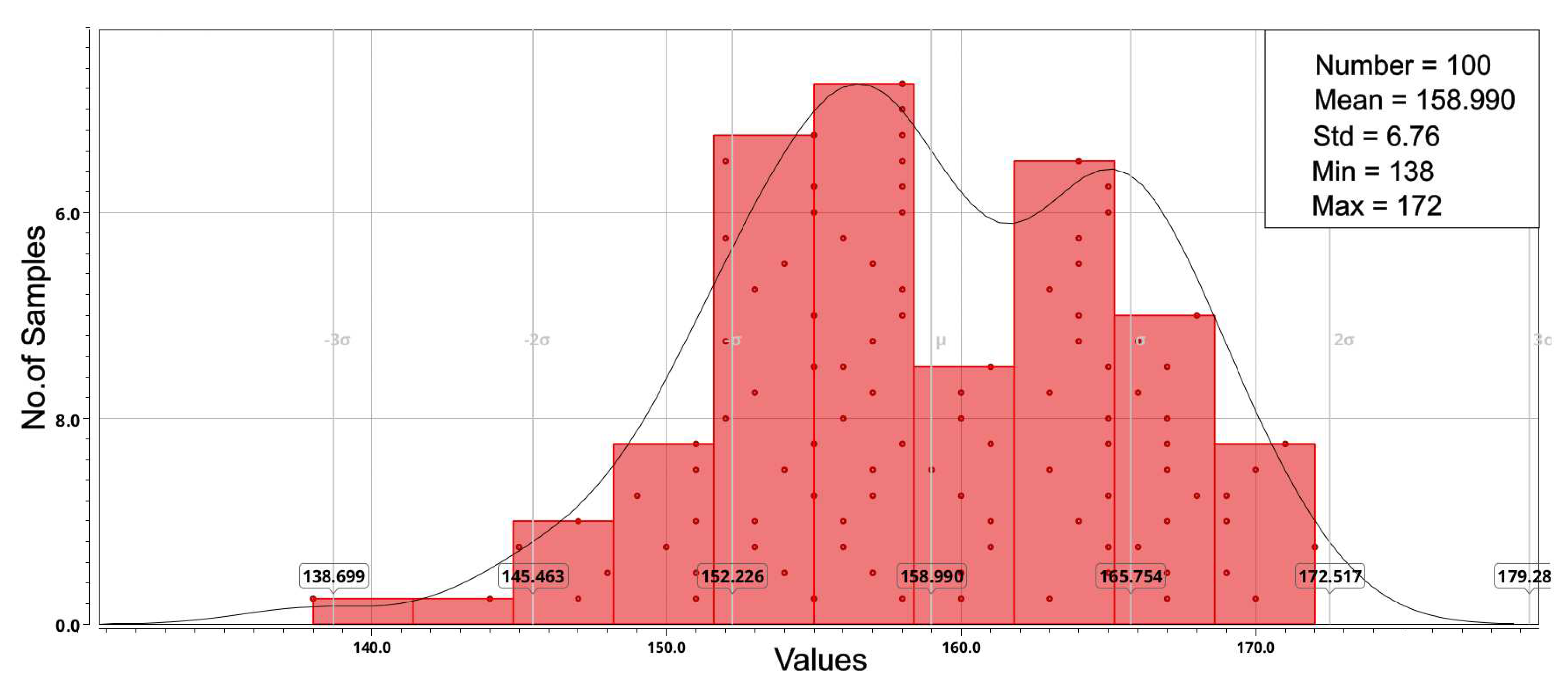
Preprints 86859 g008
Figure 8. Monte Carlo analysis: for slope=150 V/s
Figure 8. Monte Carlo analysis: for slope=150 V/s
Preprints 86859 g008
Preprints 86859 g009
Figure 9. Δ t c l k error for slope=150 V/s
Figure 9. Δ t c l k error for slope=150 V/s
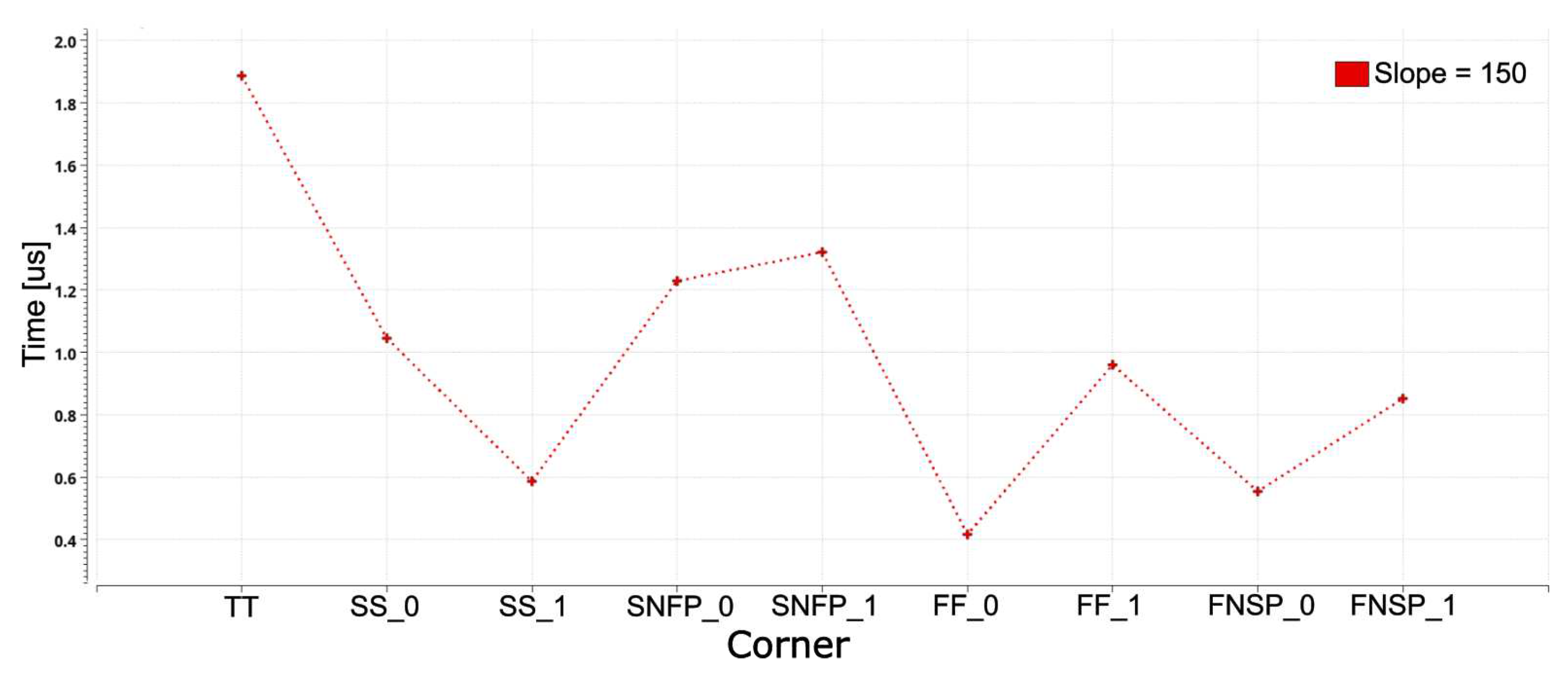
Preprints 86859 g009
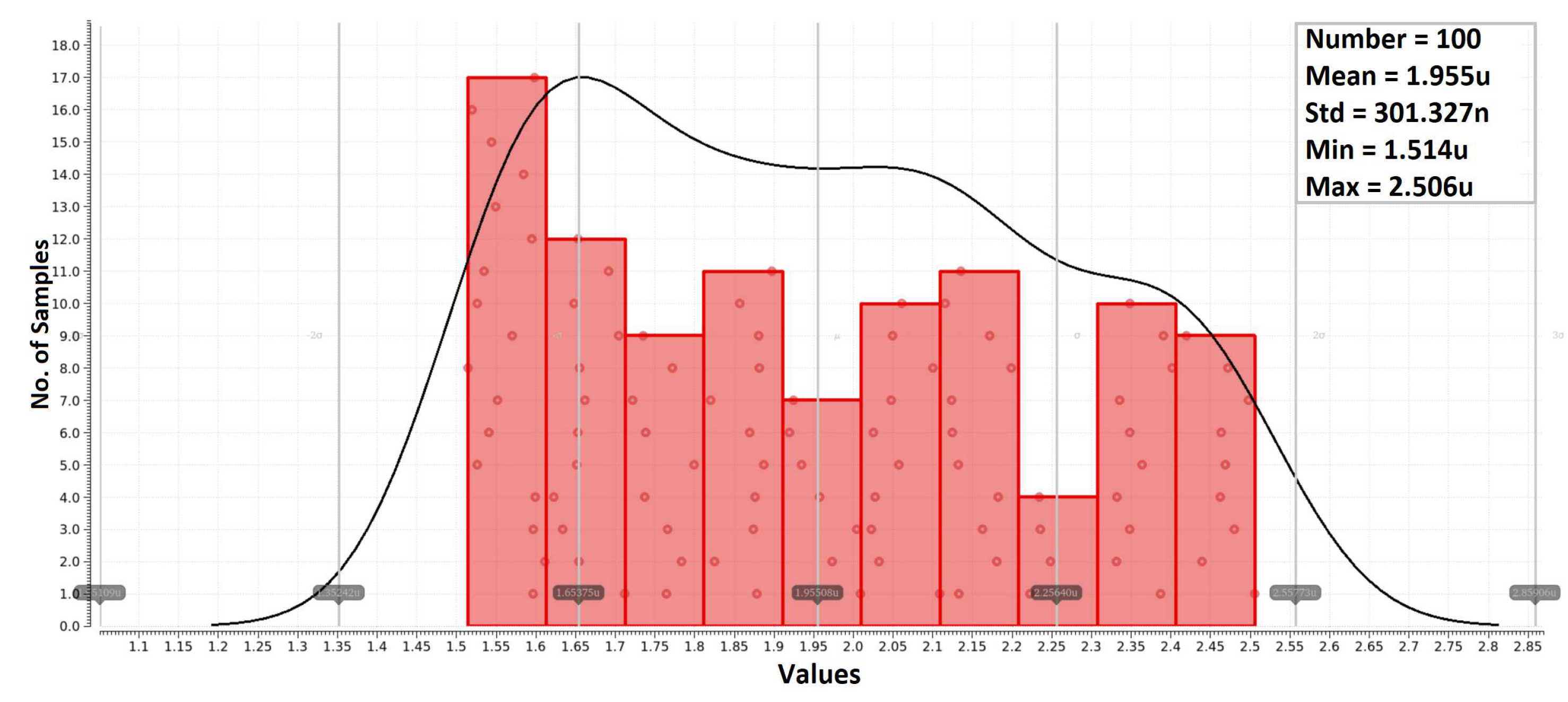
Preprints 86859 g010
Figure 10. Monte Carlo analysis: Δ t c l k error for slope=150 V/s
Figure 10. Monte Carlo analysis: Δ t c l k error for slope=150 V/s
Preprints 86859 g010
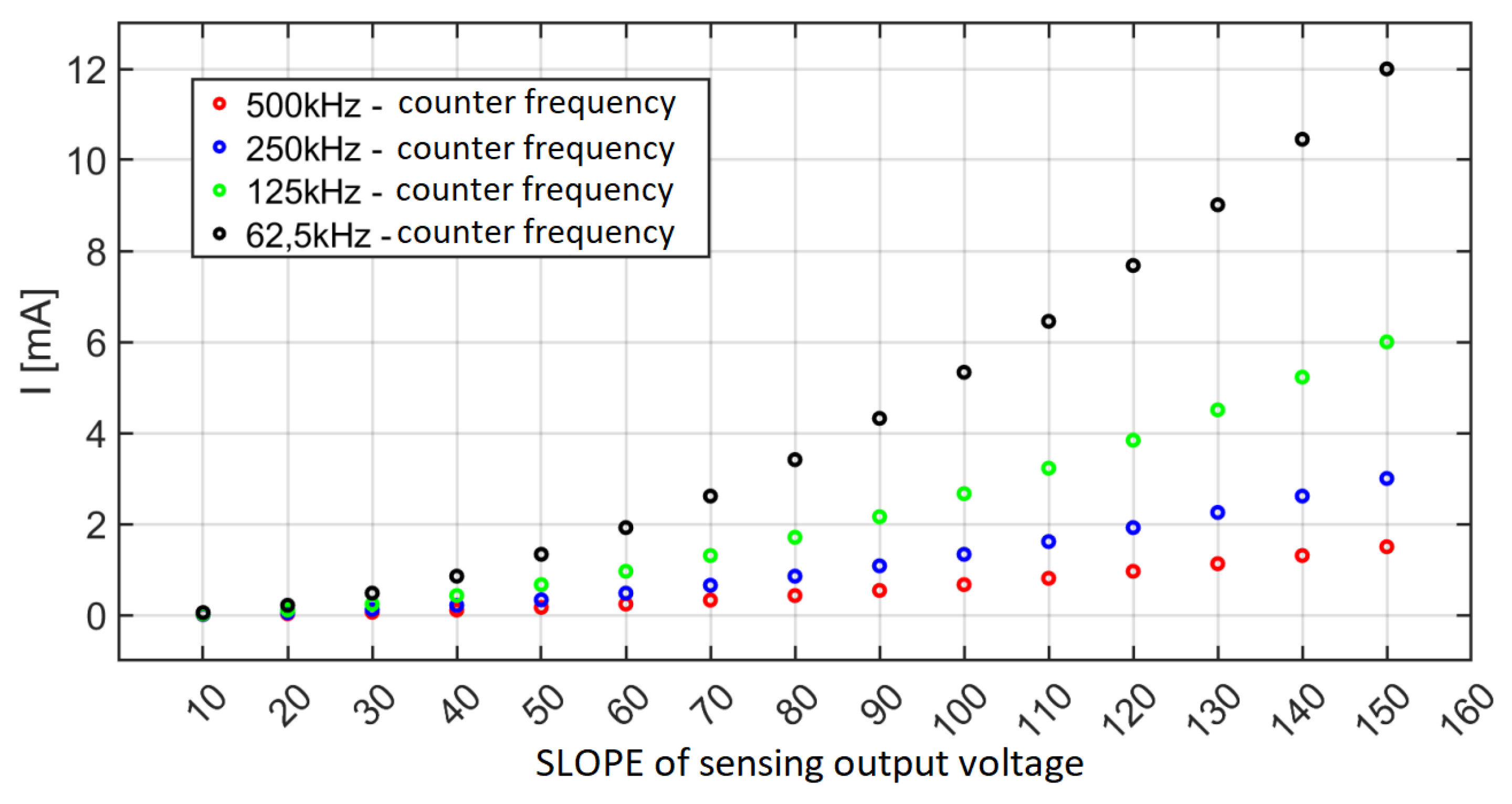
Preprints 86859 g011
Figure 11. Calculated current measurement error I[mA] for different values of counter frequency kept constant during measurement
Figure 11. Calculated current measurement error I[mA] for different values of counter frequency kept constant during measurement
Preprints 86859 g011
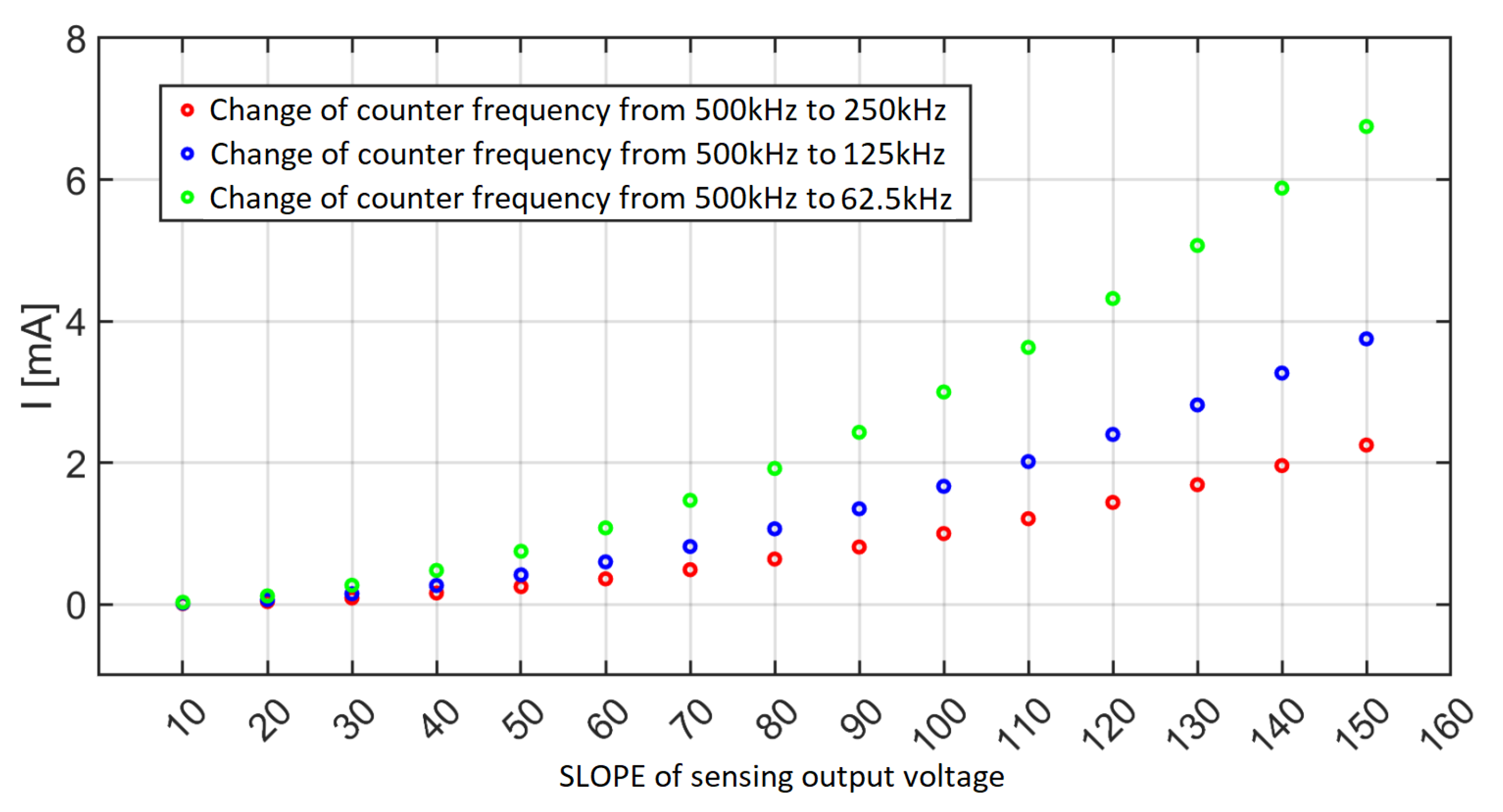
Preprints 86859 g012
Figure 12. Calculated current measurement error for counter frequency change within a certain range during measurement
Figure 12. Calculated current measurement error for counter frequency change within a certain range during measurement
Preprints 86859 g012
Preprints 86859 g013
Figure 13. Variations of time window over process corners
Figure 13. Variations of time window over process corners
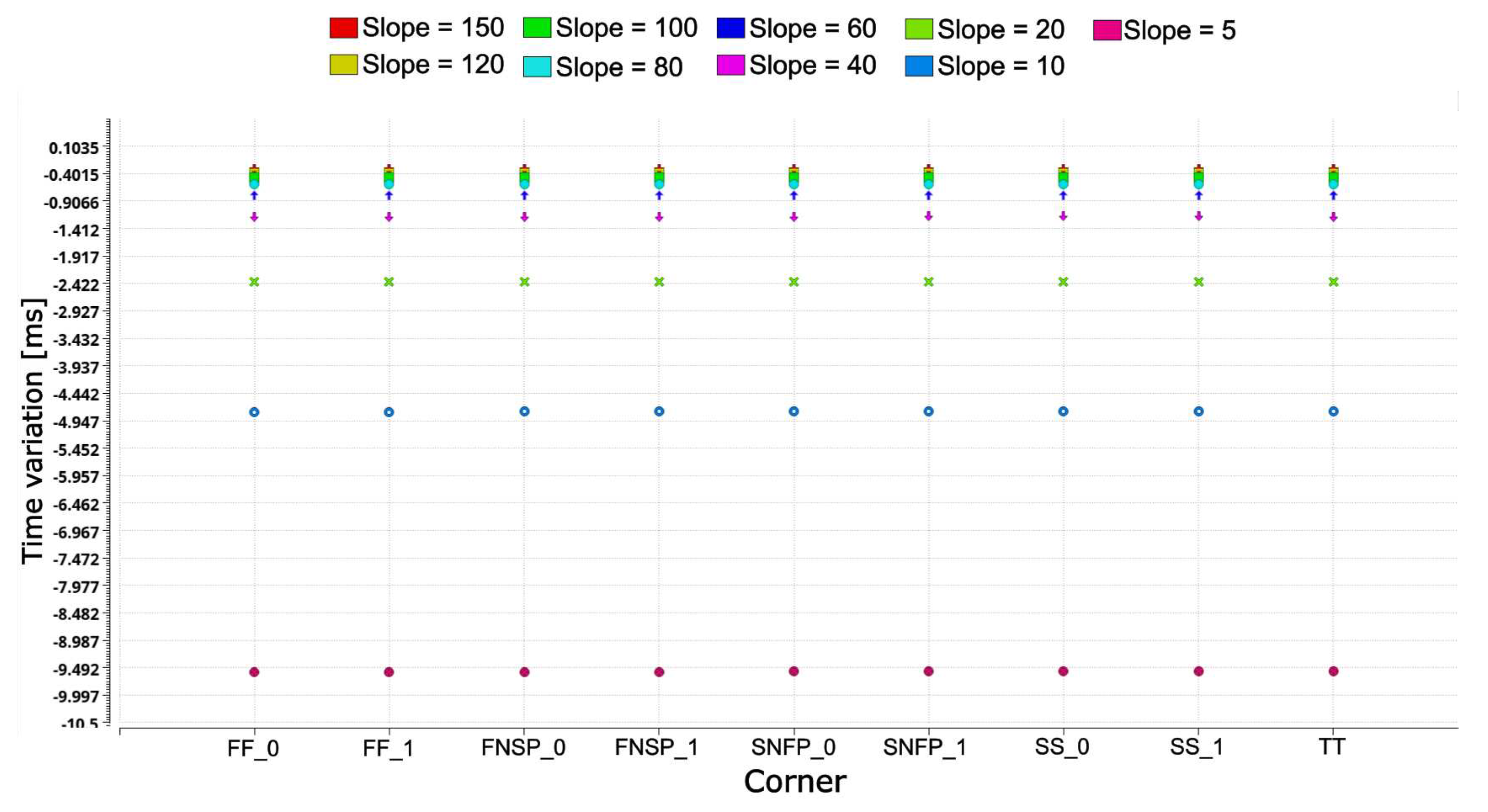
Preprints 86859 g013
Preprints 86859 g014
Figure 14. Monte Carlo analysis: Variations of time window
Figure 14. Monte Carlo analysis: Variations of time window
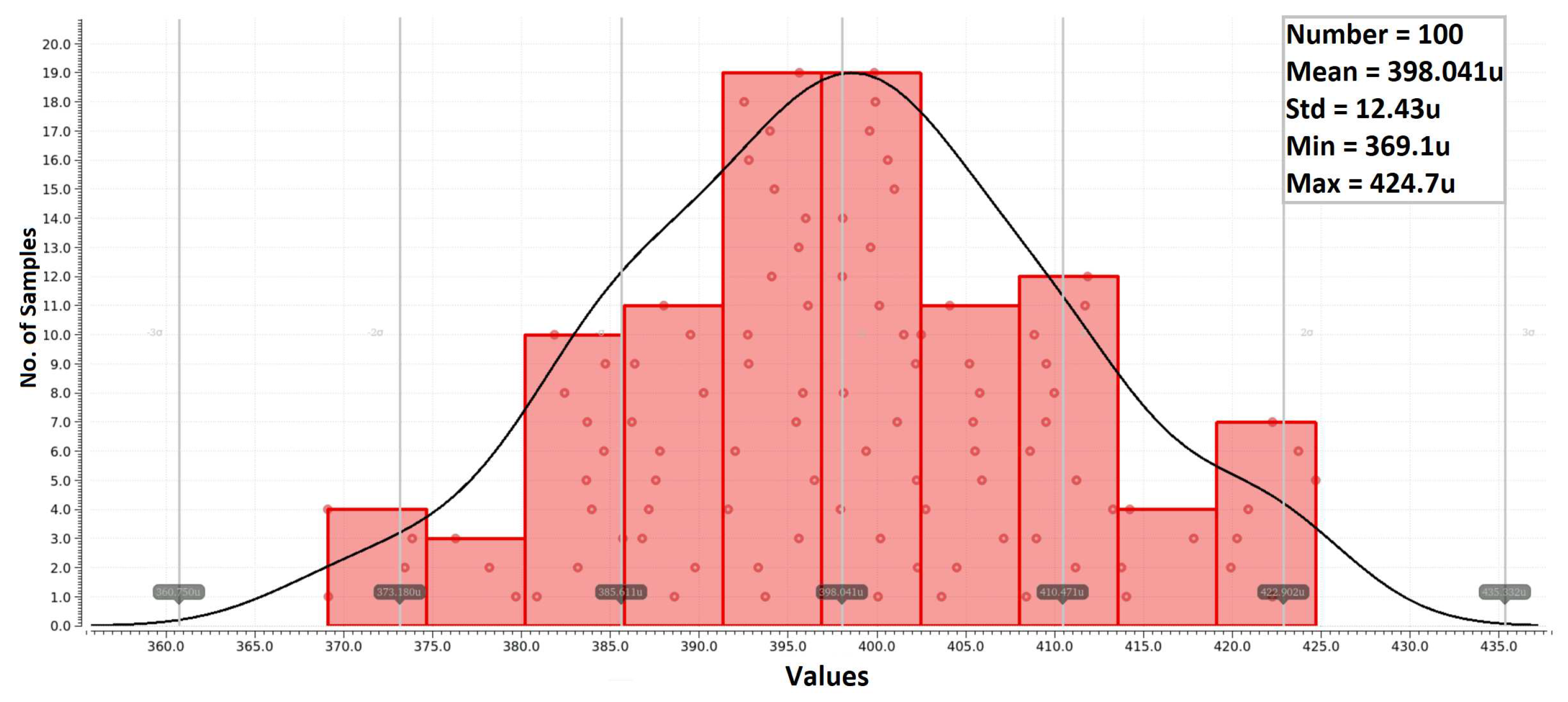
Preprints 86859 g014
Preprints 86859 g015
Figure 15. Layout of the developed slope detector
Figure 15. Layout of the developed slope detector
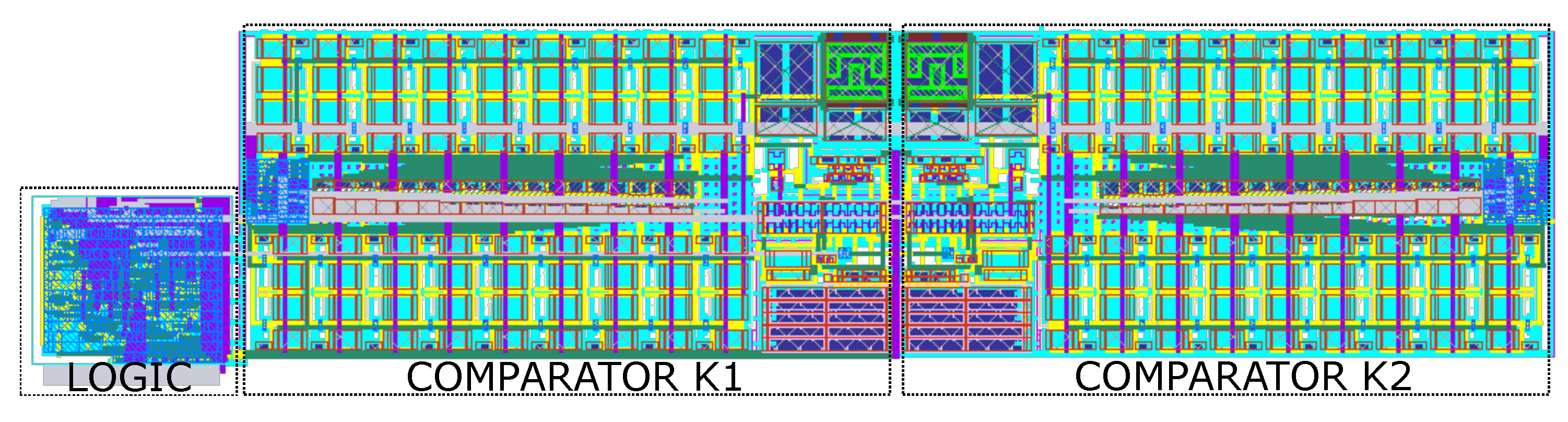
Preprints 86859 g015
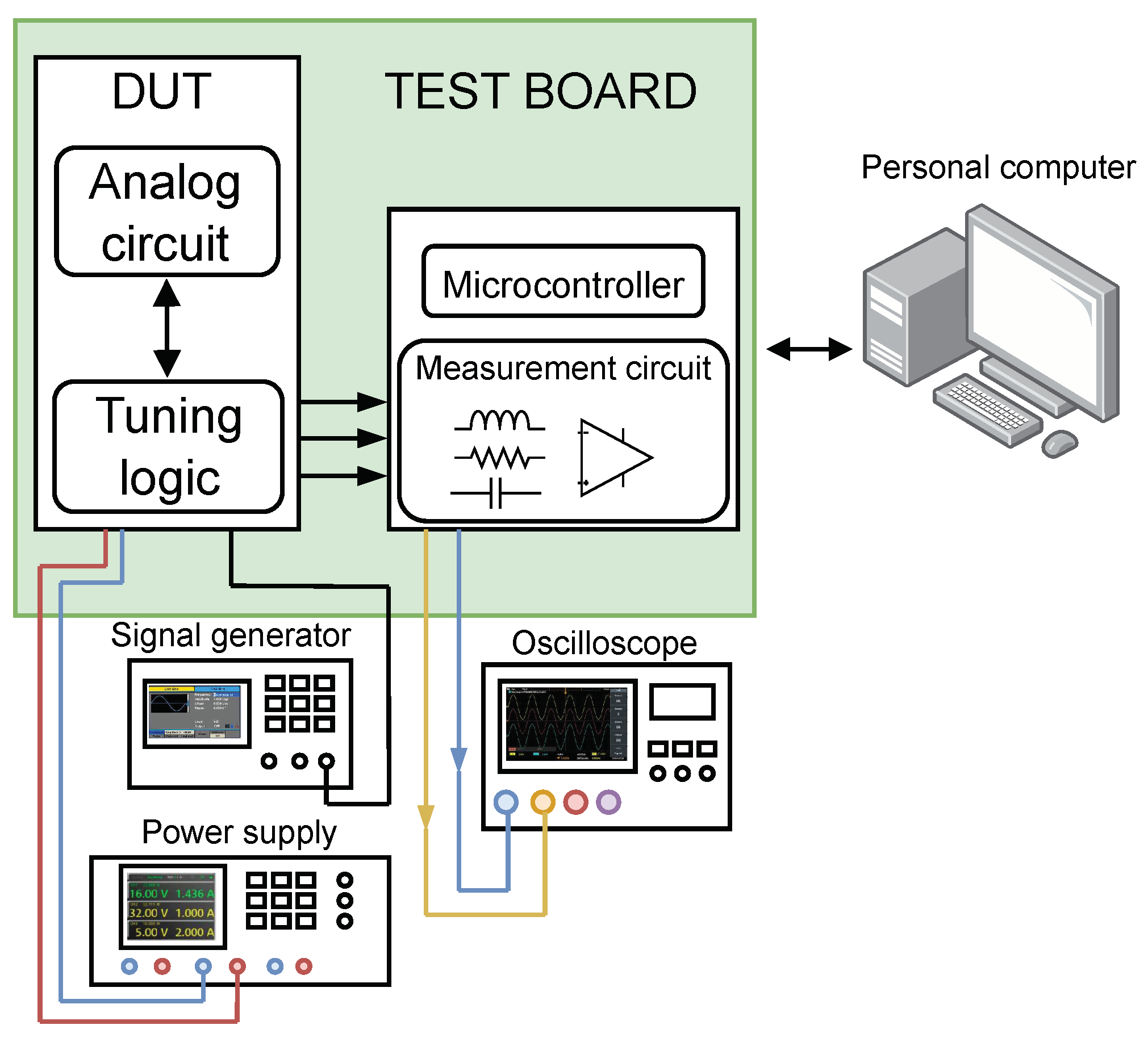
Preprints 86859 g016
Figure 16. Block diagram of measurement setup
Figure 16. Block diagram of measurement setup
Preprints 86859 g016
Table 1. Calculated conversion table between the switching frequency, the slope of sensed output voltage and the finite value of counter.
Table 1. Calculated conversion table between the switching frequency, the slope of sensed output voltage and the finite value of counter.
Counter Frequency [kHz]
SLOPE 500 250 125 62,5
10 3000 1500 750 375
20 1500 750 375 187.5
30 1000 500 250 125
40 750 375 187.5 93.8
50 600 300 150 75
60 500 250 125 62.5
70 428.6 214.3 107.1 53.6
80 375 187.5 93.8 46.9
90 333.3 166.7 83.3 41.7
100 300 150 75 37.5
110 272.7 136.4 68.2 34.1
120 250 125 62.5 31.3
130 230.8 115.4 57.7 28.8
140 214.3 107.1 53.6 26.8
150 200 100 50 25
Table 2. Measured relation between counter frequency, SLOPE of sensed output voltage, and finite value of counter.
Table 2. Measured relation between counter frequency, SLOPE of sensed output voltage, and finite value of counter.
SLOPE 500 250 125 Adaptive Frequency
10 3122 1338 826 808
20 1456 949 476 627
30 1169 645 333 555
40 911 438 241 510
50 774 389 194 470
60 623 332 164 438
70 534 256 133 407
80 481 241 122 395
90 443 210 111 379
100 389 193 98 350
110 348 175 88 332
120 322 134 82 318
130 298 149 76 302
140 272 136 69 277
150 246 124 64 249
Table 3. Time delay of comparators K1 and K2
Table 3. Time delay of comparators K1 and K2
COMP_L
Delay [us] 		COMP_H
Delay [us] 		Delay Error [ns]
Rising edge Falling edge Rising edge Falling edge COMP_L(Rising egde) - COMP_H(Falling edge)
Chip1 1.613 1.165 2.822 1.089 524
Chip2 2.054 1.1 1.89 1.170 884
Chip3 2 1.028 1.765 1.006 994
Chip4 1.9 1.034 1.983 1.056 846
Chip5 1.388 1.208 3.282 0.750 638
Table 4. Measurement results: hysteresis of comparator C O M P L across chip samples
Table 4. Measurement results: hysteresis of comparator C O M P L across chip samples
COMP_L
HYS - SLOPE 10 HYS - SLOPE 150
Rising edge Falling edge Rising edge Falling edge
HYS [mV] Time [us] HYS [mV] Time [us] HYS [mV] Time [us] HYS [mV] Time [us]
Chip1 15.2 1320 19.2 1680 7 36 14 87
Chip1 10.4 944 14.8 1340 9.6 64 17.2 110
Chip3 10 840 16.4 1370 3.2 256 9.6 780
Chip4 10 836 15.6 1270 8.8 49 17.2 106
Chip5 6.4 560 9.6 860 5.5 27 12.8 84
Table 5. Measurement results: hysteresis of comparator C O M P H across evaluated chip samples
Table 5. Measurement results: hysteresis of comparator C O M P H across evaluated chip samples
COMP_H
HYS - SLOPE 10 HYS - SLOPE 150
Rising edge Falling edge Rising edge Falling edge
HYS [mV] Time [us] HYS [mV] Time [us] HYS [mV] Time [us] HYS [mV] Time [us]
Chip1 20 1620 13.6 1250 20.8 140 11.6 74
Chip1 11.2 880 5.6 520 12.4 84 3.6 24
Chip3 7.6 700 2.4 160 10 62 1.6 8
Chip4 14 1200 10 920 16 101 7.6 50
Chip5 8 680 6 490 11.2 70 4 20
Table 6. Error in the finite counter value for the different switching frequency and slope values.
Table 6. Error in the finite counter value for the different switching frequency and slope values.
SLOPE 10 SLOPE 150
500kHz 250kHz 125kHz 500kHz 250kHz 125kHz
Chip1 35 17.5 8.75 19 9.5 4.75
Chip2 212 106 53 20 10 5
Chip3 340 170 85 124 62 31
Chip4 42 21 10.5 0.5 0.25 0.125
Chip5 35 17.5 8.75 3.5 1.75 0.875
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated