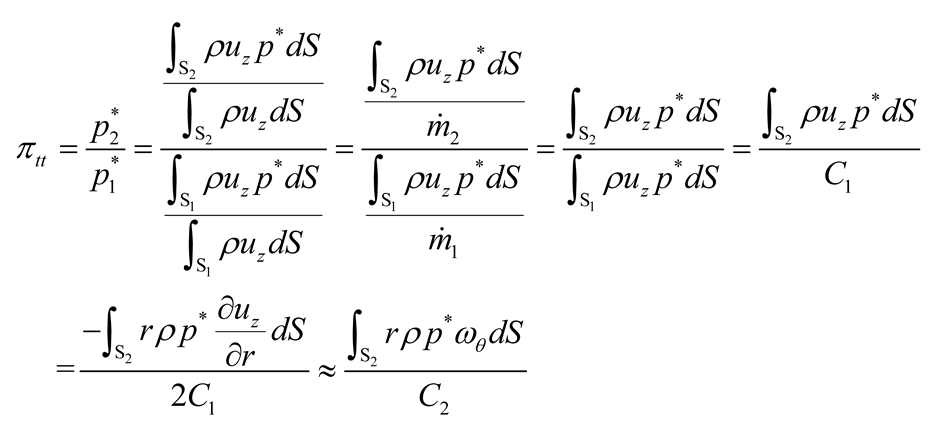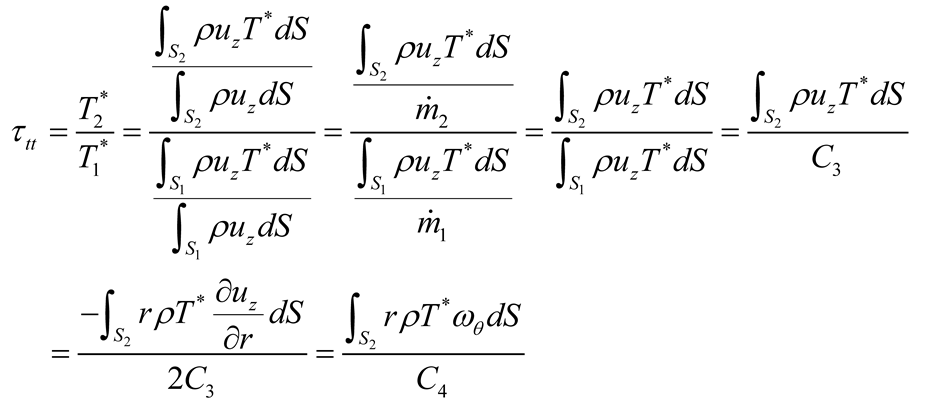New Insights into Flow for a Low-Bypass-Ratio Transonic Fan with Optimized Rotor

In order to balance the conflicts among mass flow rate, total pressure ratio, adiabatic efficiency and stall margin in a low-bypass transonic fan, the optimization of the rotor blade is implemented in this study. An advanced 3D optimization design system is adopted, and flow diagnostic methods based on vorticity dynamics are employed to discuss the flow field. Results indicate that by controlling the blade camber line curvature, significant improvements in the aerodynamic performance for the fan stage are achieved, the total pressure ratio is increased by 1.90%, while the adiabatic efficiency and mass flow rate are increased by 4.45% and 5.82%, respectively. Vorticity diagnosis suggest that there exists a close link between performance parameters and vorticity parameters in the axial fan/compressor, both azimuthal vorticity and boundary vortex flux have significant influences on the stage performance. Moreover, the boundary layer separation is accompanied by the spike of entropy and static pressure, while the derivation/gradient of these flow parameters would also suffer drastic changes under the effect of shock wave. The vorticity parameters could provide detailed flow information about the on-wall flow with high accuracy, which provides the researchers with a novel method for the turbomachinery aerodynamic design and analysis.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

As a highly integrated flow system, the overall performance of modern aircraft engines depends on the excellent matching of various functional parts, and every working unit is required to serve the whole system. Therefore, being the first part of a turbofan engine, the fan stage needs to be designed with advanced technologies to enhance its loading and efficiency while extending its stall margin. Under this background, designing theories and techniques are being proposed all the way along the development line of turbomachinery while numerous design platforms have been built over the last few decades. Quasi-3D blade design and flow analysis technique is the foundation of modern 3D design techniques, and its origin could be traced back to the 1950s when Wu [1] proposed the concept of S1/S2 stream surfaces. On the basis of this theory, a lot of solution methods are put forward with the streamline curvature method and the through-flow matrix method as representatives [2,3]. These quasi-3D blade design techniques could provide favorable initial schemes for further design, but the inevitable dependency on experimental data has restricted their further development. On the other hand, with the development of computer science and computational fluid dynamics, modern 3D design and analysis techniques based on RANS methods are developed, with which the disadvantages of quasi-3D design techniques are settled successfully. Furthermore, the application of 3D design techniques in turbomachinery has prompted the emergence of a number of advanced theories including swept and leaned blade configurations. One of the typical design is the low-noise transonic fan QF-12 which adopted the concept of swept blade [4,5]. Similarly, Wennerstorm [6,7] introduced swept blade into the design of a high through-flow transonic fan stage and received favorable effects, while a series of experiments were done by the Wright-Patterson Air Force Base in order to investigate the influence of blade sweep on the performance of the compressor [8,9]. Denton et al. [10] studied the effects of leaned and swept blade on a transonic fan, researchers in China have also conducted relevant studies [11,12].

It is obvious that the geometrical feature of blade passage has a significant influence on the aerodynamic performance of fan/compressor. However, restricted by the deficiency of design techniques, early investigations in blade optimization could only concentrate on one or few geometry features, which are not enough to satisfy the demands of practical engineering problems. Consequently, the design systems that have high efficiency and strong fault-tolerant ability are currently in great need. Many investigators have been devoted to this problem and lots of contributions have been made. Optimizations for the famous NASA Rotor 37 blade passage was done by Benini [13] and Jang et al. [14] respectively, while the NASA Rotor 67 blade passage was optimized by Lian et al. [15] using a multi-objective optimization method, the stage weight was decreased and the total pressure ratio was increased through their study. One of the other challenges that highly-load compression systems are faced with is the maintenance of the stall margin (SM>10%~15%). In the optimization work by Ellbrant et al. [16,17], a trade-off between efficiency and stall margin was made in a transonic compressor stage. Besides, the adiabatic efficiency for the NASA Rotor 67 blade was increased by 2% over the entire operating range by the redesign work conducted by Oyama et al. [18]. Recently, Mark et al. [19,20,21,22,23,24,25] has established a novel turbomachinery aerodynamic optimization design system. Based on the control of curvature for the blade geometry, the optimization system could couple the optimization and the CFD solver successfully, which was able to prove its outstanding engineering practicability in engineering application.

The formation and development of vortex structures is inevitable during the evolution of viscous flows in the fan/compressor passage, and these flow configurations are closely linked with the aerodynamic performance of the fan/compressor. The vortex structures could give important clues about the flow features in aircraft engines and work as a guidance for aerodynamic optimizations. Vorticity dynamics diagnostic methods are developed to investigate the flow according to the derivative/gradient of flow parameters [26,27]. The vorticity dynamics diagnostic method, which focuses on crucial physical principles and distinctive parameters like the boundary vorticity flux (BVF), vorticity/skin-friction vectors, and azimuthal vorticity, is an insightful aerodynamic analysis/design technique and could offer the designer completely original concepts outside of conventional design principles [28,29,30]. Investigations in this technique have obtained valuable results and further studies are expected.

There are lots of factors that could affect the performance of the fan/compressor, and the conflict between these factors would become particularly pronounced when it comes to a low bypass-ratio transonic fan stage whose hub-to-tip ratio is relatively low. Hence a proper balance of the performance index is of great significance to maximize the overall performance of the fan stage. With the challenges above, this study implements the optimization of the rotor blade for a low bypass-ratio transonic fan under stage flow conditions. The aim of the design is to raise the fan's mass flow rate and total pressure ratio when its efficiency and stall margin remain unchanged. To acquire a comprehensive of the process for transonic flow control, vorticity diagnostic methods are applied to discuss the flow. In this paper, the optimization process will be described in detail and the origin of various flow structures and their influence will be interpreted in depth using vorticity diagnostic methods.

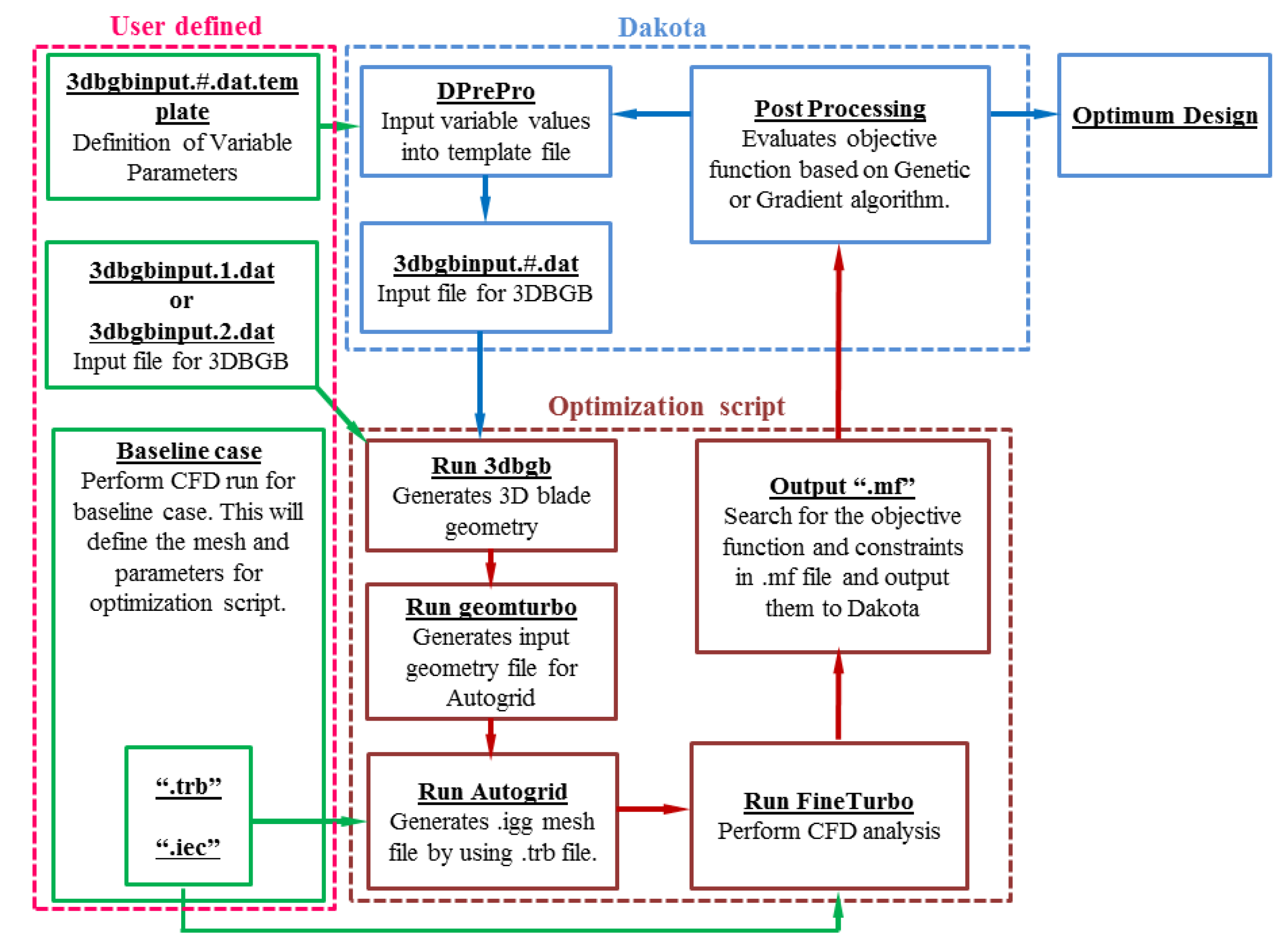
2. Optimization System

The turbomachinery aerodynamic optimization design system employed in this paper is developed by Mark et al. [19,20,21,22,23,24,25] under the Linux framework. It is made up of Shell scripts, Python scripts and Fortran executable files. The schematic diagram of the optimization system is shown Figure 1. There are three main parts in the design system: the user-defined module, the optimization script module and the Dakota optimization module. The user-defined module is executed only once in each optimization. Its main goal is to parameterize the geometry and to define the boundary conditions as well as the optimization variables using the journal files it contains. Once the optimization target is defined, the optimization script would execute the three-dimensional blade geometry builder (3DBGB) code automatically to produce the blade. The generated 3D blade geometry is in the form of the geometry input file *.geomTurbo and would get meshed by the grid generator called Autogrid5. Then, the mesh is transmitted to the CFD solver Fine/Turbo and the calculation results are collected and sent to Dakota. After each optimization step, Dakota would analyze the results automatically and extract the value of the objective function. Furthermore, based on the results from the last optimization step, Dakota would decide on the parameters in the next scheme using genetic algorithm so as to keep the optimization system running continuously.

In order to ensure the smoothness of the blade, cubic B-spline is employed when building the 3D geometry. Meanwhile, the geometrical parameters of the blade such as the curvature of the camber line and the inlet/outlet angles are modified so that diversified blade configurations could be produced. Additionally, the matching of the flow characteristics between different blade rows is also taken into consideration in the optimization system. Specific explanations about the geometric modeling process could be found in Refs. [19,20,24], the optimization process is also expounded in Ref. [19], open executables codes of the optimization modules are available online (http://gtsl.ase.uc.edu/3DBGB/).

Considering the features in both prediction precision and numerical stability, the Spalart-Allmaras turbulence model is chosen for the numerical simulations in the present study. 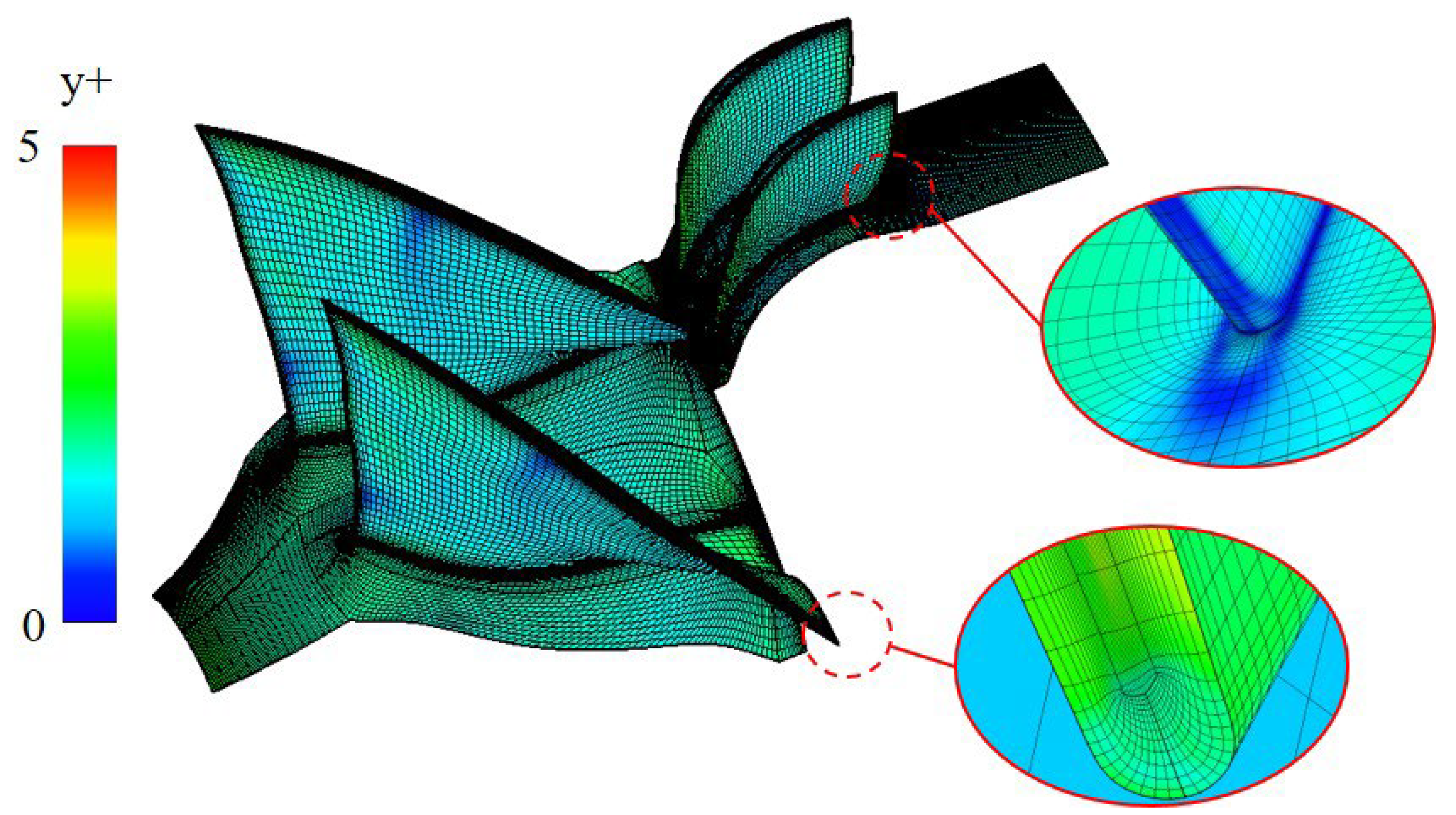The blade geometry in the baseline case (denoted as Baseline) is designed by a Turbomachinery Axisymmetric design code (known as T-AXI) [25] and the geometry generator 3DBGB [21], while the flow path is inherited from a transonic fan which has been tested by experiments [31]. Geometry and meshes for the baseline stage are displayed in Figure 2. Although the optimization is merely limited to the rotor blade, the flow in the whole stage is calculated and the total grid number is approximately 1.25 million. Furthermore, the y+ of the first grid cell is guaranteed to be less than 5 in order that the boundary layer’s flow details could be depicted accurately. The total pressure, total temperature, and the flow direction are specified at the simulation's inlet, and the calculated domain's outlet is subject to static pressure set by simple radial equilibrium. In addition, the solid boundaries are subject to the adiabatic non-slipping condition. The mixing-plane method is employed to transmit flow parameters between blade rows. Main design parameters for the fan stage are presented in Table 1. The research object of this paper is to meet the technical requirements of a new aero-engine, which needs to improve the flow rate and total pressure ratio at the design point while remaining the geometric dimension of the fan meridian passage unchanged.

3. Rotor Blade Optimization

There exist two steps in the process of rotor blade optimization. The first is to optimize the camber line of the rotor blade (denoted as Camber_Opt) and the next is to match the leading edge blade angles (denoted as Angle_Opt).The curvature of the camber line is established by the cubic B-spline formula according to numerous control points in the current optimization system, and the camber line is adjusted by modifying the variations of these control points. Since the curvature of a curve is numerically approximate to its second derivative, the curvature obtained here could be considered equivalent to the second derivate of the camber line. That is to say, the camber line could be acquired through the double integration of the defined curvature, which is just the way we do it in this study. In consideration of computational time and efficiency, five spanwise positions are chosen as the optimization plane. In addition, four variables are defined in each optimization plane. They represent the chordwise location of the control point and the curvature values for the camber line at the specified location. The constraint conditions are as follows:

Maximize: adiabatic efficiency η^* on the highest efficiency point for fan-stage;

Constraints: mass flux

\dot{m}

≥

\dot{m}

(baseline), total pressure ratio π^* ≥ π^*(baseline);

Design Variables: 20 variables on 5 spanwise sections, each section has 3 curvature control point values and 1 position value for one of the control points;

Genetic Algorithm (GA) parameters: the maximum iteration is 100, and the population size is 12.

In view of the error of inlet angles, as an empirical parameters, which is inherent and inevitable in 3D blade design, the optimization of the leading edge blade angles is essential in order to ameliorate the capacity of the fan stage in organizing viscous fluid. Similarly, following are this optimization constraint conditions:

Maximize: adiabatic efficiency η^* on the highest efficiency point for fan stage;

Constraints: mass flux

\dot{m}

≥

\dot{m}

(baseline), total pressure ratio π^* ≥ π^*(baseline);

Design Variables: 5 variables defining the added metal angle Δβ at blade leading edge;

Genetic Algorithm (GA) parameters: the maximum iteration is 100, and the population size is 12;

Constants: all other parameters from the former optimization step.

A comparison of the aerodynamic performance achieved by different optimization strategies is shown in Table 2. The fan's aerodynamic performance is greatly enhanced by the two optimization steps. The adiabatic efficiency and the total pressure ratio of the fan stage are improved by 3.87% and 2.38% in the first step of optimization by Cam-ber_Opt respectively. Additionally, the mass flow rate is increased by 4.14%, which shows that the fan passage's capacity for organizing viscous fluid is significantly improved and the shear/expansion flow is diminished in the boundary layer. Based on Camber_Opt, the Angle_Opt is adopted to ameliorate the fan stage’s aerodynamic performance. According to Table 2, the stage pressure ratio of the final design reaches 2.15, while the mass flow rate and the adiabatic efficiency are 9.45kg/s and 0.891, respectively. With these results, it is safe to conclude that a more rational structure of the flow is realized by the optimizations of the camber line and the inlet angle, hence realizing better organization of the viscous fluid while enhancing the overall performance of the whole stage.

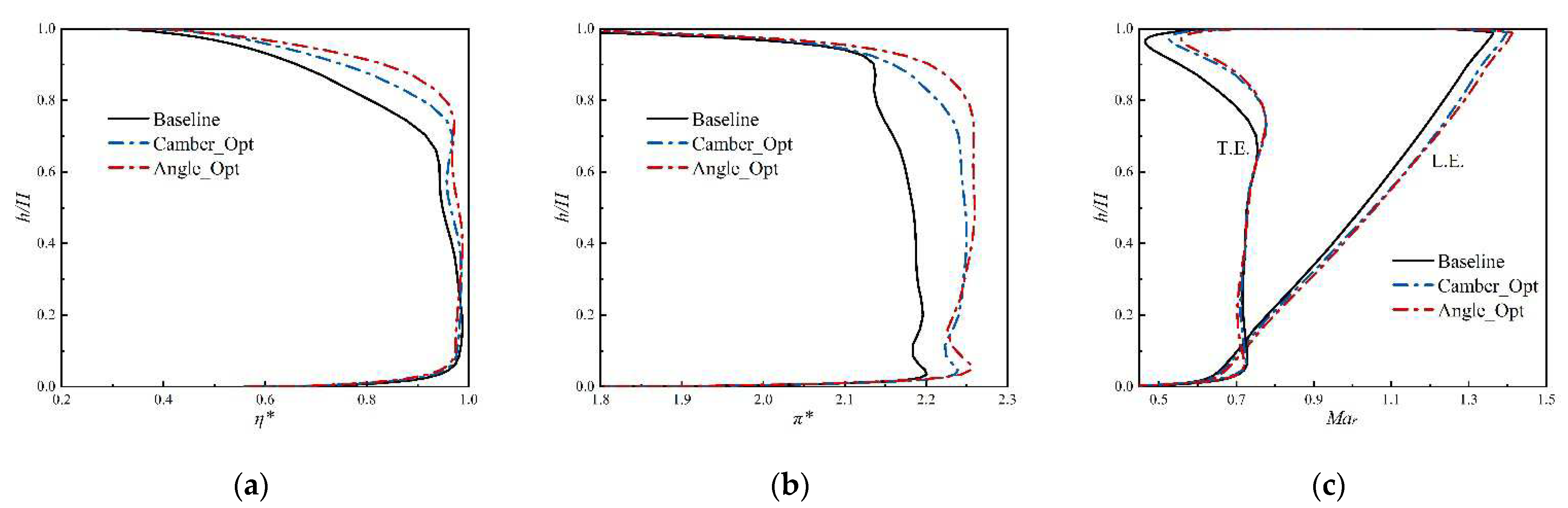
Figure 3 displays the spanwise distributions of several aerodynamic characteristics at the rotor blade outlet. Discussion about these parameters could help figure out the specific contribution rotor optimization has made. Figure 3a shows how to improve the camber line to significantly increase the adiabatic efficiency of the rotor blade, particularly in regions where h/H > 60%. The efficiency can also be increased even further by matching the leading edge angles, but the improvement is still marginal. These results suggest that the camber line optimization could reduce the shear flow downstream while weakening the shock wave intensity in the rotor channel, whereby lowering the loss caused by the shock wave and the following boundary layer separation.

The total pressure ratio of the rotor blade is evidently improved in the regions be-tween 20%H/h and 90%H/h following the camber line adjustment, according to the total pressure ratio described in Figure 3b compared to the baseline case. Moreover, Angle_Opt could further increase the pressure rise capability of the rotor blade on the basis of Camber_Opt. It can be concluded from these results that aerodynamic optimization design method in this paper is a highly recommendable one through which higher aerodynamic loading level could be obtained while maintaining the high efficiency.

As shown in Figure 3c, the increased axial flow velocity in the top half of the rotor blade is primarily responsible for the improved through-flow capacity of the fan stage. On the one hand, the increment of M_ar keeps rising along the blade's leading edge from hub to shroud. On the other hand, M_ar's apparent improvement is only seen from 60% H/h to the blade's trailing edge. Abovementioned phenomena indicate that rotor optimization mainly works on the transonic region at the upper half of the blade, i.e., the positions where the shock wave occupy. All these results have proved the optimization of the rotor blade to be an effective method to improve the aerodynamic performance of the fan stage.

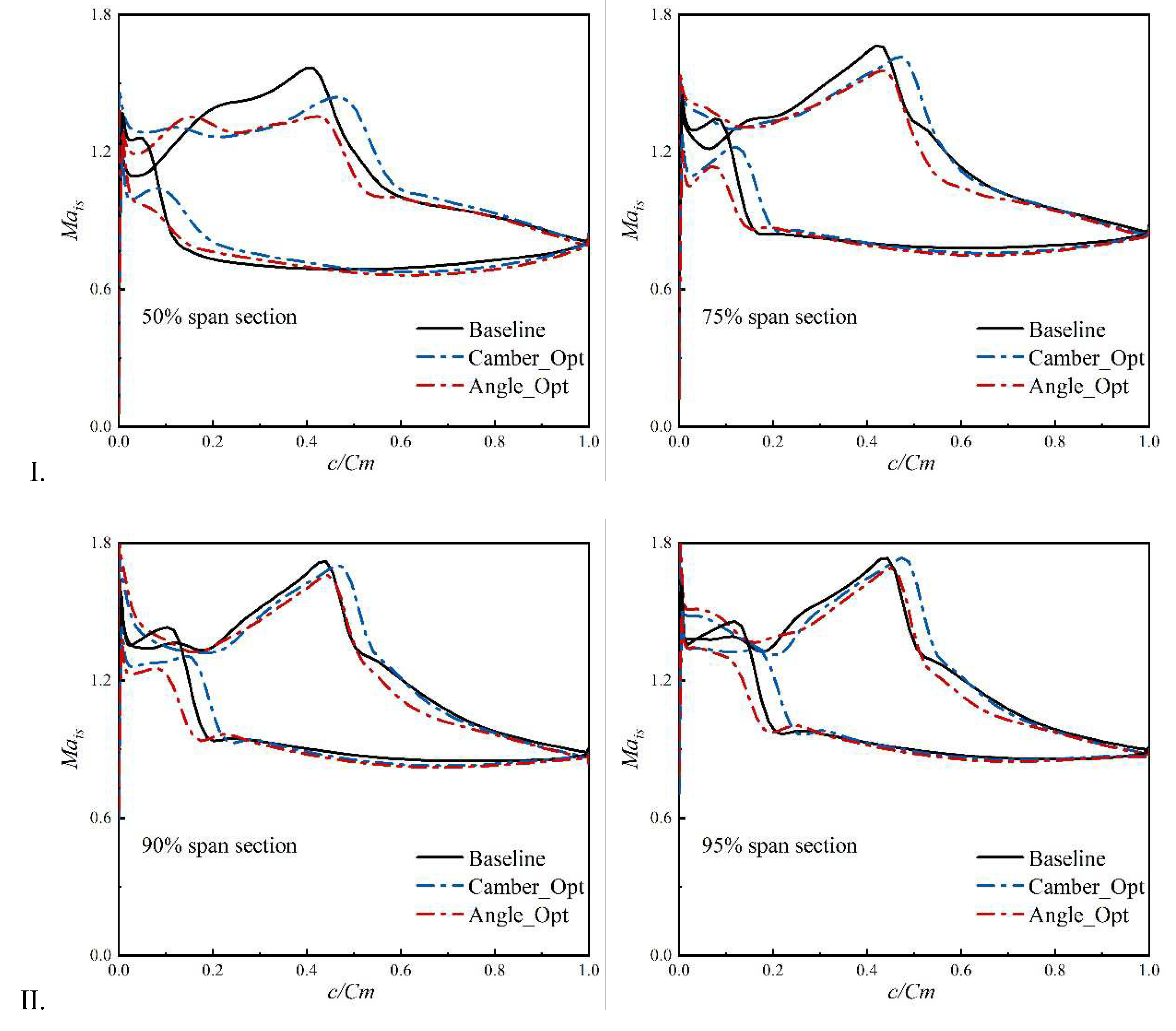
As we know, the transonic fan stage's aerodynamic performance is primarily influenced by the intensity and structure of the shock wave. The comparison of the on-wall isentropic Mach number for different cases is shown in Figure 4 in light of the fact that the shock wave's characteristics would be well mirrored by the isentropic Mach number. Results reveal that the position for the peak of M_is gets closer to the downstream after Camber_Opt, indicating that the shock wave on the blade suction surface is delayed. What’s more, the delay of the shock wave in the rotor blade passage could expand the throttling range of the transonic fan, which highlights the advantage of the design technique. After camber line optimization, the maximum value of M_is is also reduced, indicating that the shock wave's intensity has also been weakened. One of the other notable defections in the baseline configuration is the deviation of incidence angle which presented as the crossing of the M_is line at the blade leading edge. This problem is solved completely by Angle_Opt. In fact, although the position of the shock wave in Angle_Opt is moved slightly upstream compared with Camber_Opt, the location of the shock wave is still in the downstream in comparison with the baseline case, and the flow characteristics at the blade leading edge are improved greatly. In fact, near the rear region of the shock wave, the isentropic Mach number is decreased by Angle_Opt, which indicates that the rotor would have a better pressure rise capability.

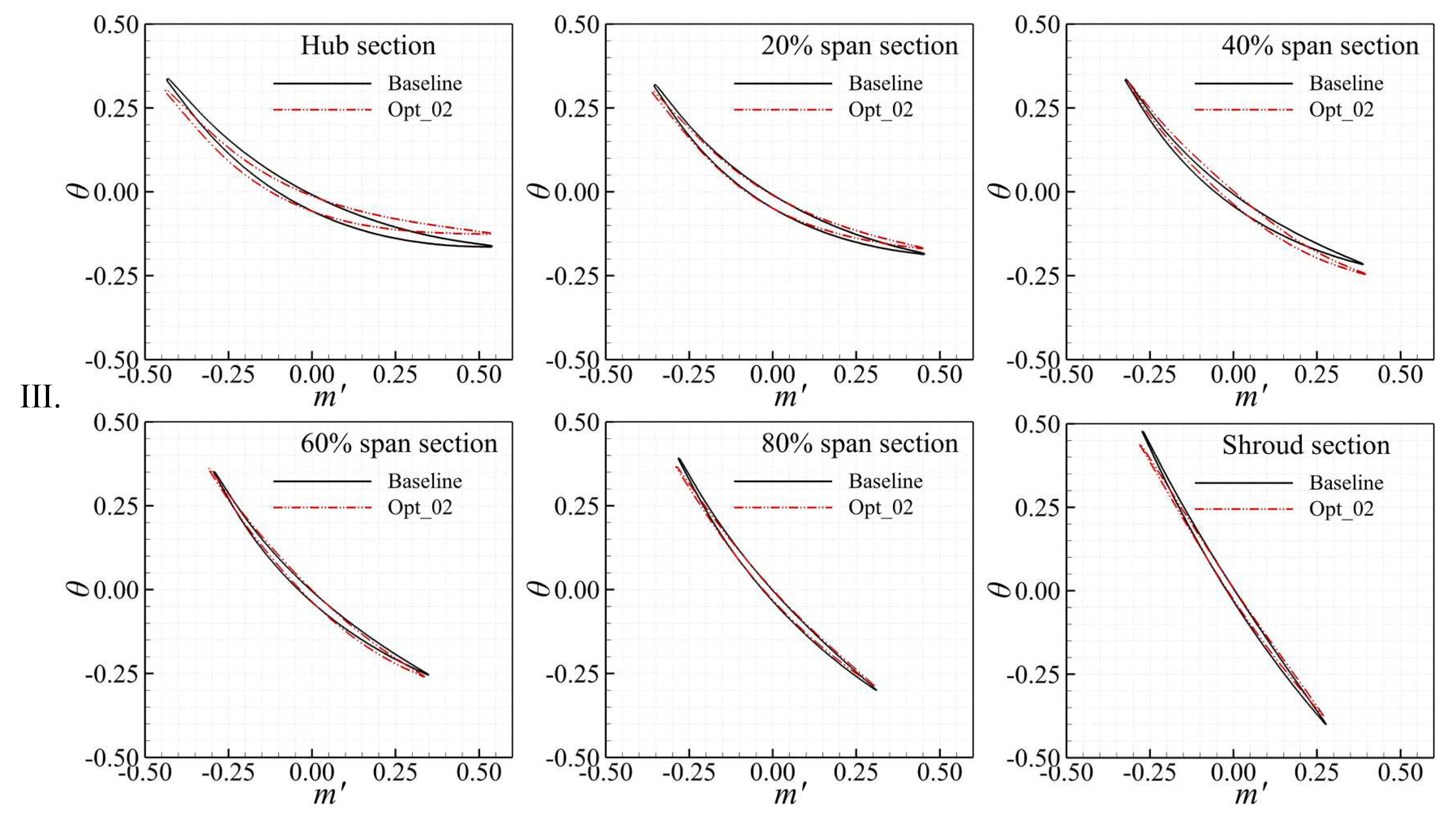
Furthermore, the enhancement of pressure rise also comes from the changes in blade geometry. The comparison of rotor blade profiles at several spanwise sections is given in Figure 5. It can be seen that the optimized case's blade camber angle is less than that of the baseline case in areas above 40%H, particularly in the tip regions. The curvature at the blade's leading edge is decreased as well, which helps to reduce the camber angle and make contributions to shock wave control. The maximum deflection of the camber line is after 50%C_m, which is in line with the design concept of the high-load transonic fan.

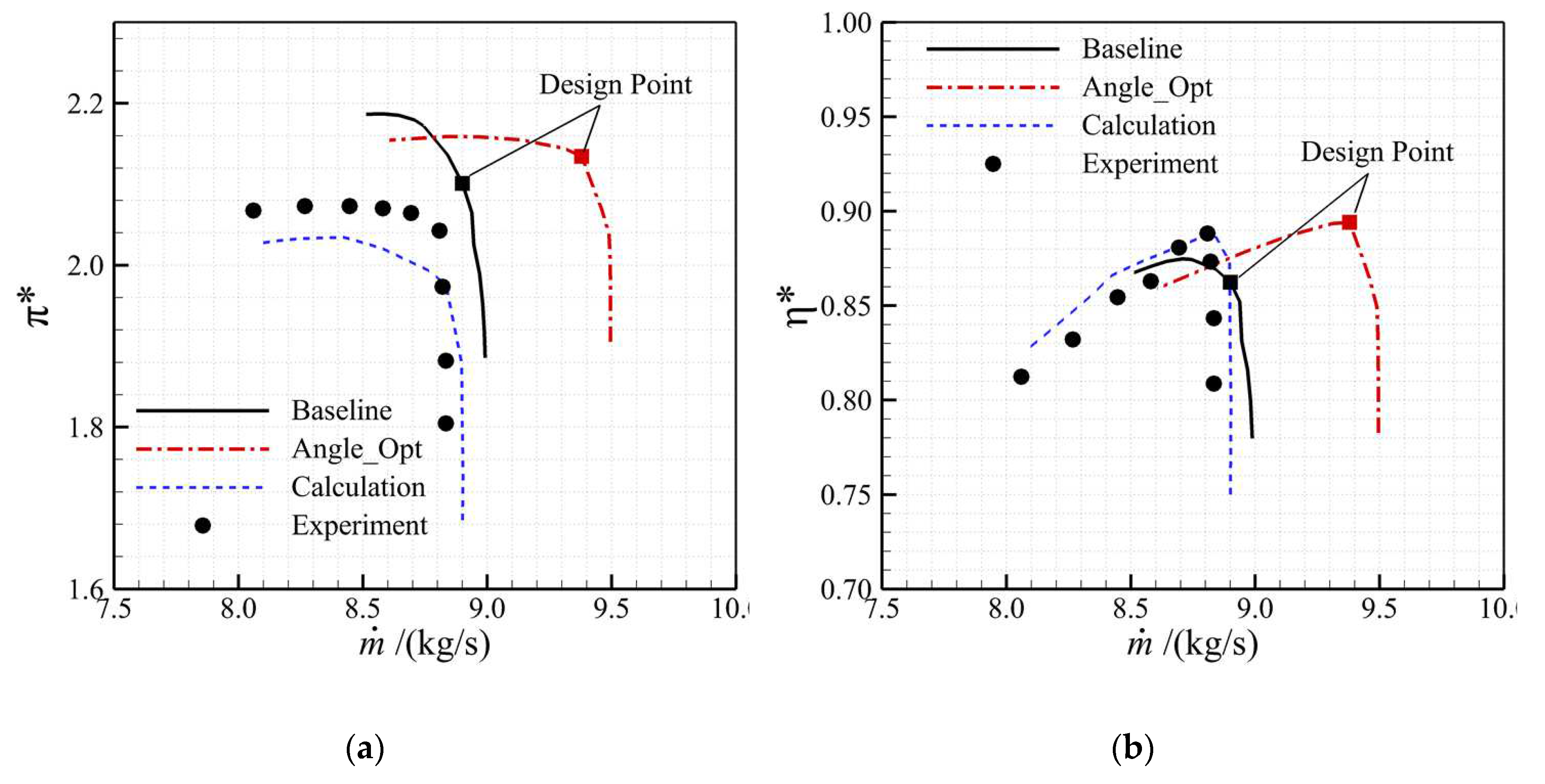
Last but not least, the performance map of the fan stage is shown in Figure 6, along with the numerical and experimental results of a fan stage with the same flow path as the present fan. [31]. Optimization of the rotor blade not only improves the performance of the fan stage at the design point, but also significantly improves the performance in off-design conditions. A notable increase in the chock mass flux is achieved by the optimization, which could greatly extend the stall margin of the fan stage. What’s more, based on the identical changing trend of both numerical and experimental results, the simulation results are within the margin of error, hence it can be concluded that the numerical method adopted in the present study is reliable with good accuracy.

4. Vorticity Dynamics Diagnosis

This section examines the physical processes controlling boundary layer separation and shock waves from the perspective of vorticity dynamics. As an important ramification in fluid dynamics, vorticity dynamics mainly focuses on the derivative/gradient of flow parameters and could be used to examine major flow information while detecting the dynamic processes. Here, the physical cause of the curvature control-induced performance increase for the fan stage will be thoroughly studied, and the mechanism of the vorticity dynamics diagnosis method will be clearly understood.

4.1. Mathematical explicit relation between vorticity dynamics parameters vs. performance parameters

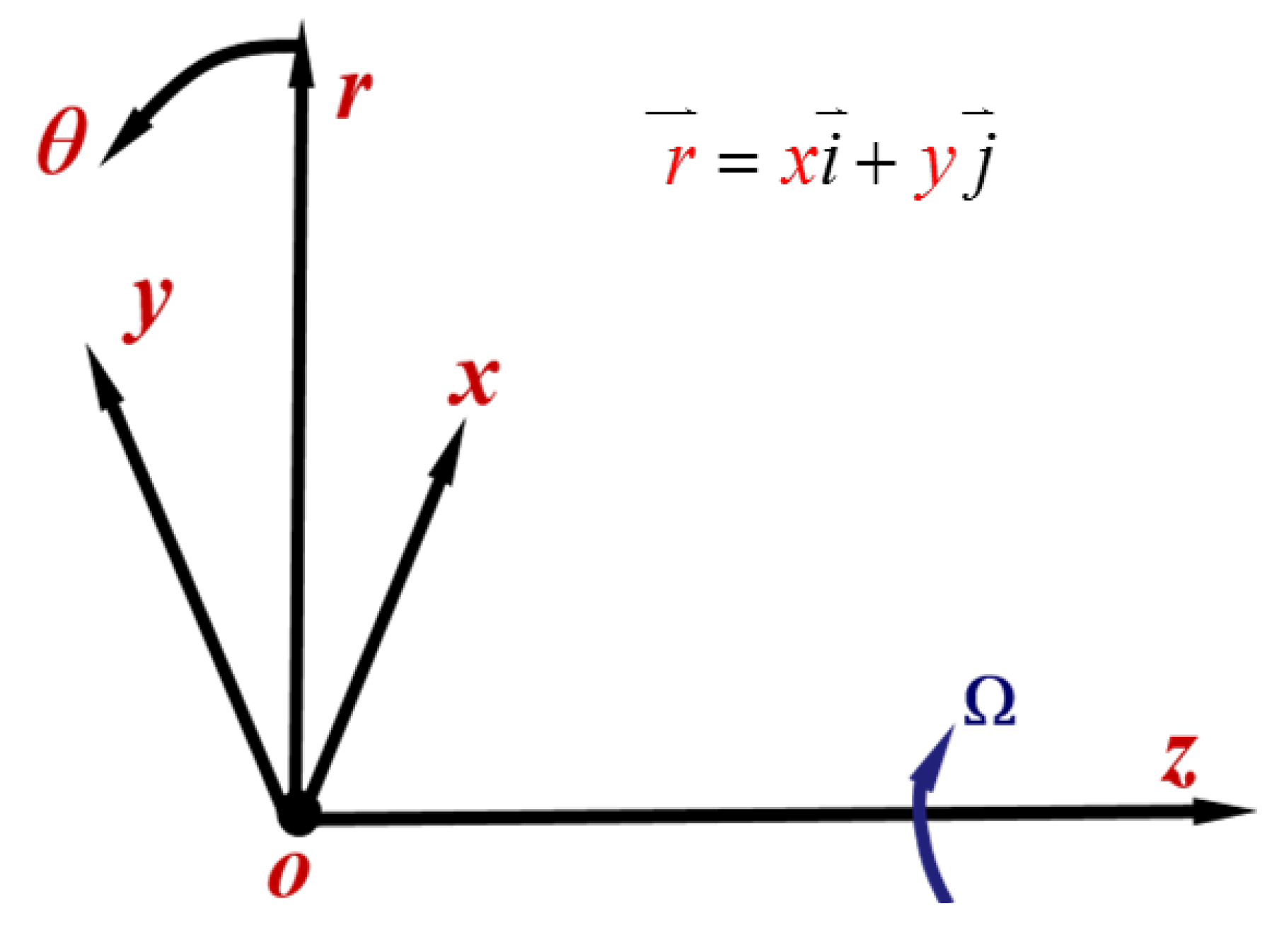
To begin with, the relationship between the vorticity dynamics parameters and the through-flow capability of axial fan/compressor is investigated. All the discussion in this section is under the cylindrical coordinates system with the z-axis being the rotation axis, as shown in Figure 7.

As we know, the mass flux of an axial fan/compressor in the cylindrical coordinates can be read as follows:

\begin{array}{l} \int_{s} ρ u_{z} d S = \int_{s} ρ u_{z} r d r d θ = \frac{1}{2} [\int_{0}^{2 π} ρ u_{z} r^{2} |_{r_{1}}^{r_{2}} d θ - \int_{s} r \frac{\partial ρ u_{z}}{\partial r} d S] = - \frac{1}{2} \int_{s} r \frac{\partial ρ u_{z}}{\partial r} d S \\ = - \frac{1}{2} \int_{s} r (u_{z} \frac{\partial ρ}{\partial r} + ρ \frac{\partial u_{z}}{\partial r}) d S = - \frac{1}{2} \int_{s} r [u_{z} \frac{\partial ρ}{\partial r} + ρ (\frac{\partial u_{r}}{\partial z} - ω_{θ})] d S \end{array}

(1)

Here, ω_θ denotes the azimuthal vorticity and is defined as:

ω_{θ} = \frac{\partial u_{r}}{\partial z} - \frac{\partial u_{z}}{\partial r}

(2)

Based on the fact that the ∂ρ/∂r and ∂u_r/∂z are ignorable at the inlet or outlet plane of fan/compressor, the Eq. (1) could be simplified as:

\int_{s} ρ u_{z} d S \approx \frac{1}{2} \int_{s} r ρ ω_{θ} d S

(3)

The Eq. (3) indicates that the mass flux of the fan/compressor depends directly on the azimuthal vorticityω_θ. Moreover, according to the Eq. (2), in the core flow region of the blade passage, ∂u_r/∂z≈∂u_z/∂r≈0, so ω_θ≈0. In the hub region where ∂u_r/∂z<<∂uz/∂r and ∂u_z/∂r>0, ω_θ≈-∂u_z/∂r<0. In the casing region where ∂u_r/∂z<<∂u_z/∂r and ∂u_z/∂r<0, ω_θ≈-∂u_z/∂r>0. Consequently, in order to improve the through flow capability of the compressor, the reduction of area for the vortex regions near the hub and the casing is required. In other words, the increase of the mass flow rate calls for the decrease of the boundary layer thickness, which is in consistence with the general principle of fluid dynamics.

Using similar numerical methods, we can get the relation between other performance parameters and the vorticity parameters, as listed below:

(a) The relation for total pressure ratio and the azimuthal vorticity:

(4)

\begin{array}{l} C_{2} = 2 C_{1} = \int_{S_{1}} ρ u_{z} p^{*} d S \approx - 0.5 \int_{S_{1}} r ρ p^{*} \frac{\partial u_{z}}{\partial r} d S \\ = - π \int_{r_{1}}^{r_{2}} r^{2} ρ p^{*} \frac{\partial u_{z}}{\partial r} d r \approx π \int_{r_{1}}^{r_{2}} r^{2} ρ p^{*} ω_{θ} d r \end{array}

(5)

(b) The relation for total temperature ratio and the azimuthal vorticity:

(6)

\begin{array}{l} C_{4} = 2 C_{3} = \int_{S_{1}} ρ u_{z} T^{*} d S \approx - 0.5 \int_{S_{1}} r ρ T^{*} \frac{\partial u_{z}}{\partial r} d S \\ = - π \int_{r_{1}}^{r_{2}} r^{2} ρ T^{*} \frac{\partial u_{z}}{\partial r} d r \approx π \int_{r_{1}}^{r_{2}} r^{2} ρ T^{*} ω_{θ} d r \end{array}

(7)

η_{t t} = \frac{{(\frac{p_{2}^{*}}{p_{1}^{*}})}^{\frac{γ - 1}{γ}} - 1}{\frac{T_{2}^{*}}{T_{1}^{*}} - 1} = \frac{π_{t t}^{\frac{γ - 1}{γ}} - 1}{τ_{t t} - 1} \approx \frac{{(\frac{\int_{S_{2}} r ρ p^{*} ω_{θ} d S}{C_{2}})}^{\frac{γ - 1}{γ}} - 1}{\frac{\int_{S_{2}} r ρ T^{*} ω_{θ} d S}{C_{4}} - 1}

(8)

(d) The relation for stall margin and the azimuthal vorticity:

(9)

Here, superscript * denotes the total condition, subscript tt denotes the total to total condition, while subscripts s and d represent the stall point and the design point, respectively.

To further reveal the mechanism of flow loss generation and find out the internal correlation between the vorticity and the compressor performance, the Boundary Vorticity Flux (BVF) is investigated in the present study. The concept of BVF was first put forward by Lighthill [32] in 1963 as a measurement for the physical generation of vorticity in the on-wall area. Following is its definition:

σ = \frac{μ}{ρ} n \cdot \nabla ω = ν \frac{\partial ω}{\partial n}

(10)

The axial moment exerted on the gas by the rotor blades of an axial fan/compressor can be represented as follows:

M_{z} = - \int_{S} {(r \times n p)}_{z} d S

(11)

Considering a sequence of mathematical transformation relations, Eq. (11) could be transformed into the following form:

M_{z} = - \int_{S} {(r \times n p)}_{z} d S = - \frac{1}{2} \int_{S_{b}} ρ r^{2} σ_{p z} d S + \frac{1}{2} \oint_{\partial S_{b}} p r^{2} d z

(12)

Here, M stands for total moment vector of acting onto the fluid by fan/compressor rotor blades, and M_z is its axial-component. σ_pz is axial-component of BVFσ_p, S_b denotes rotor blade surface and ∂S_b is the boundary of S_b. According to Eq. (12), the M_z consists of two parts: the surface integration of the second-moment of σ_pz is the first part, and the curve integration of the second-moment of static pressure p is the second. Hence, we can see that the lower σ_pz is, the higher M_z will be, which would have more beneficial effects on the total pressure ratio for the fan/compressor rotor blade passage. Therefore, the axial component of the BVF σ_pz is an important parameter that reflects the aerodynamic performance of the fan/compressor.

4.2. Flow diagnosis based on vorticity dynamics

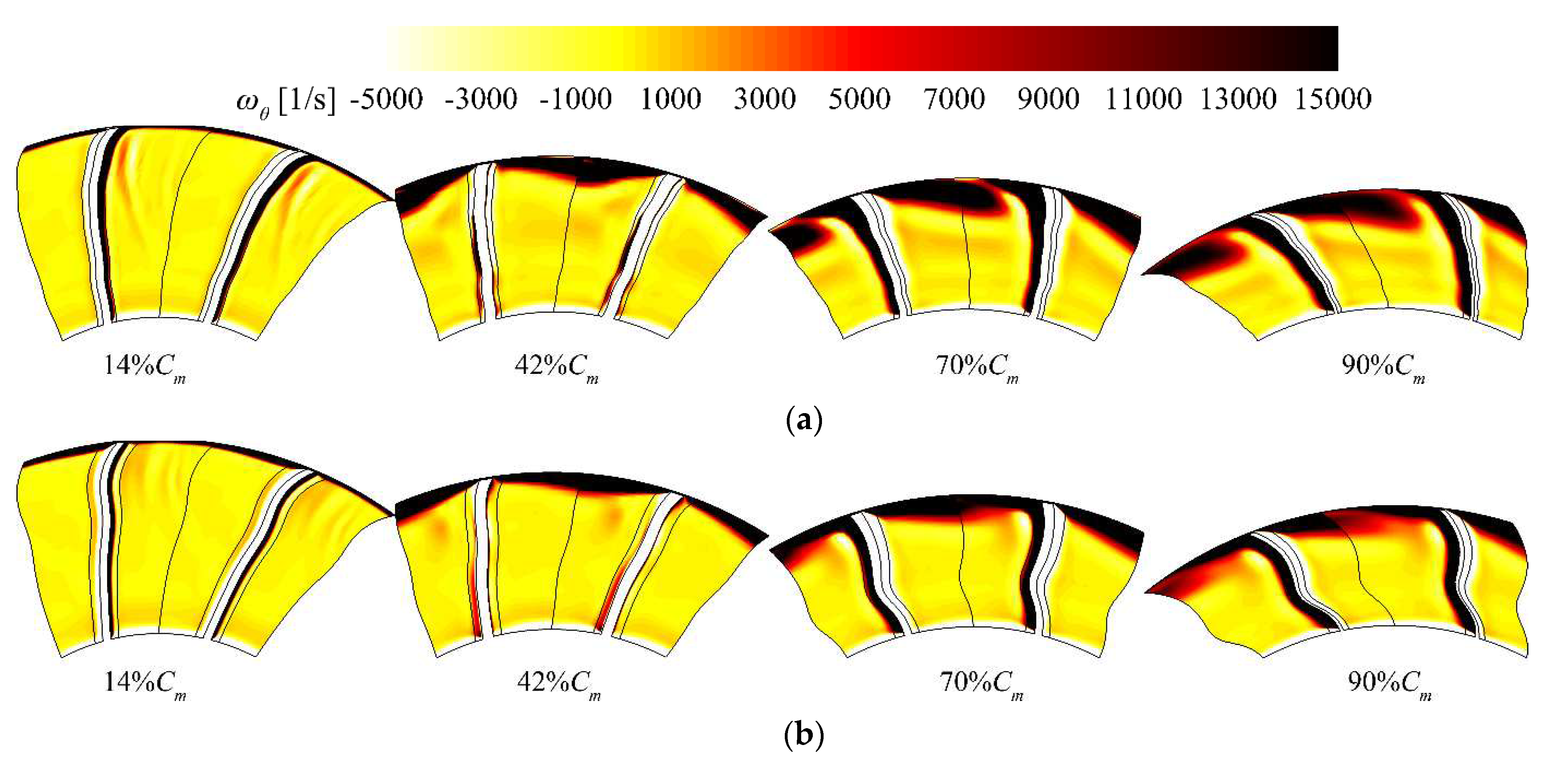
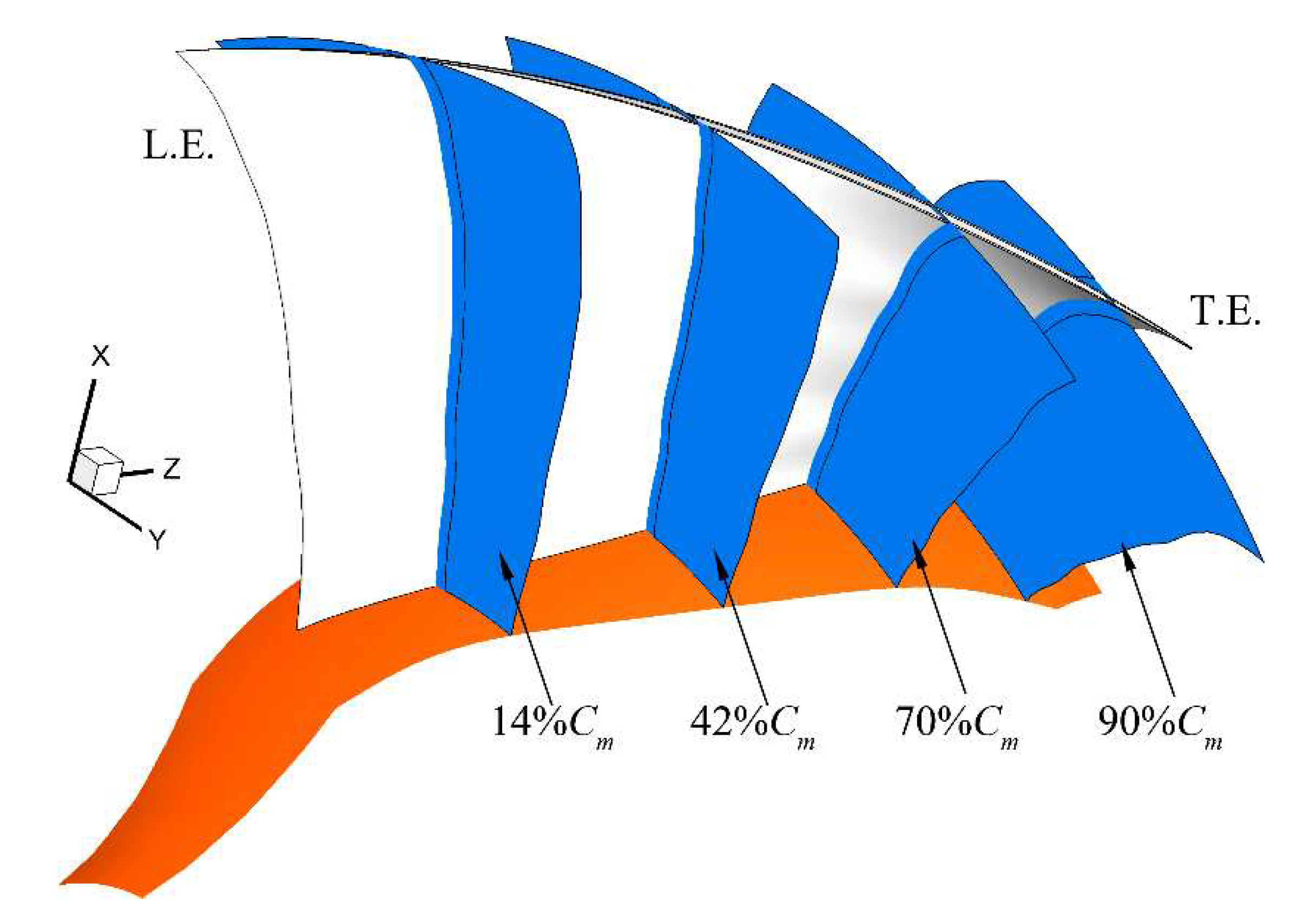
The distribution of azimuthal vorticity between the baseline and the optimized case is presented in Figure 8. Four sections are displayed, as shown in Figure 9, the chordwise locations are c/C_m=14%, c/C_m=42%, c/C_m=70% and c/C_m=90%, respectively. Compared with the baseline case, significant reduction of the vortex intensity is achieved by the optimization, which is particularly obvious in the tip region of the rotor blade. This phenomenon further demonstrates that the rotor optimization could obtain a more reasonable configuration of the shock wave in the transonic fan, which would therefore enhance the through flow capability according to Eq. (3).

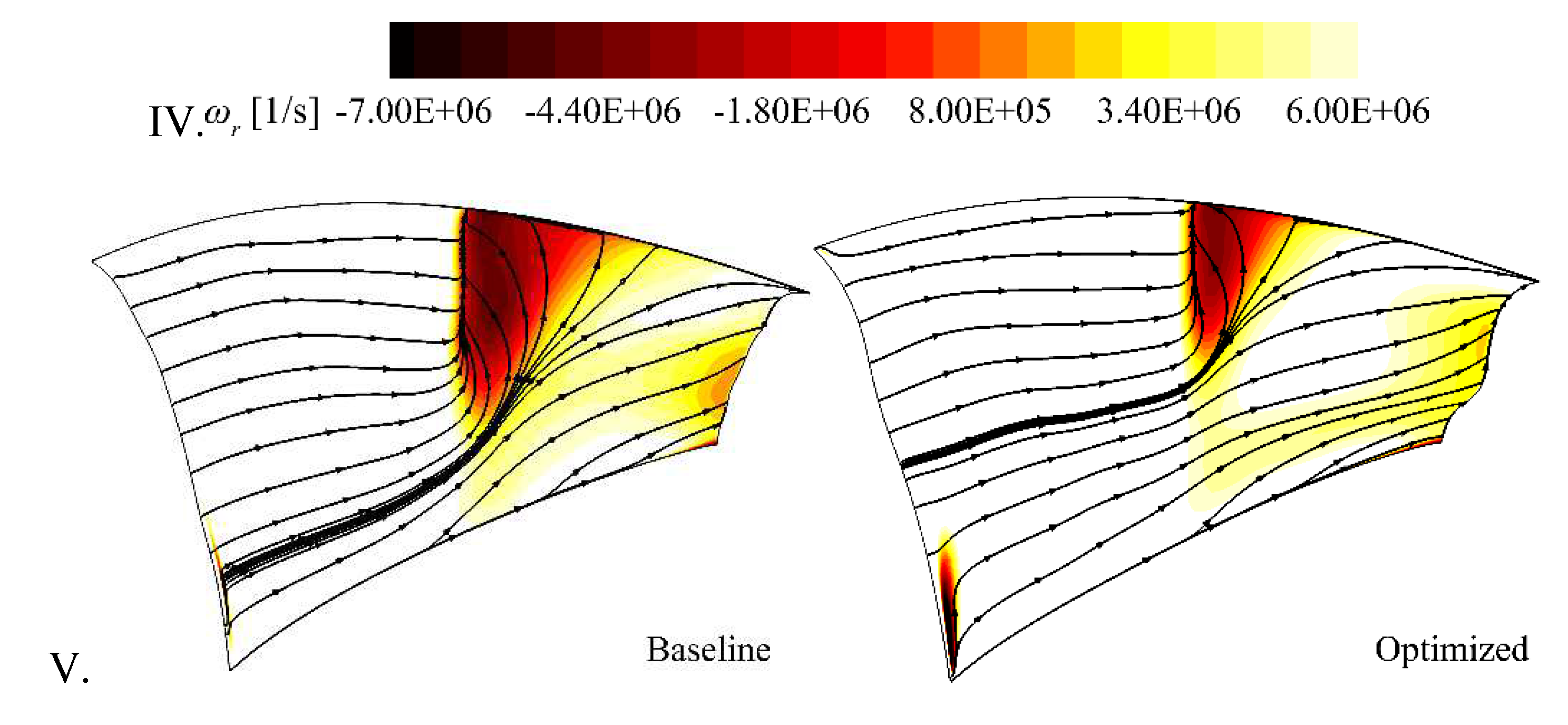
Presented in Figure 10, the radial vorticity and the skin-friction lines on the rotor blade suction surface demonstrate that boundary-layer separation caused by shock wave features as a sharp decrease in the radial vorticity, and since the optimized rotor has a smaller separation region, it has a weaker radial vorticity gradient. The weakened separation flow indicates that the optimized rotor blade in this study could achieve favorable control effect on the shock wave in the upper half of the blade, whereby improving the aerodynamic performance of the fan stage. However, the negative radial vorticity near the hub at the inlet of the optimized rotor blade indicates the lack of accuracy in leading edge metal angle at these areas, which needs to be further optimized in the future studies.

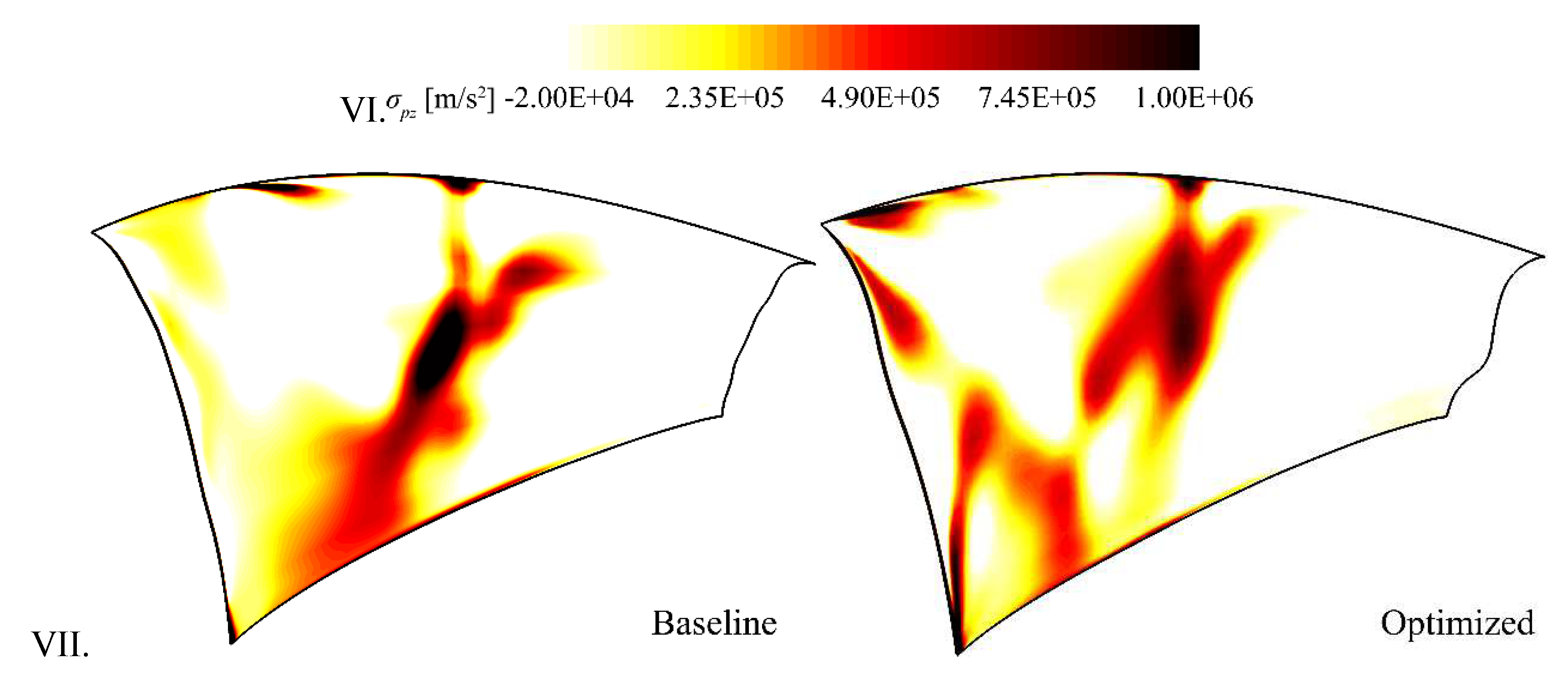
The axial component of BVF (σ_pz) on the blade suction surface is shown in Figure 11. According to the demonstrations above, the increment of σ_pz in the boundary layer area is detrimental to the performance of the compressor due to the reduction in the total aerodynamic torque. As can be seen in the Figure 11, the positive peak of σ_pz is weakened and shifted towards the upper part of the blade in the optimized case, which indicates that the flow loss caused by the shock wave is reduced significantly, and the fluid will be able to receive larger axial torque when it travels through the rotor blade passage.

According to the famous boundary layer separation criteria proposed by Wu [26] (although there have been some long-standing controversial issues), boundary layer separation is characterized by the following three features:

Separation zone warning: The distinctive vorticity vector lines on the wall have a significant positive curvature in addition to converging skin-friction lines.

Separation line criteria: The curvature of vorticity lines reach a maximum.

Separation watch: Tangent BVF lines turn to the direction of skin-friction lines on wall, or the tangent pressure gradient vector lines are basically perpendicular to the separation line.

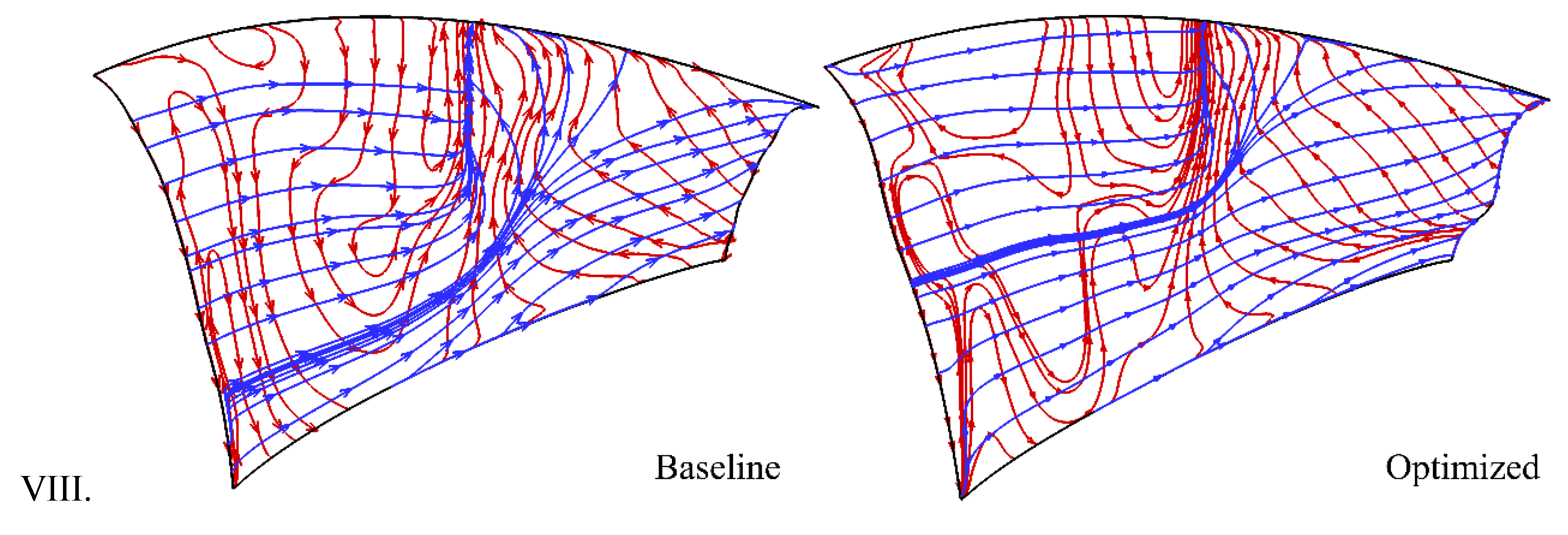
Above criteria are employed to investigate the flow in the present rotor blade passage. The skin-friction lines and the BVF lines are presented in Figure 12. The range of the shock-wave-induced separation bubble which is sketched clearly by the skin-friction lines is reduced significantly in the optimized case, and the direction of the BVF lines is just in parallel with the separation line, which is in good conformance with the above mentioned criteria.

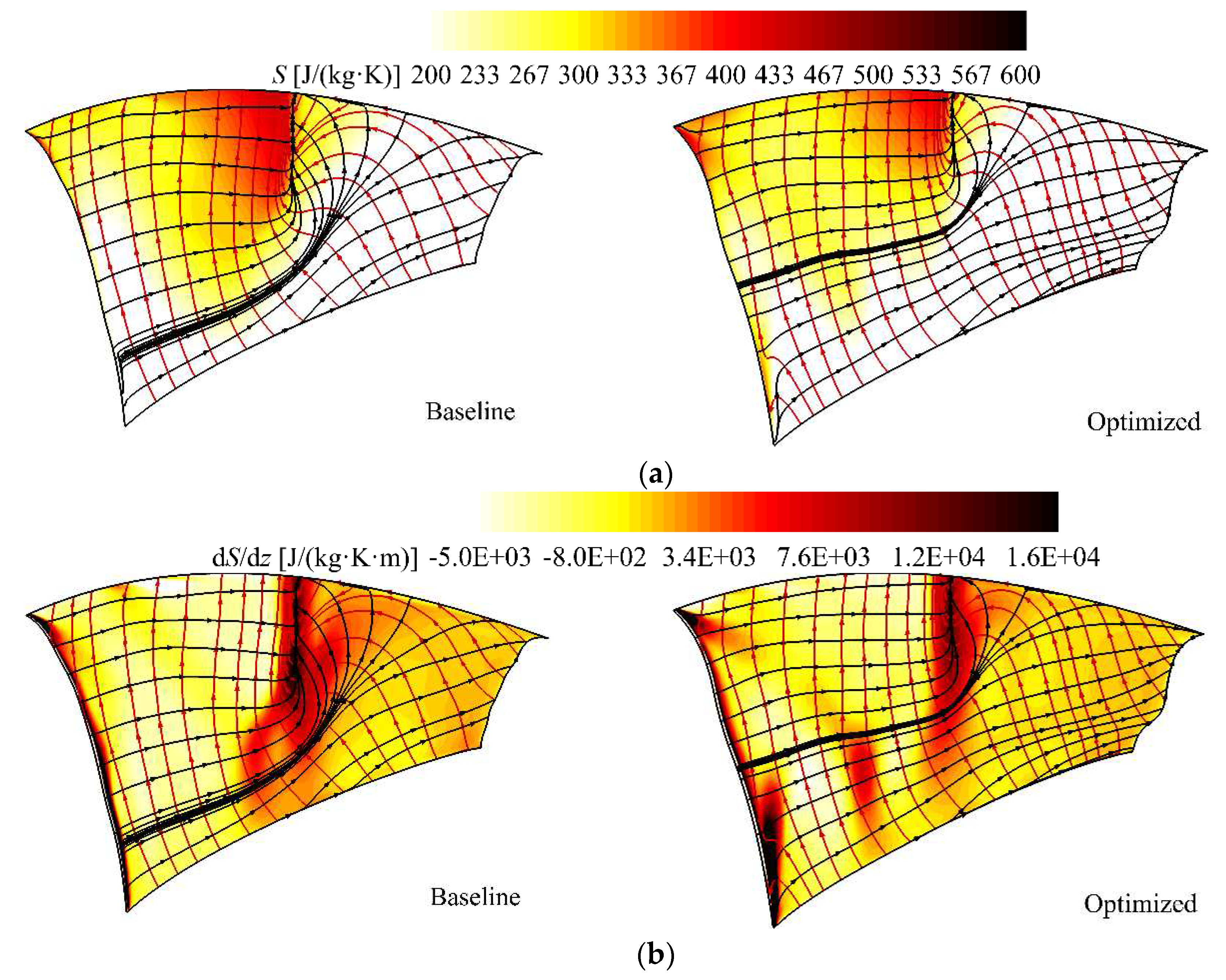
The specific entropy and its gradient on the rotor blade suction surface are presented in Figure 13, the vector lines (τ, ω) are depicted as well. For the optimized case, entropy production caused by the shock wave in the tip region of the rotor blade is reduced remarkably, and the flow separation is suppressed effectively. In fact, the fundamental principle of transonic fan optimization design is the control and utilization of the shock wave. According to Figure 13b, the spike of entropy gradient coincides well with the separation line, which is more helpful to examine boundary-layer separation. Also, the reduction of the entropy gradient in the vicinity of the separation line indicate that the intensity of the shock wave is weakened effectively by the optimization of the curvature. Moreover, it can be seen that on both sides of separation line where the skin-friction lines converge, the curvature of the vorticity lines reaches its peak, which is proved to be a valid method to identify boundary-layer separation flow.

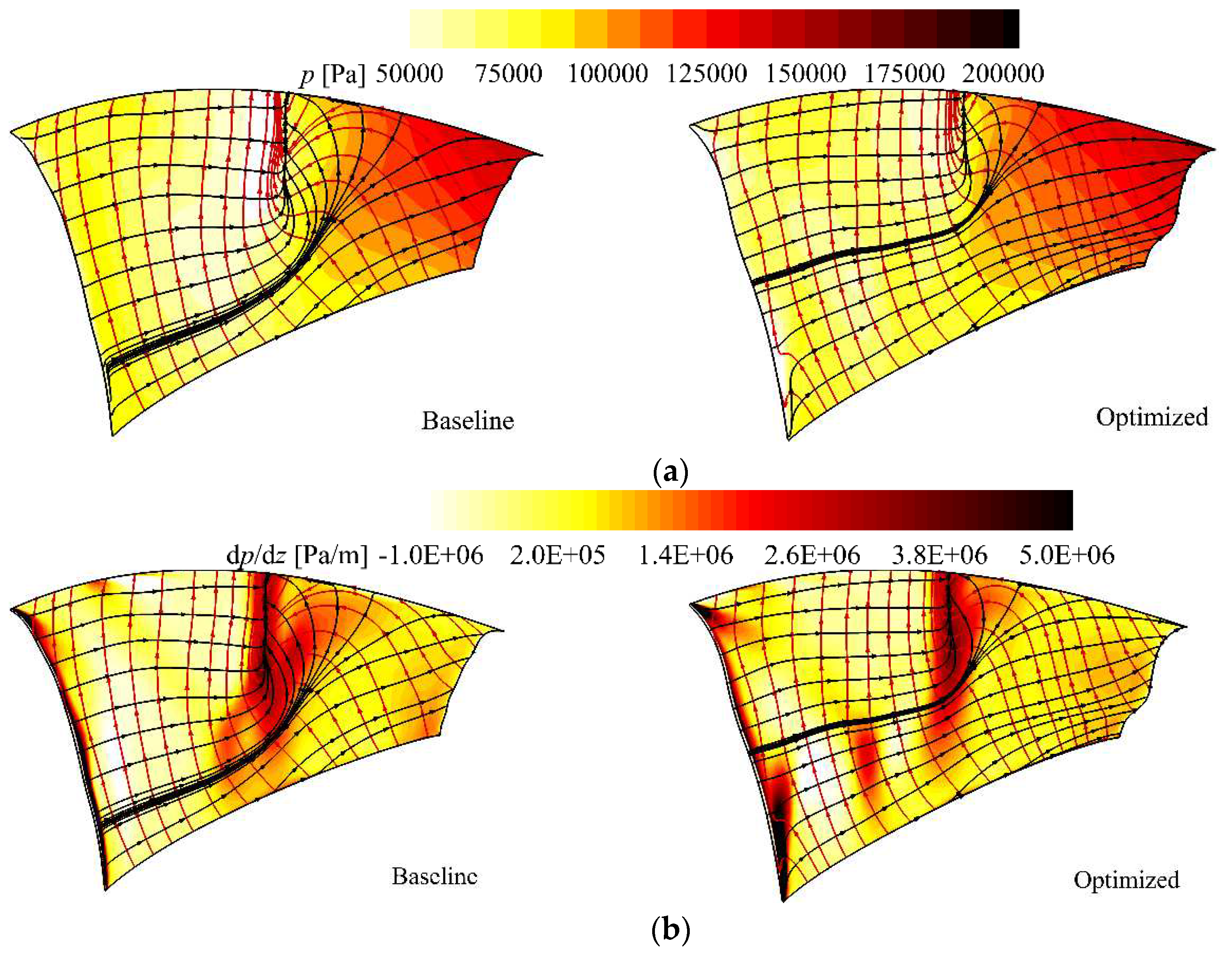
Designed to compress fluid, the main goal of a fan stage is to increase the static pressure of the fluid that flows through its blade passages. The static pressure is on the suction surface of the rotor blade is presented in Figure 14a, and the gradient of the static pressure is shown in Figure 14b. As shown in Figure 14a, the static pressure in the upstream of the separation region is higher in the optimized case than that in the baseline case, which indicates that the Mach number in front of the shock wave is lowered by the optimization. As a result, the intensity of the shock wave will be weakened and the consequent shock loss will be reduced. The gradient of the static pressure in Figure 14b has also demonstrated that gradient of the static pressure is more beneficial to check shock wave and boundary-layer separation. Moreover, the shock wave is weakened remarkably for the optimized case, which provides a more reasonable flow configuration in the rotor blade passage.

5. Conclusion

The optimizations of the rotor blade in a low-bypass transonic fan stage is implemented, flow diagnostic techniques based on vorticity dynamics are employed to discuss the flow and reveal the mechanism of three dimensional transonic blade design.

By optimizing the curvature of the camber line and matching the inlet flow angle, a novel rotor blade with continuous curvature is acquired. As a result, the intensity of the shock wave is reduced and the subsequent flow separation is delayed, increasing the fan stage's capacity for flow and pressure rise while reducing flow loss. After the optimization, the total press ratio of the fan stage is increased by 1.90%, while the adiabatic efficiency and mass flow rate are increased by 4.45% and 5.82%, respectively.

The performance parameters of axial fan/compressor depend strongly on the vorticity dynamic parameters. The azimuthal vorticity and the boundary vorticity flux have significant influences on the through-flow capability and other aerodynamic performance parameters of the fan/compressor passage. The occurrence of boundary layer separation in a transonic fan is accompanied by the spike of entropy and static pressure, and the derivation/gradient of these flow parameters would also suffer drastic changes. Other than specific flow parameters themselves, the derivative/gradient of flow parameters could provide more information about the flow with higher accuracy. Hence the utilization of flow diagnostic techniques based on vorticity/vortex dynamics provides the researchers with a novel method for turbomachinery aerodynamic analysis and design.

Acknowledgments

This work was supported by the grant from the Scientific research platform and projects of colleges and universities of Guangdong Province Department of Education (Grant No. KJ2022C010), the Guangdong Provincial Science and Technology Plan Project (Grant No. 2021A0505030013) and the National Natural Science Foundation of China (Grant No. 51506036, No. 51306042).

Nomenclature

c = Local meridian curve distance

C_m = Total meridian curve distance

h = Local span distance

H = Blade height

m’ = Normal coordinate for the streamline

\dot{m}

= Mass flow rate

Ma = Mach number

M = Moment vector, Mach number

\bar{n}

= Corrected Rotating speed

p = Pressure

r = Radial coordinates

S = Entropy

T = Temperature

u = Non-dimensional coordinate in basic airfoil plane, absolute velocity

z = Axial coordinates

α = Out flow angle

Δβ = viation on metal angle

δ = Deviation angle

η = Efficiency

θ = Circumferential coordinates

Δθ = Deviation on tangential lean angle

μ = Dynamic viscosity

ν = Kinematic viscosity

π = Pressure ratio

ρ = Density

σ_p = Boundary vorticity flux

τ = Shear stress

ω = Vorticity

Subscripts/Superscripts

1 = Inlet conditions

2 = Outlet conditions

r = Relative conditions

r,θ, z = Radial, circumferential, axial components

is = Isentropic

* = Total condition

References

Wu, C. H., “A General Theory of Three-Dimensional Flow in Subsonic and Supersonic Turbomachines of Axial-, Radial, and Mixed-Flow Types,” National Aeronautics and Space Administration. Rept. NACA-TN-2604, Cleveland, OH, Jan. 1952.
Novak, R. A., "Streamline Curvature Computing Procedures for Fluid-Flow Problems." Journal of Engineering for Power, Vol. 89, No. 4, 1967, pp. 478-490. [CrossRef]
Marsh H. A., Digital Computer Program for the Through-Flow Fluid Mechanics in an Arbitrary Turbomachine Using a Matrix Method, Her Majesty's Stationery Office, London, 1966.
Bliss, D., Hayden, R., Murray, B., and Schwaar, P., “Design Considerations for a Novel Low Source Noise Transonic Fan Stage,” 3rd Aeroacoustics Conference, Aeroacoustics Conferences, Palo Alto, CA, AIAA Paper No. 76-577, 1976. [CrossRef]
Lucas, J., Woodward. R., and Mackinnon, M., “Acoustic Evaluation of a Novel Swept Rotor Fan,” 11th Fluid and Plasma Dynamics Conference, Fluid Dynamics and Co-located Conferences, Seattle, WA, AIAA Paper No. 78-1121, 1978. [CrossRef]
Wennerstrom, A. J., and Frost, G. R., “Design of a 1500ft/sec, Transonic, High-Through-Flow, Single-Stage Axial-Flow Compressor with Low Hub/Tip Ratio,” Air Force Aero Propulsion Lab, Wright-Patterson AFB, OH, No. AFARL-TR-76-59, 1976.
Wennerstrom, A. J., Derose, R. D., Law, C. H., and Buzzell, W. A., “Investigation of a 1500ft/sec, Transonic, High-Through-Flow, Single-Stage Axial-Flow Compressor with Low Hub/Tip Ratio,” Air Force Aero Propulsion Lab, Wright-Patterson AFB, OH, No. AFARL-TR-76-92, 1976.
Frank, B., King, P., and Copenhaver, W., “Effects of Leading Edge Sweep on Stall Inception in a High-Speed Single-Stage Compressor,” 30th Joint Propulsion Conference and Exhibit, Indianapolis, IN, AIAA Paper No. 94-2696, 1994. [CrossRef]
Boyer, K., King, P., and Copenhaver, W., “Stall Inception in Single Stage, High-Speed Compressors with Straight and Swept Leading Edges,” AIAA, SAE, ASME, and ASEE, Joint Propulsion Conference and Exhibit, 29th, Monterey, CA, 1993. [CrossRef]
Denton, J. D., and Xu, L., “The Effects of Lean and Sweep on Transonic Fan Performance,” ASME Turbo Expo 2002: Power for Land, Sea, and Air, Vol. 5, American Soc. of Mechanical Engineers Paper GT 2002-30327, Amsterdam, Netherlands, Jun 2002, pp. 23-32. [CrossRef]
Shan, P., and Gui, X., “Final Report for the Design and Experiment Study of a High Loading Single-Stage Model Fan ATS-2 with a Backward Swept Rotor,” Rept. GF-A0041935, Beihang University, Beijing, China, 2000.
Hu, G. R., Zhou, Y. F., Chen, B. S., and Wei, Y. B., “Design and Test for Single Stage Transonic Fan with High Speed, High Load,” Journal of Engineering Thermophysics, Vol.22, No.1, 2001, pp.40-43.
Benini, E., “Three-Dimensional Multi-Objective Design Optimization of a Transonic Compressor Rotor,” Journal of Propulsion and Power, Vol. 20, No. 3, 2003, pp. 559–565. [CrossRef]
Jang, C. M., Li, P., and Kim, K. Y., “Optimization of Blade Sweep in a transonic Axial Compressor Rotor,” JSME International Journal Series B, Vol. 48, No. 4, 2005, pp. 793-801. [CrossRef]
Lian, Y., and Liou, M. S., (2005) “Multi-Objective Optimization of Transonic Compressor Blade Using Evolutionary Algorithm,” Journal of Propulsion and Power, Vol. 21, No. 6, 2005, pp. 979-987. [CrossRef]
Ellbrant, L., Eriksson, L.-E., and Martensson, H., “Design of Compressor Blades considering Efficiency and Stability using CFD based Optimization,” ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Vol. 8, American Soc. of Mechanical Engineers Paper GT 2012-69272, Copenhagen, Denmark, Jun 2012, pp. 371-382. [CrossRef]
Ellbrant, L., Eriksson, L. E., and Martensson, H., “Balancing Efficiency and Stability in the Design of Transonic Compressor Stages,” ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, Vol. 6B, American Soc. of Mechanical Engineers Paper GT 2013-94838, San Antonio, USA, Jun 2013, pp. V06BT37A017. [CrossRef]
Oyama, A., Liou, M. S., and Obayashi, S., “Transonic Axial Flow Blade Optimization Evolutionary Algorithms Three-Dimensional Navier-Stokes Solver,” Journal of Propulsion and Power, Vol. 20, No.4, 2004, pp. 612-619. [CrossRef]
Nemnem, A. F., “A General Multidisciplinary Turbomachinery Design Optimization System Applied to a Transonic Fan,” Ph.D. Dissertation, Department of Aerospace Engineering and Engineering Mechanics, University of Cincinnati, Cincinnati, OH, 2014.
Siddappaji, K., “Parametric 3D Blade Geometry Modeling Tool for Turbomachinery Systems,” Master’s dissertation, College of Engineering and Applied Science, University of Cincinnati, Cincinnati, OH, 2012.
Nemnem, A. F., Turner, M. G., Siddappaji, K., and Galbraith, M., “A Smooth Curvature-Defined Meanline Section Option for a General Turbomachinery Geometry Generator,” ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Vol. 2B, American Soc. of Mechanical Engineers Paper GT 2014-26363, Düsseldorf, Germany, Jun 2014, pp. V02BT39A026. [CrossRef]
Nemnem, A. F., Turner, M. G., Siddappaji, K., and Gannon, A. J., “An Automated 3D Turbomachinery Design and Optimization System,” Journal of Multidisciplinary Engineering Science and Technology, Vol. 2, No.11, 2015, pp. 3345-3359.
Siddappaji, K., Turner, M. G., Dey, S., Park, K., and Merchant, A., “Optimization of a 3-Stage Booster: Part 2—The Parametric 3D Blade Geometry Modeling Tool. ASME Turbo Expo 2011: Turbine Technical Conference and Exposition, Vol. 7, American Soc. of Mechanical Engineers Paper GT 2011-46664, Vancouver, Canada, Jun 2011, pp. 1431-1443. [CrossRef]
Siddappaji, K., Turner, M. G., and Merchant, A., “General Capability of Parametric 3D Blade Design Tool for Turbomachinery,” ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Vol. 8, American Soc. of Mechanical Engineers Paper GT 2012-69756, Copenhagen, Denmark, Jun 2012, pp. 2331-2344. [CrossRef]
Turner, M. G., Merchant, A., and Bruna, D., “A Turbomachinery Design Tool for Teaching Design Concepts for Axial-Flow Fans, Compressors, and Turbines,” Journal of Turbomachinery, Vol. 133, No. 3, 2011, pp. 937-952. [CrossRef]
Wu, J. Z., Ma, H. Y., Zhou, M. D., Vorticity and vortex dynamics. Springer, Berlin, Germany, 2006.
Wu, J. Z., Tramel, R. W., Zhu, F. L., and Yin, X., “A vorticity dynamics theory of three-dimensional flow separation,” Physics of Fluids, Vol.12, No.8, 2000, pp. 1932-1954. [CrossRef]
Wu, J. Z., Lu, X. Y., Yang, Y. T., and Zhang, R. K., “Vorticity dynamics in complex flow diagnosis and management,” Proceedings of the 13th Asian Congress Fluid Mechanics, Dhaka, Bangladesh, December 2010, pp. 1-22.
Yang, Y., Wu, H., Li, Q. S., Sheng, Z., and Wu, J. Z., “Vorticity dynamics in axial compressor flow diagnosis and design,” Journal of Fluids Engineering, Vol. 130, No. 4, 2008, pp. 041102. [CrossRef]
Li, Q. S., Wu, H., Guo, M., and Wu, J. Z., “Vorticity dynamics in axial compressor flow diagnosis and design—part ii: Methodology and application of boundary vorticity flux,” Journal of Fluids Engineering, Vol. 132, No. 1, 2010, pp. 011102. [CrossRef]
Li, S., “Design of Highly Loaded Dihedral Stator and Investigation on the Aerodynamic Stage Performance in an Axial Transonic Compressor,” Ph.D. dissertation, Harbin Institute of Technology, Harbin, China, 2007.
Lighthill, M. J., Laminar Boundary Layers, Oxford University Press, Oxford, 1963, pp. 46–113.

Figure 1. Optimization schematic.

Figure 2. Geometry and meshes for the baseline fan stage.

Figure 3. Comparisons of aerodynamic parameters for the rotor blade: (a) Adiabatic efficiency; (b) Total pressure ratio; (c) Relative Mach number.

Figure 4. Isentropic Mach number on the surface of rotor blade.

Figure 5. Blade profiles for the baseline and optimized rotor.

Figure 6. Performance map for the fan stage [31]: (a) The total pressure ratio vs. mass flow rate; (b) The adiabatic efficiency vs. mass flow rate.

Figure 7. Cylindrical coordinates system.

Figure 8. Azimuthal vorticity in cross section in the rotor passage: (a) Baseline; (b) Optimized.

Figure 9. Chordwise location for cross sections in the rotor.

Figure 10. Radial vorticity and skin-friction lines on the blade suction surface.

Figure 11. BVF-σ_pz on rotor suction surface.

Figure 12. BVF lines (in red) on and skin-friction lines (in blue) on rotor blade suction side.

Figure 13. Vector lines (τ, ω) and entropy on the rotor blade suction side: (a) Vector lines (τ, ω) and specific entropy; (b) Vector lines (τ, ω) and axial gradient of entropy.

Figure 14. Vector lines (τ, ω) and static pressure on the rotor blade suction side: (a) Vector lines (τ, ω) and specific static pressure; (b) Vector lines (τ, ω) and axial gradient of static pressure.

Table 1. Parameters of the redesigned fan stage.

Parameter	Value
Number of rotor and stator blade	13, 36
Mach number in relative coordinates for rotor blade tip	1.3848
Loading coefficient for rotor blade tip	0.463
Flow coefficient for rotor blade tip	0.500
Hub-to-tip ratio of the rotor passage	0.460
Corrected design angular velocity (rpm)	28000.0
Corrected rotor tip tangent velocity (m/s)	410.0
Clearance for rotor blade tip (mm)	0.50
Mass flow rate at design angular velocity for fan (kg/s)	≥9.34
Adiabatic efficiency at design-point	≥0.87
Total pressure ratio at design-point	≥2.05

Table 2. Aerodynamic performance for different design cases.

	Mass flux $\dot{m}$ (kg/s)		Pressure Ratio *π^ (-)**		Efficiency *η^ (-)**
	Value	(%)	Value	(%)	Value	(%)
Baseline	8.94	0	2.10	0	0.853	0
Camber_Opt	9.31	+4.14	2.15	+2.38	0.886	+3.87
Angle_Opt	9.45	+5.70	2.15	+2.38	0.891	+4.45

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer