Trajectory Smoothing Planning of Delta Parallel Robot Combining Cartesian and Joint Space

Preprint

Article

Trajectory Smoothing Planning of Delta Parallel Robot Combining Cartesian and Joint Space

Altmetrics

Downloads

108

Views

Comments

A peer-reviewed article of this preprint also exists.

Zhu Dachang^*

He Yonglong,Yu Xuezhe,

Li Fangyi^*

Zhu Dachang^*

He Yonglong,Yu Xuezhe,

Li Fangyi^*

This version is not peer-reviewed

Submitted:

03 October 2023

Posted:

09 October 2023

You are already at the latest version

Alerts

Abstract

Delta parallel robot has been widely used in precision parts processing, handling, sorting, and precision assembly, with high efficiency and motion stability being its important performance indexes. Any small line segment corner in trajectory planning causes tangential discontinuous trajectory abrupt change, and the process vibration and shock caused by it seriously affect its high-speed and high-precision performance. In this paper, a trajectory planning method combining Cartesian space and joint space is proposed. Firstly, the vector method and micro-element integration method are used to establish the complete kinematics and dynamics equations of the Delta parallel robot, and the inverse kinematics/dynamics model-solving program is written based on Matlab software. Secondly, the end-effector trajectory of the Delta parallel robot is planned in Cartesian space, and the data points and inverse control points of the end-effector trajectory are obtained by the normalization method. Finally, the data points and control points are mapped to the joint space through the inverse kinematics equation, and the fifth-order B-spline curve is adopted for quadratic trajectory planning, which realizes the high-order continuous smoothing of trajectory planning. The simulation and experiment results show that the trajectory smoothing performance of continuous high-order curvature change can be improved using the proposed method, the tracking error of the end-effector is reduced by 21.12%, and the peak torques change of three joints is reduced by 3.5%, 11.6% and 1.6%, respectively.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Delta parallel robot has been widely used in precision parts processing, hanling, sorting, and assembly because of its high speed and high precision [1]. When a straight line or an arc approaches the target curve, the acceleration curve of the trajectory of the end-effector is abrupt due to tangential discontinuity at the connecting corner of the fitted line segment, which makes the process vibration of the Delta parallel robot inevitable in high-speed operation and even causes production safety accidents [2]. Polynomial functions and interpolation methods are often used for robot trajectory planning and optimization by giving constraints on starting and ending points, including displacement, velocity, and acceleration. Boryga [3] presented a smooth trajectory planning method using higher-degree polynomial functions of acceleration to determine accurate dependencies derived for the calculation of polynomial coefficients and motion time in the case of velocity, acceleration, and jerk constraints, thus ensuring the continuity and smoothness of the trajectory. A seventh-order polynomial was applied to the trajectory planning to achieve the position, velocity, acceleration, and jerk of the actuating joints, and the positions/orientations of the parallel mechanism modules were interpolated to get a smooth trajectory without impact [4]. To achieve a smooth and precise trajectory while minimizing jerk, Damasevicius et al.[5] proposed natural cubic splines for finding a Pareto-optimal set of robot arm trajectories. When a robot is required to machine a complex curved workpiece with high precision and speed, the path is generally dispersed into a series of points and transmitted to the robot, which not only reduces precision but also causes damage to the motors and robot. Zhang et al. [6] inserted a quintic Bezier curve between small adjacent line segments to achieve velocity and acceleration continuity at the connecting points, and a quartic polynomial was adopted to achieve a constant velocity at the velocity limitation. To solve the problem of trajectory continuity, some fitting curves were presented, such as quintic and cubic non-uniform rational NURBS curves [7,8,9], quintic Pythagorean-Hodograph (PH) curve [10], combining cubic splines with a linear segment with parabolic blends [11], S-curve [12]. However, since the trajectory of the end-effector in Cartesian space needs to be mapped to the joint space through the inverse kinematic equation, it is realized by the joint actuator through the torque control according to the calculated joint variable values. Therefore, the end-effector position, joint variables, and the precise modeling of robot kinematics and dynamics equations impact trajectory smoothing planning and become a very challenging subject in robotics [13,14].

Should surfaces such as sharp corners, holes, or protrusions be considered in trajectory planning [15]? Considering the execution characteristics of joint actuators, most trajectory smoothing planning considers the planning method in joint space. It takes joint velocity, acceleration, and jerk continuity as the trajectory smoothing targets [16,17]. Considering the Gaussian interpolation of boundary conditions, a radial basis function method was proposed by Chettibi [18] to generate point-to-point smooth trajectories of robot arms. A Multi-axis real-time synchronous look-ahead trajectory planning algorithm was proposed by Liang et al. [19] based on dynamically given position and velocity sequences under the constraint of maximum velocity and acceleration of each joint axis. Shrivastava et al. [20] used the cuckoo search algorithm to suppress the linear motion equation to avoid the directional singularity in Cartesian space. Then the Bezier curve was used to depict the shape of the joint trajectory by interpolating linear polynomials with the parabolic blend. In the joint space, the joint movement was divided into acceleration, uniform speed, and deceleration parts; the fourth-order polynomial formed by the root weight was used to plan the acceleration to ensure the continuity of the displacement, speed, acceleration, and jerk of each joint and end-effector of the robot [21].

On the other hand, some literature has studied the trajectory planning of robot end-effectors in Cartesian space [22,23,24,25,26]. However, trajectory smoothing planning in a single space can not guarantee trajectory smoothness in other spaces. Moreover, in the process of high-speed reciprocating motion of a high-speed parallel robot, the influence of its nonlinear dynamic characteristics on the dynamic response and stable operation of the system can not be ignored, especially when the smooth trajectory is mapped from Cartesian space (or joint space) to joint space (or Cartesian space) [27]. Comprehensive kinematics and dynamics characteristics of the 3-DoF parallel manipulator were analyzed under the accepted link Jacobian matrices and proverbial virtual work principle, and the discretized piecewise quintic polynomials were employed to interpolate the sequence of joints’ angular position knots, which are transformed from these predefined via-points in Cartesian space [28]. Dupac [29] proposed quintic Hermite piecewise interpolants having functional continuity, and the smoothness of the end-effector path was guaranteed. At the same time, inverse kinematics and inverse dynamics were used to compute the coordinates of the joints. The smoothness of the trajectory of the robot’s end-effector is not only smoothly planned in the Cartesian space but also achieved through the kinematic and dynamic changes of the robot joints and the torque generated by the joint actuators [30]. Focus on process shock and vibration caused by abrupt trajectory change, a trajectory smoothing planning combining Cartesian and joint space is proposed in this paper. The main contribution of the current paper are summarized as follows.

(1) The vector method and microelement integration method are used to establish the complete kinematics and dynamics equations of the Delta parallel robot, and the inverse kinematics/dynamics model solving program is written based on Matlab software.

(2) The end-effector trajectory of the Delta parallel robot is planned in Cartesian space, and the data points and inverse control points of the end-effector trajectory are obtained by the normalization method.

The rest of this paper is structured as follows: In section 2, the kinematic and dynamic model of the Delta parallel robot is presented. The trajectory smoothing planning combining Cartesian and joint space is proposed in Section 3. The simulation results are shown in Section 4. Finally, Conclusions are drawn in Section 5.

2. Kinematica and Dynamic Model of the Delta Parallel Robot

2.1. Kinematic model of the Delta parallel robot

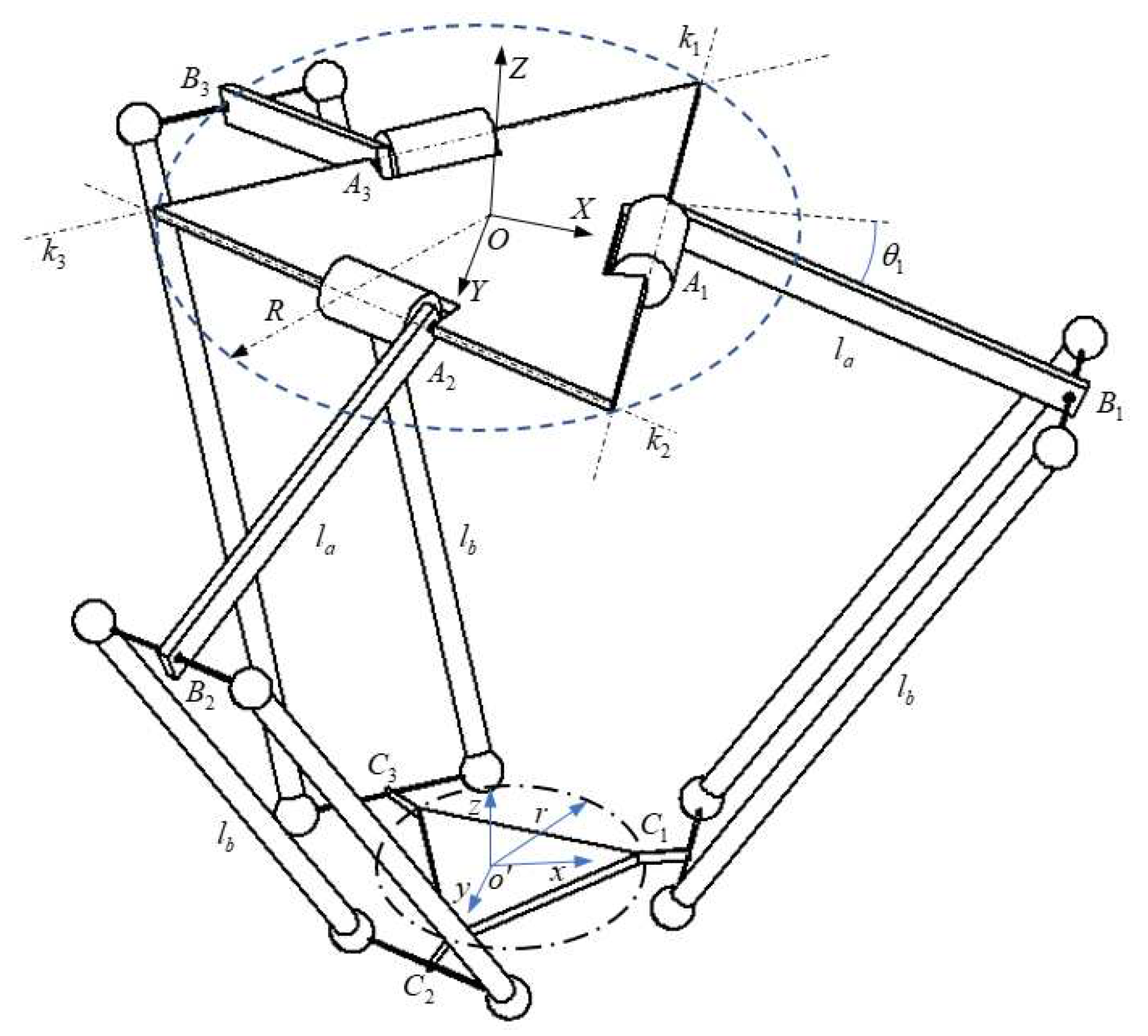
The origin O of the fixed coordinate system

{O - X Y Z}

is located in the geometric center of the equilateral triangle

A_{1} A_{2} A_{3}

which the circumradius is R, the axis of X is along with the direction of

\vec{O A_{1}}

, the axis of Y is parallel to the axis of the revolute joint

A_{1}

. The origin

o^{'}

of the moving coordinate system

\{o^{'} - x y z\}

is located in the geometric center of the equilateral triangle

C_{1} C_{2} C_{3}

which the circumradius is r. The length of active links

A_{i} B_{i}

and passive links

B_{i} C_{i}

are the constant value

l_{a}

and

l_{b}

, respectively. The variable parameters in joint space are

θ_{i}

i = 1, 2, 3

, and the output three displacements in the Cartesian space of the moving platform are x, y, and z, respectively. The geometric configuration of the Delta parallel robot is shown in Figure 1.

Assumed that the origin of the moving platform

o^{'}

{[\begin{matrix} x & y & z \end{matrix}]}^{T}

with respect to the fixed coordinate system. The inverse positional kinematic of the Delta parallel robot can be given by

\vec{B_{i}^{'} C_{i}} = \vec{O o} - \vec{O A_{i}} - \vec{A_{i} B_{i}^{'}} and ∥\vec{B_{i} C_{i}}∥ = l_{b}^{2}

(1)

The axis vectors of the revolute joint

R_{i}

are

k_{i}

(k_{i} = {[\begin{matrix} k_{x i} & k_{y i} & k_{z i} \end{matrix}]}^{T}, i = 1, 2, 3)

, respectively. According to the geometric composition characteristics of the Delta parallel robot,

k_{i}

can be derived as follows.

k_{1} = {[\begin{matrix} 0 & 1 & 0 \end{matrix}]}^{T}, k_{2} = {[\begin{matrix} \sqrt{3} / 2 & 1 / 2 & 0 \end{matrix}]}^{T}, k_{3} = {[\begin{matrix} \sqrt{3} / 2 & - 1 / 2 & 0 \end{matrix}]}^{T}

(2)

The homogeneous transformation matrix of rotation

θ

about any axis

k = {[\begin{matrix} k_{x} & k_{y} & k_{z} \end{matrix}]}^{T}

is satisfied with

Rot (k, θ) = [\begin{matrix} k_{x} k_{x} (1 - c θ) + c θ & k_{y} k_{x} (1 - c θ) - k_{z} s θ & k_{z} k_{x} (1 - c θ) + k_{y} s θ & 0 \\ k_{x} k_{y} (1 - c θ) + k_{z} s θ & k_{y} k_{y} (1 - c θ) + c θ & k_{z} k_{y} (1 - c θ) - k_{x} s θ & 0 \\ k_{x} k_{z} (1 - c θ) - k_{y} s θ & k_{y} k_{z} (1 - c θ) + k_{x} s θ & k_{z} k_{z} (1 - c θ) + c θ & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

(3)

^{o} P_{B^{'}}

can be obtained by translation and rotation based on the initial position

^{o} P_{B}

, yields to

^{o} P_{B^{'}} = Rot (k_{i}, θ_{i})^{o} P_{B} + Trans (\vec{O A_{i}})

(4)

^{o} P_{C^{'}}

can be obtained according to the motion characteristics of the moving platform, yields to

^{o} P_{C^{'}} = Trans (\vec{O o})^{o} P_{C}

(5)

Substitute (4) and (5) into (1), we obtain

{(x - m cos α_{i})}^{2} + {(y - m sin α_{i})}^{2} + {(z + l_{a} sin θ_{i})}^{2} = l_{b}^{2}

(6)

where

m = R - r + l_{a} cos θ_{i}

α_{i} = \frac{2 (i - 1) π}{3}

are the angle between

O A_{i}

and X axis,

i = 1, 2, 3

. Assumed that

sin (θ_{i}) = \frac{2 t_{i}}{1} / 1 + t_{i}^{2}

and

cos (θ_{i}) =^{1 - t_{i}^{2}} / 1 + t_{i}^{2}

, eq.(6) can be calculated as follows

θ_{i} = 2 arctan (\frac{- U_{i} \pm \sqrt{U_{i}^{2} - 4 K_{i} V_{i}}}{2 K_{i}})

(7)

where

K_{i} = l_{b}^{2} - l_{a}^{2} - x^{2} - y^{2} - z^{2} - {(R - r)}^{2} + 2 (x cos α_{i} + y sin α_{i}) (R - r - l_{a}) + 2 (R - r) l_{a}

U_{i} = - 4 z l_{a}

V_{i} = l_{b}^{2} - l_{a}^{2} - x^{2} - y^{2} - z^{2} - {(R - r)}^{2} + 2 (x cos α_{i} + y sin α_{i}) (R - r + l_{a}) - 2 (R - r) l_{a}

Assumed that

b_{i} = B_{i} C_{i}

and derivative of both sides with respect to the time, we obtain

A \dot{X} + B \dot{θ} = 0

(8)

where

B = diag (b_{1}^{T} c_{1}, b_{2}^{T} c_{2}, b_{3}^{T} c_{3})

is a diagonal matrix,

A = {[\begin{matrix} b_{1}^{T} & b_{2}^{T} & b_{3}^{T} \end{matrix}]}^{T}

, and

c_{i} = {[\begin{matrix} l_{a} sin θ_{i} cos α_{i} & l_{a} sin θ_{i} sin α_{i} & l_{a} cos θ_{i} \end{matrix}]}^{T}

\dot{X} = {[\begin{matrix} \dot{x} & \dot{y} & \dot{z} \end{matrix}]}^{T}

is the velocity vector of the end-effector of Delta parallel robot,

\dot{θ} = {[\begin{matrix} {\dot{θ}}_{1} & {\dot{θ}}_{2} & {\dot{θ}}_{3} \end{matrix}]}^{T}

is the velocity vector of the joints,

0 \in R^{3 \times 1}

is the zero matrix.

Eq.(8) can be rewritten with

\dot{θ} = - B^{- 1} A \dot{X} = J \dot{X}

(9)

where J is the kinematic Jacobian matrix of the Delta parallel robot.

Derivative (9) with respect to the time, we obtain

\ddot{θ} = J^{- 1} (\ddot{X} - \dot{J} \dot{θ})

(10)

where

\dot{J} = A^{- 1} \dot{A} A^{- 1} B - A^{- 1} \dot{B}

, and

\dot{A}

\dot{B}

satisfied with

\dot{A} = l_{a} [\begin{matrix} cos α_{1} sin θ_{1} & sin α_{1} sin θ_{1} & cos θ_{1} \\ cos α_{2} sin θ_{2} & sin α_{2} sin θ_{2} & cos θ_{2} \\ cos α_{3} sin θ_{3} & sin α_{3} sin θ_{3} & cos θ_{3} \end{matrix}] {\dot{θ}}^{T} + {\dot{X}}^{T}

(11)

and

\dot{B} = diag ({\dot{b}}_{1}^{T} c_{1} + b_{1}^{T} {\dot{c}}_{1}, {\dot{b}}_{2}^{T} c_{2} + b_{2}^{T} {\dot{c}}_{2}, {\dot{b}}_{3}^{T} c_{3} + b_{3}^{T} {\dot{c}}_{3})

(12)

2.2. Dynamic model of the Delta parallel robot

The dynamic model of the Delta parallel robot with 3-DoFs is give by

M (θ) \ddot{θ} + C (θ, \dot{θ}) \dot{θ} + G (θ) = τ

(13)

where

M (θ) \in R^{3 \times 3}

is the inertial mass matrix,

C (θ, \dot{θ}) \in R^{3 \times 3}

is the Coriolis and centripetal force,

τ \in R^{3 \times 1}

is the moment,

G (θ) \in R^{3 \times 1}

is the gravity matrix. The dynamic equation of the Delta parallel robot has the properties as follows:

Remark 1.

The inertial mass matrix

M (θ)

is a positive symmetric matrix and is bounded, and satisfy with

m I < M (θ) = M^{T} (θ) ⩽ \bar{m} I

(14)

where m and

\bar{m}

are constants more than zero,

I \in R^{3 \times 3}

is the identity matrix.

The mass of the active link is

m_{b}

, the mass of the passive link is

m_{p}

, and the mass of the moving platform is

m_{m}

. The mass matrix

M (θ)

of the Delta parallel robot consists of three parts: active link

M_{m_{b}} (θ)

, passive link

M_{m_{p}} (θ)

and moving platform

M_{m_{m}} (θ)

Considering the motion characteristics of the Delta parallel robot, the mass matrix of the moving platform can be expressed as

M_{m_{m}} (θ) = m_{p l} J^{T} J

(15)

where

m_{p} l

is the mass of the moving platform and load, J is the Jacobian matrix.

The mass matrix of the active link is given by

M_{m_{b}} (θ) = [\begin{matrix} I_{b 1} & 0 & 0 \\ 0 & I_{b 2} & 0 \\ 0 & 0 & I_{b 3} \end{matrix}]

(16)

where

I_{b 1} = I_{b 2} = I_{b 3} = I_{m} + (\frac{m_{b}}{3} + m_{c}) l_{a}^{2}

I_{m}

is the moment of inertia of the actuator,

m_{c}

is the mass of the spherical hinge. The linear velocity at any point along the link

B_{i} C_{i}

can be expressed as

v_{B_{i} C_{i}} (x) = (1 - \frac{x}{l_{b}}) v_{1} + \frac{x}{l_{b}} v_{2}

(17)

where

v_{1}

is the velocity at the connection between

B_{i} C_{i}

and

A_{i} B_{i}

v_{2}

is the velocity at the connection between

B_{i} C_{i}

and the moving platform. the elementary kinematic energy can be given by

d T = \frac{1}{2} v_{B_{i} C_{i}}^{2} d m = \frac{1}{2} v_{B_{i} C_{i}}^{2} ρ s d x

(18)

where

ρ

is the material density of the link, s is the cross-sectional area.

Integrating (17), we obtain

T = \int_{0}^{l_{b}} d T = \frac{1}{2} ρ s \int_{0}^{l_{b}} v_{B_{i} C_{i}}^{2} d x = \frac{1}{2} (\frac{1}{3} m_{l} (v_{1}^{2} + v_{2}^{2} + v_{1} v_{2}))

(19)

The Jacobian matrix of the joint

B_{i}

is defined as

J_{u, i}

M_{m_{p}} (θ)

can be derived as

M_{m_{p}} (θ) = \sum_{i = 1}^{3} \frac{1}{3} m_{l} (J^{T} J + J_{u, i}^{T} J_{u, i} + J_{u, i}^{T} J)

(20)

Assumed that the equivalent mass of the moving platform is

m_{e q} = m_{p f} + m_{l}

, there has

\sum_{i = 1}^{3} \frac{1}{3} m_{l} (J_{u, i}^{T} J_{u, i}) = \frac{1}{3} m_{l} [\begin{matrix} l_{a}^{2} & 0 & 0 \\ 0 & l_{a}^{2} & 0 \\ 0 & 0 & l_{a}^{2} \end{matrix}]

(21)

The mass matrix of the Delta parallel robot can be expressed completely as

M (θ) = I_{b t} + m_{e q} J^{T} J

(22)

where

I_{b t} = [\begin{matrix} I_{e q} & 0 & 0 \\ 0 & I_{e q} & 0 \\ 0 & 0 & I_{e q} \end{matrix}]

, and

I_{e q} = I_{m} + (\frac{m_{b}}{3} + \frac{2 m_{l}}{3} + m_{c}) l_{a}^{2}

3. Trajectory smoothing planing combining Cartesian and jiont space

Trajectory smoothing planning of the Delta parallel robot combining Cartesian and joint space is mainly to solve the problem of process vibration caused by acceleration and jerk change which is caused by discontinuity at the inflection point of the small line segment.

3.1. Trajectory planning in Cartesian space

Assume that the end-effector of the Delta parallel robot passes through the set point

p_{i} = (x_{i}, y_{i}, z_{i})

(i = 0, 1, \dots, n)

, the coordinates of each interpolation point are expressed as

x = x_{0} + λ Δ x, y = y_{0} + λ Δ y, z = z_{0} + λ Δ z

(23)

where

λ

is a normalized factor,

(x_{0}, y_{0}, z_{0})

is the initial point position,

Δ x

Δ y

and

Δ z

are increments on the x, y and z, respectivel, and satisfied with

Δ x = x_{i + 1} - x_{i}, Δ y = y_{i + 1} - y_{i}, Δ z = z_{i + 1} - z_{i}

(24)

Assume that the velocity of the line in the middle section is v, the acceleration of the parabola segment is a, the movement time and distance of the parabola segment are satisfied with

T_{p} = \frac{v}{a}, L_{p} = \frac{1}{2} a T_{p}^{2}

(25)

Considering the (24), the time, displacement and acceleration of the parabola segment after normalization can be expressed as

T_{p λ i} = T_{p} / T_{i}, L_{p λ i} = L_{p} / L_{i}, a_{p λ i} = 2 L_{p λ i} / T_{p λ i}^{2}

(26)

where

L_{i} = \sqrt{{(x_{i + 1} - x_{i})}^{2} + {(y_{i + 1} - y_{i})}^{2} + {(z_{i + 1} - z_{i})}^{2}}

T_{i} = 2 T_{p} + (L_{i} - 2 L_{p}) / v

The normalized factor

λ

is given by

λ = \{\begin{matrix} \frac{1}{2} a_{λ i} t^{2} & 0 ⩽ t ⩽ T_{p λ i} \\ \frac{1}{2} a_{λ i} T_{p λ i}^{2} + a_{λ i} T_{p λ i} (t - T_{p λ i}) & T_{p λ i} < t ⩽ 1 - T_{p λ i} \\ \frac{1}{2} a_{λ i} T_{p λ i}^{2} + a_{λ i} T_{p λ i} (t - T_{p λ i}) - \frac{1}{2} a_{λ i} {(t + T_{p λ i} - 1)}^{2} & 1 - T_{p λ i} < t ⩽ 1 \end{matrix}

(27)

where

t = i / n

i = 0, 1, \dots, n

λ = 0

is the starting point of the line segment, and

λ = 1

is the end point of the line segment.

3.2. Trajectory planning in joint space

By using Eqs. (7)-(22), the interpolation points obtained from Cartesian space are inversely mapped to joint space and used as the critical point of trajectory planning in joint space for quadratic interpolation using quintic B-spline curve, which is expressed as

θ_{i, k} (t) = \sum_{i = 0}^{k} P_{i + l} B_{l, k} (t)

(28)

where

t \in [0, 1]

θ_{i, k} (t)

is the B-spline curve of

k^{th}

P_{i + l} (l = 0, \dots, k)

are the control points,

B_{l, k} (t)

is the B-spline basis function which can be given by

B_{l, k} (t) = \frac{1}{k!} \sum_{j = 0}^{k - l} {(- 1)}^{j} C_{k + 1}^{j} {(t + k - l - j)}^{k}

(29)

where

C_{k + 1}^{j} = \frac{(k + 1)!}{j! (k + 1 - j)!}

k = 5

Substitute (29) into (28), we obtain

θ_{i, 5} (t) = \frac{1}{120} [\begin{matrix} 1 & t & t^{2} & t^{3} & t^{4} & t^{5} \end{matrix}] = A [\begin{matrix} P_{i} & P_{i + 1} & P_{i + 2} & P_{i + 3} & P_{i + 4} & P_{i + 5} \end{matrix}]

(30)

where

A = [\begin{matrix} 1 & 26 & 66 & 26 & 1 & 0 \\ - 5 & - 50 & 0 & 50 & 5 & 0 \\ 10 & 20 & - 60 & 20 & 10 & 0 \\ - 10 & 20 & 0 & - 20 & 10 & 0 \\ 5 & - 20 & 30 & - 20 & 5 & 0 \\ - 1 & 5 & - 10 & 10 & - 5 & 1 \end{matrix}]

When

t = 0

, the end-point of the B-spline curve of

5^{th}

is given by

θ_{i, 5} (0) = \frac{1}{120} (P_{i} + 26 P_{i + 1} + 66 P_{i + 2} + 26 P_{i + 3} + P_{i + 4})

(31)

Given

m + 1

data points in joint space

θ_{i} (i = 0, 1, \dots, m)

, inverse calculate the control point

P_{i}

. Since the number of the control points is

m + 5

, so four initial constraint equations are selected as follows:

\{\begin{matrix} {\ddot{θ}}_{0} (0) = 20 P_{0} + 40 P_{1} - 120 P_{2} + 40 P_{3} + 20 P_{4} = 0 \\ {\overset{⃛}{θ}}_{0} (0) = - 60 P_{0} + 120 P_{1} - 120 P_{3} + 60 P_{4} = 0 \\ {\ddot{θ}}_{m} (1) = 20 P_{m} + 40 P_{m + 1} - 120 P_{m + 2} + 40 P_{m + 3} + 20 P_{m + 4} = 0 \\ {\overset{⃛}{θ}}_{m} (1) = - 60 P_{m} + 120 P_{m + 1} - 120 P_{m + 3} + 60 P_{m + 4} = 0 \end{matrix}

(32)

Simultaneous (30) and (32), we obtain

120 [\begin{matrix} 0 \\ 0 \\ θ_{0} \\ θ_{1} \\ ⋮ \\ θ_{m} \\ 0 \\ 0 \end{matrix}] = [\begin{matrix} - 5 & - 50 & 0 & 50 & 5 \\ 20 & 40 & - 120 & 40 & 20 \\ 1 & 26 & 66 & 26 & 1 \\ 1 & 26 & 66 & 26 & 1 \\ ⋱ & ⋱ & ⋱ & ⋱ & ⋱ \\ 1 & 26 & 66 & 26 & 1 \\ 20 & 40 & - 120 & 40 & 20 \\ - 5 & - 50 & 0 & 50 & - 5 \end{matrix}] [\begin{matrix} P_{0} \\ P_{1} \\ ⋮ \\ P_{m} \\ P_{m + 1} \\ P_{m + 2} \\ P_{m + 3} \\ P_{m + 4} \end{matrix}]

(33)

The method of inverse control vertex is used to calculate NURBS curve, and the NURBS curve of degree k is defined as

p (t) = \frac{\sum_{i = 0}^{n} d_{i} ω_{i} B_{i, k} (t)}{\sum_{i = 0}^{n} ω_{i} B_{i, k} (t)} = \frac{T B_{i, k} (t) D_{i}}{T B_{i, k} (t) W_{i}}, 0 ⩽ t ⩽ 1

(34)

where

d_{i} (i = 0, 1, \dots, n)

is the control vertex of curve

p (t)

ω_{i}

is the weight factor whose number is equal to the number of the control vertices.

t = \frac{u - u_{i + k}}{u_{i + k + 1} - u_{i + k}}

D_{i} = {[\begin{matrix} ω_{i} d_{i} & ω_{i + 1} d_{i + 1} & ω_{i + 2} d_{i + 2} & ω_{i + 3} d_{i + 3} \end{matrix}]}^{T}

W_{i} = {[\begin{matrix} ω_{i} & ω_{i + 1} & ω_{i + 2} & ω_{i + 3} \end{matrix}]}^{T}

4. Experiments

The experimental platform of the Delta parallel robot based on EtherCAT com-munication mode is constructed. Motion control card selected from the Googo GEN-009-00 series, EtherCAT’s distributed clock device ensures synchronous move-ment between the various axes, thus avoiding position deviation in time response due to the strong coupling characteristics between the various axes. Based on the EtherCAT master-slave architecture, three slave stations are configured on the experimental platform. The model number is JSDG2S-15A-E, and the connection cables are CAT5E-STP industrial ethernet cable RJ45. The motor model is JSMA-PBC04AAKB, the rated torque of the motor is 3000rpm, the rated power is 400W, the moment of inertia is 0.000073kg·m2, and the reduction ratio of the motor reducer is 1:25. The experimental platform of the Delta parallel robot is shown in Figure 2.

The parameters of the Delta parallel robot are shown in Table 1.

Table 1. Parameters of the Delta parallel robot.

Parameters	Values	Parameters	Values
Length of active link $l_{a}$	0.1800 m	Radius of the fixed platform R	0.1350 m
Length of passive link $l_{b}$	0.5000 m	Radius of the moving platform r	0.0400 m
Mass of the moving platform $m_{p}$	0.2231 $k g$	Mass of the active link $m_{b}$	0.3392 $K g$ 9[2]
Mass of the passive link $m_{l}$	0.1412 $K g$	Moment of inertia of the motor $I_{m}$	0.000073 $kg \cdot m^{2}$

The test time is set to 10s, and the sampling number is set to 20001. The traditional PID controller is used to verify the single-space (Cartesian space) trajectory smoothing planning, and the proposed trajectory method is compared. PID controller parameters are set to

K_{I} = diag {[3.05, 4.05, 3.05]}^{T}

K_{P} = diag {[75, 75, 70]}^{T}

and

K_{D} = diag {[10, 15, 10]}^{T}

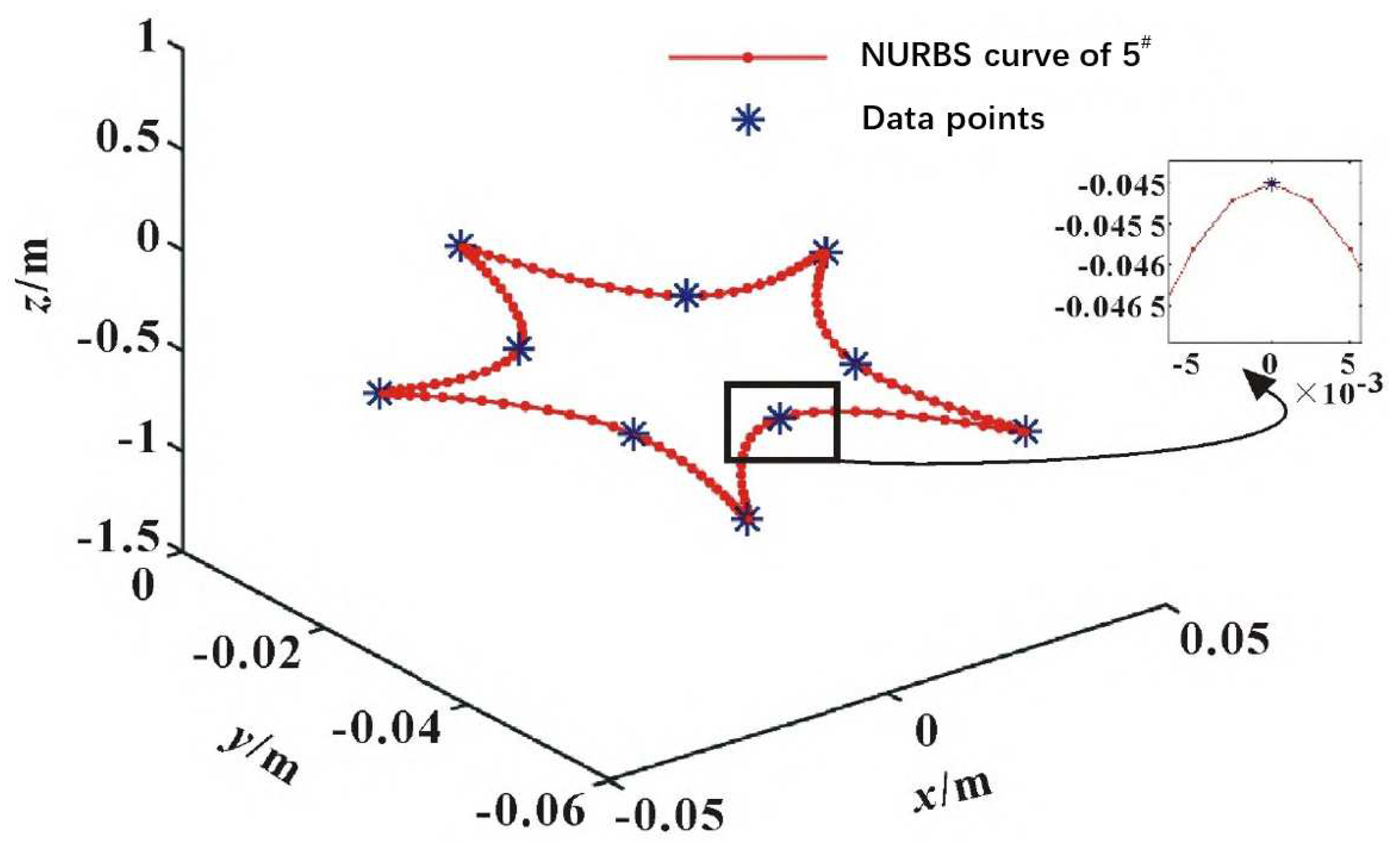
The end-effector motion trajectory of the Delta parallel robot is selected as a five-pointed star curve, 11 data points of the curve are given, and the start and end weight factors are selected as 1.0, and the rest are 0.9. The trajectory of the end-effector in Cartesian space is shown in Figure 3.

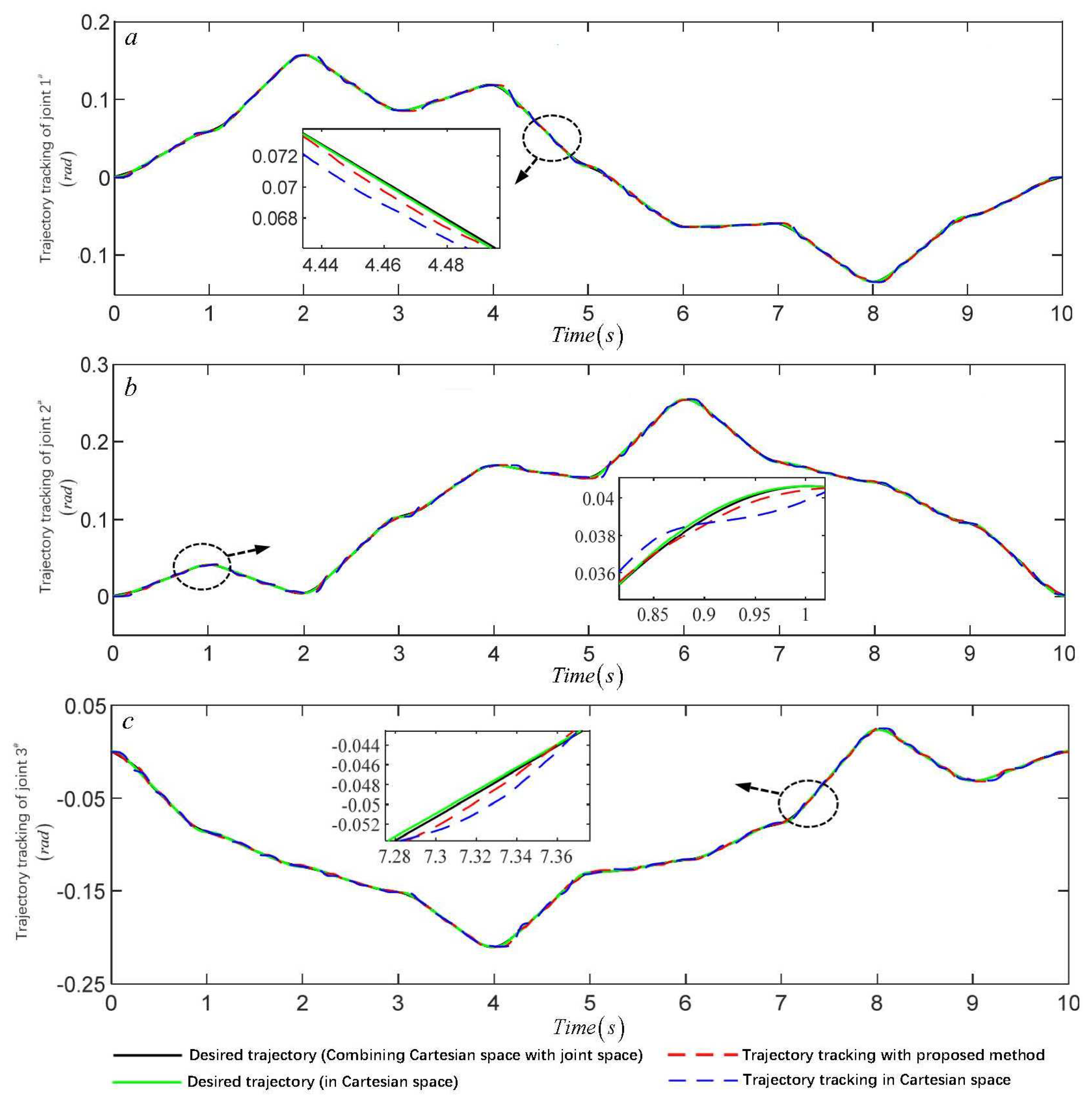
The interpolation points obtained from Cartesian space are mapped to joint space through inverse kinematics, and the fifth uniform B-spline curve is used as input data for the second interpolation and trajectory smoothing planning of the angle, angular velocity, angular acceleration, and angular jerk are obtained in joint space which are shown in Figure 4, Figure 5 and Figure 6, respectively.

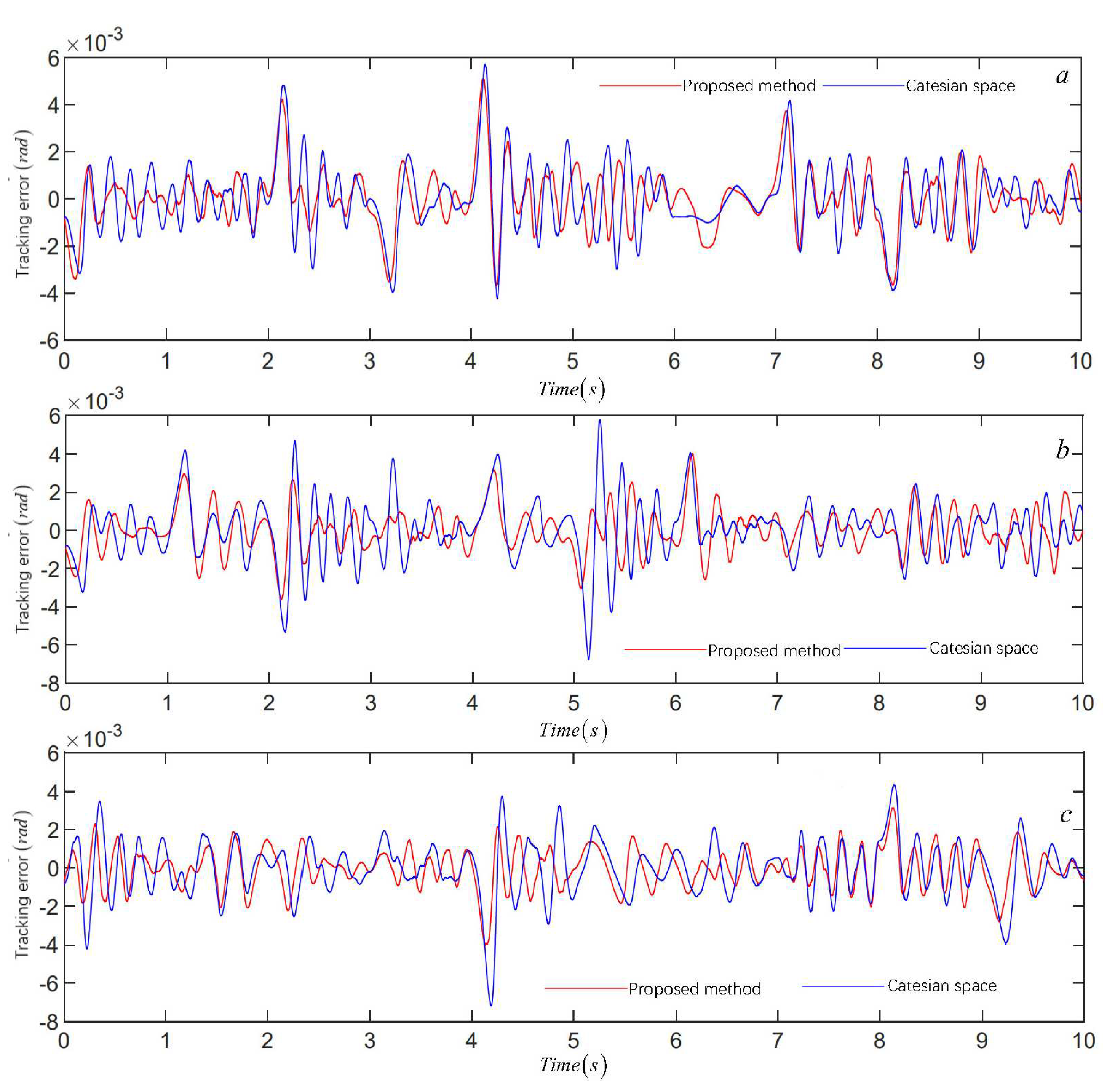
Fig.4 and Fig.5 show that compared with single space (Cartesian space) trajectory planning, the trajectory planning algorithm combining joint space can obtain a smoothing trajectory, and the discontinuity of the Jerk curve and trajectory mutation can be effectively improved under the same controller (traditional PID). Among them, the peak tracking error of joint 2 and 3 are

29 %

and

44 %

lower than that of single spatial trajectory planning, and the error value of joint 2 is smaller in the 5s transition stage. The errors are worth rapidly converging at the initial stage of the three joints.

The comparison of the peak value of trajectory tracking error is shown in Tables 2.

Table 2. Comparison of the peak value of trajectory tracking error.

	The peak value of trajectory tracking error (rad)
Joint	Cartesian space	Combining Cartesian and joint space
$1^{th}$	0.0057	0.0051
$2^{th}$	0.0068	0.0040
$3^{th}$	0.0072	0.0040

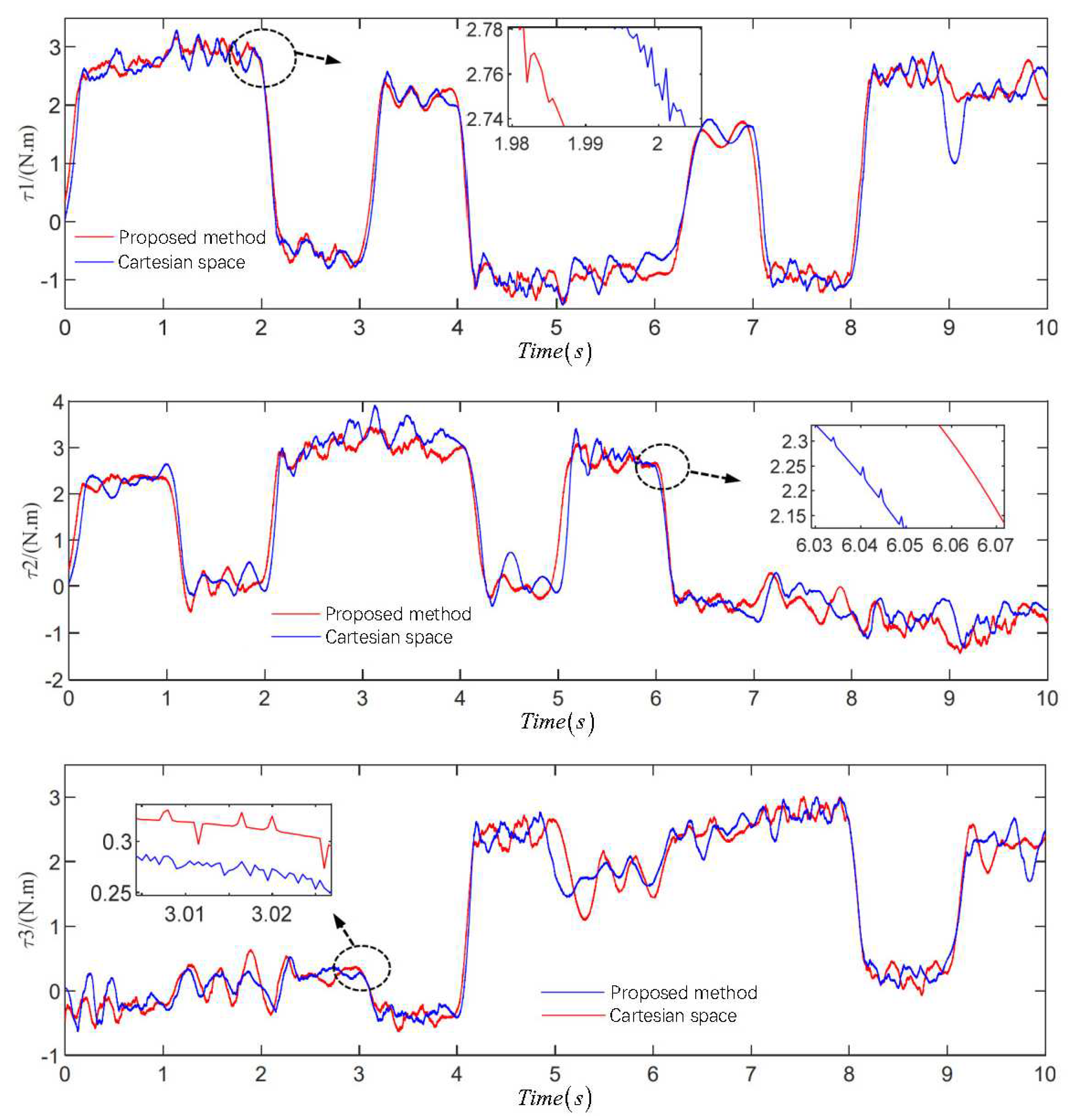
The control torque of the three joints is shown in Fig.6.

Fig.6 shows the peak torque reduction rate of joint 2 of the trajectory obtained by the proposed trajectory planning algorithm is

11.6 %

, and the torque change trend is gentle. Although the peak torque reduction rates of joints 1 and 3 are

3.5 %

and

1.6 %

, respectively, it can be seen from the torque amplification diagram that the torque vibration and shock phenomena at the transition of adjacent line segments such as 2s, 3s, and 6s are effectively reduced when the acceleration chattering is improved. A comparison of the peak value of control torque is shown in Table 3.

Table 3. Comparison of the peak value of control torque.

	Peak value of control torque $τ_{max} / ($ N.m )
Joint	Cartesian space	Combining Cartesian and joint space	reduction rate
$1^{th}$	3.2909	3.1743	$3.5 %$
$2^{th}$	3.9193	3.4657	$11.6 %$
$3^{th}$	3.0056	2.9584	$1.6 %$

5. Conclusions

In order to solve the problem of process shock and vibration caused by tangential discontinuity at the corner of small line segment in the trajectory planning of Delta parallel robot end-effector, a smooth trajectory planning method based on the combination of cubic NURBS curve in Cartesian space and quintic uniform B-spline curve in joint space is proposed in this paper. (1) The trajectory smoothing planning method combined with Cartesian space and joint space effectively solves the trajectory smoothing problem with continuous high order curvature derivatives, and the obtained joint jerk is continuously smooth. (2) The proposed method can make the robot’s end-effector move precisely along a smooth trajectory while making the angular velocity, acceleration and jerk of the joint continuously smooth without impact. (3) Smooth trajectory planning is carried out from the two aspects of robot kinematics and dynamics, which reduces the tracking error by

21.12 %

and the maximum joint torque by

11.65 %

, effectively reducing the vibration and impact during the movement.

Author Contributions

Conceptualization, Zhu Dachang and Li Fangyi; methodology, He Yonglong; software, Yu Xuezhe; validation, He Yonglong; writing—original draft preparation, Zhu Dachang; writing—review and editing, Li Fangyi; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

Simionescu, I.; Ciupitu, L.; Ionita, L.C. Static balancing with elastic systems of DELTA parallel robots. Mech Mach Theory 2015, 87, 150–162. [Google Scholar] [CrossRef]
Liu, C.; Cao, G.H.; Qu, Y.Y. Safety analysis via forward kinematics of delta parallel robot using maching learning. Safety Sci 2019, 117, 243–249. [Google Scholar] [CrossRef]
Boryga, M. The use of higher-degree polynomials for trajectory planning with jerk, acceleration and velocity constraints. Int J Comput Appl T 2020, 63(4), 337–347. [Google Scholar] [CrossRef]
Zhao, Y.J.; Yuan, F.F.; Chen, C.W.; Jin, L.; Li, J.Y.; Zhang, X.W.; Lu, X.J. Inverse kinematics and trajectory planning for a hyper-redundant bionic trunklink robot. Int J Robot Autom 2020, 35(3), 229–241. [Google Scholar]
Damasevicius, R.; Maskeliunas, R.; Narvydas, G.; Narbutaite, R.; Polap, D.; Wozniak, W. Intelligent automation of dental material analysis using robotic arm with Jerk optimized trajectory. J Amb Intel Hum Comp 2020, 11(12), 6223–6234. [Google Scholar] [CrossRef]
Zhang, S.; Liu, X.J.; Yan, B.K.; Bi, J.; Han, X.D. A real-time look-ahead trajectory planning methodology for multi small line segments path. Chin J Mech Eng En 2023, 36(1), 59. [Google Scholar] [CrossRef]
Wu, G.L.; Zhao, W.K.; Zhang, X.P. Optimum time-energy-jerk trajectory planning for serial robotic manipulators by reparameterized quintic NURBS curves. P I Mech Eng C-J Mec 2021, 235, 4382–4393. [Google Scholar] [CrossRef]
Xu, G.P.; Zhang, H.; Meng, Z.; Sun, Y.Z. Automatic interpolation algorithm for NURBS trajectory of shoe spraying based on 7-DOF robot. Int J Cloth Sci Tech 2021, 34(3), 434–450. [Google Scholar] [CrossRef]
Wu, P.; Wang, Z.Y.; Jing, H.K.; Zhao, P.F. Optimal time-jerk trajectory planning for Delta parallel robot based on improved butterfly optimization algorithm. Appl Sci -Basel 2022, 12, 8145. [Google Scholar] [CrossRef]
Liang, X.; Su, T.T. Quintic Pythagorean-Hodograph curves based trajectory planning for Delta robot with a prescribed geometrical constaint. Appl Sci -Basel 2019, 9, 4491. [Google Scholar] [CrossRef]
Bilal, H.; Yin, B.Q.; Kuma, A.; Ali, M.; Zhang, J.; Yao, J.F. Jerk-bounded trajectory planning for rotary flexible joint manipulator: an experimental approach. Appl Sci -BaseSoft Comput 2023, 27, 4029–4039. [Google Scholar] [CrossRef]
Fang, Y.; Hu, J.; Liu, W.H.; Shao, Q.Q.; Qi, J.; Peng, Y.H. Smooth and time-optimal S-curve trajectory planning for automated robots and machines. Mech Mach Theory 2019, 137, 127–153. [Google Scholar] [CrossRef]
Singh, G.; Banga, V.K. Kinematics and trajectory planning analysis based on hybrid optimization algorithm for an industrial robotic manipulators. Mech Mach Theory 2022, 26(21), 11339–11372. [Google Scholar] [CrossRef]
Dong, H.; Cong, M.; Chen, H.P. Effective algorithms to find a minimum-time yet high smooth robot joint trajectory. Int J Robot Autom 2019, 34(4), 331–343. [Google Scholar] [CrossRef]
Brown, S.; Pierson, H.A. Adaptive path planning of novel complex parts for industrial spraying operations. Prod Manuf Res 2020, 8(1), 335–368. [Google Scholar] [CrossRef]
Wang, F.; Wu, Z.J.; Bao, T.T. Time-jerk optimal trajectory planning of industrial robots based on a hybrid WOA-GA algorithm. Processes 2022, 10(5), 1014. [Google Scholar] [CrossRef]
Nadir, B.; Mohammed, O.; Minh-Tuan, N.; Abderrezak, S. Optimal trajectory generation method to find a smooth robot joint trajectory based on multiquadric radial basis functions. Int J Adv Manuf Technol 2022, 120, 297–312. [Google Scholar] [CrossRef]
Chettibi, T. Smooth point-to-point trajectory planning for robot manipulators by using radial basis functions. Robotica 2019, 37(3), 539–559. [Google Scholar] [CrossRef]
Liang, Y.Y.; Yao, C.Z.; Wu, W.; Wang, L.; Wang, Q.Y. Design and implementation of multi-axis real-time synchronous look-ahead trajectory planning algorithm. Int J Adv Manuf Technol 2022, 119, 4991–5009. [Google Scholar] [CrossRef]
Shrivastava, A.; Dalla, V.K. Multi-segment trajectory tracking of the redundant space robot for smooth motion planning based on interpolation of linear polynomials with parabolic blend. P I Mech Eng C-J Mec 2022, 236, 9255–9269. [Google Scholar] [CrossRef]
Wang, H.; Wang, H.; Huang, J.H.; Zhao, B.; Quan, L. Smooth point-to-point trajectory planning for industrial robots with kinematical constraints based on high-order polynomial curve. Mech Mach Theory 2019, 139, 284–293. [Google Scholar] [CrossRef]
Wang, G.R.; Xu, F.; Zhou, K.; Pang, Z.H. S-velocity profile of industrial robot based on NURBS curve and slerp interpolation. Processes 2022, 10(11), 2195. [Google Scholar] [CrossRef]
Grassmann, R.M.; Burgner-Kahrs, J. Quaternion-based smooth trajectory generator for via poses in SE(3) considering kinematic limits in Cartesian space. IEEE Robot Autom Let 2019, 4(4), 4192–4199. [Google Scholar] [CrossRef]
Singh, G.; Banga, V.R. Combinations of novel hybrid optimization algorithms-based trajectory planning analysis for an industrial robotic manipulators. J Field Robot 2022, 39(5), 650–674. [Google Scholar] [CrossRef]
Zhao, Y.Q.; Mei, J.P.; Niu, M.T. Vibration error-based trajectory planning of a 5-dof hybrid machine tool. Robot Cim-Int Manuf 2021, 69, 102095. [Google Scholar] [CrossRef]
Wang, Q.; Wang, Z.B.; Shuai, M. Trajectory planning for a 6-DoF manipulator used for orthopaedic surgery. Int J Intell Robot Appl 2020, 4(1), 82–94. [Google Scholar] [CrossRef]
Yang, D.; Xie, F.G.; Liu, X.J. Velocity constraints based approach for online trajectory planning of high-speed parallel robots. Chin J Mech Eng En 2022, 35(1), 127. [Google Scholar] [CrossRef]
Lu, S.; Ding, B.X.; Li, Y.M. Minimum-jerk trajectory planning pertaining to a translational 3-degree-of-freedom parallel manipulator through piecewise quintic polynomials interpolation. Adv Mech Eng 2020, 12(3), 1687814020913667. [Google Scholar] [CrossRef]
Dupac, M. Mathematical modeling and simulation of the inverse kinematic of a redundant robotic manipulator using azimuthal angles and spherical polar piecewise interpolation. Math Comput Simulat 2023, 209, 282–298. [Google Scholar] [CrossRef]
Rout, A.; Deepak, B.B.V.L.; Biswal, B.B.; Mahanta, G.B. Trajectory generation of an industrial robot with constrained kinematic and dynamic variations for improving positional accuracy. Int J Appl Metaheur 2021, 12(3), 163–179. [Google Scholar] [CrossRef]

Figure 1. The geometric configuration of Delta parallel robot with three DoFs.

Figure 2. Experimental platform of the Delta parallel robot.

Figure 3. End-effector trajectory of the Delta parallel robot in Cartesian space.

Figure 4. Trajectory tracking of each joint with proposed method and in Cartesian space. (a) joint 1. (b) Joint 2. (c) joint 3.

Figure 5. Tracking error of each joint with proposed method and in Cartesian space. Comparison of joint velocity trajectories in joint space.(a) joint 1. (b) Joint 2. (c) joint 3.

Figure 6. Comparison of joint acceleration trajectories in joint space.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Trajectory Smoothing Planning of Delta Parallel Robot Combining Cartesian and Joint Space

Abstract

1. Introduction

2. Kinematica and Dynamic Model of the Delta Parallel Robot

2.1. Kinematic model of the Delta parallel robot

2.2. Dynamic model of the Delta parallel robot

3. Trajectory smoothing planing combining Cartesian and jiont space

3.1. Trajectory planning in Cartesian space

3.2. Trajectory planning in joint space

4. Experiments

5. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe